A traveling-wave solution for bacterial chemotaxis with growth

Significance

Motility is one of the most striking bacterial behaviors common among many species. Motile bacteria can expand rapidly into previously unoccupied habitats, thus increasing fitness. Fast expansion is fostered by the sensing of gradients which the bacteria generate themselves and is further boosted by cell growth. Here we analyze the integrated dynamics of these processes mathematically. The relations obtained provide an analytical description of the expansion process and its dependence on core bacterial and environmental characteristics, like the growth rate, the abundance of chemical attractants in the surroundings, and the detection limit of the attractants.

Abstract

Bacterial cells navigate their environment by directing their movement along chemical gradients. This process, known as chemotaxis, can promote the rapid expansion of bacterial populations into previously unoccupied territories. However, despite numerous experimental and theoretical studies on this classical topic, chemotaxis-driven population expansion is not understood in quantitative terms. Building on recent experimental progress, we here present a detailed analytical study that provides a quantitative understanding of how chemotaxis and cell growth lead to rapid and stable expansion of bacterial populations. We provide analytical relations that accurately describe the dependence of the expansion speed and density profile of the expanding population on important molecular, cellular, and environmental parameters. In particular, expansion speeds can be boosted by orders of magnitude when the environmental availability of chemicals relative to the cellular limits of chemical sensing is high. Analytical understanding of such complex spatiotemporal dynamic processes is rare. Our analytical results and the methods employed to attain them provide a mathematical framework for investigations of the roles of taxis in diverse ecological contexts across broad parameter regimes.

As a fundamental part of their life cycle, bacteria spread by dispersing into and colonizing new habitats. Many species of bacteria navigate in these new habitats by sensing gradients of certain chemicals and biasing their flagellum-based swimming to move themselves along these gradients (1, 2). This process, known as chemotaxis, is among the most extensively investigated topics in molecular biology (1, 3–7) and was observed in diverse microbial habitats such as the gut (8); the soil (9); leaves (10, 11); and marine environments such as the phycosphere, sinking marine particles, and coral reefs (2, 12–14). Further, chemotaxis is employed by many eukaryotic cells such as the free-living Dictyostelium (15) and is an important element of many tissue-forming processes involved in embryogenesis (16), neuronal patterning (17), wound healing (18), and tumor metastasis (19).

Beyond promoting the movements by individual cells, chemotaxis also drives the collective movement of cells leading to emergent patterns and behaviors at the population level (20, 21). Such collective dynamics have been best studied with bacteria in culture plates and microfluidic devices. For example, when Escherichia coli cells are inoculated at the center of a soft agar plate replete with nutrients, consumption of preferred chemicals (referred to as attractants) results in collective cell movement up self-generated attractant gradients (22), leading to the emergence of striking migrating bands that propagate radially outward from the inoculation site (23–25). These migrating bands typically comprise one or two peaks in population density, which stand in contrast to the predictions of canonical models of front propagation and population expansion (26–28); they also expand at much faster speeds than predicted by canonical models. These population-level changes can strongly shape fitness and ecological interactions as recent laboratory studies have shown (29–32).

The first attempt to understand these migrating bands mathematically was made by Keller and Segel, who recovered a traveling-wave solution using a pair of reaction–diffusion–convection equations to describe the density of bacterial populations and the concentration of the attractant they consume (33). While being highly influential, the Keller–Segel (KS) model neglected cell growth, a substantial factor in the expansion process. It further required unrealistic assumptions on attractant sensing without which the migrating bands lose stability (34). Subsequent modeling efforts including cell growth managed to recover the stability of the bands, but their predictions did not match major experimental observations such as the sharply peaked density profiles and their rapid migration speeds (31, 35–38).

Recent work by Cremer et al. (39) demonstrated that the major features of the migrating bands for E. coli in soft agar can be accurately captured using a model in which bacterial growth is independent of the attractant. Numerical solutions to their growth-expansion (GE) model quantitatively described not only the boosted speed of the migrating band but also the signature spatial profile of the bands and their dependence on molecular parameters (39). Their results established the role of attractants as an environmental cue exploited by bacteria independent of possible nutritional values to promote rapid expansion.

The success of the GE model in describing E. coli in soft agar raises the possibility that the phenotype of rapid expansion and distinct density bands might also occur for chemotactic systems in the wild, in situations where growth, diffusion, and chemotaxis dominate. However, from the numerical work of Cremer et al. (39), it is not clear what aspects of their results are generalizable given that both bacterial and environmental characteristics can be vastly different in the wild. For example, bacteria living near sulphidic sediments move more than 30 times faster than E. coli (39, 40), while bacterial motility is significantly reduced by high viscosity in the gut (41, 42). Addressing the generalizability of the GE model requires a detailed mathematical analysis of the interplay of 1) growth, 2) diffusion, and 3) chemotaxis, preferably with analytical solutions. While growth and diffusion have been studied together in the canonical models of front propagation (26–28), as have diffusion and chemotaxis in the KS model (33, 36, 43–45), a sufficient understanding of the interplay of all three is still lacking.

Toward obtaining such an understanding, we describe here a detailed analytical study of the GE model. Through a heuristic analysis, we derive analytic relations that describe the dependence of the expansion speed and density profile on important molecular, cellular, and environmental parameters, including the rate of cell growth, the diffusivity and availability of the attractants, the motility and sensitivity of the bacteria, carrying capacity, and the limit of attractant sensing. Our analysis reveals the key condition for the population to attain rapid expansion speed and suggests a very broad parameter regime for which rapid expansion can be expected.

GE Model

In the GE model the evolution of the bacterial density, ρ, in space and time (t) is given by

$$\frac{\partial \rho }{\partial t}=D_{\rho }{\nabla }^2\rho -\nabla ·(\overrightarrow{v}\rho )+r\rho (1-\rho /{\rho }_c).$$ [1]

The growth of the population is given by the logistic equation where r is the growth rate and ρ_c is the carrying capacity of the system. The nondirected run-and-tumble movement of bacteria is described by a diffusion-like term with the motility coefficient $D_{\rho }$, while directed movement along the gradient of the attractant concentration a is described by a convection term with the drift velocity $\overrightarrow{v}(a,\nabla a)$, where

$$\overrightarrow{v}\equiv {\chi }_0\overrightarrow{\nabla }a/(a+a_m).$$ [2]

χ₀ is the chemotactic coefficient which describes how cells translate the sensing of the local attractant gradients into directed movement. The value of χ₀ depends on the strain, the internal cell state, the medium cells move through (e.g., liquid medium or soft agar), and the type of attractant being used (46). a_m describes the finite sensitivity of the attractant-sensing receptors (47, 48) and ensures that for $\overrightarrow{\nabla }a\to 0,\hspace{0.17em}\overrightarrow{v}\to 0$. Finally, the dynamics of the attractant are determined by its diffusion and consumption by the bacteria:

$$\frac{\partial a}{\partial t}=D_a{\nabla }^{2}a-\mu \frac{a}{a+a_k}\rho ,$$ [3]

where D_a is the molecular diffusion coefficient of the attractant, μ is the rate of uptake of the attractant by the bacteria, and a_k is the Michaelis–Menten constant describing attractant uptake. We note that the GE model defined by Eqs. 1–3 is a slight simplification of the one studied numerically in (39). However, the simplifications do not significantly impact our results, even at the quantitative level (see SI Appendix, Fig. S2, for comparison with the generalized GE model used in ref. 39).

Without growth (r = 0), the GE model resembles the original KS model which additionally also assumed negligible attractant diffusion, i.e., D_a = 0, and infinitesimal sensitivity in sensing, i.e., a_m = 0. The latter assumption of the KS model is necessary for stable traveling waves (33, 34) as otherwise the portion of the band with $a<a_m$ is not able to migrate as fast as the rest of the band and falls behind, leading to a gradually diminishing and slowing band. Many models have attempted to replenish the bands by including cell growth (35, 49–53), and while they are able to recover stability, they fail to reproduce experimental observations such as fast expansion speeds and a trailing region of increasing bacterial density behind the migrating band.

In the absence of chemotaxis (${\chi }_0=0$), the GE model reduces to the Fisher–Kolmogorov–Petrovsky–Piskunov (F-KPP) equation which describes expansion by growth and nondirected motion alone (26, 27, 54). The F-KPP equation has been extensively studied in the theory of front propagation (28) and has been used canonically to describe range expansion into unoccupied habitats (55–57), including the expansion dynamics of nonmotile bacteria in colony growth and long-range dispersal (58–62). While growth and nondirected motion movement result in a traveling-wave solution with a stable expansion speed given by $c_F=2\sqrt{D_{\rho }\hspace{0.17em}r}$ (known as the Fisher speed) (26–28, 63), it is not sufficient to explain the high expansion speeds of the bacterial front observed in populations of chemotactic bacteria (39). Indeed, as we will see in Parameter Dependences of the Expansion Speed, the expansion speed for the GE model can lead to expansion speeds orders of magnitude higher than the Fisher speed.

Remarkably, while the two different reaction–diffusion models (KS and F-KPP) fail to even qualitatively describe the experimental observation of fast-moving stable migrating bands by themselves, when combined together, they are able to quantitatively explain the prominent features of bacterial chemotaxis for a broad range of physiological and environmental conditions (39).

The GE model describes a system of nonlinear coupled partial differential equations (Eqs. 1–3) that has a degree of 4 and is accompanied by appropriate initial values and boundary conditions. For our system, we specify the initial values to be a localized profile for ρ (any localized profile converges to the same steady state solution) and a uniform attractant concentration denoted by a₀. In one dimension and with x denoting the spatial coordinate, we look for a stable traveling-wave solution of the form

$$\rho (x,t)=\rho (z),\hspace{0.17em}a(x,t)=a(z);\hspace{0.17em}\text{with}\hspace{0.17em}z=x-ct,$$

where c > 0 is the expansion speed. This converts the system of coupled partial differential equations to two one-dimensional ordinary differential equations as follows:

$$-c\frac{d\rho }{dz}=D_{\rho }\frac{d^2}{d{z}^2}\rho -{\chi }_0\frac{d}{dz}\left(\frac{\rho }{a+a_m}\frac{da}{dz}\right)+r\rho \left(1-\frac{\rho }{{\rho }_c}\right),$$ [4]

$$-c\frac{da}{dz}=D_a\frac{d^2}{d{z}^2}a-\mu \frac{a}{a+a_m}\rho .$$ [5]

In Eqs. 4 and 5, we have taken an additional simplifying assumption that a_m = a_k. For the well-characterized model organism E. coli, both the uptake and sensitivity of the major attractant aspartate are $\sim 1 \mathrm{\mu }\mathrm{M}$ (39, 64–67). Relaxing this assumption affects the results only weakly, as will be discussed below.

Eqs. 4 and 5 are supplemented by boundary conditions that describe limiting values for the bacterial density and attractant concentration far from the front:

$$\underset{z\to -\infty }{\lim }\rho \to {\rho }_c,\hspace{0.17em}\underset{z\to -\infty }{\lim }a\to 0;\hspace{0.17em}\underset{z\to \infty }{\lim }\rho \to 0,\hspace{0.17em}\underset{z\to \infty }{\lim }a\to a_0.$$ [6]

Fig. 1 shows the numerically obtained steady state profiles emerging from Eqs. 4 and 5 using experimentally established model parameters (39). All numerical solutions were obtained using finite element simulations (68, 69) (Materials and Methods). The density profile (solid red line) has a distinct peak at the front which defines the appearance of the migrating band observed in experiments (23, 24, 39) and can be divided into three distinct regimes: the growth regime (left of the density trough), the chemotaxis regime (the rising part of the density profile), and the diffusion regime (right of the density peak), as indicated in Fig. 2B. Such a division reflects the fact that as we will show in the sections dedicated to each regime, in each of these regimes, either the growth, chemotaxis, or diffusion term dominates in Eq. 4.

Fig. 1.

Profiles of bacterial density (solid red line, in optical density measured at a wavelength of 600 nm [${\text{OD}}_{600}$]), drift velocity (dashed green line, in mm/h), and attractant concentration (dotted blue line, in mM) for a steadily expanding population 14.5 h after the inoculation. Arrows indicate the different regimes used in the analytical consideration. Model parameters used are adapted from those determined in ref. 39 and are provided in SI Appendix, Table S1 (this simulation used the low-motility parameters).

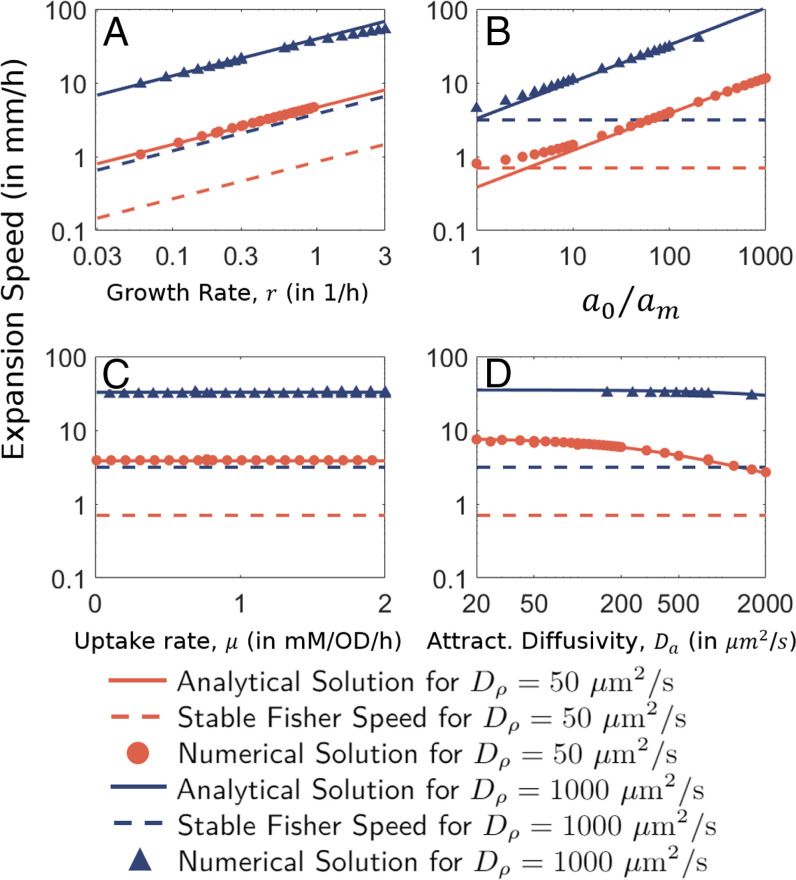
Fig. 2.

Dependence on (A) growth rate r, (B) uptake rate μ, (C) relative attractant levels $a_0/a_m$, and (D) attractant diffusion D_a. Analytical relation for the expansion speed (Eq. 23) is shown by solid lines ($D_{\rho }=50 \mathrm{\mu }{\mathrm{m}}^2/\mathrm{s},1,000 \mathrm{\mu }{\mathrm{m}}^2/\mathrm{s}$ in red and blue, respectively). The corresponding Fisher speeds, $c_F=2\sqrt{D_{\rho }·r}$, are denoted by corresponding dashed lines. Numerical solutions of the GE model (Eqs. 4 and 5) are shown by corresponding symbols. Unless specified, all parameter values are the default values given in SI Appendix, Table S1.

Chemotaxis Regime

Heuristic Derivation of the Expansion Speed

We first analyze the most striking feature of the traveling wave, the density bulge. Initially, we consider Eqs. 4 and 5 in the limit of ${\rho }_c\to \infty$ (this assumption will be relaxed later). We start with the following ansatz:

$$\rho (z)=\beta ·(a(z)+a_m),$$ [7]

with β being a proportionality constant. This reduces Eq. 5 to a homogeneous linear differential equation in a(z) with constant coefficients. The solution to such an equation is an exponential function, $a(z)\propto \exp (\lambda z)$, with λ satisfying

$$-c\lambda =D_a{\lambda }^2-\mu \beta .$$ [8]

The ansatz Eq. 7 also simplifies Eq. 4 considerably, with the penultimate term on the right-hand side (RHS) of Eq. 4 now proportional to $d^{2}a/d{z}^2$ . Another consequence of the ansatz is that $\frac{d}{dz}\rho (z)=\beta \frac{d}{dz}a(z)$, a relation that will be used often in our calculations. With the ansatz, Eq. 4 simplifies to

$$-c\lambda =(D_{\rho }-{\chi }_0){\lambda }^2+r\left(1+\frac{a_m}{a(z)}\right).$$ [9]

To proceed further, we consider the case that growth is much smaller than chemotactic drift so that the term proportional to r on the RHS of Eq. 9 may be neglected. This requires that both of the following conditions be true: The first is a condition on the parameters such that

$$r\ll \lambda c,$$ [10]

which is equivalent to assuming that the timescale of growth is much larger than the timescale of chemotactic drift, and thus, the two timescales may be separated. As we will show later, this assumption corresponds to a broad, biologically relevant parameter regime and is independent of the growth rate itself (because λc turns out to be proportional to r). The second is a condition on the values of attractant concentration a(z),

$$a(z)\gg \frac{r}{\lambda c}{a}_m.$$ [11]

As we will show in Growth Regime and the Density Trough, the quantity on the RHS of condition [11] is approximately the value of the attractant concentration at the trough of the density profile (i.e., the left boundary of the chemotaxis regime). Thus, for growth that is small compared to chemotactic drift (i.e., condition [10]), Eq. 9 becomes independent of a(z) in the chemotaxis regime. This means Eq. 4 is a linear equation involving $\rho (z)$, a(z), and their derivatives, and it (self-consistently) admits the ansatz Eq. 7 as a solution. With the last term in Eq. 9 neglected, the solution to λ is readily obtained, i.e.,

$$\lambda =\frac{c}{{\chi }_0-D_{\rho }},$$ [12]

where the solution λ = 0 is rejected as it does not solve Eq. 8. In this regime, the solution to the attractant concentration can be explicitly written as

$$a(z)=a_m\hspace{0.17em}\exp [\lambda ·(z-z_m)],$$ [13]

where z_m is defined by $a(z_m)=a_m$.

To obtain a relation for the expansion speed c and its dependence on the model parameters, we note that Eqs. 8 and 12 are by themselves insufficient since there are three unknown quantities: c, λ, and β. To obtain a defined solution, we thus invoke the boundary conditions at z = + ∞ well outside the chemotaxis regime (Eq. 6). This is done by integrating Eqs. 4 and 5 from a position $z=z^{†}$ in the chemotaxis regime to z = + ∞. For Eq. 4 with ${\rho }_c\to +\infty$, we obtain

$$c\rho (z^{†})=-D_{\rho }\frac{d\rho }{dz}(z^{†})+{\chi }_0\frac{\rho (z^{†})}{a(z^{†})+a_m}\frac{da}{dz}(z^{†})+rN(z^{†}),$$ [14]

where $N(z^{†})\equiv {\displaystyle {\int }_{z^{†}}^{\infty }\rho }(z)dz$ is the total bacterial population to the right of $z^{†}$. Note that Eq. 14 is exact and independent of our ansatz. For $z^{†}$ located in the chemotaxis regime, we plug in our ansatz Eq. 7 and Eqs. 13 to 14, yielding

$$c\beta (a(z^{†})+a_m)=-(D_{\rho }-{\chi }_0)\beta \lambda a(z^{†})+rN(z^{†}).$$ [15]

Note that while the term with growth rate r was negligible in Eq. 9, it cannot be neglected in the integral form as it involves contributions by $\rho (z)$ outside of the chemotaxis regime. Using Eq. 9, Eq. 15 simplifies to

$$c\beta a_m=r\beta (a(z^{†})+a_m)/\lambda +rN(z^{†}).$$ [16]

Now, while Eq. 16 provides us another equation for $c,\beta$ and λ, we have a new unknown, $N(z^{†})$. However, another relation for $N(z^{†})$ is obtained by integrating both sides of Eq. 5 from $z^{†}$ to $+\infty$, yielding

$$-c(a_0-a(z^{†}))=-D_a\lambda a(z^{†})-\mu [N(z^{†})-\mathrm{\Delta }N(z^{†})],$$ [17]

where $\mathrm{\Delta }N(z^{†})\equiv {\displaystyle {\int }_{z^{†}}^{\infty }{a}_m\rho (z)}/(a(z)+a_m)\hspace{0.17em}dz$. We show in SI Appendix, section S5, that $\mathrm{\Delta }N(z^{†})\sim \mathcal{O}(a_m\beta /\lambda )\ll N(z^{†})$ for $r\ll \lambda c$. Neglecting $\mathrm{\Delta }N(z^{†})$ in Eq. 17 and using Eq. 8, we obtain

$$c{a}_0\approx \mu \beta a(z^{†})/\lambda +\mu N(z^{†}).$$ [18]

Eqs. 16 and 18 allow us to eliminate $N(z^{†})+\beta a(z^{†})/\lambda$ and explicitly obtain the proportionality constant of the ansatz Eq. 7,

$$\beta =\frac{r{a}_0}{\mu a_m}\frac{1}{\left(1-\frac{r}{\lambda c}\right)}\approx \frac{r{a}_0}{\mu a_m}.$$ [19]

The explicit value of β now allows us to solve for λ and c using Eqs. 8 and 12:

$$\lambda \approx \sqrt{\frac{r\hspace{0.17em}{a}_0/a_m}{{\chi }_0-D_{\rho }+D_a}},$$ [20]

$$c\approx ({\chi }_0-D_{\rho })\sqrt{\frac{r\hspace{0.17em}{a}_0/a_m}{{\chi }_0-D_{\rho }+D_a}}.$$ [21]

From Eqs. 20 and 21, we find that the condition $r\ll \lambda c$ amounts to the following condition on the parameters:

$$\frac{a_0}{a_m}\gg 1+\frac{D_a}{{\chi }_0-D_{\rho }}.$$ [22]

Thus, the requirement for our ansatz to hold translates to an equivalent condition on the chemotactic model parameters that is independent of the growth rate r. As detailed in Parameter Dependences of the Expansion Speed, this parameter regime is typical for the study of migrating bands, with $({\chi }_0-D_{\rho })$ a few fold below D_a for bacteria in soft agar, and comparable to D_a for motile cells in liquid medium, while a_m is several orders of magnitude smaller than a₀.

Parameter Dependences of the Expansion Speed

To validate our heuristic approach we compared the derived relation for the expansion speed, Eq. 21, with numerical simulations, obtaining an excellent match for a broad range of model parameters. We show the dependences on growth rate, uptake rate, background attractant concentration, and the attractant diffusion coefficient in Fig. 2.

First, there is a square root dependence on the growth rate r, as validated by numerical results in Fig. 2A. This demonstrates that the well-known square root dependence of c_F, the Fisher speed, on growth rate is preserved in the GE model. The expansion speed is further increased by the square root of the relative background attractant concentration, $\sqrt{a_0/a_m}$ (Fig. 2B). However, the expansion speed c does not depend on the specific rate of attractant uptake μ (Fig. 2C) nor the inoculum population size (as the steady state bulge size is an emergent property, independent of the initial population size). The independence on μ is particularly counterintuitive since it is the uptake of attractant that establishes the attractant gradient which, in turn, drives the chemotactic movement. The independence on μ is in contrast to the KS model, which predicts that $c=\mu N_{KS}/a_0$ (where N_KS is the inoculum population size), but is in agreement with experimental results (23, 39). We will show in The Growth–Leakage Balance that our solution for c can be similarly expressed in terms of μ and N₀, the size of the density bulge. However, unlike the KS solution, N₀ is here an emergent quantity that turns out to be inversely proportional to μ. Thus, the dependence on μ cancels out, making the expansion speed independent of μ.

The most nontrivial aspect of Eq. 21 is perhaps the predicted dependence of the expansion speed c on the attractant diffusion coefficient D_a (Fig. 2D), which was not considered in most previous models (33, 34, 70, 71). Although this dependence itself is not so strong, it significantly affects the dependence of c on the cellular motility characteristics as we discuss next.

To see how the expansion speed depends on the cellular motility parameters $D_{\rho }$ and χ₀ we first note that $D_{\rho }$ and χ₀ result from the run-and-tumble dynamics and are thus both proportional to $v_0^2\tau$, where v₀ is the run velocity, and τ is the average duration of runs. The ratio ${\chi }_0/D_{\rho }$ results from the properties of the flagella motor, the ligand/chemotactic receptor interaction, and the chemotactic signaling network (46). To better describe the differences, we here define the chemotactic sensitivity, $\varphi \equiv ({\chi }_0-D_{\rho })/D_{\rho }$, a dimensionless parameter such that a large value of $\varphi$ represents a strong chemotactic response to a ligand. Notably, $D_{\rho }$ can vary across a broad range depending on the environment, with $D_{\rho }\sim 50 \mathrm{\mu }{\mathrm{m}}^2/\mathrm{s}$ for E. coli swimming in soft agar (39) and $D_{\rho }\sim 300$ to $1,000 \mathrm{\mu }{\mathrm{m}}^2/\mathrm{s}$ in liquid media (39, 72, 73). In contrast, $\varphi$ is not expected to be affected by environmental obstacles but by the chemotactic properties of the cell and the type of attractant and is found to vary from 2 to 8 (72, 74). We can thus keep $\varphi$ and $D_{\rho }$ as independent parameters and write the expansion speed, Eq. 21, as

$$c\approx D_{\rho }\varphi \sqrt{\frac{r\hspace{0.17em}{a}_0/a_m}{D_{\rho }\varphi +D_a}}.$$ [23]

The predicted comparison with numerical solutions confirms the dependence on cellular parameters: Notably, for high cellular motility, $D_{\rho }\varphi \gg D_a$, Eq. 23 gives $c\approx \sqrt{D_{\rho }\varphi r{a}_0/a_m}$, as seen in Fig. 3 A and B (solid dark blue lines show the analytical prediction for $\varphi =5$). The thick cyan lines show a square root fit. Meanwhile, in the range $D_{\rho }\varphi \ll D_a,\hspace{0.17em}c\propto D_{\rho }\varphi \sqrt{r{a}_0/a_m}$ and thus has a linear dependence on the motility parameter and chemotactic sensitivity (thick yellow lines).

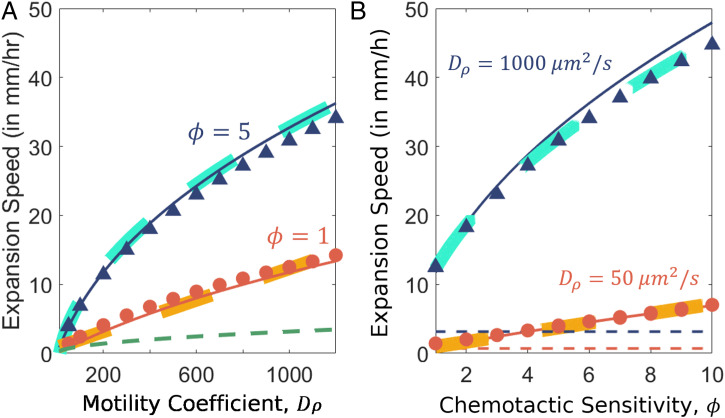
Fig. 3.

Dependence of expansion speed on motility parameters. (A) Dependence on cellular motility $D_{\rho }$. Numerical solutions for $\varphi =1$ and $\varphi =5$ are shown by red circles and dark blue triangles, respectively. Analytical solutions following Eq. 23 are shown by corresponding solid red and blue lines. The green dashed line represents the stable Fisher speed, $c_F=2\sqrt{D_{\rho }r}$, the minimum expansion speed of our system. (B) Dependence on the chemotactic sensitivity, $\varphi$. Numerical solutions for $D_{\rho }=50 \mathrm{\mu }{\mathrm{m}}^2/\mathrm{s}$ and $D_{\rho }=1,000 \mathrm{\mu }{\mathrm{m}}^2/\mathrm{s}$ are shown by red and dark blue circles, respectively. Analytic solutions following Eq. 23 are shown by the corresponding solid lines. Thick yellow and cyan dashed lines are best fits for the respective values of $\varphi$ and $D_{\rho }$ to demonstrate that $c\propto D_{\rho }\varphi$ for $D_{\rho }\varphi \mathrm{\lesssim }{D}_a$ and that $c\propto \sqrt{D_{\rho }\varphi }$ if $D_{\rho }\varphi$ is large compared to D_a. Unless specified, all parameter values are the default values given in SI Appendix, Table S1.

The dependence of the expansion speed on the value of D_a (Fig. 2D) and its relation to $D_{\rho }$ (Fig. 3) reveals a crucial role of the molecular diffusion of the attractant, which has historically been assumed to be of a much smaller scale than the motility-induced bacterial diffusion and chemotaxis (33, 34, 36, 44, 70, 71, 75). Large D_a can be understood to result in a smoothening of the attractant gradient, thereby slowing down chemotaxis. In fact, for extremely large values of D_a, we note that the bacterial population is unable to establish a gradient in the attractant concentration, and our analysis fails to hold as seen in the self-consistency condition [22]. Quantitatively, the molecular diffusivity ($D_a\approx 800 \mathrm{\mu }{\mathrm{m}}^2/\mathrm{s}$) well exceeds the chemotactic coefficient and the effective cell diffusivity of E. coli in soft agar ($D_{\rho }\approx 50 \mathrm{\mu }{\mathrm{m}}^2/\mathrm{s}$) (39). Hence, condition [22] is satisfied for $a_0>4a_m\approx 4 \mathrm{\mu }\mathrm{M}$ for aspartate, thus explaining the deviation seen at small $a_0/a_m$ for $D_{\rho }=50 \mathrm{\mu }{\mathrm{m}}^2/\mathrm{s}$ (see red circles in Fig. 2B).

We also verified the dependence of the expansion speed on $\varphi$ itself for $\varphi >1$ (Fig. 3B). For $\varphi <1$, the numerical values do not match the analytical values, as they are beyond the regime of self-consistency discussed above. Outside of this regime, the traveling-wave solution transitions to the pulled wave dynamics of the F-KPP equation, with a lower bound on the expansion speed given by the Fisher speed ($c_F=2\sqrt{D_{\rho }r}$) (SI Appendix, Fig. S3).

Effect of Carrying Capacity

Next, we consider the effect of a finite carrying capacity ρ_c and the corresponding effect on expansion. To do so, we follow a similar approach as in Heuristic Derivation of the Expansion Speed; see SI Appendix, section S6, for details of the calculations performed. Incorporating the effect of ρ_c leads us to the following form for the expansion speed:

$$c=c_{\infty }/\sqrt{1+\frac{r{a}_0}{\mu {\rho }_c}\frac{D_{\rho }\varphi \gamma }{\left(D_{\rho }\varphi +D_a\right)}\frac{a_0}{a_m}},$$ [24]

where $c_{\infty }$ is the expansion speed for infinitely large carrying capacities, ${\rho }_c\to \infty$ as given by Eq. 21, and γ is a dimensionless function determined by the shape of the density bulge. While we are unable to determine the exact functional form of γ, we find an excellent agreement between the numerical results and analytical solution for the best-fit value of γ (found to be $\gamma =0.26$ for $D_{\rho }=50 \mathrm{\mu }{\mathrm{m}}^2/\mathrm{s}$ and $\gamma =0.36$ for $D_{\rho }=1,000 \mathrm{\mu }{\mathrm{m}}^2/\mathrm{s})$ as seen in Fig. 4A.

Fig. 4.

Effect of carrying capacity. (A) Dependence of expansion speed on the ambient attractant concentration when the carrying capacity is finite (${\rho }_c=10 {\text{OD}}_{600}$). Markers (red circles and blue triangles) indicate numerical values, solid lines indicate analytical predictions as per Eq. 24, and dashed lines indicate analytical predictions with ${\rho }_c\to \infty$. All results in red are for $D_{\rho }=50 \mathrm{\mu }{\mathrm{m}}^2/\mathrm{s}$, and all results in blue are for $D_{\rho }=1,000 \mathrm{\mu }{\mathrm{m}}^2/\mathrm{s}$. (B) The ambient attractant concentration resulting in maximum expansion speed $a_0^{\text{max}}$ is shown depending on the dimensionless parameter $\mu {\rho }_c/(r{a}_m)$. The analytical solution, Eq. 24, is shown as corresponding solid lines. Dashed lines show the solutions ($c_{\infty }$) without a limiting carrying capacity (${\rho }_c\to \infty$, as shown in Fig. 3). Different symbols in B denote which model parameter was varied from its default value (square if μ, circle if ρ_c, triangle if r, and diamond if a_m) for $D_{\rho }=50 \mathrm{\mu }{\mathrm{m}}^2/\mathrm{s}$ (red) and $D_{\rho }=1,000 \mathrm{\mu }{\mathrm{m}}^2/\mathrm{s}$ (blue). For details, refer to SI Appendix, Supplemental Methods, and to SI Appendix, Table S2, for range of values used for each parameter. Parameters have the default values from SI Appendix, Table S1, unless specified.

An intriguing prediction of Eq. 24 is a peak in the relation between c and a₀ whose existence is numerically confirmed (Fig. 4A). Thus, too much attractant actually reduces the expansion speed, i.e., the expansion speed of the population cannot be arbitrarily increased merely by increasing the ambient attractant concentration, but is limited ultimately by the physiological and molecular parameters. To understand this nonmonotonic dependence, we note that in Eq. 24, the effect of ρ_c is insignificant for ${\rho }_c\gg r{a}_0^2/(\mu a_m)=\beta ·a_0$, i.e., if ρ_c is large compared to the highest density expected from the ansatz Eq. 7 when $a(z)\to a_0$. For sufficiently large a₀ such that ${\rho }_c<\beta a_0$, the quantity $\mu {\rho }_c/r$ (which describes the amount of attractant taken up by bacteria at the peak density, where $\rho (z)\approx {\rho }_c$, in one doubling time) becomes small, and the population is unable to take up the attractant fast enough to generate a substantial gradient in a(z). The lack of a substantial gradient, in turn, leads to mitigated expansion speeds. As a result, for small ρ_c, Eq. 24 simplifies to $c\propto \sqrt{\mu /a_0}$. Thus, for small carrying capacity, c increases with μ and decreases with a₀, qualitatively similar to the relation found by Keller and Segel ($c\propto \mu /a_0$). In both solutions, the decrease in expansion speed with a₀ results from a bound on the total population of the density bulge that limits its ability to consume the attractant.

We note that the existence of a peak in expansion speed for varying background attractant concentrations was observed experimentally and reported already over 30 y ago (39, 76) but was believed to be due to receptor saturation. Our analytical solution in Eq. 24, validated by simulations (Fig. 4A), provides an excellent quantitative explanation of this phenomenon even in the absence of receptor saturation.

The attractant concentration corresponding to the maximum expansion speed is found to be

$$\frac{a_0^{\text{max}}}{a_m}=\sqrt{\frac{\mu {\rho }_c}{r{a}_m\gamma }\left(1+\frac{D_a}{D_{\rho }\varphi }\right)}$$ [25]

and is validated numerically in Fig. 4B. The resulting maximum expansion speed is $c_{\text{max}}=c_{\infty }(a_0=a_0^{\text{max}})/\sqrt{2}$, and the corresponding carrying capacity is proportional to ${(a_0^{\text{max}})}^2$. Thus, for the population to maximize its expansion speed at high attractant concentrations, a very high carrying capacity is required. As the carrying capacity is typically no more than a few OD for aerobically grown cells, the attractant concentration for the maximum expansion speed, $a_0^{\text{max}}$, is not expected to be above $\sim 0.1 \text{mM}$ (Eq. 25 and Fig. 4A).

Case of $a_k\ne a_m$

If we relax the assumption that a_k = a_m and take as our ansatz $\rho (z)=\beta (a(z)+a_k)$, we note an additional term in Eq. 9 that is of the order

$$\frac{(a_m-a_k)a_{m}a(z)}{(a(z)+a_k){(a(z)+a_m)}^2}$$ [26]

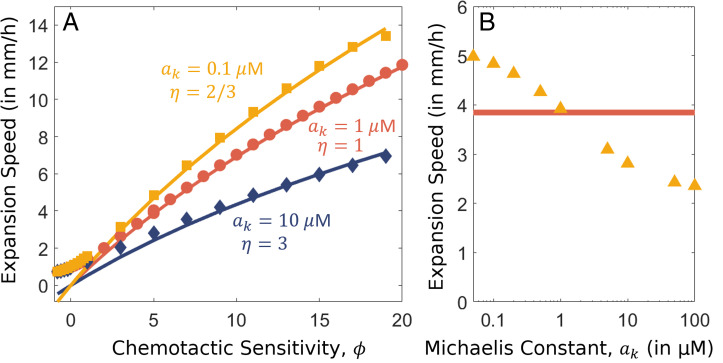
relative to the dominant chemotactic drift term. It is due to this term that our ansatz Eq. 7 fails to hold if $a_k\ne a_m$. A similar term is found in Eq. 17. While trivially negligible if a_k = a_m, the terms are also negligible for $a(z)\gg a_k,a_m$ and as $a(z)\to 0$. Thus, we expect our analysis of the chemotaxis regime (and the growth regime, which we perform in Growth Regime and the Density Trough) to also be applicable for the case that $a_k\ne a_m$ as long as $a(z)\gg a_k,a_m$. However, when $a(z)\sim a_m\sim (a_m-a_k)$, our ansatz will not hold, and the value of a(z) where $\rho (z)$ switches from being relatively constant as in the growth regime to rising exponentially as in the chemotaxis regime is undetermined by our current analysis. We expect the transition to be at $\eta a_m$, between a_k and a_m, as both of these values are crucial in determining the transition in $\rho (z)$. The coupled nature of $\rho (z)$ and a(z) make it difficult to determine η exactly. Such an assumption leads to a similar expression for expansion speed but where $\eta a_m$ replaces a_m in the final form. We find an excellent agreement with numerical results for $a_k\ne a_m$ for just one fitting parameter, η, which we find to be ∼2/3 for $a_k=0.1 \mathrm{\mu }\mathrm{M}=10a_m$ and $\eta \approx 3$ for $a_k=10 \mathrm{\mu }\mathrm{M}=0.1a_m$. The range of exponential speeds for different values of a_k while keeping a_m fixed at 1 $\mathrm{\mu }\mathrm{M}$ is shown in Fig. 5 A and B. Notably, c is seen to decrease only twofold for a 2,000-fold increase in a_k, from 50 nM to 100 $\mathrm{\mu }$M for standard parameters (Fig. 5B), while if both a_k and a_m increase 2,000-fold, c would decrease 45-fold (Fig. 2B).

Fig. 5.

Effect of varying Michaelis constant, a_k. (A) Dependence of expansion speed on the chemotactic sensitivity, $\varphi$, for different values of a_k and $D_{\rho }=50 \mathrm{\mu }{\mathrm{m}}^2/\mathrm{s}$. Solid lines indicate analytical solutions for corresponding best fit values of η, and markers denote the numerical solutions. Results for $a_k=0.1 \mathrm{\mu }\mathrm{M},\hspace{0.17em}1 \mathrm{\mu }\mathrm{M}$, and $10 \mathrm{\mu }\mathrm{M}$ are shown in yellow, red, and blue, respectively. (B) Dependence of the expansion speed on model parameter a_k. The numerical solutions obtained for $D_{\rho }=50 \mathrm{\mu }{\mathrm{m}}^2/\mathrm{s},\hspace{0.17em}\varphi =5$ are represented by yellow triangles, and the analytic solution found in Eq. 21 for $a_k=a_m={10}^{-3} \text{mM}$ is shown by the red line. Parameters have the default values from SI Appendix, Table S1, unless specified.

Diffusion Regime and the Density Peak

Next, we describe the dynamics of the propagating density profile at its asymptotic front. This is the diffusion regime which lies to the right of the density peak (Fig. 1), where the exponential increase of the concentration of the attractant observed in the chemotaxis regime is curtailed by the right boundary condition, i.e., $a(z\to \infty )\to a_0$. Here the drift velocity becomes $v\propto \frac{d}{dz}a(z)/a_0\to 0$ and thus negligible as $z\to \infty$. The equation for $\rho (z)$ is no longer affected by the attractant, and the dynamics are thus described by the F-KPP equation. The solution is

$$\rho (z)={\rho }_0\exp (-{\lambda }_D^{\pm }z)\hspace{1em}\text{with}\hspace{0.17em}{\lambda }_D^{\pm }=\frac{c_D\pm \sqrt{c_D^2-4r{D}_{\rho }}}{2D_{\rho }},$$ [27]

where ρ₀ is a proportionality constant (see Eq. 33) and c_D is the speed of propagation of the asymptotic front.

For the front to be a part of the stationary solution that propagates at the same speed as the chemotaxis regime, c (Eq. 21), we must have c_D = c, which well exceeds the F-KPP speed, $c_F=2\sqrt{r{D}_{\rho }}$. It is well known for the F-KPP equation that if the dynamical system admits a uniformly translating front solution with $c>c_F$, then the front solution corresponding to the traveling speed c is the stable solution (28). For the case that the front is asymptotic, the initial conditions are compact, and the right boundary condition is the unstable state, $\rho (z\to \infty )=0$, the steeper front solution is selected for (28) (see SI Appendix, section S7A, for a brief description). Thus, our dynamical system selects for a solution with the leading asymptotic behavior given by

$${\lambda }_D\equiv {\lambda }_D^{+}=\frac{c+\sqrt{c^2-4r{D}_{\rho }}}{2D_{\rho }}\approx c/D_{\rho }$$ [28]

for the diffusion regime.

We then turn to the form of a(z) in the diffusion regime. As $a(z)\to a_0\gg a_m$ in this regime, Eq. 5 becomes

$$-c\frac{da}{dz}=D_a\frac{d^{2}a}{d{z}^2}-\mu {\rho }_0\exp (-{\lambda }_{D}z).$$ [29]

This is a nonhomogeneous linear differential equation in a(z) with the solution

$$a(z)=a_0-\frac{\mu \exp (-{\lambda }_{D}z)}{{\lambda }_D(c-D_a{\lambda }_D)}-a_1\exp (-cz/D_a),$$ [30]

where a₁ is an undetermined constant of integration. The leading behavior is determined by whichever exponential term decays more slowly as $z\to +\infty$:

$$a_0-a(z)\propto \{\begin{array}{ll}\exp (-cz/D_a),\hfill & {\lambda }_D>\frac{c}{D_a}\hspace{0.17em}(\text{or}\hspace{0.17em}{D}_{\rho }<D_a);\hfill \\ \exp (-{\lambda }_{D}z),\hfill & {\lambda }_D<\frac{c}{D_a}\hspace{0.17em}(\text{or}\hspace{0.17em}{D}_{\rho }>D_a).\hfill \end{array}$$ [31]

As to the peak itself, it can be shown (see SI Appendix, section S9, for details) that the attractant concentration at the peak, $a(z_{\text{max}})$, is given by the bound

$$a_0\left(\frac{{\chi }_0}{{\chi }_0+D_a}\right)>a(z_{\text{max}})>\frac{a_0}{2}\left(\frac{{\chi }_0}{{\chi }_0+D_a}\right).$$ [32]

With some further approximations (that ${\chi }_0\gg D_{\rho }$ and that the ansatz Eq. 7 extends throughout the rising region of the density bulge), we obtain that

$$\frac{{\rho }_{\text{max}}}{{\rho }_{\text{min}}}\sim \frac{\lambda c}{r},$$ [33]

where ${\rho }_{\text{max}}$ is the maximal population density at the front (i.e., the density peak) and ${\rho }_{\text{min}}$ is the minimal population density left of the peak (i.e., the density dip at the transition between the chemotaxis and growth regimes). A numerical verification of Eqs. 32 and 33 for a broad parameter range is shown in SI Appendix, Fig. S4.

Growth Regime and the Density Trough

Next, we turn to the growth regime, which is the region with exponential density profile trailing the density bulge (Fig. 1B). In this regime, the increase in $\rho (z)$ as $z\to -\infty$ drives the attractant concentration to zero according to Eq. 5; i.e., $a(z)\to 0,\hspace{0.17em}da(z)/dz\to 0$ as $z\to -\infty$. Consequently, $v(z)\to 0$ and

$$\mid \frac{d}{dz}\left(v(z)\rho (z)\right)\mid \ll c·\mid \frac{d\rho }{dz}\mid$$ [34]

in the growth regime, sufficiently to the left of the density trough. Later in this section, we will quantitatively define the condition where the v term is negligible compared to c. Here we briefly describe characteristics of the solution when this condition holds.

Eliminating the term associated with chemotactic drift removes the dependence of $\rho (z)$ on a(z) in Eq. 4, with the only remaining processes determining $\rho (z)$ being growth and diffusion. Thus, we recover the F-KPP equation, with the solution $\rho (z)\propto \exp [-{\lambda }_G^{\pm }z]$, where

$${\lambda }_G^{\pm }=\frac{c_G}{2D_{\rho }}\pm \frac{\sqrt{c_G^2-4D_{\rho }r}}{2D_{\rho }},$$ [35]

c_G being the traveling velocity of the growth regime. As in the diffusion regime, here c_G must be the same as c, the speed of the chemotaxis regime, in order for Eq. 4 to admit a stationary solution. Since $c\gg c_F=2\sqrt{r{D}_{\rho }}$, the two solutions for ${\chi }_0\gg D_{\rho }$ are ${\lambda }_G^{-}\approx r/c\ll {\lambda }_F=\sqrt{r/D_{\rho }}$ and ${\lambda }_G^{+}\approx c/D_{\rho }\gg {\lambda }_F$. It is well established for the F-KPP equation that for a solution to move stably at a speed exceeding c_F, its front must be shallower than λ_F; see ref. 77 and SI Appendix, section S7B. Hence, ${\lambda }_G^{-}$ is selected. Thus, the form of density sufficiently to the left in the growth regime must be given by

$${\rho }_G(z)={\rho }_1\exp [-{\lambda }_G·z],\hspace{1em}\text{with}\hspace{0.17em}{\lambda }_G\equiv {\lambda }_G^{-}\approx r/c,$$ [36]

ρ₁ being a proportionality constant that sets the z scale as will be specified in this section.

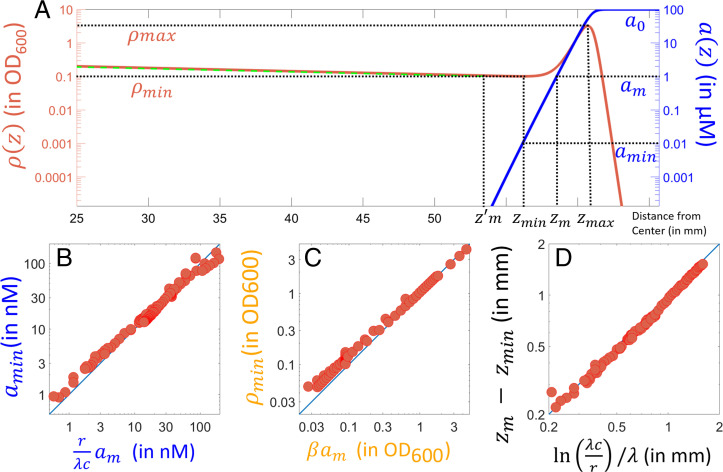
To understand how the front of the growth regime is set, we focus on the transition region between the growth and chemotaxis regimes (located close to the density trough). A magnified view of this transition region is shown in Fig. 6A, with $z_{\text{min}}$ denoting the location of the density minimum.

Fig. 6.

Transition from the chemotaxis to the growth regime. (A) Steady expansion profiles of $\rho (z)$ (solid red line) and a(z) (solid blue line) for the standard parameters (SI Appendix, Table S1; $D_{\rho }=50 \mathrm{\mu }{\mathrm{m}}^2/\mathrm{s},{\chi }_0=300\hspace{0.17em}\mathrm{\mu }{\mathrm{m}}^2/\mathrm{s}$). The profile of $\rho (z)$ as predicted by the ansatz Eq. 7 is shown using the dashed green line. Dashed horizontal lines indicate distinct values of a and ρ as indicated. (B–D) Numerically obtained values of $a(z_{\text{min}})$, $\rho (z_{\text{min}})$, and $z_m-z_{\text{min}}$ for a broad variation of parameters. Seven model parameters in Eqs. 4 and 5 (other than ρ_c, which was >1, 000 ${\text{OD}}_{600}$ for all results here) were varied across many decades (see SI Appendix, Supplemental Methods, for details of what was done and SI Appendix, Table S3, for the range of values investigated). Blue lines show y = x to demonstrate agreement with the predicted values of $a(z_{\text{min}}),\hspace{0.17em}\rho (z_{\text{min}})$, and $z_m-z_{\text{min}}$.

Previously, we have shown that for $z>z_m$ (defined by $a(z_m)=a_m$; Fig. 6A) in the chemotaxis regime, cell density is given by the ansatz Eq. 7, with the attractant concentration a(z) given by Eq. 13. We showed that the validity of this ansatz required $a(z)\gg (r/\lambda c)a_m$, i.e., Eq. 9. However, even with $r\ll \lambda c$, this condition will eventually break down for $a(z)\ll a_m$, for $z<z_m$, including possibly the vicinity of $z_{\text{min}}$ (Fig. 6A). Thus, in order to address the density profile in the transition region, we cannot rely on the ansatz Eq. 7 anymore.

Here we extend our ansatz to a modified form which we will show to be valid for both the chemotaxis and growth regimes, including all of the transition region:

$$\rho (z)=\beta \hspace{0.17em}[a(z)+a_m]·\exp [-{\lambda }_G·(z-z_m)].$$ [37]

Clearly, for $a(z)\ll a_m$, Eq. 37 recovers the form of density established for the growth regime, i.e., Eq. 36, with ${\rho }_1=\beta a_m{e}^{{\lambda }_G{z}_m}$. For $a(z)\gg a_m$ where a(z) is given by Eq. 13 in the chemotaxis regime, Eq. 37 becomes

$$\rho (z)\approx \beta a(z)·e^{-{\lambda }_G(z-z_m)}=\beta a_m·e^{(\lambda -{\lambda }_G)·(z-z_m)}\approx \beta a(z),$$

where the last approximation results from ${\lambda }_G\ll \lambda$ for our parameter regime $r\ll \lambda c$. Furthermore, we can verify that the modified ansatz Eq. 37 satisfies Eq. 4 for intermediate range of a(z), leaving behind a linear equation for a(z) that is the same as that obtained in the chemotaxis regime, with the same solution (Eq. 13) (SI Appendix, section S7B). Our modified ansatz thus leads to the following form for the cell density:

$$\rho (z)=\beta a_m\left[1+e^{\lambda ·(z-z_m)}\right]\hspace{0.17em}·\hspace{0.17em}{e}^{-{\lambda }_G(z-z_m)},$$ [38]

which we claim to be valid for the entire regime $-\infty <z<z_m$ (for $r\ll \lambda c$), including the vicinity of the density trough located at $z_{\text{min}}$.

We can now use the expression given by Eq. 38 to work out characteristics of the solution in the transition region. By setting ${\frac{d}{dz}\rho \mid }_{z=z_{\text{min}}}=0$, we obtain (for $r\ll \lambda c$):

$$z_{\text{min}}=z_m-{\lambda }^{-1}\ln \left(\frac{\lambda c}{r}\right);$$ [39]

$${\rho }_{\text{min}}=\beta a_m·\left(1+\frac{r}{\lambda c}\right)e^{-(z_{\text{min}}-z_m)·r/c}\approx \beta a_m;$$ [40]

$$a_{\text{min}}\equiv a(z_{\text{min}})=a_m·\exp [\lambda ·(z_{\text{min}}-z_m)]=\frac{r}{\lambda c}{a}_m.$$ [41]

These results are validated numerically for a range of parameters (Fig. 6 B–D).

We can determine the left boundary of the transition region, $z{\prime }_m$, by finding the range of $z<z{\prime }_m$ where Eq. 38 is described by the simple exponential form in Eq. 36 (dashed green line, Fig. 6A). This can be estimated by setting the asymptotic form

$${\rho }_G(z)\equiv \underset{z\to -\infty }{\lim }\rho (z)=\beta a_m{e}^{-{\lambda }_G·(z-z_m)}$$ [42]

to ${\rho }_G(z{\prime }_m)={\rho }_{\text{min}}$. Using Eq. 40 for ${\rho }_{\text{min}}$, we find

$$z{\prime }_m=z_{\text{min}}-{\lambda }^{-1}\ln \left(\frac{\lambda c}{r}\right).$$ [43]

In other words, Eq. 42 can be written as ${\rho }_G(z)={\rho }_{\text{min}}{e}^{-{\lambda }_G(z-z{\prime }_m)}$. Note that because ${\lambda }_G·(z_{\text{min}}-z{\prime }_m)\ll 1$ according to Eq. 43 for $r\ll \lambda c$, ${\rho }_G(z)\approx {\rho }_{\text{min}}$ for $z{\prime }_m<z<z_{\text{min}}$; i.e., the density function on the left side of $z_{\text{min}}$ is constant with relative variation of the order of $r/\lambda c$. [We can verify the self-consistency of the ansatz Eq. 38 by using it to compute the drift velocity $dv(z)/dz$ and hence evaluate the spatial domain where the condition [34] is satisfied. We find that [34] is satisfied for $e^{\lambda ·(z_{\text{min}}-z)}\gg 1$ or $z<z_{\text{min}}-{\lambda }^{-1}\ln (\lambda c/r)=z{\prime }_m$ from Eq. 43.]

To summarize, the transition region between the chemotaxis and growth regimes ranges from $z{\prime }_m<z<z_m$ where the distances from $z_{\text{min}}$ to z_m and $z{\prime }_m$ are given by Eqs. 39 and 43, respectively. The total width of the transition zone is

$$w\equiv z_m-z{\prime }_m=\frac{2}{\lambda }\ln (\lambda c/r).$$ [44]

Note that the time it takes for the wave front to migrate across the transition region is $\tau =w/c$. Thus, the key condition for our results, $r\ll \lambda c$, corresponds simply to $r\tau \ll 1$, i.e., a separation of timescale between expansion and population growth. This is a condition which we expect to hold for most expanding populations.

The Growth–Leakage Balance

We can finally use the explicit solution for $\rho (z)$ to connect the dynamics in the chemotaxis and growth regimes. We consider the total bacterial population to the right of a position $x=z+ct$, which is comoving with the population: $\tilde{N}(z;t)\equiv {\displaystyle {\int }_{z+ct}^{+\infty }d}x\prime \rho (x\prime ,t)$. The change in $\tilde{N}(z;t)$ over time is given formally by

$$\frac{d\tilde{N}}{dt}=-\tilde{J}(z;t)+r·\tilde{N}(z;t),$$ [45]

where

$$\tilde{J}(z;t)=(c-v(z+ct,t))\rho (z+ct,t)+D_{\rho }{\frac{\partial \rho }{\partial x}\mid }_{z+ct}$$

obtained from taking time derivative of $\tilde{N}$ using Eq. 1 is the leakage flux which includes the loss of cells across the position $x=z+ct$ in the laboratory frame due to chemotaxis and diffusion, and the last term in Eq. 45 describes the growth of the cells in the region $x>z+ct$.

In the absence of growth r = 0, Novick-Cohen and Segel (34) showed that incorporating the lower Weber cutoff to the KS model led to the loss of cells from the front and subsequently the slowdown of the migrating wave front. We see from Eq. 45 that the incorporation of growth, even at very low rates, allows the migrating wave front to replenish itself and thereby maintain stability.

In the stationary state ($\frac{d}{dt}\tilde{N}=0$), quantities in the moving frame have no time dependence, i.e., $\tilde{N}(z;t)=N(z)$. Thus,

$$rN(z)=J(z)\equiv (c-v(z))\rho (z)+D_{\rho }\frac{d\rho }{dz},$$ [46]

which is just Eq. 14 with v(z) given by a(z) that solves the stationary equations, Eqs. 4 and 5. Earlier, we solved Eq. 14 using the ansatz Eq. 7 that holds only in the chemotaxis regime with $z>z_m$. We can repeat the calculation using Eqs. 38 and 13 derived from our ansatz Eq. 37. We find the leakage flux to be very weakly z-dependent in the vicinity of the density trough, i.e.,

$$J(z)=J_0·\left[1+\mathcal{O}(r·(z_{\text{min}}-z)/c)\right]\hspace{1em}\text{for}\hspace{0.17em}z{\prime }_m<z<z_m,$$ [47]

where

$$J_0\equiv J(z_{\text{min}})=c{\rho }_{\text{min}}·\left[1-\frac{r}{\lambda c}\frac{{\chi }_0}{{\chi }_0-D_{\rho }}\right]\approx c{\rho }_{\text{min}}.$$ [48]

Since $|z-z_{\text{min}}|<{\lambda }^{-1}\ln (\lambda c/r)$ according to Eqs. 39 and 43, we conclude that $J(z)\approx J_0$ up to an order of $r/(\lambda c)\ln (\lambda c/r)\ll 1$. Consequently, N(z) is also nearly z-independent, reflecting the sharply peaked structure of the density front. For convenience, we define $N_0\equiv N(z_{\text{min}})$ as the size of the population in the density bulge. The above results then lead to an important biological relation,

$$r{N}_0=J_0,$$ [49]

with the bulge size given by

$$N_0=J_0/r\approx c{\rho }_{\text{min}}/r.$$ [50]

Eq. 49 describes a balance of the growth of the cells in the front and their leakage behind the front, as depicted in Fig. 7. At a given instance (time t₀), the wave front is shown as the dashed red line in the laboratory frame. The front region, composed of N₀ cells, grows at a rate rN₀. This growth is balanced by cells leaving the front (i.e., across the black dashed line indicating $x_0=z_m+c{t}_0$), with flux $J_0=-c{\rho }_{\text{min}}$. At some time δt later, the front has traversed a distance $\delta x=c·\delta t$. The total amount of cells leaving the front during this time is $\delta N=J_0\delta t$. The corresponding density of the cells left behind the propagating front is $\delta N/\delta x\approx {\rho }_{\text{min}}$ (shown as the purple region in Fig. 7A). The cells left behind will grow at the rate r. For δt much smaller than the doubling time, the density behind the front will not have grown much and will thus remain at $\sim {\rho }_{\text{min}}$ (Fig. 7A). We have shown that this is the case for the time it takes for the front to traverse the width of the trough region (Eq. 44). After a time $\mathrm{\Delta }t$ that is large compared to the doubling time, the population size at the back will become $\rho (x_0,t)=\rho (x_0,t_0)\hspace{0.17em}{e}^{r\mathrm{\Delta }t}=\rho (x_0,t_0)\hspace{0.17em}{e}^{r(t-t_0)}$ (Fig. 7B). Given that $t_0=(x_0-z_{\text{min}})/c$, we have

$$\rho (x_0,t)\approx {\rho }_{\text{min}}\exp \left[-\frac{r}{c}(x_0-ct)\right].$$ [51]

Fig. 7.

Schematic of the dynamics of the transition between chemotaxis and growth regimes. (A) In a short time $\delta t$, the density bulge shown near x₀ (dotted red line) moves forward to be near $x_0+c\delta t$ (solid red line). In that time, the density bulge grows by an amount $r{N}_0\delta t$ and is diminished by leakage given by an amount $J_0\delta t$. During steady expansion, these values match the expressions given by our ansatz (Eqs. 7 and 37). The leaked cells are deposited behind the density bulge where the bacterial density is roughly constant for a distance δx. Thus, $\rho (x_0,t_0+\delta t)\approx {\rho }_{\text{min}}$, and the total deposition over time δt, given by $\delta N_0$, is also equal to $J_0\delta t$. (B) After a long time $\mathrm{\Delta }t$, the density bulge moves to be near a position $x_0+c\mathrm{\Delta }t$ (dashed red line). Cells behind the density bulge grow at a rate r, and the density thus accumulates as $\rho (x_0,t)={\rho }_{\text{min}}\exp (r\mathrm{\Delta }t)$.

Thus, the trailing exponential density profile in Eq. 51, while looking like a moving front, is merely a result of the exponential growth of a stationary population, which is seeded by the traveling wave front at density ${\rho }_{\text{min}}$ and speed c.

Finally, we note that the picture depicted in Fig. 7A can be used directly to predict the value or ${\rho }_{\text{min}}$ without going through detailed calculation: since the bacteria are concentrated in the density bulge, the removal of the attractant is almost entirely due to uptake by cells in the density bulge. This gives us the mass conservation condition∗

$$\mu N_0\approx c{a}_0.$$ [52]

The growth–leakage balance rN₀ = J₀ then gives $J_0=c{a}_{0}r/\mu$. The consideration described in Fig. 7A then immediately gives the result that the density left behind the front bulge, which would be ${\rho }_{\text{min}}$, is given by $J_0/c=a_{0}r/\mu$. Thus, we obtain a surprisingly simple result,

$${\rho }_{\text{min}}\approx a_{0}r/\mu ,$$ [53]

independent of the other details of the system.

We can also use the expression for ${\rho }_{\text{min}}$ thus obtained to calculate the consumption of attractant around the density trough. Using $\rho (z)={\rho }_{\text{min}}$ and a(z) from Eq. 13, Eq. 5 becomes

$$-c\lambda =D_a{\lambda }^2-\frac{\mu {\rho }_{\text{min}}}{a_m}=D_a{\lambda }^2-r\frac{a_0}{a_m}.$$ [54]

This relation together with the proportionality between λ and c, Eq. 12, immediately gives the central result on the expansion speed, Eq. 21. This simple line of consideration reveals the underlying origin of the dependence of the expansion speed on $a_0/a_m$: the growth–leakage balance relates the ambient concentration a₀ to the trough density ${\rho }_{\text{min}}$ (Eq. 53), and the balance between attractant uptake $\mu {\rho }_{\text{min}}$ and drift/diffusion at the trough relates c and λ to ${\rho }_{\text{min}}$ and a_m.

Discussion

To reveal the underlying dynamics governing chemotaxis-driven population expansion, we analyzed the experimentally verified GE model mathematically (39). Following an extensive traveling-wave analysis we were able to describe the density and attractant profiles throughout the chemotaxis and growth regimes (Fig. 6 and Eqs. 13 and 37). We determined the expansion speed (Eq. 21) and the slope λ which specifies the width of the migrating band (Eq. 20).

Our results, which are in excellent agreement with numerical simulations for a broad range of model parameters tested (Figs. 2–6), recover many key experimentally observed relations of the expansion speed to biological and environmental parameters (39) that previous models based on the KS model had failed to capture (36, 37). Notably, while our model agrees with the KS model near the density bulge, with the same relation between expansion speed and the size of the peak ($c=\mu N_0/a_0$; Eq. 52), the size of the peak itself is not a constant as in the KS model but an emergent quantity. Consequently, the expansion speed depends on many of the model parameters.

First, the expansion speed depends on the ratio of the initial attractant concentration to the lower limit of attractant sensitivity (i.e., $c\propto \sqrt{a_0/a_m}$) for large carrying capacity. For finite carrying capacity our analysis predicts the nonmonotonic dependence of expansion speed with initial attractant concentration, providing an explanation for this long-known experimental observation (76): For lower attractant concentrations, increasing concentration increases the size of the bulge and hence promotes faster expansion. However, for higher concentrations, the carrying capacity limits the size of the bulge, and expansion speed decreases with increasing attractant concentration as it takes longer for the bulge to consume the attractant and establish a gradient (Eq. 24 and Fig. 4A).

Second, our results reveal a dependence of the expansion speed on the diffusion of the attractant (D_a; Fig. 2D). The effect of multiple diffusion coefficient-like parameters ($D_{\rho },{\chi }_0$, and D_a) is one of the reasons the GE model is difficult to analyze. In Cremer et al. (39), a scaling theory was developed to describe the dependence of the expansion speed on the chemotaxis coefficient χ₀. Assuming that χ₀ was the main relevant factor, the scaling theory predicted that $c\propto {\chi }_0$. Our analysis here reveal that $c\propto ({\chi }_0-D_{\rho })$ holds for large D_a but $c\propto \sqrt{{\chi }_0-D_{\rho }}$ for small D_a (Fig. 3).

The analytical understanding attained in this work quantitatively supports the role of chemotaxis in range expansion found by Cremer et al. (39). Particularly, bacterial chemotaxis does not necessarily occur to fulfill an immediate nutritional need, nor does it necessarily reflect an attempt to avoid starvation. For example, cells move chemotactically toward attractants they cannot metabolize and also swim in nutrient-replete conditions (23, 25, 39). Instead, chemotaxis could be hard-wired to promote the expansion of bacterial populations into unoccupied territories well before nutrients run out in the existing environment; low levels of attractants thus act as aroma-like cues that establish the direction of expansion and enhance the speed of population movement (39). Subsequently, cells left behind by the migrating band fully occupy the region behind the front by growing at rates determined by nutrient availability. This allows the population to expand rapidly into unoccupied territories while colonizing the traversed territories, without one compromising the other.

Our results also expand upon the general theory of front propagation into unstable states and reveal an alternative mechanism for speed selection. While many studies of front propagation involve modification of the nonlinear growth/reaction term in the original F-KPP equation (28, 78, 79), our model considers a drift term which is a functional of an environmental variable, the attractant concentration. Though the canonical results pertaining to the F-KPP equation are not expected to hold in such a two-variable system, the dynamics in the growth and diffusion regimes in our system are effectively described by the F-KPP equation. While the expansion of an F-KPP wave front pushed by the bulk (as in the diffusion regime) at rates higher than the stable Fisher speed has long been known (28, 54), our results demonstrate how F-KPP wave fronts can also be seeded by a transition regime at the front (as in the growth regime) to attain very large expansion speeds. Alternatively put, by following the chemotacting cells in the leading density bulge, the trailing region can propagate faster than predicted by F-KPP equation based on growth and diffusion alone.

Finally, we note that our analysis assumes a separation of timescales between growth (slow) and chemotactic migration (fast), i.e., $1/r\gg 1/\lambda c$, indicating that cell growth is negligible over the timescale at which the population migrates across the width of the density bulge given by $1/\lambda$. This condition is fulfilled for a broad parameter regime where the background attractant concentration is large ($a_0\gg a_m$) or when the chemotactic coefficient much exceeds the diffusion of the attractant (${\chi }_0-D_{\rho }\gg D_a$) (condition [22]). For the narrow parameter regime where condition [22] breaks down, e.g., when ${\chi }_0\to D_{\rho }$, the expansion speed approaches the stable Fisher speed c_F as it is the expected speed for a pulled wave solution determined by the asymptotic front (28) in the absence of a push from the bulk. This is supported by numerical data (SI Appendix, Fig. S3). A solution to the GE model that includes the small-χ₀ regime would provide an analytical connection to the F-KPP equation and thereby provide insight on the transition from the pushed and seeded dynamics observed when $r\ll \lambda c$ to the well-established pulled wave dynamics (28, 58, 80, 81).

Outlook

Beyond an analytical understanding of the interplay between chemotaxis, growth, and diffusion in the case of migrating bands of E. coli in soft agar [for which Cremer et al. (39) had previously established the experimental validity of the GE model], the mathematical relations obtained here offer testable predictions for settings that involve chemotaxis, growth, and diffusion independent of the specifics of the strain or the environment. First, we identify the parameter regime in which chemotaxis leads to a boost in the expansion speed (condition [22]). Outside of this regime, expansion of the population is governed by the F-KPP equation. Second, the formation of a distinct density bulge conforms to the same parameter regime (SI Appendix, section S9) and is thus also confirmed as an identifiable signature of boosted expansion for experiments and observations of bacteria in natural settings.

Quantitatively, we derive a relation between the expansion speed and the population profile in the density peak (Eq. 12) which only involves cellular motility parameters. Thus, the expansion speed can be inferred from just a snapshot of the density profile without requiring multiple measurements over an extended period of time (which can be difficult to do for bacteria outside the laboratory). Conversely, the cellular motility parameters can be inferred if measurements of the expansion speed and density profile are possible. Similarly, we derive a relation between the expansion speed and the trailing region (Eq. 51) which only involves the growth rate. We also connect the expansion speed to the chemoattractant flux generated by a source (Eq. 21). We thus provide a relation between population-level features and molecular/cellular level characteristics for chemotactic bacteria, analogous to what the solution of the F-KPP equation does for undirected motion (26–28). This relation provides an analytical framework for further studies of the effects of evolution (30) and phenotypic variability (5, 82–84) on the spread of the population.

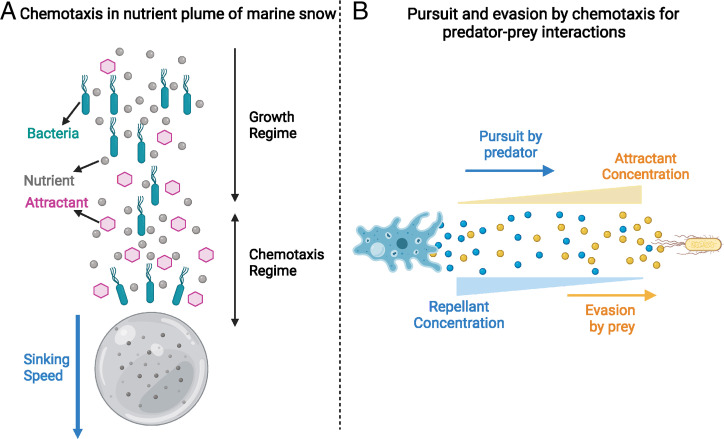
Our results may also be extended beyond expanding bacterial populations in culture plates. Fig. 8A shows an illustration of particulate organic matter, also known as marine snow, which sinks steadily in the ocean (85, 86). Nutrients and attractants generated from metabolic processes on such particles could sustain the growth of bacterial population chasing the sinking particle (87–89). To understand the resultant population distribution, the framework of the present study needs to be further extended to include nutrient and attractant generation, uptake, and diffusion on and near the particles (88, 90).

Fig. 8.

Illustrations of possible extensions of our analysis. (A) Chemotaxis in marine bacteria in the plume of sinking marine particles. The gray bead is the sinking particulate organic matter. A flux of nutrients (gray circles) and attractants (pink hexagons) diffuse into the wake of the particle. The cyan motile bacteria are able to direct their motion up the attractant gradient and thus move toward the sinking particle and keep up with it. (B) Chemotaxis in pursuit–evasion dynamics in a predator–prey system. A predator (shown as a blue amoeba) may pursue gradients of chemicals (attractant; yellow beads) left by a motile prey (a yellow bacterial cell). The motile prey may, in turn, evade the predator by performing chemotaxis and moving away from chemicals (repellent; blue beads) secreted by the predator.

More generally, the biological processes underlying chemotaxis-driven population expansion, sensing, directed movement, and the modification of the environment (as accomplished by uptake of attractant by chemotactic bacteria) are not limited to bacteria and have been reported for eukaryotic cells and higher-order organisms (15, 43). Directed movement may result from sensory cues as shown in nematodes (91) or as a consequence of area-restricted search as shown in beetles preying on aphids (92). The framework developed here may thus be employed to understand the GE dynamics of different organisms in diverse biological scenarios such as the spread of invasive species into a novel habitat (55–57, 93), the movement of cells and cell collectives during development in fruit flies and chickens (16, 94), or cancer metastasis in zebrafish and mammalian cells (19). Using this framework, we may understand the spatiotemporal dynamics of diverse ecological interactions between different species, such as predator–prey interactions where each species can direct their motion toward or away from each other, with the other species (or secretions by each species) playing the role of attractant or repellent (95) (Fig. 8B). The analysis of directed motion at the population level has largely been neglected in favor of the F-KPP dynamics (96) due to the immense body of knowledge developed for undirected motion (26–28). The mathematical understanding developed here presents a convenient framework to study directed population dynamics which has previously lacked analytical tools.

Materials and Methods

To generate all of the numerical results, finite element simulations of the system of equations were performed using FEniCS, a computing platform for solving partial differential equations (68, 69). A one-dimensional mesh of resolution 15 to 50 $\mathrm{\mu }$m was used to simulate a moving window of 30 mm (or 120 mm for very fast fronts). Finite elements of ${\mathcal{P}}_3{\mathrm{\Lambda }}^0$ type were used.

The initial bacterial density was specified with $\rho (x,t)=(\tanh ((1-x^2))+1)\times 0.029/2$ in order to initiate a sufficiently localized initial population with a differentiable functional form. The initial attractant concentration was specified to be constant everywhere. Neumann boundary conditions of zero flux were specified on both ends of the simulation domain. A difference equation was then solved to approximate the differential equation in time using a small time step (typically between 2 and 25 s). The resulting solutions were recorded and used for the subsequent iteration of the difference equation.

In order to obtain high spatial and temporal resolutions simultaneously, a moving window technique was utilized. In the moving window technique, only a 30-mm (or 120-mm for very fast fronts) interval was simulated at a time. However, when the front of the wave had gone beyond a certain threshold in the simulation domain, the simulation domain was translated to the right, and the attractant concentrations and bacterial densities were extrapolated for the sections of the new simulation domain for which the values were not previously known. This technique holds very well as long as a threshold sufficiently far from the right end of the domain is chosen (this is also desirable to ignore edge effects) such that the linear extrapolation is correct within numerical resolution.

To analyze the simulations and extract the expansion speeds, the position of the maximum drift velocity was recorded for each time step. A linear fit over time was then employed for the position to obtain the expansion speed. Only fits with a small enough sum of residuals were considered. The fits were also curated manually to ensure that the expansion speed was calculated using a period of steady and constant expansion.

Data Availability

Data and code are made available in GitHub at https://github.com/avaneeshnarla/chemotaxis-traveling-wave. All other study data are included in the article and/or SI Appendix.