A Practical Introduction to Bayesian Estimation of Causal Effects: Parametric and Nonparametric Approaches

Summary

Substantial advances in Bayesian methods for causal inference have been made in recent years. We provide an introduction to Bayesian inference for causal effects for practicing statisticians who have some familiarity with Bayesian models and would like an overview of what it can add to causal estimation in practical settings. In the paper, we demonstrate how priors can induce shrinkage and sparsity in parametric models and be used to perform probabilistic sensitivity analyses around causal assumptions. We provide an overview of nonparametric Bayesian estimation and survey their applications in the causal inference literature. Inference in the point-treatment and time-varying treatment settings are considered. For the latter, we explore both static and dynamic treatment regimes. Throughout, we illustrate implementation using off-the-shelf open source software. We hope to leave the reader with implementation-level knowledge of Bayesian causal inference using both parametric and nonparametric models. All synthetic examples and code used in the paper are publicly available on a companion GitHub repository.

1 |. INTRODUCTION

Causal inference is broadly concerned with estimating parameters governing the causal mechanisms between an intervention or treatment of interest and an outcome. These causal parameters can differ substantially from associational ones. Causal inference provides a framework for 1) constructing different estimands that have explicitly causal, rather than associational, interpretations 2) formulating the assumptions under which we can estimate these using observed data, 3) devising sensitivity analyses around violations of these assumptions, and 4) making inferences about these causal estimands via statistical modeling. These are just some of the many contributions of the causal inference literature, which we will touch on throughout this paper.

Bayesian modeling in causal inference has been growing in popularity. There are perhaps several reasons for this phenomenon. First, Bayesian modeling yields full posterior inference for any function of model parameters. For instance, point and interval estimates can be easily constructed for causal risk ratios, odds ratios, and risk differences by post-processing a single set of posterior draws from logistic regression model. Another advantage is the use of priors to induce shrinkage and sparsity in causal models - yielding more regularized causal effect estimates. We show that these can be more satisfying than the ad-hoc alternatives often employed. Priors can also be used to conduct probabilistic sensitivity analyses around violations of key causal identification assumptions. Finally, the Bayesian literature consists of a large suite of nonparametric models that can be readily applied to causal modeling. These nonparametric approaches are appealing because, unlike many classical machine learning algorithms, they allow for posterior uncertainty estimation as well as robust point estimates.

We begin with an overview of the causal identification and the Bayesian linear model before moving to confounder adjustment via standardization in the point-treatment setting. Here we highlight how priors can be used to induce shrinkage in a causal dose effect curve and partially pool conditional average treatment effect estimates across sparsely populated subgroups. Partial pooling shrinks the heterogeneous effects across subgroups towards an overall homogenous effect in the absence of data. We introduce the Bayesian bootstrap as a method for performing standardization. Next, we move to the time-varying treatment and confounding setting where we discuss Bayesian g-computation with priors that promote sparsity. Causal inference in these settings requires estimation of a large number of nuisance parameters. Priors that regularize these estimates by encouraging sparsity can be an attractive alternative to common modeling assumptions, which can be quite strict. Estimation for both static and dynamic treatment regimes are discussed. We then turn to using priors for causal sensitivity analyses. These follow from expressing violations of causal assumptions in terms of non-identifiable parameters, then conveying uncertainty about the magnitude/direction of the violation via priors on these parameters. We end with a discussion of Bayesian nonparametric causal estimation. We discuss Dirichlet process priors, Bayesian Additive Regression Trees, Gaussian processes and survey their applications to causal problems. Throughout, we present several pedagogical examples using publicly available synthetic data. We hope to demonstrate how readily these models can be implemented using existing software. A companion GitHub³ repository contains all relevant implementation code that reproduce the results in this paper.

2 |. INGREDIENTS OF BAYESIAN CAUSAL INFERENCE

2.1 |. Causal Estimands and Identification Assumptions

In order to make causal inferences, we first need to define and identify the causal estimand. After doing so, we will turn to the statistical problem of actually making inferences about this estimand. Consider estimation of the causal effect of a binary treatment assignment A ∈ {0, 1} on some observed scalar outcome Y. In this paper, we formulate estimands in terms of potential outcome Y^a1. This represents the outcome that would have been observed had a subject received treatment A = a. For subjects receiving treatment A = a, we never observe their counterfactual outcome, Y^1−a. If we did observe both potential outcomes, we could estimate each subject’s individual-level effects by taking the difference Y¹ − Y⁰. This is the difference in outcome had the subject taken treatment 1 versus 0. We could also estimate a population-level average treatment effect (ATE), Ψ = E[Y ¹] − E[Y ⁰], directly by simply taking the sample average of the difference, Y¹ − Y⁰, across all subjects. The ATE is interpreted as the average difference in the outcome had everyone in the target population received treatment A = 1 rather than A = 0. In absence of the counterfactual, we cannot estimate the individual-level effects and can only estimate Ψ under certain identification assumptions (IAs).

To understand the role of these assumptions, it is helpful to consider the data we actually observe. Along with Y (note the lack of superscript) and A, we observe a vector of confounders L - these are variables, measured pre-treatment, that impact both treatment assignment and outcome. Thus, we could estimate the conditional outcome mean, or regression, E[Y | A, L] directly from observed data. The aforementioned identification assumptions are required to express Ψ - the difference in average unobserved potential outcomes - in terms of E[Y | A = 1, L] − E[Y | A = 0, L] - the average difference in conditional outcome means between the two treatment groups. Identification refers precisely to this process of expressing (“identifying”) estimands such as Ψ in terms of observed data. In this setting with a single baseline treatment, the standard IAs² are

• IA.1: Conditional ignorability: Y^a ⊥ A | L.

• IA.2: Consistency: P(Y^a = Y | A = a) = 1, ∀a.

• IA.3: No interference: $Y_i^{a_{1:n}}=Y_i^{a_i}$.

• IA.4: Positivity: $0<P(A=1\mid L)<1,\forall L\in \mathcal{L}$.

Above, a_1:n = (a₁, a₂, …, a_i, …, a_n) is a vector of treatment interventions for each of n observed subjects and $Y_i^{a_{1:n}}$ represents subject i’s potential outcome had each subject received their corresponding treatments in a_1:n. IA.1 requires that pre-treatment variables L fully capture the confounding between treatment and outcome. That is, conditioning on L renders the potential outcome under a particular treatment, Y^a, independent of the observed treatment assignment, A. This can be violated if, for instance, we fail to condition on some confounder, such as age, when in fact older subjects tend to be treated with treatment A = 1 and are likely to have worse outcomes under this treatment, Y¹. It is important to note that conditioning on inappropriate variables (e.g. colliders or post-treatment variables) may also lead to ignorability violations³. In this paper, we will discuss ways to perform sensitivity analyses around violations of this assumption.

Consistency, IA.2, requires that the treatment be well-defined in terms of a clear intervention⁴. For example, suppose A is high/low blood pressure and Y is myocardial infarction. The outcome that occurs in a world where we intervene directly to lower blood pressure is likely not the outcome that would have occurred had everyone in the population had low blood pressure. This is because the mechanism by which we set blood pressure likely itself affects the outcome. Whether blood pressured was lowered via changes in lifestyle (exercise, better eating habits, etc) versus medication probably impacts the outcome. For this reason, consistency is often described as requiring that there is only “one version” of the treatment. A more well-defined intervention may be blood pressure medication use (versus no use). Other canonical examples of ill-defined exposures include race and BMI⁵.

IA.3 states that no subject’s treatment assignment should affect another’s potential outcome. Formally, the i^tℎ subject’s potential outcome under intervention $A_i=a,Y_i^{a_i}$, need not be indexed by the other n − 1 subjects’ interventions in the superscript. Hence, we can simplify $Y_i^{a_{1:n}}$ to just $Y_i^{a_i}$. This assumption is often violated if subjects are not independent. For example, a study of the effect of prophylactic antivirals on infection using data from patients in the same hospital may suffer from interference: the antiviral treatment of subjects roomed together affect each other’s infection probability. For concreteness, consider two such patients, i and j, with potential infection status, $Y_i^{a_i,a_j}$ and $Y_j^{a_i,a_j}$, respectively. Here, intervention a = 1 indicates antiviral therapy and a = 0 indicates control. If the infection is contagious, it may be the case that $P\left(Y_i^{0,1}\right)<P\left(Y_i^{0,0}\right)$. Even if subject i is untreated, their infection probability would likely be lower had their neighbor, subject j, been treated. Since we cannot speak of subject i’s outcome separately from subject j’s treatment, we cannot drop a_j from the superscript in $Y_i^{a_i,a_j}$. Causal inference in these settings is more complicated and an active area of research⁶.

Finally, IA.4 requires that the treatment probability be bounded so that there is no subset of the population in terms of L for whom treatment is deterministic. Intuitively, if treatment assignment was deterministic for a subpopulation of individuals, we would have no data about that group’s outcome under the other treatment condition. Positivity violations can occur at the population level (e.g. protocols forbidding treatment a for subjects over a certain age) or at the sample level due to small sample size (e.g. we observe no male diabetics with treatment a). The former are sometimes called structural violations and the latter are called random violations of positivity in the literature.

Using these assumptions we can identify both expectations in Ψ. First, under IA.3, $E\left[Y_i^{a_{1:n}}\right]=E\left[Y_i^{a_i}\right]$. Omitting subscripts for compactness,

$$\begin{gathered} E\left[Y^a\right]=\underset{\mathcal{L}}{\int }E\left[Y^a\mid L\right]dP(L) \\ =\underset{\mathcal{L}}{\int }E\left[Y^a\mid A=a,L\right]dP(L) \\ =\underset{\mathcal{L}}{\int }E[Y\mid A=a,L]dP(L) \end{gathered}$$ (1)

The first equality follows from iterated expectation over L. We use $\mathcal{L}$ to denote the space of L. From IA.1, we know that the potential outcome is independent of assignment conditional on L, which allows us to condition on A = a in the second equality. IA.4 ensures that we are not conditioning on a zero-probability event. Lastly, IA.2 allows us to drop the superscript. Intuitively, (1) identifies the average potential outcome as a regression model (under intervention A = a) that is averaged over the marginal confounder distribution. Computing marginal causal effect using this expression is called standardization. In this way, we have identified each term of Ψ in terms a regression that is estimable from observed data.

2.2 |. Statistical Assumptions

Equation (1) usually requires statistical/modeling assumptions about the regression, E[Y | A, L]. As an example, consider substituting a linear regression model E[Y | A, L] = θA + L′β (where an intercept is included in L). Then, under the IAs, standardization yields

$$\begin{gathered} \Psi =\underset{\mathcal{L}}{\int }E[Y\mid A=1,L,\omega ]-E[Y\mid A=0,L,\omega ]dP(L) \\ =\underset{\mathcal{L}}{\int }\left\{\left(\theta +L_i^{\prime }\beta \right)-\left(L_i^{\prime }\beta \right)\right\}dP(L)=\theta . \end{gathered}$$ (2)

In this special case, the ATE, Ψ, is equal to the treatment indicator coefficient, θ. Thus, an estimate of this coefficient is an estimate of the ATE. In the non-linear examples discussed later, $L_i^{\prime }\beta$ will not cancel out as it did above and a probability model for p(L) will be necessary to evaluate the integral.

2.3 |. Bayesian Modeling

Bayesian causal inference combines Bayesian modeling with the IAs discussed to compute a posterior distribution over causal estimands. In this section we introduce these key ideas, which will be expanded in future sections. Throughout much of the paper, we assume that IAs hold to keep focus on the added benefit of Bayesian modeling.

Suppose we observe data D = {Y_i, A_i, L_i}_i=1:n on n independent subjects, where A_i ∈ {0, 1} is abinary treatment indicator, L_i is a vector of confounders (including an intercept), and Y_i is the scalar outcome of interest, as defined earlier. Bayesian inference requires both a probability model for the conditional distribution of the outcome, Y, (a likelihood) as well as a probability distribution over the unknown parameter vector, ω, governing this conditional distribution (i.e. a prior). Inference then follows from making probability statements about ω having conditioned on D (via the posterior). From Bayes’ rule we have that the posterior is proportional to the likelihood times the prior, $p(\omega \mid D)\propto p(\omega )\prod _{i}p\left(Y_i\mid A_i,L_i,\omega \right)$.

For instance, if Y_i is real-valued, we could specify a Gaussian outcome model with conditional mean $\theta A_i+L_i^{\prime }\beta$ and variance $\varphi :p\left(Y_i\mid A_i,L_i,\omega \right)=N\left(Y_i\mid \theta A_i+L_i^{\prime }\beta ,\varphi \right)$. We could also set a Normal-Inverse-Gamma prior on the parameter vector ω = (θ, β, ϕ), e.g. p(ω) = N(θ | 0, 1)N(β | μ₀, Σ₀)IG(ϕ | a₀, b₀). This probability model induces a linear regression $E[Y|A_i,L_i]=\theta A_i+L_i^{\prime }\beta$, where we drop explicit conditioning on the parameters. Now it remains to find the posterior over the model parameters, p(ω | D) - which includes θ. As we showed with the linear model in the previous section, the coefficient θ is the ATE, Ψ. So a posterior over θ is a posterior over Ψ. This simple example demonstrates a general Bayesian approach to causal inference.First, identify the causal parameter of interest as a transformation of the model parameters.The IAs required to achieve this will vary by problem and strategy. Mediation⁷ and time-varying treatment⁸ settings will require extensions of the IAs discussed. Instrumental variables⁹, difference-in-differences¹⁰, and regression discontinuity¹¹ strategies all involve their own unique IAs. Second, obtain the posterior distribution (or draws from it) of these model parameters which, after transformation, yields a posterior over the causal estimand.

In practical settings, the posterior distribution, p(ω | D) does not have known form - so that we cannot analytically find the posterior after specifying the likelihood and prior. As a result, inference is instead typically conducted using draws from the posterior obtained via Markov Chain Monte Carlo (MCMC). Though a crucial topic and active area of research in itself, we omit discussion of MCMC methods and keep focus on Bayesian estimation of causal effects. We refer the reader to Andrieu et al.¹² for an introduction to MCMC. For our purposes, it is enough to know that MCMC yields a set of M draws, {ω^(m)}_1:M, from the posterior p(ω | D) given a specified likelihood and prior. Throughout, we assume we have sufficiently many draws to closely approximate the posterior. The mean or median of these samples can be used as a Bayesian point estimate of ω. Percentiles of these draws can be used for credible interval estimation (e.g. .025 and .975 percentiles for a 95% interval).

This paper relies mainly on Stan for MCMC sampling throughout. Stan is an open-source programming language for specifying Bayesian models using intuitive syntax. It back-ends to C++ to efficiently obtain posterior draws after a likelihood and prior are specified. Stan programs are often called in R via the package rstan. For those unfamiliar with Stan and R, we provide some guidance with SAS version 9.4 - a popular commercial statistical analysis software. Some of the nonparametric models to be discussed cannot be handled in either Stan or SAS. For these models, we will rely on specialized R packages.

2.4 |. Prior Information

As mentioned earlier, Bayesian inference requires specification of a prior over the parameters, p(ω). Throughout this paper we hope to illustrate that, rather than anchoring estimates to particular hard-coded values, priors can induce intricate correlation structures between parameters. These correlation structures stabilize causal effect estimates when data are sparse (as it often is in scientific applications). This is often referred to as “shrinkage”. Priors can also be used to induce “sparsity” on whole parameter vectors. Specifically, for high-dimensional vectors, we can place priors that express the belief that some portion of the vectors are nearly zero. Priors can also be used to conduct probabilistic sensitivity analyses around causal identification assumptions. All of these are pragmatic motivations for taking a Bayesian approach to causal estimation, even if one is not a Bayesian “at heart”. We will emphasize that, perhaps contrary to intuition, common frequentist approaches can often be seen as special cases of these Bayesian estimators with very rigid priors.

3 |. PARAMETRIC MODELS IN POINT-TREATMENT SETTINGS

In the following sections, we outline two examples where a Bayesian approach to causal inference offers unique benefits in the form of prior shrinkage. Although these examples use relatively simple parametric models, they reflect the general approach and intuition of Bayesian causal inference and help motivate key tools such as the Bayesian bootstrap.

3.1 |. Causal Dose Effects with AR1 Prior

Consider a setting where treatment consists of K dose levels A_i ∈ {0, 1, …, K}, with A_i = 0 indicating no treatment. Let A_ik = I(A_i = k) be an indicator that subject i was assigned to dose k ∈ {1, …, K}. Here, we assume the dose values are ordered so that they are increasing with k. That is, dose k + 1 is higher than dose k. Consider a linear outcome model,

$$E\left[Y_i\mid A,L_i\right]={\theta }_0+L_i^{\prime }\beta +\sum _{k=1}^K{\theta }_k{A}_{ik}.$$ (3)

Suppose our estimand of interest is a causal incremental dose effect curve on Ψ(k) = E[Y^A=k] − E[Y^A=k−1]. This is a curve as a function of dose, k. Each point on the curve is the causal effect of increasing dose from level k − 1 to level k. Under mild extensions of IA.1–IA.4 from the binary treatment setting to the multi-treatment setting we can again identify this estimand as

$$\Psi (k)={\theta }_k-{\theta }_{k-1}k\in \{2,\dots ,K\}$$

Where the first point is Ψ(1) = θ₁. We consider several prior choices for θ_1:K and the induced prior on Ψ(k). Throughout, u_a:b for intergers a < b denotes the vector u = (u_a, …, u_b). A first-pass approach may be to express prior independence and factorize the joint prior as $p\left({\theta }_{1:K}\right)={\prod }_{k=1}^{K}p\left({\theta }_k\right)$. We could specify each term to be Gaussian centered at some prior mean, μ_k, and standard deviation, τ_k. However, we can formulate more useful priors in this setting. The increasing dose levels may give us prior reason to believe that the effect of neighboring doses are actually correlated, not fully independent. This motivates an alternative (dependent) prior factorization: $p\left({\theta }_{1:K}\right)=p\left({\theta }_1\right)p\left({\theta }_2\mid {\theta }_1\right){\prod }_{k=3}^{K}p\left({\theta }_k\mid {\theta }_{K-1},{\theta }_{K-2}\right)$. Each term is specified as

$${\theta }_1~N\left({\mu }_1,{\tau }_1\right)$$

$${\theta }_2\mid {\theta }_1~N\left(2{\theta }_1,{\tau }_2\right)$$

$${\theta }_k\mid {\theta }_{k-1},{\theta }_{k-2}~N\left(2{\theta }_{k-1}-{\theta }_{k-2},{\tau }_k\right),k>2,$$

where μ₁, τ_1:K are all hyperparameters that we can specify. Alternatively, we could specify hyperpriors for these parameters. The above induces the following first-order autoregressive (AR1) prior on the causal curve, Ψ(k). For instance, the last line for k > 2 above implies that θ_k − θ_k−1 | θ_k−1, θ_k−2 ~ N(θ_k−1 − θ_k−2, τ_k). This follows from simply subtracting θ_k−1 from θ_k and its mean. Using the definition of Ψ(k), we see that this statement is equivalent to Ψ(k) | θ_k−1, θ_k−2 ~ N(Ψ(k − 1), τ_k). Extending this logic, the hierarchical prior on θs induces the following prior on the Ψs

$$\begin{gathered} \Psi (1)~N\left({\mu }_1,{\tau }_1\right) \\ \Psi (k)\mid \Psi (k-1)~N\left(\Psi (k-1),{\tau }_k\right),k>1 \end{gathered}$$ (4)

This expresses the prior belief that the response from increasing dose to the next level should not be too different from the response due to the previous dose level. That is, neighboring points on the curve are related. Of course, if we have data suggesting otherwise, the data will drive our posterior inference away from this prior. However, in the absence of data, this provides valuable shrinkage back towards a sensible prior belief. An example using synthetic data is presented in Figure 1a with posterior sampling done in Stan¹³. Implementation details along with a more thorough walkthrough using this synthetic data set are available in Appendix A. Implementation via PROC MCMC in SAS is also discussed. Notice in the figure that small sample sizes at each dose level lead to erratic MLE estimates. In contrast, the Bayesian estimate with the AR1 prior produces a smoother curve. In dose level 8, we only have three observations. Thus, the Bayes estimate is aggresively shrunk towards the estimate at dose 7.

FIGURE 1.

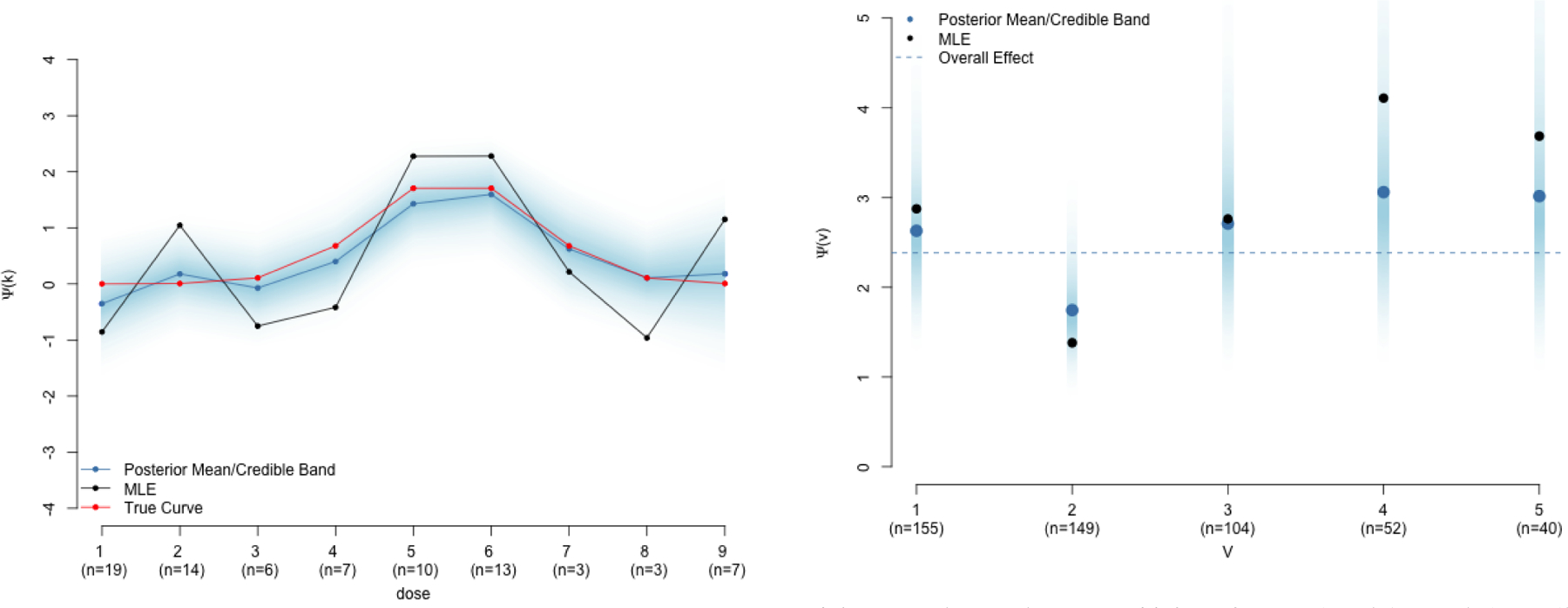
Estimates of dose effect curve (Section 3.1) and partially pooled conditional causal odds ratios (Section 3.2) using synthetic data.

(a) Posterior estimates from (3) with prior (4) with K = 10, μ₁ = 0, τ₁ = 10, and τ_k = 1 for all k. The AR1 prior smooths erratic MLEs by inducing correlation between neighboring points on the curve.

(b) Posterior estimates of Ψ(v) from (6) with partial pooling prior of Section 3.2 with q = 5, a single confounder W, an improper uniform prior on μ, and τ = .5. Posterior mean odds ratio for each stratum are shrunk towards the overall causal odds ratio (dotted line).

A common heuristic solution to this issue of decreasing sample size with increasing dose is to fully pool patients at, say, dose K and K − 1 and estimate a single effect for both rather than allowing separate effects. The prior in (4) is a compromise between these two extremes. Recall from (4) that Ψ(K) | Ψ(K − 1) ~ N(Ψ(K − 1), τ_K) for K > 1. Now notice that the heuristic alternative of combining groups K and K − 1 corresponds to the strong prior belief that τ_K ≈ 0. That is, the causal effect at dose K is a point-mass distribution at Ψ(K − 1): Ψ(K) | Ψ(K − 1) ~ δ_Ψ(K−1).

3.2 |. Partial Pooling of Conditional Causal Effects

Here we consider a more involved model for causal estimation using a logistic regression with binary outcome and treatment. Here, the mean function E[Y | A, L] is related to the covariates L through a (non-linear) logit link with inverse logit denoted by σ{·}. Thus, the integration over L in (1) must be evaluated explicitly. Consider some q–dimensional subset of pre-treatment covariates, V ⊂ L. Let W = L \ V be the set difference so that L = {W, V}. One target estimand of interest in this setting is a causal odds ratio at each level of V

$$\Psi (v)=\frac{E\left[Y^1\mid V=v\right]/\left(1-E\left[Y^1\mid V=v\right]\right)}{E\left[Y^0\mid V=v\right]/\left(1-E\left[Y^0\mid V=v\right]\right)}$$ (5)

Causally, this is contrasting the odds of the outcome had everyone in stratum V = v taken treatment 1 versus treatment 0. Since we allow for different treatment effects for each level of v, sometimes the set of Ψ(v) is referred to as a heterogenous treatment effects or conditional treatment effects (i.e. conditional on V = v). Under extensions of IA.1 – IA.4, each conditional expectation in Ψ(v) is identified as $E\left[Y^a\mid V=v\right]={\int }_{\mathcal{W}}E[Y\mid a,V=v,W]d{P}_v(W)$. Where P_v(W) = P(W | V = v) is the confounder distribution within stratum v. Note that this is just (1) conditional on V = v. The regression model is

$$E[Y\mid A=a,V,W]=\sigma \left\{{\beta }_w^{\prime }W+{\beta }_v^{\prime }V+\left({\theta }_0+{\theta }_{1:q}^{\prime }V\right)A\right\}$$ (6)

Above, we include an intercept in W. Note that the treatment effect, ${\theta }_0+{\theta }_{1:q}^{\prime }V$, varies with levels of V. We defer discussion of the integration over W to Section 3.3. For concreteness, suppose V is a vector of indicators for q = 4 race/ethnicity categories: Black, Asian, Hispanic, Native American, and White as reference. Often some categories (e.g. Hispanic, Asian, Native American) are sparse. In these settings, it is common to combine these categories into “Other” and estimate a single odds ratio for these subjects. It is also common to simply exclude these subjects and not compute causal effects for these strata at all. Neither of these may be desirable and, again, carefully formulated priors can help us strike a balance when estimating conditional causal effects. For instance, consider the prior assumption that all of these conditional (we have not marginalized over W yet) effects within race category (θ₀, θ₀ + θ₁, …, θ₀ + θ₄) are normally distributed around some “overal” treatment effect μ with standard deviation τ. We can achieve this by specifying a Gaussian prior for the conditional effect in the reference stratum θ₀ ~ N(μ, τ). For the conditional effect in stratum V = 1, we specify θ₀ + θ₁ ~ N(μ, τ). This is the same as saying θ₁ ~ N(μ − θ₀, τ). Following this logic for the other strata, the joint prior over all parameters is

$$p\left({\theta }_{0:4}\mid \mu ,\tau \right)=N\left({\theta }_0\mid \mu ,\tau \right)\prod _{j=1}^{4}N\left({\theta }_j\mid \mu -{\theta }_0,\tau \right)$$ (7)

For categories with many observations, the posterior of the conditional effects with race category will be driven mostly by data. However, for small categories, each conditional effect shrinks to the overall average across race values, μ. The hyperparameter τ controls how aggressively we shrink these conditional effects to the overall average. This allows us to estimate regularized race-specific causal effects rather than abandoning the task altogether or resorting to ad-hoc groupings of categories. Priors for μ, τ, and the other regression coefficients must be specified. Standard guidance¹⁴ can be followed when specifying priors on these nuisance parameters. Similar to the dose effect example, the heuristic approach of fully pooling sparsely populated race clusters corresponds to a rigid prior. In this case, a prior belief that the conditional effect in all the pooled strata are the same.

3.3 |. Standardization via Bayesian Bootstrap

To compute conditional causal effects in (5), we must integrate the logistic regression in the previous example over P_v(W). As shown earlier, factors involving W would cancel out in a linear model - obviating the need for explicit integration. Here, due to the non-collapsability of the logit link, W does not cancel. To compute this integral, we need an estimate of P_v(W) over which to integrate. Let S_v = {i : V_i = v} be the set of indices of subjects in stratum V = v. There are n_v subjects in stratum v, so that the size of S_v is n_v. A frequentist nonparametric approach would be to estimate the distribution empirically as ${\widehat{P}}_v(w)=\frac{1}{n_v}{\sum }_{j\in S_v}{\delta }_{W_j}(w)$, where ${\delta }_{W_j}(\cdot )$ is the degenerate distribution at W_j. This places probability mass 1/n_v on each of the n_v subjects in stratum v. This yields average potential outcome estimate

$$E\left[Y^a\mid V=v\right]\approx \frac{1}{n_v}\sum _{j\in S_v}E\left[Y\mid A=a,V=v,W=W_j\right]$$

in stratum v. This is ideal in the sense that we impose no parametric model on the conditional distribution of W, but is unsatisfactory from a Bayesian point of view because it ignores the uncertainty in the empirical estimate. This motivates the Bayesian bootstrap (BB)¹⁵. The BB begins with a model for W, $P_v(w)={{\sum }_{j\in S_v}p}_{vj}\cdot {\delta }_{W_j}(w)$. We store all the weights in this stratum in an n_v–dimensional vector p_v = {p_vj : j ∈ S_v}.This weight vector p_v live in a simplex $p_v\in \left\{{ℝ}^{n_v}:p_{vj}>0\forall j\text{and}{{\sum }_{j\in S_v}p}_{vj}=1\right\}$. Rather than fixing p_vj = 1/n_v, the BB treats the weights as unknown with a flat Dirichlet prior $p_v~Dir\left(0_{n_v}\right)$, where $0_{n_v}$ is the n_v–dimensional vector of zeros. This yields the (conjugate) posterior $p_v\mid W~Dir\left(1_{n_v}\right)$, where $1_{n_v}$ is the n_v–dimensional vector of ones. The BB makes minimal assumptions about the confounder distribution within each stratum: note the posterior mean of each weight is also 1/n_v (same as the frequentist approach), but allows uncertainty around this mean to flow through to the causal effect in that stratum.

The BB was applied to marginal ATE estimation using generalized linear models (GLMs) for the outcome by Wang et al.¹⁶. When computing a marginal ATE, the BB is used as a model for the marginal p(L) not the conditional p_v(W). In the outcome model, we no longer set V = v since V is included in L = {W, V}, which we integrate over. The BB model is now $P\left(l\mid p_{1:n}\right)={\sum }_{i=1}^n{p}_i{\delta }_{L_i}(l)$. Now we place a Dirichlet prior on the n-dimensional vector p_1:n rather than the n_v-dimensional vectors p_v. This marginal estimate will play a key role in the nonparametric estimation of Section 6.

Full posterior inference for the causal odds ratio (5) requires just a few additional steps after sampling. Suppose we obtain the m^tℎ draw of the parameters in (6), $\left\{{\beta }_w^{(m)},{\beta }_v^{(m)},{\theta }^{(m)},{\theta }_{1:q}^{(m)}\right\}$. Then, for each stratum v, we draw BB weights $p_v^{(m)}\mid W~Dir\left(1_{n_v}\right)$. Note that here $p_v^{(m)}$ denotes the collection $\left\{p_{vj}^{(m)}:j\in S_v\right\}$. Then, we do the following

1. Integrate under both interventions A ∈ {1, 0}:

   $${\mu }^{(m)}(a,v)=\sum _{j\in S_v}{p}_{vj}^{(m)}\sigma \left\{{\beta }_w^{\prime (m)}{W}_j+{\beta }_v^{\prime (m)}v+\left({\theta }^{(m)}+{\theta }_{1:q}^{\prime (m)}v\right)a\right\}$$
2. Compute Causal Effects for each v

   $${\Psi }^{(m)}(v)=\frac{{\mu }^{(m)}(1,v)/\left(1-{\mu }^{(m)}(1,v)\right)}{{\mu }^{(m)}(0,v)/\left(1-{\mu }^{(m)}(0,v)\right)}$$

Doing this for m = 1, …, M posterior parameter draws yields M draws from the posterior of the causal estimand: {Ψ^(m)(v)}_1:M for each v. These draws can be used for posterior inference. Figure 1b shows posterior estimates of Ψ(v) with the partial pooling prior in (7) using synthetic data. MCMC-based posterior inference was done using Stan. Notice that for strata V ∈ {4, 5}, we have relatively few observations. In these strata, the maximum likelihood estimate (MLE) is much higher than the others due to small sample variability. Thus, the Bayesian prior aggressively shrinks the posterior mean estimate away from MLE towards the overall effect. From a causal perspective, we can view this as shrinking the heterogenous treatment effects towards an overall treatment effect. Details of this synthetic data generation and implementation in both Stan and SAS are given in Appendix B. The latter relies on PROC MCMC for posterior sampling and PROC IML for the BB post-processing step.

4 |. TIME-VARYING TREATMENT AND CONFOUNDING

The previous sections focused on the point-treatment setting: estimating the causal effect of a single treatment administered at baseline while adjusting for a single set of pre-treatment parameters. In many applications, treatment decisions are made sequentially over time as a function of covariates measured after baseline. For example, consider a binary treatment setting where treatment at time t = 0, A₀, is assigned conditional on confounders, L₀, measured before A₀. The subsequent treatment, A₁, is assigned conditional on L₀, A₀, and L₁, where L₁ is measured between A₀ and A₁, temporally. After treatment, we observe a single outcome Y. Suppose we wish to estimate the causal ATE E[Y ^{(1, 1)} − Y ^{(0, 0)}] - the difference had everyone in the target population been always treated versus never treated. Note the potential outcomes here are indexed by a treatment vector, not scalar. In the literature this vector is often referred to as a “treatment regime” or “treatment policy”. In this section, we first discuss causal contrasts comparing outcomes that would have been realized under two different static treatment regimes while controlling for time-varying confounding. Static regimes are treatment vectors that are pre-set to fixed values in advance (e.g. always treated, never treated, alternating treatments). Afterwards, we discuss an extension to dynamic treatment regimes, where the treatment regime is set sequentially over time according to a pre-specified rule (e.g. treat at time point t if blood pressure at time t is lower than some threshold). We refer the reader to Daniel⁸ for a thorough tutorial on time-dependent confounding and modeling.

4.1 |. Comparing Static Treatment Regimes

Standard regression methods fail to properly adjust for the time-varying confounder in these settings. For instance, if we condition on L₁, then we adjust away A₀’s impact on Y that runs through L₁. However, L₁ is a confounder of A₁ and Y - so failing to adjust for it will also lead to bias. Now, generalizing to t = 0, …, T time points, under extensions of IA.1 – IA.4 to this sequential setting² we can identify each term of the causal contrast $\Psi =E\left[Y^{a_{0:T}}-Y^{a_{0:T}^{\prime }}\right]$ as

$$E\left[Y^{a_{0:T}}\right]=\underset{\mathcal{L}}{\int }E\left[Y\mid a_{0:T},L_{0:T}\right]\times \prod _{t=0}^{T}p\left(L_t\mid L_{0:t-1},a_{0:t-1}\right)d{L}_{0:T}$$ (8)

Where for t = 0, we define p(L₀ | L_0:−1,a_0:−1) = p(L₀). The expression above is known as the g-formula and the computation of the integral is referred to as g-computation - it is the multi-time point generalization of standardization in (1). Here we ignore the details of identification to focus on Bayesian modeling and computation.

In particular, note that the above requires integrating an outcome regression over the joint distribution of confounders, conditional on treatment regime a_0:T. The outcome regression here can be high-dimensional even in common data applications. If we have just two time-varying confounders and twelve (e.g. monthly) time points, the outcome model must condition on 36 variables. Similarly, each conditional confounder distribution must (usually) be modeled conditional on all previous values of L_t and A_t - another high-dimensional modeling task.

The sequential nature of treatment and confounder measurement can be visually depicted using a directed acyclic graph (DAG) in Figure 2a for T = 3 timepoints (for compactness). Notice L₂ is impacted by all previous confounder values (L₀ and L₁) and treatment values (A₀ and A₁). This is shown by arrows going into L₂. Similarly, the outcome is impacted by all past L and A values. To simplify this complexity, a Markovian assumption is commonly invoked. This assumes that each confounder distribution only depends on the previous confounder and treatment values, p(L_t | L_0:t−1, A_0:t−1) = p(L_t | L_t−1, A_t−1). A similar assumption may be used in the outcome model. This Markov-type assumption is depicted in Figure 2b, which is simply the DAG in 2a with all the gray arrows removed. After removing gray arrows, each variable is directly impacted only by variables in the preceding time point. In Figure 2b, for instance, once we know L₁ and A₁, we know the distribution of L₂. The history (A₀ and L₀) need not be considered since it only affects L₂ through L₁ and A₁. Thus, p(L₂ | L_0:1, A_0:1) = p(L₂ | L₁, A₁).

FIGURE 2.

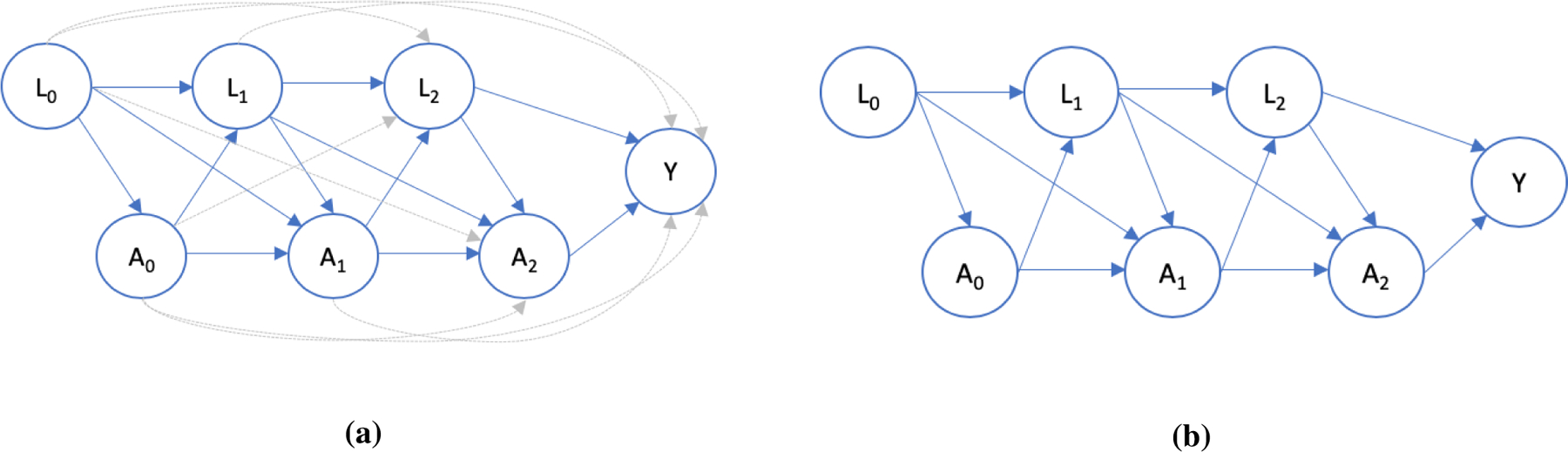
A directed acyclic graph (DAG) showing a time-varying treatment, A_t, time-varying confounder L_t, and outcome, Y, for three time points. In the first panel, treatment and confounding at each time point affects treatment and confounding in every future time point. The second panel depicts the Markov assumption described in Section 4.1 - confounders and treatment only impact variables in the next period so that p(L₂ | L_0:1, A_0:1) = p(L₂ | L₁, A₁). This is visually depicted by the deletion of the gray arrows in the first panel. Bayesian methods can help us strike a balance between these two extremes.

Neither of these extremes - conditioning on full history or invoking Markov - are completely desirable. Suppose L_t is an indicator of poor kidney function at day t. The Markov assumption presumes that two treated subjects with, say, poor kidney function on the previous day, L_t−1, have the same L_t distribution - even if one patient had poor function everyday since t = 0 and the other had good function until day t − 1. This seems unrealistic. On the other hand, it may also be unrealistic to say that kidney function on day 1, L₁, would directly impact function on, say, day 100, L₁₀₀. In the Bayesian paradigm, we can devise priors that balance these two extremes of either conditioning only on previous time period’s values versus conditioning on the entire past history. The general idea is to condition on the full history, but express a prior belief that values closer in time to the present have relatively more direct impact on the present. Conversely, values further back in time have small, if any, direct effect.

To continue this example, consider a simple setting where L_t is a continuous measure of kidney function and the outcome is viral load, with the treatment, A_t ∈ {0, 1} being anti-viral therapy at time t. Lower viral load is desirable, but comes at the expense of nephrotoxicity. So, depending on previous treatment, if the patient shows poor kidney function as measured by L, the physician may alter their treatment. To evaluate (8), we will need an outcome regression and a sequence of conditional confounder models. Consider a linear outcome regression $E\left[Y\mid A_{0:T},L_0:T\right]=\gamma +L_{0:T}^{\prime }{\beta }_Y+A_{0:T}^{\prime }{\theta }_Y$ and a Gaussian conditional model for L_t with conditional mean

$${\mu }_{L_t}\left(L_{0:t-1},A_{0:t-1}\right)=\beta +L_{0:t-1}^{\prime }{\beta }_L+A_{0:t-1}^{\prime }\theta ,$$ (9)

where β_L = (β₀, β₁, β₂, …, β_t−1) and θ are length t parameter vectors. We note that these parameters should be indexed by t (e.g. ${\beta }_L^t$) as each conditional distribution should be allowed to have their own effects, but we omit this indexing for compactness. We consider the following prior on each element of β_L

$${\beta }_{t-k}~N\left(0,{\tau }_k\varphi \right), k\in \{1,\dots ,t\}.$$ (10)

An identical prior can be used for θ. Consider the specification τ_k = (1/λ^k) for some λ > 1. This corresponds to what is often referred to as a ridge penalty in the machine learning literature. However, it differs from the standard ridge regression in that we do not apply the same penalty to all coefficients. Rather, the penalty gets increasingly aggressive for coefficients going farther back in time. For instance, for λ = 2, the prior standard deviation around 0 is halved every step backward in time, providing increasingly aggressive prior shrinkage towards 0. This implies a strong prior belief that recent confounder values are more likely to influence the present than values farther in the past. Note that the Markov assumption follows from a special (strongly informative) case of this prior, where β_t−k ~ δ₀ for k > 1: all coefficients but β_t−1 follow a point-mass distribution at 0. An example of the prior in (10) is provided in Figure 3a with T = 9. The plot shows the coefficients of β_L in the model ${\mu }_{L_9}$ getting increasingly penalized. Note that the posterior estimate of β₁ is able to break away from this prior to detect a signal (a truly non-zero coefficient value), even though it is farther in the past. However, at time point 0 the posterior estimate β₀ is strongly shrunk to zero (relative to the MLE).

FIGURE 3.

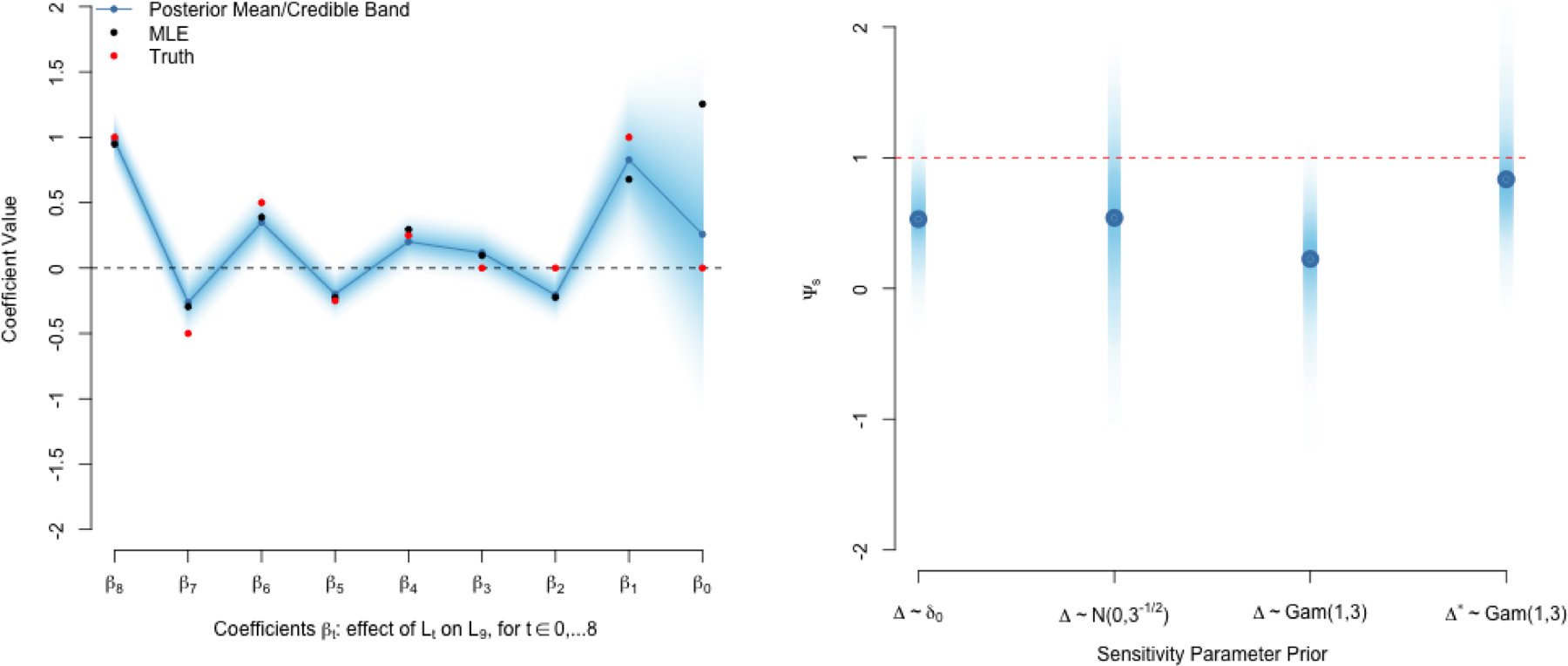
Example of g-computation on synthetic data with 10 time points, single time-varying treatment and confounder. The ridge prior in (10) was used along with Gaussian outcome and conditional confounder models.

(a) Plot of coefficient estimates from (9) with t=9. Each coefficient on the x-axis is the effect of L_t on L₉ for time points t = 0, …, 8. Note aggressive shrinkage of β₀ but ability to detect signal in the past at β₁.

(b) Sensitivity analysis of Section 5. Posterior Distribution of Ψ_s = Ψ − Δ under various priors for for Δ. Red line indicates true value.

The Bayesian literature has explored several such “sparsity” priors, including the horseshoe¹⁷, LASSO, and spike-and-slab priors¹⁸ - all of which could be applied to g-computation. These priors can all be characterized by their ability to both shrink noise, while being able to break away from the prior to detect signals¹⁷. For instance, a horseshoe type prior on the components of β_L can be specified by placing half-Cauchy hyper-priors on τ_k and ϕ in (10):

$$\begin{gathered} {\tau }_k~C^{+}\left(0,1/2^k\right) \\ \varphi ~C^{+}(0,v) \end{gathered}$$

where ν is a specified scale parameter that controls overall shrinkage across time. Similar to the ridge-type prior, the scale on the distribution of τ_k is halved every step backward in time.

The integration in (8) can be done via Monte Carlo after obtaining MCMC draws from the posterior of all the parameters governing the conditional confounder and outcome distributions. Conditional on these draws, we can simulate confounder values from these distributions and take the average of our regression model over these simulated values. Let ${\omega }_y^{(m)}$ denote the m^tℎ draw of the parameter vector governing the regression in (8). Similarly, denote the parameter vector governing each conditional confounder distribution p(L_t | L_0:t−1, a_0:t−1) by ${\omega }_{L_t}^{(m)}$. For instance, these would include draws of the regression parameters β, β_L, θ in (9) along with the Gaussian variance parameter. In the viral load example discussed earlier, ${\omega }_y^{(m)}$ would consist of ${\omega }_y^{(m)}=\left({\gamma }^{(m)},{\beta }_Y^{(m)},{\theta }_Y^{(m)}\right)$

To compute the causal ATE $\Psi =E\left[Y^{a_{0:T}}-Y^{a_{0:T}^{\prime }}\right]$ of regime a_0:T versus $a_{0:T}^{\prime }$, with each posterior draw of ${\omega }_Y^{(m)}$ and ${\omega }_{L_t}^{(m)}$ we:

1. Draw confounders, for t ∈ 0…T sequentially

   $${\tilde{L}}_t~p\left(L_t\mid {\tilde{L}}_{0:t-1},a_{0:t-1},{\omega }_{L_t}^{(m)}\right)$$

   Denote these draws ${\tilde{L}}_{0:T}=\left({\tilde{L}}_0,{\tilde{L}}_1\dots ,{\tilde{L}}_T\right)$. Repeat this a total of B times to obtain ${\left\{{\tilde{L}}_{0:T}^{(b)}\right\}}_{1:B}=\left\{{\tilde{L}}_{0:T}^{(1)},{\tilde{L}}_{0:T}^{(2)},\dots {\tilde{L}}_{0:T}^{(B)}\right\}$
2. Integrate the outcome model E[Y | a_0:T, L_0:T] over ${\left\{{\tilde{L}}_{0:T}^{(b)}\right\}}_{1:B}$ conditional on current set of draws ${\omega }_y^{(m)}$, under both interventions. In the viral load example, this would be

   $$\begin{gathered} {\mu }^{(m)}\left(a_{0:T}\right)=\frac{1}{B}\sum _{b=1}^{B}E\left[Y\mid a_{0:T},{\tilde{L}}_{0:T}^{(b)},{\omega }_y^{(m)}\right] \\ =\frac{1}{B}\sum _{b=1}^B\left({\gamma }^{(m)}+{\tilde{L}}_{0:T}^{\prime (b)}{\beta }_Y^{(m)}+{\left(a_{0:T}\right)}^{\prime }{\theta }_Y^{(m)}\right) \end{gathered}$$

   Similarly, repeat Step 1 and 2 under $a_{0:T}^{\prime }$.
3. Compute Causal Contrast

   $${\Psi }^{(m)}={\mu }^{(m)}\left(a_{0:T}\right)-{\mu }^{(m)}\left(a_{0:T}^{\prime }\right)$$

This procedure yields M posterior draws of Ψ, which can be used to form posterior mean and credible intervals. This can also be implemented in Stan using the “generated quantities” block as demonstrated in the our code on GitHub. The number of draws B should be large so that the Monte Carlo error of the integration of (8) is sufficiently low. In general, analyses with more time points and time-varying confounders will require larger B. In practice, we can try running steps 1–3 for a single posterior draw (say, draw m), over successively larger B. Keeping track of each repetition, we can check at which point increasing B only marginally increases precision in the estimate of Ψ^(m). We can then set B to this value across all posterior draws. A nice feature of this Bayesian approach is that uncertainty about the confounder and outcome models at all time points naturally flows through to the posterior of Ψ or any other causal contrast. For instance, we could have computed posterior draws of causal ratio contrast $E\left[Y^{a_{0:T}}\right]/E\left[Y^{a_{0:T}^{\prime }}\right]$ in Step 3 as ${\mu }^{(m)}\left(a_{0:T}\right)/{\mu }^{(m)}\left(a_{0:T}^{\prime }\right)$. In contrast, the frequentist approach would require many bootstrap estimates of the parameter vectors. Then, we would repeat Steps 1–3 using these bootstrap draws in place of the posterior draws. In the Bayesian framework, we need not re-estimate the model. We simply post-process the same set of draws differently.

4.2 |. Dynamic Treatment Regimes

In the previous section we compared static treatment vectors a_0:T = (a₀, a₁, …, a_T), where each element is fixed at baseline. A dynamic treatment regime is a treatment regime where the elements are determined dynamically post-baseline via a pre-specified decision rule. A decision rule is a function that, at each time point t, maps the confounder history and treatment history (L_0:T, A_0:T) to a treatment value a_t ∈ {0,1}. For simplicity, here we discuss treatment rules that determine assignment based on current confounder values only. That is, rules $r_t(\cdot ):\mathcal{L}\to \{0,1\}$ maps from the space of confounders to a treatment decision. Expanding on the viral load/kidney function example from earlier, consider a treatment rule that administers treatment at time t only if kidney function at time t is higher than some threshold κ: r_t(L_t) = r(L_t) = I(L_t > κ). We denote the average potential outcome under the dynamic treatment regime $a_{0:T}^r=\left(r\left(L_1\right),r\left(L_2\right),\dots ,r\left(L_T\right)\right)$ as $E\left[Y^{a_{0:T}^r}\right]$. Of interest may be to compare the average difference in outcome had everyone been treated according to rule r versus rule $d:\Psi =E\left[Y^{a_{0:T}^r}-Y^{a_{0:T}^d}\right]$

We note that these rules can be quite complex. For example, treatment at time t may only be assigned if kidney function has been above κ for the previous two periods as well as the current time period:

$$r_t\left(L_{(t-2):t}\right)=I\left(L_t>{\kappa }_t\right)\cdot I\left(L_{t-1}>{\kappa }_{t-1}\right)\cdot I\left(L_{t-2}>{\kappa }_{t-2}\right)$$

Here, $r_t(\cdot ):{\mathcal{L}}^3\to \{0,1\}$. In general, the rule may include previous treatment history as well as confounder history. In this section we consider the simple rule r(L_t) = I(L_t > κ), but the procedure is the same for more complicated rules.

As shown in all previous examples, Bayesian causal inference can be done quite easily provided we have posterior draws of the model parameters. Once these are obtained, computing causal contrasts is just a matter of post-processing. In this case, we only need to modify the g-computation post-processing steps from the previous section to sequentially set each element of the treatment vector as confounders are simulated, rather than use a pre-set treatment vector a_0:T.

Consider the same scenario as in the static treatment setting, with posterior draw of ${\omega }_Y^{(m)}$ and ${\omega }_{L_t}^{(m)}$, but this time with a specified dynamic treatment rule r(L_t) = I(L_t > κ). We compute a draw, μ^(m)(r), from the posterior of the average potential outcome under rule r, $E\left[Y^{a_{0:T}^r}\right]$, as follows

1. Starting from t = 1, perform the following two sub-steps sequentially until t = T

   1. Simulate Confounder

      $${\tilde{L}}_t~p\left(L_t\mid {\tilde{L}}_{0:t-1},{\tilde{a}}_{0:t-1},{\omega }_{L_t}^{(m)}\right)$$
   2. Determine Treatment according to rule

      $${\tilde{a}}_t=r\left({\tilde{L}}_t\right)=I\left({\tilde{L}}_t>\kappa \right)$$
      Denote these draws ${\tilde{L}}_{0:T}=\left({\tilde{L}}_0,{\tilde{L}}_1\dots ,{\tilde{L}}_T\right)$ and ${\tilde{A}}_{0:T}=\left({\tilde{a}}_0,{\tilde{a}}_1,\dots ,{\tilde{a}}_T\right)$. Repeat this a total of B times to obtain ${\left\{{\tilde{L}}_{0:T}^{(b)}\right\}}_{1:B}$ and ${\left\{{\tilde{A}}_{0:T}^{(b)}\right\}}_{1:B}$
2. Integrate the outcome model ${\mu }^{(m)}(r)=E\left[Y\mid a_{0:T}^r,L_{0:T}\right]$ over ${\left\{{\tilde{L}}_{0:T}^{(b)}\right\}}_{0:T}$ and ${\left\{{\tilde{A}}_{0:T}^{(b)}\right\}}_{1:B}$ conditional on current set of draws ${\omega }_y^{(m)}$ , under both interventions. In the viral load example, this would be

   $${\mu }^{(m)}(r)=\frac{1}{B}\sum _{b=1}^{B}E\left[Y\mid {\tilde{A}}_{0:T}^{(b)},{\tilde{L}}_{0:T}^{(b)},{\omega }_y^{(m)}\right]$$

Similarly, we can draw from the posterior of average potential outcome under an alternative rule d, $E\left[Y^{a_{0:T}^d}\right]$. Denote this by μ^(m)(d). Taking the difference yields a posterior draw of Ψ, Ψ^(m) = μ^(m)(r) − μ^(m)(d). The sum over B is a Monte Carlo estimate of the integral in (8). This highlights the advantage of full posterior inference. A posterior over the model parameters induces a posterior over functions of those parameters - in this case, ATEs that contrast dynamic treatment regimes.

5 |. PRIORS OVER SENSITIVITY PARAMETERS

So far we have demonstrated how priors can be used to induce various correlation structures between model parameters. In Section 3.1, we were able to estimate a smoothed causal curve by inducing correlation between neighboring points. In section 3.2, we were able to estimate conditional causal contrasts for sparsely populated subgroups by shrinking their estimates towards the overall average. Lastly, in the previous section we explored ridge-like and horseshoe priors for inducing principled sparsity on a high-dimensional covariate vector. In this section, we present a different use of priors focused explicitly on causality rather than modeling - outlining how they can be used to express uncertainty about causal identification assumptions.

We consider a binary point-treatment setting with a continuous real-valued outcome. Suppose that conditional ignorability (IA.1) does not hold, so that $Y^a\cancel{\perp }A\mid L$, for a ∈ {0, 1}. This implies that E[Y ^a | A = 1, L] ≠ [Y ^a | A = 0, L]. That is, the mean of each potential outcome differs between those actually treated and untreated, even after conditioning on L. Suppose they differ by

$${\Delta }^a(L)=E\left[Y^a\mid A=1,L\right]-E\left[Y^a\mid A=0,L\right]$$

This could be a result of selection bias. For instance, if higher outcome values are beneficial then E[Y⁰ | A = 1, L] < E[Y⁰ | A = 0, L] implies those assigned to treatment would have had worse outcomes even if they had not been treated, relative to those not assigned treatment. This could be caused by “confounding by indication” where patients worse-off to begin with are more likely to be treated with more advanced drugs. Not accounting for this selection bias may make these drugs look ineffective and, perhaps, even harmful.

In this setting, if we were to incorrectly assume IA.1, then standardization in (1) would yield a biased estimated of the causal effect Ψ = E[Y¹ − Y⁰]:

$$\underset{\mathcal{L}}{\int }\{\mu (1,L)-\mu (0,L)\}dP(L)=\Psi +\xi$$

where the bias term, ξ, is a function of Δ^a(L) and the propensity score e(L) = P(A = 1 | L)

$$\xi =\underset{\mathcal{L}}{\int }\left\{{\Delta }^0(L)e(L)+{\Delta }^1(L)[1-e(L)]\right\}dP(L).$$ (11)

Above, ξ fully characterizes the implication of an ignorability violation on our estimate, but has a complicated form: it is a function of the treatment probability and two unknown functions, Δ¹(L) and Δ⁰(L). Since ignorability is an untestable assumption, it is inherently impossible to learn about Δ¹(L) and Δ⁰(L) through the observed data. To proceed, we must make assumptions about the form of the ignorability violation. The art of sensitivity analysis lies in making assumptions that balance the tradeoff between the range of violations that can be explored against the interpretability of the sensitivity parameters. If they are not interpretable, we cannot form sensible prior beliefs about them. But if they are too simple, we will fail to explore realistic violations.

As an example, suppose that Δ¹(L) = Δ⁰(L) = Δ so that both potential outcomes differ by some constant amount between those assigned and unassigned treatments. That is, there is some constant boost that one treatment group is getting under both hypothetical treatment interventions. We also assume this bias is constant with respect to measured covariates, so that we learn nothing about the bias by conditioning on L (a worse-case scenario). In this setting, the bias reduces to $\xi =\Delta {\int }_{\mathcal{L}}dP(L)=\Delta$. These assumptions reduce (11) to be a function of a single parameter which, as mentioned earlier, can be viewed as the amount of selection bias: Δ = E[Y⁰ | A = 1, L] − E[Y⁰ | A = 0, L]. If higher Y values are beneficial, then Δ < 0 implies treated subjects would have had outcome values Δ units lower than those not assigned treatment, even had they not been treated. This could be because of a lurking unmeasured confounder (e.g. baseline disease severity) that impacts both treatment assignment and outcome. Interpretation of magnitude will depend on the units of Y. If Y were standardized, we could interpret Δ as a standard deviation difference in average potential outcomes between the two treatment groups. Suppose we believe that there is strong possibility of a selection bias in the Δ < 0 direction and no chance of bias in the other direction, we can set Δ = −Δ*. We could then specify a prior Δ* ~ Gam(a, b), which has prior mean E[Δ*] = a/b and variance V ar[Δ*] = a/b². For instance, if we have a prior belief of a one standard deviation bias, we can set (a/b) = 1 and set b to, say, b = 3. This is a fairly tight prior around Δ* = 1 with standard deviation 3^−1/2.

To illustrate, we generate some synthetic data with a single binary treatment, single continuous observed confounder, a single continuous unobserved confounder, and a Gaussian outcome with mean being a function of treatment and both confounders. We then fit the Bayesian linear regression in Equation (2), excluding the unmeasured confounder. Appendix C describes this synthetic data generation and implementation in more detail. If we had included it, standardization would yield an accurate estimate of the ATE, Ψ = E[Y¹ − Y⁰], which equals Ψ = 1 in this simulation. However, because we mistakenly exclude the unmeasured confounder, our estimate will be biased by some Δ. Conducting a sensitive analysis involves specifying different priors for Δ. Because we have no data about Δ, the posterior is the same as the prior and so the usual standardization algorithm can be modified as follows:

1. Perform standardization as usual to obtain Ψ^(m). Because we are using a linear model in this simulated example, Ψ^(m) is simply the m^tℎ posterior draw of the coefficient on the treatment dummy in our regression - as shown in Equation (2).

2. Draw sensitivity parameter from some specified prior, e.g. Δ*^(m) ~ Gam(1, 3), transform to get Δ^(m) = −Δ*^(m), and compute

   $${\Psi }_s^{(m)}={\Psi }^{(m)}-{\Delta }^{(m)}.$$

In this case, our sensitivity analysis produces the usual posterior draws Ψ^(m) that are perturbed by draws of Δ^(m). We can also view it as “subtracting off” the bias in (11) from the standardization estimate, Ψ^(m). This perturbation incorporates our prior uncertainty regarding the magnitude of the bias due to a pre-specified form and direction of an ignorability violation. Figure 3b presents perturbed posteriors under three different priors for this synthetic example: Δ ~ N(0, sd = 3^−1/2), Δ ~ Gam(1, 3), and Δ* ~ Gam(1, 3). Note that ignorability (i.e. no unmeasured confounding) can be expressed as a strong prior belief that Δ follows a point-mass distribution at 0, Δ ~ δ₀. As shown in Figure 3b, this yields a posterior estimate centered far from Ψ = 1. The first prior expresses symmetric belief about the direction of the bias, and so increases uncertainty in the posterior, without shifting its mean. Consequently, in Figure 3b we see the wider posterior interval that now has more mass around Ψ = 1. The second prior expresses prior belief that Δ > 0 and the third expresses the belief that Δ < 0. Thus, the former shifts our posterior lower to correct for the upward bias and the latter shifts our posterior up to correct for the downward bias.

While sensitivity analyses around IAs are unique and application-specific, they follow the general procedure we outlined above:

1. Find the bias induced by an IA violation, ξ.

2. Make assumptions about the nature of the violation so that ξ is expressed in terms of interpretable sensitivity parameters.

3. Express your belief about the direction and degree of the violation via priors on these sensitivity parameters.

4. Use draws from these priors to perturb the causal effect.

5. Assess the perturbed posterior.

We contrast this approach with the usual frequentist approach that computes point and interval estimates for Ψ under a pre-specified range of Δ. Usually this range is wide enough so that we can see where perturbation “reverses” some statistically significant effect, as measured by a change in p-value from significant to non-significant. In the Bayesian approach, we see how perturbation impacts the entire posterior distribution of the estimand - telling us how posterior mean, median, quantiles, variance, etc are all affected by the uncertainty in our sensitivity parameters.

The literature on Bayesian sensitivity analysis is large and growing. For instance, McCandless et al.¹⁹ develop a sensitivity analysis for unmeasured confounding of the effect of a binary exposure on an outcome and assess the quality of posterior inference via extensive simulations. Gustafson et al.²⁰ develop a Bayesian sensitivity analysis framework for unmeasured confounding where it is assumed measured confounders are measured with error. This highlights a strength of Bayesian approach: sensitivities around multiple violations (in this case, measurement error and ignorability) can be done at once with suitable priors. Mediation analyses require more complex ignorability assumptions to estimate natural direct and indirect effects. Bayesian sensitivity analyses have been developed for such problems within the context of hazard models for survival outcomes²¹. Bayesian sensitivity analysis for mediators have also been explored with nonparametric Bayesian models²². Other work by Gustafson et al. focus on Bayesian sensitivity for partially identified bias parameters²³. They discuss an application to average causal effect estimation in a randomized trial with non-compliance (i.e. not all patients randomized to treatment A = a take treatment a).

6 |. FLEXIBLE MODELS VIA NONPARAMETRIC BAYES

In previous examples, we considered parametric regression models μ(A, L) = E[Y | A, L] that were indexed by finitely many parameters. In the Gaussian example of Section 2, the regression was determined completely by (θ, β). In Section 3.2, the logistic regression was a function of (β_w, β_v, θ₀, θ_1:q). In our discussion of time-varying confounding, models for the confounder distribution were required at every time point, in addition to an outcome model. These models impose restrictive functional forms of the covariate and treatment effect. For instance, they assume that the treatment effects are linear and additive on some transformation of the conditional outcome mean. However, it is possible that the treatment effect is a complex, nonlinear function of L. Suppose all relevant confounders sufficient for IA.1 to hold are measured and included in the model. Even in this scenario, msisspecification of the functional form of that model will, in general, yield inaccurate posterior causal effect estimates. In this section we will provide a brief overview of causal effect estimation using Bayesian nonparametric (BNP) models - a class of flexible models that make minimal functional form assumptions. We focus here on the point-treatment setting, with the understanding that these methods can be applied to other settings, including conditional mean modeling in g-computation, mediation, marginal structural models, and so on. Throughout, D = {Y_i, A_i, L_i}_1:n will denote the observed data consisting of outcome, treatment, and confounder vector for n independent subjects. We will define a covariate vector X_i = (1, A_i, L_i) for compactness.

6.1 |. Dirichlet Process Mixture Models

We return to the linear model of Section 2 and specify a more flexible alternative. First, define conditional regression μ_i(X) = X′β_i. We specify the following model for the joint data distribution

$$\begin{gathered} Y_i\mid X_i,{\beta }_i,{\varphi }_i~N\left({\mu }_i\left(X_i\right),{\varphi }_i\right) \\ {X}_i\mid {\theta }_i~p\left(X_i\mid {\theta }_i\right) \\ {\omega }_i\mid G~G \\ G\mid \alpha ,G_0~DP\left(\alpha G_0\right) \end{gathered}$$ (12)

ω_i = (θ_i, β_i, ϕ_i) denotes the full parameter vector. There are two key additions in this model. First, we have saturated the model with more parameters than there are observations in the data. This is nonparametric in the sense that the number of parameters is growing with the sample size. Second, this is a generative rather than conditional model. That is, we model the joint distribution p(Y_i, X_i | ω_i) = p(Y_i | X_i, ω_i)p(X_i | ω_i) rather than just the conditional distribution of the outcome.

The parameters of the joint distribution follow an unknown prior, G. Above, we specify a Dirichlet process (DP) prior on G. Realizations of this stochastic process are discrete random probability distributions centered around a base distribution, G₀(ω_i), with dispersion controlled by α. This discreteness induces ties among the ω_i which, in turn, induces posterior clustering of data points. Specifically, subjects are partitioned into groups with similar joint data distributions and each group’s joint is modeled using a separate ω_i. In this way, the posterior conditional regression is a mixture of many cluster-specific regressions. In the machine learning literature²⁴ these are often called “mixture of experts” learners, since each component regression in the mixture (referred to as an “expert”) has “expertise” in a particular region of the data. Predictions are formed by averaging over the component experts’ predictions. These are distinct from ensemble models, which model the entire data using separate candidate models - rather than assigning different data regions to different models.

Induced Posterior Regression

Such DP mixture models have been discussed in the BNP literature for some time. Shahbaba and Neal (2007) first described a DP mixture of regressions²⁵. Blei et al. (2011) later extended this to a DP mixture of GLMs, which generalizes (12) to any conditional outcome and covariate distribution in the exponential family²⁶. There is extensive literature on posterior sampling strategies for this model, though the most common approach in causal inference tends to be Neal’s Algorithm 8²⁷. We will use software to conduct the sampling, but it is instructive to show that the posterior regression can be expressed as a mixture of regressions at each iteration in the sampler. Let ${\omega }_{1:n}^{(m)}$ be a draw of all the subject-level parameters and let ${\mu }_i^{(m)}(X)=E\left[Y\mid X,{\omega }_i^{(m)}\right]$ denote the posterior regression at each iteration, given by

$${\mu }_i^{(m)}(X)=w_0^{(m)}{\mu }_0^{(m)}(X)+\sum _{i=1}^n{w}_i^{(m)}{\mu }_i^{(m)}(X)$$ (13)

Note that this is a mixture with n + 1 components and mixture weights {$w_0^{(m)}$, $w_{1:n}^{(m)}$}. Above, ${\mu }_0^{(m)}(A,L)$ is the regression under a prior draw ${\beta }_0^{(m)}~G_0$ - we will call this a “prior regression”. The weights $w_i^{(m)}$ have the form

$$w_i^{(m)}=\frac{p\left(X\mid {\theta }_i^{(m)}\right)}{\alpha p\left(X\mid {\theta }_0^{(m)}\right)+\sum _{i=1}^{n}p\left(X\mid {\theta }_i^{(m)}\right)},$$ (14)

where ${\theta }_0^{(m)}~G_0$ is a prior draw. The weight on the prior regression is

$$w_0^{(m)}=\frac{\alpha p\left(X\mid {\theta }_0^{(m)}\right)}{\alpha p\left(X\mid {\theta }_0^{(m)}\right)+\sum _{i=1}^{n}p\left(X\mid {\theta }_i^{(m)}\right)}$$ (15)

The induced posterior regression is a complex mixture of a prior regression and several subject specific regressions. Importantly, the mixture weights are covariate-dependent, allowing us to capture non-linear and non-additive effects of X on the outcome. We refer to the specified distributions in (12) as “local” distributions as they are local to a particular mixture component. Even though the local model is parametric, we can approximate arbitrarily complicated distributions using a mixture of locally simple models. This is similar conceptually to approximating a complicated non-linear regression function using piecewise linear splines.

Local Model Choice and Hyperparameters

Specification of the model requires specifying the local distributions. In general, model fit will not be too sensitive to these choices as the resulting regression takes a complex non-linear mixtures of these local models to fit the regression. However, desired support can be a guiding concern in making this choice. For instance, it may be desirable to choose p(X_i | θ_i) such that it respects the support of the elements of X_i. Consider a vector X = (X₁, X₂, X₃) that consists of a binary, continuous/real-valued, and count confounders respectively. Assuming prior independence, we can set p(X_i | θ_i) to be the product of the Bernoulli, Gaussian, and Poisson distributions, with θ_i being the vector of parameters governing all three distributions. Similarly, if the outcome must be non-negative (e.g. blood pressure, cost, etc) then we could use a log-normal conditional outcome distribution instead of a Gaussian.

Just as with the local models, G₀ should also be set to place non-zero prior measure on the support of ω_i. In model (12) with a single count covariate L_i, we could set

$$G\left({\omega }_i\right)=N_2\left({\beta }_i;{\beta }^{*},{\Sigma }^{*}\right)IG\left({\varphi }_i;a^{*},b^{*}\right)Ber\left(p_i;p^{*}\right)IG\left({\lambda }_i;{\lambda }^{*}\right)$$

Where, θ_i = (λ_i, p_i) are the parameters governing the local covariate distribution p(X_i | θ_i) = Pois(L_i ; λ_i)Ber(A_i ; p_i).

In the causal literature, the parameters of G₀ (superscripted with asterisks above) are often set using empirical Bayes principles while a relatively flat Gamma(1, 1) hyperprior is set on α. Specifically, β* might be set to the ordinary least squares estimates, and Σ* may be set using the MLE covariance estimate. Empirical Bayes is a practical method of setting priors here as cross-validation would be too computationally intensive. Moreover, we typically have no substantive knowledge that could guide these choices. Centering the priors around empirical estimates also helps constrain the parameter draws to a reasonable range of the observed data. Simulation studies in a variety of scenarios show that this tends to yield adequate frequentist properties (i.e. credible intervals and point estimates with close to nominal coverage and bias, respectively, in repeated samples)^28,29,30. This approach is similar to Zellner’s g-prior - an empirical Bayes prior popular in the Bayesian model selection literature³¹.

Relationship to Kernel Regression

In this section, we discuss how the DP regression can be viewed as a Bayesian compromise between a fully empirical kernel regression and a parametric regression.

A kernel regression estimate for a point with covariate vector X is simply a weighted average of all the observed outcome values, each weighted by how “close” the vector X is to each observed covariate. Specifically, denote the centered Gaussian kernel as K_h(u) (i.e. this is the density of a Gaussian with zero mean and variance h). The Gaussian kernel regression³² is defined as

$$\widehat{E}[Y\mid X]=\sum _{i=1}^n{w}_i^k(X)\int Y\cdot K_h\left(Y-Y_i\right)dY.$$ (16)

Note that $\int Y\cdot K_h\left(Y-Y_i\right)dY=Y_i$ is just the Gaussian mean. The weights $w_i^k(X)$ are given by

$$w_i^k(X)=\frac{K_g\left(X-X_i\right)}{{\sum }_i{K}_g\left(X-X_i\right)}.$$ (17)

Now taking α → 0 (corresponding to an improper, flat prior) in the DP regression (13) yields

$$E\left[Y\mid X,{\omega }_{1:n}^{(m)},D\right]=\sum _{i=1}^n{w}_i^{(m)}{\mu }_i^{(m)}(X),$$ (18)

with limiting weights

$$w_i^{(m)}=\frac{p\left(X\mid {\theta }_i^{(m)}\right)}{{\sum }_{i}p\left(X\mid {\theta }_i^{(m)}\right)}.$$ (19)

Comparing these equations, it is clear that the improper extreme of the DP regression becomes a type of kernel regression. In particular, if we set p(X | θ_i) to be Gaussian with mean X_i and variance g and set ${\mu }_i^{(m)}(X)=Y_i$, then the DP regression reduces to a kernel regression estimate. Both models are covariate-weighted mixtures of subject level conditional mean models, though the DP model is more satisfying from a statistical point of view. It outputs full posterior distribution over the regression. The kernel regression typically produces a point estimate, with uncertainty estimation being more complicated. Moreover, with the DP we can specify a covariate model, p(X | θ_i), that respects the support of the various covariates. This is in contrast to the kernel regression, which uses a single kernel for the whole vector.

On the other extreme, take α >> n. Then, the DP regression becomes $E\left[Y\mid X,{\omega }_{1:n}^{(m)},D\right]\approx w_0^{(m)}{\mu }_0^{(m)}(X)$. Recall here that μ₀ is the regression with parameters drawn from the prior β₀ ~ G₀. The weights w₀ are also based on covariate parameters drawn from the prior θ₀ ~ G₀. In other words, this extreme results in a completely parametric model with parameters drawn from the prior base disstribution. So we can view the DP regression as a type of posterior compromise between the kernel regression on one extreme and a parametric regression on the other. It would also be fair to say that the DP regression is a regularized version of the kernel regression. This perspective offers more insight into the role the hyperparameters of the local outcome and covariate distributions. Specifically, if p(X | θ_i) and p(Y_i | X_i, β_i, ϕ_i) are Guassian, then the variance parameters of these distribution play the same role as h in the Kernel regression. Here, h controls the bias-variance tradeoff. Large values of h lead to a less flexible (more penalized) fit, while small values of h lead to more flexible (less penalized) fit. Similarly, prior distributions on the variance parameters of these distributions that favor small values will yield a more flexible fit with less shrinkage.

Computing Causal Effects

The MCMC scheme involves obtaining posterior draws of ${\left\{{\omega }_{1:n}^{(m)}\right\}}_{1:M}$, which we can use to construct the mean regression ${\mu }_i^{(m)}(A,L)$ at each iteration. Under IA.1 – IA.4, we can estimate causal contrasts such as Ψ = E[Y¹ − Y⁰] by integrating this regression over the confounder distribution, just as in the parameter setting. Here, integration is done over a BB draw as in Section 3.3,

1. Sample from the DP posterior to get

   $${\mu }_i^{(m)}(A,L)$$
2. Draw BB weights

   $$p_{1:n}^{(m)}\mid W~Dir\left(1_{1:n}\right)$$
3. Integrate to get posterior draw of Causal Effect:

   $${\Psi }^{(m)}\approx \sum _{i=1}^n{p}_i^{(m)}\left\{{\mu }_i^{(m)}\left(1,L_i\right)-{\mu }_i^{(m)}\left(0,L_i\right)\right\}$$

The computationally demanding portion of the above is Step 1 and can be done using off-the-shelf R packages such as ChiRP³⁰. This package runs the DP model in (12) and, by default, specifies local Gaussian distributions for non-binary and local Bernoulli distributions for binary covariates. Figure 4 visualizes predictions trained using ChiRP, where the conditional outcome distribution is simulated from a mixture of two damped harmonic oscillators. It also plots the ATE posterior from the DP model, computed as described above. The ATEs are computed using a synthetic data set with a binary treatment and single Gaussian confounder. In this example, the true treatment effect is a quadratic function of L. The figure also displays ATEs from a frequentist linear additive model, E[Y | A, L] = β₀+β₁A+β₂L, estimated using OLS. These results are biased in this scenario. Detailed descriptions of the synthetic example used for ATE computations in Appendix E. This appendix also contains implementation of the ATE computation using ChiRP.

FIGURE 4.

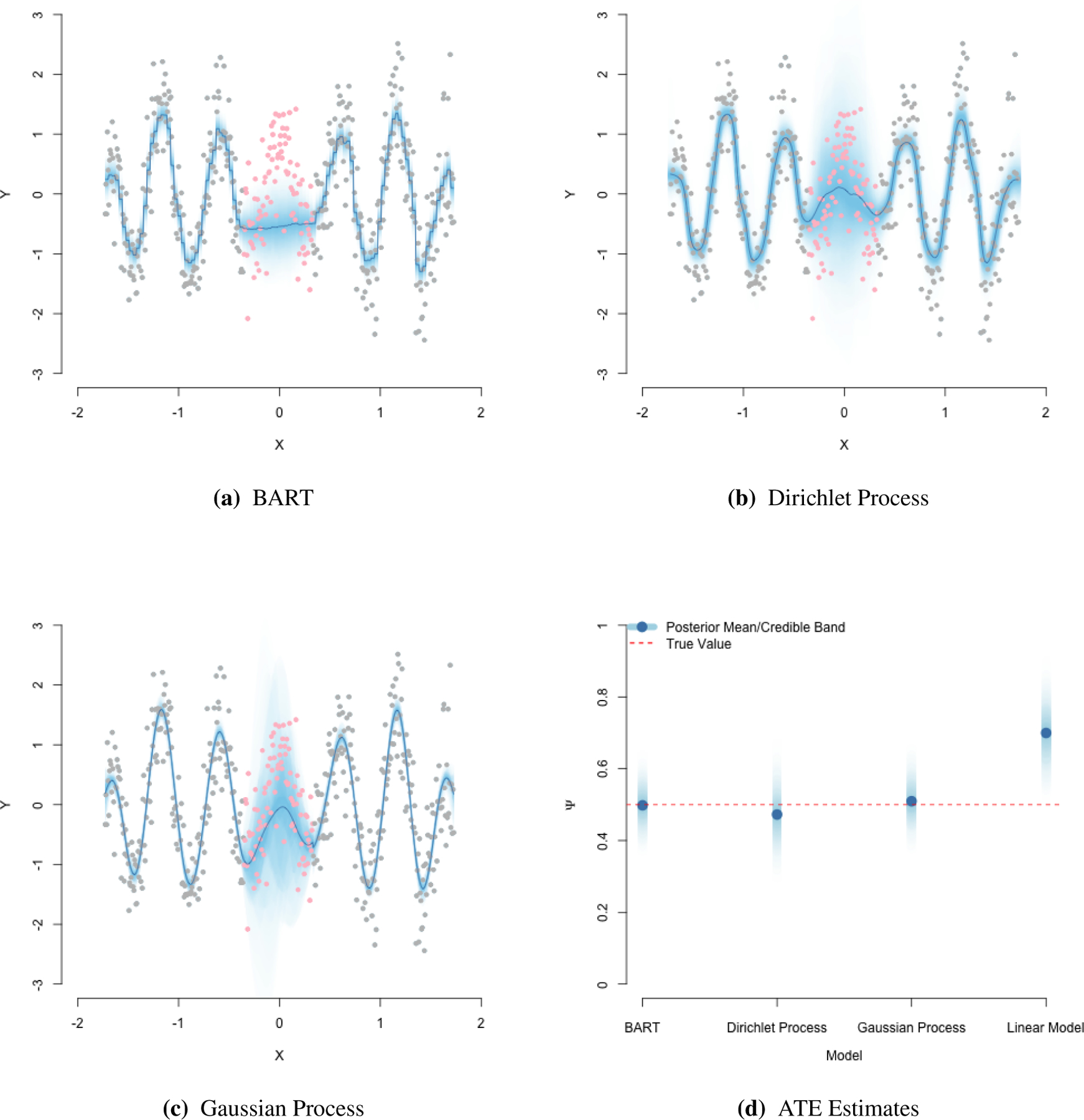
Training and test set predictions from three BNP models, along with ATE estimates from each. Red points indicate held-out test data. Gray points are training data. Notice for the DP and GP models, the increased uncertainty in the test region. BART, by contrast, has less uncertainty in this region. Relative to DP and GP, BART’s interpolation is more rigid due to its inherent tree structure.

Survey of Recent DP Applications

The DP and related priors over random probability distributions such as the enriched DP^33,34, dependent DP^35,36, and centered DP³⁷ have also been applied to causal inference. For instance, Kim et al. (2017) employ a Dirichlet Process mixture to estimate direct and indirect effects in a mediation analysis²². They specify a joint Gaussian model for the outcome, mediator, and confounders, and place a DP prior on the mean vector and covariance matrix. Later work applied DPs to latent mediators³⁸. Roy et al. (2018) use an enriched DP to model the joint distribution of the outcome and confounders, and estimate ATEs via posterior standardization over the estimated distribution of the confounders²⁹. They also describe posterior imputation of missing-at-random covariates within their model. Roy et al. (2018) use a dependent DP to estimate a marginal structural model and apply it to causal estimation with a survival outcome²⁹. Xu et al. (2016) applied a similar dependent DP model to estimate causal effects of dynamic treatment regimes³⁹. Xu et al. (2018) propose an approach for estimating quantile causal effects (e.g. difference in median outcome under one intervention versus another)⁴⁰. A Bayesian Additive Regression Tree (BART) probit model is used to to model the propensity score as a function of covariates, while a Gaussian outcome model is specified conditional on the propensity score. The parameters of the joint outcome-propensity score model are given a DP mixture prior. We will describe BART models in the next section. Oganisian et al. (2018) specify a generative model for the joint outcome, propensity score, and confounder distribution, where the conditional outcome model is a two-part zero-inflated model⁴¹. The parameters of this joint are given a DP mixture prior. Posterior standardization was conducted and a method for posterior predictive checks of positivity (IA.4) are proposed. Others⁴² have applied DP models to adjust for post-treatment variables via principal stratification⁴³. Centered DPs have also been used to estimate heterogeneous treatment effects⁴⁴. Here, the centered DP was used as a prior for an unspecified error term distribution of an accelerated failure time model.

6.2 |. Bayesian Additive Regression Trees

The original BART approach of Chipman et al.⁴⁵ models the conditional outcome distribution as a Gaussian with mean function

$$\mu (X)=\sum _{j=1}^{J}g\left(X;T_j,M_j\right)$$ (20)

Above, the conditional mean is modeled as a sum of predictions from J regression trees, T_j. In this sense BART can be viewed as an ensemble learner. Specifically, T_j consists of a set of nodes and splitting rules with an associated vector of terminal node parameters M_j. The function g maps covariates X_i to one of the terminal node parameters in M_j. The mean is then the sum of the terminal node predictions from each of the trees. The BART prior, consisting of priors on the splitting rules and terminal node parameters, is formulated to induce shrinkage towards shallow trees. This helps prevent over-fitting. This serves as a probabilistically principled alternative to pruning heuristics often used with random forests. Predictions for a toy examples are given in Figure 4. Notice that BART produces a step function as a result of the the assumed tree structure of μ(X). This holds even as BART interpolates across the covariate space with no training data (the red points in the plot indicate held out test data).

The MCMC inference engine behind BART relies on the “backfitting”⁴⁶ approach, which takes posterior draws of each tree structure and their terminal node parameters sequentially. Each tree is fit using the residual from the previously fit trees as the outcome. At every iteration m, one such cycle through the J trees yields $T_j^{(m)}$ and $M_j^{(m)}$, which we can then use to construct a regression

$${\mu }^{(m)}(A,L)=\sum _{j=1}^{J}g\left(A,L;T_j^{(m)},M_j^{(m)}\right)$$

We can use existing software in R such as BayesTree to obtain the posterior draws for μ^(m)(A, L) under both interventions. We first stack two test data sets $D_{\mathit{\text{test}}}^a={\left(A=a,L_i\right)}_{1:n}$ for a ∈ {0, 1} into a single test set {$D_{\mathit{\text{test}}}^1$, $D_{\mathit{\text{test}}}^0$}. The training data simply consists of the observed data set D_train = (Y_i, A_i, L_i)_1:n. The package will then output BART estimates of μ(X) under both interventions in the stacked test set {μ^(m)(1, L_i), μ^(m)(0, L_i)}_1:n for m = 1, … M. To compute the integral in (1), we can post-process the draws in R as follows. For each iteration, take a BB draw $p_{1:n}^{(m)}$ and compute

$${\Psi }^{(m)}=\sum _{i=1}^n{p}_i^{(m)}\left({\mu }^{(m)}\left(1,L_i\right)-{\mu }^{(m)}\left(0,L_i\right)\right)$$

In this way we obtain draws from the posterior of the ATE. Our review of BART was cursory, with a focus on causal estimation. We refer the reader to Tan et al. (2019) for a thorough tutorial on BART and its various extensions⁴⁷.

Survey of Recent BART Applications

We now provide a brief (but by no-means exhaustive) survey of BART in interesting causal inference applications. Hill (2011) first applied BART to ATE estimation⁴⁸. BART has since enjoyed wide popularity in causal estimation. For instance, it has been used to formulate fully Bayesian semi-parametric estimation of structural mean models⁴⁹, fully nonparametric estimation of optimal dynamic treatment regimes⁵⁰, and estimation of causal effects in the presence of positivity violations⁵¹. The latter augments BART with splines to extrapolate to regions of the data with deterministic treatment (i.e. non-overlap regions). Work by Hahn et al. (2017) has focused on improving the use of BART for causal inference⁵². They separate out the the treatment and confounder effects in the outcome regression, which aims to improve bias due to what the authors term “regularization-induced confounding”. We also note that the original BART model presented here has been extended for outcomes with different support. For instance, the mean function modeled using BART can be run through a probit link when the outcome is binary. Sparapani et al. proposed using BART for survival outcomes⁵³. They use a discrete-time failure model where the probability of death at each time point is modeled with a BART probit.

6.3 |. Gaussian Process (GP) Models

Here we review another BNP approach using Gaussian process (GP) priors for regression modeling^54,55. Although less widely used in the causal literature relative to DP and BART models, GPs are popular in the BNP literature. They can be implemented in Stan and so may be a practical choice for applied researchers. We consider the same problem of modeling, μ(X), the mean function of a Gaussian outcome, Y | X ~ N(μ(X), ϕ). The GP can be motivated as a prior over the space of regression functions, μ(X). We say that μ(X) follows a GP with prior mean function θ₀(X) and covariance C(X ; η, ρ). Together with the full model, this is denoted as

$$\begin{gathered} Y\mid \mu (X)~N(\mu (X),\varphi ) \\ \mu (X)~\mathcal{G}\mathcal{P}\left({\theta }_0,C\right). \end{gathered}$$ (21)

Above we have suppressed dependence of θ₀ and C on X and hyperparameters (η, ρ) for compactness. Our prior belief is that the regression function μ(X) is randomly distributed around some mean regression function θ₀, with linearity and smoothness of μ(X) relative to θ₀ being controlled by the hyperparameters. For example, a common prior mean function choice is θ₀(X) = 0 - a hyperplane through the origin. Another, approach is to set θ₀(X) = X′β. The latter specification centers our prior around a linear/additive prior mean regression function, while η and ρ allow for deviations from this prior if the data are inconsistent. The covariance can have many specified forms, but we focus on the exponential-quadratic form popular in the causal literature,

$$C_{ij}=\eta \text{exp}\left\{-\rho {\Vert X_i-X_j\Vert }^2\right\}+.01{\delta }_{ij},$$ (22)

where $\Vert v\Vert =\sqrt{v^{\prime }v}$ denotes the L₂ vector norm. C is the n × n matrix with elements given by C_ij. Intuitively, this describes the prior belief that the regression function evaluations should be similar for two subjects with similar covariate vectors. The evaluations should differ more for two subjects who have very different covariates. The parameter ρ controls how similar these function evaluations are for subjects with similar covariates. Larger ρ favors more similar regression evaluations. The parameter η controls the linearity of the regression function - with smaller η penalizing non-linearity and a priori favoring linear regression functions.

Stan can be used to sample from the posterior distribution of the regression function μ(X). Specifically, it outputs M draws from the posterior of the regression function {μ^(m)(X)}_1:m. These posterior draws are visualized in Figure 4 for both training and held-out test points. Causal ATE estimation can be done by feeding Stan two held-out test data sets, $D_{\mathit{\text{test }}}^a={\left(a,L_i\right)}_{1:n}$ for a ∈ {0, 1}. This returns posterior draws the regression function under both interventions {μ^(m)(1, L_i), μ^(m)(0, L_i)}_1:n for m = 1, … M. Within Stan, standardization can be done using BB as described before. For each iteration, take a BB draw $p_{1:n}^{(m)}$ and compute

$${\Psi }^{(m)}=\sum _{i=1}^n{p}_i^{(m)}\left\{{\mu }^{(m)}\left(1,L_i\right)-{\mu }^{(m)}\left(0,L_i\right)\right\}$$

Posterior inference for the ATE using this GP model is shown in Figure 4. Implementation details for this synthetic example are given in Appendix E. Finally, we note that GPs can easily accommodate outcomes with non-continuous/real support. For instance, with count outcomes we could specify Y | X ~ Pois exp(μ(x)). Here, we model log(E[Y | X]) = μ(X) and place a GP prior on μ(X) as in the Gaussian case.

Recent Applications in Causal Inference

Gaussian process priors have seen some usage in the causal literature. For instance, the dependent DP, used for posterior inference about marginal structural models²⁹ and dynamic treatment regimes³⁹ is essentially a combination of the DP and GP. Specifically, each cluster-specific regression function in the DP is assigned a GP prior. Just as the Guassian local model in (12) induced a posterior regression that is a mixture of linear regression functions, the dependent DP induces a posterior regression that is a mixture of GP regression functions. Other uses of GPs included modeling pollution outcomes in the presence of spatial interference (i.e. violations of IA.3 that exhibit spatial structure)⁵⁶ and estimation of propensity scores⁵⁷.

7 |. DISCUSSION

In this paper we reviewed causal effect estimation from a Bayesian perspective in point-treatment and time-varying treatment settings. For the latter, we outlined how to estimate causal effects of both static and dynamic treatment regimes. Both parameteric and nonparametric settings were discussed. Along the way, we discussed the utility of priors both for providing interpretable shrinkage and also for conducting causal sensitivity analyses. Throughout, we emphasize that the ad-hoc procedures we often use correspond to strongly informative priors. Throughout, we have highlighted various BNP techniques used for causal estimation in the literature. We hope that these surveys will be useful literature overviews that can serve as a starting point for those who want to delve further into these methods.

We note that our treatment of Bayesian causal estimation differs from that of Rubin⁵⁸ - which is fundamentally a finite-sample approach. In this approach, each subject’s counterfactual is treated as a missing data point and the target is the posterior distribution over these missing variables, $p\left({\left\{Y_i^{1-A_i}\right\}}_{1:n},\mid D\right)$. Here, $D={\left\{Y_i^{A_i},A_i,L_i\right\}}_{1:n}$ consists of the observed potential outcomes, treatment assignment, and confounder vector. Denote the parameters governing the observed data distribution as ω. By Bayes’ rule we can express the desired posterior as

$$\begin{gathered} p\left({\left\{Y_i^{1-A_i}\right\}}_{1:n},\mid D\right)=\int p\left({\left\{Y_i^{1-A_i}\right\}}_{1:n},\mid \omega \right)p(\omega \mid D)d\omega \\ \propto \int p\left({\left\{Y_i^{1-A_i}\right\}}_{1:n},\mid \omega \right)p(D\mid \omega )p(\omega )d\omega \end{gathered}$$

Suppose that n₁ of the n subjects are treated. Then the likelihood is

$$p(D\mid \omega )=p\left(Y_i^1,\dots ,Y_{n_1}^1,Y_{n_1+1}^0,\dots Y_n^0\mid L_{1:n},\omega \right)$$

Thus this approach requires a model for the joint distribution of p(Y¹, Y⁰ | L, ω), which is not identifiable in the data: we never observe both potential outcomes for any subject. By non-identifiable, we mean that the posterior (even if it is proper) over this joint distribution will be completely driven by the prior. This issue is not unique to Bayesian inference. For instance, the variance of the sample average treatment effect is not identifiable from a frequentist perspective either⁵⁹. It is a function of the covariance of the two potential outcomes, which we cannot learn. Ding et al. (2018) provide an excellent review of Bayesian causal inference from this missing data perspective⁶⁰. This missing data approach is the central idea behind the more recent PENCOMP method⁶¹, which uses a penalized splines to impute the missing counterfactuals. The approach described in our paper is what Ding et al. (2018) term the “super-population” approach, rather than the finite-sample approach. This super-population approach focuses on estimands that are a function of the parameters governing the data generation process. Once we have a good model of the process, these estimands are simply transformations of these parameters.

APPENDIX

A. CAUSAL DOSE EFFECT EXAMPLE

A.1. Data generation and implementation in Stan

This appendix provides a more detailed walkthrough of the synthetic example and model discussed in Section 3.1. We refer the reader to the Stan manual online for details about the language, syntax, and best practices. The toy example was simulated as follows. For K = 10 doese levels k ∈ {0, …, 9}, and n = 100 subjects, indexed by i we simulate:

1. single continuous confounder:

   $$L_i~N(0,1)$$
2. treatment assignment:

   $$A_i\mid L_i~P\left(A_i=k\right)\propto \text{expit}\left(1-(2/9)\cdot k+L_i-.5k{L}_i\right)$$
3. outcome:

   $$Y_i\mid A_i,L_i~N\left(5\cdot \Phi \left(A_i-5\right)-5\cdot L_i,2\right)$$

Above, Φ(·) is the standard normal CDF. Notice that the baseline probability of treatment decreases with dose level. Reflecting a realistic scenario where fewer patients are likely to be assigned to higher doses. The confounder L_i impacts both treatment and the outcome. Higher values of L_i make higher dose assignments more likely (note the −.5kL_i term). At the same time, higher L_i lead to lower outcomes. This simulation takes place in the first several lines of dose_response.R in the GitHub repository.

The logic behind using Φ is purely to have an interesting/realistic toy example. A = 5 is about the middle dose level. Using Φ we are ensuring that doses much higher than the middle have diminishing returns on the outcome. Each dose increase affects the outcome less and less. Thus the true dose effect curve is 5 · Φ(A − 5), which is plotted in red in Figure 1a. We need to adjust for L_i because patients with higher L are more likely to be treated at all levels and less likely to have higher outcomes.

The full probability model is

$$Y_i\mid A_i,L_i~N\left(\mu \left(A_i,L_i\right),\varphi \right)$$

Where, μ(A_i, L_i) is the conditional expectation in (3) - a function of θ_0:K and β. In the paper we discussed the priors on θ_1:K. These took the form of a sequence of dependent Gaussian priors, as a function of μ and τ_k. This likelihood is specifying in the ”model” block of the Stan code DR_model.stan:

model {
// specify priors 
theta[1] ~ normal( 0, 10); 
theta[2] ~ normal( 2*theta[1], 1);
for(j in 3:num_A_levels){
theta[j] ~ normal( 2*theta[j-1] - theta[j-2], 1);
}
beta ~ normal(0, 10); 
phi ~ cauchy(0,10);
// specify likelihood
Y ~ normal(L*beta + A*theta , phi);
}

Note that in the above, an intercept is included in L. Notice here we have set μ = 0, τ₁ = 10, and τ_1:K = 1. We specify a Gaussian prior with standard deviation (SD) 10. This is a relatively flat prior since this SD is larger than the sampling model SD= 2. On ϕ we place a half-Cauchy prior with scale 10 - again, fairly flat. If we wanted to place priors on, say, μ instead of setting it at μ = 0, we could have instead specified

model {
// specify priors 
mu ~ normal(0, 10); 
theta[1] ~ normal( mu, 10); …
}

We would also need to declare μ in the “parameters” block of DR_model.stan. The same idea holds for τ_0:K. We could also specify hyper-prior distributions for these variables. We fix these to constant values for simplicity of the illustrated examples and to maintain focus on the AR1 prior construction. Another important portion of DR_model.stan worth highlighting is the “generated quantities” block. In this block, we can perform post-processing of posterior draws of parameters. For instance, we can post-process draws of θ_1:K to compute the curve Ψ(k):

generated quantities { 
vector[num_A_levels] Psi;
Psi[1] = theta[1]; 
for(k in 2:num_A_levels){
Psi[k] = theta[k] - theta[k-1];
}
}

Above, we declare a vector of length num_A_levels (which is K = 10 in this example). And compute Ψ(k) = θ_k − θ_k−1 as defined in the main text. In dose_response.R we call the Stan model using the rstan package - which allows us to call Stan programs from R. Using the R function stan_model(), we compile the Bayesian model specified in DR_model.stan. Using the R function sampling() we take 500 posterior draws after a 500 draw burn-in period. Only one chain is run. In practice, more chains should be used with more posterior draws and a longer burnin period. We should check that the chains for Ψ in the generated quantities block has converged. Posterior predictive checks should also be done to evaluate model fit. Guidance for convergence and posterior predictive checks is no different in this causal setting than in the general Bayesian modeling framework, so we leave details to standard Bayesian texts such as Bayesian Data Analysis¹⁴.

A.2. Implementation in SAS

The file dose_analysis.sas in our companion GitHub repository repeats the analysis above using PROC MCMC in SAS. Within PROC MCMC, we use the “parms” statement to declare the parameters of our model. In this case, we declare the dispersion parameter “phi”, the nine conditional dose effects (t1, t2, …, t9), the confounder effect (“bL”), and the intercept (“b0”):

parms phi t1-t9 bL b0;

The AR1 prior can be specified using the “prior” statement:

prior t1 ~ normal(0, sd=10); 
prior t2 ~ normal(2*t1, sd=1); 
prior t3 ~ normal(2*t2 - t1, sd=1); 
prior t4 ~ normal(2*t3 - t2, sd=1); 
prior t5 ~ normal(2*t4 - t3, sd=1); 
prior t6 ~ normal(2*t5 - t4, sd=1); 
prior t7 ~ normal(2*t6 - t5, sd=1); 
prior t8 ~ normal(2*t7 - t6, sd=1); 
prior t9 ~ normal(2*t8 - t7, sd=1);

The Gaussian likelihood is specified using the “model” statement:

muA = t1*A1 + t2*A2 + t3*A3 + t4*A4 + t5*A5 + t6*A6 + t7*A7 + t8*A8 + t9*A9; 
model Y ~ normal( b0 + muA + bL*L , sd=phi);

Finally, for computational efficiency, we can compute the causal effects of interest directly within PROC MCMC as simple transformations of t1, t2, …t9 after specifying the likelihood. Note this is completely analogous to the generated quantities block in Stan.

Psi[1] = t1 ;
Psi[2] = t2 - t1;
Psi[3] = t3 - t2;
Psi[4] = t4 - t3;
Psi[5] = t5 - t4;
Psi[6] = t6 - t5;
Psi[7] = t7 - t6;
Psi[8] = t8 - t7;
Psi[9] = t9 - t8;

Overall, the results from SAS are quite similar to results in Stan.

B. CONDITIONAL CAUSAL EFFECTS

B.1. Data generation and implementation in Stan

This appendix walks through simulation and analysis of the synthetic example discussed in Section 3.2, including implementation of the Bayesian bootstrap in Stan. The synthetic data was simulated for n = 500 subjects (indexed here by i) as follows:

1. Confounder W_i ~ N(0, 1).

2. Stratum membership, V_i, with probability P(V_i = v) = p_v for v ∈ {1, 2, …, 5}. Where we set

   $$p_{1:v}=\left(\frac{3}{10},\frac{3}{10},\frac{2}{10},\frac{1}{10},\frac{1}{10}\right)$$
3. Treatment assignment as Bernoulli with probability

   $$P\left(A_i\mid W_i,V_i=v\right)=\text{expit}\left(1\cdot W_i+{\gamma }_v\right)$$

   Where γ_1:5 = (0, −.5, .5, .5, −.5)
4. Scalar Bernoulli outcome with probability

   $$P\left(Y_i\mid A_i,W_i,V_i\right)=\text{expit}\left[-1+W_i+\left(1+\sum _{v=2}^5{\eta }_{v}I\left(V_i=v\right)\right)A_i\right]$$

   Where η_2:5 = (−.5, 0, .5, .6) (V = 1 is the reference).

Again note that W_i and V_i both impact treatment probability and the outcome probability. The strata membership simulation mirrors practical examples where some strata are more populated (i.e. with probability 3∕10) than other strata (i.e. with probability 1∕10). In the outcome model, notice that the conditional treatment effect varies with stratum membership. Motivating the need for causal effect estimates conditional on each stratum. This simulation is done in the top portion of partial_pool.R.

The full probability model we specify for the outcome is that

$$Y_i\mid A_i,W_i,V_i~Ber\left(\mu \left(A_i,L_i\right)\right)$$

where μ(A_i, L_i) is the conditional expectation in (6), reproduced here with notation specific to this example

$$E\left[Y_i\mid A_i,L_i\right]=\sigma \left\{\gamma +{\beta }_w{W}_i+\sum _{v=2}^5{\beta }_{v}I\left(V_i=v\right)+\left[{\theta }_1+\sum _{v=2}^5{\theta }_{v}I\left(V_i=v\right)\right]A_i\right\}$$

Recall here that σ{·} is the inverse logit link. Note here that θ₁ is the conditional (on W) treatment effect in stratum 1 - which, in this parameterization, is the reference stratum. Similarly, θ₁ + θ_v is the treatment effect in stratum v for v ∈ 2, …, 5.

The Bayesian model is specified in partial_pool.stan. Below, is the “model” block where we specify the prior in (7) and likelihood. In the code, “W” is an n × 1 matrix containing each subject’s confounder value and “V” is an n × 5 matrix with i^th row (1, I(V_i = 2), I(V_i = 3), I(V_i = 4), I(V_i = 5)). Thus, I(V_i = 1) is the reference. The variable “theta” is a 5 × 1 vector, θ_1:5. The variable β_v is a 5 × 1 vector of V -specific main effects, β_2:5 including a constant (γ in the model above).

The prior for “theta” is specified to induce partial pooling as discussed. We set the standard deviation of the Gaussian priors on θ_1:5 to be τ = .5. A Gaussian hyper-prior is placed on μ. Note that on a logit scale this is quite flat. A Gaussian prior is also used on the coefficient of the confounder and intercept

model {
// specify priors 
beta_w ~ normal(0, 1); 
beta_v ~ normal(0, 1); 
mu ~ normal(0, 1);
theta[1] ~ normal( mu, .5); 
theta[2:Pv] ~ normal( mu - theta[1], .5);
// specify likelihood 
for(i in 1:N){
Y[i] ~ bernoulli_logit( W[i]*beta_w + V[i]*beta_v + ( V[i]*theta)*A[i]) ;
}
}

As before in Appendix A, we can use the generated quantities block for post-processing. As discussed in the main manuscript, this involves integrating the estimated model over a Bayesian bootstrap (BB) estimate of the conditional distribution of W | V, P_v(W). Below, we include an excerpt from partial_pool.stan that loops through each stratum of V and computes a causal odds ratio for that stratum. Below, we compute the conditional mean outcome under intervention A = 1 and A = 0 for each subject: cond_mean_y1 and cond_mean_y0, respectively. Then we take a weighted average of these conditional means, with bootstrap weights coded as bb_weights. Here, the Stan function dirichlet_rng takes a draw from $Dir\left(1_{n_v}\right)$, which is the BB posterior estimate of P_v(W). This weighted average is an estimate of the marginal mean under each intervention, coded as marg_mean_y1 and marg_mean_y0. Computing the odds ratio is done as usual using these marginal means.

generated quantities {
real marg_mean_y1; 
real marg_mean_y0; 
real odds_1; 
real odds_0; 
…
// cycle through strata of interest and compute causal Odds Ratio for each. 
vector[Pv] odds_ratio; 
for( v in 1:Pv){
// n_v = number of subjects in that stratum
// v_start:v_end are the row indices of subjects in stratum V 
int nv = n_v[v]; 
int v_start = ind[v]+1; 
int v_end = ind[v+1];
vector[nv] cond_mean_y1; 
vector[nv] cond_mean_y0; 
vector[nv] bb_weights;
// subset to stratum v
matrix[nv, Pw] Wv = W[ v_start:v_end, ];
matrix[nv, Pv] Vv = V[ v_start:v_end,];
// compute conditional means. 
cond_mean_y1 = inv_logit( Wv*beta_w +Vv*beta_v + Vv*theta); 
cond_mean_y0 = inv_logit( Wv*beta_w + Vv*beta_v);
// Bayesian bootstrap weights for P_v(W) 
bb_weights = dirichlet_rng( rep_vector(1, nv)) ;
// taking average over bayesian bootstrap weights under both treatments 
marg_mean_y1 = bb_weights’ * cond_mean_y1;
marg_mean_y0 = bb_weights’ * cond_mean_y0;
// compute odds ratio 
odds_1 = (marg_mean_y1/(1 - marg_mean_y1)); 
odds_0 = (marg_mean_y0/(1 - marg_mean_y0)); 
odds_ratio[v] = odds_1/odds_0;
}
…
}

In the sampling statement in partial_pool.R, we run a single sampling chain consisting of 1000 posterior draws after 1000 burnin draws. The results of this computation is shown in Figure 1b, which is potted in partial_pool.R.

B.2. Implementation in SAS

The code partial_pool.sas in our companion GitHub repository repeats the analysis in SAS. The main procedures involved are PROC MCMC (as in the dose effect example) and PROC IML. Here, PROC IML (Integrated Matrix Language) is used to manipulate the posterior draws obtained from PROC MCMC and conduct the Bayesian Bootstrap. Since the PROC MCMC step is very similar to the dose effect example, here we focus on the PROC IML post-processing step.

The first statements in PROC IML load in two datasets as matrices. First, dataset “posterior_draws” is loaded and stored as matrix “pm”. This is a matrix with each column corresponding to a parameter and each row corresponding to a posterior draw. This was an output from PROC MCMC. Second, dataset “mcmc_data” is loaded and stored as matrix “X”. This is the model matrix with n rows (for each of the n subjects) and covariates along the columns. Here is the relevant excerpt:

/* Read in matrix of posterior draws from SAS to IML */
use posterior_draws; read all var _ALL_ into pm; close posterior_draws;
/* Read in model matrix from SAS to IML */
use mcmc_data; read all var _ALL_ into X; close mcmc_data;
n = nrow(X); 
n_iter = nrow(pm);
/* shell to store posterior draws of Causal OR for each of the 5 strata */ 
OR_mat = j(n_iter, 5, 0);

Next, we loop through each posterior draw, indexed by “i” in the code. For each draw, we loop through the strata of V, take a BB draw of the conditional confounder distribution P_v(W), and integrate the logistic model over this BB draw of the conditional confounder distribution to attain the marginal means under each treatment. The odds ratio is computed in terms of these means. Here is the relevant excerpt:

do v = 1 to 5;
/*X[,6] is the column containing V_i. */ 
nv = sum(X[,6] = v); /* Find how many subjects in stratum v */ 
idx = loc(X[,6] = v) ; /* find which obs are in stratum v */
/* Draw from Dirichlet(1_{nv}) distribution 
to do bayesian bootstrap estimate of P_v(W) */
alpha= J(nv , 1 , 1); 
bb_w = RandDirichlet(1, alpha); 
bb_w = bb_w || 1-sum(bb_w);
/* for each strata, compute logit of event 
under treatment 1 and 0: lp1, lp0*/
/* compute reference group v=1 separately */
if v=1 then do; 
lp1 = pm[i,2] + pm[i, 3]*X[ idx , 8] + pm[i, 8] ; 
lp0 = pm[i,2] + pm[i, 3]*X[ idx , 8] ; 
end;
if v>1 then do; 
lp1 = pm[i,2] + pm[i, 3]*X[ idx , 8] + pm[i,2+v] + (pm[i, 8] + pm[i,7+v]) ; 
lp0 = pm[i,2] + pm[i, 3]*X[ idx , 8] + pm[i,2+v] ; 
end;
/* inverse logit transform to convert to probability */
p1 = exp(lp1)/(1+exp(lp1)); 
p0 = exp(lp0)/(1+exp(lp0));
/* bayesian bootstrap average of probability*/
/* dot-product: bb_w is 1-X-n vector and p1, p0 are n-X-1 */ 
mu1 = bb_w*p1; 
mu0 = bb_w*p0;
/* compute Odds Ratio for stratum v */
OR_mat[i,v] = ( mu1/(1-mu1)) / ( mu0/(1-mu0)) ; 
end;

Note that indexing of “pm” and “X” is so that we grab the appropriate columns of the model matrix and posterior parameters when forming the log odds ratio as a linear combination of these parameters. This is completely analogous to the “generated quantities” block in the Stan implementation. The SAS results are quite similar to results in Stan. Since we run relatively few MCMC iterations with different seeds across statistical software, some small differences are expected.

C. PRIORS ON SENSITIVITY PARAMETERS

C.1. Implementation in Stan

Here, we briefly describe using the generated quantities block in Stan to conduct the sensitivity analysis described in Section 5. The synthetic example underlying Figure 3b was simulated as follows in the program sensitivity.R. For i = 1, …, n = 100 subjects,

1. Simulate two confounders L_i ~ N(0, 1) and U_i ~ N(0, 1).

2. Simulate treatment assignment A_i from a Bernoulli with probability

   $$P\left(A_i=1\mid L_i,U_i\right)=\text{expit}\left(L_i+U_i\right)$$
3. Simulate outcome Y_i from

   $$Y_i\mid A_i,L_i,U_i~N\left(A_i-L_i-2U_i,1\right)$$

Notice here that subjects with higher U_i are more likely to be treated and have lower outcome values. Failing to adjust for U_i may lead us to conclude that the treatment effect is negative, while in reality is is positive (specifically, treatment has coefficient +1 in the conditional outcome model).

We specify the following misspecified Bayesian model where U_i is excluded:

$$Y_i\mid L_i,A_i~N\left(\theta A_i+\beta L_i,\varphi \right)$$

As described in the introduction, the ATE produced by standardization from this linear conditional mean model is simply θ. However, Posterior estimates of θ will be biased since we did not adjust for some unmeasured confounder U_i (i.e. IA.1 is violated). Here, we perform the sensitivity analysis described in Section 5. In the model block of sensitivity.stan, we specify the model as shown in the following excerpt

model { 
// set priors
theta ~ normal(0, 3); 
beta ~ normal(0, 3); 
delta1 ~ normal(0,1/sqrt(3));
// specify likelihood
Y ~ normal(A*theta + beta*L, phi);
}

Notice that the sensitivity parameter here is coded as delta1 and given a standard Gaussian distribution. Now, in the generated quantities block, we compute the perturbed estimate of the ATE, coded as psi3.

generated quantities { 
…
real psi3;
…
psi3 = theta + delta1; 
}

This produces the posterior estimates for Δ ~ N(0, 3^−1∕2) in Figure 3b. Note ellipses here denote ommitted code. The full code is available in the companion GitHub repository.

C.2. Derivation of Bias

Here we detail the derivation of the bias, ξ. Define the amount of bias in potential outcome Y ^a as

$${\Delta }^a(L)=E\left[Y^a\mid A=1,L\right]-E\left[Y^a\mid A=0,L\right]$$

Now, take E[Y ^a]. Iterate expectation over L and then iterate once more over A, conditional on L. We get

$$E\left[Y^a\right]=\int E\left[Y^a\mid A=0,L\right]+{\Delta }^a(L)e(L)dP(L)$$

Noting that E[Y¹ | A = 0, L] = E[Y¹ | A = 1, L]−Δ¹(L) (by definition of Δ¹(L)), we have the following expressions for each expected potential outcome

$$E\left[Y^0\right]=\int E\left[Y^0\mid A=0,L\right]+{\Delta }^0(L)e(L)dP(L)$$

and

$$E\left[Y^1\right]=\int E\left[Y^1\mid A=1,L\right]-{\Delta }^1(L)(1-e(L))dP(L)$$

Note that consistency allows us to drop the superscripts a when conditioning on A = a so that E[Y^a | A = a, L] = μ(a, L). Then subtracting yields,

$$E\left[Y^1-Y^0\right]=\int \mu (1,L)-\mu (0,L)dP(L)-\left\{\int {\Delta }^1(L)(1-e(L))+{\Delta }^0(L)e(L)dP(L)\right\}$$

Thus, under this ignorability violation, the target is equal to the usual standardization (first term on the right of the equal sign) having subtracted off the bias (the second term, which we define as ξ in the main text).

D. TIME-VARYING TREATMENTS

In the companion GitHub repository, the programs g_comp.R and gcomp.stan simulate the synthetic example and produce the posterior inference behind Figure 3a. Simulating and coding the analyses in this multi-time point setting is a little more tedious - involving more Stan syntax. We leave the details to the code comments. Briefly, the synthetic example contains a single binary treatment, time-varying confounder, and outcome for 10 time points. The confounder at each time point is simulated from a Gaussian with a conditional mean being a function of all previous confounder values. Treatment at each time point is simulated from a Bernoulli with probability being a function of all previous confounder and treatment values. Lastly, a single outcome at the end is simulated from a Gaussian with conditional mean being a function of all previous treatment and confounder values.

The generated quantities block demonstrates how we can simulate confounders sequentially conditional on “always treated” and “never treated” regimes. This is the type of simulation requires to compute ATEs of both static and dynamic treatment regimes outlined in the main text.

E. NONPARAMETRIC MODELS

This Appendix will focus on implementation details behind Section 6 - specifically the computation of ATEs in panel d of Figure 4. We will cover implementation of DP mixtures and BART in R packages ChiRP and BayesTree, respectively, as well as GP models in Stan that are contained in the program npbayes_ATE.R available in the companion GitHub repository. The synthetic data behind this example was simulated as follows. For i = 1, 2, …, n = 500 subjects,

1. Simulate confounder L_i ~ N(0, 1).

2. Simulate treatment assignment, A_i, from Bernoulli with probability

   $$P\left(A_i\mid L_i\right)=\text{expit}\left(1-\frac{1}{2}{L}_i\right)$$
3. Simulate outcome, Y_i, as

   $$Y_i\mid A_i,L_i~N\left(\left(L_i+\frac{1}{2}{L}_i^2\right)A_i,\frac{1}{5}\right)$$

Note above that the conditional treatment effect is a parabolic function of L_i. This is a complex function form. Note that the true causal effect via standardization is:

$$\begin{gathered} \Psi =E_L[E[Y\mid A=1,L]-E[Y\mid A=0,L]] \\ =E_L\left[L_i+\frac{1}{2}{L}_i^2\right] \\ =E_L\left[L_i\right]+\frac{1}{2}{E}_L\left[L_i^2\right] \\ =\frac{1}{2} \end{gathered}$$

The last line follows from the fact that L has a standard normal distribution. A parametric model will only recover this effect if it correctly specified - a tall order for such a complex functional form. Instead, Section 6 illustrates several nonparametric approaches.

Implementation of the model in (12) can be done via the fDPMix() funciton in ChiRP. We refer the reader to the companion web site¹ and R help documentation for detailed information on defaults. The simulated data set is stored in an R object called d_train in npbayes_ATE.R. Recall that we want posterior draws of the conditional outcome mean, for each subject, under both interventions. To that end, we construct the dataset d_test as follows:

d_a1 = data.frame(A=1, L=d_train$L) 
d_a0 = data.frame(A=0, L=d_train$L) 
d_test = rbind(d_a1, d_a0)

Note that d_test is the observed data set stacked twice: once with treatment set to 1 for all subjects, another with treatment set to 0 for all subjects. This will allow us to obtain predictive draws for each subject under both interventions. We now feed these data sets into fDPMix() function and specify that the conditional mean outcome model to be a function of L and A. We take 500 posterior draws after a 500 draw burnin. Initial number of clusters is set to 10. In practice, several chains with various initializations should be run and checked for mixing.

set.seed(2)
res=fDPMix(d_train = d_train, formula = Y ~ L + A,
d_test = d_test, 
iter=1000, burnin=500, init_k = 10)

The object res is a list containing a 2n× iter-burnin matrix where the first n rows are posterior predictions for each subject under treatment A = 1 and the next n rows, from n + 1 to 2n, are posterior predictions under treatment A = 0. The program npbayes_ATE.R has a short function called bayes_boot() that performs BB standardization using these draws, as described in the test. The result is a length iter-burnin vector of posterior draws for the ATE. Additional confounders can be handled accordingly.

The other nonparametric models are implemented very similarly. In the same R program, we have implemented BART using the BayesTree package as:

bart_res = bart(x.train = d_train[, c(‘L’,’A’) ],
y.train = d_train$Y, x.test = d_test, 
ndpost = 500, , nskip = 500)

Here, we take 500 posterior draws after a 500 period burn-in. Again, we stress that in practical examples, longer burnin will likely be required. By default, this implementation runs BART using a sum of 200 trees. The function can accomodate other prior settings. We refer the reader to the R documentation.

The implementation of the GP regression was taken directly from the Stan manual section on Gaussian Processes² with some minor modifications. We leave implementation details to our code and the online manual. It is quite similar to the parametric Stan implementations discussed in earlier appendices. Stan uses the following parameterization of the exponential-quadratic covariance function:

$$C_{ij}={\alpha }^2\text{exp}\left(-\frac{1}{2{ϵ}^2}{\Vert X_i-X_j\Vert }^2\right)$$

The parameter η in the main manuscript corresponds to α², while the parameter ρ in the manuscript corresponds to $\frac{1}{2{ϵ}^2}$ above. In Stan, we can conduct posterior inference on the hyperparameter by assigning them priors. In the program gaussian_process_with_HPs_multi.stan this is done in the model block. Here is the relevant excerpt:

model {
…
rho ~ inv_gamma(5, 5); 
alpha ~ std_normal(); 
…
}

Here since α is declared to be be a non-negative parameter, the specified standard normal prior defaults to a half-normal prior.