Abstract
This paper investigates the effects of Covid-19 outbreak on Turkish gasoline consumption by employing a unique data set of daily data covering the 2014-2020 period. Forecast performance of benchmark ARIMA models are evaluated for both before and after the outbreak. Even the best-fit model forecasts fail miserably after the Covid-19 outbreak. Adding volatility improves forecasts. Consumption volatility increases due to the outbreak. Policies targeting volatility can reduce adverse impacts of similar shocks on market participants, tax revenues, and vulnerable groups.
Keywords: Gasoline consumption, ARIMA models, ARCH family models
1. Introduction
The dynamics of energy markets have attracted considerable attention since the first oil crisis in the 1970s when a sudden surge in oil price in response to a supply shock was observed (Akins, 1973). Sudden declines in energy prices have also attracted attention, as in the case of the first oil glut in the 1980s (Fried, 1982) and in the case of oil price decline in 2014 (Ellwanger et al., 2017). Many studies were conducted to understand the reasons behind sudden and gradual fluctuations in both price and consumption. In high-volatility periods market fundamentals were not sufficient to explain oil price behavior patterns. There are also studies that focus on consumption rather than prices.
Demand for oil products is the primary reason for fluctuations in the global oil market (Lynch, 2002). Bilgin and Ellwanger (2019) show that fuel consumption is very important in explaining elasticities in the global oil market. They point out that demand for oil may depend on the demand for oil products and emphasize the distinction between global and local markets. Fuel consumption forecasts help policy makers in pricing and taxation decisions, and in planning energy security. Consumption forecasts are also important to investors for making future investment decisions (Makridakis et al. 2009) (Kocherlakota, 2009). Furthermore, short-run market disruptions in local fuel markets may have adverse effects on vulnerable groups in a society. Therefore, stability in local fuel markets is of high priority for policy makers.
The new oil glut has just started at the beginning of 2020 (Albulescu, 2020), with the spread of a new virus called Covid-19, namely Severe Acute Respiratory Syndrome Coronavirus 2 (SARS-CoV-2). The virus started to impact the world in a matter of weeks and became a pandemic, reducing both aggregate production and consumption globally. Although oil prices dropped to their lowest level for the last 18 years, demand still declines dramatically due to the pandemic and because of the policies followed to deal with the pandemic (David, 2020). Impacts on local markets deserve a closer look, as they have an immediate impact on households and their dynamics may differ from the global markets.
The purpose of this paper is to examine the effects of Covid-19 outbreak on Turkish gasoline consumption. To this end, we use daily gasoline consumption and make forecasts for 40-day periods before and after the announcement of the first Covid-19 case in Turkey (March 10, 2020). We use ARMA and ARCH family models to reveal the disruptive effect of Covid-19 outbreak on the Turkish gasoline market. We evaluate the forecast performance of benchmark ARMA models in the face of the pandemic and select the best-fit model as a representative model used by market participants. We observe that consumption volatility increased significantly following the announcement. Volatility dynamics are important in explaining the increased uncertainty in response to the pandemic. Our results provide insights into what to expect when a similar shock is encountered in the future. Policy makers should develop immediate response plans that target consumption volatility to mitigate the adverse effects.
The paper is organized as follows: Section II introduces the overview of Turkish gasoline market, Section III presents literature review, Section IV presents data and methodology, Section V presents empirical results and Section VI concludes the paper.
2. Turkish automotive gasoline demand
The total number of vehicles running on gasoline is increasing slowly over the years in Turkey, which is estimated to be 2.8 million in 2014 and 3.0 million by the end of March 2020 with around 1% increase each year. (TSI, 2020) Similarly, gasoline consumption appears to follow a slow upward trend that is not significant. (EMRA, 2020)
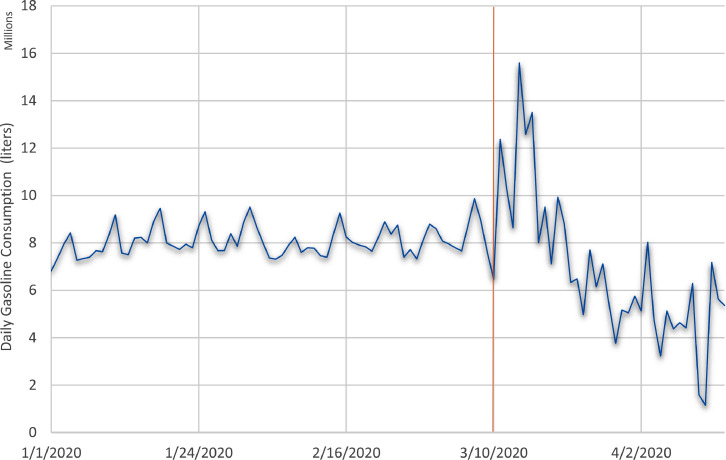
Fig. 1 shows daily gasoline consumption in Turkey over the past 6 years. This is a unique data set, as energy consumption is usually not available in daily frequency. It enables us to see daily dynamics present in the consumption data. As shown in Fig. 1, there is a seasonal trend in the gasoline fuel consumption, mainly increasing in summertime and decreasing during the winter. Moreover, the peaks in each year correspond to specific occasions such as the month of fasting and religious holidays, namely Ramadan, Eid al-Adha, etc. During these periods there is a drastic increase in demand for a short period of time, as vacations up to 10 days during and after these periods increase the demand for travel. The 2020 data presented in Fig. 2 show more clearly how the daily patterns changed after the Covid-19 outbreak.
Fig. 1.
Daily Gasoline Consumption in Turkey Full Sample.
Fig. 2.
Daily Gasoline Consumption in Turkey in 2020 (Gungor et al, 2020a).
The daily seasonality is clearer in Fig. 2. Therefore, there is not only weekly and yearly seasonality, but also daily seasonality in gasoline consumption. Furthermore, the impact of the first Covid-19 case announcement on March 10 (shown by the vertical line in Fig. 2) is evident. Initial immediate increase in consumption can be attributed to impulse purchases in response to a sudden increase in uncertainty, and then a steady declining trend governs the consumption behavior. Of note, the volatility dynamics of gasoline consumption also changed after March 10 (Güngör et al., 2020). This requires a more detailed examination of the volatility structure.
Covid-19 outbreak produced many adverse results in a very short time. It caused temporary shutdown of a fully operated refinery located in İzmir from May 5, 2020 to July 1, 2020. In addition, many oil stations lost their average sales by around 30% as shown in our calculations, especially stations located in the intercity roads lost more than 30% due to travel bans between major cities where 65 million people live (approximately 80% of the population). This shrinkage in the gasoline market also affected the government budget in terms of indirect tax incomes. According to data gathered from MoTaF (2020), liquid fuel taxes constitute 10% to 18% of the total tax revenue in Turkey between 2002 and 2019. Therefore, this 30% shrinkage also reduces government income significantly. Policy makers need immediate action plans to mitigate the adverse effects of similar shocks in the future.
3. Literature review
Over the past five decades, several studies have been carried out on consumption of energy products (oil, electricity, etc.). Many econometric applications were conducted to analyze the demand dynamics of energy products. For example, for Chinese electricity consumption forecasts Zhu and Jianzhou Wang (2011) proposed an integration of the moving average procedure and seasonal autoregressive integrated moving average model (SARIMA) with weight coefficients. Al-Qaness et al. (2018) used a modified data mining method, called as Sine-Cosine Algorithm adaptive neuro-fuzzy inference system (SCA-ANFIS), to forecast oil products’ consumption of Canada, Germany, and Japan using the data from 2007 to 2018, containing 120 records per month for each country. Öztürk and Öztürk (2018) used energy consumption data from 1970 to 2015 to forecast energy consumption of Turkey for the next 25 years using ARIMA model. Azadeh et al. (2014, s. 5), however, used integrated fuzzy mathematical programming-regression-ANOVA approach to forecast gasoline consumption in selected countries (ISE, Canada, Japan, Iran, and Kuwait) by using monthly data for the period 1992 to 2005. To project gasoline and diesel demand in India up to 2025, Agrawal (2015) adopted a different perspective and considered both long- and short-run demand relations using the autoregressive distributed lag (ARDL) and error correction mechanism (ECM) co-integration procedures. Bhutto et al. (2017) preferred a univariate approach and used Autoregressive Integrated Moving Average (ARIMA) model to forecast annual gasoline consumption in Pakistan, and policy makers demanded their forecasts, planning to make ethanol as a gasoline substitute. Li et al. (2018) considered 26 combination models based on an AI algorithm using traditional combination methods to forecast oil consumption in China. Duan et al. (2018) presented the gray-extended self-adapting intelligent gray model to predict the total crude oil consumption of China using 2002–2014 yearly data to forecast China's 2015–2020 crude oil consumption. Moreover, Li et al. (2010) provided an analysis of future gasoline demand in Australia by using eight models [including partial adjustment model (PAM), ARIMA, Holt's linear model, and Holt-Winter’ model]. They mainly concluded that more sophisticated models do not always produce better forecasting results than simple models. They recommended determining the characteristics of a time series before modeling and forecasting it. In this study we follow their suggestions.
There are few studies on Turkish gasoline consumption. Melikoglu (2014) forecasts that the annual gasoline consumption in Turkey could decline to 2.0 million m3 in 2023 in accordance with the government targets and European directives. Hasanov (2015) reports income and price inelasticity in quarterly demand for gasoline in Turkey. Mikayilov et al. (2020), also using quarterly data, show that short-run gasoline demand in Turkey is not sensitive to changes in income, prices, and car stock, suggesting that short-run fluctuations may be driven by other factors in the short run. Gungor et al. (2020b) study the volatility dynamics of Turkish diesel consumption and show that consumption volatility increased in response to the pandemic. This paper extends their discussion to gasoline consumption.
The majority of studies in the literature attempt to predict the annual or quarterly gasoline/diesel/crude oil consumption using many assumptions and applying a variety of independent variables. The data frequencies are either yearly, quarterly, or monthly in most of these studies. In this paper, we employ daily data on Turkish gasoline consumption to better capture the short-run dynamic impact of the pandemic on the market. Using high-frequency data allows us not only to understand how rapidly consumption patterns changed, but also to examine what happened to market uncertainty via consumption volatility. To the best of our knowledge, this is the first study that focuses on daily consumption patterns in a local gasoline market.
4. Data and methodology
In the empirical analysis, we use daily gasoline consumption in liters covering the period January 1, 2014 to April 19, 2020. Table 1 presents descriptive statistics of the daily gasoline consumption of Turkey.
Table 1.
Descriptive statistics (January 1, 2014 to April 19, 2020).
| Gasoline Consumption (liters) | |
|---|---|
| Mean | 8.056 million |
| Median | 7.836 million |
| Maximum | 22.315 million |
| Minimum | 1.142 million |
| Std. Dev. | 1.561 million |
| Skewness | 1.168 |
| Kurtosis | 9.302 |
| Jarque-Bera | 4332 |
| Observations | 2301 |
According to Table 1, average daily gasoline consumption is 8.056 million liters and median value is 7.836 million liters within our sample period. Maximum and minimum values are 22.314 million and 1.142 million liters, respectively, but standard deviation is 1.561 million. This implies that daily gasoline consumption does not vary a lot, but the high range indicates that occasional spikes occur. Moreover, according to Jarque-Bera test, normal distribution assumption is not valid for daily gasoline consumption. For this reason, we consider alternative distributions in the empirical model. Positive skewness value for gasoline consumption indicates right skewed distribution, whereas the kurtosis value of 9.302 shows the fat tail characteristics of the daily gasoline consumption distribution.
We apply logarithmic difference (growth rate) of gasoline consumption data to ensure stationarity condition in the econometric modeling. Following the suggestion of Li et al. (2010) we first check the stationarity properties of growth rates employing both conventional Ng-Perron unit root test and structural break unit root test of Zivot- Andrews (1992) and Lee-Strazicich (2003). We do not find any evidence of non-stationarity.
A variety of econometric methods can be used to forecast time series. A commonly used stochastic time series model is ARIMA (Autoregressive Integrated Moving Average) model. The univariate ARIMA models are simple and easy to estimate, and they are usually used as benchmark models against which forecasting performances of alternative models are compared. Under certain conditions, their forecasting performances are comparable to sophisticated models. These models analyze the stochastic properties of economic time series and use the history of the series itself instead of independent variables. In that respect, these models can be viewed as a-theoretical and are disadvantaged by omitted variable bias; however, adding independent variables may result in other complications such as endogeneity and multicollinearity. ARIMA models are the combination of differencing, moving average (MA) models and autoregressive (AR) models and they mainly focus on lagged observations lagged dependent variables and error terms.
After stationarity checks, we assess the best-fit ARIMA structure for gasoline consumption data to compare forecasting performance of this benchmark model before and after the Covid-19 outbreak.
Then we investigate volatility dynamics of the daily gasoline consumption by using alternative ARCH family models. We assess alternative ARCH family models, including ARCH, GARCH, EGARCH, and TGARCH models, and we select the best model based on forecast performance criteria. Then, we extract the conditional variance from the best-fit model as consumption volatility.
Finally, we added the volatility variable to the best-fit ARMA model as an independent variable and assess how the forecast performance of the model changes after Covid-19 outbreak when the volatility variable is added.
5. Results
The forecasting models we consider require the time series to be stationary. Therefore, we first investigate stationarity properties of growth rate of the gasoline consumption by using both conventional Ng-Perron unit root test and Zivot-Andrews (1992) structural break test for one break and Lee- Strazicich (2003) structural break unit root test for 2 breaks. Both Ng-Peron, Zivot Andrews (1992) and Lee- Strazicich (2003) tests indicate the stationarity of the growth rate of the gasoline consumption variable1 .
After stationarity checks, we estimate the best-fit AR/ARMA structure for growth rate of the gasoline consumption for the period January 1, 2014 to March 10, 2020. Table 2 presents alternative ARMA model results2 .
Table 2.
- Alternative ARMA model results (January 1, 2014 to March 10, 2020).
| ARMA(7,6) | ARMA(7,7) | SARMA(7,7)(1,1) | SARMA(7,6) (1,1) | SARMA(1,1) (7,7) | |
|---|---|---|---|---|---|
| AR(1) | (0.445)* | ||||
| MA(1) | (-0.849)* | ||||
| AR(7) | (0.470)* | (0.999)* | (0.999)* | (0.475)* | |
| MA(6) | (0.099)* | (0.078)* | |||
| MA(7) | (-0.987)* | (-0.988)* | |||
| SAR(1) | (0.445)* | (0.558)* | |||
| SMA(1) | (-0.849)* | (-0.959)* | |||
| SAR(7) | (0.999)* | ||||
| SMA(7) | (-0.988)* | ||||
| C | 0.001 | 0.004 | 0.001 | 0.001 | 0.001 |
| Model Selection Criteria and Diagnostic Checks | |||||
| AIC | -2.027 | -2.313 | -2.528 | -2.234 | -2.527 |
| SC | -2.020 | -2.305 | -2.515 | -2.221 | -2.514 |
| 74.832[0.000] | 179.463[0.000] | 0.772[0.379] | 1.464[0.219] | 0.774[0.379] | |
| Forecast Performance (Estimation 01.01.2014-30.01.2020 - Forecast 31.01.2020-3.10.2020) | |||||
| RMSE | 652890 | 456469 | 446235 | 634289 | 465563 |
| MEA | 501729 | 353847 | 348866 | 513418 | 358591 |
| MAPE | 6.077 | 4.451 | 4.351 | 6.397 | 4.527 |
| Theil | 0.040 | 0.027 | 0.026 | 0.039 | 0.028 |
Notes: Five estimated models include ARMA(7,6), ARMA(7,7), SARMA(7,7)(1,1), SARMA(7,6) (1,1), and SARMA(1,1) (7,7). Only statistically significant coefficients are shown in the table. * indicates significance at the 1% level. AIC and SC represent Akaike Information Criterion and Schwartz Criterion, respectively denotes Breusch-Godfrey test statistic which follows a χ2 distribution. RMSE is root mean square error, MEA is mean absolute error, MAPE is mean absolute percentage error, and Theil stands for the Theil inequality index.
According to Table 2, both ARMA(7,6) and ARMA(7,7) models demonstrate severe autocorrelation problems and we omit these models. Seasonal ARMA (SARMA) models seem to have better fits due to the apparent seasonality in the series. SARMA(7,7)(1,1) model is found to be the best fit model for gasoline demand variable according to both model selection criteria and forecast performance criteria.
After we define best fit model for the full sample, we make forecasts for periods before and after Covid-19 outbreak in Turkey (March 10, 2020) to show how Covid-19 outbreak distorts forecast performance of the models.
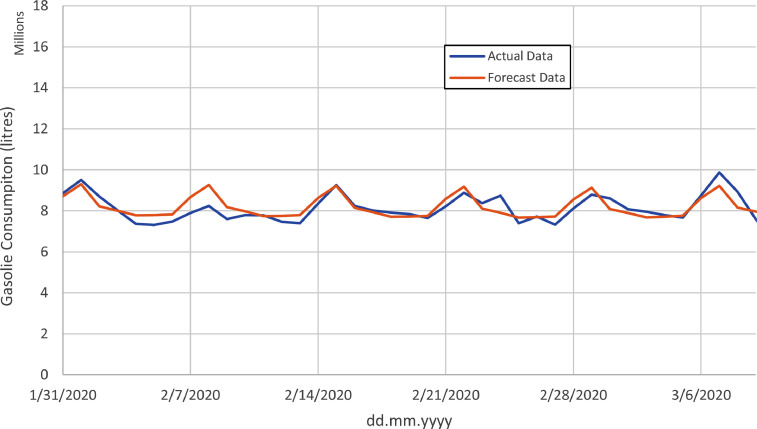
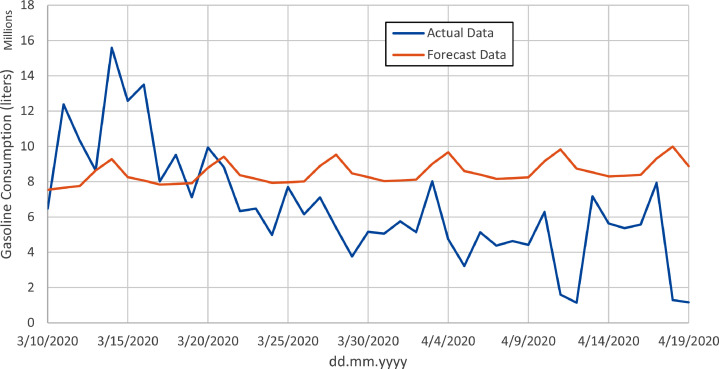
For this reason, we estimate the model for the period January 1, 2014 to January 30, 2020 and forecast for the period January 31, 2020 to March 10, 2020 (40 days) to assess the forecast performance of the model. Then, we assess the model for the period January 1, 2014 to March 10, 2020 and forecast for the period March 11, 2020 to April 19, 2020(40 days) to analyze the forecast performance of the model after Covid-19 outbreak. This enables us to compare our 40-day forecasts before and after our Covid-19 break date, March 10, 2020. Before and after forecasts along with actual data are shown in Fig. 3, Fig. 4 , respectively.
Fig. 3.
Forecasts Before Covid-19 Outbreak.
Fig. 4.
Forecasts after Covid-19 outbreak.
Fig. 3 and Fig. 4 show how Covid-19 outbreak distorts the forecast performance of the best-fit SARMA(7,7)(1,1) model. Prior to Covid-19 outbreak, there is only 0.8% difference between actual and forecasted gasoline consumption data. On the other hand, Fig. 4 shows that there is an approximately 30% difference between actual and forecasted total gasoline consumption data after Covid-19 outbreak.
The consumer behavior has revealed a vastly different situation than expected with the government sanctions because of the volatility observed in consumptions since the first appearance of the Covid-19 case in Turkey. Gasoline demand dynamics after the first case in Turkey are uncommon compared to historical movements. A downward trend and increased volatility seem to govern demand dynamics in this period following a temporary initial jump. Therefore, models that rely on historical data will have very poor forecast performances for this period. These data show how oil markets are shrinking in response to a global health crisis.
In the second part of our analysis, we investigate volatility dynamics of the gasoline consumption data. We assess alternative ARCH family models, including ARCH, GARCH, EGARCH, and TGARCH models, by employing best-fit ARMA model as mean equation for the period January 1, 2014 to April 1, 20203 . Then we select the best model according to several forecast performance criteria. Table 3 presents the results of the alternative volatility models.
Table 3.
Volatility model results.
| ARCH(1) | GARCH(1,1) | TGARCH(1,1) | EGARCH(1,1) | ||||
|---|---|---|---|---|---|---|---|
| Mean Equation | |||||||
| AR(7) | (0.999)* | (0.999)* | (0.999)* | (0.999)* | |||
| SAR(1) | (0.407)* | (0.401)* | (0.526)* | (0.525)* | |||
| MA(7) | (-0.983)* | (-0.983)* | (-0.983)* | (-0.982)* | |||
| SMA(1) | (-0.840)* | (-0.823)* | (-0.855)* | (-0.850)* | |||
| C | (-0.043) | (-0.022) | (0.002) | (0.005) | |||
| Variance Equation | |||||||
| (0.171)* | (0.150)** | (0.702)* | |||||
| (0.600)* | (0.257)* | ||||||
| (0.438)* | |||||||
| (-0.130)* | |||||||
| (0.559)* | |||||||
| (0.723)* | |||||||
| C | (0.015)* | (0.014)* | (0.001)* | (-2.047)* | |||
| Model Selection Criteria Results | |||||||
| AIC | -2.012 | -2.303 | -2.899 | -2.881 | |||
| SC | -1.992 | -2.281 | -2.877 | -2.858 | |||
| Forecast Performance (Estimation January 1, 2014 to January 30, 2020; Forecast January 30, 2020 to October 3, 2020) | |||||||
| RMSE | 448628 | 449189 | 447458 | 448406 | |||
| MEA | 356854 | 351654 | 350794 | 351711 | |||
| MAPE | 4.409 | 4,399 | 4.384 | 4.388 | |||
| Theil | 0.028 | 0.027 | 0.027 | 0.027 | |||
Notes: *, ** denote significance at the 1% and 5% levels, respectively. Variance equations are as follows. ARCH: . GARCH: . TGARCH: . EGARCH: . RMSE is root mean square error, MEA is mean absolute error, MAPE is mean absolute percentage error, and Theil stands for the Theil inequality index.
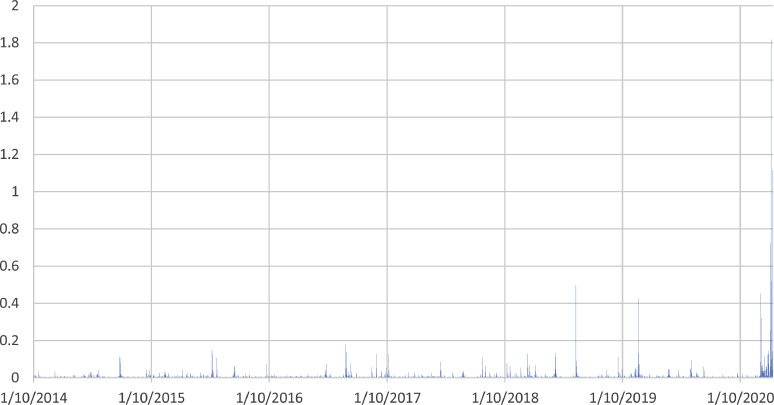
TGARCH(1,1) model performs as the best model according to both model selection and forecast performance criteria. The conditional heteroscedasticity of the best fit model is taken as the volatility of Turkish gasoline consumption. Conditional heteroscedasticity obtained from TGARCH(1,1) model is presented in Fig. 5 .
Fig. 5.
Volatility variable obtained from TGARCH(1,1) model.
As shown in Fig. 5, the uncommonly high volatility starts after March 11, 2020, which is the day after the announcement of the first Covid-19 case. Subsequently, the volatility value reaches its peak in the middle of April 2020 because of new sanctions of the government, such as weekend curfews and bans on some intercity travels.
Finally we added the volatility variable to SARMA(7,7)(1,1) model as an independent variable and investigate how forecast performance changes after adding the volatility variable to the best-fit ARMA model to have a GARCH in mean model. We have already established that Covid-19 outbreak distorts the gasoline consumption forecasts for the period March 11, 2020 to April 19, 2020. We employ SARMA(7,7)(1,1) model with and without volatility variables and estimate the model for the period January 1, 2014 to March 10, 2020 and forecast for the period March 11, 2020 to April 19, 2020. Forecast performance comparison of the SARMA(7,7)(1,1) model with and without the volatility variable for the period March 11, 2020 to April 19, 2020 is presented in Table 4 .
Table 4.
- Forecast performance comparison of the best fit model with and without the volatility variable after Covid-19 outbreak.
| SARMA(7,7)(1,1)- Without Volatility | SARMA(7,7)(1,1)- With Volatility | |
|---|---|---|
| RMSE | 3509168 | 3463934 |
| MEA | 2795437 | 2663320 |
| MAPE | 88.484 | 41.341 |
| Theil | 0.231 | 0.192 |
Notes: RMSE is root mean square error, MEA is mean absolute error, MAPE is mean absolute percentage error, Theil stands for the Theil inequality index.
Table 4 shows that the volatility variable increases the forecast performance of the best-fit SARMA(7,7)(1,1) model. Fig. 6 presents the actual gasoline consumption data and forecasts obtained from SARMA(7,7)(1,1) model with and without volatility variables.
Fig. 6.
Forecasting graph with and without volatility variable after Covid-19 outbreak.
Fig. 6 also shows that forecast performance of the SARMA(7,7)(1,1) model increases when we consider the conditional variance. For the first couple of days following the announcement of the first case, the no-volatility model forecasts appear to be closer to actual values, but these days are governed by impulse purchases caused by panic and the phenomenon does not last long. The increase in the volatility due to Covid-19 outbreak hampers the forecast performance of the best-fit model. This shows that increased uncertainty must be accounted for in the model to improve the forecast performance.
6. Conclusions
In this paper, we examined the effect of Covid-19 outbreak on daily Turkish gasoline consumption covering the period January 1, 2014 to April 19, 2020. Initial response to the announcement of the first case on March 10, 2020 shows a short-lived positive spike followed by a steady downward trend, around which an uncommonly high volatility is observed. We assess the forecast performance of benchmark ARIMA models both before and after the outbreak. Although the best-fit model forecasts fail heavily after the announcement, when the changes in the volatility structure of daily gasoline consumption are taken into account, the forecast performance improves. We next summarize the empirical steps.
In the empirical analyses, we first checked stationarity of growth rate of the gasoline consumption of Turkey. Then, we determine the best-fit AR/ARMA structure, supposedly used by market participants to forecast growth rate of gasoline consumption. SARMA(7,7)(1,1) model is the best-fit model according to both model selection and forecast performance criteria. Then, we forecast gasoline consumption 40 days before and 40 days after the announcement of the first Covid-19 case in Turkey (March 10, 2020) to indicate how Covid-19 outbreak distorts forecasting ability of market participants. We find that, before the outbreak, there is only 0.8% difference between actual and forecasted gasoline consumption data. However, there is approximately a 30% difference after the outbreak. Next, on examining the volatility dynamics of the gasoline consumption, we find that TGARCH(1,1) model is the best model according to both model selection and forecast performance criteria. We derive the conditional heteroscedasticity of the best-fit model as the volatility of Turkish gasoline consumption. We observe that gasoline consumption volatility intensifies significantly after the outbreak. The high-volatility episode starts on March 11, 2020, which is the day after the announcement of the first Covid-19 case. Subsequently, the volatility value reaches its peak in mid-April because of new sanctions imposed by the government, such as weekend curfews and intercity travel bans. Finally, we added the volatility variable to SARMA(7,7)(1,1) model as an independent variable and investigate how forecast performance changes after adding the volatility variable to the best-fit ARMA model and found that forecast performance of the SARMA(7,7)(1,1) model increases after we add the volatility variable as an independent variable. We show that the increase in the volatility due to Covid-19 outbreak causes distortion in the forecast performance of the best-fit model.
Our main conclusion is that, in response to similar shocks, policy makers should design policy responses that target consumption volatility to stabilize the market, which will reduce the uncertainty faced by market players, stabilize tax revenues, and protect vulnerable groups. Second, policy makers and traders should avoid using benchmark models to predict energy use during similar crises. They should consider models that capture the increased volatility structure. Although countries attempt to adopt policies to put their economies on track, conventional economic policies are not likely to have a significant impact on energy markets in the short run. This is because the short-run energy consumption behavior is likely to be driven by measures taken by government authorities to contain the pandemic (e.g., curfews, travel bans), by social behavior (e.g., social distancing, work from home, online meetings), and by market expectations (e.g., hoarding). Although government measures can be lifted overnight, social behavior and expectations may last longer. To relieve the disruptive effects of Covid-19 pandemic, we make two proposals: temporary rearrangement of profit margins of the dealers and liquid fuel distributors and a temporary tax regulation throughout the year to compensate the tax revenue lost. Such measures are expected to reduce volatility in gasoline consumption, stabilize the market, and mitigate the decline in tax revenues. Reduced volatility can benefit energy-poor households who tend to make low-volume but high-frequency purchases. It would be enlightening to examine the results of these measures in the near future as the pandemic and responses to the pandemic evolve.
CRediT authorship contribution statement
Bekir Oray Güngör: Data curation, Methodology, Writing - original draft, Writing - review & editing. H. Murat Ertuğrul: Data curation, Writing - review & editing. Uğur Soytaş: Writing - review & editing.
Biographies
Bekir Oray GÜNGÖR is a senior energy expert, working at Energy Market Regulatory Authority of Turkey since 2006. He received a M.Sc degree in computer engineering from Middle East Technical University of Ankara and as well as another M.Sc Degree in energy engineering from Pennsylvania State University of United States. His expertise area is mainly focusing on regulations on energy market, analyzing and reporting data gathered from energy market players and monitoring the structure of the market.
Assoc.Prof. Hasan Murat ERTUGRUL is a macroeconomics and applied macro-economic modeling professional. He received a Ph.D. degree in economics from Hacettepe University, Ankara/Turkey in 2012. His research interests focus on macroeconomics, applied macroeconomic modeling, forecasting and energy economics. He has a book, three book chapter, one international book editorship and numbers of papers indexed in SSCI and other indexes. Also, he takes a role as referee in lots of international and national journals.
Ugur Soytas is the Co-editor of Energy Economics, editor of the Routledge Handbook of Energy Economics, and Special issue editor for Energy Research Letters. He holds an MBA and a PhD in Economics from Texas Tech University. He has been working at METU since 2001. He will join the Sustainability Division of Denmark Technical University in August 2020. He will be leading the Climate Economics and Risk Management research group. He is an applied researcher in two multidisciplinary areas: energy-economy-environment-society nexus and commodity-financial market links. He published several papers in high impact peer reviewed journals such as Applied Energy, Annals of Operations Research, Economic Modelling, Energy Economics, Energy, Energy Policy, Ecological Economics, Emerging Markets Finance and Trade, Frontiers in Energy Research, Global Finance Journal, International Review of Finance, Journal of Banking and Finance, Journal of Commodity Markets, Journal of Evolutionary Economics, Journal of Policy Modeling, Managerial Finance, and Resources Policy among others. Citations to his works amount to 7793 and he has an h-index of 28 and i10 index of 44 (according to Google Scholar as of 04.19.2019). Several of his papers are recognized as highly influential in the energy economics (1 article), and environmental and ecological economics (5 articles) fields. He participates in several energy and climate change related projects at both national and international levels.
Footnotes
We did not add stationarity test results in order to save space. The results are available from authors upon request.
To estimate best-fit ARIMA model, we employ Box Jenkins 4 step procedure. We consider all possible models from SARMA(0,0)(0,0) to SARMA(7,7)(1,1), which makes 256 models and ascertained the best 5 models according to LogL (Log Likelihood), AIC (Akaike Information Criterion), and BIC (Bayesian Information Criterion).
We use student t distribution instead of normal distribution because of the Jarque-Bera test results presented.
ANNEX: ARIMA model
ARIMA method, also known as Box-Jenkins methodology, is one of the most widely used forecasting methods for univariate time series data forecasting. AR(p), MA(q), and ARMA(p,q) models are based on stationary time series. If the time series data is non-stationary ARMA model, giving a differenced d times before it becomes stationary, as non-seasonal model, which can be written as:
| (1) |
As a short version, model in lag (L) operator form can be written as:
| (2) |
where is white noise, L is the backshift operator (), and and are the polynomials of orders p and q, respectively.
However, this method does not support seasonable components, in other words time series with a repeating cycle, and a tweak is required to handle and give such a support to ARIMA, which is called seasonal ARIMA. Similarly, a seasonal ARIMA (SARIMA) model is the most common model used in many applications in industries, economics, and financial literature. (Tseng and Tzeng, 2002)
There are some new hyperparameters to the components of ARIMA in SARIMA model, named as seasonal autoregression (SAR), differencing (D), and seasonal moving average (SMA), as well an additional parameter for the period of the seasonality. (Athanasopoulos and Hyndman, 2013)
The time series is mainly represented by , where p, q, d were discussed before, the next terms represent seasonal parameters, and lastly indicates seasonal length in the data.
In the lag operator, if we transform ARIMA into a polynomial form of the SARIMA, Eq. (3) can be written as:
| (3) |
where blue parts in Eq. (3) show the new terms in the ARIMA to transform the model into SARIMA. (Camara et al., 2016) In order to assess the best SARIMA model for gasoline consumption data, the non-seasonal and seasonal components of autoregressive and moving average parameters must be estimated. To do so, the information criteria, such as Akaike Information Criterion (AIC), Bayesian Information Criterion (BIC), and the Hannan–Quinn criterion (HQ), are used to determine the best model.
Conditional variance models (Volatility Models)
ARCH model
In econometrics, the concept of conditional variance was used for the first time in the literature by
Engle (1982). Engle modeled conditional variance as a function of the past values of error term and defined the autoregressive conditional variance model as follows [ARCH(q)]:
| (4) |
Therefore, ARCH[1] can be expressed as:
| (5) |
where is the white noise error term distributed as and . Moreover, and are constant where and .
GARCH Model
One of the biggest problems of the ARCH model is that it is possible too many past values of error terms could be found statistically significant. To solve this problem, Bollerslev (1986) proposed Generalized Autoregressive Conditional Variable Variance (GARCH) model. GARCH(p,q) can be expressed as:
| (6) |
Therefore, GARCH[1,1] can be expressed as:
| (7) |
TGARCH model
Standard ARCH/GARCH models do not take asymmetry into consideration. In ARCH/GARCH models, only the magnitude of the shock is important. Its sign is ignored. TGARCH model proposed by Glosten et al. (1993) investigate the effect of asymmetry on volatility. The TGARCH model specification is presented below:
| (8) |
So TGARCH(1,1) can be expressed as;
| (9) |
The only difference between TGARCH(1,1) and GARCH(1,1) model is the term in Eq. (9). The function is an indicator function to help to model the asymmetry. Positive asymmetry parameter indicates that asymmetry is present.
EGARCH model
EGARCH model proposed by Nelson (1991) was defined as logarithmic, and by doing so negative parameter values are prevented. Thus, the coefficients could take negative values.
EGARCH (1,1) is expressed as:
| (10) |
EGARCH model takes the asymmetry into consideration.
References
- Agrawal P. India's petroleum demand: estimations and projections. Appl. Econ. 2015:1199–1212. [Google Scholar]
- Akins J.E. The oil crisis: this time the wolf is here. Foreign Aff. 1973;51(3):462–490. [Google Scholar]
- Albulescu C.T. Coronavirus and oil price crash. Soc. Sci. Res. Netw. 2020 [Google Scholar]
- Al-Qaness M.A., Elaziz M.A., Ewees A.A. Oil consumption forecasting using optimized adaptive neuro-fuzzy inference system based on sine cosine algorithm. IEEE Access. 2018;6:68394–68402. [Google Scholar]
- Athanasopoulos G., Hyndman R.J. 2013. Forecasting: Principles and Practice. [Google Scholar]
- Azadeh A., Behmanesh I., Arani H.V., Sadeghi M.H. An integrated fuzzy mathematical programming-analysis of variance approach for forecasting gasoline consumption with ambiguous inputs: USA, Canada, Japan, Iran and Kuwait. Int. J. Ind. Syst. Eng. 2014:159–184. [Google Scholar]
- Bhutto A.W., Bazmi A.A., Qureshi K., Harijan K., Karim S., Ahmad M.S. Forecasting the consumption of gasoline in transport sector in pakistan based on ARIMA model. Environ. Progr. Sustain. Energy. 2017;36(5):1490–1497. [Google Scholar]
- Bilgin D., Ellwanger R. Bank of Canada; 2019. The Simple Economics of Global Fuel Consumption (No. 2019-35) [Google Scholar]
- Bollerslev T. Generalized autoregressive conditional heteroskedasticity. J. Econ. 1986;31:307–327. [Google Scholar]
- Camara A., Feixing W., Xiuqin L. Energy consumption forecasting using seasonal ARIMA with artificial neural networks models. Int. J. Bus. Manag. 2016:11. [Google Scholar]
- David D. 2020, 03 30. BBC News.https://www.bbc.com/news/business-52089127 Retrieved from Coronavirus: Oil price collapses to lowest level for 18 years. [Google Scholar]
- Duan H., Lei G.R., Shao K. Forecasting crude oil consumption in china using a grey. Complexity. 2018:1–12. [Google Scholar]
- Ellwanger R., Sawatzky B., Zmitrowicz K. Factors behind the 2014 oil price decline. Bank of Canada Rev. 2017;2017(Autumn):1–13. [Google Scholar]
- EMRA . 2020, 05 01. Energy Market Regulatory Authority Database. Ankara, Turkey. [Google Scholar]
- Engle R.E. Autoregressive conditional heteroscedasticity with estimates of the variance of United Kingdom inflation. Econom. J. Econom. Soc. 1982:987–1007. [Google Scholar]
- Fried E.R. Brookings Institution Press; 1982. After the Oil Glut; pp. 6–11. [Google Scholar]
- Glosten L.R., Jagannathan R., Runkle D.E. On the relation between the expected value and the volatility of the nominal excess return on stocks. J. Finance. 1993:1779–1801. [Google Scholar]
- Güngör B.O., Ertuğrul H.M., Soytaş U. Effect of COVID-19 outbreak on Turkish gasoline and diesel demand. Bilkent Energy Policy Res. Center. 2020:27. [Google Scholar]
- Güngör B.O., Ertuğrul H.M., Soytaş U. The effect of the COVID-19 outbreak on the Turkish diesel consumption volatility dynamics. Energy Res. Lett. 2020;1(3) [Google Scholar]
- Hasanov M. The demand for transport fuels in Turkey. Energy Econ. 2015;51:125–134. [Google Scholar]
- Kocherlakota N. N.Kocherlakota. The Region; 2009. Modern macroeconomic models as tools for economic policy. [Google Scholar]
- Lee J., Strazicich M.C. Minimum lagrange multiplier unit root test with two structural breaks. Rev. Econ. Stat. 2003;85(4):1082–1089. [Google Scholar]
- Li J., Wang R., Jianzhou Wang Y.L. Analysis and forecasting of the oil consumption in China based on combination models optimized by artificial intelligence algorithms. Energy. 2018:243–264. [Google Scholar]
- Li Z., Rose J.M., Hensher D.A. Forecasting automobile petrol demand in Australia: An evaluation of empirical models. Transp. Res. Part A: Policy Pract. 2010:16–38. [Google Scholar]
- Lynch M.C. Forecasting oil supply: theory and practice. Q. Rev. Econ. Financ. 2002;42:373–389. [Google Scholar]
- Makridakis S., Hogarth R.M., Gaba A. Forecasting and uncertainty in the economic and business world. Int. J. Forecast. 2009;25:794–812. [Google Scholar]
- Melikoglu M. Demand forecast for road transportation fuels including gasoline, diesel, LPG, bioethanol and biodiesel for Turkey between 2013 and 2023. Renew. Energy. 2014;64:164–167. [Google Scholar]
- Mikayilov J.I., Mukhtarov S., Dinçer H., Yüksel S., Aydın R. Elasticity analysis of fossil energy sources for sustainable economies: a case of gasoline consumption in Turkey. Energies. 2020;13:731. [Google Scholar]
- MoTaF . 2020, 05 15. Tax Revenue from Fuel Oil.https://www.gib.gov.tr/yardim-ve-kaynaklar/istatistikler Retrieved from President of revenue management, Ministry of Treasury and Finance of Turkey. [Google Scholar]
- Öztürk S., Öztürk F. Forecasting Energy Consumption of Turkey by ARIMA Model. J. Asian Sci. Res. 2018:52–60. [Google Scholar]
- Tseng F.-M., Tzeng G.-H. A fuzzy seasonal ARIMA model for forecasting. Fuzzy Sets Syst. 2002:367–376. [Google Scholar]
- TSI . Turkish Statistical Institute; 2020, 04 01. Distribution of Cars Registered to the Traffic According to Fuel Type.http://www.turkstat.gov.tr/UstMenu.do?metod=temelist Retrieved from. [Google Scholar]
- Zhu S., Jianzhou Wang W.Z. A seasonal hybrid procedure for electricity demand forecasting in China. Appl. Energy. 2011:3807–3815. [Google Scholar]