Submodular generalized matching for peptide identification in tandem mass spectrometry

Motivation:

Identification of spectra produced by a shotgun proteomics mass spectrometry experiment is commonly performed by searching the observed spectra against a peptide database. The heart of this search procedure is a score function that evaluates the quality of a hypothesized match between an observed spectrum and a theoretical spectrum corresponding to a particular peptide sequence. Accordingly, the success of a spectrum analysis pipeline depends critically upon this peptide-spectrum score function. We develop peptide-spectrum score functions that compute the maximum value of a submodular function under m matroid constraints. We call this procedure a submodular generalized matching (SGM) since it generalizes bipartite matching. We use a greedy algorithm to compute maximization, which can achieve a solution whose objective is guaranteed to be at least $\frac{1}{1+m}$ of the true optimum. The advantage of the SGM framework is that known long-range properties of experimental spectra can be modeled by designing suitable submodular functions and matroid constraints. Experiments on four data sets from various organisms and mass spectrometry platforms show that the SGM approach leads to significantly improved performance compared to several state-of-the-art methods. Supplementary information, C₊₊ source code, and data sets can be found at https://melodi-lab.github.io/SGM.

1. Introduction

A shotgun proteomics experiment produces on the order of 10 mass spectra per second, each of which ideally is generated by a single peptide species. Hence, before the data can be used to answer high-level biological questions—like which functional classes of proteins are differentially expressed in one experimental condition versus another—we must first answer a simpler question, namely, “What peptide species was responsible for generating this observed spectrum?”

Over the past two decades, since the description in 1994 of the SEQUEST algorithm [1], by far the most common way to answer this question has been via database search. All such methods follow roughly the same form. The input is a set of observed spectra and a database of peptides, typically derived from the protein sequences of the organism under study. The database search algorithm is then deceptively simple: for each observed spectrum, we (1) extract from the database all peptides whose masses lie within a user-specified tolerance of the precursor mass associated with the spectrum, (2) compute a quality score for each peptide-spectrum match (PSM), and (3) assign to the spectrum the candidate peptide that received the best score.

Clearly, the success or failure of a database search method depends very strongly upon the quality of its score function. A good database search score function must exhibit at least three distinct properties. First, it must be quick to compute. At a production rate of 10 spectra per second, where each spectrum must be compared to hundreds or thousands of candidate peptides, an expensive score function will quickly become the bottleneck in any analysis pipeline. Second, the function must be accurate, in the sense that it usually succeeds in assigning the best score to the candidate peptide that actually was responsible for generating the observed spectrum. Third, the function must be well calibrated, so that the score assigned to the top peptide for one spectrum can be compared directly to the score assigned to the top peptide for a second spectrum. This third property is important because, in practice, the output of a database search algorithm is a ranked list of PSMs, one per observed spectrum. Because many observed spectra cannot be accurately identified, it is critical that the top of this ranked list of PSMs is highly enriched for correct identifications. Calibration is also important for comparing spectra containing different numbers of peaks, since an uncalibrated algorithm tends to give higher scores to more dense spectra.

Dozens of database search score functions have been described in the literature (reviewed in [2]). Most rely on first transforming the peptide sequence into a theoretical spectrum and then computing some type of similarity score between the observed and theoretical spectra. Existing similarity functions rely on cross-correlation (SEQUEST) [1], dot product (X!Tandem) [3], Poisson scoring (OMSSA) [4], hypergeometric scores (Myrimatch) [5], probabilistic models (ProbID) [6] or simple counts of overlapping peaks (Morpheus) [7].

In this work, we propose to model the affinity between an observed and theoretical spectrum using a process we call a “submodular generalized matching” (SGM). This approach generalizes and provides greater modeling power than standard bipartite matching. In order to describe SGMs, we need first to describe bipartite matchings, submodular functions and their optimization, and matroids. We briefly do so in the next few paragraphs and further discuss submodular function in Section 2.

A maximum bipartite matching starts with a non-negative weighted bipartite graph (V, U, E, w), where V is a set of “left” vertices, U is a set of “right” vertices, $E\subseteq V\times U$ is a set of edges, and $w:E\to {ℝ}_{+}$ is a weight function on the edges, where $w(A)={\sum }_{a\in A}w(a)$ for any edge set $A\subseteq E$. The goal of a maximum bipartite matching process is to find a set of edges $A\subseteq E$ that maximizes w(A) but that is a matching, i.e., no vertex may be incident to more than one edge. Conceptually, one might treat computing a peptide-spectrum matching score as finding a maximum matching in a bipartite graph consisting of an observed spectrum (represented by the vertices V), a theoretical spectrum (the vertices U), and the edges E (feasible explanations of the observed by the theoretical spectra). In other words, given an edge e ∈ E where e = (v, u) with v ∈ V, u ∈ U, the weight w(e) (which may be zero) indicates the degree to which theoretical peak u matches observed peak v.

For several reasons, however, maximum bipartite matching alone is inadequate to produce a good peptide-spectrum scoring function. First, only one edge in a traditional matching may be incident to a vertex, even though, as described below, a given theoretical fragmentation event might produce multiple effects in the observed spectrum. Conversely, several different theoretical peaks might potentially explain a single observed peak. Second, the score function of a bipartite matching w(A) is necessarily additive, meaning that the weight of an edge does not change when considered in the context of other edges added to a matching. In practice, an optimal score function might need to combine matching scores in a non-additive fashion. To address the first problem, we use matroid constraints, and to address the second problem we use submodular functions. Together, these two approaches achieve our generalization.

A set function is said to be submodular if it exhibits the quality of diminishing returns, i.e., the incremental “gain” associated with a given set v decreases as the context in which v is considered grows larger. More formally, a function $f:2^E\to ℝ$ is submodular when for any $A\subseteq B\subset E$ and $v\in E\setminus B$, f satisfies $f(A\cup \{v\})-f(A)\ge f(B\cup \{v\})-f(B)$. Submodular functions naturally model notions of information, diversity, and coverage in many applications such as information gathering [8], document summarization [9], [10], image segmentation [11], [12], [13], and string alignment [14]. If the inequality in the above definition is reversed everywhere (i.e., ≤ rather than ≥), then the function is called supermodular, and f is called modular if it is both submodular and supermodular.

A matroid $M=(E,\mathcal{I})$ is a pair consisting of a ground set E and a set of subsets $\mathcal{I}=\left(I_1,I_2,\dots \right)$ where I_i ⊆ E for all i. The subsets are said to be “independent” and to be a matroid if the subsets satisfy certain properties. Specifically, the pair $M=(E,\mathcal{I})$ is a matroid if it satisfies (i) $\varnothing \in \mathcal{I}$; (ii) $A\subset B\in \mathcal{I}$ implies that $A\in \mathcal{I}$; and (iii) given $A,B\in \mathcal{I}$ with $|A|>|B|$ then there exists $x\in A\setminus B$ such that $B\cup \left\{x\right\}\in \mathcal{I}$. Matroids are extremely powerful combinatorial objects, despite their simple definition, and have undergone years of mathematical study [15]. It is often the case that the independent sets of matroids are used as constraints in discrete optimization. For example, we may wish to maximize a set function subject to the solution being independent with respect to one or more matroids.

In fact, bipartite matching can be described in exactly this way. Given a weighted bipartite graph (V, U, E, w), we can formulate maximum bipartite matching as maximizing w(A) subject to A being independent in two matroids. Depending on the matroids (as described below) we may relax the constraint that an edge is incident only to one vertex. In fact, with this formulation, each vertex (within either V or U) may have its own limit on incident edges. This means that, for a vertex x ∈ V ∪ U, we may define a limit k_x on how many edges in a generalized matching may be incident to x.

Submodular matching generalizes this idea further as follows: rather than maximize an additive weight function w(A), we instead maximize a submodular function f. That is, submodular matching finds an edge set A ⊂ E that maximizes f(A) subject to multiple matroid constraints, $A\in {\mathcal{I}}_1\cap {\mathcal{I}}_2$. Submodular matching is NP-hard, but it can be well-approximated extremely efficiently using a greedy algorithm that has a mathematical quality guarantee, namely, that the solution provided by the greedy algorithm (Alg. 1) is no worse than 1/3 times the best possible solution—this approximation ratio is constant regardless of the problem size [16]. Submodularity can be further exploited to accelerate the greedy implementation, leading to an algorithm often called accelerated or lazy greedy [17] (Alg. 2) having almost linear time complexity in practice. Hence, computationally, the approach scales to very large data set sizes.

In this work, we demonstrate how submodular matching with matroid constraints can be used to design a natural mass spectrometry score function that incorporates two important pieces of prior knowledge about peptide fragmentation. First, the proposed score function keeps track of situations in which a single observed peak can be explained by more than one peak in the theoretical spectrum. Such a collision might occur, for example, in the fragmentation of the +2 charged peptide SSLEVHIR. One of the prefix ions (SS) has an m/z value nearly exactly equal to one of the suffix ions (R). If the observed spectrum has a peak at 175 Da/charge, then existing score functions must choose between scoring this peak as a single match or as two matches. The submodular approach, by contrast, allows us to assign a diminished score to the second match. Second, our proposed score function allows us to, in effect, assign “extra credit” to pairs of observed-theoretical matches that are mutually reinforcing. For example, when we evaluate the hypothesis that an observed spectrum was produced by the fragmentation of peptide QNSHLTIK, we expect a single cleavage event to produce a prefix ion (e.g., QNS with m/z=330 Da/charge) and its corresponding suffix ion (HLTIK with m/z=611 Da/charge). If the observed spectrum contains peaks at both 611 Da/charge and 330 Da/charge, then SGM offers full joint, or non-diminished, credit to these pair of peaks, to account for their complementary nature. The SGM approach also simultaneously discredits any other sets of peaks that should not be in a complementary relationship with each other, for the given peptide. As we see above, the edge interactions can be both local and global, and this is exactly the power of submodular functions, which can model these properties easily while allowing fast approximate maximization.

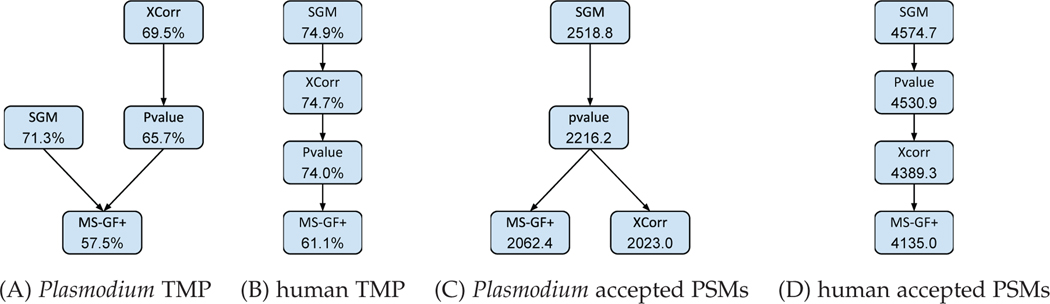
We demonstrate that our proposed score function can be computed efficiently and that the resulting score function outperforms a variety of state-of-the-art methods across multiple data sets. Specifically, we compare SGMs with four existing methods, XCorr [18], MS-GF+ [19], XCorr p-value [20] and Mascot [21]. We compute the number of spectra identified at a 1% false discovery rate (FDR) threshold, observing statistically significant improvements relative to the second-best method (p <0.05, Wilcoxon signed-rank test, Fig 10).

Fig. 10. Statistical comparison of methods.

Each panel plots, for a single data set, the comparison between four methods in terms of the target match percentage or the number of targets PSMs accepted at q < 0.01. A directed edge from A to B means that method A’s mean score is significantly larger (p < 0.05) than method B’s mean score, according to a Wilcoxon signed-rank test. The numbers in the nodes are mean values.

A related framework is called max b-matching [22]. A b-matching is a set of edges M such that at most b(v) edges in M are incident on each vertex v ∈ V. Recent studies have proposed efficient algorithms to find a b-matching of maximum weight with 1/2 guarantee. We note that this framework and SGM share a similar ability to allow multiple edges incident to one vertex. However, SGM is more flexible because it allows modelling the interaction between edges, whereas b-matching requires simply adding up the edge weights.

2. Background: Submodular Function

In this section, we give further background introduction of submodular functions. Recall that a set function $f:2^E\to ℝ$ is called submodular if and only if for any $A\subseteq B\subset E$ and $v\in E\setminus B$, f satisfies $f(A\cup \{v\})-f(A)\ge f(B\cup \{v\})-f(B)$. We define the gain of v in the context of X as $f(v\mid X)\triangleq f(X\cup \{v\})-f(X)$. Thus, f is submodular if $f(v\mid X)\ge f(v\mid Y)$ for $X\subseteq Y$ and $v\notin Y$. The function f is called monotonically non-decreasing if $f(v\mid A)\ge 0$ for all $v\in E$ and $A\subseteq E$, where $f(v\mid A)=f(\{v\}\cup A)-f(A)$ is the gain of v given A. Submodularity is preserved within a convex cone, that is, if f₁ and f₂ are both submodular functions, then λ₁f₁ + λ₂f₂ is also submodular for all ${\lambda }_1,{\lambda }_2\ge 0$.

People have studied different classes of submodular functions such as entropy [23], set cover [24], deep submodular functions [25] and so on. Among them, perhaps the most simple class is that of the concave of modular functions. Suppose that $f:2^E\to ℝ$ is a monotone non-decreasing submodular function and $g:ℝ\to ℝ$ is a monotone non-decreasing concave function, then $g(f(A))$ is submodular [26].

Optimizing an arbitrary set function is computationally intractable in polynomial time. However, submodularity provides possibilities for a variety of optimization problems. For example, minimizing a submodular function unconstrainedly can be exactly solved in polynomial time [27]. The minimum cut problem is a special case of this general minimization problem. However, the corresponding maximization problem is known to be NP-hard [28]. On the other hand, maximizing a monotonically non-decreasing submodular function under a cardinality constraint can be approximately solved by a simple greedy algorithm with a worst case lower bound of $1-\frac{1}{e}$ [29]. In recent years, due in part to the increasing set of applications in machine learning that can utilize submodularity, many other related optimization problems have been studied, including submodular cover and submodular knapsack constrained submodular optimization [30], online submodular maximization [31], and optimizing ratios of submodular functions [32], to name only a few.

Algorithm 1.

GREED for submodular maximization. [16]

1:	Input: f and m matroid constraints ${\mathcal{M}}_i=\left(E,{\mathcal{I}}_i\right)$.
2:	Output: An approximation solution $\widehat{A}$.
3:	$\widehat{A}\leftarrow \mathrm{Ø}$
4:	while exists $v\in E\setminus \widehat{A}$ s.t. $(\{v\}\cup \widehat{A})\in {\cap }_i{\mathcal{I}}_i$ do
5:	$\widehat{v}\in {\text{argmax}}_{v\in E\setminus \widehat{A},(\{v\}\cup \widehat{A})\in {\cap }_i{\mathcal{I}}_i}f(v\mid \widehat{A})$
6:	$\widehat{A}\leftarrow \left\{\widehat{v}\right\}\cup \widehat{A}$
7:	end while
8:	return $\widehat{A}$

Algorithm 2.

LAZYGREED for submodular maximization. [17]

1:	Input: f and m matroid constraints ${\mathcal{M}}_i=\left(E,{\mathcal{I}}_i\right)$.
2:	Output: An approximation solution $\widehat{A}$.
3:	$\widehat{A}\leftarrow \mathrm{Ø}$; Initialize priority queue Q.
4:	for $v\in E$ do
5:	INSERT $(Q,f(v))$
6:	end for
7:	while Q not empty do
8:	$(v,a)\leftarrow \text{POP}(Q)$
9:	if $(\{v\}\cup \widehat{A})\in {\cap }_i{\mathcal{I}}_i$ then
10:	isFresh ← $(\alpha =f(v\mid \widehat{A}))$
11:	if not isFresh then
12:	$\alpha \leftarrow f(v\mid \widehat{A})$
13:	end if
14:	if isFreash or α ≥ max(Q) then
15:	$\widehat{A}\leftarrow \widehat{A}\cup \left\{v\right\}$
16:	else
17:	INSERT(Q, (v, α))
18:	end if
19:	end if
20:	end while
21:	return $\widehat{A}$

In this paper, we consider the problem of submodular maximization under multiple matroid constraints. In 1978, Nemhauser et al. [16] proposed a GREED algorithm (Alg. 1) which is guaranteed to obtain a solution $\widehat{A}$ such that

$$f(\widehat{A})\ge \frac{1}{m+1}f\left(A^{\ast }\right),$$ (1)

where $A^{\ast }\in {\text{argmax}}_{A\in {\cap }_i}{\mathcal{I}}_{i}f(A)$ and ${\mathcal{M}}_i=\left(E,{\mathcal{I}}_i\right)$, for $i=1,\dots ,m$ are a set of m matroids to be used as constraints. The time complexity of GREED is O(n²) and can be further accelerated by LAZYGREED [17] (Alg. 2) which obtains the same solution as GREED. The $\frac{1}{m+1}$ bound can be further improved to $1-\frac{1}{e}$ [33] for m = 1 and $\frac{1}{m+ϵ}$ [34] for m ≥ 2 using multilinear extension and the continuous greedy algorithm. These algorithm are more computationally expensive, especially since they cannot use the accelerated greedy trick. Since our goal is not only to produce a good, but also a fast, scoring function, we elected to use the faster algorithms (LAZYGREED), having the $\frac{1}{m+1}$ guarantee.

Another benefit of submodularity and SGM is that we can deliberately punish certain pairs of elements by making small changes to the submodular function. This is extremely useful for designing suitable functions whenever we observe good biological properties of MS/MS, as we next show. Let $f_0:2^E\to ℝ$ be a normalized, monotonically non-decreasing submodular function, and consider two elements a, b ∈ E. Let $f^{\prime }:2^E\to ℝ$ be another submodular function where $f^{\prime }(A)=f^{\prime }(A\cap \{a,b\})$ for all $A\subseteq E$, $f^{\prime }(\varnothing )=f^{\prime }(\{a\})=f^{\prime }(\{b\})=0$ and $-{\min }_{v\in \{a,b\}}{f}_0(v\mid E\setminus \{v\})\le f^{\prime }(\{a,b\})\le 0$. Note that $f^{\prime }(a\mid E\setminus \{a\})=f^{\prime }(E)-f^{\prime }(E\setminus \{a\})=f^{\prime }(a,b)-f^{\prime }(b)=f^{\prime }(a,b)=f^{\prime }(b\mid E\setminus \{b\})$ since $f^{\prime }(v)=0$ for $v\in \{a,b\}$.

Lemma 2.1.

$f(A)=f_0(A)+f^{\prime }(A)$ is a monotonically non-decreasing submodular function.

Proof.

$f^{\prime }(A)$ is submodular by definition and so is $f(A)=f_0(A)+f^{\prime }(A)$ since submodularity is preserved when adding submodular functions.

For all $v\in E\setminus \{a,b\}$,

$$f(v\mid E\setminus \{v\})=f_0(v\mid E\setminus \{v\})+f^{\prime }(v\mid E\setminus \{v\})$$ (2)

$$=f_0(v\mid E\setminus \{v\})\ge 0.$$ (3)

For all $v\in \{a,b\}$,

$$f(v\mid E\setminus \{v\})=f_0(v\mid E\setminus \{v\})+f^{\prime }(v\mid E\setminus \{v\})$$ (4)

$$\ge f_0(v\mid E\setminus \{v\})-\underset{v\in \{a,b\}}{\min }{f}_0(v\mid E\setminus \{v\})\ge 0.$$ (5)

According to submodularity, if all the final gains are non-negative (e.g. $f(v\mid E\setminus \{v\})\ge 0$ for all $v\in E$), then f(A) is monotonically non-deceasing. □

We claim that adding f′ to f₀ discourages choosing the pair a, b when solving ${\max }_{A\in \mathcal{C}}f(A)={\max }_{A\in \mathcal{C}}{f}_0(A)+f^{\prime }(A)$ instead of ${\max }_{A\in \mathcal{C}}{f}_0(A)$ where $\mathcal{C}$ is any constraint.

Lemma 2.2.

For $A^{\ast }\in {\text{argmax}}_{A\in \mathcal{C}}{f}_0(A)$, if $\left|A^{\ast }\cap \{a,b\}\right|\le 1$, then $A^{\ast }\in {\text{argmax}}_{A\in \mathcal{C}}f(A)$ and ${\max }_{A\in \mathcal{C}}f(A)={\max }_{A\in \mathcal{C}}{f}_0(A)$. If $\left|A^{\ast }\cap \{a,b\}\right|=2$, then ${\max }_{A\in \mathcal{C}}f(A)\le {\max }_{A\in \mathcal{C}}{f}_0(A)$.

For an α-approximate solution  of ${\max }_{A\in \mathcal{C}}{f}_0(A)$, if $|\widehat{A}\cap \{a,b\}|\le 1$, then  is still an α-approximate solution of ${\max }_{A\in \mathcal{C}}f(A)$ and $f(\widehat{A})=f_0(\widehat{A})$. If $|\widehat{A}\cap \{a,b\}|=2$, $f(\widehat{A})\le f_0(\widehat{A})$.

Proof.

Immediately, we have $f(A)=f_0(A)+f^{\prime }(A)\le f_0(A)$ for all $A\subseteq E$. So ${\max }_{A\in \mathcal{C}}f(A)\le {\max }_{A\in \mathcal{C}}{f}_0(A)$.

If $\left|A^{\ast }\cap \{a,b\}\right|\le 1$, then $f^{\prime }\left(A^{\ast }\right)=0$ and $f(A)=f_0(A)+f^{\prime }(A)\le f_0(A)\le f_0\left(A^{\ast }\right)\le f\left(A^{\ast }\right)$ for all $A\subseteq E$. So $A^{\ast }\in {\text{argmax}}_{A\in \mathcal{C}}f(A)$.

For the second part, again we have $f(\widehat{A})\le f_0(\widehat{A})$.

If $|\widehat{A}\cap \{a,b\}|\le 1$, then $\frac{f(\widehat{A})}{{\max }_{A\in \mathcal{C}}f(A)}=\frac{f_0(\widehat{A})+f^{\prime }(\widehat{A})}{{\max }_{A\in \mathcal{C}}f(\widehat{A})}=\frac{f_0(\widehat{A})}{{\max }_{A\in \mathcal{C}}f(\widehat{A})}\ge \frac{f_0(\widehat{A})}{{\max }_{A\in \mathcal{C}}{f}_0(\widehat{A})}\ge \frac{1}{\alpha }$. □

Hence, adding f′ will only punish the score of the pair a and b; otherwise, the scores will be unaffected.

In practice, we use a concave over modular function, $f(A)=g\left({\sum }_{v\in A\cap \{a,b\}}{w}_v\right)$, where g is a monotonically non-deceasing concave function, and w is a non-negative weight for each element. Immediately, we have $f(A)=f_0(A)+f^{\prime }(A)$ where $f_0(A)={\sum }_{v\in A\cap \{a,b\}}g\left(w_v\right)$ and $f_0^{\prime }(A)={\mathbf{1}}_{A=\{a,b\}}\left(g\left(w_a\right)+g\left(w_b\right)-g\left(w_a+w_b\right)\right)$, and using lemma 2.2, we show that f discourages choosing the pair of a, b compared to ${\sum }_{v\in A\cap \{a,b\}}g\left(w_v\right)$, which has no interaction between elements. But unfortunately, the opposite of lemma 2.2, where we would award a particular pair of complementary elements, does not hold. It is hard to model complementary properties of multiple elements using submodularity. However, in this paper, we use an interesting trick (see Section 4.3.2 for full details) to achieve this goal.

3. Background: Mass spectrometry database search

In this section, we introduce the spectrum identification problem. Given an observed spectrum dataset S and a peptide database $\mathcal{P}$, for each s ∈ S with precursor m/z value of m^sand precursor charge value c^s, we wish to find the peptide p ∈ $\mathcal{P}$ responsible for generating s. With the knowledge of m^s and c^s, it is unnecessary to consider all p in the entire database. We assume that the responsible p has a mass approximately equal to the precursor m^s, subject to a tolerance ω determined by the settings in the first round of MS/MS. Let $P_s=P\left(m^s,c^s,\mathcal{P},\omega \right)=\left\{p:s\in \mathcal{P},\left|m(y)/c^s-m^s\right|\le \omega \right\}$. In database search, only the peptides in P_s, the candidate peptides, are scored. A scored spectrum-peptide pair is called a peptide-spectrum match (PSM).

Denoting an arbitrary scoring function as s(p, s), the spectrum identification problem, for a given s, computes:

$$p^{\ast }\in \underset{p\in P\left(m^s,c^s,\mathcal{P},\omega \right)}{\text{argmax}}\mathfrak{s}(p,s)$$ (6)

The scoring function s(p, s) is the core of any search method and a crucial determinant of the performance. We next introduce the widely used SEQUEST method and then show how we generalize it using submodular generalized matching.

3.1. The SEQUEST algorithm

SEQUEST [1] was the very first database search engine. It has a rather simple mechanism and runs very fast while having good performance. Nowadays, SEQUEST is still widely used, and many modern search engines such as MS-GF+ cite [19] and the XCorr p-value [20], which will be later described in Section 5.2, build their algorithms using ideas similar to that of SEQUEST.

We begin by describing SEQUEST because it also provides a good starting point for SGM. Prior to analysis, each observed spectrum is preprocessed in two steps. First, the intensity of each peak is replaced by its square root. Second, the m/z range spanned by the spectrum is divided into 10 regions uniformly, and the intensities within each region are normalized so that the highest intensity in that region is 50. This second step reduces the amount of intensity variation along the m/z axis.

Next, a theoretical spectrum is constructed for each candidate peptide. A peptide with namino acids is fragmented into n − 1 prefix ions (called “b-ions”) and n − 1 suffix ions (called “y-ions”). For each b-ion and y-ion with mass m_b and m_y, theoretical peaks with intensity 50 are placed at m_b and m_y, and neutral loss peaks with intensity 10 are placed at m_b − 17, m_b − 18, m_b − 28, m_y − 17. m_y − 18, corresponding to losses of ammonia (NH₃, 17 Da), water (H₂O, 18 Da) and carbon monoxide (CO, 28 Da). Furthermore, if the observed spectrum has a precursor charge greater than +2, then higher charged versions of the above peaks are also added to the theoretical spectrum.

The traditional SEQUEST score function, called XCorr, is a dot product between one theoretical and one observed spectrum, and can be calculated as follows:

$$\text{SEQUEST}(p,\tilde{s})=\langle p,\tilde{s}\rangle -\frac{1}{151}\sum _{\tau =-75}^{75}\sum _{i=1}^{N}p(i)\tilde{s}(i-\tau )$$ (7)

$$=\langle p,\tilde{s}-\frac{1}{151}\sum _{\tau =-75}^{75}{\tilde{s}}_{\tau }\rangle$$ (8)

where $\tilde{s}$ is the observed spectrum, p is the theoretical spectrum and ${\tilde{s}}^{\prime }=\tilde{s}-\frac{1}{151}{\sum }_{\tau =-75}^{75}{\tilde{s}}_{\tau }$ is called the background spectrum with ${\tilde{s}}_{\tau }(i)=\tilde{s}(i-\tau )$.

4. Submodular Generalized Matchings

Producing a score function S via SGM involves four steps. First, we create a distinct bipartite graph where the left vertices V correspond to the observed peaks and the right vertices U to theoretical peaks for each PSM needing to be scored. Second, we produce a submodular evaluation function f(A) defined over edges of that bipartite graph. Third, we define a set of matroids ${\mathcal{M}}_v=\left(E,{\mathcal{I}}_v\right)$ and ${\mathcal{M}}_u=\left(E,{\mathcal{I}}_v\right)$ whose independent sets are to be used as constraints. Fourth, we compute the score itself, $\mathfrak{s}={\max }_{A\in {\mathcal{I}}_v\cap {\mathcal{I}}_u}f(A)$. We discuss each of these steps in detail below.

4.1. Bipartite graph production

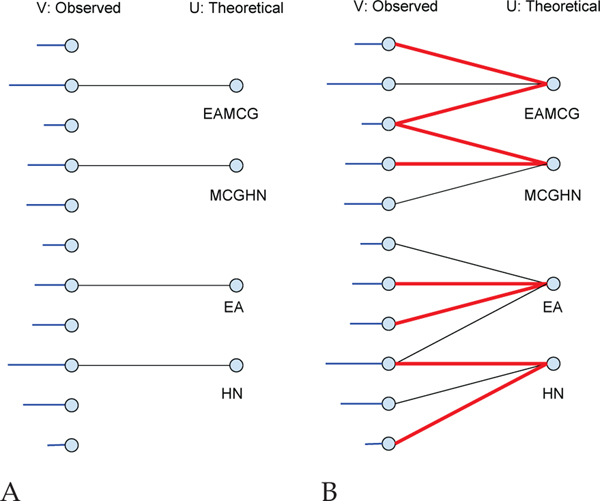
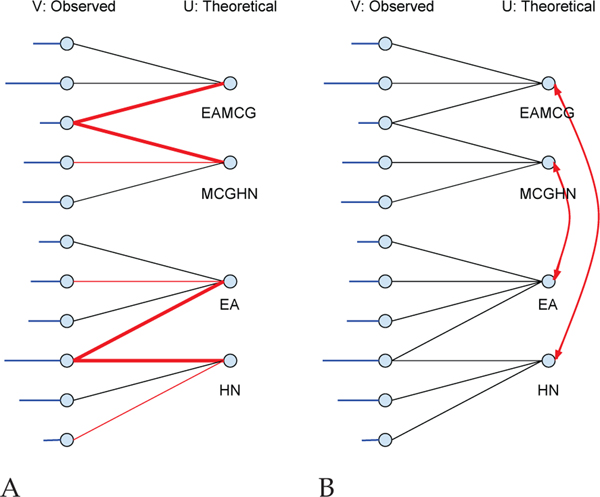
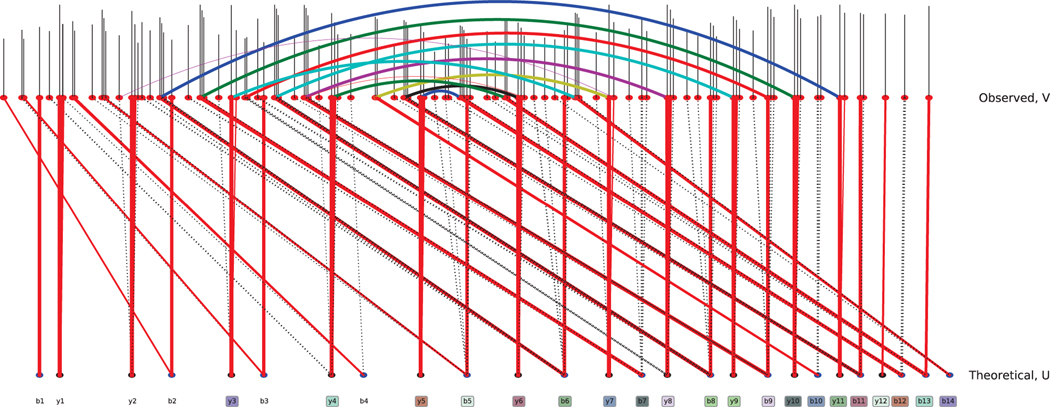
All of our models have as their core a bipartite graph representation of the matching between observed and theoretical spectra peaks (Figure 1A). A bipartite graph is one whose vertices can be divided into two disjoint sets U and V such that every graph edge e = (v, u) connects a vertex v ∈ V to a vertex u ∈ U. For each PSM, we build a bipartite graph $G=(V,U,E)$, where V and U are the sets of peaks in the observed and theoretical spectrum, respectively, and for $e=(v,u)\in E$, theoretical peak u is responsible for the existence of observed peak v with a corresponding weight w(e).

Fig. 1. PSM bipartite graphs.

(A) V is the set of all peaks in an observed spectrum. The horizontal lines attached on the left represent the peak intensities in the observed spectrum. U is the set of all fragment ions for a given theoretical spectrum derived from a given peptide. An edge (v, u) connects v ∈ V with u ∈ U if v might possibly be explained by u with an associated non-negative weight. (B) Red lines are selected edges for a particular match. Non-horizontal edges might correspond to neutral losses.

For a given edge e = {v, u}, the weight w(e) is defined $w^{\prime }(\{v,u\})x_v{y}_u$, where $w^{\prime }(\{v,u\})$ is a weight matrix and x_v, y_u are intensities of v and u. $w^{\prime }(\{v,u\})$ describes the general biological relationship between the observed and theoretical peaks given their mass-to-charge ratios, m_v and m_u. For example, if m_u − m_v is close to 0 or 18 (a water loss), then $w^{\prime }(\{v,u\})$ should be high. Note that the matrix w′ is sparse since we do not expect relationships to exist between two peaks at an arbitrary m/z difference. Also, the values of w’ are a function only of the m/z difference, i.e., $w^{\prime }(\{v,u\})=h\left(m_v-m_u\right)$ where h(·) is a function and is learned empirically using the average intensity near high-confidence b-ions and y-ions (Subsection 4.2). Note that our empirical weights may also be helpful for other scoring methods. In Section 6.3, we show that using our empirical weighting scheme does indeed yield improvements for a method like SEQUEST; however, the submodular function introduced in the next section makes better use of this weighting information.

4.2. Empirical weights

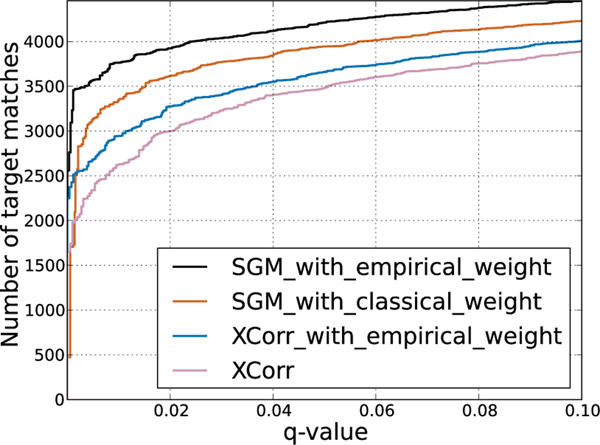
In this section, we show how we derive our empirical weights that lead to the improved performance demonstrated in Figure 12.

Fig. 12.

Evaluation of the SGM and XCorr score functions on a subset of the Plasmodium data set, with and without using the empirical weighting scheme.

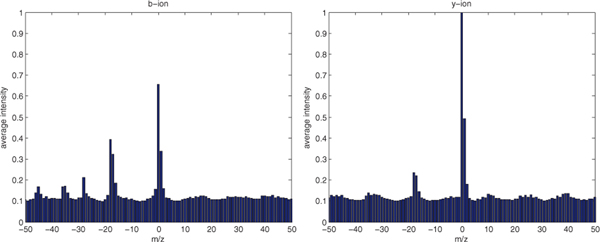
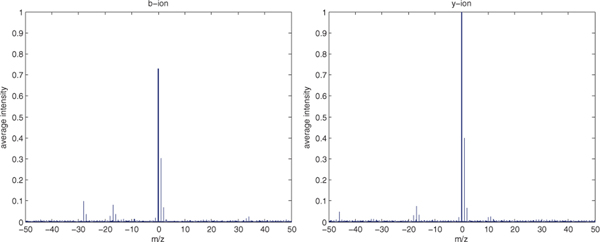
Figure 2 shows the average intensities of observed peaks near b-ions or y-ions in high confidence PSMs (q = 0.01) for the worm-01 charge +2 data set. Figure 3 shows the average intensities for one data set, Plasmodium TMT-10 (described in Section 5.1). In the figures, we see strong peaks at the band y-ions, as well as peaks with offsets of +1 Th peaks (+1 isotope peaks), −17 Th (NH₃-loss), −18 Th (H₂O-loss) and (for b-ions) −28 Th peaks (CO-loss).

Fig. 2.

Average intensity near b-ion and y-ion peaks from high-confidence (q < 0.01) PSMs in the worm-01 dataset. We see strong signals at m/z=0 (central peak), m/z=+1 (+1 isotope), m/z=−17 (NH₃ loss), m/z=−18 (H₂O loss) and m/z=−28 (CO loss for b-ion only).

Fig. 3.

Average intensity near b-ion and y-ion from high-confidence (q < 0.01) PSMs in the Plasmodium TMT-10 dataset. We see strong signals at m/z=0 (central peak), m/z=+1 (+1 isotope), m/z=−17 (NH₃ loss), m/z=−18 (H₂O loss) and m/z=−28 (CO loss for b-ion only). The intensities in this figure are also used for the empirical weights w({e_v, e_u}) for high resolution data for both Plasmodium and human. For each v and v, we compute the mass-to-charge ratio difference m_v − m_u and then use the corresponding peak intensity.

The edges are added to E based on these average intensities for b-ion and y-ions separately. The weight of each edge is $w(\{v,u\})=w^{\prime }(\{v,u\})x\left(m_v\right)$, where m_v is the m/z of v, and x is the preprocessed observed spectrum as introduced in Section 3.1. Recall that in Section 4.1 $w^{\prime }(\{v,u\})$ is determined by m_v−m_u. For low resolution data, $w^{\prime }(\{v,u\})$ is read from Table 1. For high resolution data, the $w^{\prime }(\{v,u\})$ values are obtained from Figure 3. In both settings, we calculate m_v−m_u and use the number in the table or intensity in the plot.

TABLE 1.

The empirical weights $w\left(\left\{e_v,e_u\right\}\right)$ used for low resolution data (yeast and worm). For each v and u, we compute the mass-to-charge ratio difference m_v − m_u and read the correspond entry from the table.

b-ion
$m_v-m_u$	−28	−27	−19	−18	−17	−16
$w^{\prime }(\{v,u\})$	0.1101	0.0225	0.0121	0.3128	0.2364	0.0784
$m_v-m_u$	−15	−12	−1	0	+1	+2
$w^{\prime }(\{v,u\})$	0.0112	0.0107	0.0481	0.6122	0.2514	0.0511
y-ion
$m_v-m_u$	−18	−17	−16	0	+1	+2
$w^{\prime }(\{v,u\})$	0.1364	0.1179	0.0345	1	0.4253	0.0741

For charge +3 data, where the b-ions and y-ions are charge +1 or charge +2, we do similar steps but using the mass-to-charge ratio of the higher charged ion, where $m_{v,c+}=\frac{m_{v,1+}+c-1}{c}$ is the m/z of charge c+ ion of v.

4.3. Submodular evaluation function

In this section, we define the submodular set function f(A) producing a score of an edge set A, that corresponds to how well a set of theoretical peaks (the vertex subset of U incident to edges A) explains a set of observed peaks (the vertex subset of V incident to edges A). While the function f may evaluate an arbitrary subset of edges, we only consider sets A that constitute matchings subject to the matroid constraints when producing PSM scores,. Therefore, we assume that A is a matching when describing this function.

Before discuss the particular function we have designed for PSM scoring, we describe a set of properties of fthat naturally lead us to the class of monotone non-decreasing submodular functions. First, in general, we want the theoretical spectrum to explain as much of the observed spectrum as possible. This means that if one match is a subset of the other, then we expect the first to score no greater than the second. In other words, f should be monotone non-decreasing, or $f(A)\le f(B)$ for all $A\subseteq B$. Second, in many cases, we would not wish to over-credit a given set of selected edges. For example, if an observed peak is well-explained by a given theoretical peak, then any other theoretical peak that also explains the same observed peak should be discounted or, in some sense, “explained away.” Without some kind of discounting procedure, we would be overconfident about this observed peak. Moreover, a non-discounted score function might discourage an optimization algorithm from finding alternative explanations of the theoretical peak. This is a natural diminishing returns property, and can be described as $f(A\cup \{e\})-f(A)\ge f(B\cup \{e\})-f(B),\forall A\subseteq B\subset E$ and $e\notin B$. This is equivalent to the definition of submodular functions.

In general, even approximately maximizing an arbitrary set function is hopelessly intractable since it at least costs $O\left(2^{|E|}\right)$, exponential in the number of set of edges. However, maximizing a monotonically non-decreasing submodular function subject to cardinality constraints can be approximately solved by a simple and efficient greedy algorithm with a $1-\frac{1}{e}$ guarantee [29]. The same algorithm maximizes said function subject to intersection of two matroid constraints (described below) with a 1/3 guarantee [16]. Hence, submodular functions are both natural for the problem of generalized matching for PSM scores, but also allow efficient algorithms to obtain approximate optima of high quality.

There are rich classes of submodular set functions that one might choose from. We have developed a family of such functions, as described below, that are uniquely suited for PSM scoring and that allow for a rich and powerful relationship to exist between a peptide and its observed spectrum. In the following two subsections, we describe two submodular functions f₁ and f₂, that each capture an important part of PSM scoring. Taking a convex combination of such functions preserves submodularity (e.g., f = f₁ + f₂ is submodular when the f_i’s are submodular). So our final scoring method is a mixture of two functions. This is discussed next.

4.3.1. Matching one observed peak to multiple theoretical peaks

In general, we do not want an observed peak to be over-explained and hence over-valued by multiple fragment ions. When an observed peak is accounted for on the left side, if it is matched again, then the second match should not be given as much credit as when the second match is considered alone. This diminishing returns property is exactly modeled by submodularity since if e_i is the i^th match, then $f\left(e_i\mid e_1,\dots ,e_{i-1}\right)\le f\left(e_i\right)$ whenever f is a submodular function. Here we assume that $f(\text{Ø})=0$. This relationship is depicted in Figure 4A and can be represented using the following function:

$$f_1(A)=\sum _{v\in V}{g}_1\left(\sum _{e\in A\cap \delta v}w(e)\right),$$ (9)

where $g_1(x):{ℝ}^{+}$ to $ℝ$ is a monotonically non-decreasing concave function and $\delta v\subseteq E$ are the edges incident to node $v\in V$. The function $f_1(A)$ therefore provides submodularity on the edges grouped by the observed node due to the use of $\delta v.f_1(A)$ is a submodular function since it is a sum of monotonically non-decreasing concave functions composed with non-negative modular set functions [26]. Note that we have flexibility in the choice of g₁(x), and are allowed to model this interaction in diverse ways using different g₁(x) functions. In our experiments we use $g_1(x)=\beta \log (1+{\beta }^{-1}x)$, where β is a parameter. We also experimented with $g_1=x^{\alpha }$ for α = 1/2, 1/3 and 1/4, but this class of function yielded worse empirical results (data not shown).

Fig. 4. Illustration of submodular functions.

V is the set of all peaks in an observed spectrum, with blue horizontal lines representing the observed spectrum intensities. U is the set of all fragment ions for a given theoretical spectrum. Edge (v, u) with v ∈ V and u ∈ U if v might E possibly be explained by u with an associated non-negative weight. E is set of all edges. (A) Two theoretical peaks match the same observed peak. The submodular function assigns a score intermediate between the max and the sum of the two edge scores. (B) Two complementary theoretical peaks match to different observed peaks. The submodular function assigns a “bonus” for this complementarity.

4.3.2. Scoring complementary pairs of matched observed peaks

In a spectrum produced by a well fragmented peptide, b-ions and corresponding y-ions always appear in pairs. Therefore, a score function should ideally provide a boost for a b-ion v_b if its corresponding y-ion $v_{\overline{b}}$ is also present (Figure 4B). This leads to a relationship of the inequality, $f\left(a_b\cup a_{\overline{b}}\right)>f\left(a_b\right)+f\left(a_{\overline{b}}\right)$, where $a_b\in \delta v_b$ and $a_{\overline{b}}\in \delta v_{\overline{b}}$. Unfortunately, this relationship is supermodular (essentially a negative submodular), which is a much harder or impossible to optimize with mathematical worst case guarantees. Therefore, we use a modular function to express the inherent complementarity between b- and corresponding y-ions. Such functions are as close to supermodular as possible while still being submodular. Hence, relationships among edges that are naturally supermodular use a modular function; relationships that are naturally modular use a weakly submodular function, and relationships that are naturally submodular use a strong submodular function. The “strength” of the submodularity, in this context, corresponds precisely to the curvature (magnitude of the second derivative) of the concave functions that are employed Given a concave over modular function $f(A)=g(m(A))$, we define curvature, in the current context, as ${\left|\frac{d^{2}g(x)}{d{x}^2}\right|}_{x=m(V)}$. For PSM scoring, we therefore use the following function, which acts as our submodular surrogate for a supermodular relationship between corresponding ion pairs:

$$f_2(A)={\gamma }_2\sum _{i\in U_{\text{b-ion }}}\left[\sqrt{m\left(A\cap \left(E_i\cup \sum _{j\ne i}{E}_{\overline{j}}\right)\right)}+\sqrt{m\left(A\cap E_{\overline{i}}\right)}\right]$$ (10)

where U_b-ion is the set of b-ions for a given theoretical spectrum, and if i is an b-ion then $\overline{i}$ is the corresponding y-ion, and vice versa. (We say that $\overline{i}$ is the co-ion of i, and any $j\ne i,\overline{j}$ is a “non-co” ion.) The function $m(A)={\sum }_{e\in A}{w}_e$ is a modular weight function. The coefficient ${\gamma }_2=\sqrt{{\sum }_{e\in E}w(e)}$ scales the function to be combined with the other f_i’s. Hence, we see that f₂ maximally credits any edge sets in A that correspond to an ion and its co-ion (since they are in different components in each term of the sum), whereas any edges that do not have this complementary (i.e., an ion and its non-co ions) are discounted if they are jointly selected within A.

4.3.3. Combination of submodular functions

We can use a weighted sum of the above two submodular functions as the evaluation function. The magnitude of the weight is important, because we do not want one term to dominate the other. For example, if f₁ is naturally larger than f₂ (i.e. $f_1(A)\gg f_2(A)$ for all $A\subseteq E$), then when maximizing the sum f₁ + f₂, the solution will focus primarily on f₁ with little consideration of f₂. To avoid this problem, we use the following combination:

$$f(A)=\left[{\lambda }_{\text{cal }}{f}_1(E)+\left(1-{\lambda }_{\text{cal }}\right)f_2(E)\right]\left[{\lambda }_{\text{mch }}\frac{f_1(A)}{f_1(E)}+\left(1-{\lambda }_{\text{mch }}\right)\frac{f_2(A)}{f_2(E)}\right]$$

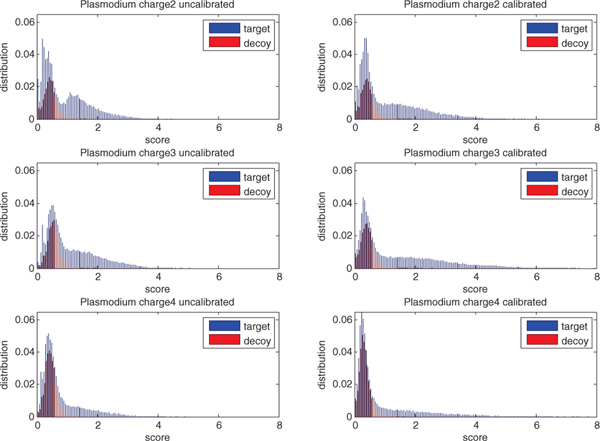
where $0\le {\lambda }_{\text{cal }},{\lambda }_{\text{mch }}\le 1$. Inside the brackets, we use a convex mixture of normalized functions so that $0\le f_1(A)/f_1(E)\le 1$ is always comparable with $0\le f_2(A)/f_2(E)\le 1$. The mixture, however, is still normalized to be in the range [0, 1] so we then calibrate this result by multiplying by ${\lambda }_{\text{cal }}{f}_1(E)+\left(1-{\lambda }_{\text{cal }}\right)f_2(E)$ which does not affect the optimization since it is independent of A. Intuitively, this calibration ensures that PSM scores are comparable across different observed spectra (Figure 6).

Fig. 6. Score calibration of SGM.

Each panel plots, for a single charge state, the SGM score distribution of top-scoring PSMs, separated into target and decoy distributions. Panels on the left are uncalibrated scores, and panels on the right are calibrated. In each plot, the x-axis is normalized so that the score threshold at q = 0.01 equals 1.

To understand further why the calibration procedure is helpful, consider the expression for f(A):

$$f(A)=\left[{\lambda }_{\text{cal}}{f}_1(E)+\left(1-{\lambda }_{\text{cal}}\right)f_2(E)\right]\left[{\lambda }_{\text{mch}}\frac{f_1(A)}{f_1(E)}+\left(1-{\lambda }_{\text{mch}}\right)\frac{f_2(A)}{f_2(E)}\right]$$

$$\begin{gathered} =\left({\lambda }_{\text{cal }}{\lambda }_{\text{mch }}{f}_1(E)+{\overline{\lambda }}_{\text{cal }}{\lambda }_{\text{mch }}{f}_2(E)\right)\frac{f_1(A)}{f_1(E)} \\ +\left({\overline{\lambda }}_{\text{cal }}{\overline{\lambda }}_{\text{mch }}{f}_2(E)+{\lambda }_{\text{cal }}{\overline{\lambda }}_{\text{mch }}{f}_1(E)\right)\frac{f_2(A)}{f_2(E)} \end{gathered}$$

$$={\alpha }_1{\overline{f}}_1(A)+{\alpha }_2{\overline{f}}_2(A),$$

where ${\overline{\lambda }}_i=1-{\lambda }_i$ for convenience, where ${\overline{f}}_i(A)=f_i(A)/f_i(E)$ for $i\in \{1,2\}$ are now two [0, 1]-normalized (and hence compatible) submodular functions as mentioned above, and where ${\alpha }_{i,}i\in \{1,2\}$ are two coefficients. These coefficients, in fact, both mix and scale the functions, because ${\alpha }_1={\lambda }_{\text{mch }}\left({\lambda }_{\text{cal }}{f}_1(E)+{\overline{\lambda }}_{\text{cal }}{f}_2(E)\right)$ and ${\alpha }_2={\overline{\lambda }}_{\text{mch}}\left({\overline{\lambda }}_{\text{cal}}{\overline{f}}_2(E)+{\lambda }_{\text{cal}}{\overline{f}}_1(E)\right)$. Hence, we see how λ_mch influences the optimization while λ_cal selects a calibration score. These are hyperparameters over the algorithm and can be tuned on a development set. Figure 4.7 below shows the effects of these parameters.

4.4. Matroid constraints

Now that we have an appropriate submodular evaluation function f, we next discuss how we produce the final PSM score $\mathfrak{s}$. One possible approach would use $\mathfrak{s}=f(E),$, thereby allowing all possible edges to comprise a score. This would be a poor choice, however, since the observed spectrum contains many noise peaks, and we have no oracle to decide whether a given peak is real signal or not. Although preprocessing steps can be very helpful to limit the influence of noise, it is impossible to fully eliminate all such cases. Moreover, the observed peaks of one fragment ion may happen to have the same m/z as other ions. In this case, the latter ion will have an unexpected co-ion, and we do not want to reward this in any way.

Thus, using all edges E will produce a final score that suffers from many false interactions. Fortunately, when we use a submodular function as described above, we expect the edges that do accurately explain the observed spectrum, in general, to have much greater weights than the noise edges. Moreover, limiting the set of edges being scored to satisfy certain constraints (which we call a “generalized matching”) forces the edges comprising a score to compete with each other. This competition limits the ability of incorrect edges to artificially boost the score. Finally, for most false PSMs, even the best set of edges will not lead to a high score.

The next question is how to set up the right constraints. A simple way is to use standard bipartite matching constraints. This, as mentioned in Section 1, is problematic since every edge in such a matching can be incident to at most only one vertex. In practice, one observed peak might be explained by multiple fragment ions, and one fragment ion might truly explain multiple observed peaks. What we would like is a “generalized matching” where every vertex may be incident to more than one, but we still limit the total number of edges.

The intersection of two matroid constraints perfectly represents this generalized matching property. As mentioned in Section 1, a matroid is a pair $(E,\mathcal{I})$, where E is a finite set and $\mathcal{I}$ is a family of what are called “independent” subsets of E. An edge set solution A satisfies a matroid constraint if and only if $A\in \mathcal{I}$. A particular kind of matroid that is useful for our model is called a partition matroid. A partition matroid is based on a partition of E into disjoint subsets sets ${\left\{E_i\right\}}_{i=1}^{\ell }$, and ℓ non-negative integers ${\left\{k_i\right\}}_{i=1}^{\ell }$, where ${\cup }_{i=1}^{\ell }{E}_i=E$ and $E_i\cap E_j=\mathrm{Ø}$ for $i\ne j$. A set $A\subseteq E$ is independent if and only if $\left|A\cap E_i\right|\le k_i,\forall i$. Therefore, $\mathcal{I}=\left\{A|A\subseteq E,|A\cap E_i\mid \le k_i,\forall i\right\}$. We have two natural partitions of edges E, namely $\{\delta v,v\in V\}$ and $\{\delta u,u\in U\}$ where, again, δ(v) is the set of edges incident to v and likewise for δ(u). Therefore, we define two partition matroids ${\mathcal{M}}_v=\left(E,{\mathcal{I}}_v\right)$ and ${\mathcal{M}}_u=\left(E,{\mathcal{I}}_u\right)$, where ${\mathcal{I}}_v=\left\{A|A\subseteq E,|A\cap \delta (v)\mid \le k_v\forall v\in V\right\}$ and ${\mathcal{I}}_u=\left\{A|A\subset E,|A\cap \delta (u)\mid \le k_u\forall u\in U\right\}$. We immediately see that a matching constraint for A is equivalent to $A\in {\mathcal{I}}_v\cap {\mathcal{I}}_u$, where $k_v=k_u=1$ for all $v\in V$ and $u\in u$. A natural and immediate generalization of bipartite matching, moreover, is to set k_v ≥ 1 and/or k_u ≥ 1, where k_v (resp. k_u) corresponds to the maximum allowed number of incident edges to vertex v (resp. u) in any generalized matching. The values k_v and k_u are seen as parameters of the constraint and correspond, for example, to allowing an observed peak to be explained by multiple fragment ions and one ion to explain multiple observed peaks in the PSM. In practice, we set k_v = ∞, because in the four datasets we studied, the maximum number of edges connected to v is only 2. Hence, there is no need for constraints on the observed side.

4.5. The final score function

Our final score, for a given PSM, is computed as ${\max }_{A\in {\mathcal{I}}_v\cap {\mathcal{I}}_u}f(A)$, where ${\mathcal{I}}_v$ and ${\mathcal{I}}_u$ are the independent sets of two partition matroids with appropriate values of k_v and k_u. An exact solution is computationally intractable, but fortunately, as mentioned previously, an approximate solution can be easily and scalably calculated using a simple greedy algorithm with a mathematical guarantee of 1/3 [35].

Our score function can be regarded as a generalization of both SEQUEST and maximum bipartite matching. SEQUEST uses a dot product operation to calculate the score which is, in fact, equivalent to maximizing a modular set function subject to a particular bipartite matching constraint, namely, one where $|\delta v|=|\delta u|=1$, i.e., where edges exist only between a theoretical peak and its corresponding observed peak. One difference between SEQUEST and such a bipartite score is that SEQUEST uses a background spectrum ${\tilde{s}}^{\prime }=\left(\tilde{s}-\frac{1}{151}{\sum }_{\tau =-75}^{75}{\tilde{s}}_{\tau }\right)$ (i.e., the difference between a foreground and average background spectra, which can be negative) rather than just a non-negative foreground spectrum. In a submodular matching, however, we cannot use the background spectrum directly since it is not always non-negative, something that would violate both the monotonicity and submodularity of our objective f(A) and render the efficient greedy algorithm mathematically vacuous. However, we can use the background information without resulting in negative values if we subtract a similar background factor after finding the maximum matching, as in: $\mathfrak{s}={\max }_{A\in {\mathcal{I}}_v\cup {\mathcal{I}}_u}f(A)-\alpha \tau$, where α is a parameter and $\tau ={\sum }_{i\in U}\frac{1}{151}{\sum }_{j=-75}^{75}\tilde{s}\left(m/z_i+j\right)$ is a background factor. Subtracting τ from the score is not precisely the same as using the background spectrum in SEQUEST but has the same intended purpose and, as we show below, works well while preserving monotonicity, submodularity, and hence the mathematical guarantees and applicability of the greedy algorithm.

4.6. Score calibration

As described in Section 1, calibration is a critical step of a good score function. We say that a PSM score function is well calibrated if a score of x assigned to spectrum s_i has the same meaning or significance as a score of x assigned to spectrum s_j. During a database search, the top-scoring PSMs from different observed spectra are combined into a final, ranked list. The ranking will be reflective of the true qualities of the PSMs only if the scores of different observed spectra are comparable. In SGM, we calibrate each PSM’s score by subtracting the average score of all the PSMs involving that spectrum, as follows

$${\mathfrak{s}}^{\ast }(p,s)=\mathfrak{s}(p,s)-\frac{{\sum }_{p^{\prime }\in P_s}\mathfrak{s}\left(p^{\prime },s\right)}{\left|P_s\right|},$$ (11)

where $\mathfrak{s}(p,s)$ is the non-calibrated score, and P_s is the set of candidate peptides associated with spectrum s.

The subtraction term is a constant with respect to each spectrum and does not affect which peptide is chosen. Rather, it only helps to produce a good overall ranking of top-scoring PSMs. Other search methods, such as MS-GF+ and the XCorr p-value, calibrate scores using dynamic programming. Using similar techniques for SGM scoring is left to future research, because SGM scoring is inherently non-linear, unlike SEQUEST which is a simple linear dot-product-based score.

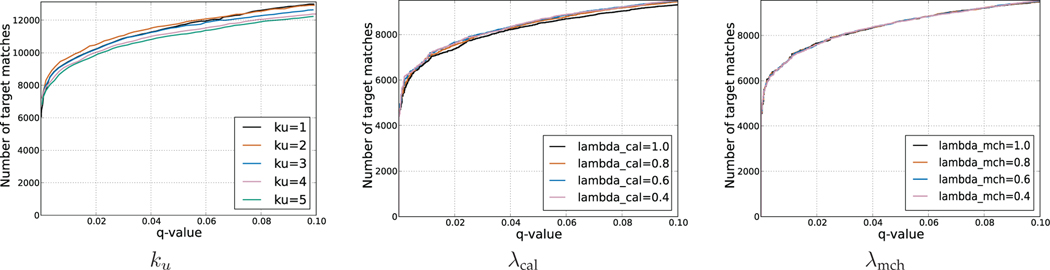
4.7. Selection of score function parameters

Our submodular functions use the hyperparameters λ_cal, λ_mch and {k_u}_u∈U. To select values for these hyperparameters, we performed an FDR-based evaluation with cases k_u ∈ {1, 2, 3, 4, 5} when λ_cal = λ_mch = 1.0 on the data set worm-01-ch2 (described in Section 5.1). The results (Figure 4.7(a)) show that k_u = 2 yields the best performance. Next, we tested cases λ_cal ∈ {0.4, 0.6, 0.8, 1.0} on yeast-01ch2, while fixing λ_mch = 1.0. We then selected λ_cal = 0.6 based on these results (Figure 4.7(b)). Next, we tested λ_mch ∈ {0.4, 0.6, 0.8, 1.0} while fixing λ_cal = 0.6. The value λ_mch = 0.8 had the best performance (Figure 4.7(c)). For α, we calculate the average score of SGM,

$${\alpha }_1=\frac{{\sum }_{s\in S}{\sum }_{p\in P_s\cup D_s}\mathfrak{s}(p,s)}{{\sum }_{s\in S}\left|P_s\cup D_s\right|}$$

and the average foreground score of SEQUEST,

$${\alpha }_2=\frac{{\sum }_{s\in S}{\sum }_{p\in P_s\cup D_s}\langle p,s\rangle }{{\sum }_{s\in S}\left|P_s\cup D_s\right|}$$

where S is the set of all observed spectra and P_s and D_s are corresponding target and decoy sets of s ∈ S. The value α is then chosen to be $\frac{{\alpha }_2}{{\alpha }_1}$. Although the derivation of these parameters was empirical in our study, we hope in future work to develop strategies that can learn these automatically.

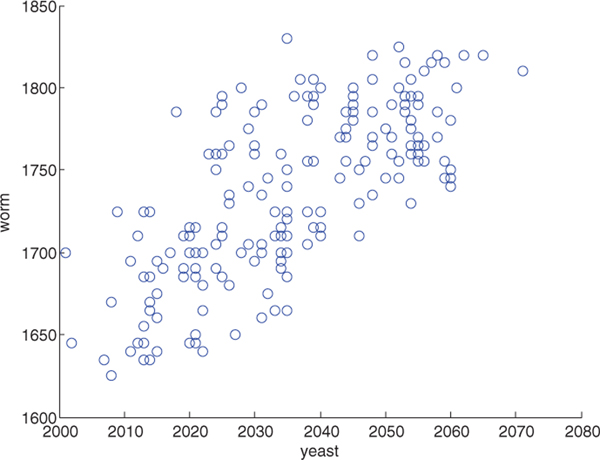
Ideally, these hyperparameters generalize across the different datasets. To test this, we tried all combinations of hyperparameters on one run from the yeast and worm data sets (yeast-01 and worm-01). The results (Figure 8) show that the parameters that work well on one dataset tend also to work well on the other dataset, implying that the parameters generalize well across datasets.

Fig. 8.

The plot shows the number of high-confidence PSMs (q ≤ 0.01) obtained by SGM on the yeast data (x-axis) versus the worm data set (y-axis). Every point represents the performance of one combination of parameters.

5. Methods

We use four different data sets to benchmark the performance of SGM relative to three state-of-the-art methods, and we employ several different quality measures to compare the results.

5.1. Data sets

The yeast (S. cerevisiae) and worm (C. elegans) data sets were collected using tryptic digestion followed by acquisition using low-resolution precursor scans and low-resolution fragment ions. A total of 108,291 yeast and 68,252 worm spectra with charges ranging from 1+ to 3+ were collected. Each search was performed using a ±3.0 Da tolerance for selecting candidate peptides. Peptides were derived from proteins using tryptic cleavage rules without proline suppression and allowing no missed cleavages. A single fixed carbamidomethyl modification was included. Further details about these data sets, along with the corresponding protein databases, may be found in [36].

The malaria parasite Plasmodium falciparum was digested using Lys-C, labeled with an isobaric tandem mass tag (TMT) relabeling agent, and collected using high-resolution precursor scans and high-resolution fragment ions. The data set consists of 240,762 spectra with charges ranging from 2+ through 6+. Searches were run using a 50 ppm tolerance for selecting candidate peptides, a 0.03 Da fragment mass tolerance, a fixed carbamidomethyl modification, and a fixed TMT labeling modification of lysine and N-terminal amino acids. Further details may be found in [37].

The human dataset was digested using trypsin, labeled with an isobaric tandem mass tag (TMT) relabeling agent, and collected using high-resolution precursor scans and high-resolution fragment ions. The data set consists of 1,133,534 spectra with charges ranging from 2+ through 6+. Searches were run using a 10 ppm tolerance for selecting candidate peptides, a 0.02 Da fragment mass tolerance, a fixed carbamidomethyl modification, and a fixed TMT labeling modification of lysine and N-terminal amino acids. Further details may be found in [38].

5.2. Database search methods

We compare SGM with four state-of-art methods: SEQUEST, MS-GF+ [19], XCorrp-value [20] and Mascot [21]. In Section 3, we have already described SEQUEST and its XCorr score function. In the experiments, we use a re-implementation of SEQUEST called “Tide” [18], available in Crux version 2.1.16790 [39]. One problem with SEQUEST in practice, as demonstrated below, is that the raw XCorr score is poorly calibrated. The MS-GF+ [19] search engine uses an alternative score function and employs dynamic programming to exactly compute the score distribution over the universe of candidate peptides for a linear scoring function. This gives far better calibration. In the experiment, we use MS-GF+ version 9980, and PSMs are ranked by the “Evalue” score. The XCorr p-value [20] uses a similar dynamic programming approach to calibration, applied to the SEQUEST XCorr score. We also use Crux for XCorr p-value. For clarity, we refer to the two variants of SEQUEST as “XCorr” (for results based on ranking with the raw XCorr score) and “p-value” (for results based on ranking by the XCorr p-value). Mascot is another traditional searching method. Unlike Sequest, Mascot uses a probabilistic metric to measure the likelihood of observed spectra and canidiate peptides. We use an online Mascot server (version 2.3.01).

To ensure a fair comparison, we use equivalent values for search settings for all search engines whenever possible. In general, we use the appropriate discretization of the fragment m/z axis for each given data set. The only exception is that, for technical reasons related to the dynamic programming procedure, the XCorr p-value can only be calculated using an m/z resolution of 1.0005079 Da. For Tide, MS-GF+ and Mascot, default search parameters are used, except that, to make a fair comparison, handling of isotope peak errors is turned off in MS-GF+. (In the Appendix, we show that this option does not affect our conclusions.) Furthermore, to avoid variability in how proteins are digested to peptides and how “decoy” peptides (see Section 5.3) are generated, we use the same digested peptide database as input to all search algorithms. We create these databases by using the “tide-index” command in Crux, with “clip-nterm-methionine” set to “True”.

5.3. Evaluation of methods

We employ a widely used approach, target/decoy search [40], to assign confidence estimates to PSM scores. These confidence estimates allow us to compare the performance of different search engines, since there is no ground truth to measure accuracy. We create a “decoy” set by randomly permuting the (non-terminal) amino acids of each peptide in a “target” set, which is the real candidate peptide set. For each spectrum, all peptides in a database comprised of targets plus decoys are searched, and the single peptide with the highest score is selected. If more than one peptide has the highest value, then ties are broken randomly.

Two complementary metrics for comparing two algorithms using target/decoy search were considered. The first, simpler approach is the “target match percentage” (TMP), defined as the fraction of observed spectra for which the top-scoring match involves a target peptide. For a perfectly random score function, the TMP is expected to be ∼50%. The best possible TMP is 100%; however, this is not achievable in practice, because any real data set will contain spectra that cannot be identified, either because the corresponding generating peptide is not in the given peptide database or because the spectrum was generated by a non-peptide contaminant. These “foreign” spectra are expected to match targets and decoys with equal frequency. TMP is not a widely used performance measure; however, we employ it here because TMP provides a measure of the quality of a score function that is independent of a score function’s calibration. This is because the TMP only compares scores for PSMs within one spectra. Hence, the distribution of PSM scores for spectrum A can be dramatically different from another spectrum B, but the TMP achieved by the score function can still be high.

Additional steps are required to evaluate the calibration of a score function. After obtaining a ranked list of the top-scoring PSM for each spectrum, we set a score threshold and label every PSM scoring better than the threshold as “accepted.” The false discovery rate at a given threshold can be estimated as $\text{FDR}=\frac{\text{number of accepted decoy PSMs}}{\text{total number of accepted PSMs}}$ [40]. In practice, we compute for each PSM its corresponding q-value, defined as the minimum FDR at which a PSM with that score is accepted [41]. Because many mass spectrometry studies report results using an FDR threshold of 1%, we sometimes report the number of target PSMs accepted at q ≤ 0.01. To evaluate the performance of a search engine over a variety of q-value thresholds, we also plot the number of accepted target PSMs as a function of q-value threshold and compute the area under the plot from 0 ≤ q ≤ 0.1. Because the FDR-based evaluation involves creating a ranked list of top-scoring PSMs from many different spectra, this metric requires good cross-spectrum calibration.

6. Results

6.1. Comparison of four search methods

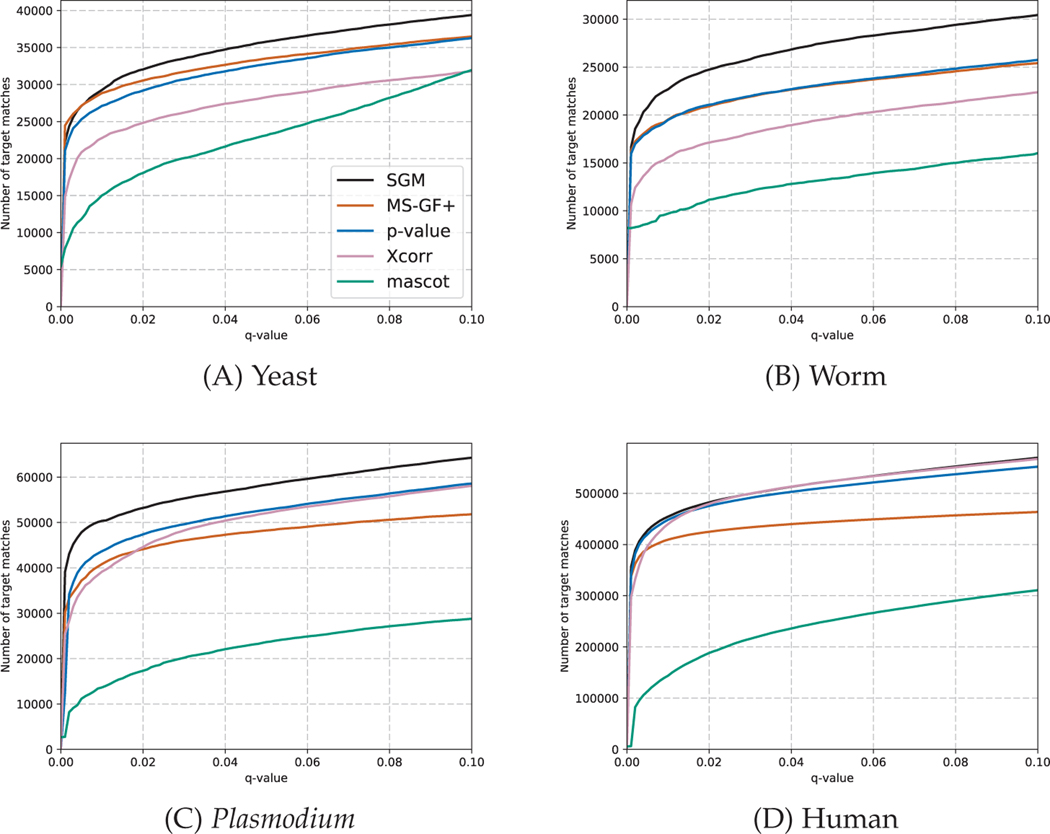
We begin by computing the target match percentage of the four search methods—SGM, MS-GF+, p-value and XCorr—on the four data sets described in Section 5.1. In all four cases, SGM achieves the greatest TMP (Table 2). Each of these data sets consists of multiple mass spectrometry runs: 3, 3, 20, and 100, for the yeast, worm, Plasmodiumand human data sets, respectively. Consequently, for the latter two data sets we were able to compute the TMP separately for each run and then use a Wilcoxon signed-rank test to identify statistically significant differences. This analysis (Figure 10) indicates that, for the malaria data set, SGM performs better than XCorr (p = 0.11), and for the human data set, SGM performs significantly better than all three competing methods (p = 1.6 × 10−⁵). The consistently good TMP performance of the SGM method on these diverse data sets indicates that, for each observed spectrum, this score function does a very good job of ranking the generating peptide above all other candidate peptides.

TABLE 2.

Target match percentage achieved by the four score functions on four data sets. In each row, the maximal value is shaded red.

Dataset	SGM	MS-GF+	p-value	XCorr
yeast	70.59	66.19	65.47	64.91
worm	82.83	77.59	77.39	76.43
Plasmodium	69.91	66.85	65.53	69.39
human	74.40	60.40	73.26	74.12

Next we evaluate the methods using false discovery rate estimation, thereby additionally taking into account the calibration of the scores. In practice, this evaluation is the most important, since it directly reflects how the end user will interpret the results of the search. The results (Figure 9) suggest that, once again, SGM performs better than MS-GF+, XCorr, XCorrp-value and Mascot for the yeast, worm and Plasmodium data sets. We quantified the performance of the first four methods by counting the number of accepted PSMs at a q-value threshold of 0.01, and we again used a Wilcoxon signed-rank test to estimate significant differences for the data sets comprised of many runs. This analysis shows that SGM significantly outperforms all three competing methods on both the Plasmodium and human data sets. The p-values relative to the second-ranked method, XCorr, are 0.0015 for Plasmodium and 0.0014 for the human data set (Figure 10).

Fig. 9. FDR-based comparison of search methods.

Each panel plots, for a single data set and a variety of score functions, the number of spectra identified as a function of FDR threshold.

6.2. Verifying the utility of submodularity

The SGM approach employs a combination of two submodular functions, each of which is designed to capture a particular property of high quality matches between spectra and peptides. To verify that the good results in Section 6.1 are indeed a reflection of these properties, we examined more closely the high-confidence identifications produced by SGM. For this analysis, we focus on a single, randomly selected run (“TMT10”) from the Plasmodium data set.

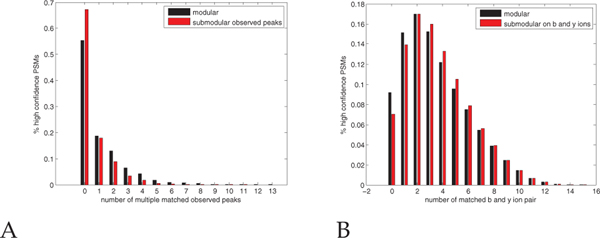
First, we show that f₁ discourages choosing multiple edges incident to one observed peak. To do so, we compare the number of multiply matched observed peaks in high confidence PSMs (q ≤ 0.01) generated using two methods: a simple, modular approach versus using f₁. The distribution of the number of multiply matched peaks decreases when we use f₁ (Figure 11A), which implies that our submodular function discourages multiply matched observed peaks.

Fig. 11. PSM properties captured by the submodular function.

(A) The number of multiple matched observed peaks decreases when we use the submodular function f₁. (B) The number of multiple matched band y-ion pairs increases when we use the submodular function f₂.

Second, we show that f₂ encourages choosing a b-ion if its corresponding y-ion is already chosen, and vice versa. As before, we compute the number of jointly matched band y-ion pairs among the high confidence PSMs, with and without inclusion of f₂. As expected, the number of matched b- and y-ion pairs increases when we use f₂ (Figure 11B), implying that our submodular function indeed encourages such matching.

6.3. Investigation of empirical weights

Our method is different from XCorr in two respects. First, we use empirically derived edge weights based on an analysis of the data (Section 4.2). Second, we generalize the dot product score to one based on a submodular generalized matching. We performed further experiments to ascertain which of these two changes are primarily responsible for the good results reported above.

In particular, we contrast our empirical weights with the “classical” weights employed by methods such as XCorr and MS-GF+. The methods use a fixed weights for each ion type. The classical weights used in the XCorr score are defined as $w^{\prime }(\{v,u\})={\delta }_{m_v,m_u}+0.2{\sum }_{l\in \{-17,-18,-28\}}{\delta }_{m_v+l,m_{u^{\prime }}}$ δ_{i, j} = 1 if i = j and 0 otherwise. Hence, the classical weight is 1 if m_v − m_u = 0; 0.2 if m_v − m_u ∈ {−17, −18, −28} and 0 otherwise.

To investigate the relative importance of SGM and the empirical weighting scheme, we analyze the contributions of these two components separately. We do the test on a single run (“TMT10”) from the Plasmodium data set, evaluating performance using target-decoy q-values. We compare four different search methods: SGM with and without empirical weights, and XCorr with and without empirical weights. In this experiment (Figure 12), the combination of SGM with empirical weights achieves by far the best performance. While the empirical weights help both XCorr and SGM, the SGM with the standard XCorr weights is still better than XCorr with our empirical weights. Hence, it is fair to say that the SGM process is the more important of the two. This is not surprising because the power of SGM, and the use of submodular functions, is that we can allow global long-range interaction amongst edge scores, something that is not possible with XCorr.

6.4. Running time

To evaluate the running time of SGM relative to other search tools, we measured the wall clock time of four search methods on a single Intel Core 2 Quad Q9550 2.83GHz CPU on the Plasmodium TMT-10 dataset. The dataset consists of 8841 spectra, each with an average of 365 target peptides and an equal number of decoy peptides. This analysis (Table 3) shows that SGM has a comparable run time with MS-GF+ and the Tide p-value. The raw XCorr score calculation is extremely fast because it simply consists of calculating a dot product, with no explicit calibration procedure.

TABLE 3.

Run time of four methods per spectrum on the Plasmodium TMT-10 data set.

SGM	MS-GF+	p-value	XCorr
8.48 × 10−2s	8.99 × 10−2s	6.89 × 10−2s	3.39 × 10−3s

7. Conclusion

We have introduced a novel class of score functions for use in tandem mass spectrometry database search. A key advantage of our SGM is that we can model many PSM properties, including long-range interactions among peaks in an observed spectrum, using a rich and powerful framework, namely that of submodularity and various matroid constraints. An additional advantage is that our model runs fast since we may use a simple accelerated greedy algorithm to find the maximum value of the submodular function with a mathematical quality guarantee of $\frac{1}{3}$. We show that our approach achieves statistically significant improvements in performance relative to several state-of-the-art methods according to two different evaluation metrics.

In SGM, we use three hyperparameters, chosen from a grid of possible values (Section 4.7). Our empirical analysis suggests that these hyperparameters generalize well across datasets. Therefore, we do not need to re-tune these hyperparameters to different datasets.

In future studies, we will explore other submodular functions in an attempt to further improve performance. For example, we can explore algorithms that can learn submodular functions and parameters from training data [10], [42]. We can will also consider other generalizations of our framework to better model the process of spectrum generation.

Fig. 5.

Visualization of the bipartite graph. The top nodes are observed peaks and the bottom ones are theoretical. Red solid lines are selected edges while dashed lines are unselected. On the top, corresponding observed peaks for b and y-ion pair are connected and thick if they are matched. On the bottom, matched b and y-ion pairs are marked in same color.

Fig. 7.

FDR-based evaluation of SGM using different hyperparameters.

Biographies

Wenruo Bai received the B.S. degrees in physics in 2013 from the School of Physics at Peking University. He was a visiting student researcher in Department of Materials Science and Engineering at University of California, Davis in 2012. He is currently working toward the PhD degree in the Department of Electrical Engineering, University of Washington, from 2013. His publications involves the topics of peptides identification, ratio of submodular function and submodular partition. His team received the best paper award of ACMBCB in 2016. His main research interests include computational biology, machine learning and submodular optimization.

Jeffrey Bilmes Jeffrey A. Bilmes is a professor at the Department of Electrical Engineering at the University of Washington, Seattle Washington. He is also an adjunct professor in Computer Science & Engineering and the department of Linguistics. Prof. Bilmes is the founder of the MELODI (MachinE Learning for Optimization and Data Interpretation) lab at UW. He received his Ph.D. from the Computer Science Division of the department of Electrical Engineering and Computer Science, University of California in Berkeley. Prof. Bilmes is a 2001 NSF Career award winner, a 2002 CRA Digital Government Fellow, a 2008 NAE Gilbreth Lectureship award recipient, and a 2012/2013 ISCA Distinguished Lecturer. Prof. Bilmes’s primary interests lie in machine learning, discrete optimization, dynamic graphical models, and signal processing for data science applications.

William S. Noble William Stafford Noble (formerly William Noble Grundy) received the Ph.D. in computer science and cognitive science from UC San Diego in 1998. After a one-year postdoc with David Haussler at UC Santa Cruz, he became an Assistant Professor in the Department of Computer Science at Columbia University. In 2002, he joined the faculty of the Department of Genome Sciences at the University of Washington. His research group develops and applies statistical and machine learning techniques for modeling and understanding biological processes at the molecular level. Noble is the recipient of an NSF CAREER award and was a Sloan Research Fellow.