Comparing Deep Learning-Based Automatic Segmentation of Breast Masses to Expert Interobserver Variability in Ultrasound Imaging

Abstract

Deep learning is a powerful tool that became practical in 2008, harnessing the power of Graphic Processing Unites, and has developed rapidly in image, video, and natural language processing. There are ongoing developments in the application of deep learning to medical data for a variety of tasks across multiple imaging modalities. The reliability and repeatability of deep learning techniques are of utmost importance if deep learning can be considered a tool for assisting experts, including physicians, radiologists, and sonographers. Owing to the high costs of labeling data, deep learning models are often evaluated against one expert, and it is unknown if any errors fall within a clinically acceptable range. Ultrasound is a commonly used imaging modality for breast cancer screening processes and for visually estimating risk using the Breast Imaging Reporting and Data System score. This process is highly dependent on the skills and experience of the sonographers and radiologists, thereby leading to interobserver variability and interpretation. For these reasons, we propose an interobserver reliability study comparing the performance of a current top-performing deep learning segmentation model against three experts who manually segmented suspicious breast lesions in clinical ultrasound (US) images. We pretrained the model using a US thyroid segmentation dataset with 455 patients and 50,993 images, and trained the model using a US breast segmentation dataset with 733 patients and 29,884 images. We found a mean Fleiss kappa value of 0.78 for the performance of three experts in breast mass segmentation compared to a mean Fleiss kappa value of 0.79 for the performance of experts and the optimized deep learning model.

Graphical Abstract

1. Introduction

Breast cancer is a leading cause of cancer death in women worldwide [1-3], causing 42,170 deaths out of 276,480 recorded breast cancer cases in women in the United States in 2020 [1]. Ultrasound (US) imaging is a relatively inexpensive, noninvasive, and widely available medical imaging technique commonly used in breast cancer screening, with growing use in developing countries [4]. Experts use morphological and textural features, including shape, margin, echo pattern, etc., to identify suspicious breast masses [5-7]. Breast masses are then scored on a visual system called the Breast Imaging Reporting and Data System (BI-RADS) scale [8]. BI-RADS categories 1, 2, 3, and 5 are mostly in agreement with the final pathological diagnosis; however, the rate of malignancy in BI-RADS category 4 can vary between 3% and 94% [9]. This process is highly dependent on the skills and experience of the experts, thereby leading to intraobserver and interobserver variability and interpretations [10, 11].

For years, investigators have attempted to develop computer-aided systems to help in clinical practice. To that end, automated segmentation of breast tumors using US has recently been investigated using deep learning convolutional neural networks (CNNs) [11, 12]. Deep learning is an increasingly popular technology for image analysis with potential use in medical applications to improve image quality [13-15], offering expertise in remote medicine [16], and automating aspects of the medical pipeline [17-20]. Owing to the strict regulation of medical data and the time and cost associated with expert processing of medical data, it is desirable to have tools that can streamline the process to reduce evaluation time and costs associated with medical care. Another consequence is that deep learning training and evaluation are often performed using the ground truth provided by a single expert [15]. However, if the performance of a deep learning model does not exactly match that of the expert-provided label, it is difficult to discern if the variation falls within an acceptable range of values. The amount of interobserver variability between experts differs depending on the modality and the organ being imaged [21].

Here, we present a top-performing deep learning segmentation model for the segmentation of suspicious breast masses in US images and compare it with the performance of three experts to evaluate interobserver reliability. The lesion segmentation task in US images is particularly challenging because of the low resolution, noisy images, complex nature of malignant pathologies, and lack of objective ground truth. Having a single observer of known reliability could potentially have a significant impact in standardizing risk estimates and reducing medical costs.

2. Materials and Methods

2.1. Patient pool

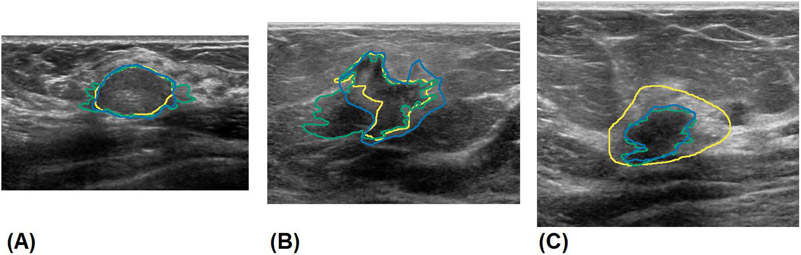
Clinical US images were obtained from patients with suspicious breast masses from different institutions using different equipment and settings. Written consent was obtained from all patients, along with proper institutional review board approval from the Mayo Clinic, while being Health Insurance Portability and Accountability Act compliant. Patients older than 19 years who underwent biopsy after US imaging for breast cancer were included in this prospective study. Patients who had breast implants or abnormalities or who had previously undergone any breast surgical procedures were excluded from the study. A total of 733 patients participated, resulting in 2,312 US clinical images from multiple orientations, which were manually segmented to provide a label. Additionally, 295 cineclips from 118 patients undergoing breast ultrasound scans were used to augment training with 28,025 additional frames. Cineclips from a previous study on 455 thyroid nodules were obtained for pretraining [20]. A subset of 121 breast US images from 85 patients were distributed to three experts (two trained radiologists and one highly expert sonographer) for breast mass segmentation. Of the total, 40 patients had malignant masses, 44 patients had benign lesions, and 1 patient was categorized as atypical and high risk, as confirmed by biopsy. The mean patient age was 57±15.0 years. There were 65 patients classified as BI-RADS 4, 18 patients classified as BI-RADS 5, and 2 patients classified as BI-RADS 6. The training set comprised 1,305 images from 486 patients, the validation set consisted of 433 images from 162 patients, and the test set comprised 121 images from 85 patients. Images from patients in the test set that had not been segmented by the experts were excluded from the training or validation set to prevent cross-contamination. The sets were divided such that no patient appeared in more than one dataset to prevent cross-contamination of data that might artificially inflate performance. The test set was labeled by three experts, and the training and validation data were segmented by the research technologists experienced in breast US. Each expert was given every US image associated with the clinical exams, including shear wave images, Doppler images, and images marked with calipers. Segmentation was performed using the software at the discretion of the experts. Figure 1 depicts manual segmentation by experts for benign and malignant breast masses. Malignant nodules tend to be more diverse and challenging, with ambiguous boundaries and complex geometries, featuring projections, spiculations, and heterogeneous echogenicity [5, 22]. An additional source of interobserver variance is disagreement over the inclusion of hyperechoic rims, a band of hyperechoic tissue surrounding some hypoechoic lesions. An example of a manual segmentation variance in a lesion with a hyperechoic band is shown in Figure 1C.

Fig. 1.

Manual segmentation of benign and malignant breast masses by experts. A) segmentations of a benign fibroadenoma, B) segmentations of a malignant invasive ductal carcinoma with indistinct margins, C) segmentations showing stylistic choice in segmenting hyperechoic rim. The results of experts 1, 2, and 3 are shown in green, blue and yellow, respectively.

2.2. Pre-Processing

The clinical US images were resized to 320 × 320 pixels or 352 × 352 pixels, depending on the training stage. The size and shape of ultrasound images depend on the geometry of the probe; curved probe images over an arc; and linear probe image in a rectangle or trapezoid area, if sweeping is used. The height and width of the resulting image are also subject to hardware settings, such as the imaging depth. To maintain consistency, the largest dimension of the US image was resized to 320 or 352 pixels, and the smallest dimension was resized to maintain the original aspect ratio. US image pixels were normalized between 0 and 1, and padding pixels were set to −1 to help differentiate between echoic shadowing and padding pixels.

2.3. Architecture

The deep learning model architecture was derived from a top-performing segmentation model, Densenet264 [23]. The model was further optimized for breast US segmentation by adding a learning scalable feature pyramid architecture, called, the Neural Architecture Search- Feature Pyramid Architecture NAS-FPN output module [24], training at multiple scales [25], and adding the ResNet-C input stem [26]. Random search optimization was applied to model training, resulting in L2 kernel normalization and input and output blocks with L = 0.5e-6. In conventional image processing, the use of multiple scales acts as a form of data augmentation and regularization, and it assists in identifying objects that appear in dramatically different scales because of an object’s distance from the camera. In US, the perceived size of an object can differ depending on the hardware and software settings. Dropout was applied after each convolutional layer in the input block to create a noisy student model [27].

2.4. Training

The deep learning model was trained in four stages. Figure 2 shows a flow chart depicting the training stages using the datasets used during training. The datasets with the patient number, image quantity, and distribution are shown in Table 1. The first stage of training was pretraining using a much larger labeled thyroid US dataset. Traditionally, models are pretrained on larger public datasets; however, it has been shown that color images of scenery translate poorly to 2D slices of anatomy [25], and, in our experience, often fail to learn or induce instability. The model was trained to segment the thyroid nodule from the surrounding tissue, which initializes the filters for use in medical US images and speeds up later training. After training for 40 epochs on the thyroid dataset, the model was modified and retrained (Table 1, row 2) on a fully labeled breast US dataset. Inspired by recent developments using multiscale training in segmentation [28, 29], the model was modified by creating a shared model and simultaneously training with input sizes of 320 × 320 pixels and 352 × 352 pixels as a form of data augmentation. The input sizes were experimentally determined to improve the performance of this model. The next stage of training used the semi-supervised self-training technique proposed by Zoph et al., He et al., and Xie et al. [25, 27]. Self-training involves using a trained model to label an unlabeled and, likely, a larger dataset for use in further training. The retrained model was used to label the unlabeled cineclip dataset (Table 1, row 3), which was more than 22 times larger than that of the manually labeled dataset. The self-training stage incorporates self-generated labeled cineclip data at a ratio of 2:1. The process was repeated twice, after which further gains were not observed. The final stage of training freezes model weights, uses a single instance at 320 × 320 pixels, adds the NAS-FPN [24] output module, and trains only on the manually labeled US data. The dataset was augmented using standard techniques, such as horizontal flipping, small rotation, shifting, and image mix-up [30]. As part of the final tuning, a simple cascaded approach used by Christ et al. [31] was implemented, wherein the trained model was used to predict the dataset. The predicted size of the lesion plus a boundary was added to each side, resulting in a cropped image. The final tuning stage was repeated using a cropped dataset. The loss function was a Matthew’s correlation coefficient adapted for segmentation from binary classification and generalized, borrowing the focal technique from Abraham et al. [32] to further penalize incorrect predictions. The loss function parameters were optimized by random search with alpha = 0.52 and beta = 1.2.

Fig. 2.

Flow chart showing the stages of model training including modifications to the model and dataset used.

Table 1.

Training stages with the number of patients and images in each dataset

Stage	Patients	Training	Validation
Pretraining	455	40,168	10,825
Retraining	733	1,305	433
Self-training	733	29,330	433
Final tuning	733	1,305	433

2.5. Final Postprocessing

The final trained model was used to predict the test set eight times: once unmodified, once with horizontal flipping, rotated 20° and −20°, and diagonally shifted four times by 20 pixels. The predicted masks were realigned and summed to a threshold value of 0.35. The augmentations, degree of augmentations, and threshold values were determined experimentally.

3. Results

To evaluate interobserver variability, we evaluated and compared features calculated from segmentation masks, compared the segmentation metrics calculated between pairs of observers, and computed the Pearson correlation coefficient and Wilcoxon signed rank tests to determine if the model’s performance aligns with that of the experts. Evaluation was performed using the common medical segmentation metric, the Dice coefficient, as well as sensitivity, specificity, Cohen’s kappa adapted for segmentation, and a relatively new metric, 95% symmetric Hausdorff distance. The 95% Hausdorff distance computes the mean distance between 95% of the boundary between segmentations, providing metric resilience against outliers [17]. Feature robustness was assessed by evaluating the two-way random single-measure intraclass correlation coefficient.

Pairwise segmentation metrics were calculated for all pairs of observers with mean values, as summarized in Table 2. According to McHugh’s interpretation of Cohen’s kappa, the model achieves a “strong” agreement with all three experts. The model’s performance most closely matches observer 3 when examining the Dice coefficient and Cohen’s kappa. This is likely due to the relatively conservative segmentations of observer 3 compared to those of observers 1 and 2, who more frequently segmented small projections and spiculations. The training dataset most closely matched the conservative style of observer 3. Fleiss’ kappa is an extension of Cohen’s kappa with the ability to assess the performance of multiple observers. Fleiss’ kappa was calculated for the experts and for all observers with resulting values of 0.790 ± 0.014 and 0.789 ± 0.013, respectively, indicating “moderate” agreement between observers with a 0.001 drop in agreement with the inclusion of the model.

Table 2.

Mean values of pairwise comparison metrics between all observers.

	SPECIFICITY	SENSITIVITY	DICE	95% HD	COHEN’S KAPPA
OBSERVERS 1-2	0.984	0.908	0.814	1.38 mm	0.804
OBSERVERS 2-3	0.987	0.838	0.804	1.64 mm	0.794
OBSERVERS 1-3	0.991	0.765	0.792	1.71 mm	0.781
OBSERVERS M-1	0.992	0.845	0.828	1.30 mm	0.820
OBSERVERS M-2	0.995	0.863	0.816	1.51 mm	0.807
OBSERVERS M-3	0.993	0.771	0.852	1.46 mm	0.844

The best values are shown in bold. The experts are numbered 1, 2, 3, and the model is labeled M.

Wilcox on signed-rank tests and Pearson’s correlation coefficients were calculated using geometric features extracted from pairwise comparison metrics in observer segmentations. Pearson’s correlation coefficient shows a strong relationship between the area, perimeter, major and minor axis length, and centroid locations (r = 0.98, 0.94, 0.97, 0.99), compared across all observers. Wilcoxon tests show that the model matches the performance of experts regarding sensitivity (p > 0.05), and it has a higher performance with regard to the Dice coefficient, specificity, and Cohen’s kappa (p > 0.05).

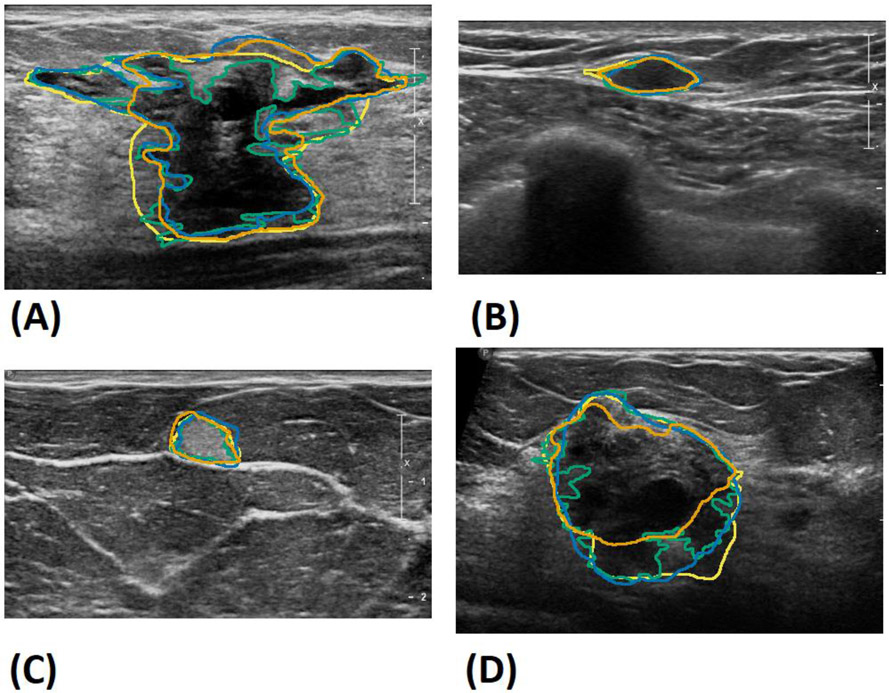
Figure 3 shows the box plots comparing the performance of the experts evaluated against each other and the model compared to the experts. A small increase in the overall performance was observed in the deep learning model compared to the experts. This suggests that the model’s segmentation is a kind of “mean” between the three observers, with fewer differences between each expert compared to the experts evaluated against each other. Figure 4 shows Bland–Altman plots showing the model results vs. the difference between each observer for the segmentation area, major axis length, and minor axis length. The mean performance is very close to zero, suggesting a close agreement between the model and the experts. Result segmentations from the model are shown in Figure 5 along with the segmentations of the other observers. Figure 5A shows a benign complex sclerosing lesion with a radial scar with large and small projections. The model fails to capture a large projection on the left side, while capturing a similar projection on the right side. The model follows small projections but is not as finely segmented as that achieved by observer 1 or 2. Figures 5B and 5C show hyperechoic and hypoechoic lesions with close agreement between all observers. Previously, a modified Unet model utilizing 10 unique instances to create a consensus prediction failed to segment hypoechoic lesions, either due to their relative rarity in the training set or the overall resemblance to background echotexture [12]. Figure 5D shows an example where the model undersegments the lower edge of a lesion, perhaps failing to distinguish the boundary from shadowing.

Fig. 3.

Box plots of Dice, Cohen’s kappa, and 95% Hausdorff metrics compared between the experts’ segmentation (ES-ES) and between experts vs. deep learning model segmentation (ES-MS)

Fig. 4.

Bland-Altmann plots show model performance vs. each expert regarding to: (A) mass area, (B) mass major axis length, (C) mass minor axis length. Observers 1, 2, and 3 are shown in green, blue and yellow, respectively.

Fig.5.

Sample segmentations of all observers from the test set. A) Benign complex sclerosing lesion, B) benign fibromatosis, C) benign mastitis, D) malignant invasive mammary carcinoma with mixed ductal and lobular features. The deep learning model’s results are shown in orange, and observers 1, 2 and 3’s results are in green, blue and yellow, respectively.

4. Discussion

This study compares the performance of an optimized deep learning automatic segmentation model against segmentation from three experts using a selection of challenging BI-RADS 4 and 5 lesions. Previous studies have used data labeled by a single expert split into the training and validation sets, creating a consistent style of segmentation data [11, 12]. By using the segmentation of the three experts, we were able to evaluate the interobserver variability of the deep learning segmentation model. The model is able to segment an image in 0.24 s using an NVIDIA Titan Xp (Santa Clara, CA) with approximately similar performance as that of an expert. However, the segmentation times of the experts were not recorded.

Segmentation comparisons were evaluated using standard comparison metrics and statistical analysis to test the model performance relative to the experts. However, we did not evaluate whether the statistical differences in performance were clinically significant. A high agreement was found in cases of fibroadenoma. Fibroadenoma is the most common benign pathology of the breast and is often hypoechoic with distinct margins. The lowest agreement occurred in difficult cases, which were heterogeneous and had unclear, indistinct margins.

The deep learning model was trained using a single label per US image provided by several US researchers, which closely matched expert performance. The data in the test, training, and validation datasets were obtained from multiple US systems using different transducers and settings. Drawing data from multiple sources provides a large, diverse dataset that can be generalized to other US systems. One limitation is that the evaluation was performed on a small number of patients relative to the size of the training and validation sets. A larger cohort would better establish the overall performance of the model; however, it is difficult to recruit experts to perform segmentation because of the time commitment and associated costs.

To compare the benefits of the model optimization, the results of ResNet152 [33], HRNet [34], EfficientNetB5 [35], InceptionV4 [36], ResNest269 [37], ResNext152 [38], and our optimized DenseNet264 base models are presented in Table 3. Each model was trained using a four-stage training regime, with results taken from the final stage. For comparison, a non-deep learning automatic segmentation algorithm was implemented using the algorithm presented by Ramadan et al. [39]. We implemented the algorithm using successive applications of contrast limited adaptive histogram equalization [40], optimized Bayesian nonlocal means filters [41], simple linear iterative clustering [42], saliency optimization [43], lazy snapping [44] and conditional post-processing with active contours model [45]. The settings were randomly optimized on a random 100-image sample of the training tests for 250 iterations. Optimal settings were applied to our test set, with a final Dice coefficient of 0.659. The relatively low performance of the algorithm seems to stem largely from the automated seed generation step. The saliency algorithm sometimes selects regions outside the suspicious mass, which causes the subsequent segmentation algorithm to segment healthy tissue instead of the suspicious mass.

Table 3.

Mean values of pairwise comparison metrics for different segmentation models.

MODEL	SPECIFICITY	SENSITIVITY	DICE	95% HD	COHEN’S KAPPA
OURS	0.993	0.826	0.832	1.42 mm	0.823
DENSENET264	0.983	0.847	0.780	1.53 mm	0.772
EFFICIENTNETB5	0.982	0.848	0.767	1.54 mm	0.756
HRNET	0.983	0.843	0.774	1.52 mm	0.763
INCEPTIONRESNETV2	0.981	0.841	0.759	1.57 mm	0.740
INCEPTIONV4	0.981	0.817	0.755	1.54 mm	0.732
RESNEST269	0.979	0.842	0.738	1.61 mm	0.725
RESNET152	0.977	0.848	0.747	1.59 mm	0.710
RESNEXT152	0.981	0.840	0.762	1.55 mm	0.740
SALIENCY GUIDED	0.747	0.900	0.659	1.89 mm	0.516

5. Conclusion

Establishing deep learning model performance and consistency is an important part of verifying the performance of a powerful and rapidly improving technology. When applied to medical data, deep learning has the potential to dramatically save time for experienced medical professionals by automating time-consuming aspects of the job and potentially reducing interobserver variability by utilizing a consistent automatic tool. Herein, we have shown that an optimized deep learning model, trained using modern techniques, performs at a level consistent with that of trained experts in a complex and challenging medical task.

Highlights.

• Automatic breast mass segmentation statistical performance was on par with that of human expert.

• Proposed Model had a mean Dice coefficient comparable to that of human expert.

• Proposed Model had a mean Hausdorff distance comparable to that of human expert.

• Proposed a focal Matthew’s correlation coefficient for loss function