Using thermodynamic equilibrium models to predict the effect of antiviral agents on infectivity: Theoretical application to SARS-CoV-2 and other viruses.

Abstract

Thermodynamic equilibrium models predict the infectivity of novel and emerging viruses using molecular data including the binding affinity of the virus to the host cell (as represented by the association constant K_{a_virus_T}) and the probability, p_virogenesis, of the virus replicating after entry to the cell. Here those models are adapted based on the principles of ligand binding to macromolecules to assess the effect on virus infectivity of inhibitor molecules which target specific proteins of the virus. Three types of inhibitor are considered using the thermodynamic equilibrium model for severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) infection of the human lung with parameters for the strength and nature of the interaction between the target virus protein and the inhibitor molecule. The first is competitive inhibition of the SARS-CoV-2 spike glycoprotein (SGP) trimer binding to its human angiotensin converting enzyme 2 (ACE2) receptor by unfractionated heparin (UFH). Using a novel approach presented here, a value of K_{a_virus_T} = 3.53 × 10¹⁷ M⁻¹ is calculated for SARS-CoV-2 from the IC₅₀ for inhibition by UFH of SARS-CoV-2 plaque formation in cell culture together with the dissociation constant K_VI of 0.73 × 10⁻¹⁰ M reported for heparin binding to SARS-CoV-2 SGP trimer. Such a high K_{a_virus_T} limits the effectiveness of competitive inhibitors such as UFH. The second is the attachment of a nanoparticle such as a zinc oxide tetrapod (ZnOT) to the virus shell as for herpes simplex virus (HSV). The increase in molecular weight through ZnOT attachment is predicted to decrease K_{a_virus_T} by orders of magnitude by making the entropy change (ΔS_{a_immob}) on immobilisation of the ZnOT:virus complex on cell binding more negative than for the virus alone. According to the model, ZnOT acts synergistically with UFH at the IC₅₀ of 33 μg/cm³ which together decrease viral infectivity by 61,000-fold compared to the two-fold and three-fold decreases predicted for UFH alone at the IC₅₀ and for ZnOT alone respectively. According to the model here, UFH alone at its peak deliverable dose to the lung of 1,000 μg/cm³ only decreases infectivity by 31-fold. Practicable approaches to target and decrease ΔS_{a_immob} for respiratory viruses should therefore be considered. The combination of decreasing ΔS_{a_immob} together with blocking the interaction of virus surface protein with its host cell receptor may achieve synergistic effects for faecal-oral viruses and HSV. The third is reversible noncompetitive inhibition of the viral main protease (M^pro) for which the decrease in p_virogenesis is assumed to be proportional to the decrease in enzyme activity as predicted by enzyme kinetic equations for a given concentration of inhibitor which binds to M^pro with dissociation constant K_i. Virologists reporting viral inhibition studies are urged to report the concentration of cells in the cell culture experiment as this is a key parameter in estimating K_{a_virus_T} here.

1. INTRODUCTION

In addition to the development of vaccines against coronavirus disease 2019 (COVID-19), both the repurposing of existing clinical drugs such as unfractionated heparin (UFH) (Tree et al. 2020) and the structure-based design of novel drugs which target severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) specific proteins are being pursued. As an example of the latter, Zhang et al. (2020) have focused on inhibitors of the main protease (M^pro, also called 3CL^pro) of SARS-CoV-2. Much research effort is directed at drugs such as UFH (Tree et al. 2020) and the monoclonal antibody MAb362 (Ejemel et al. 2020) which inhibit the entry of virus to the host cell by binding to the receptor binding domain (RBD) on the head of the SARS-CoV-2 spike glycoprotein (SGP) trimer and so blocking its interaction with the host cell receptor (Cr) angiotensin converting enzyme 2 (ACE2). This is shown in Figure 1 . Most inhibitor studies report the total inhibitor concentration (IC₅₀,) that reduces infectivity by 50%; for example the amount of UFH or MAb362 in μg/cm³ required to reduce the number of SARS-CoV-2 viral plaques on monolayers of Vero cells by 50% compared with the virus only control. The strength of an inhibitor can be also quantified by the thermodynamic dissociation constant which defines the strength of its binding either to the individual virus surface protein e.g. the SGP trimer (K_di), or to the whole virus (K_VI), or to the target viral enzyme (K_i) in the case of M^pro. It is demonstrated here that these inhibitor dissociation constants enable the theoretical modelling of the effects of inhibitors on viral infectivity in human hosts through thermodynamic equilibrium models.

Figure 1.

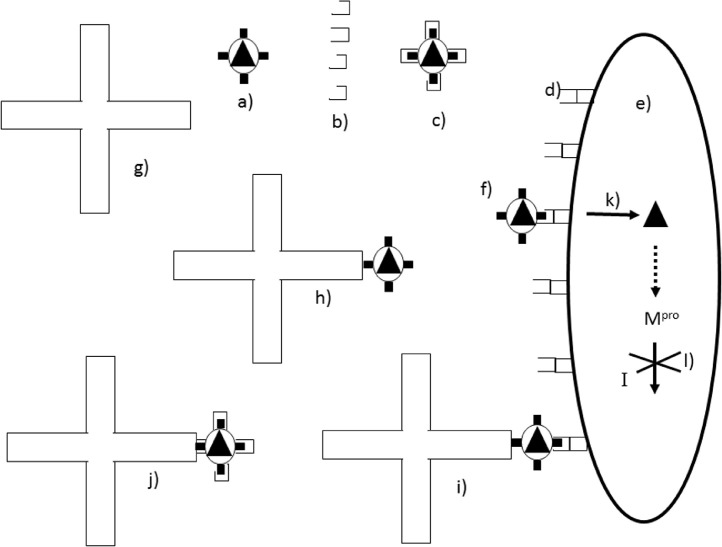
Action of inhibitors on a virus. The free virus (a) has surface spike glycoproteins (represented as black rectangles) each of which may be blocked by binding heparin molecules (b) to give a V.I complex (c) which can no longer bind to the cellular receptors (d) on the surface of the host cell (e). Free virus (f) can bind to the cellular receptors allowing entry (k) of the nucleocapsid core (black triangle) to the cell. Inhibitors such as zinc oxide tetrapods (g) can also bind to the free virus (a) to give a V.I complex (h) which could still theoretically bind to the host cell (i) with subsequent entry (k) of the viral core into the host cell (e). Binding could be prevented by a second inhibitor such as heparin (j). Once in the cell the viral main protease (M^pro) is synthesized from RNA in the nucleocapsid core. M^pro is inhibited by an inhibitor I (l).

Previously a prototype thermodynamic equilibrium model has been developed for a dose-response for a respiratory virus such as SARS-CoV-2 (Gale 2020a). That model is based on a number of biophysical and molecular parameters that can be translated into probabilities for the purpose of assessing the overall probability of infection by a single virion. The component probabilities are summarised in Table 1 . The effects of inhibitors on two of the probabilities, namely the fraction, F_B, of virus particles in the challenge dose which are bound to host cells and the probability, p_virogenesis, of the virus replicating after entry to the cell, are considered here. Central to F_B is the magnitude of the thermodynamic association constant K_{a_virus_T} which defines the binding affinity of the virus to the host cell. The magnitude of K_{a_virus_T} is not only dependent on the strength and number of SGP trimer/ACE2 interactions during virus binding but also on the entropy decrease (ΔS_{a_immob}) on immobilisation of the whole virus on the host cell surface (Liu et al 2020; Gale 2020b). An important conclusion of the work here is that the very strong binding of SARS-CoV-2 to human cells through the ACE2 receptor as represented by the high K_{a_virus_T} value reduces the effectiveness of heparin as an inhibitor. However, making ΔS_{a_immob} more negative by increasing the molecular weight of the virus on attaching to a large inert particle such as a zinc oxide tetrapod (ZnOT) nanoparticle increases the potency of heparin in reducing F_B with the two inhibitors acting synergistically.

Table 1.

Parameters for a thermodynamic equilibrium dose-response model for infection by a respiratory virus (Gale 2020a) together with possible antiviral interventions.

Parameter in Equation 2	Description	Possible interventions
Fv	Fraction of virus in lung mucus not bound to mucin, i.e. free	Blocking of viral neuraminidases and esterases if present. Not present on SARS-CoV-2
ppfu	Probability that a given virion (represented in the exposure as a viral RNA copy) is itself capable of initiating infection in a cell. In effect the inverse of the number virions in a plaque-forming unit.	N/A
FB	Fraction of virus dose bound to lung cells	Either a competitive inhibitor such as heparin that blocks ACE2 binding with a low KVI or an irreversible inhibitor that makes ΔSa_immob more negative. Possible synergistic effects on FB in combination.
pentry	Probability that a virion bound to cell surface enters that cell	Block cleavage of SGP to prevent viral membrane fusion.
pvirogenesis	Probability virus replicates within cell after entry and progeny virions are assembled.	Target viral main protease (Mpro). Major focus of research for SARS-CoV-2 (Zhang et al 2020).
pbudding	Probability progeny virions exit the infected cell

1.1. Estimation of K_{a_virus_T} from virus inhibition experiments

The magnitude of K_{a_virus_T} is known for relatively few viruses (Popovic and Minceva 2021). This may reflect the difficulty in measuring K_{a_virus_T} experimentally and to the author's knowledge there are no data on K_{a_virus_T} for SARS-CoV or SARS-CoV-2. An outcome of the thermodynamic equilibrium analysis developed here is that K_{a_virus_T} can be calculated directly from K_VI and IC₅₀ data which have been reported in drug inhibition studies. This is demonstrated for SARS-CoV-2 using data for UFH inhibition of SARS-CoV-2 plaque formation in cell culture from Tree et al. (2020). For comparison K_{a_virus_T} is also estimated for adeno-associated virus (AAV) using heparan sulphate (HS) inhibition data from Negishi et al. (2004). K_VI values for heparin binding to the virus are calculated here from dissociation constants, K_di, measured experimentally for heparin binding to the SGP trimer of SARS-CoV-2 (Kim et al. 2020) and the capsid protein of AAV-2 (Negishi et al. 2004). The K_{a_virus_T} is then used to model the effects of inhibitors on the infectivity of SARS-CoV-2 through reducing F_B.

1.2. Effect on fraction, F_B, of virus bound to host cells of competitive inhibitors that block specific virus binding through the SGP/ACE2 interaction

A competitive inhibitor such as heparin which binds reversibly to SARS-CoV-2 with a given K_VI value will compete with the ACE2 receptors on the host cell for the RBD on the SGP trimer and hence decrease the fraction, F_B, of virus bound to host cells (Figure 1) depending on the relative values of K_VI and K_{a_virus_T}. It is important to note that K_{a_virus_T} is a constant and its value will not be affected by the presence of inhibitor.

1.3. Effect on F_B of inhibitors which make ΔS_{a_immob} more negative

Liu et al. (2020) consider it is intuitive that at least some cell surface receptors are needed to provide a minimum attraction to counteract the loss in translational entropy (S_trans) of the virus on its binding to the host cell. The entropy loss on the immobilisation of the virus to the host cell has previously been formally identified and defined as ΔS_{a_immob} (Gale 2019) and has been suggested as an alternative target for antiviral therapy (Gale 2020b) based for example on the inhibition of herpes simplex virus (HSV) by binding of ZnOT nanoparticles to the virus (Antoine et al. 2012). Specifically the objective is to make ΔS_{a_immob} more negative in magnitude. Only one ZnOT has to bind to a virus (Figure 1h) to greatly increase the mass of the virus and its rotational moments of inertia and hence make ΔS_{a_immob} more negative in magnitude. It is not known whether other viruses including SARS-CoV-2 also bind to ZnOT. Specifically Antoine et al. (2012) show negative charges on the ZnOT surface attracting positively charged groups on the HSV surface and so binding the virus through non-specific electrostatic interactions. The same sites that bind heparin on the SARS-CoV-2 SGP are also positively charged (Mycroft-West et al. 2020) and therefore a SARS-CoV-2 virion could theoretically bind to ZnOT through multiple electrostatic interactions with the SGPs exactly as proposed for HSV which also binds to negatively charged HS on the cell surface through the same mechanism (Antoine et al. 2012). Similarly AAV-2 also has positive charges on its surface to bind heparin (Zhang et al. 2013) and thus could also bind ZnOT in theory. There is no reason spatially why an enveloped virion attached to a ZnOT particle could not also bind to cellular receptors in effect acting as a linker attaching the ZnOT particle to the cell (Figure 1i). Indeed many biochemical assay methods are based on specific linking of biomolecules. Membrane fusion could then proceed resulting in entry of the viral core leaving the ZnOT on the outside. Here the Sackur-Tetrode equation (Gasser and Richards 1974) is used to estimate ΔS_{a_immob} for the virus bound to a ZnOT nanoparticle using the molecular weight calculated for the ZnOT nanoparticle/virus complex (Figure 1h) and so estimate the effect of ZnOT attachment to the virus on K_{a_virus_T}. Since ZnOT targets ΔS_{a_immob} and heparin blocks SGP/ACE2 binding they inhibit virus entry in different ways and could therefore in theory act synergistically (Figure 1j). Although there would clearly be problems in inhaling thousands of ∼1 μm diameter ZnOT nanoparticles into the lungs as a therapy against SARS-CoV-2 for example, the synergistic effect of both is considered here for the purpose of developing the model for other viruses such as HSV and even faecal-oral viruses which infect humans through other routes of entry. Other approaches than attaching the virus to a massive nanoparticle need to be explored to make ΔS_{a_immob} more negative in magnitude, as these could be applied to respiratory viruses.

1.4. Effect of an inhibitor on the activity of the virus main protease

The viral main protease, M^pro, is an attractive drug target for human coronaviruses because it is a viral enzyme and with no known human proteases with a similar cleavage specificity, inhibitors are unlikely to be toxic (Zhang et al. 2020). After entry to the cell the SARS-CoV-2 RNA (Figure 1k) is translated giving a large polyprotein which is cleaved at 11 sites by M^pro. Inhibiting the activity of this enzyme would block viral replication greatly diminishing the value of p_virogenesis in Table 1. The objective of the work here is to use published K_i values for M^pro inhibition to model the effect of the concentration of inhibitor on p_virogenesis and hence predict the decrease in infectivity of the virus.

2. METHODS

The abbreviations are listed in Table 2 .

Table 2.

List of abbreviations.

Abbreviation	Full
AAV	Adeno-associated virus
ACE2	Angiotensin-converting enzyme 2
BPTI	Basic pancreatic trypsin inhibitor
Cr	Host cell receptor such as ACE2
Ctotal	Total number of cells in human lung that have ACE2 receptors and can bind SARS-CoV-2
Cfree	Total number of cells in human lung that have ACE2 receptors and can bind SARS-CoV-2 but which have no bound virus.
C.V	Number of host cells with bound virus
FB	Fraction of virus dose bound to lung cells
Fv	Fraction of virus in lung mucus not bound to mucin, i.e. free
Fi	Fraction of spike proteins with bound inhibitor on average per virion
HS	Heparan sulphate
HSV	Herpes simplex virus
IC50	Total inhibitor concentration that reduces activity by 50%.
L	Avogadro number = 6.022 × 1023 molecules per mol
Ka_virus_T	Association constant for binding of virus to host cells at temperature T
Kd_receptor_T	Dissociation constant for SGP from Cr at temperature T
Ki	Dissociation constant for inhibitor from viral enzyme
Kdi	Dissociation constant for inhibitor from individual viral surface protein (SGP)
KVI	First dissociation constant for inhibitor from Vfree.In
M	Molar (moles/dm3)
Mr	Molecular weight in Daltons
n	Number of SGP trimers on SARS-CoV-2 virion or number of capsid proteins on AAV virion that can each bind an inhibitor molecule or a cellular receptor
Nv	Number of GP/Cr contacts made on virus binding to cell
p1	Probability of initial infection of the host by a single virion in the mucus
pbudding	Probability progeny virions exit the infected cell
pentry	Probability that a virion bound to cell surface enters that cell
phost	Probability of successful infection of the host;
ppfu	Probability that a given virion (represented in the exposure as a viral RNA copy) is itself capable of initiating infection in a cell
pvirogenesis	Probability virus replicates within cell after entry and progeny virions are assembled.
R	Ideal gas constant = 8.31 J/mol/K
RBD	Receptor binding domain on virus surface protein
SARS-CoV	Severe acute respiratory syndrome coronavirus
ΔSa_immob	Change in entropy on immobilization of whole virus on binding to cell surface
ΔSrot	Change in rotational entropy of virus on binding
ΔSmem	Change in entropy as virus membrane approaches host cell membrane
ΔStrans	Change in translational entropy of virus on binding
SGP	Spike glycoprotein on SARS-CoV-2 virion surface that binds to ACE2
UFH	Unfractionated heparin
v0	Enzyme rate in absence of inhibitor
V.In	Virus with n bound inhibitor molecules
Vfree	Virus not bound to host cells
vInhib	Enzyme rate in presence of inhibitor
Vmucus	Total virus dose entering lung mucus

On inhalation of aerosols containing respiratory viruses such as SARS-CoV-2, a proportion enter the mucus in the respiratory tract and lung lining fluid. The probability, p_host, of initial infection of the host (Gale 2020a) is given by

$${\mathit{p}}_{\mathit{host}}=1-{\left(1-{\mathit{p}}_1\right)}^{{\mathit{V}}_{\mathit{mucus}}}$$ (1)

where V_mucus is the total virus dose entering lung mucus during initial exposure of the host and p₁ is the probability of initial infection of the host by a single virion in the mucus.

On the basis of the dose-response for infection of a respiratory virus (Gale 2020a), p₁ may be broken down into a series of probabilities according to

$$p_1=F_v\times p_{pfu}\times F_B\times p_{entry}\times p_{virogenesis}\times p_{budding}$$ (2)

where F_v is the fraction of virus in lung mucus not bound to mucin, i.e. free to bind to epithelial cells, p_pfu is the probability that a given virion is itself capable of initiating infection in a cell, F_B is the fraction of virus bound to epithelial cells, p_entry is the probability that a virion bound to the cell surface enters that cell, p_virogenesis is the probability that the virus replicates within the cell after entry and progeny virions are assembled, and p_budding is the probability that the progeny virions exit the infected cell. With the exception of p_pfu each of these probability steps could be targeted by drug therapies as shown in Table 1.

In the absence of data on whether SARS-CoV-2 binds to human mucin (Chatterjee et al 2020), F_v is set to 1. The value of p_pfu is set to 0.0001 based on there being ∼10⁴ RNA copies per pfu for SARS-CoV-2 replicating in human airway tissues over 5 days post infection (Plante et al. 2020). Of 39,778 lung cells studied by Lukassen et al. (2020), 206 expressed ACE2 and of those only 104 expressed both ACE2 and transmembrane protease/serine protease (TMPRSS2) and/or furin. TMPRSS2 is required to cleave the SGP resulting in membrane fusion and cell entry of the virion. Thus given SARS-CoV-2 has bound to a cell there is a 0.5 (104/206) probability that it will be able to enter and p_entry is set to 0.5. The values of p_virogenesis and p_budding are set to 1 (Gale 2020a). Modelling F_B is now described.

2.1. Modelling the effect on F_B of competitive inhibitors such as UFH that block specific virus binding through the RBD/ACE2 interaction

2.1.1. Competitive reversible binding of inhibitor to the surface spike glycoprotein trimers on the virus

Each SGP trimer binds reversibly to an inhibitor (I) molecule such as UFH with a dissociation constant, K_di, which is determined experimentally (Kim et al. 2020). The lower the magnitude of K_di the stronger the binding. Many viruses contain multiple (n) copies of the surface proteins that bind to the cellular receptors and hence also to competitive inhibitors. For example one AAV-2 capsid has n = 20 HS binding sites (Negishi et al. 2004) and the SARS-CoV and SARS-CoV-2 virions each have n = 74 SGP trimers (Popovic and Minceva 2020). According to Price and Dwek (1979) the number, i, of molecules of an inhibitor bound to each virion with n equivalent inhibitor binding sites (i.e. SGP trimers in the case of SARS-CoV-2) increases with concentration [I] of inhibitor as

$$i=\frac{n\left[I\right]}{K_{\mathit{di}}+\left[I\right]}$$ (3)

On dividing by n, the fraction, F_i, of SGP trimers with bound inhibitor on average per virion in a sample is given by

$$F_i=\frac{\left[I\right]}{K_{di}+\left[I\right]}$$ (4)

This assumes all the 74 SGP trimers have the same K_di and that each binds a single I molecule independently (Price and Dwek 1979). The K_di determined experimentally for SARS-CoV-2 SGP trimer binding to heparin is 0.73 × 10⁻¹⁰ M (Kim et al. 2020). For the purpose of demonstration here, an inhibitor concentration, [I], of 2.1 μM is used for UFH. This represents the average IC₅₀ of 33 μg/cm³ for UFH reported for SARS-CoV-2 Australia/VIC01/2020 (Tree et al. 2020) based on a M_r of 16,000 Da for UFH (Table 3 ). Thus 33 μg/cm³ is equivalent to 0.033 g/dm³ which on dividing by 16,000 g/mol give 2.1 × 10⁻⁶ mol UFH per dm³. At an inhibitor concentration [I] = 2.06 × 10⁻⁶ M and using K_di = 0.73 × 10⁻¹⁰ M, then F_i = 0.99997 according to Equation 4 such that 99.997% of the n = 74 SGP trimers have bound UFH in the absence of host cells. Thus at the IC₅₀ used by Tree et al. (2020) the free SARS-CoV-2 virion exists almost exclusively as V_free(UFH)₇₄ with a small proportion existing as V_free(UFH)₇₃ following the dissociation of a single UFH molecule according to:

$$V_{free}{\left(UFH\right)}_{74}\leftrightarrow V_{free}{\left(UFH\right)}_{73}+UFH$$

Table 3.

Values of K_{a_virus_T} calculated for SARS-CoV-2 and AAV-2 with Equation 10 using published data for K_VI and IC₅₀. The first dissociation constant for the heparin-saturated virus, K_VI, equals the dissociation constant, K_di, measured experimentally for a single SGP binding to a single heparin (see Methods for justification).

Virus	Inhibitor	IC50 (μg/cm3)	Mr (Da)	IC50 (M)	KVI (M)	aKa_virus_T (M−1)
SARS-CoV-2	UFH	b33.0	f16,000	d2.1 × 10−6	e0.73 × 10−10	3.53 × 1017
AAV-2	HS			c0.3 × 10−6	c3.4 × 10−9	1.09 × 1015

^aCalculated with [C_free] ∼ [C_total] = 8 × 10⁻¹⁴ M in Equation 10 as for human lung model (see text).

^bAverage of 25 and 41 μg/cm³ range for plaque inhibition assay of Vero E6 cells by UFH from Tree et al. (2020)

^cData for HS binding to AAV-2 from Negishi et al. (2004)

^dValue in units of M used in Equation 10 calculated as IC₅₀ in μg/cm³ converted to g/dm³ and then divided by M_r in Da.

^eTrimeric SARS-CoV-2 SGP binding to immobilized heparin (Kim et al. 2020).

^fM_r UFH (Tree et al. 2020)

More generally for a free virus with n binding sites on its surface

$$V_{free}{I}_n\leftrightarrow V_{free}{I}_{\left(n-1\right)}+I$$ (5)

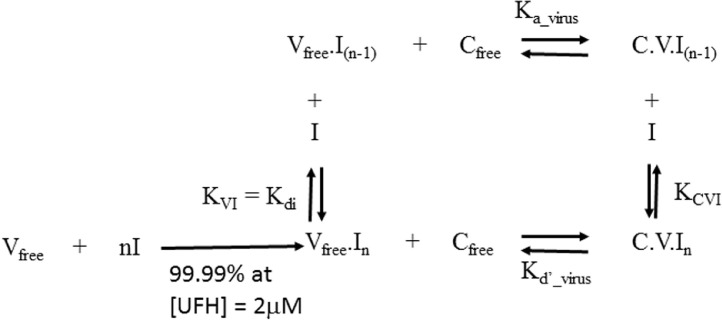
and the dissociation constant for the first inhibitor molecule from the saturated virus is given by K_VI.

$$K_{VI}=\frac{\left[V_{free}{I}_{\left(n-1\right)}\right].\left[I\right]}{\left[V_{free}.I_n\right]}$$ (6)

For a virion with an inhibitor molecule bound to each and every one of the n SGP trimers, the K_VI is related to the dissociation constant, K_di, measured in a laboratory for a single SGP trimer/I interaction by

$$K_{VI}=\left(\frac{n}{1}\right)K_{di}$$

This is because statistically each I molecule can dissociate from a V_free.I_n complex in n ways but the free I molecule can only associate with V_free.I_(n-1) in one way (Price and Dwek 1979). Thus in the case of SARS-CoV-2 for which K_di = 0.73 × 10⁻¹⁰ M for SGP/heparin interaction (Kim et al. 2020), the dissociation constant for the V_free(UFH)₇₄ entity is given by

$$K_{VI}=\left(\frac{74}{1}\right)\times 0.73\times {10}^{-10}M=5.4\times {10}^{-9}M$$

For the purpose of simplifying the model here in Figure 2 , it is assumed that the V_free.I_(n-1) entity makes the first SGP/ACE2 interaction with its one free SGP trimer in the cases of SARS-CoV and SARS-CoV-2. However, the virion is spherical and the 74 SGP trimers all point in different directions being normal to the sphere surface. There are therefore spatial considerations to be considered in that only the one SGP trimer of the n = 74 trimers on the virus surface that is immediately opposite to an ACE2 receptor molecule on the host cell surface can result in binding. Therefore there is only one in 74 UFH dissociations that can result in a binding and it is proposed that the effective K_VI is reduced by a factor of n such that

$$K_{VI}\equiv K_{di}$$

Figure 2.

Thermodynamic equilibrium constants for interaction of virus (V) with its host cell (C) and inhibitor (I).

2.1.2. Model for competitive inhibition of virus binding to host cell

The scheme for the interaction of the virus (V) with a host cell (C) and a specific inhibitor (I) is set out in Figure 2 and is based on the binding of ligands to macromolecules (Price and Dwek 1979). The free virus, V_free.I_(n-1), binds to a host cell, C_free, to give a cell with bound virus, C.V.I_(n-1), with a binding affinity given by the association constant K_{a_virus_T} in units of dm³ mol⁻¹ (M⁻¹) where

$$K_{a\_virus\_T}=\frac{\left[C.V.I_{\left(n-1\right)}\right]}{\left[C_{free}\right]\left[V_{free}.I_{\left(n-1\right)}\right]}$$ (7)

From Figure 2 the fraction, F_B, of virus bound to host cells is expressed as

$$F_B=\frac{\left[C.V.I_{\left(n-1\right)}\right]+\left[C.V.I_n\right]}{\left[V_{free.}{I}_{\left(n-1\right)}\right]+\left[C.V.I_{\left(n-1\right)}\right]+\left[V_{free}{I}_n\right]+\left[C.V.I_n\right]}$$

For competitive inhibition the fully saturated virus complex (V_free.I_n) cannot bind to the host cell (C) because an inhibitor molecule I is bound to the RBD of every SGP trimer on the virus thus blocking all interaction of the virus with the cellular receptors (Cr). This is called competitive inhibition because I and Cr compete for the same site on the viral SGP trimers in the case of SARS-CoV-2 or the viral capsid proteins in the case of AAV. It has been demonstrated that heparin directly competes with ACE2 for the RBD on the head of the SGP from SARS-CoV-2 (Mycroft-West et al. 2020; Tree et al. 2020) and binding of AAV-2 to heparan sulphate proteoglycans on the host cell surface is competitively inhibited by soluble HS (Negishi et al. 2004). This confirms competitive inhibition. Since in competitive inhibition the binding of I and C to the virus is mutually exclusive the C.V.I_n complex cannot exist. Thus [C.V.I_n] = 0 M for competitive inhibition and

$$F_B=\frac{\left[C.V.I_{\left(n-1\right)}\right]}{\left[V_{free.}{I}_{\left(n-1\right)}\right]+\left[C.V.I_{\left(n-1\right)}\right]+\left[V_{free}{I}_n\right]}$$

Substituting [C.V.I_(n-1)] and [V_free.I_n] with Equation 7and Equation 6 respectively allows F_B to be expressed in terms of the concentration [I] of inhibitor and its dissociation constant, K_VI, from the virus:

$${\mathit{F}}_{\mathit{B}}=\frac{1}{1+\frac{1}{{\mathit{K}}_{\mathit{a}\_\mathit{virus}\_\mathit{T}}\times \left[{\mathit{C}}_{\mathit{free}}\right]}\left(1+\frac{\left[\mathit{I}\right]}{{\mathit{K}}_{\mathit{VI}}}\right)}$$ (8)

For low challenge doses such that the number of viruses is much fewer than the number of target cells, C_free may be approximated by C_total which is calculated in the case of SARS-CoV-2 as the fraction of lung cells expressing ACE2 on their surface (Gale 2020a). Of 39,778 lung cells studied by Lukassen et al. (2020), the number expressing ACE2 was 206 accounting for 0.52% of the 230 × 10⁹ cells in the human lung (Crapo et al 1982). The value for [C_free] is 8.0 × 10⁻¹⁴ M on the basis of 1.2 × 10⁹ susceptible lung cells expressing ACE2 in 0.025 dm³ of lung lining fluid (Gale 2020a).

2.1.3. Heparin binds reversibly to both SARS-CoV-2 and AAV-2

While inhibitor binding to SGP trimers must be tight to be effective with small K_di values, it must also be reversible for the model in Figure 2 as represented by the two way arrows. The kinetic dissociation rate of 1.2 × 10⁻⁷ s⁻¹ for heparin dissociating from the SGP trimer of SARS-CoV-2 confirms the reversible nature of the binding (Kim et al. 2020) as does the dissociation rate of 1.2 × 10⁻³ s⁻¹ reported for heparin dissociating from AAV-2 by Zhang et al. (2013).

2.2. Estimating K_{a_virus_T} for SARS-CoV-2 from published IC₅₀ and K_VI values

When the fraction of viruses bound to host cells in the presence of inhibitor, F_Bi, is equal to half that in the absence of inhibitor, F_B0, then the probability, p_host, of infection will be halved because p₁ in Equation 1 is halved according to Equation 2. Therefore the inhibitor concentration [I] at which

$$F_{Bi}=0.5\times F_{B0}$$

is the IC₅₀. By setting [I] = 0 M in Equation 8, F_B0 can be expressed as

$$F_{B0}=\frac{1}{1+\frac{1}{K_{a\_virus\_T}\times \left[C_{free}\right]}}$$

Substituting into Equation 8 gives

$$0.5\times F_{B0}=\frac{1}{\frac{1}{F_{B0}}+\frac{I{C}_{50}}{K_{a\_virus\_T}\times \left[C_{free}\right]\times K_{VI}}}$$

from which the IC₅₀ is calculated as:-

$$I{C}_{50}=K_{VI}\left(1+K_{a\_virus\_T}\times \left[C_{free}\right]\right)$$ (9)

in agreement with the classic expression for competitive inhibition of enzymes (Cer et al 2009). The value of K_{a_virus_T} is then derived from Equation 9 as

$$K_{a\_virus\_T}=\frac{1}{\left[C_{free}\right]}\left(\frac{I{C}_{50}}{K_{VI}}-1\right)$$ (10)

and is calculated here using published data for dissociation constants and IC₅₀s for UFH binding to SARS-CoV-2 and for HS binding to AAV-2 (Table 3). Equation 10 gives a negative K_{a_virus_T} when IC₅₀ < K_VI which is meaningless. It should be stressed that K_VI is not the same as the IC₅₀ and in all systems with host cells present IC₅₀ will be greater than K_VI. pH and other factors including temperature (Gale 2020b) affect the strength of virus binding and it is assumed here for the purpose of demonstration that conditions are similar in the cell culture experiments, the human lung and in the SGP/UFH binding experiments.

2.3. Modelling the effect on F_B of inhibitors which make ΔS_{a_immob} more negative

2.3.1. Estimating the effect of changing ΔS_{a_immob} on K_{a_virus_T}

As presented previously (Gale 2019, 2020b), the magnitude of K_{a_virus_T} can also be estimated from thermodynamic parameters as

$${\mathrm{K}}_{\mathrm{a}\_\text{virus}\_\mathrm{T}}=\frac{1}{{\left({\mathrm{K}}_{\mathrm{d}\_\text{receptor}\_\mathrm{T}}\right)}^{N_v}}\times {\mathrm{e}}^{\frac{\Delta {\mathrm{S}}_{\mathrm{a}\_\text{immo}\mathrm{b}}}{\mathrm{R}}}$$ (11)

where K_{d_receptor_T} is the dissociation constant for the SARS-CoV-2 SGP trimer from its ACE2 at temperature T, N_v is the number of SGP/ACE2 interactions on virus/host cell binding and ΔS_{a_immob} is the change in entropy on immobilization of whole virus on binding to the cell surface. Increasing ΔS_{a_immob} by the amount ΔΔS_{a_immob} (i.e. the difference between the values of ΔS_{a_immob(virus)} for the SARS-CoV-2 virion and ΔS_{a_immob(virus:ZnOT)} for the SARS-CoV-2 virion attached to ZnOT) therefore increases K_{a_virus_T} by a factor of

$$\frac{K_{a\_\mathit{virus}\_T\left(\mathit{virus}\right)}}{K_{a\_\mathit{virus}\_T(\mathit{virus}:\mathit{ZnOT})}}=e^{\frac{1}{R}\left(\Delta \Delta S_{a\_\mathit{immob}}\right)}$$ (12)

where $\Delta \Delta S_{a\_immob}=\Delta S_{a_{immob}\left(virus\right)}-\Delta S_{a_{immob}\left(virus:ZnOT\right)}$

2.3.2. Estimation of ΔS_{a_immob} for the virus and for the virus attached to ZnOT

The ΔS_{a_immob} term in Equation 11 is itself comprised of several entropy terms

$$\Delta {\mathit{S}}_{\mathit{a}\_\mathit{immob}}=\Delta {\mathit{S}}_{\mathit{trans}}+\Delta {\mathit{S}}_{\mathit{rot}}+\Delta {\mathit{S}}_{\mathit{mem}}$$ (13)

including the changes in translational and rotational entropy of the whole virus (ΔS_trans and ΔS_rot respectively) and an entropic pressure (ΔS_mem) associated with bringing two membranes close together, as for example, when the virus envelope approaches the host cell membrane (Sharma, 2013).

The ΔS_trans and ΔS_rot terms are now considered.

2.3.3. Translational entropy

The absolute translational entropy per mol of the free virus, S_trans(free virus), is estimated here by the Sackur-Tetrode equation (Gasser and Richards 1974) on the basis of its molecular weight (M_r) in Daltons (Da)

$$S_{trans}\left(freevirus\right)=Rln\left({\left(2\pi \frac{M_r}{1000L}\times \frac{k_{B}T}{h^2}\right)}^{3/2}\times \frac{k_{B}T}{p}\times e^{5/2}\right)$$ (14)

where R is the ideal gas constant, h is the Planck constant, k_B is the Boltzmann constant, p is the atmospheric pressure (101,325 Nm⁻²), L is the Avogadro number and T is the temperature (298 K). The change in translational entropy on virus binding, ΔS_trans, is calculated as:-

$$\Delta S_{trans}=S_{trans}\left(boundvirus\right)-S_{trans}\left(freevirus\right)$$ (15)

where S_trans(bound virus) is the absolute translational entropy of the virus bound to the host cell. The virus has to adopt a certain orientation (Liu et al. 2020) at the point of entry to the cell as the virus membrane fuses with the cell membrane in the case of enveloped viruses such as SARS-CoV-2. Some viruses involve chlathrin-coated pits which would give considerable immobilisation of the virus both in terms of lateral diffusion and rotation. For example African swine fever virus enters macrophages through chlrathin-mediated endocytosis (Andres 2017). It is tempting to assume that S_trans(bound virus) = 0 J/mol/K because the bound virus is immobilised and thus cannot move in the x, y or z directions. However, even in a protein crystal the individual atoms can vibrate in the principal directions about their mean positions with r.m.s. amplitudes of 0.03 to 0.05 nm and the whole proteins themselves can move within a crystal by distances of 0.02 to 0.025 nm (Finkelstein and Janin 1989). Such motions no doubt occur in the atoms of a bound virus, and in the case of enveloped viruses the phospholipids in the envelope will still be able to diffuse within the bilayer. Furthermore, depending on the mobility of the Cr molecule(s) to which the virus is bound, the virus-Cr complex may be able to undergo lateral diffusion within the two dimensional lipid bilayer. Kukura et al. (2009) reported sliding and tumbling motions of individual virions of Simian virus 40 bound to receptors in supporting lipid bilayers and also a repeated back and forth rocking motion of the virion. Some Cr molecules may be anchored to the cytoskeleton thus limiting diffusion, and lateral diffusion may be reduced as the number N_v of GP/Cr contacts increases. To the author's knowledge there are no data for entropy changes on virus binding to the host cell and therefore this work draws on analogies from protein studies, namely the basic pancreatic trypsin inhibitor (BPTI). For BPTI Finkelstein and Janin (1989) estimated S_trans (bound) was half that of S_trans (free). For the purpose of the work here it is therefore assumed that the same holds for viruses and substituting in Equation 15 gives

$$\Delta S_{trans}\sim -\frac{1}{2}{S}_{trans}\left(freevirus\right)$$ (16)

The negative value of ΔS_trans reflects the increase in order as the virus is immobilised.

2.3.4. Rotational entropy

On binding of the virus to the cell surface rotation about two of the three principal axes will be prevented, although some rotation through the Cr molecule(s) about the normal axis to the membrane could occur depending on the rotational diffusion constant of the Cr molecule(s) within the phospholipid bilayer. Finkelstein and Janin (1989) estimated ΔS_rot for BPTI to be slightly more negative than that of the ΔS_trans of -96.2 J/mol/K at -125 to -100 J/mol/K. Estimating the magnitude of the ΔS_rot term involves calculation of the moments of inertia around the three principal axes using the atomic coordinates from the crystal structure as for BPTI (Finkelstein and Janin 1989). This is not possible here for viruses, and for the demonstration purpose of this paper it is assumed that ΔS_rot ∼ ΔS_trans as for BPTI and therefore that

$$\Delta S_{a\_immob}=\Delta S_{trans}+\Delta S_{rot}\approx -S_{trans}\left(freevirus\right)$$ (17)

where S_trans(free virus) is given in Equation 14.

2.3.5. Molecular weights of the SARS-CoV-2 virion and the ZnOT nanoparticle

The M_r of the SARS-CoV-2 virion is 2.20 × 10⁸ Da as calculated from its molecular compositions (Popovic and Minceva 2020). The ZnOT nanoparticles used by Antoine et al. (2012) for HSV treatment were large with arm diameters in the range of 200 nm to 1 μm and arm lengths in the range of 5 μm to 30 μm. Smaller particles may have a broader application because they can be applied at higher particle densities and theoretically could be inhaled. The ZnOT particles used here in the model assumed arm diameters of 200 nm but arm lengths of only 800 nm to give a sphere diameter of ∼ 1 μm. Thus a volume of 1.0 × 10⁻¹⁹ m³ is calculated as four cylindrical arms each of diameter 200 nm and length 800 nm and multiplying by the density of zinc oxide (5.61 g/cm³) gives a mass of 5.6 × 10⁻¹³ g per ZnOT nanoparticle. Multiplying by L gives the M_r as 3.396 × 10¹¹ Da. The M_r of the SARS-CoV-2 virion attached to a ZnOT nanoparticle is therefore 3.398 × 10¹¹ Da.

2.4. Modelling the effect of inhibitors that block the virus main protease

The strength of binding of an inhibitor to an enzyme is defined by the thermodynamic dissociation constant K_i in units of M. The rate, v_Inhib, of an enzyme reaction in the presence of a reversible inhibitor at a concentration [I] with dissociation constant K_i relative to the rate, v₀, of that enzyme in the absence of inhibitor (Bacha et al. 2004) is given by:-

$$\frac{v_{Inhib}}{v_0}=\frac{K_m+\left[S\right]}{K_m\left(1+\left[I\right]/K_i\right)+\left[S\right]\left(1+\left[I\right]/\alpha K_i\right)}$$ (18)

where K_m is the Michaelis constant and [S] is the substrate concentration. The parameter α equals ∞ for competitive inhibition and approaches zero for uncompetitive inhibition. It is assumed here that the effect of [I] on p_virogenesis is directly proportional to the decrease in v_Inhib relative to the rate, v₀, in the absence of inhibitor, i.e. with [I] = 0 M. For the purpose of the prototype dose-response model for infection of humans by respiratory coronaviruses (Gale 2020a) it was assumed that p_virogenesis equals 1, that is once the viral core has entered the cell then replication and capsid assembly are highly efficient. Thus p_virogenesis in the presence of I is given by:-

$${\mathit{p}}_{\mathit{virogenesis}}=\frac{{\mathit{v}}_{\mathit{Inhib}}}{{\mathit{v}}_0}$$ (19)

since when [I] = 0 M in Equation 18 then p_virogenesis = 1.

3. RESULTS

3.1. Estimating K_{a_virus_T} for SARS-CoV-2 and AAV-2 from the published IC₅₀ and K_VI values

Values of K_{a_virus_T} are estimated in Table 3 for SARS-CoV-2 and AAV-2 using data for inhibition of infection by UFH (Tree et al. 2020) and HS (Negishi et al. 2004) respectively in Equation 10.

3.2. Effect on F_B of the competitive inhibitor UFH that blocks specific virus binding to host cells through the SGP/ACE2 interaction

3.2.1. Predicted effect of K_{a_virus_T} on the fraction of virus bound to host cells in the presence of inhibitors of different strengths

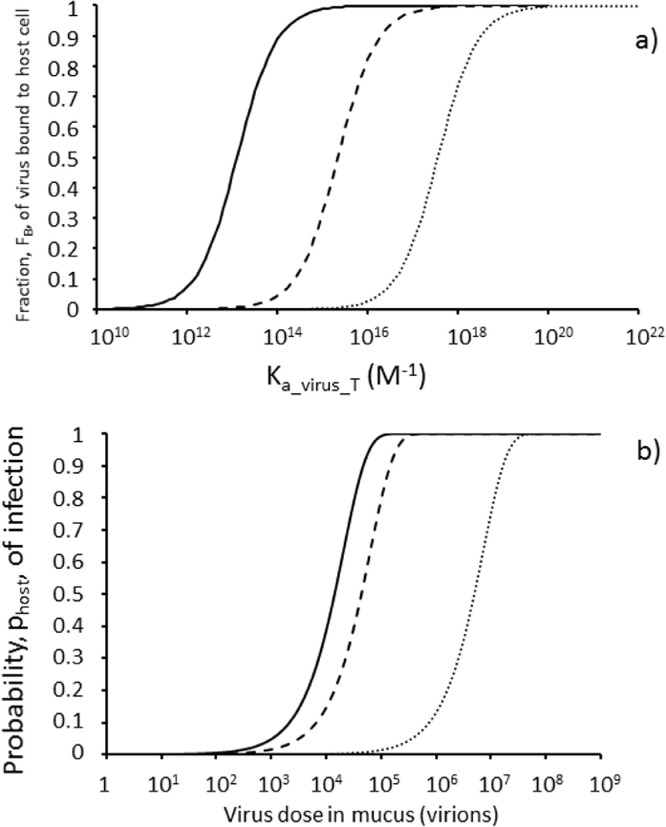
The fraction, F_B, of virus bound to host cells calculated as a function of K_{a_virus_T} according to Equation 8 is shown in Figure 3 a for no inhibitor (solid line), with a weak inhibitor (K_VI of 1.22 × 10⁻⁸ M as for HS binding to AAV-6 capsid protein (Zhang et al. 2013)) (dashed line) and with a strong inhibitor (K_VI of 0.73 × 10⁻¹⁰ M as for heparin binding to SARS-CoV-2 SGP trimer (Kim et al. 2020)) (dotted line). For all three systems, increasing the strength of virus binding to the host cell as represented by K_{a_virus_T} increases the fraction, F_B, of virus bound to host cells. However, the presence of the competitive inhibitor UFH (Figure 3a dashed and dotted lines) requires higher magnitudes of K_{a_virus_T} to achieve the same F_B as for the virus in the absence of inhibitor (Figure 3a solid line). From the inhibitor perspective, a stronger inhibitor (dotted line) is required to achieve the same F_B for a virus with a higher K_{a_virus_T} as a weak inhibitor (dashed line) achieves against a virus which binds host cells less strongly i.e. with a lower K_{a_virus_T}. So for example a 2.1 μM concentration of weak inhibitor (K_VI of 1.22 × 10⁻⁸ M) can achieve 90% inhibition (i.e. F_B = 0.1) of a virus which binds cells with a K_{a_virus_T} = 2.5 × 10¹⁴ M⁻¹ (dashed line Figure 3a). However, to achieve 90% inhibition of a virus which binds cells more strongly (K_{a_virus_T} = 3.9 × 10¹⁶ M⁻¹) requires a stronger inhibitor (K_VI of 0.73 × 10⁻¹⁰ M) according to the model (dotted line Figure 3a). Figure 3a demonstrates the nature of competitive inhibition with increasing K_{a_virus_T} offsetting the effect on F_B of increasing inhibitor binding affinity as represented by lower K_VI. Thus, higher values of K_{a_virus_T} greatly reduce the effectiveness of the inhibitor such that for viruses with very high K_{a_virus_T} values almost 100% of the virus may be bound to cells in the presence of 2.1 μM inhibitor in this model. Only with K_{a_virus_T} <10¹⁷ M⁻¹ does a strong inhibitor (K_VI = 0.73 × 10⁻¹⁰ M) have any sizeable effect on F_B (dotted line Figure 3a). For a weaker inhibitor (K_VI = 1.22 × 10⁻⁸ M), K_{a_virus_T} must be less than 10¹⁵ M⁻¹ for the inhibitor to begin to have an effect on F_B (dashed line Figure 3a).

Figure 3.

Modelling the effect of the competitive inhibitor unfractionated heparin (UFH) which binds to virus spike glycoprotein blocking binding to the cell surface receptor; a) Fraction, F_B, of virus bound to host cells in human lung increases as a function of K_{a_virus_T} according to Equation 8 with [C_free] ∼ [C_total] = 8 × 10⁻¹⁴ M (see text); b) Dose-response (Equation 1 with p_pfu = 10⁻⁴; F_v = 1, p_entry = 0.5, p_virogenesis = 1, p_budding = 1 in Equation 2) for infection with F_B calculated from Equation 8 with K_{a_virus_T} = 10¹⁵ M⁻¹. No inhibitor (solid line) and UFH concentrations of 2.1 μM with K_VI = 1.22 × 10⁻⁸ M (weak) for heparin:AAV-6 (Zhang et al. 2013) (dashed line) and K_VI = 0.73 × 10⁻¹⁰ M (strong) for heparin:SARS-CoV-2 (Kim et al. 2020) (dotted line).

3.2.2. Predicted effect of UFH on the infectivity of the virus

The predicted effect of 2.1 μM UFH on the virus dose response according to Equation 1 is shown in Figure 3b with K_{a_virus_T} = 10¹⁵ M⁻¹. Thus a relatively weak inhibitor with K_VI = 1.22 × 10⁻⁸ M (dashed line representing HS binding to AAV-6 capsid protein (Zhang et al. 2013)) has relatively little effect, reducing the risk of infection by just three-fold according to p₁ values in Table 4 . In contrast a stronger inhibitor with K_VI = 0.73 × 10⁻¹⁰ M (dotted line representing heparin binding to SARS-CoV-2 SGP trimer (Kim et al. 2020)) reduces the risk of infection by 350–fold with p₁ decreasing from 4.9 × 10⁻⁵ to 1.4 × 10⁻⁷ and the predicted ID₅₀ (virion dose which infects half of a population when given to each every member of that population) increasing from 1.4 × 10⁴ virions to 4.9 × 10⁶ virions (Table 4).

Table 4.

Summary of the predicted effects of inhibitors on virus infection parameters using the thermodynamic equilibrium model.

Virus parameters	Inhibitor action	Inhibitor parameters	Probability, p1, of initial infection of the host by a single virion in the mucus	ID50 (virions or viral RNA copies)
Virus with Ka_virus_T = 1015 M−1 (Figure 3b)	None	[I] = 0 μM	4.9 × 10−5	1.4 × 104
	Heparin blocks RBD of SGP with low affinity (Figure 1c)	[I] = 2.1 μM with KVI = 1.22 × 10−8 M	1.6 × 10−5	4.3 × 104
	Heparin blocks RBD of SGP with high affinity (Figure 1c)	[I] = 2.1 μM with KVI = 0.73 × 10−10 M	1.4 × 10−7	4.9 × 106
SARS-CoV-2 virion with Ka_virus_T = 3.53 × 1017 M−1 (Figure 4)	None	[I] = 0 μM	5.0 × 10−5	1.39 × 104
	Heparin at measured IC50 (33 μg/cm3) blocks RBD of SGP with high affinity (Figure 1c)	[I] = 2.1 μM (IC50) with KVI = 0.73 × 10−10 M	2.5 × 10−5	2.77 × 104
	Heparin at very high dose (1,000 μg/cm3) blocks RBD of SGP with high affinity (Figure 1c)	[I] = 62.5 μM with KVI = 0.73 × 10−10 M	1.6 × 10−6	4.34 × 105
ZnOT:SARS-CoV-2 complex with Ka_virus_T = 5.76 × 1012 M−1 (Figure 4)	ZnOT attached to virion (Figure 1h)	Assume irreversible binding of ZnOT	1.6 × 10−5	4.39 × 104
	ZnOT attached to virion and heparin at measured IC50 (33 μg/cm3) blocks RBD of SGP with high affinity (Figure 1j)	[I] = 2.1 μM (IC50) with KVI = 0.73 × 10−10 M	8.2 × 10−10	8.49 × 108
SARS-CoV-2 virion with FB = 1 (Figure 5)	None		5.0 × 10−5	1.39 × 104
	FL-101 inhibits viral main protease Mpro (Figure 1l)	[I] = 20 μM with Ki = 1.6 × 10−5 M, α = 4,2.	2.6 × 10−5	2.65 × 104
	FL-166 inhibits viral main protease Mpro (Figure 1l)	[I] = 20 μM with Ki = 4.0 × 10−8 M, α = 1.8.	1.2 × 10−7	5.85 × 106
	FL-166 at double concentration inhibits viral main protease Mpro (Figure 1l)	[I] = 40 μM with Ki = 4.0 × 10−8 M, α = 1.8.	5.9 × 10−8	1.17 × 107

3.3. Effect on F_B of inhibitors which make ΔS_{a_immob} more negative

The magnitudes of ΔS_{a_immob} for the SARS-CoV-2 virion and for the SARS-CoV-2 virion bound to a ZnOT nanoparticle as approximated from their M_rs using the Sackur-Tetrode equation (Equation 14) are -348.3 J/mol/K and -439.9 J/mol/K respectively such that ΔΔS_{a_immob} = 91.6 J/mol/K. Thus attaching a ZnOT nanoparticle to a SARS-CoV-2 virion decreases K_{a_virus_T} by 61,000-fold (Equation 12) from 3.53 × 10¹⁷ M⁻¹ (Table 3) for free SARS-CoV-2 to 5.76 × 10¹² M⁻¹. The dose-response curves with F_B in Equation 2 calculated using these K_{a_virus_T} values in Equation 8 are plotted in Figure 4 . Complexing the virion with ZnOT decreases p₁ by three-fold (Table 4) increasing the ID₅₀ three-fold from 1.39 × 10⁴ virions for the free virion (Figure 4 solid line) to 4.39 × 10⁴ virions for the ZnOT/virion complex (Figure 4 dotted line).

Figure 4.

Predicted effect of a combination of unfractionated heparin (UFH) and ZnOT which affect virus binding to the host cell on dose-response for SARS-CoV-2 infection (Equation 1 with p_pfu = 10⁻⁴; F_v = 1, p_entry = 0.5, p_virogenesis = 1, p_budding = 1 in Equation 2) with F_B calculated from Equation 8 with K_{a_virus_T} = 3.53 × 10¹⁷ M⁻¹ as estimated for SARS-CoV-2 (Table 3). No UFH and no ZnOT (solid line); UFH alone at concentration of 2.1 μM (IC₅₀) (dashed line) and at concentration of 62.5 μM (1,000 μg/cm³) (dash single dot line) with K_VI = 0.73 × 10⁻¹⁰ M (for heparin binding to SARS-CoV-2 SGP trimer (Kim et al 2020)); ZnOT alone with K_{a_virus_T} = 5.76 × 10¹² M⁻¹ as estimated for SARS-CoV-2 complexed to ZnOT (see text) (dotted line); and UFH at concentration of 2.1 μM with ZnOT acting synergistically (dash double dot line).

3.4. Enhancing the effectiveness of competitive inhibitors (UFH) that block SGP/ACE2 binding by adding a second inhibitor (ZnOT) that makes ΔS_{a_immob} more negative

UFH blocks SGP/ACE2 binding. Addition of UFH at a concentration of 2.1 μM (equal to the IC₅₀) to free virus (Figure 4 solid line) decreases the infectivity as represented by p₁ by two-fold as expected for the IC₅₀ (Table 4) doubling the ID₅₀ from 1.39 × 10⁴ virions to 2.77 × 10⁴ virions (Figure 4 dashed line). With the UFH concentration still at 2.1 μM, the addition of ZnOT decreases p₁ by 61,000-fold (Table 4) compared to the free virus increasing the predicted ID₅₀ from 1.39 × 10⁴ to 8.49 × 10⁸ virions (Figure 4 dash double dot line). For comparison increasing the UFH concentration to 1,000 μg/cm³ (62.5 μM) (in the absence of ZnOT) only decreases the infectivity by 31-fold (Figure 4 dash single dot line) relative to the free virus (Figure 4 solid line).

3.5. Modelling effectiveness of inhibitors that block the virus main protease of SARS-CoV

Bacha et al. (2004) report a K_m of 9 μM for a peptide substrate containing the Gln-Ala cleavage sequence for SARS-CoV main proteinase. Bacha et al. (2004) reported K_i values between 40 nM and 16 μM for five aryl boronic compounds which inhibit SARS-CoV M^pro. The five compounds bound reversibly to SARS-CoV M^pro with values for the α parameter in Equation 18 between 1.8 and 5.6 consistent with noncompetitive enzyme inhibition. The K_i for one aryl boronic compound, FL-166, was 40 nM with α = 1.8 (Bacha et al. 2004) and with a substrate concentration [S] of 5 μM (as used by Bacha et al. (2004)) predicts a v_Inhib/v₀ ratio of 0.0024 according to Equation 18 at an inhibitor concentration of 20 μM (in the range of 10 to 40 μM used by Bacha et al. (2004)). Thus p_virogenesis and hence p₁ are decreased by a factor of 422-fold increasing the ID₅₀ from 1.39 × 10⁴ virions to 5.85 × 10⁶ virions (Table 4) as shown by the shift in the dose response curve to the right (Figure 5 dashed line). Doubling the inhibitor concentration to 40 μM halved p₁ doubling the ID₅₀ to 1.17 × 10⁷ virions (Table 4) as shown by the further right shift in the dose-response curve (Figure 5 dash dot dot line). A second weaker aryl boronic inhibitor, FL-101, with a much higher K_i value of 16 μM and a value for the α parameter = 4.2 only halved p_virogenesis having relatively little effect on the dose-response at a concentration of 20 μM (Figure 5 dotted line) with the predicted ID₅₀ approximately doubling from 1.39 × 10⁴ virions to 2.65 × 10⁴ virions (Table 4).

Figure 5.

Modelling the effect of two noncompetitive aryl boronic inhibitors (FL-101 and FL-166 according to Bacha et al. (2004)) of SARS-CoV main protease (M^pro) on the dose-response (Equation 1 with p_pfu = 10⁻⁴, F_v = 1, F_B = 1, p_entry = 0.5, p_budding = 1 in Equation 2) for infection with p_virogenesis calculated from Equation 19 with [S] = 5 μM and K_m = 9 μM in Equation 18; no inhibitor (solid line); the weaker inhibitor compound FL-101 [I] = 20 μM, K_i = 16 μM, α = 4.2 (dotted line); the stronger inhibitor compound FL-166 [I] = 20 μM, K_i = 40 nM, α = 1.8 (dashed line); and the stronger inhibitor compound FL-166 at higher concentration [I] = 40 μM (dash dotted line).

4. DISCUSSION

Previously a thermodynamic equilibrium model estimated the probability, p₁, of initial infection of humans by a single SARS-CoV-2 virion to be 0.0014 (Gale 2020a). This was based on a p_pfu value of 0.0028 from data for SARS-CoV reporting 360 RNA copies per pfu (Vicenzi et al. 2004) and an F_B of 1.0 based on the strength of the interaction between the SARS-CoV-2 virion and the ACE2 receptors (Gale 2020a). Updating the model with a p_pfu value of 0.0001 based on data showing 10⁴ RNA copies per pfu for SARS-CoV-2 (Plante et al 2020) decreases the predicted p₁ to 5.0 × 10⁻⁵ (Table 4) which is in better agreement with the values of 1.5 × 10⁻⁶ to 1.6 × 10⁻⁵ estimated by Zhang and Wang (2020) The RNA:pfu ratio of 10⁴ used here to parameterise p_pfu is for SARS-CoV-2 with the amino acid aspartate (D) at residue 614 of the SGP which was common before March 2020. Since May 2020 a variant with the amino acid glycine (G) at residue 614 has become more common. The D614G substitution gives a statistically significant increase in p_pfu and hence infectivity (Plante et al 2020) and is not considered in this work. Here that thermodynamic equilibrium model is combined with well-established biochemical inhibition models for ligands binding to macromolecules (Price and Dwek 1979) to predict the effect of inhibitors on the infectivity and dose-response for a virus as illustrated for SARS-CoV-2. The model is based not only on the fraction, F_B, of virions bound to host cells according to Equation 8 but also on the effect of the inhibitor on the rate of virogenesis according to Equation 18 (Figure 1). The predicted effects on the virus dose-response of competitive inhibitors of different binding affinity for the RBD on the virus surface proteins are shown in Figure 3b. In Figure 4, the predicted effect of attaching a large ZnOT nanoparticle to the SARS-CoV-2 virion is shown together with the synergistic effect of adding a competitive inhibitor such as UFH that blocks the RBD of the SARS-CoV-2 SGP from binding to ACE2 on the host cell surface. The predicted effect on the dose-response of an inhibitor that blocks virogenesis of SARS-CoV-2 is demonstrated in Figure 5.

4.1. Estimation of K_{a_virus_T} for SARS-CoV-2 and AAV-2

The value of K_{a_virus_T} is of key importance not only in determining the strength of cell binding (Popovic and Minceva 2021) but also in influencing the effect of a competitive inhibitor on the fraction, F_B, of virus bound to host cells as shown in Figure 3a. It is difficult to measure experimentally and there do not appear to be data for SARS-CoV-2 as yet (Popovic and Minceva 2021). However it can be calculated in Equation 10 from the K_VI and the IC₅₀ values which are easier to measure and have been quantified in SARS-CoV-2 and AAV-2 inhibition studies (Table 3). A value for K_{a_virus_T} of 3.53 × 10¹⁷ M⁻¹ is estimated here for SARS-CoV-2 using heparin inhibition data and represents high affinity binding. This is in agreement with theoretical estimates made previously using the K_{d_receptor_T} of 1.47 × 10⁻⁸ M reported for SARS-CoV-2 SGP trimer binding to a single ACE2 protein (Wrapp et al. 2020) in Equation 11 with N_v up to 4 or 5 to overcome the large negative entropy change (ΔS_{a_immob}) on virus binding to the host cell (Gale 2020a). Using the data of Negishi et al. (2004) in Equation 10 a value of 1.09 × 10¹⁵ M⁻¹ is calculated for K_{a_virus_T} for AAV-2 which is also high affinity.

One apparent anomaly in the model is that K_VI is based on just one inhibitor molecule dissociating from the V_free.I_n entity (Equation 5) allowing just one SGP trimer to bind to an ACE2 receptor while the value of K_{a_virus_T} predicted in Table 3 is so high as to require N_v to be greater than one in Equation 11. This can be explained as follows. Once the first SGP trimer/ACE2 receptor interaction has been made, further interactions will be made by neighbouring ACE2 receptors on the host cell competitively displacing heparin molecules from adjacent SGP trimers on the virus with very similar K_di values to K_VI because each SGP trimer/heparin interaction is assumed to be identical and independent (Price and Dwek 1979). The key point is that while the virus can bind to multiple (N_v) ACE2 receptors giving a very high K_{a_virus_T} by Equation 11, each inhibitor can only bind one SGP trimer and therefore each of the multiple SGP trimer/inhibitor interactions on the virus is independent of the others. This may not apply to MAb362 sIgA which being dimeric contains four binding sites each of which could bind to one SGP (Kumar Bharathkar et al. 2020). Thus each MAb362 sIgA could contact up to four SGP trimers on a SARS-CoV-2 virion such that K_VI is much lower than the K_di reported by Ejemel et al. (2020). For this reason K_{a_virus_T} is not calculated with MAb362 inhibition data here.

4.2. Uncertainty in the estimates of K_{a_virus_T} for SARS-CoV-2 and AAV-2

One source of uncertainty in K_{a_virus_T} estimated for SARS-CoV-2 and AAV-2 in Table 3 using Equation 10 from inhibition studies is the molar concentration of Vero E6 cells in the plaque assays used. Here it is assumed that the [C_total] value in the plaque inhibition assay and used as an approximation for [C_free] in Equation 10 to calculate K_{a_virus_T} is the same as that estimated for cells expressing ACE2 in the human lung epithelium at 8 × 10⁻¹⁴ M (Gale 2020a). This also ensures the measured IC₅₀ also achieves a 50% reduction in the probability of infection in the dose-response for infectivity in Figure 4 for the purpose of demonstration of the models here. It is likely that the concentration of cells in the plaque inhibition assays in Tree et al. (2020) is lower such that the predicted K_{a_virus_T} values using Equation 10 would be higher than those in Table 3.

4.3. The high K_{a_virus_T} for SARS-CoV-2 hinders the effectiveness of competitive inhibitors such as UFH which block SGP/ACE2 binding

It is concluded from Figure 3a that the high binding affinity of the SARS-CoV-2 virion to its host cell based on its high K_{a_virus_T} diminishes the effectiveness at decreasing F_B by inhibitors that competitively block the RBD of the SGP binding to ACE2. Specifically high values of K_{a_virus_T} at >10¹⁵ M⁻¹ and >10¹⁷ M⁻¹ undermine inhibition by competitive inhibitors with K_VI values of ∼10⁻⁸ and ∼10⁻¹⁰ M, respectively with at least 20% of the virus still bound to host cells (Figure 3a). From Equation 9 the higher the K_{a_virus_T} then the higher the inhibitor concentration required to achieve a 50% inhibition of the virus as represented by the IC₅₀. Thus, heparin may be more effective against AAV-2 due to the lower K_{a_virus_T} for AAV-2 than against SARS-CoV-2 even though heparin binds more tightly to SARS-CoV-2 SGP than to AAV-2 according to the K_VI values (Table 3). The peak amount of UFH that can be delivered to the lung is 400 – 2,600 μg/ cm³ (Tree et al. 2020). Even at a concentration of 1,000 μg/cm³ (62.5 μM), UFH only decreases the infectivity by 31-fold according to the model here (Figure 4). From Figure 3a an approach is needed to reduce K_{a_virus_T} for SARS-CoV-2 to <10¹⁵ M⁻¹ at which UFH at a concentration of just 2.1 μM (assuming K_VI of 0.73 × 10⁻¹⁰ M for SARS-CoV-2 SGP trimer (Kim et al. 2020)) would reduce F_B to 0.003 (dotted line in Figure 3a) in effect inhibiting infectivity by 99.7% and shifting the dose-response curve for SARS-CoV-2 by almost three orders of magnitude (dotted line in Figure 3b).

4.4. Using a second inhibitor to target ΔS_{a_immob} greatly enhances the effectiveness of inhibitors such as UFH which block the SGP/ACE2 interaction

Decreasing the magnitude of K_{a_virus_T} for SARS-CoV-2 to <10¹⁵ M⁻¹ could be achieved by a second inhibitor which specifically binds to the virus and increases its overall M_r so making ΔS_{a_immob} more negative in magnitude. According to the approximation here based on the Sackur-Tetrode equation the attachment of a ZnOT nanoparticle to a SARS-CoV-2 virion decreases the K_{a_virus_T} to 5.76 × 10¹² M⁻¹. This is in the range where competitive inhibition of the SGP/ACE2 binding by UFH at relatively low concentration (2.1 μM) has a significant effect on the fraction, F_B, of SARS-CoV-2 bound to host cells (dotted line in Figure 3a) and even has a considerable effect on F_B for a virus which is more weakly inhibited as for HS binding to AAV-6 capsid protein (dashed line in Figure 3a). In summary, while UFH alone at a concentration of 2.1 μM reduces the risk two–fold for SARS-CoV-2 as expected at the IC₅₀ concentration, UFH still at 2.1 μM concentration but combined with ZnOT gives a 61,000–fold decrease in infectivity (Figure 4).

4.5. Uncertainty in the estimate of K_{a_virus_T} for SARS-CoV-2 bound to ZnOT

The importance of the loss of translational entropy in ΔS_{a_immob} on virus binding to the host cell is acknowledged by Liu et al. (2020). While the M_r of the virion is known with great accuracy for SARS-CoV-2 (Popovic and Minceva 2020), the values of ΔS_{a_immob} calculated here using the Sackur-Tetrode equation (Equation 14) for such large particles are at best approximations. However they are sufficient for the purpose of demonstrating the potential for developing drugs to target ΔS_{a_immob}.

4.6. Attaching a large nanoparticle may not be an efficient way to decrease ΔS_{a_immob}

While the magnitude of K_{a_virus_T} is very sensitive to changes in ΔS_{a_immob} according to Equation 12, ΔS_{a_immob} is not very sensitive to M_r and to significantly decrease ΔS_{a_immob} for a virus requires attachment of a much larger particle such as ZnOT. This is because of the logarithmic nature of the effect of M_r on the magnitude of S_trans according to the Sackur Tetrode equation (Equation 14). Thus, even though the M_r of the ZnOT nanoparticle is 1,540–fold greater than that of the SARS-CoV-2 virion it only decreases ΔS_{a_immob} by 26% from -348.3 J/mol/K to -439.8 J/mol/K. The effect on decreasing K_{a_virus_T} of attaching a ZnOT will be greater for a smaller virus compared to a larger virus such as SARs-CoV-2. For example ΔS_{a_immob} is approximated by the Sackur-Tetrode equation at -307.4 J/mol/K for the smaller foot-and-mouth disease virus virion on the basis of its Mr = 8.3 × 10⁶ (van de Woude et al. 1972) and would be decreased by 43% by attachment to a ZnOT.

4.7. Other approaches to target ΔS_{a_immob} and application to other viruses

The logarithmic relationship of ΔS_{a_immob} and M_r in the Sackur-Tetrode equation demonstrates a practical limitation in attaching large particles to virions as a means disrupting the thermodynamics of virus binding to host cells although physical entrapment itself may be important as shown for HSV binding within the crevice of a ZnOT nanoparticle (Antoine et al. 2012). Furthermore the inhalation of ZnOT nanoparticles will not be practicable to a respiratory virus such as SARS-CoV-2. Other approaches to targeting ΔS_{a_immob} should be considered including the entropy decrease (ΔS_mem) when the virus and host membranes approach on binding (Sharma 2013).

The K_{a_virus_T} needs to be <10¹² M⁻¹ in the absence of UFH to have a major impact on F_B (Figure 3a solid line). Thus with K_{a_virus_T} estimated to be 5.76 × 10¹² M⁻¹ for the SARS-CoV-2:ZnOT complex it is not surprising in the model here that attachment of ZnOT alone has a relatively small effect on SARS-CoV-2 infectivity in the absence of heparin (dotted line Figure 4). This is in part because of the very high concentration of susceptible cells in the human lung estimated at [C_total] = 8 × 10⁻¹⁴ M which serve to keep F_B high in Equation 8 by providing a lot of high affinity ACE2 receptors to “attract” the virus SGPs. In the model for infection by faecal-oral viruses of the human intestine where the concentration of host cells is estimated to be 36-fold lower than that in the lung at [C_total] = 2.2 × 10⁻¹⁵ M (Gale 2018), the attachment of ZnOT decreases the probability of infection by 80-fold. Thus with [C_free] = 2.2 × 10⁻¹⁵ M as for the human intestine, F_B from Equation 8 ([I] = 0 M) for SARS-CoV-2 attached to ZnOT is 0.012 compared to 0.31 for the human lung with [C_free] = 8 × 10⁻¹⁴ M. It is concluded that the combination of targeting ΔS_{a_immob} together with blocking the interaction of virus surface protein with its host cell receptor may be more applicable for faecal-oral viruses and HSV than for respiratory viruses such as SARS-CoV-2. The model here predicts that ZnOT alone only reduces infectivity by three-fold (Figure 4 dotted line) based on its effect on ΔS_{a_immob} alone In practice the effect of ZnOT on infectivity may be greater than just three-fold because its attachment to the virus surface would also prevent some of the n = 74 SGP trimers on the SARS-CoV-2 (Figure 1h) from interacting with ACE2 and the tetrapod structure may entrap virions so they are not physically able to contact the cell surface. The purpose of the model here is merely to demonstrate the effect of an inhibitor that targets ΔS_{a_immob}. The larger ZnOT particles used by Antoine et al. (2012) for HSV have much larger M_r and hence would decrease ΔS_{a_immob} even more in magnitude.

4.8. Modelling the effect of protease inhibitors on virus dose-response

The effect of inhibitors of the SARS-CoV main protease (M^pro) is taken directly from enzyme kinetics (Basha et al. 2004) and applied to p_virogenesis as the decrease in reaction rate in the presence of inhibitor, v_Inhib, relative to the rate in the absence of inhibitor, v₀ in Equation 19. This allows the decreases in predicted infectivity to be related to published K_i values and inhibitor concentrations as shown in Figure 5.

4.9. K_VI values should be reported where possible in addition to IC₅₀ values

The IC₅₀ is always greater than the K_VI in Equation 10 because the Cr receptors on the host cells compete against the inhibitor for the binding sites on the surface proteins on the virus. The IC₅₀ value is often reported in inhibition studies instead of the K_VI. The K_VI has the advantage that it is a thermodynamic dissociation constant that can be used directly as a parameter in the models developed here which can be adapted to model different hosts for example. In contrast the IC₅₀ value is less flexible because it depends on the system in which it was measured (Cer et al. 2009). Specifically according to Equation 9 the IC₅₀ depends both on the host cell concentration ([C_free]) and on the strength of virus binding to those host cells as represented by K_{a_virus_T}. Both these parameters in cell culture may be different from those in a live host such that the IC₅₀ is not necessarily representative of the concentration that will give a 50% decrease in the probability of infection of the host. Thus if the concentration of susceptible cells is higher in the human lung than in the experimental cell culture study, then the IC₅₀ measured in the laboratory may need to be revised upwards for effective therapy in the patient according to Equation 9. The beauty of reporting both the IC₅₀ and the K_VI value is that K_{a_virus_T} can be also calculated provided [C_total] is also reported in to order to approximate [C_free] in Equation 10.

4.10. Development of the model

The assumption in Equation 5 that free virus is either in the V_free.I_n or V_free.I_(n-1) form will not hold at low [I] according to Equation 4. However it is satisfactory for the demonstration of proof of principle here. The model should be developed further to include the complete range of V.I entities from V_free, V_free.I, V_free.I₂, ….., V_free.I_(n-2), V_free.I_(n-1), to V_free.I_n. This is complicated mathematically and indeed each of these entities will have its own K_VI based on K_di and the number of ways I can dissociate and associate as set out by Price and Dwek (1979). Furthermore consideration needs to be taken of the spatial distribution of the I molecules on the virus. For example for SARS-CoV-2, a V_free.I₇₀ entity has four SGP trimers free to bind to ACE2 receptors. If these four free SGP trimers are adjacent on the virus surface (which is statistically very unlikely) then they can each bind an ACE2 molecule on the initial contact with the host cell surface giving N_v = 4 in Equation 11 such that K_{a_virus_T} is very high. Statistically it is much more likely that the four free SGP trimers on V_free.I₇₀ will be on opposite sides of the sphere so that initial binding of V_free.I₇₀ is through one SGP trimer/ACE2 interaction. At the other extreme at low [I], the bound inhibitor will have very little effect on the binding to host cells of V_free.I₄ for example which still has 70 free SGP trimers with which to initiate binding to the host cell. For this reason no attempt is made here to model F_B as a function of [I] using Equation 8. However, at the relatively high [I] = 2.1 × 10⁻⁶ M used in the demonstrations here most if not all of the virus will be saturated with inhibitor molecules according to Equation 4 such that Equation 5 is appropriate.

During viral replication in the host cell, a substantial number of progeny virions do not contain RNA and are not infectious such that p_virogenesis = 0. These "empty viruses" could act as inhibitors by binding to ACE2 receptors on the host cell surface, although their SGP trimers would also mop up UFH and could even bind to mucins thus locally overcoming the host innate response (see Gale 2020a). Further development of the thermodynamic model should consider these empty viruses. The model can be parameterised for other SARS-CoV-2 variants once IC₅₀ and K_di are obtained experimentally.

4.11. Interpretation of outputs of the model

The response considered here, namely initial infection of the host, happens before the innate immune response and the acquired immune response both of which are important for stopping progression of coronavirus infection in the host (Lim et al. 2016). The objective of the inhibitor in this prototype model is to decrease p₁ and no attempt is made here to allow for the stage in the infection process at which the inhibitor is applied. The prototype model is therefore theoretical and could also be applied to modelling the effect of viral inhibitors on human lung cell culture lines where the response is production of at least one plaque. In the human host, once initial infection has taken place for example in the nasal epithelium of a person infected with SARS-CoV-2, infection progresses to the bronchioles and alveoli of the lung (Hou et al 2020). There are not sufficient data and understanding to model the innate and acquired immune responses and these are therefore ignored in this prototype model, although removal by mucus is considered through F_v. The aim of this paper is to produce a prototype model for the effect of inhibitors on the infectivity of the virus and focuses on the effect of inhibitors on p₁ in Equation 2 through F_B (Equation 8) and p_virogenesis (Equation 18 and Equation 19). Thus assuming the innate and acquired immune responses are constant and are not affected by the drugs, then their effect on the relative decrease in p₁ with the drug compared to without the drug cancels out, such that the model allows the changes in p₁ (and hence ID₅₀) with and without drugs to be modelled. The reader should therefore focus on the changes in p₁ (and hence ID₅₀) on addition of drugs rather than their absolute values. The dose-response parameters (namely p₁ and ID₅₀) presented here are representative of initial infection in an immunologically naïve person in the absence or presence of the drug.

5. CONCLUSIONS

A thermodynamic equilibrium model previously developed to model the infectivity of a novel respiratory virus based on measured biophysical parameters is adapted by applying biochemical principles on the binding of ligands to macromolecules to model the effects of antiviral drugs including heparin that inhibit SARS-CoV-2. Specifically the effect of the strength of the inhibitor on the probability, p₁, of infection by a single respiratory virion in the mucus in the lung lining fluid is calculated. In the absence of inhibitor, p₁ is predicted to be 5.0 × 10⁻⁵ for SARS-CoV-2 representing an ID₅₀ of 13,900 virions.

Central to the model is the dissociation constant, K_VI, for the virus/inhibitor complex which defines the strength of the inhibitor. Although each SARS-CoV-2 virion can bind multiple inhibitor molecules through its 74 surface spike glycoprotein (SGP) trimers, it is shown that the K_VI value for use in the model at high inhibitor concentration is the same as that determined experimentally for the dissociation of a heparin molecule from a single virus SGP trimer.

Also key to the model is the strength of binding of the virus to the host cell through viral SGP interactions with cell receptors (ACE2 for SARS-CoV-2) as represented by the association constant K_{a_virus_T}. Although there are many published studies on the strength of the SGP/ACE2 interaction for SARS-CoV-2, there is no information on K_{a_virus_T} which depends on unknowns such as the number of SGP/ACE2 interactions made on cell surface binding and also the change in entropy on immobilisation of the virus (ΔS_{a_immob}). It is demonstrated here how the magnitude of K_{a_virus_T} for a virus binding to a host cell may be estimated using the K_VI and IC₅₀ data obtained from cell culture inhibition studies, providing the concentration of cells is known. The value calculated here for K_{a_virus_T} for SARS-CoV-2 from heparin inhibition studies is very high at 3.53 × 10¹⁷ M⁻¹. This value may be underestimated here due to uncertainty in the concentration of cells in cell culture.

Such a high K_{a_virus_T} value for SARS-CoV-2 would hinder the effectiveness of competitive inhibitors such as heparin that block SGP binding to the ACE2 receptor on the host cell, i.e. those viruses which bind the host cell more strongly are more difficult to inhibit and require inhibitors with lower K_VI values than viruses that bind more weakly. An alternative approach is to find a second inhibitor to decrease the magnitude of K_{a_virus_T} prior to use of heparin.

In theory, K_{a_virus_T} may be decreased by orders of magnitude by attachment of a ZnOT nanoparticle to the virus as used for inhibition of herpes simplex virus binding. This targets the entropy of immobilisation of the virus as opposed to the SGP/ACE2 interaction and renders the virus infectivity much more susceptible to inhibitors that block SGP/ACE2 binding. At the IC₅₀ concentration, heparin decreases infectivity by 50% as expected, but with the attachment of a ZnOT nanoparticle to the virion, its infectivity is decreased 61,000-fold at the same heparin concentration, demonstrating the synergistic effect of these competitors. Increasing the heparin concentration to 1,000 μg/ cm³ only achieves a 31-fold reduction in infectivity according to the model here.

Since inhaling ZnOT nanoparticles is not practicable as a therapy for respiratory viruses, other approaches to targeting the entropy of immobilisation of the virus should be considered. These include the entropy decrease when the virus and host membranes approach.

The combination of targeting the entropy of immobilisation together with blocking the interaction of virus surface protein with its host cell receptor may achieve synergistic effects for non-respiratory viruses for example herpes simplex virus and faecal-oral viruses. The limited effect on SARS-CoV-2 predicted for ZnOT alone reflects the high concentration of susceptible cells in the lung. The application of ZnOT alone will be more effective at lower host cell concentrations such as in the intestine.

Thermodynamic equilibrium models have a role to play in understanding the effect of drug treatments on virus infectivity. The case is made for also publishing K_VI values which unlike IC₅₀s represent the interaction between virus and its inhibitor and are not affected by the concentration of host cells or the virus association constant. Specifically if the concentration of susceptible cells is higher in the human lung than in the experimental cell culture study, then the IC₅₀ measured in the laboratory may need to be revised upwards for effective therapy in the patient.

Author Statement

I wrote this paper based on my previous thermodynamic dose-response models with no funding. It is my contribution to the global response against COVID-19.

Disclaimer

The views expressed in this paper are those of the author and not necessarily those of any organisations.

Declaration of Competing Interest

None declared.