Generalizability and Transportability of the National Lung Screening Trial Data: Extending Trial Results to Different Populations

Abstract

Background:

Randomized controlled trials (RCT) play a central role in evidence-based healthcare. However, the clinical and policy implications of implementing RCTs in clinical practice are difficult to predict as the studied population is often different from the target population where results are being applied. This study illustrates the concepts of generalizability and transportability, demonstrating their utility in interpreting results from the National Lung Screening Trial (NLST).

Methods:

Using inverse-odds weighting, we demonstrate how generalizability and transportability techniques can be used to extrapolate treatment effect from (i) a subset of NLST to the entire NLST population and from (ii) the entire NLST to different target populations.

Results:

Our generalizability analysis revealed that lung cancer mortality reduction by LDCT screening across the entire NLST [16% (95% confidence interval [CI]: 4–24)] could have been estimated using a smaller subset of NLST participants. Using transportability analysis, we showed that populations with a higher prevalence of females and current smokers had a greater reduction in lung cancer mortality with LDCT screening [e.g., 27% (95% CI, 11–37) for the population with 80% females and 80% current smokers] than those with lower prevalence of females and current smokers.

Conclusions:

This article illustrates how generalizability and transportability methods extend estimation of RCTs' utility beyond trial participants, to external populations of interest, including those that more closely mirror real-world populations.

Impact:

Generalizability and transportability approaches can be used to quantify treatment effects for populations of interest, which may be used to design future trials or adjust lung cancer screening eligibility criteria.

Introduction

Randomized controlled trials (RCT) are the de facto approach to assessing the efficacy of interventions. As of July 1, 2021, over 382,000 research studies have been registered on ClinicalTrials.gov (1), highlighting the large number of studies that have been conducted or are currently underway. Nevertheless, the translation of this knowledge to clinical practice is often problematic. External validity (i.e., generalizing the study findings to an external population) is a longstanding challenge in utilizing RCT results. Study participants are often different from the target populations of non-participants who may or may not have been eligible for the RCTs. Currently, clinical guidelines are often based on systematic reviews or meta-analyses of RCTs conducted in populations that do not necessarily mirror such target populations. Approaches are needed to extrapolate the findings of RCTs, generalizing them to other populations of interest, informing clinical, policy, and public health interventions for that population (2, 3). Furthermore, although stratification of RCT results by participant characteristics (covariates) allows us to estimate the causal effect within a defined subpopulation (e.g., all female or male participants), this analysis does not estimate the causal effects when the population characteristics are varied (e.g., increasing the proportion of female participants). Thus, more flexible analysis methods are needed.

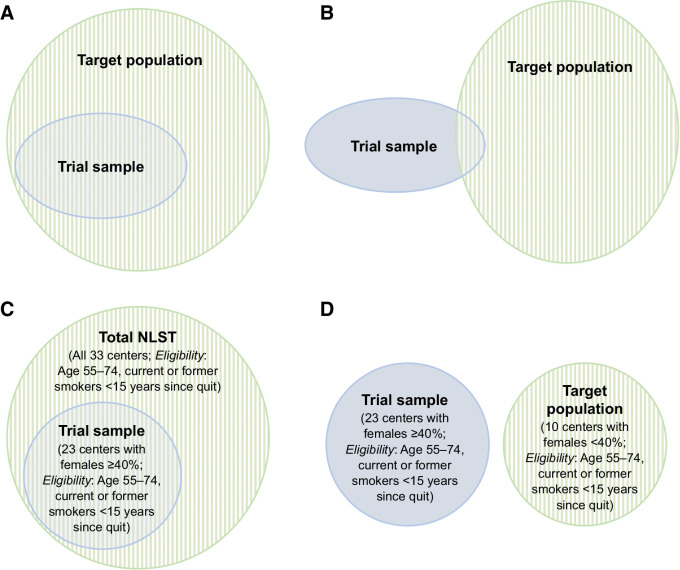
Whereas careful attention has been given to RCT internal validity (i.e., obtaining the unbiased causal effect for the study participants), methods for drawing inferences related to the generalizability and transportability of trial results have been under-utilized in health science research (4, 5). Generalizability and transportability are concepts that have recently received renewed interest in causal inference literature (6–9). Techniques exist for extrapolating results from RCT participants to a target population, given knowledge about the characteristics of a population for which an intervention is being considered (8–13). Generalizability is considered when the target population completely subsumes the study participants (e.g., the study participants are people in California, and the target population is the entire United States population; Fig. 1A). Transportability is applicable when the target population partially includes or does not include the study participants [e.g., the study participants are people in the United States, and the target population includes people in the Western hemisphere (partial inclusion) or people in Europe (no inclusion; Fig. 1B)]. Given RCTs' role in formulating clinical guidelines, informing evidence-based physician decision making, and contributing to health policy management, understanding how these approaches can be used to interpret RCT results for different populations is imperative.

Figure 1.

Concepts of generalizability and transportability. Diagrams illustrating generalizability (A) and transportability (the target population may or may not include any RCT-eligible individuals; B). C, In our example using the NLST, generalizability applies when we consider participants from 23 centers with females ≥40% as the trial sample and those from the entire NLST as the target population (i.e., the study participant population is a subset of the target population). D, Transportability applies when we consider participants from 23 centers with females ≥40% as the trial sample and those from the other 10 centers with females <40% as the target population (i.e., the study participant population is external to the target population).

To ground our discussion, we demonstrate how these concepts are applied to a large, multicenter trial that evaluated lung cancer screening efficacy using low-dose CT (LDCT). The National Lung Screening Trial (NLST) was the first randomized clinical trial to demonstrate a reduction in lung cancer mortality after three annual screens with LDCT of the chest relative to chest x-ray (CXR; ref. 14). These findings, complemented by a comparative simulation study of different eligibility criteria and screening intervals, informed lung cancer screening recommendations made by the United States Preventive Services Task Force (USPSTF; refs. 15, 16). Recently, the primary outcome of the NLST has been further supported by additional large RCTs conducted in Europe, the Nederlands–Leuvens Longkanker Screenings Onderzoek (NELSON) trial (17) and the Multicentric Italian Lung Detection (MILD) trial with ten years of follow-up (18). More recently, the German Lung cancer Screening Intervention (LUSI) also showed beneficial effects of regular LDCT screening on reduction in lung cancer mortality, particularly among females (19). However, several other RCTs reported no significant lung cancer mortality benefit (20–23). While these trials studied distinct populations from the NLST, NELSON, and MILD trials, they also have smaller sample sizes or shorter follow-up periods. Recognizing the substantial resources required to conduct such trials, the ability to generalize findings from the NLST cohort (whether a subset of, or the entire population) to a target population would be of great public benefit. Through the examples of generalizability and transportability formula, we demonstrate the utility of such techniques to extend RCT results to other populations of interest without conducting additional trials.

Materials and Methods

Data sources and study population

The NLST was conducted at 33 sites as a collaborative effort of (i) a contract called the Lung Screening Study (LSS), sponsored by the National Cancer Institute (NCI) Division of Cancer Prevention, and (ii) a grant to the American College of Radiology Imaging Network (ACRIN) sponsored by the NCI Division of Cancer Treatment and Diagnosis, Cancer Imaging Program (24). A total of 53,452 participants were enrolled from August 2002 to April 2004. In total, 26,722 individuals were randomized to LDCT screening and 26,730 to CXR screening. Eligibility criteria included current or former smokers aged 55 to 74 years, a history of cigarette smoking of at least 30 pack-years, and among former smokers, no more than 15 years since quit (14, 24, 25).

Given a previous NLST report of the difference in the lung cancer mortality risk ratio (RR) by sex [male, n = 31,530 (59%), RR = 0.92; female, n = 21,922 (41%), RR = 0.73; ref. 26], we selected 23 screening centers having female prevalence ≥40% (the threshold which is close to the overall prevalence of females in the entire NLST population) as our trial sample to estimate the effect of screening on lung cancer mortality. We then defined the remainning subset of the NLST (i.e., 10 centers having female prevalence <40%) as target population that is assumed, for illustration purposes, to be NLST-eligible nonparticipants.

Measurements

Demographic characteristics including age (years), sex (male or female), race (Asian, Black, American Indian or Alaska Native, Native Hawaiian or Other Pacific Islander, or White), ethnicity (Hispanic, Non-Hispanic), education status (less than college, college or higher, others), marital status (single, married, widowed, or divorced), and smoking status (current or former smokers) were self-reported at randomization. Body mass index (BMI) was calculated as weight (kilograms) divided by height (meters) squared. Mortality data were ascertained by annual questionnaires and searches on the National Death Index. Participants were followed for up to 8.2 years.

Statistical analyses

Using generalizability and transportability formula, we extended the results from our trial sample (N = 29,848) to the entire participants in the NLST (N = 53,452; Fig. 1C) and the target population (N = 23,604; Fig. 1D), respectively, without knowing their outcomes. Table 1 summarizes assumptions necessary to conduct generalizability and transportability analysis, also called identifiability conditions. For example, due to the nature of RCT, the intervention group and control group were exchangeable (i.e., no confounders between the intervention and the outcome), and the probability of being in the intervention group was not zero in any stratum of covariates. Other assumptions were not testable but expected to hold in our example of ideal settings within the NLST data. We employed an inverse-odds weighting approach to control for participants' preintervention demographic characteristics (age, sex, race/ethnicity, education, marital status, smoking, and BMI) and the recruitment arm of the NLST (i.e., whether the center was part of LSS or ACRIN). In this approach, we emulate the target population from the sample of trial participants using the weights calculated by an inverse of odds of being in the trial sample instead of the target population (6, 7, 27);

Table 1.

Conditions for identifying causal quantities for generalizability and transportability.

Key identifiability conditions	Meaning	Example illustrations using the NLST
(i) Conditional exchangeability over study participation, S (S-admissibility)	The participants enrolled in the trial sample are exchangeable with individuals in the target population conditional on some pre-intervention or background variables; i.e., the mean potential outcome conditional on these variables is independent of RCT participation.	The participants enrolled in the trial sample of our example illustration (23 centers with females ≥40%) are exchangeable with those in the target population (10 centers with females <40%) or with the entire NLST conditional on sex, age, race/ethnicity, education, marital status, smoking, body mass index, and the recruitment arm of NLST (LSS or ACRIN).
(ii) Conditional exchangeability over intervention in the study participant population	The participants in the intervention group are exchangeable with the participants in the control group conditional on some pre-intervention or background variables.	The participants in the LDCT screening group are exchangeable with the participants in the radiography group, which is expected to hold by randomization in the NLST.
(iii) Positivity of RCT participation and intervention assignment	a) There is a non-zero probability of trial participation in any stratum defined by covariates that are needed to ensure conditional exchangeability.a	a) The probability of being in the trial sample is not zero in any stratum defined by age, sex, race/ethnicity, education, marital status, smoking, body mass index, and the recruitment arm of NLST.
	b) There is a non-zero probability of intervention assignment in any stratum defined by covariates that are needed to ensure conditional exchangeability.a	b) The probability of being in the LDCT screening group is not zero, which is expected to hold by randomization of intervention assignment in the NLST.
(iv) Consistency	The potential outcome under a specified intervention for any individual who received that intervention is equal to the individual's observed outcome.	The potential outcome under LDCT screening for any individual who received that screening is equal to the individual's observed outcome.
(v) No interference	One individual's intervention does not affect another individual's outcome.b	One participant's lung screening using LDCT does not influence other participants' lung cancer mortality.
(vi) No measurement error	Each variable used in the analyses is correctly measured.	All variables in the NLST are correctly measured.
(vii) Correct model specification	The models used in the analyses are statistically correctly specified.	The logistic regression model used to determine whether the participant is in the trial sample and the Cox proportional hazard model used to predict lung cancer mortality were correctly specified.

Abbreviations: ACRIN, American College of Radiology Imaging Network; LSS, Lung Screening Study.

^aFor transportability, the probability is considered for the superpopulation that gave rise to the trial sample.

^bOr the pattern of interference is the same between the trial sample and the target population.

As an additional analysis, we recategorized the NLST participants into two different groups defined by the recruitment arm of NLST (i.e., ACRIN and LSS). We then generalized the results of the participants from ACRIN centers to the entire NLST population and transported the results to the participants from LSS centers.

Lastly, we assessed changes in the estimated effect derived from the entire NSLT population to the hypothesized target populations by varying the distribution of sex and smoking status. We compared our analysis with previously reported RR of lung cancer mortality in these sample populations: current smokers, n = 25,760 (48%), RR = 0.81; former smokers, n = 27,692 (52%), RR = 0.91 (26). For all experiments, 95% confidence intervals (95% CI) were estimated by repeating the analyses on 200 bootstrapped samples. All analyses were conducted using R 4.0.3.

Ethical Approval

The study was exempted from human subjects review by the institutional review board at University of California, Los Angeles.

Data sharing

Available at https://biometry.nci.nih.gov/cdas.

Results

Table 2 presents participant characteristics for the entire NLST and two study populations: a subset of centers where the distribution of female participants is ≥40% (called the “trial sample”), and an example target population where the distribution of female participants is < 40% (called the “target population”). Compared with the target population (centers with <40% female participants), participants among the trial sample were more likely to be single or divorced/widowed, current smokers, and from centers enrolled through ACRIN.

Table 2.

Demographic characteristics of participants in the two study populations of the NLST determined by the center's distribution of sex.^a

	Total NLST 33 Centers	Trial sample: 23 Centers with females ≥40%	Target population: 10 Centers with females <40%
Characteristics	(N = 53,452)	(N = 29,848)	(N = 23,604)	P valueb
Age at randomization	61.4 ± 5.0	61.4 ± 5.0	61.5 ± 5.0	0.01
Sex				<0.001
Male	59.0	55.8	63.0
Female	41.0	44.2	37.0
Ethnic group				0.47
Hispanic	1.8	1.7	1.8
Non-Hispanic	97.5	97.7	97.3
Others or missing	0.7	0.6	0.9
Education status				0.79
Less than college	43.8	43.8	43.7
College or higher	53.9	53.7	54.2
Others or missing	2.3	2.5	2.1
Marital status				<0.001
Single	4.7	4.9	4.2
Married	66.6	65.3	68.2
Widowed/divorced	28.1	29.0	27.1
Missing	0.6	0.7	0.5
Smoking status				0.001
Current	48.2	48.9	47.4
Former	51.8	51.1	52.6
BMI (kg/m2)				0.74
<25	28.6	28.8	28.5
25 to <30	42.6	42.5	42.8
≥30	28.1	28.1	28.1
Missing	0.7	0.7	0.7
Study				<0.001
LSS	64.8	46.1	88.4
ACRIN	35.2	53.9	11.6

Abbreviations: ACRIN, American College of Radiology Imaging Network; BMI, body mass index; LSS, Lung Screening Study.

^aData are presented as a percentage or mean ± standard deviation otherwise indicated.

^b P value for the difference between the trial sample and target population was calculated by t test for age and χ² test for other categorical variables.

Generalizing the result from one subpopulation to the entire NLST population

Table 3 summarizes our analysis of generalizing results from the trial sample to the entire NLST population. Among 29,848 participants in the trial sample, during the median (interquartile range) follow-up of 6.6 (6.2–6.9) years, 579 died of lung cancer. The rates of death from lung cancer in the LDCT group versus the CXR group were 274 deaths and 334 deaths per 100,000 person-years, respectively. The relative reduction in the rate of lung cancer mortality with LDCT screening in the trial sample was 18% (95% CI, 6–29).

Table 3.

Effect of lung screening by LDCT on lung cancer–related mortality in the two study populations of the National Lung Screening Trial (NLST) determined by the center's distribution of sex.

Cohort	Estimated effect [HR (95% CI)]	Generalized/transported effect [HR (95% CI)] from the estimated effect in the trial sample using inverse-odds weighting approacha,b
Trial sample: 23 centers with females ≥40%	0.82 (0.71–0.94)	—
Target population: 10 centers with females <40%	0.90 (0.72–1.09)	0.89 (0.71–1.08)
Total NLST	0.84 (0.76–0.95)	0.84 (0.72–0.99)

Abbreviations: ACRIN, American College of Radiology Imaging Network; LSS, Lung Screening Study.

^aRobust 95% CIs were estimated by repeating the analyses on 200 bootstrapped samples.

^bThe estimated effect in the original cohort was transported/generalized to the target cohort controlling for age, sex, race/ethnicity, education, marital status, smoking, BMI, and the recruitment arm of NLST (LSS or ACRIN).

Across the entire NLST population of 53,452 participants during the median (interquartile range) follow-up of 6.7 (6.2–7.0) years, 1,021 deaths from lung cancer were observed. The rates of death from lung cancer in the LDCT arm and CXR arm were 273 deaths and 324 deaths per 100,000 person-years, respectively. On the basis of the observed outcome data across the entire NLST population, the relative reduction in the rate of lung cancer mortality with LDCT screening was 16% (95% CI, 5–24). The generalized effect (i.e., the effect calculated by applying the generalizability formula across the trial sample without knowing the outcome across the entire NLST population) of LDCT screening on lung cancer mortality across the entire NLST population was 16% (95% CI, 1–28). This analysis demonstrates the successful application of the inverse-odds weighting approach to estimate the causal effect on the target population from only a subset of the NLST.

Transporting the result from one subpopulation of the NLST to another

Among 23,604 participants in the target population, during the median (interquartile range) follow-up of 6.7 (6.3–7.1) years, 442 deaths from lung cancer were observed. The rates of death from lung cancer in the LDCT arm and CXR arm were 272 deaths and 309 deaths per 100,000 person-years, respectively. On the basis of the observed outcome data across the target population, the relative reduction in the rate of lung cancer mortality with LDCT screening was 10% (95% CI, −9–28). The transported effect (i.e., the effect calculated by applying the transportability formula across the trial sample without knowing the outcome across the target population) of LDCT screening on lung cancer mortality across this target population was 11% (95% CI, −8–29).

Generalizing and transporting the result from ACRIN to the entire NLST and LSS populations

Among 18,840 participants in ACRIN centers, the relative reduction in the rate of lung cancer mortality with LDCT screening was 23% (95% CI, 7–36). The generalized effect of LDCT screening on lung cancer mortality among the entire NLST population was 21% (95% CI, 2–35) which was toward the observed effect [16% (95% CI, 5–24)] among the entire NLST participants (Supplementary Table S1). The transported effect of LDCT screening on lung cancer mortality among participants in LSS centers was 20% (95% CI, −2–34), which was larger than the observed effect among 34,612 participants in LSS centers [11% (95% CI, −4–25), and the 95% CI of both estimates included the null.

Extending the trial result to a range of target populations

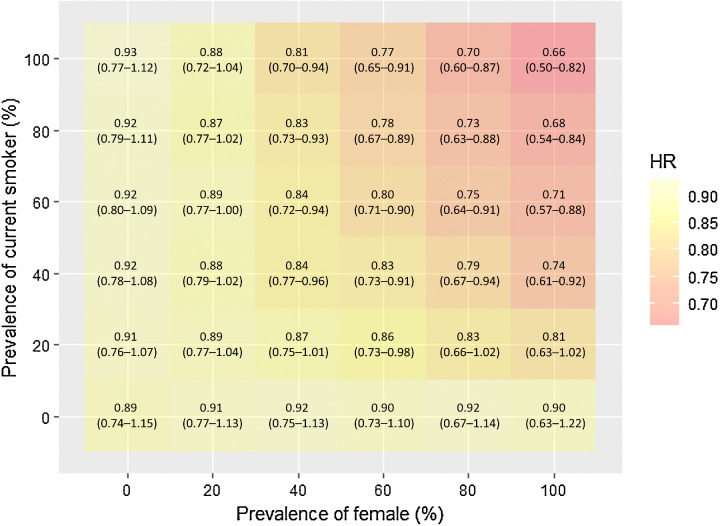
As shown in Fig. 2, the hypothesized target populations with a higher prevalence of females and current smokers showed a greater reduction in lung cancer mortality with LDCT screening than the hypothesized populations with a lower prevalence of females and current smokers. For example, the relative reduction was 27% (95% CI, 11–37) for the population with 80% females and 80% current smokers, while the relative reduction was 11% (95% CI, −4–23) for the population with 20% females and 20% current smokers.

Figure 2.

Transported effect of lung screening by LDCT on lung cancer–related mortality varying the distribution of sex and smoking status in the NLST.

Discussion

This article illustrates the application of generalizability and transportability analysis to extend the results obtained from an RCT to an external target population using data from the NLST. This approach provides the estimated effect of the intervention (in this case, LDCT screening) on the outcome (lung cancer mortality) with not only high internal validity (due to RCT study design) but also high external validity (due to the application of generalizability and transportability techniques). Even well-designed, adequately powered conventional RCTs do not necessarily provide the potential impact of the intervention if the target population differs from the trial sample. When all variables that modify the effect of the intervention and differentiate the trial sample from the target population are observed, the generalizability and transportability formulae allow us to obtain externally valid estimates in the target population by controlling for differences in the distribution of such variables between the two populations.

Our work builds on a growing foundation of literature related to generalizability and transportability (4–13, 28–31). Despite the theoretical advancement of the methodology in statistics and epidemiology, it has not yet been sufficiently demonstrated in the clinical literature, so we aimed to not only introduce these concepts to physicians and biomedical researchers but also to provide a practical demonstration. In our example, we found that both estimates for the target population (10 centers with the female prevalence of <40%) and the entire NLST calculated from the trial sample (23 centers with the female prevalence of ≥40%) using the generalizability and transportability formulae were nearly identical to the observed estimates in each population, respectively. Moreover, we showed that the transportability formula allowed us to transport the estimated effects in the NLST to hypothesized external populations varying the distribution of sex and smoking status. Through these examples, we observed a higher mortality reduction in a population with a higher prevalence of females when screened using LDCT, which is consistent with a recent result at 10 years of follow-up from the NELSON trial [males (n = 13,195), rate ratio = 0.76 (95% CI, 0.61–0.94); females (n = 2,594), rate ratio = 0.67 (95% CI, 0.38–1.14)] while the heterogeneity by sex was not statistically significant (17). Notably, while we illustrate this principle using only two variables, results can be transported to any target population by varying the distribution of multiple covariates using a single transportability formula. These examples reinforce that extending the results from an RCT to the appropriate target population can provide clinicians and decision-makers novel insights about the population that would benefit from the intervention.

Defining the target population is essential to make meaningful generalizations of RCT results (3, 32–34). When the trial sample is a random subset of the target population, we can often generalize study results to the target population without additional analysis. However, there is rarely an ideal setting in which the RCT-eligible population is an exact random subsample of the entire population of interest. Furthermore, researchers and practitioners must consider the extent to which trial results can be applied when the target population consists of individuals who were RCT-eligible but did not participate (e.g., the nearest study site was too far away) or who were not eligible but could have benefitted from the intervention under study (e.g., the individual fell short of the minimum smoking pack-year history) (2). Even when the trial sample is a random subset of the target population, transportability can be used to estimate the treatment effect over time if the distribution of the trial participants' characteristics changes. For example, results from the NLST (conducted during 2002–2009) may not be directly interpreted in the same population in 2020, given the declining number of current smokers over the last decade (35).

Several limitations of this approach are noted. The presence of unmeasured variables could modify the effect of interest when the distribution of such variables is different between the trial sample and the target population. Although our main example was an ideal setting for illustration purposes, our additional example of ACRIN and LSS showed some gaps between observed treatment effects and generalized or transported effects, indicating that some key variables were not included in our generalizability and transportability formula. The assumption of this conditional exchangeability over study participation (i.e., enumerating a comprehensive set of variables that modify the effect of treatment as related to the sampling of the original study population) is even more challenging when attempting to extrapolate the results to general populations. Sensitivity analysis could provide ranges of the transported effect in the target population, assuming the distribution of variables that modify the effect in the trial sample but were not measured in the target population (36). A statistical approach of modeling the outcome by inserting the interaction term between the intervention and the covariates may be helpful. Still, we cannot rule out the possibility of interaction even when the interaction term's obtained coefficient is not statistically significant. In this context, a conservative approach may include a broader set of variables in the transportability formula with the assumption that they may modify the treatment effect (36). Recently, several approaches including tree-based methods have been developed to detect heterogeneous treatment effects by a complex set of covariates and predict treatment effects at finely categorized subgroups (37, 38). The combination of these methods with generalizability and transportability would further increase the utility of RCT results towards both population-based and individualized clinical decision making.

The generalizability and transportability formula needs to be properly specified. Several techniques have been developed to detect model misspecification (27, 39). In addition, to avoid the violation of the positivity assumption (i.e., a non-zero probability of trial participation for each individual in the target population), the target population should meet the study inclusion and exclusion criteria of the original trials, particularly for variables that could modify the treatment effect. Here, the results from the NLST may not be transported to the population of never smokers because the RCT included only current or former smokers. Therefore, the external validity of the trial must be carefully considered when designing the study. Given the variability of CT screening across guidelines and trials (14–17), we also need to carefully consider the type and methods of screening when extending and interpreting the intervention effects. Lastly, we utilize individual-level data from the NLST to show that our formula works using existing RCT data. Access to individual-level data on baseline covariates for both trial and target populations is crucial for correctly specifying generalizability and transportability formulae. Given such data, we can determine the expected treatment effect on the target population of interest. The ability to flexibly estimate effect size across a wide number of covariates can help readers understand the implications of RCT results in a range of external populations and have broader implications beyond lung cancer screening. For example, the recent SARS-CoV-2 outbreak underscored the need for rapid recruitment and execution of clinical trial studies on potential vaccines. Generalizability and transportability may be used to estimate these vaccines' treatment effect on patient groups who may not have been well-represented in these trials.

In healthcare literature, RCTs have been considered the de facto standard clinical to provide evidence to inform clinical guidelines. However, estimates obtained from an RCT are insufficient to estimate the benefits of interventions in real-world settings if the population of interest differs from the trial sample. The concepts and applications of generalizability and transportability help us to minimize this longstanding limitation of RCTs. Although these quantitative techniques have well-documented assumptions, they are particularly informative when clinical trials are not feasible or ethical, allowing us to transport the results of an RCT to an external population of interest. Such information is critical for academic society to build clinical guidelines targeting a specific population that has a different distribution of baseline characteristics from the trial sample. Moreover, even if these approaches do not entirely overcome the barriers that limit external validity of existing RCTs, they allow researchers to efficiently and effectively define the study population of future trials by knowing which populations would receive the greatest benefit from an intervention. Including generalizability and transportability analysis as part of RCT reporting would maximize the utility of the RCT, informs the quality of future trials, and translates experimental data into rational clinical guidelines.

Authors' Disclosures

W. Hsu reports grants from Siemens Medical Solutions and personal fees from Radiological Society of North America outside the submitted work. O.A. Arah reports grants from NIH during the conduct of the study. D.R. Aberle reports grants from NIH R01 CA226079, NIH U01 CA233370, NIH R01 CA210360, PCORI (Kaiser Foundation), NIH U01 CA196408, and grants from Johnson and Johnson and Boston University during the conduct of the study. A.A.T. Bui reports grants from NIH during the conduct of the study. No disclosures were reported by the other authors.

Authors' Contributions

K. Inoue: Conceptualization, data curation, software, formal analysis, supervision, methodology, writing–original draft, writing–review and editing. W. Hsu: Conceptualization, supervision, funding acquisition, validation, investigation, methodology, writing–original draft, writing–review and editing. O.A. Arah: Conceptualization, methodology, writing–review and editing. A.E. Prosper: Conceptualization, software, writing–review and editing. D.R. Aberle: Conceptualization, investigation, methodology, writing–review and editing. A.A.T. Bui: Conceptualization, formal analysis, funding acquisition, investigation, writing–review and editing.