Self-fusion ^{for OCT noise reduction}

Abstract

Reducing speckle noise is an important task for improving visual and automated assessment of retinal OCT images. Traditional image/signal processing methods only offer moderate speckle reduction; deep learning methods can be more effective but require substantial training data, which may not be readily available. We present a novel self-fusion method that offers effective speckle reduction comparable to deep learning methods, but without any external training data. We present qualitative and quantitative results in a variety of datasets from fovea and optic nerve head regions, with varying SNR values for input images.

1. INTRODUCTION

Speckle noise can be a barrier to both visual assessment and automated analysis of OCT scans, which are widely used for retinal imaging. Many approaches have been proposed for reducing speckle noise. Hardware-based methods typically consist of acquiring multiple scans of the same or similar location and averaging to boost SNR; variants include multiple backscattering angles¹ and joint aperture detection.² Software-based methods include adaptive methods^3-9 and variational methods.^10,11 Others have proposed wavelet-based methods^12-15 that seek to suppress speckle in the wavelet, curvelet,¹⁶ wave atom¹⁷ or spectral¹⁸ domains. Classic Perona-Malik gradient anisotropic diffusion filtering, which works well for additive noise, will enhance speckle rather than reducing it; however, speckle-reducing variants have been developed.^19-21 Many of these traditional methods only offer moderate speckle reduction (software) or require additional acquisition time (hardware). In recent years, several learning and deep learning approaches have been proposed to better address this task. Fang et al.²² build a sparse representation dictionary from high-SNR images. Yu et al.²³ proposes to use PCANet in conjunction with non-local means filtering. Ma et al.²⁴ proposes an edge-sensitive conditional generative adversarial network (cGAN). Halupka et al.²⁵ propose a GAN architecture with Wasserstein distance and perceptual similarity. Huang et al.²⁶ also use a GAN structure, with the aim of simultaneous de-speckling and super-resolution. While these deep learning approaches are typically more successful than traditional methods in reducing speckle, they suffer from a need to re-train for different image appearances (such as images acquired with systems from different vendors). In this paper, we propose a non-learning method with a speckle reduction ability comparable to that of deep learning methods without requiring any external data.

Multi-atlas label fusion methods have been widely used for medical image segmentation.²⁷ These methods rely on multiple so-called ‘atlases’ that are (often manually) labeled training samples. To segment a new test image, each atlas is deformably registered to the test image, allowing both the atlas image and the corresponding segmentation label map to be aligned to the test image. In the common space of the test image, each atlas is assigned a spatially varying weight, typically based on the residual registration error between the registered atlas and the test image. The segmentation result is then obtained through a weighted vote between the atlas labels.

In previous work, we introduced multi-atlas intensity fusion.²⁸ This method also relies on atlases registered to a test image, but uses the weight maps to combine the atlases themselves rather than associated label maps. The outcome is a new image that represents the same anatomy as the test image using the atlases as basis functions. The weighted averaging allows noise reduction. The atlas set can be manipulated to achieve additional effects, such as the removal of lesions from the test image by using atlases that do not contain any lesions.²⁸

In this paper, we propose a new ‘self-fusion’ technique that does not require any atlases. Instead, for each B-scan in an OCT volume, we use the neighboring B-scans as ‘atlases’. Since the entire volume is acquired through the same camera from the same eye, these B-scans offer exceptionally well-fitting atlases, in terms of both image appearance and anatomy, making registration and weight estimation very robust. The outcome is speckle reduction abilities comparable to that of hardware-based averaging without requiring multiple acquisitions. Unlike deep learning methods, no external training data is needed, as the volume serves as its own ‘atlas’.

2. METHODS

2.1. Data acquisition

One volume was acquired on a 400 kHz 1060±100 nm Axsun swept-source OCT engine (9.6 μm axial resolution in air) and sampled at 2560 × 500 × 400 pix. (spectral × lines × frames) with 4 repeated frames. OCT signal was acquired on a balanced photodiode and digitized at 2GS/s. 12 additional OCT volumes were acquired using a spectral-domain (SD-OCT) system with a 845±85 nm superluminescent diode light source (1.85 μm axial resolution in air) detected on a 4096 pix. line-scan CMOS sensor. Volumes were sampled at 4096 × 500 × 500 pix. (spectral × lines × frames) with 5 repeated frames at each position for a total of 2500 frames per volume. OCT SNR was adjusted by varying the detector exposure time from 6.7 μs, 3.35 μs, and 2 μs resulting in SNR values of 101 dB, 96 dB, and 92.5 dB, respectively. Volumes were acquired in two healthy volunteers in foveal and optic nerve head (ONH) region at each exposure setting.

On each volume, motion correction was performed by compensating for measured lateral and axial motion shifts using discrete Fourier transform registration on sequential B-scans. The repeated frames (4 for the first dataset, 5 for the second) were split into separate volumes. A single acquisition was used as the input to the denoising algorithm. The repeated acquisitions were averaged together to create the ‘ground truth’ for evaluation.

2.2. Self-fusion for OCT noise reduction

Given an input 3D OCT volume, we consider each 2D B-scan individually. For each input B-scan, we synthesize a new 2D B-scan that represents the same anatomy but with less noise. Then, we tile the synthesized B-scans together to obtain the final result, a denoised 3D OCT volume.

Let us consider an arbitrary input 2D B-scan B_i, where i indicates the slice index within the 3D OCT volume. We define a slice neighborhood by considering the set of B-scans within a radius R to B_i: N_R(B_i) = {B_j∣i–R≤j≤i+R}. Then, we use the joint label fusion model of Wang et al.²⁹ We note that in this interpretation of the multi-atlas fusion framework, we use the neighboring slices B_j ∈ N_R(B_i) as the ‘atlases’. We call this method ‘self-fusion’ because, unlike traditional multi-atlas methods that rely on external atlases, our approach does not require any input other than the 3D OCT volume to be denoised. We further note that there are no ‘labels’ in our fusion approach: we rather use the intensity fusion technique, where the weight maps assigned to each atlas are used to combine the atlas intensities, rather than atlas labels.²⁸ The result of intensity fusion is a synthesized image that represents the target image as a weighted combination of the atlas images.

Specifically, we begin the synthesis process by registering each 2D B-scan B_j ∈ N_R(B_i) to the current B-scan B_i. Then, for each pixel (x, y) on each registered slice B_j, we compute a weight w_j(x, y) following the joint label fusion model. The joint label fusion model takes into account both the local patch similarity between the atlas B_j and the target slice B_i, as well as the patch similarities between pairs of atlases B_j and B_k (B_j, B_k ∈ N_R(B_i)). We use a 5 × 5 pixel neighborhood to compute patch similarity.

We note that we use B_i itself as an atlas to synthesize B_i. This is desirable since B_i naturally contains the most information about the anatomy represented in B_i, and it is thus highly valuable for successful fusion. However, B_i has, by definition, perfect similarity to the target image B_i, which means it would be assigned an extremely high weight that would dominate any contribution from other atlases. This would lead to a synthesis result that is practically identical to the input image. We avoid this problem by using a very high value for α, the weight of the conditioning identity matrix used to compute the atlas similarity matrix M in the joint label fusion framework.²⁹ This makes it possible to emphasize B_i by assigning its pixels relatively high weights in the fusion, while still allowing nontrivial contribution from the other atlases in N_R(B_i).

3. RESULTS

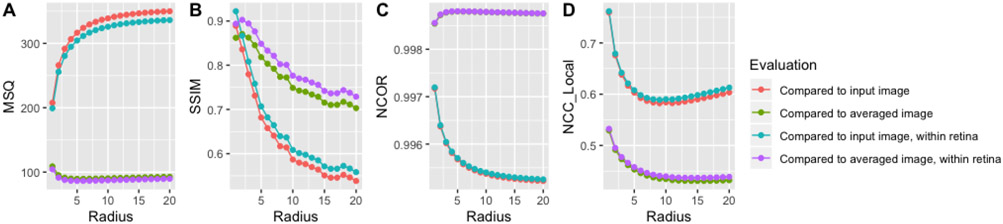
Figure 1 shows quantitative evaluation of the self-fusion results on the first dataset as a function of the neighborhood radius R. As can be expected, these metrics are similar to each other in overall trend, but the comparison to the average image performs better than the comparison to the noisy input, and the metrics improve when only considering the voxels within the retina. We note that some metrics improve with increasing radius, as the SNR becomes stronger, whereas other metrics deteriorate, likely due to the increased blurring. Based on this analysis, we choose a radius of 5 voxels for the second dataset.

Figure 1.

Quantitative evaluation for one OCT volume (first dataset) for varying radius R. A Mean square difference (MSQ), B structural similarity index (SSIM, 2-voxel radius), C image-wide normalized cross-correlation (NCC), D local (patch-based, patch radius 4 voxels) NCC. We report each metric between the self-fusion result and the input image (single acquisition) or the ground truth (4 acquisitions averaged), for the whole image or within the retina (manual mask).

Figures 2 and 3 show qualitative results for varying SNR levels, in the ONH and fovea regions respectively, in images from the second dataset. We note the good performance of our self-fusion method on even very noisy images. This is potentially useful in clinical applications for patients who may suffer from cataracts, vitreal haze, or corneal opacity. We also note the preservation of fine features, such as blood vessels and their shadows, as well as tissue layers.

Figure 2.

Self-fusion in the ONH. Left: input noisy image. Middle: Self-fusion of the single input noisy image. Right: average of 5 noisy images. The three rows are from SNR levels of 92.5dB, 96dB and 101dB respectively.

Figure 3.

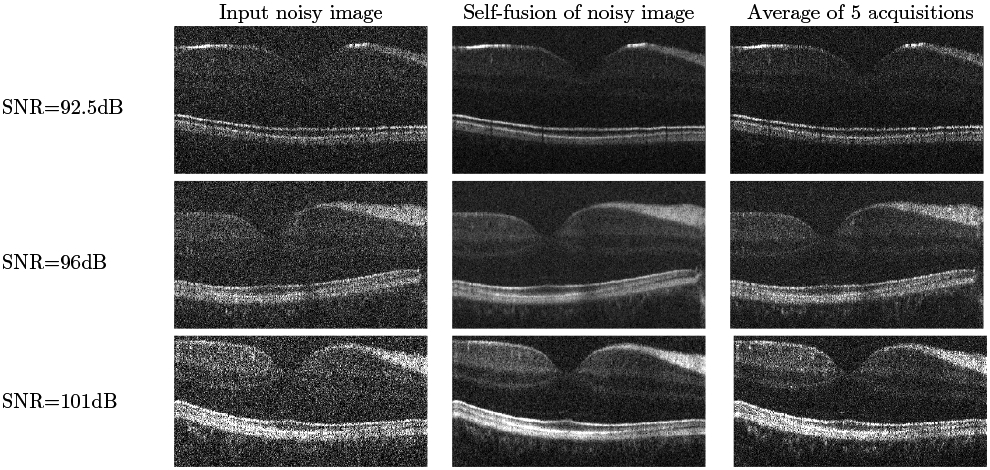
Self-fusion in the fovea. Left: input noisy image. Middle: Self-fusion of the single input noisy image. Right: average of 5 noisy images. Note the external limiting membrane is visible on the 96 dB and 101 dB self-fusion and averaged images but not on the raw single images.

Finally, we note that for many settings, the self-fusion result visually has better contrast than the average of 5 repeated frames, which is often considered the gold standard for despeckling. We hypothesize that this is likely because the self-fusion method allows us to leverage more data in the reconstruction: while the ‘ground truth’ is limited to the average of only 5 repeated frames at the same location, the self-fusion results shown in Figures 2 and 3 use a radius R of 5, which means 11 B-scans (5 on each side, and the central B-scan itself) were fused together. This is made possible because of two complementary components of self-fusion: on one hand, the deformable registration step allows data from further B-scans to be leveraged. On the other hand, the use of the joint fusion metric²⁹ rather than simple averaging helps suppress the contribution of inappropriate data within this larger set, whether caused by registration error, image artifacts, noise or anatomical mismatch. This helps slow down the degradation caused by incorporating B-scans from increasingly distant locations. Figure 4 illustrates the filtering output for radius R in range [1..20]. We observe that the overall image quality is relatively stable even for R=20, which corresponds to 41 self-fused B-scans. While some edge blurring can be observed, especially for small features such as blood vessels, this blurring is minimal compared to simple averaging of the same number of images, even after registration. The image artifact visible on the left side of the input B-scan is noteworthy: the averaging of 4 repeated frames can only mildly softens this artifact, while self-fusion is able to alleviate it considerably.

Figure 4.

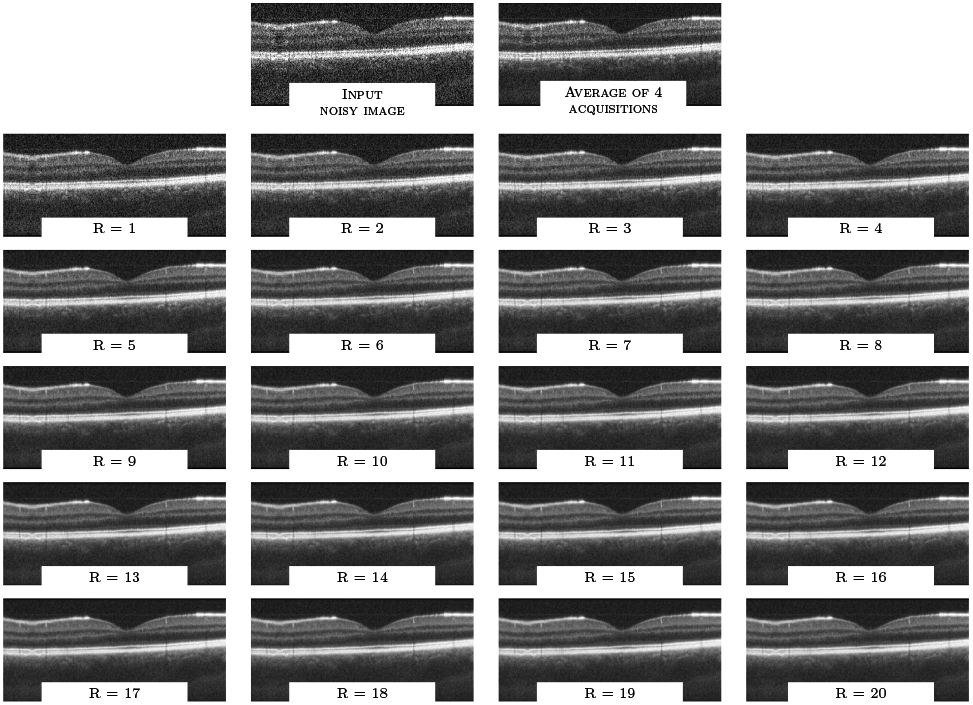
Qualitative evaluation for one OCT volume (first dataset) for varying radius R.

4. DISCUSSION AND CONCLUSION

We presented the novel self-fusion algorithm for speckle noise reduction in OCT images of the retina. The quantitative and qualitative results illustrate the performance of this method on a variety of settings. One current drawback of the method is that it is considering each B-scan independently, which may potentially cause consistency artifacts in 3D space; we plan on exploring this issue in future work.