Longitudinal subcortical segmentation with deep learning

Abstract

Longitudinal information is important for monitoring the progression of neurodegenerative diseases, such as Huntington’s disease (HD). Specifically, longitudinal magnetic resonance imaging (MRI) studies may allow the discovery of subtle intra-subject changes over time that may otherwise go undetected because of inter-subject variability. For HD patients, the primary imaging-based marker of disease progression is the atrophy of subcortical structures, mainly the caudate and putamen. To better understand the course of subcortical atrophy in HD and its correlation with clinical outcome measures, highly accurate segmentation is important. In recent years, subcortical segmentation methods have moved towards deep learning, given the state-of-the-art accuracy and computational efficiency provided by these models. However, these methods are not designed for longitudinal analysis, but rather treat each time point as an independent sample, discarding the longitudinal structure of the data. In this paper, we propose a deep learning based subcortical segmentation method that takes into account this longitudinal information. Our method takes a longitudinal pair of 3D MRIs as input, and jointly computes the corresponding segmentations. We use bi-directional convolutional long short-term memory (C-LSTM) blocks in our model to leverage the longitudinal information between scans. We test our method on the PREDICT-HD dataset and use the Dice coefficient, average surface distance and 95-percent Hausdorff distance as our evaluation metrics. Compared to cross-sectional segmentation, we improve the overall accuracy of segmentation, and our method has more consistent performance across time points. Furthermore, our method identifies a stronger correlation between subcortical volume loss and decline in the total motor score, an important clinical outcome measure for HD.

1. INTRODUCTION

Huntington’s disease (HD) is an autosomal dominant neurodegenerative disorder known to affect subcortical structures.¹ Specifically, changes in caudate and putamen volume are the primary imaging-based markers of HD pathology even in the early stages of disease progression,^2-4 whereas other structures such as the pallidum appear to be more mildly affected, and the thalamus is relatively preserved. Understanding the relationship between subcortical atrophy and clinical outcome measures such as the total motor score (TMS) is of interest for HD studies. Given the large inter-subject variability in brain anatomy and disease progression, longitudinal MRI studies are especially important in this context. While many large-scale studies indeed collect longitudinal MRI data, many segmentation methods treat each MRI scan as an independent sample even if they belong to the same subject, and only consider the longitudinal structure of the data in post-processing, i.e., in the statistical analysis stage. Such an approach limits the benefits of longitudinal datasets.

In recent years, deep learning based segmentation methods have dominated the field, and state-of-the-art deep learning based methods produced promising results for segmenting subcortical structures.^5-8 Dolz et al.⁵ proposed a 3D fully convolutional neural network (FCNN) on subcortical segmentation, and they applied their method to a large-scale dataset to prove the model robustness and segmentation accuracy. Based on the work of Dolz et al.,⁵ Li et al.⁶ further improved segmentation results by exploring variants on augmentation strategies and network architecture. Wu et al.⁷ proposed a 2D + 3D framework for segmenting the subcortical structures, which demonstrated promising performance. In a concurrent submission, we propose⁸ a cascaded 3D framework and a 3D FCNN to segment subcortical structures, which provides more accurate segmentations than Dolz et al.,⁵ Li et al.⁶ and Wu et al.⁷ However, none of these methods are designed for longitudinal subcortical segmentation, and the development of such methods is an important need in the field.

In related previous studies, the convolutional long short-term memory (C-LSTM)⁹ approach has been used for joint segmentation of multiple images and produced promising results^10-12 by extracting and passing useful inter-image information. He et al.¹¹ used C-LSTM to leverage inter-slice information and improved segmentation consistency in retinal OCT scans. Bai et al.¹² achieved aortic image sequence segmentation by applying C-LSTM. In a closely related work, Gao et al.¹⁰ stacked C-LSTMs into an FCNN for joint 4D medical image segmentation. This allows the model to learn the overall trend and the correlations from MRIs at multiple time-points.

In this paper, we propose a longitudinal subcortical segmentation method, which uses two 3D MRIs acquired at different time points from a given subject as input and jointly computes the corresponding segmentations. Inspired by the work from Gao et al.,¹⁰ we use two different time-point MRIs for each subject and focus on the relationship between these inputs to improve the segmentation accuracy. Additionally, we use a network architecture specifically optimized for the subcortical segmentation task.⁸ With the bi-directional C-LSTM blocks, our model is able to extract, pass and fuse useful longitudinal information to form segmentations. Thus, we leverage the inherent dependency between longitudinal scans instead of treating them as independent samples and discarding the useful contextual information. We test our method on the PREDICT-HD dataset and evaluate our results against a cross-sectional variant.⁸ The Dice coefficient, average surface distance and 95-percent Hausdorff distance are used as evaluation metrics. We also report the correlation of the volume loss with the decline in total motor score.

2. METHODS

2.1. Convolutional LSTM

The long short-term memory (LSTM)¹³ is a specific type of recurrent neural network (RNN) for increasing learning ability based on previous information. Furthermore, the LSTM minimizes the effect of the “gradient vanishing” problem in the training process. Based on fully connected LSTM,¹⁴ Shi et al. proposed the C-LSTM⁹ which can be incorporated in the fully convolutional neural network (FCNN) architecture and leverages spatiotemporal information due to the convolution operation. The C-LSTM can be described as:

$$\begin{gathered} i_t=\sigma (W_{xi}\ast x_t+W_{hi}\ast h_{t-1}+b_i) \\ {f}_t=\sigma (W_{xf}\ast x_t+W_{hf}\ast h_{t-1}+b_f) \\ {o}_t=\sigma (W_{xo}\ast x_t+W_{ho}\ast h_{t-1}+b_o) \\ {c}_t=f_t\otimes c_{t-1}+i_t\otimes \tanh (W_{xc}\ast x_t+W_{hc}\ast h_{t-1}+b_c) \\ {h}_t=o_t\otimes \tanh (c_t) \end{gathered}$$ (1)

where x_t is the input, c_t is the output cell state and h_t is the hidden state. c_t–1 and h_t–1 are the output from previous hidden layer. i_t, f_t and o_t are the input, forget and output gates respectively. * denotes convolution operation, ⊗ denotes pixel-wise multiplication, and σ is the sigmoid function. Finally, the Ws contain the weights and the bs contain the bias.

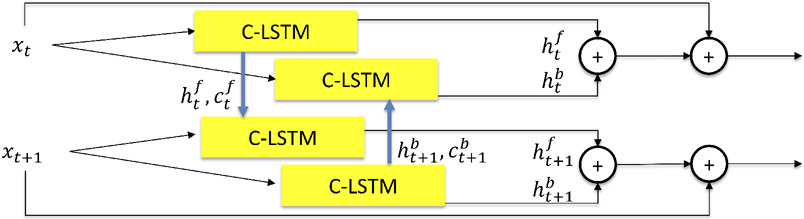
For our work, to allow each input scan to leverage information from the other scan, we added a backward path to form a bi-directional C-LSTM, as shown in Fig. 1. Additionally, to reinforce current information, we used an addition before outputting. Along the training processes, C-LSTMs will extract, pass and fuse the useful longitudinal information between scans. Thus, our segmentations take into account the longitudinal context.

Figure 1.

The bi-directional convolutional long short-term memory (C-LSTM) block. h^f, c^f and h^b, c^b are the output cell and hidden state in forward and backward path. t denotes the time-point.

2.2. Network Architecture

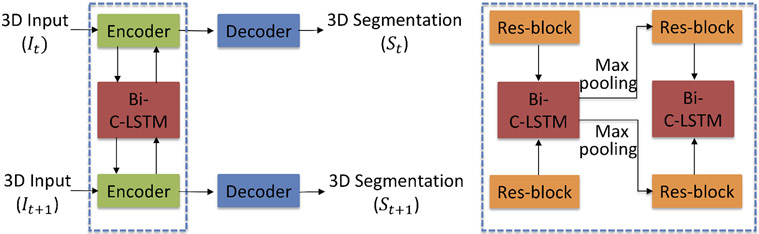
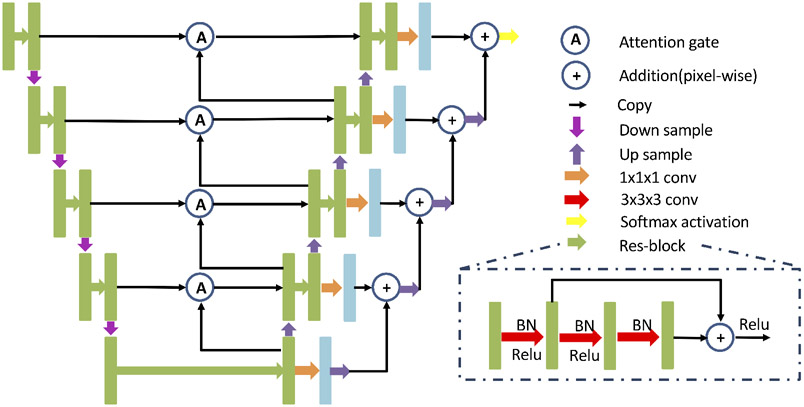
Fig. 2 shows our framework for longitudinal subcortical segmentation. The framework contains 2 paths, such that each path receives the 3D image from one time-point as input and outputs the corresponding 3D segmentation. The output has the same size as the input volume but contains 9 channels (8 considered subcortical structures and 1 background). Similar to Gao et al.,¹⁰ in the encoder phase, the bi-directional C-LSTM blocks serve as the bridge between paths to achieve the extraction, transmission and fusion of longitudinal information. Thus, the feature maps containing both inter-scan and intra-scan information are forwarded to each decoder path separately to form segmentations. The encoder and decoder include 4 3D max-pooling and 3D nearest neighbor upsampling operations. Besides that, 8 residual blocks are stacked in encoder and decoder evenly, and 1 is used in bottleneck path. Residual blocks are modified from He et al.,¹⁵ and consist of a 3 × 3 × 3 convolution operation, batch normalization and ReLU activation. Like the 3D U-Net,¹⁶ there is a skip connection with an attention gate¹⁷ between encoder and decoder. An addition operation is applied in the decoders before the final output. The detailed network architecture is shown as Fig. 3, which is same as the architecture of cross-sectional subcortical segmentation method.⁸

Figure 2.

The longitudinal subcortical segmentation framework. The dashed square shows the connection between blocks. Is are the input 3D MRIs and Ss are the corresponding segmentations. t represents the time-point.

Figure 3.

The network architecture. The feature maps are represented by rectangular boxes. The green boxes at each level contain 32, 64, 128, 256, 512 channels respectively. For all levels, light blue boxes have 9 channels (8 subcortical structures and background).

2.3. Experimental Setup

Dataset.

Our dataset is a subset of the multi-site PREDICT-HD database and contains 40 healthy control subjects and 119 HD subjects. The HD subjects were classified into three groups based on their CAP scores, which is a marker of HD progression:¹⁸ high-CAP (n=39), medium-CAP (n=40) and low-CAP (n=40). Each subject has 2 T1-weighted MRIs with at least 2 years between the two scans. We randomly select 20 subjects in each category for training and 5 subjects for validation. The rest of the subjects were used for testing. The subcortical structures that are considered in our study are the left and right pairs of thalamus, caudate, pallidum and putamen.

Pre-processing.

We employed the BRAINSAutoWorkup pipeline to pre-process^19,20 the images. This process includes: (1) non-local mean filter denoising, (2) rigid intra-subject and inter-subject registration, and resampling to 1 × 1 × 1mm³ resolution, (3) bias field correction and intensity normalization (4) multi-atlas label fusion method²¹ for segmenting subcortical structures. The segmentations produced by the multi-atlas method were visually quality controlled and used as “ground truth” for training and testing our models. In addition, skull-stripping was applied, and histogram matching was performed to alleviate the variability of tissue contrast produced by different scanners and acquisition sequences between study sites.

Data Augmentation.

Random affine transformation, random elastic deformation, and the combination of random affine transformation and random elastic deformation were used as our augmentation strategy. The same type of transformation was applied to both time-points of a given subject. Using these augmentations helps reduce overfitting. Additionally, our augmentations could improve model robustness and help bi-directional C-LSTM block to extract useful longitudinal information.

Implementation Details.

During training, we used the Dice Loss²² as our loss function, with weight = 1 for all foreground labels and weight = 0.1 for background. We used an Adam optimizer with β₁ =0.9, β₂ = 0.999, and weight decay = 10⁻⁵. We set the initial learning rate to 0.01 and decayed by a factor of 0.5 every 50 epochs. The weights of bi-directional C-LSTM blocks and C-LSTM cells are not shared. With a batch size of 2, the whole training process took around 450 epochs with early stop. However, we set the maximum epoch number to 1000, in case the early stop condition is not triggered. We randomly switched the input order in each iteration to increase the model robustness and boost the ability of the bi-directional C-LSTM for extracting useful information. Due to GPU memory limitation, we applied the method described in⁸ to automatically crop input images to a region of 96 × 96 × 48mm³ which includes the subcortical area. The model is implemented using PyTorch and trained with a NVIDIA Titan RTX.

Evaluation methods.

We compare the results of our longitudinal subcortical segmentation method to its cross-sectional counterpart.⁸ We note that this cross-sectional method⁸ outperforms previous state-of-the-art methods such as those presented in.^5-7 All pre-processing and data augmentation pipelines as well as train/validation/test splits of the data were the same between the cross-sectional and longitudinal methods, with the only difference being the introduction of a second path in the longitudinal network as well as the bi-directional C-LSTM blocks connecting the two paths. For evaluation, we use the Dice coefficient, the average surface distance and the 95-percent Hausdorff distance as our metrics. Statistical significance was determined using a 2-tail, paired t-test with significance threshold p < 0.05. We also report the Pearson’s correlation coefficient between the change in total motor score (TMS) between the two visits and the volume loss between these two time-points.

3. RESULTS

The Dice results for all subjects (control and HD) are shown in Tab. 1. The top panel shows that the Dice score of our longitudinal approach was significantly higher than the cross-sectional analysis for all 8 structures. To assess the consistency of the performance, we report the absolute value of the difference between the Dice scores of the two time-points, averaged over all subjects. These results are shown in the bottom panel of Tab. 1, where we observe that the longitudinal approach was more consistent for 6 out of 8 structures.

Table 1.

(Top) Segmentation Dice scores. Statistically significant improvements (2-tailed paired t-test, p < 0.05) over the cross-sectional method⁸ are denoted in bold. (Bottom) The performance consistency, computed as the absolute difference of Dice score between two time-points of a subject. Underlined entries highlight better performance consistency. For both tables, results are presented as mean ± std. dev.

Dice score
	R thalamus	L thalamus	R caudate	L caudate	R pallidum	L pallidum	R putamen	L putamen
Cross-sec.8	0.979±0.005	0.980±0.004	0.975±0.008	0.974±0.007	0.967±0.011	0.965±0.014	0.980±0.005	0.980±0.006
Longitudinal	0.980±0.004	0.980±0.004	0.976±0.007	0.975±0.007	0.969±0.009	0.968±0.011	0.981±0.004	0.981±0.006
Absolute difference of Dice score between time points (×10−1)
	R thalamus	L thalamus	R caudate	L caudate	R pallidum	L pallidum	R putamen	L putamen
Cross-sec.8	0.021±0.020	0.029±0.024	0.040±0.036	0.048±0.046	0.067±0.052	0.069±0.059	0.033±0.026	0.036±0.029
Longitudinal	0.023±0.016	0.028±0.025	0.036±0.040	0.035±0.034	0.061±0.050	0.068±0.063	0.036±0.027	0.034±0.027

It is well known that the Dice score cannot capture small features that do not contribute substantially to overall volume, such as the thin tail of the caudate. For this reason, we also report the surface distances in Tab. 2, specifically, the average surface distance and the 95-percent Hausdorff distance. Both metrics are improved in the longitudinal segmentation for all 8 structures, with the difference reaching statistical significance for 10 out of the 16 comparisons.

Table 2.

(Top) Average surface distance. (Bottom) 95-percent Hausdorff distance. For both tables, results are presented as mean±std. dev. Statistically significant improvements (2-tailed paired t-test, p < 0.05) over the cross-sectional method⁸ are denoted in bold.

Average surface distance
	R thalamus	L thalamus	R caudate	L caudate	R pallidum	L pallidum	R putamen	L putamen
Cross-sec.8	0.051±0.016	0.051±0.018	0.030±0.016	0.030±0.012	0.035±0.014	0.040±0.030	0.032±0.035	0.029±0.011
Longitudinal	0.049±0.017	0.048±0.017	0.029±0.014	0.028±0.019	0.031±0.012	0.035±0.019	0.028±0.015	0.028±0.014
95-percent Haussdorf distance
	R thalamus	L thalamus	R caudate	L caudate	R pallidum	L pallidum	R putamen	L putamen
Cross-sec.8	0.585±0.495	0.568±0.497	0.093±0.292	0.119±0.325	0.161±0.369	0.253±0.448	0.051±0.221	0.076±0.267
Longitudinal	0.508±0.502	0.492±0.502	0.051±0.221	0.093±0.292	0.102±0.304	0.169±0.377	0.008±0.092	0.059±0.237

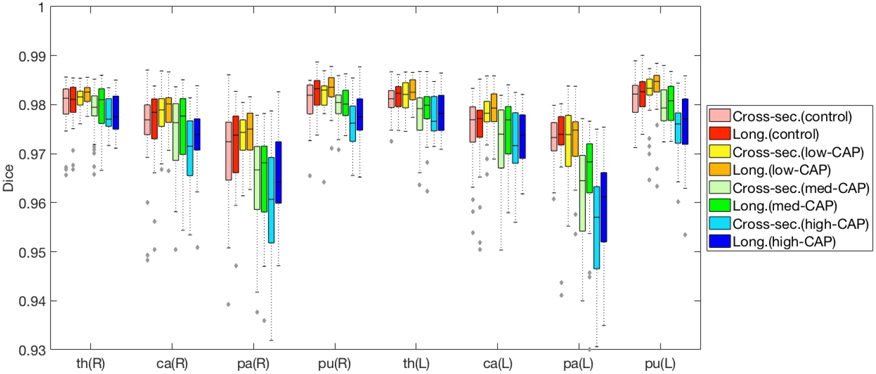
Fig. 4 shows the breakdown of Dice scores across the 3 disease stages (low-, med-, high-CAP) as well as controls. We note that the longitudinal accuracy is consistently superior to cross-sectional segmentation, and it is more robust to increased amounts of atrophy known to be present in later disease stages.

Figure 4.

Comparison of segmentation performance. In HD subjects, many subcortical structures are increasingly atrophied in higher CAP groups. (L)eft and (R)ight pairs of (th)lamus, (ca)daute, (pa)llidum and (pu)tamen are considered. Compared to the cross-sectional method,⁸ our proposed longitudinal method obtained consistently superior Dice scores.

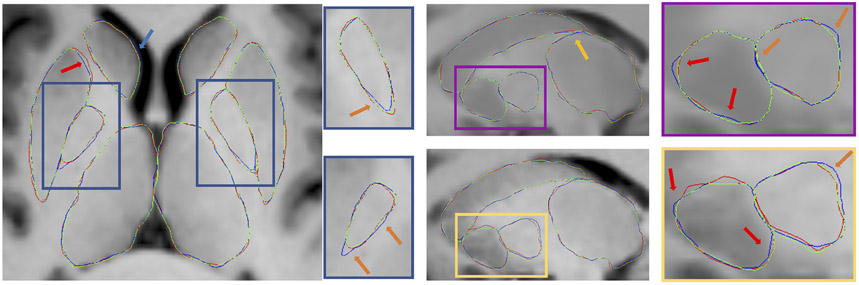
The qualitative results are shown in Fig. 5. From axial and sagittal slices, we can see the clear improvements of pallidum (blue zoomed-in panels, orange arrows). The yellow and pink panels highlight improvements in the putamen segmentation accuracy (red arrows), where the most noticeable changes visible in sagittal slices. Furthermore, axial slices show our method delivered more plausible thalamus segmentations, since the boundary between the left and right thalamus should follow the mid-sagittal plane.

Figure 5.

Qualitative results. Red, blue and green lines represent “ground truth”, cross-sectional⁸ and proposed longitudinal segmentations respectively. Yellow, blue, orange and red arrows highlight the improvements of thalamus, caudate, pallidum and putamen, respectively.

In Tab. 3, we report the Pearson’s correlation coefficient between the change in TMS between the two visits and the volume loss between these two time points. The volumes were normalized by the total brain volume prior to this analysis. We expect to see strong correlations for the caudate and putamen which are known to be affected in HD, and an increase in correlation strength in later disease stages. We note that the findings in Tab. 3 are preliminary, since the number of test subjects in each group was limited, and several subjects had to be excluded due to missing TMS scores. Nevertheless, we note that the longitudinal segmentation method produced stronger correlations between volume loss and TMS decline for most of the comparisons in the caudate and putamen, the most affected structures. Interestingly, we also find robust correlations in the pallidum, which suggests that our methods might be more sensitive to HD changes in the pallidum than previously reported HD studies^2-4 that relied on an older generation of segmentation algorithms such as multi-atlas methods. In line with the literature,^2-4 the thalamus does not appear to be strongly associated with the HD pathology, although the correlation in the high-CAP group suggests that this structure may become affected in later disease stages. Replicating these preliminary findings in a larger dataset remains as future work.

Table 3.

Pearson’s correlation coefficient between volume loss between two time-points and the TMS decline during the same time period. Bold numbers denote the method identifying a stronger correlation. We observe that some structures like the thalamus show weak correlations with both methods, in line with the existing HD literature. Note that subjects with missing TMS data were excluded from this analysis (n=3, 2, 2 for high-CAP, medium-CAP and low-CAP categories respectively).

All HD Subjects (low-CAP, med-CAP, high-CAP)
	R thalamus	L thalamus	R caudate	L caudate	R pallidum	L pallidum	R putamen	L putamen
Cross-sec.8	−0.1985	−0.0232	−0.3800	−0.2826	−0.3233	−0.4280	−0.3750	−0.3431
Longitudinal	−0.1345	0.0743	−0.3809	−0.3654	−0.3712	−0.4587	−0.3152	−0.3482
Low-CAP Subjects
	R thalamus	L thalamus	R caudate	L caudate	R pallidum	L pallidum	R putamen	L putamen
Cross-sec.8	−0.0639	−0.2707	−0.2342	−0.1888	−0.4166	−0.2540	−0.2987	−0.4645
Longitudinal	−0.0840	−0.2680	−0.2764	−0.2871	−0.4079	−0.3044	−0.2922	−0.4730
Med-CAP Subjects
	R thalamus	L thalamus	R caudate	L caudate	R pallidum	L pallidum	R putamen	L putamen
Cross-sec.8	−0.1258	0.3095	−0.3268	−0.2676	−0.3877	−0.4911	−0.3082	−0.3169
Longitudinal	−0.1034	0.4050	−0.3270	−0.3185	−0.4349	−0.5535	−0.2327	−0.4000
High-CAP Subjects
	R thalamus	L thalamus	R caudate	L caudate	R pallidum	L pallidum	R putamen	L putamen
Cross-sec.8	−0.5348	−0.2763	−0.627	−0.5513	−0.4162	−0.6226	−0.6836	−0.4264
Longitudinal	−0.3254	−0.0960	−0.6549	−0.6006	−0.6017	−0.6232	−0.5589	−0.3597

4. DISCUSSION AND CONCLUSIONS

In this work, we proposed a 3D subcortical segmentation method leveraging longitudinal information. We used two 3D scans of a given subject as inputs and took advantage of the longitudinal context by using the bi-directional C-LSTM, such that information from both time points were learned by our model jointly. With the longitudinal information, the model learns the relationship between the scans and achieves superior segmentation performance with higher accuracy and better consistency for the considered subcortical structures. Additionally, our segmentations better correlate with TMS decline in a limited dataset. We note that our bi-directional C-LSTM blocks and C-LSTM cells are not using shared weights in our experiments. However, the shared weights blocks and cells produced nearly identical results to those reported in this paper. Extending our framework to allow more than 2 time-points per subject remains as future work; an important step towards this goal will be to optimize the network architecture to avoid GPU memory limitation issues. Another potential extension might be a multi-task network that handles the registration of the two time-points along with the longitudinal segmentation.