Abstract
The subcortical structures of the brain are relevant for many neurodegenerative diseases like Huntington’s disease (HD). Quantitative segmentation of these structures from magnetic resonance images (MRIs) has been studied in clinical and neuroimaging research. Recently, convolutional neural networks (CNNs) have been successfully used for many medical image analysis tasks, including subcortical segmentation. In this work, we propose a 2-stage cascaded 3D subcortical segmentation framework, with the same 3D CNN architecture for both stages. Attention gates, residual blocks and output adding are used in our proposed 3D CNN. In the first stage, we apply our model to downsampled images to output a coarse segmentation. Next, we crop the extended subcortical region from the original image based on this coarse segmentation, and we input the cropped region to the second CNN to obtain the final segmentation. Left and right pairs of thalamus, caudate, pallidum and putamen are considered in our segmentation. We use the Dice coefficient as our metric and evaluate our method on two datasets: the publicly available IBSR dataset and a subset of the PREDICT-HD database, which includes healthy controls and HD subjects. We train our models on only healthy control subjects and test on both healthy controls and HD subjects to examine model generalizability. Compared with the state-of-the-art methods, our method has the highest mean Dice score on all considered subcortical structures (except the thalamus on IBSR), with more pronounced improvement for HD subjects. This suggests that our method may have better ability to segment MRIs of subjects with neurodegenerative disease.
Keywords: MRI, Subcortical Segmentation, CNN, Neurodegeneration, Huntington’s Disease
1. INTRODUCTION
Subcortical structures are related to many neurodegenerative diseases, such as Alzheimer’s, Parkinson’s and Huntington’s (HD) diseases.1 To better understand HD, quantitative measurements of subcortical structures are essential. In the past, many automatic subcortical segmentation methods from magnetic resonance images (MRIs) were proposed.2–7 Many of these methods are based on multi-atlas label fusion, which is time-consuming due to the deformable registration process. In more recent years, convolutional neural network (CNN) based methods have dominated many segmentation fields with superior performance,8–10 and subcortical segmentation is no exception.11–13 Dolz et al.11 developed a fully convolutional neural network with small kernels and multi-concatenation to segment the subcortical area. Li et al.12 explored variants based on the work of Dolz et al.11 to improve the performance of CNNs for subcortical segmentation. Wu et al.13 proposed a joint 3D+2D framework to achieve accurate subcortical segmentation.
Hierarchically learning parameters with linear and non-linear layers, CNNs leverage local and global information from images for predicting segmentations. Once the training process is completed, CNN-based methods have high accuracy and are computationally efficient to predict the output. However, the ability of CNNs is highly dependent on the amount of training data, and it is desirable for the training data to be tightly matched to the test data. For neurodegeneration studies, small in-house datasets are widely used and it is hard to find public datasets with manual annotations. In such situations, generating new training data for each considered disease population is expensive and time-consuming. Alternatively, datasets of healthy control subjects may be used in training, and improving the generalizability of models from healthy controls to neurodegenerative disease populations is therefore important.
In this paper, we propose a 2-stage cascaded framework for subcortical segmentation, with a 3D CNN architecture at each stage. In the first stage, we downsample the original image and use it as input to create a coarse segmentation. Then we find an extended subcortical region of interest (ROI) from this coarse segmentation. In the second stage, we obtain the final segmentation from the cropped subcortical ROI at full resolution. Note that both stages use the same model, which is a 3D U-Net14 based CNN. In our model, residual blocks15 and attention gates16 are used. Additionally, we connect feature maps from every level to preserve global information.
We evaluate our model on 2 datasets, the publicly available IBSR* and a subset of the PREDICT-HD database,17 which consists of both healthy control and HD subjects. For PREDICT-HD, we train our model only on healthy control subjects, and test on both healthy control and HD subjects to evaluate the generalization ability of our model. We use the Dice similarity coefficient as our metric to validate the results.
2. METHODS
2.1. Segmentation framework
We propose a 2-stage 3D subcortical segmentation framework (Fig. 1) to handle the memory limitation problem in 3D segmentation. After pre-processing, we feed downsampled images into the proposed CNN to create a coarse segmentation in the first stage. Then we upsample the coarse segmentation back to its original size, and find the bounding box of the subcortical areas. We extend the bounding box generously (see Fig. 1) to make sure any initially under-segmented areas are preserved. In the second stage, we crop this extended subcortical area at full resolution, and use this cropped area as the input of the proposed CNN to have the final segmentation.
Figure 1.
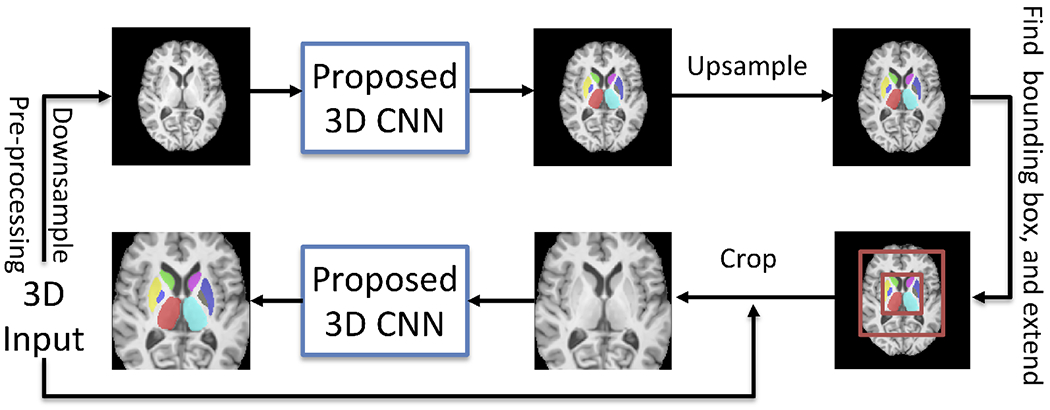
Overall workflow of the proposed framework.
2.2. Network architecture
Our network (Fig. 2) is a 3D fully convolutional neural network adopted from the 3D U-Net.14 Residual blocks15 and attention gates16 are used in our network to minimize the degradation problem and emphasize the ROI. In the residual blocks, batch normalization and ReLU-activation are followed by the convolution operation, and ReLU-activation is applied before outputting. We used 3D max-pooling and 3D nearest neighbor upsampling in the encoder and the decoder. Furthermore, we use skip connections between the encoder and the decoder, which preserves the coding information for the decoder. Before outputting the final segmentation, we further reinforce information by adding the outputs from the different scales.
Figure 2.
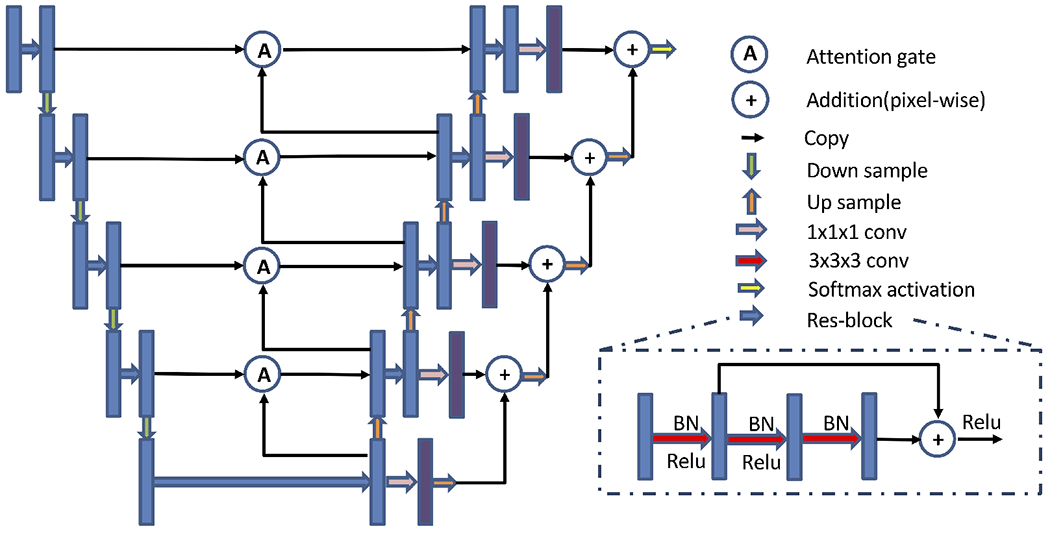
Proposed network architecture. Blue and purple boxes are feature maps. The number of channels for blue boxes at each level is 32, 64, 128, 256, 512 and the number of channels for purple boxes is 9 for all levels. The input size is N × 1 × 128 × 128 × 96, and the output size is N × 9 × 128 × 128 × 96, where N is the batch size and 9 is the number of output channels (8 subcortical structures+background).
2.3. Implementation details
The Adam optimizer was used with L2 penalty 0.00001, β1 = 0.9, β2 = 0.999 and initial learning rate 0.01. The learning rate was decayed by a factor of 0.5 every 50 epochs. Inspired by Milletari et al.,18 we used one minus mean of Dice coefficients from all labels as loss function during training, with equal weight (wFG = 1) for all foreground labels and decayed weight (wBG = 0.1) for the background. With a batch size of 2, we trained our model for 1000 total epochs and early stop was used in the training process. With the early stop, the training process is finished around 400 epochs and each epoch took 97 seconds. Total number of parameters of model is 36,290,202. The whole training process was conducted on an NVIDIA Titan RTX with 24 GB memory and was implemented using PyTorch.
2.4. Datasets and preprocessing
Two datasets were used for our experiments. One of these is a publicly available dataset, which allows us to compare our results to state-of-the-art methods reported in the literature.11, 13 The second dataset includes HD subjects, which allows us to assess the generalizability of our model to neurodegeneration studies.
The first dataset, IBSR, includes 18 T1w MRIs (resolution: 0.8 × 0.8 × 1.5mm3 to 1.0 × 1.0 × 1.5mm3). The publicly available manual segmentations are used as ground truth for this dataset. We randomly select 12, 3, and 3 as training, validation and testing sets respectively. Leave-three-out cross-validation is used on this dataset. For preprocessing, we use the publicly provided skull-stripped images and normalize the intensities using histogram matching.
The second dataset is a subset of the multi-site PREDICT-HD study17 (1mm isotropic resolution T1w). This subset contains 37 health controls, 13 diagnosed HD subjects, and 13 pre-manifest HD subjects in each of the high-CAP, medium-CAP and low-CAP categories, for a total of 37+13×4=89 subjects. The CAP score is a well-known measurement for disease progression of HD.17 Each subject was scanned at 2 different time points. From the healthy controls, we randomly select 20 subjects for training and 2 for validation. The remaining 15 healthy controls and all HD subjects are used for testing, to assess the generalizability of our model to atrophied brains. We employ a leave-two-out cross-validation strategy. The full preprocessing pipeline for this dataset is described in detail elsewhere.19, 20 Briefly, this includes: (1) non-local mean filter denoising, (2) intra-subject and inter-subject alignment by rigid registration, (3) bias field correction and intensity normalization. Since this dataset does not contain manual segmentations, we segment the subcortical structures with a Multi-Atlas (MA) method21 and use this as ‘ground truth’ after visual quality control. Finally, skull-stripping and histogram matching are also applied.
2.5. Data augmentation
We used 3 types of random data augmentation: affine transformation, elastic deformation, and combination of affine and elastic deformation. In addition to reducing overfitting, these augmentations serve the purpose of mimicking atrophy present in HD, such that the model can be trained on only healthy subjects and still generalize well to HD subjects. Fig. 3 shows examples of augmentations.
Figure 3.
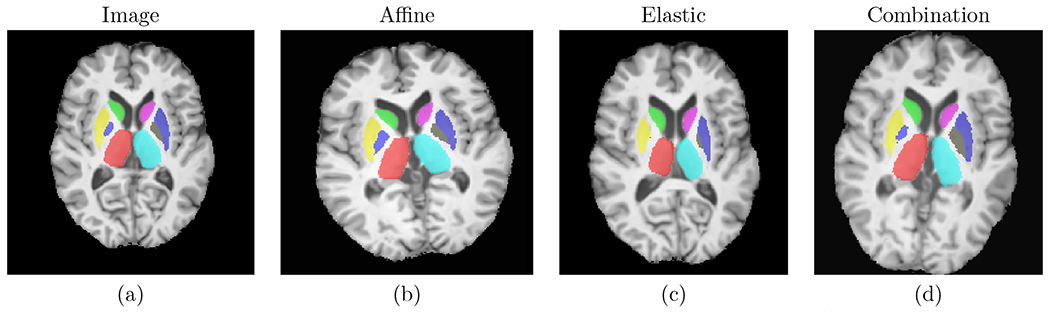
Examples of the used data augmentations. Left to right: original image, random affine, random elastic deformation, combination of random affine and random elastic deformation.
3. RESULTS
Tab. 1 shows the results of all 8 considered subcortical structures for the IBSR dataset. Compared to the results reported by Wu et al.,13 our method produced higher mean Dice scores except for the left thalamus. Compared to Dolz et al.,11 our method obtained superior performance for all structures except the thalamus.
Table 1.
Dice scores on IBSR, presented as mean ± std. dev.. Highest mean Dice scores are presented in bold. The left and right structures are reported jointly by Dolz et al.11 The train/test splits may differ between the compared methods, as these are not reported.11, 13
| R thalamus | L thalamus | R caudate | L caudate | R pallidum | L pallidum | R putamen | L putamen | |
|---|---|---|---|---|---|---|---|---|
| Wu et al. | 0.917±0.013 | 0.913±0.013 | 0.899±0.022 | 0.898±0.019 | 0.839±0.042 | 0.846±0.027 | 0.910±0.015 | 0.911±0.015 |
| Dolz et al. | 0.92 | 0.91 | 0.83 | 0.90 | ||||
| Proposed | 0.918±0.016 | 0.913±0.015 | 0.915±0.000 | 0.909±0.008 | 0.858±0.016 | 0.876±0.026 | 0.912±0.020 | 0.917±0.007 |
For the PREDICT-HD dataset, we trained our model only on healthy control subjects, and tested on both diagnosed HD patients and healthy controls. The results are shown in Tab. 2. Bold numbers indicate significant improvements (p < 0.05, 2-tail, paired t-test) compared to the work from Li at al.12 Additionally, Dice scores from all subcortical structures were significantly better than the method from Dolz et al.11 (these are not explicitly denoted on Table 2, for brevity). We observe that the improvement is especially pronounced for the caudate, putamen and pallidum of the HD subjects, which is noteworthy since these structures are known to be impacted in HD. This suggests our method may have better generalizability to brains that present neurodegeneration.
Table 2.
Dice scores on PREDICT-HD, presented as mean±std. dev. Compared to the method from Li et al.,12 significant improvements (p < 0.05 with 2-tailed paired t-test) are presented in bold. For all 8 structures, the proposed method significantly outperformed the Dolz et al.11 method.
| Control Subject Dice score | ||||||||
|---|---|---|---|---|---|---|---|---|
| R thalamus | L thalamus | R caudate | L caudate | R pallidum | L pallidum | R putamen | L putamen | |
| Dolz et al. | 0.965±0.008 | 0.964±0.006 | 0.951±0.031 | 0.951±0.019 | 0.938±0.012 | 0.937±0.011 | 0.962±0.009 | 0.964±0.009 |
| Li et al. | 0.970±0.008 | 0.970±0.006 | 0.962±0.018 | 0.959±0.016 | 0.951±0.015 | 0.954±0.012 | 0.972±0.007 | 0.972±0.007 |
| Proposed | 0.972±0.006 | 0.973±0.005 | 0.965±0.008 | 0.961±0.013 | 0.963±0.009 | 0.956±0.029 | 0.976±0.004 | 0.974±0.009 |
| Diagnosed Subject Dice score | ||||||||
| R thalamus | L thalamus | R caudate | L caudate | R pallidum | L pallidum | R putamen | L putamen | |
| Dolz et al. | 0.955±0.021 | 0.957±0.013 | 0.820±0.240 | 0.868±0.149 | 0.855±0.110 | 0.887±0.056 | 0.924±0.060 | 0.921±0.067 |
| Li et al. | 0.963±0.020 | 0.963±0.015 | 0.875±0.181 | 0.894±0.128 | 0.882±0.123 | 0.901±0.058 | 0.931±0.064 | 0.933±0.055 |
| Proposed | 0.970±0.007 | 0.970±0.008 | 0.925±0.080 | 0.932±0.059 | 0.933±0.028 | 0.938±0.019 | 0.959±0.018 | 0.955±0.023 |
Finally, our method produced the highest mean Dice scores over all subcortical structures for the 3 pre-manifest HD populations as well, as can be seen in Figure 4. This further suggests that our model is more generalizable to atrophied structures. Importantly, the Dice score of our method is more consistent across the disease progression (low-, medium-, high-CAP) than the compared methods, which suggests that it is more robust to increasing amounts of atrophy.
Figure 4.
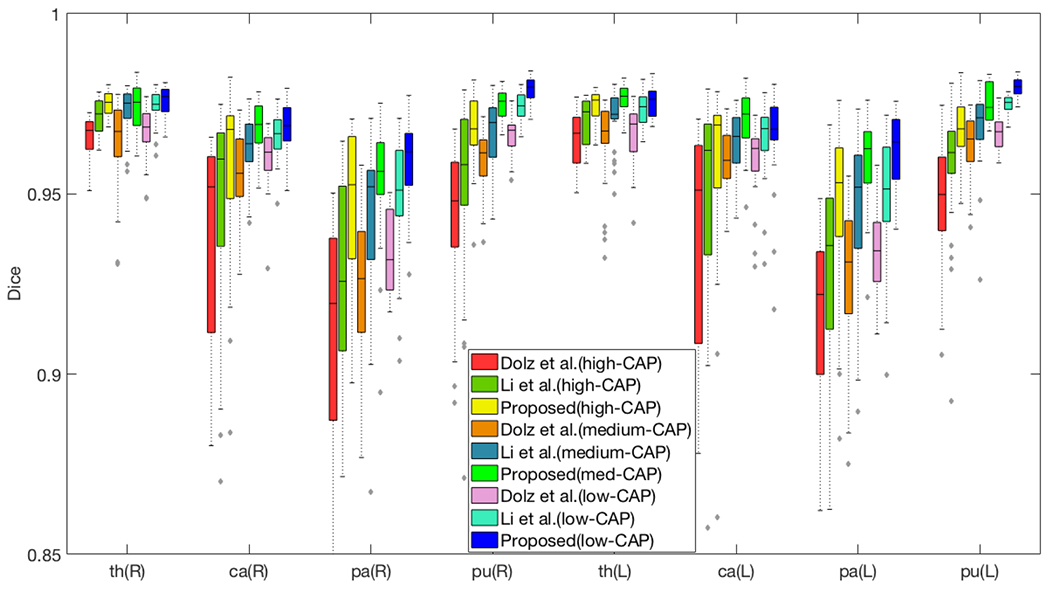
Segmentation performance of 39 HD pre-manifest subjects (13 subjects in each category). Higher CAP scores indicate patients further along the HD disease progression, and are associated with more atrophy. The horizontal axis lists the (R)ight and (L)eft pairs of thalamus, caudate, pallidum and putamen.
The qualitative results are shown in Fig. 5. We observe that the proposed method is visually the most similar to the ‘ground truth’. Our method is also more smooth than the ‘ground truth’, as can be seen in the thalamus of the control subject (red arrows). We further observe that the thin tail of the caudate in the HD subject (diagnosed) is captured well by the proposed approach, but it is substantially under-segmented by the other two methods (green arrows). Furthermore, our proposed approach produced superior putamen segmentations for the HD subject (diagnosed), which can be observed in the axial and coronal views (blue arrows).
Figure 5.

The comparison of segmentation results. Top 3 rows are from a (C)ontrol subject and bottom 3 rows are from a (D)iagnosed HD subject. Methods are marked on the top. Our method has better performance in the thalamus (red arrows), the putamen (blue arrows), the pallidum (orange arrows), as well as on the caudate tail (green and purple arrows).
It is noteworthy that Li et al.12 used spatial coordinates to encapsulate global context, but this is a relatively inefficient approach. Our currently proposed model better preserves global context thanks to its more robust architecture, and it produces superior results as shown in Fig. 5 and Tab. 2. Finally, we note that these two methods11, 12 include a postprocessing step to eliminate spurious islands from the CNN result, while our approach does not require such a postprocessing step.
4. DISCUSSION AND CONCLUSIONS
In this work, we proposed a 2-stage cascaded framework for subcortical segmentation, with a 3D CNN architecture at each stage. Our results indicate that our method is the best among the compared state-of-the-art methods. Our model can be trained efficiently on the relatively small IBSR dataset, and it generalizes well from healthy training subjects to HD test subjects in the PREDICT-HD dataset. Compared to the state-of-the-art methods, our model produces the highest mean Dice scores on all considered subcortical structures, except for the thalamus on the IBSR dataset. Furthermore, for HD subjects, our model has a dramatic improvement of accuracy for the caudate and the putamen, which are the most atrophied subcortical structures in HD.17, 22, 23 These findings indicate that our method has better generalizability not only to unseen healthy subjects, but also from healthy controls to an HD population. Our findings suggest that the skip connections, residual blocks, attention gates, and output adding in our architecture all play important roles for preserving global information and improving segmentation accuracy.
This study also indicates several directions for further research. Tables 1 and 2 suggest that our method may have more consistent performance between left and right hemispheres compared to the alternative methods (e.g., diagnosed pallidum in Table 2). This behavior could potentially be further enhanced by developing a symmetric attention gate. Additionally, the loss function could be further investigated to improve segmentation. Finally, validating our method in a larger dataset as well as exploring multi-modal segmentation remain as future work.
Acknowledgements.
This work was supported, in part, by NIH grant R01-NS094456. The PREDICT-HD study was funded by the NCATS, the NIH (NIH; NS040068, NS105509, NS103475) and CHDI.org.
Footnotes
REFERENCES
- [1].Bates GP, Dorsey R, Gusella JF, Hayden MR, Kay C, Leavitt BR, Nance M, Ross CA, Scahill RI, Wetzel R, et al. , “Huntington disease,” Nature reviews Disease primers 1(1), 1–21 (2015). [DOI] [PubMed] [Google Scholar]
- [2].Nugent AC, Luckenbaugh DA, Wood SE, Bogers W, Zarate CA Jr, and Drevets WC, “Automated subcortical segmentation using first: test–retest reliability, interscanner reliability, and comparison to manual segmentation,” Human brain mapping 34(9), 2313–2329 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3].Wang J, Vachet C, Rumple A, Gouttard S, Ouziel C, Perrot E, Du G, Huang X, Gerig G, and Styner MA, “Multi-atlas segmentation of subcortical brain structures via the autoseg software pipeline,” Frontiers in neuroinformatics 8, 7 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4].Patenaude B, Smith SM, Kennedy DN, and Jenkinson M, “A bayesian model of shape and appearance for subcortical brain segmentation,” Neuroimage 56(3), 907–922 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Fischl B, Salat DH, Busa E, Albert M, Dieterich M, Haselgrove C, Van Der Kouwe A, Killiany R, Kennedy D, Klaveness S, et al. , “Whole brain segmentation: automated labeling of neuroanatomical structures in the human brain,” Neuron 33(3), 341–355 (2002). [DOI] [PubMed] [Google Scholar]
- [6].Oguz I, Kashyap S, Wang H, Yushkevich P, and Sonka M, “Globally optimal label fusion with shape priors,” in [International Conference on Medical Image Computing and Computer-Assisted Intervention], 538–546, Springer; (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7].Oguz BU, Shinohara RT, Yushkevich PA, and Oguz I, “Gradient boosted trees for corrective learning,” in [International Workshop on Machine Learning in Medical Imaging], 203–211, Springer; (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8].Zhang H, Valcarcel AM, Bakshi R, Chu R, Bagnato F, Shinohara RT, Hett K, and Oguz I, “Multiple Sclerosis Lesion Segmentation with Tiramisu and 2.5D Stacked Slices,” MICCAI, 338–346 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Han S, Carass A, He Y, and Prince JL, “Automatic cerebellum anatomical parcellation using u-net with locally constrained optimization,” NeuroImage , 116819 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10].He Y, Carass A, Liu Y, Jedynak BM, Solomon SD, Saidha S, Calabresi PA, and Prince JL, “Fully convolutional boundary regression for retina oct segmentation,” in [MICCAI; ], 120–128, Springer (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Dolz J, Desrosiers C, and Ayed IB, “3d fully convolutional networks for subcortical segmentation in mri: A large-scale study,” NeuroImage 170, 456–470 (2018). [DOI] [PubMed] [Google Scholar]
- [12].Li H, Zhang H, Hu D, Johnson H, Long JD, Paulsen JS, and Oguz I, “Generalizing mri subcortical segmentation to neurodegeneration,” in [Machine Learning in Clinical Neuroimaging and Radiogenomics in Neuro-oncology], 139–147, Springer; (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13].Wu J, Zhang Y, and Tang X, “A joint 3d+ 2d fully convolutional framework for subcortical segmentation,” in [MICCAI; ], 301–309 (2019). [Google Scholar]
- [14].Cicek O, Abdulkadir A, Lienkamp SS, Brox T, and Ronneberger O, “3D U-Net: learning dense volumetric segmentation from sparse annotation,” in [MICCAI; ], 424–432 (2016). [Google Scholar]
- [15].He K, Zhang X, Ren S, and Sun J, “Deep residual learning for image recognition,” in [CVPR; ], (2016). [Google Scholar]
- [16].Schlemper J, Oktay O, Schaap M, Heinrich M, Kainz B, Glocker B, and Rueckert D, “Attention gated networks: Learning to leverage salient regions in medical images,” MedIA 53, 197–207 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [17].Long JD, Paulsen JS, et al. , “Multivariate prediction of motor diagnosis in Huntington’s disease: 12 years of PREDICT-HD,” Mov. Disorders 30(12), 1664–1672 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [18].Milletari F, Navab N, and Ahmadi S-A, “V-net: Fully convolutional neural networks for volumetric medical image segmentation,” in [2016 fourth international conference on 3D vision (3DV)], 565–571, IEEE; (2016). [Google Scholar]
- [19].Pierson R, Johnson H, Harris G, Keefe H, Paulsen JS, Andreasen NC, and Magnotta VA, “Fully automated analysis using brains: Autoworkup,” NeuroImage 54(1), 328–336 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [20].Kim EY and Johnson HJ, “Robust multi-site mr data processing: iterative optimization of bias correction, tissue classification, and registration,” Frontiers in neuroinformatics 7, 29 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [21].Kim EY, Lourens S, Long JD, Paulsen JS, and Johnson HJ, “Preliminary analysis using multi-atlas labeling algorithms for tracing longitudinal change,” Frontiers in neuroscience 9, 242 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [22].Long JD, Paulsen JS, Marder K, Zhang Y, Kim J-I, Mills JA, and of the PREDICT-HD Huntington’s Study Group, R., “Tracking motor impairments in the progression of huntington’s disease,” Movement Disorders 29(3), 311–319 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [23].Paulsen JS, Long JD, Ross CA, Harrington DL, Erwin CJ, Williams JK, Westervelt HJ, Johnson HJ, Aylward EH, Zhang Y, et al. , “Prediction of manifest huntington’s disease with clinical and imaging measures: a prospective observational study,” The Lancet Neurology 13(12), 1193–1201 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]


