Scan-rescan repeatability of axonal imaging metrics using high-gradient diffusion MRI and statistical implications for study design

Abstract

Axon diameter mapping using diffusion MRI in the living human brain has attracted growing interests with the increasing availability of high gradient strength MRI systems. A systematic assessment of the consistency of axon diameter estimates within and between individuals is needed to gain a comprehensive understanding of how such methods extend to quantifying differences in axon diameter index between groups and facilitate the design of neurobiological studies using such measures. We examined the scan-rescan repeatability of axon diameter index estimation based on the spherical mean technique (SMT) approach using diffusion MRI data acquired with gradient strengths up to 300 mT/m on a 3T Connectom system in 7 healthy volunteers. We performed statistical power analyses using data acquired with the same protocol in a larger cohort consisting of 15 healthy adults to investigate the implications for study design. Results revealed a high degree of repeatability in voxel-wise restricted volume fraction estimates and tract-wise estimates of axon diameter index derived from high-gradient diffusion MRI data. On the region of interest (ROI) level, across white matter tracts in the whole brain, the Pearson’s correlation coefficient of the axon diameter index estimated between scan and rescan experiments was r = 0.72 with an absolute deviation of 0.18 μm. For an anticipated 10% effect size in studies of axon diameter index, most white matter regions required a sample size of less than 15 people to observe a measurable difference between groups using an ROI-based approach. To facilitate the use of high-gradient strength diffusion MRI data for neuroscientific studies of axonal microstructure, the comprehensive multi-gradient strength, multi-diffusion time data used in this work will be made publicly available, in support of open science and increasing the accessibility of such data to the greater scientific community.

1. Introduction

Axon diameter estimation in the living human brain has attracted great interests in recent years with the growing availability of high-gradient strength human MRI systems (Jones et al., 2018; Setsompop et al., 2013), which sensitize the diffusion MRI measurement to intra-axonal water diffusion (Huang et al., 2020; Veraart et al., 2018; Veraart et al., 2019; Veraart et al., 2020; Veraart et al., 2021). The effective axon diameters can be measured by diffusion MRI using gradient strengths up to 300 mT/m but are dominated by the largest axons in the tail of the distribution and weighted by compartment-specific volume fractions and T₂ values within the voxel (Alexander et al., 2010; Burcaw et al., 2015; Veraart et al., 2020), and may be modulated by time-dependent diffusion in the extra-axonal space as well (Andersson et al., 2020; Burcaw et al., 2015; Fieremans et al., 2016; Lee et al., 2018; Lee et al., 2020a; Lee et al., 2020b). Despite these caveats and limitations, the relative trends in axon diameter extracted from high-gradient strength measurements in the living human brain spanning from the anterior to posterior tips of mid-sagittal corpus callosum (Alexander et al., 2010; Huang et al., 2015) and other white matter tracts extracted from high-gradient strength measurements in the living human brain are consistent with those from histology (Assaf et al., 2013; Huang et al., 2020; Veraart et al., 2018; Veraart et al., 2020). Several studies have demonstrated the potential of such noninvasive measurements in providing unique neuro-scientific insights into white matter microstructure and plasticity, including serving as a probe of axonal conduction velocity (Drakesmith et al., 2019; Horowitz et al., 2015), microstructural alterations due to aging (Fan et al., 2019) and axonal damage in neurological diseases such as multiple sclerosis (Huang et al., 2016; Santis et al., 2019).

The scan-rescan repeatability of a simplified AxCaliber approach (Assaf et al., 2008) for mapping mean axon diameter was initially investigated in the corpus callosum of both humans and non-human primates (Alexander et al., 2010; Dyrby et al., 2013). More recently, assessments were performed in the human spinal cord (Duval et al., 2018) and brain (Veraart et al., 2021) using a relatively larger group size. These studies provided supportive evidence for the feasibility of robustly extracting quantitative axonal metrics in healthy adults. A drawback of the AxCaliber type of approach that limits its application to whole brain analysis lies in the assumption of a single fiber bundle, which contradicts the known prevalence of complex white matter structures in the brain, such as fiber crossings and other complex fiber configurations (Anderson, 2005; Behrens et al., 2007; Dyrby et al., 2014; Fan et al., 2017; Fan et al., 2014; Jeurissen et al., 2013; Lee et al., 2019; Mollink et al., 2017; Mortazavi et al., 2017; Nilsson et al., 2012; Schilling et al., 2018; Tournier et al., 2004). We have recently generalized the AxCaliber approach under the spherical mean technique (SMT) framework (Callaghan et al., 1979; Kaden et al., 2016a; Kaden et al., 2016b) to obtain per-voxel averaged apparent axon diameter index estimates that are independent of fiber orientation distribution (Fan et al., 2020). The results are in line with findings by (Veraart et al., 2020), in which convincing theoretical and experimental evidence was provided to support the validity of in vivo axon diameter mapping using diffusion MRI at 300 mT/m gradient strengths, with averaged in vivo MR-estimated radii reported in the range of ~2–3 μm in both studies (Fan et al., 2020; Veraart et al., 2020). Before the next step can be taken to generalize the axon diameter mapping method to larger scale studies of axonal microstructure across the lifespan and in neurological disorders, the scan-rescan repeatability of such measurements still needs to be assessed. The consistency of axon diameter estimates should be characterized within and between individuals, and also compared on a voxel-wise versus tract-specific basis, in order to gain a comprehensive understanding of how such methods extend to quantifying differences in axon diameter for specific fiber bundles between groups. Furthermore, understanding the reliability of axon diameter measurements in the living human brain using currently available hardware will aid in guiding the design of next-generation gradient systems for more robust and precise measurements of axonal microstructure.

The goal of this work was to assess the scan-rescan repeatability of axon diameter index estimation based on the SMT approach using diffusion MRI data acquired with gradient strengths up to 300 mT/m on the 3T Connectom scanner in 7 healthy volunteers, and to examine the implications for study design using data acquired with the same protocol in 15 healthy volunteers. Our repeatability analysis included an examination of voxel-wise absolute errors and correlation coefficients of the quantitative diffusion metrics between scan and rescan sessions, followed by tract-wise examinations of repeatability and intraclass correlation coefficients (ICCs) of ROI-averaged axonal metrics. To characterize the consistency and variation between individuals, tract-wise statistics were obtained, upon which statistical power analyses were performed to achieve a better understanding of the implications in designing future biological studies. To encourage the greater use of high-gradient strength diffusion MRI data for neuroscientific studies of axonal microstructure, the comprehensive multi-gradient strength, multi-diffusion time data from all individuals included in this work will be made publicly available.

2. Material and Methods

2.1. Signal Model

The signal model is the same as described in (Fan et al., 2020). In brief, the total diffusion weighted signal written in the spherical mean form $\overline{S}$ is composed of signals originating from three compartments, i.e.,

$$\overline{S}=f_r\overline{S_r}+f_h\overline{S_h}+f_{csf}\overline{S_{csf}},$$ (1)

where, $\overline{S_r}$, $\overline{S_h}$ and $\overline{S_{csf}}$ are the spherical mean signals for the restricted, hindered, and CSF compartments, respectively, and f_r, f_h, and f_csf are the corresponding relaxation-weighted volume fractions, which sum to 1. The SMT framework applied to this signal model uses diffusion MRI data acquired at multiple diffusion times to fit for axon diameter and to differentiate the contributions of the restricted, intra-axonal diffusion signal and the hindered, extra-axonal diffusion signal to the overall diffusion signal.

In the intracellular compartment, $\overline{S_r}$ is dependent on the signal components that are perpendicular and parallel to the fiber axis, respectively. The perpendicular component is a function of the inner diameter of a cylinder derived using the Gaussian phase distribution approximation for a finite gradient pulse (van Gelderen et al., 1994), and thus is dependent on diffusion time Δ and gradient duration δ as well. The intrinsic diffusivity was assumed to equal the parallel diffusivity and took on a fixed value of D_∥ = 1.7 × 10⁻³ mm²/s for white matter in all subjects, which was based on the average longitudinal diffusivity in the cerebral white matter estimated from our in vivo human diffusion data. The parallel signal component was assumed to obey mono-exponential decay based on the empiric signal decays observed in the cerebral white matter with a fixed intrinsic/parallel diffusivity of D_∥ = 1.7 × 10⁻³ mm²/s. Hindered diffusion in the extra-axonal compartment is assumed to be 3D Gaussian (Fieremans et al., 2011) and modeled by an axially symmetric tensor with a fitted perpendicular diffusivity of D_h and a fixed intrinsic/parallel diffusivity of D_∥ = 1.7 × 10⁻³ mm²/s (Alexander et al., 2010; Daducci et al., 2015; Dyrby et al., 2013; Huang et al., 2020; Kaden et al., 2016a; Zhang et al., 2012). Isotropic diffusion in the free water / cerebrospinal fluid (CSF) compartment is modeled by Gaussian diffusion with a fixed diffusivity of D_cxf = 3 × 10⁻³ mm²/s.

Voxel-wise fitting for apparent axon diameter, restricted and hindered volume fractions, and perpendicular hindered diffusivity D_h was performed using the Markov chain Monte Carlo (MCMC) sampling approach described in (Fan et al., 2020). A total of 200,000 MCMC samples were calculated for each voxel and saved at intervals of 100 iterations with a burn-in of 20,000 iterations (i.e., 1,800 samples were saved for each voxel). The mean of the estimates for apparent axon diameter, perpendicular hindered diffusivity D_h, and volume fractions f_r, f_h and f_csf were then calculated for each voxel by taking the mean over the saved MCMC samples.

2.2. Data Acquisition

This study was conducted with approval from the Institutional Review Board of Mass General Brigham. 15 healthy, cognitively normal adults participated in this study (22–72, 39.2 ± 18.6 years old, 11 females), among which 7 subjects (22–72, 37.1 ± 18.4 years old, 4 females) participated in the scan-rescan experiments. The 7 scan-rescan participants were scanned twice on the same day and were removed from the scanner between the scan and rescan sessions for a rest period of approximately one hour. Written informed consent was obtained from each participant.

Imaging data was acquired on the 3T Connectom scanner (Siemens MAGNETOM Connectom) with a maximum gradient strength of 300 mT/m. A custom-built 64 channel head coil (Keil et al., 2013) was used for signal reception. Diffusion MRI data were acquired using a pulsed gradient spin-echo, echo planar imaging (EPI) sequence with an in-plane field-of-view (FOV) of 216 × 216 mm and 2 mm isotropic voxel size. The duration of the diffusion weighting gradient (δ) was 8 ms. Two diffusion times were sampled (Δ= 19/49 ms), and 8 diffusion encoding gradient strengths linearly spaced from 30 to 290 mT/m were sampled for each diffusion time, with 32 diffusion-encoding directions sampled for b < 2,400 s/mm² and 64 diffusion-encoding directions for b ≥ 2,400 s/mm^2. Interleaved b = 0 images were collected every 16 diffusion weighted volumes. Five b = 0 images with reversed phase-encoding direction (posterior-to-anterior) were also acquired to correct for susceptibility-induced image distortions. Other parameters include: repetition time (TR) / echo time (TE) = 4000/77 ms, in-plane acceleration factor of 2 using the generalized autocalibrating partial parallel acquisition (GRAPPA) method (Griswold et al., 2002; Polimeni et al., 2015), slice acceleration factor of 2 using simultaneous multi-slice (SMS) techniques (Feinberg et al., 2010; Feinberg and Setsompop, 2013; Setsompop et al., 2012a; Setsompop et al., 2012b), and partial Fourier of 6/8. The total acquisition time was approximately 55 min. The current imaging protocol resulted from an empiric optimization effort that sought to keep the acquisition time to within an hour, similar to the constraints adopted in the ActiveAx approach (Alexander et al., 2010), while acquiring enough data to ensure robust estimates without losing important anatomical detail. In brief, the protocol optimization involved examining the precision of the fitted model parameters with the inclusion of a minimum number of diffusion times and b-shells per diffusion time for sufficient sampling of the diffusion signal decay, as described in (Huang et al., 2020). We were able to acquire the two diffusion times with 8 b-shells per diffusion time across the whole brain within 55 min with accelerated acquisition methods such as GRAPPA and SMS. The diffusion MRI sequence was also adapted to export phase images in addition to the magnitude images, and the real-valued diffusion data were obtained by removing the nuisance background phase caused by physiological noise, motion, and instrumental imperfections such as inhomogeneity in the B₁-transmit field (Eichner et al., 2015; Fan et al., 2020).

T₁ -weighted structural images with 1 mm isotropic voxel size were also acquired using an multi-echo magnetization-prepared gradient echo (MEMPRAGE) sequence (van der Kouwe et al., 2008) with the following imaging parameters: TR/TE = 2530/1.15 ms, GRAPPA = 3, inversion time TI = 1100 = ms, flip angle = 7°, and acquisition time = 4 min.

2.3. Image Processing

All imaging data were corrected for gradient nonlinearity distortions using our in-house Matlab codes, as in (Fan et al., 2016). Diffusion data were corrected for susceptibility and eddy current distortions using TOPUP (Andersson et al., 2003) and EDDY (Andersson and Sotiropoulos, 2016; Andersson et al., 2016) tools in FSL (Jenkinson et al., 2012). FreeSurfer reconstruction (stable version v6.0.0, https://surfer.nmr.mgh.harvard.edu/) was performed using T₁-weighted images to obtain masks of the cerebral white matter.

Voxel-wise estimations of axon diameter index (a), relaxation-weighted restricted (f_r) and hindered (f_h) volume fractions, and hindered diffusivity (D_h) were performed under the SMT framework using the real-valued diffusion data (Fan et al., 2020) using the Markov Chain Monte Carlo sampling approach (Huang et al., 2020). In addition, diffusion tensor imaging (DTI) fitting was performed using the data acquired at b = 950 s/mm^2. All model fitting was performed in the original native space of the scan and rescan sessions.

For the 7 participants who underwent scan and rescan experiments, assessment of the scan-rescan repeatability of the voxel-based metric estimates was performed in the half-way space between the scan and rescan diffusion spaces for each participant to ensure that the image registration process exerted an equivalent influence on the scan and rescan data. Briefly, the following image registration steps were taken to attain voxel-wise correspondence between scan and rescan images. First, within each scan session, the average of the interleaved b = 0 images was registered to the T₁-weighted image using boundary-based registration (Greve and Fischl, 2009) with 6 degrees of freedom. The T₁-weighted image of the rescan session was then registered to that of the scan session. The resulting transformations were then concatenated to obtain a single transformation from the diffusion space of the rescan data to the diffusion space of the original scan data. A transformation to a position halfway between the two diffusion spaces was then calculated, which is henceforth referred to as a “halfway transformation”. This halfway transformation was applied to the scalar maps calculated in each imaging session’s native space, bringing each map to the halfway point between the scan and rescan sessions.

To assess the tract-wise repeatability on the region-of-interest (ROI) level, the Johns Hopkins University (JHU) - International Consortium for Brain Mapping (ICBM) -DTI-81 white matter atlas (https://fsl.fmrib.ox.ac.uk/fsl/fslwiki/Atlases) was used to define the white matter segments. The fractional anisotropy (FA) maps from the scan and rescan sessions were first registered to their mid-way point and averaged, and the averaged map was then nonlinearly registered to the JHU-ICBM template 1 mm FA map using the FMRIB nonlinear image registration tool (FNIRT) (https://fsl.fmrib.ox.ac.uk/fsl/fslwiki/FNIRT). The resulting warp-field was then inverted and applied simultaneously with the linear halfway transformation to the binary masks in the standard space to obtain the alignment with the scalar maps calculated in the native diffusion spaces, where ROI-averages were calculated.

Statistical power analyses were performed with all 15 participants, where only the first scan session was used for the 7 scan-rescan participants. Specifically, the native FA maps were nonlinearly registered to the JHU-ICBM 1 mm FA map using FNIRT, and the resulting warp-field was then applied to the maps of FA, restricted volume fraction and axon diameter index using tri-linear interpolation. For each segment in the cerebral white matter, an ROI average was calculated, and the mean and standard deviation across all participants were obtained for statistical power analyses.

2.4. Data Analysis

2.4.1. Scan-Rescan Repeatability

Scan-rescan repeatability was first assessed on the voxel-based metric estimation. Voxels within the white matter masks were included, and a mild threshold on FA (i.e., FA > 0.2) was used to exclude voxels substantially contaminated by partial volume effects. Pearson’s correlation was performed between corresponding voxels of scan and rescan sessions throughout the brain across all subjects and the average absolute errors per voxel were also reported.

On the tract level, the repeatability of ROI averages of diffusion metrics was assessed. Similarly, the Pearson’s correlation was performed between measures obtained in the scan and rescan sessions throughout all subjects, and the mean absolute deviation was reported. To explore whether the tract-level results were critically dependent on how tracts/ROIs were defined, a different white matter atlas was also adopted to perform similar assessments (Figure S2 in Supplementary Materials).

The intraclass correlation coefficient (ICC) was computed in each tract-ROI as in (Duval et al., 2018) to assess the capability of the metrics to identify genuine inter-subject microstructural differences given the measured intra-subject variability. The ICC was calculated as:

$$ICC=\frac{{s_{inter}}^2}{{s_{intra}}^2+{s_{inter}}^2}$$

Where ${s_{inter}}^2=va{r}_i\left({\overline{m}}_i\right)$ and ${s_{intra}}^2=mea{n}_i\left(\frac{1}{2}\left({\left(m_{i,scan}-\overline{m_i}\right)}^2+{\left(m_{i,rescan}-\overline{m_i}\right)}^2\right)\right)$, $m_{i,scan}$ is the metric value within a particular tract for subject i. $\overline{m_i}$ is the average between the scan and rescan sessions. Here, an ICC value closer to 1 means that the between-subject variation is much higher than intra-subject scan-rescan error. A one-way analysis of variance (ANOVA) was performed to assess for differences in ICC among the three metrics (FA, restricted volume fraction and axon diameter index) using the full list of tracts presented in the Supplementary Materials (Table S1), which was followed by pairwise two-sample T-tests to identify the specific relationship.

2.4.2. Statistical Power Analysis

A statistical power analysis was performed for each of the diffusion metrics, including FA, restricted volume fraction and apparent axon diameter index, to obtain an estimation on the effect size and number of participants needed to meet the statistical significance in a group of interest as compared to a reference standard. The sample mean (μ) and standard deviation (σ) of these diffusion metrics were calculated for each white matter segment in the ICBM template space using the data acquired in the 15 healthy, cognitively normal adult participants (i.e., as a reference standard). The statistical power analyses can be presented in two ways. First, for a given known group size, what is the minimum effect size detectable (i.e., Δμ in absolute value or Δμ/μ in percentage) with respect to the reference standard? The other way to frame this question is: given a known effect size, how many participants are needed to detect a statistically significant group difference? We address both questions in this work in order to inform study design in a straightforward and practical way. To answer the first question, equal group size was assumed for both groups of interest and reference standard (N = 15), assuming the difference in group mean values was tested using a two-tailed two-sample T-test at a significance level of α = 0.05 and power of π = 0.8. To answer the second question, the minimum group size (i.e., equal number of participants, N, for both groups) was estimated for 5% and 10% effect sizes, respectively.

3. Results

3.1. Scan-Rescan Repeatability

The consistency in diffusion metrics between scan and rescan sessions is shown in Figure 1, in which exemplary maps of FA, restricted volume fraction, and axon diameter index are shown for are presentative subject. The axon diameter index maps demonstrated reproducible patterns of variation across the whole brain between the two separate sessions, including an anterior-to-posterior gradient with smaller diameters in the frontal lobes and larger diameters in the parietal and occipital lobes, in keeping with previously observed trends (Fan et al., 2020; Huang et al., 2020; Tomasi et al., 2012). The performance of the registration between scan and rescan sessions was qualitatively assessed in checkerboard plots (Figure S1 in the Supplementary Materials), which showed accurate registration of the scan and rescan images. The alignment between the scan and rescan images was verified quantitatively by linear correlation analyses between the average b = 0 images of the scan and rescan sessions after registration, which demonstrated strong correlations with correlation coefficients ranging from 0.87 to 0.93.

Fig. 1.

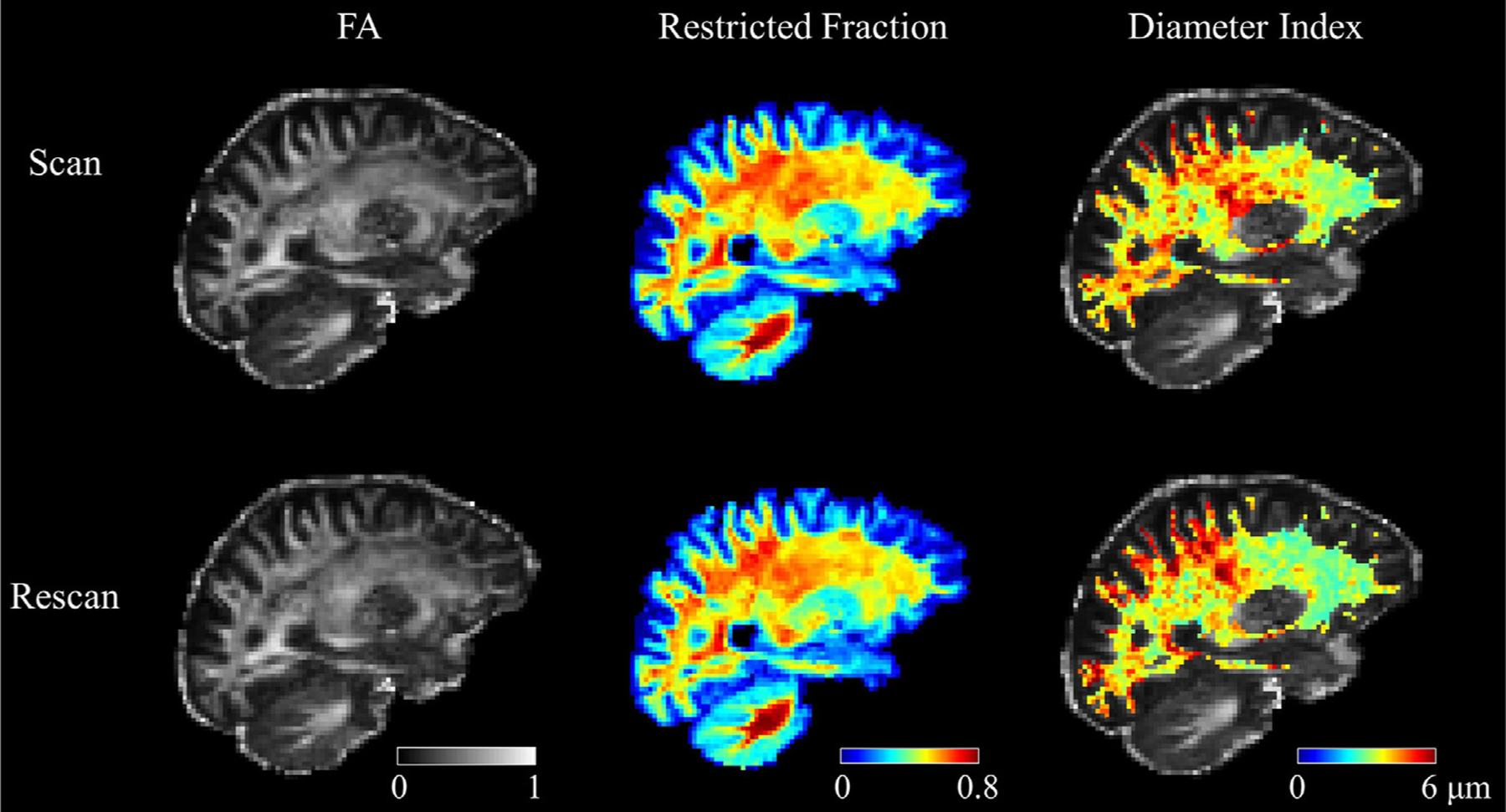
Representative FA, restricted volume fraction, and apparent axon diameter index maps in a healthy subject from scan (upper panel) and rescan (lower panel) sessions. The maps are displayed in the halfway point between the two sessions, such that identical anatomical regions can be compared. The visual consistency between the scan and rescan results can be appreciated from the maps.

Scatterplots of the voxel-wise estimates from the scan and rescan sessions are shown in Fig. 2. Each plot was generated with all white matter voxels pooled from all subjects. The restricted volume fraction estimates showed the highest Pearson’s correlation coefficient (r = 0.94), with an average absolute deviation of 0.03 between scan and rescan measures. The results for FA were in the same range, with a correlation coefficient of r = 0.93 and average absolute deviation of 0.04. The axon diameter index was the most the challenging metric to estimate, and the correlation coefficient was r = 0.53 between voxel-wise estimates of the scan and rescan sessions.

Fig. 2.

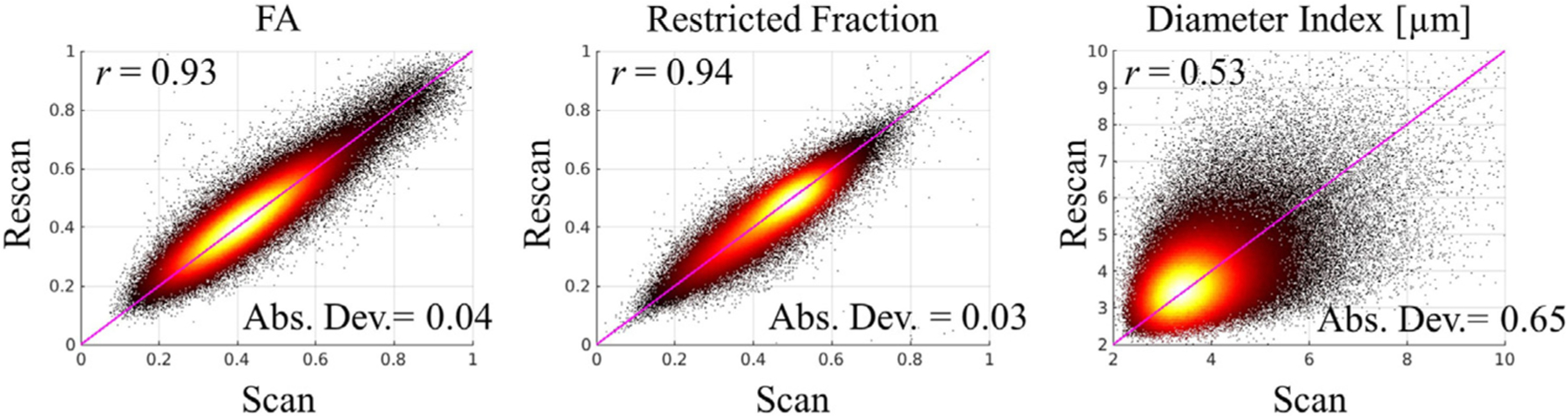
Voxel-wise estimates of diffusion metrics from scan and rescan sessions. The plots were generated by pooling together all white matter voxels across all subjects. The Pearson’s correlation coefficient (r) and absolute deviation (Abs. Dev.) are labeled on each plot. The line of unity is marked in pink.

The repeatability of ROI-averaged diffusion metrics is shown in Fig. 3. Each point in the scatterplot corresponds to one white matter segment in one participant, and all white matter segments across all subjects were pooled together to show the scan-rescan repeatability on one plot. Similar to the voxel-wise results, the ROI-averaged estimates also demonstrated the highest scan-rescan correlation in the restricted volume fraction. Note that the repeatability of the ROI-averaged estimates of axon diameter index markedly improved as compared to the voxel-wise estimates, with a Pearson’s correlation coefficient of r = 0.72 and absolute deviation of 0.18 μm.

Fig. 3.

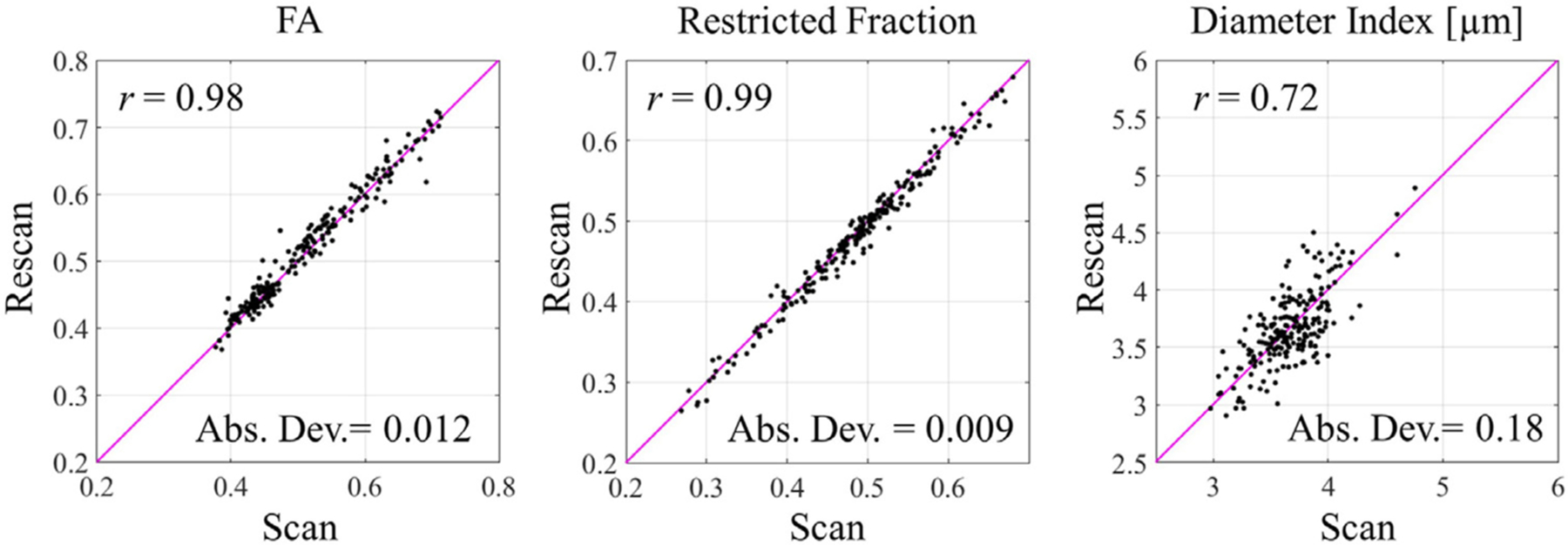
ROI-averaged diffusion metrics of scan and rescan sessions. The plots were generated by pooling together all white matter segments across all subjects. The Pearson’s correlation coefficient (r) and absolute deviation (Abs. Dev.) were labeled on each plot. The line of unity is marked in pink.

To assess the capability of detecting reliable differences between subjects using these metrics, Table 1 lists the ICC scores for FA, restricted volume fraction, and axon diameter in segments of several major white matter tracts in the brain, with the full list presented in the Supplementary Material (Table S1). In general, good to excellent reliability was observed for FA, restricted volume fraction and axon diameter across the major white matter tracts, with the highest ICC scores observed in the largest and most coherent bundles in the brain. The ICC scores derived from FA, f_r and a differed significantly from one another (p < 0.001). The ICC scores for the estimated f_r weresignificantly higher than those for FA (t = 3.49, p < 0.001), which were in turn higher than those for the axon diameter index a (i.e., FA vs. a, t = 7.5, p < 0.001).

Table 1.

Intraclass Correlation Coefficients

Tracts	FA	f r	a
Genu of corpus callosum	0.98	0.99	0.78
Body of corpus callosum	0.98	0.98	0.92
Splenium of corpus callosum	0.95	0.98	0.84
Posterior limb of internal capsule R	0.91	0.98	0.91
Posterior limb of internal capsule L	0.94	0.98	0.88
Superior corona radiata R	0.95	0.89	0.91
Superior corona radiata L	0.87	0.95	0.87
Posterior thalamic radiation (include optic radiation) R	0.96	0.99	0.63
Posterior thalamic radiation (include optic radiation) L	0.81	0.99	0.68
Cingulum (cingulate gyrus) R	0.90	0.95	0.75
Cingulum (cingulate gyrus) L	0.93	0.96	0.67
Superior longitudinal fasciculus R	0.90	0.98	0.92
Superior longitudinal fasciculus L	0.83	0.98	0.65

Given that DTI is a widely accepted and adopted technique in the community, we included the repeatability measure of FA in addition to the microstructural metrics of f_r and a in this paper, to assist appreciation of the degree of repeatability of the microstructural metrics being studied. It is worth noting that FA and the microstructural metrics of f_r and a are distinct physical quantities, reflecting different aspects of the diffusion properties of neuroaxonal tissue. In particular, FA has been observed to have no correlation with axon diameter estimates (Alexander et al., 2010; Fan et al., 2019).

3.2. Statistical Power Analysis

The group mean (μ) and standard deviation (σ) were calculated among the 15 participants (see detailed statistics in Table S2), based on which the minimum effect size detectable (Δμ and Δμ/μ) was estimated, assuming that the control group and the group of interest consisted of N = 15 participants each.

The results are presented in the form of an atlas. Fig. 4 a shows the atlas of group means (μ) for FA, restricted volume fraction (f_r) and axon diameter index (a), respectively. Overall, the maps demonstrated left-right symmetry, with regional variations consistent with expected trends. For example, FA was lower in the centrum semiovale than in regions consisting of highly oriented, coherent fiber bundles such as the corpus callosum, internal capsules and cerebral peduncles. The restricted volume fraction increased moving from superior to inferior along the corticospinal tract as the fiber bundles are more tightly packed in the basal ganglia and brainstem. On the map of axon diameter index, a low-high-low pattern was observed in the genu, body and splenium of the corpus callosum on the sagittal view. Across the whole brain, the anterior-to-posterior gradient in the axon diameter index was observed, with the anterior portions of the brain demonstrating smaller axonal sizes than the posterior portions. Note that the maps of restricted volume fraction and axon diameter index demonstrated relatively consistent values across the whole brain, presumably due to the use of the SMT framework which accounts for potential confounding effects caused by crossing fibers.

Fig. 4. a.

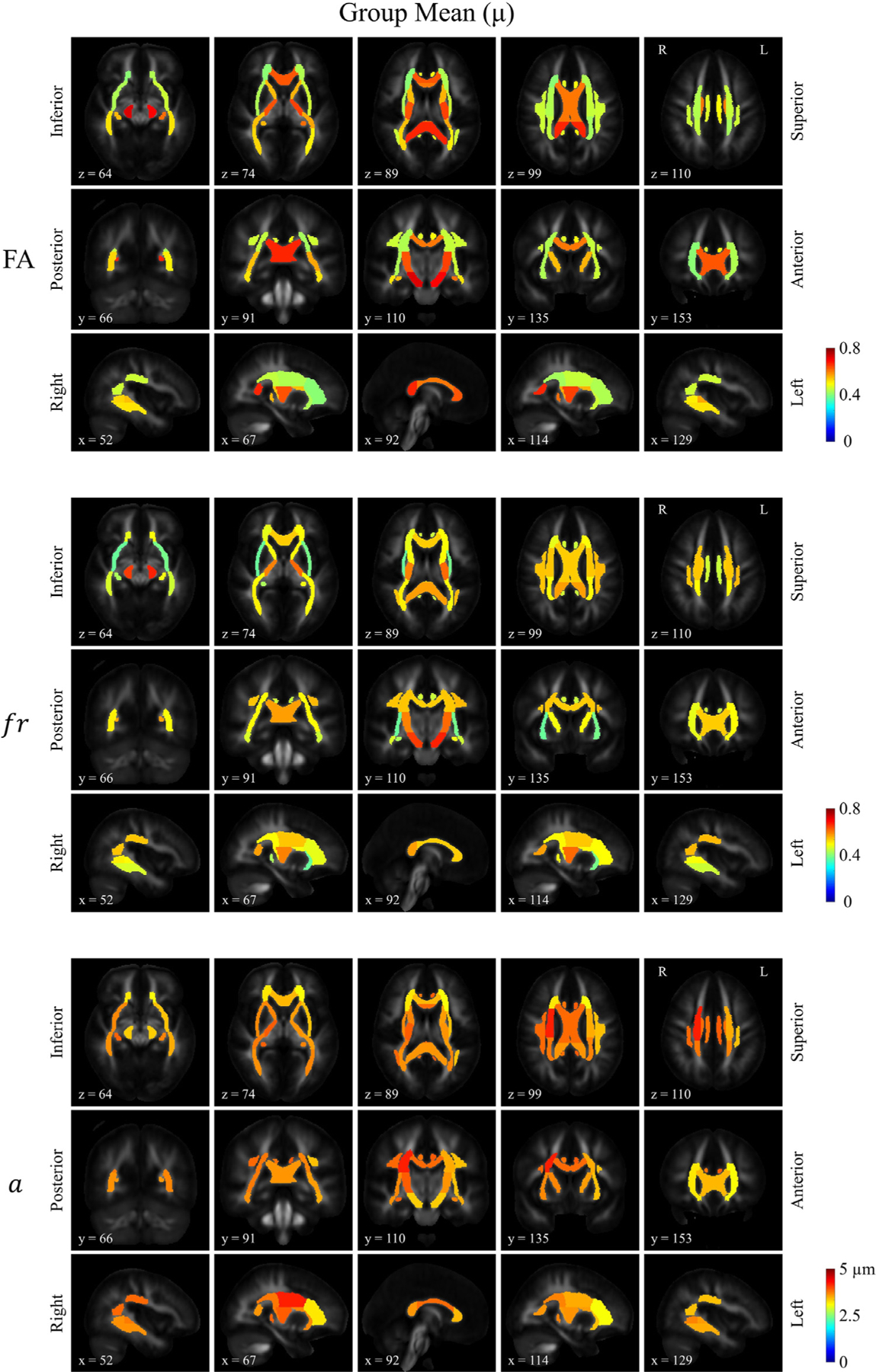
Atlases of the group means for FA, restricted volume fraction (f_r) and apparent axon diameter index (a) for different tract ROIs derived from the ICBM-DTI-81 white matter atlas. A striking feature in the map of f_r lies in the relatively uniform distribution throughout the whole brain cerebral white matter regardless of crossing structures, in distinction to that of FA. The slice number (i.e., first slice counted as slice 0) of the template FA in the ICBM space was labeled on each individual map.

The distribution of the minimum effect size detectable (Δμ) was shown in Figure 4b, which also demonstrates a left-right symmetric pattern in general. Δμ reflects the variation across individuals in the cohort being studied, inclusive of the effect of the reliability of the measurement itself. A hotter color on the map of Δμ means a higher threshold to resolve a significant group difference, and cooler colors mean it is easier to detect a group difference. Along the corticospinal tracts, both f_r and a demonstrated relatively high thresholds in the most inferior segments (i.e., cerebral peduncles), where the average axon diameter index was smaller and approached the resolution limit of axon diameter estimation using 300 mT/m gradient strength, which is approximately 2~3 μm (Dyrby et al., 2013; Fan et al., 2020; Nilsson et al., 2017). Furthermore, the Signal-to-Noise Ratio (SNR) in the central brain was lower as this area is relatively farther away from the receiver coil, with temporal SNR ranging from 20 in the central white matter tracts to 40 in the hemispheric white matter. The combination of factors – smaller diameter axons near the resolution limit of diffusion MRI and lower temporal SNR (tSNR) – likely made it more difficult to estimate parameters such as a reliably. Variations in both f_r and a were observed along tracts such as the corticospinal tracts (Fig. 4a), whereas the minimum detectable group difference in percentage seemed less variable along the tract in f_r than a (Fig. 4c). Our previous simulation studies on how Gaussian noise affects SMT parameter estimation (Supplementary Materials in (Fan et al., 2020)) show that the error bars for f_r estimation are relatively narrow throughout the range of f_r between 0.2 to 0.8, as compared to the estimation of a. The high precision in the estimation of f_r suggests that the variation along the tract in f_r observed in (Fig. 4a) likely reflects true biological variation. In comparison, the precision of a is more contingent on having sufficient SNR in the data, and thus the higher Δμ/ μ observed in the bilateral cerebral peduncle (CP) (i.e., the most inferior portion of the corticospinal tract) is thought to be dominated by the low SNR in this region. Besides, another important factor appears to be the size of the structure, with larger/thicker segments demonstrating a lower Δμ, and smaller/thinner structures such as the fornix and cingulum showing a higher threshold, likely due at least in part to the difficulty in registration and hence partial volume effects on the estimation of microstructural measures in the smallest tracts. Similar rationale also applies to the trend observed in the mid-sagittal view of the corpus callosum. Generally speaking, larger axons (i.e. in the body of the corpus callosum) are easier to be estimated, but the thinner structure with a higher fraction of border voxels makes it more susceptible to the partial volume effects. The lower restricted signal fraction in the border voxels contributed to the difficulty of estimating axon diameter index, which should also be taken into consideration when interpreting the results.

Fig. 4. b.

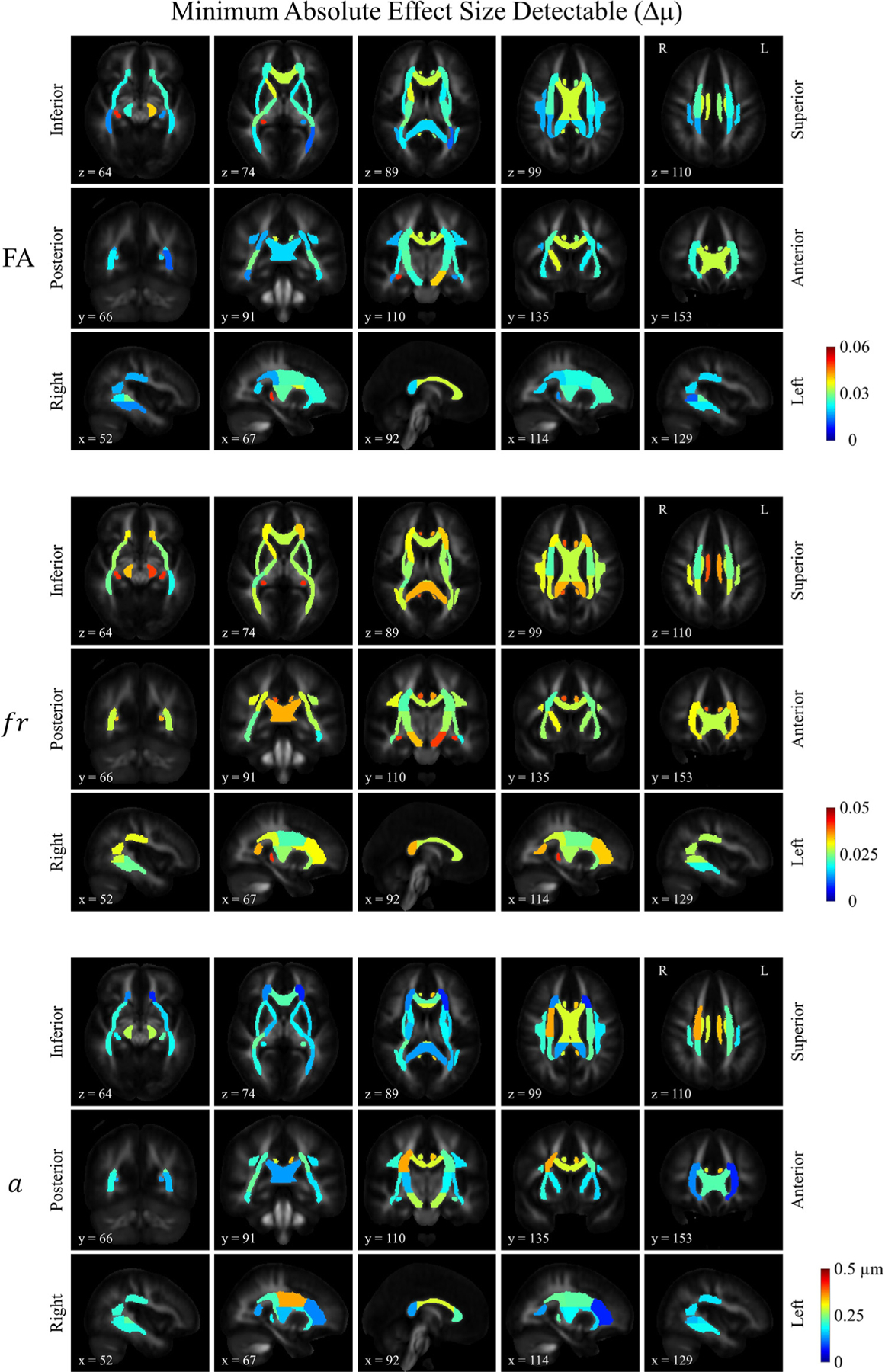
Distribution of the estimated minimum absolute effect size detectable for FA, restricted volume fraction (f_r) and axon diameter index (a). The same slices were shown as in Figure 4a.

Fig. 4. c.

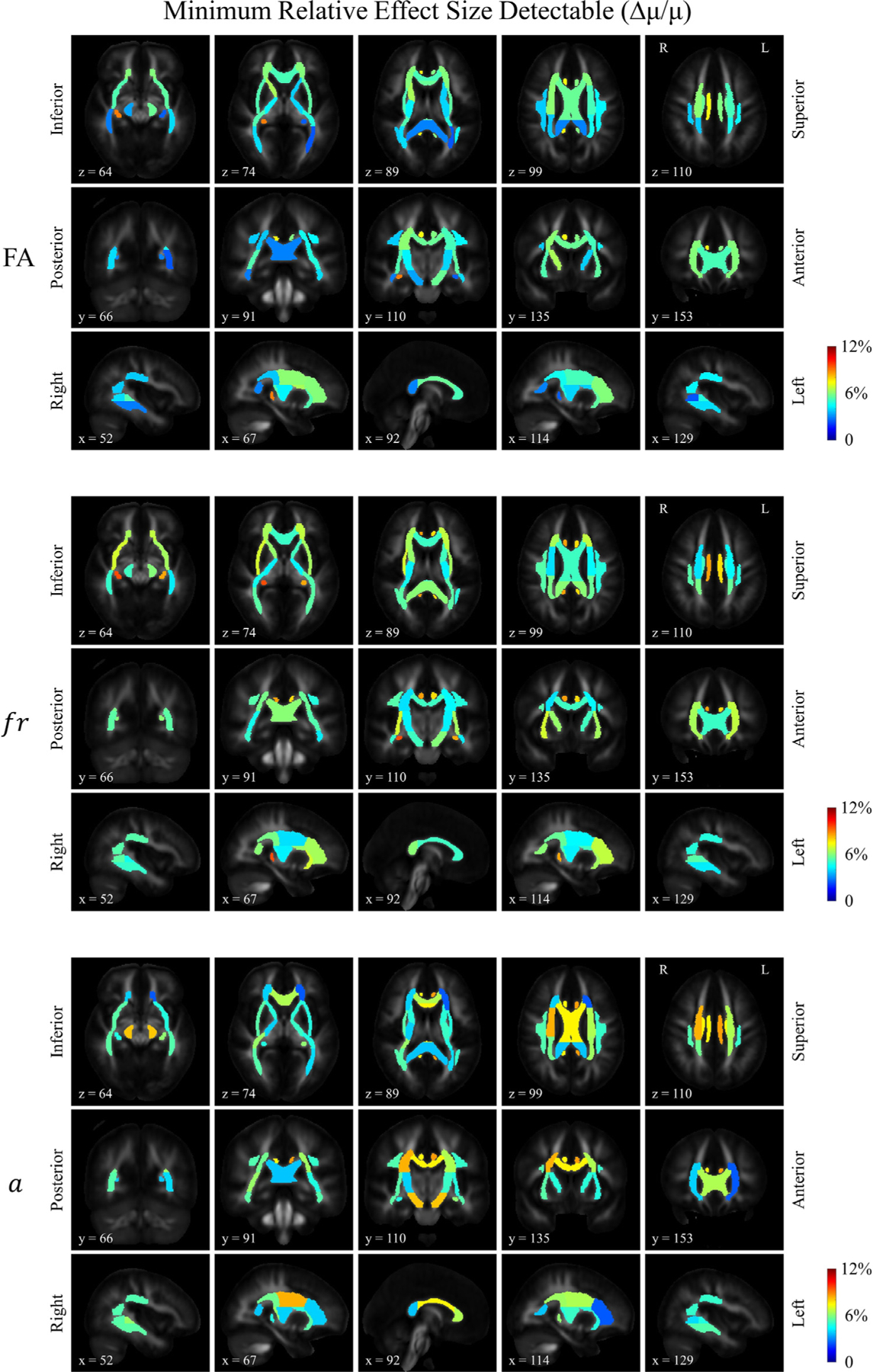
Distribution of the estimated minimum relative effect size detectable for FA, restricted volume fraction (f_r) and axon diameter index (a). The minimum detectable relative effect size was calculated by dividing the minimum absolute detectable effect sizes in Figure 4b by the group means in Figure 4a.

The relative effect size shown in Fig. 4c is a composite score, consisting of the ratio between Δμ and μ (Δμ/ μ), which we present here to give a visual representation of the statistical power of different metrics on the same scale. When inspecting the maps of μ (Fig. 4a), Δμ (Fig. 4b), and Δμ/μ (Fig. 4c) alongside each other, the patterns revealed by the whole brain maps (e.g., variations between white matter segments across the whole brain) seemed to show a higher degree of similarity between the maps of Δμ and Δμ/μ as opposed to the map of μ, suggesting that the variations in relative effect size (Δμ/μ) are dominantly driven by variations in Δμ rather than the group average value (μ). The same results were also listed in numbers in Table S2 in the Supplementary Materials.

The numbers of participants required to ensure sufficient power to detect a difference between groups in FA, restricted volume fraction, and diameter index were also calculated and are shown in Fig. 5. As an example, for a given effect size of 10%, the bar plot in Fig. 5 summarizes the projected number of participants needed to observe a meaningful difference between groups for different white matter segments. Results for smaller effect size (5%) are shown in the Supplementary Materials (Figure S3).

Fig. 5.

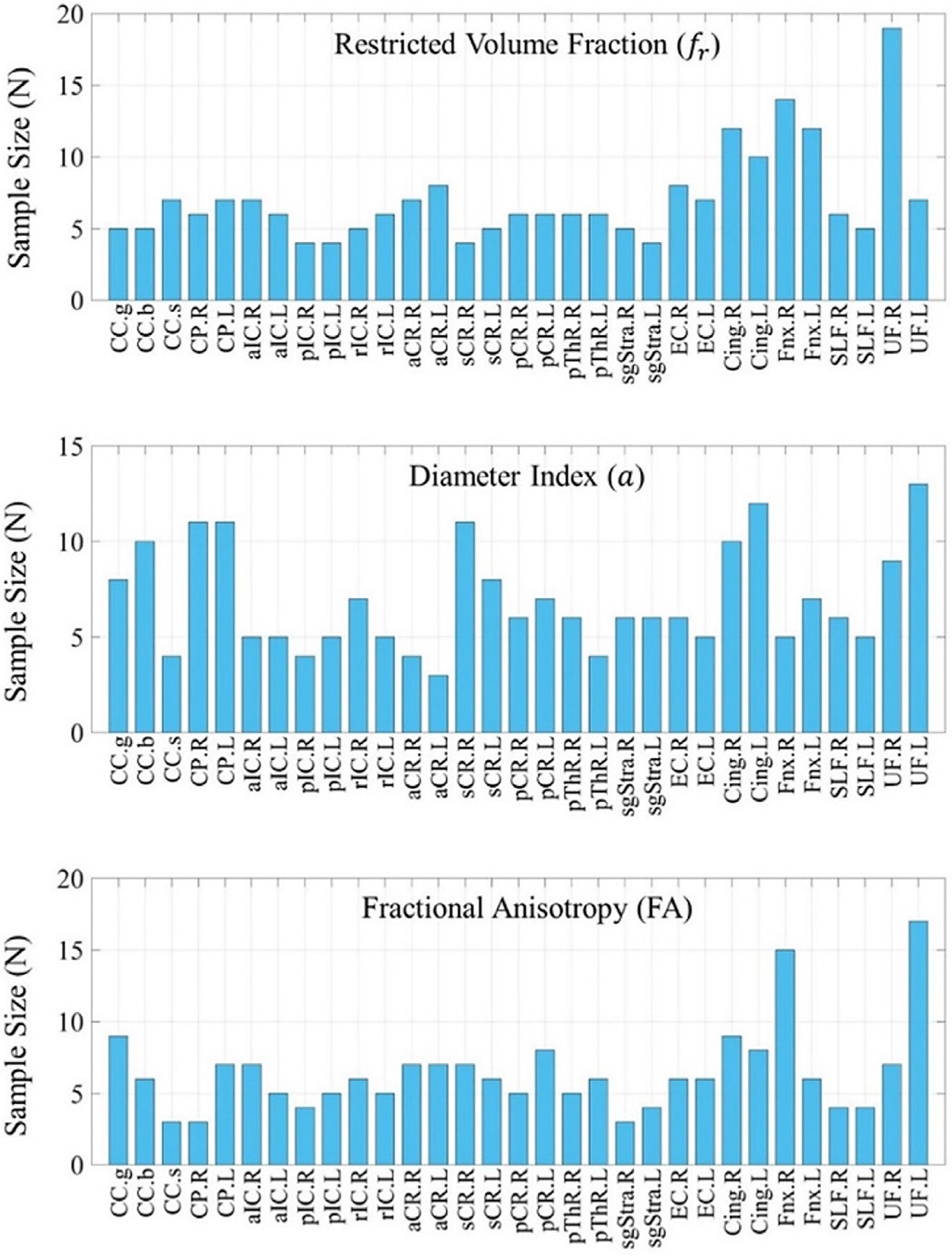
Projected number of participants needed to observe a meaningful difference between groups for different regions in the cerebral white matter. The calculation was based on the group mean and standard deviation of a cohort of 15 healthy adults, estimated to reach a significance level of α = 0.05 for a 10% effect size with a statistical power of 0.8.

Abbreviations: CC.g: genu of Corpus Callosum, CC.b: body of Corpus Callosum, CC.s: splenium of Corpus Callosum, CP.R: Cerebral Peduncle R, CP.L: Cerebral Peduncle L, aIC.R: anterior limb of Internal Capsule R, aIC.L: anterior limb of Internal Capsule L, pIC.R: posterior limb of Internal Capsule R, pIC.L: posterior limb of Internal Capsule L, rIC.R: retrolenticular part of Internal Capsule R, rIC.L: retrolenticular part of Internal Capsule L, aCR.R: anterior Corona Radiata R, aCR.L: anterior Corona Radiata L, sCR.R: superior Corona Radiata R, sCR.L: superior Corona Radiata L, pCR.R: posterior Corona Radiata R, pCR.L: posterior Corona Radiata L, pThR.R: posterior Thalamic Radiation R, pThR.L: posterior Thalamic Radiation L, sgStra.R: sagittal Stratum R, sgStra.L: sagittal Stratum L, EC.R: External Capsule R, EC.L: External Capsule L, Cing.R: Cingulum (cingulate gyrus) R, Cing.L: Cingulum (cingulate gyrus) L, Fnx.R: Fornix (cres) / stria terminalis R, Fnx.L: Fornix (cres) / stria terminalis L, SLF.R: Superior Longitudinal Fasciculus R, SLF.L: Superior Longitudinal Fasciculus L, UF.R: Uncinate Fasciculus R, UF.L: Uncinate Fasciculus L.

4. Discussion

In this work, we applied the previously developed SMT-based axon diameter mapping method to scan-rescan experimental data acquired in seven healthy subjects on the Connectom scanner. We then performed statistical power analyses with data acquired using the same protocol in 15 healthy volunteers to determine the minimum effect size and project the number of participants that would be needed to observe a meaningful difference between groups in different cerebral white matter regions-of-interest throughout the whole brain. Our findings provide valuable data that will inform the experimental design and interpretation of results in group studies of high gradient diffusion MRI measures, taking into account the intra-scan variability represented in our scan-rescan cohort alongside measures of variation in FA, restricted volume fraction and axon diameter index in a larger group of healthy adults. Our results reveal a high degree of repeatability in the restricted volume fraction estimates, and advocate for a certain degree of spatial averaging such as ROI- or tract-based averaging for robust diameter index measurements.

Axon diameter mapping in the living human brain has attracted great interest in the last decade, and the growing evidence that these measures are reliable within and between subjects, and even between sites (Fan et al., 2020; Huang et al., 2020; Veraart et al., 2020; Veraart et al., 2021) lends promise to the broader use of these methods for studying changes in brain structure across the lifespan and in pathology. Our results suggest that measures of relative axonal size obtained with diffusion MRI in vivo are repeatable. Our findings are in agreement with those of (Veraart et al., 2021), in which a different analysis method was applied to data acquired on two separate Connectom scanners and yielded consistent results in terms of both estimated values of axon diameter index and test-retest repeatability. We anticipate that the results of this work will be helpful for projecting sample sizes based on the minimum detectable effect size and informing the design of future group studies using similar methods. We acknowledge that the current study only examines the statistical implications of scan-rescan repeatability, i.e., sample size and effect size estimation, assuming a pre-fixed imaging protocol such as the one used here, and there is potential to shorten the imaging protocol and reduce the acquisition time further through a critical assessment of the impact of varying b- or q-values on the precision of axon diameter index estimation. Nevertheless, as a first step to placing our results in the context of existing, albeit limited, axon diameter mapping studies in the living human brain, we present a review of axon diameter index values reported in the literature from in vivo human diffusion MRI studies (Table 2) of such studies, which indicate that the anticipated effect size for axon diameter indices in different white matter regions (e.g., genu, body and splenium of the corpus callosum and forceps minor versus forceps major) and in different populations (e.g., multiple sclerosis and aging) is on the order of 10% or higher. For a 10% effect size, the results of our current power analyses indicate that most white matter regions require less than 15 people to observe a measurable difference between groups (Fig. 5), which is an encouraging finding. The sample size calculation accounts not only for scan-rescan robustness but is also inclusive of inter-subject variation.

Table 2.

Axon diameter index values reported in the literature from in vivo human diffusion MRI studies

Condition	Demographics	Regions of Interest	Effect Size (Δμ/ μ)	References
MS	6 patients (30.7 ± 9.0 y, 2 F)	Corpus Callosum (lesion vs. NAWM)	Genu: 30.4% Body: 13.0% Splenium: 29.3%	(Huang et al., 2016)
MS	9 patients (27–59 y, 6 F) 6 HC (22–53 y, 4 F)	Whole brain tissue (MS vs. HC)	12.81 %	(De Santis et al., 2019)
MS	23 HC (40.2 ± 11.9 y, 14 F) 7 Progressive MS (48.1 ± 12.8 y, 5 F) 30 MS in total (43.9 ± 11.2 y, 24 F)	Corpus Callosum	Lesion vs. NAWM: 20.7% NAWM in progress MS vs. HC: 11.7% NAWM in total MS vs. HC: 5.6%	(Huang et al., 2019)
Healthy	9 HC (29 ± 5 y)	Corpus Callosum	0.5–1.1 μm spanning from anterior to posterior tips of mid-sagittal corpus callosum (range/ μ≈ 71.2%)	(De Santis et al., 2016)
Healthy	9 HC (23–66 y, 9 M)	Corpus Callosum	3.1–4.6 μm between five segments of the corpus callosum projecting to various cortical regions (range/ μ≈ 38.9%)	(Yu et al., 2017)
Healthy	36 HC (22–72 y, 23 F)	Corpus Callosum	~4.5–4.9 μm spanning from 20–72 years old (range/ μ≈ 8.9%)	(Fan et al., 2019)
Healthy	4 HC (22–45 y, 1 F)	Corpus Callosum Cerebral WM	5.7–6.5 μm spanning from anterior to posterior tips of mid-sagittal corpus callosum (range/ μ≈ 12.5%) 5.7–6.2 μm between 6 major cerebral white matter tracts (range/ μ≈ 8.2%)	(Veraart et al., 2020)
Healthy	6 HC (29 ± 12 y, 6 F)	Cerebral WM	CST vs. Forceps Major: ~20% Forceps Major vs. Forceps Minor: ~12%	(Fan et al., 2020)

Abbreviations: MS: Multiple Sclerosis, HC: Healthy Control, y: years old, F: Female, M: Male, NAWM: Normal Appearing White Matter, CST: Corticospinal Tract

A major strength of this work is the presentation of results for both intra- and inter-subject variability of diffusion MRI measures obtained with high gradient strengths. To our knowledge, this is the largest study of scan-rescan repeatability of axon diameter estimates in the human brain using high-gradient strength diffusion MRI data reported to date. Our findings are in line with previous smaller-scale studies of scan-rescan repeatability of axon diameter estimation using ActiveAx in the human and Vervet monkey brains (Alexander et al., 2010; Dyrby et al., 2013), in which broad trends in axon diameter index across the corpus callosum were shown to be quite reproducible, although individual voxel-wise estimates were shown to have greater variability. Of note, many previous studies have assessed the reproducibility of FA measures in the healthy population (Besseling et al., 2012; Boekel et al., 2017; Grech-Sollars et al., 2015; Koller et al., 2021; Lin et al., 2015; Marenco et al., 2006), with reported ICC scores that fall within a range of ~0.7 to 0.98. Our data also yielded ICC scores in the same range for FA, allowing us to compare our results to the existing literature and supporting the consistency of our data and analyses with prior studies.

It is important to note that the scan-rescan reproducibility of axon diameter estimation reflects the precision of such measurements and does not guarantee that such estimates will match histology-derived measures. The MR-effective axon diameter estimated by diffusion MRI is an apparent value that is more heavily weighted by the larger axons in the voxel (Alexander et al., 2010; Burcaw et al., 2015). The axon diameters estimated by diffusion MRI are thus larger compared to histology-derived values. However, previous studies (Fan et al., 2020; Huang et al., 2020; Veraart et al., 2020; Veraart et al., 2021) have shown that the MR-effective axon diameter index calculated from histological data largely fall within the range estimated by diffusion MRI. Moreover, these distinct yet complementary approaches converge upon strikingly similar estimates and patterns of apparent axon diameter in whole brain white matter, which supports the consistency of the overall approach in extracting reliable diameter estimates in the living human brain.

Given the scarcity of high-gradient diffusion MRI data and limited availability of high-gradient human MRI systems, this work will be accompanied by a public release of all the data that was used to perform the reported analyses and power calculations. This data can be used practically to project sample sizes and potentially design studies on white matter development, aging and pathologic alterations using high-gradient diffusion MRI measures. In comparison to approaches that focus exclusively on the intra-axonal component of the diffusion MRI signal (Veraart et al., 2020; Veraart et al., 2021), our data was acquired using a comprehensive, multi-diffusion time, multi-gradient strength protocol to enable estimation of both restricted volume fraction and axon diameter index. This acquisition retains the capability of exploring the time-dependence of the diffusion MRI signal and should thus be amenable to a wide range of analyses. At the same time, our acquisition protocol has been successfully implemented in at least 40 healthy individuals and patients with MS, demonstrating the ability to acquire 55 min of dedicated high-gradient diffusion MRI data in the whole brain successfully within reasonable scan times that are tolerated by the majority of healthy individuals and patients with chronic neurologic disorders such as multiple sclerosis. Building on our success in acquiring such data, we seek to make this valuable dataset more widely available to those who do not have convenient access to MRI scanners equipped with 300 mT/m gradient strengths and have thus deliberately sought to recruit adult subjects across the lifespan and of both sexes to make the data more informative for future group studies.

The measurement of axon diameter in vivo relies on sensitizing the diffusion MRI measurement to micron-sized axons, which is difficult if not impossible to achieve using gradient strengths available on conventional scanners. Advances in gradient technology over the past decade have generated significant interest in tissue microstructural imaging using diffusion MRI, and we anticipate that the increasing availability of high-gradient systems will increase the relevance and translational potential of our findings to clinical and research scanners. In addition to the Connectom MRI scanner manufactured by Siemens, other scanner vendors have developed highly efficient gradient coils for clinical use. For example, the MAGNUS gradient developed by General Electric achieves 200 mT/m maximum gradient strength and 500 T/m/s slew rate and will be used for exploring tissue microstructure in patients undergoing clinical 3T MRI (Foo et al., 2020). The higher gradient strengths available on preclinical systems allow the straightforward application of our findings to axon diameter mapping on small-bore systems, as the estimated axon diameter indices should approach the actual values of axon diameters measured on electron microscopy, within the limitations of the pulsed gradient spin echo experimental design and acquisition protocol (Dyrby et al., 2013; Sepehrband et al., 2016).

That being said, an accurate and reliable estimation of axon diameter in vivo is challenging. The measurements are limited by the low SNR of the diffusion MRI measurement when acquired at high b-values, even with dedicated high-gradient scanners (Huang et al., 2020; Veraart et al., 2020). It is a common strategy to ameliorate SNR losses by spatial averaging, which motivated our assessment of the tract-wise ROI average repeatability between the scan and rescan sessions. The correlation coefficient (i.e., precision) and absolute errors (i.e., accuracy) (Duval et al., 2018) on the ROI level were remarkably improved in axon diameter index compared to f_r and FA (Fig. 2 and Fig. 3). Our results advocate for applying spatial averaging to boost the SNR and obtain more reliable measurements, as evidenced by the stronger correlation of tract-wise ROI-averaged measures of axon diameter (r = 0.72) and smaller absolute error ~0.18 μm, lending confidence to axon diameter mapping as a tool for probing white matter microstructure in the living human brain. The concept of spatial averaging along the tract or within white matter segments is supported by other recently proposed approaches (Koller et al., 2021) such as the “tractometry”-based approach (Bells et al., 2011; Chamberland et al., 2019), which leverage the robustness of the reported metrics along tracts without sacrificing anatomical specificity. The recent work by (Veraart et al., 2021) also examined the variability of estimates along major white matter tracts and found that averaging along the tracts improved the repeatability of measurements of effective radii, suggesting that tract-based averaging is a viable strategy to ameliorate challenges posed by low SNR measurements at high b-values.

The definition of the ICC is based on the discrepancies between intra-subject and inter-subject variations. In addition to the scan-rescan variability, any genuine biological variations throughout the selected ROI also contribute to the intra-subject variation. Thus, it is logical to calculate ICC in an ROI that is anatomically uniform, rather than throughout the whole brain. In our study, the ICC’s were calculated per white matter segment. Given the observed variation along tracts, for example, in longer tracts such as the corticospinal tract, it is worthwhile to consider different segments of such tracts separately to preserve the homogeneity within the ROI. The along-tract variation could introduce intra-subject variation leading to underestimation of the ICC. On the other hand, smaller tracts are more susceptible to the registration errors. Also, the number of voxels within the ROI need to be sufficient to guarantee that the calculation of standard deviation is meaningful. Thus, the definition of ROI should be wisely chosen depending on the research question, and the related effects should be taken into consideration when interpreting the results. Our results show that the relaxation-weighted restricted volume fraction f_r has an ICC that is slightly higher than the ICC of FA, suggesting that f_r offers at least comparable sensitivity to differences between individuals and robustness in identifying group differences of interest as more commonly used diffusion metrics derived from DTI. It is worth noting that FA is sensitive to fiber orientation distribution in contrast to the SMT based methods, and thus the inter-subject variation ${s_{inter}}^2$ for FA reflects inter-subject differences in fiber orientation distribution in the same anatomical region, in addition to inter-subject differences in microscopic anisotropy. See (Andersen et al., 2020) for an example of how the orientation distribution-independent anisotropy measures can improve group comparisons in neurobiological studies. Despite their limitations in the presence of crossing fibers, DTI-derived metrics have been widely used and accepted as providing stable and highly repeatable measures. The finding that f_r derived from the SMT-based microstructural imaging methods can achieve comparable or even slightly superior performance to FA lends great promise for the exploration of such measures in future studies.

Limitations of the current study design include the lack of systematic examinations into possible experimental factors that could influence the scan-rescan repeatability, such as temperature and head positioning. We chose to conduct the study in a pragmatic manner to mirror what would be done for a typical clinical study, applying reasonable experimental procedures (e.g., applying head/neck cushions and padding around the ears to immobilize the head and providing lumbar support for comfort) to mitigate against motion. Our results demonstrated good scan-rescan repeatability using these measures. Care was also taken in the processing/analysis stream to mitigate against bias that could be introduced therein, such as the strategy of registering scan-rescan images to the halfway transform space and calculating the statistics (mean and standard deviation values) of scalar maps in their native space instead of the interpolated up-sampled counterparts in the atlas space. We acknowledge that the relative effect size could still be affected by registration errors, especially for smaller structures such as the fornix and uncinate fasciculus. Also, the template approach to defining white matter ROIs minimizes variability between individuals but may be susceptibility to minor registration errors. Future work should examine data-driven approaches to defining white matter ROIs and their effect on the scan-rescan repeatability of high-gradient diffusion MRI measures.

The current work focuses on the scan-rescan repeatability of the previously published spherical mean approach to axon diameter index mapping (Fan et al., 2020), in which diffusion in the intra-axonal space was modeled as occurring in impermeable cylinders. The advantage of using a simple geometrical model of cylindrical axons lies in the closed-form analytical expression for the spherically averaged diffusion MRI signal within cylindrical compartments (Callaghan et al., 1979; Panagiotaki et al., 2012; Yablonskiy et al., 2002). However, we acknowledge that modeling axons as impermeable cylinders is far from realistic given the extensive morphological variations known to occur in white matter (Andersson et al., 2020; Lee et al., 2020a; Lee et al., 2020b), including axonal caliber variations and undulations, which contribute to time-dependent diffusion along the axonal axis and can result in overestimation of the axon diameter (Andersson et al., 2020; Lee et al., 2020a; Lee et al., 2020b). Nevertheless, the effects of axonal dispersion and undulation can be greatly mitigated by spherical averaging (Lee et al., 2020a; Veraart et al., 2020), as adopted in the SMT approach used here.

5. Conclusions

Our study revealed a high degree of repeatability in restricted volume fraction estimates from high-gradient diffusion MRI data, and advocate for a degree of spatial averaging such as ROI- or tract-based averaging to derive robust axon diameter index measurements. Along with statistical power analyses that account for inter-subject variation, our study provides confidence in axon diameter index as a potential imaging biomarker for group studies of white matter microstructure across the lifespan and in disease populations.