Abstract
This study investigates the impact of COVID‐19 pandemic on stock returns, conditional volatility, conditional skewness and bad state probability. This study utilizes an asymmetric exponential generalized autoregressive conditional heteroscedasticity model to capture the asymmetric effect of positive and negative shocks (news) on conditional volatility. Using a sample consisting of international stock market indices in Brazil, China, Italy, India, Germany, Russia, Spain, United Kingdom, and United States, over the period from January 1, 2013 to December 31, 2020, we find unprecedented increases in conditional volatilities and bad state probabilities across all the markets. However, this impact is not symmetric across markets. Furthermore, we find that the negative affect of deaths is more pronounced, compared to the positive impact of recovered cases.
Keywords: bad state probability, COVID‐19, pandemic, stock market, volatility
1. INTRODUCTION
In late 2019, a new virus called “COVID 19” had started to spread, causing “severe pneumonia.” Thus, this virus led to an extraordinary rate of death between the elderly and the most vulnerable in society, leading to an international social distancing and home isolation of more than 2 billion people worldwide, with tremendous social, political and economic consequences (Goodell, 2020; Sharif et al., 2020). Moreover, one of the commercial effects of this virus was an unexpected disruptions in the flow of goods and services, commodity prices and financial conditions, creating an economic disasters across many countries because of its impact on the production and supply chains in China, the United States, Europe, and Japan, as well as the most important economies in the world (IMF, 2020).
Significant changes in the financial structures of countries was caused by the “domino effect” created by retrenched investors in many countries (Kenourgios et al., 2011). This contagion effect in the global market led to unprecedented disturbing effects in different economies that were only comparable to the depression of 1920 (Corbet et al., 2020). Moreover, all the countries face a great health crisis, severe external demand shock, dramatic shrinking in global financial conditions, and a plunge in the commodity prices that will have a severe effect on economic activity in commodity exporters (IMF, 2020). In addition, the outbreak of COVID‐19 has been declared as a global pandemic on June, 2020 by the World Health Organization (WHO), which shaken the global financial markets. As of June 16, 2020, there are 9,653,048 confirmed cases and 491,128 deaths across the world for 216 Countries, areas or territories with cases, including emerging and developed countries (WHO, 2020).
The objective of this research is to analyze the influence of COVID‐19 on the stock price behavior of equity market indices of selected nine countries. We selected the countries that had the largest confirmed cases of COVID‐19 at the end of March and June 2020. Accordingly, the final sample included United States, Italy, Spain, United Kingdom, Germany, China, Brazil, Russia, and India. We also compare how the stock price behavior differs across the periods pre‐ and during the COVID‐19 (to examine the initial effect of the shock of COVID‐19 on the markets) and then between the first and second quarters during the COVID‐19 period (to explore whether the markets are rebounded after the shock is being assessed and absorbed). Our analysis of stock market behavior is based on examining stock returns, conditional volatility, conditional skewness, and bad state probability, measured using a widely applied econometric model, an asymmetric exponential generalized autoregressive conditional heteroscedasticity (EGARCH) model.
The advantage of this model is to allow for capturing the well‐documented asymmetric effect of positive and negative shocks on conditional volatility as positive shocks may have less impact on volatility than the negative shocks (Alberg et al., 2008; Hentschel, 1995; Nelson, 1991). It is commonly known fact that volatility clustering produces heavier tails, as documented by Engle's (1982) seminal paper on autoregressive conditional heteroscedasticity (ARCH) model and its generalization by Bollerslev's (1986) paper on generalized autoregressive conditional heteroscedasticity (GARCH) model, and others (e.g., Tsay, 2010). However, since normal GARCH model links directly the kurtosis to the variance, it is unable to well capture the excess kurtosis that exists in financial returns and produces low probability of extreme realizations (extreme returns) than observed in the data. In addition, inclusion of conditional skewness in the model captures the asymmetry, and also impacts the persistence in conditional variance as highlighted by Harvey and Siddique (1999). To overcome these drawbacks when using the normal GARCH model, our EGARCH model adds two extra parameters in the distribution of returns, namely the skewness and kurtosis. Moreover, this model is augmented to capture the impact of the number of death and recovered cases to distingue between the effects of negative information (deaths) verses positive information (recovered cases). Moreover, as any other major crisis, the COVID‐19 pandemic was associated with an adverse impact on the financial markets, caused by panic, uncertainty, negative sentiment and investor pessimism during the pandemic. Hence, it was crucial for us to estimate bad state probabilities (i.e., the probability that stock market returns might fall below the expected returns) to quantify the likelihood of bad events, and assess the probability of markets downturns in bad times of high uncertainty.
Therefore, this paper contributes to the literature in several ways. First, this study extends the evolving literature on the impact of COVID‐19 on stock market behavior. Although several studies have investigated how financial markets have been affected during COVID‐19 period (Baker et al., 2020; Corbet et al., 2020), to the best of our knowledge, none have examined the impact of COVID‐19 on global stock markets, using an asymmetric exponential EGARCH model with an emphasis on conditional volatility, conditional skewness and bad state probability. This allows for not only capturing the dynamic behavior of conditional variance but also taking into account the asymmetric impact of negative versus positive return innovations. Second, this study aims to estimate the impact of COVID‐19 recovered cases and deaths on the conditional mean, conditional volatility and conditional skewness of the returns of equity market indices. By doing that, we distinguish between the impact of positive and negative information on stock market behavior to examine the asymmetric characteristics of stock market behavior. Third, we demonstrate how the COVID‐19 pandemic can amplify bad state probability, which is important in a period when financial markets experience extreme uncertainty and investors' behavior is driven by their fear and panic. Therefore, this study adds not only to the literature on COVID‐19's effect on stock markets but also to the overall literature on financial market crashes and crises. Fourth, our long analysis period (January 1, 2013 to December 31, 2020) enables us to compare the stock price behavior across not only the periods pre‐ and during the COVID‐19 pandemic but also the first and second quarters during the COVID‐19 period. This allows for better understanding of how stock markets have initially reacted to the shock of COVID‐19, compared to how they are rebounded after the shock is being absorbed. Moreover, our findings provide important implications for investors, practitioners and policy makers. For traders and investors seeking to invest in international stock markets, the results indicate which markets are most correlated and risky, which have strong consequences for portfolio optimization and implementation of profitable trading strategies. For practitioners, the findings allow to get insights into the dynamic behavior of stock markets in the countries that are heavily affected by the pandemic in order to examine the best investment options. For policy makers, the findings confirm the critical role that the political leadership and governments can play, via mitigating the spread of pessimistic views and negative feelings amid citizens, in conveying positive signals to the investors and thereby decreasing market uncertainty.
2. LITERATURE REVIEW
Following such a huge worldwide crisis, the literature on the economic effects of COVID‐19 has emerged quickly in recent months. For example, Ramelli and Wagner (2020) and Zaremba et al. (2020), among other, have investigated the adverse impact of COVID 19 on stock returns and volatility. Other studies have examined how the outbreak of COVID‐19 affected the financial contagion in financial markets. For example, Akhtaruzzaman et al. (2020) examine how the COVID‐19 period has affected the financial contagion between China and G7 countries and show that stocks listed across China and G7 countries have been associated with a significant increase in conditional correlations between their stock returns. Consistently, Just and Echaust (2020) show close dependence between S&P 500 index returns and both implied volatility and implied correlation during the COVID‐19 period.
Other studies focus on exploring how COVID‐19 has affected commodity markets. Gharib et al. (2021) examine the economic impact of COVID‐19 on the causal relationship between crude oil and gold prices and find a bilateral contagion effect of bubbles in oil and gold markets during the recent COVID‐19 outbreak. Sharif et al. (2020) analyze the connectedness between COVID‐19, oil price volatility shock, the stock market, geopolitical risk and economic policy uncertainty in the United States. Their finding show that the effect of the COVID‐19 on the geopolitical risk substantially higher than on the US economic uncertainty. In related context, Conlon and McGee (2020) examine the price behavior of Bitcoin during the COVID‐19 bear market and provide empirical evidence casting doubt on the ability of Bitcoin to act as a safe‐haven asset. While other studies focus on assessing the role of governmental policies in mitigating the negative impact of the pandemic on financial markets. For instance, Narayan et al. (2020) examine the effect of government responses of G7 countries to the coronavirus pandemic (COVID‐19) on stock market returns, showing that lockdowns, travel bans, and economic stimulus packages have exerted a positive effect on the G7 stock markets. Ma et al. (2020) reveal that countries with more aggressive government fiscal policy exhibit a superior ability to decrease the adverse impact of the pandemic on GDP growth, while emerging market are most likely to experience superior negative influences from COVID‐19. Table 1 outlines a summary of related literature to provide more insights into the research approaches adopted by the studies depicted in Table 1. In‐depth analysis has been conducted to categorize these studies in Table 1.
TABLE 1.
Summary of related literature
| Study | Sample | Methodology | Main results |
|---|---|---|---|
| 1. Albulescu (2020) | US stock market from March 11, 2020 to May 15, 2020. | OLS regression, stepwise procedure | The new confirmed cases are associated with higher financial volatility. |
| 2. Baek et al. (2020) | US stock market from January 2, 2020 to April 30, 2020. | Two‐regime Markov switching model | The volatility is more sensitive to the news of COVID‐19 more than the economic indicators. Moreover, the negative COVID‐19 news (number of deaths) is twice as impactful as positive COVID‐19 news (recovered cases) suggesting a negativity bias. |
| 3. Baig et al. (2021) | US stock market from January 13, 2020 to April 17, 2020 | GARCH (1,1) model | The confirmed cases and deaths during COVID‐19 are associated with a significant upturn in volatility and market illiquidity. |
| 4. Bissoondoyal‐Bheenick et al. (2020) | G20 countries stock market from January 22, 2020 to May 20, 2020 | Bivariate fractionally integrated vector autoregressive model | The connectedness between stock return and volatility has increased during the COVID‐19 pandemic. |
| 5. Chaudhary et al. (2020) | United States, China, Japan, Germany, India, United Kingdom, France, Italy, Brazil, and Canada from January 1, 2019 to June 30, 2020 | Unit root test; the ARCH effect test; and GARCH (1,1) model | The COVID‐19 period is associated with negative mean returns for all market indices and higher volatility. |
| 6. Choi (2020) | US stock market from January 2008 to May 2020. | Wavelet coherence analysis | The economic policy uncertainty during COVID‐19 affects the sector volatility more than the global financial crisis for all sectors. |
| 7. Liu et al. (2020) | Abu Dhabi, France, Germany, United States, United Kingdom, Malaysia, Indonesia, Korea, Russia, Japan, Australia, Canada, Singapore, Taiwan, Asia ex Japan, Thailand, Hong Kong, Shanghai, Shenzhen, Italy, and India from February, 21, 2019 to March, 18, 2020. | Market model; and OLS regression | The new confirmed cases during COVID‐19 have a negative effect on stock abnormal returns. Countries in Asia, compared to other countries, experience more negative abnormal returns. |
| 8. He, Sun, et al. (2020) | China stock market from June 3, 2019, to March 13, 2020. | Average adjusted return rate model; the market index adjusted return rate model; and the market model | COVID‐19 has a negative effect on some industries; mining, electricity and heating, transportation, and environment. In contrast, other industries, for example, information technology, manufacturing, education, and health‐care are more resilient to the pandemic. |
| 9. He, Liu, et al. (2020) | Republic of China, Italy, South Korea, France, Spain, Germany, Japan, and the US stock market. | Conventional t tests; and nonparametric Mann–Whitney tests. | COVID‐19 has a negative—but short term—effect on stock markets of affected countries. |
| 10. Jelilov et al. (2020) | Nigeria stock market from February 27, 2020 to April 30, 2020. | Standard GARCH and the GJR‐GARCH model | COVID‐19 is associated with higher volatility and negative market returns. |
| 11. Kotishwar (2020) | United States, Spain, France, Italy, China, and India from March 11, 2020 to April, 2020 | VECM and CAAR model | All the selected indices have positively responded more in the post period after declaring the COVID‐19 as pandemic on March 11, 2020, compared with the pre‐period. |
| 12. Lyocsa and Molnár (2020) | US stock market from November 2019 and ends in May 2020, | Nonlinear smooth transition regime switching model | Market volatility tends to motivate the returns autocorrelation of during times of great volatility. |
| 13. Just and Echaust (2020) | US stock market from June 3, 2019 to June 12, 2020. | Two‐regime Markov switching model | There is a close dependence between returns and both implied correlation and implied volatility but not with liquidity. |
| 14. Mazur et al. (2020) | US stock market for the month of March 2020. | OLS regression | There are high positive stock returns in some sectors; healthcare natural gas, software stocks, and food. However, it falls dramatically in other sectors; petroleum, real estate, entertainment, and hospitality. Furthermore, lose‐making stocks reveal a great volatility that is negatively correlated with stock returns. |
| 15. Narayan et al. (2020) | G7 countries stock market, from July 1, 2019 to April 16, 2020. | Time‐series regression model | All the government polices during COVID 19 had a positive effect on the stock markets of the G7 countries. |
| 16. Sharif et al. (2020) | US stock market from January 21, 2020 to March 30, 2020 | Continuous wavelet transform, the wavelet coherence and the wavelet‐based granger causality tests. | COVID‐19 outbreak exhibits a greater effect on the US geopolitical risk and economic uncertainty more than on the US stock market. |
| 17. Waheed et al. (2020) | Pakistani stock market from February 26, 2020 to April 17, 2020. | Auto regressive integrated moving average; and exponential smoothing (ES) approach | COVID‐19 has a positive effect on KSE‐100 index that has a positive increment in stock returns. |
| 18. Yousef (2020) | G7 stock market indices for the period 2000–2020. | GARCH; and GJR‐GARCH models | COVID‐19 is associated with higher volatility in the G7 markets. |
| 19. Zaremba et al. (2020) | Argentina, Australia, Austria, Bahrain, Belgium, Brazil, Bulgaria, Canada, Chile, China, Colombia Croatia, Cyprus, Czechia, Denmark, Egypt, and Estonia from January 1, 2020 to April 3, 2020. | Capital asset pricing model (CAPM); three‐factor model (FF); and four‐factor model (CAR). | COVID‐19 is associated with higher volatility |
| 20. Zhang et al. (2020) | United States, Italy, China Mainland, Spain, Germany, France, United Kingdom, Switzerland, Korea, South, Netherlands, Japan, and Singapore from February 7, 2020 to March 27, 2020. | Pairwise correlations | COVID‐19 is associated with higher volatility and systematic risk. |
The first category considers mainly samples from developed countries. These studies adopt different methodology and statistical models using time‐series regression model (e.g., Narayan et al., 2020); Two‐regime Markov switching model (e.g., Baek et al., 2020; Just & Echaust, 2020); ordinary least square (OLS) (e.g., Albulescu, 2020; Mazur et al., 2020); GARCH (1,1) model (e.g., Baig et al., 2021; Yousef, 2020); Wavelet coherence analysis (e.g., Choi, 2020); nonlinear smooth transition regime switching model (e.g., Lyocsa & Molnár, 2020) and the wavelet coherence and the wavelet‐based Granger causality tests (e.g., Sharif et al., 2020). On the other hand, the second category focus on samples from developing countries. The approaches used in these studies include: the average adjusted return rate model (e.g., He, Sun, et al., 2020); the market index adjusted return rate model and the market model (e.g., Jelilov et al., 2020); GARCH model (e.g., Waheed et al., 2020) and auto regressive integrated moving average and exponential smoothing.
While, in the third category, other studies provides empirical evidence based on both developed and developing markets. Those studies adopted various models, such as bivariate fractionally integrated vector autoregressive model (e.g., Bissoondoyal‐Bheenick et al., 2020); unit root test, the ARCH effect test, and the GARCH (1,1) model (e.g., Chaudhary et al., 2020); conventional t tests and nonparametric Mann–Whitney tests (e.g., He, Liu, et al., 2020); market model, and the OLS (e.g., Liu et al., 2020); pairwise correlations (e.g., Zhang et al., 2020); CAAR model (Kotishwar, 2020); and capital asset pricing model (CAPM), three‐factor model (FF), and four‐factor model (e.g., Zaremba et al., 2020).
3. METHODOLOGY
3.1. Data collection
In order to conduct this study, the selection of our sample covers both pre‐COVID‐19 period (January 1, 2013 to December 31, 2019) and during COVID‐19 period (January 1, 2020 to December 31, 2020). We take the starting date of COVID‐19 period as January 1, 2020, the next day when the first case of COVID‐19 was reported to the WHO. On the other hand, we choose the first date of pre‐COVID‐19 period as January 1, 2013, to avoid and exclude the effect of the two crisis which are the worldwide financial crisis between 2007 and 2009 and European sovereign debt crisis between 2010 and 2012. So, it can be said that the data started from January 1, 2013 to the December 31, 2020 which has been divided into pre COVID‐19 and during COVID‐19. Then, to explore how the markets initially reacted and got rebounded after the shock is being absorbed, we divide the first 6‐month period during COVID‐19 into two quarters to compare and examine the effect of COVID‐19 over time where quarter 1 covers the period (January 1, 2020 to March 31, 2020) and quarter 2 covers the period (April 1, 2020 to June 30, 2020).
To investigate the effect of COVID‐19 on the stock returns of the selected countries as a sample of this study. We have chosen the countries in our sample according to the following steps. First, we nominated the top 10 countries that have confirmed cases of COVID‐19 at the end of March 2020 (quarter 1) and at the end of June 2020 (quarter 2) as shown in Figure 1. Second, we selected the intersection (repeated) countries between the two groups (quarters) which are United States, Italy, Spain, United Kingdom, and Iran. We excluded Iran from our sample where we did not find any data of return index in the DataStream for this country. Third, we selected the unrepeated countries from the top highest five countries that have confirmed cases at the end of March and June 2020 (WHO, 2020). We found that Germany and China are the countries selected from group of March 2020 and Brazil, Russia and India are the countries selected from the group of June 2020. Finally, the total countries that should be included in our sample after excluding Iran are nine countries which are United States, Italy, Spain, United Kingdom, Germany, China, Brazil, Russia, and India.
FIGURE 1.
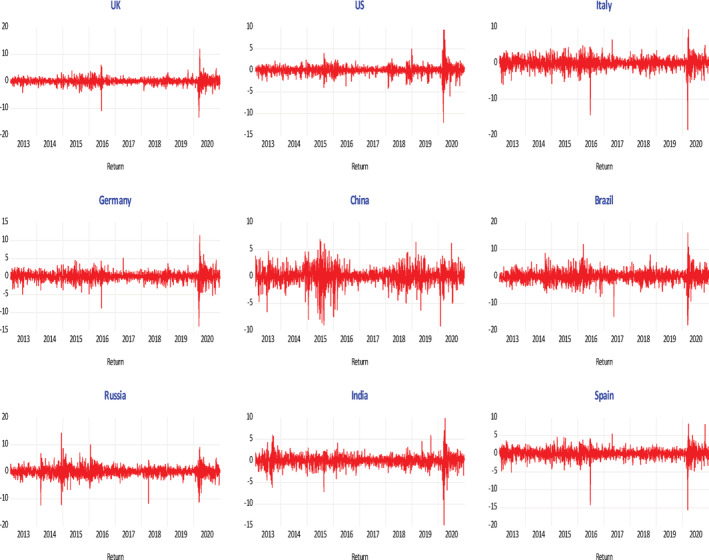
Time series plot of stock return from January 1, 2013, to December 31, 2020
We collected the data in a daily basis for the return indices, confirmed cases, death cases and recovered cases for the nine countries and the world. The data obtained from the DataStream and the WHO. Daily returns were computed from the return index: using log‐returns , where is return and are the return and the price index obtained from DataStream. More details on the list of stock indexes, and the number of confirmed cases, deaths and recovered cases per country is provided in Table B1.
3.2. Model specification
To model the marginal distribution of returns, we use the skewed t distribution of Hansen (1994). The density probability function of the rescaled skewed t distribution of Hansen has the following form:
| (1) |
here is the country return, is the conditional mode of the return,1 is its conditional variance, is the shape parameter (2 < < ), the parameter is the conditional skewness parameter that governs the asymmetry of the distribution (−1 < < 1) and
The function (.) is the Gamma function given by
The skewed t distribution reduces to the t distribution when the skewness parameter = 0. This distribution is used in financial econometrics by Patten (2018). The distribution is asymmetric to the left if −1 < < 0, and it is asymmetric to the right if 0 < <1.
We allow for time‐varying conditional means and variances of returns. The return equation is given by
Where
| (2) |
is world return, the total number of death due to COVID‐19 and is the total number of recovered individuals and, , , , and are constant parameters.
To capture the dynamic behavior of conditional variance and take into account the asymmetric impacts of negative versus positive return innovations, the conditional variance is modeled as an asymmetric EGARCH(1,1) of Nelson (1991) augmented by additional regressors and given by
| (3) |
The parameters , , and capture respectively the news effect, the volatility persistence and the leverage effect. While and capture the effect of the number of death and recovered cases on the volatility. If − < 0 and then bad news have higher effect on volatility than good news. This can be seen clearly by rewriting the variance equation as
| (4) |
Since < 0 and , bad news have higher effect on the volatility than good news . We use also a constant and time varying covariates to model skewness which results in time varying skewness. To constrain the conditional skewness between −1 and 1, we use the shifted logistic function and model the conditional skewness as
where , , , and are constant parameters capturing the skewness dynamics.
Proposition 1
The probability for the market to be in bad state is given by 2:
4. EMPIRICAL RESULTS
Table 2 the daily stock returns for the nine countries during the period of pre‐COVID‐19 that starts from January 1, 2013 to December 31, 2019 and the COVID‐19 period that starts from January 1, 2020 to December 31, 2020. The descriptive statistics show that the mean of stock returns for the period of pre‐COVID‐19 are positive for all countries in the sample except India that has a negative return as shown in Panel (A). The mean of United States refers to the highest positive stock return while Spain and United Kingdom returns experienced the lowest positive mean. On the other hand, during the period of COVID‐19, Panel (B) demonstrates that the United Kingdom, Brazil, Russia and Spain have, on average, negative returns, while the United States, Italy, Germany, China, and India have positive returns. As it can be also shown in Figure 1, the markets initially exhibit a sharp decline in 2020 before being rebounded for the remainder of the year.
TABLE 2.
Descriptive statistics of returns for pre and during COVID‐19
| Panel A: Descriptive statistics of returns (Pre COVID‐19) | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| United Kingdom | United States | Italy | Germany | China | Brazil | Russia | India | Spain | |
| Mean | 0.0059 | 0.0468 | 0.0192 | 0.0268 | 0.0314 | 0.0141 | 0.0315 | −0.0108 | 0.0057 |
| Median | 0.0355 | 0.0348 | 0.0347 | 0.0338 | 0.0000 | 0.0000 | 0.0069 | 0.0056 | 0.0284 |
| Maximum | 5.9245 | 4.9594 | 6.4805 | 5.0559 | 6.8463 | 14.2929 | 5.9577 | 12.3657 | 5.4454 |
| Minimum | −10.8713 | −4.0979 | −14.2922 | −8.7517 | −8.9720 | −12.3383 | −7.0767 | −6.6138 | −14.1669 |
| SD | 0.9691 | 0.7929 | 1.3780 | 1.0796 | 1.4745 | 1.6564 | 1.0859 | 1.0076 | 1.1884 |
| Skewness | −0.7968 | −0.4670 | −0.7167 | −0.4296 | −0.6992 | −0.1340 | −0.1838 | 0.7654 | −0.9843 |
| Kurtosis | 14.8623 | 6.7980 | 10.5345 | 6.8779 | 8.7818 | 13.0588 | 6.9780 | 18.8094 | 14.9519 |
| Panel B: Descriptive statistics of returns (During COVID‐19) | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| United Kingdom | United States | Italy | Germany | China | Brazil | Russia | India | Spain | |
| Mean | −0.0277 | 0.0787 | 0.0381 | 0.0704 | 0.1197 | −0.0385 | −0.0121 | 0.0663 | −0.0079 |
| Median | 0.0715 | 0.1791 | 0.1527 | 0.0999 | 0.0599 | 0.0482 | 0.0877 | 0.1758 | 0.0000 |
| Maximum | 11.8153 | 9.3828 | 9.3046 | 11.3622 | 6.1692 | 16.1127 | 9.0132 | 9.7535 | 8.1936 |
| Minimum | −13.2503 | −11.9841 | −18.3670 | −13.7633 | −9.1178 | −17.8490 | −11.2529 | −14.7715 | −15.5523 |
| SD | 2.0921 | 2.1352 | 2.2645 | 2.1562 | 1.5162 | 3.4942 | 2.3786 | 2.1748 | 2.1801 |
| Skewness | −0.5975 | −0.5526 | −2.2623 | −0.7685 | −0.9316 | −0.8835 | −0.7567 | −1.4416 | −1.2572 |
| Kurtosis | 12.7612 | 11.1900 | 21.3181 | 12.2151 | 9.2821 | 10.2674 | 7.6175 | 14.2676 | 13.7444 |
Note: This table reports descriptive statistics for daily stock returns. Panel A reports the results during the period per‐the COVID‐19 period (January 1, 2013 to December 31, 2019). Panel B reports the results during the COVID‐19 period (January 1, 2020 to December 31, 2020).
Next, we seek examine how the markets initially reacted and got rebounded after the shock is being absorbed. Therefore, we focus our analysis on the first 6 months that have been divided into two quarters to compare and examine the effect of COVID‐19 over time where quarter 1 covers the period (January 1, 2020 to March 31, 2020) and quarter 2 covers the period (April 1, 2020 to June 30, 2020). Table 3 depicts the returns during the period of COVID‐19 for the first two quarters of the year 2020. The mean of stock returns for all nine countries are negative for the quarter 1 (starts from January 1, 2020 to march 31, 2020) which indicates that all countries had shock in their stock markets resulted from the pandemic COVID‐19. Brazil, India, Russia and Spain are the highest countries that have been affected dramatically by the decrease in their stock returns. Finally, Panel (B) shows that all countries have been shifted their means of returns to be positive in the second quarter of the pandemic which indicates that these countries have taken actions and adopted some strategies to deal with the COVID‐19.
TABLE 3.
Descriptive statistics of returns for COVID‐19 (Quarter 1 and 2)
| Panel A: Descriptive statistics of returns (COVID‐19—Quarter 1) | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| United Kingdom | United States | Italy | Germany | China | Brazil | Russia | India | Spain | |
| Mean | −0.4920 | −0.2817 | −0.4676 | −0.4332 | −0.1689 | −0.5880 | −0.5501 | −0.5634 | −0.5116 |
| Median | −0.1075 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | −0.1963 | −0.1827 | −0.1686 | −0.1201 |
| Maximum | 11.8153 | 9.3828 | 9.3046 | 11.3622 | 3.7682 | 9.0132 | 6.9799 | 4.7954 | 8.1936 |
| Minimum | −13.2503 | −11.9841 | −18.3670 | −13.7633 | −9.1178 | −11.2529 | −14.7715 | −11.6703 | −15.5523 |
| SD | 3.0563 | 3.5030 | 3.3811 | 2.9335 | 2.0539 | 3.4945 | 3.2786 | 2.4860 | 3.0374 |
| Skewness | −0.3791 | −0.2062 | −2.2717 | −0.8181 | −1.3578 | −0.4817 | −1.4128 | −1.5467 | −1.7786 |
| Kurtosis | 10.1960 | 5.6172 | 15.3190 | 11.9562 | 7.2691 | 5.0898 | 8.1837 | 8.2286 | 11.8126 |
| Panel B: Descriptive statistics of returns (COVID‐19—Quarter 2) | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| United Kingdom | United States | Italy | Germany | China | Brazil | Russia | India | Spain | |
| Mean | 0.1461 | 0.2995 | 0.2559 | 0.3942 | 0.1963 | 0.3061 | 0.2908 | 0.2092 | 0.1570 |
| Median | 0.0683 | 0.4250 | 0.1741 | 0.4017 | 0.0599 | 0.3524 | 0.1786 | 0.3361 | 0.0000 |
| Maximum | 4.8707 | 7.0331 | 3.8729 | 6.0529 | 2.8512 | 5.3739 | 9.7535 | 4.0199 | 5.0776 |
| Minimum | −4.8315 | −5.8944 | −5.3393 | −4.4606 | −2.8501 | −7.7157 | −6.7127 | −4.5935 | −4.7903 |
| SD | 2.1118 | 1.9766 | 2.1604 | 2.3807 | 0.9559 | 2.3143 | 2.3296 | 1.7088 | 2.1649 |
| Skewness | −0.2542 | −0.1233 | −0.5369 | −0.0708 | 0.1400 | −0.3938 | 0.5056 | −0.0853 | −0.1120 |
| Kurtosis | 2.7575 | 5.0620 | 2.9465 | 2.9249 | 4.4629 | 4.0272 | 6.7496 | 3.9342 | 2.6639 |
Note: This table reports descriptive statistics for daily stock returns. Panel A reports the results during the first quarter in the COVID‐19 period (Jan. 1, 2020 to March 31, 2020). Panel B reports the results during the second quarter in the COVID‐19 period (April 1, 2020 to June 30, 2020).
Table 4 reveals that all countries are positively correlated and pairwise correlations are strongly significant. Therefore, there is no possible risk diversification for investors via buying all countries' indices. However, the investors can invest in US market and Chinese market as the market give positive average returns even during COVID‐19 period as demonstrated in Table 2. This fact is supported by the results in Table 3 since the average returns during the first quarter of COVID‐19 are −02817 for United States and −0.1689 for China exhibiting lower losses after the shock.
TABLE 4.
Correlation matrix
| United Kingdom | United States | Italy | Germany | China | Brazil | Russia | India | Spain | |
|---|---|---|---|---|---|---|---|---|---|
| United Kingdom | 1.00 | ||||||||
| ‐ | |||||||||
| United States | 0.68 | 1.00 | |||||||
| (0:00) | ‐ | ||||||||
| Italy | 0.87 | 0.66 | 1.00 | ||||||
| (0:00) | (0:00) | ‐ | |||||||
| Germany | 0.91 | 0. 66 | 0.92 | 1.00 | |||||
| (0:00) | (0:00) | (0:00) | ‐ | ||||||
| China | 0.38 | 0.28 | 0.28 | 0.35 | 1.00 | ||||
| (0:00) | (0:00) | (0:00) | (0:00) | ‐ | |||||
| Brazil | 0.66 | 0.75 | 0.67 | 0.66 | 0.31 | 1.00 | |||
| (0:00) | (0:00) | (0:00) | (0:00) | (0:00) | ‐ | ||||
| Russia | 0.78 | 0.51 | 0.74 | 0.77 | 0.28 | 0.59 | 1.00 | ||
| (0:00) | (0:00) | (0:00) | (0:00) | (0:00) | (0:00) | ‐ | |||
| India | 0.61 | 0.39 | 0.56 | 0.56 | 0.45 | 0.51 | 0.49 | 1.00 | |
| (0:00) | (0:00) | (0:00) | (0:00) | (0:00) | (0:00) | (0:00) | ‐ | ||
| Spain | 0.89 | 0.65 | 0.92 | 0.90 | 0.31 | 0.70 | 0.73 | 0.58 | 1.00 |
| (0:00) | (0:00) | (0:00) | (0:00) | (0:00) | (0:00) | (0:00) | (0:00) |
‐ |
Note: p values are in parenthesis.
As demonstrated in Tables 2 and 3, all indices' returns exhibit skewed distribution with fat tails. That is, the returns have negative skewness, meaning that the probability of losing an amount of money buying a country index is higher than the probability of gaining the same amount. Also, fatter tails of the distribution of returns reveal that there is high probability to get extreme returns than the normal, that is, either extreme gains or extreme losses. In the other side, Figure 1 shows that there is a volatility clustering and volatility persistence, as there are periods of high volatility followed by periods of high volatility and periods of low volatility followed by periods of low volatility. Accordingly, the conditional volatility is computed using an asymmetric EGARCH (1, 1) of Nelson (1991) to capture these stylized facts of returns. That is, the model (skewed t‐distribution of Hansen) comprises two key parameters capturing the dynamics of the asymmetry and fat tailedness of the distribution. In one side, the parameter controls the shape of the distribution and hence capture the degree asymmetry and hence governs the probability of bad state of the market. In the other side, the parameter captures the likelihood of extreme returns. Model speciation is presented in Section 3.
Figure 2 displays the dynamics of the estimated conditional volatility across the selected countries. As mentioned, we compute the conditional volatility, using an asymmetric EGARCH (1, 1) of Nelson (1991). Stock price crashes unfolded extreme volatility during the COVID‐19 pandemic, which led to unprecedented rise in conditional volatilities across all the markets, as it can be apparent in the graph. Unsurprisingly, the highest levels of volatility are observed in the United States and the United Kingdom while countries, like China and Germany, exhibit less conditional volatility. The surge in new cases and deaths despite the government's efforts to mitigate the spread of COVID‐19 in the United States and the United Kingdom were associated with the spread of pessimistic views and negative feelings amid both the political leadership and citizens, which has adversely affected market uncertainty. In contrast, the stock markets in China and Germany appear to have suffered less and the prompt intervention of their governments to control the spread of the virus appeared to convey positive signals to the investors and mitigate the prevailing market uncertainty. As it can be also shown, the excessive increase in conditional volatility appears not to be persistent during the COVID‐19 period as for all the markets the figure exhibits a significant fall in the conditional volatility once the shock has been absorbed.
FIGURE 2.
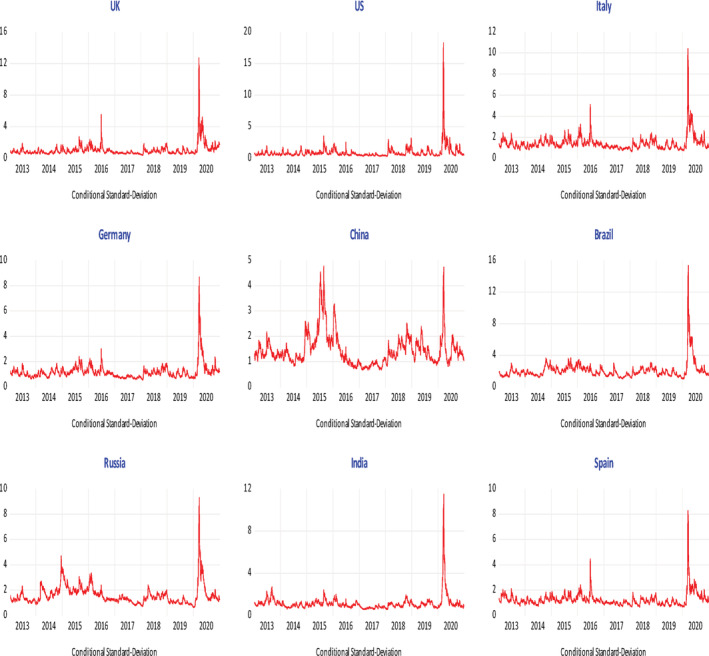
Time series plot of conditional volatility from January 1, 2013, to December 31, 2020
As any other major crisis, the initial market reaction to the COVID‐19 pandemic is associated with panic, uncertainty, negative sentiment and investor pessimism, which exerted an adverse impact on the financial markets. To get more insights into this impact, we estimate the bad state probabilities to compare how the likelihood of bad events differs across the periods pre‐ and during the COVID‐19 (to examine the initial effect of the shock of COVID‐19 on the markets) and between the first and second quarters during the COVID‐19 period (to examine whether the markets get rebounded after the shock is being assessed and absorbed). As demonstrated in Table 5 and Figure 3, the impact of the COVID‐19 was visible worldwide on the major equity markets, which generally experienced noticeable increase in bad state probabilities, indicating that market participants perceived the event as a global shock and so it has reflected on their adverse expectation with respect to the market behavior. In comparison with the time period before COVID‐19, we observe—on average‐ an increase in bad state probabilities across the United Kingdom, Germany, Brazil and India. In contrast, the United States, Russia, China, Italy, and Spain exhibit a decrease in bad state probabilities.
TABLE 5.
Bad state probability during periods per‐ and during the COVID‐19
| Panel A: Bad state probability (Before COVID‐19) | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| United Kingdom | United States | Italy | Germany | China | Brazil | Russia | India | Spain | |
| Mean | 0.5362 | 0.5677 | 0.5525 | 0.5322 | 0.4850 | 0.4985 | 0.5299 | 0.5174 | 0.5487 |
| Median | 0.5350 | 0.5671 | 0.5529 | 0.5314 | 0.4842 | 0.4981 | 0.5295 | 0.5170 | 0.5486 |
| Maximum | 0.6035 | 0.6019 | 0.5643 | 0.5758 | 0.5268 | 0.5211 | 0.5541 | 0.5418 | 0.5576 |
| Minimum | 0.4890 | 0.5441 | 0.5346 | 0.5024 | 0.4572 | 0.4834 | 0.5136 | 0.5011 | 0.5428 |
| SD | 0.0141 | 0.0070 | 0.0036 | 0.0089 | 0.0084 | 0.0045 | 0.0049 | 0.0049 | 0.0018 |
| Skewness | 0.7147 | 0.7318 | −0.7860 | 0.7431 | 0.7746 | 0.7714 | 0.7596 | 0.7641 | 0.7663 |
| Kurtosis | 4.6610 | 4.7326 | 4.8657 | 4.7506 | 4.8248 | 4.8296 | 4.8014 | 4.8118 | 4.8220 |
| Panel B: Bad state probability (During COVID‐19) | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| United Kingdom | United States | Italy | Germany | China | Brazil | Russia | India | Spain | |
| Mean | 0.5798 | 0.5472 | 0.5180 | 0.5805 | 0.5050 | 0.4863 | 0.4958 | 0.5416 | 0.4919 |
| Median | 0.5619 | 0.5625 | 0.5345 | 0.5693 | 0.5235 | 0.4814 | 0.5090 | 0.5049 | 0.4833 |
| Maximum | 0.7908 | 0.6298 | 0.6023 | 0.7390 | 0.6000 | 0.5595 | 0.7093 | 0.7798 | 0.5709 |
| Minimum | 0.4903 | 0.3683 | 0.2404 | 0.4403 | 0.3712 | 0.4361 | 0.0586 | 0.4676 | 0.4265 |
| SD | 0.0604 | 0.0495 | 0.0558 | 0.0514 | 0.0494 | 0.0208 | 0.1110 | 0.0759 | 0.0468 |
| Skewness | 1.8032 | −1.7234 | −3.1002 | 0.6441 | −1.2085 | 1.0957 | −2.3606 | 1.8215 | 0.2462 |
| Kurtosis | 5.6327 | 5.6377 | 12.8640 | 3.2700 | 3.8491 | 4.8427 | 9.7593 | 5.0637 | 1.5943 |
Note: This table reports descriptive statistics for bad state probability. Panel A reports the results during the period per‐the COVID‐19 period (January 1, 2013 to December 31, 2019). Panel B reports the results during the COVID‐19 period (January 1, 2020 to December 31, 2020). Bad state probability is estimated using an asymmetric EGARCH (1, 1) of Nelson (1991). See model speciation in Section 3.
Abbreviation: EGARCH, exponential generalized autoregressive conditional heteroscedasticity.
FIGURE 3.
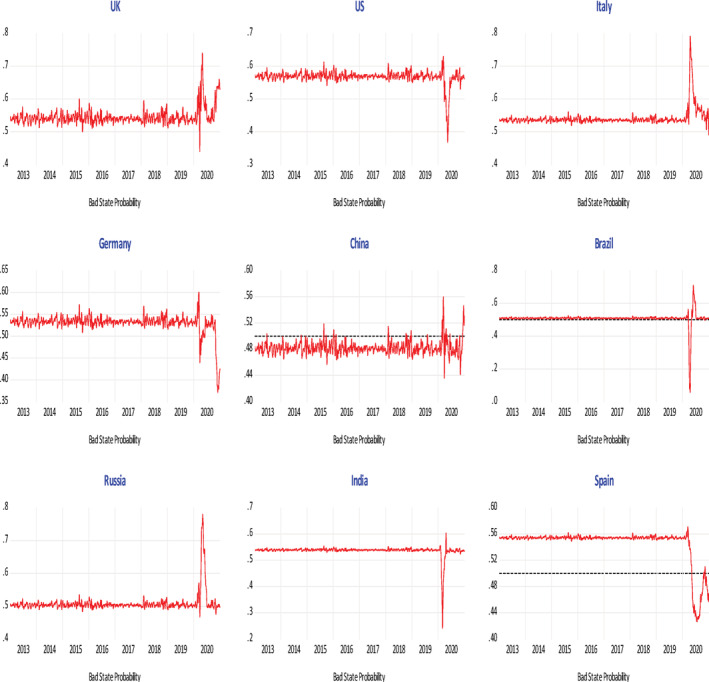
Time series plot of bad state probability from January 1, 2013, to December 31, 2020
Again, these findings should not be surprising due to the pessimistic views and negative feelings which were prevailing amid both the political leadership and citizens in markets, such as the United Kingdom and Germany, after the COVID‐19 pandemic; in contrast other markets (e.g., Russia and China) were associated with relatively lower market uncertainty not only due to their economic/political strength but also to their prompt response to markets' fears and investors' worries. It is also worth mentioning that bad state probability exhibited larger SD and maximum values in all the markets, which indicates that the probability of stock market declines becomes more volatile and is expected to move up to larger highest values compared the period pre‐COVID‐19 pandemic.
A closer examination of the behavior of bad state probability during the first two quarters in the COVID‐19 period, as displayed in Table 6, reveals that bad state probability differs during the second quarter in the COVID‐19 period (April 1, 2020 to June 30, 2020) as compared to that of the first quarter period (January 1, 2020 to March 31, 2020). This difference between the two quarters varies across countries. For example, except for Germany, China and Spain, bad state probability becomes—on average—higher during the second quarter. As expected, Italy exhibits the highest increase in bad state probability (by ~35% from 0.5642 to 0.7638) during the second quarter in the COVID‐19 period caused by soaring levels of uncertainty and investors' pessimism due to the surge in new cases and deaths despite the government's efforts (e.g., lockdowns, stimulus packages and travel bans) to mitigate the spread of COVID‐19. Again, among the markets that experienced higher bad state probability during the second quarter, Russia has the lowest increase (by 0.73% from 0.5361 to 0.5400), which can be attributed to Russia's policies that helped subdue panic and so mitigated the adverse effects of the pandemic on the stock markets, in addition to the impact of the positive news associated with Russia's experimental COVID‐19 vaccines. On the other hand, China, Germany and Spain experienced lower bad state probability during the second quarter in the COVID‐19 period, which might reflect that investors' confidence has been resorted, and so stock markets in these counties have recovered quicker than the other markets. The prompt intervention of the government in China and Germany to control the spread of the virus managed to maintain business and confidence and conveyed positive signals to the stock markets, whereas in Spain the noticeable decline in daily new cases and deaths starting from April might have positively influenced the financial markets and so reflected on the fall in bad state probability in the second quarter during the COVID‐19 period. Taken together, these findings suggest that for risk‐averse investors, Chinese market is more attractive since the average of bad state probability is the lowest among all countries and is less than 50% during the second quarter of COVID‐19 period as shown in Tables 5 and 6.
TABLE 6.
Bad state probability during the COVID‐19 period
| Panel A: Bad state probability (COVID‐19—First quarter) | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| United Kingdom | United States | Italy | Germany | China | Brazil | Russia | India | Spain | |
| Mean | 0.5490 | 0.5748 | 0.5642 | 0.5415 | 0.5104 | 0.5052 | 0.5361 | 0.5242 | 0.5573 |
| Median | 0.5376 | 0.5683 | 0.5528 | 0.5330 | 0.5020 | 0.5001 | 0.5304 | 0.5190 | 0.5501 |
| Maximum | 0.6418 | 0.6338 | 0.6750 | 0.6142 | 0.6144 | 0.5473 | 0.5808 | 0.5692 | 0.6388 |
| Minimum | 0.4294 | 0.5091 | 0.5324 | 0.4693 | 0.4024 | 0.4696 | 0.4931 | 0.4843 | 0.4598 |
| SD | 0.0435 | 0.0264 | 0.0377 | 0.0320 | 0.0567 | 0.0166 | 0.0185 | 0.0181 | 0.0269 |
| Skewness | −0.0151 | 0.0989 | 2.1395 | 0.2484 | 0.1151 | 0.7884 | 0.4838 | 0.6865 | 0.6808 |
| Kurtosis | 3.5721 | 3.5546 | 6.2434 | 3.3359 | 2.2083 | 3.5398 | 3.5053 | 3.4929 | 7.4751 |
| Panel B: Bad state probability (COVID‐19—Second quarter) | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| United Kingdom | United States | Italy | Germany | China | Brazil | Russia | India | Spain | |
| Mean | 0.6655 | 0.6275 | 0.7638 | 0.5082 | 0.4854 | 0.5681 | 0.5400 | 0.6327 | 0.4042 |
| Median | 0.6473 | 0.6347 | 0.7613 | 0.5140 | 0.4805 | 0.5533 | 0.5247 | 0.6428 | 0.3868 |
| Maximum | 0.8028 | 0.8487 | 0.8495 | 0.5584 | 0.6056 | 0.7598 | 0.7984 | 0.7950 | 0.7070 |
| Minimum | 0.5796 | 0.4578 | 0.6554 | 0.3997 | 0.4374 | 0.3488 | 0.4934 | 0.5079 | 0.1649 |
| SD | 0.0679 | 0.0964 | 0.0630 | 0.0407 | 0.0324 | 0.1047 | 0.0594 | 0.0754 | 0.1776 |
| Skewness | 0.5293 | −0.1579 | −0.2771 | −1.2338 | 1.9720 | 0.1336 | 2.7601 | −0.0306 | 0.0394 |
| Kurtosis | 1.9312 | 2.2201 | 1.6978 | 3.9283 | 7.3752 | 2.4528 | 10.5667 | 1.9907 | 1.4047 |
Note: This table reports descriptive statistics for bad state probability. Panel A reports the results during the first quarter in the COVID‐19 period (January 1, 2020 to March 31, 2020). Panel B reports the results during the second quarter in the COVID‐19 period (April 1, 2020 to June 30, 2020). Bad state probability is estimated using an asymmetric EGARCH (1, 1) of Nelson (1991). See model speciation in Section 3.
Abbreviation: EGARCH, exponential generalized autoregressive conditional heteroscedasticity.
After gaining insights into how the risk–return behavior of stock markets differed across the periods pre‐ and during the COVID‐19 and between the first and second quarters during the COVID‐19 period, we further investigate the impact of COVID‐19 (proxied by the number of deaths and recovery cases) on stock returns, conditional volatility and conditional skewness. Table 7 reports the results. Our dependent variable is mean return that represents the daily percentage changes in the selected markets' stock indices in Panel A, while it is conditional volatility modeled using an asymmetric EGARCH (1,1) of Nelson (1991) in Panel B, and it is conditional skewness estimated using an asymmetric EGARCH (1,1) of Nelson (1991) in Panel C. In general, our results are in line with the findings on the adverse impact of financial crises in general (e.g., Novotny, 2010; Sarkar & Patel, 1998) and the COVID‐19 pandemic in specific (e.g., Baek et al., 2020; Chaudhary et al., 2020; Zhang et al., 2020). Particularly, for our independent variable “mean return,” we observe a consistently negative relationship between coronavirus death cases and stock return only in the Italy, whereas the coefficients are insignificant in the other markets. As for the impact of recovery, the coefficient is only consistently positive and statistically significant in the United Kingdom, Italy and Brazil while it remains insignificant in other markets. In economic terms, an increase in death cases by 1000—in Italy, for example,—is associated with about 0.014% decrease in average stock returns while an increase in recovered cases by 1000 is associated with about 0.0044% increase in average stock returns.
TABLE 7.
The influence of COVID‐19 deaths and recovered cases on stock returns, conditional volatility, and conditional skewness
| United Kingdom | United States | Italy | Germany | China | Brazil | Russia | India | Spain | |
|---|---|---|---|---|---|---|---|---|---|
| Panel A: Mean return | |||||||||
| W.Return | 0.21452*** | −0.05065** | 0.1165*** | 0.19813*** | 0.22967*** | 0.03282 | 0.26894*** | 0.35395*** | 0.21442*** |
| Death | 0.000085 | −0.00055 | −0.00014* | 0.00045 | 0.00110 | −0.00094 | 0.00400 | −0.00191 | 0.00019 |
| Recovery | 0.00764*** | −0.00029 | 0.000044** | −0.0000 | −0.0000 | 0.00104*** | −0.00025 | 0.00014 | −0.0000 |
| Panel B: Conditional volatility | |||||||||
| W.Return | −0.13901*** | −0.14547*** | −0.09288*** | −0.07532*** | −0.05982*** | −0.0856*** | −0.07210*** | −0.07293*** | −0.08029*** |
| Death | 0.00018*** | 0.00719* | 0.0000*** | 0.0000* | −0.00013 | −0.0000 | 0.00077 | 0.00015 | 0.0000* |
| Recovery | 0.00068 | −0.0000 | −0.000016*** | −0.0000 | 0.0000 | 0.0000 | −0.0000 | 0.0000* | −0.0000 |
| Panel C: Conditional skewness | |||||||||
| W.Return | 0.17341*** | 0.12271** | 0.06966 | 0.10813** | 0.10326*** | 0.03841 | 0.08670* | 0.03899 | 0.02154 |
| Death | −0.00069*** | 0.00916 | −0.00036** | 0.00014 | −0.0005 | 0.00738*** | −0.00611 | −0.00151 | 0.00030 |
| Recovery | 0.01420** | 0.00083 | 0.0000* | 0.0000* | 0.0000 | −0.00225* | 0.00011 | 0.00036 | 0.0000 |
Note: This table provides the results from the regression estimation of COVID‐19 deaths and recovered cases on stock returns, conditional volatility and conditional skewness. Dependent variable is mean return that represents the daily percentage changes in the selected markets' stock indices in Panel A, while it is conditional volatility modeled using an asymmetric EGARCH (1,1) of Nelson (1991) in Panel B, and it is conditional skewness estimated using an asymmetric EGARCH(1,1) of Nelson (1991) in Panel C. See model specification in Section 3. W.Return is average daily percentage returns of MSCI World Index; Death is the total number of daily deaths; Recovery is the total number of daily recovered cases.
Abbreviation: EGARCH, exponential generalized autoregressive conditional heteroscedasticity.
Significant at 10%.
Significant at 5%.
Significant at 1%.
With respect to our dependent variable “conditional volatility,” the number of coronavirus death cases is found to be significantly positively associated with conditional volatility in the United Kingdom, the United States, Italy, Germany, and Spain. For example, an increase in the number of death cases in the United Kingdom by 1000 is associated with about a 0.018% increase in conditional volatility. In contrast, the findings across the other markets exhibit generally insignificantly positive coefficients (Russia, and India) or inconsistently negative coefficients (Brazil and China). The findings on the impact of recovered cases reveal a consistently negative and significant association only in Italy. For our dependent variable “conditional skewness,” we find a significant impact of the number of deaths on conditional skewness in the United Kingdom, Italy, and Brazil. We observe mixed results on the relationship with number of recovered cases and conditional skewness across the markets.
5. ROBUSTNESS TESTS
To further explore the robustness of our analysis, diagnoses tests will be performed as follows:
The CDF skewed t distribution of Hansen is given by
Let be the error term, then the distribution of is
If the model is well specified, then will follow the uniform distribution on (0, 1). In addition, the standardized residual will follow the normal distribution with mean zero and SD one, where is the cumulative distribution function of the standard normal distribution and is its quantile, that is, is the inverse of . To assess the quality of the model (robustness check) and test the specification of the models, we estimated residual which under a correct specification should be independent and uniformly distributed. Following Vlaar and Palm (1993) and Berkowitz (2001), if the model is well specified, the estimated residual follows the standard normal distribution with mean zero and SD one. Using the normalized run four classical tests: Cramervon Mises, Anderson–Darling, Watson empirical distribution, and Jarque–Bera tests. Table 8 summarized the results of the four tests. We notice from the table that the null hypothesis that the model is well specified is not rejected at least at 1% confidence level for all the four test and hence the model does capture all the stylized facts highlighted in the literature concerning returns.
TABLE 8.
Diagnostic tests
| JB | CM | W | AD | |
|---|---|---|---|---|
| United Kingdom |
3:11 (0:21) |
0:06 (0:81) |
0:05 (0:68) |
0:40 (0:84) |
| United States |
5:04 (0:08) |
0:11 (0:54) |
0:11 (0:24) |
0:76 (0:51) |
| Italy |
2:47 (0:29) |
0:10 (0:56) |
0:09 (0:33) |
0:82 (0:47) |
| Germany |
2:00 (0:37) |
0:04 (0:95) |
0:03 (0:88) |
0:26 (0:96) |
| China |
9:08 (0:02) |
0:16 (0:37) |
0:13 (0:14) |
1:19 (0:27) |
| Brazil |
7:39 (0:02) |
0:31 (0:13) |
0:28 (0:01) |
2:12 (0:08) |
| Russia |
6:12 (0:05) |
0:19 (0:29) |
0:19 (0:05) |
1:40 (0:20) |
| India |
4:24 (0:12) |
0:05 (0:88) |
0:05 (0:76) |
0:37 (0:88) |
| Spain |
0:06 (0:97) |
0:05 (0:88) |
0:05 (0:68) |
0:38 (0:87) |
Abbreviations: AD, Anderson–Darling test; CM, Cramer–von Mises test; JB, Jarque–Bera test; W, Watson test.
As mentioned before, since normal GARCH model link directly the kurtosis to the variance, it is unable to well capture the excess kurtosis that exists present in financial returns, resulting in having low probability of extreme realizations (extreme returns) than observed in the data. Therefore, we also conduct a Lagrange multiplier (LM) test for the presence of GARCH effect, as Table 9 illustrates, the null hypothesis is strongly rejected for all countries, testifying for the existence of the effect of GRACH on extreme returns.
TABLE 9.
ARCH‐LM test for conditional heteroscedasticity
| Panel A: Residuals autoregressive conditional heteroscedasticity LM test | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| United Kingdom | United States | Italy | Germany | China | Brazil | Russia | India | Spain | |
| Statistic | 278.9342 | 798.0081 | 132.7790 | 252.9038 | 209.8375 | 580.3271 | 299.4189 | 500.9419 | 164.2774 |
| p value | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
Note: This table reports residuals autoregressive conditional heteroscedasticity LM test (ARCH test).
In addition, Table 10 provides the descriptive statistics of the GARCH conditional volatility and conditional variance of the proposed model. While in the normal GARCH they are equal, in our model the conditional variance is higher that the GARCH volatility. This testifies that the estimated risk implied by the proposed model is higher than in the normal case, with the case of Brazil exhibiting the highest level. Furthermore, in the normal GARCH model the distribution is symmetric (skewness = 0) meaning that there is equal probability of losing or gaining the same amount of money investing in the financial market, the results of our model produces in average negative skewness () as Table 11 (second row) shows. These results signify that the distribution is left asymmetric which translate in higher probability of losing an amount of money than gaining the same amount except for the case of China where and hence the likelihood of gain is higher than the likelihood of loss.
TABLE 10.
Descriptive statistics of GARCH volatility and model's implied volatility estimates
| Panel A: Descriptive statistics of GARCH volatility estimate | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| United Kingdom | United States | Italy | Germany | China | Brazil | Russia | India | Spain | |
| Mean | 1.7663 | 1.7979 | 2.5892 | 1.8007 | 2.4452 | 5.3868 | 3.1208 | 1.8084 | 1.8911 |
| Median | 0.7329 | 0.4883 | 1.6719 | 1.1545 | 1.6705 | 3.3963 | 1.9388 | 1.0192 | 1.3203 |
| Maximum | 152.7427 | 315.4359 | 110.2596 | 81.2990 | 22.6002 | 212.1903 | 81.7621 | 130.1726 | 70.6085 |
| Minimum | 0.1561 | 0.1058 | 0.3961 | 0.2977 | 0.4427 | 0.9992 | 0.3907 | 0.3148 | 0.4380 |
| SD | 7.0897 | 12.1587 | 5.3752 | 4.1293 | 2.5897 | 11.5398 | 4.7278 | 6.2353 | 3.6070 |
| Skewness | 15.0822 | 18.0271 | 12.8925 | 11.9263 | 3.6957 | 11.4057 | 8.9267 | 13.8604 | 13.0494 |
| Kurtosis | 264.4052 | 367.1540 | 206.1879 | 175.2792 | 20.4280 | 163.1646 | 114.4171 | 223.4008 | 203.6618 |
| Panel B: Descriptive statistics of conditional variance estimate | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| United Kingdom | United States | Italy | Germany | China | Brazil | Russia | India | Spain | |
| Mean | 2.8938 | 3.0164 | 3.2559 | 2.1051 | 2.5414 | 8.4952 | 3.6843 | 2.0532 | 2.0798 |
| Median | 0.7808 | 0.5571 | 1.7562 | 1.1948 | 1.6934 | 3.4044 | 1.9404 | 1.0668 | 1.4317 |
| Maximum | 613.6490 | 1065.3360 | 228.3696 | 173.5321 | 43.0289 | 633.4338 | 124.5595 | 174.0941 | 94.4947 |
| Minimum | 0.1575 | 0.1210 | 0.4045 | 0.3016 | 0.4482 | 1.0015 | 0.3919 | 0.3244 | 0.4753 |
| SD | 20.4377 | 33.2760 | 9.5061 | 7.1241 | 2.9790 | 35.5551 | 7.9912 | 7.7245 | 4.2972 |
| Skewness | 22.8204 | 25.6049 | 14.4875 | 16.0421 | 5.0390 | 11.0604 | 8.6459 | 13.5524 | 14.2181 |
| Kurtosis | 609.7289 | 727.8897 | 282.3976 | 312.5928 | 41.8738 | 147.6355 | 95.3432 | 224.7273 | 243.1128 |
Note: This table reports descriptive statistics for GARCH volatility and model's implied volatility estimates.
TABLE 11.
Skewness (degree of asymmetry)
| United Kingdom | United States | Italy | Germany | China | Brazil | Russia | India | Spain | |
|---|---|---|---|---|---|---|---|---|---|
| Skewness | −0.0928 | −0.1362 | −0.0838 | −0.0587 | 0.0348 | −0.0148 | −0.0178 | −0.0742 | −0.0924 |
| Kurtosis | 6.5146 | 5.6191 | 6.3843 | 5.3717 | 3.5579 | 4.7521 | 4.5341 | 4.4694 | 7.1694 |
The model also captures also the likelihood of extreme events (extreme returns) since the kurtosis parameter is small than 303 (infinite for the normal distribution) as Table 11 (third row) shows. It is even smaller for the case of China, Brazil, Russia, and India compared with other countries, attesting that the likelihood of extreme returns is higher in the emerging countries than the developing ones. We mention that the case of China is the most extreme.
6. CONCLUSION
This study attempts to explain how COVID‐19 pandemic has affected the stock market behavior of international equity indices in nine markets. Unlike other studies we focus on several dimensions of a stock market, that is, stock returns, conditional volatility, conditional skewness, and bad state probability, measured using an asymmetric exponential GARCH model. Furthermore, we have examined the influence of COVID‐19‐related death cases and recovered cases on these indicators. Unsurprisingly, our findings show that COVID‐19 has exerted adverse impact on major equity markets, which led to unprecedented rise in conditional volatilities and bad state probabilities across all the markets. However, this impact is not symmetric across all the markets. For example, China and Germany exhibit less conditional volatility; in contrast, Italy, the United States and the United Kingdom experience excessive volatility and bad state probability. Furthermore, we also find that the excessive increase in conditional volatility appears not to be persistent during the COVID‐19 period as for all the markets the conditional volatility exhibits a significant fall once the shock has been absorbed. With respect to the impact of COVID‐19‐related deaths and recovered cases on stock price behavior, the overall findings reveal that the negative affect of deaths is more pronounced, compared to the positive impact of recovered cases. These findings confirm prior empirical findings on the adverse impact triggered by financial crises (Novotny, 2010; Sarkar & Patel, 1998) and the COVID‐19 pandemic (Baek et al., 2020; Chaudhary et al., 2020; Zhang et al., 2020). Moreover, our findings provide important implications for investors, practitioners and policy makers. For traders and investors seeking to invest in international stock markets, the results indicate which markets are most correlated and risky, which have strong consequences for portfolio optimization and implementation of profitable trading strategies. For practitioners, the findings allow to get insights into the dynamic behavior of stock markets in the countries that are heavily affected by the pandemic in order to examine the best investment options. For policy makers, the findings confirm the critical role that the political leadership and governments can play, via mitigating the spread of pessimistic views and negative feelings amid citizens, in conveying positive signals to the investors and thereby decreasing market uncertainty.
AUTHOR CONTRIBUTIONS
Mohamed A. K. Basuony developed the idea, collected all the required data, and drafted and revised the manuscript, in addition to supervising the work. Mohammed Bouaddi performed the model and empirical analysis (tables and figures), in addition to writing the methodology. He also revised the manuscript. Heba Ali wrote and interpreted the empirical results, introduction and conclusion, in addition to revising the final manuscript. Rehab EmadEldeen wrote the literature section and provided a summary table of all the papers, in addition to revising the final manuscript. All authors read and approved the final manuscript.
Biographies
Mohamed A. K. Basuony is associate professor of Accounting at the School of Business at the American University in Cairo. Prior to that, he worked at the German University in Cairo and Faculty of Commerce, Ain Shams University. He received both his bachelor with honors and master degree from the same university. He obtained his PhD degree from Brunel University in the United Kingdom. His work experience includes more than 25 years teaching undergraduates as well as post‐graduates in Egypt, Kuwait, and the United Kingdom. His areas of research are in performance management, balanced scorecard, management and strategic control, corporate governance, and corporate social responsibility.
Mohammed Bouaddi is associate professor in Economics at the American University in Cairo. He is currently appointed as the director of graduate programs in Economics at the American University in Cairo. Bouaddi's research focuses primarily in applied econometrics with specialties asset pricing, time series analysis, and financial economics. He has published papers in refereed journals involving applications of econometric methods in the fields of portfolio selection, macro‐finance, and corporate finance. His actual interest is in the econometrics of factor models.
Heba Ali is an assistant professor in Finance at the Faculty of Management Technology, the German University in Cairo (GUC). She received her Master and PhD degrees in Finance and Investment from Exeter Business School, University of Exeter, United Kingdom. She has 10 years academic teaching experience in reputable educational institutions such as University of Exeter, the GUC, and Cairo University. Her research interests focus on the areas of behavioral finance, corporate finance, risk, financial modeling, sustainability performance, the SDGs, and equity issues. She published a number of papers in reputable academic journals, such as Emerging Markets Review, Journal of Cleaner Production, and Journal of Behavioural Finance. Her experience also includes working in the field of stock market in the areas of technical analysis and portfolio management. She participated in several international conferences.
Rehab Emadeldeen is full‐time assistant professor of Accounting at the School of Business at the Egyptian Chinese University and part‐time at the School of Business at American University in Cairo. She received both her bachelor, master, and PhD degrees from the Faculty of Commerce, Ain Shams University. Her work experience includes more than ten years teaching undergraduates. She had publications in several journals, including Journal of Islamic Marketing, and Corporate Ownership & Control.
APPENDIX A.
In the following proof, we derive the probability of bad state. The probability at time t of the market to be in bad state at time t + 1 is given by
Let then
The last equality follows from the fact that is the CDF of the standard Student t distribution of (with degree of freedom ) evaluated at zero.
TABLE B1.
Descriptive statistics
| Panel A: List of stock indexes | |
|---|---|
| Country | Index |
| United Kingdom | FTSE100 |
| United States | S&P 500 COMPOSITE |
| Italy | FTSE MIB INDEX |
| Germany | DAX 30 PERFORMANCE |
| China | SHANGHAI SHENZHEN CSI 300 |
| Brazil | BRAZIL BOVESPA |
| Russia | MOEX RUSSIA INDEX |
| India | The BSE SENSEX |
| Spain | IBEX 35 |
| Panel B: COVID‐19 related cases | ||||||
|---|---|---|---|---|---|---|
| Confirmed cases | Death cases | Recovered cases | ||||
| Country | June, 30 | March, 31 | June, 30 | March, 31 | June, 30 | March, 31 |
| United Kingdom | 221,904 | 17,766 | 43,730 | 1789 | 344 | 135 |
| United States | 1,912,534 | 134,071 | 127,393 | 3883 | 781,655 | 5507 |
| Italy | 166,865 | 71,844 | 34,767 | 12,428 | 190,248 | 15,729 |
| Germany | 143,512 | 47,094 | 8957 | 687 | 177,795 | 13,656 |
| China | 64,450 | 63,056 | 4634 | 3311 | 78,479 | 76,238 |
| Brazil | 1,044,929 | 4135 | 59,594 | 201 | 790,040 | 127 |
| Russia | 457,063 | 1703 | 9320 | 17 | 412,650 | 121 |
| India | 396,142 | 1070 | 16,893 | 35 | 334,821 | 123 |
| Spain | 194,143 | 69,802 | 28,355 | 8464 | 150,376 | 19,259 |
Note: This table reports the list of stock indexes (Panel A), and the number of confirmed cases, deaths and recovered cases per country.
Basuony, M. A. K. , Bouaddi, M. , Ali, H. , & EmadEldeen, R. (2021). The effect of COVID‐19 pandemic on global stock markets: Return, volatility, and bad state probability dynamics. Journal of Public Affairs, e2761. 10.1002/pa.2761
Footnotes
Notice that, because the distribution is asymmetric, is the conditional mode rather than conditional mean.
Appendix A: Proof of Proposition 1.
We note that lower value of means fatter tails and thus higher likelihood of extreme returns. We also note that when , the normal distribution approximate very well the Student distribution.
DATA AVAILABILITY STATEMENT
The data that support the findings of this study are available from the corresponding author upon reasonable request.
REFERENCES
- Akhtaruzzaman, M. , Boubaker, S. , & Sensoy, A. (2020). Financial contagion during COVID–19 crisis. Finance Research Letters, 38, 101604. 10.1016/j.frl.2020.101604 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alberg, E. , Shalit, H. , & Yosef, R. (2008). Estimating stock market volatility using asymmetric GARCH models. Applied Financial Economics, 18, 1201–1208. [Google Scholar]
- Albulescu, C. (2020). COVID‐19 and the United States financial markets' volatility. Finance Research Letters, 38, 101699. 10.1016/j.frl.2020.101699 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baek, S. , Mohanty, S. , & Glambosky, M. (2020). COVID‐19 and stock market volatility: An industry level analysis. Finance Research Letters, 37, 101748. 10.1016/j.frl.2020.101748 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baig, A. , Butt, H. , Haroon, O. , & Rizvi, S. (2021). Deaths, panic, lockdowns and US equity markets: The case of COVID‐19 pandemic. Finance Research Letters, 38, 101701. 10.1016/j.frl.2020 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baker, S. , Bloom, N. , Davis, S. , Kost, K. , Sammon, M. , & Viratyosin, T. (2020). The unprecedented stock market impact of COVID‐19. National Bureau of Economic Research, 26945. [Google Scholar]
- Berkowitz, J. (2001). Testing density forecasts, with applications to risk management. Journal of Business & Economic Statistics, 19(4), 465–474. [Google Scholar]
- Bissoondoyal‐Bheenick, E. , Do, H. , Hu, X. , & Zhong, A. (2020). Learning from SARS: Return and volatility connectedness in COVID‐19. Finance Research Letters, 41, 101796. 10.1016/j.frl.2020.101796 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bollerslev, T. (1986). Generalized autoregressive conditional heteroskedasticity. Journal of Econometrics, 31, 307–327. [Google Scholar]
- Chaudhary, R. , Bakhshi, P. , & Gupta, H. (2020). Volatility in international stock markets: An empirical study during COVID‐19. Journal of Risk and Financial Management, 13(9), 208. 10.3390/jrfm13090208 [DOI] [Google Scholar]
- Choi, S. (2020). Industry volatility and economic uncertainty due to the COVID‐19 pandemic: Evidence from wavelet coherence analysis. Finance Research Letters, 37, 101783. 10.1016/j.frl.2020.101783 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Conlonm, T. , & McGee, R. (2020). Safe haven or risky hazard? bitcoin during the COVID‐19 bear market bitcoin during the COVID‐19 bear market. Finance Research Letters, 35, 101607. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Corbet, S. , Hou, Y. , Hu, Y. , Lucey, B. , & Oxley, L. (2020). Aye Corona! The contagion effects of being named Corona during the COVID‐19 pandemic. Finance Research Letters, 38, 101591. 10.1016/j.frl.2020.101591 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Engle, R. (1982). Autoregressive conditional heteroscedasticity with estimates of the variance of United Kingdom inflation. Econometrica, 50, 987–1007. [Google Scholar]
- Gharib, C. , Mefteh‐Wali, S. , & Jabeur, S. (2021). The bubble contagion effect of COVID‐19 outbreak: Evidence from crude oil and gold markets. Finance Research Letters, 38, 101703. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goodell, J. (2020). COVID‐19 and finance: Agendas for future research. Finance Research Letters, 35, 101512. 10.1016/j.frl.2020.101512 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harvey, C. , & Siddique, A. (1999). Conditional skewness in asset pricing tests. The Journal of Financial and Quantitative Analysis, 34, 465–487. [Google Scholar]
- Hansen, B. (1994). Autoregressive conditional density estimation. International Economic Review, 35(3), 705–730. [Google Scholar]
- He, P. , Sun, Y. , Zhang, Y. , & Li, T. (2020). COVID–19's impact on stock prices across different sectors—An event study based on the Chinese stock market. Emerging Markets Finance and Trade, 56(10), 2198–2212. 10.1080/1540496X.2020.1785865 [DOI] [Google Scholar]
- He, Q. , Liu, J. , Wang, S. , & Yu, J. (2020). The impact of COVID‐19 on stock markets. Economic and Political Studies, 8(3), 275–288. 10.1080/20954816.2020.1757570 [DOI] [Google Scholar]
- Hentschel, L. (1995). All in the family: Nesting symmetric and asymmetric GARCH models. Journal of Financial Economics, 39, 71–104. [Google Scholar]
- IMF . (2020, April). The great lockdown . Retrieved from https://www.imf.org/en/Publications/WEO/Issues/2020/04/14/weo-april-2020.
- Jelilov, G. , Iorember, P. , Usman, O. , & Yua, P. (2020). Testing the nexus between stock market returns and inflation in Nigeria: Does the effect of COVID‐19 pandemic matter? Journal of Public Affairs, 20, 1–9. 10.1002/pa.2289 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Just, M. , & Echaust, K. (2020). Stock market returns, volatility, correlation and liquidity during the COVID‐19 crisis: Evidence from the Markov switching approach. Finance Research Letters. doi: 10.1016/j.frl.2020.101775, 37, 101775 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kenourgios, D. , Samitas, A. , & Paltalidis, N. (2011). Financial crises and stock market contagion in a multivariate time‐varying asymmetric framework. Journal of International Financial Markets, Institutions and Money, 21(1), 92–106. 10.1016/j.intfin.2010.08.005 [DOI] [Google Scholar]
- Kotishwar, A. (2020). Impact of COVID‐19 pandemic on stock market with reference to select countries—A study. Academy of Accounting and Financial Studies Journal, 24(4), 1–9. [Google Scholar]
- Liu, H. , Manzoor, A. , Wang, C. , Zhang, L. , & Manzoor, Z. (2020). The COVID‐19 outbreak and affected countries stock markets response. International Journal of Environmental Research and Public Health, 17(8), 2800. 10.3390/ijerph17082800 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lyocsa, S. , & Molnár, P. (2020). Stock market oscillations during the corona crash: The role of fear and uncertainty. Finance Research Letters, 36, 101707. [Google Scholar]
- Ma, C. , Rogers, J. , & Zhou, S. (2020). Global economic and financial effects of 21st century pandemics and epidemics . Retrieved from https://papers.ssrn.com/sol3/papers.cfm?abstract_id=3565646.
- Mazur, M. , Dang, M. , & Vega, M. (2020). COVID‐19 and the march 2020 stock market crash. Evidence from S&P1500. Finance Research Letters, 38, 101690. 10.1016/j.frl.2020.101690 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Narayan, P. , Phan, D. , & Liu, G. (2020). COVID‐19 lockdowns, stimulus packages, travel bans, and stock returns. Finance Research Letters, 38, 101732. 10.1016/j.frl.2020.101732 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nelson, D. (1991). Conditional heteroskedasticity in asset return: A new approach. Journal of the Econometric Society, 59(2), 347‐370. doi: 10.2307/2938260 [DOI] [Google Scholar]
- Novotny, J. (2010). Were stocks during the financial crisis more jumpy: A comparative study (Vol. 416). Center for Economic Research and Graduate Education and Economics Institute (CERGEEI) Working Paper Series. [Google Scholar]
- Patten, J. (2018). Time‐varying systemic risk: Evidence from a dynamic copula model of CDS spreads. Journal of Business & Economic Statistics, 36(2), 181–195. [Google Scholar]
- Ramelli, S. , & Wagner, A. (2020). Feverish stock price reactions to COVID‐19. Swiss Finance Institute Research, 9, 622–655. 10.1093/rcfs/cfaa012 [DOI] [Google Scholar]
- Sarkar, A. , & Patel, S. (1998). Stock market crises in developed and emerging markets (SSRN 76168). 10.2139/ssrn.76168 [DOI]
- Sharif, A. , Aloui, C. , & Yarovaya, L. (2020). COVID‐19 pandemic, oil prices, stock market, geopolitical risk and policy uncertainty nexus in the US economy: Fresh evidence from the wavelet‐based approach. International Review of Financial Analysis, 70, 101496. 10.1016/j.irfa.2020.101496 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tsay, R. (2010). Analysis of financial time series. John Wiley & Sons. [Google Scholar]
- Waheed, R. , Sarwar, S. , Sarwar, S. , & Khan, M. (2020). The impact of COVID‐19 on Karachi stock exchange: Quantile‐on‐quantile approach using secondary and predicted data. Journal of Public Affairs, 20(4), e2290. 10.1002/pa.2290 [DOI] [PMC free article] [PubMed] [Google Scholar]
- WHO . (2020). Coronavirus disease (COVID‐19), situation report 152 . Retrieved from https://www.who.int/emergencies/diseases/novel-coronavirus-2019/situation-reports/.
- Yousef, I. (2020). Spillover of COVID‐19: Impact on stock market volatility. International Journal of Psychosocial Rehabilitation, 24(6), 18069–18081. [Google Scholar]
- Vlaar, P. J. , & Palm, F. C. (1993). The message in weekly exchange rates in the European monetary system: mean reversion, conditional heteroscedasticity, and jumps. Journal of Business & Economic Statistics, 11(3), 351–360. [Google Scholar]
- Zaremba, A. , Kizys, R. , Aharon, D. , & Demir, E. (2020). Infected markets: Novel coronavirus, government interventions, and stock return volatility around the globe. Finance Research Letters, 35, 101597. 10.1016/j.frl.2020.101597 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang, D. , Hu, M. , & Ji, Q. (2020). Financial markets under the global pandemic of COVID‐19. Finance Research Letters, 36, 101528. 10.1016/j.frl.2020.101528 [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.


