A calibrated piecewise-linear FGM approach for travel destination recommendation during the COVID-19 pandemic

Abstract

After months of lockdown due to the COVID-19 pandemic, more people are planning regional trips because overseas travel is still not feasible. However, choosing a suitable travel destination during the COVID-19 pandemic is challenging because the factors critical to the selection process are very different from those usually considered. Furthermore, without sufficient literature or data for reference, existing methods based on psychological analyses or mining past experiences may not be applicable. Consequently, a fuzzy multi-criteria decision-making method – the calibrated piecewise-linear fuzzy geometric mean (FGM) approach – is proposed in this study for travel destination recommendation during the COVID-19 pandemic. The contribution of this research is twofold. First, the critical factors that affect the selection of a suitable travel destination during the COVID-19 pandemic are discussed. Second, the accuracy and efficiency using existing fuzzy analytic hierarchy process (FAHP) methods have been enhanced. The calibrated piecewise-linear FGM approach has been successfully applied to recommend suitable travel destinations to fifteen travelers for regional trips in Taiwan during the COVID-19 pandemic.

1. Introduction

Since the outbreak of the COVID-19 pandemic in Wuhan, China, the tourism industry has been severely affected. The most obvious example is the cruise industry. Almost all cruise lines have suspended their operations to reduce the spread of the pandemic [1]. Later, as the epidemic gradually eased, people began to resume regional tourism in some countries and regions [2]. However, because the epidemic had not yet ended, methods of recommending suitable travel destinations to travelers were worth discussing.

The factors considered for choosing a travel destination during the COVID-19 pandemic differ markedly from those usually considered [3], [4]. For example, before the COVID-19 outbreak, the number of countries visited was a key factor [5]. However, since the outbreak of the COVID-19 pandemic, the possibility of cross-country travel has been reduced dramatically, making the number of countries visited an irrelevant issue [6]. In contrast, during the COVID-19 pandemic, the number of confirmed cases in the region of a travel destination became an essential factor.

Furthermore, population density is an inverse indicator. Densely populated travel destinations are less popular due to the higher risk of infection. Travelers also avoid using public transportation systems. Moreover, outdoor attractions have priority over indoor facilities (such as museums, churches, castles, and amusement parks). These factors can be classified as natural risks that have never been of universal importance. Some travel destinations have also received government subsidies to encourage tourists to visit. Consequently, the amount of government subsidies has become a critical factor. Table 1 compares the factors that are critical to travel destination recommendation (or selection) before and during the COVID-19 pandemic [3], [4], [5], [7], [8], [9].

Table 1.

Comparison of factors critical to travel destination recommendation (or selection) before and during the COVID-19 pandemic.

	Before COVID-19 outbreak	During COVID-19 pandemic
Factors	$•$ Travelers’ attitude $•$ Traveler’s subjective norm $•$ Traveler’s perceived behavioral control $•$ Traveler’s past behavior $•$ Traveler’s perception of a country’s products $•$ The number of countries visited $•$ The number of countries visited for pleasure $•$ Stay length $•$ The number of people in the tour group $•$ Travel mode $•$ Availability of public transportation systems $•$ Expected satisfaction $•$ Expected service quality $•$ Expected value $•$ Likelihood to return $•$ Natural disaster risk $•$ Physical risk $•$ Political risk $•$ Performance risk	$•$ The number of confirmed cases in the region $•$ Population density $•$ The amount of government subsidy $•$ The number of outdoor attractions $•$ Travelers’ attitude $•$ Traveler’s subjective norm $•$ Traveler’s perceived behavioral control $•$ Traveler’s past behavior $•$ Traveler’s perception of a region’s products $•$ Stay length $•$ The number of people in the tour group $•$ Travel mode $•$ Expected satisfaction $•$ Expected service quality $•$ Expected value $•$ Likelihood to return $•$ Natural disaster risk $•$ Physical risk $•$ Performance risk

In the literature, several methods for recommending travel destinations have been proposed, such as behavior analysis [10], [11], [12], weighted average (WA) or fuzzy-weighted average (FWA) [13], association or correlation analysis [5], [14], structural equation modeling (SEM) or regression analysis [15], [16], and analytic hierarchy process (AHP) [17], [18], [19]. Websites – such as TripAdvisor, Yelp, and travel agencies – and numerous apps are recommending suitable travel destinations for travelers. Existing websites and apps for recommending travel destinations cannot distinguish whether there is an epidemic outbreak. Existing methods in this field face the following difficulties:

• (1)The current situation differs markedly from the situation before the COVID-19 pandemic. Therefore, it is impossible to infer a traveler’s choice from her or her past behavior.
• (2)For the same reason, it is not feasible to recommend a destination to a traveler based on other travelers’ past choices.
• (3)The selection and recommendation process during the COVID-19 pandemic is much more uncertain than that before the COVID-19 pandemic.

This study addresses these difficulties by proposing a fuzzy multi-criteria decision-making method – the calibrated piecewise-linear fuzzy geometric mean (FGM) approach – for travel destination recommendation during the COVID-19 pandemic. The calibrated piecewise-linear FGM approach does not rely on the analysis of travelers’ behaviors or the knowledge generated by mining their traveling histories but rather on a traveler’s subjective evaluation. Accordingly, it is not subject to the first two difficulties. Furthermore, fuzzy logic is a viable means for modeling uncertainties, such as the uncertainty involved in the travel destination selection and recommendation process during the COVID-19 pandemic.

In the proposed methodology, a fuzzy AHP (FAHP) problem is solved to determine the fuzzy priorities of factors critical to the selection of a travel destination. However, existing FAHP methods are subject to inaccuracy or inefficiency [20]. The calibrated piecewise-linear FGM approach tackles this problem by efficiently and accurately estimating the fuzzy priorities of critical factors. Subsequently, based on the derived fuzzy priorities, a fuzzy technique for order preference by similarity to ideal solution (FTOPSIS) [21] is applied to evaluate the overall performance of a travel destination. The traveler destination with the highest overall performance will be recommended to the traveler.

The remainder of this paper is organized as follows. Section 2 is dedicated to the literature review. Section 3 introduces the calibrated piecewise-linear FGM approach proposed in this study. Section 4 details the application of the proposed methodology for recommending travel destinations to fifteen travelers for regional trips in Taiwan during the COVID-19 pandemic. Finally, Section 5 provides the conclusions of this study and some possible topics for future investigation.

2. Literature review

2.1. Travel destination selection and recommendation

Lam and Hsu [10] considered attitude, subjective norm, perceived behavioral control, and past behavior as factors critical to the selection of a travel destination. They applied the theory of planned behavior (TPB) to simulate a traveler’s decision-making mechanism based on these critical factors. Weaver et al. [5] applied a canonical correlation analysis to investigate the effects of nine factors (the number of countries visited, the number of countries visited for pleasure, stay length, the number of people in the tour group, travel mode, expected satisfaction, expected service quality, expected value, and likelihood to return) on the selection of a travel destination.

In the study by An et al. [7], four risks (natural disaster risk, physical risk, political risk, and performance risk) associated with a travel destination were defined that affect travelers’ satisfaction and purchase intentions. However, for travelers with different characteristics, the effects were not identical. Karl [9] found similar results, demonstrating that travelers with higher educational levels and travel frequencies had affine risks, whereas elderly travelers were risk-averse and uncertainty-averse. These attitudes were reflected in their choices of travel destinations.

Ban [13] applied FWA to evaluate the overall performance of each travel destination. The travel destination with the highest overall performance was recommended to a traveler. Lee and Lockshin [8] believed that a consumer’s perception of a country’s products affects her or her perception of the country as a travel destination. Furthermore, a traveler’s experience at a destination affects her or her intention to revisit [22]. Juwattanasamran et al. [14] mined association rules to predict a traveler’s destination based on his or her characteristics. Abubakar and Ilkan [16] applied SEM to analyze the impact of online word of mouth (WOM) on a traveler’s trust in a destination and intention to travel. Ferns and Walls [15] also adopted the same method. Zhou et al. [19] applied AHP to evaluate the competitiveness of a travel destination. Factors considered in their study included the availability of adventure-based and nature-based activities, hospitality, friendliness of residents, safety and security, shopping ability, the variety and quality of restaurants, and the availability of activities for children.

Yuzhanin and Fisher [11] studied the effectiveness of TPB in predicting travelers’ choice of travel destinations and produced mixed results. Consequently, they claimed that different constructs should be developed for travelers with different characteristics. Qiu et al. [12] described the psychological process of a traveler choosing a travel destination as a cell system. while updating the information in this process, the intention of visiting each destination was successively compared.

2.2. Travel destination recommendation amid the COVID-19 pandemic

In this section, some recent references on travel destination recommendation amid the COVID-19 pandemic are reviewed to show the relevance and contribution of this study. Lee et al. [23] summarized the seven types of measures to control cross-border travel related to the COVID-19 pandemic as travel warning, travel advisory, suspend transportation, visa requirement or refusal, expediting the entry of selected foreign nationals, and restricting the entry of selected foreign nationals, and closing national borders, showing the importance of travel advisory/recommendation for cross-border travel during the COVID-19 pandemic. Wilson and Chen [24] highlighted the impact of the COVID-19 pandemic on the tourism industry and emphasized the importance of restarting tourism to restore the economy. In their view, factors to consider in pre-travel consultation can be classified into three categories: traveler’s personal risk stratification, trip-based determinants, and policies including health insurance, employer mandate and government regulations (origin and destination). This view is consistent with the proposition of this research, as illustrated by Table 2. Wilson and Chen [24] also detailed the components of these categories. However, the factors listed in this study are clearer and more operable. In the view of Anzai et al. [25], the decision to control travel by restricting the freedom of movement should strike a balance between the epidemiological impact and the expected economic fallout. For this reason, gradually resuming tourism and the corresponding tourism consultation (or recommendation) is a critical task. According to Nilashi et al. [26], during the COVID-19 pandemic, tourists are using electronic word of mouth (eWOM) more and more for travel planning. However, recommendation agents supported by applications of machine learning or soft computing techniques may be more effective. In addition, such recommendation agents need to be very efficient. This study aims to fill these gaps.

Table 2.

Factors to consider in pre-travel consultation.

Wilson and Chen [24]	This study
Traveler’s personal risk stratification	$•$ Traveler’s perceived behavioral control $•$ Natural disaster risk $•$ Physical risk $•$ Performance risk
Trip-based determinants	$•$ The number of outdoor attractions $•$ Travelers’ attitude $•$ Traveler’s subjective norm $•$ Traveler’s past behavior $•$ Traveler’s perception of a region’s products $•$ Stay length $•$ Travel mode $•$ Expected satisfaction $•$ Expected service quality $•$ Expected value $•$ Likelihood to return
Policies (including health insurance, employer mandate and government regulations)	$•$ The number of confirmed cases in the region $•$ Population density $•$ The amount of government subsidy $•$ The number of people in the tour group

Compared with these state-of-the-art research, the contribution of this research is twofold. First, this study lists critical factors that affect the selection of a suitable travel destination during the COVID-19 pandemic. Some of these critical factors have not been considered in past travel recommendation studies. In addition, these critical factors are not only used in the proposed methodology, but can also be applied to other types of travel destination recommendation methods. Second, the accuracy and efficiency using existing FAHP methods have been enhanced. Although FAHP methods have been widely discussed and applied, the estimation error generated by approximating the values of weights will lead to the wrong decision. In a recent experiment [27], such estimation error led to incorrect decisions in 15% to 30% of cases. As the risk of making wrong decisions increases during the COVID-19 pandemic, passengers (decision makers) will pay more attention to this.

2.3. Fuzzy Analytic Hierarchy Process (FAHP)

The AHP proposed by Saaty [28] is an established multi-criteria decision-making method. AHP is based on the pairwise comparison of criteria, a subjective process. Fuzzy logic has been incorporated into AHP to consider such subjectivity, resulting in various FAHP methods [29]. FAHP has been widely applied to several topics in various fields, such as supplier selection [20], [30], [31], [32], projects selection and risk assessment and management [33], [34], [35], personnel selection [36], [37], failure mode and effect analysis [38], [39], and strategy analysis and technology selection [40], [41], [42], [43], [44], [45], [46].

In an FAHP problem, deriving the values of fuzzy eigenvalues and eigenvectors requires many fuzzy multiplication operations, a time-consuming task [47] that can be completed using alpha-cut operations (ACO) [48]. Some researchers improved computational efficiency by modifying the definition of consistency to obtain fuzzy eigenvalues and vectors using different methods (i.e., not a fuzzy eigenanalysis) [49], [50], [51]. Furthermore, many FAHP applications used techniques such as fuzzy extent analysis (FEA) [52], [53], [54], FGM [45], [55], [56], and the fuzzy inverse of column sum (FICSM) [54] to approximate, rather than derive, the values of fuzzy eigenvalues and eigenvectors. However, such approximation may lead to incorrect decisions [57], [58]. Chen et al. [59] solved this problem by modifying ACO and proposed the approximating ACO (xACO) method to derive the values of fuzzy eigenvalues and eigenvectors without enumerating all possible $\alpha$ cuts of a fuzzy judgment matrix. However, their method was still time-consuming for a large-scale FAHP problem.

A calibrated piecewise-linear FGM approach is proposed in this study to improve the efficiency and accuracy of solving an FAHP problem. The calibrated piecewise-linear FGM approach is as a hybrid of FGM and ACO. In the calibrated piecewise-linear FGM method, some $\alpha$ cuts of fuzzy eigenvalues and eigenvectors are estimated using FGM. These $\alpha$ cuts are then connected with straight lines. Consequently, the membership functions of fuzzy eigenvalues and eigenvectors are approximated with piecewise linear functions instead of triangular functions. Accordingly, the estimated fuzzy eigenvalue and eigenvector more accurately approximate their exact values. Furthermore, even for a large-scale FAHP problem, the required calculations can be completed quickly because FGM is applied instead of ACO to estimate the $\alpha$ cuts of fuzzy eigenvalues and eigenvectors. The differences between the proposed methodology and some existing methods are summarized in Table 3.

Table 3.

Differences between the proposed methodology and some existing methods.

Method	Type of eigenvalue and eigenvector	Shape of membership functions	Efficiency	Accuracy
FGM	Fuzzy	Triangular	Very high	Low
FEA	Crisp	–	Very high	Very low
FICSM	Fuzzy	Triangular	Very high	Low
ACO	Fuzzy	Nonlinear	Very low	Very high
xACO	Fuzzy	Logarithmic	Low $\sim$ moderate	High
The proposed methodology	Fuzzy	Piecewise Linear	Very high	Moderate to High

2.4. Other methods for deriving the fuzzy priorities of critical factors

Conventional FAHP methods follow the rules established by Saaty [28]: a linguistic scale mapped to [1], [9], meeting the multiplicative requirement, ${\lambda }_{\max }$-based consistency measure, and minimizing the sum of squared deviations between the derived fuzzy priorities and pairwise comparison results [47], [48], [49], [50], [51], [52], [53], [54], [55], [56], [57], [58], [59]. However, it is difficult for these methods to optimize accuracy and efficiency simultaneously, even if the simplest forms of fuzzy numbers are adopted.

Other types of FAHP methods alter the rules [60]. For example, Ozdemir and Nalbant [61] proposed a fuzzy preference relationship method to solve an FAHP problem, in which pairwise comparison results (within [1], [9]) were converted into preference values (within [0, 1]) before deriving the fuzzy priorities of critical factors. Wan et al. [62] proposed a similar approach to address an FAHP problem in which pairwise comparison results were mapped to Atanassov intuitionistic fuzzy numbers. Dožić et al. [63] solved a nonlinear programming problem to optimize the minimum satisfaction level of the derived fuzzy priorities in the pairwise comparison results. Zhang et al. [64] proposed a fuzzy logarithmic least square method that minimized the sum of squared deviations from the derived fuzzy priorities to the pairwise comparison results, both in their logarithmic values.

In addition to FAHP, there are also other methods, such as fuzzy measuring attractiveness using a categorical-based evaluation technique (fuzzy MACBETH) [65], that derive the fuzzy priorities of critical factors from pairwise comparison results. However, fuzzy MACBETH uses an interval scale, whereas FAHP adopts a ratio scale. Furthermore, fuzzy MACBETH solves a mathematical programming problem to derive the fuzzy priorities of critical factors [66], [67].

This study aims to improve the accuracy and efficiency of FAHP methods that follow the original rules of Saaty [28], and therefore will not compare with FAHP methods that follow different rules.

3. Proposed methodology

3.1. Calibrated piecewise-linear FGM

In FAHP, a decision-maker compares the priority of a critical factor over that of another with linguistic terms [68] such as “as equal as”, “weakly more important than”, “strongly more important than”, “very strongly more important than”, and “absolutely more important than”. These linguistic terms are usually mapped to triangular fuzzy numbers (TFNs) within [1], [9] (Table 4) [45], [69], [70].

Table 4.

Linguistic terms for expressing relative priorities.

Symbol	Linguistic term	TFN
L1	As equal as	(1, 1, 3)
L2	As equal as or weakly more important than	(1, 2, 4)
L3	Weakly more important than	(1, 3, 5)
L4	Weakly or strongly more important than	(2, 4, 6)
L5	Strongly more important than	(3, 5, 7)
L6	Strongly or very strongly more important than	(4, 6, 8)
L7	Very strongly more important than	(5, 7, 9)
L8	Very or absolutely strongly more important than	(6, 8, 9)
L9	Absolutely more important than	(7, 9, 9)

Based on pairwise comparison results, the fuzzy judgment matrix ${\tilde{\mathbf{A}}}_{n\times n}=\left[{\tilde{a}}_{ij}\right]$ is constructed as

$$\begin{array}{c}{\tilde{a}}_{ji}=(a_{ji1},a_{ji2},a_{ji3})\hfill \\ =1/{\tilde{a}}_{ij}\hfill \\ \cong (1/a_{ij3},1/a_{ij2},1/a_{ij1})\hfill \end{array}$$ (1)

$${\tilde{a}}_{ii}=1$$ (2)

The fuzzy eigenvalue and eigenvector of $\tilde{\mathbf{A}}$, indicated by $\tilde{\lambda }$ and $\tilde{\mathbf{x}}$ respectively, satisfy [71]

$$det\left(\tilde{\mathbf{A}}(-)\tilde{\lambda }\mathbf{I}\right)=0$$ (3)

and

$$\left(\tilde{\mathbf{A}}(-)\tilde{\lambda }\mathbf{I}\right)(\times )\tilde{\mathbf{x}}=0$$ (4)

where ($-$) and ($\times$) are the fuzzy subtraction and multiplication. Deriving the values of $\tilde{\lambda }$ and $\tilde{\mathbf{x}}$ requires that many fuzzy multiplication operations are performed. However, the multiplication of TFNs does not yield a TFN [72]. Therefore, $\tilde{\lambda }$ and $\tilde{\mathbf{x}}$ are no longer TFNs. The fuzzy priority of critical factor i, indicated by ${\tilde{w}}_i$, can be derived as

$$\begin{array}{cc}{\tilde{w}}_i\hfill & =\frac{{\tilde{x}}_i}{\sum _{j=1}^n{\tilde{x}}_j}\hfill \\ \hfill & =\frac{1}{1+\sum _{j\ne i}\frac{{\tilde{x}}_j}{{\tilde{x}}_i}}\hfill \end{array}$$ (5)

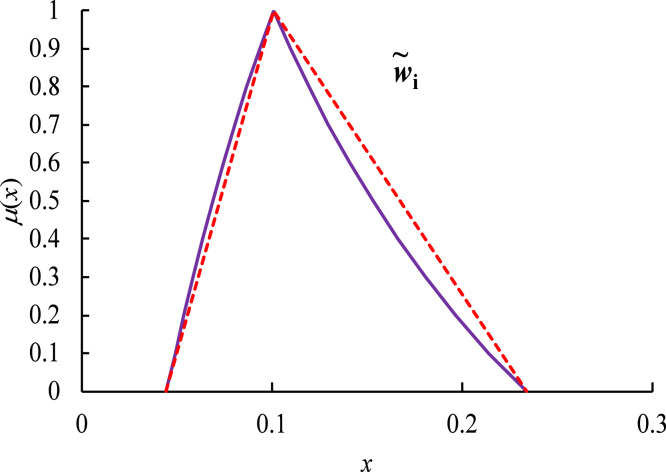
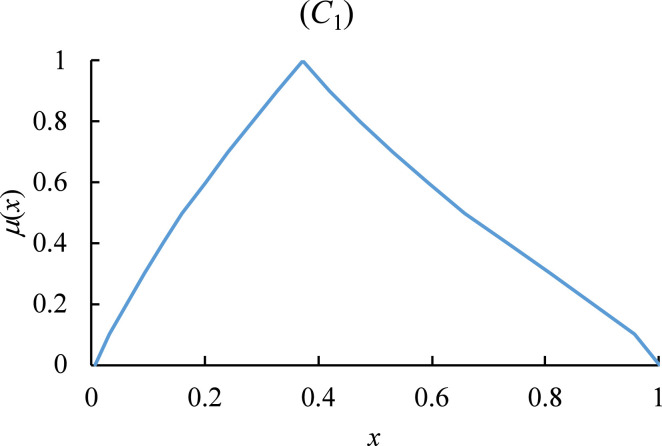
Consequently, ${\tilde{w}}_i$ is not a TFN either, as illustrated in Fig. 1. Approximating ${\tilde{w}}_i$ with a TFN may lead to an incorrect decision. This problem becomes more severe because all fuzzy priorities add up to 1, so the inaccuracy of one fuzzy priority aggravates that of another fuzzy priority.

Fig. 1.

Non-TFN nature of a fuzzy priority.

The FGM method estimates ${\tilde{w}}_i$ as [70]

$${\tilde{w}}_i\cong \frac{\sqrt[n]{\prod _{j=1}^n{\tilde{a}}_{ij}}}{\sum _{k=1}^n\sqrt[n]{\prod _{j=1}^n{\tilde{a}}_{kj}}}$$ (6)

When ${\tilde{w}}_i$ is approximated with a TFN, i.e., ${\tilde{w}}_i=(w_{i1},w_{i2},w_{i3})$, the following theorem holds.

Theorem 1 [45] —

$$w_{i1}\cong \frac{1}{1+\sum _{k\ne i}\frac{\sqrt[n]{\prod _{j=1}^n{a}_{kj3}}}{\sqrt[n]{\prod _{j=1}^n{a}_{ij1}}}}$$ (7)

$$w_{i2}\cong \frac{1}{1+\sum _{k\ne i}\frac{\sqrt[n]{\prod _{j=1}^n{a}_{kj2}}}{\sqrt[n]{\prod _{j=1}^n{a}_{ij2}}}}$$ (8)

$$w_{i3}\cong \frac{1}{1+\sum _{k\ne i}\frac{\sqrt[n]{\prod _{j=1}^n{a}_{kj1}}}{\sqrt[n]{\prod _{j=1}^n{a}_{ij3}}}}$$ (9)

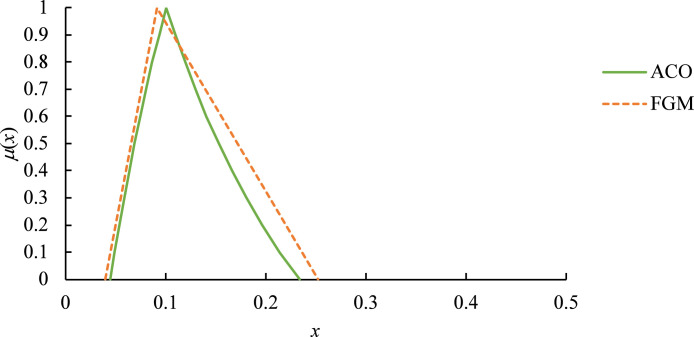
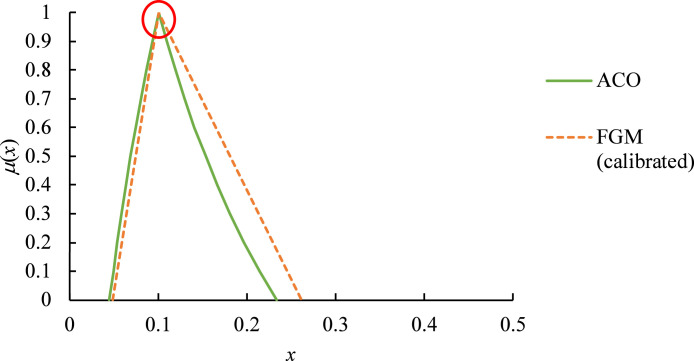
A fuzzy priority estimated using FGM is illustrated in Fig. 2. the core (with a membership of 1) of an estimated fuzzy priority was not equal to the actual value (derived using ACO). Therefore, the estimated fuzzy priority can be calibrated so that its core overlaps with the actual value, thereby improving the estimation accuracy, as illustrated in Fig. 3:

$${\tilde{w}}_i\left(\mathrm{FGM}\right)\to {\tilde{w}}_i\left(\mathrm{FGM}\right)+w_{i2}\left(\mathrm{ACO}\right)-w_{i2}\left(\mathrm{FGM}\right)$$ (10)

Accordingly, only a single eigenanalysis based on the core of the fuzzy judgment matrix, which can be done in an instant, is performed.

Fig. 2.

Fuzzy priority estimated using FGM.

Fig. 3.

Calibrating estimated fuzzy priority.

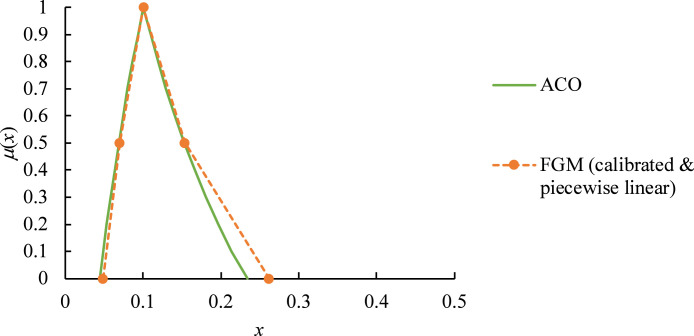
However, the edges of an estimated fuzzy priority using FGM are linear, whereas those of the actual values are nonlinear. Accordingly, the $\alpha$ cuts of a fuzzy priority can be estimated using FGM and then connected to form piecewise linear edges similar to curved edges (Fig. 4). Because such $\alpha$ cuts are estimated using FGM, the required calculations can also be completed in an instant.

Fig. 4.

Calibrated estimated fuzzy priority with piecewise linear edges.

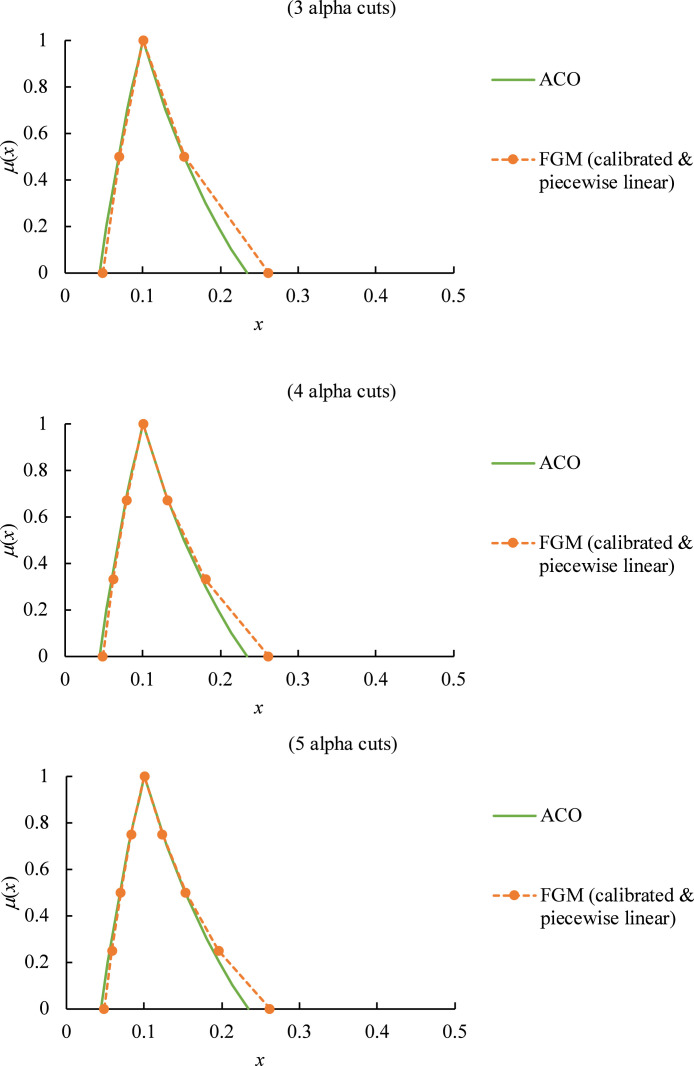
The estimation accuracy improves when more $\alpha$ cuts are connected, as illustrated in Fig. 5.

Fig. 5.

Improvement in estimation accuracy by connecting more $\alpha$ cuts.

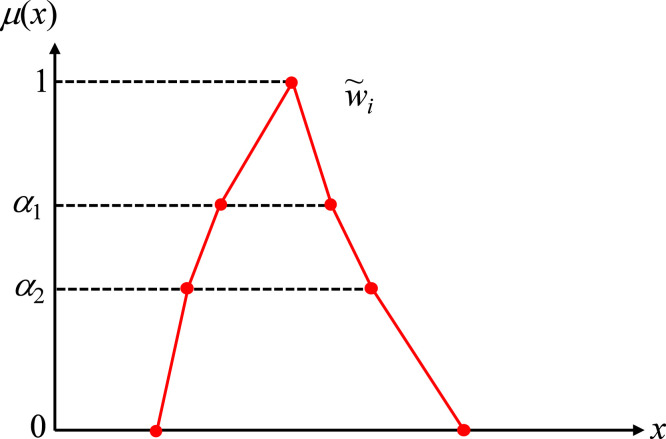
The procedure is described as follows. Assume the left and right $\alpha$ cuts of ${\tilde{w}}_i$ are indicated by $w_i^L\left(\alpha \right)$ and $w_i^R\left(\alpha \right)$, respectively. According to Theorem 1,

$$w_i^L\left(\alpha \right)\cong \frac{1}{1+\sum _{k\ne i}\frac{\sqrt[n]{\prod _{j=1}^n{a}_{kj}^R\left(\alpha \right)}}{\sqrt[n]{\prod _{j=1}^n{a}_{ij}^L\left(\alpha \right)}}}$$ (11)

$$w_i^R\left(\alpha \right)\cong \frac{1}{1+\sum _{k\ne i}\frac{\sqrt[n]{\prod _{j=1}^n{a}_{kj}^L\left(\alpha \right)}}{\sqrt[n]{\prod _{j=1}^n{a}_{ij}^R\left(\alpha \right)}}}$$ (12)

Then, a fuzzy priority is estimated by connecting some of its $\alpha$ cuts with straight lines, as illustrated in Fig. 6, in which the membership function on either side is approximated by connecting four $\alpha$ cuts with straight lines:

Fig. 6.

Fuzzy priority estimated by connecting some of its $\alpha$ cuts with straight lines.

(Left-hand side)

$${\mu }_{w_i}\left(x\right)=\left\{\begin{array}{c}\frac{x-w_i^L\left(0\right)}{w_i^L\left({\alpha }_1\right)-w_i^L\left(0\right)}\cdot {\alpha }_1\hfill \\ if{w}_i^L\left(0\right)\le x<w_i^L\left({\alpha }_1\right)\hfill \\ \frac{x-w_i^L\left({\alpha }_1\right)}{w_i^L\left({\alpha }_2\right)-w_i^L\left({\alpha }_1\right)}\cdot ({\alpha }_2-{\alpha }_1)+{\alpha }_1\hfill \\ if{w}_i^L\left({\alpha }_1\right)\le x<w_i^L\left({\alpha }_2\right)\hfill \\ \frac{x-w_i^L\left({\alpha }_2\right)}{w_i^{\ast }\left(1\right)-w_i^L\left({\alpha }_2\right)}\cdot (1-{\alpha }_2)+{\alpha }_2\hfill \\ if{w}_i^L\left({\alpha }_2\right)\le x<w_i^{\ast }\left(1\right)\hfill \end{array}\right)$$ (13)

(Right-hand side)

$${\mu }_{w_i}\left(x\right)=\left\{\begin{array}{c}\frac{x-w_i^{\ast }\left(1\right)}{w_i^R\left({\alpha }_2\right)-w_i^{\ast }\left(1\right)}\cdot ({\alpha }_2-1)+1\hfill \\ if{w}_i^{\ast }\left(1\right)\le x<w_i^R\left({\alpha }_2\right)\hfill \\ \frac{x-w_i^R\left({\alpha }_2\right)}{w_i^R\left({\alpha }_1\right)-w_i^R\left({\alpha }_2\right)}\cdot ({\alpha }_1-{\alpha }_2)+{\alpha }_2\hfill \\ if{w}_i^R\left({\alpha }_2\right)\le x<w_i^R\left({\alpha }_1\right)\hfill \\ \frac{x-w_i^R\left({\alpha }_1\right)}{w_i^R\left(0\right)-w_i^R\left({\alpha }_1\right)}\cdot (0-{\alpha }_1)+{\alpha }_1\hfill \\ if{w}_i^R\left({\alpha }_1\right)\le x<w_i^R\left(0\right)\hfill \end{array}\right)$$ (14)

FGM is a special case of calibrated piecewise-linear FGM because only the $\alpha$ cuts for $\alpha =0$ and 1 are connected.

Calibrated piecewise-linear FGM is more accurate than FGM and FEA. In contrast, it is much more efficient than existing enumeration-based methods such as ACO and xACO. When $\alpha$ takes 11 possible values (0, 0.1, …, 1), the numbers of FGM operations and the eigenanalyses required for various methods are compared, as presented in Table 5.

Table 5.

Number of iterations required when $\alpha$ takes 11 possible values.

Method	Number of FGM operations	Number of eigenanalyses
FEA	3	0
FGM	3	0
ACO	0	$11\cdot 2^{{\mathrm{C}}_2^n}$
xACO	0	$10\text{\%}\cdot 11\cdot 2^{{\mathrm{C}}_2^n}$
Calibrated piecewise-linear FGM	20	1

3.2. FTOPSIS for evaluating overall performance of a travel destination

Subsequently, FTOPSIS [73] is applied to assess the overall performance of a travel destination. First, the performance of a travel destination in optimizing each critical factor is normalized using fuzzy distributive normalization:

$$\begin{array}{cc}{\tilde{\rho }}_{qi}\hfill & =\frac{{\tilde{p}}_{qi}}{\sqrt{\sum _{\varphi =1}^Q{\tilde{p}}_{\varphi i}^2}}\hfill \\ \hfill & =\frac{1}{\sqrt{1+\sum _{\varphi \ne q}{\left(\frac{{\tilde{p}}_{\varphi i}}{{\tilde{p}}_{qi}}\right)}^2}}\hfill \end{array}$$ (15)

where ${\tilde{p}}_{qi}$ is the performance of the q-th travel destination in optimizing the $i$th critical factor and ${\tilde{\rho }}_{qi}$ is the normalized performance. Replacing all variables in Eq. (15) with their $\alpha$ cuts gives

$${\rho }_{qi}^L\left(\alpha \right)=\frac{1}{\sqrt{1+\sum _{j\ne i}{\left(\frac{p_{qj}^R\left(\alpha \right)}{{\tilde{p}}_{qi}^L\left(\alpha \right)}\right)}^2}}$$ (16)

$${\rho }_{qi}^R\left(\alpha \right)=\frac{1}{\sqrt{1+\sum _{j\ne i}{\left(\frac{p_{qj}^L\left(\alpha \right)}{{\tilde{p}}_{qi}^R\left(\alpha \right)}\right)}^2}}$$ (17)

Subsequently, the fuzzy weighted scores are calculated based on the fuzzy priorities derived using the calibrated piecewise-linear FGM approach:

$${\tilde{s}}_{qi}={\tilde{w}}_i(\times ){\tilde{\rho }}_{qi}$$ (18)

Equivalently,

$$s_{qi}^L=w_i^L\left(\alpha \right){\rho }_{qi}^L\left(\alpha \right)$$ (19)

$$s_{qi}^R=w_i^R\left(\alpha \right){\rho }_{qi}^R\left(\alpha \right)$$ (20)

The fuzzy ideal (zenith) point and fuzzy anti-ideal (nadir) point are specified, respectively, as

$${\tilde{\Lambda }}^{+}=\left\{{\tilde{\Lambda }}_i^{+}\right\}=\left\{\underset{q}{max}{\tilde{s}}_{qi}\right\}$$ (21)

$${\tilde{\Lambda }}^{-}=\left\{{\tilde{\Lambda }}_i^{-}\right\}=\left\{\underset{q}{min}{\tilde{s}}_{qi}\right\}$$ (22)

Their $\alpha$ cuts are as follows:

$$[{\Lambda }^{+L}\left(\alpha \right),{\Lambda }^{+R}\left(\alpha \right)]=\left\{[{\Lambda }_i^{+L}\left(\alpha \right),{\Lambda }_i^{+R}\left(\alpha \right)]\right\},=\left\{[\underset{q}{max}{s}_{qi}^L\left(\alpha \right),\underset{q}{max}{s}_{qi}^R\left(\alpha \right)]\right\}$$ (23)

$$[{\Lambda }^{-L}\left(\alpha \right),{\Lambda }^{-R}\left(\alpha \right)]=\left\{[{\Lambda }_i^{-L}\left(\alpha \right),{\Lambda }_i^{-R}\left(\alpha \right)]\right\},=\left\{[\underset{q}{min}{s}_{qi}^L\left(\alpha \right),\underset{q}{min}{s}_{qi}^R\left(\alpha \right)]\right\}$$ (24)

The fuzzy distance from each travel destination to the two reference points are calculated respectively as

$${\tilde{d}}_q^{+}=\sqrt{\sum _{i=1}^n{\left({\tilde{\Lambda }}_i^{+}(-){\tilde{s}}_{qi}\right)}^2}$$ (25)

$${\tilde{d}}_q^{-}=\sqrt{\sum _{i=1}^n{\left({\tilde{\Lambda }}_i^{-}(-){\tilde{s}}_{qi}\right)}^2}$$ (26)

Equivalently,

$$d_q^{+L}\left(\alpha \right)=\sqrt{\sum _{i=1}^n{(max(\underset{i}{\overset{+L}{\Lambda }}\left(\alpha \right)-s_{qi}^R\left(\alpha \right),0))}^2}$$ (27)

$$d_q^{+R}\left(\alpha \right)=\sqrt{\sum _{i=1}^n{({\Lambda }_i^{+R}\left(\alpha \right)-s_{qi}^L\left(\alpha \right))}^2}$$ (28)

$$d_q^{-L}\left(\alpha \right)=\sqrt{\sum _{i=1}^n{(min(\underset{i}{\overset{-R}{\Lambda }}\left(\alpha \right)-s_{qi}^L\left(\alpha \right),0))}^2}$$ (29)

$$d_q^{-R}\left(\alpha \right)=\sqrt{\sum _{i=1}^n{({\Lambda }_i^{-L}\left(\alpha \right)-s_{qi}^R\left(\alpha \right))}^2}$$ (30)

Finally, the fuzzy closeness of each travel destination is obtained as

$${\tilde{C}}_q=\frac{{\tilde{d}}_q^{-}}{{\tilde{d}}_q^{+}(+){\tilde{d}}_q^{-}}$$ (31)

Therefore,

$$C_q^L\left(\alpha \right)=min(\frac{\underset{q}{\overset{-R}{d}}\left(\alpha \right)}{\underset{q}{\overset{+R}{d}}\left(\alpha \right)+d_q^{-R}\left(\alpha \right)},\frac{\underset{q}{\overset{-L}{d}}\left(\alpha \right)}{\underset{q}{\overset{+R}{d}}\left(\alpha \right)+d_q^{-L}\left(\alpha \right)})$$ (32)

$$C_q^R\left(\alpha \right)=max(\frac{\underset{q}{\overset{-R}{d}}\left(\alpha \right)}{\underset{q}{\overset{+L}{d}}\left(\alpha \right)+d_q^{-R}\left(\alpha \right)},\frac{\underset{q}{\overset{-L}{d}}\left(\alpha \right)}{\underset{q}{\overset{+L}{d}}\left(\alpha \right)+d_q^{-L}\left(\alpha \right)})$$ (33)

A travel destination with a higher fuzzy closeness is more suitable. For an absolute ranking, the fuzzy closeness can be defuzzified using the center-of-gravity (COG) method:

$$D\left({\tilde{C}}_q\right)=\frac{{\int }_0^1\alpha \left(\frac{C_q^L\left(\alpha \right)+C_q^R\left(\alpha \right)}{2}\right)d\alpha }{{\int }_0^1\alpha d\alpha }$$ (34)

4. Application

The proposed methodology has been applied to recommend suitable travel destinations to fifteen travelers that would like to take regional trips in Taiwan after several months of lockdown from to the COVID-19 pandemic. at the time of this study, the period during which the Taiwan government banned residents from traveling abroad had been extended to the end of August.

Five factors are critical to the selection of a suitable travel destination during the COVID-19 pandemic:

• •the number of confirmed cases in the region,
• •the population density of the region,
• •the amount of government subsidies for traveling to the region,
• •the number of outdoor attractions in the region, and
• •the expected value of the travel destination.

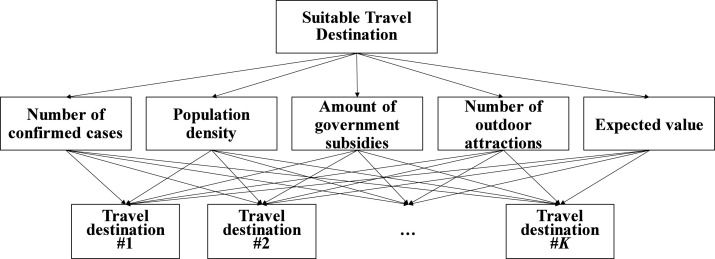
Among these critical factors, the number of confirmed cases and the amount of government subsidies have rarely been considered by travelers before the COVID-19 pandemic [74], [75], [76]. Population density used to be a positive indicator, but it has become a negative indicator. The number of outdoor attractions was once an indicator for specific populations, but it is now pursued by everyone. The expected value of a travel destination is equally important before and during the COVID-19 pandemic. The FAHP problem is illustrated in Fig. 7.

Fig. 7.

FAHP problem.

Consider the details of the first traveler as an example. The traveler first compared the relative priorities of these critical factors with linguistic terms. The results are summarized in Table 6.

Table 6.

Results of pairwise comparisons.

Critical factor #1	Critical factor #2	Relative priority of critical factor #1 over critical factor #2
Number of confirmed cases	Population density	Weakly more important than
Number of confirmed cases	Amount of government subsidies	Strongly more important than
Number of outdoor attractions	Number of confirmed cases	Weakly or strongly more important than
Expected value	Number of confirmed cases	As equal as
Amount of government subsidies	Population density	Weakly or strongly more important than
Number of outdoor attractions	Population density	Strongly more important than
Expected value	Population density	Weakly more important than
Number of outdoor attractions	Amount of government subsidies	Strongly more important than
Amount of government subsidies	Expected value	Weakly more important than
Number of outdoor attractions	Expected value	Weakly more important than

Based on Table 6, the following fuzzy judgment matrix was constructed:

$$\tilde{\mathbf{A}}=\left[\begin{array}{ccccc}\hfill 1\hfill & \hfill (1,3,5)\hfill & \hfill (3,5,7)\hfill & \hfill 1/(2,4,6)\hfill & \hfill 1/(1,1,3)\hfill \\ \hfill 1/(1,3,5)\hfill & \hfill 1\hfill & \hfill 1/(2,4,6)\hfill & \hfill 1/(3,5,7)\hfill & \hfill 1/(1,3,5)\hfill \\ \hfill 1/(3,5,7)\hfill & \hfill (2,4,6)\hfill & \hfill 1\hfill & \hfill 1/(3,5,7)\hfill & \hfill (1,3,5)\hfill \\ \hfill (2,4,6)\hfill & \hfill (3,5,7)\hfill & \hfill (3,5,7)\hfill & \hfill 1\hfill & \hfill (1,3,5)\hfill \\ \hfill (1,1,3)\hfill & \hfill (1,3,5)\hfill & \hfill 1/(1,3,5)\hfill & \hfill 1/(1,3,5)\hfill & \hfill 1\hfill \end{array}\right]$$ (35)

The consistency ratio of $\tilde{\mathbf{A}}$ was approximately 0.19, which was considered acceptable because the COVID-19 pandemic was highly uncertain. The fuzzy priorities of critical factors were derived from the fuzzy judgment matrix using the calibrated piecewise-linear FGM approach. The calibrated piecewise-linear FGM approach was implemented using MATLAB on a PC with a 3.60 GHz Intel Core i7-7700 CPU 3.60 with 8 GB of RAM. The execution time was less than 1 s. The results, in terms of their $\alpha$ cuts for $\alpha =0$, 0.5, and 1, are presented in Table 7. These $\alpha$ cuts were calibrated. The results are depicted in Table 8.

Table 7.

Fuzzy priorities of critical factors.

i	${\tilde{w}}_i\left(0\right)$	${\tilde{w}}_i(0.5)$	${\tilde{w}}_i\left(1\right)$
1	[0.08, 0.36]	[0.13, 0.27]	[0.20, 0.20]
2	[0.03, 0.17]	[0.04, 0.09]	[0.05, 0.05]
3	[0.06, 0.28]	[0.09, 0.19]	[0.13, 0.13]
4	[0.25, 0.68]	[0.37, 0.59]	[0.48, 0.48]
5	[0.06, 0.35]	[0.09, 0.21]	[0.12, 0.12]

Table 8.

Calibrated fuzzy priorities.

i	${\tilde{w}}_i\left(0\right)$	${\tilde{w}}_i(0.5)$	${\tilde{w}}_i\left(1\right)$
1	[0.11, 0.39]	[0.16, 0.30]	[0.23, 0.23]
2	[0.03, 0.17]	[0.04, 0.09]	[0.05, 0.05]
3	[0.07, 0.29]	[0.10, 0.20]	[0.14, 0.14]
4	[0.23, 0.66]	[0.35, 0.57]	[0.46, 0.46]
5	[0.06, 0.35]	[0.09, 0.21]	[0.12, 0.12]

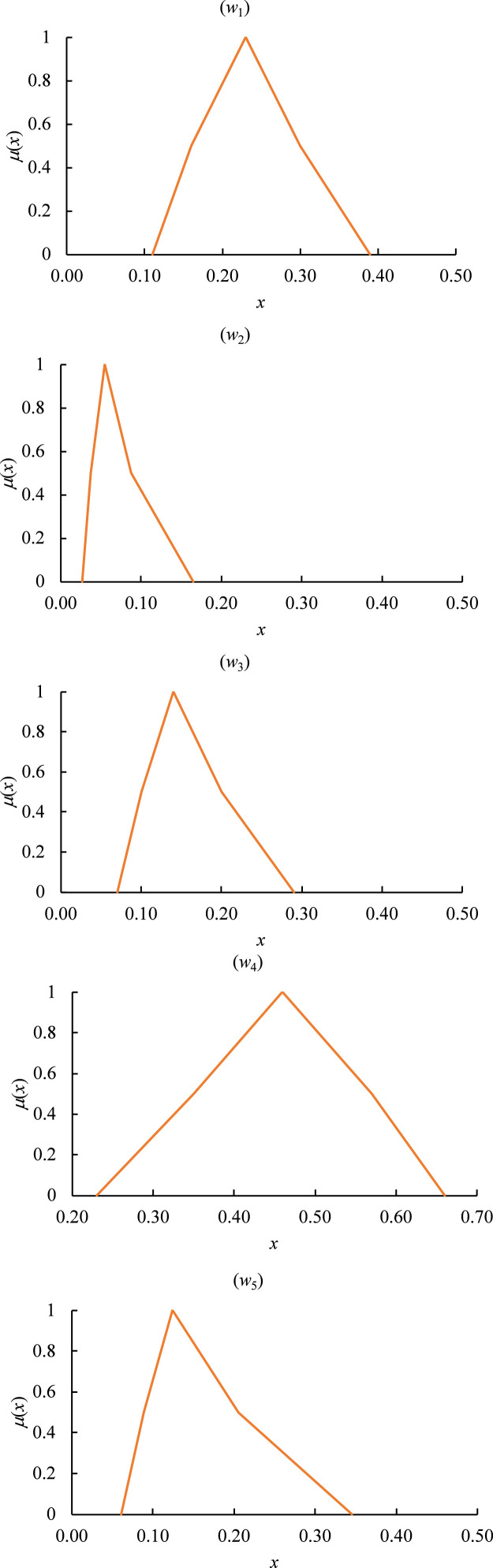
These calibrated $\alpha$ cuts were connected to form the piecewise-linear membership functions of fuzzy priorities, as depicted in Fig. 8.

Fig. 8.

Fuzzy priorities estimated using calibrated piecewise-linear FGM.

The most important critical factor was “the number of outdoor attractions”, followed by “the number of confirmed cases room rate discount” and “expected value”.

There are hundreds of travel destinations in the geographic database. Each traveler chose at most ten travel destinations in which he or she was most interested. Then, the traveler applied the proposed methodology to help make a choice. Consider the first traveler as an example. The five travel destinations the traveler considered are represented by A to E. The collected data on the five travel destinations are summarized in Table 9.

Table 9.

Data on five travel destinations.

Travel destination	Number of confirmed cases	Population density	Amount of government subsidies (NTD)	Number of outdoor attractions	Expected value
A	0	827.88	1200	4	Moderate to High
B	0	70.27	700	14	High
C	2	211.74	700	10	Moderate
D	43	1271.81	700	16	Low to moderate
E	12	293.91	700	21	Very high

Among the five critical factors, “the amount of government subsidies”, “the number of outdoor attractions”, and “expected value” exhibited the-higher-the-better performance, whereas “the number of confirmed cases” and “population density” exhibited the-lower-the-better performance. The performance was evaluated according to the rules depicted in Table 10. Consider “number of confirmed cases” as an example. The minimum and maximum of this critical factor in the regions of all travel destinations are first derived as ${min}_r{x}_r$ and ${max}_r{x}_r$, respectively. If the number of confirmed cases in the region of a travel destination is more than $0.9\cdot {min}_r{x}_r+0.1\cdot {max}_r{x}_r$ but less than $0.65\cdot {min}_r{x}_r+0.35\cdot {max}_r{x}_r$, the performance of the travel destination in optimizing this critical factor is (3, 4, 5).

Table 10.

Rules for evaluating performance.

Critical factor	Rule
Number of confirmed cases	${\tilde{p}}_{q1}\left(x_q\right)=\left\{\begin{array}{ccc}(0,0,1)\hfill & \mathrm{if}\hfill & 0.1\cdot {min}_r{x}_r+0.9\cdot {max}_r{x}_r\le x_q\text{or data not available}\hfill \\ (0,1,2)\hfill & \mathrm{if}\hfill & 0.35\cdot {min}_r{x}_r+0.65\cdot {max}_r{x}_r\le x_q<0.1\cdot {min}_r{x}_r+0.9\cdot {max}_r{x}_r\hfill \\ (1.5,2.5,3.5)\hfill & \mathrm{if}\hfill & 0.65\cdot {min}_r{x}_r+0.35\cdot {max}_r{x}_r\le x_q<0.35\cdot {min}_r{x}_r+0.65\cdot {max}_r{x}_r\hfill \\ (3,4,5)\hfill & \mathrm{if}\hfill & 0.9\cdot {min}_r{x}_r+0.1\cdot {max}_r{x}_r\le x_q<0.65\cdot {min}_r{x}_r+0.35\cdot {max}_r{x}_r\hfill \\ (4,5,5)\hfill & \mathrm{if}\hfill & x_q<0.9\cdot {min}_r{x}_r+0.1\cdot {max}_r{x}_r\hfill \end{array}\right)$ where $x_q$ is the number of confirmed cases in the region.
Population density	${\tilde{p}}_{q2}\left(x_q\right)=\left\{\begin{array}{ccc}(0,0,1)\hfill & \mathrm{if}\hfill & 0.1\cdot {min}_r{x}_r+0.9\cdot {max}_r{x}_r\le x_q\text{or data not available}\hfill \\ (0,1,2)\hfill & \mathrm{if}\hfill & 0.35\cdot {min}_r{x}_r+0.65\cdot {max}_r{x}_r\le x_q<0.1\cdot {min}_r{x}_r+0.9\cdot {max}_r{x}_r\hfill \\ (1.5,2.5,3.5)\hfill & \mathrm{if}\hfill & 0.65\cdot {min}_r{x}_r+0.35\cdot {max}_r{x}_r\le x_q<0.35\cdot {min}_r{x}_r+0.65\cdot {max}_r{x}_r\hfill \\ (3,4,5)\hfill & \mathrm{if}\hfill & 0.9\cdot {min}_r{x}_r+0.1\cdot {max}_r{x}_r\le x_q<0.65\cdot {min}_r{x}_r+0.35\cdot {max}_r{x}_r\hfill \\ (4,5,5)\hfill & \mathrm{if}\hfill & x_q<0.9\cdot {min}_r{x}_r+0.1\cdot {max}_r{x}_r\hfill \end{array}\right)$ where $x_q$ is the population density of the region.
Amount of government subsidies	${\tilde{p}}_{q3}\left(x_q\right)=\left\{\begin{array}{ccc}(0,0,1)\hfill & \mathrm{if}\hfill & x_q<0.9\cdot {min}_r{x}_r+0.1\cdot {max}_r{x}_r\text{or data not available}\hfill \\ (0,1,2)\hfill & \mathrm{if}\hfill & 0.9\cdot {min}_r{x}_r+0.1\cdot {max}_r{x}_r\le x_q<0.65\cdot {min}_r{x}_r+0.35\cdot {max}_r{x}_r\hfill \\ (1.5,2.5,3.5)\hfill & \mathrm{if}\hfill & 0.65\cdot {min}_r{x}_r+0.35\cdot {max}_r{x}_r\le x_q<0.35\cdot {min}_r{x}_r+0.65\cdot {max}_r{x}_r\hfill \\ (3,4,5)\hfill & \mathrm{if}\hfill & 0.35\cdot {min}_r{x}_r+0.65\cdot {max}_r{x}_r\le x_q<0.1\cdot {min}_r{x}_r+0.9\cdot {max}_r{x}_r\hfill \\ (4,5,5)\hfill & \mathrm{if}\hfill & 0.1\cdot {min}_r{x}_r+0.9\cdot {max}_r{x}_r\le x_q\hfill \end{array}\right)$ where $x_q$ is the amount of government subsidies for traveling to the region.
Number of outdoor attractions	${\tilde{p}}_{q4}\left(x_q\right)=\left\{\begin{array}{ccc}(0,0,1)\hfill & \mathrm{if}\hfill & x_q<0.9\cdot {min}_r{x}_r+0.1\cdot {max}_r{x}_r\text{or data not available}\hfill \\ (0,1,2)\hfill & \mathrm{if}\hfill & 0.9\cdot {min}_r{x}_r+0.1\cdot {max}_r{x}_r\le x_q<0.65\cdot {min}_r{x}_r+0.35\cdot {max}_r{x}_r\hfill \\ (1.5,2.5,3.5)\hfill & \mathrm{if}\hfill & 0.65\cdot {min}_r{x}_r+0.35\cdot {max}_r{x}_r\le x_q<0.35\cdot {min}_r{x}_r+0.65\cdot {max}_r{x}_r\hfill \\ (3,4,5)\hfill & \mathrm{if}\hfill & 0.35\cdot {min}_r{x}_r+0.65\cdot {max}_r{x}_r\le x_q<0.1\cdot {min}_r{x}_r+0.9\cdot {max}_r{x}_r\hfill \\ (4,5,5)\hfill & \mathrm{if}\hfill & 0.1\cdot {min}_r{x}_r+0.9\cdot {max}_r{x}_r\le x_q\hfill \end{array}\right)$ where $x_q$ is the number of outdoor attractions in the region.
Expected value	${\tilde{p}}_{q5}\left(x_q\right)=\left\{\begin{array}{ccc}(0,0,1)\hfill & \mathrm{if}\hfill & x_q=“{\text{very low}}^{\prime \prime }\hfill \\ (0,1,2)\hfill & \mathrm{if}\hfill & x_q=“{\mathrm{low}}^{\prime \prime }\hfill \\ (1.5,2.5,3.5)\hfill & \mathrm{if}\hfill & x_q=“{\text{moderate}}^{\prime \prime }\hfill \\ (3,4,5)\hfill & \mathrm{if}\hfill & x_q=“{\text{high}}^{\prime \prime }\hfill \\ (4,5,5)\hfill & \mathrm{if}\hfill & x_q=“{\text{very high}}^{\prime \prime }\hfill \end{array}\right)$ where $x_q$ is the expected value of the travel destination.

Table 11 presents the evaluation results. There was no perfect travel destination that dominated the others.

Table 11.

Evaluation results.

q	${\tilde{p}}_{q1}$	${\tilde{p}}_{q2}$	${\tilde{p}}_{q3}$	${\tilde{p}}_{q4}$	${\tilde{p}}_{q5}$
1	(4.00, 5.00, 5.00)	(1.50, 2.50, 3.50)	(4.00, 5.00, 5.00)	(0.00, 0.00, 1.00)	(2.25, 3.25, 4.25)
2	(4.00, 5.00, 5.00)	(4.00, 5.00, 5.00)	(0.00, 0.00, 1.00)	(1.50, 2.50, 3.50)	(3.00, 4.00, 5.00)
3	(4.00, 5.00, 5.00)	(3.00, 4.00, 5.00)	(0.00, 0.00, 1.00)	(1.50, 2.50, 3.50)	(1.50, 2.50, 3.50)
4	(0.00, 0.00, 1.00)	(0.00, 0.00, 1.00)	(0.00, 0.00, 1.00)	(3.00, 4.00, 5.00)	(0.75, 1.75, 2.75)
5	(3.00, 4.00, 5.00)	(3.00, 4.00, 5.00)	(0.00, 0.00, 1.00)	(4.00, 5.00, 5.00)	(4.00, 5.00, 5.00)

FTOPSIS was applied to assess the overall performance of each travel destination. First, the performance of a travel destination in optimizing each criterion was normalized using fuzzy distributive normalization. The results are summarized in Table 12.

Table 12.

Normalized performance.

q	${\tilde{\rho }}_{q1}$	${\tilde{\rho }}_{q2}$	${\tilde{\rho }}_{q3}$	${\tilde{\rho }}_{q4}$	${\tilde{\rho }}_{q5}$
1	(0.42, 0.52, 0.62)	(0.17, 0.31, 0.51)	(0.89, 1.00, 1.00)	(0.00, 0.00, 0.18)	(0.26, 0.42, 0.63)
2	(0.42, 0.52, 0.62)	(0.45, 0.63, 0.74)	(0.00, 0.00, 0.20)	(0.17, 0.34, 0.63)	(0.35, 0.51, 0.74)
3	(0.42, 0.52, 0.62)	(0.34, 0.50, 0.74)	(0.00, 0.00, 0.20)	(0.17, 0.34, 0.63)	(0.17, 0.32, 0.52)
4	(0.00, 0.00, 0.12)	(0.00, 0.00, 0.15)	(0.00, 0.00, 0.20)	(0.35, 0.55, 0.91)	(0.09, 0.22, 0.41)
5	(0.31, 0.42, 0.62)	(0.34, 0.50, 0.74)	(0.00, 0.00, 0.20)	(0.46, 0.68, 0.91)	(0.46, 0.64, 0.74)

Second, the fuzzy weighted scores of all travel destinations, in terms of $\alpha$ cuts, were calculated based on the derived fuzzy priorities. The results are summarized in Table 13.

Table 13.

Fuzzy weighted scores.

q	${\tilde{s}}_{q1}$ ($\alpha$: $\alpha$ cut)	${\tilde{s}}_{q2}$ ($\alpha$: $\alpha$ cut)	${\tilde{s}}_{q3}$ ($\alpha$: $\alpha$ cut)	${\tilde{s}}_{q4}$ ($\alpha$: $\alpha$ cut)	${\tilde{s}}_{q5}$ ($\alpha$: $\alpha$ cut)
1	0.0: [0.05, 0.24] 0.1: [0.05, 0.23] 0.2: [0.06, 0.21] 0.3: [0.06, 0.20] 0.4: [0.07, 0.18] 0.5: [0.08, 0.17] 0.6: [0.08, 0.16] 0.7: [0.09, 0.15] 0.8: [0.10, 0.14] 0.9: [0.11, 0.13] 1.0: [0.12, 0.12]	0.0: [0.01, 0.09] 0.1: [0.01, 0.08] 0.2: [0.01, 0.07] 0.3: [0.01, 0.06] 0.4: [0.01, 0.05] 0.5: [0.01, 0.04] 0.6: [0.01, 0.03] 0.7: [0.01, 0.03] 0.8: [0.01, 0.02] 0.9: [0.01, 0.02] 1.0: [0.02, 0.02]	0.0: [0.06, 0.29] 0.1: [0.07, 0.27] 0.2: [0.08, 0.25] 0.3: [0.08, 0.24] 0.4: [0.09, 0.22] 0.5: [0.09, 0.20] 0.6: [0.10, 0.19] 0.7: [0.11, 0.18] 0.8: [0.12, 0.16] 0.9: [0.13, 0.15] 1.0: [0.14, 0.14]	0.0: [0.00, 0.12] 0.1: [0.00, 0.10] 0.2: [0.00, 0.09] 0.3: [0.00, 0.08] 0.4: [0.00, 0.06] 0.5: [0.00, 0.05] 0.6: [0.00, 0.04] 0.7: [0.00, 0.03] 0.8: [0.00, 0.02] 0.9: [0.00, 0.01] 1.0: [0.00, 0.00]	0.0: [0.02, 0.22] 0.1: [0.02, 0.20] 0.2: [0.02, 0.17] 0.3: [0.02, 0.15] 0.4: [0.03, 0.13] 0.5: [0.03, 0.11] 0.6: [0.03, 0.10] 0.7: [0.04, 0.08] 0.8: [0.04, 0.07] 0.9: [0.05, 0.06] 1.0: [0.05, 0.05]
2	0.0: [0.05, 0.24] 0.1: [0.05, 0.23] 0.2: [0.06, 0.21] 0.3: [0.06, 0.20] 0.4: [0.07, 0.18] 0.5: [0.08, 0.17] 0.6: [0.08, 0.16] 0.7: [0.09, 0.15] 0.8: [0.10, 0.14] 0.9: [0.11, 0.13] 1.0: [0.12, 0.12]	0.0: [0.01, 0.12] 0.1: [0.02, 0.11] 0.2: [0.02, 0.10] 0.3: [0.02, 0.09] 0.4: [0.02, 0.07] 0.5: [0.02, 0.06] 0.6: [0.02, 0.06] 0.7: [0.03, 0.05] 0.8: [0.03, 0.04] 0.9: [0.03, 0.04] 1.0: [0.03, 0.03]	0.0: [0.00, 0.06] 0.1: [0.00, 0.05] 0.2: [0.00, 0.04] 0.3: [0.00, 0.03] 0.4: [0.00, 0.03] 0.5: [0.00, 0.02] 0.6: [0.00, 0.02] 0.7: [0.00, 0.01] 0.8: [0.00, 0.01] 0.9: [0.00, 0.00] 1.0: [0.00, 0.00]	0.0: [0.04, 0.42] 0.1: [0.05, 0.39] 0.2: [0.06, 0.36] 0.3: [0.07, 0.33] 0.4: [0.08, 0.30] 0.5: [0.09, 0.28] 0.6: [0.10, 0.25] 0.7: [0.11, 0.23] 0.8: [0.13, 0.20] 0.9: [0.14, 0.18] 1.0: [0.16, 0.16]	0.0: [0.02, 0.26] 0.1: [0.02, 0.23] 0.2: [0.03, 0.20] 0.3: [0.03, 0.18] 0.4: [0.03, 0.15] 0.5: [0.04, 0.13] 0.6: [0.04, 0.12] 0.7: [0.05, 0.10] 0.8: [0.05, 0.09] 0.9: [0.06, 0.07] 1.0: [0.06, 0.06]
3	0.0: [0.05, 0.24] 0.1: [0.05, 0.23] 0.2: [0.06, 0.21] 0.3: [0.06, 0.20] 0.4: [0.07, 0.18] 0.5: [0.08, 0.17] 0.6: [0.08, 0.16] 0.7: [0.09, 0.15] 0.8: [0.10, 0.14] 0.9: [0.11, 0.13] 1.0: [0.12, 0.12]	0.0: [0.01, 0.12] 0.1: [0.01, 0.11] 0.2: [0.01, 0.10] 0.3: [0.01, 0.08] 0.4: [0.02, 0.07] 0.5: [0.02, 0.06] 0.6: [0.02, 0.05] 0.7: [0.02, 0.04] 0.8: [0.02, 0.04] 0.9: [0.02, 0.03] 1.0: [0.03, 0.03]	0.0: [0.00, 0.06] 0.1: [0.00, 0.05] 0.2: [0.00, 0.04] 0.3: [0.00, 0.03] 0.4: [0.00, 0.03] 0.5: [0.00, 0.02] 0.6: [0.00, 0.02] 0.7: [0.00, 0.01] 0.8: [0.00, 0.01] 0.9: [0.00, 0.00] 1.0: [0.00, 0.00]	0.0: [0.04, 0.42] 0.1: [0.05, 0.39] 0.2: [0.06, 0.36] 0.3: [0.07, 0.33] 0.4: [0.08, 0.30] 0.5: [0.09, 0.28] 0.6: [0.10, 0.25] 0.7: [0.11, 0.23] 0.8: [0.13, 0.20] 0.9: [0.14, 0.18] 1.0: [0.16, 0.16]	0.0: [0.01, 0.18] 0.1: [0.01, 0.16] 0.2: [0.01, 0.14] 0.3: [0.02, 0.12] 0.4: [0.02, 0.10] 0.5: [0.02, 0.09] 0.6: [0.03, 0.08] 0.7: [0.03, 0.07] 0.8: [0.03, 0.06] 0.9: [0.03, 0.05] 1.0: [0.04, 0.04]
4	0.0: [0.00, 0.05] 0.1: [0.00, 0.04] 0.2: [0.00, 0.03] 0.3: [0.00, 0.03] 0.4: [0.00, 0.02] 0.5: [0.00, 0.02] 0.6: [0.00, 0.01] 0.7: [0.00, 0.01] 0.8: [0.00, 0.01] 0.9: [0.00, 0.00] 1.0: [0.00, 0.00]	0.0: [0.00, 0.02] 0.1: [0.00, 0.02] 0.2: [0.00, 0.02] 0.3: [0.00, 0.01] 0.4: [0.00, 0.01] 0.5: [0.00, 0.01] 0.6: [0.00, 0.00] 0.7: [0.00, 0.00] 0.8: [0.00, 0.00] 0.9: [0.00, 0.00] 1.0: [0.00, 0.00]	0.0: [0.00, 0.06] 0.1: [0.00, 0.05] 0.2: [0.00, 0.04] 0.3: [0.00, 0.03] 0.4: [0.00, 0.03] 0.5: [0.00, 0.02] 0.6: [0.00, 0.02] 0.7: [0.00, 0.01] 0.8: [0.00, 0.01] 0.9: [0.00, 0.00] 1.0: [0.00, 0.00]	0.0: [0.08, 0.60] 0.1: [0.09, 0.56] 0.2: [0.11, 0.52] 0.3: [0.12, 0.48] 0.4: [0.14, 0.45] 0.5: [0.16, 0.41] 0.6: [0.17, 0.38] 0.7: [0.19, 0.34] 0.8: [0.21, 0.31] 0.9: [0.23, 0.28] 1.0: [0.25, 0.25]	0.0: [0.01, 0.14] 0.1: [0.01, 0.12] 0.2: [0.01, 0.11] 0.3: [0.01, 0.09] 0.4: [0.01, 0.08] 0.5: [0.01, 0.07] 0.6: [0.02, 0.06] 0.7: [0.02, 0.05] 0.8: [0.02, 0.04] 0.9: [0.02, 0.03] 1.0: [0.03, 0.03]
5	0.0: [0.03, 0.24] 0.1: [0.04, 0.22] 0.2: [0.04, 0.20] 0.3: [0.05, 0.19] 0.4: [0.05, 0.17] 0.5: [0.06, 0.16] 0.6: [0.07, 0.14] 0.7: [0.07, 0.13] 0.8: [0.08, 0.12] 0.9: [0.09, 0.11] 1.0: [0.10, 0.10]	0.0: [0.01, 0.12] 0.1: [0.01, 0.11] 0.2: [0.01, 0.10] 0.3: [0.01, 0.08] 0.4: [0.02, 0.07] 0.5: [0.02, 0.06] 0.6: [0.02, 0.05] 0.7: [0.02, 0.04] 0.8: [0.02, 0.04] 0.9: [0.02, 0.03] 1.0: [0.03, 0.03]	0.0: [0.00, 0.06] 0.1: [0.00, 0.05] 0.2: [0.00, 0.04] 0.3: [0.00, 0.03] 0.4: [0.00, 0.03] 0.5: [0.00, 0.02] 0.6: [0.00, 0.02] 0.7: [0.00, 0.01] 0.8: [0.00, 0.01] 0.9: [0.00, 0.00] 1.0: [0.00, 0.00]	0.0: [0.11, 0.60] 0.1: [0.12, 0.57] 0.2: [0.14, 0.54] 0.3: [0.16, 0.51] 0.4: [0.18, 0.48] 0.5: [0.20, 0.45] 0.6: [0.22, 0.42] 0.7: [0.24, 0.39] 0.8: [0.27, 0.37] 0.9: [0.29, 0.34] 1.0: [0.31, 0.31]	0.0: [0.03, 0.26] 0.1: [0.03, 0.23] 0.2: [0.04, 0.21] 0.3: [0.04, 0.19] 0.4: [0.04, 0.17] 0.5: [0.05, 0.14] 0.6: [0.05, 0.13] 0.7: [0.06, 0.12] 0.8: [0.07, 0.10] 0.9: [0.07, 0.09] 1.0: [0.08, 0.08]

Based on the fuzzy weighted scores, the fuzzy ideal and anti-ideal points were defined, respectively, as presented in Table 14. Subsequently, the distances from each travel destination to the two reference points were measured. The results are summarized in Table 15.

Table 14.

Fuzzy ideal point and fuzzy anti-ideal point.

Reference point	${\tilde{\Lambda }}_1^{\mathrm{\ast }}$ ($\alpha$: $\alpha$ cut)	${\tilde{\Lambda }}_2^{\mathrm{\ast }}$ ($\alpha$: $\alpha$ cut)	${\tilde{\Lambda }}_3^{\mathrm{\ast }}$ ($\alpha$: $\alpha$ cut)	${\tilde{\Lambda }}_4^{\mathrm{\ast }}$ ($\alpha$: $\alpha$ cut)	${\tilde{\Lambda }}_5^{\mathrm{\ast }}$ ($\alpha$: $\alpha$ cut)
Fuzzy ideal point	0.0: [0.05, 0.24] 0.1: [0.05, 0.23] 0.2: [0.06, 0.21] 0.3: [0.06, 0.20] 0.4: [0.07, 0.18] 0.5: [0.08, 0.17] 0.6: [0.08, 0.16] 0.7: [0.09, 0.15] 0.8: [0.10, 0.14] 0.9: [0.11, 0.13] 1.0: [0.12, 0.12]	0.0: [0.01, 0.12] 0.1: [0.02, 0.11] 0.2: [0.02, 0.10] 0.3: [0.02, 0.09] 0.4: [0.02, 0.07] 0.5: [0.02, 0.06] 0.6: [0.02, 0.06] 0.7: [0.03, 0.05] 0.8: [0.03, 0.04] 0.9: [0.03, 0.04] 1.0: [0.03, 0.03]	0.0: [0.06, 0.29] 0.1: [0.07, 0.27] 0.2: [0.08, 0.25] 0.3: [0.08, 0.24] 0.4: [0.09, 0.22] 0.5: [0.09, 0.20] 0.6: [0.10, 0.19] 0.7: [0.11, 0.18] 0.8: [0.12, 0.16] 0.9: [0.13, 0.15] 1.0: [0.14, 0.14]	0.0: [0.11, 0.60] 0.1: [0.12, 0.57] 0.2: [0.14, 0.54] 0.3: [0.16, 0.51] 0.4: [0.18, 0.48] 0.5: [0.20, 0.45] 0.6: [0.22, 0.42] 0.7: [0.24, 0.39] 0.8: [0.27, 0.37] 0.9: [0.29, 0.34] 1.0: [0.31, 0.31]	0.0: [0.03, 0.26] 0.1: [0.03, 0.23] 0.2: [0.04, 0.21] 0.3: [0.04, 0.19] 0.4: [0.04, 0.17] 0.5: [0.05, 0.14] 0.6: [0.05, 0.13] 0.7: [0.06, 0.12] 0.8: [0.07, 0.10] 0.9: [0.07, 0.09] 1.0: [0.08, 0.08]
Fuzzy anti-ideal point	0.0: [0.00, 0.05] 0.1: [0.00, 0.04] 0.2: [0.00, 0.03] 0.3: [0.00, 0.03] 0.4: [0.00, 0.02] 0.5: [0.00, 0.02] 0.6: [0.00, 0.01] 0.7: [0.00, 0.01] 0.8: [0.00, 0.01] 0.9: [0.00, 0.00] 1.0: [0.00, 0.00]	0.0: [0.00, 0.02] 0.1: [0.00, 0.02] 0.2: [0.00, 0.02] 0.3: [0.00, 0.01] 0.4: [0.00, 0.01] 0.5: [0.00, 0.01] 0.6: [0.00, 0.00] 0.7: [0.00, 0.00] 0.8: [0.00, 0.00] 0.9: [0.00, 0.00] 1.0: [0.00, 0.00]	0.0: [0.00, 0.06] 0.1: [0.00, 0.05] 0.2: [0.00, 0.04] 0.3: [0.00, 0.03] 0.4: [0.00, 0.03] 0.5: [0.00, 0.02] 0.6: [0.00, 0.02] 0.7: [0.00, 0.01] 0.8: [0.00, 0.01] 0.9: [0.00, 0.00] 1.0: [0.00, 0.00]	0.0: [0.00, 0.12] 0.1: [0.00, 0.10] 0.2: [0.00, 0.09] 0.3: [0.00, 0.08] 0.4: [0.00, 0.06] 0.5: [0.00, 0.05] 0.6: [0.00, 0.04] 0.7: [0.00, 0.03] 0.8: [0.00, 0.02] 0.9: [0.00, 0.01] 1.0: [0.00, 0.00]	0.0: [0.01, 0.14] 0.1: [0.01, 0.12] 0.2: [0.01, 0.11] 0.3: [0.01, 0.09] 0.4: [0.01, 0.08] 0.5: [0.01, 0.07] 0.6: [0.02, 0.06] 0.7: [0.02, 0.05] 0.8: [0.02, 0.04] 0.9: [0.02, 0.03] 1.0: [0.03, 0.03]

Table 15.

Distances between each travel destination and the two reference points.

q	${\tilde{d}}_q^{+}$ ($\alpha$: $\alpha$ cut)	${\tilde{d}}_q^{-}$ ($\alpha$: $\alpha$ cut)
1	0.0: [0.00, 0.72] 0.1: [0.02, 0.67] 0.2: [0.05, 0.62] 0.3: [0.08, 0.58] 0.4: [0.12, 0.53] 0.5: [0.15, 0.49] 0.6: [0.18, 0.45] 0.7: [0.21, 0.41] 0.8: [0.25, 0.38] 0.9: [0.28, 0.34] 1.0: [0.32, 0.32]	0.0: [0.00, 0.46] 0.1: [0.02, 0.42] 0.2: [0.04, 0.39] 0.3: [0.06, 0.35] 0.4: [0.08, 0.32] 0.5: [0.09, 0.29] 0.6: [0.11, 0.26] 0.7: [0.13, 0.24] 0.8: [0.15, 0.22] 0.9: [0.17, 0.20] 1.0: [0.19, 0.19]
2	0.0: [0.00, 0.71] 0.1: [0.02, 0.65] 0.2: [0.03, 0.60] 0.3: [0.05, 0.55] 0.4: [0.06, 0.49] 0.5: [0.07, 0.44] 0.6: [0.09, 0.39] 0.7: [0.10, 0.34] 0.8: [0.13, 0.30] 0.9: [0.17, 0.25] 1.0: [0.21, 0.21]	0.0: [0.00, 0.56] 0.1: [0.01, 0.52] 0.2: [0.02, 0.47] 0.3: [0.03, 0.43] 0.4: [0.05, 0.39] 0.5: [0.07, 0.35] 0.6: [0.10, 0.32] 0.7: [0.12, 0.29] 0.8: [0.15, 0.26] 0.9: [0.18, 0.23] 1.0: [0.20, 0.20]
3	0.0: [0.00, 0.71] 0.1: [0.02, 0.66] 0.2: [0.03, 0.60] 0.3: [0.05, 0.55] 0.4: [0.06, 0.50] 0.5: [0.07, 0.44] 0.6: [0.09, 0.40] 0.7: [0.10, 0.35] 0.8: [0.13, 0.30] 0.9: [0.17, 0.26] 1.0: [0.21, 0.21]	0.0: [0.00, 0.53] 0.1: [0.01, 0.49] 0.2: [0.02, 0.45] 0.3: [0.03, 0.41] 0.4: [0.05, 0.37] 0.5: [0.07, 0.34] 0.6: [0.09, 0.31] 0.7: [0.12, 0.28] 0.8: [0.15, 0.25] 0.9: [0.17, 0.22] 1.0: [0.20, 0.20]
4	0.0: [0.00, 0.70] 0.1: [0.02, 0.64] 0.2: [0.04, 0.59] 0.3: [0.06, 0.53] 0.4: [0.08, 0.48] 0.5: [0.10, 0.42] 0.6: [0.11, 0.37] 0.7: [0.13, 0.33] 0.8: [0.15, 0.28] 0.9: [0.17, 0.24] 1.0: [0.20, 0.20]	0.0: [0.00, 0.62] 0.1: [0.00, 0.57] 0.2: [0.02, 0.53] 0.3: [0.05, 0.49] 0.4: [0.08, 0.45] 0.5: [0.10, 0.42] 0.6: [0.13, 0.38] 0.7: [0.16, 0.35] 0.8: [0.19, 0.31] 0.9: [0.22, 0.28] 1.0: [0.25, 0.25]
5	0.0: [0.00, 0.66] 0.1: [0.02, 0.60] 0.2: [0.03, 0.54] 0.3: [0.05, 0.48] 0.4: [0.06, 0.42] 0.5: [0.07, 0.36] 0.6: [0.09, 0.30] 0.7: [0.10, 0.25] 0.8: [0.11, 0.21] 0.9: [0.13, 0.17] 1.0: [0.14, 0.14]	0.0: [0.00, 0.71] 0.1: [0.02, 0.66] 0.2: [0.05, 0.62] 0.3: [0.09, 0.58] 0.4: [0.12, 0.54] 0.5: [0.15, 0.50] 0.6: [0.19, 0.46] 0.7: [0.22, 0.43] 0.8: [0.26, 0.40] 0.9: [0.30, 0.36] 1.0: [0.33, 0.33]

Finally, the fuzzy closeness of each travel destination was derived. The results are depicted in Table 16. Consider travel destination A as an example. Its fuzzy closeness is depicted in Fig. 9, with curved edges on both sides.

Table 16.

Fuzzy closeness of each travel destination.

q	${\tilde{C}}_q$ ($\alpha$: $\alpha$ cut)
1	0.0: [0.01, 1.00] 0.1: [0.03, 0.96] 0.2: [0.06, 0.88] 0.3: [0.09, 0.81] 0.4: [0.13, 0.73] 0.5: [0.16, 0.66] 0.6: [0.20, 0.59] 0.7: [0.24, 0.53] 0.8: [0.28, 0.47] 0.9: [0.33, 0.42] 1.0: [0.37, 0.37]
2	0.0: [0.00, 0.99] 0.1: [0.02, 0.96] 0.2: [0.04, 0.93] 0.3: [0.06, 0.90] 0.4: [0.09, 0.86] 0.5: [0.14, 0.83] 0.6: [0.20, 0.78] 0.7: [0.26, 0.74] 0.8: [0.33, 0.66] 0.9: [0.41, 0.58] 1.0: [0.49, 0.49]
3	0.0: [0.00, 0.99] 0.1: [0.02, 0.96] 0.2: [0.04, 0.93] 0.3: [0.06, 0.89] 0.4: [0.09, 0.86] 0.5: [0.14, 0.82] 0.6: [0.19, 0.78] 0.7: [0.26, 0.73] 0.8: [0.33, 0.66] 0.9: [0.40, 0.57] 1.0: [0.48, 0.48]
4	0.0: [0.00, 0.99] 0.1: [0.00, 0.96] 0.2: [0.03, 0.93] 0.3: [0.08, 0.89] 0.4: [0.14, 0.85] 0.5: [0.20, 0.81] 0.6: [0.26, 0.77] 0.7: [0.33, 0.72] 0.8: [0.41, 0.67] 0.9: [0.48, 0.62] 1.0: [0.55, 0.55]
5	0.0: [0.00, 0.99] 0.1: [0.03, 0.97] 0.2: [0.09, 0.95] 0.3: [0.15, 0.92] 0.4: [0.22, 0.90] 0.5: [0.30, 0.87] 0.6: [0.38, 0.84] 0.7: [0.47, 0.81] 0.8: [0.56, 0.78] 0.9: [0.64, 0.74] 1.0: [0.70, 0.70]

Fig. 9.

Fuzzy closeness of travel destination A.

Subsequently, COG was applied to defuzzify the fuzzy closeness of each travel destination. The results are summarized in Table 17.

Table 17.

Defuzzification results.

q	Defuzzified closeness
1	0.396
2	0.490
3	0.485
4	0.527
5	0.637

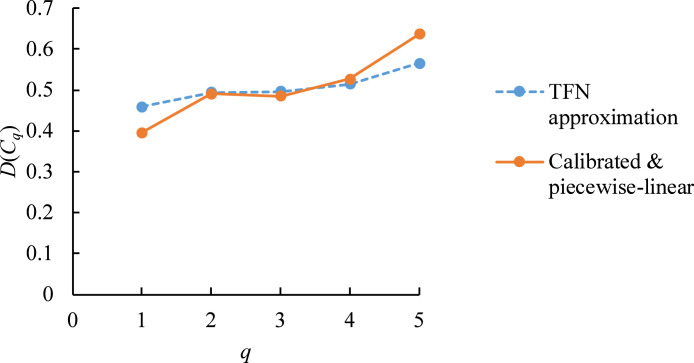
According to the experimental results,

• (1)The differences between the overall performance of travel destinations were significant.
• (2)In contrast, if TFNs were used to approximate fuzzy priorities, the differences between the travel destinations were insignificant, as illustrated in Fig. 10.
• (3)Among the five travel destinations, travel destination E achieved the highest overall performance, evidently due to its numerous outdoor attractions and high expected value.
• (4)In contrast, travel destination A was considered the least suitable travel destination because of its few outdoor attractions.
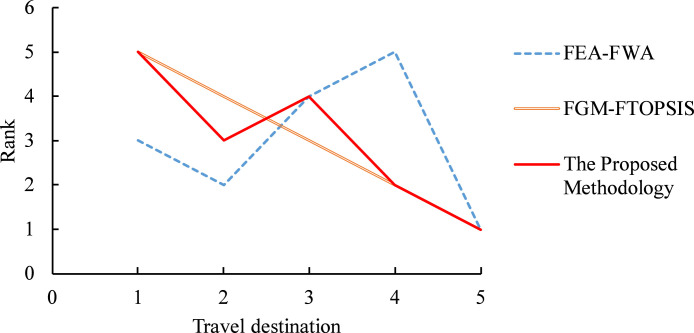
• (5)Two existing methods, FEA–FWA and FGM–FTOPSIS, were also applied to compare these travel destinations. In FEA–FWA, the fuzzy priorities of critical factors were estimated using FEA. Then, FWA was applied to assess the overall performance of each travel destination. In FGM–FTOPSIS, fuzzy priorities were approximated with TFNs using FGM. Subsequently, FTOPSIS was applied to derive the overall performance of a travel destination. The ranking results, which differed by method, are compared in Fig. 11. Existing methods estimated, rather than derived, the fuzzy priorities of critical factors, which might lead to incorrect decisions. Nevertheless, travel destination E was always the best choice, demonstrating the correctness of the recommendation result using the proposed methodology.
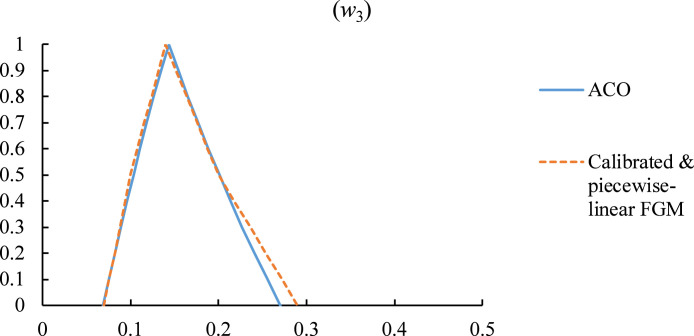
• (6)ACO was also applied to derive the exact values of fuzzy priorities for comparison to assess the effectiveness of the calibrated piecewise-linear FGM approach. The membership functions fitted using the calibrated piecewise-linear FGM approach resembled the exact membership functions, as illustrated in Fig. 12. Furthermore, the calibrated piecewise-linear FGM approach required less than 1 s to fit the membership functions, while xACO and ACO required 5 and 24 s, respectively, on the same platform to approximate or derive the membership functions.
• (7)It is interesting to know whether the consideration of different criteria changes the recommendation result. An experiment was conducted to investigate this issue by eliminating one of the five criteria at a time. Travel destinations were ranked based on the remaining criteria. The experimental results are summarized in Table 18. In most cases, travel destination E was the best choice, demonstrating the correctness of the recommendation result using the proposed methodology. However, without considering the criterion “number of outdoor attractions”, travel destinations with higher expected values and fewer confirmed cases were more suitable.

Fig. 10.

Differences between travel destinations using various methods.

Fig. 11.

Comparison of the ranking results using various methods.

Fig. 12.

Comparing the fitted membership function to the exact membership function.

Table 18.

Rankings after eliminating one criterion at a time.

Considered criteria	Ranking
Population density, amount of government subsidies, number of outdoor attractions, expected value	E $\to$ D $\to$ B $\to$ C $\to$ A
Number of confirmed cases, amount of government subsidies, number of outdoor attractions, expected value	E $\to$ D $\to$ B $\to$ C $\to$ A
Number of confirmed cases, population density, number of outdoor attractions, expected value	E $\to$ D $\to$ B $\to$ C $\to$ A
Number of confirmed cases, population density, amount of government subsidies, expected value	A $\to$ B $\to$ C $\to$ E $\to$ D
Number of confirmed cases, population density, amount of government subsidies, number of outdoor attractions	E $\to$ D $\to$ B $\to$ C $\to$ A

The recommended travel destinations to all travelers, and their choices, are summarized in Table 19. The travel destinations considered by each traveler and the defuzzified closeness of the recommended travel destination are also presented. The defuzzified closeness of a travel destination varied by case because fuzzy closeness was a relative measure. Furthermore, the expected value of a travel destination was not the same for different travelers. Consequently, a travel destination was not always superior or inferior to another.

Most of the travelers followed the recommendations, confirming that travelers relied heavily on the information provided by the recommendation system during the COVID-19 pandemic. The appropriateness of the recommendation results using the proposed methodology was also supported. The recall rate, precision rate, and F1 metric [77], [78] were all 87%. However, if the top two performing travel destinations were recommended to each traveler, then the recall rate was 100%, the precision rate was 50%, and the F1 metric was 67%.

Table 19.

Destinations recommended to travelers.

Traveler	Considered travel destinations	Recommended travel destination (Defuzzified Closeness)	Traveler’s choice
1	A, B, C, D, E	E (0.637)	E
2	F, G, H, I, J, K	K (0.673)	K
3	L, M, N, O, P	L (0.647)	L
4	A, C, M	C (0.683)	C
5	G, I, L, P	L (0.630)	L
6	N, P, Q, R	N (0.675)	N
7	B, C, H, M	B (0.629)	C
8	L, O, P, S, T	L (0.629)	L
9	C, E, G	E (0.628)	E
10	C, D, E, G	E (0.633)	E
11	B, L, N, Q, U	N (0.733)	L
12	G, L, P	L (0.687)	L
13	E, H, L, M	E (0.676)	E
14	C, H, M, P	C (0.617)	C
15	B, D, F, P	B (0.649)	B

5. Conclusions

After several months of experiencing the COVID-19 pandemic, people want to travel regionally because cross-border travel is still not viable. However, choosing a suitable travel destination during the COVID-19 pandemic has become challenging because people are now paying more attention to health-related issues. A calibrated piecewise-linear FGM approach is proposed in this study to accomplish this task. In the proposed methodology, the factors critical to the selection of a suitable travel destination are different from those usually considered. Furthermore, by hybridizing ACO and FGM, the accuracy and efficiency of deriving the fuzzy priorities of critical factors can be improved.

The proposed methodology has been applied to recommend suitable travel destinations to fifteen travelers for regional trips during the COVID-19 pandemic. The following conclusions can be drawn from the experimental results:

• (1)“The number of outdoor attractions” and “the number of confirmed cases room rate discount” were considered as the most important critical factors, evidently due to the COVID-19 pandemic.
• (2)The most suitable travel destination was usually a destination with many outdoor attractions in the region, while the least suitable destination for travel was usually one of the destinations with few outdoor attractions or high population density.
• (3)After improving the accuracy of approximating the fuzzy priorities of critical factors, the differences between the overall performance of travel destinations became more evident.
• (4)Most of the travelers followed the recommendations, demonstrating that they relied heavily on the information provided by the recommendation system during the COVID-19 pandemic.

The piecewise linear FGM approach must be applied to more real cases to elaborate further on its effectiveness. Furthermore, it is difficult to predict the duration of the COVID-19 pandemic. Therefore, the priorities of critical factors may change, so the same analysis must be conducted again to determine whether the experimental results obtained in this study remain applicable.

CRediT authorship contribution statement

Toly Chen: Data curation, Methodology, Writing - original draft, Writing - review and editing. Yu-Cheng Wang: Data curation, Methodology, Writing - original draft, Writing - review and editing.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.