Sample sizes for cluster-randomised trials with continuous outcomes: Accounting for uncertainty in a single intra-cluster correlation estimate

Abstract

Sample size calculations for cluster-randomised trials require inclusion of an inflation factor taking into account the intra-cluster correlation coefficient. Often, estimates of the intra-cluster correlation coefficient are taken from pilot trials, which are known to have uncertainty about their estimation. Given that the value of the intra-cluster correlation coefficient has a considerable influence on the calculated sample size for a main trial, the uncertainty in the estimate can have a large impact on the ultimate sample size and consequently, the power of a main trial. As such, it is important to account for the uncertainty in the estimate of the intra-cluster correlation coefficient. While a commonly adopted approach is to utilise the upper confidence limit in the sample size calculation, this is a largely inefficient method which can result in overpowered main trials. In this paper, we present a method of estimating the sample size for a main cluster-randomised trial with a continuous outcome, using numerical methods to account for the uncertainty in the intra-cluster correlation coefficient estimate. Despite limitations with this initial study, the findings and recommendations in this paper can help to improve sample size estimations for cluster randomised controlled trials by accounting for uncertainty in the estimate of the intra-cluster correlation coefficient. We recommend this approach be applied to all trials where there is uncertainty in the intra-cluster correlation coefficient estimate, in conjunction with additional sources of information to guide the estimation of the intra-cluster correlation coefficient.

Introduction

Cluster randomised controlled trials (cRCTs) are studies which randomise groups (clusters) of patients or participants – rather than individuals – to health interventions. Example units of randomisation include general practices, hospitals, schools or geographical areas. The decision to undertake a cluster randomised trial is often made for practical reasons such as to prevent contamination across arms. ¹ Alternatively, the intervention may be a system of care that necessitates a whole unit, such as a hospital, to be randomised.

With a cluster randomised trial, the outcomes of patients within clusters may be correlated, introducing an additional level of complexity to the design and analysis of the studies. This correlation can be quantified by the intra-cluster correlation coefficient (ICC). While different outcomes will usually have different ICCs, usually only that for the primary outcome is calculated and it is this which we refer to as ‘the ICC’ in this paper. This correlation can occur for many reasons, including the common care or clinical practice of the patients within a cluster, where the cluster may be a GP practice or a clinician.

Sample size calculations for cluster randomised trials require inclusion of an inflation factor taking into account the ICC. ² This in turn requires a reasonable estimate of the value of the ICC. Like other parameters, such as the variance, the ICC is regularly estimated from pilot trials. However, estimates of ICCs gained from pilot studies are often very imprecise, with large uncertainty about the estimate.^3,4

ICCs vary markedly, with ICCs less than 0.001 or more than 0.8 having been documented depending on the intervention, population and outcome being investigated.^3,5–7 Even a small ICC can have a considerable impact on the power of a study. For example, an individually randomised trial might require 100 participants per arm. The same study using a cluster randomised design, with clusters of size 20 and an ICC of 0.02, would require 138 participants per arm (using result 1, the ‘Sample size for cRCTs’ section ). With an ICC of 0.05, it would require 195 participants per arm. Given the impact on the sample size of the ICC, it is important to have a robust estimate of the ICC to preserve the power of a main trial.

Researchers^3,4 recommend being guided by ICCs from multiple studies or databases that have studied patterns in ICCs ⁵ to select an appropriate estimate rather than using a single estimate from an external pilot trial. However, this is not always straightforward, particularly if few studies report relevant ICCs, or if they are largely inconsistent. As such, in practice, estimates from external pilot trials are frequently used to calculate main trial sample size. Given the imprecision of ICC estimates from single pilot trials, utilising such estimates without in some way controlling for the likely imprecision in that estimate is not recommended. ICC estimates that are too small will result in an underpowered study and estimates that are too large will result in an overpowered study. The use of internal pilot studies to facilitate a recalculation of the ICC may lead to a more accurate estimate, ⁸ but internal pilot studies may not be feasible. It is also not recommended simply to assume large ICCs (e.g. the upper bound of a confidence interval around the ICC estimate) to ensure sufficient power, ⁴ not only due to the likely overpowering that will result, but the known diminishing returns associated with increasing cluster size in cRCTs ⁹ suggest this would be an extremely inefficient means of controlling for imprecision in an ICC estimate.

Existing studies have examined the methods of accounting for imprecision of estimated parameters required to calculate sample size. For example, Julious and Owen ¹⁰ presented a method for accounting for the imprecision in the estimate of the variance from pilot studies of individually randomised trials. In this paper, we address the problem of accounting for the uncertainty in the ICC when calculating sample size for a main trial, and we make practical recommendations.

Estimating the uncertainty in the ICC

We define $\rho$ to be the true parameter estimate for the ICC and $\hat{\rho }$ to be the maximum likelihood estimate. The uncertainty in $\hat{\rho }$ must itself be estimated, and there are several established methods for estimating the uncertainty of $\hat{\rho }$ .^11–15 It is beyond the scope of this paper to perform an exhaustive investigation of all these available methods. In order to explore a broad yet feasible range of methods, we examine three methods compared by Ukoumunne. ¹²

Ukoumunne ¹² divided a number of methods into three categories; those based on

1. Large sample approximations to the standard error of $\hat{\rho };$

2. The variance ratio statistic;

3. A large sample approximation to the standard error of a normalising transformation of $\hat{\rho }$ .

In the following, we utilise one method from each of these three categories: Swiger's variance, ¹⁶ Searle's method ¹⁷ and Fisher's transformation, ¹⁸ respectively. These specific methods are considered here due to their relative accessibility and ease of implementation, and are detailed in Supplementary material S1.

While we restrict the present study to three methods, the numerical approach proposed in this paper to account for uncertainty in the ICC estimate may be used with any of the methods for estimating the uncertainty in $\hat{\rho }$ , since it requires only a plausible distribution (including defined upper and lower limits) for $\hat{\rho }$ . When designing a trial, given the properties of the estimated parameters and expected results, one method may be preferred, with an alternative approach used to assess the sensitivity of the calculations.

Methods

In this section, we present a method to account for the uncertainty in the estimate of an ICC from a pilot trial with a continuous outcome and a known sample size, using a numerical integrative adjustment to the sample size calculation for a main trial. For simplicity, throughout, we assume a two-armed trial design with equal cluster sizes and equal numbers of clusters in each arm, and the same ICC and variance in both arms.

Sample size for cRCTs

The number of participants in each arm, n, in a cluster randomised trial is usually estimated by ¹

$$n=\frac{2{\left(Z_{1-\frac{\alpha }{2}}+Z_{1-\beta }\right)}^2{\sigma }^2(1+(m_f-1)\hat{\rho })}{{({\mu }_1-{\mu }_2)}^2}$$ (1)

where σ² is the variance, ${\mu }_1$ and ${\mu }_2$ are the means in the two trial arms, $\hat{\rho }$ the estimated ICC, and $m_f$ is the desired cluster size for the main trial. $Z_{1-\frac{\alpha }{2}}$ and $Z_{1-\beta }$ are the standard normal values associated with the probabilities of $1-\frac{\alpha }{2}$ and $1-\beta$ , where $\alpha$ is the type I error rate (often 0.05) and $\beta$ the type II error rate (often either 0.1 or 0.2). $\beta -1$ is the desired power.

Worked example

Consider the following scenario: a pilot cluster randomised trial has been performed, from which an estimate of the ICC has been generated to calculate the sample size for a main trial, such that $\hat{\rho }=0.05$ . The effect size (the standardised mean difference between study arms) is estimated to be $d=({\mu }_1-{\mu }_2)/\sigma =0.25$ , and the desired cluster size for the main trial $m_f=40$ . Requiring 90% power with α  =  0.05 in result (1), the required number of participants per arm rounded up to the nearest whole number, is

$$n=\frac{2{(1.96+1.29)}^2(1+(39*0.05))}{{0.25}^2}=998$$ (2)

The required number of clusters per arm for the main trial, $k_f$ , again rounded up to the nearest whole number is then given by

$$k_f=\frac{n}{m_f}=25$$ (3)

For a two-armed trial, this equates to a trial of 50 clusters and 2000 individuals.

Table 1 shows main trial sample sizes (clusters per arm) for a range of cluster sizes, effect sizes and estimated ICCs using result (1).

Table 1.

Clusters per arm $k_f$ required for a main trial with 90% power for a two-tailed test and $\alpha =0.05$ , without accounting for the uncertainty in the ICC, calculated according to result (1).

Estimated ICC $\hat{\rho }$	Effect size d  =  0.1					Effect size d  =  0.25					Effect size d  =  0.5
	Cluster size $m_f$					Cluster size $m_f$					Cluster size $m_f$
	5	10	15	20	30	5	10	15	20	30	5	10	15	20	30
0.01	440	231	161	126	91	71	37	26	21	15	18	10	7	6	4
0.05	507	307	240	206	173	82	50	39	33	28	21	13	10	9	7
0.10	592	402	339	307	275	95	65	55	50	44	24	17	14	13	11
0.20	761	592	536	508	479	122	95	86	82	77	31	24	22	21	20

ICC: intra-cluster correlation.

Accounting for uncertainty

Result (1) requires an estimate of the ICC. A straightforward way to account for the imprecision in the estimate of the ICC is to take the sample size formula for a cluster randomised trial and integrate this over all plausible values of the ICC. This then provides an ‘average’ sample size over those values.

Where $\hat{\rho }$ is the estimated ICC, the following result can then be used

$$n=\int \left(\frac{2{\left(Z_{1-\frac{\alpha }{2}}+Z_{1-\beta }\right)}^2{\sigma }^2(1+(m_f-1)\hat{\rho })}{{({\mu }_1-{\mu }_2)}^2}\right)d\hat{\rho }$$ (4)

Result (4) cannot be solved analytically, so we may solve numerically though the trapezoidal rule whereby

$${\int }_a^{b}f(x)dx\approx \sum _{i=0}^{Np-1}\frac{f(x_i)+f(x_{i+1})}{2}\mathrm{\Delta }x$$ (5)

where $x_0=a$ , $x_{Np}=b$ and $\mathrm{\Delta }x=x_{i+1}-x_i$ , representing a suitable partition of the interval $[a,b]$ to balance the accuracy of the approximation to the true integral and computational feasibility. Although other numerical integration methods are known to produce more accurate approximations, the trapezoidal rule is easily understood, straightforward to apply and fast to calculate. ¹⁹ A suitably small $\mathrm{\Delta }x$ will ensure a reasonable approximation.

We take $f(x)$ to be the sample size calculation for cRCTs (result 1). Using a partition size $\mathrm{\Delta }x=0.001$ , taking ${\hat{\rho }}_i$ as the $i\mathrm{th}$ percentile of the 99.8% confidence interval around $\hat{\rho }$ , and utilising this in place of $\hat{\rho }$ in $f(x)$ , we can then substitute this in result (5), giving

$$n\approx \sum _{i=0.001}^{0.998}0.0005\left[\frac{2{\left(Z_{1-\frac{\alpha }{2}}+Z_{1-\beta }\right)}^2{\sigma }^2(1+(m_f-1){\hat{\rho }}_i)}{{({\mu }_1-{\mu }_2)}^2}+\frac{2{\left(Z_{1-\frac{\alpha }{2}}+Z_{1-\beta }\right)}^2{\sigma }^2(1+(m_f-1){\hat{\rho }}_{i+1})}{{({\mu }_1-{\mu }_2)}^2}\right]$$ (6)

Upper and lower limits for $\hat{\rho }$ and its distribution must be estimated to implement this approach. As discussed in the introduction, there are several established methods for estimating this uncertainty and calculating possible limits.

In the following demonstrations, we use Swiger's method, Searle's method and Fisher's normalising transformation, respectively, to estimate 99.8% confidence intervals around $\hat{\rho }$ ; these CI limits are then used as the upper and lower limits for result (6). Each method makes assumptions about the distribution of $\hat{\rho }:$ Swiger's method assumes a normal distribution, Searle's method assumes an F-distribution and Fisher's method assumes a normal distribution of the transformation of $\hat{\rho }$ (see Supplementary Material S1). Demonstrations were implemented in R version 3.6.3 ²⁰ on 64-bit Windows.

Demonstrations

Demonstration 1: Worked example revisited

To illustrate the impact of the integrative adjustment described in the ‘Accounting for uncertainty’ section, we first revisit the example introduced in the ‘Worked example’ section. We recalculated the sample size for the worked example using Swiger's method, Searle's method and Fisher's transformation, respectively, to calculate the uncertainty in the estimate of the ICC. In each case, we calculated the main trial sample size using our integrative adjustment described above, and also using the upper limit of the 95% confidence interval around the ICC to illustrate the difference in approaches.

Since the size of the pilot trial will affect the precision of the estimate of the ICC, we present four alternative scenarios under which the ICC has been estimated. In all scenarios, the effect size, estimated ICC and target cluster size for the main trial are the same. However, the details of the pilot trial from which the ICC is estimated are varied, such that:

• Scenarios 1 and 2 have the same sized clusters, but a different number of clusters;

• Scenarios 1 and 3 have the same number of clusters but a different cluster size;

• Scenarios 1 and 4 have the same number of participants, but a different cluster size;

• Scenarios 2 and 3 have the same number of participants but a different cluster size;

• Scenarios 2 and 4 have the same number of clusters but a different cluster size.

Results are shown in Table 2. In each case, the estimated effect size $(d)$ was 0.25, estimated ICC $(\hat{\rho })$ was 0.05 and target main trial cluster size $(m_f)$ was 40.

Table 2.

Results for the worked example, calculated four different configurations of pilot trial to estimate the ICC. Integrative approach uses result (6).

	Scenario 1	Scenario 2	Scenario 3	Scenario 4
Pilot cluster size (m)	20	20	40	10
Total clusters in pilot (K)	4	8	4	8
Total participants in pilot (N)	80	160	160	80
Swiger's method
Estimated ICC 95% CI	0, 0.201	0, 0.149	0, 0.163	0, 0.201
Integrative approach
Total clusters	58	54	54	58
Total participants	2320	2160	2160	2320
Upper 95% CI limit approach
Total clusters	150	116	126	150
Total participants	6000	4640	5040	6000
Searle's method
Estimated ICC 95% confidence interval	0, 0.581	0, 0.275	0, 0.514	0, 0.353
Integrative approach
Total clusters	100	70	92	78
Total participants	4000	2800	3680	3120
Upper 95% CI limit approach
Total clusters	400	200	356	250
Total participants	16000	8000	14240	10000
Fisher's transformation
Estimated ICC 95% confidence interval	0, 0.322	0, 0.200	0, 0.268	0, 0.263
Integrative approach
Total clusters	70	58	64	64
Total participants	2800	2320	2560	2560
Upper 95% CI limit approach
Total clusters	230	150	194	192
Total participants	9200	6000	7760	7680

ICC: intra-cluster correlation.

The sample sizes in Table 2 compare with a trial of 50 clusters and 2000 individuals without adjusting for imprecision in the estimate of the ICC. It is clear from this example that the choice of method to estimate the uncertainty in the variance can have an impact on the overall sample size calculation. Searle's method is the most conservative and results in the largest sample sizes; Swiger's method is the least conservative and results in the smallest sample size.

While the total number of individuals in the pilot trial is important for estimating the ICC, the relative number and size of clusters impacts on the precision of the estimate. For example, scenario 2, with more, medium sized clusters, estimates the ICC with greater precision than scenario 3, which has the same number of participants but fewer, larger clusters. All methods, however, result in a more efficient cRCT sample size than using the upper 95% CI for the ICC, which is likely to result in heavily overpowered trials.

Demonstration 2: Main trial sample size

To expand on the worked example, we used the integrative adjustment in result (6) to calculate sample sizes for main trials based on a broader range of example scenarios:

• Pilot trial cluster size: 2–60, increments of 1

• Pilot trial clusters per arm: 2–20, increments of 1

• Estimated ICC: 0.01, 0.05, 0.1, 0.15, 0.2

• Effect size: 0.01, 0.05–0.75, increments of 0.05

We also calculated sample sizes for these scenarios according to the unadjusted result (1) for comparison.

Table 3 shows selected results for this demonstration. These can be compared to the central set of columns in Table 1 (where d  =  0.25), which shows corresponding sample sizes without accounting for this uncertainty. In almost all cases, the adjusted sample size is larger than the unadjusted sample size, though the degree to which this differs depends on the cluster size, and the number of clusters in the pilot trial, with larger cluster sizes and larger pilot trials leading to less uncertainty, and subsequently a sample size closer to the unadjusted calculation. As such, as the size of the pilot trial increases, the adjusted sample size asymptotes at the unadjusted size. A broader range of results are given in tables in Supplementary Material S2. Complete results for this demonstration are extensive, and are available from https://github.com/JenLSheffield/ICC_imprecision; despite this, however, there will be many scenarios not covered in this demonstration. As such, R code to generate estimates for custom scenarios is available in Supplementary Material S4 and from https://github.com/JenLSheffield/ICC_imprecision.

Table 3.

Selected main trial sample sizes (clusters per arm) accounting for the uncertainty in the ICC, for a range of cluster sizes, ICCs and pilot clusters per arm, calculated using result (6). Cluster size is assumed to be equal in pilot and main trials. Effect size d  =  0.25.

ICC	Clusters per arm	Swiger's method					Searle's method					Fisher's transformation
		Cluster size					Cluster size					Cluster size
		5	10	15	20	30	5	10	15	20	30	5	10	15	20	30
0.01	4	82	43	30	23	17	90	50	35	28	20	85	45	32	25	18
	8	78	41	28	22	16	82	44	31	24	17	80	42	29	23	16
	10	77	40	28	22	16	80	42	30	23	17	78	41	29	22	16
	15	76	40	27	21	15	77	41	28	22	16	77	40	28	22	16
	20	75	39	27	21	15	76	40	28	22	16	75	39	27	21	15
0.05	4	90	53	41	35	29	99	62	49	42	36	92	56	43	37	31
	8	86	51	39	34	28	90	55	43	37	31	87	52	41	35	29
	10	85	50	39	34	28	88	54	42	36	31	86	52	40	35	29
	15	84	50	39	33	28	86	52	41	35	30	84	51	40	34	29
	20	83	50	39	33	28	85	51	40	35	29	84	50	39	34	29
0.10	4	101	67	56	50	45	110	77	66	61	55	103	70	59	54	48
	8	97	65	55	50	44	102	70	60	54	49	99	67	57	51	46
	10	97	65	55	49	44	100	69	59	53	48	98	66	56	51	46
	15	96	65	54	49	44	98	67	57	52	47	97	66	56	50	45
	20	95	65	54	49	44	97	67	56	51	46	96	65	55	50	45
0.20	4	125	96	86	82	77	135	108	99	95	90	126	99	90	86	81
	8	122	95	86	81	77	128	101	92	88	83	124	97	88	84	79
	10	122	95	86	81	77	127	100	91	86	82	123	97	88	83	79
	15	122	95	86	81	77	125	98	89	85	80	123	96	87	83	78
	20	122	95	86	81	77	124	97	88	84	79	123	96	87	82	78

ICC: intra-cluster correlation.

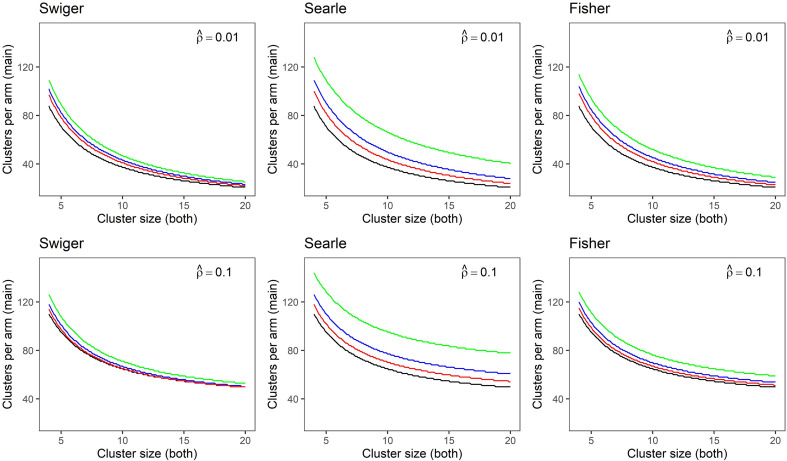
Figure 1 expands on Table 3 and the worked example above, and illustrates the difference in required clusters per arm for a main trial as cluster size varies, and contrasts results across the three methods of estimating the imprecision in the ICC estimate. Black graphs show the unadjusted sample size for the main trial. The green, blue and red graphs show the sample size for the main trial calculated using the integrative adjustment, with ICC estimates from a pilot trial of two, four and eight clusters per arm, respectively. In this figure, cluster size is the same for the main trial as for the pilot trial. Each panel shows results for an estimated effect size of 0.25. The top row shows results for an estimated ICC of 0.01, the bottom row shows results for an estimated ICC of 0.1.

Figure 1.

Sample size in clusters-per-arm for a main trial calculated for small and medium estimated intra-cluster correlation (ICCs) of $\hat{\rho }=0.01$ (top), $\hat{\rho }=0.1$ (bottom) and medium effect size (d = 0.25), using each method of estimating imprecision in the ICC. Plots show sample size accounting for imprecision in the ICC estimate from a pilot trial with two clusters-per-arm (green), four clusters-per-arm (blue), eight clusters-per-arm (red) and without accounting for imprecision (black). Main trial and pilot trial cluster sizes are assumed to be equal.

In all cases, when more clusters are used to estimate the ICC, the precision of that estimate is improved, and thus the ultimate sample size for the main trial is smaller and closer to that calculated without accounting for uncertainty. Searle's method is the most conservative of the three estimates, and results in the largest sample size. This difference between methods is more pronounced for medium to large cluster sizes, where Swiger's and Fisher's methods asymptote more quickly at the unadjusted sample size as ICC precision increases. Swiger's and Fisher's methods tend to produce similar estimates, particularly for smaller cluster sizes.

For Figure 1, while the three calculations of sample size in each plot appear similar, close inspection of the y-axis indicates a large difference in the calculated clusters-per-arm for the main trial. For example, consider Swiger's method and an estimated ICC of 0.01 (top left). When the cluster size is small $(m=m_f=4)$ , the calculated main trial sample size using the integrative adjustment with a small pilot trial (four clusters per arm, blue line) is 102 clusters per arm. In contrast, the calculated sample size without accounting for uncertainty (black line) is 88 clusters per arm: an underestimation of 13.7%. Similar underestimations persist with larger cluster sizes: at $m=m_f=8$ , the corresponding main trial sample sizes equate to 43 and 37 clusters per arm, respectively, reflecting a relative underestimation of 14.0%.

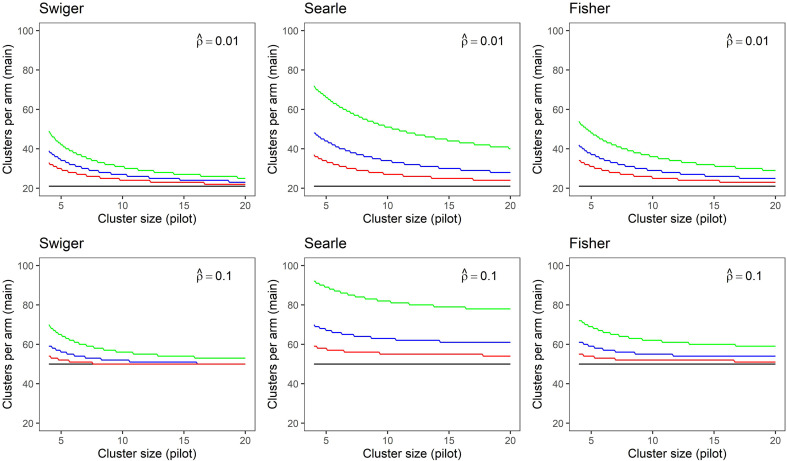
In Figure 2, the same results are shown as in Figure 1, but the main trial cluster size is held at $m_f=20$ , and only the pilot cluster size m is varied. This figure highlights the large amount of uncertainty in the estimate of the ICC that is attributable to the chosen cluster size in the pilot trial. The main trial sample size asymptotes more quickly for larger numbers of clusters in the pilot trial and larger $\hat{\rho }$ , although the use of Searle's method with the integrative adjustment continues to produce main trial sample size calculations markedly larger than the unadjusted sample size even with larger clusters in the pilot trial.

Figure 2.

Sample size in clusters-per-arm for a main trial calculated for small and medium estimated intra-cluster correlation (ICCs) of $\hat{\rho }=0.01$ (top), $\hat{\rho }=0.1$ (bottom) and medium effect size (d = 0.25), using each method of estimating imprecision in the ICC. Plots show sample size accounting for imprecision in the ICC estimate from a pilot trial with two clusters-per-arm (green), four clusters-per-arm (blue), eight clusters-per-arm (red) and without accounting for imprecision (black). Main trial cluster size is fixed at m_f = 20.

Sensitivity analysis

We explored the sensitivity of the sample size estimate using the integrative adjustment, compared with the unadjusted sample size, to the ICC, in an investigation similar to that performed by Julious. ²¹

1. First, we calculated the adjusted sample size based on an estimated ICC of 0.05, according to result (6) as well as the unadjusted sample size based on result (1).

2. Second, in two scenarios, we calculated plausibly large values for the ICC which corresponded to the 70th and 95th percentile of the confidence interval for the ICC. In the main paper, this CI has been calculated using Searle's method as the most conservative (see Supplementary Material S3 for results using the other approaches).

3. Finally, using these upper percentile estimates as the ICC, we calculated the resulting power for a main trial using the adjusted and unadjusted sample size calculated in step 1.

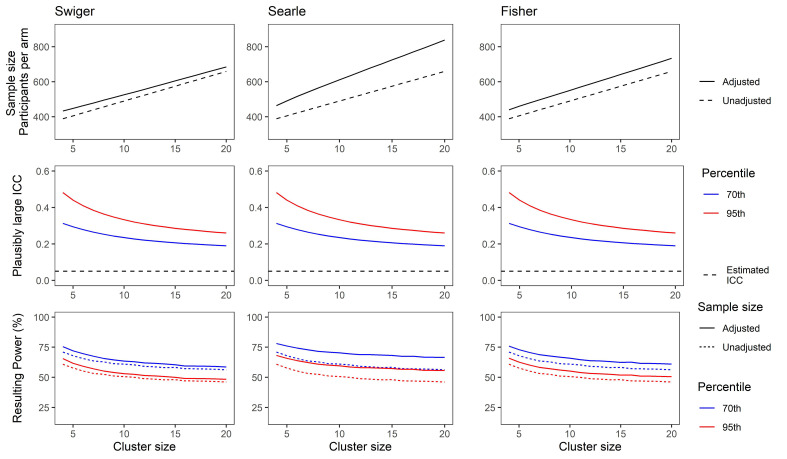
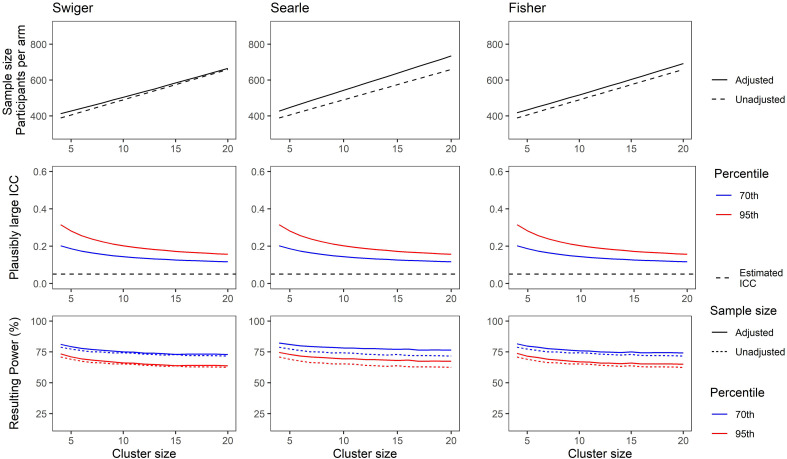
Figures 3 and 4 show the results for this demonstration. For Figure 3, the ICC was considered to be estimated based on a pilot trial with four clusters per arm. For Figure 4, the pilot trial was considered to have eight clusters per arm. The x-axes show the cluster size, which is the same for the pilot and the main trial.

Figure 3.

(Top) Adjusted and unadjusted sample size for a range of cluster sizes based on an estimated intra-cluster correlation (ICC) of 0.05, and a pilot trial of four clusters per arm, using each method of estimating imprecision in the ICC. (Middle) Plausibly large ICC set at the 70th (blue) and 95th (red) percentile of the ICC CI as calculated using Searle's method. (Bottom) Resulting power for a main trial powered using sample size from top plots and plausibly large ICCs from middle plots. Solid lines show power for a trial using the unadjusted sample size. Dotted lines show power for a trial using the adjusted sample size. Colour as in middle plots.

Figure 4.

(Top) Adjusted and unadjusted sample size for a range of cluster sizes based on an estimated intra-cluster correlation (ICC) of 0.05, and a pilot trial of eight clusters per arm, using each method of estimating imprecision in the ICC. (Middle) Plausibly large ICC set at the 70th (blue) and 95th (red) percentile of the ICC CI as calculated using Searle's method. (Bottom) Resulting power for a main trial powered using sample size from top plots and plausibly large ICCs from middle plots. Solid lines show power for a trial using the unadjusted sample size. Dotted lines show power for a trial using the adjusted sample size. Colour as in middle plots.

The sample size for a main trial, calculated using result (1) with no adjustment, and using the integrative adjustment in result (6) with the three respective methods, is shown by the number of participants per arm (top panels). These indicate the large differences in sample size using the unadjusted versus the adjusted calculations, and also across the different methods. The middle panels show the plausibly large values for the ICC for this simulation, which equate to the 70th (blue) and 95th (red) percentiles of the confidence interval around the ICC estimate $\hat{\rho }$ , as calculated according to Searle's method. The bottom panels show the resulting power in a scenario in which the main trial has the sample size shown in the top panels, when the ICC is that shown in the middle panels. For instance, in the bottom left panel, the solid blue line indicates the power of a main trial which has a sample size as shown by the solid line in the top left panel, and an ICC as indicated by the blue line in the middle left panel.

Figure 4 shows the same, but for the scenario where the pilot cluster size was larger, with eight clusters per arm used to estimate the ICC. Note that the adjusted sample sizes are closer to the unadjusted sample size due to a greater precision in the estimate of the ICC, and the resulting power losses in the bottom panels are relatively smaller.

These illustrate the losses in power that can result when no adjustments are made for uncertainty in the estimate of the ICC in the sample size calculation (compare dashed lines with solid lines in the bottom panels). This is particularly noticeable when the pilot trial has few clusters per arm. The use of Searle's method, being the most conservative, is more likely to preserve power when $\hat{\rho }$ is very imprecisely estimated. Swiger's method shows the greatest loss in power of the three methods in this scenario; however, this still shows an improvement of around 10% of the power loss for an unadjusted sample size. The minimum power achieved using the integrative approach and an ICC at the 95^th percentile of the CI was 46.1%, using Swiger's method, and with a smaller pilot trial. The greatest power achieved for the same scenario was 74.6%, using Searle's method and a larger pilot trial.

Discussion

Previous research shows that ICC estimates from pilot trials are frequently imprecise. ⁴ While recommendations exist not to utilise a single ICC estimate from one pilot trial for estimating main trial sample size, this remains commonly done in practice. We have presented an approach to help mitigate some of the potential impacts on main trial power that can result from using a single ICC estimate by adjusting the calculated main cRCT sample size according to the imprecision in the ICC estimate in the case of continuous outcomes. Our approach can be used with any means of estimating the uncertainty in the estimate of the ICC. In this initial study, we have assumed a two-armed trial, with equally sized clusters and the same number of clusters per arm.

Our worked example illustrated the interplay of cluster size and number of clusters in the pilot trial on the resulting imprecision of the ICC estimate, and the further impacts of this on the calculated main trial sample size. This showed that a pilot trial with more, medium-sized clusters resulted in a more precisely estimated ICC than a pilot with larger, fewer clusters but the same overall number of participants. In all cases however, our approach resulted in a more efficient main trial than utilising the upper limit of the 95% CI around the estimated ICC.

In the ‘Demonstration 2: Main trial sample size’ section, we demonstrated the impact of the size of the pilot trial, in terms of number of clusters and the cluster size, on the resulting main trial sample size, compared with the unadjusted calculation. This suggested large gains in precision when increasing the size of the pilot trial from two to eight clusters per arm, particularly for smaller cluster sizes.

Finally, we showed the implications of using this method on the subsequent power of a main trial, using a plausibly large value for the ICC. This demonstrated that while utilising the adjusted sample size results in additional recruitment demands on a main trial, it could result in potentially large increases in power relative to the case in which no adjustment is made.

Implications for trial design

It is clear that the size of a pilot trial used to generate an estimate of the ICC can have a considerable impact on the main trial sample size when adjusting for the uncertainty of this estimate. Small pilot trials will generally lead to very large main trials using this approach, and more, medium-size clusters will tend to result in a more precise estimate of the ICC than fewer, larger clusters. This should be considered when designing both pilot and main cRCTs.

The use of multiple methods to estimate the uncertainty in the ICC in the present manuscript indicated that in some cases, particularly for small pilot trials, very different estimates for a main trial sample size can result. The differences between these methods were reduced as the pilot trial sample size increased; however, since pilot trials are typically small, it is unlikely that full agreement between the methods will be reached for a given pilot trial. In this case, an understanding of the likely distribution of $\hat{\rho }$ would be helpful in order to assess which method is most appropriate. In the absence of such an understanding, it may be convenient to be guided by Searle's method as the most conservative to maximise the likelihood of maintaining reasonable power, whilst risking significantly less overpowering than other conservative approaches such as utilising the upper limit of the 95% CI around the ICC. A sensible approach would be to estimate the sample size using all three methods and combine this with other sources of information regarding the ICC to generate a final well-rounded estimate.

As such, the work presented here is most usefully considered as an additional tool to support a broader approach to determining a sensible ICC estimate for a sample size calculation. Our approach should be considered in the context of other methods, which together may gain a more accurate overall picture of the ICC to lead to a sensible estimate, consistent with the approach recommended by previous researchers.^3,4 Such an approach should consider, for example, surveys to study patterns in ICCs.

Relation to existing methods

A Bayesian approach has previously been taken to accounting for imprecision in the estimate of the ICC when designing a cRCT. ²² This approach generates posterior distributions for the true ICC $\rho$ based on an estimate $\hat{\rho }$ , and also examines the use of Swiger's method, Searle's method and Fisher's transformation to achieve this. These distributions are further used to generate probability distributions for power for a main trial of a given sample size. The methods presented in the present manuscript provide an alternative approach to Turner et al., which may be preferred in some circumstances. It is more straightforward to apply, and may be used to generate a main trial sample size estimate, in contrast to the Bayesian approach which estimates the mean power for a chosen sample size. Most usefully however, and in line with the recommendations above, these methods may be used in conjunction to support a multi-method approach: our method may estimate a range of sample sizes, then Turner's method ²² may be used to estimate the mean resulting power for those candidate sample sizes.

Limitations

This study has several limitations. This manuscript only addresses the case of continuous outcomes. We have not accounted for other sources of uncertainty, such as in the variance estimate, and in practice, this would further affect the power of a main trial. It is also clear from Figures 3 and 4 that the recommended adjustment will still result in a loss of power if the ICC estimate is very imprecise. We have also assumed equal cluster sizes throughout; many cRCTs will inevitably recruit unequally sized clusters which will have a non-trivial impact on both precision and power.

The sample for a pilot trial may not be representative of the wider population meaning that an ICC estimated from a pilot trial may not be directly applicable to a larger main trial. Additionally, the variance calculated according to any of the three methods of estimating the uncertainty in $\hat{\rho }$ is itself an estimate and likely to be imprecise; as a result, the estimated distribution of $\hat{\rho }$ may be too conservative or too liberal. There may also be many scenarios in which none of these methods is appropriate; each relies on certain assumptions, and results will be inaccurate if these assumptions are violated. It may be difficult to know which of the three methods is most appropriate in a given case. Finally, the use of the sample size formula in result (1) itself relies on an adequately sized pilot trial for the estimation of the ICC to be applicable. The question of what is ‘adequately sized’ is complex due to the interplay of the number of clusters, the ICC, the effect size and the cluster size, and will vary accordingly. However, Figures 1 and 2, along with tables in Supplementary Material S2 imply that 4–8 clusters of 15–20 individuals per arm will approach the asymptote of the unadjusted sample size in many cases.

Future work will aim to address these shortcomings by exploring additional means of calculating imprecision in the ICC estimate, and addressing the case of unequal cluster size and binary outcomes. Additionally, for cases where assumptions such as the normality of $\hat{\rho }$ may not hold, alternative methods without parametric assumptions, such as bootstrapping, will be investigated.

Conclusions

Despite the limitations discussed above, particularly regarding the imprecision of the estimate of the variance of $\hat{\rho }$ , this paper contributes a new approach which may be utilised in concert with additional information and methods to reach a sensible estimate of the ICC for calculating main trial sample size. This is a straightforward approach which may be applied quickly and easily utilising the code we have made available in Supplementary Material S4, and may be further developed for use with any means of calculating the variance of $\hat{\rho }$ , beyond those we have considered here, making it broadly applicable. Many scenarios are also covered in Supplementary Tables S2.1–S2.36 and those in the associated GitHub repository, which may serve as guidance for main trial sample size, providing a resource which may support the multi-method approach advocated here.