Comparing the electric fields of transcranial electric and magnetic perturbation

Abstract

Significance.

Noninvasive brain stimulation (NIBS) by quasistatic electromagnetic means is presently comprised of two methods: magnetic induction methods (transcranial magnetic perturbation or TMP) and electrical contact methods (transcranial electric perturbation or TEP). Both methods couple to neuronal systems by means of the electric fields they produce. Both methods are necessarily accompanied by a scalp electric field which is of greater magnitude than anywhere within the brain. A scalp electric field of sufficient magnitude may produce deleterious effects including peripheral nerve stimulation and heating which consequently limit the spatial and temporal characteristics of the brain electric field. Presently the electromagnetic NIBS literature has produced an accurate but non-generalized understanding of the differences between the TEP and TMP methods.

Objective.

The aim of this work is to contribute a generalized understanding of the differences between the two methods which may open doors to novel TEP or TMP methods and translating advances, when possible, between the two methods.

Approach.

This article employs a three shell spherical conductor head model to calculate general analytical results showing the relationship between the spatial scale of the brain electric fields and: (1) the scalp-to-brain mean-squared electric field ratio for the two methods and (2) TEP-to-TMP scalp mean-squared electric field ratio for similar electric fields at depth.

Main results.

The most general result given is an asymptotic limit to the TEP-to-TMP ratio of scalp mean-squared electric fields for similar electric fields at depth. Specific example calculations for these ratios are also given for typical TEP electrode and TMP coil configurations. While TMP has favorable mean-squared electric field ratios compared to TEP this advantage comes at an energetic cost which is briefly elucidated in this work.

1. Introduction

The neuronal tissue of the brain can be perturbed noninvasively by the application of an electric field generated by two means: magnetic induction and electrical contact [1, 2]. The magnetic induction method uses a time varying current within coils external to the head, and not in electrical contact with the head, to produce a time varying magnetic field within the brain. This time varying magnetic field induces an electric field in the electrically conductive head. The electric contact method uses a source of current and electrodes in contact with the head to produce an electric field within the brain. Regardless of which method is used, the electric field is stronger in the scalp than in the brain. Therefore, when designing new systems to perturb brain function, it is of considerable importance to understand with some generality the characteristics of the brain and scalp electric fields of each method. In addition it is important for the researcher to understand the energetic costs of generating electric fields by each method.

Here the electric contact method will be referred to as transcranial electric perturbation (TEP) and the magnetic induction method will be referred to as transcranial magnetic perturbation (TMP). Therefore TMS (transcranial magnetic stimulation) [1], which is an induction method that employs brief (approximately 250 μs) and possibly intense pulses (requiring as much as 6 kA of coil current) capable of producing suprathreshold electric fields (greater than 40 V m⁻¹) within the brain, is a TMP method. Similarly TES (transcranial electric stimulation) [3, 4], which is a electric contact method that employs sustained (300–1800 s) subthreshold electric fields (approximately 0.5 V m⁻¹) generated from relatively small contact currents (typically up to 2.0 mA in the DC–kHz range) or electroconvulsive therapy [5], which is an electric contact method that employs brief pulses (0.2–2.0 ms) delivered as a train of brief pulses (0.2–1.0 ms square wave pulse, 20–240 pulses s⁻¹, ⩽8 s total duration) using contact current amplitudes in the range of 100–900 mA, are both TEP methods.

Regardless of the method used the resulting electric field couples to neurons and may perturb their state in a short or long term manner. When the electric field is suprathreshold, robust effects such as spiking and electrical nerve blocking [6] can be elicited with kHz continuous waveforms. When the electric field is subthreshold effects such as entrainment [7, 8] and motor threshold changes [9, 10] can be elicited. The dynamics of the coupling of the applied electric field to any given neuron can be described by equations that predict the change in the neuron’s transmembrane potential (the output) which are in general nonlinear with respect to the applied electric field (the input) [11]. If the electric field amplitude is much smaller than threshold then the electrodynamics of the neuronal system can often be described by a linear relationship between the input electric field and the output transmembrane potential. As the input amplitude increases the linear approximations will fail and nonlinear relationships must ultimately be employed.

Most TEP and TMP modeling employs the finite element method in conjunction with volume conductor models built from magnetic resonance images [12–16] to estimate the electric field within the head. However such detail is not necessarily needed or even desirable when trying to establish general physical and engineering principles associated with the TEP and TMP methods. In fact, when making comparisons between these methods, numerical calculation of electric fields generated by specific TEP electrode geometries or specific TMP coil geometries can miss general principles, like those described in the body of this paper, which are obtainable through analytical calculations.

The work herein makes clear, in a general manner, that the choice between the TEP or TMP methods depends primarily upon the temporal and spatial characteristics of the desired electric field as well as the energy consumption of the respective current sources. With respect to the electric field spatial characteristics it is shown that the TEP and TMP methods differ fundamentally with respect to the electric field subspaces they span and the scalp-to-brain power dissipation ratios they produce. All other differences, such as field focality, follow from these two general differences.

To compare the feasibility, benefits and trade-offs of TEP versus TMP electric fields a detailed model of the electric field established in the human head is not needed. Detailed models are important for estimating electric field dosing [17, 18] but are unnecessary to elucidate and compare general design and feasibility issues concerning the TEP and TMP methods. Instead it suffices to employ a spherical head model which can yield generic comparisons of the brain versus scalp electric fields. To make such comparisons it is helpful to have a single number for each region of the head to characterize the ‘distance’ between the electric field in that region and the zero electric field. In other words, this single number should behave as a mathematical norm for the electric field in a region. Any norm has three properties: it is nonzero except when the field is zero, it scales linearly with the scaling of the field and it obeys the triangle inequality expected of any distance metric. Many norms for a field exist. For example the absolute value norm (L1 norm), the Euclidian norm (root-mean-square norm or L2 norm) and the maximum norm. The root-mean-square norm is particularly useful because it is analytically easier to manipulate than the other norms. Additionally, as will be seen, this choice of the norm does not require a unique determination of the electric fields when making comparisons between similar TEP and TMP fields as would be necessary for meaningful comparisons using the maximum norm.

Throughout this paper comparisons will be made between TEP and TMP electric fields using the root-mean-square or mean-squared norms within the brain and scalp regions. These particular norms are useful proxies for the electric field magnitude and the absorbed power respectively. These quantities are of great experimental consequence since the amplitude of the scalp electric field may limit the safely obtainable amplitude of the cortical electric field. Indeed, scalp peripheral nerve stimulation (which can range from distracting to painful) scales with root-mean-square electric field amplitude while scalp heating (which can range from benign to burning) scales with mean-square electric field amplitude. Note that since the conductivities of the brain and scalp regions are comparable and often assumed to be equal, as is often the case in three-shell models, then the scalp-to-brain power dissipation ratio is equivalent to the scalp-to-brain mean-squared electric field ratio. Also note that most extant quasistatic EM noninvasive brain stimulation (NIBS) methods are limited by peripheral nerve stimulation rather than tissue heating. However, this may not apply to future methods in which electric field amplitude, frequency (although still quasistatic) and duration of the perturbing waveforms could be increased.

To present the differences between TEP and TMP electric fields in a clear manner a three-shell head model is employed and solved analytically. In this model the head is assumed to consist of three concentric spherically symmetric regions of differing conductivities which adequately represent the electromagnetic properties of the scalp, skull and brain. Vector spherical harmonics [19] are used to describe the TEP and TMP electromagnetic fields and sources of current. This is a natural choice for the vector fields given the spherical geometry of the model.

Most of the earlier treatments of the electric field within a spherically symmetric conductor did not make use of vector spherical harmonics and as a result the derivations were somewhat long and cumbersome [20]. The authors know of only two publications [21, 22] (articles concerned with TMS coil design) which make use of vector spherical harmonics in the treatment of such problems. However, scalar spherical harmonics have been used in the analytic solution of the three-shell TEP model [23] albeit with skull, cerebrospinal fluid (CSF) and brain as the three compartments of the model. That publication noted that the results of their calculations were only slightly dependent upon the conductivity and thickness of the CSF hence that compartment is not included in the present work. Here, for the first time, vector spherical harmonics are used to describe both the TMP and TEP electric fields thereby allowing for a direct comparison of the respective electric fields and properties. While these solutions will be used in this paper to establish general properties of the TMP and TEP electric fields it is important to stress that they will also be of importance to future general work requiring these solutions as input to dynamical calculations such as, for example, the evolution of the head temperature distribution. A real head will of course not be spherically symmetric nor will it be precisely separable into only three regions of differing electric conductivity, however the general principles and estimates established in this work apply approximately to more realistic models as well.

This paper is organized as follows: In section 2 the three-shell model is solved for the electric field in the three regions modeling the scalp, skull and brain. Briefly the spatial differences between the TEP and TMP electric fields are mentioned. In section 3 the quantities R^TEP, R^TMP and R are calculated. The quantities R^TEP and R^TMP are the scalp-to-brain ratios of power dissipation for the TEP and TMP cases respectively whereas R is the TEP-to-TMP ratio of scalp energy dissipation for the case of similar TEP and TMP electric fields at the radial position of the cortex. Example calculations of each ratio are given for the case of typical electrode and coil geometries. The energetic cost of generating an electric field within the brain depends upon the method used. Therefore section 3.5 presents a simple analysis of the power utilization of TEP and TMP current sources. In this manner a more complete picture of the benefits and costs of each method can be understood. The paper ends with a discussion of future methods that could potentially take advantage of the benefits of TMP albeit at a cost in power utilization and requiring new designs for TMP coil cooling systems.

2. Methods

The electric fields of TEP and TMP, from which all results herein will be obtained, were derived by solving the quasistatic Maxwell Equations in terms of a vector spherical harmonic representation. Figure 1 depicts the three-shell spherical head model which will be used in the derivation of the TEP and TMP electric fields. The spherical head of volume V consists of three conducting spherical shells in which the regions from outermost to innermost are the scalp (region 2), skull (region 1) and brain (region 0) respectively with scalar conductivities σ_i (i = 0, 1, 2). Reasonable estimates for the radii of the three shell model corresponding to human anatomy are r₀ = 80 mm, r₁ = 86 mm and r₂ = 92 mm [24]. Typical values of the conductivities which will be used here are such that σ₀ = σ₂ and σ₁/σ₀ = 1/80 [25] although, for sake of generality, these values will not be enforced initially.

Figure 1.

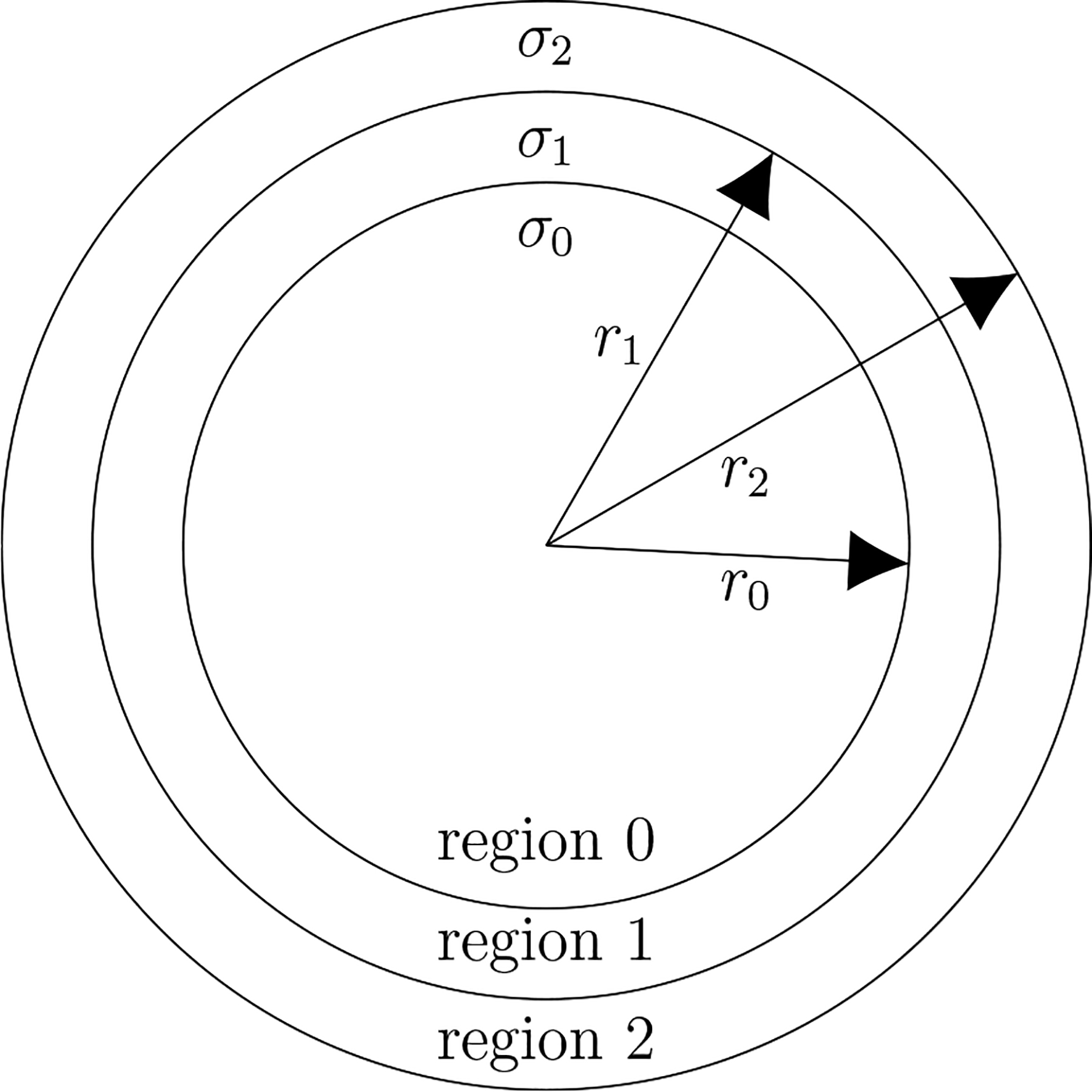
The three-shell spherical head model in which the regions from outermost to innermost are the scalp, skull and brain respectively. Typical estimates for three shell model radii are r₀ = 80 mm, r₁ = 86 mm and r₂ = 92 mm whereas typical estimates σ₀ = σ₂ and ϵ = σ₁/σ₀ = 1/80. Note that only the ratio ε, rather than the specific values of the conductivities, is of importance in this work since the focus is on the calculation of mean-squared electric field ratios between the brain and scalp regions. The mean-squared electric field is a single number proxy for the energy dissipation in a region whereas it is square root is a single number proxy for the electric field amplitude in a region.

In TMP the electric field arises from a current density J(x, t) within a coil, supported external to V only, driven by a current source. In TEP the electric field arises from an electric current density J(x, t) in electrical contact with the external boundary of the scalp region. Regardless of the method the electric field is given (in the Gaussian system of units) at all positions x and times t by [26]:

$$E(x,t)=-\nabla \Phi (x,t)-\frac{1}{c}\frac{\partial A(x,t)}{\partial t}$$ (1)

where Φ is the scalar potential and A is the vector potential. It will be convenient in this work to use the nondimensional position vector r = x/r₂. The electric field is then given everywhere by:

$$\text{e}(r,t)=-\frac{1}{r_2}\nabla \phi (r,t)-\frac{1}{c}\frac{\partial a(r,t)}{\partial t}$$ (2)

where the derivatives of the ∇ operator are with respect to the components of r and where the field quantities are given by e(r, t) = E(rr₂, t), φ(r, t) = Φ(rr₂, t), a(r, t) = A(rr₂, t) and j(r, t) = J(rr₂, t).

Given the frequencies of interest (less than 100 kHz) we will make the usual quasistatic approximations (see [27] for nuance concerning the quasistatic approximation). Under these approximations: (1) the scalar potential φ within V obeys Laplace’s equation ∇² φ = 0, (2) polarization and magnetization currents can be ignored so that the current within V is Ohmic only (j(r, t) = σ(r)e(r, t) where σ(r) is the conductivity), (3) the vector potential within V depends only upon currents external to V since the secondary Ohmic currents, established within V due to the electric field caused by the time varying external current, are relatively small by comparison and (4) the boundary conditions at the interface between regions n and n + 1 are $\widehat{r}\cdot j_n=\widehat{r}\cdot j_{n+1}$ and $\widehat{r}\times e_n=\widehat{r}\times e_{n+1}$ where $\widehat{r}$ is unit vector in the radial direction of a spherical coordinate system. The first boundary condition is a consequence of the quasistatic condition ∇ · j = 0 whereas the second boundary condition is valid in general.

2.1. TEP

To calculate e(r, t) within V we require a convenient form of the scalar potential φ(r, t) and vector potential a(r, t) suitable to the assumed spherical geometry. Given the geometry of the model a natural choice for representing the electric fields of both methods is the complete set of vector spherical harmonics. The electric scalar potential, obeying Laplace’s equation ∇² φ = 0 within V, can be written as sums of scalar spherical harmonics Y_jm(θ, ϕ) in the three regions of the three-shell model as:

$${\phi }_0(r,\theta ,\varphi ,t)=r_2\sum _{jm}{A}_{jm}(t)r^j{Y}_{jm}(\theta ,\varphi )$$ (3)

$$\begin{gathered} {\phi }_1(r,\theta ,\varphi ,t)=r_2\sum _{jm}{B}_{jm}(t)r^j{Y}_{jm}(\theta ,\varphi ) \\ +C_{jm}(t)r^{-(j+1)}{Y}_{jm}(\theta ,\varphi ) \end{gathered}$$ (4)

$$\begin{gathered} {\phi }_2(r,\theta ,\varphi ,t)=r_2\sum _{jm}{D}_{jm}(t)r^j{Y}_{jm}(\theta ,\varphi ) \\ +E_{jm}(t)r^{-(j+1)}{Y}_{jm}(\theta ,\varphi ) \end{gathered}$$ (5)

where the subscript k = 0, 1, 2 of φ_k(r, θ, ϕ, t) denotes the region and where the indices of the double summation have values j = 0, …, ∞ and m = −j, …, j. The quantities A_jm, B_jm, C_jm, D_jm and E_jm will be determined by the boundary conditions. Since the vector potential can be neglected in the TEP case (the vector potential due to current in V is negligible) the electric field is given by $e(r,\theta ,\varphi ,t)=-\frac{1}{r_2}\nabla \phi (r,\theta ,\varphi ,t)$ and in the three regions:

$${\text{e}}_0(r,\theta ,\varphi )=-\sum _{jm}{A}_{jm}{[j(2j+1)]}^{1/2}{r}^{j-1}{\text{Y}}_{jm}^{j-1}(\theta ,\varphi$$ (6)

$$\begin{gathered} e_1\left(r,\theta ,\varphi \right)=-\sum _{jm}{B}_{jm}{\left[j\left(2j+1\right)\right]}^{1/2}{r}^{j-1}{Y}_{jm}^{j-1}\left(\theta ,\varphi \right) \\ -\sum _{jm}{C}_{jm}{\left[\left(j+1\right)\left(2j+1\right)\right]}^{1/2}{r}^{-\left(j+2\right)} \\ \times Y_{jm}^{j+1}\left(\theta ,\varphi \right) \end{gathered}$$ (7)

$$\begin{gathered} e_2\left(r,\theta ,\varphi \right)=-\sum _{jm}{D}_{jm}{\left[j\left(2j+1\right)\right]}^{1/2}{r}^{j-1}{Y}_{jm}^{j-1}\left(\theta ,\varphi \right) \\ -\sum _{jm}{E}_{jm}{\left[\left(j+1\right)\left(2j+1\right)\right]}^{1/2}{r}^{-\left(j+2\right)} \\ \times Y_{jm}^{j+1}\left(\theta ,\varphi \right) \end{gathered}$$ (8)

where the time dependence has been suppressed for the sake of a compact notation and the $Y_{jm}^l(\theta ,\varphi )$ are complex valued vector spherical harmonics (see appendix A).

The boundary conditions at r = 1, r = α₁ = r₁/r₂ and r = α₀ = r₀/r₂ are

$${\sigma }_2{e}_2(1,\theta ,\varphi )\cdot \widehat{r}=j(1,\theta ,\varphi )\cdot \widehat{r}$$ (9)

$$\begin{gathered} {\sigma }_1{\text{e}}_1\left({\alpha }_1,\theta ,\varphi \right)\cdot \widehat{r}={\sigma }_2{\text{e}}_2\left({\alpha }_1,\theta ,\varphi \right)\cdot \widehat{r} \\ \widehat{r}\times e_1\left({\alpha }_1,\theta ,\varphi \right)=\widehat{r}\times e_2\left({\alpha }_1,\theta ,\varphi \right) \end{gathered}$$ (10)

$$\begin{gathered} {\sigma }_0{\text{e}}_0\left({\alpha }_0,\theta ,\varphi \right)\cdot \widehat{r}={\sigma }_1{\text{e}}_1\left({\alpha }_0,\theta ,\varphi \right)\cdot \widehat{r} \\ \widehat{r}\times e_0\left({\alpha }_0,\theta ,\varphi \right)=\widehat{r}\times e_1\left({\alpha }_0,\theta ,\varphi \right). \end{gathered}$$ (11)

By applying these five boundary conditions we obtain a system of five linear equations which can be solved (see appendix B) for the quantities A_jm, B_jm, C_jm, D_jm and E_jm. Defining ϵ = σ₁/σ₀ and making the reasonable assumption that σ₂ = σ₀ the following solution is obtained:

$$\begin{gathered} A_{jm}=a_j{\alpha }_0^{-(2j+1)}{\alpha }_1^{-(2j+1)}{\mathcal{D}}_j^{-1}{I}_{jm} \\ {B}_{jm}=b_j{\alpha }_0^{-(2j+1)}{\alpha }_1^{-(2j+1)}{\mathcal{D}}_j^{-1}{I}_{jm} \\ {C}_{jm}=c_j{\alpha }_1^{-(2j+1)}{\mathcal{D}}_j^{-1}{I}_{jm} \\ {D}_{jm}=\left[d_{0j}{\alpha }_0^{-(2j+1)}+d_{1j}{\alpha }_1^{-(2j+1)}\right]{\alpha }_1^{-(2j+1)}{\mathcal{D}}_j^{-1}{I}_{jm} \\ {E}_{jm}=e_j\left[{\alpha }_0^{-(2j+1)}-{\alpha }_1^{-(2j+1)}\right]{\mathcal{D}}_j^{-1}{I}_{jm} \end{gathered}$$ (12)

where, for the sake of compact notation, we have defined

$$\begin{gathered} a_j=ϵ{\left(2j+1\right)}^2 \\ {b}_j=\left(2j+1\right)\left(\left[1+ϵ\right]j+ϵ\right)] \\ {c}_j=-\left(1-ϵ\right)j\left(2j+1\right) \\ {d}_{0j}=\left(\left[1+ϵ\right]j+ϵ\right)\left(\left[1+ϵ\right]j+1\right) \\ {d}_{1j}=-{\left(1+ϵ\right)}^{2}j\left(j+1\right) \\ {e}_j=\left(1-ϵ\right)j\left(\left[1+ϵ\right]j+ϵ\right)] \end{gathered}$$ (13)

and

$$\begin{gathered} {\mathcal{D}}_j=-ϵj^3{\alpha }_0^{-\left(2j+1\right)}{\alpha }_1^{-\left(2j+1\right)}-{ϵ}^2{j}^2\left(j+1\right){\alpha }_0^{-\left(2j+1\right)} \\ \times {\alpha }_1^{-\left(2j+1\right)}-ϵj^2\left(j+1\right){\alpha }_1^{-\left(4j+2\right)}+{ϵ}^2{j}^2\left(j+1\right) \\ \times {\alpha }_1^{-\left(4j+2\right)}-j^2\left(j+1\right){\alpha }_0^{-\left(2j+1\right)}{\alpha }_1^{-\left(2j+1\right)} \\ -ϵj{\left(j+1\right)}^2{\alpha }_0^{-\left(2j+1\right)}{\alpha }_1^{-\left(2j+1\right)}+j^2\left(j+1\right) \\ \times {\alpha }_1^{-\left(4j+2\right)}-ϵj^2\left(j+1\right){\alpha }_1^{-\left(4j+2\right)}-ϵj^2\left(j+1\right) \\ \times {\alpha }_0^{-\left(2j+1\right)}-{ϵ}^{2}j{\left(j+1\right)}^2{\alpha }_0^{-\left(2j+1\right)}-ϵj{\left(j+1\right)}^2 \\ \times {\alpha }_1^{-\left(2j+1\right)}-{ϵ}^{2}j{\left(j+1\right)}^2{\alpha }_1^{-\left(2j+1\right)}-j^2\left(j+1\right) \\ \times {\alpha }_0^{-\left(2j+1\right)}+ϵj{\left(j+1\right)}^2{\alpha }_0^{-\left(2j+1\right)} \\ -j^2\left(j+1\right){\alpha }_1^{-\left(2j+1\right)}+ϵj^2\left(j+1\right){\alpha }_1^{-\left(2j+1\right)} \end{gathered}$$ (14)

and

$$I_{jm}=\frac{1}{{\sigma }_2}{\int }_0^{2\pi }{\int }_0^{\pi }\mathbf{\text{j}}(1,\theta ,\varphi )\cdot \widehat{r}{Y}_{jm}^{*}(\theta ,\varphi )\text{ sin}\theta d\theta d\varphi .$$ (15)

Note that since ∇ · j = 0 for a quasistatic system then, according to Gauss’s Law, I₀₀ = 0 therefore the indices of the double summation are now j = 1, …, ∞ and m = −j, …, j.

Considering the solutions for the electric field within the brain as given by equation (6) together with equation (15) it is apparent that the electric field is independent of the size of the head r₂. Therefore for two different size three-shell model heads, with the same relative size shells, the electric fields will be identical at any given nondimensional position within the head if the current densities j(1, θ, ϕ) are identical. However for a fixed angular distribution of current density, since the surface area of the electrodes increases as $r_2^2$, then so does the total current delivered to the electrodes by the current source.

2.2. TMP

In accordance with equation (2) both the scalar potential φ(r, t) and vector potential a(r, t) must be considered to obtain the TMP electric field e(r, t) within V. In terms of the dimensionless spatial coordinate r the vector potential in the quasistatic case is given by [26]

$$a(r,t)=\frac{r_2^2}{c}\iiint \frac{j\left(r^{\prime },t\right)}{\left|r-r^{\prime }\right|}{d}^3{r}^{\prime }.$$ (16)

Expanding the integrand in terms of vector spherical harmonics (see [19, p 229]) we can write the electric field within V as

$$a(r,t)=c\sum _{ljm}\frac{r^l}{2l+1}{Y}_{jm}^l(\theta ,\varphi )J_{jm}^l(t)$$ (17)

where l = j − 1, j, j + 1 and

$$\begin{gathered} J_{jm}^l(t)=\frac{4\pi r_2^2}{c^2}\iiint \frac{1}{r^{\prime l+1}}j\left(r^{\prime },{\theta }^{\prime },{\varphi }^{\prime },t\right) \\ \cdot {\mathbf{\text{Y}}}_{jm}^{*l}\left({\theta }^{\prime },{\varphi }^{\prime }\right)r^{\prime 2}\text{ sin}{\theta }^{\prime }d{r}^{\prime }d{\theta }^{\prime }d{\varphi }^{\prime }. \end{gathered}$$ (18)

Since the ohmic current within V can be neglected in the calculation of the vector potential then it follows that ∇ × b = ∇ × ∇ × a = 0 within V. Applying this constraint (making use of identities given in [19, pg 217]) one finds that $J_{jm}^{j+1}=0$ and therefore

$$\begin{gathered} a(r,t)=c\sum _{jm}\frac{r^j}{2j+1}{J}_{jm}^j(t)Y_{jm}^j(\theta ,\varphi ) \\ +c\sum _{jm}\frac{r^{j-1}}{2j-1}{J}_{jm}^{j-1}(t)Y_{jm}^{j-1}(\theta ,\varphi ). \end{gathered}$$ (19)

Since the quasistatic vector potential given by equation (16) satisfies ∇ · a = 0 everywhere and since ∇ · e = 0 within V then according to equation (2) the scalar potential must satisfy the Laplace equation within V. Therefore within V the scalar potential in the three regions can written as:

$${\phi }_0(r,\theta ,\varphi )=r_2\sum _{jm}{A}_{jm}{r}^j{Y}_{jm}(\theta ,\varphi )$$ (20)

$$\begin{gathered} {\phi }_1(r,\theta ,\varphi )=r_2\sum _{jm}{B}_{jm}{r}^j{Y}_{jm}(\theta ,\varphi )+C_{jm}{r}^{-(j+1)} \\ \times Y_{jm}(\theta ,\varphi ) \end{gathered}$$ (21)

$$\begin{gathered} {\phi }_2(r,\theta ,\varphi )=r_2\sum _{jm}{D}_{jm}{r}^j{Y}_{jm}(\theta ,\varphi )+E_{jm}{r}^{-(j+1)} \\ \times Y_{jm}(\theta ,\varphi ) \end{gathered}$$ (22)

and the corresponding electric fields are:

$${\mathbf{\text{e}}}_0(r,\theta ,\varphi )=-\sum _{jm}[j{\left(2j+1\right)}^{1/2}{A}_{jm}{r}^{j-1}{\mathbf{\text{Y}}}_{jm}^{j-1}(\theta ,\varphi )\text{}-\sum _{jm}\frac{r^j}{2j+1}\frac{\partial J_{jm}^j}{\partial t}{Y}_{jm}^j(\theta ,\varphi )\text{}-\sum _{jm}\frac{r^{j-1}}{2j-1}\frac{\partial J_{jm}^{j-1}}{\partial t}{Y}_{jm}^{j-1}(\theta ,\varphi )$$ (23)

$$\begin{gathered} e_1\left(r,\theta ,\varphi \right)=-{\sum _{jm}\left[j\left(2j+1\right)\right]}^{1/2}{B}_{jm}{r}^{j-1}{Y}_{jm}^{j-1}\left(\theta ,\varphi \right) \\ -\sum _{jm}{\left[\left(j+1\right)\left(2j+1\right)\right]}^{1/2}{C}_{jm}{r}^{-\left(j+2\right)} \\ \times Y_{jm}^{j+1}\left(\theta ,\varphi \right)-\sum _{jm}\frac{r^j}{2j+1}\frac{\partial J_{jm}^j}{\partial t}{Y}_{jm}^j \\ \times \left(\theta ,\varphi \right)-\sum _{jm}\frac{r^{j-1}}{2j-1}\frac{\partial J_{jm}^{j-1}}{\partial t}{Y}_{jm}^{j-1}\left(\theta ,\varphi \right) \end{gathered}$$ (24)

$$\begin{gathered} e_2\left(r,\theta ,\varphi \right)=-{\sum _{jm}\left[j\left(2j+1\right)\right]}^{1/2}{D}_{jm}{r}^{j-1}{Y}_{jm}^{j-1}\left(\theta ,\varphi \right) \\ -\sum _{jm}{\left[\left(j+1\right)\left(2j+1\right)\right]}^{1/2}{E}_{jm}{r}^{-\left(j+2\right)} \\ \times Y_{jm}^{j+1}\left(\theta ,\varphi \right)-\sum _{jm}\frac{r^j}{2j+1}\frac{\partial J_{jm}^j}{\partial t}{Y}_{jm}^j \\ \times \left(\theta ,\varphi \right)-\sum _{jm}\frac{r^{j-1}}{2j-1}\frac{\partial J_{jm}^{j-1}}{\partial t}{Y}_{jm}^{j-1}\left(\theta ,\varphi \right). \end{gathered}$$ (25)

Note that once again the time dependence of the fields has been suppressed for the sake of compact notation.

The boundary conditions are still those given by equations (9)–(11) albeit with j · n = 0 and now the electric field has a component due to induction as well as that due to surface charges. By applying the five boundary conditions we again obtain a system of five linear equations which can be solved (see appendix C) for the quantities A_jm, B_jm, C_jm, D_jm and E_jm. For all three regions the following simple solution is obtained:

$$\mathbf{\text{e}}(r,\theta ,\varphi )=-\sum _{jm}\frac{r^j}{2j+1}\frac{\partial J_{jm}^j}{\partial t}{Y}_{jm}^j(\theta ,\varphi ).$$ (26)

Note that the electric field due to the surface charge exactly cancels the l = j − 1 components of the magnetically induced components of the electric field and therefore the conductivities do not appear anywhere in the solution. Nondimensional spatial coordinates have been used in equation (26) and the only quantity which depends on the size of the head r₂ is $J_{jm}^j$ as defined in equation (18). Accordingly as r₂ is decreased the current density must increase as $r_2^2$ in order to achieve the same electric field magnitude at the nondimensional radial position r within the head. This presents a challenge for creating small animal TMP systems [28–30] with electric fields of angular resolution and magnitude comparable to those in humans. If smaller coils are used to try to achieve angular resolution comparable to that in humans the resistance of such coils will, for frequencies of interest here, increase approximately as $r_2^{-2}$ while the current needed to obtain similar electric fields in the cortex is unchanged. As a result the power dissipated in the coil will increase approximately as $r_2^{-1}$ demanding efficient and relatively small cooling systems to prevent damage to the TMP coil. Of course a more complete description of the differences between humans and small animals would include differences in the size of each shell of the three shell model and the conductivities therein.

One important point to note is that TEP and TMP electric fields within the brain region exist in orthogonal subspaces. This follows from the VSH property ${\int }_0^{\pi }{\int }_0^{\pi }{Y}_{jm}^l(\theta ,\varphi )\cdot Y_{j^{\prime }{m}^{\prime }}^{l^{\prime }}(\theta ,\varphi )\text{ sin}\theta d\theta d\varphi ={\delta }_{l{l}^{\prime }}{\delta }_{j{j}^{\prime }}{\delta }_{m{m}^{\prime }}$ and from equations (6) and (23) which show that the TEP and TMP brain electric fields are spanned by the l = j − 1 and l = j VSH components respectively. Also note that the TMP electric field, unlike the TEP field, has no radial component (see appendix A). The orthogonality of the TEP and TMP fields has great consequence since the coupling of the electric field to neurons is dependent upon the relative direction of the field and the neuronal fibers. Consequently even if the electric field of TEP and TMP are angularly ‘focused’ on the same regions of the cortex completely different populations of neurons may be affected by each. This may be of particular importance to studies which use suprathrsehold TMS to probe changes in cortical excitability due to TES.

3. Results

Here, estimates are given, in the context of the three-shell TEP/TMP model, for select metrics of the relative power dissipated in the scalp and brain regions. In addition a simple estimate of the relative power utilized by the methods is presented to give a balanced understanding of the limitations and strengths of each.

Three power metrics are calculated: R^TEP, R^TMP and R. The quantities R^TEP and R^TMP are the scalp-to-brain ratios of power dissipation for the TEP and TMP cases respectively. These quantities enable one to estimate the power dissipated in the scalp for a given power dissipated in the brain. However the radial dependence of the TEP and TMP electric fields are fundamentally different making it difficult to directly compare the relative energy dissipated (or mean-squared electric field) in the scalp for the two methods. To yield a better direct comparison the quantity R is calculated which gives the TEP-to-TMP ratio of scalp energy dissipation for the case of similar TEP and TMP electric fields at the radial position of the cortex. Example calculations of each ratio are given for the case of typical electrode and coil geometries. In addition the three quantities are calculated in the case where only one VSH of index j contributes to the field. This leads to the calculation of an asymptotic limit to the ratio R. Note that since the conductivities of the brain and scalp are taken to be equal in this three-shell model then the dissipated power ratios are equivalent to mean-squared electric field ratios.

3.1. Relative power dissipation in brain and scalp: TEP case

In this subsection we calculate R^TEP, the ratio of the spatiotemporal averaged power dissipated in the scalp and brain regions for the TEP electric field. The averaged power dissipated in region k is given by:

$$P_k=\frac{{\sigma }_k}{V_{k}T}{\int }_0^T{\int }_{R_k}|\mathbf{\text{e}}(r,\theta ,\varphi ,t){|}^2{r}^2\text{ sin}\theta drd\theta d\varphi dt$$ (27)

where V_k is the volume of region R_k, σ_k is its conductivity and T is the temporal averaging interval. The interval T could be any meaningful time interval for the temporal waveform of the current source. For example, it could a period of a periodic waveform or it could be an interval which is large compared to such a period. Note that if the current density is separable with respect to the spatial and temporal variables (that is j(r, t) = I(t) f(r)) then temporal averaging is inconsequential since the time dependence cancels in the ratio R^TEP. All but one of the current densities considered in this work will be separable. The exceptions, as discussed in section 3.4, will be a TMP system comprised of two circular coils and a TEP system comprised of two electrode pairs each driven by independent sinusoidal current sources of different frequencies. Also note that P_k can also be interpreted as the product of the mean-square electric field and the conductivity for region k.

Using equations (6), (12) and (27) we can write the average power dissipated in region 0 due to the TEP electric field as:

$$\begin{gathered} P_0^{TEP}=\frac{{\sigma }_0}{r_2^2{V}_0}\sum _{jm}\overline{j{\left|A_{jm}\right|}^2}{\alpha }_0^{2j+1} \\ =\frac{3{\sigma }_0}{4\pi r_2^2{\alpha }_0^3}\sum _{jm}j{a}_j^2{\alpha }_0^{-(2j+1)}{\alpha }_1^{-(4j+2)}{\mathcal{D}}_j^{-2}\overline{{\left|I_{jm}\right|}^2} \end{gathered}$$ (28)

where the line over time dependent quantities denotes a time average. Similarly the average power dissipated in region 2 is:

$$\begin{gathered} P_2^{TEP}=\frac{{\sigma }_0}{V_2}\sum _{jm}[\overline{{\left|D_{jm}\right|}^2}j\left(r_2^{2j+1}-r_1^{2j+1}\right)+\overline{{\left|E_{jm}\right|}^2} \\ \times (j+1)\left(r_1^{-(2j+1)}-r_2^{-(2j+1)}\right)] \\ =\frac{3{\sigma }_0}{4\pi \left(1-{\alpha }_1^3\right)r_2^2}\sum _{jm}j[d_{0j}{\alpha }_0^{-(2j+1)}{\alpha }_1^{-(2j+1)}{+d_{1j}{\alpha }_1^{-(4j+2)}]}^2 \\ \times {\mathcal{D}}_j^{-2}\overline{{\left|I_{jm}\right|}^2}\left(1-{\alpha }_1^{2j+1}\right)+\frac{3{\sigma }_0}{4\pi \left(1-{\alpha }_1^3\right)r_2^2} \\ \times \sum _{jm}(j+1)e_j^2{\left[{\alpha }_0^{-(2j+1)}-{\alpha }_1^{-(2j+1)}\right]}^2 \\ \times {\mathcal{D}}_j^{-2}\overline{{\left|I_{jm}\right|}^2}\left[{\alpha }_1^{-(2j+1)}-1\right]. \end{gathered}$$ (29)

Each term in the summation of equation (28) or (29) is the average power $P_{jm}^{TEP,k}$ dissipated in the VSH component of the TEP electric field indexed by (j, m) in regions k = 0, 2. The ratio, $R^{TEP}=P_2^{TEP}/P_0^{TEP}$, of the average power dissipated in the scalp to that dissipated in the brain is then

$$\begin{gathered} R^{TEP}=\frac{{\alpha }_0^3}{1-{\alpha }_1^3}\frac{\sum _{jm}j{\left[d_{0j}{\alpha }_0^{-(2j+1)}{\alpha }_1^{-(2j+1)}+d_{1j}{\alpha }_1^{-(4j+2)}\right]}^2{\mathcal{D}}_j^{-2}\overline{{\left|I_{jm}\right|}^2}\left(1-{\alpha }_1^{2j+1}\right)}{\sum _{jm}j{a}_j^2{\alpha }_0^{-(2j+1)}{\alpha }_1^{-(4j+2)}{\mathcal{D}}_j^{-2}\overline{{\left|I_{jm}\right|}^2}} \\ +\frac{{\alpha }_0^3}{1-{\alpha }_1^3}\frac{\sum _{jm}(j+1)e_j^2{\left[{\alpha }_0^{-(2j+1)}-{\alpha }_1^{-(2j+1)}\right]}^2{\mathcal{D}}_j^{-2}\overline{{\left|I_{jm}\right|}^2}\left[{\alpha }_1^{-(2j+1)}-1\right]}{\sum _{jm}j{a}_j^2{\alpha }_0^{-(2j+1)}{\alpha }_1^{-(4j+2)}{\mathcal{D}}_j^{-2}\overline{{\left|I_{jm}\right|}^2}}. \end{gathered}$$ (30)

In general R^TEP depends upon I_jm, that is, it depends upon the geometry of the TEP electrodes and the magnitude of the current supplied to the electrodes. However general features can be elucidated by considering the separable case when the current source is such that I_jm = 0 for all but one value of j (m not restricted). In that case the power ratio for the jth component, $R_j^{TEP}=P_{jm}^{TEP,2}/P_{jm}^{TEP,0}$, is given by:

$$\begin{gathered} R_j^{TEP}=\frac{{\alpha }_0^3}{1-{\alpha }_1^3}{\left[\left(d_{0j}/a_j\right){\alpha }_0^{-(2j+1)}+\left(d_{1j}/a_j\right){\alpha }_1^{-(2j+1)}\right]}^2 \\ \times \left[1-{\alpha }_1^{2j+1}\right]{\alpha }_0^{2j+1}+\frac{{\alpha }_0^3}{1-{\alpha }_1^3}\frac{j+1}{j}{\left(e_j/a_j\right)}^2 \\ \times {\left[{\alpha }_0^{-(2j+1)}-{\alpha }_1^{-(2j+1)}\right]}^2\left[1-{\alpha }_1^{2j+1}\right] \\ \times {\alpha }_0^{2j+1}{\alpha }_1^{2j+1}. \end{gathered}$$ (31)

Figure 2 shows the dependence of $R_j^{TEP}$ upon j for a three shell conductor model. It is clear from the figure that $R_j^{TEP}$ increases as j increases. In other words, as the spatial detail of the electric field increases (e.g. more focality) so does the energy dissipated in the scalp relative to that dissipated in the brain. Note that for any value of j the spatial detail is not equal in the θ and ϕ directions.

Figure 2.

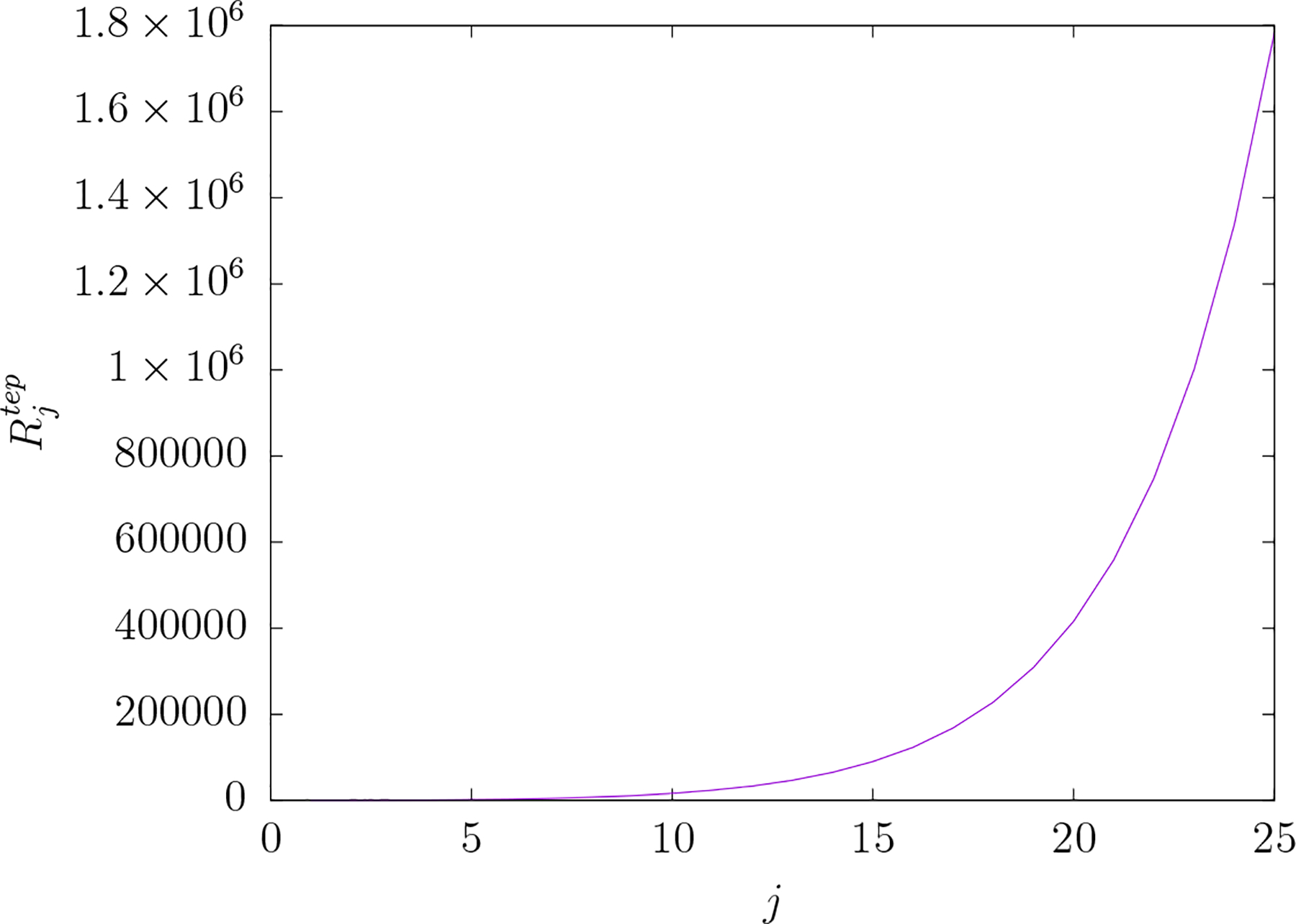
$R_j^{TEP}$ versus j for TEP electric fields. $R_j^{TEP}$ is the ratio of the mean-squared electric field over the scalp region to that over the brain region for an electric field comprised of a single vector spherical harmonic component indexed by the pair of integers j and m. The index j of the vector spherical representation of the electric field is reciprocally related to spatial scale in the field. Note that $R_j^{TEP}$ is independent of index m for any given value of j. The cost of greater electric field focality in the brain is greater mean-squared electric field in the scalp relative to the brain.

To estimate R^TEP for a typical TEP system consider the scalp electrode system depicted in figure 3. In this example the system is comprised of two electrodes each subtending an angle θ_o on the scalp surface, with electrode centers separated by the angle β. Appendix D derives the I_jm for such a system which is found to be:

$$\begin{gathered} I_{jm}=I_{j0}^{+}\left[{\delta }_{m0}-\sqrt{\frac{(j-m)!}{(j+m)!}}{P}_j^m(\text{cos }\beta )\right] \\ =I_{j0}^{+}\left[{\delta }_{m0}-\sqrt{\frac{4\pi }{2j+1}}{\tilde{P}}_j^m(\text{cos }\beta )\right] \end{gathered}$$ (32)

where

$$\begin{gathered} I_{j0}^{+}=2\pi I_o\sqrt{\frac{1}{2j+1}}[\sqrt{\frac{1}{2j+3}}{\tilde{P}}_{j+1}\left(\text{cos }{\theta }_o\right) \\ -\sqrt{\frac{1}{2j-1}}{\tilde{P}}_{j-1}\left(\text{cos }{\theta }_o\right)] \end{gathered}$$ (33)

and where I_o is the radial component of a uniform current density provided by the electrodes. Note that the $P_j^m$ are associated Legendre functions and that the ${\tilde{P}}_j^m$ are the more numerically stable renormalized associated Legendre functions (see appendix D).

Figure 3.

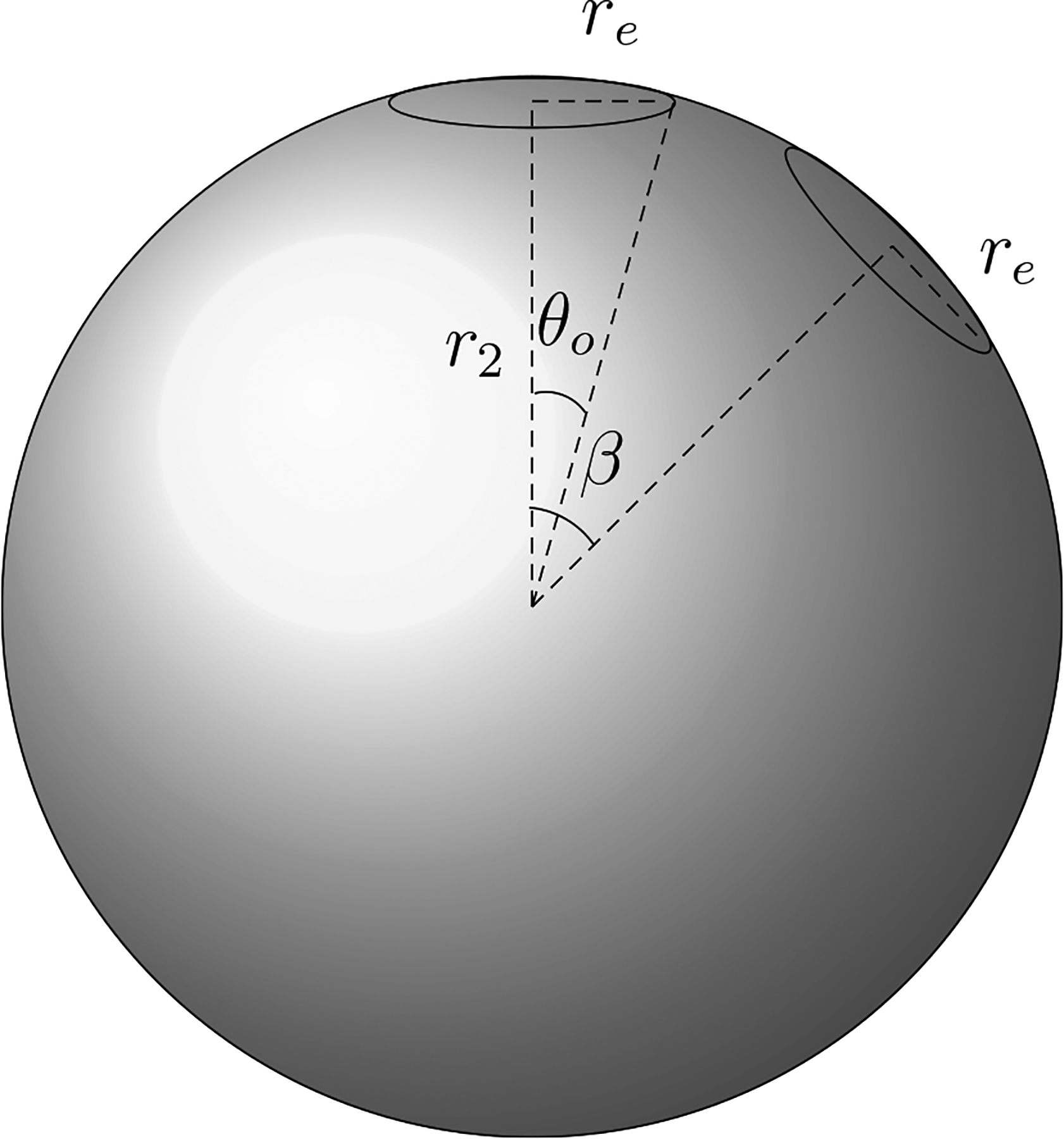
Spherical head model with two TEP electrodes on the scalp surface (r = r₂). Each electrode (outlined) subtends the angle θ_o from its center and the centers of the two electrodes are separated by the angle β.

C++ computer code (available upon request) was written to perform all summations within this work. The computation of the normalized associated Legendre functions $P_j^m$ was adopted from a standard [31]. Figure 4 shows the dependence of R^TEP versus electrode separation angle β for four different electrode sizes θ_o. R^TEP increase as spatial detail increases with smaller electrodes or smaller separation between the electrodes.

Figure 4.

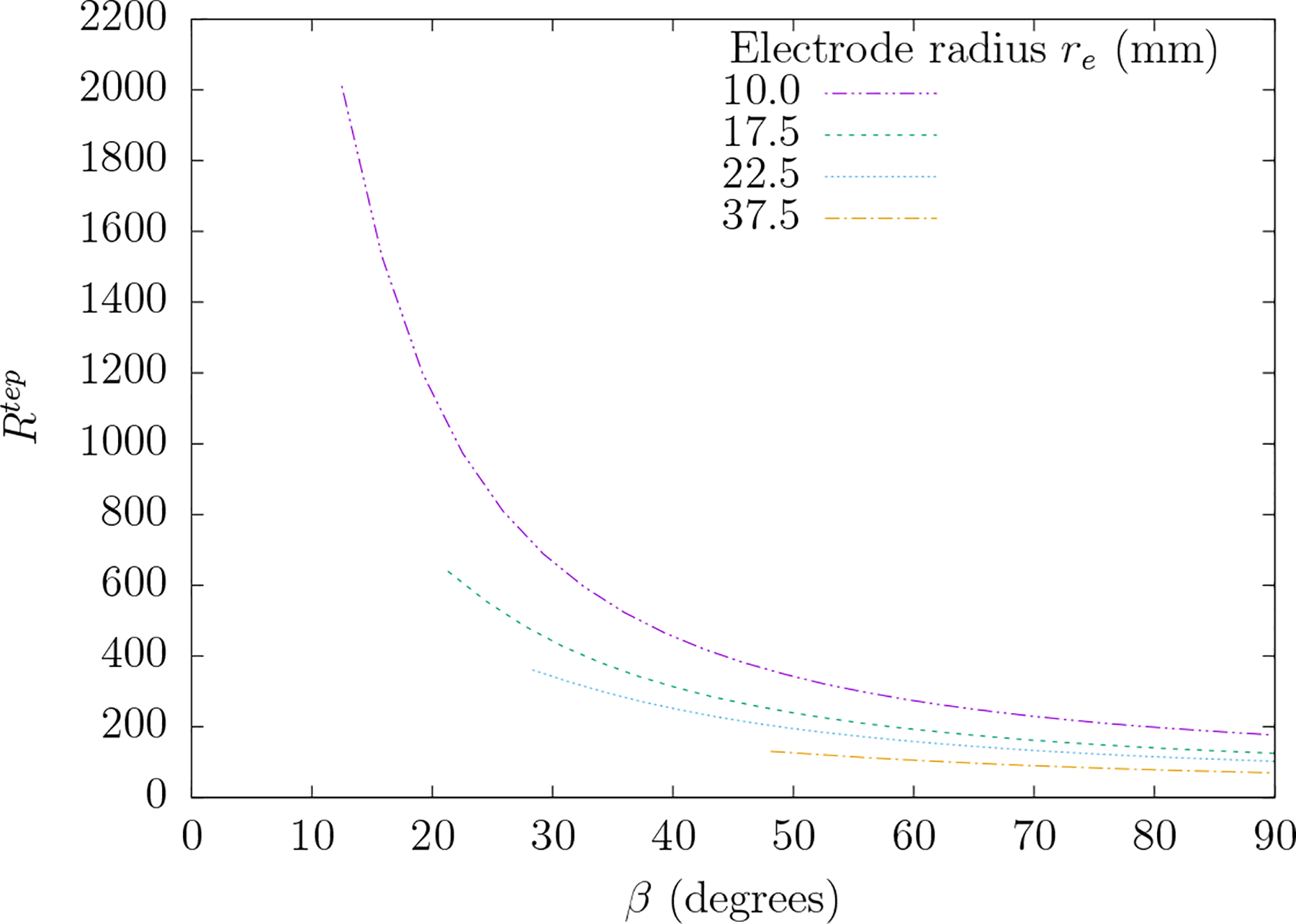
A plot of ratio R^TEP versus electrode separation angle β for four different electrode radii r_e. R^TEP is the ratio of the mean-squared electric field over the scalp region to that of the brain region for the specific electrode system depicted in figure 3. The angle θ_o which subtends the electrode from its center is determined according to ${\theta }_o={\text{cos }}^{-1}\sqrt{1-r_e^2}$. Each plot extends over the range β = [2θ_o, 90] so that the electrodes do not overlap.

3.2. Relative power dissipation in brain and scalp: TMP case

In this subsection we calculate the ratio of the spatially-averaged power dissipated in the brain and scalp regions for the TMP electric field. Using equations (26) and (27) we can write the average power dissipated in region 0 as:

$$P_0^{TMP}=\frac{3{\sigma }_0}{4\pi {\alpha }_0^3}\sum _{jm}\frac{{\alpha }_0^{2j+3}}{{(2j+1)}^2(2j+3)}\overline{{\left|\frac{\partial J_{jm}^j}{\partial t}\right|}^2}.$$ (34)

Similarly the average dissipated power in region 2 is:

$$P_2^{TMP}=\frac{3{\sigma }_0}{4\pi \left(1-{\alpha }_1^3\right)}\sum _{jm}\frac{1-{\alpha }_1^{2j+3}}{{(2j+1)}^2(2j+3)}\overline{{\left|\frac{\partial J_{jm}^j}{\partial t}\right|}^2}$$ (35)

and the ratio $R^{TMP}=P_2^{TMP}/P_0^{TMP}$ is:

$$R^{TMP}=\frac{{\alpha }_0^3}{1-{\alpha }_1^3}\frac{\sum _{jm}\left(1-{\alpha }_1^{2j+3}\right){\left[{(2j+1)}^2(2j+3)\right]}^{-1}\overline{{\left|\frac{\partial J_{jm}^j}{\partial t}\right|}^2}}{\sum _{jm}{\alpha }_0^{2j+3}{\left[{(2j+1)}^2(2j+3)\right]}^{-1}\overline{{\left|\frac{\partial J_{jm}^j}{\partial t}\right|}^2}}.$$ (36)

If the current source is such that J_jm = 0 for all but one value of j (m not restricted) then $R_j^{TMP}=P_{jm}^{TMP,2}/P_{jm}^{TMP,0}$ is

$$R_j^{TMP}=\frac{{\alpha }_0^3}{1-{\alpha }_1^3}\frac{1-{\alpha }_1^{2j+3}}{}{\alpha }_0^{2j+3}.$$ (37)

Figure 5 shows the dependence of $R_j^{TMP}$ upon j. Again, as in the case of TEP, the spatial detail of the electric field comes at a cost. The energy dissipated in the scalp relative to the energy dissipated in the brain increases as the electric field is made more spatially detailed. However, in contrast to the TEP electric field, $R_j^{TMP}$ is much smaller than $R_j^{TEP}$ for a given j. For example at $j=20R_j^{TEP}$ is approximately 35 times greater than $R_j^{TMP}$.

Figure 5.

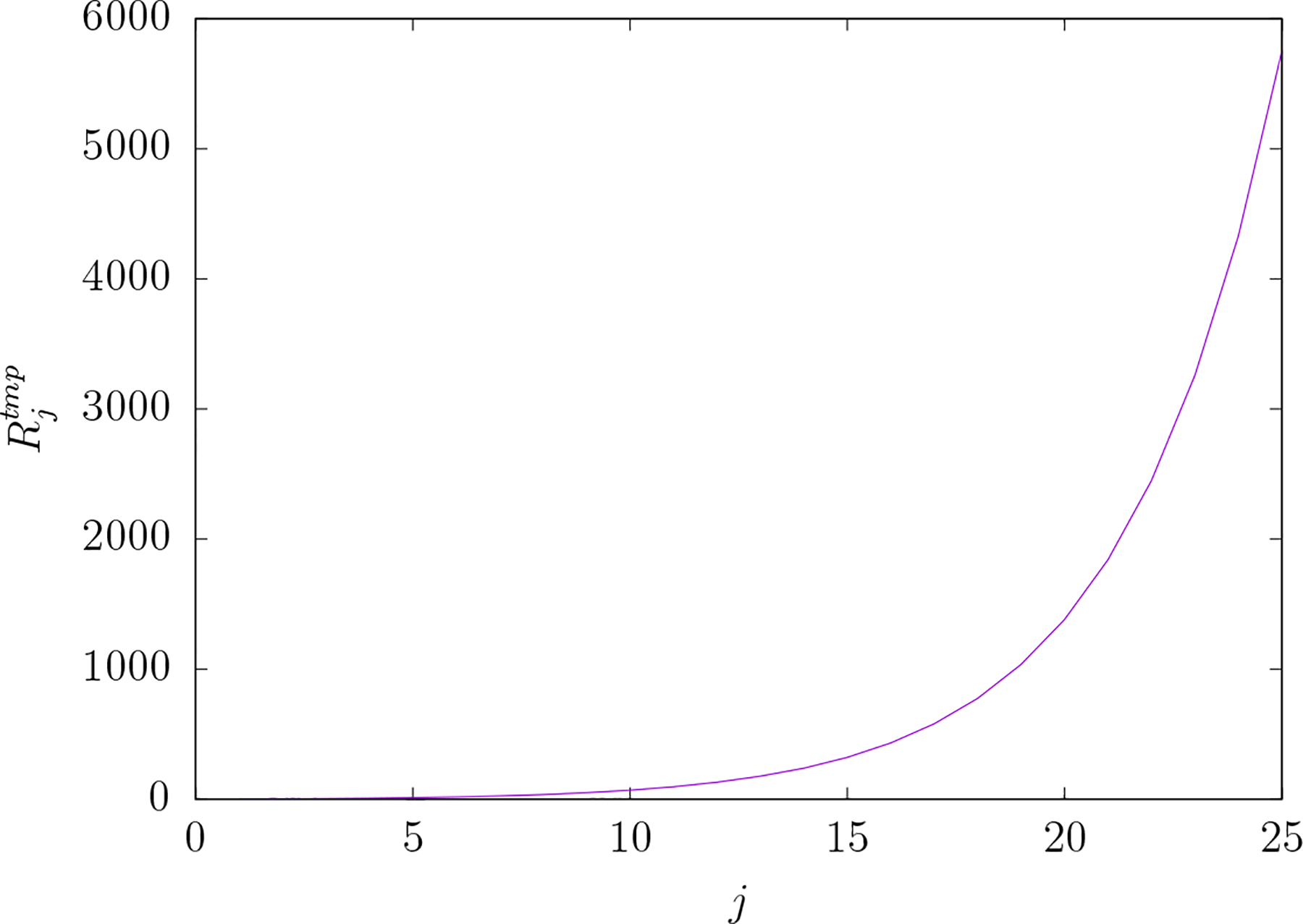
$R_j^{TMP}$ versus j for TMP electric fields. $R_j^{TMP}$ is the ratio of the mean-squared electric field over the scalp region to that over the brain region for an electric field comprised of a single vector spherical harmonic component indexed by the pair of integers j and m. The index j of the vector spherical representation of the electric field is reciprocally related to spatial scale in the field. Note that $R_j^{TMP}$ is independent of index m for any given value of j. As with TEP the cost of greater electric field focality in the brain is greater mean-squared electric field in the scalp relative to the brain. However that cost is much greater for TEP as compared to TMP.

The value of R^TMP will of course depend on the geometry of the TMP coil. That is it will depend upon J_jm. Here calculations of R^TMP are given for simple thin circular TMS coils and figure-8 coils as depicted in figure 6. The specifications for TMS coils, which typically contain many windings of Litz wire, are usually given in terms of an inner and outer radius for the winding. Here the coils are approximated by a single winding at the average of typical inner and outer radii. For the circular coil (coil 1 of figure 6) assume the current density j is a thin ring of current of amplitude I(t) and radius r_c (in units of r₂) inscribed on a plane tangent to the outer surface of the scalp region and centered on the vertical axis. Appendix E calculates $J_{jm}^j$ for this simple coil to be:

$$J_{jm}^j=i{\delta }_{m0}\frac{8{\pi }^2{r}_2^2}{c^2{\rho }_o^j}I\sqrt{1-{\text{cos }}^2{\theta }_o}{\tilde{P}}_j^1\left(\text{cos}{\theta }_o\right)$$ (38)

where ${\theta }_o={\text{cos}}^{-1}\left(1/\sqrt{r_c^2+1}\right)$. A figure-8 coil can be constructed from two circular coils (coils 1 and 2 of figure 6) with currents circulating in opposite senses and with coil 2 rotated by an angle 2 θ_o relative to coil 1. For this figure-8 coil $J_{jm}^j=J_{jm}^{j+}-J_{jm}^{j-}$ where $J_{jm}^{j+}$ and $J_{jm}^{j-}$ are contributions from coil 1 and 2 respectively. Appendix E calculates $J_{jm}^j$ for this figure-8 coil to be:

$$\begin{gathered} J_{jm}^j=i\frac{8{\pi }^2{r}_2^2}{c^2{\rho }_o^j}I\sqrt{1-{\text{cos}}^2{\theta }_o} \\ \times \left[{\delta }_{m0}-{(-1)}^m\sqrt{\frac{4\pi }{2j+1}}{\tilde{P}}_j^m\left(\text{cos }2{\theta }_o\right)\right] \\ \times {\tilde{P}}_j^1\left(\text{cos }{\theta }_o\right). \end{gathered}$$ (39)

Figure 7 gives a plot of R^TMP versus coil radii for the circular and figure-8 coils. Clearly the value of R^TMP increases as the radius of the coil decreases. Note that for coil radii less than 10 mm the difference between the figure-8 R^TMP and circular coil R^TMP is quite large. However for coil radii greater than 10 mm the difference is not near as stark.

Figure 6.

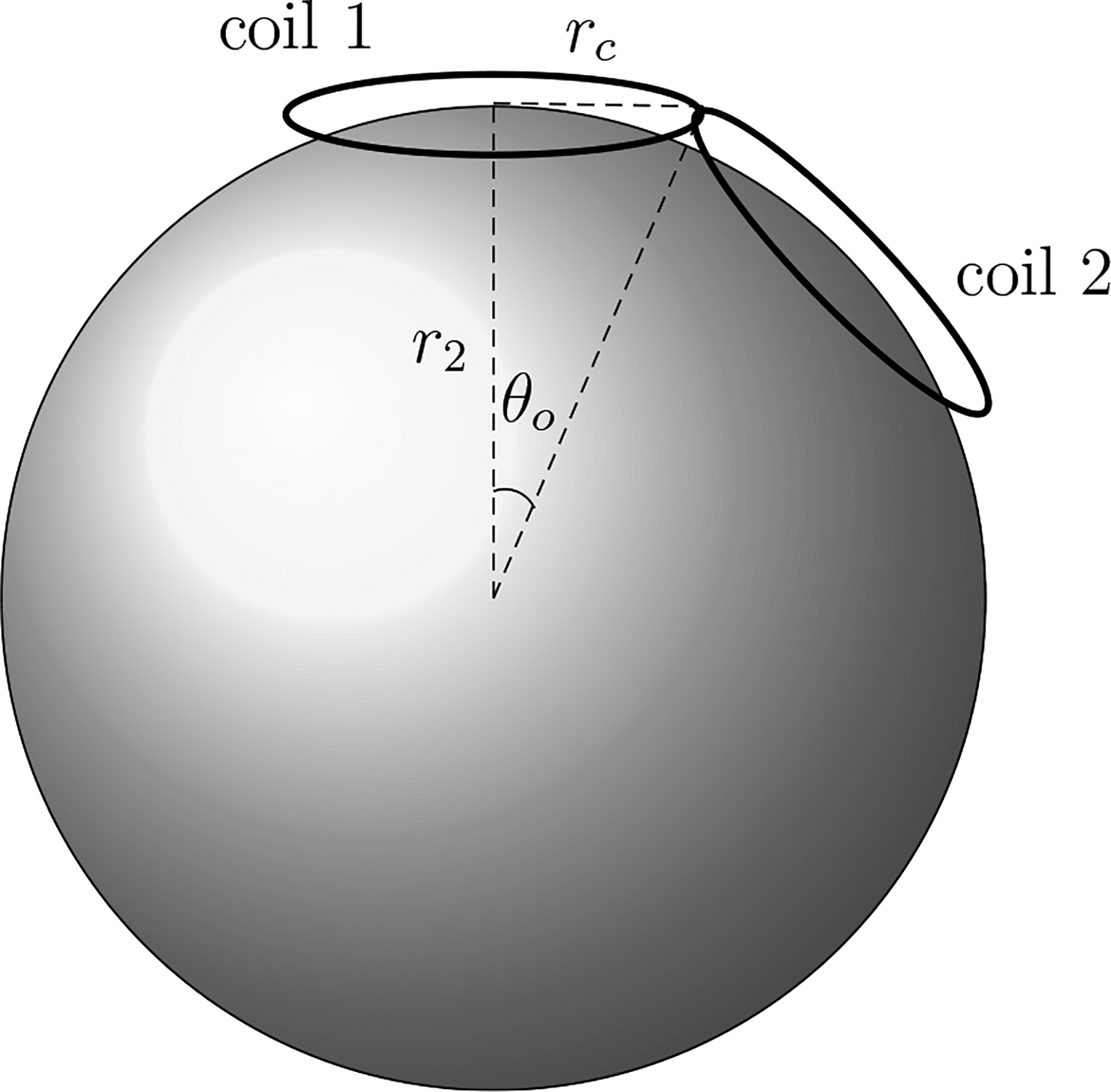
Spherical head model with two circular TMP coils with radii r_c. The centers of coil 1 and 2 are on the scalp scalp surface (r = r₂). Note that the angle between the planes of the two coils is π − 2 θ_o.

Figure 7.

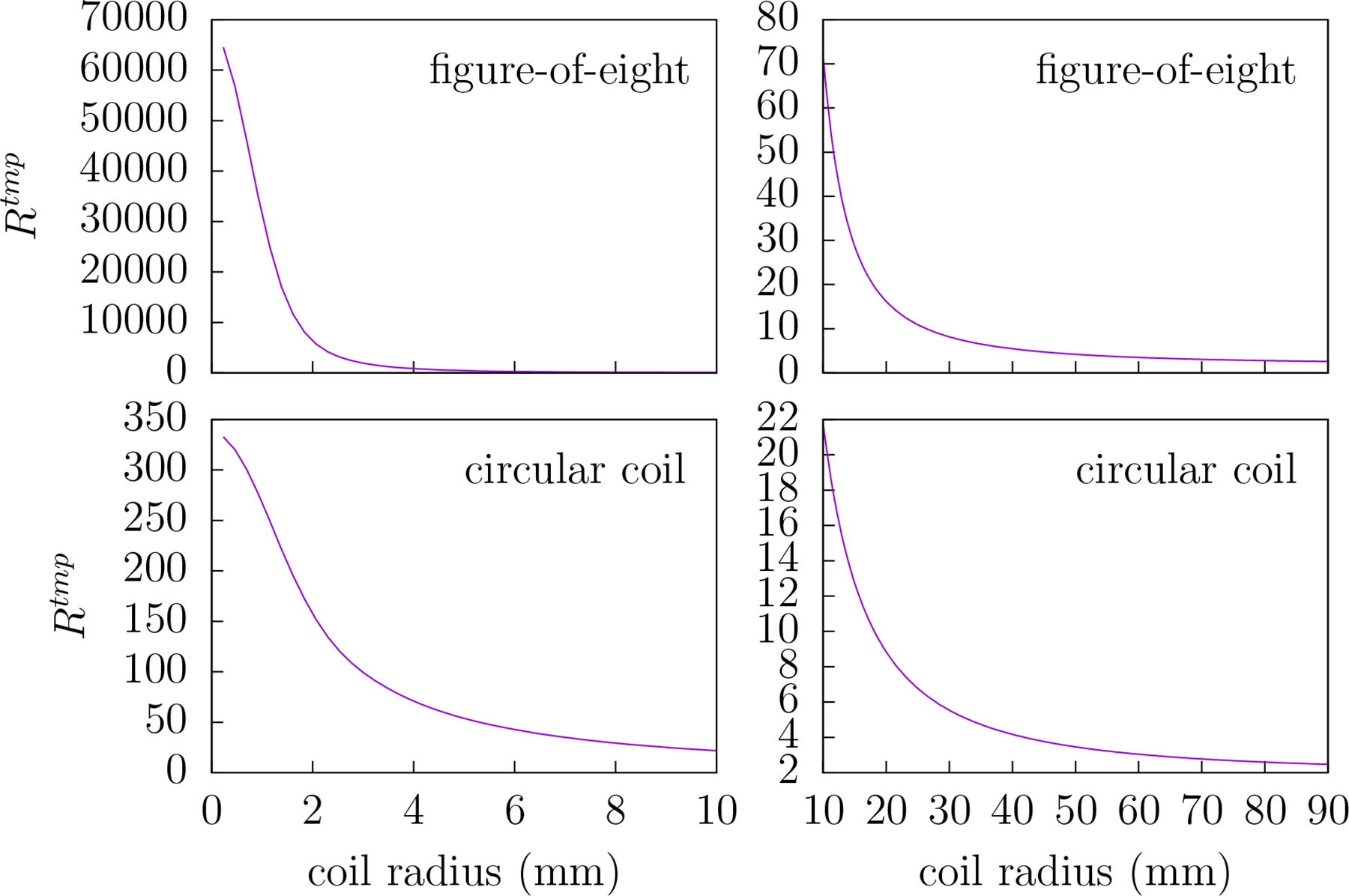
The ratio R^TMP versus coil radius r_c for circular coils (bottom row) and figure-8 (top row) coil. R^TMP is the ratio of the mean-squared electric field over the scalp region to that of the brain region for the coil geometries depicted in figure 6. For small radii the difference between the values of R^TMP for the circular and figure-8 coils is quite pronounced. Therefore, to draw attention to this difference, the left plots cover 0–10 mm radii whereas the right plots cover 10–90 mm.

The quantities R^TEP and R^TMP are useful for estimating the mean-squared electric field in the scalp (brain) given an estimate for mean-squared electric field in the brain (scalp). Even though the plots of R^TEP and R^TMP given in figures 4 and 7 respectively show that the values of R^TMP are typically much smaller than R^TEP for standard TEP electrode and TMP coil configurations a direct comparison of these quantities may be inadequate for estimating the relative intensities of the TEP and TMP scalp electric fields. This direct comparison is complicated by the fact that the electric fields of TEP and TMP have different radial dependences which may skew the volume averages over the brain region. Furthermore, while it is the scalp electric field that often limits the brain electric field amplitude, the usual target of the electric field is the cortex. Therefore a better comparison of TEP-to-TMP scalp electric fields might be obtained when their respective electric fields at the radial distance of the cortex were similar.

3.3. Comparison of TMP and TEP power dissipation

This section examines the ratio of TEP-to-TMP power dissipated in the scalp for similar electric fields at the radial distance of the cortex. That is, the quantity R given by

$$R=\frac{P_2^{TEP}}{P_2^{TMP}}=\frac{\sum _{jm}{P}_{jm}^{TEP,2}}{\sum _{jm}{P}_{jm}^{TMP,2}}$$ (40)

is calculated where $P_{jm}^{TEP,2}$ and $P_{jm}^{TMP,2}$ are respectively the TEP and TMP power dissipated in region 2 for the VSH component indexed by (j, m). Such a quantity would allow one to meaningfully compare TEP to TMP electric fields with respect to the energy they dissipate in the scalp.

Importantly, the TEP and TMP electric fields cannot be equal since they reside in orthogonal subspaces. Given this limitation, a metric of the electric field similarity must be defined. The metric used here defines similar TEP and TMP electric fields as those which have identical cortical surface-area-averaged power dissipation for each component of their VSH expansion at all times t. This condition is insufficient to uniquely define the similar electric fields but it is a reasonable definition of similarity and is, as will bee seen, sufficient to derive R.

For the TEP or TMP electric field the power P_S(α₀) averaged over the spherical surface S at r = α₀ (the cortical surface) is given by

$$P_S\left({\alpha }_0\right)={\sigma }_k{\int }_{S_0}{|\mathbf{\text{e}}\left({\alpha }_0,\theta ,\varphi \right)|}^2\text{ sin}\theta d\theta d\varphi .$$ (41)

The chosen metric of similarity requires that $P_S^{TMP}\left({\alpha }_0\right)=P_S^{TEP}\left({\alpha }_0\right)$ and according to equations (6) and (26) similarity is obtained when:

$$\overline{{\left|\frac{\partial J_{jm}^j}{\partial t}\right|}^2}=\frac{a_j^2}{r_2^2{\alpha }_0^2}j{(2j+1)}^3{\alpha }_0^{-(4j+2)}{\alpha }_1^{-(4j+2)}{\mathcal{D}}_j^{-2}\overline{{\left|I_{jm}\right|}^2}$$ (42)

or alternatively

$${\mathcal{D}}_j^{-2}\overline{{\left|I_{jm}\right|}^2}=\frac{r_2^2{\alpha }_0^2}{a_j^2}\frac{1}{j{(2j+1)}^3}{\alpha }_0^{4j+2}{\alpha }_1^{4j+2}\overline{{\left|\frac{\partial J_{jm}^j}{\partial t}\right|}^2}.$$ (43)

According to equations (29) and (35) the ratio of volume-averaged power dissipated in the scalp (region 2) is

$$\begin{gathered} R=\frac{\sum _{jm}j{\mathcal{D}}_j^{-2}\overline{{\left|I_{jm}\right|}^2}{\left[d_{0j}{\alpha }_0^{-(2j+1)}{\alpha }_1^{-(2j+1)}+d_{1j}{\alpha }_1^{-(4j+2)}\right]}^2\left[1-{\alpha }_1^{2j+1}\right]}{r_2^2\sum _{jm}\overline{{\left|\frac{\partial J_{jm}^j}{\partial t}\right|}^2}{\left[{(2j+1)}^2(2j+3)\right]}^{-1}\left[1-{\alpha }_1^{2j+3}\right]} \\ +\frac{\sum _{jm}(j+1){\mathcal{D}}_j^{-2}\overline{{\left|I_{jm}\right|}^2}{e}_j^2{\left[{\alpha }_0^{-(2j+1)}-{\alpha }_1^{-(2j+1)}\right]}^2\left[{\alpha }_1^{-(2j+1)}-1\right]}{r_2^2\sum _{jm}\overline{{\left|\frac{\partial J_{jm}^j}{\partial t}\right|}^2}{\left[{(2j+1)}^2(2j+3)\right]}^{-1}\left[1-{\alpha }_1^{2j+3}\right]} \end{gathered}$$ (44)

and substituting (42) into (44) yields:

$$\begin{gathered} R=\frac{{\alpha }_0^2\sum _{jm}j{\left[d_{0j}{\alpha }_0^{-(2j+1)}{\alpha }_1^{-(2j+1)}+d_{1j}{\alpha }_1^{-(4j+2)}\right]}^2\left[1-{\alpha }_1^{2j+1}\right]{\mathcal{D}}_j^{-2}\overline{{\left|I_{jm}\right|}^2}}{\sum _{jm}j(2j+1){(2j+3)}^{-1}{a}_j^2{\alpha }_0^{-(4j+2)}{\alpha }_1^{-(4j+2)}\left[1-{\alpha }_1^{2j+3}\right]{\mathcal{D}}_j^{-2}\overline{{\left|I_{jm}\right|}^2}} \\ +\frac{{\alpha }_0^2\sum _{jm}(j+1)e_j^2{\left[{\alpha }_0^{-(2j+1)}-{\alpha }_1^{-(2j+1)}\right]}^2\left[{\alpha }_1^{-(2j+1)}-1\right]{\mathcal{D}}_j^{-2}\overline{{\left|I_{jm}\right|}^2}}{\sum _{jm}j(2j+1){(2j+3)}^{-1}{a}_j^2{\alpha }_0^{-(4j+2)}{\alpha }_1^{-(4j+2)}\left[1-{\alpha }_1^{2j+3}\right]{\mathcal{D}}_j^{-2}\overline{{\left|I_{jm}\right|}^2}}. \end{gathered}$$ (45)

Alternatively by substituting equation (43) into (44) the ratio for similar electric fields within the brain (region 0) becomes

$$\begin{gathered} R=\frac{{\alpha }_0^2\sum _{jm}{a}_j^{-2}{(2j+1)}^{-3}\overline{{\left|\frac{\partial J_{jm}^j}{\partial t}\right|}^2}{\left[d_{0j}+d_{1j}{\left({\alpha }_0/{\alpha }_1\right)}^{2j+1}\right]}^2\left[1-{\alpha }_1^{2j+1}\right]}{\sum _{jm}{\left[{(2j+1)}^2(2j+3)\right]}^{-1}\left[1-{\alpha }_1^{2j+3}\right]\overline{{\left|\frac{\partial J_{jm}^j}{\partial t}\right|}^2}} \\ +\frac{{\alpha }_0^2\sum _{jm}{\left(e_j/a_j\right)}^2\frac{j+1}{j{(2j+1)}^3}{\left[{\alpha }_1^{2j+1}-{\alpha }_0^{2j+1}\right]}^2\left[{\alpha }_1^{-(2j+1)}-1\right]{\left|\overline{\frac{\partial J_{jm}^j}{\partial t}}\right|}^2}{\sum _{jm}{\left[{(2j+1)}^2(2j+3)\right]}^{-1}\left[1-{\alpha }_1^{2j+3}\right]\overline{{\left|\frac{\partial J_{jm}^j}{\partial t}\right|}^2}}. \end{gathered}$$ (46)

Whether to choose equation (45) or (46) depends upon whether one is comparing similar fields generated by a given TEP electrode configuration (I_jm are known) or by a given TMP field ($J_{jm}^j$ are known).

If the I_jm are zero for all but one value of j (m unrestricted) then

$$\begin{gathered} R_j={\left(\frac{{\alpha }_0}{a_j}\right)}^2\frac{2j+3}{2j+1}{\left[d_{0j}+d_{1j}{\left({\alpha }_0/{\alpha }_1\right)}^{2j+1}\right]}^2 \\ \times \left[\frac{1-{\alpha }_1^{2j+1}}{1-{\alpha }_1^{2j+3}}\right]+{\left(\frac{{\alpha }_0}{a_j}\right)}^2\frac{2j+3}{2j+1}\frac{j+1}{j}{e}_j^2{\alpha }_1^{2j+1} \\ \times {\left[1-{\left({\alpha }_0/{\alpha }_1\right)}^{2j+1}\right]}^2\left[\frac{1-{\alpha }_1^{2j+1}}{1-{\alpha }_1^{2j+3}}\right]. \end{gathered}$$ (47)

As j → ∞ the value of R_j → R_∞ where

$$R_{\infty }=\frac{1}{16}\frac{{(1+ϵ)}^4}{{ϵ}^2}{\alpha }_0^2.$$ (48)

That is, R_j asymptotically approaches an upper limit determined by the relative size of the brain region α₀ and the scalp-to-skull conductivity ratio ε. Note that if the TEP and TMP electric fields are constrained to be similar at arbitrary depth, rather than at the cortical surface, then α_o is replaced by α = r/r₂. Therefore the advantage of TMP over TEP with respect to the scalp-to-brain ratio of the root-mean-squared electric field is linear with respect to radial depth at which the fields are taken to be similar.

Figure 8 gives the plot of R_j versus j for three different conductivity ratios ε although ε = 0.0125 is the value most often assumed in the literature. The plot shows that R_j clearly increases with respect to j, an index of decreasing spatial scale of the electric field, but reaches an asymptotic value. For the particular dimensions of three-shell model used in this work the asymptotic values corresponding to the conductivity ratios ε = 0.0075, 0.0125 and 0.0175 are 865.6, 317.9 and 165.4.

Figure 8.

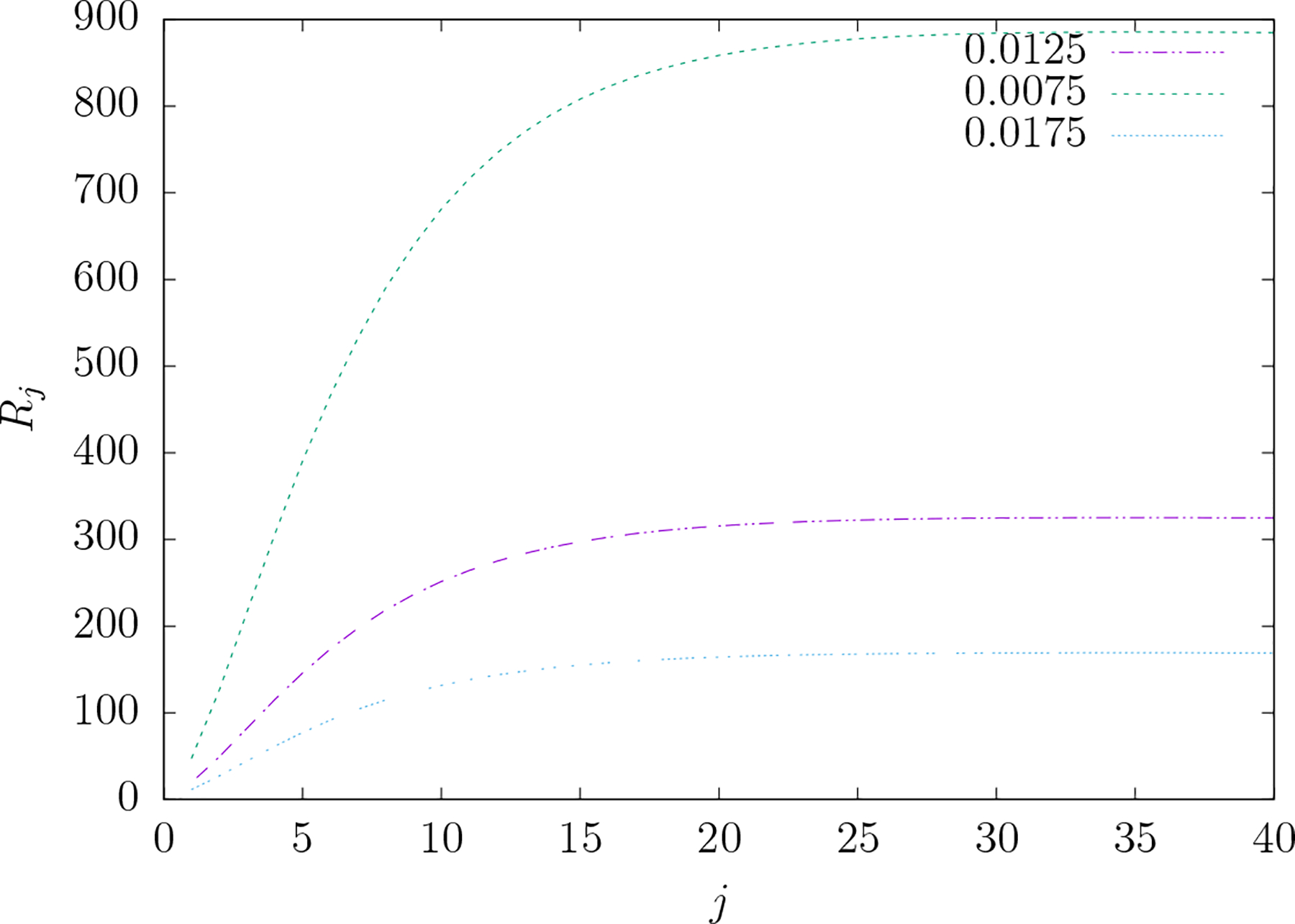
The ratio R_j versus j for three different values of the skull-to-scalp conductivity ratio ε. R_j is the ratio of the TEP to TMP mean-squared electric field over the scalp for similar electric fields at the level of the cortical surface when the electric field is comprised of a single vector spherical harmonic component indexed by integers j and m. The literature typically uses the value ϵ = 1/80 = 0.0125. Note that each curve approaches an asymptotic limit given by $R_{\infty }=\frac{1}{16}\frac{{(1+ϵ)}^4}{{ϵ}^2}{\alpha }_0^2$. For similar electric fields at the level of the cortex, TEP produces much larger mean-squared scalp electric fields compared to TMP as electric field focality increases at the cortex.

Figure 9 gives a plot of R versus electrode separation angle for five different electrode radii typical in TEP systems. As the electrode separation or the electrode radii decrease—that is, the spatial detail in the field increases—the value of R increases. Figure 10 gives a plot of R versus coil radius for the simple circular TMS coil and the figure-8 coil. Again note that as the spatial detail increases (coil size decreases) R increases. For typical circular coils with average radii of 20–40 mm the value of corresponding values of R range from 105 to 171. Also note that, as compared to the circular coil of the same radius, the figure-8 coil has a modestly increased value of R.

Figure 9.

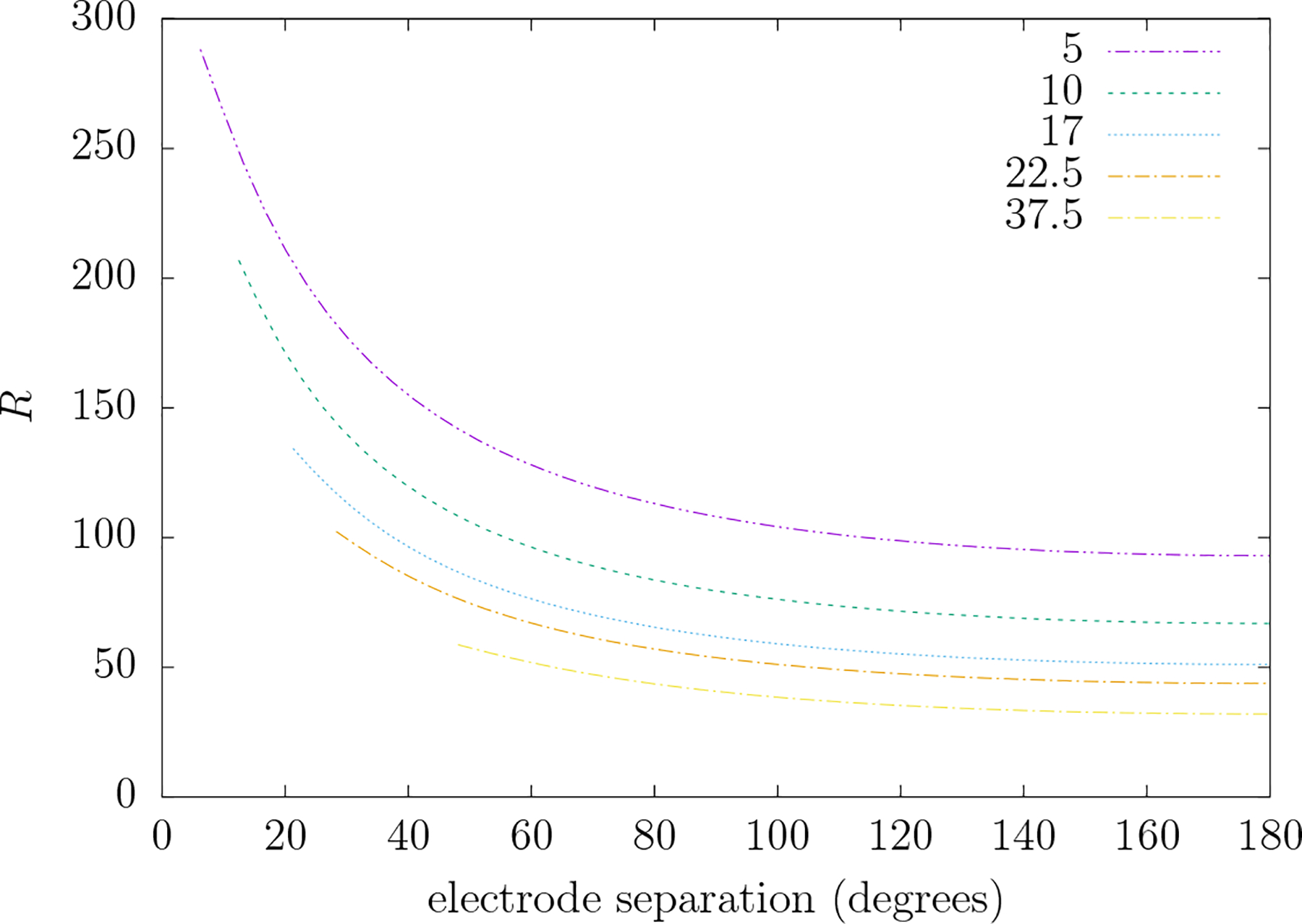
R versus the electrode separation angle (degrees) for five different electrode radii (mm) that are typical of commercial TEP electrode systems depicted in figure 3. R is the ratio of the TEP to TMP mean-squared electric field over the scalp when the TMP electric field at the level of the cortical surface is similar to that produced by the TEP system depicted in figure 3. Each plot extends from the minimal separation between electrodes (twice the angle subtended by the electrode from its center) up to 180°.

Figure 10.

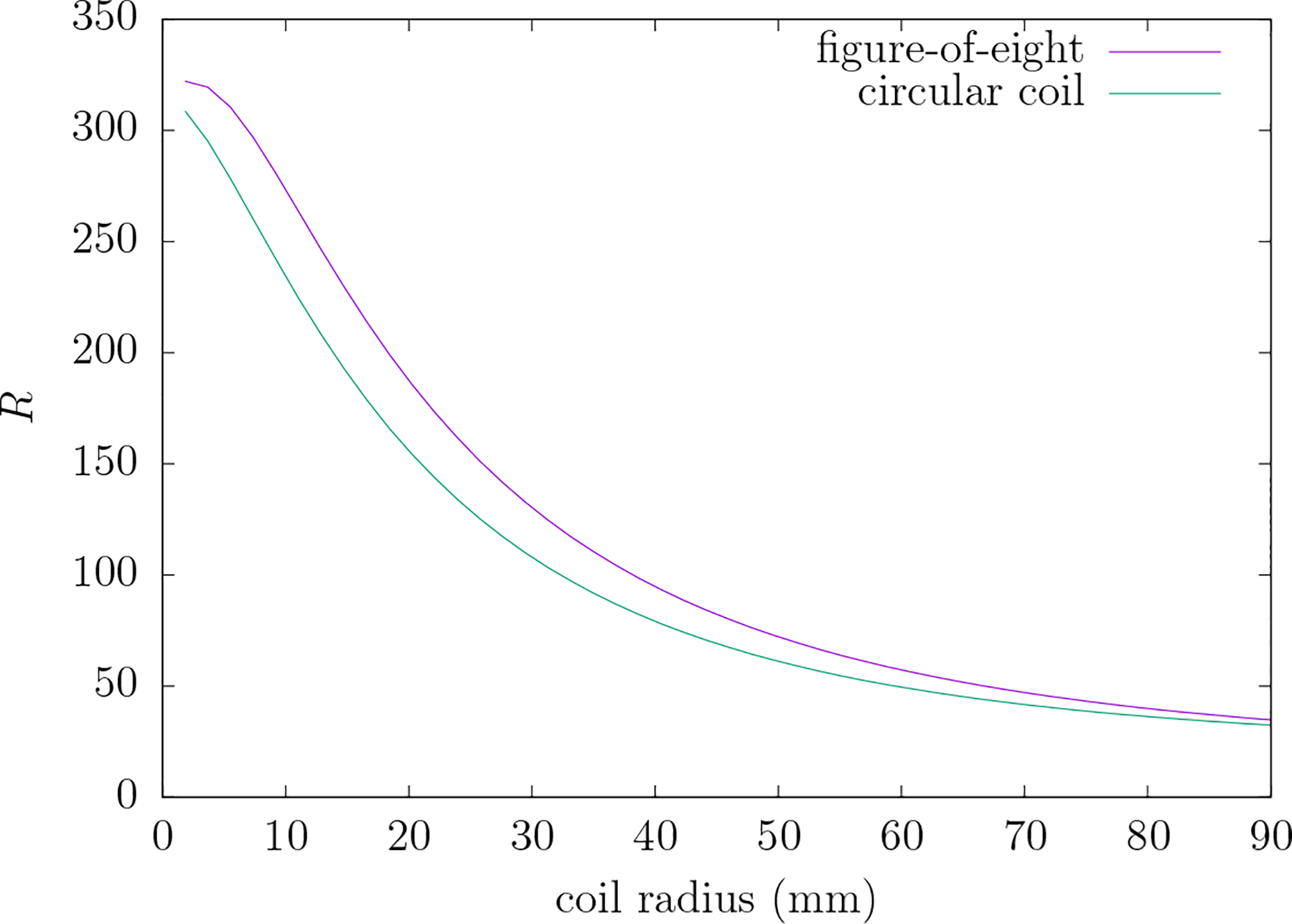
R versus coil radius of the circular and figure-8 coils (ε = 1/80). R is the ratio of the TEP to TMP mean-squared electric field over the scalp when the TEP electric field at the level of the cortical surface is similar to that produced by the TMP system depicted in figure 6.

Note, by referring to equation (40), that R_∞, the asymptotic value of R_j, is additionally an upper bound to the value of R. Therefore although R, the TEP-to-TMP ratio of power dissipated in the scalp for similar electric fields at the cortex, increases with increasing spatial detail of the field there is an upper limit to this value. Also note that the electric field of a figure-8 coil, which is in common use in TMS research, would be expected to yield values of R considerably greater than that of the circular coil used here due to its more focal field.

3.4. TMP and TEP power dissipation for nonseparable current densities

All of the current densities considered in this work have, up to this point, been separable with respect to time and spatial coordinates as is typical of extant TEP and TMP systems. However, interesting TEP work has recently been done with nonseparable current densities to produce spatially dependent temporal interference effects in mice brains [32]. Consider now the nonseparable case of a TMP system comprised of the two circular coils of the figure-8 example albeit with each coil driven independently. Coil 1 has time dependence sinω₁t and coil 2 has time dependence sinω₂t. In such a case:

$$\begin{gathered} \sum _m{|\frac{\partial J_{jm}^j}{\partial t}|}^2=\sum _m{|{\omega }_1\text{ cos}{\omega }_{1}t{J}_{jm}^{j+}-{\omega }_2\text{ cos}{\omega }_{2}t{J}_{jm}^{j-}|}^2 \\ ={\omega }_1^2{\text{ cos}}^2{\omega }_{1}t\sum _m{|J_{jm}^{j+}|}^2+{\omega }_2^2{\text{ cos}}^2{\omega }_{2}t \\ \times \sum _m{|J_{jm}^{j-}|}^2-{\omega }_1{\omega }_2\text{ cos}{\omega }_{1}t\text{ cos}{\omega }_{2}t \\ \times \sum _m\left(j_{jm}^{j+*}{J}_{jm}^{j-}+J_{jm}^{j+}{J}_{jm}^{j-*}\right) \\ ={\omega }_1^2{\text{ cos}}^2{\omega }_{1}t\sum _m{|J_{jm}^{j+}|}^2+{\omega }_2^2{\text{ cos}}^2{\omega }_{2}t \\ \times \sum _m{|J_{jm}^{j-}|}^2-\frac{{\omega }_1{\omega }_2}{2}[\text{ cos}\left({\omega }_1-{\omega }_2\right)t \\ +\text{ cos}\left({\omega }_1+{\omega }_2\right)t]\sum _m[j_{jm}^{j+*}{J}_{jm}^{j-}+J_{jm}^{j+}\times J_{jm}^{j-*}] \end{gathered}$$ (49)

where $J_{jm}^{j+}$ and $J_{jm}^{j-}$ are the coefficients corresponding to coils 1 and 2 (see appendix E). For time averages over an interval T such |ω − ω₂|⁻¹ ≪ T

$$\sum _m\overline{{\left|\frac{\partial J_{jm}^j}{\partial t}\right|}^2}\approx \frac{1}{2}\left({\omega }_1^2\sum _m{|J_{jm}^{j+}|}^2+{{\omega }_2^2\sum _m|j_{jm}^{j-}|}^2\right)$$ (50)

where the horizontal line denotes a time average. Finally, since the coils are assumed to be identical in their shape

$$\sum _m\overline{{\left|\frac{\partial J_{jm}^j}{\partial t}\right|}^2}\approx \frac{1}{2}\left({\omega }_1^2+{\omega }_2^2\right)\sum _m{|J_{jm}^{j+}|}^2.$$ (51)

For the TEP case of two pairs of electrodes, each pair driven by current sources of different frequencies, a similar result is obtained:

$$\sum _m\overline{{\left|I_{jm}\right|}^2}\approx \sum _m{|I_{jm}^{+}|}^2.$$ (52)

Therefore in the long-time average case a system of two pairs of TEP electrodes, in which each pair is identical except for a rotation on the sphere’s surface, the power ratios calculated for the interfering pair are the same as that for a single pair of electrodes. A similar statement can be made for interfering TMP coils except that the single coil power ratio is multiplied by the average of the squared frequencies of each coil. These results can be extrapolated to an arbitrary number of coils or electrode pairs rotated to different positions on a spherical surface in which the long-time average extends over an time interval large compared to the reciprocal of the smallest frequency differences.

3.5. Current source energy utilization

From the results given in the previous sections it is clear that TMP has the distinct advantage of producing a much smaller scalp electric field than TEP for similar cortical fields and therefore capable of diminishing potential deleterious scalp effects. However many TEP applications target specific brain electric field frequencies in the range of 0–200 Hz. This frequency range covers most of the brain frequencies which are measured by electroencephalography and magnetoencephalography. As the simple analysis of this section will show, within this frequency range it is energetically costly to generate TMP electric fields of significant amplitude to potentially alter brain activity (at least 0.5 V m⁻¹).

The source of electric current for TEP or TMP delivers power to a load which is comprised of cables, electrodes (TEP) or coils (TMP) and a head. For standard TES and TMS systems there is one source of current driving the TES electrodes or the TMS coil. Because of this the quasistatic electric field E(r, t) induced in the brain will be separable with respect to temporal and spatial variables. As already noted the TES electric field depends linearly upon the current amplitude I_e(t) whereas the TMS electric field depends linearly upon the temporal derivative of the current I_m(t) supplied to the coil. In the following it will be assumed that I_m(t) = I_mo sin(2πft) and I_e(t) = I_eo sin(2πft) where f is the frequency of a continuous applied field. We can then write the corresponding electric fields as

$$\begin{gathered} E_m(r,t)=e_m\frac{d{I}_m(t)}{dt}{e}_m(r) \\ =e_{m}2\pi f{I}_{mo}\text{cos}(2\pi ft)e_m(r) \end{gathered}$$ (53)

$$E_e(r,t)=e_e{I}_e(t)e_e(r)=e_e{I}_{eo}\text{sin}(2\pi ft)e_e(r)$$ (54)

where e_m(r) and e_e(r) are vector fields with magnitude normalized to one at some point r_o in the cortex, and e_m and e_e are the corresponding magnitudes at that point in units of (Vs Am⁻¹) and (V Am⁻¹) respectively.

Typical TMS coils (figure-8 shape with inductance of 12.0 μH and resistance of 12.0 mΩ) are known to produce a peak electric field amplitude of approximately 100 V m⁻¹ electric in the cortex near the coil (ie r_o) when I_mo = 5.0 kA and f = 4 kHz. Using equation (53) an estimate of e_m = (100V m⁻¹)/(2πI_mof) = 7.9 × 10⁻⁷ Vs Am⁻¹ is obtained. For a typical TES system the peak electric field is known to be approximately 0.5 V m⁻¹ for I_eo = 2.0 mA. This yields an estimate of e_e = (0.5V m⁻¹)/I_eo = 250V Am⁻¹.

To obtain estimates of the power supplied to the TES and TMS loads it is assumed that typical TES and TMS systems are used to create electric fields which have equal amplitudes at some some point r_o in the brain region. The point r_o will be assumed to be a relative spatial maximum (true extrema cannot exist) for both the TEP and TMP electric fields but the distribution of the electric field about r_o will be assumed to be only as similar as present methods allow. The ratio of temporally-averaged power (averaged over one period of a sinusoidal source of frequency f) supplied by the TES or TMS current source to the respective loads can be written as:

$$r=\frac{I_{eo}^2{R}_e}{I_{mo}^2{R}_m}$$ (55)

where R_e and R_m are the resistances of the TEP and TMP loads respectively. The TES load is primarily due to the resistance at the scalp-electrode interface and to lesser degree on the conductivity of the head and cables. The resistance of the TMS load is primarily due the resistance of the TMS coil and cable. We have previously noted that I_eo = |E_e|/e_e and I_mo = |E_m|/(2πe_mf) where |E_e| and |E_m| are values for the fields at r_o. Therefore we can write:

$$r={\left(\frac{2\pi f{e}_m}{e_e}\right)}^2{\left(\frac{\left|E_e\right|}{\left|E_m\right|}\right)}^2\frac{R_e}{R_m}.$$ (56)

Since the electric field amplitudes are assumed to be equal at r_o we can write

$$r={\left(\frac{2\pi f{e}_m}{e_e}\right)}^2\frac{R_e}{R_m}.$$ (57)

Since R_e is primarily due to the scalp-electrode interface it is roughly independent of the position of the TES electrodes. Also R_m is roughly independent of the presence of the head. Reasonable estimates for the two quantities are R_e = 10 kΩ and R_m = 12 mΩ. These estimates correspond to those given for NeuroConn TES electrodes and a figure-eight MagVenture TMS coil. If we insert the values for e_e and e_m (determined in the previous section) for the human head along with resistances R_e and R_m of typical human head systems we obtain

$$r\approx f^2\left(3.3\times {10}^{-10}\right).$$ (58)

Notice that this estimate depends on the square of the frequency. For a frequency of 10 Hz we have r ≈ 3.3 × 10⁻⁸ whereas for a frequency of 55 kHz we have r ≈ 1.0. Clearly TEP is far more energy efficient than TMP at low frequencies whereas the reverse is true at very high frequencies. To obtain a 10 Hz 0.5 V m⁻¹ TES electric field amplitude within the cortex requires the current source to supply approximately 2.0 mA to an electrode pair. The average power per cycle is then 0.5 × (2.0mA)² × 10 kΩ = 0.02W. Using equation (58) we can estimate that achieving the same TMP electric field using a typical human TMS coil would require approximately 610 kW.

4. Discussion

It is well known that TEP amd TMP electric fields cannot have extremal points within the interior of the head. The extremal points must always occur at the boundaries hence the scalp electric field will always be of greater magnitude than the brain electric field regardless of the method. As scalp electric fields increase in magnitude they may elicit pain due to coupling with peripheral nerves. At higher magnitudes still potentially dangerous effects due to scalp heating may occur. These deleterious effects set a maximum electric field magnitude within the scalp and consequently within the brain. However with low frequency TMP (e.g. 0–200 Hz) it is energetically costly to generate electric fields of sufficient magnitude to significantly influence neuronal state. Understanding how electric field focality, scalp heating and energy utilization shape the experimental TEP and TMP space is of value to the researcher and inventor of new noninvasive brain perturbation methods and technology.

In this work the analytic solutions of the TEP and TMP three shell model are derived and used to demonstrate important features of the respective electric fields and to estimate scalp-to-brain mean-square electric field ratios as well as the TEP-to-TMP ratio scalp mean-squared electric fields for similar electric fields at the cortex. When looking for general principles and model-based estimates analytic solutions are superior to numerical solutions since they obtain a general solution based on system variables rather a set of specific solutions based on specific choices of variables. Of the general features elucidated here:

1. TEP and TMP electric fields exist in orthogonal subspaces spanned by the vector spherical harmonics $Y_{jm}^{j-1}(\theta ,\varphi )$ and $Y_{jm}^j(\theta ,\varphi )$ respectively. The $Y_{jm}^j(\theta ,\varphi )$ vector spherical harmonics have no radial component whereas the $Y_{jm}^{j-1}(\theta ,\varphi )$ do. Therefore a TMP electric field can only be tangential to the surface of the spherical head (as has been noted elsewhere [22]).

2. TEP and TMP can have similar focality in the absence of the restrictions set by scalp mean-square electric field. A given value of index j adds similar levels of angular spatial detail on a sphere of arbitrary radius within the head for both TEP and TMP electric fields.

3. For both methods as the angular spatial detail (indexed by j) in the electric field increases so does the ratio of power dissipated in the scalp (or mean square scalp electric field) to that in the brain. For typical conductance values of the three-shell human head model this ratio is much higher in TEP ($R_j^{TEP}$) than TMP ($R_j^{TMP}$).

4. For similar electric fields at the radial distance of the cortex there exists an upper bound to the ratio of TEP-to-TMP mean-square scalp electric field given by the quantity R_∞. A value of approximately 318 was calculated for typical human head three-shell model parameters. Note that the root-mean-square electric field ratio would therefore be 17.8.

5. At low frequencies (0–200 Hz) the energetic cost for a current source to generate electric fields of appreciable magnitude within the brain region are much higher for TMP as compared to TEP.

The energetic cost associated with TMP could be made practical if electric fields of frequency greater than 1 kHz were used to perturb brain function. Recent publications suggest that this may be possible. It is well known that suprathreshold electric fields are able to robustly produce electrical nerve block in peripheral nerves [6]. It has recently been shown that amplitude modulation of suprathreshold kilohertz frequency TEP electric fields [32] may allow some degree of spatial localization with respect to the radial variable r by means of spatially distributed interference effects. The proposed mechanism is such that the amplitude of the modulation, rather than the amplitude and frequency of the electric field alone, plays a role in the coupling to neurons. The amplitude of the modulation can vary spatially thereby allowing additional spatial localization of effects in a manner not restricted by the extremum principle. Furthermore subthreshold TEP at 2–5 kHz and 2.0 mA has been shown to effect motor evoked potentials with approximately the same efficacy as TEP in the 0–100 Hz range [10]. These results suggest that continuously applied kHz TMP electric fields may be an effective and energetically feasible method to perturb brain states and function.

It should be noted that if kHz amplitude modulation does play a role in spatial focusing of TEP electric fields then this method could allow one to increase the spatial localization of electric field effects without increasing the mean-squared electric field within the scalp. Although this would be a welcome finding, kHz TMP amplitude modulation methods could increase the localization or amplitude of brain electric fields amplitude obtained from kHz even further. However this increase would come at a cost since, as has been shown, TEP systems are less energetically costly as compared to TMP systems.

Finally it should be noted the three shell spherical shell model has many obvious shortcomings. For example, the head and brain is more hemispherical rather than spherical [22] and the brain can be further partitioned in CSF, white matter and gray matter regions each with different conductivities. However this paper concerns generic comparisons between the TEP and TMP methods which are accessible through the three shell model. That said, extending the results given here, to the degree that it may be possible, to a more general model of the human head could be of interest to the field of NIBS.

Appendix A. Vector spherical harmonic definitions and properties

The l = j − 1, j, j + 1 VSH components are defined as follows:

$$\begin{gathered} {\mathbf{\text{Y}}}_{jm}^{j+1}(\theta ,\varphi )=\sqrt{\frac{j+1}{2j+1}}(-\widehat{\mathbf{\text{r}}}{Y}_{jm}(\theta ,\varphi )+\widehat{\theta }\frac{1}{j+1}\times \frac{\partial Y_{jm}(\theta ,\varphi )}{\partial \theta }+\widehat{\varphi }\frac{im}{j+1}\frac{Y_{jm}(\theta ,\varphi )}{\text{sin}\theta }) \\ {\mathbf{\text{Y}}}_{jm}^j(\theta ,\varphi )=-\widehat{\theta }\frac{m}{\sqrt{j(j+1)}}\frac{Y_{jm}(\theta ,\varphi )}{\text{sin}\theta }-\widehat{\varphi }\frac{i}{\sqrt{j(j+1)}}\times \frac{\partial Y_{jm}(\theta ,\varphi )}{\partial \theta } \\ {\mathbf{\text{Y}}}_{jm}^{j-1}(\theta ,\varphi )=\sqrt{\frac{j}{2j+1}}(\widehat{\mathbf{\text{r}}}{Y}_{jm}(\theta ,\varphi )+\widehat{\theta }\frac{1}{j}\frac{\partial Y_{jm}(\theta ,\varphi )}{\partial \theta }+\widehat{\varphi }\frac{im}{j}\frac{Y_{jm}(\theta ,\varphi )}{\text{sin}\theta }) \end{gathered}$$ (59)

The VSH components have many interesting properties. The following properties will be of use in the derivations presented in this work:

$$\begin{gathered} \widehat{\mathbf{\text{r}}}\cdot Y_{jm}^{j+1}(\theta ,\varphi )=-{\left(\frac{j+1}{2j+1}\right)}^{1/2}{Y}_{jm}(\theta ,\varphi ) \\ \widehat{\mathbf{\text{r}}}\cdot Y_{jm}^j(\theta ,\varphi )=0 \\ \widehat{\mathbf{\text{r}}}\cdot Y_{jm}^{j-1}(\theta ,\varphi )={\left(\frac{j}{2j+1}\right)}^{1/2}{Y}_{jm}(\theta ,\varphi ) \end{gathered}$$ (60)

$$\begin{gathered} \widehat{\mathbf{\text{r}}}\times Y_{jm}^{j+1}(\theta ,\varphi )=i{\left(\frac{j}{2j+1}\right)}^{1/2}{Y}_{jm}^j(\theta ,\varphi ) \\ \widehat{\mathbf{\text{r}}}\times Y_{jm}^j(\theta ,\varphi )=i{\left(\frac{j+1}{2j+1}\right)}^{1/2}{Y}_{jm}^{j-1}(\theta ,\varphi ) \\ +i{\left(\frac{j}{2j+1}\right)}^{1/2}{Y}_{jm}^{j+1}(\theta ,\varphi ) \\ \widehat{\mathbf{\text{r}}}\times Y_{jm}^{j-1}(\theta ,\varphi )=i{\left(\frac{j+1}{2j+1}\right)}^{1/2}{Y}_{jm}^j(\theta ,\varphi ). \end{gathered}$$ (61)

Appendix B. Solving for the TEP E field

We will assume that σ₂ = σ₀ and write ϵ = σ₁/σ₀. In all cases of interest the conductivity of the skull will be much less than the conductivity of the scalp or brain and therefore ϵ ≪ 1. For our purpose we will use the usual ratio of ϵ = 1/80 = 0.0125. Applying the boundary condition at r = 1 we have

$$j(1,\theta ,\varphi )\cdot \widehat{r}=-{\sigma }_2\sum _{jm}{\left[j\left(2j+1\right)\right]}^{1/2}{D}_{jm}{Y}_{jm}^{j-1}(\theta ,\varphi )\cdot \widehat{r}\text{}-{\sigma }_2\sum _{jm}{\left[\left(j+1\right)\left(2j+1\right)\right]}^{1/2}{E}_{jm}\text{}\times Y_{jm}^{j+1}(\theta ,\varphi )\cdot \widehat{r}\text{}=-{\sigma }_2\sum _{jm}\left[j{D}_{jm}-\left(j+1\right)E_{jm}\right]Y_{jm}(\theta ,\varphi )$$ (62)

and using the VSH orthogonality relationship we get

$$-j{D}_{jm}+(j+1)E_{jm}=I_{jm}$$ (63)

where

$$I_{jm}=\frac{1}{{\sigma }_2}{\int }_0^{2\pi }{\int }_0^{\pi }j(1,\theta ,\varphi )\cdot \widehat{\mathbf{\text{r}}}{Y}_{jm}^{*}(\theta ,\varphi )\text{sin}\theta d\theta d\varphi .$$ (64)

Note that since ∇ · j = 0 for a quasistatic system then, according to Gauss’s Law, I₀₀ = 0 therefore the double summation indices are now j = 1, …, ∞ and m = −j, …, j.

Applying the first boundary condition at r = α₁ we have

$$\begin{gathered} {\sigma }_1\sum _{jm}{\left[j\left(2j+1\right)\right]}^{1/2}{B}_{jm}{\alpha }_1^{j-1}{Y}_{jm}^{j-1}(\theta ,\varphi )\cdot \widehat{\mathbf{\text{r}}} \\ +{\sigma }_1\sum _{jm}{\left[\left(j+1\right)\left(2j+1\right)\right]}^{1/2}{C}_{jm}{\alpha }_1^{-(j+2)} \\ \times Y_{jm}^{j+1}(\theta ,\varphi )\cdot \widehat{\mathbf{\text{r}}} \\ ={\sigma }_0\sum _{jm}{\left[j\left(2j+1\right)\right]}^{1/2}{D}_{jm}{\alpha }_1^{j-1}{Y}_{jm}^{j-1}(\theta ,\varphi )\cdot \widehat{\mathbf{\text{r}}} \\ +{\sigma }_0\sum _{jm}{\left[\left(j+1\right)\left(2j+1\right)\right]}^{1/2}{E}_{jm}{\alpha }_1^{-(j+2)} \\ \times Y_{jm}^{j+1}(\theta ,\varphi )\cdot \widehat{\mathbf{\text{r}}} \end{gathered}$$ (65)

or

$$\begin{gathered} {\sigma }_1\sum _{jm}\left[j{B}_{jm}{\alpha }_1^{j-1}-(j+1)C_{jm}{\alpha }_1^{-(j+2)}\right]Y_{jm}(\theta ,\varphi ) \\ ={\sigma }_0\sum _{jm}\left[j{D}_{jm}{\alpha }_1^{j-1}-(j+1)E_{jm}{\alpha }_1^{-(j+2)}\right] \\ \times Y_{jm}(\theta ,\varphi ) \end{gathered}$$ (66)

therefore

$$\begin{gathered} ϵj{B}_{jm}-ϵ(j+1)C_{jm}{\alpha }_1^{-(2j+1)}-j{D}_{jm}+(j+1) \\ \times E_{jm}{\alpha }_1^{-(2j+1)}=0. \end{gathered}$$ (67)

Applying the second boundary condition at r = α₁ we have

$$\begin{gathered} \sum _{jm}{[j(2j+1)]}^{1/2}{B}_{jm}{\alpha }_1^{j-1}\widehat{\mathbf{\text{r}}}\times Y_{jm}^{j-1}(\theta ,\varphi ) \\ +\sum _{jm}{[(j+1)(2j+1)]}^{1/2}{C}_{jm}{\alpha }_1^{-(j+2)}\widehat{\mathbf{\text{r}}} \\ \times Y_{jm}^{j+1}(\theta ,\varphi ) \\ =\sum _{jm}{[j(2j+1)]}^{1/2}{D}_{jm}{\alpha }_1^{j-1}\widehat{\mathbf{\text{r}}}\times Y_{jm}^{j-1}(\theta ,\varphi ) \\ +\sum _{jm}{[(j+1)(2j+1)]}^{1/2}{E}_{jm}{\alpha }_1^{-(j+2)}\widehat{\mathbf{\text{r}}} \\ \times Y_{jm}^{j+1}(\theta ,\varphi ) \end{gathered}$$ (68)

or

$$\begin{gathered} \sum _{jm}{\left[j\left(j+1\right)\right]}^{1/2}{B}_{jm}{\alpha }_1^{j-1}{Y}_{jm}^j(\theta ,\varphi ) \\ +\sum _{jm}{\left[j\left(j+1\right)\right]}^{1/2}{C}_{jm}{\alpha }_1^{-(j+2)}{\mathbf{\text{Y}}}_{jm}^j(\theta ,\varphi ) \\ =\sum _{jm}{\left[j\left(j+1\right)\right]}^{1/2}{D}_{jm}{\alpha }_1^{j-1}{Y}_{jm}^j(\theta ,\varphi ) \\ +\sum _{jm}{\left[j\left(j+1\right)\right]}^{1/2}{E}_{jm}{\alpha }_1^{-(j+2)}{Y}_{jm}^j(\theta ,\varphi ) \end{gathered}$$ (69)

which yields

$$B_{jm}+C_{jm}{\alpha }_1^{-(2j+1)}-D_{jm}-E_{jm}{\alpha }_1^{-(2j+1)}=0.$$ (70)

Similarly applying the first and second boundary conditions at r = α₀ yields:

$$j{A}_{jm}-ϵj{B}_{jm}+ϵ(j+1)C_{jm}{\alpha }_0^{-(2j+1)}=0,$$ (71)

and

$$A_{jm}-B_{jm}-C_{jm}{\alpha }_0^{-(2j+1)}=0.$$ (72)

We will write equations (63), (67) and (70)–(72) in the following compact form

$$\left[\begin{array}{ccccc}0& 0& 0& d_1^j& e_1^j\\ 0& b_2^j& c_2^j& d_2^j& e_2^j\\ 0& b_3^j& c_3^j& d_3^j& e_3^j\\ a_4^j& b_4^j& c_4^j& 0& 0\\ a_5^j& b_5^j& c_5^j& 0& 0\end{array}\right]\left[\begin{array}{c}{A}_{jm}\\ B_{jm}\\ C_{jm}\\ D_{jm}\\ E_{jm}\end{array}\right]=\left[\begin{array}{c}{I}_{jm}\\ 0\\ 0\\ 0\\ 0\end{array}\right]$$ (73)

where

$$\begin{array}{rr}\hfill d_1^j=-j& e_1^j=(j+1)\hfill \\ \hfill d_2^j=-j& e_2^j=(j+1){\alpha }_1^{-(2j+1)}\hfill \\ \hfill d_3^j=-1& e_3^j=-{\alpha }_1^{-(2j+1)}\hfill \\ \hfill b_2^j=ϵj& \hfill c_2^j=-ϵ(j+1){\alpha }_1^{-(2j+1)}\\ \hfill b_3^j=1& c_3^j={\alpha }_1^{-(2j+1)}\hfill \\ \hfill a_4^j=j{b}_4^j=-ϵj& c_4^j=ϵ(j+1){\alpha }_0^{-(2j+1)}\hfill \\ \hfill a_5^j=1b_5^j=-1& c_5^j=-{\alpha }_0^{-(2j+1)}.\hfill \end{array}$$ (74)

Using Cramer’s Rule the solution of this simultaneous set of equations yields the results given in equations (12)–(14).

Appendix C. Solving for the TMP E field

Here we apply boundary conditions to the TMP electric field, as given by equations (23)–(25), to determine the coefficients A_jm, B_jm, C_jm, D_jm and E_jm. The boundary conditions are still those given by equations (9) and (10) albeit with $\mathbf{\text{j}}·\widehat{\mathbf{\text{r}}}=0$. Applying the boundary condition at r = 1 gives:

$$\begin{gathered} 0=-\sum _{jm}[{[j(2j+1)]}^{1/2}{D}_{jm}{\mathbf{\text{Y}}}_{jm}^{j-1}(\theta ,\varphi ) \\ +{[(j+1)(2j+1)]}^{1/2}{E}_{jm}{Y}_{jm}^{j+1}(\theta ,\varphi )]\cdot \widehat{\mathbf{\text{r}}} \\ -\sum _{jm}[\frac{1}{2j+1}\frac{\partial J_{jm}^j}{\partial t}{\mathbf{\text{Y}}}_{jm}^j(\theta ,\varphi )+\frac{1}{2j-1}\times \frac{\partial J_{jm}^{j-1}}{\partial t}{Y}_{jm}^{j-1}(\theta ,\varphi )]\cdot \widehat{\mathbf{\text{r}}} \\ =\sum _{jm}[j{D}_{jm}-(j+1)E_{jm}+{\left(\frac{j}{2j+1}\right)}^{1/2}\frac{1}{2j-1}\times \frac{\partial J_{jm}^{j-1}}{\partial t}]Y_{jm}(\theta ,\varphi ) \end{gathered}$$ (75)

or

$$-j{D}_{jm}+(j+1)E_{jm}={\left(\frac{j}{2j+1}\right)}^{1/2}\frac{1}{2j-1}\frac{\partial J_{jm}^{j-1}}{\partial t}.$$ (76)

Applying the first boundary condition of equation (10) at r = α₁ we have

$$\begin{gathered} {\sigma }_1\sum _{jm}[{\left[j\left(2j+1\right)\right]}^{1/2}{B}_{jm}{\alpha }_1^{j-1}{Y}_{jm}^{j-1}(\theta ,\varphi )+{\left[\left(j+1\right)\left(2j+1\right)\right]}^{1/2}{C}_{jm}{\alpha }_1^{-(j+2)}\times Y_{jm}^{j+1}(\theta ,\varphi )]\cdot \widehat{\mathbf{\text{r}}} \\ +{\sigma }_1\sum _{jm}[\frac{{\alpha }_1^j}{2j+1}\frac{\partial J_{jm}^j}{\partial t}{Y}_{jm}^j(\theta ,\varphi )+\frac{{\alpha }_1^{j-1}}{2j-1}\times \frac{\partial J_{jm}^{j-1}}{\partial t}{Y}_{jm}^{j-1}(\theta ,\varphi )]\cdot \widehat{\mathbf{\text{r}}} \\ ={\sigma }_0\sum _{jm}[{\left[j\left(2j+1\right)\right]}^{1/2}{D}_{jm}{\alpha }_1^{j-1}{Y}_{jm}^{j-1}(\theta ,\varphi )+{\left[\left(j+1\right)\left(2j+1\right)\right]}^{1/2}{E}_{jm}{\alpha }_1^{-(j+2)}\times Y_{jm}^{j+1}(\theta ,\varphi )]\cdot \widehat{\mathbf{\text{r}}} \\ +{\sigma }_0\sum _{jm}[\frac{{\alpha }_1^j}{2j+1}\frac{\partial J_{jm}^j}{\partial t}{Y}_{jm}^j(\theta ,\varphi )+\frac{{\alpha }_1^{j-1}}{2j-1}\times \frac{\partial J_{jm}^{j-1}}{\partial t}{Y}_{jm}^{j-1}(\theta ,\varphi )]\cdot \widehat{\mathbf{\text{r}}} \end{gathered}$$ (77)

or

$$\begin{gathered} {\sigma }_1\sum _{jm}[j{B}_{jm}{\alpha }_1^{j-1}{Y}_{jm}(\theta ,\varphi )-(j+1)C_{jm}{\alpha }_1^{-(j+2)} \\ \times Y_{jm}(\theta ,\varphi )]+\left({\sigma }_1-{\sigma }_0\right)\sum _{jm}{\left[\frac{j}{2j+1}\right]}^{1/2} \\ \times \frac{{\alpha }_1^{j-1}}{2j-1}\frac{\partial J_{jm}^{j-1}}{\partial t}{Y}_{jm}(\theta ,\varphi ) \\ ={\sigma }_0\sum _{jm}[j{D}_{jm}{\alpha }_1^{j-1}{Y}_{jm}(\theta ,\varphi )-(j+1)E_{jm}\times {\alpha }_1^{-(j+2)}{Y}_{jm}(\theta ,\varphi )] \end{gathered}$$ (78)

or

$$\begin{gathered} {\sigma }_1\left[j{B}_{jm}{\alpha }_1^{j-1}-(j+1)C_{jm}{\alpha }_1^{-(j+2)}\right]+\left({\sigma }_1-{\sigma }_0\right) \\ \times {\left[\frac{j}{2j+1}\right]}^{1/2}\frac{{\alpha }_1^{j-1}}{2j-1}\frac{\partial J_{jm}^{j-1}}{\partial t} \\ ={\sigma }_0\left[j{D}_{jm}{\alpha }_1^{j-1}-(j+1)E_{jm}{\alpha }_1^{-(j+2)}\right] \end{gathered}$$ (79)

$$\begin{gathered} ϵj{B}_{jm}-ϵ(j+1)C_{jm}{\alpha }_1^{-(2j+1)}-j{D}_{jm}+(j+1)E_{jm} \\ \times {\alpha }_1^{-(2j+1)}=(1-ϵ){\left[\frac{j}{2j+1}\right]}^{1/2}\frac{1}{2j-1}\frac{\partial J_{jm}^{j-1}}{\partial t}. \end{gathered}$$ (80)

Applying the second boundary condition of equation (10) at r = α₁ we have

$$\begin{gathered} \sum _{jm}[{[j(2j+1)]}^{1/2}{B}_{jm}{\alpha }_1^{j-1}{Y}_{jm}^{j-1}(\theta ,\varphi ) \\ +{[(j+1)(2j+1)]}^{1/2}{C}_{jm}{\alpha }_1^{-(j+2)}{Y}_{jm}^{j+1}(\theta ,\varphi )]\times \widehat{\mathbf{\text{r}}} \\ =\sum _{jm}[{[j(2j+1)]}^{1/2}{D}_{jm}{\alpha }_1^{j-1}{Y}_{jm}^{j-1}(\theta ,\varphi )+[\left(j+1\right){\left(2j+1\right)}^{1/2}{E}_{jm}{\alpha }_1^{-(j+2)}\times Y_{jm}^{j+1}(\theta ,\varphi )]\times \widehat{\mathbf{\text{r}}} \end{gathered}$$ (81)

or

$$\begin{gathered} \sum _{jm}[{[j(j+1)]}^{1/2}{B}_{jm}{\alpha }_1^{j-1}{Y}_{jm}^j(\theta ,\varphi )+{[j(j+1)]}^{1/2}\times C_{jm}{\alpha }_1^{-(j+2)}{Y}_{jm}^j(\theta ,\varphi )] \\ =\sum _{jm}[{[j(j+1)]}^{1/2}{D}_{jm}{\alpha }_1^{j-1}{Y}_{jm}^j(\theta ,\varphi )+{[j(j+1)]}^{1/2}{E}_{jm}{\alpha }_1^{-(j+2)}{Y}_{jm}^j(\theta ,\varphi )] \end{gathered}$$ (82)

or

$$B_{jm}+C_{jm}{\alpha }_1^{-(2j+1)}-D_{jm}-E_{jm}{\alpha }_1^{-(2j+1)}=0.$$ (83)

Similarly the first and second boundary conditions applied at r = α₀ yield:

$$\begin{gathered} j{A}_{jm}-ϵj{B}_{jm}+ϵ(j+1)C_{jm}{\alpha }_0^{-(2j+1)} \\ =(ϵ-1){\left(\frac{j}{2j+1}\right)}^{1/2}\frac{1}{2j-1}\frac{\partial J_{jm}^{j-1}}{\partial t}, \end{gathered}$$ (84)

and

$$A_{jm}-B_{jm}-C_{jm}{\alpha }_0^{-(2j+1)}=0.$$ (85)

We write equations (78), (80) and (83)–(85) as:

$$\left[\begin{array}{ccccc}0& 0& 0& d_1^j& e_1^j\\ 0& b_2^j& c_2^j& d_2^j& e_2^j\\ 0& b_3^j& c_3^j& d_3^j& e_3^j\\ a_4^j& b_4^j& c_4^j& 0& 0\\ a_5^j& b_5^j& c_5^j& 0& 0\end{array}\right]\left[\begin{array}{c}{A}_{jm}\\ B_{jm}\\ C_{jm}\\ D_{jm}\\ E_{jm}\end{array}\right]=I_{jm}\left[\begin{array}{c}1\\ (1-ϵ)\\ 0\\ (ϵ-1)\\ 0\end{array}\right]$$ (86)

where

$$\begin{array}{rr}\hfill d_1^j=-j& e_1^j=(j+1)\hfill \\ \hfill d_2^j=-j& e_2^j=(j+1){\alpha }_1^{-(2j+1)}\hfill \\ \hfill d_3^j=-1& e_3^j=-{\alpha }_1^{-(2j+1)}\hfill \\ \hfill b_2^j=ϵj& c_2^j=-ϵ(j+1){\alpha }_1^{-(2j+1)}\hfill \\ \hfill b_3^j=1& c_3^j={\alpha }_1^{-(2j+1)}\hfill \\ \hfill a_4^j=j{b}_4^j=-ϵj& c_4^j=ϵ(j+1){\alpha }_0^{-(2j+1)}\hfill \\ \hfill a_5^j=1b_5^j=-1& c_5^j=-{\alpha }_0^{-(2j+1)}\hfill \end{array}$$ (87)

and

$$I_{jm}={\left(\frac{j}{2j+1}\right)}^{1/2}\frac{1}{2j-1}\frac{\partial J_{jm}^{j-1}}{\partial t}.$$ (88)

Using Cramer’s Rule the solution of this simultaneous set of equations is:

$$A_{jm}=B_{jm}=D_{jm}=-\frac{I_{jm}}{j}{C}_{jm}=E_{jm}=0.$$ (89)

By substituting equations (89) into equations (23) through (25) the following expression for the electric field in regions 0, 1 and 2 is obtained:

$$\mathbf{\text{e}}(r,\Omega ,t)=-\sum _{jm}\frac{r^j}{2j+1}\frac{\partial j_{jm}^j}{\partial t}{\mathbf{\text{Y}}}_{jm}^j(\theta ,\varphi ).$$ (90)

In fact for an arbitrary number of concentric spherical conductors the expression for E(r, θ, ϕ, t) in all regions will be given by equation (90). The electric field due to the surface charge exactly cancels the l = j − 1 components of the induced part of the electric field.

Appendix D. Calculating I_jm for typical electrode pairs

Assume there are two TEP electrodes, the first will have outgoing (directed along an outward oriented unit normal vector at the surface of the three shell sphere) current and the second will have ingoing current. The center of the first electrode is located at the upper pole of the sphere and the center of the second electrode is located at some angle β relative to the z-axis (the z-axis runs through the poles). The perimeter of each electrode subtends an angle θ_o (from its center) on the surface of the sphere and it is assumed that the radial component of the current density provided by the electrodes are uniform and of magnitude I_o.

For the single electrode located at the pole with out-going uniform current density:

$$\begin{gathered} I_{jm}^{+}=I_o{\int }_0^{{\theta }_o}{\int }_0^{2\pi }{Y}_{jm}^{*}(\theta ,\varphi )\text{ sin }\theta d\varphi d\theta \\ =I_o\sqrt{\frac{2j+1}{4\pi }\frac{(j-m)!}{(j+m)!}}{\int }_0^{2\pi }{e}^{im\varphi }d\varphi {\int }_0^{{\theta }_o}{P}_j^m \\ \times (\text{cos }\theta )\text{ sin }\theta d\theta \\ =2\pi {\delta }_{m0}{I}_o\sqrt{\frac{2j+1}{4\pi }}{\int }_1^{\text{cos }{\theta }_0}{P}_j(\text{cos }\theta )d\text{ cos }\theta \\ ={\delta }_{m0}{I}_o\sqrt{\frac{\pi }{2j+1}}{\left[P_{j+1}(\text{cos }\theta )-P_{j-1}(\text{cos }\theta )\right]}_1^{\text{cos }{\theta }_o} \\ ={\delta }_{m0}{I}_o\sqrt{\frac{\pi }{2j+1}}[P_{j+1}\left(\text{cos }{\theta }_o\right)-P_{j-1}\left(\text{cos }{\theta }_o\right) \\ -P_{j+1}(1)+P_{j-1}(1)] \\ ={\delta }_{m0}{I}_o\sqrt{\frac{\pi }{2j+1}}\left[P_{j+1}\left(\text{cos }{\theta }_o\right)-P_{j-1}\left(\text{cos }{\theta }_o\right)\right] \\ ={\delta }_{m0}2\pi I_o\sqrt{\frac{1}{2j+1}}[\sqrt{\frac{1}{2j+3}}{\tilde{P}}_{j+1}\left(\text{cos }{\theta }_o\right) \\ -\sqrt{\frac{1}{2j-1}}{\tilde{P}}_{j-1}\left(\text{cos }{\theta }_o\right)] \\ ={\delta }_{m0}{I}_{j0}^{+} \end{gathered}$$ (91)

where the ${\tilde{P}}_j=\sqrt{\frac{2j+1}{4\pi }}{P}_j$ are the renormalized (numerically stable) Legendre Functions and the definition of $I_{j0}^{+}$ should be obvious. The $I_{jm}^{+}$ are by definition the coefficients of a spherical harmonic expansion of the outgoing current contribution to the function $I^{+}(\theta ,\varphi )=J\left(r_2,\Omega \right)\cdot \widehat{\mathbf{\text{r}}}$ and therefore using equation (91) we can write

$$I^{+}(\theta ,\varphi )=\sum _j{I}_{j0}^{+}{Y}_{j0}(\theta ,\varphi )=\sum _j\sqrt{\frac{2j+1}{4\pi }}{I}_{j0}^{+}\times P_j(\text{cos }\theta ).$$ (92)

The contribution to I_jm by a second electrode of the same size rotated to a position β relative to the pole with ingoing uniform current density can be found by rotating by β the function I⁺(θ, ϕ) for the electrode at the pole given by equation (92) and changing sign. The Y_j0 spherical harmonic transforms under a rotation operator $\widehat{D}(\alpha ,\beta ,\gamma )$ (where α, β and γ are Euler angles) according to:

$$\begin{gathered} \widehat{D}(\alpha ,\beta ,\gamma )Y_{j0}(\theta ,\varphi )=\sqrt{\frac{4\pi }{2j+1}}\sum _{m=-j}^j{Y}_{jm}(\theta ,\varphi ) \\ \times Y_{jm}^{*}(\beta ,\alpha ) \end{gathered}$$ (93)

therefore the ingoing contribution to I⁻ due to the second electrode is

$$\begin{gathered} I^{-}(\Omega )=-\widehat{D}(\alpha ,\beta ,\gamma )I^{+}(\Omega ) \\ =-\sum _j{I}_{j0}^{+}\widehat{D}(\alpha ,\beta ,\gamma )Y_{j0}(\theta ,\varphi ) \\ =-\sum _j\sum _{m=-j}^j{I}_{j0}^{+}\sqrt{\frac{4\pi }{2j+1}}{Y}_{jm}(\theta ,\varphi )Y_{jm}^{*}(\beta ,\alpha ) \end{gathered}$$ (94)

and $I_{jm}^{-}$, the contribution to I_jm by the ingoing current density of the second electrode, is given by

$$\begin{gathered} I_{jm}^{-}=-{\int }_1^{-1}{\int }_0^{2\pi }{I}^{-}(\theta ,\varphi )Y_{jm}^{*}(\theta ,\varphi )d\varphi d\text{cos}\theta \\ =-I_{j0}^{+}\sqrt{\frac{4\pi }{2j+1}}{Y}_{jm}^{*}(\beta ,\alpha ). \end{gathered}$$ (95)

Here we assume that α = 0 and allow β to vary the position of the second electrode in which case:

$$\begin{gathered} I_{jm}^{-}=-I_{j0}^{+}\sqrt{\frac{4\pi }{2j+1}}{Y}_{jm}^{*}(\beta ,0) \\ =-I_{j0}^{+}\sqrt{\frac{(j-m)!}{(j+m)!}}{P}_j^m(\text{cos }\beta ) \end{gathered}$$ (96)

and therefore

$$\begin{gathered} I_{jm}=I_{j0}^{+}\left[{\delta }_{m0}-\sqrt{\frac{(j-m)!}{(j+m)!}}{P}_j^m(\text{cos }\beta )\right] \\ =I_{j0}^{+}\left[{\delta }_{m0}-\sqrt{\frac{4\pi }{2j+1}}{\tilde{P}}_j^m(\text{cos }\beta )\right] \end{gathered}$$ (97)

where the definition of the renormalized associated Legendre functions ${\tilde{P}}_j^m$ should be obvious.

Appendix E. Calculating $J_{jm}^j$ for circular and figure-8 TMS coils

The specifications of TMS coils, which contain many windings, are usually given in terms of an inner and outer radius for a simple circular coil. Here the simple circular coil (see figure 6) is approximated by a single winding at the average of the inner and outer radii. Assume the current density j is a thin ring of current of amplitude I(t) and radius r_c (in units of r₂) inscribed on a plane tangent to the outer surface of the scalp region and centered on the vertical axis. Then

$$j=I(t)e_{\varphi }\delta \left(r-{\rho }_o\right)\delta \left(\text{cos }\theta -\text{cos }{\theta }_o\right)r^{-1}\text{sin }\theta$$ (98)

where ${\rho }_o=\sqrt{r_c^2+1}$ and ${\theta }_o={\rho }_o^{-1}$. It follows that

$$\begin{gathered} J_{jm}^j=\frac{4\pi r_2^2}{c^2}\iiint \frac{1}{r^{\prime j+1}}j\left(r^{\prime },{\theta }^{\prime },{\varphi }^{\prime }\right)\cdot Y_{jm}^{*j}\left({\theta }^{\prime },{\varphi }^{\prime }\right)r^{\prime 2} \\ \times d{r}^{\prime }d{\varphi }^{\prime }d\text{ cos }{\theta }^{\prime } \\ =\frac{4\pi r_2^2}{c^2}I\iiint \frac{1}{r^{\prime j+1}}\delta \left(r^{\prime }-{\rho }_o\right)\delta \left(\text{cos }{\theta }^{\prime }-\text{cos }{\theta }_o\right) \\ \times \text{ sin }{\theta }^{\prime }{e}_{\varphi }\cdot Y_{jm}^{*j}\left({\theta }^{\prime },{\varphi }^{\prime }\right)r^{\prime }d{r}^{\prime }d{\varphi }^{\prime }d\text{ cos }{\theta }^{\prime } \\ =\frac{4\pi r_2^2}{c^2{\rho }_o^j}I\iint \delta \left(\text{cos }{\theta }^{\prime }-\text{cos }{\theta }_o\right)\text{ sin }{\theta }^{\prime }{e}_{\varphi } \\ \cdot Y_{jm}^{*j}\left({\theta }^{\prime },{\varphi }^{\prime }\right)d{\varphi }^{\prime }d\text{ cos }{\theta }^{\prime } \\ =\frac{i}{\sqrt{j(j+1)}}\frac{4\pi r_2^2}{c^2{\rho }_o^j}I\iint \delta \left(\text{cos }{\theta }^{\prime }-\text{cos }{\theta }_o\right)\text{ sin }{\theta }^{\prime } \\ \times \frac{\partial Y_{jm}^{*}}{\partial {\theta }^{\prime }}d{\varphi }^{\prime }d\text{ cos }{\theta }^{\prime }. \end{gathered}$$ (99)

Since

$$\begin{gathered} \frac{\partial Y_{jm}}{\partial {\theta }^{\prime }}=\frac{1}{2}\sqrt{j(j+1)-m(m+1)}{Y}_{jm+1}{e}^{-i\varphi } \\ -\frac{1}{2}\sqrt{j(j+1)-m(m-1)}{Y}_{jm-1}{e}^{i\varphi } \end{gathered}$$ (100)

then

$$\begin{gathered} J_{jm}^j=i\frac{2\pi r_2^{2}I}{c^2{\rho }_o^j}{\left(\frac{j(j+1)-m(m+1)}{j(j+1)}\right)}^{1/2} \\ \times \iint \delta \left(\text{cos }{\theta }^{\prime }-\text{cos }{\theta }_o\right)\text{ sin }{\theta }^{\prime }{Y}_{jm+1}^{*}\left({\theta }^{\prime },{\varphi }^{\prime }\right)e^{i{\varphi }^{\prime }} \\ \times d{\varphi }^{\prime }d\text{cos }{\theta }^{\prime } \\ -i\frac{2\pi r_2^{2}I}{c^2{\rho }_o^j}{\left(\frac{j(j+1)-m(m-1)}{j(j+1)}\right)}^{1/2} \\ \times \iint \delta \left(\text{cos }{\theta }^{\prime }-\text{cos }{\theta }_o\right)\text{ sin }{\theta }^{\prime }{Y}_{jm-1}^{*}\left({\theta }^{\prime },{\varphi }^{\prime }\right) \\ \times e^{-i{\varphi }^{\prime }}d{\varphi }^{\prime }d\text{ cos }{\theta }^{\prime } \\ =i\frac{2\pi r_2^{2}I}{c^2{\rho }_o^j}{\left(\frac{j(j+1)-m(m+1)}{j(j+1)}\right)}^{1/2} \\ \times \iint \delta \left(\text{cos }{\theta }^{\prime }-\text{cos }{\theta }_o\right)\text{ sin }{\theta }^{\prime }{e}^{-im\varphi }{\tilde{P}}_j^{m+1}(\text{cos }\theta ) \\ \times d{\varphi }^{\prime }d\text{ cos }{\theta }^{\prime } \\ -i\frac{2\pi r_2^{2}I}{c^2{\rho }_o^j}{\left(\frac{j(j+1)-m(m-1)}{j(j+1)}\right)}^{1/2} \\ \times \iint \delta \left(\text{cos }{\theta }^{\prime }-\text{cos }{\theta }_o\right)\text{ sin }{\theta }^{\prime }{e}^{-im\varphi }{\tilde{P}}_j^{m-1} \\ \times (\text{cos }\theta )d{\varphi }^{\prime }d\text{ cos }{\theta }^{\prime } \\ =i{\delta }_{m0}\frac{4{\pi }^2{r}_2^{2}I}{c^2{\rho }_o^j}\int \delta \left(\text{cos }{\theta }^{\prime }-\text{cos }{\theta }_o\right)\text{ sin }{\theta }^{\prime }{\tilde{P}}_j^1 \\ \times (\text{cos }\theta )d\text{ cos }{\theta }^{\prime } \\ -i{\delta }_{m0}\frac{4{\pi }^2{r}_2^{2}I}{c^2{\rho }_o^j}\int \delta \left(\text{cos }{\theta }^{\prime }-\text{cos }{\theta }_o\right)\text{ sin }{\theta }^{\prime }{\tilde{P}}_j^{-1} \\ \times (\text{cos }\theta )d\text{ cos }{\theta }^{\prime } \\ =i{\delta }_{m0}\frac{4{\pi }^2{r}_2^{2}I}{c^2{\rho }_o^j}\sqrt{1-{\text{cos }}^2{\theta }_o}{\tilde{P}}_j^1\left(\text{cos }{\theta }_o\right) \\ -i{\delta }_{m0}\frac{4{\pi }^2{r}_2^{2}I}{c^2{\rho }_o^j}\sqrt{1-{\text{cos }}^2{\theta }_o}{\tilde{P}}_j^{-1}\left(\text{cos }{\theta }_o\right) \\ =i{\delta }_{m0}\frac{8{\pi }^2{r}_2^{2}I}{c^2{\rho }_o^j}\sqrt{1-{\text{cos }}^2{\theta }_o}{\tilde{P}}_j^1\left(\text{cos }{\theta }_o\right) \end{gathered}$$ (101)

where the identities $Y_{jm}(\theta ,\varphi )=e^{im\varphi }{\tilde{P}}_j^m(\text{cos }\theta )$ and ${\tilde{P}}_j^{-m}(\text{cos }\theta )={(-1)}^m{\tilde{P}}_j^m(\text{cos }\theta )$ have been used.

If a second coil is added with its current circulating in the direction opposite that of coil 1 then a figure-of-eight type coil can be obtained. The position and orientation of coil 2 is obtained by rotating coil 1 by an angle β = 2θ_o from the z-axis such that the two coils osculate (see figure 6) at one point. For this figure-8 coil $J_{jm}^j=J_{jm}^{j+}-J_{jm}^{j-}$ where $J_{jm}^{j+}$ is the contribution from coil 1 (given by equation (101)) and $J_{jm}^{j-}$ is the contribution from coil 2. $J_{jm}^{j-}$ can be found by performing either a rotation of the current density by angle β or a rotation of the spherical harmonic $Y_{jm}^{*j}(\theta ,\varphi )$ by angle −β. Using the later approach

$$\begin{gathered} J_{jm}^{j-}=\frac{4\pi r_2^2}{c^2}\iiint \frac{1}{r^{\prime j+1}}j\left(r^{\prime },{\theta }^{\prime },{\varphi }^{\prime }\right) \\ \cdot \left[\widehat{D}(0,-\beta ,0){\mathbf{\text{Y}}}_{jm}^{*j}\left({\theta }^{\prime },{\varphi }^{\prime }\right)\right]r^{\prime 2}d{r}^{\prime }d{\varphi }^{\prime }d\text{ cos }{\theta }^{\prime } \\ =\frac{4\pi r_2^2}{c^2{\rho }_o^j}I\iint \delta \left(\text{cos }{\theta }^{\prime }-\text{cos }{\theta }_o\right){\mathbf{\text{e}}}_{\varphi } \\ \cdot \left[\widehat{D}(0,-\beta ,0){\mathbf{\text{Y}}}_{jm}^{*j}\left({\theta }^{\prime },{\varphi }^{\prime }\right)\right]\text{ sin }{\theta }^{\prime }d{\varphi }^{\prime }d\text{ cos }{\theta }^{\prime } \\ =\frac{4\pi r_2^2}{c^2{\rho }_o^j}I\iint \delta \left(\text{cos }{\theta }^{\prime }-\text{cos }{\theta }_o\right)\sum _{m^{\prime }}{D}_{m^{\prime }m}^j \\ \times (0,-\beta ,0)e_{\varphi }\cdot Y_{j{m}^{\prime }}^{*j}\left({\theta }^{\prime },{\varphi }^{\prime }\right)\text{ sin }{\theta }^{\prime }d{\varphi }^{\prime }d\text{ cos }{\theta }^{\prime } \\ =\frac{i4\pi I}{\sqrt{j(j+1)}}\frac{r_2^2}{c^2{\rho }_o^j}\iint \delta \left(\text{cos }{\theta }^{\prime }-\text{cos }{\theta }_o\right)\sum _{m^{\prime }}{D}_{m^{\prime }m}^j \\ \times (0,-\beta ,0)\frac{\partial Y_{j{m}^{\prime }}^{*}}{\partial {\theta }^{\prime }}\text{ sin }{\theta }^{\prime }d{\varphi }^{\prime }d\text{ cos }{\theta }^{\prime } \end{gathered}$$ (102)

where $\widehat{D}(0,-\beta ,0)$ is the rotation operator with Euler angle arguments and $D_{m^{\prime }m}^j$ are the Wigner D-functions [19]. But the integration with respect to ϕ′ yields

$$\begin{gathered} \int \frac{\partial Y_{j{m}^{\prime }}^{\ast }}{\partial {\theta }^{\prime }}d{\varphi }^{\prime }=\frac{1}{2}\int \sqrt{j(j+1)-m^{\prime }\left(m^{\prime }+1\right)} \\ \times Y_{j{m}^{\prime }+1}^{\ast }\left({\theta }^{\prime },{\varphi }^{\prime }\right)e^{i{\varphi }^{\prime }}d{\varphi }^{\prime } \\ -\frac{1}{2}\int \sqrt{j(j+1)-m^{\prime }\left(m^{\prime }-1\right)} \\ \times Y_{j{m}^{\prime }-1}^{\ast }\left({\theta }^{\prime },{\varphi }^{\prime }\right)e^{-i{\varphi }^{\prime }}d{\varphi }^{\prime } \\ =\frac{1}{2}\int \sqrt{j(j+1)-m^{\prime }\left(m^{\prime }+1\right)} \\ \times {\tilde{P}}_j^{m^{\prime }+1}\left(\text{cos }{\theta }^{\prime }\right)e^{-i{m}^{\prime }{\varphi }^{\prime }}d{\varphi }^{\prime } \\ -\frac{1}{2}\int \sqrt{j(j+1)-m^{\prime }\left(m^{\prime }-1\right)} \\ \times {\tilde{P}}_j^{m^{\prime }-1}\left(\text{cos }{\theta }^{\prime }\right)e^{i{m}^{\prime }{\varphi }^{\prime }}d{\varphi }^{\prime } \\ =\pi {\delta }_{m^{\prime }0}\sqrt{j\left(j+1\right)}[{\tilde{P}}_j^1\left(\text{cos }{\theta }^{\prime }\right) \\ -{\tilde{P}}_j^{-1}\left(\text{cos }{\theta }^{\prime }\right)] \\ =2\pi {\delta }_{m^{\prime }0}\sqrt{j(j+1)}{\tilde{P}}_j^1\left(\text{cos }{\theta }^{\prime }\right). \end{gathered}$$ (103)

Substituting equation (103) into (102) and making use of the identity $D_{0m}^j(\alpha ,\beta ,\gamma )=\sqrt{4\pi /(2j+1)}{Y}_{j,-m}(\beta ,\gamma )$ [19] the result is obtained:

$$\begin{gathered} J_{jm}^{j-}=i\frac{8{\pi }^2{r}_2^2}{c^2{\rho }_o^j}I{D}_{0m}^j(0,-\beta ,0)\int \delta \left(\cos {\theta }^{\prime }-\cos {\theta }_o\right) \\ \times {\tilde{P}}_j^1\left(\cos {\theta }^{\prime }\right)\mathrm{ sin }{\theta }^{\prime }d\cos {\theta }^{\prime } \\ =i\frac{8{\pi }^2{r}_2^2}{c^2{\rho }_o^j}I\sqrt{1-{\cos }^2{\theta }_o}{D}_{0m}^j(0,-\beta ,0){\tilde{P}}_j^1\left(\cos {\theta }_o\right) \\ =i\frac{8{\pi }^2{r}_2^2}{c^2{\rho }_o^j}I\sqrt{1-{\cos }^2{\theta }_o}\sqrt{4\pi /(2j+1)}{Y}_{j,-m} \\ \times (-\beta ,0){\tilde{P}}_j^1\left(\cos {\theta }_o\right) \\ ={i(-1)}^m\frac{8{\pi }^2{r}_2^2}{c^2{\rho }_o^j}I\sqrt{1-{\cos }^2{\theta }_o}\sqrt{4\pi /\left(2j+1\right)} \\ \times {\tilde{P}}_j^m(\cos \beta ){\tilde{P}}_j^1\left(\cos {\theta }_o\right) \end{gathered}$$ (104)

which reduces to the result given by equation (101) when β = 0. For the figure-8 coil the coefficients $J_{jm}^j$ are then given by:

$$\begin{gathered} J_{jm}^j=J_{jm}^{j+}-J_{jm}^{j-}=i\frac{8{\pi }^2{r}_2^2}{c^2{\rho }_o^j}I\sqrt{1-{\text{cos }}^2{\theta }_o} \\ \times \left[{\delta }_{m0}-{(-1)}^m\sqrt{\frac{4\pi }{2j+1}}{\tilde{P}}_j^m\times \left(\text{cos }2{\theta }_o\right)\right]{\tilde{P}}_j^1\left(\text{cos }{\theta }_o\right). \end{gathered}$$ (105)

Data availability statement

No new data were created or analysed in this study.