Abstract
An algorithm for automatic spinal pedicle screw planning is reported and evaluated in simulation and first clinical studies. A statistical atlas of the lumbar spine (N = 40 members) was constructed for active shape model (ASM) registration of target vertebrae to an unsegmented patient CT. The atlas was augmented to include ‘reference’ trajectories through the pedicles as defined by a spinal neurosurgeon. Following ASM registration, the trajectories are transformed to the patient CT and accumulated to define a patient-specific screw trajectory, diameter, and length. The algorithm was evaluated in leave-one-out analysis (N = 40 members) and for the first time in a clinical study (N = 5 patients undergoing cone-beam CT (CBCT) guided spine surgery), and in simulated low-dose CBCT images. ASM registration achieved (2.0 ± 0.5) mm root-mean-square-error (RMSE) in surface registration in 96% of cases, with outliers owing to limitations in CT image quality (high noise/slice thickness). Trajectory centerlines were conformant to the pedicle in 95% of cases. For all non-breaching trajectories, automatically defined screw diameter and length were similarly conformant to the pedicle and vertebral body (98.7%, Grade A/B). The algorithm performed similarly in CBCT clinical studies (93% centerline and screw conformance) and was consistent at the lowest dose levels tested. Average runtime in planning five-level (lumbar) bilateral screws (ten trajectories) was (312.1 ± 104.0) s. The runtime per level for ASM registration was (41.2 ± 39.9) s, and the runtime per trajectory was (4.1 ± 0.8) s, suggesting a runtime of ~(45.3 ± 39.9) s with a more fully parallelized implementation. The algorithm demonstrated accurate, automatic definition of pedicle screw trajectories, diameter, and length in CT images of the spine without segmentation. The studies support translation to clinical studies in free-hand or robot-assisted spine surgery, quality assurance, and data analytics in which fast trajectory definition is a benefit to workflow.
Keywords: surgical planning, image-guided surgery, surgical robotics, atlas-based registration, automatic planning, surgical data science, quality assurance
1. Introduction
Spinal pedicle screw placement is intrinsic to treating a wide variety of spinal trauma, tumors, deformity, and degenerative conditions (Attar et al 2001). The procedure typically involves the posterior insertion of screws into two or more vertebrae. The screw heads are then fastened to fusion hardware, such as rods or plates, providing stabilization of the spine (Sethi et al 2012). Screws must be placed accurately through a narrow corridor of the vertebrae known as the pedicle, which is in close proximity to the spinal cord, dural sac, nerve roots, and blood vessels. Improperly placed screws can lead to neurological complications, including paralysis (Slone et al 1993). Conventionally, pedicle screw placement involves free-hand insertion using anatomical landmarks along with preoperative imaging (Yoshii et al 2015). Suboptimal placement and/or breach was found in up to ~13.5% of cases—of which 40.2% correspond to a medial breach with potential damage to the spinal cord (Jamalaldini and Etemadifar 2017).
A variety of methods aim to improve the safety of pedicle screw placement, including fluoroscopic guidance, 3D navigation, and most recently robot-assistance (Puvanesarajah et al 2014, Joseph et al 2017, Yoshii et al 2015). Related efforts include improved intraoperative imaging (Silbermann et al 2011, Hecht et al 2015) as well as intraoperative guidance and quality assurance (QA) of device placement using 3D–2D image registration (Uneri et al 2015). Additionally, research involving retrospective analysis of screw placement in large image datasets may help in understanding factors underlying variations in spine surgery outcome (De Silva et al 2019).
Common to these efforts is the need for a reliable definition of transpedicle trajectory. In free-hand screw placement using navigation, a surgeon views the position of tracked instruments (e.g. drill, tap, and screwdriver) with respect to the planned trajectories. The planned trajectories can be planned preoperatively or intraoperatively using the ‘drop-screw’ technique (i.e. tracking an instrument relative to CT and ‘dropping’ a virtual screw in the CT image at the desired location). Despite its simplicity, the technique requires manual positioning of the tracked tool for each trajectory and introduces additional time and workflow.
Image guidance improves the accuracy of screw placement, but free-hand image-guided procedures still exhibit suboptimal screw placement. In a study of lumbar pedicle screw placement using fluoroscopic guidance, 28% of lumbar pedicle screws resulted in medial breaches with neurological complications in 17% of patients (Puvanesarajah et al 2014). With stereotactic navigation, breach rates of 15.7% and 4.5% have been reported for 2D and 3D fluoroscopic navigation, respectively (Mason et al 2014). In addition to suboptimal surgical product, the extended fluoroscopy time raises concern regarding radiation exposure to surgical staff, increased operating time, and workflow interruption (Puvanesarajah et al 2014).
As an alternative, robot-assisted spinal pedicle screw placement is becoming more prevalent. Examples include the Excelsius (Globus, Audubon PA), Mazor X (Mazor, Caesarea, Israel), and Cirq (Brainlab, Munich, Germany). Each uses optical tracking to position the robot end effector (e.g. a pedicle drill guide) at each vertebra entry point, providing the surgeon with a precisely placed corridor through which trans-pedicle instrumentation can be delivered. Several studies concluded that these systems provide improved geometric accuracy compared to fluoroscopically guided freehand screw placement (Joseph et al 2017). Operating time, however, may increase (~15%) and would benefit from further improvements to workflow (Ghasem et al 2018).
A potential bottleneck is manual planning of screw trajectories, which serves as the basis for target positions communicated to the robot. Similar to free-hand techniques, trajectories for robot-assisted procedures can be planned using a drag-and-drop interface, which is typically performed using intraoperative cone-beam CT (CBCT). The process introduces a slight interruption to workflow, and manual planning carries the potential for error and/or inter-operator variability.
Motivated by the need for streamlined workflow and rigorous, reproducible trajectory definition, we developed an automatic trajectory planning algorithm that could improve workflow and reproducibility in free-hand navigated and robot-assisted screw placement. It could also provide a definitive reference trajectory for purposes of intraoperative QA (e.g. comparing actual screw placement to an automatically defined reference) and image analytics (retrospective review of image data in relation to surgical outcomes).
A variety of methods for automatic spine screw planning have been reported. One technique uses parametric models of vertebral bodies and pedicles that are registered to the patient CT, and screw trajectories are computed based on geometric and structural properties evident in the target image (Knez et al 2016). Additional work (Knez et al 2018) augments this technique to accommodate spinal curvature in the trajectory plan. The methods aim to increase purchase within the vertebral body by maximizing overlap of the screw with subchondral bone density (Hounsfield Units, HU) in the CT image. The methods also exercise pre-defined geometric constraints, such as orientation of the screw parallel to the superior endplate. The methods demonstrated close agreement between automatically planned trajectories and manually defined plans, with mean absolute differences (MAD) of (0.4 ± 0.4) mm for screw diameter, (5.8 ± 4.2) mm for screw length, (2.0 ± 1.4) mm for the pedicle cross point, and (7.6° ± 5.8°) for insertion angle.
Another algorithm (Xiaozhao et al 2016) automatically segments vertebral bodies and pedicles and uses similar geometric and structural properties to plan trajectories. The method first identifies the pedicle area and initializes a path in the region, and then solves an optimization problem to adjust the path such that the length of the screw path and the overlap of the screw with image intensities (HU) in the CT image are maximized, which in turn is believed to maximize screw purchase. The methods incorporate several planning guidelines from studies that discuss concepts of optimal trajectory planning, and the authors recognize that definition of optimality may vary from surgeon to surgeon. Planned screw trajectories were shown to be in close agreement with manual definitions and to provide a high degree of screw purchase. Recognizing possible variations in surgeon’s planning preferences, automatically determined trajectory plans may require some adjustment in direction or screw size.
Additional work (Li et al 2017) used a spine landmark detection method in conjunction with multi-atlas vertebral segmentation to segment the target vertebra and create a distance map representing the distance between voxels and the vertebral edge. The algorithm then determines pedicle regions within the vertebra from the segmentation by performing clustering and morphological operations on the distance map. Safe regions are then determined within the pedicle, and similar geometric considerations as described in Knez et al and Xiaozhao et al are incorporated, allowing adjustment according to additional clinical parameters (e.g. patient age, where older patients with lower bone mineral density may require more conservative insertion schemes). The addition of such clinical parameters give the surgeon a degree of control over the otherwise fully automatic plans in a manner that may better reflect unique planning preferences. The large number of (often qualitative) clinical parameters present a challenge to the planning algorithm, since the parameters considered to be relevant may vary based on the surgeon’s experience.
The algorithm reported below is based on the method reported by Goerres et al (2017), using an atlas of vertebral shapes and reference trajectories as a basis for definition of trajectories in a patient’s CT image. As with other atlas-based approaches, the atlas defines vertebral shape models based on normal vertebral body morphology, which is reasonable in that the vertebrae receiving pedicle screws are relatively normal (i.e. not fractured, degenerative, or deformed). Moreover, the reference trajectories defined in the atlas can be adjusted to reflect patterns of biomechanically optimal constructs and a surgeon’s individual planning preferences.
The methods and experiments detailed below are distinct in several respects from those in initial studies in Goerres et al (2017). First, the ASM registration is performed without segmentation of the patient CT (whereas the previous work required segmentation of the target vertebrae). The atlas reported below involves a greater number of members (Nmember = 40, compared to Nmember = 20 in previous work) and spans a larger number of vertebrae (the complete lumbar spine, Nlevel = 5, compared to Nlevel = 3 isolated vertebrae in previous work). The trajectory planning method has also been modified to improve runtime and reduce sensitivity to parameter selection. We also describe a method to automatically define the screw diameter and length. The algorithm is tested for the first time in intraoperative cone-beam CT (CBCT, whereas previous work used diagnostic-quality CT) and as a function of dose in low-dose CBCT.
2. Methods
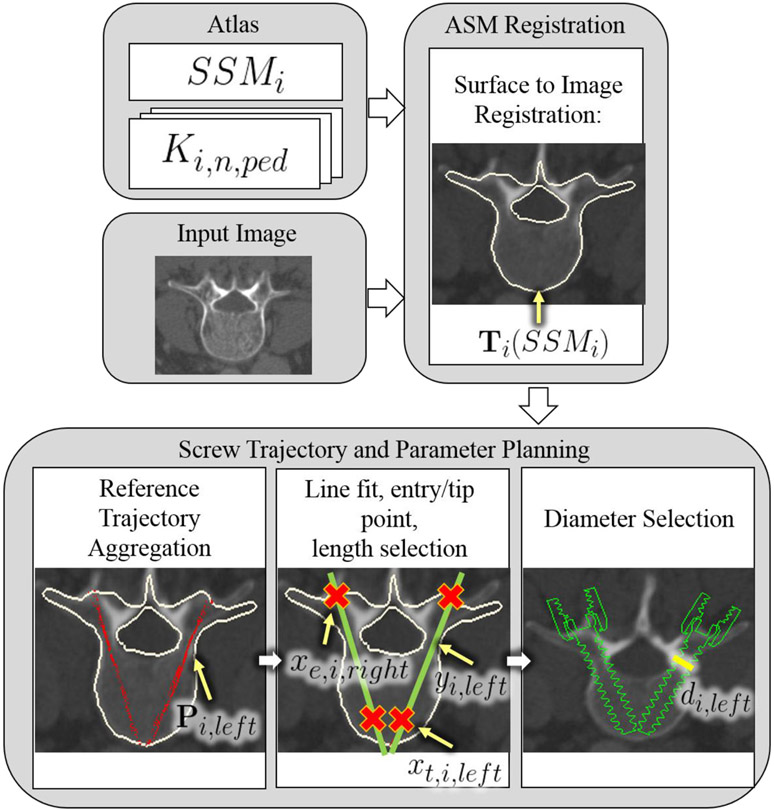
An overview of the method for automatic planning of screw trajectory, length, and diameter in unsegmented CT images is shown in figure 1 and summarized in table 1. The algorithm uses two co-registered atlases: an anatomical atlas; and a trajectory atlas. The anatomical atlas is in the form of statistical shape models (SSMs) with a unique SSM for each vertebral level. The trajectory atlas contains expert definitions of bilateral, transpedicle trajectories. With the patient CT (‘target image’) as input, the algorithm registers the SSMs for each vertebral target using a surface-to-image ASM registration method. Using the resulting transformation, each member of the trajectory atlas is then transformed onto each target level and aggregated. A line fit to the aggregated point cloud defines the trajectory. The intersection of the line fit and the registered SSM is used to determine the screw entry point and length, and the distances from the line to the cortical walls of the pedicle are used to determine screw diameter.
Figure 1.
Illustration of the automatic trajectory planning algorithm. Terms are defined in table 1.
Table 1.
Summary of variables and notation.
| Variable | Description |
|---|---|
| i ∈ [1, 5] | Vertebral level index (L1–L5) |
| n ∈ [1, 40] | Atlas member index |
| ped = {left, right} | Pedicle side |
| SSMi | SSM for vertebral level i |
| Ki,n,ped | Atlas trajectory for vertebral level i, atlas member n, and side ped |
| Ti | Resulting transformation from ASM registration for vertebral level i |
| P i,ped | Aggregated point cloud of atlas trajectories for vertebral level i, side ped |
| yi,ped | Trajectory centerline fit for vertebral level i, side ped |
| xe,i,ped | Location of planned screw entry point (e) for vertebral level i, side ped |
| xt,i,ped | Location of planned screw tip point (t) for vertebral level i, side ped |
| di,ped | Planned screw diameter for vertebral level i, side ped |
2.1. Anatomical atlas (SSMs)
CT images from 40 patients were acquired from the cancer image archives (TCIA) (N = 20), (Roth et al 2014), Spineweb (N = 10) (Jianhua et al 2016), and an IRB-approved retrospective study (N = 10) of patients undergoing spine surgery at our institution. The average voxel spacing was 0.6 × 0.6 × 1 mm, with a range of 0.28 mm to 0.98 mm axial voxel size and from 0.5 mm to 2.5 mm slice thickness. All images were resampled with bilinear interpolation to 0.5 mm isotropic voxel spacing. To build the anatomical atlas, the lumbar spine in each image was manually segmented to provide a basis for generating surface meshes for SSM calculation. Manual segmentation was the preferred method in this work (see, automatic segmentation), since it is accurate, does not add to registration runtime (i.e. was performed once offline simply to generate the atlas), and provided reliable ‘ground-truth’ definition for analysis of registration accuracy. Surface meshes were then generated for each vertebra. All vertebral meshes were resampled to 4000 vertices, which was sufficiently fine (~0.5–1.0 mm spacing between vertices) to capture vertebral shape variations. For each vertebral level (L1–L5), coherent point drift deformable point-set registration (Myronenko et al 2010) established correspondence between an arbitrarily designated template mesh and the remaining meshes in the atlas. Generalized Procrustes analysis (Gower et al 1975) then superimposed the meshes to a common coordinate frame after correcting any misalignment due to translation, rotation, and scale. Principal component analysis (PCA) was performed on the aligned meshes to generate statistical shape models (SSMi, i = 1, 2, 3, 4, 5) separately for each vertebra using the Statismo software package (Lüthi et al 2012). The statistical shape model can be represented as:
| (1) |
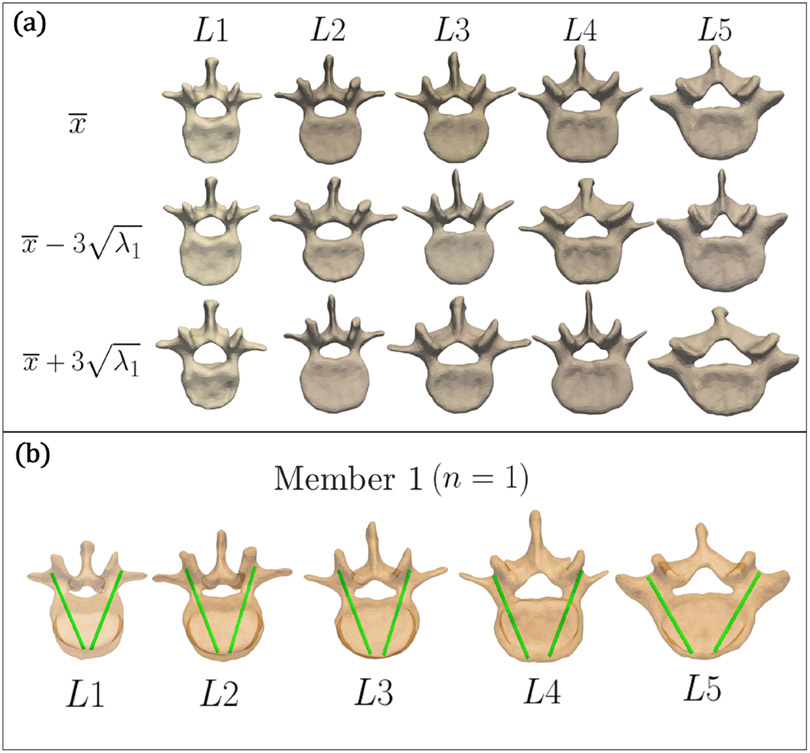
where x is the generated shape, is the mean shape, P contains the eigenvectors of the covariance matrix (representing the principal modes of shape variation) and b is a set of weight parameters (Cootes et al 1994). The eigenvalues, λi, represent the variance of each element in b. Thus, by limiting the values of bi to within , the generated shape x is reasonably within the scope of variation observed in the training data set. Figure 2(a) shows the SSMs developed for L1–L5, with visualizations of the mean shape () and the SSM deformed ±3 standard deviations from the mean shape along the first principal component.
Figure 2.
(a) Illustration of the anatomical atlas. Mean shape for SSMs L1–L5 (top row) and deformation ±3 standard deviations from the mean shape along the first principal component (second and third row). (b) Illustration of the trajectory atlas. Visualizations of reference trajectories in the first member of the atlas (n = 1), for L1–L5.
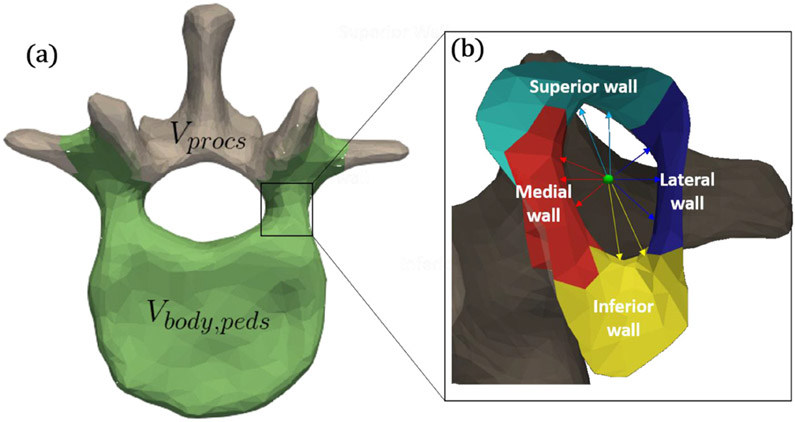
As shown in figure 3(a), multiple anatomical sub-components were defined within each SSM by manually selecting vertices on the SSM mean-shape mesh and assigning a label to them. Specifically, vertices belonging to the vertebral body and pedicles (denoted Vbody,peds) were distinguished from those belonging to the spinous processes (denoted Vprocs). The body and pedicle vertices, Vbody,peds, consisted of all vertices anterior to (but not including) the transverse processes of both sides, the region containing the pars interarticularis (extending both superiorly and inferiorly around the transverse process towards the pedicle), and the region lateral to the mamillary process, The process vertices Vprocs, consisted of all other vertices. To improve the performance of ASM registration within regions containing the screw (i.e. Vbody,peds), the Vprocs vertices were not used in the shape deformation and regularization steps of ASM registration, as discussed in section 2.2.2. Within the region of the pedicle, vertices belonging to the medial, lateral, superior, and inferior regions of the pedicle corridor were also defined in each SSM (figure 3(b)) and were used as a basis for determining screw diameter, as described below.
Figure 3.
Illustration of components defined within a vertebral level. (a) Vertices belonging to the vertebral body and pedicle distinguished from those of the spinous process (L1 SSM is shown). (b) Sub-components within the pedicle corridor: medial, lateral, superior, and inferior walls (L1 left pedicle is shown). Also shown in (B) are pertinent distances from the centerline (green): medial (dmed,i,ped), lateral (dlat,i,ped), superior (dsup,i,ped), and inferior (dinf,i,ped).
2.2. ASM registration
2.2.1. Initialization
Initialization of the ASM registration uses a single point label (e.g. vertebral centroid) in each level of interest in the patient CT. A variety of methods have been reported to define such points automatically—for example FastSpine (Siemens Healthineers) and machine learning methods (Levine et al 2019). In the work reported below, the vertebral centroids were manually annotated. Registration was initialized by positioning each SSM to align with the corresponding centroid in the target CT. Subsequently, an exhaustive search over a coarse grid of rotation, scaling, and translation was performed to determine a rigid fit for each SSM to maximize overlap in gradient magnitude between the SSM and CT. Rotation ranged from −15° to 15° (1° increments) about each Cartesian axis, scaling ranged from 0.85 to 1.15 (0.05 increments, all uniform scaling), and translation ranged from −1 to 1 mm with (1 mm increments) along each Cartesian axis.
2.2.2. Active shape model (ASM) registration
ASM registration aligns the SSM with the patient CT image as shown in figure 1 without segmentation of the target image. In each ASM registration iteration, a search is performed along the SSM vertex normals (using only vertices Vbody,peds) to identify peaks in the gradient magnitude image, xm, and random sample consensus (RANSAC) adjusts the pose of the SSM. A total of 4000 Procrustes alignments are performed using 20 corresponding vertex samples between the peak points xm and the SSM, and the alignment with the highest gradient image overlap between the SSM and the target image is chosen. This step in the algorithm effectively adjusts the pose of the SSM rigidly to improve gradient magnitude image overlap. After alignment, residuals between the peak points and the pose-adjusted SSM are projected onto the PCA space, and the deformation is computed from PCA coefficients applied in a regularized manner. This process is performed iteratively until convergence, yielding the transformation:
| (2) |
where i denotes the target level (1 to 5, corresponding to L1 to L5 in the current work), Ti is the transformation for the target vertebral level, and SSMi is the SSM for the target level. The target image is denoted I.
The ASM algorithm implementation in this work used a five-level coarse-to-fine hierarchical structure. The convergence criterion for each level was defined in terms of the root-mean-square-difference (RMSD) between consecutive iterations falling below a threshold distance. Once this threshold is reached, the ASM registration proceeds to the next level of the hierarchy. A sensitivity analysis of parameters in the ASM hierarchy was shown in previous work, identifying nominal parameter settings and robust operating points (Vijayan et al 2019), including: the initial search distance along the vertex normals for peaks in the gradient magnitude image (PLinitial); the number of Procrustes alignments performed during pose adjustment (Niter); and the maximum number of principal components used for shape regularization (PCmax). Consistent with that sensitivity analysis, we selected PLinitial = 4 mm, Niter = 4000, and PCmax = 8 components.
2.3. Trajectory atlas
Each vertebra was manually annotated with bilateral transpedicle trajectories by a spinal neurosurgeon with >20 years of experience. Specifically, a trajectory annotation was defined by a line between a designated entry point (at the posterior aspect of the vertebra) and a tip point located at the anterior cortex of the vertebral body. The trajectory line is denoted as Ki,n,ped, where i is the vertebral level, n is the atlas member, and ped is the pedicle (left or right).
The trajectory atlas reflects the neurosurgeon’s planning preferences and incorporates numerous quantitative and qualitative planning criteria for pedicle screw placement. It encapsulates experiential considerations in path planning implicit in surgical approach—for example, consideration of the accessibility of the entry point, or achieving greater purchase by slight lateral offset, or modifying the attitude of the screw within the vertebral body to increase screw purchase. The method thus does not necessarily aim to achieve the ‘center’ of the pedicle (exercising considerations beyond geometry as reflected in the trajectory atlas), and in the current work, it does not seek to maximize overlap in image intensity (a surrogate for bone density, as in Schreiber et al (2011)), although the potential value of such overlap is recognized. An example of annotated trajectories is shown in figure 2(b) for the first member of atlas.
2.4. Trajectory planning
2.4.1. Calculation of trans-pedicle trajectory
Following ASM registration, the atlas of reference trajectories for each target vertebral level is transformed to the target CT using the ASM transformation result. For each target vertebral level, and each pedicle (left and right), each reference trajectory is uniformly sampled along the line between the entry point and tip point to generate 50 points along the trajectory. The mean value coordinates (MVC) method is used to interpolate the deformation field from Ti along the length of the reference trajectory to transform the reference trajectory points to the target image. Each transformed trajectory is aggregated into a 3D point cloud in the patient CT image space:
| (3) |
where Pi,ped is the point cloud for vertebral level i and target pedicle ped (left or right). A linear trajectory yi,ped is determined by fitting a straight line to the point cloud:
| (4) |
This is a distinction from the method described in previous work (Goerres et al 2017), which generated cylinders for each reference trajectory, transformed each cylinder using MVC, added binarized images of each transformed cylinder into an ‘accumulation map’, and performed a rigid intensity-based registration of a straight binary cylindrical trajectory to the accumulation map to compute a trajectory line. That method required several parameters for determining the resolution of the accumulation map and for registration optimization, and consequently required parameter tuning. Additionally, it carried higher computational requirements for generating the accumulation map, including binning atlas trajectories into images, and accumulating these images, leading to costlier runtime. The method reported here achieves the trajectory definition result without these parameter tuning requirements at a lower computational cost, since trajectories are accumulated in 3D space without binning and accumulation of images.
2.4.2. Calculation of screw length
After a trajectory has been computed, the entry point xe,i,ped and tip of the trajectory xt,i,ped are determined by calculating the intersection of the linear trajectory with the registered SSM mesh using an OBBtree ray-triangle intersection algorithm (Gottschalk et al 1996), giving:
| (5) |
where is the intersection of the trajectory with the anterior aspect of the vertebral body, and xe,i,ped is the intersection of the trajectory with the posterior of the vertebra. Keeping xe,i,ped fixed, xt,i,ped is then calculated such that the length of the screw (distance from entry point to tip point) is rounded down to the nearest 5 mm:
| (6) |
| (7) |
noting that commercially available screws typically vary in length increments of 5 mm. Equation (7) includes a ‘safety margin’ via the floor operation, rounding the screw length down to the nearest 5 mm. This allows for potential registration error of the vertebral body, especially in the anterior-most aspect.
2.4.3. Calculation of screw diameter
Following the length calculation, the distances between the linear trajectory and the medial, lateral, superior, and inferior regions of the pedicle cortical wall of the SSM are calculated. As illustrated in figure 3(b), the maximum screw diameter was computed from these distributions of distances as:
| (8a) |
| (8b) |
| (8c) |
| (8d) |
| (8e) |
where min and med are the minimum and median operators, respectively on the distributions dX, representing the distance from the linear trajectory to cortex ‘X’ for each pedicle in each target vertebral level. Note that the min operator is invoked with respect to dmed, whereas the med is used for dlat, dsup, and dinf, reflecting the distinction among breaches of medial, lateral, superior, and inferior cortex. Specifically, medial breaches are considered unacceptable due to proximity to the spinal dura, whereas lateral, superior, and inferior breaches are considered acceptable within 2 mm (Grades A and B according to the Gertzbein–Robbins classification scale (Gertzbein et al 1990): 0 mm (Grade A); 0–2 mm (Grade B); 2–4 mm (Grade C); 4–6 mm (Grade D), and >6 mm (Grade E). A robust variation of the min operator (viz., the average over the lower decile of the distribution) was implemented to avoid outliers and noise in the ASM registration. The resulting diameter di,ped was rounded down to the nearest 0.5 mm.
2.5. Performance evaluation
2.5.1. Atlas size and member selection
To examine the sensitivity of ASM registration to the number of atlas members used to build the SSMs, 30 L1 SSMs were generated with atlas size ranging from 10 to 39 members—in each case with members randomly selected from 39 cases from the N = 40 dataset. The left-out case was chosen as a ‘test image’ (an L1 vertebra with mean shape similar to that of the original N = 40 L1 SSM). Each of the 30 SSMs were registered to the test image a total of 20 times each to include stochastic variations in the ASM algorithm.
Additionally, the effect of SSM member composition on ASM registration accuracy was examined. From 39 cases taken from the N = 40 dataset, 100 groups of N = 20 were randomly selected, and an SSM was generated for each group. Each SSM was then registered to the L1 vertebra of the test image (which was the same test image used in the atlas size experiment), and the RMSE was calculated for each.
2.5.2. Leave-one-out analysis
The performance of the planning algorithm was evaluated using leave-one-out analysis of trajectory plans over each case in the atlas, giving a total of (40 cases) × (5 vertebrae) × (2 bilateral) = 400 trajectories. The accuracy of ASM registration was evaluated for each case in terms of the RMSE distance between the registered and true vertebral surface (generated from the manual segmentations performed for the SSM member dataset), using only Vbody,peds in the calculation.
The entry point difference and angular difference between each planned trajectory and its corresponding atlas trajectory was calculated to determine the similarity between the planned trajectory and the trajectory as defined by the surgeon in the atlas trajectory. Note that this analysis does not consider that the planned trajectory may still be acceptable even with significant deviation from the surgeon’s original plan—i.e. surgeons may choose to plan the same case using different but equally acceptable approaches; therefore, limiting the analysis of planned trajectories to comparisons with atlas trajectories does not consider such variability. The acceptability of planned trajectories was also evaluated in terms of the conformance of the planned trajectory and screw within bone—i.e. absence of breach. The distance between the planned trajectory centerline and the pedicle cortex was measured as a function of distance along the length of each trajectory. The planned screw diameters and lengths were compared to typical screw sizes available in clinical practice for adult lumbar spine fixation procedures. In addition, the distance from the edge of the screw to the cortex was measured, with negative values indicating breach. These breaches were additionally classified according to the Gertzbein–Robbins scale.
2.5.3. Performance in CBCT
To assess the performance of the algorithm for automatic planning in CBCT, five images were acquired containing L3–L5 under an IRB-approved protocol for offline analysis of CBCT images acquired with the O2 O-arm (Medtronic, Minneapolis MN) using standard clinical imaging techniques. Manual segmentations were performed in order to provide a ground-truth reference for ASM registration accuracy calculations. Bilateral trajectories were planned in each image for each vertebra, giving a total of (5 cases) × (3 vertebrae) × (2 bilateral) = 30 trajectories. The acceptability of the trajectories was evaluated using the same criteria established in the leave-one-out analysis in 2.5.1.
2.5.4. Performance in low-dose CBCT
Additionally, the performance of the algorithm was evaluated in low-dose CBCT. For one of the cases in the study in 2.5.2, three additional simulated low-dose CBCT images were generated using a noise injection method (Wang et al 2014). The noise injection method generates a simulated low-dose CBCT image by injecting quantum and electronics noise in the CBCT scan data acquired at a nominal clinical dose. The noise injection corresponds to both magnitude and correlation of noise exhibited in a CBCT images acquired at lower dose levels, as previously reported in Wang et al (2014) and Zhang et al (2019). The dose level associated with CBCT images acquired at nominal clinical dose is denoted Dfull, and the simulated low-dose levels are denoted Dsim. Bilateral trajectories were planned in each image for each vertebra, giving a total of (1 case) × (4 images with different dose levels, including the nominal clinical dose level) × (3 vertebrae) × (2 bilateral) = 24 trajectories. The nominal clinical dose (Dfull) was 32.7 mGy (372.5 mAs), with low-dose simulations (Dsim) of 3.3 mGy (37.5 mAs), 6.5 mGy (75.0 mAs), and 16.4 mGy (186.0 mAs). The accuracy of ASM registration was evaluated for each image in terms of the RMSE distance between the registered and true vertebral surface, using only Vbody,peds in the calculation, and plotted against dose level. The distance between corresponding planned trajectory centerlines and the pedicle cortex was measured as a function of distance along the length of each trajectory. Additionally, the chosen screws lengths and diameters are reported for each dose level.
3. Results
3.1. Atlas size and member selection
3.1.1. Effect of atlas size on ASM registration accuracy
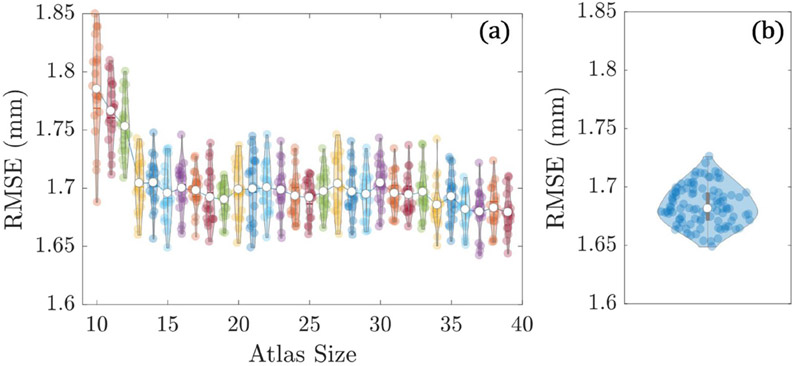
Figure 4(a) shows the effect atlas size on registration accuracy. The RMSE appears to stabilize for N > 20, with only marginal improvement for larger atlas size. A slight reduction in RMSE and variance in distributions is suggested above N ~ 35 members. The N = 40 atlas (and N = 39 for the leave-one-out study) was therefore used, providing the lowest average RMSE value of all tested atlas sizes.
Figure 4.
Effect of atlas size and membership on registration accuracy. (a) Registration RMSE for atlases ranging from 10 to 39 members.
3.1.2. Effect of atlas member selection on ASM registration accuracy
Figure 4(b) shows the RMSE of each registration, for all 100 SSMs. The average RMSE across all groups was 1.68 ± 0.02 mm, indicating that despite random variations in SSM atlas member selection, the SSMs are registering to the target image with high precision.
3.2. Leave one out study
3.2.1. ASM registration accuracy
The algorithm successfully registered cases in 191/200 cases as summarized below. Outliers were observed in 9/200 cases due to poor image quality in the target CT (thick slices and/or high noise) and anatomical variation (specifically, lumbosacral transition vertebrae in 2/200 cases). These outliers resulted in a transformation by which the SSM centroid was outside the target vertebral body, presenting a conspicuous failure mode. Such outliers were not included in subsequent analysis. For the successful registrations, the RMSE between surfaces was calculated using the vertebral body and pedicle vertices of the registered SSM (Vbody,peds).
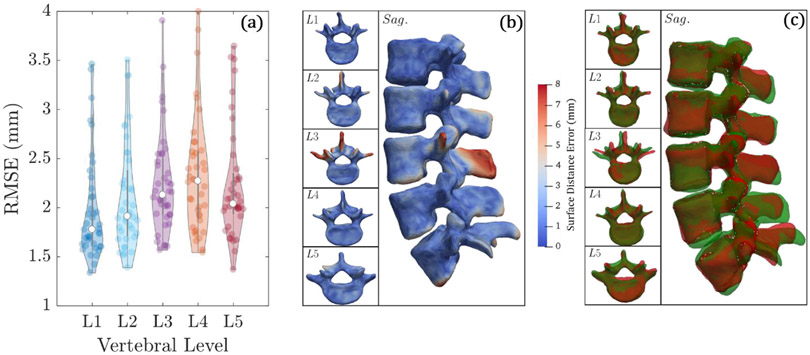
The average RMSE after centroid-based initialization of the SSMs was 2.3 ± 0.5 mm. The average RMSE after ASM registration was 2.0 ± 0.5 mm, indicating improved alignment of the SSM with the target CT. Figure 5(a) shows violin plots of the RMSE for L1–L5, showing reasonable performance across all vertebral levels. Figures 5(b) and (c) show an example ASM registration reflecting the median performance. Since the ASM registration is driven by the Vbody,peds components, the method yields high accuracy registration for the vertebral body and pedicles and allows a higher surface distance error in Vprocs. For comparison, ASM registration was also performed without separating the SSM vertices (i.e. ASM registration using Vbody,peds + Vprocs), and the average RMSE after registration was 2.2 ± 1.1 mm (RMSE calculated using only Vbody,peds). The result shows that disregarding the process vertices does not diminish the trajectory planning process, since they are not pertinent anatomical regions for the planned trajectories.
Figure 5.
Accuracy of ASM registration in the leave-one study over 40 (unsegmented) CT images. (a) Violin plots of average RMSE for each vertebral level. (b) Surface rendering of the surface distance error for each vertebral level. (c) Surface overlays for true vertebral surface (green) and registered surface (red).
3.2.2. Trajectory centerline conformance
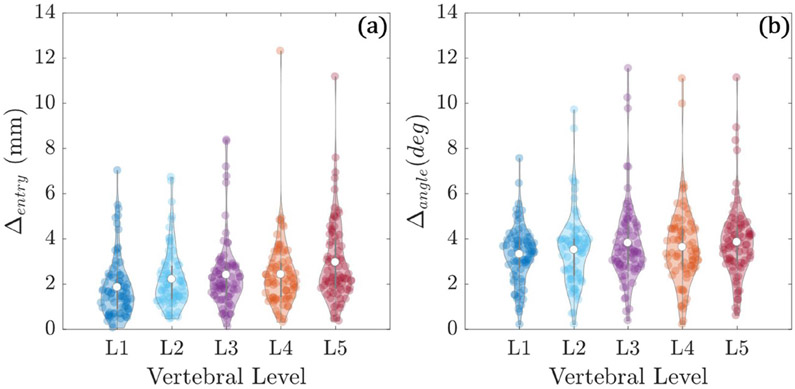
Figure 6 shows the trajectory centerline differences between planned trajectories and their corresponding surgeon-defined atlas trajectories. The distributions reflect differences from 382 cases (191 left pedicle and 191 right pedicle). The entry point differences were 2.4 ± 1.6 mm with a range of 0.05 mm to 12.3 mm. The average angular difference was 3.6° ± 0.8°, with a range of 0.2° to 11.54°. The results suggest reasonable agreement between the planned trajectories and their corresponding atlas trajectories as designated by the surgeon, noting that some degree of intra-operator variability exists (not quantified in the current work).
Figure 6.
Trajectory centerline differences between automatically planned trajectories and atlas definitions. (a) Entry point differences (in mm). (b) Angular differences (in degrees).
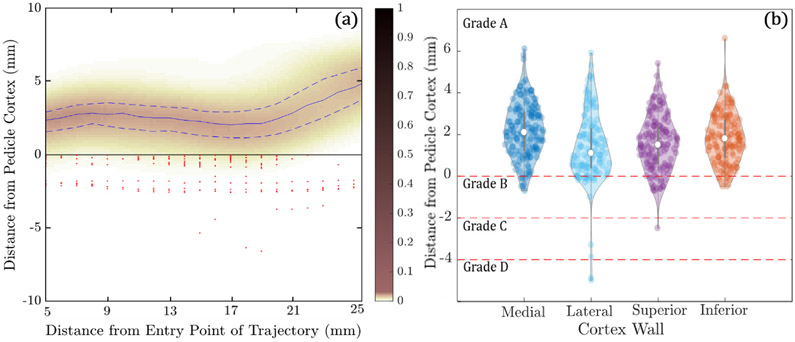
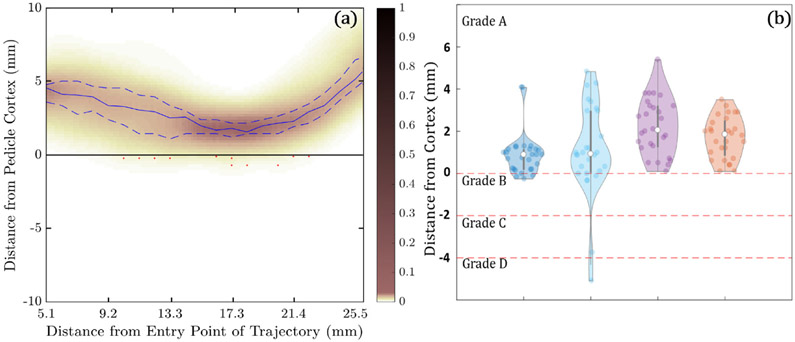
Figure 7(a) shows the minimum distance between the planned trajectory and the pedicle wall computed as a function of distance along the trajectory through the narrowest region of the pedicle (5–26 mm diameter). The heat map reflects the distance distribution along the length of the trajectory in 382 cases (191 left pedicle and 191 right pedicle) with median values indicated by the solid blue line, interquartile ranges represented by the dashed blue lines, and red markers indicating breach. With few exceptions, the trajectories are seen to reside within bone corridors, with 94.7% (362/382) of trajectories not breaching the corridor (Grade A), 4.2% (16/382) suggesting Grade B breach (<2 mm), 0.3% (1/382) Grade C (<4 mm), 0.5% (2/382) Grade D (<6 mm), and 0.3% (1/382) Grade E (>6 mm). The analysis shown here does not distinguish between actual breach and false positives/negatives owing to noise in the truth definition (segmentation error).
Figure 7.
Conformance of automatically defined trajectory centerlines and screw plans within bone corridors in the leave-one-out study over 40 cases. (a) Heatmap probability distribution of the distance of the planned trajectory centerlines to the pedicle cortex as a function of distance along the trajectory. The solid blue line indicates the median distance, and the dashed blue lines indicate the interquartile range. Red markers indicate breaches of the cortical wall. (b) Violin plots of the minimum distance of planned screws to the medial, lateral, superior, and inferior cortical walls, along with GB classifications.
3.2.3. Planned screw conformance
For each trajectory computed, the algorithm reports maximum screw diameter and length rounded down to the nearest 0.5 mm and 5 mm, respectively. The median planned screw diameter in the leave-one-out study was 6 mm (range 4–10 mm diameter). The median screw length was 45 mm (range 30–65 mm). These values are comparable to the maximum screw diameter and screw length reported in Takeshita et al (2009) for 1100 pedicles in CT images. In that study, the average maximum screw diameter for the lumbar spine was 7.1 ± 1.6 mm, with a range of 2.6–11.5 mm, while the average maximum screw length was 44.2 ± 4.3 mm, with a range of 32.8–59.1 mm.
Figure 7(b) shows the minimum distance (along the entire length of the trajectory) between the edge of the planned screw (see, the trajectory centerline as in figure 7(a)) and the medial, lateral, superior, and inferior pedicle cortex, for all trajectories with no centerline breach (N = 362). Trajectory centerlines that breached the cortex were not included in figure 7(b) or the accompanying analysis, thereby showing the frequency with which acceptable centerline trajectories (i.e. within the pedicle cortex) might breach by way of the selected screw diameter. In other words, if a centerline was found to breach, then the resulting screw plan would also breach. Note that centerline breaches can be automatically detected by intersection with the SSM segmentation, prompting the user to intervene. The analysis of planned screw conformance was therefore limited to acceptable (non-breaching) centerlines. A negative value indicates cortical breach by the screw. Of all planned screws, 86.7% had no breach (Grade A), 11.9% (43/362) had calculated diameters that caused a Grade B breach (<2 mm), 0.8% (3/362) caused a Grade C breach (<4 mm), 0.6% (2/362) caused a Grade D breach (<6 mm), and there were no Grade E breaches. None of the medial breaches exceeded Grade B, reflecting the tendency imparted by surgeon preferences established in the trajectory atlas—viz., a tendency to lateralize the screw for improved cortical purchase.
The distributions indicated a slight (but systematic) underestimation in screw diameter compared to typical clinical patterns, arising from the fairly conservative selection rule of equation (8). Specifically, the average distance between the centerline and medial, lateral, superior, and inferior pedicle cortex was 2.2 mm, 1.4 mm, 1.6 mm, and 1.8 mm, respectively—suggesting that there is still room in the pedicle (~1–2 mm to avoid significant breach of the lateral, superior, or inferior walls) for a larger screw than what was prescribed using equation (8). This idea is further supported from the results mentioned above (median of 6 mm for planned screw diameters versus average of 7.1 mm in the literature). Future work will consider variations in the selection rule in equations (8b)-(8d)—for example, using the upper quartile instead of the median.
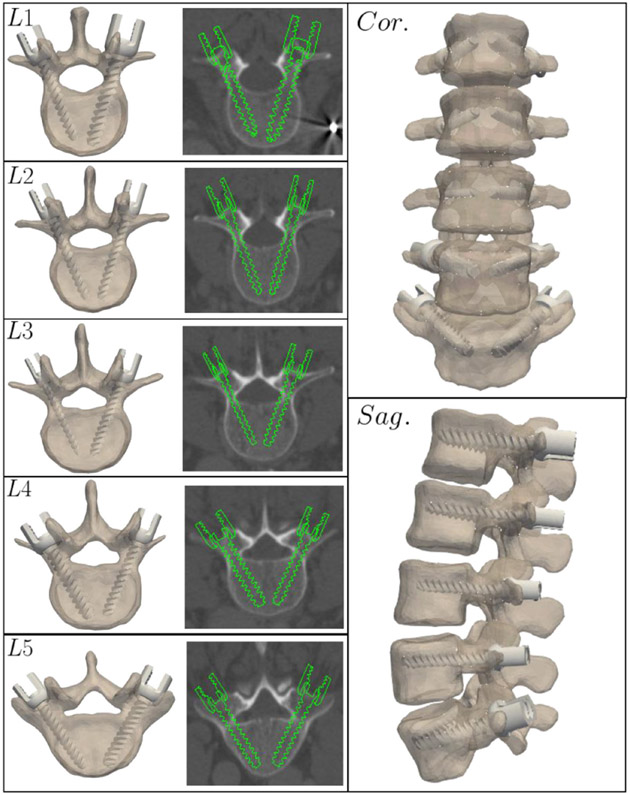
Figure 8 shows an example rendering of a complete trajectory plan for an example case from the leave-one-out study. The algorithm outputs the coordinates of each entry point, trajectory, screw diameter, and length along with a 3D rendering of the screw, facilitating easy interpretation of the result and potential integration with various navigation and robotic surgery software platforms. In a conservative clinical implementation, the algorithm is envisioned as a means of automatic initialization subject to the surgeon’s review, modification, and approval prior to transmitting the plan to the navigation system and robot.
Figure 8.
Automatically determined pedicle screw plans (including 3D trajectory as well as screw diameter and length) for an example case reflecting median performance in the leave-one-out study.
3.3. Cone-beam CT study
3.3.1. ASM registration accuracy
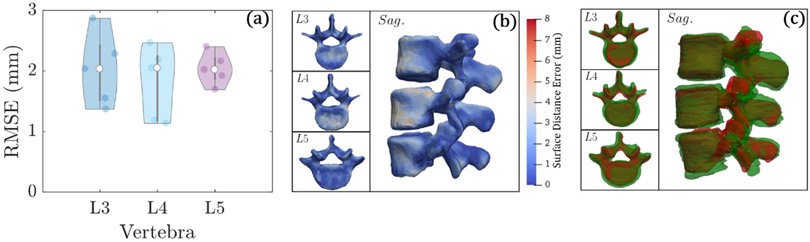
All 5 cases (15 vertebrae) in the CBCT clinical study were successfully registered, as shown in figure 9. The target image (CBCT) was not segmented, and the images reflected realistic image quality in CBCT acquired with standard clinical protocols, including noise, shading, streak, and truncation effects typical of CBCT. The average RMSE after ASM registration was 2.0 ± 0.5 mm. The violin plots of figure 9(a) show similar performance in L3, L4, and L5 in this initial clinical pilot study.
Figure 9.
Accuracy of ASM registration in the CBCT study over 5 (unsegmented) CBCT images. (a) Violin plots of average RMSE for each vertebral level. (b) Surface rendering of the surface distance error for each vertebral level. (c) Surface overlays of the ground truth vertebral surface (green) and registered surface (red).
3.3.2. Trajectory centerline conformance
Figure 10(a) shows the minimum distance between the planned trajectory and the pedicle wall plotted as a function of distance along the trajectory through the narrowest region (5–26 mm) of the pedicle for the CBCT clinical study. The heat map reflects the distance distribution along the length of the trajectory in 30 cases (15 left pedicle and 15 right pedicle (blue)), with median values indicated by the solid blue line, interquartile ranges represented by the dashed blue lines, and red markers indicating breach. The trajectories are seen to reside within bone corridors, with 93.3% (28/30) of trajectories not breaching the corridor (Grade A), and 6.7% (2/30) suggesting Grade B breach (<2 mm). The analysis shown here does not distinguish between actual breach and false positives/negatives owing to noise in the truth definition (segmentation error).
Figure 10.
Conformance of automatically planned trajectory centerlines and screws within bone corridors in the clinical CBCT study. (a) Heatmap probability distribution of the distance of the planned trajectory centerlines to the pedicle cortex as a function of distance along the trajectory. The solid blue line indicates the median distance, and the dashed blue lines indicate the interquartile range. Red markers indicate breaches of the cortical wall. (b) Violin plots of the minimum distance of planned screws to the medial, lateral, superior, and inferior cortical walls, along with GB classifications.
3.3.3. Planned screw conformance
The median planned screw diameter in the CBCT clinical study was 7 mm with a range of 4 to 8 mm. The median screw length was 50 mm with a range of 40–55 mm. These values are similar to sizes reported in Takeshita et al (2009) (diameter = 7.1 ± 1.6 mm, range of 2.6–11.5 mm, length = 44.2 ± 4.3, range of 32.8–59.1 mm).
Figure 10(b) shows the minimum distance (along the entire length of the trajectory) between the edge of the planned screw (see, the trajectory centerline as in figure 10(a)) and the medial, lateral, superior, and inferior pedicle cortex, for all trajectories with no centerline breach (N = 28). Of all planned screws, 21.4% (6/28) had calculated diameters that caused a Grade B breach (<2 mm), 3.6% (1/28) caused a Grade C breach (<4 mm), 3.6% (1/28) caused a Grade D breach (<6 mm), and there were no Grade E breaches in the current study. Of the Grade B breaches, 14.3% (4/28) were medial, and none of the medial breaches exceeded Grade B.
3.4. Low-dose CBCT study
3.4.1. ASM Registration
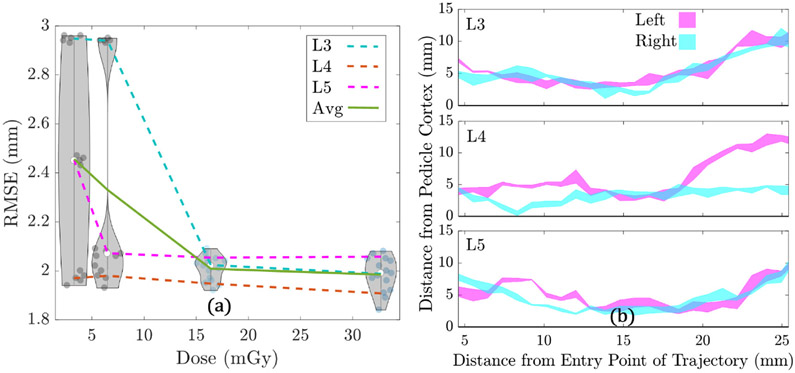
Figure 11(a) shows the RMSE for ASM registration of L3–L5 for the low-dose CBCT study plotted as a function of dose. The average RMSE across all vertebrae (L3–L5) is also plotted as a function of dose. Violin plots are overlaid in figure 11(a) at each dose level, representing the distribution in RMSE across all 3 vertebrae, with 5 runs performed for each vertebra. Recognizing stochasticity in the ASM registration algorithm, the algorithm was run 5 times on the same image, and the RMSE was calculated for each run to determine if there was variability in planning for the same image, especially at lower dose levels. As shown in figure 11(a), at the low dose level Dsim = 3.3 mGy, there are 3 distinct clusters of points corresponding to L3, L4, and L5, suggesting that despite challenges to image quality (stochasticity in the ASM algorithm), the method robustly registered the SSMs with high repeatability. Figure 11(a) also shows that the RMSE of registered surfaces improves and the variability of RMSE across vertebrae generally decreases as the dose level increases, owing to improved image quality. However, the algorithm appears robust at dose levels less than one-third of current clinical scan protocols.
Figure 11.
Automatic planning in low-dose CBCT. (a) RMSE versus dose level for the low-dose CBCT study. Violin plots represent the distributions at each dose level for all 3 vertebrae, with a total of 5 runs performed for each vertebrae (3 vertebrae × 5 runs = 15 total runs). (b) Interval plot for left and right trajectories, for L3–L5, in the low-dose cone-beam CT study. The intervals represent the range of distance profiles across all 4 dose levels.
3.4.2. Trajectory and screw planning
Figure 11(b) shows the range of distances between the planned trajectory and the pedicle wall plotted as a function of distance along the trajectory through the narrowest region of the pedicle (5–26 mm diameter). Each subplot contains a left interval and a right interval, and each interval represents the range of distances to the pedicle cortex for planned trajectories across all 4 dose levels. (Thin intervals suggest that there is little difference in planned trajectory centerlines for each dose level.) The plot shows that across all vertebrae (L3–L5), and for both sides (left and right), the planned trajectories are visibly consistent across dose levels. This furthers the findings of figure 11(a) that the planned trajectories are robust despite variations in ASM registration accuracy.
3.5. Runtime analysis
The trajectory planning algorithm can be divided into 3 main steps: (1) SSM initialization, (2) ASM registration, and (3) trajectory and screw planning. SSM initialization was performed on a GPU (GeForce GTX 780 Ti, Nvidia, Santa Clara, CA) and since an exhaustive search over a coarse grid was performed to determine a transformation with the highest gradient magnitude overlap, the runtime was fairly consistent across all cases. The mean runtime for SSM initialization was 7.2 ± 1.4 s, with a ~2 s GPU initialization runtime and ~0.5 s metric calculation runtime. Remaining runtime was due to CPU-based calculations. Due to the large size of the exhaustive search performed over the coarse grid (~10 000 possible orientations), the GPU provided a ~100 × speedup compared to a CPU implementation for computing the gradient magnitude overlap metric. Thus, the GPU implementation provides an overall speedup of 7–8 × compared to a CPU implementation for SSM initialization.
ASM registration was also performed on a GPU, and convergence for the stochastic algorithm varies somewhat between cases (e.g. due to differences from the mean SSM shape). The mean runtime and standard deviation for ASM registration was 201.7 ± 105.3 s for bilateral screws in five levels (ten trajectories). For the high number of RANSAC iterations used in this algorithm (4000), the GPU provided a 110–120 × speedup compared to a CPU implementation for calculating gradient magnitude overlap. Considering other calculations that do not involve the GPU, the GPU provided an overall speedup of 7–8 × compared to a CPU implementation for ASM registration. Better initialization of the SSM could further improve the runtime of ASM registration.
Trajectory and screw planning involved a line-fitting process through a point cloud and a series of distance calculations between the trajectory and walls of the SSM. As a result, the runtime for trajectory planning was relatively consistent across all cases. The mean runtime for bilateral screw planning in five levels (ten trajectories) was 42.1 ± 2.7 s. During the atlas trajectory transformation process, a set of points along each trajectory was transformed and accumulated to form the point cloud. The number of points affects the runtime, and future improvements could reduce the required density of the point cloud via more robust linear fitting.
The total runtime for the current implementation of the algorithm was 312.1 ± 104.0 s for bilateral screws in five vertebral levels (ten trajectories). The runtime per level for ASM registration was 41.2 ± 39.9 s, and the runtime per trajectory was 4.1 ± 0.8 s. This suggests an achievable runtime of 45.3 ± 39.9 s for a more fully parallelized implementation in which each SSM is registered independently and in parallel, and afterwards, each trajectory is computed independently and in parallel. While no studies (to our knowledge) have been reported regarding the length of time for manual trajectory planning of pedicle screw trajectories, observations of robotic-assisted surgeries at our institution (Globus Excelsius planning interface) indicated that manual trajectory definition requires ~30–60 s per trajectory. For a five-level lumbar fixation procedure, such as the one performed in the leave-one-out studies in this work, this results in ~300–600 s for all ten trajectories. Therefore, with further parallelization the algorithm could reduce the time required to plan screw trajectories in intraoperative CBCT and improve quality by reducing spurious intra- or inter-operator variability.
4. Discussion and conclusions
An algorithm for automatic planning of spinal pedicle screw placement was presented and evaluated, extending the method reported by Goerres et al (2017) to operate without segmentation of the patient CT and to define screw length and diameter. The atlas of vertebrae and pedicle trajectories was extended to cover the full lumbar spine, applied for the first time in clinical data for patients undergoing CBCT-guided spine surgery, and evaluated in simulated low-dose CBCT (i.e. artificially generated low-dose CBCT images using a previously validated noise injection method). The atlas of reference trajectories allows surgeon preferences to be reflected within the reference set—e.g. preferences on entry point (giving better alignment of the screw heads with spinal rods), lateralization (option for increased purchase in lateral cortex), and attitude (e.g. screw placement parallel to vertebral endplates or maximal linear extent within the vertebral body for increased pullout strength).
The leave-one-out study over 40 cases (×5 levels ×2 pedicles = 400 trajectories) demonstrated acceptable plans in ~95% of trajectories (382/400), with outliers attributed primarily to poor CT image quality (high noise or thick slices). Pedicle trajectories conformed within bone corridors (i.e. absence of breach, excluding outliers mentioned above) in 94.8% of trajectories (362/382) and reflected biomechanical rationale and surgical preferences intrinsic to the atlas. The planned trajectories were also similar to the atlas trajectories defined by the surgeon, with an average entry point difference ~2.5 mm and average angular difference of ~3.5°. The predicted screw lengths and diameters were similar to common screw sizes in the adult lumbar spine and were similarly conformal within bone corridors in ~99% of trajectories (357/362 with GR Grade A breach <0–2 mm).
The method was evaluated for the first time in a clinical study of patients undergoing CBCT-guided spine surgery (five patients, three vertebrae, for a total of 30 trajectories), demonstrating the robustness of the algorithm in images exhibiting realistic levels of noise and artifact. The method yielded acceptable pedicle screw trajectories in ~93% of trajectories (28/30) and similarly conformant screw lengths and diameters. Outliers were attributed to poor CBCT image quality (high noise and streak artifacts).
The method exhibited similar performance in clinical CBCT images modified to simulate low-dose imaging protocols. Planned trajectories showed minimal variability over the range of dose levels investigated in this study (down to Dsim = 3.3 mGy, compared to Dfull = 32.7 mGy for standard clinical protocol), demonstrating that the algorithm has some level of robustness to increases in quantum and electronics noise associated with lower-dose imaging. Such robustness is attributed to the use of a gradient-based objective function and RANSAC sampling. However, the algorithm may not be similarly robust to outlier images with spuriously high levels of streak artifacts. Moreover, the method showed that screw trajectories were fairly robust against errors in anatomical registration due to the accumulation and regression over the entire atlas of registered trajectory centerlines.
The work here adds to a body of literature on automatic spine planning, including (Knez et al 2016, 2018, Xiaozhao et al 2016, Li et al 2017). The methods vary in the technique by which the pedicle region is identified, including parametric modeling, image segmentation and clustering/morphological operations, and the ASM method as reported above. There are similarly a variety of techniques to determine a trajectory plan, including geometric constraints, biomechanical constraints, and the atlas-based aggregation method reported in this work. All of these methods have demonstrated performance that is potentially suitable to clinical use, though direct, quantitative comparison among methods is challenged by a lack of standard methodology or figures of merit reported. However, all of these methods appear to perform well, with certain benefits associated with certain algorithm design choices. Parametric modeling techniques (Knez et al 2016, 2018) offer the ability to model anatomical deformities and abnormalities by simply introducing new parameters, whereas SSM-based methods must have a large number of atlas members representative of such deformities to provide a reliable mode of variation in principal component analysis. Such methods also use image features (such as HU) as a surrogate for bone mineral density to increase screw purchase and pullout strength (Xiaozhao et al 2016). The SSM, atlas-based method presented in this work offers a variety of potential advances and/or advantages. One is the ability of the surgeon to reflect patterns of biomechanically optimal constructs and his/her own planning preferences in the trajectory atlas, which results in an atlas that may reflect factors beyond typical geometric and biomechanical considerations. Additionally, the method is generalizable to other surgical planning applications operating on the same underlying principle of a statistical atlas of anatomical shape complemented by an atlas of trajectories therein. For example, an analogous method was shown for automatic planning in pelvic trauma surgery (Han et al 2018), where SSMs of the pertinent anatomy (in this case, the pelvis) were constructed, and trajectories (in this case, k-wire trajectories) were annotated in the atlas. The method presented in this work also offers a relatively fast computation time (45.3 ± 39.9 s) for a one-level, unilateral trajectory, compared to previously reported runtimes for the same plan of ~140 s (Knez et al 2016), recognizing that each could benefit from further parallelization and acceleration.
The method is subject to a variety of limitations and factors that remain to be fully addressed to support translation to routine clinical use. In the current work, initialization of the ASM registration used manually labeled vertebral centroids. While manual labels were fairly quick and easy to define, a more fully automatic workflow under development in ongoing work invokes automatic centroid definition—e.g. the FastSpine method (Siemens Healthineers) or a machine learning method (e.g. Levine et al (2019)). A small number of outliers observed in ASM registration were primarily related to poor image quality in preoperative CT, and routine clinical use would benefit from more standardized control/QA of the imaging protocols in preoperative imaging—for example, slice thickness no greater than ~1.0—1.5 mm. Alternatively, intraoperative CBCT (which typically achieves isotropic spatial resolution better than 1.0 mm) was found to provide a reliable basis for planning. Further investigation is warranted to improve the criteria for screw diameter selection. In the current work, screw diameter was selected based on the minimum/median criteria of equation (7) rounded down to the nearest 0.5 mm, which is likely a conservative choice (i.e. biased low in diameter selection). There was also no constraint or regularization for bilateral symmetry in screw selection between left and right pedicles. Rather, each screw was planned independently and did not reflect common practice of bilaterally symmetric screws. Future work will investigate methods to regularize the estimation of screw diameter and length, considering both pedicles and adjacent vertebrae.
Another potential improvement is to plan screws in a manner that considers the number of screws and vertebral levels comprising the overall surgical product—rather than planning each screw independently in isolation. For example, optimal screw trajectories within a two-level fusion may differ from those in a three-, four-, or five-level fusion. A brute force solution to this consideration may reside in the trajectory atlas approach—e.g. a separate trajectory atlas for constructs of various extent.
An investigation of the effect of atlas size and member selection was reported in this work, showing that an atlas size of N = 40 was suitable to the registration task. The effect of member selection was investigated by performing registrations based on randomly selected subgroup SSMs (of N = 20 members each), showing that atlas member selection did not have substantial influence on registration accuracy in the current study. However, it is certainly possible that registration accuracy could be improved using a more targeted, statistically motivated selection process that uses features or statistical properties to identify optimal atlas membership. For instance, multi-atlas brain segmentation algorithms have been reported using image similarity between atlas members and the target image (Aljabar et al 2009, Zaffino et al 2018) to choose more optimal atlas subsets for segmentation, showing improved performance over non-selective atlases. Similarly, principal component analysis of shape similarity could be used to identify subtypes/clusters within the population of atlas members used to generate an SSM (Ramsay et al 2018). By choosing members that have similar shape features and identifying a common underlying characteristic for this cluster, a particular cluster can be used to generate an SSM that registers with improved accuracy compared to an SSM computed from an atlas of equal size but indiscriminate shape. Such studies suggest that the algorithm reported above may benefit from statistically targeted atlas member selection.
The algorithm was automated insofar as it generated trajectory plans for all vertebral levels in the input CT (or CBCT) for which a vertebral label (‘centroid’ position) was provided. Given the vertebral label points as initialization, the algorithm ran with the runtimes described above (e.g. 312.1 ± 104.0 s for five-level bilateral planning, potentially reduced to a total of 45.3 ± 39.9 s with improved parallelization). The algorithm did not presume to plan which vertebrae should be instrumented for a given pathology; rather, it merely computed trajectories for all labeled vertebrae in the input CT. Recognizing the potential for outliers (registration failures) and patient-specific variations (e.g. unusual pedicle morphology or low bone density) that may not be reflected in the trajectory atlas, the output of the algorithm may be conservatively viewed as an initialization of the plan, subject to refinement and approval by the surgeon.
The method may also provide a new component of operating room quality assurance (ORQA) (Uneri et al 2016) for assessing the quality of screw placement near the end of a case. For example, the true screw positions could be determined by (low-dose) intraoperative CBCT or 3D–2D registration (e.g. the KC-Reg method in Uneri et al (2015)), and the discrepancy between planned and delivered trajectory could form a quality check on each screw. Action levels for revision are yet to be determined and warrant clinical studies to inform what level of revision is likely to provide clinical benefit.
In related work, the algorithm is being used to define reference trajectories in support of retrospective analysis of large spine surgery image datasets. Specifically, reference trajectories defined in preoperative image data are compared to the position of screws evident in postoperative data, and differences between the two are analyzed as a potential factor underlying variability in surgical outcome. The method forms one component of a larger image-analytic framework called SpineCloud (De Silva et al 2019) that combines automatically determined, image-based features with patient demographic data as input to predictive models on surgical outcome. The ability to automatically define reference trajectories in large retrospective datasets provides a useful tool in support of such data intensive methods.
Acknowledgments
The work was supported by NIH Grant R01-EB-017226. Thanks to Felicia Wang (Biomedical Engineering, Johns Hopkins University) for collection and segmentation of CT images used in this work.
References
- Aljabar P et al. 2009. Multi-atlas based segmentation of brain images: atlas selection and its effect on accuracy NeuroImage 46 726–38 [DOI] [PubMed] [Google Scholar]
- Attar A et al. 2001. Lumbar pedicle: surgical anatomic evaluation and relationships ‘Eur. Spine J 10 10–5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cootes TF, Hill A, Taylor CJ and Haslam J 1994. The use of active shape models for locating structures in medical images Image Vis. Comput 12 355–66 [Google Scholar]
- De Silva T et al. 2019. SpineCloud: image analytics for predictive modeling of spine surgery outcomes American Society of Neuro-Radiology (ASNR) Annual Meeting 2019 accepted [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gertzbein SD and Robbins SE 1990. Accuracy of pedicular screw placement in vivo Spine 15 11–4 [DOI] [PubMed] [Google Scholar]
- Ghasem A, Sharma A, Greif D, Alam M and Maaieh M 2018. The arrival of robotics in spine surgery Spine 42 1670–7 [DOI] [PubMed] [Google Scholar]
- Goerres J et al. 2017. Spinal pedicle screw planning using deformable atlas registration Phys. Med. Biol 62 2871–91 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gottschalk S et al. 1996. OBBTree Proc. of the 23rd Annual Conf. on Computer Graphics and Interactive Techniques—SIGGRAPH ‘96 ( 10.1145/237170.237244) [DOI] [Google Scholar]
- Gower JC 1975. Generalized procrustes analysis Psychometrika 40 35–51 [Google Scholar]
- Han R et al. 2018. Automatic definition of surgical trajectories and acceptance window in pelvic trauma surgery using deformable registration Medical Imaging 2018: Image-Guided Procedures, Robotic Interventions, and Modeling ( 10.1117/12.2292927) [DOI] [Google Scholar]
- Hecht N et al. 2015. Accuracy and workflow of navigated spinal instrumentation with the mobile AIRO® CT scanner Eur. Spine J 25 716–23 [DOI] [PubMed] [Google Scholar]
- Jamalaldini M and Etemadifar M 2017. Evaluating accuracy of free-hand pedicle screw insertion in adolescent idiopathic scoliosis using postoperative multi-slice computed tomography scan Adv. Biomed. Res 6 19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jianhua Y et al. 2016. A multi-center milestone study of clinical vertebral CT segmentation Comput. Med. Imaging Graphics 49 16–28 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Joseph J, Smith B, Liu X and Park P 2017. Current applications of robotics in spine surgery: a systematic review of the literature Neurosurg. Focus 42 E2. [DOI] [PubMed] [Google Scholar]
- Knez D et al. 2016. Computer-assisted screw size and insertion trajectory planning for pedicle screw placement surgery IEEE Trans. Med. Imaging 35 1420–30 [DOI] [PubMed] [Google Scholar]
- Knez D et al. 2018. Computer-assisted pedicle screw placement planning: towards clinical practice 2018 IEEE 15th Int. Symp. on Biomedical Imaging (Washington, DC: 4–7 April 2018) ( 10.1109/isbi.2018.8363566) [DOI] [Google Scholar]
- Levine M. et al. Automatic vertebrae localization in spine CT: a deep-learning approach for image guidance and surgical data science. Proc. SPIE. 2019;10951:1091510S. [Google Scholar]
- Li M, Liao S, Reda FA, Zhan Y, Zhou XS and Kleinszig G 2017. Image based pedicle screw postioning US Patent Specification 15/281182. (Washington, DC: US Patent and Trademark Office; )
- Lüthi M et al. 2012. Statismo—a framework for PCA based statistical models Insight J. 1 1–18 (http://hdl.handle.net/10380/3371) [Google Scholar]
- Mason A et al. 2014. The accuracy of pedicle screw placement using intraoperative image guidance systems J. Neurosurg. Spine 20 196–203 [DOI] [PubMed] [Google Scholar]
- Myronenko A and Song X 2010. Point-set registration: coherent point drift IEEE Trans. Pattern Anal. Mach. Intell 32 2262–75 [DOI] [PubMed] [Google Scholar]
- Puvanesarajah V. Techniques and accuracy of thoracolumbar pedicle screw placement World. J. Orthop. 2014;5:112. doi: 10.5312/wjo.v5.i2.112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ramsay B. et al. Clustered iterative sub-atlas registration for improved deformable registration using statistical shape models. Medical Imaging 2018: Image-Guided Procedures, Robotic Interventions, and Modeling. 2018;10576:105760C. [Google Scholar]
- Roth HR, Lu L, Seff A and Summers RM 2014. A new 2.5D representation for lymph node detection using random sets of deep convolutional neural network observations MICCAI 2014 pp 520–7 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schreiber JJ et al. 2011. Hounsfield units for assessing bone mineral density and strength: a tool for osteoporosis management J. Bone Joint Surg. Am Vol. 93 1057–63 [DOI] [PubMed] [Google Scholar]
- Sethi A. et al. Lumbar pedicle screw placement: using only AP plane imaging Indian. J. Orthop. 2012;46:434. doi: 10.4103/0019-5413.98832. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Silbermann J et al. 2011. Computer tomography assessment of pedicle screw placement in lumbar and sacral spine: comparison between free-hand and O-arm based navigation techniques Eur. Spine J 20 875–81 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Slone RM et al. 1993. Spinal fixation. Part 3. Complications of spinal instrumentation RadioGraphics 13 797–816 [DOI] [PubMed] [Google Scholar]
- Takeshita K et al. 2009. Diameter, length, and direction of pedicle screws for scoliotic spine Spine 34 798–803 [DOI] [PubMed] [Google Scholar]
- Uneri A et al. 2015. Known-component 3D–2D registration for quality assurance of spine surgery pedicle screw placement Phys. Med. Biol 60 8007–24 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Uneri A et al. 2016. WE-AB-BRA-07: operating room quality assurance (ORQA) for spine surgery using known-component 3D–2D image registration Med. Phys 43 3792–2 [Google Scholar]
- Vijayan RC et al. 2019. Automatic trajectory and instrument planning for robot-assisted spine surgery Medical Imaging 2019: Image-Guided Procedures, Robotic Interventions, and Modeling ( 10.1117/12.2513722) [DOI] [Google Scholar]
- Wang AS, Stayman JW, Otake Y, Vogt S, Kleinszig G, Khanna AJ, Gallia GL and Siewerdsen JH 2014. Low-dose preview for patient-specific, task-specific technique selection in cone-beam CT Med. Phys 41 071915. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xiaozhao C et al. 2016. A method of lumbar pedicle screw placement optimization applied to guidance techniques Comput. Assist. Surg 21 142–7 [Google Scholar]
- Yoshii T. et al. Lumbosacral pedicle screw placement using a fluoroscopic pedicle axis view and a cannulated tapping device. J. Orthop. Surg. Res. 2015;10:79. doi: 10.1186/s13018-015-0225-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zaffino P. et al. Multi atlas based segmentation: should we prefer the best atlas group over the group of best atlases? Phys. Med. Biol. 2018;63:12NT01. doi: 10.1088/1361-6560/aac712. [DOI] [PubMed] [Google Scholar]
- Zhang X. et al. Improved intraoperative imaging in spine surgery: clinical translation of known-component 3D image reconstruction on the O-Arm system. Proc. SPIE. 2019;10951:1095103. doi: 10.1002/mp.13652. [DOI] [PMC free article] [PubMed] [Google Scholar]