C-arm orbits for metal artifact avoidance (MAA) in cone-beam CT

Abstract

Metal artifacts present a challenge to cone-beam CT (CBCT) image-guided surgery, obscuring visualization of metal instruments and adjacent anatomy—often in the very region of interest pertinent to the imaging/surgical tasks. We present a method to reduce the influence of metal artifacts by prospectively defining an image acquisition protocol—viz., the C-arm source-detector orbit—that mitigates metal-induced biases in the projection data. The metal artifact avoidance (MAA) method is compatible with simple mobile C-arms, does not require exact prior information on the patient or metal implants, and is consistent with 3D filtered backprojection (FBP), more advanced (e.g. polyenergetic) model-based image reconstruction (MBIR), and metal artifact reduction (MAR) post-processing methods. The MAA method consists of: (i) coarse localization of metal objects in the field-of-view (FOV) via two or more low-dose scout projection views and segmentation (e.g. a simple U-Net) in coarse backprojection; (ii) model-based prediction of metal-induced x-ray spectral shift for all source-detector vertices accessible by the imaging system (e.g. gantry rotation and tilt angles); and (iii) identification of a circular or non-circular orbit that reduces the variation in spectral shift. The method was developed, tested, and evaluated in a series of studies presenting increasing levels of complexity and realism, including digital simulations, phantom experiment, and cadaver experiment in the context of image-guided spine surgery (pedicle screw implants). The MAA method accurately predicted tilted circular and non-circular orbits that reduced the magnitude of metal artifacts in CBCT reconstructions. Realistic distributions of metal instrumentation were successfully localized (0.71 median Dice coefficient) from 2–6 low-dose scout views even in complex anatomical scenes. The MAA-predicted tilted circular orbits reduced root-mean-square error (RMSE) in 3D image reconstructions by 46%–70% and ‘blooming’ artifacts (apparent width of the screw shaft) by 20–45%. Non-circular orbits defined by MAA achieved a further ~46% reduction in RMSE compared to the best (tilted) circular orbit. The MAA method presents a practical means to predict C-arm orbits that minimize spectral bias from metal instrumentation. Resulting orbits—either simple tilted circular orbits or more complex non-circular orbits that can be executed with a motorized multi-axis C-arm—exhibited substantial reduction of metal artifacts in raw CBCT reconstructions by virtue of higher fidelity projection data, which are in turn compatible with subsequent MAR post-processing and/or polyenergetic MBIR to further reduce artifacts.

1. Introduction

Cone-beam CT (CBCT) systems are increasingly prevalent in dental, (Baba et al 2004) orthopedic, (Zbijewski et al 2011) breast, (Boone et al 2005) head, (Wu et al 2019) and interventional imaging scenarios. (Siewerdsen et al 2005, Fahrig et al 2006, Uneri et al 2019) Among the challenges to image quality in applications like image-guided surgery (IGS) are artifacts arising from highly attenuating metal instrumentation within the field-of-view (FOV), such as surgical clips, dental fillings, staples, screws, and orthopedic implants. For example, in spine surgery, metal artifacts can arise from pedicle screws and spinal fixation rods, where it is important to clearly visualize regions adjacent to instrumentation—e.g. to verify that a spinal pedicle screw is contained within the pedicle and is not impinging on the spinal cord, adjacent nerves, or vessels.

Metal artifacts arise from a mismatch/bias between the forward model (physical process of x-ray image formation) and the inverse model (image reconstruction with a variety of idealized model assumptions). Factors underlying the shading and streaks commonly termed ‘metal artifacts’ include a number of distinct effects: beam hardening (spectral shift of the polychromatic x-ray beam transmitted through metal compared to surrounding tissue); x-ray scatter (increased scatter-to-primary ratio behind metal objects); photon starvation (strong attenuation and correspondingly increased influence of detector electronic noise); lag (increased view to view signal fluctuation behind metal objects); sensitivity to geometric calibration; view sampling; and patient motion. (Boas and Fleischmann 2012) Each of these factors is particularly important for interventional C-arm CBCT—for example: the influence of scatter is high for a volumetric beam; the lower power associated with a mobile C-arm combined with the higher level of electronic noise for a flat-panel detector (FPD) results in greater susceptibility to photon starvation (compared to multi-detector CT, MDCT).

In IGS, metal artifacts can confound visualization of features in the very region-of-interest (ROI) for which the images are acquired—e.g. determining the placement of an implant relative to surrounding bone and soft tissue. Previously reported algorithms for metal artifact reduction (MAR) can be considered in three broad categories. (i) Classic MAR methods that treat metal regions in the projection domain as missing data and rely on various segmentation and sinogram ‘in-painting’ approaches. (Wang et al 1996, Meyer et al 2010, Zhang and Yu 2018) Accurate segmentation and in-painting is challenging without additional prior information, and even small errors can cause significant residual artifacts. (Uneri et al 2019) (ii) A second category uses 3D image-domain restoration to improve the quality of reconstructed images. Popular restoration methods include total variation denoising, radial adaptive filters, (Bal et al 2005, Mouton et al 2013) and machine learning methods. (Ketcha et al 2020, Lin et al 2019) These methods are helpful especially when working without access to underlying projection data. Methods in both categories (i) and (ii) involve post-processing (either in the projection or image domain—or both) to reduce artifacts (i.e. biases encumbered in the projection data) and are therefore referred to as MAR post-processing in this work. (iii) Alternatively, a physical model of the system and source of metal artifacts (e.g. beam hardening) can be invoked within the system model for 3D image reconstruction to improve image quality using model-based image reconstruction (MBIR) (e.g. polyenergetic MBIR (Elbakri and Fessler 2002, Morsbach et al 2013)). Both MAR post-processing and polyenergetic MBIR can utilize prior information of the metal objects (shape and material of implants) or the patient (prior CT or CBCT images) to realize substantial gains in performance. (Stayman et al 2012, Uneri et al 2019) They also benefit from imaging protocols that yield projection data that are of higher fidelity to begin with—which is the goal of the approach described below.

We propose a method to acquire data in a manner that minimizes the factors of bias from which metal artifacts arise—i.e. to avoid metal artifacts in the first place—and is compatible with MAR post-processing or polyenergetic MBIR. A number of methods have been reported whereby the orbit of the source and detector are modified to positively affect image quality. In head CT, for example, the CT gantry is sometimes tilted relative to the patient’s longitudinal axis to improve image quality in the region of the skull base (van Straten et al 2007) and/or to reduce dose to eye lens. (Nikupaavo et al 2015) The gantry may also be tilted to improve localization in CT-guided biopsies. (Yamagami et al 2004) Other methods seek to mathematically optimize the scan orbit to reduce the influence of x-ray scatter, (Zhao et al 2019) cone-beam artifacts, (Gang et al 2018, 2020) or to maximize the spatial-frequency-dependent signal and noise transfer characteristics with respect to the imaging task. (Gang et al 2017, Stayman et al 2019, Capostagno et al 2019)

The method described below (referred to as metal artifact avoidance, MAA) prospectively identifies a source-detector orbit that minimizes (or at least reduces) metal-induced biases in the projection data. The MAA method utilizes low-dose scout views (e.g. acquired during the pre-scan collision check) and operates without other sources of strong prior information (such as the exact shape or material of the metal objects or patient anatomy). Furthermore, the MAA method is compatible with MAR post-processing and either filtered backprojection (FBP) or polyenergetic MBIR. As shown below, the MAA orbit optimization can be constrained to identify simple tilted (circular or semi-circular) orbits that are commonly available on mobile C-arms, and the method naturally extends to more elaborate, non-circular orbits that can be executed on multi-axis motorized C-arms.

2. Materials and methods

2.1. Mobile C-Arm for intraoperative CBCT

Increasingly, mobile or fixed-room C-arms are capable of source-detector orbits beyond that of a fixed circular scan (i.e. semi-circular, 180° + fan angle) in a plane perpendicular to the long axis of the patient. For example, figure 1 illustrates a simple tilted orbit for a mobile C-arm (Cios Spin 3D, Siemens Healthineers, Forcheim, Germany), with rotation angle (θ) varying from 0° to 196° and tilt angle (ϕ) varying from −30° to 30° without table collision. In clinical practice, such C-arms commonly permit scanning within ±15° gantry tilt, and scans at increased tilt angle are possible given suitable geometric calibration. Such C-arms are also potentially capable of executing non-circular orbits via motorized variation of θ and ϕ during the scan. For some systems, in fact, a non-circular orbit with multiple motorized axes is standard for CBCT imaging (e.g. Ziehm Vario 3-D (Ziehm Imaging, Orlando, Florida)).

Figure 1.

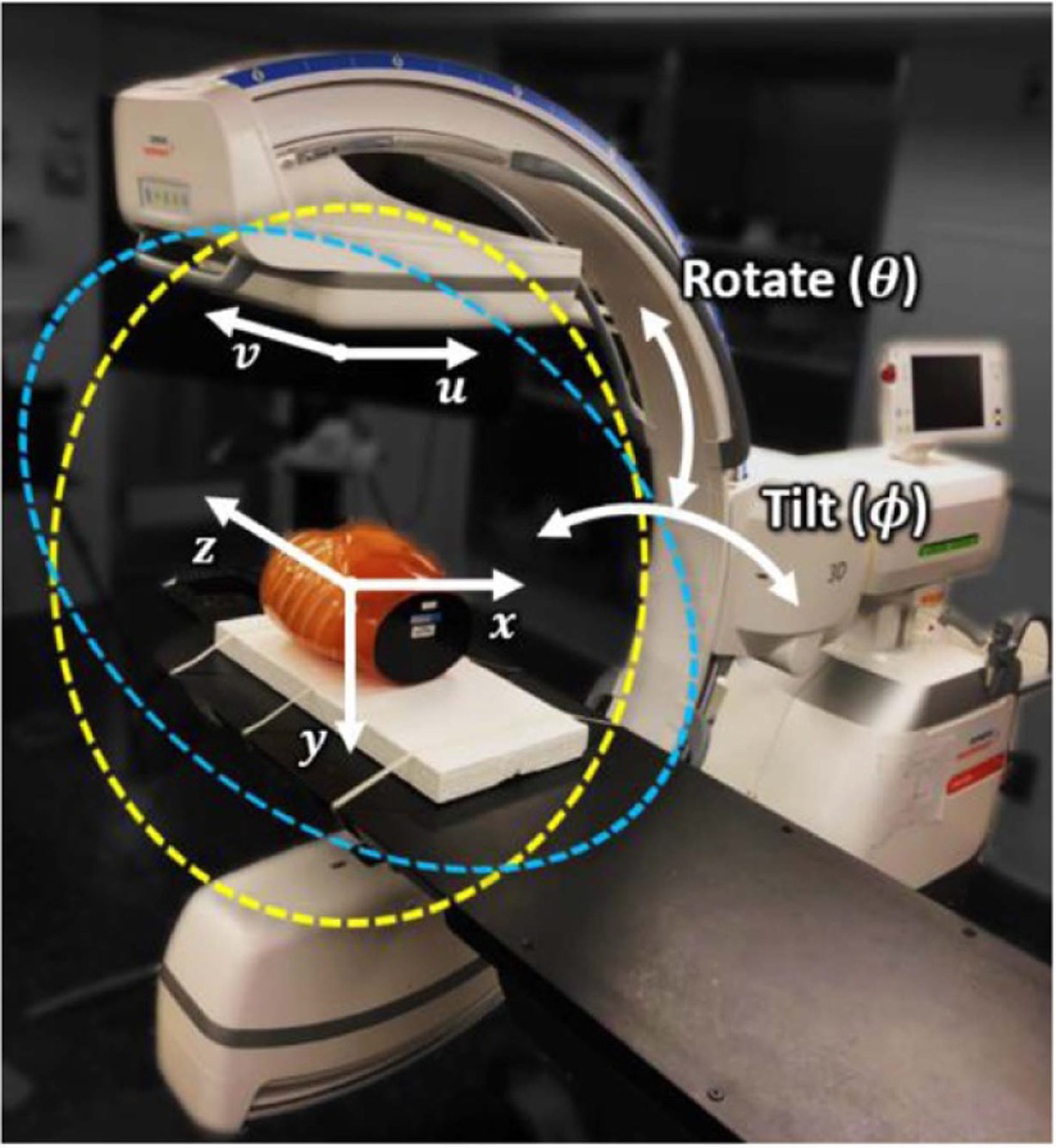
Mobile C-arm for intraoperative CBCT. The isocentric C-arm nominally acquires CBCT data from a (untilted) semi-circular half-scan orbit in rotation angle θ = 0°–196° (yellow circle). Such an orbit can also be acquired at a specified gantry tilt angle (ϕ, marked in blue). Computer-controlled motorization of both θ and ϕ during the scan allows non-circular orbits that may improve sampling characteristics and MAA performance.

The mobile C-arm in figure 1 was used for testing and preclinical validation of the MAA approach. The system has an x-ray tube with a rotating tungsten anode (0.3/0.5 FS focal spot), tube output up to 1.65 mAs/view at 125 kV, and an indirect-detection, CMOS-based flat panel detector (FPD) (Xineos 3030 HS, Teledyne Dalsa, Waterloo, Canada) with 30 × 30 cm² detector area (0.3 × 0.3 mm² pixel size with 2 × 2 hardware binning). The source-axis distance (SAD) is 62.3 cm, and the source-detector distance (SDD) is 116.4 cm, giving a 16 × 16 × 16 cm³ volumetric field-of-view (FOV). An example body scan protocol involves 400 projections acquired over a 196° scan arc at 110 kV with a 30 s scan time (588 mAs), giving a dose level of 31.4 mGy (weighted central and peripheral air kerma measured with a stack of three 32 cm diameter CTDI phantoms) (Sheth et al 2019).

2.2. Source-detector orbits for metal artifact avoidance (MAA)

A flowchart representation of the MAA algorithm is shown in figure 2. The main stages include: (i) coarse localization of metal objects from scout views; (ii) predictive calculation of metal-induced bias for all possible views; and (iii) orbit optimization.

Figure 2.

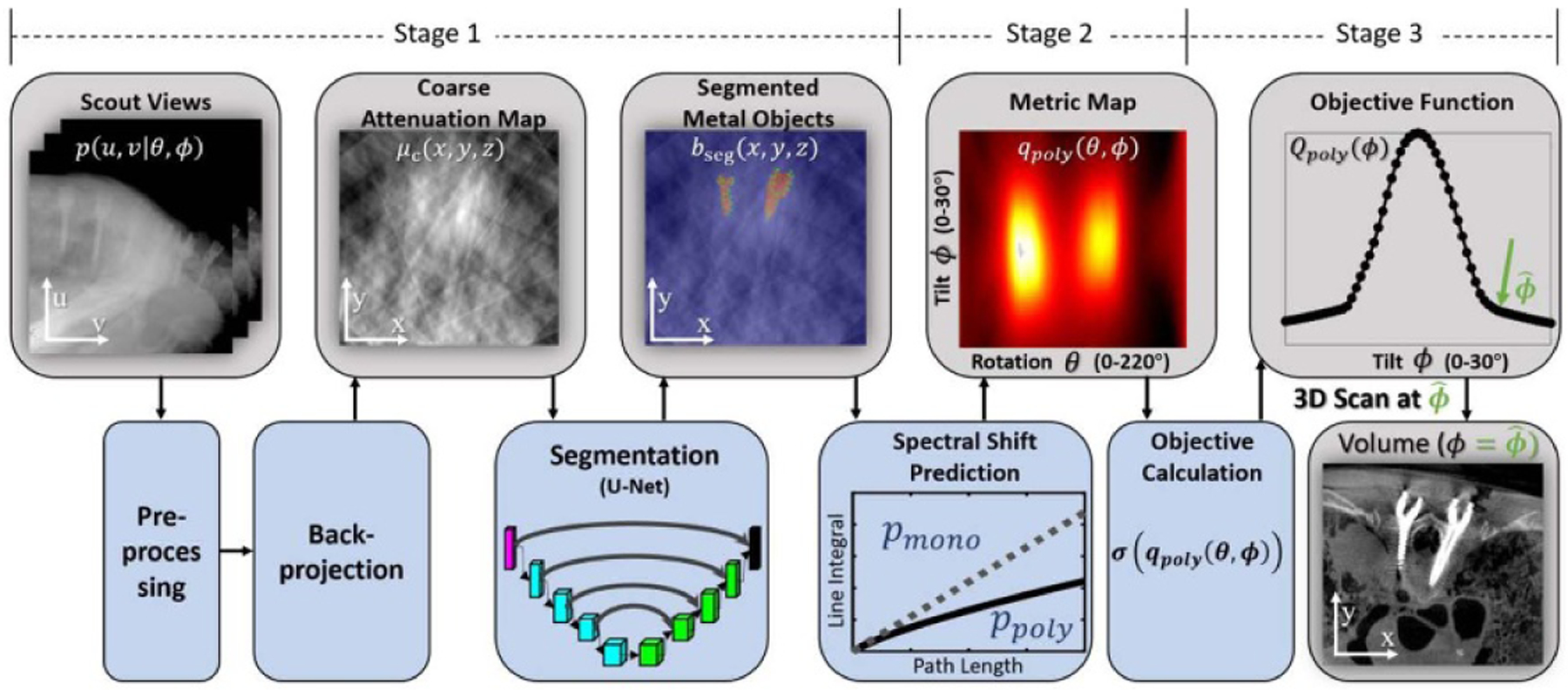
Flowchart for the MAA algorithm. Scout views (2 or more) are pre-processed and backprojected to form a coarse attenuation map (μ_c), which is segmented using a U-Net to localize metal objects (b_seg). Biases associated with spectral shift are then predicted as a function of gantry rotation (θ) and tilt (ϕ) angles to yield a metric map, denoted q_poly(θ, ϕ). An orbit that minimizes metal artifacts is determined by finding a path in q_poly(θ, ϕ) that minimizes errors and/or bias associated with the presence of metal (e.g. finding a path that minimizes the standard deviation (σ) of q_poly). A horizontal row in q_poly(θ, ϕ) represents a circular orbit at gantry tilt ϕ, and a curved path in q_poly(θ, ϕ) represents a noncircular orbit.

2.2.1. Localization of metal objects from scout views

Given two or more scout views, the MAA algorithm begins with preprocessing (e.g. adaptive histogram equalization, AHE) followed by backprojection (without the ramp filter used in FBP) to form a coarse attenuation map (μ_c), which is then segmented to a binary volume (b_seg) describing the 3D location of metal objects within the FOV. As substantiated below, a fairly coarse segmentation was found to be sufficient for the MAA method, requiring only a rough, low-resolution segmentation that reasonably captured the size, shape, and orientation of metal objects to determine a desirable C-arm orbit (cf., MAR methods that typically require very accurate segmentation (Uneri et al 2019)).

Coarse segmentation was achieved using a convolutional neural network (CNN) implemented as a four-level 2D U-Net (Ronneberger et al 2015) architecture (applied slice-by-slice) with ReLU activation function, batch normalization (added after each ReLU activation function), and general Dice loss function. (Sudre et al 2017) The network was initialized with the ‘He normal’ method (He et al 2015) and trained using the Adam optimizer with an initial learning rate of 5 × 10⁻³ for 50 epochs.

For simplicity and to avoid the requirement for manufacturer-specific models of surgical instruments, the U-Net was trained with only simulated data in the current work. Digitally reconstructed radiographs (DRRs) (computed at various projection views, θ, as in the scout views) were computed from 10 abdominal and thoracic CT images drawn from The Cancer Imaging Archive (TCIA) and overlaid with a random number of forward-projected metal objects: ellipsoids ranging in size and eccentricity (10–80 mm major and minor axes) and coarsely segmented spine screw models obtained from CT images. Future work could certainly involve addition of higher fidelity object models (e.g. vendor-specific designs) and other application-specific objects (e.g. fracture fixation plates) to improve performance. The effects of data truncation, partial volume effect, noise (quantum and electronic), scatter, and beam hardening were included in DRR generation. The DRRs were then preprocessed (AHE) and backprojected (without ramp filter) to form μ_c for network training. Data augmentation included variation in the location, size, orientation, shear ratio, and attenuation of simulated metal objects in each DRR. A total of ~36 000 (34 000 training + 2000 validation) images (patches of 128 × 128 voxels, μ_c) were used for network training.

2.2.2. Predictive estimate of bias in projection data: spectral shift

The second step of the MAA algorithm estimates the metal-induced bias in the projection domain for all rotation (θ) and tilt (ϕ) angles. Primary sources of error/bias include increased scatter-to-primary ratio, photon starvation, and beam hardening (Barrett and Keat 2004, Meyer et al 2010)—the last being the focus of this work. The line integral for a monoenergetic beam at detector position (u, v) is:

$$p_{\mathit{\text{mono}}}(u,v\mid \theta ,\varphi )={\mu }_m\left(A{b}_{seg}\right)$$ (1)

where b_seg is the binary metal segmentation described in the previous section, μ_m is an empirically estimated scalar representing the attenuation coefficient of the metal object (titanium in this work), and A is the system matrix defined by the Siddon ray tracing method (Siddon 1985). The corresponding polyenergetic line integral is:

$$p_{\mathit{\text{poly}}}(u,v\mid \theta ,\varphi )=\sum _{i=1}^N{\alpha }_i{p}_{\mathit{\text{mono}}}^i(u,v\mid \theta ,\varphi )$$ (2)

where $p_{\mathit{\text{mono}}}^i(u,v\mid \theta ,\varphi )$ denotes raising the pixel value p_mono (u, v|θ, ϕ) to the power of i, α_i are precalculated polynomial mapping coefficients, which are determined not only by the spectrum but also the metal material (since the energy dependence of attenuation coefficient is material dependent) (Joseph and Spital 1978). The number of polynomial coefficients (N) was empirically set to 5 in this work. The MAA method is relatively insensitive to both the spectral model and the metal material (including μ_m), since each are only used to predict desirable orbits (not to perform an actual beam-hardening correction). In this work, α_i was pre-computed for titanium (Z = 22) and a 110 kV spectrum, (Punnoose et al 2016) μ_m was set to be the attenuation coefficient of titanium at the mean energy of the used 110 kV spectrum. While more sophisticated polyenergetic forward projection models have been reported, (Joseph and Spital 1978) the simple form of equation (2) was chosen due to its computational efficiency, as it can be precomputed as a simple lookup table with 1D linear interpolation illustrated as a plot of the line integral versus path length in the flowchart of figure 2.

The difference between mono- and poly-energetic line integrals defines a metric of x-ray spectral shift in the projection domain:

$$q_{\mathit{\text{poly}}}(\theta ,\varphi )=\sum _{u,v}\left|p_{\mathit{\text{mono}}}(u,v\mid \theta ,\varphi )-p_{\mathit{\text{poly}}}(u,v\mid \theta ,\varphi )\right|$$ (3)

where, in the current work, q_poly is summed over (u, v) in each projection to reflect the total spectral shift influencing the projection data at each θ and ϕ. (A variation of q_poly limited to a particular region of interest—e.g. the central region of the projection—can certainly be envisioned.)

2.2.3. Orbit optimization

The third step of the MAA algorithm is to identify the orbit (characterized by tilt angle at each rotation angle, ϕ(θ)) that will minimize metal artifacts in the 3D image reconstruction. A number of objective functions can be envisioned based on the q_poly (θ, ϕ) ‘metric map’ described by equation (3) and illustrated in figure 2. Rather than simply aggregating (i.e. summing) the spectral shift at each θ, we formulated an objective that describes the inconsistency in spectral shift between projection views, since it is the disparity in spectral shift that underlies the non-uniform shading and streaks commonly identified as beam-hardening effects or metal artifacts. Specifically, we defined an objective denoted Q_poly based on the standard deviation in q_poly (θ, ϕ) as follows:

$$Q_{\mathit{\text{poly}}}(\varphi (\theta ))=\sigma \left[q_{\mathit{\text{poly}}}(\theta ,\varphi (\theta ))\right]$$ (4)

where σ is the standard deviation operator.

Circular Orbits with Optimal Gantry Tilt:

The objective of equation (4) can be simplified to the case of finding the optimal tilt (for a semi-circular orbit)—i.e. a constant, optimal tilt angle $\widehat{\varphi }$ for all θ:

$$\widehat{\varphi }=\underset{\varphi }{\text{arg}\text{min}}=Q_{\mathit{\text{poly}}}(\varphi )=\sigma \left[q_{\mathit{\text{poly}}}(\theta ,\varphi )\right]$$ (5)

This simplification amounts to finding a ‘horizontal’ row of the q_poly (θ, ϕ) metric map with minimum standard deviation—i.e. a scalar value of ϕ that can be easily solved by exhaustive search of the limited variable space. In practice, there are a number of potential challenges associated with increasingly larger tilt angle, including reduced reproducibility in geometric calibration and an increased risk of collision with the operating table. Therefore, the ‘optimal’ tilt may be practically interpreted as the $\widehat{\varphi }$ that is as small as possible, but as large as necessary. In this work, we used a semi-heuristic choice (not a true minimization) of $\widehat{\varphi }$ such that Q_poly (ϕ) was reduced to 5% of its maximum-to-minimum range over all possible ϕ.

Non-Circular Orbits:

Modern C-arms with motorized control of multiple axes are potentially capable of non-circular CBCT orbits—e.g. large fixed-room robotic C-arms (such as the Artis Pheno, Siemens Healthineers) or some mobile C-arms, (Overley et al 2017, Sheth et al 2019) such as the one shown in figure 1, which provides motorized control of θ and ϕ. This opens the possibility of using non-circular orbits to achieve even lower values of the objective function (Q_poly). For a non-circular orbit, ϕ changes with θ. To reduce the dimensionality of the problem and encourage a more practical, smooth, and realistic orbit, we modeled ϕ(θ) as a superposition of cubic b-spline kernels, each centered at one of M = 10 knots equally distributed over the 196° scan arc:

$$\widehat{f}=\underset{f}{\text{arg}\text{min}}=Q_{\mathit{\text{poly}}}(f)=\sigma \left[q_{\mathit{\text{poly}}}\left(\theta ,\sum _{i=0}^M{f}_{i}B\left(\theta -{\theta }_i\right)\right)\right]$$ (6)

where B is a cubic B-spline, and f_i is the control parameter for spline knot control points i. The optimization in equation (6) is non-convex and thus challenging to solve with conventional gradient-based methods. Therefore, we used the covariance matrix adaptation evolution strategy (CMA-ES) (Hansen and Kern 2004) as a robust solver of equation (6) operating in near real-time (~0.5 s for the 196 × 61 (θ, ϕ) search space).

2.2.4. Reconstruction with MAA Orbit

Images were reconstructed on a volumetric grid covering 16 × 16 × 16 cm³ FOV with isotropic voxel size of 0.4 × 0.4 × 0.4 mm³. For the simple semi-circular, tilted orbit resulting from minimization of equation (5), 3D image reconstruction was performed using 3D filtered backprojection, (Kak et al 2002) modified to transform backprojected rays according to the system geometry of the untilted (ϕ = 0°) orbit. The resulting volumetric image is thus oriented the same irrespective of tilt angle (detailed in §2.3 below). Projection data at the edge of the detector was linearly extrapolated to mitigate truncation artifacts. A 2D Hann apodization with cutoff frequency set to 60% of the Nyquist frequency in both row and column directions was used for projection domain noise reduction.

For the non-circular orbit resulting from minimization of equation (6), the image was reconstructed with a penalized weighted least-squares (PWLS) (Fessler 1994) method with a Huber loss function to penalize pairwise differences between voxels in a first-order neighborhood around each voxel. The method included multi-resolution reconstruction to mitigate truncation artifacts (as in (Wu et al 2018)), and the objective function was minimized using separable quadratic surrogates (SQS) solver with ordered subsets (OS-SQS), (Erdogan and Fessler 1999) with 80 iterations and 10 subsets.

Both FBP and PWLS methods were implemented in MATLAB (The MathWorks, Natick MA), with forward and back projection operations executed on GPU using CUDA-based libraries. All image reconstructions were performed on a workstation equipped with a GeForce GTX TITAN X (Nvidia, Santa Clara CA) graphics card.

2.3. Studies and system geometry

The MAA approach was tested and evaluated in a series of studies beginning with a digital simulation (Study #1, below) and extending to more realistic scenarios in an anthropomorphic chest phantom experiment (Study #2), a pre-clinical cadaver experiment (Study #3), and another digital simulation study focusing on MAA with non-circular orbits (Study #4). In all studies, the system geometry was that of the C-arm in figure 1.

A reproducible orbit and geometric calibration (i.e. specification of the source-detector pose relationship for all θ) is prerequisite to accurate 3D image reconstruction. For the MAA approach, the mechanical flex of the gantry depends on tilt angle (ϕ), necessitating a separate geometric calibration for each ϕ. Geometric calibrations were performed over a range ϕ = (−30°, 30°) at 5° intervals. Calibration at arbitrary tilt angles within that range were estimated by linear/spherical-linear interpolation (Dam et al 1998) of the intrinsic and extrinsic parameters.

Geometric calibration followed the method of Cho et al (Cho et al 2005) using a cylindrical BB placed at the same tilt angle as the C-arm gantry. In this way the calibration determines the source-detector trajectory within a common reference frame (untilted relative to the phantom), allowing simple interpolation of intrinsic and extrinsic parameters at any tilt. For 3D images to be reconstructed in a common coordinate system (i.e. so that the image does not appear rotated by the gantry tilt angle), the resulting projection matrices included the following tilt transformations:

$$P_{\varphi =0}=P_{\varphi ={\varphi }^{*}}\times T_{\mathit{\text{tilt}}}\times T_w$$ (7)

$$T_{\mathit{\text{tilt}}}=\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& \text{cos}\left({\varphi }^{*}\right)& -\text{sin}\left({\varphi }^{*}\right)& 0\\ 0& \text{sin}\left({\varphi }^{*}\right)& \text{cos}\left({\varphi }^{*}\right)& 0\\ 0& 0& 0& 1\end{array}\right]T_w=\left[\begin{array}{cccc}1& 0& 0& t_x\\ 0& 1& 0& t_y\\ 0& 0& r_z& t_z\\ 0& 0& 0& 1\end{array}\right]$$ (8)

where P_ϕ=ϕ* is the projection matrix at tilt angle ϕ*, T_tilt is a transformation through tilt angle ϕ*, and T_w accounts for possible discrepancy in displacement (t) and tilt (r_z) between the BB phantom and the gantry tilt angle. The ‘true’ C-arm gantry tilt ϕ* was taken as that reported by the C-arm axis encoders, and T_w was determined by 3D-3D image registration of reconstructions at ϕ = 0° (using P_ϕ=0 as the projection matrix) and at ϕ = ϕ* (using P_ϕ=ϕ* × T_tilt as the projection matrix).

2.3.1. Study #1: basic feasibility in digital simulation (cylinder + metal objects)

A simulation study was first conducted to investigate feasibility of the MAA approach over a broad range of simulated metal objects and orbits. Study #1 simulated a 16 cm diameter water cylinder containing a variety of metallic (Titanium) spheres and cylindrical rods as illustrated in figure 3(a). A 100 kV x-ray spectrum was computed using the spektr toolkit, (Punnoose et al 2016) modeling beam-hardening effects, while ignoring x-ray scatter for present purposes. Geometry was defined to match the Cios Spin system (figure 1). Orbit optimization was constrained to semi-circular orbits with tilt angle ϕ ranging (−30°, 30°). We hypothesized that the MAA objective described by equation (5) would identify tilted orbits that avoided overlap of multiple metal objects and/or projections through the long axis of metal objects. Performance was evaluated in terms of the root-mean-squared-error (RMSE) between 3D image reconstructions from the MAA orbit and the ground truth image for various orbits.

Figure 3.

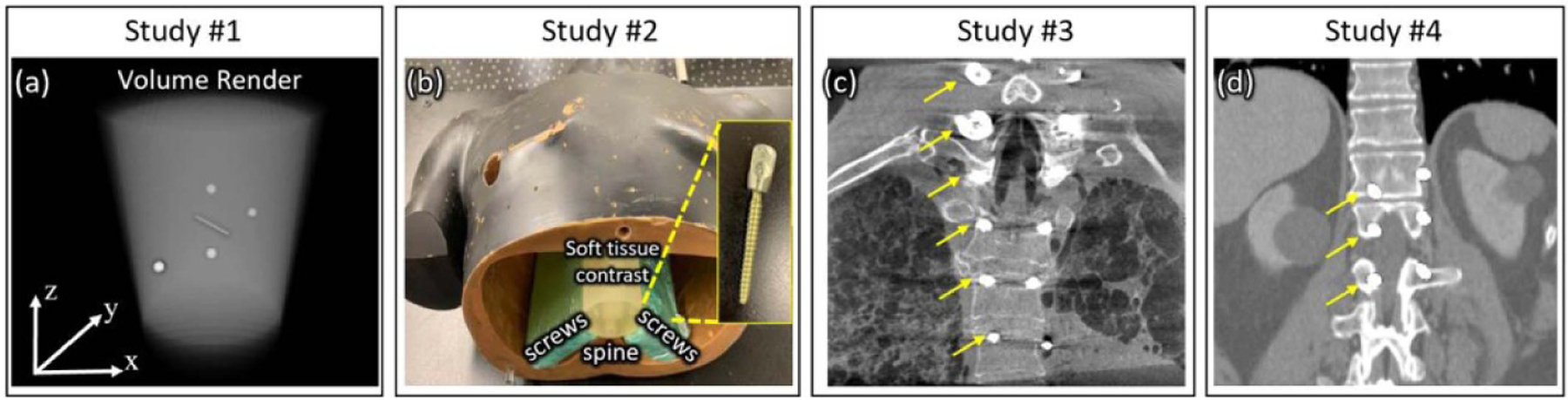
Illustration of the object used in digital simulation, phantom, and cadaver studies in this work. (a) Volume rendering of a simple digital cylindrical phantom containing simulated metal spheres and rods in Study #1. (b) Photograph of the anthropomorphic chest phantom with pedicle screws placed in slabs of tissue-equivalent bolus adjacent to the spine in Study #2. (c) Coronal slice from a CBCT scan of the cadaver implanted with cervical and thoracolumbar pedicle screws in Study #3. (d) Coronal slice of the digital anatomy phantom containing simulated spine screws in Study #4. Arrows in (c) and (d) mark the location of pedicle screws on one side of the spine.

2.3.2. Study #2: chest phantom experiment with spine screws

The MAA approach was translated to physical experiments using the mobile C-arm of figure 1 and a chest phantom (figure 3(b)) containing a natural human skeleton in tissue-equivalent plastic and a collection of spinal pedicle screws. Study #2 focused on identification of the tilted circular orbit (i.e. minimization of equation (5)) to minimize metal artifacts. Four pairs of solid spinal pedicle screws (DePuy Synthes, Raynham MA) were incorporated in the chest phantom, ranging 30–60 mm in length and 3.5–6 mm in diameter. The 8 screws were embedded in tissue-equivalent material and placed adjacent to the spine as shown in figure 3(b), presenting a broad range of orientation (out-of-plane angles ranging ~(−15°, 20°)) and rotation relative to the scan plane and longitudinal axis. Screw arrangement in this study was therefore a bit more challenging to the MAA approach than in a real patient implant, where the range in out-of-plane angles is usually less (following the curvature of the spine within the FOV). The screws used in Study #2 were solid (not cannulated, as in Study #3) and were therefore expected to give stronger magnitude of metal artifacts (given similar screw length/diameter).

The MAA orbit predicted to minimize metal artifacts was computed using 6 low-dose scout views (each acquired at ϕ = 0°, with rotation angle θ = 0° to 150° in steps of 30°). C-arm CBCT scans were acquired at tilt angles ranging ϕ = −30° to +30° at 10° intervals (7 scans total) using the body scan protocols described in §2.1. The segmentation (b_seg in figure 2) was evaluated using Dice coefficient compared to threshold-based segmentation computed in CBCT reconstruction with 400 views and minimal metal artifacts. The improvement in metal artifacts achieved with the MAA method was quantified in terms of the magnitude of ‘blooming’ artifact, defined in terms of the full-width-at-half-maximum (FWHM) of the screw shaft compared to its specified diameter.

2.3.3. Study #3: cadaver experiment with implanted spine screws

A cadaver study was performed to validate the performance of MAA with realistic anatomy and spinal pedicle screw implants. The cadaver featured 6 pairs of pedicle screws (NuVasive, San Diego CA), including one pair of solid cervical screws (35 mm length and 2 mm diameter) and five pairs of cannulated thoracolumbar spine screws (50 mm length and 4.5 mm diameter). The MAA method for predicting optimal tilt was the same as in §2.3.2, including 6 scout projection views and minimization of equation (5) to find the tilted circular orbit that would minimize metal artifacts. CBCT images were acquired at tilt angles ranging ϕ = (−15°, 15°) at 5° intervals (7 scans total). Metal artifacts magnitude was assessed in terms of ‘blooming’ (FWHM) about the shaft of the pedicle screw, comparing the image quality for the scan performed at optimal tilt angles to that for other tilt angles (including no tilt). This cadaver study was conducted in accordance with all ethical and biosafety requirements of our institution.

Study #2 and #3 were designed to challenge the MAA approach in different aspects. While the screw arrangement in Study #3 was more realistic and thus not as challenging to the MAA approach as in Study #2, Study #3 featured much more complex anatomical structures and challenged other aspects of the MAA approach like metal object localization (i.e. testing the generalizability of the U-Net with realistic anatomy and spine screws very different from those in the training set, which comprised relatively simple simulated metal objects).

In addition to comparison with (uncorrected) 3D image reconstructions from the conventional orbit (results below denoted as ‘Conventional’), uncorrected reconstructions from the MAA orbit (denoted ‘MAA’) were also compared to MAR-corrected reconstructions from both the conventional orbit (denoted ‘Conventional + MAR’) the MAA orbit (denoted ‘MAA + MAR’). The MAR method employed in this work was the frequency splitting MAR (FS-MAR) method (Meyer et al 2012) as implemented in the manufacturer’s release of the mobile C-arm in figure 1.

2.3.4. Study #4: extension to non-circular orbits (digital simulation)

Finally, the MAA approach was tested in relation to non-circular orbit optimization with another digital simulation study. As shown in figure 3(d), Study #4 used a CT scan of a human thorax (also drawn from the TCIA dataset, but distinct from the training data of the U-Net segmentation method) implanted with three pairs of bilateral spinal pedicle screws. The out-of-plane orientation of screws with respect to the central axial plane was 0°, −11°, and −22° on the right side of the spine, and 0°, 11°, and 22° on the left side of the spine. The simulated screw model was based on segmentation of one of the screw models in Study #2 (a solid pedicle screw with 60 mm length and 6 mm diameter). To add a further degree of complexity and variability in the data (e.g. screws of varying material type), the attenuation of the right-side screws was increased by 10% compared to left-side screws. Optimization of equation (6) yielded the non-circular orbit that minimized variations in x-ray spectral shift. Performance was analyzed in terms of the degree to which the non-circular orbit reduced metal artifacts compared to the optimal tilted circular orbit, characterized in terms of visual image quality and RMSE from ground truth. To reconstruct 3D images from non-circular orbits, the PWLS method (§2.2.4) was used, noting that iterative reconstruction was only invoked to handle the non-circular system geometry (and not for purposes of improved noise-resolution tradeoffs of MBIR). To ensure fair comparison between images in this study—i.e. to focus on benefits to image quality associated with the MAA orbit (and not the reconstruction method)—all images in this study (both circular and non-circular orbits) were reconstructed using the PWLS method.

3. Results

3.1. Study #1: basic feasibility in digital simulation (cylinder + metal objects)

Figures 4(a) and (b) show μ_c and b_seg calculated from two scout views (AP and lateral) of the digital cylinder phantom, clearly localizing the 3D position of simple metal spheres and rods using U-Net based segmentation. Although b_seg was found often to overestimate the true object (as evident in the sphere in figure 4(b)), the coarse segmentation provided sufficient information for calculation of the metric map for MAA, as illustrated in figure 4(c), which shows the predicted map of spectral shift (q_poly (θ, ϕ)) computed from b_seg. Bright regions in the metric map correspond to views (θ, ϕ) with strong metal-induced bias, from which strong metal artifacts in the image domain can be expected to arise. For example, views at ϕ ~ 0° and θ ~ 0° are particularly problematic (high spectral shift) for this phantom arrangement, as it results in overlapping metal spheres in the central axial plane (two spheres shown in the top row of figure 4(e)).

Figure 4.

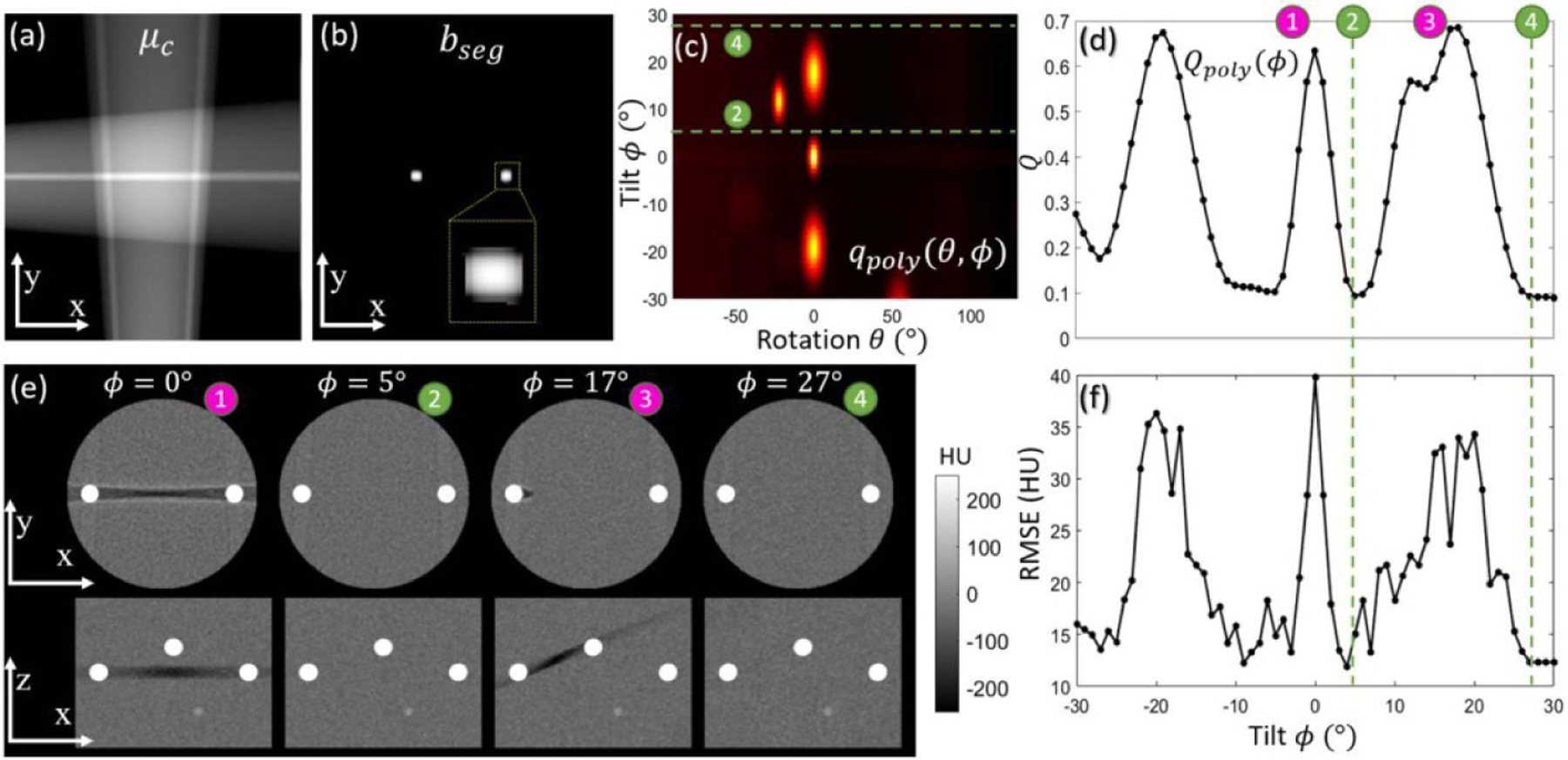
Study #1: Simulation study involving a water cylinder with a variety of metal spheres and rods. (a) Coarse attenuation map μ_c computed from 2 scout views. The central axial (x, y) plane is shown, recognizing that the coarse attenuation map is computed over the full 3D volume. (b) Segmentation b_seg computed by the U-Net. (c) Metric map q_poly (θ, ϕ) computed over a realistic range of rotation (θ) and tilt (ϕ) angles. Optimal tilted semi-circular orbits are marked by dashed green lines labeled ➁ and ➃, which avoid projection views with high spectral shift. (d) Objective function Q_poly (ϕ) computed from equation (5). (e) Axial and sagittal slices from FBP image reconstructions of data acquired at various tilt angles. (f) The RMSE analyzed as a function of tilt angle ϕ is seen to follow a similar trend as the objective function in (d), confirming the basic notion that minimization of variation in spectral shift (from q_poly (θ, ϕ)) minimizes metal artifacts in 3D image reconstructions.

Desirable tilt angles are evident in the objective function Q_poly (ϕ) in figure 4(d)—for example, ϕ ~ 5° and ϕ ~ 27°, marked with green circles and corresponding to horizontal lines in figure 4(c) that avoid the low-fidelity views (high spectral shift). A comparison between Q_poly (ϕ) at ϕ ~ 5° and ϕ ~ 17° shows that a larger tilt angle is not always a better choice—in this case resulting in overlap of spheres from out-of-plane. Figure 4(e) shows axial and sagittal reconstructions at example tilt angles, confirming that the optimal semi-circular orbit predicted by MAA minimizes the magnitude of metal artifacts in 3D image reconstructions. Figure 4(f) quantifies the reduction in metal artifacts magnitude (RMSE from ground truth). The trend in RMSE evaluated as a function of ϕ closely matches the MAA objective function (Q_poly (ϕ)), confirming the MAA prediction over a large range of tilted semi-circular orbits. Compared to an untilted orbit, the MAA orbit at ϕ = 5° or 27° reduced RMSE by ~70%, with little or no streak artifact visibly evident. As mentioned in §2.2.3, ϕ = 5° is preferred over 27°, since smaller tilt angles tend to give more reproducible geometric calibration and reduced chance of table collision.

3.2. Geometric calibration (studies #2 and #3)

Pertinent to studies conducted in Studies #2 and #3, figures 5(a) and (b) shows that the system geometry (e.g. piercing point location (u₀, v₀), detrended with its mean value) for the mobile C-arm in figure 1 was reproducible to a high degree, for both untilted and tilted semicircular orbits. Over a 10-hour period of normal use, the standard deviation (computed from 5 repeat calibrations) of the location of the piercing point was below 0.15 mm for both orbits at ϕ = 0° and ϕ = 30°. This degree of reproducibility was sufficient to maintain accurate image reconstruction, as illustrated in reconstructions of a 0.2 mm wire in figure 5(c) for both measured and interpolated calibrations. Note that mismatch of the geometric calibration from that of the actual tilt angle (figure 5(c3)) results in strong degradation of the image, and even small mismatches (figure 5(c4)) resulted in visible degradation of the point-spread function (PSF). Interpolation of the geometric calibration to match the actual tilt angle (figure 5(c5)) maintained the fidelity of the reconstruction (comparable to figures 5(c1) and (c2), where acquisition and calibration are at matched tilt angle).

Figure 5.

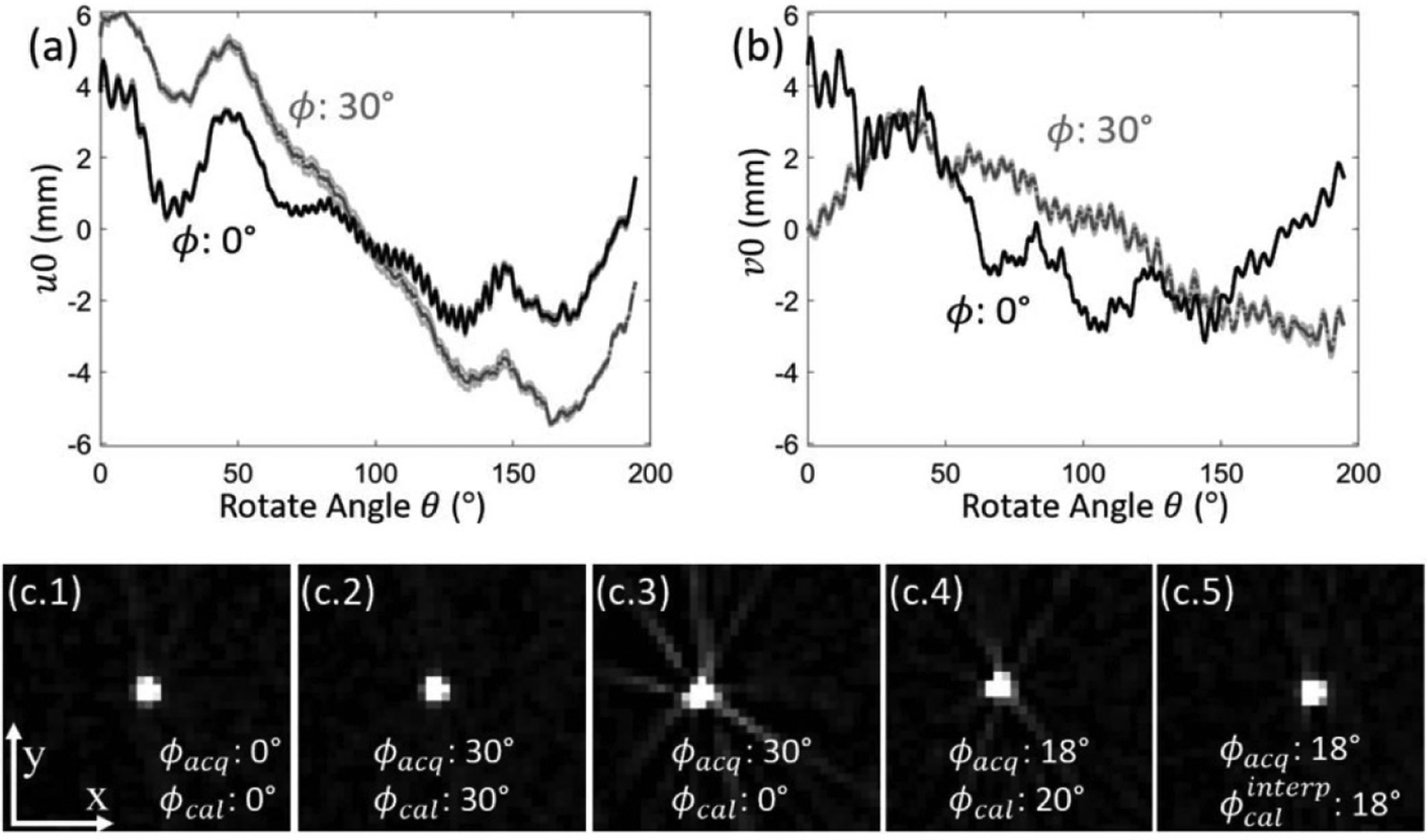
Geometric calibration of the tilted C-arm gantry. The reproducibility of calibration is demonstrated in the location of the piecing point (u₀, v₀) in (a) and (b) for tilt angles ϕ = 0° and ϕ = 30°. The 5 repeated calibrations over a 10-hour interval are overlaid in the shaded region for each curve. The PSF of a wire phantom in five different scenarios was shown in (c.1–5), where ϕ_acq denotes the gantry tilt for scanning, and ϕ_cal the tilt at calibration.

3.3. Metal localization (studies #2 and #3)

Figure 6 shows example μ_c and b_seg obtained from 6 projection views of the chest phantom (Study #2) and cadaver (Study #3). In each case, the optimal threshold-based segmentation (i.e. best case for which the threshold maximized Dice coefficient) is shown in comparison to b_seg obtained with the U-Net. The Dice coefficient (figure 6(e)) computed over all axial slices containing metal objects shows that the simple U-Net demonstrated better performance in segmenting the screws. The method was robust with sparsely sampled, coarse backprojections (N = 6 scout views) and was relatively insensitive to highly attenuating anatomy (e.g. bones). The method appears generalizable to a range of screw types, sizes, and materials (including types not seen in the training data), and it demonstrated robust performance in complex, realistic anatomy beyond that of the training data. Overall, compared with the best-case threshold segmentation, the U-Net segmentation yielded superior median Dice coefficient (0.71, compared to 0.53) and reduced variability (interquartile range, IQR) in Dice coefficient by 59%. While the median Dice coefficient would still be considered low for some applications (e.g. MAR), it appears to be sufficient in localizing metal objects for purposes of MAA orbit definition. Conversely, threshold-based segmentation was much less robust to other bright regions in μ_c (e.g. high attenuating anatomy) and resulted in large areas of false positives (figure 6(b)), which were observed to confound MAA orbit prediction (e.g. orbit tilt angle (ϕ) prediction from threshold based segmentation was off by 15° in study #3) and fail to capture important differences between positive and negative tilt angles.

Figure 6.

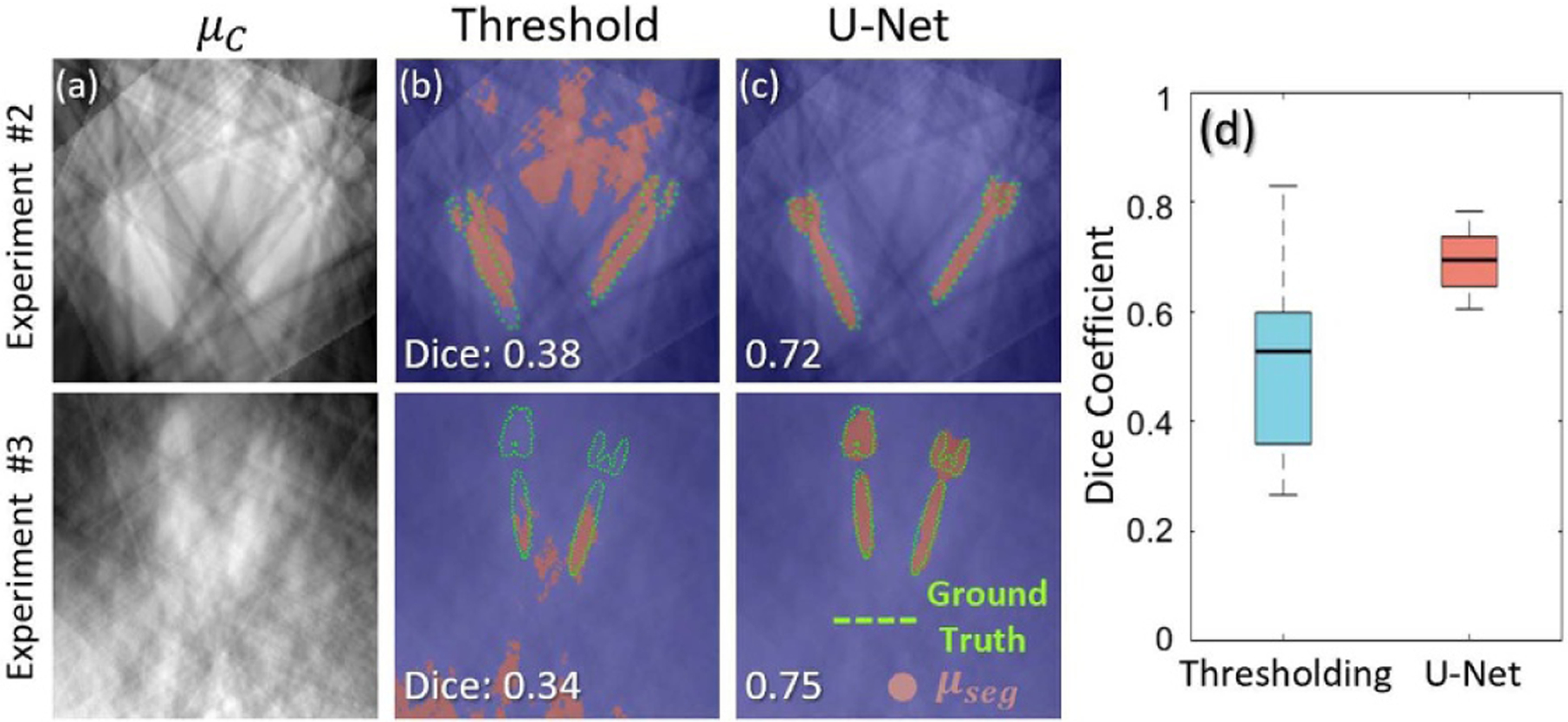
Coarse localization of metal objects from sparse projection views in Studies #2 and #3. (a) Axial plane (x-y plane) coarse backprojections (μ_c) from 6 scout projection views. (b) Example segmentation results (b_seg) using optimal-threshold-based method (threshold tuned to maximize Dice coefficient), showing false positives that can confound MAA performance. (c) Example segmentation results using a simple U-Net. Segmentation results are marked with red overlays, and ground truth is outlined with green dots. Example results from Study #2 (chest phantom) and #3 (cadaver) are shown in the first and second row, respectively. (d) Dice coefficient computed for optimal-threshold-based and U-Net segmentation methods.

3.4. Chest phantom experiment with spine screws (study #2)

Figure 7 shows MAA results for the chest phantom (Study #2), with the q_poly (θ, ϕ) metric map in figure 7(a) showing that positive tilt angles are likely to result in strong metal artifacts for this particular arrangement of spine screws (even worse than zero tilt). The corresponding Q_poly (ϕ) objective function monotonically decreases (improves) with negative tilt angle. The criterion for 5% of maximum-to-minimum range is achieved at ϕ ~ −24° as shown in in figure 7(b), and the tilted orbit at ϕ = −20° (labeled ➁, close to the MAA optimal tilt angle) shows strong reduction in metal artifacts compared to a conventional untilted orbit (ϕ = 0°, labeled ➂). The improvement is evident qualitatively in side-by-side comparison in figures 7(e) and (f) in terms of blooming and shading artifacts about the screw and visualization of surrounding tissues. Quantitative assessment of metal artifact reduction for 4 pedicle screws (one selected from each bilateral pair) is shown in figure 7(c). The metal artifacts magnitude for each screw peaks at a different value of ϕ, corresponding roughly to the out-of-plane angle of that particular screw, but the magnitude for all screws is lowest at ϕ = −20°, as predicted by MAA. Comparison of figures 7(d) and (b) confirms the predictive power of MAA in that the measured trend in artifact magnitude (figure 7(d)) matches well with the objective function Q_poly (ϕ) in figure 7(b).

Figure 7.

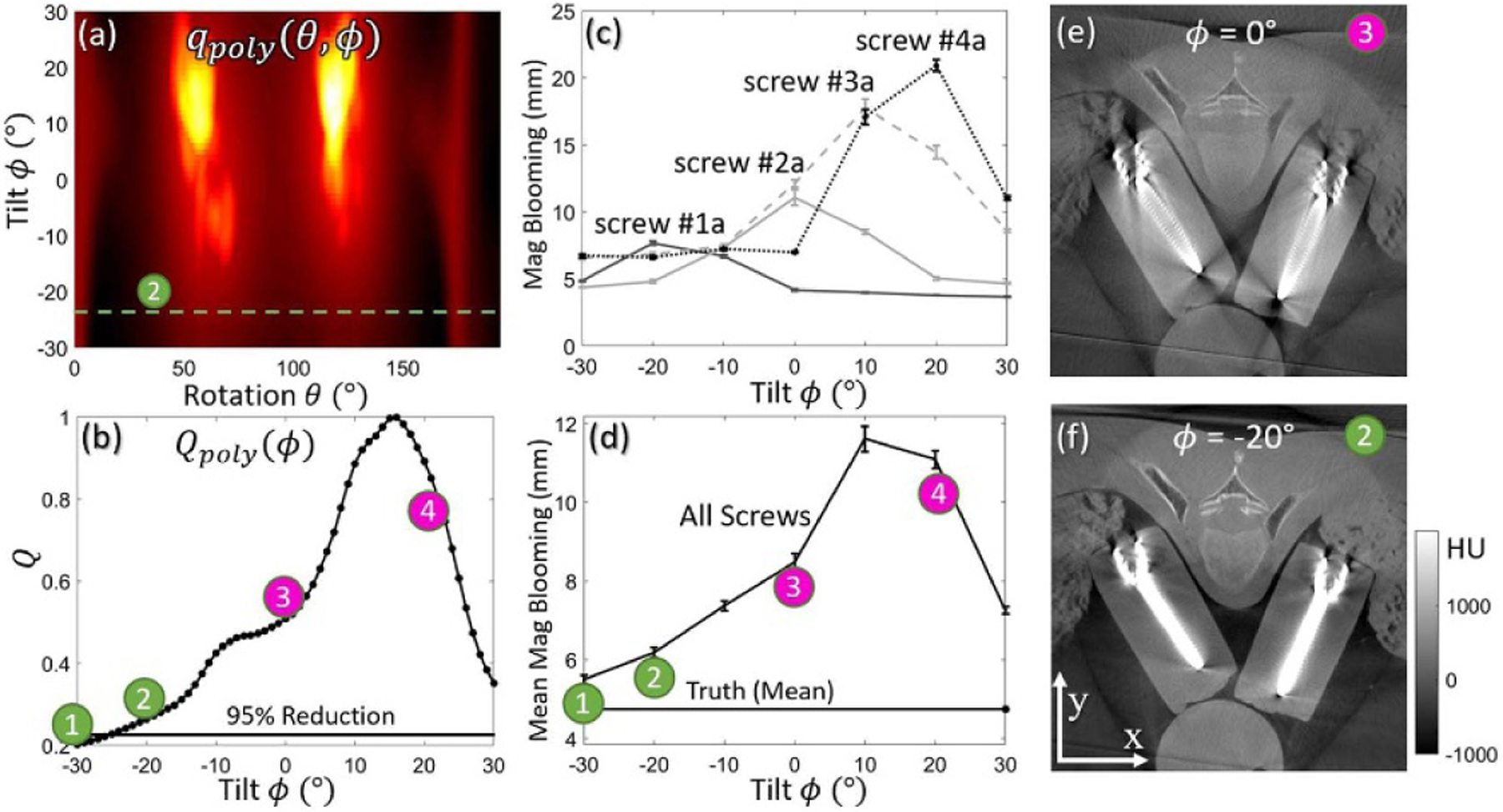
The MAA method applied to a chest phantom with four pairs of bilateral pedicle screws in Study #2. (a) Spectral shift metric map q_poly (θ, ϕ), with a tilted semi-circular orbit marked in green satisfying the 5% of maximum-to-minimum range criterion. (b) Objective function Q_poly (ϕ) determined from (a). (c) Magnitude of blooming artifacts vs. tilt angle for four screws. (d) Magnitude of blooming artifact averaged over eight screws measured as a function of tilt angle. Artifact magnitude was found to minimize at the tilt angle predicted by MAA (and same trend as (b)). (e–f) Axial image (through the shaft of screws #2 (a and b) acquired at gantry tilt angles, ϕ = 0° (➂) and ϕ = −20° (➁).

3.5. Cadaver experiment with implanted spine screws (study #3)

Results from the cadaver study (Study #3) are summarized in figure 8. The q_poly (θ,ϕ) metric map in figure 8(a) again suggests that negative tilt angles are strongly preferred (compared to zero or positive gantry tilt). The Q_poly (ϕ) objective function minimizes near ϕ ~ −10° (labeled ➀), and the MAA prediction is confirmed in terms of visual image quality in figures 8(c)–(e). Quantitation of metal artifacts (blooming) is shown in figure 8(b), where the overlaid plot (thin line with symbols and error bars) shows close correspondence with MAA prediction. The potential benefit of MAA artifact is evident with respect to the clinical task of visualizing the pedicle cortex immediately adjacent to the screws in figures 8(c.1)–(e.1); in many cases, only the MAA image provides unambiguous assessment of whether the screw has breached the cortex. In addition to reducing blooming artifacts, the MAA method also reduced soft-tissue noise and high-frequency streaks arising from the region of the pedicle screw. Compared to orbits at ϕ = 10° and ϕ = 0°, the MAA orbit (ϕ = −10°) achieved 39%–56% reduction in noise and high frequency streaks (as characterized by the standard deviation in voxel values with soft-tissue ROIs near the screw).

Figure 8.

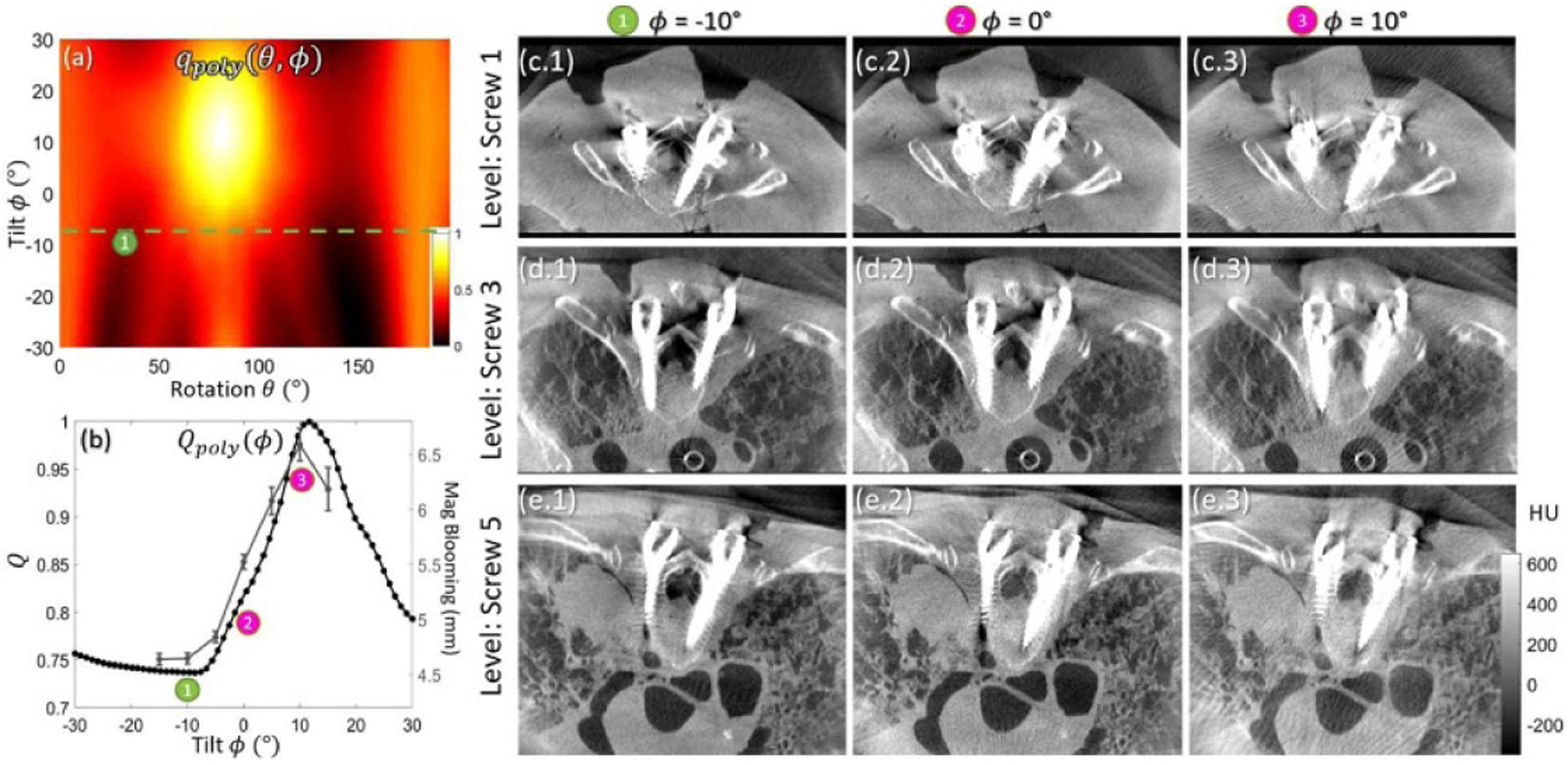
Study #3: Cadaver study with 6 pairs of implanted pedicle screws. (a) Spectral shift q_poly (θ, ϕ) metric map, showing reduction in spectral shift for tilt angles of ϕ ⩽ −10°. (b) The Q_poly (ϕ) objective computed as a function of C-arm gantry tilt. The minimum near ϕ = −10° suggests an optimal tilted orbit. Overlaid on the plot is a measurement of artifact magnitude (blooming) averaged over all 12 screws, in agreement with the MAA prediction. (c)–(e) Quasi-axial image slices (each slice oriented in plane with the screw shaft for purposes of visualization) at three vertebral levels. The optimal orbit as predicted by MAA was marked with ➀ in (a)–(e).

Figure 9 shows the image quality for the cadaver study with different scan orbits and post-processing methods. As in previous studies, the MAA method (figure 9(c)) substantially improved image quality compared to the Conventional case (figure 9(a)). Interestingly, MAA also outperformed the Conventional + MAR case (figure 9(b)), illustrating the importance of higher fidelity projection data acquired with the MAA orbit. As anticipated, the MAA + MAR case (figure 9(d)) appears best overall, confirming the compatibility of MAA with MAR post-processing.

Figure 9.

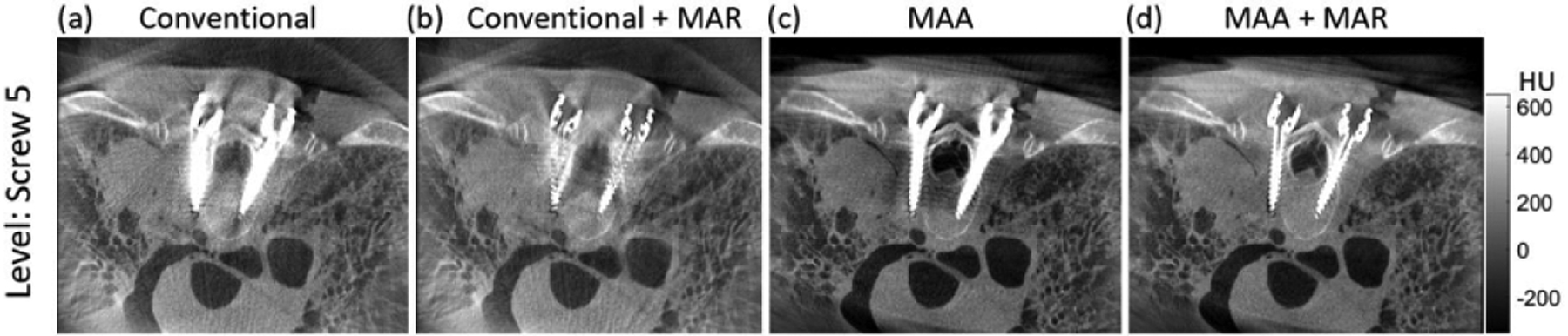
Quasi-axial image slice (in plane with one pair of pedicle screws) from the cadaver study. Four cases of orbit and processing method are illustrated: (a) ‘Conventional’ (untilted) orbit without metal artifact correction; (b) Conventional untilted orbit with MAR; (c) MAA orbit without metal artifact correction; and (d) MAA orbit with MAR.

3.6. Extension to non-circular orbits (study #4)

Figure 10(a) shows the q_poly (θ, ϕ) metric map computed for the simulated spine phantom in Study #4. Note the two bright regions corresponding to low-fidelity views (strong metal-induced bias) through the screw shaft. The optimal tilted semi-circular orbit based on Q_poly (ϕ) (minimization of equation (5)) features a tilt angle of ϕ ~ 4°, which avoids some of the low-fidelity views, but not all of them, as shown in figure 10(c), which exhibits fairly strong residual metal artifacts (though still an improvement over the untilted orbit, not shown for brevity). Note that Q_poly (ϕ) is an objective for the overall metal artifacts arising from all screws evident in the projection data; therefore, while a larger tilt angle (e.g. ϕ = −20°) might reduce the artifact associated with screw #3 (which has 0° out-of-plane angle as shown in figure 10(c)), it would result in increased metal artifacts for other screws like screw #1 and #2 (which have large, negative out-of-plane angles). For this case, there is therefore no single gantry tilt that substantially reduces metal artifacts for all screws.

Figure 10.

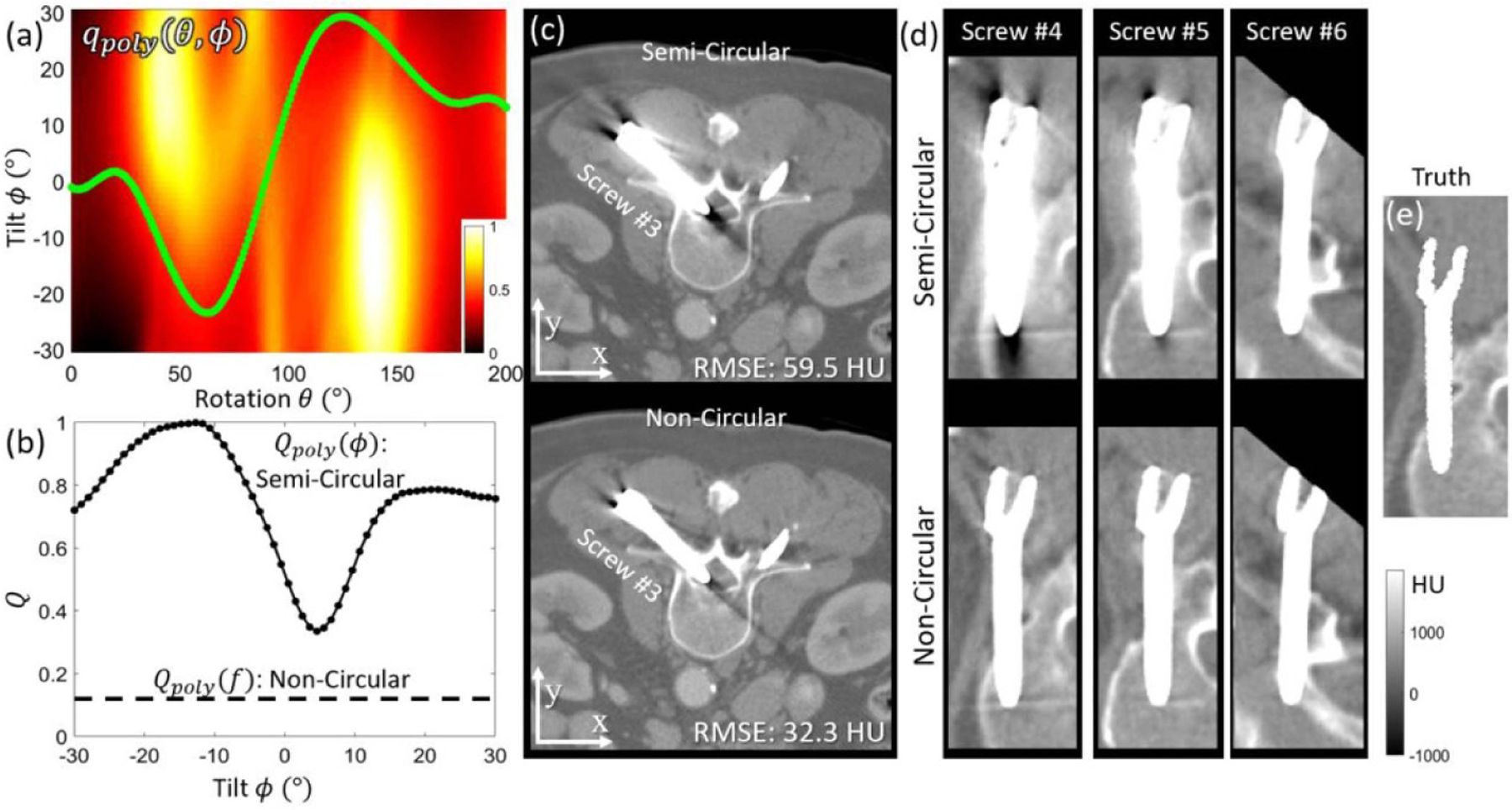
The MAA method for definition of a non-circular orbit in Study #4. (a) The q_poly (θ, ϕ) metric map with optimal non-circular orbit marked in green. (b) The Q_poly (ϕ) (semi-circular) objective plotted over a range of gantry tilt angles shows that the non-circular Q_poly (f) achieves a lower value than any setting of semi-circular orbit. (c) Axial slices (screw #3, which has 0° out-of-plane angle) imaged with optimal circular orbit (top) and non-circular orbit (bottom). Both were reconstructed with the PWLS method. (d) Three example screws (#4–6, with out-of-plane angles 0°, 11°, and 22°, respectively) acquired with the optimal semi-circular (top) and non-circular (bottom) orbit. The images correspond to quasi-axial slices oriented in plane with the shaft of each screw for purposes of visualization (e) Ground truth image of the simulated screw.

The issue is resolved by minimization of equation (6), resulting in a non-circular MAA orbit. The optimal non-circular orbit (computed by equation (6) and marked by the green curve overlaid in figure 10(a)) avoids most of the low-fidelity views and as shown in figure 10(b), resulted in a much lower Q_poly (f) characteristic compared to the semi-circular orbit (Q_poly (ϕ)). The optimal non-circular MAA orbit achieved a strong reduction in metal artifact for all screws—evident in figures 10(c) and (d). While some residual artifacts are still evident, the MAA orbit reduced overall RMSE by ~46%, confirming the effectiveness of the MAA method for definition of non-circular orbits. Moreover, it bears reiteration that the MAA method is compatible with MAR post-processing, which would presumably benefit from higher fidelity input associated with the MAA projection data.

4. Discussion and conclusions

The MAA method was demonstrated to accurately predict C-arm orbits that avoid metal artifacts by minimizing (or at least strongly reducing) biases in projection data associated with x-ray spectral shift (i.e. beam-hardening effects) imparted by metal objects. The method operates without strong priors on the patient (no need for a preoperative 3D image or anatomical model) or instrumentation (no need for exact knowledge of devices implanted in the patient). The MAA approach is fairly straightforward to implement on common intraoperative CBCT systems without major modification to image acquisition or reconstruction—e.g. FBP for tilted circular orbits or MBIR for complex non-circular orbits. Although not specifically examined in the current work, the MAA method could also be constrained to orbits suitable to other analytic reconstruction methods. (Katsevich 2003, 2004, Zou and Pan 2004, Pack et al 2005) Moreover, the method is compatible with post-processing MAR approaches (both in projection or image domain) and various forms of polyenergetic MBIR approaches to further reduce metal artifacts.

Such orbits require calibration of the C-arm geometry beyond the conventional single, untilted, circular scan. Phantom and cadaver studies on the mobile C-arm in figure 1 demonstrated that geometric calibration of tilted semi-circular MAA orbits could be achieved based on a set of calibrations acquired at various gantry tilt (e.g. circular scan calibrations performed at ±30° tilt in increments of 5° or 10°). Such calibrations demonstrated reproducible intrinsic and extrinsic parameters, permitting interpolation of projection matrices to estimate calibration at intermediate tilt angles with 3D image reconstruction indistinguishable from that acquired using calibration performed for the particular tilt angle. The feasibility and geometric calibration of non-circular orbits on the mobile C-arm system are subjects of other ongoing work. (Wu et al 2020a) Note also that the spline models for non-circular orbit prediction yields a smooth solution that does not require abrupt changes to the motor drives during the scan. Initial studies demonstrate non-circular orbits on the C-arm with simultaneous adjustment of ϕ and θ during the scan, and the geometric parameters for such non-circular orbits can be obtained by interpolating a library of pre-calibrated (tilted) circular orbits. (Wu et al 2020a)

A simple U-Net was implemented to segment metal objects in sparsely sampled coarse backprojection data (μ_c). The network performed well with as few as 2 views for simple objects (spheres and rods) and 6 views for more complicated objects (spine screws). Importantly, the MAA method does not require a highly accurate segmentation for orbit definition, and segmentation errors of several voxels did not strongly affect the resulting orbit. This is not the case for MAR, which can exhibit strong sensitivity to segmentation error, and even small errors on the order of 1 pixel can result in strong residual streak artifacts. (Pauwels et al 2014, Uneri et al 2019) The simple U-Net used in this work only segments metal objects within the FOV. Ongoing/future work includes improving the robustness of metal segmentation with fewer scout views (as few as 2 views), improving segmentation related to truncated metal objects, and integration of scout view acquisition within realistic clinical workflow. Work in progress suggests that a neural network that segments metal directly from scout views (with backprojection incorporated as a connection layer within the network) could achieve reasonable segmentation with just 2 scout views. (Wu et al 2020a) Other segmentation methods (e.g. Superpixel (Zhang et al 2016)) may also be investigated in future work.

The current work incorporated x-ray spectral shift (beam-hardening effects) as a surrogate for metal-induced bias in projection data. The q_poly (θ, ϕ) metric from equation (3) (and figures 4(c), 7(a), 8(a), and 10(a)) relates the magnitude of spectral shift in each view, and the Q_poly objective describes the variation in spectral shift from view to view, recognizing such inconsistencies as a source of metal artifacts. In this work, spectral shift at each pixel was treated equally (i.e. an unweighted summation in equation (3)). Assigning spatially-varying weights to each pixel (e.g. stronger weights to pixels attributing to clinically relevant ROIs—or weighting in accordance with the variance of pixel values as in PWLS) is the subject of possible future work.

A variety of alternative metrics (q) can be envisioned—for example, a metric based on the magnitude of the line integral (path length in metal) as a surrogate for photon starvation effects:

$$q_{\mathit{\text{atten}}}(\theta ,\varphi )=\sum _k\text{maxk}\left(p_{\mathit{\text{mono}}}(u,v\mid \theta ,\varphi )\right)$$ (9)

where terms are the same as in equation (3), and the summation over maxk identifies the k largest monoenergetic line integrals for each value of θ and ϕ. Such a metric reflects aspects of signal-to-noise ratio and could help to reduce noise and high-frequency streaks from the screw, improving soft-tissue contrast-to-noise ratio (CNR) and detectability. And because the magnitude of attenuation and spectral shift are closely related for a polyenergetic beam, the q_atten metric was found to follow q_poly in some situations. One can also envision a hybrid combination of q_poly and q_atten in the objective function to jointly minimize spectral and photon starvation effects. However, the q_poly metric was found to perform better in scenarios for which metal objects were the source of artifact—as often the case in image-guided surgery—with blooming and shading artifacts (from spectral shift) often being a more dominant source of image degradation than photon starvation. (Wu et al 2020bb) The computational cost for q_poly and q_atten metrics is similar, since the limiting step (p_mono calculation) is required for both, and both can still be calculated in near real-time. A metric such as that in equation (9) based on the magnitude of the line integral can be naturally extended to the spatial-frequency-dependent signal-to-noise ratio (i.e. the noise-equivalent quanta, NEQ), amounting to the ‘task-driven’ imaging paradigm that seeks an orbit to maximize 3D NEQ relative to the spatial frequencies associated with the imaging task. (Stayman et al 2019, Capostagno et al 2019) Other alternatives include metrics to minimize the influence of x-ray scatter (Zhao et al 2019), view sampling effects (Zhao et al 2014), lag/ghosting effects, and to improve sampling characteristics with respect to completeness and Tuy’s condition and ‘cone-beam’ artifacts. (Gang et al 2020) A combination of these metrics could also be envisioned.

Alternative objective functions (Q) can be envisioned as well—e.g. maximum/summation of q_poly at each θ—and were investigated in separate studies. (Wu et al 2020bb) The results for such objectives were similar in some cases to those shown below, and given the specific task of avoiding metal artifacts in IGS applications, the objective to minimize variations in spectral shift (equation (4)) was found to perform best overall. (Wu et al 2020bb) More complicated objective functions (e.g. leveraging the histogram of q_poly) is the subject of future work.

Another important point of consideration with applying the MAA method in clinical settings is potential collisions between C-arm and patient. In this work, the optimization problem for orbit prediction was constrained with an empirically chosen tilt angle range (ϕ = (−30°, 30°), which is a conservative range to avoid collision with the patient or the table). In current clinical practice, the standard methodology to avoid collision is a pre-scan check performed by moving the C-arm through the (untilted) orbit. There is currently no commonly available system to integrate the positions of the mobile C-arm with the position of the patient or table. In the current work, we ensured freedom from collision via pre-scan check after MAA orbit prediction, recognizing the additional step in workflow. One can certainly envision solutions that could relate the positions of the C-arm, patient, and table—e.g. using optical surface reconstruction. (Ladikos et al 2008) If such relationship is known, then a collision zone (represented by ranges of θ and ϕ) can be included as constraints in the MAA optimization problem. Other physical constraints, including limits on maximum acceleration (ϕ and θ direction), can also be included for a given system. Such constraints are not problematic for the optimizer used in this work (exhaustive search for circular orbits, and CMA-ES for non-circular orbits).

Another important point is the extent to which the proposed MAA method can be implemented with clinically acceptable runtime. Owing to the use of a pre-trained network for metal objects localization and a simple polyenergetic model (LUT) for spectral shift calculation, the MAA method yields an orbit prediction in near real-time (seconds). For non-circular orbits, 3D image reconstruction invites the use of MBIR method, and while little effort was paid to image reconstruction runtime in the current work, acceleration strategies are emerging that could yield MBIR images with clinically acceptable runtime. (Wang et al 2015, Sisniega et al 2019)

In conclusion, the studies reported in this work demonstrate the first testing and evaluation of the MAA approach over a range of anatomical contexts and metal instrumentation, focusing on imaging in the presence of spine screws. MAA correctly predicted tilted circular or non-circular orbits for realistic arrangements of surgical instrumentation and reduced the influence of metal artifacts in images both visually and quantifiably. Tilted circular orbits identified by MAA were shown to substantially avoid metal artifacts (i.e. reduce the magnitude of metal artifacts in raw, uncorrected 3D image reconstructions), and extension of the MAA approach to non-circular orbits showed further improvement.

It bears reiteration that MAA is not intended as a blanket substitute for MAR post-processing or polyenergetic MBIR. In some instances, the raw 3D image reconstruction resulting from an MAA orbit may be sufficient for the imaging task. More generally, however, the MAA method provides a relatively simple, practical means to obtain projection data that are less influenced by metal-induced bias, allowing MAR post-processing or iterative methods to perform even better.