Significance
Nonlinear optics in topological semimetals is a burgeoning field of research with an expanding list of new materials but limited choice of probes. We devised, modeled, and implemented an approach for investigating nonlinear optics at the nanoscale with a metallic tip. Far-field nonlinear optics are diffraction-limited and probe the in-plane response only. Our tip-based approach circumvents the diffraction limit and provides strong field enhancement for both in-plane and out-of-plane fields. We therefore gain access to complete nonlinear tensors including components not attainable before. One immediate application of our approach is the separation of surface state and bulk nonlinear responses in Weyl semimetals. Applying near-field probes to topological semimetals constitutes a new paradigm of research on nanoscale nonlinearity.
Keywords: Weyl semimetal, near-field optics, nonlinear photocurrent
Abstract
Chiral Weyl fermions with linear energy-momentum dispersion in the bulk accompanied by Fermi-arc states on the surfaces prompt a host of enticing optical effects. While new Weyl semimetal materials keep emerging, the available optical probes are limited. In particular, isolating bulk and surface electrodynamics in Weyl conductors remains a challenge. We devised an approach to the problem based on near-field photocurrent imaging at the nanoscale and applied this technique to a prototypical Weyl semimetal TaIrTe4. As a first step, we visualized nano-photocurrent patterns in real space and demonstrated their connection to bulk nonlinear conductivity tensors through extensive modeling augmented with density functional theory calculations. Notably, our nanoscale probe gives access to not only the in-plane but also the out-of-plane electric fields so that it is feasible to interrogate all allowed nonlinear tensors including those that remained dormant in conventional far-field optics. Surface- and bulk-related nonlinear contributions are distinguished through their “symmetry fingerprints” in the photocurrent maps. Robust photocurrents also appear at mirror-symmetry breaking edges of TaIrTe4 single crystals that we assign to nonlinear conductivity tensors forbidden in the bulk. Nano-photocurrent spectroscopy at the boundary reveals a strong resonance structure absent in the interior of the sample, providing evidence for elusive surface states.
Nonlinear optical effects emerge when a material’s polarization density reacts to second- or higher-order powers of the electric field of light (1). For example, the second-harmonic generation (SHG) describes the phenomenon where the incoming light frequency ω is transformed to 2ω after interacting with the nonlinear medium, characterized by the SHG susceptibility . A close counterpart of the SHG is the bulk photovoltaic effect (BPVE), where a direct current (dc) is generated in the bulk of the sample with finite frequency excitation at ω, described by the nonlinear conductivity . Optical nonlinearities play a preeminent role in modern photonics. Applications aside, nonlinear effects are connected to geometrical properties of the electronic wavefunctions (2–5) often categorized under the notions of Berry curvature/connection and have emerged as key probes of topological effects in semimetals (6–12).
Along with band topologies, crystal symmetries play a preeminent role in optical nonlinearities. Nonmagnetic Weyl semimetals break the inversion symmetry and therefore fulfill the requirement for the observation of various second-order nonlinear responses. Extraordinarily strong SHG has been observed in the Weyl semimetal TaAs (6). However, the energy scale associated with the large SHG ( eV) exceeds that of the Weyl bands by at least an order of magnitude (13, 14) and contributions irrelevant to Weyl physics have to be considered. Since the Berry curvature Ω associated with the Weyl points is divergent in the momentum space (3, 5) as , low-energy midinfrared and terahertz photons are best suited to probe the electrodynamics associated with Weyl points. Indeed, giant BPVE [also known as shift current (15, 16)] has been observed in TaAs in the midinfrared at ( cm– 1) (7) and in TaIrTe4 at m () (8). The shift current tensor encodes the nonlinear light–matter interaction in a steady-state dc , where ( or c) is the light electric field. Beyond bulk Weyl points, another defining aspect of the Weyl semimetal is the unique surface states connecting the projection of the bulk Weyl points (13, 14). Due to the metallic nature of the bulk, such surface conducting channels are extremely challenging to disentangle from bulk response using linear transport and conventional optical measurements (17).
Nonlinear responses offer a symmetry-based approach to distinguish the surface and bulk responses. Indeed, both SHG (18) and photocurrent (19) are adept at isolating the surface states response of a three-dimension topological insulator from that of the bulk because the latter vanishes by virtue of inversion symmetry. However, this elegant approach is inept for nonmagnetic Weyl semimetals where inversion symmetry is broken both in the bulk and at the surfaces. Novel nonlinear observables with the bulk and surface selectivity are therefore highly desirable. In this work, we establish near-field nano-photocurrent imaging as a powerful symmetry-sensitive approach for investigating nonlinear optical responses with a metallic tip. Different nonlinear conductivity tensors are differentiated by their distinct real-space photocurrent patterns. The net effect is that the bulk and surface contributions of Weyl semimetals are disentangled by their inherent “symmetry fingerprint” in real space.
We utilized a near-field optical microscope for nano- photocurrent measurements in the midinfrared range (11 to 4.5 µm) with -nm spatial resolution limited by the metallic tip apex (Fig. 1A). We focused on the type-II Weyl semimetal TaIrTe4 (20, 21) and the measured nano-photocurrent pattern shows intriguing reversals in sign that depend on the crystal axis. This pattern was successfully reproduced using the Shockley–Ramo (SR) formalism adapted for nonlocal photocurrent response (22). We augmented this analysis approach for experimental settings with an optical antenna: the metallic tip in our near-field apparatus. The antenna simultaneously provides the in-plane (Ea, Eb) and the out-of-plane (Ec) electric fields and generates the nonlinear shift current via (i = a or b). The photocurrent patterns in the interior of the crystals reveal strong directionality in TaIrTe4. The spectral characteristics of the nano-photocurrent in the interior include a broad maximum around 1,400 cm– 1 that is accounted for by the density functional theory (DFT) calculations. We also discovered robust photocurrent responses near the edges of the crystal that can be understood with a nonlinear tensor forbidden in the bulk. The spectral response of edges reveals an additional resonance structure compared to the interior photocurrent. We discuss the spectroscopic features of these resonances in relation to the expected surface states in TaIrTe4.
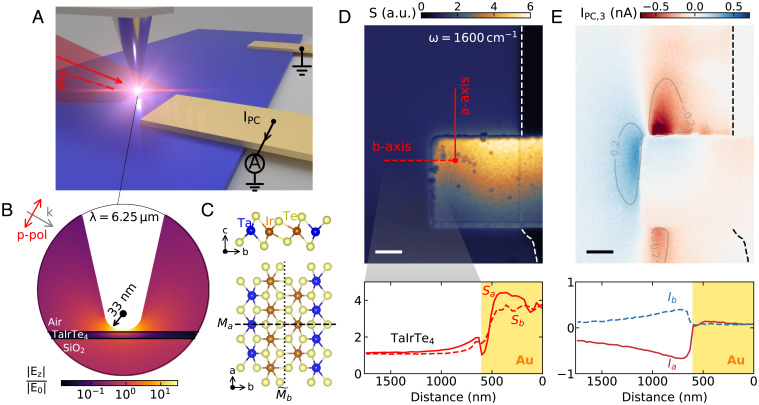
Fig. 1.
Near-field nano-optical and nano-photocurrent experiments on TaIrTe4. (A) Schematic for nano-infrared and nano-photocurrent measurements where the scattering (S) and zero-bias photocurrent () signals are collected simultaneously. (B) Simulation of the field enhancement for the z-component of the electric field (Ez) for a metallic tip ( 30-nm radius) close to TaIrTe4 surface with p-polarized incident light. (C) Crystal structure of TaIrTe4 for the side view (Upper) and top view (Lower). (D) Nano-infrared image of the scattering amplitude at (m) for a 12-nm-thick sample (Sample 1) at ambient conditions. (Lower) The linecuts along the a-axis (red solid line) and b-axis (red dashed line). (E) Nano-photocurrent map of the same region as in D, showing clear direction-switching pattern near the Au contact. (Lower) The linecuts of taken along the same paths as in D. (Scale bars in D and E, 600 nm.)
We exfoliated the bulk crystal and deposited gold electrical contacts on the thin TaIrTe4 flakes, as shown schematically in Fig. 1A (see Methods for details). A midinfrared laser was focused on a metallic atomic force microscope tip that raster-scans across the sample in the tapping mode. Local near-field signal is scattered out by the tip and detected in the far field while the photocurrent signal is amplified and detected via one of the Au contacts. Both the scattering signal and the photocurrent signal are demodulated at high harmonics of the tip-tapping frequency to suppress the far-field background (see Methods). The deep-subdiffractional mapping concurs with strong field enhancement under the metallic tip (Fig. 1B), allowing access of the nonlinear shift current tensor components with z axis electric field.
We begin with a direct comparison of the scattering and photocurrent signals for a 12-nm-thick TaIrTe4 nanocrystal (Sample 1). In Fig. 1 D and E we display the local near-field scattering amplitude and photocurrent signal collected at laser frequency at room temperature, respectively. At , the reflectance contrast along a- and b-axis is around Ra (ω)/Rb (ω) = 1.7 (SI Appendix, Fig. S1). However, this anisotropy is not readily captured in antenna-based nano-infrared experiments (23, 24). Indeed, Fig. 1D shows a homogeneous scattering amplitude along the a- and b-axis. Remarkably, the nano-photocurrent map in Fig. 1E evinces a completely different picture. We observe strong “hot spots” near the Au contact and the polarity of the photocurrent at these hot spots depends on the crystal axes. The photocurrent signal also vanishes close to the sample edge (black dashed line) aligned with the a-axis of the crystal. We emphasize that in Fig. 1E the wavelength of laser light (m) is larger than the entire image and the direction-switching behavior will be smeared out with conventional far-field scanning photocurrent measurements. Furthermore, through the analysis of signal decay with the increasing tip-tapping harmonic, we confirmed that the observed nano-photocurrent signal originates from the local evanescent fields underneath the tip (see SI Appendix, Figs. S2 and S3).
The characteristic direction-switching photocurrent pattern is also robust with changing laser frequencies (SI Appendix, Fig. S17). In Fig. 2A, the nano-photocurrent at m () for Sample 1 is shown, with direction-switching pattern on both the collecting and the ground contacts. To gain insights into the spatial nanotextures of the photocurrent, we utilized the standard SR formalism (22, 25) to model the nano-photocurrent map. The SR theorem provides a basis for understanding complex spatial patterns of photocurrent where current collection is nonlocal. Specifically, the measured current (IPC) between electrical contacts is related to the local source of photocurrent via
| [1] |
where C is a prefactor governed by the device configuration. is an auxiliary weighting field determined by solving the Laplace equation for a suitable potential and boundary conditions. Modeling based on the SR formalism has been successfully applied to graphene (26, 27) and topological insulators (28) to interpret experimental real-space photocurrent patterns. The SR analysis involves first solving the auxiliary weighting field and then collecting the product of local photocurrent and . Among the seven symmetry-allowed shift current tensors in TaIrTe4 (, σcaa, σcbb, σccc), only σaac and σbbc give rise to in-plane photocurrent (8), provided out-of-plane electric fields are present. In our experiment and simulations, the tip provided both the in-plane and out-of-plane electric fields that generate local in-plane photocurrent in the sample via . We remark that while the c-axis electric field (Ec) originating from the tip is rotationally symmetric and has a definite sign (Fig. 1B), the in-plane components (Ea and Eb) have a dipole-like pattern, as shown in Fig. 2B. Both the c-axis (Fig. 1B) and in-plane tip electric fields (Fig. 2B) were simulated based on the experimental configurations taking into account the dielectric functions of TaIrTe4 (SI Appendix, Fig. S1). The calculated electric field distribution can be well-approximated with the simple point-charge model and for the tip, where d is the height of the charge and r is the in-plane distance away from it (see SI Appendix, Figs. S5 and S6).
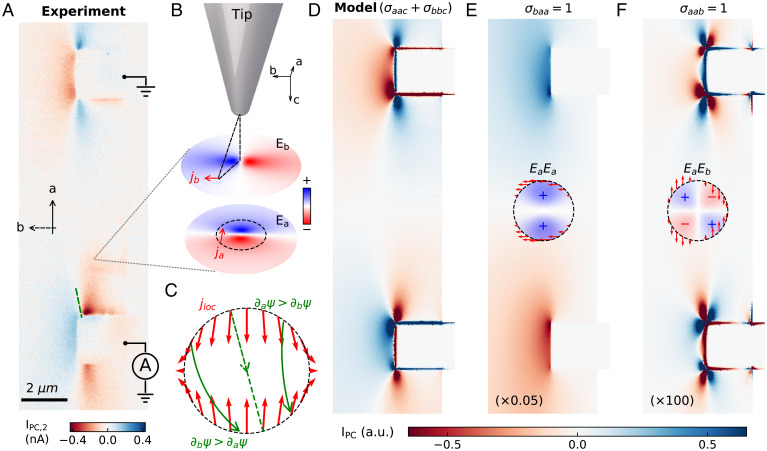
Fig. 2.
Nano-photocurrent experiment and modeling based on the SR theorem. (A) Nano-photocurrent map of Sample 1 at m, showing similar direction-switching behavior as in Fig. 1E. (B) Tip-mediated nonlinear photocurrent generation in the interior of the sample. Color plots are numerical calculation of the tip electric fields in the sample. (C) Magnitude and direction of the (red arrows) on a 100-nm-diameter circle centered at the tip position according to . Green arrows are schematics of the auxiliary field distribution . (D) Model simulation of the nano-photocurrent pattern with the profile in C, showing good agreement with the experiment. (E) Model simulation using , showing no direction-switching pattern near the contact. (Inset) The simulated distribution and the corresponding photocurrent (red arrows). (F) Model simulation using , showing more sign changes near the contacts compared to the experiment in A. (Inset) The simulated distribution and the corresponding photocurrent (red arrows). The magnitudes of the simulated photocurrent in E and F are scaled by 0.05 and 100 times, respectively. a.u., arbitrary units.
In general, the two shift current tensors σaac and σbbc in an anisotropic material are different and may have opposite signs (3, 5). Accordingly, the direction of deviates from the direction of the local field produced by the tip (). Therefore, both the magnitude and the direction of varies as a function of in-plane angle with respect to the tip. In Fig. 2C, we illustrate an example of the calculated using the point-charge model of the optical antenna with . The magnitude of the generated photocurrent follows the decay of the tip electric fields away from the tip center position . As a result, from a finite area of the sample will contribute to the final collected at each tip location (see SI Appendix, section III). We emphasize that reverses sign when r is reversed, as shown by the two red arrows connected with a green dashed arrow in Fig. 2C. This symmetry of is imposed by the tip electric fields as is odd in r (Fig. 2B) while is even in r (Fig. 1B). Because depends both on and , finite difference in (green solid arrows in Fig. 2C) will lead to finite photocurrent even in the interior of the sample. This nanoscale asymmetry in combined with the nonlinear mechanism of leads to the observed direction-switching behavior around the contact.
The combination of SR formalism (Eq. 1) and the tip-mediated shift current generation (Fig. 2 B and C) determine the at any point inside the sample, thus facilitating detailed comparisons with experiments. Indeed, the real-space simulation shown in Fig. 2D exhibits an excellent agreement with the experimental photocurrent map (Fig. 2A) using . The direction-switching behavior near the contact is captured in the simulation using (Fig. 2C). We remark that direction-switching pattern is only weakly sensitive to the precise ratio of (SI Appendix, Fig. S11) but is strongly influenced by the dc anisotropy ratio . With increasing , the “zero-crossing” photocurrent direction (green dashed line in Fig. 2A) will bend toward the a-axis of the crystal (SI Appendix, Fig. S9). We therefore conclude that our observed photocurrent pattern is dominated by the bulk TaIrTe4 through shift current tensors σaac and σbbc.
The tip-promoted shift current generation mechanism yields verifiable predictions for other nonlinear tensors. For example, the surface of the TaIrTe4 breaks the glide mirror symmetry () (10) and allows σbaa and σaab to appear at the surface and contribute to . Since depends on even order of the in-plane electric field Ea, it always points to the same direction (Fig. 2E inset). Therefore, the direction-switching photocurrent pattern near the contact is absent for σbaa (Fig. 2E). On the other hand, has a quadruple-like pattern (Fig. 2F, Inset) and leads to additional sign reversals for (Fig. 2F). Furthermore, we also considered the photothermoelectric (PTE) effect [reported in nano-photocurrent experiments on graphene (29–31)] and the direction-switching pattern is also absent in the PTE simulation (SI Appendix, Fig. S10). We refer to these distinct photocurrent patterns (Fig. 2 D–F) as the inherent “symmetry fingerprints” of the underlying nonlinear conductivities.
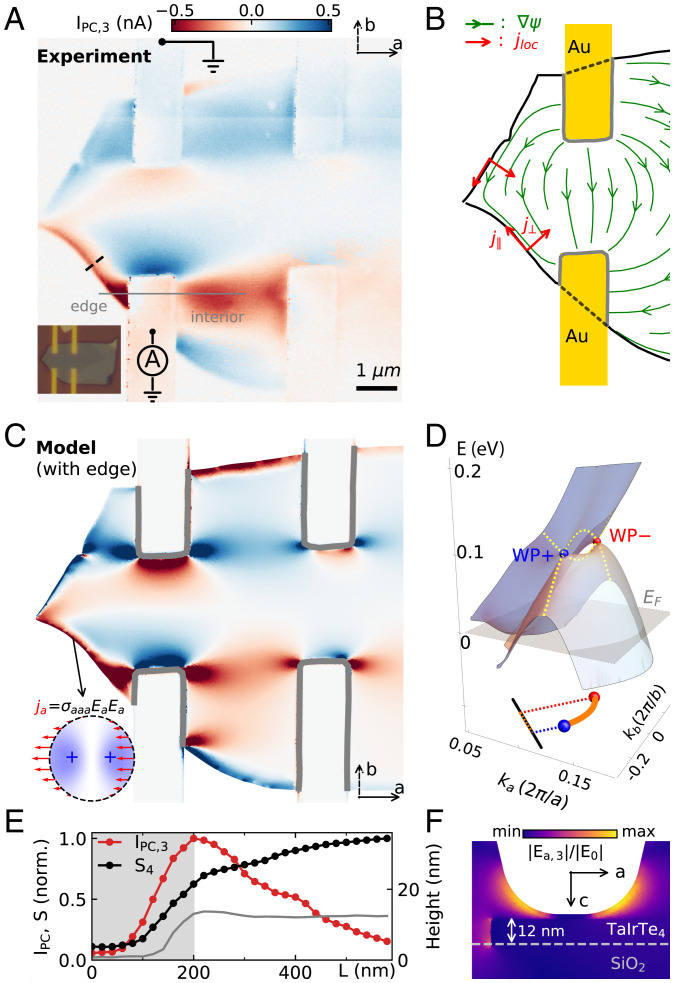
By analyzing the photocurrent along the perimeter of the TaIrTe4 crystal we gain a complimentary access to the surface response of a Weyl semimetal. To explore the photocurrent at the boundary, an additional device with contacts along both a- and b-axis was fabricated and investigated: Sample 2 in Fig. 3A. The nano-photocurrent map demonstrates direction-switching behavior near the Au contacts similar to that in Figs. 1E and 2A (Sample 1). Remarkably, we also observe prominent photocurrent localized near the boundary of the sample, in stark contrast to Sample 1 with the edge oriented along the a-axis. These contrasting trends are understood from the symmetry of the edges within the SR formalism (26, 32). In TaIrTe4, the mirror symmetry Ma (Fig. 1C) will force any local boundary photocurrent to be perpendicular to the a-axis. Since the boundary condition ensures that only tangential components of exist near the sample boundaries (Fig. 3B), no photocurrent will be collected if mirror symmetries force to be perpendicular to the edge. The observation of boundary photocurrent in Sample 2 (Fig. 3A) therefore suggests local photocurrent flowing parallel to the mirror-symmetry-breaking edges ( in Fig. 3B). Among the six shift current tensors allowed at the boundaries (SI Appendix, Fig. S12), we find that σaaa and σabb give a consistent boundary photocurrent pattern as observed in the experiment. In Fig. 3C the simulation using for the interior and at the edge is shown, again exhibiting good agreement with the data (Fig. 3A). The mirror-symmetry-braking edges therefore offer an additional photocurrent response devoid of bulk contributions.
Fig. 3.
Boundary photocurrent in TaIrTe4. (A) Experimental photocurrent map in a four-terminal device (Sample 2), displaying direction-switching real-space pattern near the ground (top left) and collecting (bottom left) contacts. The two contacts on the right are floated. (Inset) An optical image of the device. (B) Simulation of the auxiliary field (green arrow) for Sample 2 under the SR scheme. Red arrows indicate local photocurrent generated near the boundary of the sample. (C) Model simulation of the nano-photocurrent pattern with the profile in Fig. 2C for the interior and additional boundary photocurrent contribution (Inset), showing good agreement with the experiment. (D) Band structure of TaIrTe4 showing two of the four Weyl points at around 0.1 eV above the Fermi energy (EF). (Bottom Inset) The finite projection of Fermi-arc states on a mirror-symmetry breaking edge (black line). (E) Photocurrent (red) and scattering amplitude (black) along the black dashed line in A. The photocurrent is peaked at the physical edge ( nm). The gray solid line is the corresponding topography profile. (F) Numerical simulation of the in-plane electric field (Ea) in the ac-plane (side view) for tip position located 40 nm away from the sample edge.
The boundary photocurrent signals described by σaaa and σabb may entail the surface state response in TaIrTe4. In Fig. 3D, the band structure of TaIrTe4 near the Weyl points obtained from DFT calculations is shown. The bottom schematic illustrates the nonvanishing projection of the Fermi-arc surface state (orange curve) on the mirror-symmetry-breaking edge and surface. We examine the photocurrent and the concurrent near-field scattering amplitude through a linecut across the edge (black dashed line in Fig. 3A), shown in Fig. 3E. The scattering amplitude (S4) is enhanced at the boundary of the sample ( nm) and keeps increasing gradually toward the interior of the sample. In contrast, the photocurrent signal is peaked at the boundary and slowly decays in the interior. Such a slow decay of boundary photocurrent can be understood by the slow decay of in-plane electric field Ea. Physically, the photocurrent in Fig. 3E contain contributions from both the one-dimensional boundary in the ab-plane and the side surface of the sample due to its finite thickness. In Fig. 3F (SI Appendix, Fig. S6) the simulated in-plane electric fields on the side (top) surface remain prominent even as the tip is 40 nm ( nm) away from the edge. As a result, the photocurrent due to the boundary and side surface could still be collected as the tip is located a few hundred nanometers away from the edge.
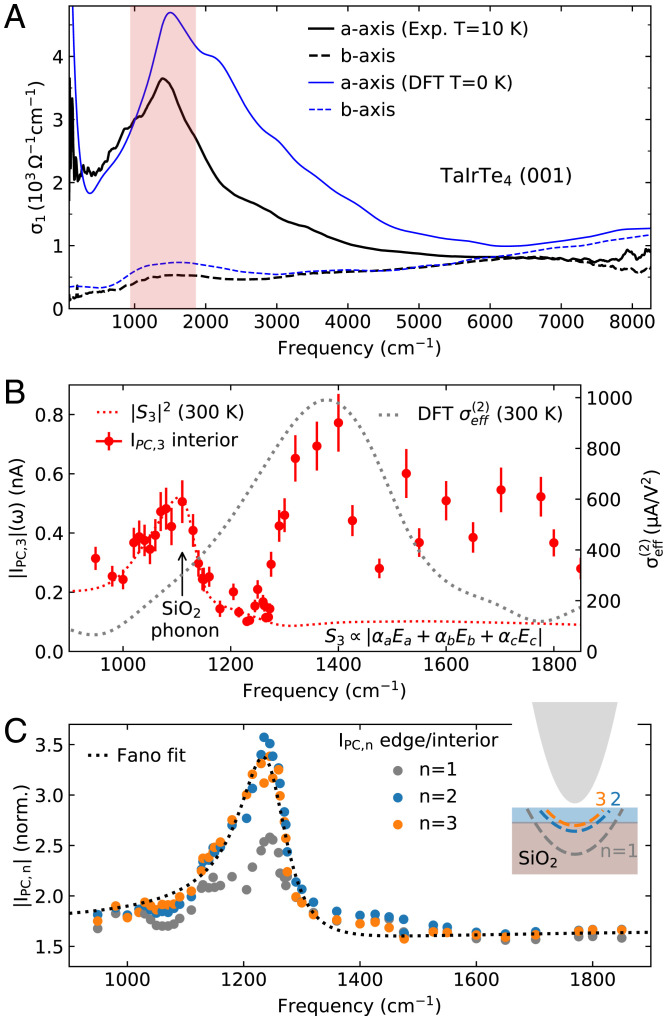
Complementary to spatial patterns, spectroscopic measurements offer additional insights on the origin of the photocurrent. We begin with the linear optical conductivity spectra extracted from the broadband infrared reflectance spectra (SI Appendix, Fig. S1). In Fig. 4A, the real part of the experimental optical conductivity () at T = 10 K is compared with DFT calculations (0 K) for both the a- and b-axis. The overall agreement between the experimental and DFT calculations for TaIrTe4 is excellent among topological semimetals (33, 34). The dramatically enhanced optical conductivity along the a-axis compared to the b-axis is consistent with the quasi-one-dimensional Ta and Ir chains along the a-axis of the crystal (Fig. 1C).
Fig. 4.
Linear and nonlinear spectroscopy of TaIrTe4. (A) Comparison of experimental linear optical conductivity at 10 K (black) with DFT calculations (blue solid and dashed lines). Red-shaded region corresponds to the frequency range where the photocurrent spectroscopy measurements were performed. (B) Photocurrent spectroscopy for the interior of the sample (red dots), showing a narrow peak due to the SiO2 phonon and a broad peak near 1,400 cm– 1. Gray dotted line is the DFT calculation of at 300 K. Red dotted line is the calculated near-field scattering amplitude square using experimental dielectric function at 300 K (SI Appendix, Fig. S1). (C) Photocurrent spectroscopy of the edge response normalized by the interior response at different tip-tapping harmonics (n = 1, 2, 3). The normalized spectra show asymmetric behaviors that are fitted by a Fano line shape (dotted line). (Inset) A schematic of the extent of the tip electric field into the sample for different tip-tapping harmonics.
Near-field photocurrent spectroscopy augments the nano-photocurrent pattern with crucial frequency-domain information. We performed spectroscopic nanoimaging along the gray line in Fig. 3A, which contains both the boundary and interior regions. The photocurrent amplitude at the boundary and in the interior are spatially averaged to compare their frequency dependence. In Fig. 4B, the interior photocurrent spectrum is represented as red dots, with a peak near 1,130 cm– 1 that comes from the SiO2 phonon (35). Interestingly, this phonon feature from the substrate can be well-described by the square of the near-field scattering amplitude ( red dotted line) calculated via the lightning-rod model (36) (see SI Appendix, section V). The scattering amplitude S encodes the local tip–sample interaction but is still a linear function of the dielectric function (or equivalently the optical conductivity ). As a result, large deviation appears near 1,400 cm– 1, where a broad peak appears in the photocurrent yet is absent in the calculation based on experimental . The DFT calculation for the effective shift current tensor (dotted gray line) reproduces the photocurrent peak near 1,400 cm– 1, further attesting to the nonlinear shift current mechanism observed through real-space patterns (Figs. 2 and 3).
The agreement of the interior photocurrent with DFT calculations of bulk shift current tensors provide a basis for understanding the photocurrent at the boundary. We normalized the boundary photocurrent by the interior photocurrent as depicted in Fig. 4C for different tip-tapping harmonics. Interestingly, a clear resonance near 1,240 cm– 1 ( 0.15 eV) appears in all three harmonics. Such a resonance is distinct from the SiO2 resonance ( 1,130 cm– 1) and is also not predicted by the bulk shift current calculations (Fig. 4B). As we have demonstrated from spatial modeling, the photocurrent at the boundary originates from σaaa and/or σabb allowed at mirror-symmetry-breaking edges. It is likely that this additional resonance comes from σaaa and σabb where surface-state-related optical transitions around 0.15 eV can contribute (21, 37, 38). Such a scenario is consistent with the tip-modulation pattern of the normalized photocurrent spectrum and also with the asymmetric spectral shape of the resonance. As demonstrated in near-field studies of topological insulator surface states (39), higher tip-tapping harmonics are dominated by response of the surface since the electric fields are more confined spatially (Fig. 4C, Inset). Compared to n = 1, the normalized at n = 2 and 3 indeed show less influence from the SiO2 resonance at 1,130 cm– 1 and stronger resonance near 1,240 cm– 1. Furthermore, the asymmetric lineshape of and can be well-described by a fit with a Fano-type line shape (40): (fitting parameters are listed in SI Appendix, Table S2). This formula describes the interaction of a resonant transition at frequency ω0 and a continuum of background transitions, where γ is the width of the resonance, b is an offset, and q is the Fano parameter. The good agreement of the Fano-type asymmetric lineshape and the harmonic dependence of the boundary photocurrent provide evidence for the elusive surface states in TaIrTe4.
In this work, we investigated the Weyl semimetal TaIrTe4 with near-field nano-photocurrent imaging and spectroscopy. Unique direction-switching patterns appear in the photocurrent map and are successfully identified as tip-mediated nonlinear shift current through extensive spatial modeling. Surface- and bulk-related nonlinear contributions are further distinguished through their distinct “symmetry fingerprints” in the photocurrent maps. We also discovered robust boundary photocurrent features that are not explained by the bulk nonlinear response. Asymmetrical spectral line shape and the harmonic dependence of the nano-photocurrent spectra further support the surface-state origin of the photocurrent at the boundary. Applying near-field probes to topological semimetals constitutes a new paradigm of research on nanoscale nonlinearity. Our combined experimental and theoretical approach also paves the way for investigating more complex correlated electronic phenomena in real space (41, 42).
Methods
Single Crystal Growth
High-quality single crystals of TaIrTe4 crystals were grown using the self-flux method with Te as the flux (43). Ta powder, arc-melted Ir, and Te chunks with a molar ratio of Ta:Ir:Te = 3:3:94 were loaded into a 5-mL alumina crucible. The crucible was then sealed inside a quartz tube under one-third of atm of Ar. The growth ampule was heated up to 1,200 ∘C in 5 h, held at 1,200 ∘C for 3 h and then slowly cooled to 550 ∘C at a rate of 2 ∘C/h. Single crystals of TaIrTe4 were then separated from the liquid flux using a centrifuge.
Device Fabrication
TaIrTe4 flakes were mechanically exfoliated from single crystals to the target Si/SiO2 (285 nm) substrate using Scotch tape. After we chose thin flakes based on optical contrast, we deposited the contacts (Cr/Au: 5 nm/45 nm) using e-beam evaporation (angstrom). The thickness of the flakes was measured by atomic force microscopy.
Nano-Optical and Nano-Photocurrent Measurements
Room-temperature nano-optical and nano-photocurrent measurements were performed in a commercial s-SNOM from Neaspec GmbH. We used tunable quantum cascade lasers from Daylight Solutions and the incident laser power was around 20 mW. The photocurrent was amplified using a Femto DLPCA-200 current amplifier and then demodulated at higher order (n > 1) of the tip-tapping frequencies (around 75 kHz). A function generator that outputs known alternating current voltages at different harmonics of the tip tapping was used to convert the measured current signal to physical units.
Acknowledgments
Nano-photocurrent research is a collaborative pro- ject between the Center for Novel Pathways to Quantum Coherence in Materials, an Energy Frontier Research Center funded by the US Department of Energy (DOE), Office of Science, Basic Energy Sciences (BES) and the Energy Frontiers Center on Programmable Quantum Materials funded by the US DOE, Office of Science, BES, under award DE-SC0019443. Synthesis and characterization of TaIrTe4 single crystals at the University of California, Los Angeles was supported by the US DOE, Office of Science, BES under award DE-SC0021117. J.O. was supported by the Quantum Materials program, Director, Office of Science, BES, Materials Sciences and Engineering Division, of the US DOE under Contract No. DE-AC02-05CH11231 and the Gordon and Betty Moore Foundation’s EPiQS Initiative through Grant No. GBMF4537 at University of California, Berkeley. D.H. is supported by a fellowship from the Simons Foundation (579913). The Flatiron Institute is a Division of the Simons Foundation.
Footnotes
The authors declare no competing interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at https://www.pnas.org/lookup/suppl/doi:10.1073/pnas.2116366118/-/DCSupplemental.
Data Availability
All study data are included in the article and/or SI Appendix.
References
- 1.Boyd R., Nonlinear Optics (Burlington, ed. 3, 2008). [Google Scholar]
- 2.Morimoto T., Nagaosa N., Topological nature of nonlinear optical effects in solids. Sci. Adv. 2, e1501524 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Yang X., Burch K., Ran Y., Divergent bulk photovoltaic effect in Weyl semimetals. arXiv [Preprint] (2017). https://arxiv.org/abs/1712.09363 (Accessed 11 November 2021).
- 4.Sotome M., et al., Spectral dynamics of shift current in ferroelectric semiconductor SbSI. Proc. Natl. Acad. Sci. U.S.A. 116, 1929–1933 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Ahn J., Guo G. Y., Nagaosa N., Low-frequency divergence and quantum geometry of the bulk photovoltaic effect in topological semimetals. Phys. Rev. X 10, 041041 (2020). [Google Scholar]
- 6.Wu L., et al., Giant anisotropic nonlinear optical response in transition metal monopnictide Weyl semimetals. Nat. Phys. 13, 350–355 (2017). [Google Scholar]
- 7.Osterhoudt G. B., et al., Colossal mid-infrared bulk photovoltaic effect in a type-I Weyl semimetal. Nat. Mater. 18, 471–475 (2019). [DOI] [PubMed] [Google Scholar]
- 8.Ma J., et al., Nonlinear photoresponse of type-II Weyl semimetals. Nat. Mater. 18, 476–481 (2019). [DOI] [PubMed] [Google Scholar]
- 9.Ma Q., et al., Observation of the nonlinear Hall effect under time-reversal-symmetric conditions. Nature 565, 337–342 (2019). [DOI] [PubMed] [Google Scholar]
- 10.Kumar D., et al., Room-temperature nonlinear Hall effect and wireless radiofrequency rectification in Weyl semimetal TaIrTe . Nat. Nanotechnol. 16, 421–425 (2021). [DOI] [PubMed] [Google Scholar]
- 11.Orenstein J., et al., Topology and symmetry of quantum materials via nonlinear optical responses. Annu. Rev. Condens. Matter Phys. 12, 247–272 (2021). [Google Scholar]
- 12.Ma Q., Grushin A. G., Burch K. S., Topology and geometry under the nonlinear electromagnetic spotlight. Nat. Mater., 10.1038/s41563-021-00992-7 10.1038/s41563-021-00992-7 (2021). [DOI] [PubMed] [Google Scholar]
- 13.Xu S. Y., et al., Discovery of a Weyl fermion semimetal and topological Fermi arcs. Science 349, 613–617 (2015). [DOI] [PubMed] [Google Scholar]
- 14.Lv B. Q., et al., Experimental discovery of Weyl semimetal TaAs. Phys. Rev. X 5, 031013 (2015). [Google Scholar]
- 15.von Baltz R., Kraut W., Theory of the bulk photovoltaic effect in pure crystals. Phys. Rev. B Condens. Matter 23, 5590–5596 (1981). [Google Scholar]
- 16.Sipe J. E., Shkrebtii A. I., Second-order optical response in semiconductors. Phys. Rev. B Condens. Matter Mater. Phys. 61, 5337–5352 (2000). [Google Scholar]
- 17.Chang G., et al., Unconventional photocurrents from surface fermi arcs in topological chiral semimetals. Phys. Rev. Lett. 124, 166404 (2020). [DOI] [PubMed] [Google Scholar]
- 18.Hsieh D., et al., Nonlinear optical probe of tunable surface electrons on a topological insulator. Phys. Rev. Lett. 106, 057401 (2011). [DOI] [PubMed] [Google Scholar]
- 19.McIver J. W., Hsieh D., Steinberg H., Jarillo-Herrero P., Gedik N., Control over topological insulator photocurrents with light polarization. Nat. Nanotechnol. 7, 96–100 (2011). [DOI] [PubMed] [Google Scholar]
- 20.Koepernik K.et al., TaIrTe: A ternary type-II Weyl semimetal. Phys. Rev. B 93, 201101 (2016). [Google Scholar]
- 21.Belopolski I., et al., Signatures of a time-reversal symmetric Weyl semimetal with only four Weyl points. Nat. Commun. 8, 942 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Song J. C. W., Levitov L. S., Shockley-Ramo theorem and long-range photocurrent response in gapless materials. Phys. Rev. B Condens. Matter Mater. Phys. 90, 075415 (2014). [Google Scholar]
- 23.Schneider S. C., Grafström S., Eng L. M., Scattering near-field optical microscopy of optically anisotropic systems. Phys. Rev. B Condens. Matter Mater. Phys. 71, 115418 (2005). [Google Scholar]
- 24.Yao Z., et al., Probing subwavelength in-plane anisotropy with antenna-assisted infrared nano-spectroscopy. Nat. Commun. 12, 2649 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Shockley W., Currents to conductors induced by a moving point charge. J. Appl. Phys. 9, 635–636 (1938). [Google Scholar]
- 26.Ma Q., et al., Giant intrinsic photoresponse in pristine graphene. Nat. Nanotechnol. 14, 145–150 (2019). [DOI] [PubMed] [Google Scholar]
- 27.Cao H., et al., Photo-Nernst current in graphene. Nat. Phys. 12, 236–239 (2016). [Google Scholar]
- 28.Seifert P., et al., Quantized conductance in topological insulators revealed by the Shockley-Ramo theorem. Phys. Rev. Lett. 122, 146804 (2019). [DOI] [PubMed] [Google Scholar]
- 29.Woessner A., et al., Near-field photocurrent nanoscopy on bare and encapsulated graphene. Nat. Commun. 7, 10783 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Sunku S. S., et al., Hyperbolic enhancement of photocurrent patterns in minimally twisted bilayer graphene. Nat. Commun. 12, 1641 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Hesp N. C. H., et al., Nano-imaging photoresponse in a moiré unit cell of minimally twisted bilayer graphene. Nat. Commun. 12, 1640 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Wang Q., et al., Robust edge photocurrent response on layered type II Weyl semimetal WTe 2. Nat. Commun. 10, 1–7 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Shao Y., et al., Optical signatures of Dirac nodal lines in NbAs2. Proc. Natl. Acad. Sci. U.S.A. 116, 1168–1173 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Pronin A. V., Dressel M., Nodal semimetals: A survey on optical conductivity. Phys. Status Solidi B 258, 2000027 (2021). [Google Scholar]
- 35.Fei Z., et al., Infrared nanoscopy of Dirac plasmons at the graphene-SiO2 interface. Nano Lett. 11, 4701–4705 (2011). [DOI] [PubMed] [Google Scholar]
- 36.McLeod A. S., et al., Model for quantitative tip-enhanced spectroscopy and the extraction of nanoscale-resolved optical constants. Phys. Rev. B Condens. Matter Mater. Phys. 90, 085136 (2014). [Google Scholar]
- 37.Wawrzik D., You J. S., Facio J. I., van den Brink J., Sodemann I., Infinite Berry curvature of Weyl Fermi arcs. Phys. Rev. Lett. 127, 056601 (2021). [DOI] [PubMed] [Google Scholar]
- 38.Cao J., Wang M., Yu Z. M., Yao Y., Bulk-Fermi-arc transition induced large photogalvanic effect in Weyl semimetals. arXiv [Preprint] (2021). https://arxiv.org/abs/2108.08138 (Accessed 11 November 2021).
- 39.Mooshammer F., et al.; Nanoscale near-field tomography of surface states on (BiSb)Te. Nano Lett. 18, 7515–7523 (2018). [DOI] [PubMed] [Google Scholar]
- 40.Fano U., Effects of configuration interaction on intensities and phase shifts. Phys. Rev. 124, 1866–1878 (1961). [Google Scholar]
- 41.Shao Y., et al., Electronic correlations in nodal-line semimetals. Nat. Phys. 16, 636–641 (2020). [Google Scholar]
- 42.Ku M. J. H., et al., Imaging viscous flow of the Dirac fluid in graphene. Nature 583, 537–541 (2020). [DOI] [PubMed] [Google Scholar]
- 43.Zhou X., et al., Coexistence of tunable Weyl points and topological nodal lines in ternary transition-metal telluride TaIrTe. Phys. Rev. B 97, 241–102 (2018). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
All study data are included in the article and/or SI Appendix.