Complex Diffusion in Bacteria

Abstract

Diffusion within bacteria is often thought of as a “simple” random process by which molecules collide and interact with each other. New research however shows that this is far from the truth. Here we shed light on the complexity and importance of diffusion in bacteria, illustrating the similarities and differences of diffusive behaviors of molecules within different compartments of bacterial cells. We first describe common methodologies used to probe diffusion and the associated models and analyses. We then discuss distinct diffusive behaviors of molecules within different bacterial cellular compartments, highlighting the influence of metabolism, size, crowding, charge, binding, and more. We also explicitly discuss where further research and a united understanding of what dictates diffusive behaviors across the different compartments of the cell are required, pointing out new research avenues to pursue.

2.1. Introduction

Diffusion is the consequence of a particle randomly colliding with the other particles in its surroundings. The diffusion speed, directionality, and trajectory of a particle contain rich information about how the particle interacts with its surroundings, offering an invaluable window to examine molecular interactions in live cells.

In bacterial cells, random diffusion is sufficient to allow molecules to reach their desired target sites efficiently because of the small cellular volumes (on the order of ~10⁻¹⁵ L). For example, a protein molecule with a diffusion coefficient (D) of 1 μm²/s can sample the entire cytoplasm in ~100 ms. In contrast, eukaryotic cells have volumes that are three orders of magnitude larger and simple diffusion is no longer sufficient. Directional motor proteins such as kinesin and myosin are hence required to deliver molecules to different cellular addresses. Since diffusion is a major mechanism behind how molecules find their “place” in bacterial cells, it is vital to understand the characteristics of diffusion in the different compartments of bacterial cells. In this review, we present a critical summary and evaluation of commonly used methods and analyses to probe complex diffusive behaviors observed in bacterial cells, with a major focus on single-molecule tracking (SMT). We then elucidate various diffusion dynamics with specific examples in the bacterial cytoplasm, nucleoid, and membranes.

2.2. Common Methods to Characterize Diffusion in Bacterial Cells

Commonly used methods to characterize molecules’ diffusion in live cells are fluorescence recovery after photobleaching (FRAP), fluorescence correlation spectroscopy (FCS) and single molecule tracking (SMT). Here we briefly describe FRAP and FCS, and then discuss SMT in depth, due to its wide use and vast potential in probing diffusion in bacterial cells.

2.2.1. Fluorescence Recovery After Photobleaching (FRAP)

In FRAP, a focused laser is used to photobleach a small region of a cell containing fluorescently labeled molecules, and subsequently the fluorescence recovery of the region is monitored (Fig. 2.1a). Depending on the diffusion speed, diffusive mode, and the geometry of the selected region and cell, the FRAP curve can be fit to specific models to extract diffusion coefficients and kinetic rates associated with particular molecular interactions (Rayan et al. 2010). As an ensemble method, FRAP is relatively simple to implement; the apparent FRAP rate serves as a straightforward measure to allow comparison of the same system under different conditions even in the absence of a specific model. Therefore, FRAP has been widely used in diffusion studies. However, one should be aware of the limitation of using FRAP to extract quantitative parameters such as diffusion coefficients and kinetics. These values are ensemble-averaged means pertinent to and only valid in specific models. Finally, FRAP is unable to depict heterogeneous diffusion properties of molecules limiting its use in terms of determining diffusive behavior (Elowitz et al. 1999) – except for “relatively” specific situations (Lorén et al. 2009).

Fig. 2.1.

Three most common methodologies used to quantify diffusion. (a) Fluorescence Recovery after Photobleaching (FRAP): the recovery of fluorescence signal (shown as green color) in a region of interest (ROI, shown as gray dashed circle) is monitored after bleaching (bleached region shown as black circle). The “rate” at which the signal recovers is related to the mobility of the particle of interest, shown as red and blue curves. (b) Fluorescence Correlation Spectroscopy (FCS): fluctuations within a small diffraction-limited excitation volume are monitored throughout time, illustrated as counts vs time. The fluctuations of slower diffusing particles are shown in red and the higher frequency fluctuations of the faster diffusing particles are shown in blue. The autocorrelation functions of each system can be calculated, providing information about the diffusion of the particles. (c) Single Molecule Tracking (SMT): The location of individual molecules or particles within a cell are monitored through time (arrows indicate direction of time). The displacements along the trajectories can then be analyzed with different methodologies, which are further illustrated in Fig. 2.2 and explained in detail in text

2.2.2. Fluorescence Correlation Spectroscopy (FCS)

FCS is a methodology that monitors the fluctuations of fluorescence within a small region to determine many different parameters, including the diffusion coefficients. The mechanism behind the technique is that the fluctuations in fluorescence are due to molecules moving into and out of the illuminated region, allowing the dynamics of the system to be quantified (Fig. 2.1b). FCS often includes calculating the autocorrelation function and then fitting it to specific models to extract the desired parameters. When compared to FRAP, the theoretical interpretations of the data often have the same limitations in regards to quantifying the diffusive behavior (Elson 2011).

2.2.3. Single-Molecule Tracking (SMT)

SMT is a method where one follows the movement of individual molecules (or particles in some cases) labeled with fluorophores to determine how the molecule interacts with its surroundings and potential targets (Fig. 2.1c). Because of the single-molecule nature of the method, SMT allows one to identify not only the molecule’s diffusive mode and diffusion coefficient, but also the population heterogeneity and in vivo kinetics of switching between diffusive states, which are often indicative of specific molecular interactions.

2.3. Practical Concerns of SMT

A successful SMT experiment requires a few critical parameters be within an optimal range. These parameters are the single molecule signal to noise ratio (SNR), the length (L) and number (N) of SMT trajectories. These parameters have large influences on the theoretical limitations of quantifying diffusion coefficients and diffusive behaviors with different forms of analyses, discussed throughout (Michalet and Berglund 2012).

2.3.1. Signal to Noise Ratio (SNR)

The first parameter, SNR, is often defined as the ratio between the numbers of photons emitted by the fluorophore and the cell’s autofluorescence background. SNR dictates how well one can determine the position of a molecule at each time point, i.e., the precision at which the molecule can be localized. This concept is the same as the localization precision from single-molecule localization superresolution microscopy (SMLM) (Betzig et al. 2006; Rust et al. 2006; Hess et al. 2006). In live bacterial cells, the SNR for commonly used fluorescent proteins and organic dyes are sufficient for a localization precision of ~10–30 nm (Betzig et al. 2006; Rust et al. 2006; Hess et al. 2006). When the SNR is low due to a short camera exposure time or a high cellular autofluorescence background, individual displacements along the SMT trajectory cannot be determined accurately, leading to large uncertainties in determining the corresponding D (Das et al. 2009; Bohrer et al. 2017; Persson et al. 2013; Slator and Burroughs 2018; Matsuda et al. 2018). As such, metrics used to quantify the diffusive dynamics of molecules (Weber et al. 2010a, 2012a; He et al. 2008; Condamin et al. 2008; Thapa et al. 2018) are often distorted, making the interpretation of the data difficult and complex (Weber et al. 2012a). For instance, when the SNR is low, the mean squared displacement (MSD, discussed in detail below) can show sub-diffusive behaviors at short timescales, even when the diffusion is purely Brownian (Martin et al. 2002). Additionally, the quantified diffusive states and corresponding kinetic switching rates can be ill-defined, due to the low confidence in defining D values along a trajectory (Bohrer et al. 2017; Persson et al. 2013; Michalet and Berglund 2012).

2.3.2. Trajectory Length (L)

The second parameter, L, describes how long in time a molecule can be tracked. In practice, L is limited by the time a fluorophore remains fluorescent before it photobleaches – as long as the molecule does not diffuse out of focus. Due to the stochastic nature of photobleaching (photobleaching time is usually exponentially distributed (Lee et al. 2012; Yeow et al. 2006)), only a small portion of all SMT trajectories are relatively long. As such, a large number of total SMT trajectories are often required to obtain a sufficient number of long SMT trajectories.

Long SMT trajectories are vital to determine if the diffusive behavior of molecules is ergodic, if there is dynamic heterogeneity along single trajectories, and if the molecule transitions between different diffusive states. Here ergodicity refers to whether the average behavior across all molecules equals the behavior of individual molecules over long periods of time, which can be used as a metric to discriminate between different models of diffusion (Deng and Barkai 2009; Parry et al. 2014); dynamic heterogeneity means the diffusion coefficient of an individual molecule varies through time or space (Lampo et al. 2017a); transition kinetics refer to the rates of a molecule switching from one to the other diffusive state characterized by distinct diffusion coefficients.

How long is long enough for SMT? In ensemble kinetic measurements of chemical reactions, a “rule of thumb” is to monitor the reaction for at least five reaction halftimes (so that the reaction has proceeded >95%) in order to determine the rate constant accurately. The equivalent should be applied to SMT as well. For example, for a transition rate of 1 s⁻¹, the minimal average trajectory length should be at least ~5 s long to capture a sufficient number of transition events. In practice, SMT tracking trajectories should be even longer in order to observe the two different states before and after the transition with confidence. In theory, one can also obtain a large number of shorter SMT trajectories (>10,000) and analyze the data using statistical methods to extract the kinetic information (Bohrer et al. 2017; Das et al. 2009; Persson et al. 2013). These statistical methods often require additional assumptions about the kinetic rates and steady states, and hence need to be carefully evaluated.

2.3.3. How to Achieve High SNR and Obtain Long Trajectories

To achieve a high SNR, the key is to use bright fluorophores. To obtain long trajectories, the key is to use photostable fluorophores – as it is often important to use a high frame rates, which often requires high laser intensities. Bright, red-colored organic fluorophores such as the newly developed Janelia Fluor Dyes (JFD) (Lukinavičius et al. 2013) (now commercially available) in conjunction with Halo or SNAP tag (Los et al. 2008; Cole 2013) satisfy both requirements. The unique, rigid fluorophore structure of JF646 ensures high fluorescence quantum yield and low photobleaching quantum yield, and the lengthened conjugation plane allows red-shifted excitation at 647 nm, which avoids the autofluorescence background that usually comes from flavin proteins (Xiao 2009). Halo- or SNAP-ligand modified JF646 is membrane permeable (even for Gram negative bacteria such as E. coli) and can be directly added into cell’s growth medium and subsequently washed for live cell labeling.

In the event that the Halo/SNAP-JF646 labeling system or its alike is not feasible (for example, the fusion protein is not functional or there is a high level of nonspecific dye binding), other strategies can be employed. Fluorescent proteins (FPs) usually tolerate fusions well and do not require the addition of exogenous fluorophore, simplifying sample preparation. In our experience, the red-colored fluorescent protein TagRFP-t (Beilharz et al. 2015), even though not comparable to JF646, is sufficiently bright and is the most photostable when compared to the other FPs we tested (EGFP, EYFP, mCherry, mNeonGreen, mEos3.2, and PAmCherry) (Zhang et al. 1996, 2012; Ormö et al. 1996; Shaner et al. 2004, 2013; Subach et al. 2009). If other less bright or photostable fluorophores are the only option, one could try to [1] minimize cellular autofluorescence background by avoiding the green-colored fluorophores and by growing cells in defined (such as M9 or EZRDM) instead of complex (such as LB) media; and [2] conduct multiple rounds of SMT experiments in which the dark interval between adjacent imaging frames is systematically varied so that trajectories of different dark intervals can be computationally stitched together to cover longer time scales (Gebhardt et al. 2013). Lastly, recent advances in microscopy methodologies, such as MINFLUX, show promise for expanding the limits of SMT – as the low number of photons needed to reach a comparable resolution allows one to obtain much longer trajectories (Balzarotti et al. 2017).

2.3.4. Trajectory Number (N)

A final requirement for a successful SMT experiment is to obtain a sufficient number of trajectories. As with any single-molecule experiment, diffusive trajectories of individual molecules are inherently stochastic and therefore a large sample size is needed to quantify and account for these fluctuations. Generally speaking, to obtain a single mean diffusion coefficient (D) a hundred trajectories with an average length of at least five to ten tracking frames may be sufficient. If there are multiple populations with different Ds, a few hundred to a thousand trajectories are necessary to separate the different populations. To extract kinetic rates, greater than 10,000 trajectories may be needed (see below for more details).

The above requirement demands collecting as many trajectories from as many single cells as possible. However, SMT also requires a low labeling density in single cells so that individual molecules can be spatially isolated. A low labeling density can be achieved by carefully tuning the fusion protein’s expression level using repressible promoters and/or low copy plasmids, so that on average in one bacterial cell there is only one or two fluorescent molecules. Such a low expression level leads to a low imaging throughput since the majority of cells would not have any expressed fluorescent molecules due to the Poissonian distribution of lowly expressed molecules in a population of cells. Furthermore, the expression level is often difficult to control experimentally due to the leakiness of most prokaryotic promoters.

One way to bypass this experimental difficulty is to use the Halo/SNAP-JF dye labeling system. The fusion protein can be expressed normally in cells, but the concentration of the dye can be tuned at will so that only a small percentage of fusion protein molecules are labeled to allow SMT. This strategy, however, still does not circumvent the issue of low data throughput, since one can only obtain on average one or two trajectories per cell.

The ideal strategy is to use a photoactivatable fluorophore that is not fluorescent unless activated (Stepanenko et al. 2011; Ando et al. 2002; Gurskaya et al. 2006; Subach et al. 2009). A fusion protein could thus be 100% labeled with a photoactivatable fluorophore but remain nonfluorescent; only upon a low dose of activation light one or a few molecules are stochastically turned on to be tracked. After they are photobleached, new molecules are turned on, allowing continuous SMT of many molecules in the same cells. Commonly used photoactivatable fluorophores include mEso3.2 (Zhang et al. 2012) and PAmCherry (Subach et al. 2009), but none of their photochemistry properties are as good as the stable JF646. Photoactivable JF dyes have been developed (Grimm et al. 2016), but their low activation rates require further optimization for SMT. Furthermore, continuous photoactivation using high energy light (405 or 488 nm) can cause photo-damage of cells, limiting the number of trajectories one can continuously collect from individual cells. Finally, one technology which could help in the accumulation of trajectories from a large number of cells is the mother-machine – though this technology has not yet been thoroughly utilized by the SMT community (Wang et al. 2010; Camsund et al. 2020).

2.4. Data Analysis and Interpretation of SMT

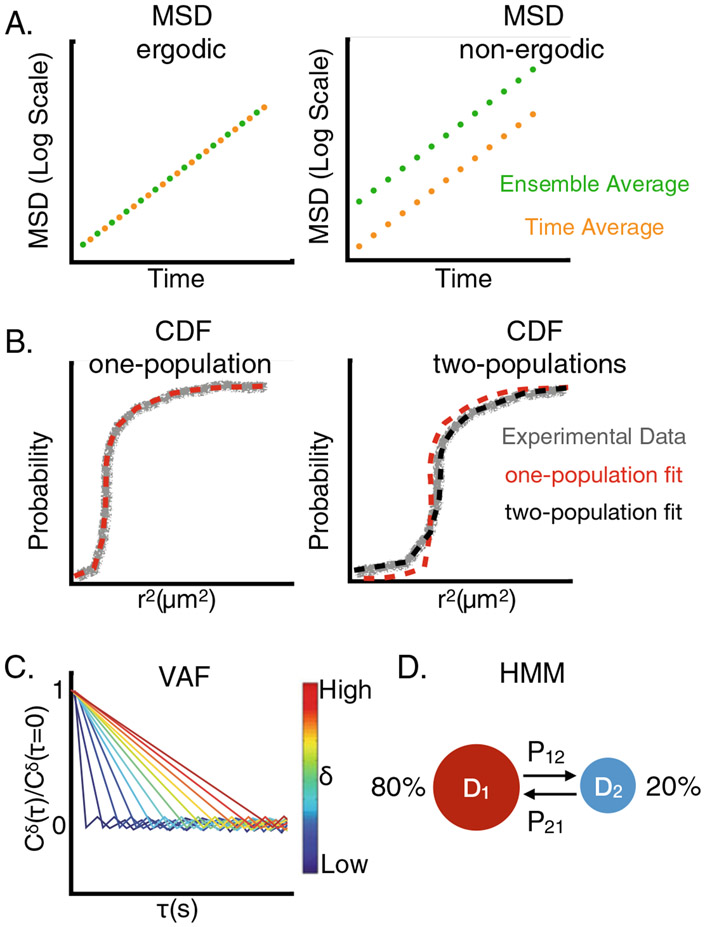
SMT trajectories can be analyzed multiple ways depending on what quantitative information one wishes to extract. Commonly used analyses include mean squared displacement (MSD), cumulative displacement distribution function (CDF), velocity autocorrelation function (VAF), and Hidden Markov Model (HMM). Below we describe each analysis and what information can be determined independently and collectively from these analyses.

2.4.1. Mean Squared Displacement (MSD)

The mean squared displacement (MSD) is the most commonly used metric to estimate the apparent diffusion coefficient D, which helps quantify the diffusion mode of single molecules (also see the section: Commonly encountered diffusion mechanisms below). The ensemble-averaged MSD is calculated by taking the squared distance a molecule travels for a certain time and then averaging over all molecules (Fig. 2.2a):

$$MSD(t)=\frac{1}{n}\sum _{i=1}^n(x_i(t)-x_i(0){)}^2$$ (2.1)

where x(t) is the coordinate of the molecule at time t and n is the number of trajectories. Note that in all experimentally measured MSD curves, the square root of the y-axis intercept, or the apparent MSD value when t = 0, indicates the uncertainty in determining a molecule’s position, hence serving as a useful indicator to estimate experimental localization precision. Because different SMT trajectories have different lengths, to ensure that each molecule contributes equally to the final MSD curve for each t, a common practice is to select trajectories that have a minimal length and truncate longer trajectories to the minimal length.

Fig. 2.2.

Data analyses of SMT. (a) An example of an MSD for an ergodic system and for a non-ergodic system. (b) An example a CDF fit for a one state system and a two state system. (c) An example VAF for Brownian diffusion. (d) A two state Markov model with its corresponding diffusion coefficients, transition probabilities and percentages of each state

For individual trajectories, the time averaged MSD of each trajectory is computed using the following equation:

$$MS{D}_{\tau }(t)=\frac{1}{T-t}\sum _{\tau =0}^{T-t}(x(t+\tau )-x(\tau ){)}^2,$$ (2.2)

where T is the total time of the individual trajectory and τ ranges over all possible values up to T – t based on the time interval of the SMT experiment. If a system is ergodic, the MSD_τ(t) = MSD(t) and it can be used to discriminate between different modes of diffusion, Fig. 2.2a. Note that a combination of the two can be used to examine ergodicity if trajectories are not of sufficient length (Parry et al. 2014):

$$MS{D}_{\tau }^{avg}(t)=\frac{1}{n}\sum _{i=1}^n\frac{1}{T-t}\sum _{\tau =0}^{T-t}(x_i(t+\tau )-x_i(\tau ){)}^2.$$ (2.3)

2.4.2. Cumulative Displacement Distribution Function (CDF)

As mentioned above, dynamic heterogeneity means that D values of individual molecules vary through time and/or space. Dynamic heterogeneity can exist simply because the molecule of interest has multiple diffusive states depending on its interactions with other molecules. For instance, in E. coli, RNA polymerase (RNAP) molecules exhibit a D of ~1 μm²/s in the cytoplasm, ~0.4 μm²/s in the nucleoid, and ~0.1 μm²/s when bound to chromosomal DNAs (Stracy et al. (2015) and see Section: Diffusion of DNA binding proteins). These different D values indicate different modes of DNA interactions of RNAP, with the slowest one most likely bound to DNA, the fastest one freely diffusing in the cytoplasm, and the intermediate one interacting with the nucleoid nonspecifically. Dynamic heterogeneity can also result from the molecule experiencing different local environments within the cell (Lampo et al. 2017b). When a “continuum” of heterogeneity is observed, the varying diffusive properties could be due to the local environment changing with time or the molecule moving to a different environment.

One useful way to examine whether there are multiple diffusive populations is to inspect the single-step displacement distribution. For a single population with 1d-Brownian motion (random collisions of the molecule with other molecules within the medium), the displacement distribution for a molecule to move a distance x away from the origin in the time interval t follows a normal distribution

$$p(x,t)=\frac{e^{\frac{-x^2}{4Dt}}}{(4\pi Dt{)}^{\frac{1}{2}}},$$ (2.4)

with a characteristic diffusion coefficient D, that is dependent upon the size of the molecule, the temperature and the viscosity of the medium. The corresponding cumulative distribution function (CDF), can also be fit to a single exponential function to extract D. When the displacement distribution cannot be described adequately with a single population, the linear combination of multiple terms with different D values and respective population fractions can be used (Vrljic et al. 2007) (Fig. 2.2b). For 2d-diffusion, the CDF for two populations of diffusing molecules can be fit with the following equation:

$$CDF(r^2,t)=1-\alpha \times e^{\frac{-r^2}{4D_{1}t+4{\sigma }^2}}-(1-\alpha )\times e^{\frac{-r^2}{4D_{2}t+4{\sigma }^2}}$$ (2.5)

where D₁ and D₂ are the diffusion coefficients of the two diffusion populations, α accounts for the fraction of each population, r is the radial distance and σ is the localization precision of the experiment. Once different populations with characteristic diffusion coefficients are identified, one can analyze each population’s behavior as described below.

2.4.3. Velocity Autocorrelation Function (VAF)

If one wishes to characterize the diffusive behavior and dissect the mechanisms behind it, the velocity autocorrelation function (VAF) is an important tool (Weber et al. 2012a). The function identifies the correlation in the velocity of a molecule at different timescales and allows one to distinguish between different diffusive processes and is particularly useful for sub-diffusion (Weber et al. 2012a). The function is defined as the following (Fig. 2.2c):

$$C_v^{\delta }(\tau )=\langle \overrightarrow{v}(t+\tau )\cdot \overrightarrow{v}(t)\rangle ,$$ (2.6)

where

$$v(t)=\frac{1}{\delta }([\overrightarrow{R}(t+\delta )-\overrightarrow{R}(t)].$$ (2.7)

Here $\overrightarrow{R}(t)$ is the position vector of the molecule at time t and $\langle \overrightarrow{v}(t+\tau )\cdot \overrightarrow{v}(t)\rangle$ is the mean dot product averaged over all trajectories. The values of δ and τ are varied across all possible time intervals of the trajectories. As we will describe more in detail below, specific characteristics of the VAF are indicative of different diffusion modes and when combined with other analyses, it is often possible to delineate the underlying diffusion mechanism.

2.4.4. Hidden Markov Model (HMM)

In some cases where there exist multiple “well defined” diffusive populations, it will be of interest to identify the transition kinetics between the different states of the molecule. The ability to monitor the change of a molecule’s diffusive behavior in real time, which reflects its interactions with targets without perturbing the system is one of the most powerful benefits of SMT (Bohrer et al. 2017; Das et al. 2009; Persson et al. 2013). In order to extract the kinetic rates between different diffusive states, the individual states must have different diffusion coefficients and the displacement distributions need to be known (Das et al. 2009; Persson et al. 2013). One can then use likelihood and Bayesian approaches to quantify the transition kinetics of the system by fitting to a hidden Markov model (HMM, Fig. 2.2d), see Das et al. for further details (Das et al. 2009). Note: an alternative methodology, analytical diffusion distribution analysis, was recently developed which can also extract kinetic parameters when the system of interest has two diffusive states with fast transition rates (Vink et al. 2020). Finally, the field has not yet determined a methodology for particles that exhibit non-Brownian diffusion – though methodologies are beginning to take the mechanisms responsible for non-Brownian motion into account (Bohrer et al. 2017; Slator and Burroughs 2018).

2.5. Commonly Encountered Diffusion Mechanisms

2.5.1. Brownian Motion

Brownian motion, in which a molecule randomly collides with the surrounding molecules (Fig. 2.3a), is the most common and the simplest diffusion mechanism. The MSD plot of a SMT experiment is a straight line, with the slope of the line providing the diffusion coefficient (Fig. 2.3b). The corresponding single-step displacement distribution’s CDF can be well described by a single exponential function. Additionally, due to the fact that all displacements are independent of each other, the VAF decays to zero for all τ ≥ δ (Fig. 2.3c). Note, if the experiment has a low localization precision, the VAF will show a negative peak for τ = δ, which approaches zero as τ increases.

Fig. 2.3.

Cartoons showing different modes of diffusion, with each row showing a different mode of diffusion through time (light gray circles illustrate the medium), the mean squared displacement (MSD, shown on a linear scale (except for K), green ensemble average, yellow time average), and the corresponding velocity autocorrelation function (VAF, color indicates δ as in Fig. 2.2). [Specifics] (d) Super Diffusion: dark gray Line is track on which a particle travels in a directed manner (For example actin). (g) Confined: dark gray line indicates a barrier where the diffusion of a particle is restricted (For example the membrane). (k) MSD is shown on a log scale. (l) Viscoelastic: the springs between the particles of the medium represent the elastic property of the medium. (o) Continuous Time Random Walk (CTRW): the overlap between the particle of interest with a particle of the medium indicates a binding event. For all rows arrows show direction of time as well as previous locations

2.5.2. Anomalous Diffusion

Any type of diffusion process that does not result in a linear MSD is considered anomalous. There are two types of anomalous diffusion, sub-diffusion and super-diffusion. Most of the time, anomalous diffusion has an MSD that scales with time to an exponent, MSD = 4Dt^α. (For sub-diffusion 0 < α < 1 and for super-diffusion α > 1) Examples of the MSDs for both types of anomalous diffusion are shown in Fig. 2.3e,h,k,m,p.

Super-diffusion usually results from directional movement of molecules (Fig. 2.3d) and is rare in bacterial cells, as they do not have linear motor proteins such as kinesin or myosin. However, directional movement of cytoskeletal proteins such as MreB (Fu et al. 2018), cell wall remodeling enzymes PBP2 and PBP3 (Yang et al. 2017; Perez et al. 2019; Bisson-Filho et al. 2017) and segregating plasmid DNAs (Ringgaard et al. 2009; Hu et al. 2015) have been observed. The VAF of super-diffusion will show positive values across multiple τ values as the directionality of individual displacements is positively correlated (Fig. 2.3f) (Kim et al. 2006).

Sub-diffusion is commonly observed in bacterial cells and can result from a number of different mechanisms. A first step to differentiate different diffusion mechanism is to compare the exponent value of the MSD curve with what would be expected from the different diffusion models, as what was done previously on the diffusion of chromosomal DNA segments and mRNA molecules (Weber et al. 2010a). However, because different sub-diffusion processes can result in similar MSD curves, other metrics are normally needed to support specific models. Below we focus on a few models pertinent to diffusing molecules in bacterial cells.

2.5.2.1. Diffusion with Confinement (Sub-diffusion)

The most common mechanism behind sub-diffusion in bacterial cells is confinement, which results from diffusion in a finite space (Fig. 2.3g). With confinement, the space a molecule can explore is limited and the MSD reaches a plateau at long time scales (Fig. 2.3h), causing the MSD to scale with an exponent α < 1. The value of the plateau can be used to extract the size of the confinement zone, which corresponds to the finite size of space where the molecule could freely diffuse (Kusumi et al. 1993). For 1d diffusion (along x) within a box of length L_x, the MSD_x(t) follows:

$$\begin{gathered} MS{D}_x(t)=\frac{L_x^2}{6}-\frac{16L_x^2}{{\pi }^4}\sum _{n=1(odd)}^{\infty }\frac{1}{n^4} \\ \times exp[-\frac{1}{2}(\frac{n\pi 2D_x}{L_x}{)}^{2}t] \end{gathered}$$ (2.8)

Here it can be seen that as t → ∞ the MSD will asymptotically approach $\frac{L_x^2}{6}$, which defines the value of the plateau. If diffusion is Brownian, sub-diffusion caused by confinement will still appear Brownian at short time scales before the molecules can experience the barriers. Therefore, the single-step displacement distribution will still be approximately Gaussian. At long time scales, the displacement distribution or CDF will deviate from that expected from Brownian motion.

The characteristics of confinement can be quantified using VAF. Confinement results in an “anti-persistent” behavior, in which a molecule is reflected off of the barrier and returns to its previous position. The resulting VAF $C_v^{\delta }(\tau )$ shows a small negative peak or a zero at small δ and τ (due to the molecule not having time to experience the barriers) and then develops into a large negative peak as δ and τ increase, Fig. 2.3i. This resulting behavior within the VAF is due to the barrier reflecting the molecule, leading to the negative velocity relative to the previous velocity.

Confinement often leads to difficulties in identifying the true diffusive behavior of molecules. For instance, confinement eliminates long timescale correlations in the VAF (Weber et al. 2012a) and reduces D values, and hence leads to mis-identified diffusion modes and states, creating error in the associated kinetic rates (Bohrer et al. 2017).

To limit the amount of confinement in rodshaped bacterial cells, it is a common practice to take the displacements along the long axis of the cell, as it introduces less confinement when compared to the short axis of the cell due the longer length (Bohrer et al. 2017; Bakshi et al. 2013; Persson et al. 2013; Weber et al. 2010a). However, this practice eliminates a significant amount of data, leading to less accurate determination of Ds and transition kinetics of a system. Bohrer et al. developed an algorithm, termed Single-Particle tracking Improvement with Confinement Error Reduction or SPICER, to selectively incorporate the displacements along the confined dimension of the cell by quantifying the distance of a molecule to the barrier that is needed to minimize the effects of confinement. The new algorithm significantly improves the accuracy in determining both the D values of different diffusive species and also the associated kinetic transition rates of the systems (Bohrer et al. 2017).

2.5.2.2. Diffusion Near a Liquids Glass Transition (Sub-diffusion)

Another mechanism of sub-diffusion can be due to a disordered/heterogeneous medium (Havlin and Ben-Avraham 1987). For instance, it is well known that diffusion deviates from Brownian motion in amorphous solids (Hunter and Weeks 2012; Weeks and Weitz 2002). Interestingly, the bacterial cytoplasm has been reported to have “glass like properties” and changes from liquid-like to solid-like in a metabolism-dependent fashion (Fig. 2.3j) (Parry et al. 2014).

The MSD curve of molecules diffusing in a glass-forming liquid can take on a variety of different shapes, but the “characteristic curve” has three distinct characteristics: [1] At short timescales the log of the MSD displays a linear relationship; [2] at intermediate timescales, the log of the MSD approaches a plateau due to the molecules being trapped in “cages” formed by the relatively immobile solvent molecules; and [3] at long timescales the cages rearrange allowing the molecules to escape and the MSD increases again (Weeks and Weitz 2002) (Fig. 2.3k).

Additionally, diffusion within a “glass-like” medium is non-ergodic, meaning that the average MSD over all trajectories does not equal the average of individual trajectories (over time) (Equation 2.1 ≠ Equation 2.2, Fig. 2.3k) (Cipelletti and Ramos 2005). The non-ergodicity is the result of the medium having an “infinite” phase space, in that there is an “infinite” number of ways to create local cages and unique arrangements of molecules and the timescales at which the “cages” rearrange vary greatly. A medium that is approaching its glass-like transition will have certain areas displaying glass-like properties while others display fluid-like properties, leading to heterogeneities in the diffusion modes of different molecules within the same cell. This mechanism results in individual cells having more than a single population of diffusing molecules, some confined to cages and others freely diffusing (Parry et al. 2014).

Finally, molecules diffusing in a medium approaching its glass transition also exhibit the anti-persistent behavior (Parry et al. 2014; Weeks and Weitz 2002). The anti-persistent behavior is exemplified by a strong negative correlation between adjacent displacements. For adjacent displacements there is a strong linear dependence for the magnitudes of adjacent displacements (in the direction of the first displacement) up to the “cage size” of the medium (Fig. 2.6b) (Weeks and Weitz 2002). The anti-persistent behavior arises because molecules are reflected by the cage barriers (similar to that of confinement), causing the molecules to return to their previous positions. However, analyzing the anti-persistent behavior using the relatively simple negative correlation of adjacent displacements instead of the VAF (which has not been extensively investigated with this type of system) limits the understanding of this system, as we further discuss below (Weber et al. 2012a; Weeks and Weitz 2002; Parry et al. 2014).

Fig. 2.6.

The cytoplasm of E. coli has glass-like properties. (a) The radiation of gyration (R_g) of individual trajectories vs. the particle size for individual GFP-fused avian reovirus protein μNS particles, without (green) and with (black) ATP-depletion (DNP). (Figure from Parry et al. 2014) (The dashed line indicates the separation between the “caged” population (small R_g) and the freely diffusive population (large R_g)). (b) The anti-persistent behavior of adjacent displacements for the same data in (a). Here the directionality was assigned a negative value if the second displacement was in the opposite direction of the first. (Figure from Parry et al. 2014)

2.5.2.3. Diffusion Within a Viscoelastic Medium (Sub-diffusion)

In Brownian diffusion, each step a molecule takes is independent of the previous steps. In other diffusion modes there may exist temporal correlations throughout an individual trajectory, which are thought to be a hallmark of complex systems containing many interacting components. Temporal correlations themselves lead to anomalous diffusive behavior (Balakrishnan 1985): positively correlated subsequent displacements lead to super-diffusion, whereas all other types of temporal correlations produce sub-diffusion.

One common mechanism that leads to temporally correlated sub-diffusion is diffusion within a viscoelastic medium (Fig.2.3l). For example, the diffusive motion of bacterial chromosomal loci in the cytoplasm has been modeled as a polymer within a viscoelastic medium; the viscoelasticity of the fluid leads to “fluid memory”, which propagates past “deformations” to the future (Weber et al. 2010b; Weiss 2013). Fractal calculus has been shown to be a useful tool in the modeling of mechanical memory of viscoelastic materials (Deng and Barkai 2009). Therefore, within bacteria, the viscoelasticity of the medium has been most frequently modeled with the fractional Langevin equation (Weber et al. 2012a; Lutz 2001; Deng and Barkai 2009; Weber et al. 2010a, 2012b). We should also note that the diffusion of molecules within homogeneous protein solutions have been successfully modeled using the fractional Langevin equation (Pan et al. 2009) (and the resulting MSD’s of the fractional Langevin motion are ergodic, Fig. 2.3m) (Deng and Barkai 2009). Finally, as with all previously mentioned models of sub-diffusion, fractional Langevin motion also results in anti-persistent behavior, in that when a molecule moves the medium “pushes back” (Weber et al. 2010a). The corresponding VAF $C_v^{\delta }(\tau )$ shows a consistent negative peak when δ and τ are equal for all measurable δ and τ (Fig. 2.3n) (Weber et al. 2012a). This behavior indicates that there is a “restoring force”, causing the anti-persistent behavior over a large range of timescales due to the elastic nature of the medium. There are two major biological implications if a cell’s cytoplasm is a viscoelastic medium; (1) molecules would take longer to reach distant targets than a freely diffusing molecule; and (2) molecules would retrace their previous locations, which could have interesting implications for the timescales of any process which depends upon two molecules coming together.

2.5.2.4. Continuous Time Random Walk (Sub-diffusion)

A fourth type of sub-diffusion behavior is described by the Continuous Time Random Walk (CTRW) model. In the CTRW the diffusion of a molecule is modelled as jumps on a lattice with random waiting times between individual jumps. The waiting time distribution follows a power law probability distribution, leading to large heterogeneities when comparing the MSDs of individual molecules. The proposed biological mechanism behind the CTRW are binding events along a trajectory (Weber et al. 2010a) (Fig. 2.3o), whose power law distribution for waiting times has been observed before (Nagle 1992). The long tail of the waiting time distribution leads to the breaking of ergodicity, where the ensemble average does not equal the time averages of individual trajectories (Fig. 2.3p) (He et al. 2008). Here we should note that CTRW does not show anti-persistent behavior and the VAF does not have a negative peak (Fig. 2.3q).

2.6. Diffusion in Different Subcellular Compartments

2.6.1. Diffusion in the Cytoplasm

The cytoplasm is the largest compartment of a bacterial cell and the main reaction chamber for essential cellular processes such as signal transduction, protein degradation and gene regulation (Fig. 2.4). As diffusion is the main means for bacterial macromolecules to reach their target sites in the cytoplasm, it is important to understand how the properties of bacterial cytoplasm influence diffusion.

Fig. 2.4.

A “simplistic” overview of diffusion within the different compartments of the cell. The three different regions of the cell are shown in yellow with their specific label. Below a characteristic diffusion coefficient is shown that has been observed for that compartment (Note: the characteristic diffusion coefficient for the nucleoid is for the DNA itself (DNA) and for a protein non-specifically binding DNA (DNA-Binder))

A defining difference between the cytoplasm of eukaryotic cells versus bacteria cells is the level of crowding. For instance, in bacterial cells the concentration of proteins was measured at 200 g/L in laboratory growth conditions, whereas that in mammalian cells was measured at 50–100 g/L (Cayley et al. 1991; Winick 1968). Under special conditions such as increased osmotic stress, the macromolecular concentration in bacterial cells can approach that of protein crystals (Mika and Poolman 2011). The extreme crowding of cytoplasm has a massive influence on the diffusive properties of cytoplasmic molecules and is likely the main origin of sub-diffusion.

2.6.1.1. Diffusion of Particles of Different Sizes

Early studies characterized the diffusion of fluorescent proteins (FPs) in live E. coli cells using FRAP (Elowitz et al. 1999). By bleaching half of a cell and monitoring the fluorescence recovery, the diffusion coefficient D of GFP was determined at ~8μm²/s. This D value is ~10 times slower than that in water (Terry et al. 1995) and ~4 times slower than that in the cytoplasm of eukaryotic cells (Swaminathan et al. 1997), suggesting that the bacterial cytoplasm is indeed highly viscous, and that the diffusion of macromolecules in the cytoplasm could set the reaction timescales for certain cellular processes (Elowitz et al. 1999).

Interestingly, when a FP is fused to proteins of different molecular weights (MWs), although the trend holds true that the larger the MW is, the lower the diffusion coefficient, the quantitative relationship is different from what would be expect from the Stokes-Einstein equation (Einstein 2007). Instead of scaling with MW with an exponent of −1/3, the experimentally measured scaling exponent is between −0.5 to −0.8 for proteins (Mika and Poolman 2011; Kumar et al. 2010). As such, proteins exhibit a rapid reduction of D as MW increases. As we discuss below, other properties of proteins and the bacterial cytoplasm are likely responsible for this behavior.

For large and non-globular molecules such as mRNAs labeled with the MS2-FP fusion system (Golding and Cox 2006) (MW > 2 MDa), studies observed sub-diffusive motions with an MSD exponent α of ~0.7 on timescales from seconds to minutes (Golding and Cox 2006; Weber et al. 2010a, 2012b; Lampo et al. 2017b). The sub-diffusive behavior did not appear to be dependent on the growth condition or the genetic backgrounds used in the experiments, as the exponent α remained similar under various conditions (Weber et al. 2010a). In one study two diffusive states were qualitatively observed, with one essentially immobile (“trapped”) and the other freely diffusing throughout the cytoplasm. With these results, the first model in which the heterogeneous, crowded cytoplasm traps/cages individual mRNA molecules was proposed for bacteria (Golding and Cox 2006). A more recent study found that the diffusion of mRNA molecules exhibited dynamic heterogeneity through time and space and was ergodic (Fig. 2.5a) (Lampo et al. 2017b). Intriguingly, the diffusion coefficients of individual mRNA molecules followed an exponential distribution, showing more of a continuum instead of two distinct states, one immobile and one mobile. It should also be mentioned that a similar trend was also found for mRNA within Yeast cells, suggesting the behavior may be a universal trait (Fig. 2.5a). Notably, VAF analysis of these studies all showed anti-persistent behaviors over various timescales (Fig. 2.5b), suggesting that the mRNA’s diffusive motion resembled that of fractional Langevin motion, i.e. mRNA molecules diffused within an viscoelastic medium (Weber et al. 2012a; Lampo et al. 2017a).

Fig. 2.5.

(a) Dynamic Heterogeneity of individual molecules: the probability density function of the diffusion coefficient of individual mRNA molecules normalized by their mean. (Adapted from Lampo et al. 2017a). (b) The VAF of the mRNA resembles that of diffusion within a viscoelastic medium. (Adapted from Lampo et al. 2017a)

A recent study explored the diffusive properties of even larger particles in the bacterial cytoplasm (Parry et al. 2014). GFP-fused avian reovirus protein μNS, when expressed at different levels, self-assembles into large particles of different sizes. Parry et al. tracked the diffusion of these nanoparticles in E. coli and C. crescentus cells and found that these large particles exhibited different diffusion properties when compared to molecules of smaller sizes.

First, the MSD curve of these nanoparticles showed sub-diffusive behavior that was qualitatively similar to what was observed for mRNA (Golding and Cox 2006). They also exhibited two subpopulations, one immobile and one mobile. The presence of these two populations was independent of the corresponding particle size and the metabolic activity of cells, but the fractions of the two populations varied with both (Fig. 2.6a). The displacement distribution of nanoparticles was not Gaussian, and the larger the particles, the more they deviated from that expected for Brownian motion.

Second, the mobility of nanoparticles was related to the metabolic state of the cells: in metabolically inactive cells (ATP-depleted for example), there were more immobile particles (Fig. 2.6a), the MSD exhibited non-ergodic behavior, and the larger particles deviated from Brownian motion to an even greater extent when compared to smaller particles (< 30–40 nm) (Parry et al. 2014). These results indicate that smaller particles within the cytoplasm “see” the cytoplasm as more of a fluid medium and the apparent diffusion coefficient of particles is greatly affected by the metabolism of the organism.

The differential diffusive behavior of small and large molecules/particles in the bacterial cytoplasm have also been reported under stressed conditions. In osmotically upshifted cells, the diffusion of GFP (quantified using FRAP) was found to decrease drastically compared to unshifted cells (Konopka et al. 2006; van den et al. 2007), while small molecules such as sugar molecules remained mobile and freely diffused throughout the cell (van den et al. 2007).

Lastly, these nanoparticles showed an anti-persistent behavior where adjacent displacements exhibited opposite directions (Fig. 2.6b), suggesting that these particles have a preference to return to their previous positions (Weeks and Weitz 2002). As such, the bacterial cytoplasm was proposed to have glass-like properties, which affects the diffusion of molecules of different sizes differentially (Parry et al. 2014).

How does the bacterial cytoplasm behave like a glass-forming liquid? The differential mobility of small and large molecules/particles, the presence of the mobile and immobile states, non-ergodicity (in metabolically inactive cells) and the anti-persistent behavior, all suggest that the highly crowded cytoplasm likely traps particles in pockets/cages and that the cytoplasm is near its glass transition, at least in the metabolically inactive cells. These cages would confine the molecules/particles until the surrounding molecules in the cages rearrange themselves, which have been proposed to be depend upon mechanic perturbations and small volume changes resulting from various enzymatic activities (Parry et al. 2014; Oyama et al. 2019). In metabolically inactive cells, the local cages would persist for a longer period of time compared to normal cells, explaining why molecules are trapped in heterogenous pockets for longer times and why the deviation from typical Brownian motion grows larger. This effect directly links the timescales at which the cytoplasmic medium rearranges to the metabolism of the cell, providing a useful window to investigate bacterial cell metabolism. Notably, similar responses of chromosomal loci and an outer membrane protein (discussed later) to the cell’s metabolism (Weber et al. 2012b; Winther et al. 2009) have also been reported, suggesting that it may be a universal rule that active metabolism of the cell increases the diffusion of molecules beyond what could be caused by simple thermal motion alone.

Many questions remain unanswered. Exactly how at the molecular level does the metabolic activity of a cell perturb the local cages in the cytoplasm? How are the diffusive dynamics of trapped molecules/particles influenced by the relative sizes of the surrounding molecules and chemical compositions? Do these glass-like properties influence any cellular processes in metabolically active cells, considering that most molecules in cells are likely too small to exhibit these effects with active enzymatic activity? Also, given that the cytoplasm of metabolically active cells exhibited only a fraction of the behaviors for a medium with “glass like properties”, how should the viscoelastic properties, ergodicity, and specific distributions of dynamic diffusion coefficients that were seen for the mRNA molecule (Weber et al. 2012a; Lampo et al. 2017a), chromosome (discussed later), and nucleoid associated proteins (discussed later) (Sadoon and Wang 2018) be incorporated into the theory? Finally, further studies are needed to investigate the timescales over which the μNS trajectories show anti-persistent behavior (the velocity autocorrelation function) to determine whether the behavior is consistent with the other studies/does diffusion within an “active glass” exhibit a similar VAF as a viscoelastic medium (Weber et al. 2012a; Lampo et al. 2017a; Sadoon and Wang 2018).

2.6.1.2. Diffusion of Molecules of Different Surface Properties

In the bacterial cytoplasm, the diffusive behavior has also been shown to be influenced by the surface properties of molecules. An early example came from the observation that the addition of a small (<1 kD) but highly charged 6xHis tag to GFP caused a two-fold reduction of its D value in E. coli cells (Elowitz et al. 1999). Another study systematically modified the surface net charge of GFP from −30 to 25 across multiple bacterial species and found that the most positively charged GFP variants had a D value 100-fold slower than those of the negatively charged ones, likely caused by their electrostatic interactions with negatively charged ribosome (Fig. 2.7). Interestingly, the study pointed out that as the majority of cytoplasmic proteins in most bacteria are negatively charged, it is possible that these organisms evolved to limit nonspecific interactions with the ribosome in order to maintain a sufficient diffusion coefficient for its cytoplasmic contents (Schavemaker et al. 2017).

Fig. 2.7.

The relation between the charge of GFP and their diffusion coefficients: the filled histogram shows the distribution for the charged particle referenced in the individual subplots and the empty histogram shows the diffusion coefficients of the −30 GFP in each subplot for reference Schavemaker et al. (2017)

A note of caution is that the D measurement of relatively small molecules such as GFP in above studies were done using FRAP. As mentioned earlier, FRAP is an ensemble method and unable to differentiate different types of diffusion and corresponding transition kinetics (Elowitz et al. 1999). SMT of freely diffusing small protein molecules in live bacterial cells has been difficult in the past because of the molecules’ relative fast diffusion. However, with recent development of bright organic fluorophores such as the Halo-JF dye system, and fast, sensitive cameras such as the new generation of Scientific cMOS cameras, it is foreseeable that new information of the bacterial cytoplasm and dynamic interactions of normal-sized protein molecules with their interacting partners will emerge.

2.6.2. Diffusion in the Nucleoid

The majority of the bacterial cytoplasm volume is occupied by the nucleoid, an enormous DNA-RNA-protein complex (Fig. 2.4). The macromolecular structure and compaction of the nucleoid are maintained and regulated by small RNAs and many proteins such as histone-like nucleoid-associated proteins (NAPs) (Drlica and Rouviere-Yaniv 1987), topoisomerases (Stracy et al. 2018) and the structural maintenance of chromosome (SMC) proteins (Fudenberg et al. 2016). The chromosome also dynamically rearranges when exposed to different stimuli (Dorman and Dorman 2016). Consequently, the organization and dynamics of the nucleoid itself influences how DNA binding proteins such as RNAP and transcription factors (TFs) find their targeting DNA sites.

For instance, chromosomal DNA loops (Postow et al. 2004) play important roles in transcription regulation and the overall compaction of the chromosome (Bohrer and Roberts 2016; Chong et al. 2014). DNA loops form when specific chromosomal regions come into contact with each other in space and the ends are restrained by protein binding. Chromosomal DNA segments of different genes could also be spatially positioned in proximity with each other to form the scaffold of the so-called transcription factories for RNAP and transcription factors binding. In E. coli and B. subtilis RNA polymerases were shown to form spatial clusters, where the synthesis of rRNA takes place (Weng et al. 2018). Due to the local high concentration of RNAP, the diffusion of genes and/or transcription factors into and out of the RNAP clusters is a likely mechanism of transcription regulation. Therefore, it is important to understand the diffusive properties and associated time scales of the dynamics of the chromosome and its interacting proteins (Kapanidis et al. 2018).

2.6.2.1. Diffusion of Chromosomal DNA

One important consideration of describing the diffusion of chromosomal DNAs is that chromosomal DNA is a polymer itself, thus its diffusive dynamics are different from that of any nontethered particles within the cytoplasm. Note that while there were only limited numbers of studies on the chromosome’s dynamics in bacteria, it has been shown that the general diffusive properties of the chromosome are conserved across different bacterial species.

In one study Weber et al. (2010a) used the ParB-GFP/parS system to label chromosomal loci in both E. coli and C. crescentus (Nielsen et al. 2006). The labeled chromosomal loci exhibited sub-diffusive motion with an MSD exponent α ~ 0.4. Under different perturbation conditions, although the D varied over ~4-fold, the α value was unchanged, indicating that the dynamics of these individual loci are likely dominated by one universal physical process (Fig. 2.8a). The α value is also different from that of mRNA molecules measured using the MS2-GFP system (α ~ 0.7) (Golding and Cox 2006; Weber et al. 2010a; Lampo et al. 2017a). This difference suggests that the physical interactions of chromosomal DNA and mRNAs with their surroundings are likely very different. Incorporating the chromosomal polymer property into the diffusion model led to an exponent of ~0.5 (Weber et al. 2010b), indicating that additional factors must be at play. Interestingly, when the viscoelastic property of the cytoplasm (modelled by fractional Langevin motion Deng and Barkai 2009) was incorporated together with the polymer model, an exponent of α ~ 0.35 was predicated, matching experimental measurements. Correspondingly, the velocity correlation function showed long timescale correlations for chromosomal loci (Fig. 2.8b, and mRNAs too, Fig. 2.5b). These results hence provide strong support that the cytoplasm possesses viscoelastic properties that create “fluid memory” (Weber et al. 2010a, 2012a).

Fig. 2.8.

(a) The behavior of the DNA’s sub-diffusive diffusion (exemplified by the exponent of MSD curve α) remains the same when exposed to different perturbations. (Figure from Weber et al. 2010a). (b) The VAF of the DNA resembles that of diffusion within a viscoelastic medium. (Figure from Weber et al. 2012a)

One interesting discrepancy of this work is that a viscoelastic cytoplasm modelled by the fractional Langevin equation is fundamentally different from a cytoplasm with glass-like properties as what was proposed by Parry et al. A recent work by Sadoon et al. shed light on the discrepancy (Sadoon and Wang 2018). In this study the diffusive behavior of the DNA binding protein H-NS was investigated. The histone like H-NS oligomerizes on DNA and regulates the expression of ~5% of the E. coli genome. Using SMT of mEos3.2-fused H-NS, the apparent D value was determined to be similar to that of the chromosomal loci with α ~ 0.6, suggesting that the diffusion of H-NS is likely linked to that of the chromosome. The velocity autocorrelation function showed characteristics that were consistent with previous studies (Weber et al. 2010a, 2012a; Lampo et al. 2017b) suggesting a viscoelastic cytoplasm as modeled by the fractional Langevin equation (Weber et al. 2012a). Interestingly, when they quantified the complex modulus of the medium as a function of frequency (0.1–20 s⁻¹) the bacterial cytoplasm showed a glass-like transition over the different timescales, suggesting that the cytoplasm exhibited properties as reported by Parry et al. (2014). This study suggests that the cytoplasm of bacteria behaves differently at different timescales, highlighting the importance of taking timescales of different cellular processes into consideration.

In another study, Weber et al. found that their previous model of the viscoelastic cytoplasm coupled with the DNA polymer model was inadequate to capture the temperature dependence of the diffusion of labeled chromosomal DNA loci. The apparent diffusion coefficient D of chromosomal DNA loci scaled exponentially with temperature, termed “super-thermal”, instead of linearly as predicted in the Stokes-Einstein equation when the system is at equilibrium (Weber et al. 2012b). Most interestingly, this super-thermal diffusion only existed in cells of active metabolism – in cells depleted of ATP, D scaled linearly with temperature as expected. These results indicate that the non-equilibrium state of the cell, most certainly caused by enzymatic activities, leads to “faster” diffusion than what would be produced solely by thermal fluctuations. Here the influence of metabolism on diffusion is consistent with the previously discussed study done by Parry et al. (2014).

2.6.2.2. Diffusion of DNA Binding Proteins

Since the chromosome is within the same compartment as the ribosomes within bacteria, all of the components that regulate the conformation of the chromosome, transcription and translation must function together within the same environment. Since the diffusion of chromosomal DNA is very small compared to that of DNA-binding proteins, different diffusive states of DNA-binding proteins, judged by their differential apparent diffusion coefficients, are commonly used to identify the bound and unbound states, providing an invaluable technique to study protein-DNA binding kinetic and functions in live cells.

An early SMT experiment done by Elf et al. probed the binding of the transcription factor LacI to its specific chromosomal binding site lacO. While both 1d and 3d diffusion had been proposed as the mechanism for how transcription factors find their specific DNA targets in the presence of overwhelmingly nonspecific chromosomal DNA (von Hippel and Berg 1989), the authors found that the a single LacI dimer spends the majority of its time (90%) performing 1d diffusion along the DNA, demonstrating this mechanism in vivo. A similar result was found for RNAP, which spends 85% of its time binding non-specifically within the nucleoid (Stracy et al. 2014, 2015; Kapanidis et al. 2018). Furthermore, transient non-specific binding has also been observed for the nucleoid-associated protein HU and was proposed to be important for maintaining the “dynamic” nature of the chromosome (Bettridge et al. 2019) – suggesting this may be a common trait of many DNA associating proteins.

In another recent study, the diffusion dynamics of gyrase in E. coli was investigated using SMT (Stracy et al. 2018). Gyrase helps maintain the supercoiling state of the chromosome, which has a large effect on transcription (Dorman and Dorman 2016; Bohrer and Roberts 2016). It was found that the average time gyrase molecules spent in the specific DNA bound states is ~2 s, with replication-proximal gyrase molecules having longer dwell times (~8 s). Such a difference suggests that different gyrase molecules may work at different capacities depending on the local topological need, highlighting the unique power of SMT as an imaging technique to identify spatial information in live cells.

Along the same line, SMT studies helped resolve a discrepancy between biochemical and microscopic data regarding the spatial arrangement between transcription and translation in bacterial cells (Hobot et al. 1985; Wang et al. 2011; Bakshi et al. 2012). Biochemical studies showed that in bacterial cells translation occurs co-transcriptionally when mRNA is still being transcribed and physically attached to the DNA. Fluorescence microscopy however showed that ribosomes are excluded from the nucleoid while RNAP is predominately nucleoid-associated (Stracy et al. 2015; Bakshi et al. 2012). Using SMT of the ribosomal protein L1 and S2 tagged with mEos2, the diffusion coefficients of the free subunit and the incorporated, translating ribosome were found to be significantly different, and that the free subunits could diffuse freely throughout the nucleoid. Therefore, ribosome could assemble inside the nucleoid to initiate translation. Fully assembled, translating ribosomes, however, are mainly excluded from the nucleoid, suggesting that as translation is initiated, the transcribing mRNA could gradually move out of the nucleoid to continue translation. Indeed, such movement of actively transcribing gene loci has been observed in E. coli cells (Stracy et al. 2014).

2.6.3. Diffusion in the Cell Envelope

The cell envelope of gram-negative bacteria has three layers, the outer membrane (OM), and the inner membrane (IM), and the space in between where the cell wall resides (periplasm) (Fig. 2.4). Gram-positive bacteria do not have an outer membrane but have a thick cell wall and an inner membrane. The outer membrane acts as the first barrier between the cell and the environment for gram-negative bacteria. It is rich in β-barrel proteins, which allows small molecules to access the periplasm and cytoplasm through the inner membrane (Ruiz et al. 2006). Another function of the outer membrane comes from its mechanical properties, as a recent study predicts that the outer membrane’s β-barrel proteins play a large part in the ability of the cell to handle external forces (Lessen et al. 2018). The periplasm of gram-negative bacteria is often described as being “highly viscous” (Cho et al. 2014; Ruiz et al. 2006; Goemans et al. 2014; Denoncin et al. 2014; Mas et al. 2019; Grote et al. 2018) and contains a thin layer of peptidoglycan, or cell wall, although in reality it is likely not much more viscus than the cytoplasm (Foley et al. 1989; Mullineaux et al. 2006; Sochacki et al. 2011). The peptidoglycan layer dictates the cell shape and allows the cell to survive osmotic stress. The incorporation of this layer during division has been shown to be a major driving force for proper constriction (Yang et al. 2017). Finally, the inner membrane directly links molecules in the cytoplasm to the environment on the outside and is important for a multitude of different signal transduction processes. The organization of bacterial membranes has been shown to be highly regulated and likely composed of many scattered microdomains (Rudner and Losick 2010; Lopez and Koch 2017; Dempwolff et al. 2016).

2.6.3.1. Diffusion Within the Outer Membrane

Despite the importance of the outer membrane and its associated outer membrane proteins (OMPs), there are relatively few studies in which the diffusive behaviors of OMPs were investigated when compared to that of cytoplasmic proteins.

In an early work, where OMPs were nonspecifically labeled with a dye-conjugated reactive succinimidyl ester and chased with dye-free medium, it was found that a significant proportion of the outer membrane proteins OMPs remained immobile in particular at the cell poles (de Pedro et al. 2004). This observation is consistent with the notion that cell poles are essentially metabolically inert and stable.

For OMPs not specifically targeted to cell poles, many of them were found to be largely confined as well. SMT experiments of the outer membrane λ receptor protein tagged with large beads (20–500 nm) showed that that a subpopulation of the receptor was confined in small domains of 20–50 nm, and that a relatively faster population explored regions about 100–300 nm in size (Fig. 2.9a) (Oddershede and Dreyer 2002; Gibbs et al. 2004). SMT of two other outer membrane proteins labeled with fluorescent antibodies, the porin OmpF and the cobalamin receptor BtuB, showed that OmpF was confined to domains of ~100 nm in diameter, similar to the λ receptor, while BtuB was much more mobile with a D of 0.05 μm²/s, an order of magnitude larger than that of OmpF (Spector et al. 2010).

Fig. 2.9.

(a) The confined diffusion of the OMP λ receptor with the filled circles calculated using the fast particles and the open circles the slow. (Figure from Gibbs et al. 2004). (b) Top shows an illustration of the colors representing the diffusive states of the individual molecules. Bottom shows how the diffusion of individual BtuB (OMP) was affected by the addition of different amounts of more BtuB or non-interacting OmpF. The addition of an engineered maltose binding protein with a single transmembrane helix (TM-MBP) was also used as a control. (Figure from Rassam et al. 2015)

What determines the differences in the mobility of OMPs and why do some OMPs exhibit confined diffusion? On one hand, depleting ATP, or inhibiting cell wall synthesis, caused a significant further reduction of the mobility of the λ receptor at long time scales (Winther et al. 2009), similar to what was observed for cytoplasmic proteins and the chromosome (Parry et al. 2014; Weber et al. 2012b). On the other hand, because λ receptor is anchored to the cell wall covalently, it was proposed that the constant and dynamic energy-consuming reconstruction of the peptidoglycan layer underlies the diffusive behavior of the λ receptor (Winther et al. 2009). A later study that quantified the dynamics of OmpA with and without the ability to bind the cell wall however showed essentially the same immobility, arguing against this hypothesis (Verhoeven et al. 2013).

Later the work of Rassam et al. showed that protein-protein interactions within the outer membrane appear to play an important role in restricting OMP diffusion. Using SMT, a mutated BtuB protein unable to interact with its cytoplasmic membrane protein partner TonB showed >10-fold increase of mobility. Interestingly, even nonspecific protein-protein interactions were shown to be important. Rassam et al. further showed that two other OMPs, Cir and BamA, which do not interact with BtuB directly, clustered with BtuB in 0.5-μ m diameter “islands” on the outer membrane of E. coli cells. When the diffusion of BtuB was measured in vitro in a supported lipid bilayer made from E. coli membrane extract (Fig. 2.9b), SMT of BtuB showed Brownian diffusion at low concentrations. When the concentration of BtuB or a non-interacting OMP (OmpF) increased, BtuB exhibited orders of magnitude reduced diffusion and increased confinement. These results strongly suggest that the mechanism behind the previously observed confined diffusion was due to the “promiscuous” interactions among OMPs in confined areas of the outer membrane, which was proposed to be individual islands of different molecular compositions (Rassam et al. 2015). The proposed OMP islands formed by non-specific protein-protein interactions however need to be further verified. In particular, it would be interesting to examine whether all or just a few specific OMPs make up these islands, whether the characteristics of these OM islands vary with metabolism, and how the response changes the diffusion of other OMPs.

2.6.3.2. Diffusion Within the Periplasm

Even fewer studies have investigated the diffusive behaviors of proteins in the periplasm. In an early study where the diffusion of the maltose-binding protein (MBP) within the periplasm of E. coli was monitored using FRAP, the lateral diffusion coefficient of MBP was found to be at 0.009μm²/s (Brass et al. 1986). The extremely small diffusion coefficient was later shown to result from the harsh experimental conditions used to permeabilize the cells. Later FRAP studies found that the diffusion coefficients of FP tagged periplasmic proteins were ~3μm²/s (Foley et al. 1989; Mullineaux et al. 2006; Sochacki et al. 2011), only “slightly”smaller than that in the cytoplasm. Additionally, when under osmotic stress (water leaves the cytoplasm and moves into the periplasm), the diffusion coefficient of these periplasmic proteins increased ~3 fold, similar to what was observed for the cytoplasm (Sochacki et al. 2011). Most interestingly, the periplasms of multiple gram-negative bacteria have been shown to form heterogenous, diffusion-confined domains, suggesting that the proteins in the periplasm likely exhibit a level of crowding that influences each other’s diffusion dynamics (Foley et al. 1989; Zhang et al. 2008, 2013). Clearly, further investigations especially with SMT methodologies are needed to elucidate the diffusion dynamics of proteins in the periplasm.

While no SMT studies have been done on a purely periplasmic protein at this time, various studies have quantified the diffusive properties of the enzymes responsible for maintaining the peptidoglycan layer during cell division (mostly inner membrane proteins). Of particular interest to the study of diffusive behavior within bacteria, many of these proteins show super-diffusion, whose corresponding velocities are likely directly linked to their state. Furthermore, studies are beginning to show how the information within the dynamic behavior of molecular assemblies within the cytoplasm are propagated into the periplasmic compartment.

In most bacteria, for cell division to take place, a large macromolecular complex, the divisome, must form and direct the synthesis of septal peptidoglycan. The formation of this complex is initiated by FtsZ, a tubulin homolog, which polymerizes at the middle of dividing cells. While FtsZ SMT studies have shown that the individual monomers of the FtsZ filaments are stationary (Niu and Yu 2008), recent works utilizing total internal reflection fluorescence microscopy have shown that the filaments themselves show directional movement, the result of treadmilling (Yang et al. 2017; Bisson-Filho et al. 2017). The FtsZ filaments’ dynamics are thought to direct/-coordinate the incorporation of the peptidoglycan and organize many of the other proteins in the divisome.

Interestingly, even though many of the enzymes important for septal peptidoglycan incorporation show the same super-diffusive motion, the mechanisms behind their motions seem to vary between different bacterial species. In Bacillus subtilis it was found that the velocity of bPBP2b (penicillin-binding protein) was directly linked with the velocity of the FtsZ filaments and that the velocities of these components were directly linked to septum closure (Bisson-Filho et al. 2017). Similarly, in E. coli it was shown that the velocity of the synthase enzyme bPBP3 (FtsI) was also directly correlated with the velocity of the FtsZ filaments, but interestingly the velocity of the two were not limiting in terms of septum closure (Yang et al. 2017). Lastly, unlike the other two species in Streptococcus pneumoniae it was recently found that the bPBP2x:FtsW complex exhibits directional motion, but its velocity is independent of the velocity of the FtsZ filaments (Perez et al. 2019). Considering the similarities in the diffusion dynamics and the rarity of directional motion within bacteria future work quantifying the mechanisms responsible for the diffusion of these enzymes is an exciting direction of study.

2.6.3.3. Diffusion Within the Inner Membrane

Compared to proteins in the outer membrane, inner membrane proteins (IMPs) appear to be more mobile. The first SMT study of an IMP tracked the membrane-bound histidine kinase PleC fused with a YFP in C. crescentus cells. PleC localizes to the cell pole of Caulobacter cells and was shown to be important for the asymmetric cell division (Wheeler and Shapiro 1999). A subpopulation of PleC-YFP indeed was found at the cell pole and was largely immobile, and the other subpopulation diffused within the cell body with normal Brownian motion with a D of ~0.01μm²/s. This observation suggests that at least some IMPs can freely diffuse throughout the entire inner membrane within C. crescentus cells (Deich et al. 2004). Another IMP, TatA, forms large complexes (~600 KDa) with itself and the other two proteins TaB and TacC in the twin-arginine translocon (Bolhuis et al. 2001). TatA diffused faster than PleC with an apparent D of ~0.13μm²/s measured by FRAP (Mullineaux et al. 2006). Such a high mobility is comparable to what was observed within Eukaryotic membranes (Zhang et al. 1993). SMT of TatA-YFP in another study showed similar Brownian motion with a comparable D value, although the trajectories were not long enough to identify whether there were other diffusive modes at long time scales (Leake et al. 2008).

The relationship between the size of an IMP and its diffusion coefficient was also investigated. For TatA-YFP, for example, SMT found that the apparent diffusion coefficient value decreased when the number of TatA-YFP molecules in self-assembled complexes increased from ~10 to 100. Interestingly, the relationship can be strictly described as logarithmic, mimicking what has been observed for the relationship between the size of cytoplasmic proteins and the corresponding diffusion coefficient (Leake et al. 2008; Kumar et al. 2010). Another work by Oswald et al. investigated the diffusion coefficients of eight different inner membrane proteins and showed a clear relationship between the apparent diffusion coefficient and the radii, but not the molecular weight, of each protein (Fig. 2.10) (Oswald et al. 2016). This interesting finding suggested that it is the “amount/volume of the protein” that interacts with the membrane that dictates the apparent diffusion coefficient (Saffman and Delbrück 1975). A more recent and exhaustive study has verified this finding, which investigated ~200 membrane proteins within Bacillus subtilis (Lucena et al. 2018).

Fig. 2.10.

Diffusion coefficients of IMPs vs. the radius of the IMP (R). (Figure from Oswald et al. 2016)

Not all IMPs exhibit Brownian motion. The cytochrome bd-I complex (CydB), when fused to GFP, was found to form clusters of ~100 nm in diameter and contain approximately 76 cydB-GFP proteins per cluster. A similar logarithmic relationship between the apparent diffusion coefficient and the number of CydB within the complex as that of TatA-YFP was also observed. However, some CydB-GFP clusters clearly exhibited confined diffusion. By fitting the MSD curves to a mobility-confinement model, the confinement zone of CydB-GFP, defined as an area in which the molecules can diffuse freely and above which a barrier confines the diffusion of the molecules was determined to have a diameter of 160 nm (Lenn et al. 2008). A similar confinement zone was observed for another IMP, Tsr, a chemotaxis proteins that forms clusters at cell poles (Oh et al. 2014). A few other IMPs that do not form clusters also showed sub-diffusive behavior based on their MSD plots, suggesting that sub-diffusion may be a common feature of IMPs.

What contributes to the confinement of IMPs? The inner membranes of B. subtilis and E. coli stained with membrane dyes Nile Red and Dil-C12 respectively, showed a clustered, heterogenous fluorescence distribution (Strahl et al. 2014; Oswald et al. 2016). As it is known that both dyes are more specific for fluid rather than rigid regions of the membrane, it is likely that there existed fluid macrodomains on the membrane, and that these macrodomains may be responsible for the confined movement of IMPs. In eukaryotic cells it is known that cytoskeleton proteins such as actin are involved in the formation of membrane microdomains (Chichili and Rodgers 2009). Therefore, it is not surprising that when the polymerization of the bacterial actin homolog MreB was inhibited, the apparent Ds of many IMPs increased, confinement disappeared, and that the proportion of Tsr molecules that experienced confined diffusion diminished significantly (Oswald et al. 2016).

Based on these results, a general model behind the confinement caused by MreB was proposed (Oswald et al. 2016), similar to what was proposed for actin in eukaryotic cells (Goiko et al. 2016). Filaments formed by MreB and its membrane anchors may act as diffusion barriers/fences for inner membrane proteins, leading to their apparent confinement observed in the MSD plots. However, Lucena et al. found that the diffusion of >200 IMPs along the long axis of the cell and the short axis did not exhibit any markable differences, arguing that the MreB filaments, which mainly form along the short axis of the cell, may not be confining the diffusion of the proteins using the same mechanism as actin, or that MreB filaments may not be as dense or well organized as long actin filaments in eukaryotic cells (Lucena et al. 2018).

2.7. Summary

Within this review we have described the various methodologies used to characterize diffusion within bacteria with a primary focus on single molecule tracking. We have described the different forms of analysis one can use to determine the behavior of diffusion as well as described the most common models of diffusion within bacteria. We then went into detail, describing the studies that have characterized the diffusion within the different compartments of bacteria, and several different themes emerged from the various studies. First, in every compartment of the cell, diffusion is much more complicated than normal Brownian motion, with a vast array of different mechanisms leading to sub-diffusion. Second, the metabolism of the cell can have a large impact on the diffusion of particles in any compartment of the cell, where the higher the metabolism the faster the diffusion of the particles. Third, the cytoplasm likely has viscoelastic properties and influences the diffusion of particles on a variety of different timescales. Fourth, diffusion within the cell envelope has not been quantified as in depth as within the other compartments. And fifth, different protein-protein interactions can lead to different types of diffusion, including confinement. Finally, we would like to emphasize that no real consensus has been made for any compartment and no model can yet explain all the experimental work at this time, leaving room for many new discoveries.