Abstract
The world is now facing the Covid-19 pandemic and the control of Covid-19 spread in health care facilities is a serious concern. The ventilation system in hospital isolation rooms with infectious patients plays a significant role in minimizing the spread of viruses and the risk of infection in hospital. In this study, computational fluid dynamics (CFD) simulation is applied to investigate the important factors on transport and evaporation of multi-component cough droplets in the isolation room with different ventilation configurations. We analyzed the effects of various air outlet positions on the removal efficiency of infectious droplets in isolation room and proposed the optimum location of exhaust vent in hospital isolation room to maximize the droplet removal efficiencies. We found that the evaporation rate of droplets is strongly dependent on the relative humidity (RH) and, at low RH, the large-sized droplets with Covid-19 virus can evaporate quickly and become small-sized aerosols to stay in air for a long time and the Covid-19 can propagate more easily through the respiratory organs during breathing. It also explains why the Covid-19 can propagate faster in winter with low humidity than in summer with high humidity.
Keywords: Covid-19, Isolation room, Ventilation designs, Droplet evaporation, CFD simulation
Nomenclature
Droplet surface area
Spalding mass number
Drag coefficient
initial concentration of solid compounds
Heat capacity
- D
Diffusion coefficient of vapor
Mass diffusivity of species i
- ddry
Final diameter when all water in droplet evaporates completely
Particle diameter
- E
Energy
Drag force
Gravity acceleration
Enthalpy
Latent heat of vaporization
- J
Diffusive flux
Mass transfer coefficient
Mass
Molecular weight of air
Molecular weight of water
- p
Static pressure
- Re
Reynolds number
- Sc
Schmidt number
Mass added to the fluid phase
Saturated vapor pressure
- t
Time
- T
Temperature
Velocity
- Y
Species fraction
Greek letter
Thermal conductivity
Molecular viscosity
Fluid density
Droplet density
Density of mixture of solutes
Molar fraction of water at the droplet surface
Stress tensor
1. Introduction
Almost 2 years have passed after the outbreak of Covid-19 and the world is still struggling to respond to this pandemic as well as racing to develop the vaccine and medicine against the coronavirus and its new variants. According to the statistics provided by the World Health Organization (WHO), about 234 million cases and 4.8 million deaths have been reported globally until October 1, 2021. This is putting great pressure on medical facilities due to the sudden increase in need for isolation rooms for the treatment of Covid-19 patients. The isolation room occupies a lower air pressure than the adjacent spaces (negative pressure) to prevent the spread of contaminated air to the outside environment [1,2]. The negative pressure in isolation room is created by keeping the exhaust volume flow rate higher than the supply volume flow rate [3]. The results of this study can be applicable to prevent the transmission of not only Covid-19 but also other respiratory diseases such as SARS, MERs and tuberculosis by droplets containing pathogens.
The isolation room in hospitals, especially, have a high risk of Covid-19 infections which might strongly depend on ventilation configuration. For isolation room design, the specifications of exhaust and supply airflow rates and the layout of ventilation system are quite important [4], because the risk of virus propagation in hospital can be critically influenced by the direction, velocity and pattern of airflow in the room. It is also important to understand the transport of droplets containing Covid-19 in the isolation room to protect other patients, visitors and healthcare workers. This can be accomplished by investigating the droplet dynamics combined with the flow patterns in isolation room to calculate the droplet removal efficiency.
The computational fluid dynamic (CFD) simulation has been applied to calculate the contaminant transport in isolation rooms and to predict the effect of airflow behavior on virus transmission [[4], [5], [6], [7], [8], [9]]. Cho et al. [10] and Hang et al. [11] used the tracer gas simulation to analyze the possibility of pathogen propagation through airflow in isolation rooms and showed that the locations of supply and outlet air streams are the most important elements that directly affect the pollutants dispersion. The ventilation strategies were optimized to reduce the pollutant's exposure level of healthcare workers from the patient. Cheong et al. [6] and Jacob et al. [9] reported that selecting the right type of supply air diffuser can minimize inter-mixing between the supply air and the air in the room and that the extract grill should be located near the infectious source. Richmond et al. [8] investigated the dispersion of particle carrying pathogen from the patient in isolation room during the single cough or sneeze and showed the evidence that a health care worker could be exposed to infectious aerosolized agents in an infected isolation room. Most airborne transmissions are caused by the dispersion of droplets/particles and, in the particle model, particle distribution is affected by gravity force and deposition, which is different from the tracer gas simulation. The cough droplets carrying viruses are aqueous solution containing some amount of non-volatile components including sodium chloride, carbohydrate, lipids, protein, mucus, and potentially infectious virus [12]. These components will affect the droplet evaporation rate and the size of droplets and will eventually influence the behavior of droplets in isolation room. However, there has been no publication yet to investigate the Covid-19 transport in isolation room for various designs of ventilation system considering multi-component droplet evaporation.
The droplet evaporation can play a significant role in the Covid-19 spread because of two main reasons: firstly, droplet size changes by evaporation and can affect dramatically the droplet movement and residence time in gas phase and, secondly, the compositions of water and some organic compounds in the droplet may influence the virus's survival [13]. Many droplets are expelled from human body during coughing, water component in droplets would evaporate and the droplets gradually shrink and the equilibrium state between droplet and vapor phases will finally be reached. If the particle becomes completely desiccated, the droplet diameter during drying, , can be determined by the following equation [14]:
| (1) |
where , and are the initial diameters of droplets, density of mixed solutes after drying (g/mL) and initial concentration of non-volatile compounds in droplets (g/mL), respectively. The droplets generated from coughing is in the size range of 1–750 μm [15] and can become smaller quickly in the air by evaporation, because they are quite small and have large surface area [16]. Small droplets become stable aerosols and can be suspended in the air for a long time without settling down to the ground and they can be transported to distant position by airflow by air conditioner or other ventilation systems. In this way, the aerosols will have more chances to participate in the transmission of Covid-19 to other persons.
In this study, CFD simulation with the Eulerian-Lagrangian model is used to investigate several important factors on the transport of cough droplets in hospital isolation room and the evaporation and dispersion of multi-component cough droplets were considered for different ventilation configurations of isolation room. The effects of initial droplet size and relative humidity (RH) on the evaporation of droplets were analyzed. We considered several locations of air outlet ventilation in isolation room and tried to evaluate the droplet removal efficiency of all designs and proposed the optimum location of exhaust ventilation to reduce cough droplet concentration. The results obtained from this study can be used to establish efficient and optimum design of isolation rooms in hospital, which can be significant to reduce the propagation of not only the Covid-19 disease but also the other possible respiratory diseases in the future.
2. Modelling and numerical simulation
2.1. Model cases for numerical simulation
We considered 5 types of gas outlet configurations in the hospital isolation room with a Covid-19 patient lying on the bed (Fig. 1 ). The air comes into the room via an air supply inlet placed on the ceiling and goes out via an exhaust grill. The patient coughs and expels a gas jet stream with given flow rate at an angle of 20° off from vertical direction. Many droplets are injected into the isolation room for 0.35 s during a single cough. We investigated the ventilation flow patterns and droplet dynamics in the isolation room after a cough for 5 different geometrical setups of exhaust grill position (Fig. 1).
Fig. 1.
5 different ventilation configurations considered for isolation room.
The isolation room considered in this study has dimensions of 4 m (length) × 3.5 m (width) × 2.6 m (height). The height of patient is 1.75 m and the mouth is assumed to have a rectangular shape (4 cm × 1 cm) during cough. We believe that it is more reasonable to assume that the droplets are accompanied with the cough flow in mouth, not being released in a conical shape. The rectangular shape of mouth is assumed because of some geometric convenience in numerical simulation.
The bed has a size of 2.0 m × 0.9 m × 0.1 m and is placed at a height of 0.6 m above the ground. The air inlet is fixed on the ceiling at the same position for all 5 cases and has a size of 0.46 m × 0.46 m. The air outlet for the isolation room is assumed to have a size of 0.46 m × 0.46 m for one outlet (Case 1, Case 2, Case 3) or size of 0.23 m × 0.46 m for two outlets (Cases 4 and 5).
The following 5 cases of exhaust air grill location are considered in this study and the exact locations of exhaust air grill are illustrated in Fig. 1.
Case 1
Exhaust air grill placed over the patient's head.
Case 2
Exhaust air grill placed on the ceiling.
Case 3
Exhaust air grill placed on the left sidewall.
Case 4
Two exhaust air grills on either side of the patient head.
Case 5
Two exhaust air grills on either side of the bed bottom.
2.2. Governing model equations
2.2.1. Model equations for continuous phase (air flow)
With the Eulerian descriptions, the airflow field in the isolation room can be predicted by solving the conservation laws. Major governing equations considered in this study are summarized as follows:
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
| (7) |
2.2.2. Model equations for cough droplet transport and evaporation
The Lagrangian approach is employed to track the trajectory of multi-component droplets. The equation of motion of droplets is given by applying Newton's 2nd law,
| (8) |
where is the drag force on droplet,
| (9) |
Here Re is Reynolds number, which is defined as
| (10) |
With an assumption that droplets keep the spherical shape throughout the calculated domain, the drag coefficient is given by
| (11) |
Resuspension of some particles sticking to surfaces might happen after evaporation. There would be several factors that can affect the resuspension of particles, but the resuspension of particles after evaporation is not included in this study, because the resuspension of particles is not clearly elucidated yet. The droplets after evaporation will become solid particles which might have the core-shell structure or porous microstructures. However, there is no experimental data yet about the final shape of solid particles after evaporation and we assumed the spherical shape of droplets during evaporation in this study.
The heat and mass balance equations of droplets need to be solved to calculate the droplet diameter in each time step. The droplet temperature changes by the effects of heat conduction and liquid evaporation and the energy balance equation for multi-component droplet can be written as follows,
| (12) |
For diffusion-controlled vaporization model, the evaporation rate of component i is given by
| (13) |
where is mass transfer coefficient of component i at the droplet surface and is given by
| (14) |
is the Spalding mass number for species ( ) and and are the water vapor mass fraction ( ) and water vapor molar fraction ( ), respectively, at the droplet surface assuming a liquid-vapor equilibrium [17].
2.3. Boundary and initial conditions
It is recommended that, in an isolation room, the ventilation rate needs to be 12 air changes per hour (ACH) at least, and the pressure in isolation room should be lower than the environment by 2.5–15 Pa [3,8,18]. In this work, the inlet air flow rate was assumed to be 12 ACH, which is equivalent to 0.5734 m/s at the entrance. The gauge pressure at exhaust position was assumed to be −5.5 Pa to keep the negative pressure in isolation room. The temperature and RH of cough air stream are assumed to be 36 °C and 100%, respectively, and the isolation room temperature is 20 °C. The standard RH in isolation room is assumed to be 50% in most simulations and the effect of RH on droplet evaporation was investigated for 3 other RH's of 30%, 70%, and 90%.
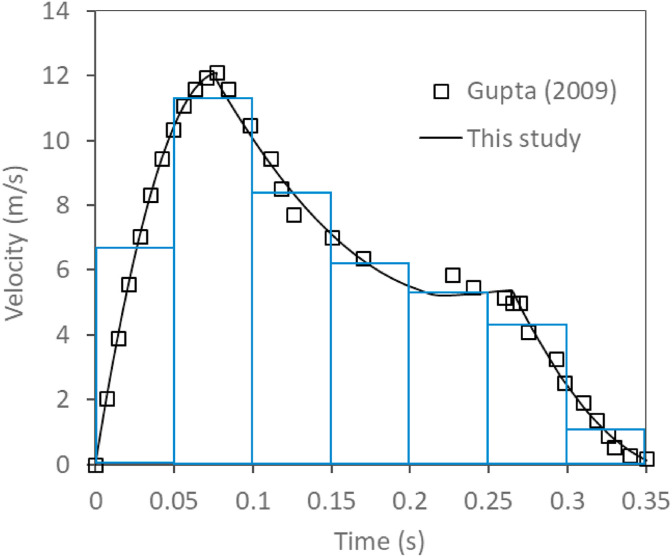
Based on Gupta's experimental study [19], the coughing air stream velocity is given as a function of time with a maximum velocity of 12.1 m/s as shown in Fig. 2 . In this study, the coughing air velocities were interpolated separately for 3 different time intervals as follows and were implemented into numerical simulation.
| (15) |
Fig. 2.
Coughing air stream velocities as a function of time.
In this study, the droplet volume fraction was far less than 10% (even in cough stream, the particle volume fraction is about 3.38 × 10−5%) and the discrete phase model (DPM) can be applied successfully to model the movement of cough droplets. We assumed that droplets have a spherical shape and a uniform temperature of 36 °C. Droplets from a few to hundreds of micrometers are emitted from mouth during cough and their velocity at the mouth outlet is assumed to be same as cough air stream velocity.
We choose 5 typical sizes of cough droplets and their numbers for calculation in this study based on Chao's results [15], which are 5 μm (1200 particles), 10 μm (500 particles), 20 μm (150 particles), 50 μm (50 particles), and 175 μm (100 particles) for total 2000 droplets per cough. The injection rates of droplets into isolation room during cough are calculated by dividing the air stream velocity into 7 intervals as shown in Fig. 2 and it is assumed that the droplet numbers in each interval are proportional to the gas flow rate. Based on the report of Effros et al. [20], the droplets contain several non-volatile components which are [Na+] = 91 ± 8 mM, [K+] = 60 ± 11 mM, [Cl+] = 102 ± 17 mM, [lactate] = 44 ± 17 mM, and [protein] = 7.63 ± 1.82 g/L, respectively. To simplify, we assumed that the NaCl represents those salts and the glycerin represents the lactate and protein in the cough droplets. The initial mass ratio of water, salt and glycerin in cough droplets is 912:8:80. The heat exchange between patient body and around environment was neglected. For the walls and patient body, the boundary condition for droplets in DPM is set as trap condition with the assumption that the trajectory calculation will be terminated when the droplets touch the surfaces of walls and patient body. The escape condition in DPM was applied to the droplets at inlet and outlet of isolation room. The other boundary conditions for numerical modeling are summarized in Table 1 .
Table 1.
Boundary conditions for numerical modeling.
| Inlet – Air stream | Inlet air velocity = 0.5734 m/s, water mass fraction = 0.00726, temperature = 293 K, droplet: escape (DPM) |
| Outlet – Air stream | Pressure outlet (gauge pressure) = −5.5 Pa, droplet: escape (DPM) |
| Inlet – Cough through mouth | Inlet velocity: Eq. (15), user defined velocity function, water mass fraction = 0.03534, temperature = 309 K, droplet: escape (DPM) |
| Patient body, bed and wall | Heat flux = 0 W m−2, droplet: trap (DPM) |
2.4. Numerical method to solve governing equations
The governing equations are solved by ANSYS Fluent code. Due to high Reynolds number at the mouth outlet when a cough occurs, an RNG k-ε turbulent model is applied. At first, a steady-state model is used to compute the airflow profile in the isolation room. This airflow state is regarded as the initial condition to calculate the trajectory and evaporation of droplets. After that, all governing equations for airflow with coughing, droplet movement and evaporation are solved using a transient model. A first-order discretization method is used for turbulent equations and second-order discretization is applied for other equations. In each time step, droplet will lose some water by evaporation and its temperature changes due to heat transfer and heat of evaporation. In this study, a new user defined function (UDF) is programmed to solve the heat and mass balance equations of droplets (equation (12) and (13)) by calculating the updated temperature and mass fractions of droplet in each time step. We also tried to investigate the effect of Brownian diffusion on droplet trajectory for Case 1. However, we found that there is no significant change in droplet distribution because Brownian diffusion is the dominant particle deposition mechanism for fine particles smaller than 0.1 μm [21]. The present work aims to investigate the distribution of droplets in size ranges of 5–175 μm (after drying, it becomes 2.05–20.5 μm) so the effect of particle diffusion could be ignored.
3. Results and discussion
3.1. Air velocity distributions in the isolation room for different ventilation configurations
The droplet distributions in isolation room after coughing will strongly depend on the airflow patterns. Fig. 3 shows the air velocity patterns at vertical plane of z = 1.75 m for 5 cases (Fig. 3a–b, 3d-3f)) and at vertical plane of x = 0.93 m for Case 3 (Fig. 3c). The air velocity distributions in isolation room for 5 cases are quite different in the region near the outlet position, while they are similar in the region opposite the patient's bed. Therefore, the air velocity distributions for full cross section of plane are shown only for Case 1 (Fig. 3a) and they are shown for partial cross section of plane around the patient for Case 2, Case 3, Case 4, Case 5 (Fig. 3b. 3d-f). For Case 3, the air velocity distributions at the plane passing through the center of outlet (x = 0.93 m) are also added in Fig. 3c. It can be seen that the airflow patterns are relatively well-developed for air ventilation in the isolation room for all 5 cases. At all positions near the patient's body, the air velocity needs to be less than 0.15 m/s within the threshold value as recommended by the ASHRAE Standard [22] to satisfy the patient's comfort. The air velocities near the patient's head for all 5 cases are kept low and less than 0.07 m/s. However, some air recirculation is found in the region under patient's bed for Case 1, Case 2, Case 3, Case 4 and, if some droplets happen to move to this zone, they will be captured there and cannot escape the zone easily. We also checked if there is any recirculation, especially, in the region near the corners of isolation room for all ventilation configurations we are considering, but no significant recirculation was found. Generally, the inlet air flows evenly in all places of the isolation room for all 5 cases and makes good ventilation for the isolation room via exhaust grilles mounted on the wall or ceiling.
Fig. 3.
Airflow patterns in the vertical sectional view at z = 1.75 m (a-c and e-f) and at x = 0.93 m (d) of isolation rooms at 90 s (ACH = 12).
3.2. Cough droplet distributions in isolation room for different ventilation configurations
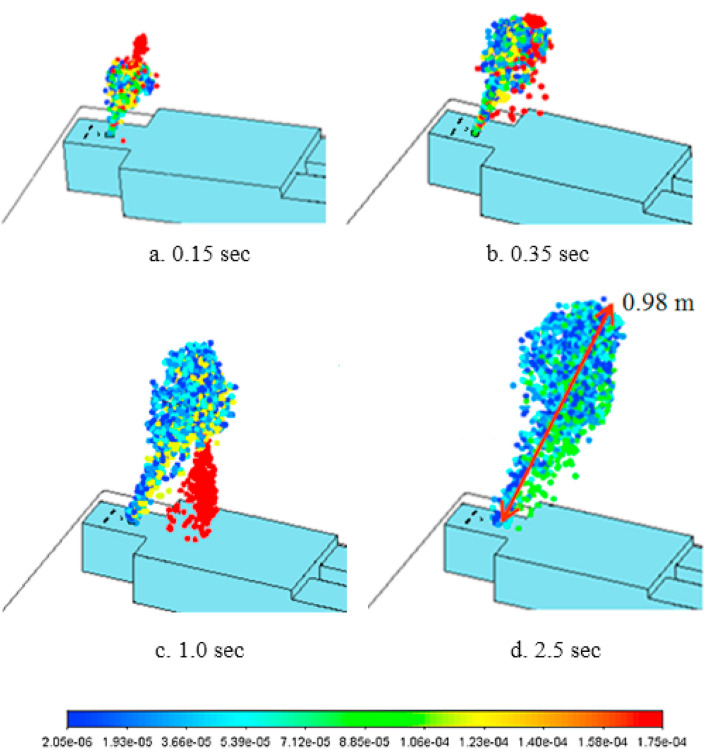
Fig. 4 shows the droplet distributions of various sizes in isolation room for different times just after the start of cough until t = 2.5 s and these results are almost similar for all 5 cases because of the fast cough velocity comparing to the ventilation air velocity near patient. Generally, the emitted droplet distribution looks like ice cream cone-shaped cloud. At t = 0.15 s, the large-sized particles are mostly on the top of ice cream cone, because they have a higher momentum and move faster. As shown in Equation (15), the cough stops at t = 0.35 s and most of droplets still follow the flow patterns in isolation room, while the larger-sized droplets (for example, 175 μm droplets) stop earlier because of the higher drag force from air and heavier gravitational force and start to settle down (t = 0.35s). At t = 1.0 s, the larger-sized droplets are separated from the droplet cloud and start to fall down to the patient's body, while smaller-sized droplets are still suspended in the air and move with the coughing airflow over a long distance. At 2.5 s, some droplets can travel a maximum distance of 0.98 m. From Fig. 4, it can be seen that the size of droplets decreases rapidly with time, because the small-sized droplets have large surface area and, accordingly, fast evaporation rate and, at 2.5 s, the droplets suspended in the air become to have the size range of 2.05–20.5 μm. For the case of 50 μm droplets, some of them settle down early by gravity, while the others become smaller-sized droplets by evaporation and are suspended in air drifting with the flow pattern in isolation room.
Fig. 4.
Droplet distributions of various sizes in isolation room just after a cough(a: t = 0.15s, b: t = 0.35s, c: t = 1.0s, d: t = 2.5s) (RH = 50%).
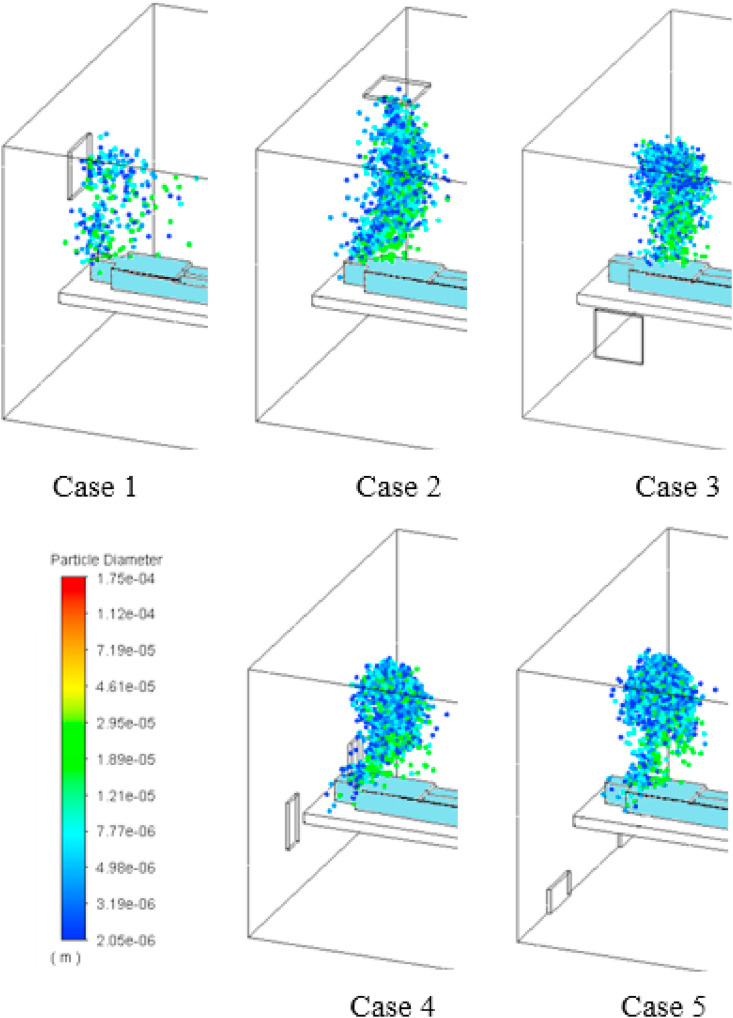
Fig. 5 illustrates the droplet distributions of various sizes in isolation room for 5 cases at 10 s after the start of a cough. There are some differences in droplet distributions depending on the ventilation configurations because the movement of droplets is mainly affected by the airflow patterns in isolation room. For Case 1, some droplets are already discharged from isolation room by ventilation, but, for other cases, it can be clearly seen that many droplets are still remaining in the isolation room, especially, more concentrated above the patient. For Case 2, some droplets have the tendency to go up towards ceiling where the exhaust grill is located and, for Case 3, the droplet distribution is perverted towards the exhaust grill in side wall, while, for Cases 4 and 5, the droplet distributions are affected by the airflow to exhaust grills located on both sides of patient.
Fig. 5.
Droplet distributions in isolation room for 5 cases at 10 s after coughing (RH = 50%).
Fig. 6 shows the droplet distributions in the isolation room for 5 cases at 60 s. For Case 1, most droplets are removed from the isolation room by ventilation. For other cases, droplets are distributed widely more or less in the isolation room depending on their flow patterns. It is found that for Cases 2 and 3, the droplets are more concentrated in the region near the patient, while, for Cases 4 and 5, the droplets are more spread out to the whole isolation room, which might increase the possible region of Covid-19 transmission.
Fig. 6.
Droplet distributions in isolation room for 5 cases at 60 s after coughing (RH = 50%).
Fig. 7, Fig. 8 show the percentages of droplets for various initial sizes escaped from isolation room through exhaust grill and suspended in the air of isolation room for 5 cases at 60 s, respectively. The rest of droplets are supposed to have settled down in the isolation room by gravity. No droplet with initial size of 175 μm is found for all 5 cases in Fig. 7, Fig. 8, because they have already settled down because of strong gravitational force. For Case 1, it is found that most of droplets for all sizes have escaped from isolation room and the droplet removal efficiency by ventilation is about 98%. For Case 4, Case 5, many droplets are still remaining suspended in isolation room and the droplet removal efficiencies by ventilation are about 5–7% and are far lower than even for Case 2, Case 3 of 43–50%.
Fig. 7.
Percentage of droplets for various initial sizes escaped from isolationroom through exhaust grill for 5 cases at 60 s after coughing (RH = 50%).
Fig. 8.
Percentage of droplets for various initial sizes suspended in isolationroom for 5 cases at 60 s after coughing (RH = 50%).
For the droplets with initial size of 50 μm, the sum of escaped and suspended droplets is far lower than other droplets with smaller initial sizes, mainly because many of them have already settled down by gravity before they become small enough to be suspended in isolation room by evaporation.
Total numbers of cough droplets suspended in isolation room for 5 cases are shown as a function of time in Fig. 9 . For Case 1, droplet concentration in isolation room decreases quickly by ventilation from the beginning and becomes almost zero after 40 s. For Case 2, droplet concentration decreases fast for 5s < t < 20 s when many droplets approach the exhaust grill on ceiling by the flow pattern in isolation room and, then, decreases slowly and the percentage of droplets suspended in the room becomes 35.3% at 90 s. For Case 3, droplet concentration decreases fast for 35s < t < 55s when the droplets from the perverted distribution approach the exhaust grill on side-wall by the flow pattern here and the final percentage of droplets suspended in the room is 29.8% at 90 s. For Cases 4 and 5, the droplet removal from isolation room by ventilation is not so much efficient compared with other ventilation cases here and their removal efficiencies increase slowly and reach about 31% at 90 s. It can be seen that the droplet removal efficiencies are quite different for Cases 1, 4, and 5 where the heights of air outlet are just different on the same wall, (Case 1: about 100%, Cases 4 and 5: about 31% at t = 90 s). We can propose that the exhaust outlet should be placed above the patient's head on the backside wall.
Fig. 9.
Total numbers of droplets suspended in isolation room as a function of time for 5 cases after coughing (RH = 50%).
3.3. Change of droplet sizes by evaporation for different initial droplet sizes and relative humidities
Fig. 10 shows the change of droplet sizes by evaporation for different initial sizes in the isolation room as a function time (Case 1). For this calculation, we assumed that droplets are injected into the isolation room simultaneously with the same velocity of 10 m/s to investigate the effect of time. The smaller-sized droplets have faster heat and mass transfer rates because of the larger specific surface area and they evaporate faster and reach the final size more quickly than the larger-sized droplets as shown in Fig. 10. The large droplets with initial size of 175 μm deposit fast by the strong gravitational force before they are dried completely by evaporation and they are not found in the air of isolation room after 1.4 s. At 20 °C and RH = 50%, the cough droplets with initial diameter smaller than or equal to 20 μm need less than 0.5 s to evaporate completely and to reach the final size, while those with 50 μm need about 2.32 s for complete evaporation. The droplet size doesn't change after reaching the equilibrium state of water between the liquid droplet and vapor phase. After evaporation, the final droplet size shrink to around 41% of initial size, and the final droplet size ranges from 2.05 μm to 20.5 μm. The changes of droplet compositions with initial sizes of 20 μm and 50 μm m are shown in Fig. 11 . The water content in droplets decreases by evaporation, while the salt and glycerin mass fractions gradually increase with time and finally become about 0.09 and 0.909, respectively. Because the solutes in droplet will cause some depression of water vapor pressure at the droplet surface (based on Raoult's law) compared with that of pure droplet, more water can remain in the droplet at equilibrium and the equilibrium droplet diameter becomes larger than d dry.
Fig. 10.
Change of droplet sizes by evaporation for different initial sizes in the isolation room (Case 1). The air temperature is 293 K with RH = 0.5 and initial droplet velocity = 10 m/s.
Fig. 11.
Time-dependent composition of droplets with initial sizes of 20 μm and 50 μm at 298 K and RH = 50%.
To show the changes of droplet size in each size bin with time, the particle size distributions for different times after coughing are shown for Case 1 in Fig. 12 . The droplets with the initial size of 175 μm cannot stay in gas phase longer than 1.5 s because they fall down quickly. The droplets smaller than 50 μm can be suspended in gas phase without sedimentation and the droplet size decreases with time by evaporation. The particle concentration decreases with time because the particles are lost by the entrainment to exit gas stream and the deposition on the surface.
Fig. 12.
Particle size distributions for different times after coughing for Case 1.
The relative humidity plays an important role to determine the evaporation rate of droplets. Fig. 13 shows the change of droplet size with time for different RH's from 30% to 90% for initial droplet size of 50 μm at ambient temperature of 293 K (Case 1). The main driving force for droplet evaporation is the pressure difference between the saturated vapor pressure at the droplet surface and partial vapor pressure in the ambient air (∼RH) and, accordingly, the droplet evaporation rate decreases as RH increases. At low RH, the ambient air has low partial vapor pressure, resulting in larger pressure difference and faster evaporation rate and it takes shorter time for complete evaporation. For example, at RH = 30%, the time needed for 50 μm droplet to shrink to its final equilibrium size is 1.7 s, while, at RH = 50%–70% and 90%, it becomes 2.4 s, 4.2 s and 5.4 s (∼3.2 times longer than at RH = 30%), respectively.
Fig. 13.
Droplet size change with time for initial droplet size of 50 μm under different RH's in isolation room (Case 1).
Fig. 14 illustrates the number of droplets suspended in isolation room for different initial droplet sizes and RH's as a function of time for Case 1, which shows the removal efficiency of droplets from the isolation room. It is assumed that the same number of droplets of different sizes from 50 to 80 μm are injected together into the isolation room with the same velocity of cough stream. For all droplets of different sizes, the number of droplets suspended in the isolation room is higher when the RH is lower. At low RH, because the large-sized cough droplets emitted from Covid-19 patients evaporate more quickly (within a few seconds) and become smaller in size, they can be suspended in the air as stable aerosols for a longer time. These droplets can have more chances to propagate the Covid-19 virus to other persons through breathing in isolation room. This also explains why the respiratory diseases transmitted through cough droplets including the Covid-19 can propagate faster in winter with low humidity than in summer with high humidity. For the case of droplets with initial size of 80 μm, the number of droplets suspended in isolation room is small and we cannot see a big difference in number of droplets for various RH's, because most of these droplets fall down quickly by gravity before they are evaporated due to their heavy weight. From this result, we can propose to use the humidifier to increase the humidity of isolation room and, therefore, the efforts to reduce the droplets in isolation room can occur without the changes in ventilation pattern of room. By changing the ACH of the room, the ventilation efficiency can also be changed dramatically. Additionally, droplet removal efficiency can be enhanced by installing filtration equipment such as HEPA in the isolation room. For physicians and nurses, some mitigation efforts can also be achieved to minimize the exposure to pathogens by keeping physical distance, using masks, teleworking and preparing flexible work schedules.
Fig. 14.
Number of droplets suspended in isolation room for different initial droplet sizes and RH's as a function of time for Case 1.
4. Conclusion
This study is focused on investigating the transport and evaporation of multi-component droplets in the hospital isolation room with a coughing Covid-19 patient. The outlet position of various ventilation designs has great impacts on the airflow patterns and also the contaminated droplet distributions in the isolation room. For all 5 cases of outlet configuration considered, the air velocity near the patient's bed is within the recommended threshold value of less than 0.15 m/s. Air supply and exhaust grill should be designed to allow inlet air stream to remove the contaminated air around the patient to outlet. Case 1 where the exhaust outlet is placed above the patient's head shows the best performance of ventilation with the droplet removal efficiency of 99% after 90 s. The droplet size is quite important for the particle trajectory in isolation room and is strongly dependent on the evaporation rate of multi-component droplets which is determined by initial droplet size and RH. The lower the ambient humidity is, the higher the droplet evaporation rate is, and, at 20 °C, the evaporation time for droplets of 50 μm is about 1.7 s at RH = 30%, while it becomes 3.2 times longer at RH = 90%. In an environment with low RH, the droplets containing Covid-19 viruses will shrink more quickly by evaporation and can stay in the air as stable aerosols for a longer time (for droplets with initial size less than 70 μm) and, therefore, the risk of Covid-19 propagation to other persons by inhalation of these droplets increases in hospital. This study can be a basis to design the hospital isolation room to remove effectively the droplets containing Covid-19 and/or other respiratory disease viruses from the isolation room.
CRediT authorship contribution statement
Huyen Thi Dao: Writing – original draft, Investigation. Kyo-Seon Kim: Writing – review & editing, Validation, Project administration, Conceptualization.
Declaration of competing interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- 1.Al-benna S. Negative pressure rooms and COVID-19. J. Perioperat. Pract. 2021;31:18–23. doi: 10.1177/1750458920949453. [DOI] [PubMed] [Google Scholar]
- 2.Qian H., Zheng X. Ventilation control for airborne transmission of human exhaled bio-aerosols in buildings. J. Thorac. Dis. 2018;10:2295–2304. doi: 10.21037/jtd.2018.01.24. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Hyttinen M., Rautio A., Pasanen P., Reponen T., Earnest G.S., Streifel A., Kalliokoski P. Airborne infection isolation rooms - a review of experimental studies. Indoor Built Environ. 2011;20:584–594. doi: 10.1177/1420326X11409452. [DOI] [Google Scholar]
- 4.Mui K.W., Wong L.T., Wu C.L., Lai A.C.K. Numerical modeling of exhaled droplet nuclei dispersion and mixing in indoor environments. J. Hazard Mater. 2009;167:736–744. doi: 10.1016/j.jhazmat.2009.01.041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Alhamid M.I., Raymond A. Design of the ventilation system and the simulation of air flow in the negative isolation room using FloVent 8 . 2. AIP Conf. Proc. 2019 doi: 10.1063/1.5046600. [DOI] [Google Scholar]
- 6.Cheong K.W.D., Phua S.Y. Development of ventilation design strategy for effective removal of pollutant in the isolation room of a hospital. Build. Environ. 2006;41:1161–1170. doi: 10.1016/j.buildenv.2005.05.007. [DOI] [Google Scholar]
- 7.Villafruela J.M., Castro F., San José J.F., Saint-Martin J. Comparison of air change efficiency, contaminant removal effectiveness and infection risk as IAQ indices in isolation rooms. Energy Build. 2013;57:210–219. doi: 10.1016/j.enbuild.2012.10.053. [DOI] [Google Scholar]
- 8.Richmond-Bryant J. Transport of exhaled particulate matter in airborne infection isolation rooms. Build. Environ. 2009;44:44–55. doi: 10.1016/j.buildenv.2008.01.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Jacob S., Yadav S.S., Sikarwar B.S. Springer Singapore; 2019. Design and Simulation of Isolation Room for a Hospital. [DOI] [Google Scholar]
- 10.Cho J. Investigation on the contaminant distribution with improved ventilation system in hospital isolation rooms: effect of supply and exhaust air diffuser configurations. Appl. Therm. Eng. 2019;148:208–218. doi: 10.1016/j.applthermaleng.2018.11.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Hang J., Li Y., Jin R. The influence of human walking on the flow and airborne transmission in a six-bed isolation room: tracer gas simulation. Build. Environ. J. 2014;77:119–134. doi: 10.1016/j.buildenv.2014.03.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Bellagambi F.G., Lomonaco T., Salvo P., Vivaldi F., Ghimenti S., Biagini D., Di F., Fuoco R., Hangou M. Saliva sampling : methods and devices . An overview. Trends Anal. Chem. J. 2019;124 doi: 10.1016/j.trac.2019.115781. [DOI] [Google Scholar]
- 13.Dbouk T., Drikakis D. Weather impact on airborne coronavirus survival. Phys. Fluids. 2020;32 doi: 10.1063/5.0024272. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Nicas M., Nazaroff W.W., Hubbard A. Toward understanding the risk of secondary airborne infection : emission of respirable pathogens. J. Occup. Environ. Hyg. 2005:143–154. doi: 10.1080/15459620590918466. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Chao C.Y.H., Wan M.P., Morawska L., Johnson G.R., Ristovski Z.D., Hargreaves M. Characterization of expiration air jets and droplet size distributions immediately at the mouth opening. Aerosol Sci. 2009;40:122–133. doi: 10.1016/j.jaerosci.2008.10.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Vedovoto M. Evaluation of droplet evaporation models and the incorporation of natural convection effects, flow. Turbul. Combust. 2018;102:537–558. doi: 10.1007/s10494-018-9973-8. [DOI] [Google Scholar]
- 17.Deprédurand V., Castanet G., Lemoine F. Heat and mass transfer in evaporating droplets in interaction : influence of the fuel. Int. J. Heat Mass Tran. 2010;53:3495–3502. doi: 10.1016/j.ijheatmasstransfer.2010.04.010. [DOI] [Google Scholar]
- 18.Memarzadeh F., Xu W. Role of air changes per hour (ACH) in possible transmission of airborne infections. Build. Simul. 2012;5:15–28. doi: 10.1007/s12273-011-0053-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Gupta J.K., Lin C.H., Chen Q. Flow dynamics and characterization of a cough. Indoor Air. 2009;19:517–525. doi: 10.1111/j.1600-0668.2009.00619.x. [DOI] [PubMed] [Google Scholar]
- 20.Effros R.M., Hoagland K.W., Bosbous M., Castillo D., Foss B., Dunning M., Gare M., Lin W.E.N., Sun F. Dilution of respiratory solutes in exhaled condensates. Am. J. Respir. Crit. Care Med. 2002;165:663–669. doi: 10.1164/rccm.2101018. [DOI] [PubMed] [Google Scholar]
- 21.Liu D.L. Particle deposition onto enclosure surfaces. Dev. Surf. Contam. Clean. Part. Depos. Control Remov. 2010:1–56. doi: 10.1016/B978-1-4377-7830-4.10001-5. [DOI] [Google Scholar]
- 22.ANSI/ASHRAE standard 55-2004, thermal environmental conditions for human occupancy. Am. Soc. Heating, Refrig. Air-Conditioning Eng. 2004 2004. [Google Scholar]