ABSTRACT
Background
Link prediction is an important and well-studied problem in network biology. Recently, graph representation learning methods, including Graph Convolutional Network (GCN)-based node embedding have drawn increasing attention in link prediction.
Motivation
An important component of GCN-based network embedding is the convolution matrix, which is used to propagate features across the network. Existing algorithms use the degree-normalized adjacency matrix for this purpose, as this matrix is closely related to the graph Laplacian, capturing the spectral properties of the network. In parallel, it has been shown that GCNs with a single layer can generate more robust embeddings by reducing the number of parameters. Laplacian-based convolution is not well suited to single-layered GCNs, as it limits the propagation of information to immediate neighbors of a node.
Results
Capitalizing on the rich literature on unsupervised link prediction, we propose using node similarity-based convolution matrices in GCNs to compute node embeddings for link prediction. We consider eight representative node-similarity measures (Common Neighbors, Jaccard Index, Adamic-Adar, Resource Allocation, Hub- Depressed Index, Hub-Promoted Index, Sorenson Index and Salton Index) for this purpose. We systematically compare the performance of the resulting algorithms against GCNs that use the degree-normalized adjacency matrix for convolution, as well as other link prediction algorithms. In our experiments, we use three-link prediction tasks involving biomedical networks: drug–disease association prediction, drug–drug interaction prediction and protein–protein interaction prediction. Our results show that node similarity-based convolution matrices significantly improve the link prediction performance of GCN-based embeddings.
Conclusion
As sophisticated machine-learning frameworks are increasingly employed in biological applications, historically well-established methods can be useful in making a head-start.
Availability and implementation
Our method, SiGraC, is implemented as a Python library and is freely available at https://github.com/mustafaCoskunAgu/SiGraC.
1 Introduction
Graphs (networks) are commonly used to represent a broad range of interactions and associations (as edges) among biomedical entities (as nodes) (Cowen et al., 2017). Developing computational methods to analyze and understand these networks is one of the major research challenges in bioinformatics. A common problem that arises in the analysis of biomedical networks is the prediction of new associations or interactions using existing information on the network(s). This problem is often abstracted in the form of ‘link prediction’, a commonly studied problem in data mining and machine learning (Lü and Zhou, 2011). In the context of biomedical networks, link prediction is useful in discovering previously unknown associations or interactions, as well as identifying missing or spurious interactions (Yue et al., 2020). Link prediction problems on biological networks include disease gene prioritization (Erten et al., 2011a), prediction of drug–disease associations (DDAs) (Liang et al., 2017), functional annotation of long non-coding RNAs (Zhang et al., 2018), de-noising of protein interaction networks (Yoo et al., 2017) and prediction of drug response in cancer cell lines (Stanfield et al., 2017).
Earlier approaches to link prediction aim to assess the similarity between pairs of nodes based on local topological features (Zhou et al., 2009). These local features usually focus on the shared neighborhood of node pairs and differ from each other in terms of how they evaluate the size of the overlap and the individual nodes in the overlap. Post-genomic developments in network biology establish the relevance of global network topology in delineating the functional relationships between biomolecules (Cowen et al., 2017; Pandey et al., 2008). Motivated by these insights, network proximity quantified via random walk-based algorithms is commonly utilized for link prediction (Valdeolivas et al., 2019).
While powerful in capturing global network topology, random walk-based methods have several limitations, including degree bias (Coşkun and Koyutürk, 2015; Erten et al., 2011a), over-emphasis of proximity information at the expense of structural information (Devkota et al., 2020; Ribeiro et al., 2017) and dependency on the choice of hyper-parameters (usually, the damping factor) (Grover and Leskovec, 2016; Perozzi et al., 2014). Topological similarity-based algorithms aim to circumvent these issues by using random walk-based proximity scores as topological features (Cao et al., 2014; Erten et al., 2011b; Lei and Ruan, 2013). The concept of topological similarity is further generalized by node embeddings, which provide representations of nodes in a multi-dimensional latent feature space (Grover and Leskovec, 2016; Perozzi et al., 2014). The objective of node embedding is to optimize the embedding space and the mapping of nodes to this space in such a way that nodes that are ‘similar’ in the network are ‘close’ to each other in the embedding space. By representing nodes as vectors in multi-dimensional feature space, node embeddings enable use of off-the-shelf machine-learning algorithms for link prediction (Perozzi et al., 2014).
Earlier algorithms for node embedding utilize random walk-based objectives to define node ‘similarity’ (Grover and Leskovec, 2016; Hamilton et al., 2019; Perozzi et al., 2014; Tang et al., 2015). With the advent of deep learning, neural network-based algorithms, including Graph Convolutional Networks (GCNs), are also applied to the computation of node embeddings (Gilmer et al., 2017; Kipf and Welling, 2016b). In a recent study, Yue et al. (2020) extensively investigate the effectiveness of network embedding techniques in the context of supervised link prediction on a broad range of biomedical networks. Among various embedding techniques, GCN-based embedding delivers encouraging results for most of the biomedical link prediction tasks (Yue et al., 2020).
Graph Auto-Encoder (GAE) is a direct application of GCNs to the computation of node embeddings (Gilmer et al., 2017; Kipf and Welling, 2016b). GAE uses a loss function that aims to reconstruct the adjacency matrix of the network using a dot product decoder. Veličković et al. (2019) propose Deep Graph Infomax (DGI), which uses an improved loss function and limit the neural network to a single layer, thereby reducing the number of parameters to be learned. Despite DGI’s effectiveness, its use of the degree-normalized adjacency matrix as the convolution matrix limits its ability to propagate features across the network.
In this article, we aim to develop an effective method for the computation of node embeddings in biological networks by integrating three key insights: (i) GCNs are potentially effective in computing powerful node embeddings for biological networks. (ii) Reduced number of layers in GCNs renders the computation of node embeddings more stable and robust. (iii) Local measures of node similarity, which demonstrated effectiveness in early applications of unsupervised link prediction, can provide ‘shortcuts’ for shallow neural networks to propagate features across the network in a way that is useful for link prediction. In other words, we propose using node-similarity matrices (computed using local measures of node similarity) as convolution matrices for GCNs that are used to compute node embeddings for link prediction. To comprehensively investigate the promise of this idea, we explore the effectiveness of node-similarity measures as convolution matrices in DGI’s single-layered GCN encoder, by focusing on eight representative measures of node similarity (Zhou et al., 2009).
In our computational experiments, we use BIONEV, a framework developed by Yue et al. (2020) to benchmark link prediction algorithms in biomedical applications. We focus on three-link prediction tasks: (i) prediction of DDAs (Gottlieb et al., 2011), (ii) prediction of drug–drug interactions (DDIs) (Zhang et al., 2018) and (iii) prediction of protein–protein interactions (PPIs) prediction (Cho et al., 2016; Wang et al., 2017). Our results show that GCN encoders equipped with node similarity-based convolution matrices significantly outperform those that utilize the degree-normalized adjacency convolution matrix across all datasets. These results show that insights provided by established techniques in unsupervised link prediction can help improve the accuracy of new machine-learning techniques in a large margin.
2 Materials and methods
2.1 Link prediction and node embedding
In a general setting, the link prediction problem can be stated as follows: given a network , where denotes the set of n entities (e.g. genes/proteins, biological processes, functions, diseases, drugs etc.) and denotes a set of m interactions/associations among these entities, predict pairs of entities that may also be interacting or associated with each other (Yue et al., 2020). Link prediction can be supervised or unsupervised, where unsupervised link prediction aims to directly score and rank pairs of nodes using features derived from network topology. Supervised link prediction, on the other hand, uses a set of ‘training’ edges and non-edges to learn the parameters of a function that relates these topological features to the likelihood of the existence of an edge.
To extract features that represent network topology, graph representation learning techniques are used to embed the nodes of the network into a multi-dimensional feature space. For a given network , a network embedding is defined as a matrix , where and d is a parameter that defines the number of dimensions in the embedding space. Each row of this matrix represents, for each biomedical entity , the embedding of u as .
To facilitate supervised link prediction using node embeddings as features, a given number of edges are randomly sampled from . To generate a set of ‘negative’ samples, the same number of node pairs from the set is also randomly sampled. Next, for a given pair of nodes , their corresponding embeddings, are concatenated to a single score via Hadamard product with the label 1 or 0 depending on whether (u, v) represents a positive (extant edge) or negative (non-extant edge) sample. Finally, these combined latent features’ scores with their labels are fed into a supervised machine-learning algorithm (e.g. support vector machine, Random Forest), to train a classifier for link prediction (Yue et al., 2020).
2.2 Network embedding via GCNs
GCNs are simplified versions of Graph Convolutional Neural Networks, which are generalizations of conventional Convolutional Neural Networks on graphs (Li et al., 2018). In the context of various machine-learning tasks, GCNs facilitate the use of network topology in computing latent features from input features associated with network nodes. GCNs are also used to compute node embeddings, i.e. features that represent network topology, by setting the loss function appropriately to capture the correspondence between the embeddings and network topology.
In GCNs, each graph convolution layer involves three steps: (i) feature propagation, (ii) linear transformation and (iii) application of a non-linear activation function (Wu et al., 2019). Feature propagation is accomplished by using a convolution matrix that is computed from graph topology. In the context of computing network embeddings, the choice of convolution matrix is critical as it defines the relationship between network topology and computed embeddings. The parameters of linear transformation are learned by training the GCN to minimize a loss function and standard non-linear functions are used for activation (e.g. sigmoid or ReLU). Thus, the key ingredients of a GCN-based network embedding technique are the choice of the convolution matrix and the loss function.
2.2.1 Graph Auto-encoder
Kipf and Welling (2016b) propose GAE as a direct application of their GCN model (Kipf and Welling, 2016a) to the computation of node embeddings in a network. GAE uses the degree-normalized adjacency matrix as the convolution matrix in a two-layer neural network. In this context, the convolution matrix is defined as
| (1) |
where A denotes the adjacency matrix of the network, denotes the adjacency matrix with self-loops added and denotes the degree matrix, . Since is equal to the graph Laplacian, we refer to as Laplacian-based convolution matrix throughout this article.
Using as the convolution matrix, GAE defines the network embedding matrix as:
| (2) |
where and are trainable weight matrices. These weight parameters are trained using the following loss function:
| (3) |
where σ denotes logistic sigmoid function.
2.2.2 Deep Graph Infomax
Veličković et al. (2019) develop DGI using the infomax principle (Linsker, 1988) to define a loss function that can be used in various learning settings. In the context of link prediction, DGI computes the embedding matrix using a single-layered neural network:
| (4) |
where PReLU denotes parametric ReLU (Veličković et al., 2019) as the non-linear activation function and is a trainable weight matrix. The loss function used to train is defined as binary cross entropy loss:
| (5) |
where represents the global graph-level summary, for denote the corrupted embedding vectors that are obtained by shuffling the nodes (randomly permuting the rows of I) and is a trainable scoring matrix.
Although DGI has not yet been implemented in biological applications, it has demonstrated great potential in other applications (Veličković et al., 2019). DGI owes its promising results to two factors: (i) capturing the global information of the network by incorporating node summaries and corrupted embeddings in its loss function, and (ii) utilizing the power of this loss function to reduce the number of layers, thereby the number of parameters to be learned and avoiding oversmoothing. Namely, the number of parameters to be learned for DGI is , while this number is , where represents the number of nodes in the network, d represents the number of dimensions in the embedding space and represents the number of nodes in the hidden layer of the GAE neural network.
However, the single-layered nature of DGI also limits its ability to diffuse information across the network. In the context of link prediction, node embeddings are utilized to assess the similarity between pairs of nodes. Motivated by this consideration, we hypothesize that coupling of DGI’s neural network architecture and loss function with convolution matrices that are based on node similarities can deliver superior link prediction performance as compared to convolution matrices that directly incorporate the adjacency matrix of the network.
2.3 Node-similarity measures as convolution matrices
An important design choice in GCN-based network embedding is the choice of the convolution matrix. As discussed above, most of the existing algorithms use the Laplacian-based convolution matrix. To date, the effect of the convolution matrix on algorithm performance has not been comprehensively characterized in the context of link prediction in biomedical networks.
We stipulate that network similarity measures can be effective as convolution matrices in conjunction with a single-layered neural network. Such measures include those that have demonstrated success in earlier applications of link prediction, including Common Neighbors (CNs), Adamic-Adar (AA) and others (Liben-Nowell and Kleinberg, 2007; Zhou et al., 2009), Below, we describe these measures and discuss how they can be adopted into the framework of DGI as convolution matrices. For this purpose, we consider the following formulation for computing node embeddings [where is optimized using the loss function in (5)]:
| (6) |
Below, we discuss various options for the convolution matrix C based on the rich literature on unsupervised link prediction. Observe that, for both DGI and GAE, .
(i) CNs: for a given node , let be the set of neighbors of u. Then, the number of CNs of nodes and is defined as:
| (7) |
Since and for , , the convolution matrix representing count of CNs can be formulated as:
| (8) |
(ii) Jaccard Index (JI): this measure assesses the overlap between the neighbors of two nodes by normalizing the size of the intersection by the size of the union:
| (9) |
In matrix form, JI can be formulated as a convolution matrix as follows:
| (10) |
Here, N denotes an all-ones matrix with the same size as A and denotes element-wise (Hadamard) division.
(iii) AA: this commonly utilized measure of node similarity refines the notion of CNs by assigning more weight to less-connected CNs (Adamic and Adar, 2003):
| (11) |
This notion of node similarity can be formulated as a convolution matrix as follows:
| (12) |
(iv) Resource Allocation (RA): this measure also aims to reduce the effect of highly connected CNs, but does so more agressively by normalizing with the degree of the neighbor. Thus, RA-based convolution matrix can be formulated as:
| (13) |
(v) Hub-Depressed Index (HDI): similar to JI, HDI aims to normalize the overlap between neighbors of two nodes based on the degrees of the nodes, but does so by focusing on the node with higher degree (thus penalizing hubs):
| (14) |
Using the notation introduced above, HDI-based convolution matrix can be formulated as:
| (15) |
(vi) Hub-Promoted Index (HPI): in contrast to HDI, HPI normalizes the size of the overlap of the neighbors of two nodes by the degree of the less-connected node, thereby promoting hubs. This index can be represented as a convolution matrix as:
| (16) |
(vii) Sørenson Index (SI): similar to JI, SI normalizes the size of the overlap of the two nodes by taking into account the degree of both nodes, but uses the average of the degrees instead of the size of the union:
| (17) |
Thus, compared to JI, SI is more conservative toward high-degree nodes as the common neighborhood is counted twice in the denominator. SI can be formulated as a convolution matrix as follows:
| (18) |
(viii) Salton Index (ST): ST also normalizes the size of the overlap by the degrees of the two nodes, but uses the geometric mean of the degrees instead of the arithmetic mean:
| (19) |
ST can be formulated as a convolution matrix as follows:
| (20) |
To summarize our approach, we use the node-similarity measures to compute node embeddings for all nodes in the network as follows in Algorithm 1:
Algorithm 1: Similarity-Based Graph Convolution (SiGraC)
Input: given the adjacency matrix of a network
Output: Embedding matrix, H
1 Compute the convolution matrix C based on the specified node-similarity index (CN, JI, AA, RA, HDI, HPI, SI, or ST)
2 Compute embeddings using the single-layered GCN encoder.
3 Randomly row-wise shuffle I to obtain corrupted node identities .
4 Compute corrupted embeddings , using the single-layered GCN encoder
5 Compute network-level summary of embeddings .
6 Update and M using gradient descent to minimize (5)
Once the node embeddings are computed using the above (unsupervised) procedure, we feed these embeddings into BIONEV, the supervised link prediction algorithm implemented by Yue et al. (2020). BIONEV takes as input a training network and node embeddings, uses these embeddings to train supervised link prediction models and uses a test dataset to evaluate the performance of the embeddings.
3 Results and discussion
3.1 Datasets and experimental setup
In our experiments for within-network link prediction, we use four biomedical networks compiled by Yue et al. (2020). The descriptive statistics of these four networks are shown on Table 1. These networks represent link prediction tasks in the context of three different biomedical applications:
Table 1.
Descriptive statics of the networks used in computational experiments
| # Nodes () | # Edges () | Avg. degree | Density | |
|---|---|---|---|---|
| Datasets | ||||
| DrugBank DDI | 2191 | 242 027 | 110.5 | 0.1 |
| CTD DDA | 12 765 | 92 813 | 7.3 | 0.0011 |
| NDFRT DDA | 13 545 | 56 515 | 4.2 | 0.0006 |
| STRING PPI | 15 131 | 359 776 | 23.8 | 0.0031 |
Note: Avg. degree is defined as , density is defined as
DrugBank DDIs: the DrugBank–DDI network is composed of verified pairwise interactions between chemical compounds used as drugs, obtained from DrugBank, a freely accessible online database that contains detailed information about drugs and drug interactions (Wishart et al., 2018).
Comparative Toxicogenomics Database (CTD) DDAs: CTD is a database that catalogues the effects of environmental exposures. It contains associations between chemicals and diseases, representing toxic effects of chemicals (Davis et al., 2019).
National Drug File Reference Terminology (NDFRT) DDAs: This dataset contains DDAs based on NDFRT in the unified medical language system. In the network, there is an edge between a disease and drug if the drug is used for the treatment of the disease (Bodenreider, 2004).
PPIs: The PPI network contains Homo sapiens PPIs extracted from the STRING database (Szklarczyk et al., 2015).
In addition, we use four additional molecular interaction networks for cross-network link prediction, provided by Cho et al. (2016). These networks represent two different types of interactions among genes/proteins of Saccharomyces cerevisiae and H.sapiens, obtained from the STRING database v9.1 (Franceschini et al., 2013). This collection contains two types of networks for each organism: (i) co-expression networks obtained using correlation of the expression of genes coding for respective proteins across a range of biological states (thus, these are statistical networks indicating potential functional association) and (ii) experimentally identified PPI networks (thus, these networks contain potential functional/physical interactions). The descriptive statistics of these networks are shown on Table 2.
Table 2.
Descriptive statistics of the networks used in cross-network link prediction experiments
| Datasets | # Nodes | # Co-expression edges | # Experimental edges | # Overlapping edges |
|---|---|---|---|---|
| Yeast PPI | 6400 | 314 602 | 220 226 | 34 898 |
| Human PPI | 18 362 | 775 319 | 302 400 | 75 910 |
3.1.1 Baseline embedding methods
For GAE and DGI algorithms, we use the Python implementation provided respectively by Kipf and Welling (2016a) and Veličković et al. (2019). For other state-of-the-art network embedding methods (Table 3), we use OpenNE (https://github.com/thunlp/OpenNE), Python source code implementation. We implement our node-similarity measure-based embedding methods on top of PyTorch implementation provided by Veličković et al. (2019).
Table 3.
Comparison of the link prediction performance of neural network-based node embeddings and other state-of-the-art algorithms on four biological networks
| Datasets | Node similarity-based-NN |
Laplacian-based-NN |
Random Walk |
||||||
|---|---|---|---|---|---|---|---|---|---|
| CN | HPI | Salton | GAE | DGI | Line | DeepWalk | Node2vec | Struct2vec | |
| DrugBank | 0.918±0.019 | 0.905±0.007 | 0.933±0.003 | 0.853±0.005 | 0.864±0.003 | 0.782±0.004 | 0.845±0.004 | 0.853±0.004 | 0.857±0.007 |
| CTD_DDA | 0.922±0.005 | 0.959± 0.004 | 0.950±0.004 | 0.804±0.003 | 0.862±0.012 | 0.813±0.012 | 0.903±0.005 | 0.871±0.023 | 0.913±0.007 |
| NDFRT | 0.919±0.005 | 0.935±0.002 | 0.943±0.004 | 0.904±0.007 | 0.912±0.003 | 0.907±0.009 | 0.893±0.010 | 0.885±0.009 | 0.859±0.004 |
| STRING | 0.943±0.003 | 0.917±0.006 | 0.952±0.004 | 0.876±0.005 | 0.887±0.003 | 0.843±0.006 | 0.912±0.006 | 0.881±0.004 | 0.903±0.007 |
Note: Node similarity-based-NN refers to node embeddings computed using node similarity-based convolution matrices (CN, Common Neighbor; HPI, hub-promoted index; Salton, Salton Index), Laplacian-Based-NN refers to node embeddings using Laplacian-based convolution and Random Walk refers to methods that use random walk-based proximity measures to predict links. For each dataset, the best performing method(s) is (are) underlined and shown in bold.
3.1.2 Within-network link prediction
For the networks presented on Table 1, we assess the performance of the algorithms using randomized test and training tests, where the randomized tests are repeated 10 times for each algorithm/parameter setting. For each randomized test, we select a certain fraction (referred to as test ratio) of the edges in the network uniformly at random, remove these edges from the network and reserve them as the positive test set. We then compute node embeddings and perform training on the remaining network.
3.1.3 Cross-network link prediction
For the networks presented on Table 2, we use one network type (e.g. yeast co-expression network) to compute node embeddings and use these embeddings as features to train and use a supervised link prediction model on the other network type (e.g. yeast experimentally identified PPI network) after removing overlapping edges from the test network.
3.1.4 Training supervised link prediction models
For training, we use the Hadamard product of node embedding vectors to construct a feature set for each pair of nodes. For each node pair, we assign label ‘1’ if the pair has an edge in the training network and label ‘0’ otherwise. We use these data to train a Logistic Regression-based binary classifier by dividing feature scores to 80% train set and 20% test set. Subsequently, we make predictions for the pairs of nodes in the positive and negative test sets and compute the area under the receiver operating characteristic curve (AUC) accordingly. The negative test sets are obtained by sampling, uniformly at random, pairs of nodes with no edge in between such that the number of these ‘true negative’ pairs is equal to the number of test edges that were removed; i.e. for each test instance, we create a ‘true positive’ and a ‘true negative’ set of equal size. Then we score all pairs in these two sets and compute the AUC using these scores. We repeat this process 10 times.
For the test ratio for embedding, we use 10%, 30% and 50% as the fraction of edges removed from the networks. For the neural networks used in computing node embeddings, we use default hyper-parameters suggested by the baseline papers; namely embedding dimension d = 100, training epoch =200.
3.2 Link prediction performance
We compare the link prediction performance of node similarity-based convolution matrices (using DGI’s single-layered GCN encoder) against encoders that use Laplacian-based convolution. Specifically, we use the following methods for comparison: (i) DGI (which uses the single-layered GCN encoder, we also use for the convolution matrices) and (ii) GAE (which uses a double-layered GCN encoder). Selection of these two methods for comparison enables assessment of the effect of the convolution matrix (similarity-based versus DGI), as well as effect of the architecture of the GCN (DGI versus GAE).
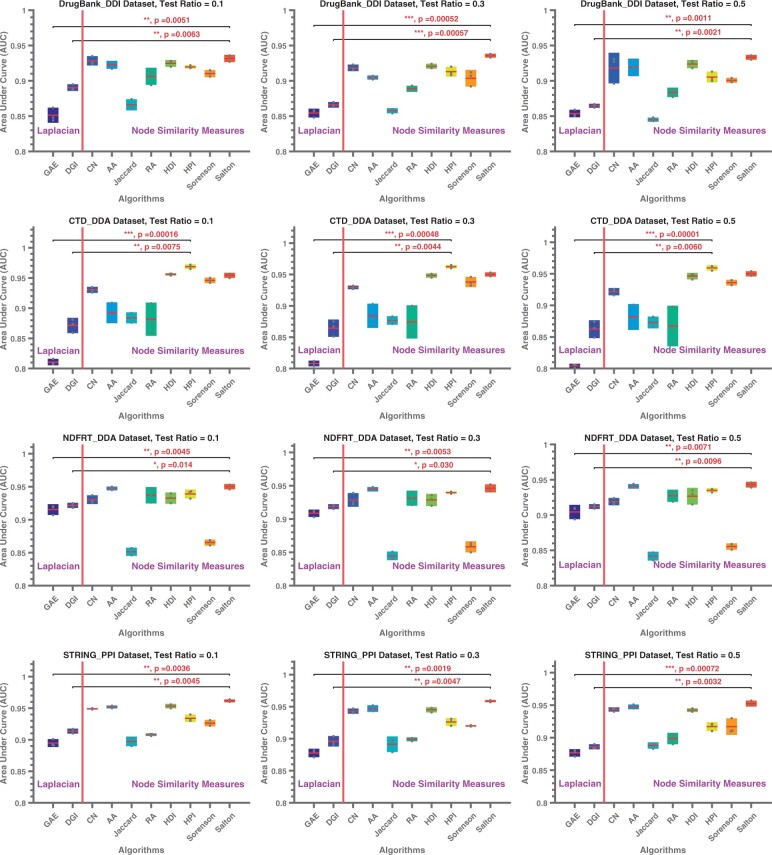
The comparison of the link prediction performance of node similarity-based convolution matrices against that of Laplacian-based convolution for within-network link prediction is shown in Figure 1. Based on these results, we make the following observations:
Fig. 1.
Link prediction performance of node embeddings computed using different convolution matrices. In each figure, the x-axis shows the neural network architecture (on the left of the red line; these methods use Laplacian-based convolution) or convolution matrix (on the right of the red line; these methods use a node similarity-based convolution matrix on a single-layered neural network as in DGI), the y-axis shows the AUC for link prediction. Asterisks indicate the significance of performance gain provided by the best node-similarity method against the two baseline methods (*P < 0.05, **P < 0.01, ***P < 0.001). Each row corresponds to a different dataset, each column represents different test ratios (e.g. on the left-most column 10% of the edges in the network are deleted and used as positive test samples, the remaining 90% of the edges are used for training), where the training data get smaller as we move from left to right. GAE, Graph Auto-encoder; DGI, Deep Graph Infomax; CN, Number of common neighbors; AA, Adamic-Adar; RA, Resource Allocation; HDI, Hub-deprived index; HPI, Hub-promoted index
With Laplacian-based convolution, DGI’s single-layered neural network delivers superior prediction performance over GAE’s two-layered neural network, except multiplex human PPI.
The link prediction performance of DGI and all node similarity-based convolution matrices (all using single-layer neural network) is robust to decreasing size of training data.
The accuracy provided by node similarity-based convolution matrices tend to depend on the dataset.
For all datasets, most of the node similarity-based convolution matrices deliver more accurate predictions as compared to DGI.
For node similarity-based convolution, ST, HPI and CN deliver better accuracy than other node-similarity measures.
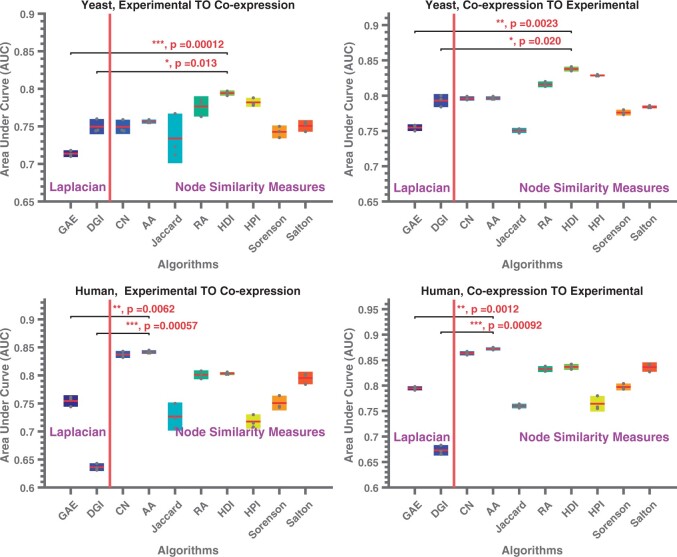
The results of computational experiments for cross-network link prediction are shown in Figure 2. We observe that the overall predictive performance of cross-network link prediction is worse than that of within-network link prediction compared to within-network link prediction, but the embeddings computed on the other network are still informative. Interestingly, the single-layered GCN (DGI) performs better than the double-layered GCN (GAE) on the yeast networks, while performing significantly worse on the human networks. The improvement provided by node similarity-based convolution matrices is consistent with the patterns observed for within-network link prediction, in that HDI and HPI significantly outperform DGI with Laplacian-based convolution on yeast networks, while common neighborhood and AA significantly outperform GAE with Laplacian-based convolution on human networks.
Fig. 2.
Link prediction performance of supervised link prediction using network embeddings computed on a different network. The figures show the link prediction performance of a logistic regression-based classifier on one type of network trained using node embeddings computed using a different type of network. The top and bottom rows respectively show results for S.cerevisiae and H.sapiens networks. The left column shows results for link prediction performance on co-expression networks using embeddings computed on experimentally identified PPI networks. The right column shows results for link prediction performance on experimentally identified PPI networks using embeddings computed on co-expression networks. In each figure, the x-axis shows the neural network architecture (on the left of the red line; these methods use Laplacian-based convolution) or convolution matrix (on the right of the red line; these methods use a node similarity-based convolution matrix on a single-layered neural network as in DGI), the y-axis shows the AUC for link prediction. Asterisks indicate the significance of performance gain provided by the best node-similarity method against the two baseline methods (*P < 0.05, **P < 0.01, ***P < 0.001)
These results demonstrate that node similarity-based convolution matrices can be more effective than Laplacian-based convolution in computing node embeddings for various link prediction tasks on biological networks. As suggested by the superior performance and low variance of DGI as compared to GAE, the use of a single-layered neural network improves and stabilizes predictive performance. The use of node-similarity matrices in a single-layered network adds to this improvement by enabling the network to take multiple steps during convolution. Node similarity-based convolution accomplishes this by using established ‘features’ that are proven to be useful in unsupervised link prediction.
3.3 Effect of graph density
Node similarity-based convolution matrices perform substantially better than DGI and GAE on all six networks, we consider in our experiments. To further investigate the robustness of methods and effects of network density on the accuracy of link prediction, we perform another set of experiments by sparsifying a network. For this purpose, we use the densest network in our datasets, namely DrugBank_DDI. We randomly sample edges from the DrugBank_DDI to construct networks with density ranging from 0.0005 to 0.1 (the network’s original density). We then perform cross-validation on these sampled networks with 50% test ratio. Observe that as the network gets sparser, the availability of training data declines drastically.
The results of our density analysis are shown in Figure 3. As seen in the figure, the network’s density plays a major role on the performance of link prediction algorithms. While the accuracy provided by all methods declines steadily as density goes down, the accuracy of node similarity-based convolution stays above that of DGI until the graph becomes extremely sparse. When graph density goes down to 0.001, we observe that the accuracy of node-similarity convolution becomes more variable and comparable to DGI.
Fig. 3.

The relationship between topological properties of input graphs and the link prediction performance of convolution matrices. AUC for the single-layered neural network using graph Laplacian (DGI), CN and Salton Index as a function of network density. Networks are generated by randomly sampling edges from the Drugbank–DDI dataset
3.4 Comparison to other link prediction algorithms
Algorithms that are used for link prediction in biological networks are not limited to those that utilize neural network-based node embeddings. Many other approaches exist, including unsupervised methods that use node similarity (which we use as convolution matrices in this work), and random walk-based algorithms (which use random walks to compute node embeddings). To further evaluate the performance of the node similarity-based graph convolution against state-of-the-art methods in link prediction, we consider multiple algorithms in two categories: (i) Neural Network-based algorithms and (ii) Random Walk-based algorithms. For each of these three categories, we select three algorithms that are reported to perform best on biological networks (Yue et al., 2020) and compare the link prediction performance of these algorithms on our four networks. The results of these experiments are shown on Table 3. As seen, our proposed approach significantly outperforms the exiting node embedding algorithms and set the new state-of-the-art.
4 Conclusion
In this article, by capitalizing on the rich literature on unsupervised link prediction, we proposed using node similarity-based convolution to compute GCN-based node embeddings for link prediction. We comprehensively tested eight different node-similarity measures (CNs, JI, AA, ResourceAllocation, HDI, HPI, Sorenson Index and SI) using four different networks representing different link prediction problems in biomedical applications as well as two multiplex networks. Our results showed that node similarity-based convolution in a single-layered GCN encoder delivers superior performance as compared to GCNs that use Laplacian-based convolution. Future efforts in this direction would include incorporation of other similarity measures into our framework, consensus learning of these proximity measures all together, and their applications, such as node classification and clustering.
Acknowledgements
We would like to thank Kaan Yorganc ioğlu and Serhan Yilmaz from Case Western Reserve University for their valuable insights and useful discussions.
Funding
This work was supported, in whole or in part, by US National Institutes of Health grants [U01-CA198941] from the National Cancer Institute.
Conflict of Interest: none declared.
Contributor Information
Mustafa Coşkun, Department of Computer Engineering, Abdullah Gül University, Kayseri, Turkey; Hakkari University, Kayseri 38080, Turkey.
Mehmet Koyutürk, Department of Computer and Data Sciences, Case Western Reserve University, Cleveland, OH 44106, USA; Center for Proteomics and Bioinformatics, Case Western Reserve University, Cleveland, OH 44106, USA.
References
- Adamic L.A., Adar E. (2003) Friends and neighbors on the web. Soc. Netw., 25, 211–230. [Google Scholar]
- Bodenreider O. (2004) The unified medical language system (UMLS): integrating biomedical terminology. Nucleic Acids Res., 32, D267–D270. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cao M. et al. (2014) New directions for diffusion-based network prediction of protein function: incorporating pathways with confidence. Bioinformatics, 30, i219–i227. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cho H. et al. (2016) Compact integration of multi-network topology for functional analysis of genes. Cell Syst., 3, 540–548. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Coşkun M., Koyutürk M. (2015) Link prediction in large networks by comparing the global view of nodes in the network. In: 2015 IEEE International Conference on Data Mining Workshop (ICDMW), pp. 485–492. IEEE, New Orleans.
- Cowen L. et al. (2017) Network propagation: a universal amplifier of genetic associations. Nat. Rev. Genet., 18, 551–562. [DOI] [PubMed] [Google Scholar]
- Davis A.P. et al. (2019) The comparative toxicogenomics database: update 2019. Nucleic Acids Res., 47, D948–D954. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Devkota K. et al. (2020) GLIDE: combining local methods and diffusion state embeddings to predict missing interactions in biological networks. Bioinformatics, 36, i464–i473. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Erten S. et al. (2011a) DADA: degree-aware algorithms for network-based disease gene prioritization. BioData Min., 4, 19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Erten S. et al. (2011b) Vavien: an algorithm for prioritizing candidate disease genes based on topological similarity of proteins in interaction networks. J. Comput. Biol., 18, 1561–1574. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Franceschini A. et al. (2013) STRING v9. 1: protein-protein interaction networks, with increased coverage and integration. Nucleic Acids Res., 41, D808–D815. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gilmer J. et al. (2017) Neural message passing for quantum chemistry. In: Proceedings of the 34th International Conference on Machine Learning, Vol. 70. pp. 1263–1272. Sydney, NSW, Australia.
- Gottlieb A. et al. (2011) PREDICT: a method for inferring novel drug indications with application to personalized medicine. Mol. Syst. Biol., 7, 496. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grover A., Leskovec J. (2016) node2vec: scalable feature learning for networks. In: Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, pp. 855–864. San Francisco. [DOI] [PMC free article] [PubMed]
- Hamilton W.L. et al. (2019) Representation learning on graphs: methods and applications (2017). IEEE Data Engineering Bulletin. [Google Scholar]
- Kipf T.N., Welling M. (2016a) Semi-supervised classification with graph convolutional networks. In ICLR. [Google Scholar]
- Kipf T.N., Welling M. (2016b) Variational graph auto-encoders. In NIPS Workshop on Bayesian Deep Learning. [Google Scholar]
- Lei C., Ruan J. (2013) A novel link prediction algorithm for reconstructing protein–protein interaction networks by topological similarity. Bioinformatics, 29, 355–364. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li Q. et al. (2018) Deeper insights into graph convolutional networks for semi-supervised learning. In: Thirty-Second AAAI Conference on Artificial Intelligence. New Orleans.
- Liang X. et al. (2017) LRSSL: predict and interpret drug–disease associations based on data integration using sparse subspace learning. Bioinformatics, 33, 1187–1196. [DOI] [PubMed] [Google Scholar]
- Liben-Nowell D., Kleinberg J. (2007) The link-prediction problem for social networks. J. Am. Soc. Inf. Sci. Technol., 58, 1019–1031. [Google Scholar]
- Linsker R. (1988) Self-organization in a perceptual network. Computer, 21, 105–117. [Google Scholar]
- Lü L., Zhou T. (2011) Link prediction in complex networks: a survey. Physica A, 390, 1150–1170. [Google Scholar]
- Pandey J. et al. (2008) Functional coherence in domain interaction networks. Bioinformatics, 24, i28–i34. [DOI] [PubMed] [Google Scholar]
- Perozzi B. et al. (2014) Deepwalk: online learning of social representations. In: Proceedings of the 20th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. pp. 701–710. New York.
- Ribeiro L.F. et al. (2017) struc2vec: learning node representations from structural identity. In: Proceedings of the 23rd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. pp. 385–394. Halifax, Canada.
- Stanfield Z. et al. (2017) Drug response prediction as a link prediction problem. Sci. Rep., 7, 40321. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Szklarczyk D. et al. (2015) STRING v10: protein–protein interaction networks, integrated over the tree of life. Nucleic Acids Res., 43, D447–D452. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tang J. et al. (2015) LINE: large-scale information network embedding. In: Proceedings of the 24th International Conference on World Wide Web. pp. 1067–1077. Florence, Italy.
- Valdeolivas A. et al. (2019) Random walk with restart on multiplex and heterogeneous biological networks. Bioinformatics, 35, 497–505. [DOI] [PubMed] [Google Scholar]
- Veličković P. et al. (2019) Deep graph infomax. In: 7th International Conference on Learning Representations (ICLR 2019). New Orleans.
- Wang Y.-B. et al. (2017) Predicting protein–protein interactions from protein sequences by a stacked sparse autoencoder deep neural network. Mol. Biosyst., 13, 1336–1344. [DOI] [PubMed] [Google Scholar]
- Wishart D.S. et al. (2018) DrugBank 5.0: a major update to the DrugBank database for 2018. Nucleic Acids Res., 46, D1074–D1082. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu F. et al. (2019) Simplifying graph convolutional networks. In: ICML. Long Beach, California.
- Yoo B. et al. (2017) Improving identification of key players in aging via network de-noising and core inference. IEEE/ACM Trans. Comput. Biol. Bioinform., 14, 1056–1069. [DOI] [PubMed] [Google Scholar]
- Yue X. et al. (2020) Graph embedding on biomedical networks: methods, applications and evaluations. Bioinformatics, 36, 1241–1251. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang W. et al. (2018) Manifold regularized matrix factorization for drug-drug interaction prediction. J. Biomed. Inform., 88, 90–97. [DOI] [PubMed] [Google Scholar]
- Zhou T. et al. (2009) Predicting missing links via local information. Eur. Phys. J. B, 71, 623–630. [Google Scholar]