Cluster Gauss-Newton and CellNOpt Parameter Estimation in a Small Protein Signaling Network of Vorinostat and Bortezomib Pharmacodynamics

Abstract

Ordinary differential equation (ODE) based models of signal transduction pathways often contain parameters that are unidentifiable or unmeasurable by experimental data, and calibrating such models to data remains challenging. Here, two efficient parameter estimation methods, Cluster Gauss-Newton (CGN) and CellNOpt (CNO), were applied to fit a signaling network model of U266 multiple myeloma cells to the activity dynamics of key proteins in response to vorinostat and/or bortezomib. A logic-based network model was constructed and transformed to 17 ODEs with 79 parameters estimated within broad ranges of biologically plausible values. The top 10% best-fit parameters by both methods had high uncertainties with CV > 50% for the majority of parameters. The root mean square and prediction errors were comparable without statistically significant differences between the two methods. Despite uncertain parameter estimation, prediction of protein dynamics after the sequential combination of bortezomib and vorinostat was predicted with reasonable accuracy and precision. Global sensitivity analyses of partial rank correlation coefficients and Sobol sensitivity demonstrated that apoptosis induction was most sensitive to parameters governing the activity of the proteasome-JNK-caspase-8 axis. Simulations revealed that the greatest magnitude of pharmacodynamic drug interactions between bortezomib and vorinostat occurred at caspase-9, AKT, and Bcl-2. Two sequential combinations were explored in silico, and the outcome matched qualitatively with an empirical evaluation of the pharmacodynamic interaction based on cell viability. Overall, the CGN and CNO algorithms performed similarly for this ODE-based network model calibration, and the calibrated model provided meaningful insights into cellular signaling mechanisms in response to pharmacological perturbations.

INTRODUCTION

Mathematical models based on ordinary differential equations (ODEs) have been used to analyze complex signal transduction pathways in biological systems (1-4). These models provide a quantitative description of biological processes that are regulated by the dynamic interplay of signaling pathways, and often integrate numerous gene and protein interactions by codifying prior knowledge and experimental data. The development of mathematical models for signal transduction presents two main challenges: first, the need to collect rich experimental data systematically for the components of the pathways of interest (e.g., genes, proteins, and metabolites); second, the need for operational parameter estimation methods to calibrate these models to experimental data (5). The parameter estimation challenge is transformed to an optimization problem in order to identify the best-fit parameters that characterize the experimental data. However, under limited data conditions, the parameters are estimated with a high degree of uncertainty, and/or there exist multiple possible solutions in an otherwise over-parameterized model.

The Cluster Gauss-Newton (CGN) method and CellNOpt (CNO) are two established algorithms for calibrating complex systems models to experimental data (6, 7). CGN is an optimization method that provides a cluster of possible solutions to parameter estimation when the number of parameters exceeds the observed data (6). It is an extension of the Cluster Newton method, which was applied successfully to an ODE physiologically-based pharmacokinetic model of irinotecan and its metabolites (8, 9). CNO is a software package designed to train signaling networks to genomic and proteomic data under perturbation using different logic-based formalisms, including logic-derived ODEs (10). A workflow for training a model with logic-based ODEs against temporal experimental data with CNO has been described for prostate cancer cells (11).

In this study, signal transduction in U266 multiple myeloma (MM) cells in response to treatment with two drugs, vorinostat and bortezomib, was selected as a test case for evaluating the CGN and CNO algorithms for parameter estimation. Aberrations in signaling pathways are implicated in the progression of MM and affect its treatment outcomes to vorinostat and bortezomib (12, 13).Mathematical models that incorporate and replicate the dynamics of key mediators of signaling pathways might facilitate the prediction of treatment outcomes for new combinatorial drug regimens. Vorinostat is a histone deacetylase (HDAC) inhibitor indicated for cutaneous T-cell lymphoma and affects gene transcription, cell cycle arrest, and apoptosis in malignant cells (14). Bortezomib is a proteasome inhibitor used to treat MM and mantle cell lymphoma and promotes pro-apoptotic signals in malignant cells by reducing proteasome-mediated degradation of pro-apoptotic proteins (15). The pharmacodynamics of these two drugs on signal transduction in MM cells was investigated using a logic-based (Boolean) network model (12), which can be converted to and ODE model for calibration to the dynamic protein activity profiles in response to the two drugs alone and in combination. Most of the parameters for the relationships defined by the ODE-model are not measured experimentally, and therefore a robust parameter estimation algorithm is required for developing a model that contains numerous parameters with missing data for certain sets of state variables.

This study aims to compare the parameter estimation, prediction accuracy, and model sensitivity by CGN and CNO using a small protein signaling network of MM in response to vorinostat and/or bortezomib, in order to establish the quantitative pharmacodynamic relationships within this specific system. The calibrated model was used to predict 1. the dependence of apoptosis on vorinostat concentration after the model was trained to protein activity data from cells exposed to two different static concentrations of vorinostat; and 2. proteomic signaling after sequential combination of bortezomib and vorinostat after the model was trained to data from single-drug and simultaneous combination treatments.

METHODS

Data sources

Temporal activity data for select proteins following control and drug treatments were extracted from two prior studies, included here as cases. In case 1, U266 MM cells were treated with 2 and 5 μM vorinostat for 48h, and Bcl-xL, cleaved PARP, p21, p53, and phosphorylated and total NF-κB were quantified using semi-quantitative western blot analysis (Dataset 1) (13). In case 2, protein activity profiles were quantified using the MAGPIX Luminex system for Bcl-2, p21, p53, phosphorylated and total NF-κB, AKT, JNK, and cleaved caspases-8, 9 and 3 in U266 cells treated with (i) 3 nM bortezomib for 48h, (ii) 2 μM vorinostat for 48h, (iii) 3 nM bortezomib + 2 μM vorinostat for 48h, and (iv) 3 nM bortezomib for 24h followed by addition of 2 μM vorinostat for another 24h (Dataset 2) (12). To explore signal transduction activity in this protein-based network, the active forms of proteins were quantified. For example, the ratio of phosphorylated divided by total protein intensities was used as model input for signal transduction proteins such as NF-κB, AKT, and JNK. Cleaved caspases and cleaved PARP were quantified because they catalyze proteolytic activities. All protein activity data were normalized between 0 and 1 with the following equation, as required by the CNO method:

$$NF{C}_i=\frac{{\log }_{2}F{C}_i-Min({\log }_{2}FC)}{Max({\log }_{2}FC)-Min({\log }_{2}FC)}$$ (1)

in which NFC_i is the normalized fold change for protein i, FC_i represents the original fold-change of protein i compared to its value at time 0. In this way, the baseline for all proteins at time 0 was converted to 0.419 for Dataset 1 and to 0.189 for Dataset 2. The drug concentrations were normalized to their highest concentration in the experimental datasets. Specifically, vorinostat concentrations of 2 and 5 μM were converted to 0.4 and 1.0, and bortezomib 3 nM was converted to 1.0.

Model development

The structural network for MM signaling was retrieved from the dissertation of Nanavati (12) (Supplement Fig. S1). The original Boolean network was constructed based on previously established signaling motifs for apoptotic and survival pathways, and the overall structure underwent a Boolean model reduction procedure to arrive at the final model containing 17 nodes (2 for therapeutic interventions and 15 for proteins) and 44 edges (interactions) (Fig. S1). The reduced logic-based network model was converted into ODEs using the “Normalized HillCube” method in Odefy, a MATLAB toolbox (16). In this manner, the value for each node was constrained between 0 and 1 in continuous manner. The activity of a protein is determined by its first-order turnover rate constant τ and its interaction with other protein(s). Each interaction is represented by a Hill function. The Hill coefficient n determines the slope of the relationship and the parameter k corresponds to a potency or threshold term that turns on the state of an interaction. The model contained 79 parameters in total. A generalized equation for a protein i (x_i) that is either activated or inhibited by protein j can be defined as:

$$\frac{d(x_i)}{dt}=\frac{1}{{\tau }_i}\left(\sum _j^{M_i}{f}_{j,i}(x_{j,i})-x_i\right)$$ (2)

with

$$f_{j,i}(x_{j,i})=\{\begin{array}{cc}\frac{x_j^{n_{j,i}}}{x_j^{n_{j,i}}+k_{j,i}^{n_{j,i}}}\cdot (1+k_{j,i}^{n_{j,i}}),\hfill & foractivation\hfill \\ 1-\frac{x_j^{n_{j,i}}}{x_j^{n_{j,i}}+k_{j,i}^{n_{j,i}}}\cdot (1+k_{j,i}^{n_{j,i}}),\hfill & forinactivation\hfill \end{array}\phantom{\}}$$ (3)

in which M_i is the total number of proteins interacting with i, and j is one of them, and f_j,i(x_j,i) is the Hill function for j’s effect on i. The Hill equation can be used to describe nonlinear capacity-limited relationships between an upstream and downstream protein. The advantages of this equation include: 1. the capacity and sensitivity parameters characterizing the relationship quantitatively are ubiquitous in biological and pharmacological systems including protein-protein interactions; and 2. it has the inherent flexibility to describe gradual to quantal signals by adjusting the value of a Hill coefficient, which controls the steepness of the curve. The Hill equation bridges a gap between the qualitative dynamics of signaling models and quantitative interaction networks and has been applied to Boolean protein networks (17). Some of the assumptions of this equation include (among others): 1. a capacity limit for protein signals, which is consistent with physiological ranges for proteins in a cell; and 2. the interaction relationship is unidirectional.

Parameter estimation with Cluster Gauss-Newton method

The CGN method uses a global linear approximation method to search multiple possible solutions of parameters (6). Briefly, a group of initial parameter sets (a cluster of 1000 for the 79-parameter vector) was prepared with a uniformly distributed random sampling from given parameter ranges (Supplemental Table S1). The whole parameter cluster was optimized iteratively, similar to the Gauss-Newton method, but using a linear approximation instead of a gradient. The maximal number of iterations was set to 100, and the top 500 solutions (out of the 1000) with lowest root mean square error (RMSE) were selected as initial terms for the next round of optimization. This step was repeated 2 more times on the next top 200/500 and 100/200 solutions. Then the top 10/100 (10%) solutions were selected for further optimization. For each of the 10 solutions, a cluster of 100 was generated around each parameter (ranging ±20%), and the search range was narrowed down by 5% with each iteration. The multiple steps were applied to accelerate the optimization process by narrowing down the search range for parameters based on the best parameter solutions. The median value for each cluster was then calculated as the estimated parameter value. The workflow in this study with the CGN method is summarized in Supplemental Fig. S2A, and additional details can be found in Supplemental Methods. The CGN method was implemented in MATLAB R2018b, and ODEs were integrated using the ode15s solver.

Parameter estimation with CellNOpt

Previously developed (reduced) network of MM signaling was encoded in simple interaction file (sif) format using Cytoscape software (v. 3.7.1), implemented in the R package CellNOptR and converted to a continuous model with the add-on package CNOROde as described previously (4). The optimization problem of estimating the Hill function parameters k and n and the turnover parameter τ to each logic gate was solved using a global population-based stochastic algorithm based on enhanced scatter search (18), with dynamic hill climbing (DHC) as the local search algorithm, which was implemented in the MEIGOR package. The optimization procedure was performed in two stages. In the first stage, each parameter was given a wide range of values (Supplemental Table S1). The problem was solved 20 times with different random initial parameter values, and each optimization was set to a maximum run time of 10 hours. In the second stage, the upper and lower boundaries for each parameter were set to 20% above the maximum value and 20% below minimum value of solutions obtained in the first stage. The problem was then solved 100 times with different random initial parameter values within new boundaries, and each optimization was set to have a maximum run time of 3 hours. In both stages, the initial condition for each node was set to the basal state (at time 0). Final solutions were rank-ordered based on the objective function value (OFV), and the top 10/100 (10%) solutions with the best OFV were selected for further evaluation. The workflow with the CGN method is summarized in Supplemental Fig S2B.

Model projections

For case 1, parameter values were obtained by training the model with Dataset 1 by both methods. There were 10 best solutions obtained using each method. The final 20 sets (10 from CGN and 10 from CNO) of estimated parameter values were used separately to generate 20 predicted profiles of cleaved PARP at 48h in response to vorinostat at 1-6 μM. For case 2, the same model was trained using data from single-drug and simultaneous combination treatments (groups btz, vor, and btz+vor). The final parameter values from both methods were used to simulate protein expression profiles after the sequential treatment of bortezomib followed by vorinostat (Dataset 2, group btz-vor). The sequential treatment group was not used in the parameter estimation step, and therefore represents an external validation. To assess the model predictive performance, a null hypothesis was tested. Briefly, model simulations were conducted with 20 randomized parameter vectors drawn from the initial parameter space (Table S1). The differences between the observed and model predicted data were calculated for each protein and were compared with those differences based on the 20 best-fit parameter solutions with unpaired Student’s t-test.

Global sensitivity analyses

Two global sensitivity analyses were conducted, the partial rank correlation coefficient (PRCC) and the Sobol sensitivity analysis, for case 2 in which cells were treated with the simultaneous combination of vorinostat and bortezomib. The PRCC assumes a monotonic relationship between the model parameters and system output (19). Sobol sensitivity decomposes the variance of the model output into the variances in combinations of parameters (20). The first and total order Sobol indices quantify the contribution of one parameter and by a parameter with all its interactions to the output variance. The model output was the area under the curve (AUC) for cleaved caspase-3 after 48h of drug exposure because cleaved caspase-3 is responsible for the execution of apoptosis (21). The trapezoidal rule was used to calculate the AUC for caspase-3 expression, which was simulated at each hour following treatment. The varying parameters were the protein turnover rate constants (τ) and the threshold parameters for protein-protein interactions (k). The ranges for variation were set as ±20% of the median values of the final 20 sets of estimated parameters. The Latin hypercube sampling method with 10⁶ samples was implemented in MATLAB R2018b with the function “lhsdesign” and was used for PRCC analysis using “partialcorr” with Spearman’s method. The first and total orders of Sobol indices, along with their 95% confidence interval values, were calculated with the function “sobol_indices”, which utilizes the Saltelli method in the R package “sensobol”. The sampling matrix with 2.04×10⁵ samples of 47 parameters was generated by “sobol_matrices” function, which is based on Sobol’s quasi-random number sequences.

RESULTS

Model calibration and estimated parameters by CGN and CNO

Case 1.

The network model was converted to 15 ODEs with 79 parameters and calibrated to the experimental activity profiles of Bcl-xL, NF-κB, p21, p53, and cleaved PARP in U266 cells following exposure to vorinostat at 2 and 5 μM for 48h (Dataset 1, 48 data points). The experimental data showed concentration-dependent induction of p21 and cleaved PARP by vorinostat, as well as concentration-dependent reduction of Bcl-xL. NF-κB was increased, but p53 decreased with vorinostat treatment. The profiles of all proteins were assumed stable without drug treatment (baseline condition). Fitted profiles for the top 10 out of 100 solutions with the least RMSE by CGN and CNO are shown in Fig 1. These final 20 sets of parameters (10 from each method) were used for subsequent model simulations. Both methods captured the temporal activity profiles reasonably well from visual inspection, with an average Pearson’s correlation coefficient value of 0.89 between the observed values and model predictions. Consistent with the observations, the 90% prediction intervals for vorinostat at 2 and 5 μM did not overlap for Bcl-xL, p21, or cleaved PARP (Fig 1). The statistics for the estimated parameter values are listed in Supplement Table S2.

Figure 1.

Model fitted profiles for protein activity in Case 1: U266 cells were exposed to vorinostat at 2 or 5 μM and vehicle control for 48h. Shaded area represents the 90% prediction intervals based on the top 10 solutions from each of the two methods.

Multiple possible solutions to the parameter values were possible when the model was fitted to observed data. The top 10 solutions from both methods showed comparable goodness-of-fit and similar RMSE values (Supplemental Figs. S3). There were no statistically significant differences in the RMSE values between the two methods (Supplemental Fig. S3C, p-value = 0.19 with unpaired Student’s t-test). The two methods performed comparably for estimating parameter sets for an over-parameterized model. A substantial proportion of the parameters were distributed throughout the search boundaries in both methods, with the protein turnover rate constant parameters ranging from 0-120h, Hill coefficient parameters for protein interactions ranging from 0-12, and the threshold parameters for protein interactions ranging from 0-24 (Supplemental Table S2 and Figure S4 A-C). The mean and standard deviation was calculated for each parameter in the final 20 sets. Only 4 parameters (n_Prot,JNK, n_HDAC1,Cas8, n_JNK,P53 and n_Cas8,Cas3) showed CV < 50% (CV = standard deviation/mean×100%). There were no highly correlated pairs of parameters (Spearman's rank correlation coefficient > 0.9, Supplemental Fig. S5) among the final 20 sets, although the 10 sets from the CNO method demonstrated a slightly greater correlation among each other compared to the CGN method. Overall, the final 20 sets of parameters were well separated from each other. The lack of convergence for the parameter values is likely owing to parameter unidentifiability, which might arise from both structural and practical identifiability issues in quantitative system pharmacological models (22). In the original datasets, 9 out of the 15 proteins in the signaling network were quantified, with at least one upstream or downstream protein quantified for the 6 proteins that were not measured directly. In addition, the temporal protein activity profiles were quantified to help further constrain the parameter space. Despite this design, the estimated parameter values by the CGN and CNO methods were not precise. In summary, the network models were able to recapitulate the protein activity profiles after vorinostat treatment at two concentrations, albeit with imprecise parameter estimation.

Case 2.

The same network model with 15 ODEs and 79 parameters were calibrated to the experimental profiles of AKT, Bcl-2, caspases-3, -8 and -9, JNK, NF-κB, p21, and p53 when U266 cells were treated with bortezomib at 3 nM, vorinostat at 2 μM, or both drugs simultaneously for 48h (Dataset 2, 108 data points). Bortezomib induced the activity of JNK, p21, and cleaved caspases-3, -8 and -9, but reduced AKT, Bcl-2, NF-κB, and p53. Vorinostat induced p21 and cleaved caspase-9 activity, but reduced the activity for AKT, Bcl-2, and p53. The simultaneous combination changed the activity of these proteins to greater extents as compared to either single-drug treatment, especially for p21. Fitted profiles from the top 10/100 solutions with the least RMSE by each method are shown in Fig. 2. Both methods recapitulated the temporal activity profiles reasonably well, although the model-predicted baseline appeared more stable with the CNO method as compared to CGN, especially for Bcl-2, NF-κB, p53, and cleaved caspase-9 (Fig. 2). The average Pearson’s correlation coefficient value was 0.72 between the observed and model-predicted values. The two methods showed comparable goodness-of-fit and similar RMSE values (Supplemental Figs. S3). There were no statistically significant differences in the RMSE between the two methods (Supplemental Fig. S3C, p-value = 0.097 with un-paired t-test). Statistics of the estimated parameter values are listed in Supplemental Table S3.

Figure 2.

Model fitted profiles for protein activity in Case 2: U266 cells were exposed to a bortezomib 3 nM, b vorinostat 2 μM, or c two-drug combination simultaneously for 48h.

The number of observations were greater than the number of parameters (108 vs. 79), but parameter identifiability remains an issue owing to the nonlinear nature of the model and the lack of experimental testing of logical relationships. Therefore, most of the parameter values were still distributed throughout the search limits similar to case 1 (Supplemental Table S3 and Figure S4 D-F), and there were no highly correlated pairs of parameter sets (Supplemental Fig. S5). There were 8 parameters (n_Cas8,Cas3, n_Prot,JNK, τ_Prot, n_JNK,Cas8, n_P53,p21, n_Cas9,Cas3, n_P53,AKT and n_Cas3,AKT) that showed CV < 50% in the final 20 best-fit sets. Most of these parameters are Hill coefficients for protein interactions where both proteins were measured. In summary, the network model was able to describe the dynamics of 9 proteins when exposed to bortezomib, vorinostat and their simultaneous combination despite the uncertain estimation of the parameters.

Model prediction of vorinostat concentration dependence

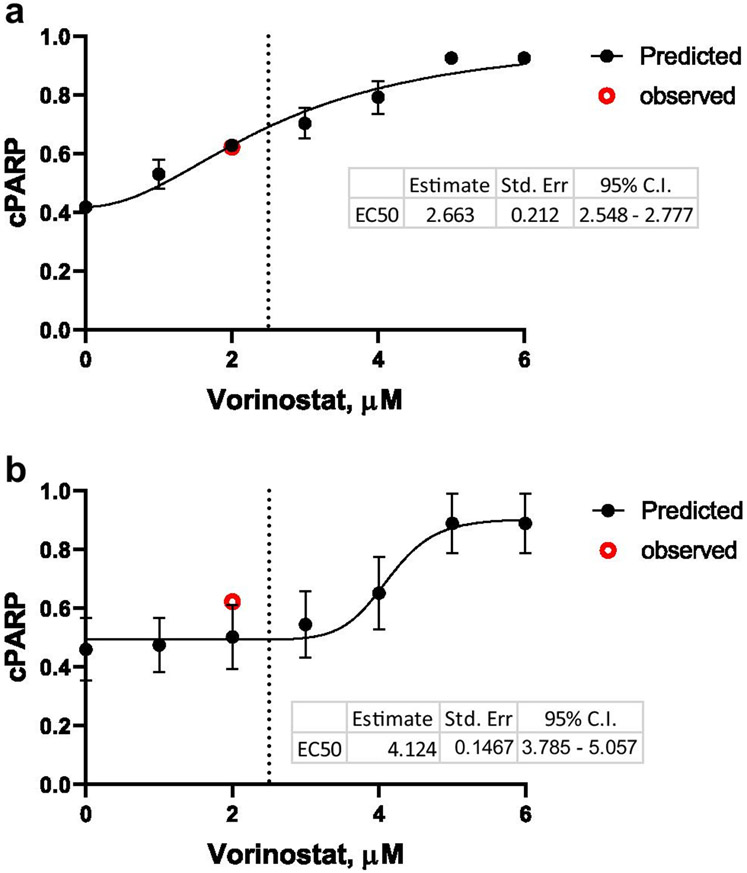
The final 20 parameter sets from case 1 were applied to predict the activity of cleaved PARP at 48h when exposed to 0, 1, 2, 3, 4, 5, and 6 μM of vorinostat. These concentrations were converted to 0, 0.2, 0.4, 0.6, 0.8, 1.0 and 1.2 in the model. The mean and standard deviation of the simulated values of cleaved PARP were calculated at each concentration(Fig. 3A). Vorinostat-induced cleaved PARP showed a clear concentration dependence, which was well described by a fitted Hill function. The EC₅₀ value (concentration to induce half maximal stimulation) was calculated to be 2.66 μM. This is consistent with the literature reported EC₅₀ value (2.5 μM) for vorinostat-induced apoptosis, which was quantified by the percentage of Annexin V positive cells (23). Training the model with data following vorinostat 5 μM exposure only resulted in a final model that failed to predict the increased cleaved PARP observed at 2 μM (Fig. 3B). Under this condition, the predicted EC₅₀ value for vorinostat was 1.5-fold greater, and the induction of cleaved PARP by vorinostat exhibited a steep concentration-effect relationship (Fig 3B). As expected for pharmacodynamic systems, concentration-effect relationships are best inferred only when a suitable concentration range is evaluated. Interestingly, the potency of vorinostat for increased cleaved PARP was reasonably predicted from the network trained with temporal activity data for only 2 concentrations of the drug.

Figure 3.

Concentration dependency for vorinostat-induced cleaved PARP at 48h. a Cleaved PARP was simulated 20 times based on the 20 best-fit parameter sets obtained by training the model with protein activity profiles of vorinostat at both 2 and 5 μM. b Cleaved PARP was simulated 20 times based on parameter values obtained by training the model with the protein activity data in response to vorinostat 5 μM only. The red circle indicates the observed cPARP activity in response to vorinostat 2 μM. Black dots and error bars indicate the mean and standard deviations of the 20 simulated cPARP activities at each vorinostat concentration. Dotted line indicates the reported EC₅₀ (2.5 μM) for vorinostat-induced apoptosis from the literature (23).

Model validation and sequential effects of bortezomib followed by vorinostat

To test whether the model could predict accurately a different treatment strategy with the same concentrations of the drugs as in case 2, the final 20 estimated parameter sets were used to predict the activity profiles of AKT, Bcl-2, caspases-3, -8 and -9, JNK, NF-κB, p21, and p53 when cells were pre-treated with bortezomib at 3 nM for 24h, followed by the addition of vorinostat of 2 μM for another 24h. These data served as external validation of the model because they were not used for parameter estimation. The addition of vorinostat increased the activity of JNK, p21, and cleaved caspases-3, -8 and -9, but further decreased AKT, Bcl-2, NF-κB, and p53 as compared to the pre-treatment of bortezomib alone. The 90% prediction interval from the 20 parameter sets overlaid with the observed data show reasonable prediction for all protein activity profiles (Fig. 4), with an average Pearson’s correlation coefficient value of 0.70 between the observed values and model predictions. The prediction from both CGN and CNO methods showed similar profiles (Supplement Fig. S6) except for NF-κB, where parameters estimated using the CNO method predicted an increasing trend and those from the CGN algorithm predicted a slightly decreasing trend. The mean absolute percentage error values were calculated: $MAPE=\frac{1}{n}\left({\sum }_{i=1}^n\mid \frac{y_{pred,i}-y_{obs,i}}{y_{pred,i}}\mid \right)$, and the CNO method showed a slightly lower MAPE (Supplement Fig. S7). Overall, both estimation methods demonstrated good predictability for the sequential treatment of bortezomib followed by vorinostat when the model was calibrated based on the activity profiles from both single-agent treatments and their simultaneous combination. This sequential exposure, but not the simultaneous combination treatment, has been shown to elicit synergistic cell killing of U266 MM cells (24).

Figure 4.

Prediction of the protein activity profiles overlaid with experimental observations for the sequential treatment of bortezomib 3 nM followed by the addition of vorinostat 2 μM. Shaded area represents the 90% prediction intervals from the top 20 parameter sets. The p-value for hypothesis testing (details explained in Methods – Model projections) is shown in each panel.

Model sensitivity analyses suggests potential targets for apoptosis induction

Global sensitivity analyses by both the PRCC and Sobol methods were conducted to identify the parameters to which the model is most sensitive to in terms of induced cell death in U266 cells. The AUC of cleaved caspase-3 was used as the model output based on its role as a key mediator for apoptosis. Among the 79 parameters in the network model, the final 20 sets of protein turnover rate constants (τ) and the threshold parameters for interactions (k) were selected to be varied by ±20% around the median or by the range of the estimated values (whichever was narrower). The PRCC and Sobol methods resulted in the same 6 parameters to which the model is most sensitive (Fig. 5). The most influential parameter based on PRCC was the threshold parameter k_Cas8,Cas3 (for cleaved caspase-8 to activate caspase-3), which was expected given that the interaction acts directly on the model output (caspase-3). Accordingly, a greater threshold parameter would be associated with less activation of caspase-3 by caspase-8. The second most influential parameter was τ_Prot (turnover rate constant for proteasome). This parameter determines how quickly the proteasome is inhibited by bortezomib. A greater τ_Prot parameter would be associated with slower proteasome inhibition, and thus potentially slower downstream signal accumulation affecting caspase-3. The next 4 identified parameters included: k_Prot,JNK, k_JNK,Cas8, k_P53,Cas8, and k_JNK,p53, which are threshold parameters for protein interactions within the Proteasome– JNK – p53 – caspase-8 axis that mediate the downstream signals for bortezomib through the apoptotic pathway. The partial correlation coefficient for k_Prot,JNK was positive because proteasome inhibits the activation of JNK. Sobol indices also confirmed the rank order of importance of these 6 parameters in the model. Given the parameter ranges for this study, the variance of k_Cas8,Cas3 and τ_Prot determined 76% and 22% of the variance in the AUC of caspase-3. The variance in the output from all the other parameters were much smaller compared to these two terms. The values for the first and total order Sobol indices were similar, suggesting negligible interaction between parameters. Inhibiting proteasome or activating the JNK-p53-caspase-8 axis could result in the accumulation of cleaved caspase-3 in U266 cells and result in increased apoptosis.

Figure 5.

Global sensitivity analyses showing the six most sensitive parameters for the AUC of cleaved caspase-3 in response to the simultaneous combination of bortezomib 3 nM and vorinostat 2μM at 48h. a Partial rank correlation coefficients (PRCC) for the parameters sorted by their absolute values. The sign of the coefficient indicates a positive or negative correlation between the parameter and the output. b The first- and total-order Sobol indices (S1 and St) for parameters sorted by St values.

Identification of protein(s) mediating bortezomib-vorinostat interactions

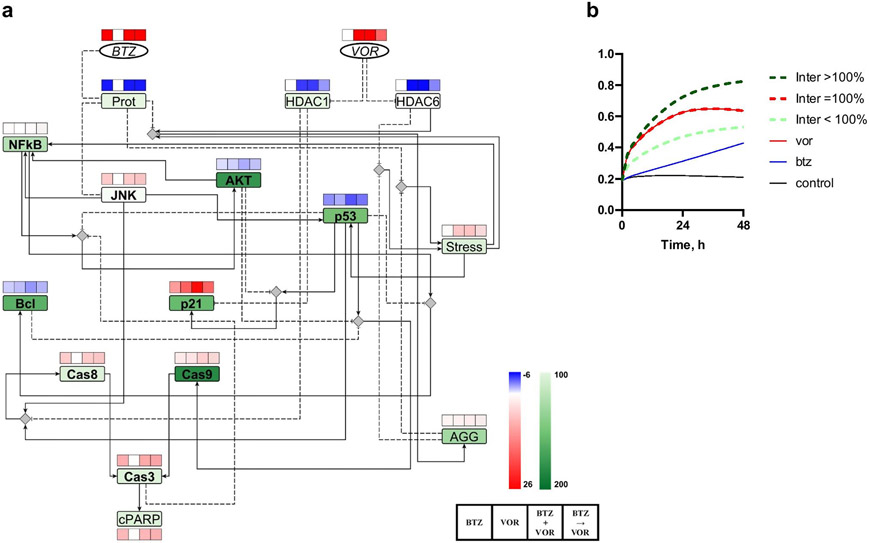
In order to identify the proteins that mediate the pharmacodynamic interactions between bortezomib and vorinostat in the signal transduction network, the net exposure for each protein in response to the combination was compared to values for single-agent treatments. Specifically, the mean activity profiles for each protein were simulated based on the final 20 sets of parameters under baseline conditions, or with vorinostat, bortezomib, or their combination for 48h. The AUC_0-48 for each protein was calculated under the four conditions, and the treatment-mediated effect was calculated as the AUC differences between any treatment group and the baseline condition. For example, dAUC_BTZ,i = AUC_BTZ,i − AUC_Baseline,i for protein i. The dAUC value is positive if the protein activity is increased compared to baseline and negative if decreased. The AUC was integrated based on log-transformed data, and the negative and positive values were weighed equally. The percent change in the absolute dAUC of the sequential combination (btz+vor) group, relative to the greater absolute dAUC of the single-agent groups, was calculated as an interaction index: $Inte{r}_i=\frac{\mid dAU{C}_{comb,i}\mid }{\max \left(\mid dAU{C}_{BTZ,i}\mid ,\mid dAU{C}_{VOR,i}\mid \right)}\times 100\%$. This index characterizes the extent of the response to the bortezomib-vorinostat combination relative to the maximum of the single-agent responses. If greater than 100% for a protein, the index suggests that the protein activity in response to the combination exceeded the maximal responses by either single-agent treatment, thus implying that the responses overlapped at this protein (i.e., the protein might be a potential mediator for the interaction). The absolute value was used to handle negative values. The interaction index as well as the dAUC values for all proteins are shown in Fig. 6. The combination of bortezomib and vorinostat resulted in the highest interaction index for cleaved caspase-9 (184%), followed by AKT (177%), Bcl-2 (161%), p21 (155%), p53 (162%), AGG (aggresome, 129%), and NF-κB (121%). The sign of dAUC for any proteins in the combination btz+vor group was the same as for any single-agent group. The downstream signals of bortezomib and vorinostat appear to be enhanced by the increases in Caspase-9, p21, AGG, and NF-κB, and by the decreases in AKT, Bcl-2, and p53 within the signal transduction network.

Figure 6.

Pharmacodynamic interactions between bortezomib and vorinostat within the signal transduction network. a The mean AUC for each protein until 48h was predicted. AUC differences between treatment groups and the baseline (dAUC) was calculated and color coded in the squares. The interaction index $(Inter=\frac{\mid dAU{C}_{comb}\mid }{\max (\mid dAU{C}_{BTZ}\mid ,\mid dAU{C}_{VOR}\mid )}\cdot 100\%)$ for each node was color coded in the rectangles. The squares from left to right are: 1. bortezomib 3 nM, 2. vorinostat 2 μM, 3. simultaneous combination, and 4. bortezomib followed by vorinostat. b Illustrative temporal profiles of proteins in which the index is less than, equal to, or greater than 100%.

Mean protein activity profiles were simulated using the final 20 estimated parameter sets for the sequential treatment of bortezomib for 24h followed by addition of vorinostat for another 24h, or the reverse exposure regimen. The dAUC values for both sequential treatment groups were calculated for the later 24h when both drugs were present (Fig. 7A-B). Bortezomib followed by vorinostat exposure increased the activity of p21, JNK, and caspases-8, -9 and -3 and decreased the activity of proteasome, p53, and AKT compared to the regimen with the reverse schedule (Fig. 7C). Although this network model was not linked quantitatively to cell growth or death directly, the increase in anti-proliferation proteins and decrease in pro-survival proteins implies that bortezomib followed by vorinostat could be more effective than the reverse regimen. This is consistent qualitatively with a previous report that bortezomib followed by vorinostat exhibited synergistic inhibition on MM cell viability, but the reverse regimen was simply additive (24). Simulation of protein activity profiles from this network helped to identify pharmacodynamic interaction mechanisms and to compare potential outcomes between sequential treatment regimens.

Figure 7.

Comparison of accumulated protein activity when exposed to two regimens of sequential combinations: bortezomib 3 nM followed by vorinostat 2 μM (blue), or vorinostat 2 μM followed by bortezomib 3 nM (red). The activity profiles of a p21 and b AKT are shown as examples of proteins induced and reduced by the two sequential combination regimens. Shaded areas are illustrated for calculating the AUC differences between treatment groups and the baseline (dAUC) from 24 to 48h. c dAUC values for each protein in the network for the two regimens.

DISCUSSION

The complexity of biological regulatory networks, coupled with sparse experimental observations, often results in parameter estimation difficulties for ODE-based quantitative systems pharmacology models. Gutenkunst and colleagues examined 17 system biology models and found that the existence of parameters with great uncertainties (so-called “sloppy” parameters) was universal (25). They conclude that a system biology model with sloppy parameters can provide well-constrained predictions about the components within the biological system (25). However, there is still a knowledge gap in determining whether such a model can both recapitulate and learn from the biological data such that the model can be used for extrapolation (e.g., to predict the systemic responses under new perturbations). Here, an ODE-based signaling network model was applied to the time-series data of dynamic protein activity profiles for U266 MM cells, and parameters were estimated by two methods. Both methods provided poorly-constrained parameter values (Supplemental Tables S1-2) with neither algorithm emerging as superior in terms of the accuracy and precision of the predictions (Figs. 1-2). Although the CNO method by default does not allow for the simultaneous fitting of responses to multiple drug concentrations, the addition of dummy nodes representing concentration levels were sufficient for accommodating multiple exposure level pharmacodynamics (Supplemental Methods). The CGN algorithm is more flexible for such a scenario, and the model equations are fully customizable. The CNO method appeared to be slightly better suited to data representing different perturbations (case 2), with a relatively smaller mean prediction error for the bortezomib/vorinostat sequential combination (Supplemental Figure S7). The model and final parameter sets captured the experimental data, but more importantly, were successfully extrapolated to infer concentration-dependency in steady-state variables, identify mediators for drug-drug interactions, and explore alternative combination regimens. The model was also externally validated by providing good predictions of the protein dynamic profiles for the sequential combination regimen (Fig. 4), which were not used for model development. The CGN and CNO methods allowed for the effective calibration of a small signaling network to experimental data and provided a platform for making predictions for additional perturbation conditions. There are other optimization algorithms that could be applied for parameter estimation, such as Particle Swarm Optimization (PSO) and Scatter Search (SS). However, the CGN and CNO methods have demonstrated utility in PBPK (6, 8, 9) and QSP network models (7, 26, 27), are relatively easy to implement, and can be readily integrated with ODE solvers and efficient optimization procedures.

The network model was calibrated separately using two different datasets instead of jointly modeling both datasets simultaneously. The two datasets were obtained from different experimental platforms (Western blot vs. Luminex MAGPIX assay), and consistent signature profiles were difficult to identify owing to differences in assay procedures and the semi-quantitative nature of both methods. One of the primary goals was to test the performance of two parameter optimization methods, and so clean and comparable datasets were preferred. Considering the rich temporal data available for both cases, the datasets were used separately to avoid unnecessary “contamination” in the model input data from different experimental platforms. The two algorithms tested here, especially the CNO method, works well with single-source data with rich temporal profiles and unique perturbation conditions (7). In addition, data normalization was necessary to scale all the available experimental data for protein activity within the range of 0-1 (7). The “baselines” (T=0) for each protein were different in both datasets because of the different ranges of the raw experimental data. The difference in the baseline value also affects the estimation of EC₅₀ values for protein interactions, because the network steady-state under control conditions is dependent on the relative values of baseline protein expression and EC₅₀ values. Best approaches for combining disparate data sources and types is the subject of ongoing research.

The activity profiles for proteins in response to bortezomib followed by vorinostat were in good agreement with experimental data, which were not used to calibrate the model. On comparing the accumulated signals for proteins under bortezomib followed by vorinostat vs. the reverse schedule, the balance shifted toward enhanced anti-proliferative signals (e.g., increased p21 and cleaved caspase-3, and decreased AKT), suggesting a more effective regimen schedule. This matches qualitatively with the observed synergy (i.e., better than additive) in the former schedule compared to additivity for the latter (24). The sequence of administration for drug combinations may be important for relapsed and refractory MM treatment (28). Heeg and colleagues used a statistical modeling approach to compare overall survival for different sequences and found that survival associated with treatment sequences starting with thalidomide, lenalidomide, or bortezomib in combination with melphalan/prednisone was significantly better than sequences starting with melphalan/prednisone alone (29). Further expansion of our mechanistic signaling model, as well as appropriate links for preclinical to clinical translation, may provide a platform for improving the predictions of the probability of patient survival for different combination regimens from nonclinical experiments.

Global sensitivity analysis offers insights into the most influential parameters to a specific model output given the model structure and can be used to identify potential key pharmacological targets of interest (19, 30-34). There are multiple metrics to quantify global parameter sensitivity, and they should be chosen according to considerations such as computational cost, purpose of use, and model features. In this study, PRCC was used because the model followed monotonic input-output relationship (as suggested in Fig. 3). The use of Sobol indices is a variance-based approach that makes no assumptions on the relationship between the model input and output (20, 35). Parallelized computing (32 cores) was implemented in order to obtain enough samples for the evaluation of variance. The rank-order of the top 6 sensitive parameters by PRCC and Sobol indices were the same in this analysis, despite the quantitative differences in the two metrics. The quantitative differences might stem from their calculation formulas: PRCC calculates the correlation coefficient for ranked values for each variable rather than the raw data, but Sobol indices quantify the contribution to variances in decomposed dimensions with raw values. Based on their calculation formulas, a PRCC ranges from −1 to 1, but a Sobol index ranges from 0 to 1. The goal of the sensitivity analyses in this work was to search for the signaling proteins/axes controlling cell death (cleaved caspase-3) to generate hypotheses for potential additional pharmacological targets. Therefore, the qualitative information represented by the rank order of the most sensitive parameters was more important than the quantitative values for the two metrics. Global sensitivity analyses suggested that the accumulated signal of cleaved caspase-3 was sensitive to the signals of caspase-8, proteasome, JNK, and p53. The most sensitive parameter was the threshold of cleaved caspase-8 to activate cleaved caspase-3 by both sensitivity matrices, and there was a negative association with this parameter to apoptosis. This is consistent with a previous report that bortezomib-induced cell death was effectively inhibited by pan-caspase inhibitor ZVAD-FMK or caspase-8 inhibitor IETD-FMK, but was inhibited to a lesser extent by a caspase-9 inhibitor LEHD-FMK and a caspase-3/7 inhibitor DEVD-FMK (36). The second most sensitive parameter was the turnover rate constant for proteasome, in which faster inhibition of proteasome should result in a greater apoptotic signal. This is consistent with target-binding kinetics of ixazomib, a 2^nd generation of proteasome inhibitor showing a proteasome dissociation half-life 5-fold lower than bortezomib, which resulted in apoptosis induction in MM cells resistant to bortezomib (37, 38). Besides the two targets that have been associated with improved cytotoxicity of bortezomib by other scientific reports, new potential pharmacological targets were identified by the global sensitivity analysis of our final model, including: activation of JNK or p53, or relieving the proteasome-mediated degradation/inhibition of JNK. The targeting these proteins requires further pharmacological validation as the sensitivity analysis could identify erroneous targets. The consistency of the rank order of the top 6 sensitive parameters for PRCC and Sobol sensitivity provides some confidence; however, even if the identified proteins fail to improve efficacy, the high sensitivities of cell death to these proteins 0still imply that these parameters affect the robustness of the prediction. Therefore, these proteins should be assigned a greater priority for quantification in the future experimental designs. In addition, the proteasome-JNK-caspase-8 axis identified in the current network can be further expanded for potential target screening,

The key mediators for the pharmacodynamic interaction of bortezomib and vorinostat were identified, and cleaved caspase-9, AKT, and Bcl-2 were the top 3 proteins whose activity altered the most in response to the combination compared to single-drug exposure (Fig. 6). The interaction index is a simple variation based on the highest single-agent method or Gaddum’s non‐interaction to identify drug interactions (39, 40). The objective is to identify the potential signaling proteins that might mediate the combination effects in the signaling network based on response magnitudes rather than the pharmacological definitions of synergy or antagonism, which typically quantify whether the response to the combination is greater than the additive effect of the single agent responses (40). The intracellular signals by each drug transduce through and integrate at those critical proteins, which were experimentally measured in this study (case 2). Pharmacodynamic models can also be used to infer the time-course of unmeasured variables (e.g., AGG or Stress), the interaction strength of which could be quantified using modeling and simulation. Identifying the potential proteins responsible for pharmacodynamic drug-drug interactions could aid the discovery of predictive biomarkers for combination therapies, which could be incorporated into mathematical models linking protein activity to treatment outcomes (40). Further experimental data are needed to validate the predicted impact of the signaling factors identified in this study.

The final systems model (Fig. 6) and 20 best parameter sets are specific to U266 MM cells and does not account for subtleties arising from cell specific properties, such as different functional genetic mutations in signaling pathways in different MM cell lines, which can alter sensitivity to drug treatment (41). However, cell-specific models can be obtained by calibrating general network to signaling dynamics in different cell models, which will allow comparison of network connectivity across a panel of cell lines and highlight any functional differences that stem from genetic defects (27, 42). The advantage of using efficient parameter estimation methods lies in ability to preserve prior knowledge about biological processes while working with diverse datasets; this approach circumvents the need to rewire the model for every new experimental scenario, which hinders the predictive ability. New algorithms are evolving to allow integration of literature-constrained and data-driven networks to infer novel interactions and missing links (26, 43).

Estimating all 79 parameters was plausible because of the usage of effective optimization methods CGN and CNO. A more common effort to handle these many unknown parameters is to draw some values from the literature (e.g. from in vitro measurements) (44), fix them and then adjust remaining parameters to fit the existing data (45). This approach works because the models in system biology are often “sloppy”: they are uncertain and sensitive to only a few parameters (25). Another approach is to summarize the directional interactions among measured proteins from prior knowledge, and simplify all other interactions with hypothetical transit compartments. An example is the model developed by Nanavati et al. using the same data as in case 1 (13). The network consisted of 5 proteins shown in Fig. 1, each with a series of hypothetical transit compartments representing regulation interactions. The effects of vorinostat were projected to the proteins or the transit compartments. This approach dramatically reduced the number of parameters needed for the model, thus reducing the uncertainty in parameter estimation, but compromised the ability of the model to identify potential pharmacological target(s). For example, the underlying interaction(s) among proteins might be masked by the hypothetical construct of the model (transit compartments) when conducting parameter sensitivity analysis. In contrast to the previous approach in which the signaling network served as a guide to construct a smaller dynamical model that included only quantified proteins linked through the hypothetical interactions, the signaling network was converted to ODEs in this study, and parameters for the full network were calibrated against experimental data by two parameter optimization methods that provided insights into the intracellular processes of drug action despite relatively limited information. Whereas the previous approach resulted in well-constrained parameter estimates that enable a fit-for-purpose application, it does not allow for an evalutation of the potential dynamics of unmeasured proteins and limits any investigation of potential mediators of drug interactions owing to the limited scope of the final model. In this work, the temporal responses to the sequential btz-vor combination were not used in the training of the model, but rather provided a validation dataset for the final model calibrated on the btz, vor, and simultaneous btz+vor combination. In summary, model development approaches should be selected based on the purpose of the study with considerations such as data quality, computational cost, and practical utility.

CONCLUSION

The CGN and CNO parameter estimation methods were found to show similar predictive performance for calibrating an ODE-based model of signal transduction in U266 MM cells in response to vorinostat and bortezomib. The model suggested sensitive parameters for apoptosis induction, the mediators for pharmacodynamic interactions between the two drugs, and the difference in responses to two sequential regimens in silico.