Time-independent harmonics dispersion relation for time-evolving nonlinear waves

The inner makings of an evolving or balanced nonlinear wave are revealed by the discovery of the harmonics dispersion relation.

Abstract

We present a theory for the dispersion of generated harmonics in a traveling nonlinear wave. The harmonics dispersion relation (HDR), derived by the theory, provides direct and exact prediction of the collective harmonics spectrum in the frequency–wave number domain and does so without prior knowledge of the u = u(x, t) solution. It is valid throughout the evolution of a distorting unbalanced wave or the steady-steady propagation of a balanced wave with waveform invariance. The new relation is shown to be a special case of the general nonlinear dispersion relation (NDR), which is also derived. The theory is examined on a diverse range of cases of one-dimensional elastic waves and shown to hold irrespective of the spatial form of the initial wave profile, type and strength of the nonlinearity, and the level of dispersion in the linear limit. Another direct outcome of the general NDR is an analytical condition for soliton synthesis.

INTRODUCTION

Wave motion lies at the heart of many disciplines in the physical sciences and engineering. For example, natural phenomena involving atomic motion, seismic motion, fluid flow, heat transfer, or propagation of light and sound all involve wave physics at some level (1). While the theory of linear dispersive waves is fairly complete, much has remained to be understood about nonlinear waves and their characterization. For linear systems, it is customary to obtain dispersion relations that relate the frequency ω and wave number κ of propagating modes. A dispersion relation provides valuable information and is often used to characterize a range of physical properties of the medium admitting the wave motion (2). In nonlinear systems, on the other hand, the notion of a dispersion relation has been treated with caution because superposition does not apply. Yet, the appeal of retaining nonlinear effects in the study of dispersion has motivated several studies in a variety of disciplines, including quantum mechanics (3), solid mechanics (4–9), fluid dynamics (10–13), acoustics (14), electromagnetics (15, 16), plasma physics (17–20), geophysics (21–23), astrophysics (24), and biophysics (25, 26), among others. Aside from explicit examination of dispersion, classical methods for solving the initial-value problem for a wide class of nonlinear evolution equations have been developed since the late 1960s (27–30).

In many problems, it is often sufficient to consider the effects of weak nonlinearities; in such cases, these effects are augmented over the linear dispersion relation in the form of perturbations (31). Nonlinear dispersion relations for systems exhibiting weak nonlinearities were derived by small-parameter expansions, for example, for discrete chains (5, 7), elastic rods (4), and plasma (17). For strong nonlinearities, however, exact derivations of NDR are needed. While relatively rare, a few exact NDR formulations have been produced for certain problems; for example, Schürmann et al. (32) provided an exact NDR for TE-polarized electromagnetic waves in a layered structure and Huang et al. (18) and Ginzburg et al. (19) for surface plasmon waves.

However, a key question remains, and that is what does it mean to have a dispersion relation for nonlinear waves, especially when the nonlinearity is strong? One challenge stems from the fact that an unbalanced nonlinear wave distorts as it travels and appears to ultimately fully lose its original shape, and in many instances, the final outcome is onset of a form of instability (1). Inherent to this distortion is an intricate mechanism of harmonic generation, a phenomenon that is widely used in laser science (33) and ultrasound nondestructive evaluation (34–36). Harmonic generation also takes place in balanced waves that do not experience distortion (37). In the presence of harmonic generation, a Fourier transform of the space-time response reveals a fundamental harmonic and a series of higher-order harmonics. The distortion that we observe is a manifestation of energy exchange from one harmonic to the other (38, 39). Aside from dispersion analysis, rigorous theory has been developed for the analysis of the spatial response of multiple harmonics. Early works in this area include papers by Thurston and Shapiro (40), Tiersten and Baumhauer (41), and Thompson and Tiersten (42). Common techniques applied on weakly nonlinear systems seek spatial solutions for harmonics using perturbation expansions, e.g., see publications on elastic waves by Auld (43), Deng (44), and de Lima and Hamilton (45). This body of theory follows key experimental work on harmonic generation in ultrasonic waves in metals (34–36, 46, 47); see review by Matlack et al. (48).

In an earlier study (8), we presented an exact dispersion relation for a thin elastic rod modeled by a nonlinear second-order partial differential equation (PDE). The term “thin” designates a rod model with a cross-sectional thickness much smaller than the wavelengths of the propagating waves; a thin rod is nondispersive in the small-amplitude linear limit. Validation by numerical simulation was performed, whereby a cosine waveform with a specific value of amplitude and a specific value of wave number was initially prescribed and the derived NDR was shown to predict, exactly, the instantaneous change in the frequency from what is otherwise dictated by the linear dispersion relation. No connection was established between the derived NDR and the evolved nonlinear wave, either in its spatial form or by considering its generated harmonics. An elastic beam, modeled by a fourth-order PDE, was also investigated by the same approach, and an exact NDR was derived for a simplified version of that system (49); however, no validation by numerical simulation was performed, as the model appeared overly complex to integrate numerically.

Here, we provide a theory that characterizes the nature of a nonlinear wave, through its harmonic generation, as it evolves over long times. The prediction is in the form of an exact analytical dispersion relation that describes the distribution of the generated harmonics in the frequency–wave number domain; it is valid at all times for a balanced wave or up to the point of breaking if the wave reaches an unstable state. This result thus introduces a new insight into the notion of an NDR and a new finding pertaining to the spectral characterization of harmonic generation.

We present the theory not only for a thin rod but also for a thick rod. A “thick” rod is modeled by a fourth-order PDE, exhibits lateral inertia, and is dispersive in the linear limit as the wave amplitude B → 0. For both systems, we first derive a general NDR as a function of B and wave number κ and then specialize our derivation to yield a harmonics dispersion relation that predicts the harmonic generation spectrum associated with a wave having an initially prescribed amplitude–wave number pair: B = B_e and κ = κ_e. Upon presenting the theory, we provide validation by numerical simulation followed by Fourier transformation, demonstrating applicability for (i) large amplitudes, (ii) different types of nonlinearity, (iii) different times throughout the evolution, (iv) the presence or lack of dispersion in the linear limit, and (v) different initial wave profiles. Last, we provide an analytical condition for soliton synthesis, which represents yet another outcome of the general NDR.

RESULTS

Theory

Thick elastic rod

We consider an infinite one-dimensional (1D) rod with polar radius of gyration r and constant material properties. The rod admits longitudinal displacements u(x, t) under uniaxial stress σ(x, t), where x and t denote position and time, respectively. The governing nonlinear equation of motion (EOM) is obtained by Hamilton’s principle $\mathrm{\delta }{\int }_0^t(\mathcal{T}-\mathcal{U})\mathrm{\partial }t=0$, where $\mathcal{T}=\mathrm{\rho }[{({\mathrm{\partial }}_{t}u)}^2+{\mathrm{\nu }}^2{r}^2{({\mathrm{\partial }}_{\mathit{tx}}^{2}u)}^2]/2$ and 𝒰 = σϵ/2 define the kinetic and strain energy densities, respectively. Here, ρ and ν denote the mass density and Poisson’s ratio, and the stress in our model follows Hook’s law σ = Eϵ, where E is the elastic modulus. A linear constitutive law is considered for simplicity, but the theory is directly applicable to material nonlinearities as well. Geometric nonlinearity is introduced through the definition of strain; a finite strain ϵ may, in principle, take the form of any of the Seth-Hills family of strain measures (50, 51). Here, we consider, separately, the Green-Lagrange strain (GLS) and Hencky strain (HS) measures, which are defined as ϵ = ∂_xu + (∂_xu)²/2 and ϵ = ln (1 + ∂_xu), respectively. The EOM for the displacement gradient $\overline{u}={\mathrm{\partial }}_{x}u$ takes the general form

$${\mathrm{\partial }}_{\mathit{tt}}\overline{u}-{\mathrm{\partial }}_{\mathit{xx}}(\mathrm{\alpha }\overline{u}+\mathrm{\beta }\mathcal{N}(\overline{u})+\mathrm{\gamma }{\mathrm{\partial }}_{\mathit{tt}}\overline{u})=0$$ (1)

where α = β = c² and $\mathcal{N}(\overline{u})=3{\overline{u}}^2/2+{\overline{u}}^3/2$ for the GLS measure and α = 0, β = c², and $\mathcal{N}(\overline{u})=\text{ln} (1+\overline{u})/(1+\overline{u})$ for the HS measure. For both cases, the quasistatic speed of sound is given by $c=\sqrt{E/\mathrm{\rho }}$, and for compactness, we have introduced the parameter γ = r²ν². In this model, the effect of the lateral inertia is considered only on the longitudinal displacement; however, the theoretical framework is fully valid in the absence of this modeling simplification.

For the limiting configuration of a thin rod, the lateral inertia is omitted by setting r = 0. In this medium, a traveling wave profile with an initial finite-amplitude B_e will experience, in the course of its evolution, forward self-steepening in the case of Green-Lagrange nonlinearity and backward self-steepening in the case of Hencky nonlinearity. Eventually, each wave experiences instability at time τ_S. An analysis of this steepening effect and its path to instability is given in the Supplementary Materials, where in fig. S1, both self-steepening scenarios are demonstrated.

General nonlinear dispersion relation

We introduce a traveling phase variable ξ = κx − ωt and substitute it into Eq. 1, resulting in the transformation from $\overline{u}(x,t)$ to $\overline{U}(\mathrm{\xi })$. This gives

$${\mathrm{\omega }}^2{\overline{U}}_{\mathrm{\xi }\mathrm{\xi }}-{\mathrm{\kappa }}^2{(\mathrm{\alpha }\overline{U}+\mathrm{\beta }\mathcal{N}(\overline{U})+{\mathrm{\omega }}^2\mathrm{\gamma }{\overline{U}}_{\mathrm{\xi }\mathrm{\xi }})}_{\mathrm{\xi }\mathrm{\xi }}=0$$ (2)

which, upon integration twice, yields

$$({\mathrm{\kappa }}^2\mathrm{\alpha }-{\mathrm{\omega }}^2)\overline{U}+{\mathrm{\kappa }}^2\mathrm{\beta }\mathcal{N}(\overline{U})+\mathrm{\gamma }{\mathrm{\kappa }}^2{\mathrm{\omega }}^2{\overline{U}}_{\mathrm{\xi }\mathrm{\xi }}=0$$ (3)

The integration constants leading to Eq. 3 represent coefficients of a constant term and a secular term and have been set equal to zero, which is consistent with a bounded traveling wave solution for an initially bounded displacement field.

Now, we seek a general NDR that we associate with any arbitrary initial waveform $\overline{f}(x,0)$ belonging to the family of wave functions F that is consistent with the following conditions at ξ = 0

$$\overline{U}(0)=B\mathrm{\kappa },{\overline{U}}_{\mathrm{\xi }}(0)=0,{\overline{U}}_{\mathrm{\xi }\mathrm{\xi }}(0)=-B\mathrm{\kappa }$$ (4)

The choice of “Bκ” is not unique, but this quantity is selected because the deviation from the linear dispersion curve depends directly on this product. Setting ξ = 0, by definition, restricts the spatial (κx) and temporal (ωt) phases to be equal. This, in turn, enables a moving reference frame that follows the traveling wave, which allows for a time-independent nonlinear dispersion analysis. Examples of F functions include cosine, hyperbolic secant, Gaussian, and Lorentzian functions. Upon substitution of Eq. 4 into Eq. 3, we obtain the exact NDR for the GLS and HS measures, respectively, as

$${\mathrm{\omega }}^{\text{GLS}}=c\mathrm{\kappa }\sqrt{(2+3B\mathrm{\kappa }+B^2{\mathrm{\kappa }}^2)/(2+2\mathrm{\gamma }{\mathrm{\kappa }}^2)}$$ (5)

and

$${\mathrm{\omega }}^{\text{HS}}=c\mathrm{\kappa }\sqrt{\text{ln} (1+B\mathrm{\kappa })/(B\mathrm{\kappa }(1+B\mathrm{\kappa })(1+\mathrm{\gamma }{\mathrm{\kappa }}^2))}$$ (6)

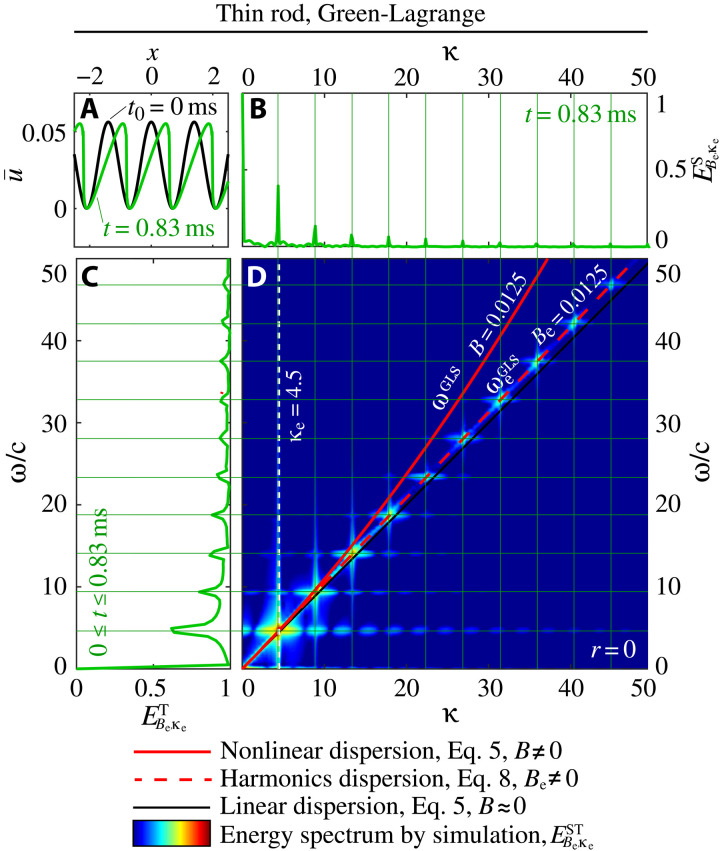
These reduce to a linear dispersive form in the limit of B → 0 and a linear nondispersive form in the limit B → 0, γ → 0. Figure 1D presents a plot of the general NDR for the GLS model, as defined in Eq. 5, for a thin rod and B = 0.0125 (see solid red curve). Note that nonlinearity by itself causes wave dispersion (8).

Fig. 1. Nonlinear cosine wave experiencing distortion (steepening) and harmonic generation.

(A) Spatial profiles captured at the initial time and at a later time; initial amplitude is B_e = 0.0125, and initial wave number is κ_e = 4.5. (B) Wave number spectrum, (C) frequency spectrum, and (D) frequency–wave number spectrum of harmonics demonstrating exact prediction by the harmonics dispersion relation of Eq. 8. The result is based on the GLS measure.

Harmonics dispersion relation

We now uncover that the general NDR derived above inherently encompasses information on the harmonic generation mechanism associated with nonlinear waves characterized initially by a specific amplitude B = B_e and wave number κ = κ_e. Starting with Eq. 3, we impose the set of conditions

$$\overline{U}(0)=B_{\mathrm{e}}{\mathrm{\kappa }}_{\mathrm{e}},{\overline{U}}_{\mathrm{\xi }}(0)=0,{\overline{U}}_{\mathrm{\xi }\mathrm{\xi }}(0)=-B_{\mathrm{e}}{\mathrm{\kappa }}_{\mathrm{e}}$$ (7)

which is a special case of the conditions prescribed in Eq. 4. This yields the following exact harmonics dispersion relation for the GLS and HS models, respectively

$${\mathrm{\omega }}_{\mathrm{e}}^{\text{GLS}}=c\mathrm{\kappa }\sqrt{(2+3B_{\mathrm{e}}{\mathrm{\kappa }}_e+B_{\mathrm{e}}^2{{\mathrm{\kappa }}_e}^2)/(2+2\mathrm{\gamma }{\mathrm{\kappa }}^2)}$$ (8)

and

$${\mathrm{\omega }}_{\mathrm{e}}^{\text{HS}}=c\mathrm{\kappa }\sqrt{\text{ln} (1+B_{\mathrm{e}}{\mathrm{\kappa }}_e)/(B_{\mathrm{e}}{\mathrm{\kappa }}_e(1+B_{\mathrm{e}}{\mathrm{\kappa }}_e)(1+\mathrm{\gamma }{\mathrm{\kappa }}^2))}$$ (9)

Each of these relations predicts the exact frequency–wave number curve on which all the harmonics will lie following a Fourier transform of the time response of a traveling nonlinear pulse of any arbitrary form provided that the initial conditions of the solved PDE are consistent with the corresponding ξ = 0 conditions stated in Eq. 7. If the pulse is not balanced, e.g., is experiencing self-steepening, then the prediction will be valid up to time τ_S, the instant of onset of instability. Alongside the general NDR curve plotted in Fig. 1D for the thin-rod GLS model, a harmonics dispersion relation based on Eq. 8 is plotted for B_e = 0.0125 and κ_e = 4.5 (see dashed red curve). The notion of a harmonics dispersion relation represents a new paradigm in nonlinear wave science.

Single generic forms of the general NDR and the harmonics dispersion relation in terms of the nonlinear function, $\mathcal{N}(\overline{U})$, and the strain gradient at ξ = 0, $\overline{U}(0)$, for the two types of nonlinearity, are provided in the Supplementary Materials. These generic forms allow us to apply the general NDR and the harmonics dispersion relation to other types of nonlinearities in a modular fashion.

Validation by direct numerical simulations

In this section, we seek a numerical solution of Eq. 1 to validate our assertion that each of Eqs. 8 and 9 (for the GLS and HS measures, respectively) represents a dispersion relation for harmonic generation. We use a spectral method in conjunction with an efficient explicit time-stepping method to obtain the response as a function of position and time. Afterward, a discrete Fourier transform is performed on the simulated space-time field to reveal the spectrum of the emerging harmonics and compare their distribution in the frequency–wave number domain with the analytically derived harmonics dispersion relation (see the Supplementary Materials for details on the numerical approach).

We consider a 1D computational domain and prescribe initially as an “excitation” a spatially harmonic or a solitary wave profile that is characterized by an amplitude B_e and a wave number κ_e. In principle, any arbitrary but well-defined and smooth wave function $\overline{f}(x,0)\in \mathcal{F}$ that is consistent with Eq. 7, which are the conditions used to derive the harmonics dispersion relation, may be used in these simulations. Once a function $\overline{f}(x,0)$ is selected, we set $\overline{u}(x,0)=B_{\mathrm{e}}{\mathrm{\kappa }}_{\mathrm{e}}[1+\overline{f}(x,0)/(B_{\mathrm{e}}{\mathrm{\kappa }}_{\mathrm{e}})]/2$; the “1/2” offset is introduced as a preprocessing step to facilitate direct comparison with theory. The space-time domain is defined by −x* < x ≤ x* (large enough to allow an unbalanced nonlinear wave to fully evolve up to the point of breaking) with a grid spacing of h = 1 cm and 0 ≤ t ≤ τ_S with a constant time step of Δt = 1 μs.

First, we examine a simple cosine wave profile [for which $\overline{f}(x,t)=B_{\mathrm{e}}{\mathrm{\kappa }}_{\mathrm{e}}\text{cos} ({\mathrm{\kappa }}_{\mathrm{e}}(x-\mathrm{ct}))$] as an excitation signal and apply it to the case of the thin rod with GLS nonlinearity. This wave profile has the form $\overline{u}(x,t)=B_{\mathrm{e}}{\mathrm{\kappa }}_{\mathrm{e}}[1+\text{cos} ({\mathrm{\kappa }}_{\mathrm{e}}(x-\mathit{ct}))]/2$ and is characterized by B_e = 0.0125 and κ_e = 4.5. We prescribe this $\overline{u}$ field along the entire computational domain at initial time t = t₀ = 0 and let the simulation run freely afterward. Periodic boundary conditions are applied for all simulations involving a cosine signal excitation; otherwise, when a localized excitation is prescribed, the simulations are not allowed to run beyond the time when boundary reflections occur. A time snapshot of the simulated motion is plotted in Fig. 1A, showing a clear distortion of the wave profile after some traveling time. This distortion is caused by the nonlinear GLS inherently present in the model.

Performing Fourier analysis separately in space and in time on the evolved wave field, on a time window that ends at t = 0.83 ms, indicates the generation of harmonics in both the wave number and frequency domains. The spatial energy spectrum $E_{B_{\mathrm{e}},{\mathrm{\kappa }}_{\mathrm{e}}}^{\mathrm{S}}$ and the temporal energy spectrum $E_{B_{\mathrm{e}},{\mathrm{\kappa }}_{\mathrm{e}}}^{\mathrm{T}}$ are plotted in Fig. 1(B and C, respectively) (the subscripts indicate that the spectrum is associated with a prescribed initial wave with amplitude B_e and wave number κ_e). In Fig. 1D, we show the contour of $E_{B_{\mathrm{e}},{\mathrm{\kappa }}_{\mathrm{e}}}^{\text{ST}}=\text{ln}\mid {\mathcal{E}}_{B_{\mathrm{e}},{\mathrm{\kappa }}_{\mathrm{e}}}^{\text{ST}}\mid$, where ${\mathcal{E}}_{B_{\mathrm{e}},{\mathrm{\kappa }}_{\mathrm{e}}}^{\text{ST}}$ is the evolved energy spectrum produced by Fourier analysis in both space and time, noting that the Fourier transformation is always done at a time close to τ_S (see the Supplementary Materials for details of the numerical scheme). The brightened areas in the contour plot represent the harmonics, which are consistent with each of the separately obtained spatial (Fig. 1B) and temporal (Fig. 1C) harmonics. The frequency–versus–wave number distribution of the generated harmonics, as produced by standard direct simulations, accurately coincides with the theoretical harmonics dispersion curve derived in Eq. 8, thus providing firm validation of the theory.

Validation for large wave amplitudes and different types of nonlinearity

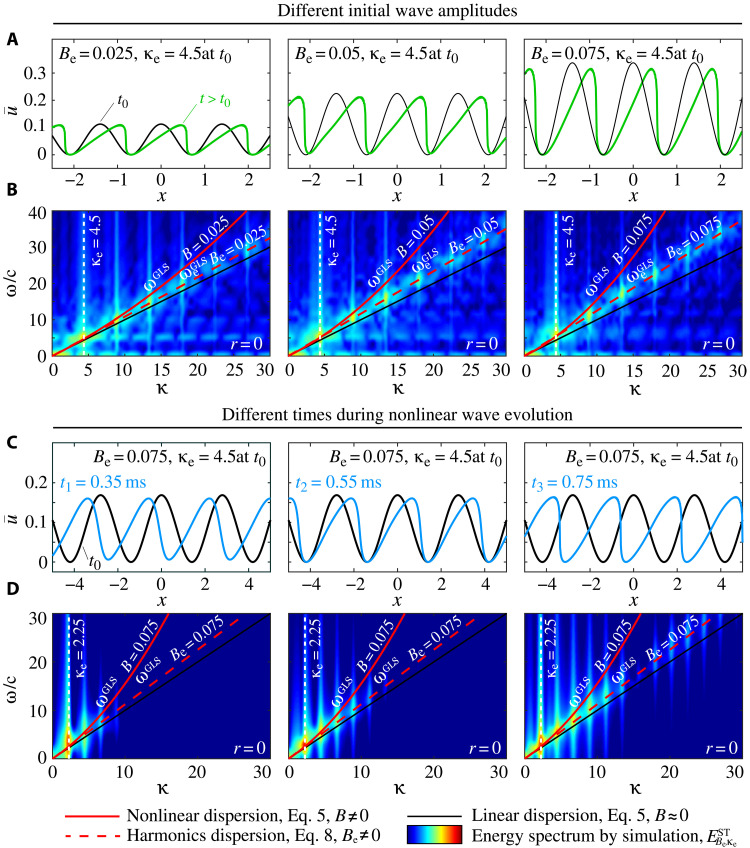
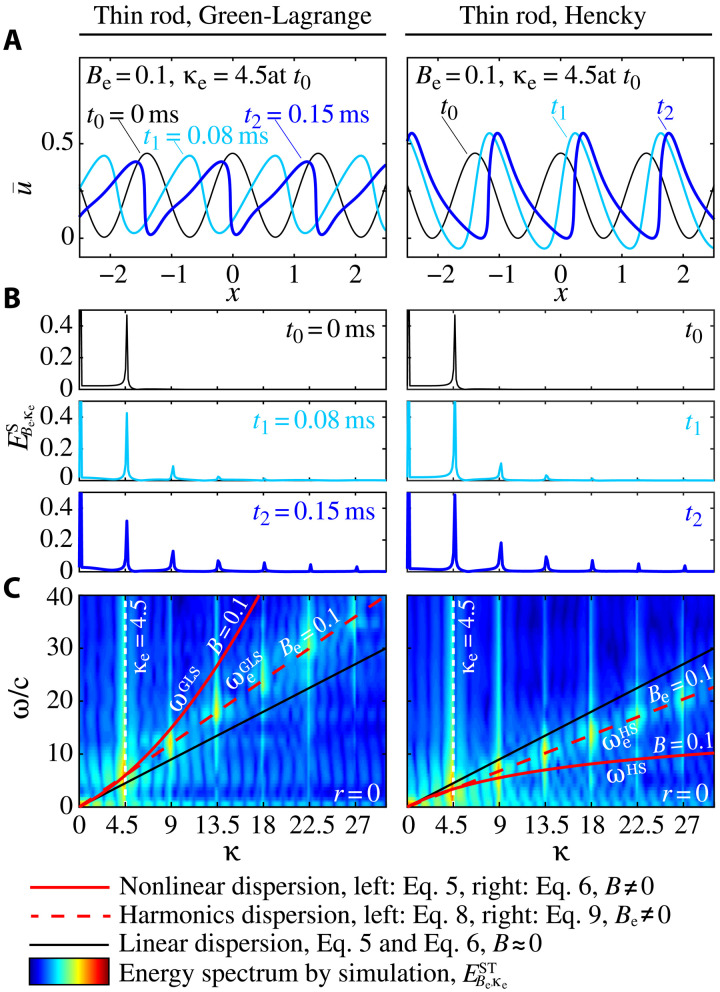
We repeat the simulation of Fig. 1, considering higher amplitudes and also considering both the GLS and HS models. In Fig. 2A, we show the time evolution of the same cosine wave but for initial amplitudes B_e = 0.025, 0.05, and 0.075, and, in Fig. 2B, provide the corresponding energy spectra in the frequency–wave number domain. For all cases, the harmonics dispersion relation of Eq. 8 perfectly predicts the distribution of the harmonics. In Fig. 3, we extend the excitation signal amplitude further to a value of B_e = 0.1 and, once again, show perfect prediction. A wave with an initial amplitude of B_e = 0.1 is considered strongly nonlinear; this is evident from the significant deviation of the general NDR curve for B = 0.1 compared to the infinitesimal dispersion relation. The validation is successful not only for the GLS model (which exhibits a hardening nonlinearity) but also for the HS model (which exhibits a softening nonlinearity), thus demonstrating generality of the theory to different types of nonlinearities.

Fig. 2. Validation of theory for large wave amplitudes and at different times during wave evolution.

Top two panels: Validation of the harmonics dispersion relation of Eq. 8 for nonlinear cosine waves of various prescribed amplitudes: B_e = 0.025, 0.05, and 0.075. (A) Spatial profile experiencing distortion (steepening) after some evolution in time. (B) Corresponding frequency–wave number spectra of harmonics. All results are based on the GLS measure. Bottom two panels: Validation of the harmonics dispersion relation of Eq. 8 for a nonlinear cosine wave at different stages of evolution, considering the following times during the simulation: t₁ = 0.35 ms, t₂ = 0.55 ms, and t₃ = 0.75 ms. (C) Spatial profile experiencing progressive distortion (steepening). (D) Corresponding frequency–wave number spectra of harmonics. All results are based on the GLS measure.

Fig. 3. Validation of theory for different types of nonlinearity.

Strongly nonlinear cosine wave experiencing progressive distortion (steepening) and harmonic generation, considering both the GLS and HS models: (A) spatial profiles captured at three different times, (B) corresponding wave number spectra, and (C) frequency–wave number spectrum of harmonics at a highly evolved state demonstrating precise prediction by the harmonics dispersion relations of Eqs. 8 and 9, respectively. The spike at zero frequency in (B) is an artifact of the numerical Fourier transform.

Validation throughout wave evolution

Now, we consider the validity of the harmonics dispersion relation at different stages of evolution of a nonlinear wave. We refer again to Fig. 3 where, in Fig. 3A, we show the initial cosine signal corresponding to B_e = 0.1 and κ_e = 4.5 and overlay two subsequent time snapshots of the simulated motion. Performing Fourier analysis in space on the wave profile at the time of excitation t₀ and at the two time instants t₁ and t₂ elucidates the nature of the temporal evolution of the wave number spectrum. At t₀, only a single harmonic exists (which is of the cosine excitation signal). As the wave evolves, the nonlinear effects increasingly cause distortion and generation of more energized higher harmonics, as shown in Fig. 3B. It is noticeable, however, that the wave number distribution of the harmonics gets established early in the simulation and is sustained as the evolution progresses. To investigate this aspect of harmonic generation further, we consider, in Fig. 2 (C and D), the same problem but for a slightly smaller excitation amplitude, B_e = 0.075. Figure 2C displays the spatial distortion at three different time instants, t₁ = 0.35 ms, t₂ = 0.55 ms, and t₃ = 0.75 ms. The corresponding spectral response is shown in Fig. 2D. Once again, the distribution is shown to get established at an early stage and sustain itself throughout the evolution; now, we see this to be the case in the frequency–wave number domain representing a state of spatiotemporal spectral invariance. These results confirm that the harmonics dispersion relation of Eq. 8 is applicable at all times during the nonlinear evolution as long as the wave remains stable.

Validation for linearly dispersive models

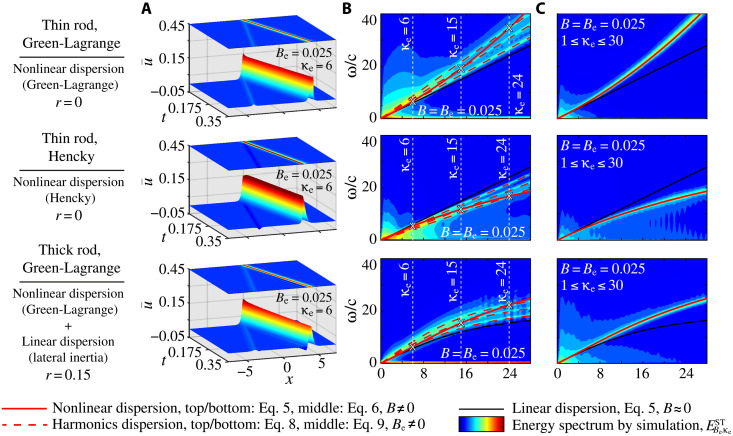
We also consider a thick rod under the GLS measure and propagate the same cosine excitation but now characterized by B_e = 0.05 and κ_e = 4.5 with various rod thicknesses. Unlike conventional techniques such as the method of characteristics that fall short in the presence of linear dispersion (52), our theory predicts the harmonic generation frequency–wave number spectrum even for systems that are linearly dispersive (e.g., r ≠ 0), as is shown in Fig. 4. We observe that for all r ≠ 0 cases (Fig. 4, C to E), the harmonics dispersion relation exhibits dispersion, indicating a nonlinear softening trend for the generated harmonics in line with the dispersive nature stemming from lateral inertia.

Fig. 4. Validation of theory for linearly dispersive models.

Harmonics dispersion relation predicts harmonics generated by direct simulations for both linearly nondispersive (r = 0) and linearly dispersive (r ≠ 0) rods: (A) effect of lateral inertia on the general NDR and (B to E) frequency–wave number spectra of harmonics with general NDR and harmonics dispersion relation for each case overlaid. Near balance of linear and nonlinear dispersion is demonstrated in (D). All results are based on the GLS measure, and a cosine wave is prescribed as an initial condition in the simulations.

Validation for different initial wave profiles

Next, we simulate the nonlinear wave propagation of a localized pulse defined by a hyperbolic secant function, $\overline{f}(x,t)=B_{\mathrm{e}}{\mathrm{\kappa }}_{\mathrm{e}}\text{sech}({\mathrm{\kappa }}_{\mathrm{e}}(x-\mathit{ct}))$. We apply $\overline{u}(x,t)=B_{\mathrm{e}}{\mathrm{\kappa }}_{\mathrm{e}}[1+\text{sech}({\mathrm{\kappa }}_{\mathrm{e}}(x-\mathit{ct}))]/2$, which is consistent with Eqs. 4 and 7, as the initial waveform at t = 0. Figure 5A shows the results for B_e = 0.025 and κ_e = 6. The initial wave packet propagates along the positive direction; also observed is a characteristic trailing wave of modest amplitude radiating in the opposite direction of the traveling wave. The spatial profile of the waves feature the eventual formation of shocks at the leading and trailing edges of the wave packet for the GLS and HS measures, respectively, in analogy with the behavior observed in Fig. 3A and analyzed further in the Supplementary Materials and fig. S1. In Fig. 5B, we consider excitations at two more κ_e values and superpose the Fourier-transformed spectra for all three cases. It is seen that the analytical harmonics dispersion curves predict with full conformity the distribution of the harmonics for each of the excitations, including in the linearly dispersive case shown in the bottom panel. Note that since the hyperbolic secant function has a rich frequency content, the excited energy spectrum for each of the three cases displayed in Fig. 5B conforms continuously to the harmonics dispersion relations plotted in dashed red; this is in contrast to the cosine wave profile cases where the spectrum comprises discrete energy spots. Furthermore, the set of the intersections of each harmonics dispersion curve with its corresponding κ_e value exactly follows the path of the general NDR plotted in solid red. We learn from this perfect matching of intersections that the general NDR curve traces the fundamental harmonic associated with each excitation wave number (for a given value of B_e). This characteristic is confirmed further in Fig. 5C by superimposing the energy spectra of 30 separate simulations for distinct initial wave packets sharing the same amplitude B_e = 0.025 but covering the range of excitation wave numbers κ_e = 1 to 30, with increments of 1. Here, the quantity plotted is ${\sum }_{{\mathrm{\kappa }}_{\mathrm{e}}}{E}_{B_{\mathrm{e}},{\mathrm{\kappa }}_{\mathrm{e}}}^{\text{ST}}={\sum }_{{\mathrm{\kappa }}_{\mathrm{e}}}[\text{ln}\mid {\mathcal{E}}_{B_{\mathrm{e}},{\mathrm{\kappa }}_{\mathrm{e}}}^{\text{ST}}\mid ]$, shown as a superposition of windows of energy spectra around the fundamental harmonic where each corresponds to a particular value of κ_e. The correlation of an NDR with a superposition of the fundamental harmonic frequencies discretely identified from the Fourier spectra corresponding to multiple wave number excitations, from separate simulations, was demonstrated in (53).

Fig. 5. Validation of theory for localized nonlinear waves and demonstration of the connection between harmonics dispersion relation and general NDR.

(A) Space-time numerical simulation of a large-amplitude hyperbolic secant wave profile. (B) Frequency–wave number spectra showing distribution of harmonics in evolved field. The intersections of the harmonics dispersion relations (dashed red curves) for three distinct excitation wave numbers are shown to coincide with the general NDR for the selected value of wave amplitude. (C) Superposition of harmonics spectra from 30 distinct simulations covering a range of excitation wave numbers is shown to match with full conformity with the general NDR for the selected value of wave amplitude. Different cases are considered in each of the top, middle, and bottom panels.

The results of Fig. 5 (B and C) confirm that our derived NDR and harmonics dispersion relation hold for arbitrary excitation profiles such as the hyperbolic secant function considered, as long as the excitation signal is initially characterized by B_e and κ_e and is consistent with Eqs. 4 and 7. Two more examples of different initial wave profiles, namely, a Gaussian profile and a Lorentzian profile, are examined in the Supplementary Materials and are shown to be also accurately characterized by the NDR and harmonics dispersion relation.

Soliton synthesis by general NDR

Solitons research traces back to its first observation in a canal by J. S. Russell (54) and key early theoretical developments that followed (55, 56). Other than their solitary spatial profile, a unique aspect of this class of waves is their inherent stability which is commonly attributed to a balance between nonlinear and dispersion effects (52). Using the general NDR, we are able to find a condition for balance between hardening dispersion (stemming from the nonlinear kinematics) and softening dispersion (stemming from the linear lateral inertia). This represents a formal approach for the analysis, characterization, and engineering of solitons. This approach has been presented recently by the authors in the context of 1D periodic rods (57). For a thick rod, we formulate the soliton synthesis condition as

$$r=\text{arg min}\{{\Vert {\mathrm{\omega }}_{\text{GLS}}/c-\mathrm{\alpha }B\mathrm{\kappa }\Vert }_{[0,1]}/\underset{[0,1]}{\text{max}}({\mathrm{\omega }}_{\text{GLS}}/c)\le 1\%,\mathrm{\alpha }\in \mathbb{R}\}$$ (10)

which gives an optimal value of r = 0.166 for B = 0.05. These values generate a linear-nonlinear dispersion balance within 1% error for the range 0 ≤ Bκ ≤ 1, which is the case displayed in Fig. 4D, where the general NDR appears nearly as a perfect linear (straight) curve. The harmonic generation of this nearly balanced wave is dispersive. Thus, while minimum dispersion in the general NDR is needed for the creation of a soliton (with some error tolerance for a given Bκ range), the associated harmonic generation spectrum is not necessarily nondispersive. Figure 6A decomposes the balancing components in the general NDR, and Fig. 6 (B to D) illustrates the effect in the spatial domain showing, in Fig. 6C, the stable and nearly invariant propagation of a synthesized soliton. Future work may extend this soliton synthesis concept to more complex models, for example, rods/beams with varying cross section (58, 59) or prestretch (60), to name a few.

Fig. 6. Illustration of soliton synthesis in a thick rod.

(A) Balance of hardening (nonlinear) dispersion with softening (linear) dispersion. The solid black curves represent an initial hyperbolic secant wave; the corresponding colored curves represent the evolved wave profile for (B) nonlinear dispersion, (C) nearly balanced dispersion (soliton), and (D) linear dispersion.

DISCUSSION

We have provided a unified theory of nonlinear waves consisting of a general NDR and a harmonics dispersion relation, where the former encompasses the latter. A general NDR defines, (i) for a given amplitude B and wave number κ, the instantaneous dispersion of a nonlinear wave (8) and, (ii) for a given excitation amplitude B_e, the frequency–wave number trajectory of the fundamental harmonic in a superposition of isolated windows of Fourier-transformed nonlinear wave fields spanning a range of excitation wave numbers κ_e. Prescription of a condition for soliton synthesis is a natural outcome of the general NDR, as demonstrated in Figs. 4 (A and D) and 6 (A and C). A harmonics dispersion relation, which is a novel concept, defines the frequency–wave number spectrum of the generated harmonics in a nonlinear wave field for a given excitation amplitude B_e and wave number κ_e. This relation effectively unravels the inner makings of a nonlinear wave. It is derived directly from the governing nonlinear PDE; thus, it provides a pathway for prediction of the spectral content of harmonic generation without knowledge of the time-dependent spatial solution or any treatment of the problem in the spatial-temporal domain. The HDR is shown to be a special case of the general NDR by comparing Eqs. 8 and 9 to 5 and 6. This connection establishes a fundamental unification of two key tenets of wave propagation: nonlinear dispersion and harmonic generation. Both relations are derived exactly (i.e., without any expansions or perturbation analysis).

As shown in the diverse sets of examples given, considering thin and thick elastic rods, there is no limitation by the type and strength of the nonlinearity, or by the shape of the initial wave profile provided that it belongs to the family of functions F. There is also no restriction on the presence of linear dispersion. The derived relations are applicable at any state of evolution in time as long as the wave is balanced or has not yet reached its breaking point if unbalanced. These findings underscore the nature of general nonlinear dispersion and harmonic generation dispersion as time-independent characteristics of the medium and its wave propagation properties, for a given amplitude and a given class of initial profiles for the evolving or balanced waveform.

Given that the theory at its foundation is based on the introduction of the traveling wave conditions of Eqs. 4 and 7, it is, in principle, agnostic to the type of wave considered. It is therefore applicable to other disciplines of wave propagation beyond elastic waves, as well as being amenable to extension to multidimensional problems.

MATERIALS AND METHODS

The numerical results presented in this study were obtained using an in-house code; see details in the Supplementary Materials. The material properties considered are for aluminum: ρ = 2700 kg/m³, E = 70 GPa, and ν = 0.33. All reported units are in the SI system.

Supplementary Materials

This PDF file includes:

Supplementary Text

Figs. S1 to S3

Table S1

Legends for movies S1 and S2

References

Other Supplementary Material for this manuscript includes the following:

Movies S1 and S2