Abstract
Objectives
Heart failure (HF) is a common disease with a high hospital readmission rate. This study considered class imbalance and missing data, which are two common issues in medical data. The current study’s main goal was to compare the performance of six machine learning (ML) methods for predicting hospital readmission in HF patients.
Methods
In this retrospective cohort study, information of 1,856 HF patients was analyzed. These patients were hospitalized in Farshchian Heart Center in Hamadan Province in Western Iran, from October 2015 to July 2019. The support vector machine (SVM), least-square SVM (LS-SVM), bagging, random forest (RF), AdaBoost, and naïve Bayes (NB) methods were used to predict hospital readmission. These methods’ performance was evaluated using sensitivity, specificity, positive predictive value, negative predictive value, and accuracy. Two imputation methods were also used to deal with missing data.
Results
Of the 1,856 HF patients, 29.9% had at least one hospital readmission. Among the ML methods, LS-SVM performed the worst, with accuracy in the range of 0.57–0.60, while RF performed the best, with the highest accuracy (range, 0.90–0.91). Other ML methods showed relatively good performance, with accuracy exceeding 0.84 in the test datasets. Furthermore, the performance of the SVM and LS-SVM methods in terms of accuracy was higher with the multiple imputation method than with the median imputation method.
Conclusions
This study showed that RF performed better, in terms of accuracy, than other methods for predicting hospital readmission in HF patients.
Keywords: Patient Readmission, Heart Failure, Machine Learning, Classification, Data Analysis
I. Introduction
Heart failure (HF) is a common, chronic, and complex clinical syndrome that significantly diminishes quality of life [1]. The lifetime risk of HF through the ages of 45–95 years is 20% to 45% [2]. More than 37 million people around the world suffer from HF [3]; however, the prevalence of HF varies worldwide. The American Heart Association estimated that the HF prevalence is between 1.26% to 6.7% [4], with the expectation that it will increase by 32% from 2012 to 2030 [5]. In Iran, its prevalence has been reported to be high (8%) [6]. According to the World Health Organization, the annual incidence of HF is estimated to be 660,000 per year worldwide, and this figure is expected to double in the next 30 years [7]. According to previous studies, the HF incidence in Iran is higher than in other Asian countries [8].
Furthermore, HF is a common cause of hospitalization in the adult and elderly population [9]. The annual readmission rate due to HF is quite high, at 56.6% [10]. Approximately 30% of patients experience readmission 30 to 60 days after discharge [11]. Hospital readmission imposes high economic costs for both patients and the healthcare system, and this issue therefore needs more attention due to its negative impacts on healthcare systems’ costs [12].
In the past decade, several machine learning (ML) methods, such as the support vector machine (SVM), least-square SVM (LS-SVM), bagging, random forest (RF), AdaBoost, and naïve Bayes (NB) methods, have been widely applied for the management of cardiovascular diseases. SVM and LS-SVM are kernel-based learning methods that are widely employed for classification and regression problems. These methods have an outstanding capability to solve nonlinear and high-dimensional problems [13,14]. Bagging, RF, and AdaBoost are ensemble learning methods that achieve better learning performance by aggregating several weak learners [14,15]. These ML methods can improve predictions by utilizing higher-dimensional, complex, and nonlinear relationships between variables [16]. These methods also have been used to predict hospital readmission in various studies [5,16–18]. For instance, Lorenzoni et al. [18] compared the performance of eight ML methods to predict hospitalization in HF patients. Their results showed that the generalized linear model net had the best performance. Similarly, Landicho et al. [5] used four ML methods to predict readmission in HF patients. According to their results, SVM had the best performance.
One of the major problems in ML methods for classification is the class imbalance issue. This issue is common in medical data and leads to the poor classification of minority classes. Several methods have been developed to address class imbalance. Among them, the Synthetic Minority Over-Sampling Technique (SMOTE) is a widely used method that was proposed by Chawla et al. [19]. Another common issue in medical research is missing data. There are three types of missing data: missing completely at random (MCAR), missing at random, and missing not at random. If missingness is completely random (i.e., MCAR), it can be ignored [20]; otherwise, removing incomplete data may lead to bias and reduce the power of ML methods [20,21]. To overcome this problem, imputation methods such as median, mean, and multiple imputations can be used [5,18].
ML methods are nonparametric methods that require no distributional assumptions. These methods consider complex and nonlinear relationships among variables. Previous studies have shown positive performance of ML methods in prediction and classification problems [13–15]. However, the performance of these methods is data-dependent, and no single method is always is the best for classification problems [14]. Meanwhile, despite the considerable number of studies in the field of predicting hospital readmission in HF patients, only a few of them have been performed in Iran [8,22]. Hospital readmission not only reduces the quality of life, but also increases medical costs. Therefore, with the increasing prevalence of HF and related readmission worldwide, it is essential to identify HF patients at a higher risk of readmission in order to manage these patients better [12]. Furthermore, in developing countries such as Iran, hospital readmission problems are exacerbated by resource limitations [23]. Hence, this study’s main goal was to compare the performance of six ML methods for predicting hospital readmission in HF patients and to find the best method for our data.
II. Methods
1. Data Collection and Preparation
In this retrospective cohort study, information on 1,856 HF patients was analyzed. These patients were hospitalized in Farshchian Heart Center in Hamadan Province from October 2015 to July 2019. This center is the referral heart center in Hamadan Province in Western Iran. Data were extracted from hospital records using a checklist of items according to the context of the patients’ records and clinical examinations performed by cardiologists. The checklist included data on demographic variables, vital signs, past medical history, and laboratory tests. We extracted all available variables in patients’ records and considered them all. There was a total of 46 variables. The continuous variables were normalized. The outcome was hospital readmission during the follow-up period. The SMOTE method was used for handling the imbalanced dataset problem. This study was approved by the Institutional Review Board of Hamadan University of Medical Sciences (No. IR.UMSHA.REC.1398.276). All patients were informed of the purpose of the study and informed written consent was obtained from all of them.
2. Missing Data
The data used in this study suffered from data missingness, although it should be noted that data were only missing for continuous variables. Hence, two imputation methods were used to deal with missing data: (1) missing values were imputed with the median (median imputation method) and (2) multiple imputations were used (multiple imputation method). Little’s MCAR test was performed to evaluate MCAR.
3. Machine Learning Methods
SVM was proposed by Vapnik [13]. This method tries to construct an optimal hyperplane that separates data points based on their classes. When observations are not linearly separable, SVM converts nonlinear input to a linear state in high-dimensional feature space using a kernel function. The radial basis kernel function was utilized in this study due to its excellent performance. LS-SVM was applied by Tapak et al. [14], such that LS-SVM uses a set of linear equations instead of a quadratic programming problem in the dual space. Further information about the SVM and LS-SVM methods can be found elsewhere in the literature [13,14].
Bagging, one of the earliest ensemble methods, was proposed by Leo Breiman [14]. This method utilizes bootstrap sampling, which involves forming training subsets by randomly resampling the training dataset. A separate classifier-based model is used to train each of the subsets. Then, all classifier-based models are aggregated into the final model [14]. RF is a modification to bagging developed by Leo Breiman and his colleagues [15]. This method fits the number of decision tree classifiers on subsamples of the dataset. The averaging method is then applied to control overfitting and increase accuracy [15]. AdaBoost is one of the first boosting algorithms that was proposed by Yoav Freund and Robert E. Schapire [15]. This method generates a subset of the training dataset and constructs an initial classifier-based model with equal weights assigned for instances. Then, in each boosting iteration, the training instances are reweighted so that the next learner concentrates on the instances that were misclassified previously. The final model is obtained based on a weighted sum of all the classifier-based models [15]. Further details about the bagging, RF, and AdaBoost methods can be found in the above-mentioned references [14,15].
NB is a probabilistic classifier based on Bayes’ theorem with strong independence assumptions between every pair of variables. This assumption is difficult to satisfy in the real world, so it is characterized as “naive.” However, NB performs well, even when the independence assumption is violated [24].
4. Performance Criteria
The discrimination ability of ML methods was assessed using several criteria, including sensitivity, specificity, positive predictive value (PPV), negative predictive value (NPV), and accuracy. The performance of each method was assessed using a cross-validation approach, in which the dataset was randomly divided into training (70%) and test (30%) sets. This procedure was repeated 100 times, and the average values for evaluation criteria were computed.
5. Software Packages
Statistical analysis was performed using R version 3.6.3, with the following packages: “e1071” for SVM; “kernlab” for LS-SVM; “adabag” for bagging, RF, and AdaBoost; “naivebayes” for NB; “randomForest” for variable importance (VIMP) in the RF; “naniar” for the Little MCAR test; and “DMwR” for balancing the dataset.
III. Results
Of the 1,856 HF patients, 542 (29.9%) had at least one hospital readmission. The mean age of these patients was 71.7 ± 13.4 years. The majority of them (64.4%) were men. More than half (57.0%) of the hospital-readmitted patients had a history of hypertension. The characteristics of the HF patients are given in Tables 1 and 2.
Table 1.
Clinical characteristics of heart failure patients
| Variable | Hospital readmission | |||||
|---|---|---|---|---|---|---|
| No (n = 1,314) | Yes (n = 542) | |||||
| Median | Min–Max | Mean ± SD | Median | Min–Max | Mean ± SD | |
| Age (yr) | 76.0 | 22.0–97.0 | 74.0 ± 13.5 | 73.0 | 27.0–97.0 | 71.7 ± 13.4 |
| BMI (kg/m2) | 25.3 | 14.3–53.3 | 25.8 ± 5.1 | 25.0 | 13.8–47.3 | 25.8 ± 4.9 |
| Ejection fraction (%) | 25.0 | 10.0–55.0 | 26.4 ± 10.9 | 20.0 | 10.0–50.0 | 22.8 ± 10.1 |
| SBP (mmHg) | 121.0 | 67.0–220.0 | 125.4 ± 24.4 | 125.0 | 70.0–220.0 | 126.0 ± 24.1 |
| DBP (mmHg) | 80.0 | 40.0–137.0 | 77.9 ± 15.6 | 80.0 | 44.0–140.0 | 78.1 ± 15.1 |
| FBS (mg/dL) | 98.5 | 38.0–455.0 | 113.3 ± 51.2 | 97.0 | 31.0–453.0 | 112.6 ± 53.0 |
| BUN (mg/dL) | 23.0 | 10.0–127.5 | 26.5 ± 13.6 | 24.0 | 11.5–95.0 | 27.2 ± 12.1 |
| Creatinine (mg/dL) | 1.3 | 0.5–10.7 | 1.4 ± 0.8 | 1.3 | 0.7–10.2 | 1.4 ± 0.7 |
| Cholesterol (mg/dL) | 141.0 | 50.0–386.0 | 146.7 ± 43.5 | 135.0 | 30.0–317.0 | 142.3 ± 41.2 |
| Triglycerides (mg/dL) | 103.0 | 25.0–437.0 | 115.3 ± 52.3 | 99.0 | 28.0–358.0 | 110.8 ± 50.5 |
| HDL (mg/dL) | 36.0 | 20.0–85.0 | 38.0 ± 9.7 | 38.0 | 20.0–74.0 | 38.8 ± 9.8 |
| LDL (mg/dL) | 81.0 | 24.0–313.0 | 86.7 ± 32.9 | 80.0 | 26.0–382.0 | 84.2 ± 32.7 |
| CK-MB (U/L) | 22.0 | 2.0–980.0 | 34.5 ± 57.6 | 22.0 | 7.0–1089.0 | 32.5 ± 60.3 |
| Sodium (Na) (mmol/L) | 139.5 | 116.0–164.5 | 139.1 ± 4.0 | 140.0 | 121.5–148.0 | 139.6 ± 3.7 |
| Potassium (K) (mmol/L) | 4.2 | 2.9–7.3 | 4.2 ± 0.5 | 4.2 | 2.7–6.6 | 4.2 ± 0.4 |
| WBC (×109/L) | 7.6 | 2.5–23.6 | 8.1 ± 2.9 | 7.4 | 2.4–20.9 | 7.9 ± 2.7 |
| RBC (×109/L) | 4.6 | 2.6–8.4 | 4.6 ± 0.7 | 4.6 | 2.7–7.5 | 4.7 ± 0.7 |
| Hemoglobin (Hb) (g/dL) | 13.6 | 6.0–19.9 | 13.5 ± 2.1 | 13.7 | 8.1–19.8 | 13.7 ± 2.1 |
| Hct (%) | 41.8 | 19.7–63.3 | 41.8 ± 6.0 | 41.8 | 25.2–62.8 | 42.3 ± 5.9 |
| RDW (%) | 14.5 | 11.5–24.6 | 14.9 ± 2.0 | 14.5 | 11.8–23.6 | 15.0 ± 2.0 |
| Platelet (×103/μL) | 188.0 | 40.0–573.0 | 197.1 ± 69.5 | 185.0 | 50.0–578.0 | 198.3 ± 71.9 |
| MCV (fL) | 90.1 | 58.3–118.1 | 89.4 ± 7.1 | 90.9 | 62.3–112.3 | 90.3 ± 6.9 |
| MCH (pg) | 29.3 | 16.4–43.1 | 29.0 ± 2.9 | 29.6 | 17.8–37.7 | 29.2 ± 2.9 |
| MCHC (g/dL) | 32.4 | 25.9–43.5 | 32.3 ± 1.6 | 32.4 | 26.2–36.3 | 32.3 ± 1.6 |
| PT (s) | 13.2 | 12.0–36.0 | 14.4 ± 3.5 | 13.3 | 12.0–36.0 | 14.4 ± 3.4 |
| INR | 1.1 | 1.0–10.5 | 1.3 ± 0.7 | 1.1 | 1.0–6.5 | 1.3 ± 0.6 |
| PTT (s) | 27.0 | 20.0–120.0 | 29.5 ± 9.5 | 27.0 | 20.5–120.0 | 29.6 ± 10.0 |
BMI: body mass index, SBP: systolic blood pressure, DBP: diastolic blood pressure, FBS: fasting blood glucose, BUN: blood urea nitrogen, HDL: high-density lipoprotein, LDL: low-density lipoprotein, CK-MB: creatine kinase-MB, WBC, white blood cell, RBC: red blood cell, RDW: red cell distribution width, Hct: hematocrit, MCV: mean corpuscular volume, MCH: mean corpuscular hemoglobin, MCHC: mean corpuscular hemoglobin concentration, PT: prothrombin time, INR: international normalized ratio, PTT: partial thromboplastin time, SD, standard deviation.
Table 2.
Baseline characteristics of heart failure patients
| Hospital readmission | ||
|---|---|---|
| No (n = 1,314) | Yes (n = 542) | |
| Hospital departments (ward) | 803 (61.1) | 356 (65.7) |
| Sex (male) | 742 (56.5) | 350 (64.4) |
| History of diabetes (yes) | 377 (28.7) | 158 (29.2) |
| History of hypertension (yes) | 780 (59.4) | 309 (57.0) |
| History of blood lipids (yes) | 152 (11.6) | 52 (9.6) |
| Smoking (yes) | 175 (13.3) | 113 (20.8) |
| Substance abuse (yes) | 179 (13.6) | 99 (18.3) |
| History of MI (yes) | 57 (4.3) | 41 (7.6) |
| Family history of HF (yes) | 59 (4.5) | 40 (7.4) |
| History of stroke (yes) | 65 (4.9) | 21 (3.9) |
| COPD (yes) | 57 (4.3) | 34 (6.3) |
| Thyroid disease (yes) | 75 (5.7) | 29 (5.4) |
| Respiratory disease (yes) | 142 (10.8) | 65 (12.0) |
| Kidney disease (yes) | 143 (10.9) | 61 (11.3) |
| CABG (yes) | 128 (9.7) | 79 (14.6) |
| CAG (yes) | 125 (9.5) | 60 (11.1) |
Values are presented as number (%).
MI: myocardial infarction, HF: heart failure, COPD: chronic obstructive pulmonary disease, CABG: coronary artery bypass graft, CAG: coronary angiography.
Overall, 937 (50.48%) patients had missing data for at least one variable. The most common variable with missing data was ejection fraction (25.59%), followed in descending order by body mass index (19.39%), and creatine kinase-MB (CK-MB) (10.82%). The percentages of missing laboratory test variables were roughly 0.1% to 8%. No other variables had missing data. The results of Little’s MCAR test showed a significance value of less than 0.05, meaning that the missing data were not MCAR.
Tables 3 and 4 show the discriminative ability of the six ML methods for predicting hospital readmission in HF patients with two imputation methods for missing data. The performance of the LS-SVM method, in terms of specificity, PPV, NPV, and accuracy, was higher with the multiple imputation method than with the median imputation method. With the median imputation method, the specificity of SVM was similar to that of RF (0.95). Bagging had the highest specificity among the ML methods (0.96). Bagging and LS-SVM had the lowest and highest sensitivity, respectively. The mean PPV of the ML methods ranged between 0.27 to 0.78 for the test sets, with the lowest and highest values belonging to LS-SVM and RF, respectively. Furthermore, the mean NPV of all ML methods was greater than 0.90. RF outperformed the other ML methods in terms of accuracy (Table 3). Moreover, with the multiple imputation method, SVM and RF had the highest accuracy (Table 4).
Table 3.
Performance criteria of machine learning methods using the median imputation method
| Methods | Set | Sensitivity | Specificity | PPV | NPV | Accuracy |
|---|---|---|---|---|---|---|
| SVM | Train | 0.66 (0.010) | 0.99 (0.001) | 0.98 (0.007) | 0.93 (0.001) | 0.94 (0.001) |
| Test | 0.62 (0.016) | 0.95 (0.011) | 0.75 (0.049) | 0.92 (0.005) | 0.89 (0.009) | |
| LS-SVM | Train | 0.87 (0.008) | 0.53 (0.070) | 0.28 (0.027) | 0.95 (0.005) | 0.59 (0.057) |
| Test | 0.86 (0.015) | 0.51 (0.073) | 0.27 (0.032) | 0.94 (0.007) | 0.57 (0.059) | |
| Bagging | Train | 0.54 (0.017) | 0.99 (0.001) | 0.95 (0.015) | 0.91 (0.003) | 0.91 (0.003) |
| Test | 0.52 (0.021) | 0.96 (0.011) | 0.75 (0.060) | 0.90 (0.006) | 0.88 (0.009) | |
| AdaBoost | Train | 1.00 (0) | 1.00 (0) | 1.00 (0) | 1.00 (0) | 1.00 (0) |
| Test | 0.85 (0.012) | 0.87 (0.020) | 0.58 (0.044) | 0.96 (0.003) | 0.86 (0.016) | |
| RF | Train | 0.81 (0.008) | 1.00 (0) | 1.00 (0) | 0.96 (0.001) | 0.97 (0.001) |
| Test | 0.72 (0.016) | 0.95 (0.011) | 0.78 (0.047) | 0.94 (0.004) | 0.91 (0.009) | |
| NB | Train | 0.67 (0.007) | 0.96 (0.004) | 0.77 (0.020) | 0.93 (0.001) | 0.91 (0.004) |
| Test | 0.64 (0.017) | 0.93 (0.011) | 0.66 (0.041) | 0.92 (0.004) | 0.88 (0.009) |
The number in parenthesis denotes standard deviation.
PPV: positive predicted value, NPV: negative predicted value; SVM: support vector machine, LS-SVM: least-square support vector machine, RF: random forest, NB: naïve Bayes.
Table 4.
Performance criteria of machine learning methods using the multiple imputation method
| Methods | Set | Sensitivity | Specificity | PPV | NPV | Accuracy |
|---|---|---|---|---|---|---|
| SVM | Train | 0.66 (0.010) | 0.99 (0.001) | 0.98 (0.006) | 0.93 (0.001) | 0.94 (0.001) |
| Test | 0.62 (0.017) | 0.95 (0.011) | 0.75 (0.052) | 0.92 (0.004) | 0.90 (0.008) | |
| LS-SVM | Train | 0.87 (0.009) | 0.55 (0.061) | 0.29 (0.026) | 0.95 (0.004) | 0.60 (0.049) |
| Test | 0.86 (0.015) | 0.54 (0.060) | 0.28 (0.028) | 0.95 (0.005) | 0.60 (0.049) | |
| Bagging | Train | 0.48 (0.024) | 0.99 (0.001) | 0.95 (0.016) | 0.90 (0.004) | 0.90 (0.004) |
| Test | 0.46 (0.027) | 0.95 (0.014) | 0.69 (0.066) | 0.89 (0.006) | 0.87 (0.010) | |
| AdaBoost | Train | 1.00 (0) | 1.00 (0) | 1.00 (0) | 1.00 (0) | 1.00 (0) |
| Test | 0.84 (0.012) | 0.84 (0.021) | 0.54 (0.039) | 0.96 (0.003) | 0.84 (0.017) | |
| RF | Train | 0.80 (0.009) | 1.00 (0) | 1.00 (0) | 0.96 (0.001) | 0.96 (0.001) |
| Test | 0.69 (0.018) | 0.94 (0.013) | 0.73 (0.051) | 0.93 (0.004) | 0.90 (0.010) | |
| NB | Train | 0.69 (0.008) | 0.94 (0.005) | 0.71 (0.019) | 0.93 (0.001) | 0.89 (0.004) |
| Test | 0.66 (0.017) | 0.90 (0.018) | 0.59 (0.046) | 0.92 (0.004) | 0.86 (0.014) |
The number in parenthesis denotes standard deviation.
PPV: positive predicted value, NPV: negative predicted value; SVM: support vector machine, LS-SVM: least-square support vector machine, RF: random forest, NB: naïve Bayes.
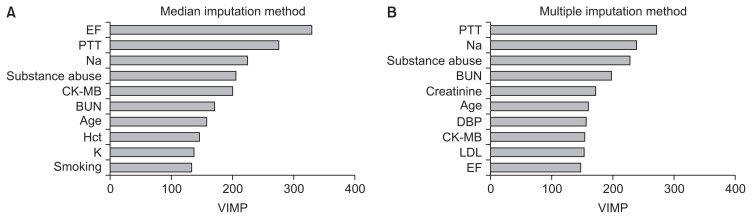
Figure 1 displays the top 10 VIMPs obtained from RF using both imputation methods for missing data. Ejection fraction, prothrombin time (PTT), and sodium were found to be the three most important variables for predicting hospital readmission in HF patients with the median imputation method (Figure 1A). Using the multiple imputation approach, the highest VIMP for RF was PTT (Figure 1B). Ejection fraction, PTT, sodium, substance abuse, CK-MB, blood urea nitrogen (BUN), and age were similarly important variables using both imputation methods.
Figure 1.
Top 10 variable importance (VIMP) values for predicting hospital readmission in heart failure patients using two imputation methods for missing data: (A) median imputation method and (B) multiple imputation method. EF: ejection fraction, PTT: partial thromboplastin time, CK-MB: creatine kinase-MB, BUN: blood urea nitrogen, Hct: hematocrit, DBP: diastolic blood pressure, LDL: low-density lipoprotein.
IV. Discussion
The results of this study show that, in terms of accuracy, RF performed better than other ML methods for predicting hospital readmission in HF patients. Other ML methods, except LS-SVM, had highly similar performance and showed good discrimination, with accuracy in the range of 0.84–0.90.
Various studies have investigated readmission among HF patients using different ML methods. However, it is difficult to compare the results of these studies, because each study considered different characteristics of HF patients. For instance, Landicho et al. [5] compared the performance of logistic regression, SVM, RF, and neural network SVMs to predict hospital readmission in HF patients with a cost-sensitive approach. They found that SVM had better performance than other methods. Similar results were also reported in a study conducted by Artetxe et al. [25]. In another study, Awan et al. [17] used different ML methods to predict 30-day readmission or death with an imbalanced dataset. They showed that the multi-layer perceptron approach had the highest performance compared to other methods. Angraal et al. [26] also found the performance of RF was better than other ML methods. This finding is consistent with our results.
In the current study, we also identified the importance of variables by RF. The results of this method showed that ejection fraction, PTT, sodium, substance abuse, BUN, and CK-MB were important variables for hospital readmission in HF patients. These results are in agreement with previous studies [26–28]. Frizzell et al. [27] compared traditional and ML methods for predicting readmission in HF patients. The results of the logistic regression model indicated that HF readmission was associated with some variables such as BUN, ejection fraction, age, and sodium. These variables were identified as important variables based on RF in our study.
A systematic review by Ouwerkerk et al. [28] also reported that BUN, sodium, and race were the top three most important variables for HF hospitalization. In another study, Angraal et al. [26] showed that BUN was the second most important variable for HF hospitalization. These findings are also consistent with our results, according to which BUN was the fourth most important variable.
Based on our findings, age and creatinine were important variables for HF readmission. Previous studies have confirmed this result [17,18,29]. In a study conducted by Landicho et al. [5], 12 variables were significantly associated with hospital readmission in HF patients. However, none of them were identified as important variables in our study. This may be due to differences in the methods of considering variables between both studies. They used the filter and wrapper feature selection methods, and the initial variables were also different from those used in the present study.
Missingness of data could affect the performance of ML methods. Using imputation methods to deal with missing data may improve the discrimination ability of ML methods. In this study, the performance of the ML methods was highly similar using both imputation methods and showed good discrimination. Lorenzoni et al. [18] showed that the performance of ML methods was better when they excluded missing data. This may have been due to the low percentage of missing data in their study; furthermore, they did not assess whether the missingness was random.
The primary limitation of this study is that the data did not include patients’ medication and psychosocial information, which may have improved the performance of the ML methods. Despite this limitation, our study showed that ML methods had good performance in predicting hospital readmission in HF patients. These results can improve cardiologists’ ability to identify HF patients at high risk for hospital readmission. Identifying high-risk patients provides a valuable opportunity to perform early clinical interventions, which may reduce patients’ risk of readmission. In fact, preventing hospital readmission can improve patients’ quality of life and reduce medical costs.
In conclusion, this study showed that the performance of RF provided better results, in terms of accuracy, than other ML methods for predicting hospital readmission in HF patients.
Acknowledgments
This paper is part of a PhD thesis of the first author in Biostatistics. The authors would like to express gratitude to the Vice-Chancellor of Research and Technology, Hamadan University of Medical Sciences for the approval and support of this study (Ethical Code No. IR.UMSHA.REC.1398.276). It is also necessary to thank the staff of the clinical research department of Farshchian medical education heart center for their cooperation.
Footnotes
Conflict of Interest
No potential conflict of interest relevant to this article was reported.
References
- 1.Ponikowski P, Voors AA, Anker SD, Bueno H, Cleland JG, Coats AJ, et al. 2016 ESC Guidelines for the diagnosis and treatment of acute and chronic heart failure: the Task Force for the diagnosis and treatment of acute and chronic heart failure of the European Society of Cardiology (ESC) Developed with the special contribution of the Heart Failure Association (HFA) of the ESC. Eur Heart J. 2016;37:2129–200. doi: 10.1093/eurheartj/ehw128. [DOI] [PubMed] [Google Scholar]
- 2.Virani SS, Alonso A, Benjamin EJ, Bittencourt MS, Callaway CW, Carson AP, et al. Heart Disease and Stroke Statistics-2020 Update: a report from the American Heart Association. Circulation. 2020;141:e139–e596. doi: 10.1161/CIR.0000000000000757. [DOI] [PubMed] [Google Scholar]
- 3.Braunwald E. The war against heart failure: the Lancet lecture. Lancet. 2015;385:812–24. doi: 10.1016/S0140-6736(14)61889-4. [DOI] [PubMed] [Google Scholar]
- 4.Rajadurai J, Tse HF, Wang CH, Yang NI, Zhou J, Sim D. Understanding the epidemiology of heart failure to improve management practices: an Asia-Pacific perspective. J Card Fail. 2017;23:327–39. doi: 10.1016/j.cardfail.2017.01.004. [DOI] [PubMed] [Google Scholar]
- 5.Landicho JA, Esichaikul V, Sasil RM. Comparison of predictive models for hospital readmission of heart failure patients with cost-sensitive approach. Int J Healthc Manag. 2020. Jul 21, [Epub]. [DOI]
- 6.Ahmadi A, Soori H, Mobasheri M, Etemad K, Khaledifar A. Heart failure, the outcomes, predictive and related factors in Iran. J Mazandaran Univ Med Sci. 2014;24:180–8. [Google Scholar]
- 7.Sahle BW, Owen AJ, Mutowo MP, Krum H, Reid CM. Prevalence of heart failure in Australia: a systematic review. BMC Cardiovasc Disord. 2016;16:32. doi: 10.1186/s12872-016-0208-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Negarandeh R, Zolfaghari M, Bashi N, Kiarsi M. Evaluating the effect of monitoring through telephone (tele-monitoring) on self-care behaviors and readmission of patients with heart failure after discharge. Appl Clin Inform. 2019;10:261–8. doi: 10.1055/s-0039-1685167. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Gupta A, Fonarow GC. The Hospital Readmissions Reduction Program-learning from failure of a healthcare policy. Eur J Heart Fail. 2018;20:1169–74. doi: 10.1002/ejhf.1212. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Maggioni AP, Orso F, Calabria S, Rossi E, Cinconze E, Baldasseroni S, et al. The real-world evidence of heart failure: findings from 41 413 patients of the ARNO database. Eur J Heart Fail. 2016;18:402–10. doi: 10.1002/ejhf.471. [DOI] [PubMed] [Google Scholar]
- 11.Jackson JD, Cotton SE, Bruce Wirta S, Proenca CC, Zhang M, Lahoz R, et al. Burden of heart failure on patients from China: results from a cross-sectional survey. Drug Des Devel Ther. 2018;12:1659–68. doi: 10.2147/DDDT.S148949. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Tripoliti EE, Papadopoulos TG, Karanasiou GS, Naka KK, Fotiadis DI. Heart failure: diagnosis, severity estimation and prediction of adverse events through machine learning techniques. Comput Struct Biotechnol J. 2016;15:26–47. doi: 10.1016/j.csbj.2016.11.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Vapnik V. The nature of statistical learning theory. New York (NY): Springer Science & Business Media; 2013. [Google Scholar]
- 14.Tapak L, Shirmohammadi-Khorram N, Amini P, Alafchi B, Hamidi O, Poorolajal J. Prediction of survival and metastasis in breast cancer patients using machine learning classifiers. Clin Epidemiol Glob Health. 2019;7:293–9. [Google Scholar]
- 15.Carreira-Perpinan MA, Zharmagambetov A. Ensembles of bagged TAO trees consistently improve over random forests, AdaBoost and gradient boosting.. FODS ‘20: ACM-IMS Foundations of Data Science Conference; 2020 Oct 19–20; Virtual Event, USA. pp. 35–46. [Google Scholar]
- 16.Mortazavi BJ, Downing NS, Bucholz EM, Dharmarajan K, Manhapra A, Li SX, et al. Analysis of machine learning techniques for heart failure readmissions. Circ Cardiovasc Qual Outcomes. 2016;9:629–40. doi: 10.1161/CIRCOUTCOMES.116.003039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Awan SE, Bennamoun M, Sohel F, Sanfilippo FM, Dwivedi G. Machine learning-based prediction of heart failure readmission or death: implications of choosing the right model and the right metrics. ESC Heart Fail. 2019;6:428–35. doi: 10.1002/ehf2.12419. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Lorenzoni G, Sabato SS, Lanera C, Bottigliengo D, Minto C, Ocagli H, et al. Comparison of machine learning techniques for prediction of hospitalization in heart failure patients. J Clin Med. 2019;8:1298. doi: 10.3390/jcm8091298. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Chawla NV, Bowyer KW, Hall LO, Kegelmeyer WP. SMOTE: synthetic minority over-sampling technique. J Artif Intell Res. 2002;16:321–57. [Google Scholar]
- 20.Groenwold RHH, Dekkers OM. Missing data: the impact of what is not there. Eur J Endocrinol. 2020;183:E7–E9. doi: 10.1530/EJE-20-0732. [DOI] [PubMed] [Google Scholar]
- 21.Haji-Maghsoudi S, Rastegari A, Garrusi B, Baneshi MR. Addressing the problem of missing data in decision tree modeling. J Appl Stat. 2018;45:547–57. [Google Scholar]
- 22.Sohrabi B, Vanani IR, Gooyavar A, Naderi N. Predicting the readmission of heart failure patients through data analytics. J Inf Knowl Manag. 2019;18:1950012. [Google Scholar]
- 23.Kalateh Sadati A, Bagheri Lankarani K, Tabrizi R, Rahnavard F, Zakerabasali S. Evaluation of 30-day unplanned hospital readmission in a large teaching hospital in Shiraz, Iran. Shiraz E-Med J. 2017;18:e39745. [Google Scholar]
- 24.Mughal MO, Kim S. Signal classification and jamming detection in wide-band radios using Naïve Bayes classifier. IEEE Commun Lett. 2018;22:1398–401. [Google Scholar]
- 25.Artetxe A, Larburu N, Murga N, Escolar V, Grana M. In: Innovation in Medicine and Healthcare 2017. Chen YW, Tanaka S, Howlett R, Jain L, editors. Cham, Switzerland: Springer; 2017. Heart failure readmission or early death risk factor analysis: A case study in a telemonitoring program; pp. 244–53. [Google Scholar]
- 26.Angraal S, Mortazavi BJ, Gupta A, Khera R, Ahmad T, Desai NR, et al. Machine learning prediction of mortality and hospitalization in heart failure with preserved ejection fraction. JACC Heart Fail. 2020;8:12–21. doi: 10.1016/j.jchf.2019.06.013. [DOI] [PubMed] [Google Scholar]
- 27.Frizzell JD, Liang L, Schulte PJ, Yancy CW, Heidenreich PA, Hernandez AF, et al. Prediction of 30-day all-cause readmissions in patients hospitalized for heart failure: comparison of machine learning and other statistical approaches. JAMA Cardiol. 2017;2:204–9. doi: 10.1001/jamacardio.2016.3956. [DOI] [PubMed] [Google Scholar]
- 28.Ouwerkerk W, Voors AA, Zwinderman AH. Factors influencing the predictive power of models for predicting mortality and/or heart failure hospitalization in patients with heart failure. JACC Heart Fail. 2014;2:429–36. doi: 10.1016/j.jchf.2014.04.006. [DOI] [PubMed] [Google Scholar]
- 29.Au AG, McAlister FA, Bakal JA, Ezekowitz J, Kaul P, van Walraven C. Predicting the risk of unplanned readmission or death within 30 days of discharge after a heart failure hospitalization. Am Heart J. 2012;164:365–72. doi: 10.1016/j.ahj.2012.06.010. [DOI] [PubMed] [Google Scholar]