Hydration, Prediction of the pK_a, and Infrared Spectroscopic Study of Sulfonated Polybenzophenone (SPK) Block-Copolymer Hydrocarbon Membranes and Comparisons with Nafion

Abstract

We used long-range-corrected density functional theory to investigate the hydration, pK_a values, and harmonic vibrational spectroscopy of sulfonated polybenzophenone (SPK) block-copolymer hydrocarbon membranes to ascertain the reasons why this gives comparable or higher proton conductivities against Nafion over a wide range of humidity. It was found that a minimum of three water molecules are required for proton dissociation in both membranes. From natural population analysis, it was noticed that the proton dissociation of SPK membranes is nearly comparable to Nafion at relatively low water content. Next, we explored the applicability of the appropriate treatment for pK_a and proton’s energy with a benchmark set (AKB) scheme to compute the pK_a values for these membranes. These results indicate that the proton dissociative abilities of sulfonic acid groups of the SPK membrane are higher than those of Nafion. This could be one of the reasons for the SPK membrane to show higher proton conductivities at high relative humidity. Furthermore, the effect of hydration on the proton conductivity of membranes illustrates that asymmetric stretching of the SO₃^– mode was in agreement with Nafion ones but opposite trends were found in the case of symmetric stretching of the SO₃^– mode upon hydration.

Introduction

From the past few decades, significant efforts on the design and development of polymer electrolyte fuel cells (PEFCs) or proton-exchange membrane fuel cells (PEMFCs) have been made as alternative energy devices because of their high energy efficiency and minimal environmental pollution. Their lightweight and compactness have made them a good choice in stationary and portable devices. However, the performance, durability, and cost of their component materials need further improvement to commercialize fuel cell vehicles.^1,2 A proton-exchange membrane (PEM) is one of the important components that transport protons from the anode to the cathode. The indispensable requirements for a good PEM include (i) high proton conductivity even under low humidity and elevated temperature conditions, (ii) low gas permeability, (iii) high durability and stability, (iv) low cost, and (v) environmentally friendly properties.

Nafion, perfluorinated sulfonic acid (PFSA) ionomer-based membrane, is still used as the state-of-the-art membrane in fuel-cell applications because of high proton conductivity and reasonably good mechanical and chemical stability.³ However, high production cost, less environmental compatibility, relatively larger gas permeability, and a bit complicated synthetic processes are the major drawbacks that limit the widespread commercialization of PEMFCs. Therefore, an alternative to Nafion is in great demand.

Among the alternative membranes, aromatic hydrocarbon PEMs with acidic functions have emerged as one of the promising candidates due to many approaches used by many researchers across the globe. They demonstrated that such membranes have high stability and high susceptibility toward sulphonation and phosphonation reactions. Furthermore, it will also be easy to modify the structures to tune their properties.⁴⁻⁷ Some representative membranes include polyphenylenes,⁸ poly(arylene ether ketone)s,⁹ polybenzimidazoles,^10,11 poly(arylene ether sulfone)s,^12,13 and polyimides.^14,15 These PEMs show high proton conductivity, reasonable stability, and very low gas permeability, but none of them could compete with Nafion because of insufficient durability and poor proton conductivity under relatively low humidity conditions. To achieve these conflicting properties with a single ionomer membrane, block-copolymer proton conductive membranes came into the picture.

The block copolymer constructs phase-separated morphology, that is, molecular hydrophilic and hydrophobic phase separation. Hydrophilic parts facilitate pathways for the ionic channel, while hydrophobic domains provide mechanical strength and gas permeation. Vallejo et al.¹⁶ found that block copolymers showed better proton conductivity than random copolymers. Recently, Watanabe and his co-workers studied a series of aromatic block copolymers composed of highly sulfonated fluorenyl groups in the hydrophilic blocks,^17,18 but ¹H NMR and IR spectra indicated that the sulfonated fluorenyl groups and ether linkages undergo oxidative degradation.¹⁹ To overcome this drawback, sulfonated polybenzophenone (SPK) block-copolymer membranes without fluorine and ether groups were reported.²⁰ It was expected that the carbonyl groups, electron-withdrawing groups, would not only enhance the oxidative stability but also increase the acidity of sulfonic acid groups present in the same phenylene rings. The experimental results showed that the proton conductivity of the SPK membrane with higher ion-exchange capacity (IEC = 2.57 m equiv/g) was 0.45 S/cm at 90% relative humidity (RH) which was 3.7 times higher than that of Nafion at 80 °C, while the conductivity of the same membrane was 6.5 mS/cm at 20% RH and comparable to that of Nafion (5.9 mS/cm). Unfortunately, the higher IEC led to large water uptake and swelling under fully hydrated conditions. Hence, mechanical failure was inevitable. Therefore, a molecular-level understanding of the membrane is warranted for further improvements of proton conductivities of the membranes. However, morphology is another major factor in achieving good proton conductivity of a membrane, but such a study is beyond the scope of this work.

Nowadays, molecular modeling study has become a powerful tool to provide the necessary physical, chemical, and mechanistic insights at the molecular level. To the best of our knowledge, a fundamental molecular-level understanding of proton conductivities under varied hydration conditions for multiblock-copolymer membranes in general and SPK block-copolymer membranes, in particular, has not been investigated in detail. This prompted us to undertake a modeling effort to understand the hydration and proton dissociation at low hydration levels for rational development of the SPK membranes using the long-range-corrected density functional theory (LCDFT). To compare the results, Nafion is also taken under this study.

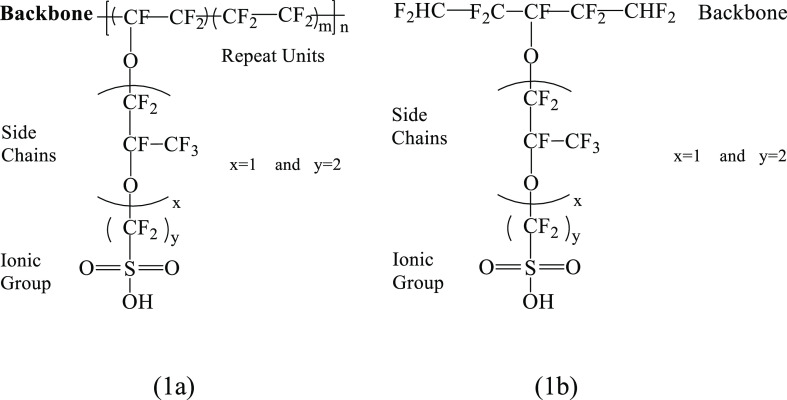
It is a well-established fact that the backbone of the polymer electrolyte membrane also plays a crucial role in the proton conduction apart from the hydrophilic side chains with terminal acidic functional groups.² Despite knowing this, many researchers have studied Nafion after considering much smaller models such as CF₃SO₃H, CF₃CF₂SO₃H, and CF₃O(CF₂)₂SO₃H.²¹⁻³⁰ However, Paddison and Elliott studied the role of the side chain in affecting proton transfer in the short-side-chain perfluorosulfonic acid membrane under minimal hydration levels.³¹ Therefore, a good choice of the model becomes very important to investigate the energetics of any membrane quantitatively and qualitatively as well. Because of this, we considered the model of Nafion and SPK membranes, as shown in Figures 1b and 2b, respectively, while Figures 1a and 2a depict the chemical structure of Nafion and SPK membranes, respectively.

Figure 1.

Chemical structure of the Nafion membrane (a) and model Nafion (b).

Figure 2.

Chemical structure of sulfonated polybenzophenone (SPK) block-copolymer membrane (a) and model SPK membrane (b).

The pK_a value is one of the methods to indicate the strength of an acid. The lower the pK_a value, the stronger is the acid. In other words, the lower value indicates that the acid fully dissociates in water. To gain insights into the proton dissociative capability of the acidic functional groups of the hydrophilic component of the SPK membranes, we have also estimated their acid strengths.

According to Bower and Maddams, infrared spectroscopy is a powerful tool to elucidate polymer structures at many levels right from specific normal modes to molecular configurations.³² The intensity and widths of the vibrational peaks provide information regarding macroconformations of the polymer, and the IR methods benefit from the simplicity of the spectrum obtained from the repetitive nature of the polymer chain. Since the SPK membrane undergoes different humidity conditions in operating fuel cells, the IR spectrum analysis under the hydration/dehydration conditions is, therefore, required to investigate the proton conductivity of SPK in further detail.

Results and Discussion

The optimized geometries of SPK and Nafion membranes were obtained without water molecules and with the addition of explicit one, two, three, and four water molecules per sulfonic acid groups in gas-phase calculation, as shown in Figures 3 and 4, respectively. The distance between the oxygen of sulfonic acid/sulfonate and the acidic proton (−SO₂O···H bond length) and the distance between the oxygen of the sulfonic acid/sulfonate and the oxygen of the water molecule/hydronium ion (−SO₂O···H···OH₂ bond length) are presented in Table 1.

Figure 3.

Optimized structures of the SPK membrane at various hydration numbers: 0, 1, 2, 3, and 4 at the LC-BLYP/6-311+G(d,p) level. The dotted circle represents the position of the proton attached to the sulfonic acid moiety and lambda (λ) means the number of water molecules per sulfonic acid group.

Figure 4.

Optimized structures of the Nafion membrane at various hydration numbers: 0, 1, 2, 3, and 4 at the LC-BLYP/6-311+G(d,p) level. The dotted circle represents the position of the proton attached to the sulfonic acid moiety and lambda (λ) means the number of water molecules per sulfonic acid group.

Table 1. Optimized Distances (d) between the O Atom of the Sulfonic Acid Group Protonated in the Initial Structures and Protons and the O Atom of the Closest Water Molecule in Hydrated Nafion and SPK Membrane Models (Å).

	d(−SO2O···H)		d(−SO2O···H···OH2)
λ	SPK	Nafion	SPK	Nafion
λ = 0	0.97 (0.97)	0.97
λ = 1	1.00 (1.00)	1.01	2.60 (2.59)	2.56
λ = 2	1.03 (1.04)	1.06	2.52 (2.49)	2.46
λ = 3	1.49 (1.53)	1.58	2.50 (2.52)	2.54
λ = 4	1.81 (1.81)	1.88	2.72 (2.71)	2.75

The equilibrium structures of both membranes without the addition of any water molecule exhibit a nearly uniform O–H bond length of 0.97 Å. Upon the addition of a single water molecule, this O–H bond length increased to 1.00 Å in the SPK membrane, while the same was found to be 1.01 Å in Nafion. However, the −SO₂O···H···OH₂ bond lengths in the SPK were 2.60 and 2.59 Å, which is 0.04 Å more than that of Nafion.

The addition of a second water molecule (i.e., at λ = 2) resulted in the O–H bond length increase from 0.97 to 1.06 Å approximately, while −SO₂O···H···OH₂ bond lengths decreased in comparison with the one water case. It indicates that one water molecule approaches toward O–H of the sulfonic acid to accept the hydrogen bond and acts as a hydrogen-bond donor to the other water molecule which was also a hydrogen-bond donor to a different oxygen atom of the acid group. Eventually, partial proton dissociation was observed in both membranes as can been seen in Figures 3 and 4.

Proton dissociation was first observed upon the addition of a third water molecule per sulfonic acid group (i.e., at λ = 3) in both SPK and Nafion, as shown in Figures 3 and 4. The O–H bond length increased to 1.49 and 1.58 Å in SPK and Nafion, respectively, and the −SO₂O···H···OH₂ bond lengths were 2.50–2.54 Å. It was found that two of the oxygen atoms of the sulfonate group are now involved in a hydrogen bond with two individual water molecules, and the remaining oxygen and, now, hydronium ion are involved in a contact ion pair. Furthermore, the hydronium ion is also hydrogen-bonded to the two water molecules, maintaining a ring-like network of hydrogen bonds.

Figures 3 and 4 display the optimized structures of the SPK and Nafion membranes having four water molecules per sulfonic acid group (i.e., λ = 4). This shows that proton dissociation has taken place. Furthermore, the O–H bond length tabulated in Table 1 is 1.81 and 1.88 Å. It means that the detached protons from the sulfonic acid groups of the membranes are transporting from one place to another through the hydrogen bonds with water clusters and the hydronium ion form an Eigen cation as it is hydrogen. Therefore, one can conclude that both SPK and Nafion membranes require a minimum of three water molecules for proton dissociation from the sulfonic acid groups of the membranes. To understand the lower proton conductivity of the SPK membrane against Nafion at a low humidity case, which is below the λ = 3 case, we focused on the charge distribution analyzed by the natural bonding orbital (NBO).⁴²

In the deprotonation process of the sulfonic acid group, the proton approaches the negatively charged oxygen atoms in water molecules. Since oxygen atoms are more electronegative than sulphur atoms, the electrons are localized on the oxygen atoms. If electrons are highly localized on oxygen atoms, there would be a larger repulsive force between the oxygen atoms of the water molecule and the sulfonic group. Hence, we focus on the NBO charge distribution of the sulfonic group. The NBO charges of sulphur, oxygen, and hydrogen atoms of the sulfonic group are shown in Table 2. The charge on hydrogen atoms for both SPK and Nafion has almost the same values for λ = 0 to 4. This seems to show that the NBO charge of the H atom does not affect the deprotonation process. Next, we concentrated on the NBO charges of the oxygen atoms of the sulfonic group. In the case of λ = 0 to 2, the NBO charge on the oxygen atoms increased from 0.02 to 0.07. However, from λ = 3 onward, it decreases to 0.01 for both membranes, but comparing the sum of the NBO charge of the three oxygen atoms, the total for SPK was −2.73, −2.82, −2.86, −3.08, and −3.07 and those for the Nafion were −2.64, −2.73, −2.79, −3.01, and −3.01 for λ = 0, λ = 1, λ = 2, λ = 3, and λ = 4, respectively. This result indicates that the proton dissociation of SPK is nearly comparable to Nafion at relatively low water content.

Table 2. Natural Population Analysis of the Sulfonic Acid Group in SPK and Nafion Membranes.

	λ = 0	λ = 1	λ = 2	λ = 3	λ = 4
SPK
S	2.34 (2.34)	2.36 (2.37)	2.37 (2.38)	2.38 (2.38)	2.39 (2.38)
O	–0.93 (−0.90)	–0.98 (−0.98)	–1.00 (−0.91)	–1.02 (−1.01)	–1.02 (−1.02)
O	–0.91 (−0.94)	–0.92 (−0.91)	–0.93 (−1.01)	–1.03 (−1.03)	–1.03 (−1.03)
O	–0.89 (−0.90)	–0.92 (−0.92)	–0.93 (−0.94)	–1.02 (−1.03)	–1.02 (−1.02)
H	0.52 (0.52)	0.54 (0.54)	0.53 (0.54)	0.54 (0.54)	0.52 (0.53)
SO3–	–0.39 (−0.39)	–0.46 (−0.45)	–0.49 (−0.49)	–0.68 (−0.70)	–0.69 (−0.69)
Nafion
S	2.28	2.30	2.33	2.33	2.33
O	–0.90	–0.95	–0.88	–1.00	–1.01
O	–0.88	–0.91	–0.92	–1.01	–0.99
O	–0.87	–0.88	–0.98	–1.00	–1.01
H	0.52	0.54	0.53	0.54	0.52
SO3–	–0.36	–0.43	–0.46	–0.68	–0.68

Prediction of the pK_a

Acid dissociation constant, pK_a, is a physical quantity that measures the ability of a molecule to donate or accept a proton from another molecule. In other words, one can say that pK_a of the molecules tells us about their protonation states in the solution at particular pH, that is, the larger the pK_a value, the lesser is the proton dissociation ability. It can be measured experimentally but it becomes difficult many times because of detection of the protonation state changes for a small amount of solute. To circumvent this problem, quantum chemical calculation methods have become a powerful tool to predict the pK_a value of many compounds with reasonable accuracy.

SPK and Nafion membranes have the sulfonic acid (−SO₃H) moieties through which they release protons. To apply the AKB method as mentioned in the previous section, a linear regression curve using a set of reference molecules must be required. Here, we have considered nine reference molecules, as shown in Figure 5, having sulfonic acid moieties: (i) fluorosulfonic acid, (ii) chlorosulfonic acid, (iii) trifluoromethane sulfonic acid, (iv) 4-nitrobenzene sulfonic acid, (v) methyl hydrogen sulfate, (vi) 4-bromobenzene sulfonic acid, (vii) benzene sulfonic acid, (viii) methane sulfonic acid, and (ix) ethane sulfonic acid. The experimental pK_a values of the reference molecules were taken from the work done reported by Guthrie.⁴³

Figure 5.

Reference molecules and their experimental pK_a values.

Figure 6 shows a scattered plot between experimental pK_a and computed ΔG₀ (free-energy difference between neutral and its anion) of all nine reference compounds in water solvent using implicit solvation models such as conductor-like polarizable continuum model (CPCM). This plot indicates a linear correlation between them with the square of correlation coefficient (R²) of 0.9288. It means that the fitness of the linear regression is reasonably good. To access the reliability of this method, we calculated the pK_a values of these nine reference compounds and tabulated them in Table 3. Considering the difference between the calculated and the experimental pK_a for these compounds, the mean actual error is around 0.01 pK_a units. Thus, these data indicate that the AKB scheme is reliable and applicable to our systems, that is, SPK and Nafion membranes.

Figure 6.

Linear correlations between experimental pK_a values and calculated free-energy differences, ΔG₀, in water at CPCM-LC-BLYP levels using 6-311+G(d,p) basis sets.

Table 3. Calculated and Experimental pK_a Values of Reference Molecules in Water at the CPCM-LC-BLYP Level Using 6-311+G(d,p) Basis Sets.

s. no.	compounds	pKa (calc.)	pKa (expt.)43
(i)	FSO3H	–6.40	–6.40 ± 0.50
(ii)	ClSO3H	–6.18	–6.00 ± 0.50
(iii)	CF3SO3H	–5.39	–5.90 ± 0.50
(iv)	p-NO2C6H4SO3H	–3.25	–4.00 ± 1.00
(v)	CH3OSO3H	–4.26	–3.40 ± 0.50
(vi)	p-BrC6H4SO3H	–2.93	–3.10 ± 1.00
(vii)	C6H5SO3H	–2.55	–2.80 ± 1.00
(viii)	CH3SO3H	–2.12	–1.92 ± 0.01
(ix)	CH3CH2SO3H	–1.99	–1.68 ± 0.02

Next, we substituted the free-energy difference of neutral SPK and its anion in the linear regression equation obtained in Figure 6. The computed pK_a of SPK comes to be −5.82. A similar procedure was followed for Nafion, for which the computed pK_a is −5.64, as shown in Figure 7. Since pK_a of SPK is lower than those of Nafion, the proton dissociative ability from the sulfonic acid group of SPK would be more than Nafion under relatively high humidity conditions. These findings could be one of the reasons to support the experimental observation.²⁰

Figure 7.

Predicted pK_a value of SPK and Nafion at the CPCM-LC-BLYP/6-311+G(d,p) level.

Vibrational Peak Analysis

The hydrophilic component of the SPK membrane unit has two sulfonic acid groups and one ketone functional group. Therefore, one must get two values for S=O symmetric, S=O asymmetric, O–H stretching, SO₃^– symmetric/asymmetric, and H₃O⁺ symmetric/asymmetric vibrational peaks. Table 4 displays theoretical assignments of some important harmonic vibrational peaks of the SPK membrane at various hydration numbers (λ = 0 to 4) at the LC-BLYP/6-311+g(d,p) level. The sulfonic acid group which is not toward the hydrophobic components of the membrane, their peaks’ wavenumbers are written in parentheses. Let us first discuss the vibrational peak assignments of the membrane in a dry state (i.e., λ = 0). The results tabulated in Table 4 indicates that the S=O symmetric stretching modes, ν_sym (S=O), have peaks at 1228 cm^–1, while the S=O antisymmetric stretching modes, ν_asym (S=O), of the sulfonic acid groups have 1430 and 1445 cm^–1. Since the proton is attached to one of the oxygen atoms of the acidic moieties, the O–H vibrational stretching, ν_str (O–H), appeared at 3834 and 3843 wavenumbers. However, in the C=O stretching, ν_str (C=O), the vibration was noticed at 1849 cm^–1. When SPK started to hydrate with explicit one and two water molecules per sulfonic acid groups, all the abovementioned four vibrational peaks were found with relatively lower wavenumbers. However, the significant decrease in ν_str (O–H) at λ = 2 depicts that the O–H bond is weakening and is on the verge of proton dissociation from the sulfonic acid group.

Table 4. Theoretical Assignments of Some Important IR Peaks of the SPK Membrane at Various Hydration Numbers (λ = 0 to 4) at the LC-BLYP/6-311+G(d,p) Level.

λ	νsym(S=O)	νasym(S=O)	νstr(O–H) (−SO3H group)	νsym(SO3–)	νasym(SO3–)	νsym(C=O)	νsym(H3O+)	νasym(H3O+)
0	1228 (1228)	1430 (1445)	3834 (3843)			1849
1	1193 (1193)	1430 (1439)	3118 (3195)			1851
2	1181 (1189)	1360 (1367)	2449 (2629)			1852
3	1074 (1084)	1184 (1186)		1074 (1084)	1184 (1186)	1851	2991 (3000)	2748 (2800)
4	1077 (1087)	1239 (1240)		1077 (1087)	1239 (1240)	1849	3048 (3078)	2663 (2713)

In the case of λ = 3, the ν_str (O–H) peak is absent, but two new peaks were noticed at 1074 (1084) and 1184 (1186) cm^–1 for symmetric stretching of SO₃^–, ν_sym (SO₃^–), and asymmetric stretching vibration mode of the SO₃^–, ν_asym(SO₃^–), group, respectively, along with symmetric stretching vibration of H₃O⁺, ν_sym (H₃O⁺), at 2991 and 3000 cm^–1, and asymmetric stretching of H₃O⁺, ν_asym (H₃O⁺), at 2748 and 2800 cm^–1. These results ensured that the proton dissociation has taken place and there is no formation of Eigen cations. In other words, a minimum of three water molecules are required for proton dissociation. Similarly, for the case of λ = 4, ν_sym (SO₃^–), ν_asym(SO₃^–), ν_sym(H₃O⁺), ν_asym(H₃O⁺), and ν_str(C=O) were also found, but their wavenumbers are lower than those of λ = 3, as shown in Table 4. This trend seems to show that vibrational frequencies of these modes will keep decreasing upon increasing hydration.

To understand the effect of dehydration or hydration on the proton conductivity of SPK, Figure 8 depicts the peak strength of symmetric stretching of SO₃^–, ν_sym(SO₃^–), and asymmetric stretching of SO₃^–, ν_asym(SO₃^–), as a function of λ. These results show that the peak intensities of ν_sym(SO₃^–) for 1074–1077 cm^–1 increase upon increasing hydration, while the peak intensities of asymmetric stretching of the SO₃^– mode for 1184–1239 cm^–1decrease with increasing lambda (λ) values. This means that upon dehydration, the peak intensities of ν_sym(SO₃^–) stretching modes decrease and the peak intensities of ν_asym(SO₃^–) stretching modes increase. It is assumed that these results will be helpful for the experimentalists during IR spectra measurements of this membrane under relatively low humidity conditions.

Figure 8.

Calculated IR spectra of the SPK membrane for various hydration numbers (λ = 3 and 4) at the LC-BLYP/6-311+G(d,p) level.

Nafion is still considered as the state-of-the-art membrane as far as proton conductivity at low humidity is concerned. Therefore, it becomes pertinent to compute vibration peaks of Nafion to compare them with those of SPK to ascertain the reasons why SPK failed to give more proton conductivity at low water content than that of Nafion. However, experimental and theoretical infrared studies on Nafion had also been discussed in detail elsewhere.⁴⁰

Table 5 show important peaks assignments of Nafion at different hydration numbers (λ): 0, 1, 2, 3, and 4. Before investigating the hydration of Nafion, let us first discuss the main harmonic vibrational peaks of a dry Nafion membrane, that is, λ = 0 case. It was found that the S=O symmetric stretching and the S=O asymmetric stretching modes were 25 and 47–62 cm^–1, respectively, on the higher side of its counterparts in SPK. However, the O–H vibrational stretching was reported at 3821 cm^–1 which is nearly 13–22 cm^–1 than that of SPK.

Table 5. Theoretical Assignments of Some Important IR Peaks of the Nafion Membrane at Various Hydration Numbers (λ = 0 to 4) at the LC-BLYP/6-311+G(d,p) Level.

λ	νsym(S=O)	νasym(S=O)	νstr(O–H) (−SO3H group)	νsym(SO3–)	νasym(SO3–)	νsym(H3O+)	νasym(H3O+)
0	1253	1492	3821
1	942	1479	3037
2	1207	1428	2184
3	1097	1286		1097		3060	2777
4	1099	1295		1099		3075	2450

When Nafion is hydrated with explicit one and two water molecules per sulfonic acid group, then wavenumbers of ν_sym (S=O), ν_asym (S=O), and ν_str (O–H) keep decreasing in comparison with its dry state. The IR spectra become different at λ = 3. There is absence of ν_str (O–H) mode and the peaks appeared at 1097, 3060, and 2777 cm^–1 correspond to ν_sym (SO₃^–), ν_sym (H₃O⁺), and ν_asym (H₃O⁺) stretching modes of vibration, respectively. These results indicate that the proton is completely detached from the sulfonic acid groups. Furthermore, similar observations were found in the λ = 4 case. It is interesting to note that at λ = 3 and onward, all the significant peaks appeared at nearly the same wavenumbers.

Next, we investigated the effect of dehydration/hydration on the proton conductivity of Nafion using the hydration numbers, 3 and 4. Figure 9 illustrates the calculated IR spectra (peak strength vs frequency) of the hydrated Nafion membrane. As shown in the figure, the peak intensity of the SO₃^– symmetric stretching mode for 1097–1099 cm^–1 is slightly increased but there is a significant increase in the peak intensity of the SO₃^– asymmetric stretching mode for 1286–1295 cm^–1 upon increasing the hydration. However, this trend is just contrary to the experimental result.⁴⁴ We, therefore, compare the hydration effect on the proton conductivity of SPK with the experimental ones of Nafion. It was found that asymmetric stretching of the SO₃^– mode is in line with Nafion ones, but opposite trends were noticed in the case of symmetric stretching of the SO₃^– mode upon dehydration or hydration.

Figure 9.

Calculated IR spectra of the Nafion membrane for hydration numbers (λ = 3 and 4) at the LC-BLYP/6-311+G(d,p) level.

Conclusions

In this article, we have first studied optimized geometries of SPK block-copolymer hydrocarbon membranes without any water molecule in the gas phase and then with explicit addition of one, two, three, and four water molecules per sulfonic acid group using LCDFT. To compare the proton detachability against the benchmark polymer electrolyte, Nafion, we also investigated it. The results show that a minimum of three water molecules is required to detach a proton from the hydrophilic component of sulfonic acid groups in both membranes. Next, we performed NBO calculation. The natural population analysis results indicated that the proton dissociation of SPK is nearly comparable to Nafion under relatively low humidity conditions.

Since pK_a is one of the important parameters to measure the ability of a molecule for proton dissociation in an aqueous solution, the applicability of the AKB methods to compute the pK_a values for these membranes was explored by us for the first time. The computed free-energy difference of the neutral membrane and its anion was used in the linear regression equation of Figure 6. It was found that the computed pK_a values of the SPK membrane are lower than that of Nafion. This seems to show that the proton dissociative ability of the sulfonic acid group of SPK in water would be more than that of Nafion under relatively high humidity conditions.

Finally, we performed harmonic vibrational peak analysis. The absence of the ν_str (O–H) mode and the presence of peaks for ν_sym(SO₃^–), ν_asym(SO₃^–), ν_sym(H₃O⁺), and ν_asym(H₃O⁺) stretching modes of vibration at hydration number 3 (λ = 3) confirmed the complete detachment of the proton from the sulfonic acid groups. It means that a minimum of three water molecules per sulfonic acid group is indispensable for proton dissociation. Furthermore, the effect of hydration on the proton conductivity of membranes was also explored in terms of the peak strength of symmetric stretching of SO₃^–, ν_sym(SO₃^–), and asymmetric stretching of SO₃^–, ν_asym(SO₃^–), as a function of hydration numbers. These results indicate that asymmetric stretching of the SO₃^– mode was in agreement with Nafion ones but opposite trends were found in the case of symmetric stretching of the SO₃^– mode upon hydration. All in all, structural tuning in the SPK membrane is warranted to produce more proton conductivity at low IEC against Nafion and the predicted pK_a values would be helpful for the experimentalist for better membrane synthesis.

Computational Details and Theory

The geometry optimization of the molecules considered under this study has been performed using the LCDFT method, LC-BLYP,³³⁻³⁶ in conjunction with 6-311+G(d,p) basis sets.³⁷ The symmetry restrictions were not imposed in any calculations. To confirm that the local minima are obtained, vibrational frequency calculation was carried out with the same method and basis sets as mentioned above. It was found that the optimized geometries have no imaginary frequencies. To examine the high humidity conditions, we studied solvent effects using the CPCM method.³⁸ All the computations have been performed using the Gaussian 16 suite of the program³⁹ and GaussView⁴⁰ software was used to visualize and analyze the calculated results.

Recently, Matsui et al.⁴¹ had proposed appropriate treatment for pK_a and proton’s energy with a benchmark set (AKB) scheme to compute the pK_a values and reported its advantages over the other methods. While this method had been applied on various small molecules to predict the quantum chemical pK_a values, its application on the PEM is yet to be investigated. Therefore, we apply the AKB method systematically as mentioned below.

Let us consider a polymer electrolyte having a terminal acidic group, −SO₃H. When the membrane is subjected to humidity, a deprotonating reaction takes place with the per sulfonic acid group. This can be represented by the following general reaction.

1

where ⊗ stands for the remaining parts of the PEM.

If K_a is the dissociation constant for the reaction (1), then one can write

2

We know that

3

and

4

where ΔG(aq) is called the Gibbs free-energy difference for the deprotonating reaction in the aqueous phase.

Therefore, the expression for the pK_a can be obtained after rearranging the abovementioned eq 4. That is

5

6

In the abovementioned eq 5, R is called the universal gas constant and T is the temperature in kelvin. With the advent of implicit solvation models such as CPCM and others, it became feasible to get the free-energy values of the anion and neutral species from the vibrational frequency analysis. In the case of the proton (H⁺), it has no electron and hence the G(H⁺) results from any quantum chemical calculation appeared impossible.

To circumvent these problems, a scaling factor, γ, was introduced and multiplied with the Gibbs free energy of the deprotonating reaction. Following this, eqs 5 and 6 can be written as

7

8

9

which means that

10

11

12

Equation 9 provides an apparent linear correlation between ΔG₀ and pK_a values. These parameters m and C₀ were determined by the least square fitting with typical experimental pK_a values of several reference molecules of our interests for which experimental pK_a values in aqueous solutions are known.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.1c04484.

• Cartesian coordinates of optimized geometries (PDF)

The authors declare no competing financial interest.