Abstract
Accurate prediction of protein–ligand binding free energies is important in enzyme engineering and drug discovery. The molecular mechanics/generalized Born surface area (MM/GBSA) approach is widely used to estimate ligand-binding affinities, but its performance heavily relies on the accuracy of its energy components. A hybrid strategy combining MM/GBSA and machine learning (ML) has been developed to predict the binding free energies of protein–ligand systems. Based on the MM/GBSA energy terms and several features associated with protein–ligand interactions, our ML-based scoring function, GXLE, shows much better performance than MM/GBSA without entropy. In particular, the good transferability of the GXLE model is highlighted by its good performance in ranking power for prediction of the binding affinity of different ligands for either the docked structures or crystal structures. The GXLE scoring function and its code are freely available and can be used to correct the binding free energies computed by MM/GBSA.
1Introduction
Reliable estimation of protein–ligand binding free energies is a core issue in drug screening and design.1−3 In traditional drug discovery, direct measurement of protein–ligand binding affinity mostly relies on experimental techniques, which are costly and time-consuming for high-throughput screening of a great number of compounds. Various computational approaches have emerged for calculating the binding free energy between ligands and their target proteins. These range from the high-end free-energy methods such as free-energy perturbation (FEP)4−6 and thermodynamic integration (TI),7,8 which are physically rigorous but prohibitively expensive for high-throughput screening, to the low-end empirical scoring functions (SFs). Classical SFs can be typically divided into three classes, namely, force field (FF)-based SFs,9−16 empirical SFs,17−21 and knowledge-based SFs.22−24 FF-based SFs characterize the protein–ligand interactions by linear combination of nonbonding interaction components (such as electrostatic, van der Waals, and hydrogen bonding), while the other more difficult components such as desolvation and entropic contributions are usually simplified or even neglected. Consequently, these SFs show diversified performance in predicting the protein–ligand binding affinity.
The FF-based molecular mechanical/generalized Born surface area (MM/GBSA) approach is a fast and popular method for binding free-energy prediction.25,26 MM/GBSA is usually more accurate than most SFs and less demanding in computational cost than FEP and TI methods. In the MM/GBSA approach, the binding free energy of the ligand can be computed from the difference between the free energies of the protein receptor (R), the ligand (L), and the complex (RL) in solution (eq 1). The binding free energy can be decomposed into a gas-phase MM energy, polar and nonpolar solvation terms, and a conformational entropy term (eq 2),27,28 in which the polar solvation energies are estimated using an implicit solvation GB29 model, while the calculation of the nonpolar solvation energy is based on the approximation of solvent-accessible surface area.30 The conformational entropy term (−TΔS), which is normally calculated by normal-mode analysis, is usually neglected due to the high computational cost and technical errors associated with its calculation.
| 1 |
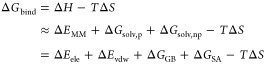 |
2 |
Recently, machine learning (ML)-based scoring functions have emerged as promising techniques for the prediction of protein–ligand binding free energies.31−36 Unlike conventional SFs, ML-based SFs are able to capture the relationship between protein–ligand binding affinity through a nonlinear algorithm and have been shown to outperform the conventional SFs in terms of scoring power. For instance, Ballester and Mitchell developed a random forest-based SF (RF-Score),37 in which the occurrence of the key protein–ligand atom-type pairs within a cutoff distance was used as an input feature. Using the PDBbind v2007 as the training set (1105 complexes) and test set (195 complexes), a high Pearson’s correlation coefficient (R) of 0.776 was obtained for the scoring power.37 Subsequently, RF-Score was further improved by tuning the parameters and adding extra empirical energy terms.38 On the basis of 50 descriptors related to protein–ligand interactions, Li et al. developed a support vector regression (SVR) algorithm-based SF named ID-Score, which achieved a higher scoring power (Rp = 0.753).39 Wang and Zhang developed a scoring function ΔvinaRF20,40 in which the RF algorithm was employed to simultaneously improve the scoring, ranking, docking, and screening power of the AutoDock Vina scores. Using the features in AutoDock Vina and an additional 20 features, ΔvinaRF20 achieved superior performance compared to classical scoring function in both the CASF-2007 and CASF-2013 benchmarks.40 By taking into account the explicit water molecule binding and ligand conformation stability, Zhang and co-workers developed a new scoring function named ΔvinaXGB41 that shows better performance than the previous ΔvinaRF20.
In addition to the traditional ML, deep learning-based SFs have also emerged as a promising tool in predicting the binding free energy of protein–ligand complexes.42−47 Unlike the traditional machine learning algorithms, deep learning-based SFs depend strongly on algorithms and data, as well as the hardware.48−50 With the improvement of hardware computing speed and the storage capacity, the quantum chemistry-based SFs have been developed to predict the binding affinity of protein–ligand complexes.51,52
Inspired by the aforementioned work, we describe herein a hybrid MM/GBSA and ML method to predict the binding free energy of protein–ligand complexes. Using the MM/GBSA energy components and other descriptors associated with protein–ligand binding, we have shown that the hybrid MM/GBSA and ML approach (named GXLE) has superior performance in scoring power compared to the pure MM/GBSA. Compared with many other ML methods, fewer physicochemical features have been used in GXLE, which renders robustness and transferability of binding affinity prediction to this model.
2. Methods
2.1. Data Sets
The PDBbind database (http://www.pdbbind-cn.org/)53,54 developed by Wang et al. provides 3D structures of protein–ligand complexes and their binding affinity data, which has been widely used as the benchmark for scoring functions. In this study, we chose a PDBbind refined set as part of our training set, which consists of high-resolution crystal structures with reliable experimental binding affinities (3 < pKd < 12). In addition to the refined set from PDBbind, we also used part of the general set from PDBbind (0.4 < pKd < 3) in our training set. According to the time-split cross-validation method,55 we divided the training set into two sections. One section of the set, whose structures were released after 2018, was used as a validation set, while the remainder of the set was used as the new training set. The validation set was used to select a model that could perform well with different structure types. The core set (CASF-2016),56 which consists of high-quality protein–ligand complexes, was used as the test set. The structures in the test set were excluded from both the training set and validation set. Due to some technical problems in the Amber setup, a small part of problematic complexes from the training set and validation set were ignored. In total, our system has 3511 complexes in the training set, 301 complexes in the validation set and 285 complexes in the test set (Table 1).
Table 1. Summary of the Data Sets.
| Source | numbers | |
|---|---|---|
| traning set | PDBbind refined set (before 2018) | 3511 |
| validation set | PDBbind refined set (after 2018) | 301 |
| test set | CASF-2016 | 285 |
2.2. Preparation of Structures
All absent hydrogen atoms were added to the proteins using the LEAP module in AMBER18.57 The Amber ff14SB58 FF was employed for the protein residues, while the general AMBER FF (GAFF)59 and AM1-BCC60,61 charges were used for ligands. The resulting protein–ligand complex was solvated in a rectangular box of TIP3P62 waters extending up to at least 12 Å from the protein surface. Counterions, Na+ or Cl–, were added to neutralize the total charge of each system. After an ideal setup, the whole system was fully minimized using combined steepest descent and conjugate gradient method. All optimizations were performed using the AMBER18 program.57,63 The fully optimized structures were used in the subsequent MM/GBSA calculations.
2.3. MM/GBSA Binding Free-Energy Calculations
| 3 |
The MM/GBSA binding free-energy calculations can be decomposed into five interaction terms as shown in eq 3. ΔEele and ΔEvdW are electrostatic energies and the van der Waals energies from the gas-phase molecular mechanics, respectively. The electrostatic solvation energy between the solute and the continuum solvent (ΔGGB) is calculated with the GB model, while the nonpolar contribution (ΔGSA) is estimated by the solvent-accessible surface area. The entropy term (−TΔS) can be calculated by MMPBSA.py64 using the normal mode method. However, some studies have shown that the calculated entropy is far from accurate. As such, we chose only the first four terms (ΔEele, ΔEvdw, ΔGGB, and ΔGSA) of the MM/GBSA method featured in the work described below.
2.4. Feature Selection and Preprocessing
In addition to the four features derived from the MM/GBSA equation, other key features are also included in our ML models, including the number of rotatable bonds (RT), hydrogen-bond interactions (HB), experience-based van der Waals interactions (VDW), hydrophobic interaction terms (HP, HM, and HS), the total charges of the ligand, the number of atoms of each element, and the number of heavy atoms. These features can be divided into three categories: physical interaction energy terms, empirical interaction energy terms, and the ligand information.
For empirical interaction energy terms, the RT feature represents the number of rotatable bonds in the ligand (eq 4), which can be used to approximate the entropy term upon ligand binding. The HB feature, which is taken from the empirical X-Score,18 measures the hydrogen-bonding interactions between H-bond donors (D) and the H-bond acceptors (A). The strength of a hydrogen bond is related to the A–D bond length, as well as the two bond angles involved in H-bond interactions (eq 5). In addition, the VDW obtained from X-Score is calculated by considering all the atom pairs between the ligand and the protein (eq 6). The hydrophobic interaction terms (HP, HM, and HS) obtained from empirical SFs17,65,66 were also considered in our ML models. Hydrophobic pairs (HPs) are calculated by summing the hydrophobic atom pairs formed between the ligand and the protein (eq 7). The overall hydrophobic matching (HM) between the ligand and the protein is calculated with eq 8. The hydrophobic surface (HS) calculates the buried hydrophobic surface of the ligand (eq 9).
| 4 |
| 5 |
| 6 |
| 7 |
| 8 |
| 9 |
For the ligand information, a total of 12 features were considered and the total charges of the ligand, the number of atoms of each element (C, N, O, F, P, S, Cl, Br, I, and H), and the number of heavy atoms were included.
In order to eliminate the influence of unit and scale differences between features, each feature was subsequently standardized using sklearn.preprocessing.StandardScaler class.
2.5. Machine Learning Models
Scikit-Learn 0.24.167 was used to generate all ML models. For linear regressions (LR), ridge regressions (RR), decision trees (DTs), extra trees (ETs), support vector machines (SVMs), random forests (RFs), and deep neural networks (DNN), the classes sklearn.linear_model.LinearRegression, sklearn.linear_model.Ridge, sklearn.tree.DecisionTreeRegressor, sklearn.ensemble.ExtraTreesRegressor, sklearn.svm.SVR, sklearn.ensemble.RandomForest-Regressor, and sklearn.neural_network.MLPRegressor were invoked. We also tested the recently developed extreme gradient boosting (XGB).68 A brief description and tuned hyperparameters of each ML method are shown in Table S1 in the Supporting Information. The ML models are used for predicted binding free energy according to eq 10
| 10 |
where (x1,x2,...xn) is the vector of input features, in which n is the number of features. F is the ML model that adopts a nonlinear function. The output is the predicted binding free energy for protein–ligand complex i. Different models have different ways to define and obtain minimum loss through eq 11
| 11 |
where ΔGpre,i and ΔGexp,i are the binding free energy of the protein–ligand complex from prediction and experiment, respectively, and i and N are the number of samples in the training set.
2.6. Performance Evaluation
The scoring power is gauged by Pearson’s correlation coefficient (Rp) and mean square error (MSE). Rp is the correlation coefficient between predicted binding free energy and experimental binding free energy (eq 12), while MSE is the mean-squared error between the predicted binding free energy and the experimental binding free energy (eq 13), which quantifies the bias in free-energy predictions.
| 12 |
| 13 |
In eqs 12 and 13, ΔGpre,ave and ΔGexp,ave are the average binding free energy from prediction and experiment, respectively, while N is the number of samples in the data set used for testing. The larger the value of Rp, the better is the correlation between them.
3. Results
3.1. Features and Model Analysis
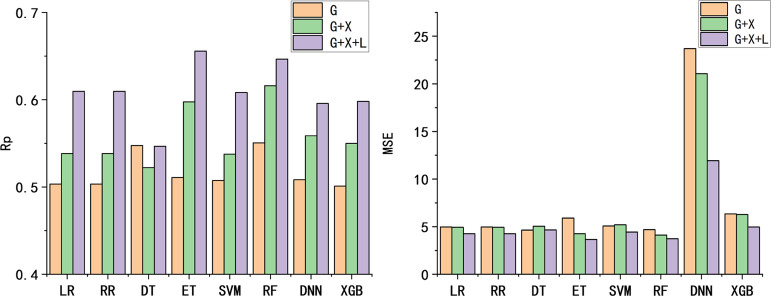
Consistent with previous studies, ML model selection and parameter adjustment are carried out on the basis of the validation set. As mentioned in the Methods section, above, our features contain three categories: GBSA-based (G), X-Score-based (X), and ligand-based entries (L). Accordingly, we used three feature sets, G, G + X, and G + X + L. For each model training, the results were obtained 100 times and the mean values were used as the final results. Figure 1A presents the Rp of eight ML models for the validation set. According to the results on the validation set in Figure 1, Pearson’s correlation coefficient of each model improves as the feature dimensions increase (G < G + X < G + X + L), with the exception of one from the decision tree model (DT). In addition to Pearson’s correlation coefficient, the addition of more features also decreases the MSE. For regression models, especially for ensemble learning-related ET and RF, the increase in feature sets can greatly improve its performance. All these results confirm the effectiveness of selected features in prediction power.
Figure 1.
Performance of eight ML models on the validation set with three different feature sets (G, G + X, and G + X + L). (A) Pearson’s correlation coefficient (Rp). (B) Mean square error (MSE).
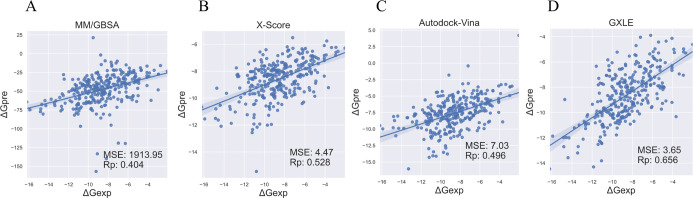
As shown in Figure 1, the extreme tree regression model using G + X + L features (22 features in total) yielded the best performance in the validation set (also see Table S2 in the Supporting Information for detailed data), in which the Rp is 0.656, while the MSE value is 3.65. As expected, use of ML significantly improved the results of MM/GBSA, in which MM/GBSA leads to a huge MSE value of 1913.95 and a low correlation coefficient of 0.404 (Figure 2A). As summarized in Table S2 in the Supporting Information, the worst DT achieved Rp = 0.547, while the best ET achieved Rp = 0.656, which are both better than the empirical scoring function X-Score (0.528) and AutoDock Vina (0.496) (Figure 2B,C). In addition, the Rp of linear regression (LR) is 0.610, which is better than that of linear regression-based X-Score and AutoDock Vina, indicating the effectiveness of our feature selection. As the extreme tree regression model using G + X + L features (labeled GXLE model) produced the best results (Figure 2D), we will use GXLE in the following test studies. According to feature importance analysis results (Figure S1), VDW from X-Score, ΔGSA from MM/GBSA, and the number of heavy atoms from ligands are ranked as top 1, 2, and 3, respectively, among 22 features. It should be noted that they come from different categories of features, which proves the effectiveness of three feature categories.
Figure 2.
Pearson correlation coefficients and mean-squared error between the experimental data and the predicted binding free energies: (A) calculated by MM/GBSA, (B) X-Score, (C) AutoDock Vina, and (D) GXLE on the validation set.
3.2. Results from a Test Set, CASF-2016
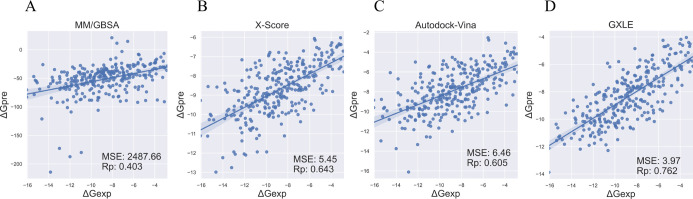
To evaluate the performance of the GXLE model, the CASF-2016 benchmark contained 285 complexes were used as a test set. As is shown in Figure 3, compared with MM/GBSA and X-Score, our GXLE model significantly reduces the error and improves the correlation. In line with the validation test in Figure 2, MM/GBSA yields large error in terms of the MSE value, and its correlation coefficient is only 0.403 (Figure 3A). This is because the entropy term was ignored in our MM/GBSA calculations due to the high computational cost, while the neglection of entropy term would result in the significant overestimation of the predicted binding free energies (see Figure 3A). Interestingly, the experience-based X-Score performs much better than MM/GBSA, while the former has a coefficient of 0.643 and an MSE of 5.45, respectively (Figure 3B). In particular, our GXLE model affords a correlation coefficient of 0.762 and an MSE of 3.97 (Figure 3D), respectively, which is better than X-Score and AutoDock Vina (Figure 3C).
Figure 3.
Pearson correlation coefficients and mean-squared error between the experimental data and predicted binding free energies: (A) calculated by MM/GBSA, (B) X-score, (C) AutoDock Vina, and (D) GXLE on the test set CASF-2016.
3.3. Comparison with Other Scoring Functions
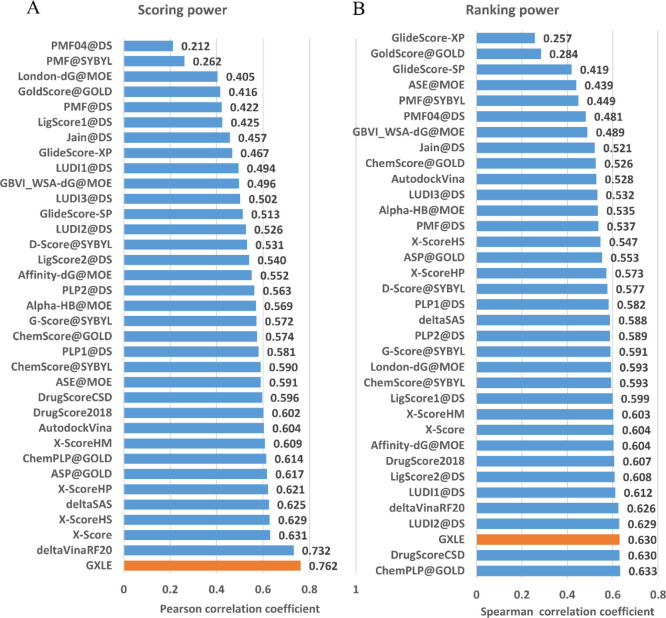
For CASF-2016, more than 30 common scoring functions have been tested and included in the data set. Figure 4 compares our model GXLE against 30 scoring functions included in the CASF-2016 data set, while the detailed data are shown in Table S3 in the Supporting Information.
Figure 4.
Performance of scoring functions on the CASF-2016 benchmark. (A) Scoring power measured by the Pearson correlation coefficient and (B) ranking power measured by the Spearman correlation coefficient. GXLE’s performances are colored orange and other scoring functions’ performances are blue.
Since the training set of the published ΔvinaRF20 contains 140 complexes that have been included in the test set of CASF-2016, we retrained the ΔvinaRF20 by excluding these 140 complexes from CASF-2016. As displayed in Figure 4, the retrained ΔvinaRF20 yielded a Pearson correlation coefficient of 0.732 and a Spearman correlation coefficient of 0.626, respectively. Inspection of Figure 4 shows that our GXLE has a Pearson correlation coefficient of 0.762 and a Spearman correlation coefficient of 0.63, which is among one of the best scoring functions in CASF-2016 data set.
3.4. Extended Application of GXLE
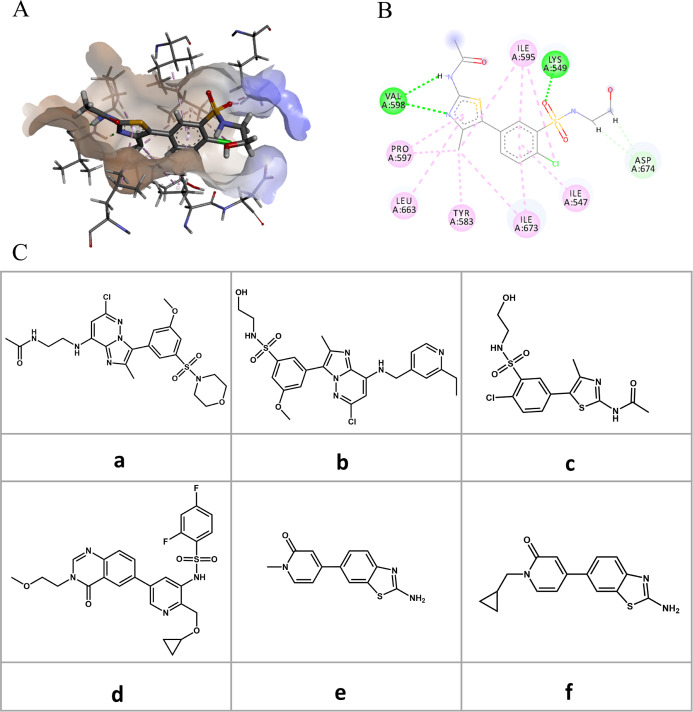
In this section, we examine the ranking power of an extended application of GXLE. For this purpose, we selected a test set (a, b, c, d, e, and f, Figure 5C) of six lipid kinases, PI4KIIIβ inhibitors, whose bioactivities (IC50) are considerably different from each other.69 For the ligand c, the crystal structure of PI4KIIIβ in complex with c was available (PDB id: 4D0L).70 As such, the hydrophilicity and hydrophobicity of protein pocket (Figure 5A) and the interactions of c with the important residues of the binding pocket (Figure 5B) were analyzed first. As shown in Figure 5B, LYS549 and VAL598 form H-bond interactions with c and are key to the binding of inhibitors. Indeed, the vital role of LYS549 in ligand binding has been confirmed experimentally.70 On the basis of PDB 4D0L, five other inhibitors were docked into the binding site of PI4KIIIβ using the SYBYL program. Among different docked poses, the docking pose (I) is able to form the H-bond interactions with LYS549; (II) has the similar binding pose with c; and (III) has the highest docking score and was selected for subsequent scoring. Figure S2 in the Supporting Information shows more details about these and it depicted the selected binding pose for each inhibitor a, b, d, e, and f.
Figure 5.
Interaction between the ligand and the protein in the crystal structure 4D0L. (A) Interaction analysis of the binding pocket, brown for the hydrophobic part and blue for the hydrophilic part. (B) Interaction of the important residues, green for hydrogen bonding and pink for hydrophobicity. (C) Molecular formulas of six inhibitors. The ligand c is contained in the crystal structure (PDB id: 4D0L), while the other ligands (a, b, d, e, and f) are docked to the pocket of the target.
Then, GBSA, X-score,18 D-score,9 PMF-score,22 G-score,14 ChemScore,17 and AutoDock Vina,21 as well as GXLE, were used to rank the binding affinity of the selected poses (Figure S2). Table 2 compares the calculated scores from the seven selected scoring functions and our GXLE model. It is seen that GXLE yielded exactly the same ranking order as experiments (IC50), while all other seven scoring functions failed to give the correct ranking order. Notably, the performance of GBSA is even much poorer than the empirical X-score. All these results indicate that for different ligands of the same target, GXLE shows good performance in its ranking power for the docked structures.
Table 2. Evaluation of the Ranking Power of Selected Scoring Functions Using a Set of PI4KIIIβ Inhibitors.
| ID | IC50 (nM) | GXLE | GBSA | X-score | D-score | PMF-score | G-score | ChemScore | Vina |
|---|---|---|---|---|---|---|---|---|---|
| a | 0.98 | –10.09 | –46.05 | 6.37 | –160.81 | –50.87 | –127.24 | –24.44 | –5.12 |
| b | 6.1 | –9.95 | –52.02 | 6.35 | –150.30 | –54.91 | –125.00 | –27.58 | –4.46 |
| c | 19 | –9.83 | –44.94 | 6.10 | –47.85 | 91.31 | –149.75 | –7.71 | –4.47 |
| d | 220 | –9.68 | –57.55 | 6.30 | –190.07 | –76.92 | –248.21 | –25.67 | –4.77 |
| e | 316 | –6.31 | –29.61 | 5.70 | –86.48 | –66.81 | –162.86 | –23.89 | –6.17 |
| f | 1250 | –3.80 | –20.36 | 5.00 | –83.48 | –31.16 | –125.92 | –12.76 | –2.87 |
3.5. Assessment on Different Biological Targets
In this section, the performance of GXLE with different biological targets will be evaluated. For this purpose, we selected a test set consisting of 10 targets that cover different biological target types. For each target, we collected all the crystal structures of complexes that contain small molecular ligands with their bioactivity data available from the PDBbind general set. Complexes presented in the training set, validation set, or test set were removed (for a PDBid list of all the collected crystal structures of the 10 selected targets, see Table S4 in the Supporting Information). For each target, the performance of GXLE on the collected complexes was evaluated and was characterized by Rp and Rs. Table 3 shows the calculated Rp and Rs values for each target. The Rp values for the 10 targets are in the range of 0.467–0.844 and on average are 0.736. The Rs values are between 0.399 and 0.873, and the average is 0.697. For comparison, using the same data and evaluation method, we also tested MM/GBSA without the entropy term, X-score, and AutoDock Vina. All the results are listed in Table 3. Compared with MM/GBSA without the entropy term, GXLE shows higher Rp and Rs values, respectively, in eight targets. The Rp values of GXLE in six systems are higher than those of X-score, while the Rs values in seven targets are higher than those of X-score. In addition, we also compared our GXLE model against the recently developed geometric and topological invariant-based ML models, which have shown superior performance in benchmark studies.71−74 To this end, we have retrained the open-sourced PSH-ML using the same training set as ours (including 3511 complexes). Then, we have tested it on the same extended test set, as shown Table 3. Compared with PSH-ML, our GXLE model shows slightly higher average Rp and Rs values. Overall, GXLE achieved the highest average values in both Rp and Rs. These results clearly indicate that GXLE can achieve better and more consistent performance on all the test targets, suggesting that it can be applied to a broad range of biological target types.
Table 3. Performances of GXLE, MM/GBSA, X-Score, AutoDock Vina, and PSH-ML Evaluated against a Set Consisting of 10 Selected Diverse Biological Targetsa.
| method |
GXLE |
MM/GBSA |
X-score |
AutoDock
Vina |
PSH-ML |
||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| test target | number | Rp | Rs | Rp | Rs | Rp | Rs | Rp | Rs | Rp | Rs |
| BACE-1 | 73 | 0.833 | 0.746 | 0.836 | 0.783 | 0.810 | 0.711 | 0.660 | 0.710 | 0.836 | 0.752 |
| CHK1 | 15 | 0.777 | 0.737 | 0.687 | 0.293 | 0.736 | 0.564 | 0.876 | 0.787 | 0.924 | 0.755 |
| DPP4 | 13 | 0.467 | 0.399 | 0.197 | 0.250 | 0.456 | 0.285 | 0.191 | 0.316 | 0.711 | 0.301 |
| ER | 7 | 0.844 | 0.857 | 0.794 | 0.786 | 0.642 | 0.857 | 0.601 | 0.750 | 0.391 | 0.571 |
| LTA-4H | 22 | 0.770 | 0.873 | 0.700 | 0.749 | 0.774 | 0.859 | 0.606 | 0.613 | 0.769 | 0.894 |
| P38a | 18 | 0.793 | 0.780 | 0.689 | 0.706 | 0.814 | 0.851 | 0.765 | 0.764 | 0.849 | 0.685 |
| PPAR | 11 | 0.750 | 0.645 | 0.485 | 0.600 | 0.756 | 0.581 | 0.734 | 0.573 | 0.528 | 0.509 |
| PTP1B | 14 | 0.675 | 0.737 | –0.292 | –0.189 | 0.713 | 0.724 | –0.025 | 0.070 | 0.526 | 0.530 |
| thrombin | 15 | 0.840 | 0.679 | 0.926 | 0.821 | 0.823 | 0.707 | 0.621 | 0.546 | 0.874 | 0.732 |
| renin | 22 | 0.611 | 0.514 | –0.165 | 0.225 | 0.398 | 0.463 | 0.187 | 0.213 | 0.601 | 0.423 |
| average values | 0.736 | 0.697 | 0.486 | 0.502 | 0.692 | 0.660 | 0.522 | 0.534 | 0.701 | 0.615 | |
BACE-1, β-secretase 1; CHK1, serine/threonine-protein kinase chk1; DPP4, dipeptidyl peptidase 4; ER, estrogen receptor; LTA-4H, leukotriene A-4 hydrolase; P38a, mitogen-activated protein kinase 14; PPAR-γ, peroxisome proliferator-activated receptor; and PTP1B, protein tyrosine phosphatase 1B.
4. Discussion and Conclusions
A few and simple features taken either from MM/GBSA terms or associated with protein–ligand interactions have been used here to develop the ML-based scoring functions for ligand binding affinity predictions. Among a variety of nonlinear regression ML methods, the extreme tree regression was found to have the best performance. The best model GXLE we trained in this study remarkably improves the accuracy of the prediction compared to MM/GBSA without entropy. On the benchmark CASF-2016, our method achieves a Pearson correlation coefficient of 0.762 in scoring power and a Spearman correlation coefficient of 0.63 in ranking power, which is among one of the best scoring functions contained in CASF-2016 data sets. In particular, our model shows good transferability in its extended ranking power for binding affinity prediction of different ligands of the same target for either the docked structures or crystal structures. Due to both the efficiency and accuracy, our GXLE model is expected to find wide applications in a broad range of protein–ligand complexes. To further improve the predicting power of GXLE, extended training sets comprising the docked complexes40,41,75,76 and more features associated with protein–ligand interactions may be useful.39,77
5. Data and Software Availability
Code for processing data and acquiring features, data related to training set, validation set, and test set, and code for ML-related modeling are available (https://github.com/LinaDongXMU/GXLE).
Acknowledgments
This work was supported by the National Key Research and Development Program of China (2019YFA0906400) and NSFC (nos. 22122305, 22121001, and 22073077). We thank Dr. Jianing Lu and Dr. Junjie Hu for valuable discussions.
Glossary
Abbreviations
- FEP
free-energy perturbation
- TI
thermodynamic integration
- SF
scoring function
- FF
force field
- MM/GBSA
molecular mechanical/generalized Born surface area
- RT
rotatable bonds
- HB
hydrogen-bond interaction
- VDW
van der Waals
- HP
hydrophobic pairs
- HM
hydrophobic matching
- HS
hydrophobic surface
- MSE
mean square error
- LR
linear regression
- RR
ridge regression
- DT
decision tree
- ET
extra tree
- SVM
support vector machine
- RF
random forest
- DNN
deep neural network
- XGB
extreme gradient boosting
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.1c04996.
ML methods and corresponding hyperparameters, performance of different features and methods on the validation set, and performance of various scoring functions on the test set CASF-2016 associated data (PDF)
The authors declare no competing financial interest.
Supplementary Material
References
- Li C.; Deng X.; Zhang W.; Xie X.; Conrad M.; Liu Y.; Angeli J. P. F.; Lai L. Novel Allosteric Activators for Ferroptosis Regulator Glutathione Peroxidase 4. J. Med. Chem. 2019, 62, 266–275. 10.1021/acs.jmedchem.8b00315. [DOI] [PubMed] [Google Scholar]
- Jin Z.; Du X.; Xu Y.; Deng Y.; Liu M.; Zhao Y.; Zhang B.; Li X.; Zhang L.; Peng C.; Duan Y.; Yu J.; Wang L.; Yang K.; Liu F.; Jiang R.; Yang X.; You T.; Liu X.; Yang X.; Bai F.; Liu H.; Liu X.; Guddat L. W.; Xu W.; Xiao G.; Qin C.; Shi Z.; Jiang H.; Rao Z.; Yang H. Structure of M(pro) from SARS-CoV-2 and discovery of its inhibitors. Nature 2020, 582, 289–293. 10.1038/s41586-020-2223-y. [DOI] [PubMed] [Google Scholar]
- Zhang Q.; Sang F.; Qian J.; Lyu S.; Wang W.; Wang Y.; Li Q.; Du L. Identification of novel potential PI3Kalpha inhibitors for cancer therapy. J. Biomol. Struct. Dyn. 2021, 39, 3721–3732. 10.1080/07391102.2020.1771421. [DOI] [PubMed] [Google Scholar]
- Chen J.; Wang X.; Pang L.; Zhang J. Z. H.; Zhu T. Effect of mutations on binding of ligands to guanine riboswitch probed by free energy perturbation and molecular dynamics simulations. Nucleic Acids Res. 2019, 47, 6618–6631. 10.1093/nar/gkz499. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee T.-S.; Allen B. K.; Giese T. J.; Guo Z.; Li P.; Lin C.; McGee T. D. Jr.; Pearlman D. A.; Radak B. K.; Tao Y.; Tsai H.-C.; Xu H.; Sherman W.; York D. M. Alchemical Binding Free Energy Calculations in AMBER20: Advances and Best Practices for Drug Discovery. J. Chem. Inf. Model. 2020, 60, 5595–5623. 10.1021/acs.jcim.0c00613. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scheen J.; Wu W.; Mey A. S. J. S.; Tosco P.; Mackey M.; Michel J. Hybrid Alchemical Free Energy/Machine-Learning Methodology for the Computation of Hydration Free Energies. J. Chem. Inf. Model. 2020, 60, 5331–5339. 10.1021/acs.jcim.0c00600. [DOI] [PubMed] [Google Scholar]
- Steinbrecher T.; Mobley D. L.; Case D. A. Nonlinear scaling schemes for Lennard-Jones interactions in free energy calculations. J. Chem. Phys. 2007, 127, 214108. 10.1063/1.2799191. [DOI] [PubMed] [Google Scholar]
- Bhati A. P.; Wan S.; Wright D. W.; Coveney P. V. Rapid, Accurate, Precise, and Reliable Relative Free Energy Prediction Using Ensemble Based Thermodynamic Integration. J. Chem. Theory Comput. 2017, 13, 210–222. 10.1021/acs.jctc.6b00979. [DOI] [PubMed] [Google Scholar]
- Ewing T. J. A.; Makino S.; Skillman A. G.; Kuntz I. D. DOCK 4.0: Search strategies for automated molecular docking of flexible molecule databases. J. Comput.-Aided Mol. Des. 2001, 15, 411–428. 10.1023/a:1011115820450. [DOI] [PubMed] [Google Scholar]
- Venkatachalam C. M.; Jiang X.; Oldfield T.; Waldman M. LigandFit: a novel method for the shape-directed rapid docking of ligands to protein active sites. J. Mol. Graphics Modell. 2003, 21, 289–307. 10.1016/s1093-3263(02)00164-x. [DOI] [PubMed] [Google Scholar]
- Liu X.; Liu J.; Zhu T.; Zhang L.; He X.; Zhang J. Z. H. PBSA_E: A PBSA-Based Free Energy Estimator for Protein-Ligand Binding Affinity. J. Chem. Inf. Model. 2016, 56, 854–861. 10.1021/acs.jcim.6b00001. [DOI] [PubMed] [Google Scholar]
- Bao J.; He X.; Zhang J. Z. H. Development of a New Scoring Function for Virtual Screening: APBScore. J. Chem. Inf. Model. 2020, 60, 6355–6365. 10.1021/acs.jcim.0c00474. [DOI] [PubMed] [Google Scholar]
- Wang E.; Liu H.; Wang J.; Weng G.; Sun H.; Wang Z.; Kang Y.; Hou T. Development and Evaluation of MM/GBSA Based on a Variable Dielectric GB Model for Predicting Protein-Ligand Binding Affinities. J. Chem. Inf. Model. 2020, 60, 5353–5365. 10.1021/acs.jcim.0c00024. [DOI] [PubMed] [Google Scholar]
- Jones G.; Willett P.; Glen R. C.; Leach A. R.; Taylor R. Development and Validation of a Genetic Algorithm for Flexible Docking. J. Mol. Biol. 1997, 267, 727–748. 10.1006/jmbi.1996.0897. [DOI] [PubMed] [Google Scholar]
- Marchand J.-R.; Knehans T.; Caflisch A.; Vitalis A. An ABSINTH-Based Protocol for Predicting Binding Affinities between Proteins and Small Molecules. J. Chem. Inf. Model. 2020, 60, 5188–5202. 10.1021/acs.jcim.0c00558. [DOI] [PubMed] [Google Scholar]
- Fu H.; Chen H.; Cai W.; Shao X.; Chipot C. BFEE2: Automated, Streamlined, and Accurate Absolute Binding Free-Energy Calculations. J. Chem. Inf. Model. 2021, 61, 2116–2123. 10.1021/acs.jcim.1c00269. [DOI] [PubMed] [Google Scholar]
- Eldridge M. D.; Murray C. W.; Auton T. R.; Paolini G. V.; Mee R. P. Empirical scoring functions: I. The development of a fast empirical scoring function to estimate the binding affinity of ligands in receptor complexes. J. Comput.-Aided Mol. Des. 1997, 11, 425–445. 10.1023/a:1007996124545. [DOI] [PubMed] [Google Scholar]
- Wang R.; Lai L.; Wang S. M. Further development and validation of empirical scoring functions for structure-based binding affinity prediction. J. Comput.-Aided Mol. Des. 2002, 16, 11–26. 10.1023/a:1016357811882. [DOI] [PubMed] [Google Scholar]
- Friesner R. A.; Banks J. L.; et al. Glide: A New Approach for Rapid, Accurate Docking and Scoring. 1. Method and Assessment of Docking Accuracy. J. Med. Chem. 2004, 47, 1739–1749. 10.1021/jm0306430. [DOI] [PubMed] [Google Scholar]
- Halgren T. A.; Murphy R. B.; et al. Glide: A new approach for rapid, accurate docking and scoring. 2. Enrichment factors in database screening. J. Med. Chem. 2004, 47, 1750–1759. 10.1021/jm030644s. [DOI] [PubMed] [Google Scholar]
- Trott O.; Olson A. J. Vina, AutoDock improving the speed and accuracy of docking with a new scoring function, efficient optimization, and multithreading. J. Comput. Chem. 2010, 31, 455–461. 10.1002/jcc.21334. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Muegge I.; Martin Y. C. A general and fast scoring function for protein–ligand interactions: A simplified potential approach. J. Med. Chem. 1999, 42, 791–804. 10.1021/jm980536j. [DOI] [PubMed] [Google Scholar]
- Mooij W. T. M.; Verdonk M. L. General and targeted statistical potentials for protein-ligand interactions. Proteins 2005, 61, 272–287. 10.1002/prot.20588. [DOI] [PubMed] [Google Scholar]
- Velec H. F. G.; Gohlke H.; Klebe G. DrugScore(CSD)-knowledge-based scoring function derived from small molecule crystal data with superior recognition rate of near-native ligand poses and better affinity prediction. J. Med. Chem. 2005, 48, 6296–6303. 10.1021/jm050436v. [DOI] [PubMed] [Google Scholar]
- Wang E.; Sun H.; Wang J.; Wang Z.; Liu H.; Zhang J. Z. H.; Hou T. End-Point Binding Free Energy Calculation with MM/PBSA and MM/GBSA: Strategies and Applications in Drug Design. Chem. Rev. 2019, 119, 9478–9508. 10.1021/acs.chemrev.9b00055. [DOI] [PubMed] [Google Scholar]
- Greenidge P. A.; Kramer C.; Mozziconacci J.-C.; Wolf R. M. MM/GBSA binding energy prediction on the PDBbind data set: successes, failures, and directions for further improvement. J. Chem. Inf. Model. 2013, 53, 201–209. 10.1021/ci300425v. [DOI] [PubMed] [Google Scholar]
- Kollman P. A.; Massova I.; Reyes C.; Kuhn B.; Huo S.; Chong L.; Lee M.; Lee T.; Duan Y.; Wang W.; Donini O.; Cieplak P.; Srinivasan J.; Case D. A.; Cheatham T. E. Calculating Structures and Free Energies of Complex Molecules: Combining Molecular Mechanics and Continuum Models. Acc. Chem. Res. 2000, 33, 889–897. 10.1021/ar000033j. [DOI] [PubMed] [Google Scholar]
- Gohlke H.; Case D. A. Converging free energy estimates: MMPB(GB)SA studies on the protein–protein complex Ras–Raf. J. Comput. Chem. 2004, 25, 238–250. 10.1002/jcc.10379. [DOI] [PubMed] [Google Scholar]
- Massova I.; Kollman P. Combined molecular mechanical and continuum solvent approach (MM-PBSA/GBSA) to predict ligand binding. Perspect. Drug Discovery Des. 2000, 18, 113–135. 10.1023/a:1008763014207. [DOI] [Google Scholar]
- Weiser J.; Shenkin P. S.; Still W. C. Approximate atomic surfaces from linear combinations of pairwise overlaps (LCPO). J. Comput. Chem. 1999, 20, 217–230. . [DOI] [Google Scholar]
- Shen C.; Ding J.; Wang Z.; Cao D.; Ding X.; Hou T. From machine learning to deep learning: Advances in scoring functions for protein–ligand docking. Wiley Interdiscip. Rev.: Comput. Mol. Sci. 2019, 10, e1429 10.1002/wcms.1429. [DOI] [Google Scholar]
- Li H.; Sze K. H.; Lu G.; Ballester P. J. Machine-learning scoring functions for structure-based virtual screening. Wiley Interdiscip. Rev.: Comput. Mol. Sci. 2020, 11, e1478 10.1002/wcms.1478. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shen C.; Hu Y.; Wang Z.; Zhang X.; Zhong H.; Wang G.; Yao X.; Xu L.; Cao D.; Hou T. Can machine learning consistently improve the scoring power of classical scoring functions? Insights into the role of machine learning in scoring functions. Briefings Bioinf. 2021, 22, 497–514. 10.1093/bib/bbz173. [DOI] [PubMed] [Google Scholar]
- Soni A.; Bhat R.; Jayaram B. Improving the binding affinity estimations of protein-ligand complexes using machine-learning facilitated force field method. J. Comput.-Aided Mol. Des. 2020, 34, 817–830. 10.1007/s10822-020-00305-1. [DOI] [PubMed] [Google Scholar]
- Su M.; Feng G.; Liu Z.; Li Y.; Wang R. Tapping on the Black Box: How Is the Scoring Power of a Machine-Learning Scoring Function Dependent on the Training Set?. J. Chem. Inf. Model. 2020, 60, 1122–1136. 10.1021/acs.jcim.9b00714. [DOI] [PubMed] [Google Scholar]
- Tran-Nguyen V. K.; Bret G.; Rognan D. True Accuracy of Fast Scoring Functions to Predict High-Throughput Screening Data from Docking Poses: The Simpler the Better. J. Chem. Inf. Model. 2021, 61, 2788–2797. 10.1021/acs.jcim.1c00292. [DOI] [PubMed] [Google Scholar]
- Ballester P. J.; Mitchell J. B. A machine learning approach to predicting protein-ligand binding affinity with applications to molecular docking. Bioinformatics 2010, 26, 1169–1175. 10.1093/bioinformatics/btq112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ballester P. J.; Schreyer A.; Blundell T. L. Does a more precise chemical description of protein-ligand complexes lead to more accurate prediction of binding affinity?. J. Chem. Inf. Model. 2014, 54, 944–955. 10.1021/ci500091r. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li G. B.; Yang L. L.; Wang W. J.; Li L. L.; Yang S. Y. ID-Score a new empirical scoring function based on a comprehensive set of descriptors related to protein-ligand interactions. J. Chem. Inf. Model. 2013, 53, 592–600. 10.1021/ci300493w. [DOI] [PubMed] [Google Scholar]
- Wang C.; Zhang Y. Improving scoring-docking-screening powers of protein-ligand scoring functions using random forest. J. Comput. Chem. 2017, 38, 169–177. 10.1002/jcc.24667. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lu J.; Hou X.; Wang C.; Zhang Y. Incorporating Explicit Water Molecules and Ligand Conformation Stability in Machine-Learning Scoring Functions. J. Chem. Inf. Model. 2019, 59, 4540–4549. 10.1021/acs.jcim.9b00645. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jimenez J.; Skalic M.; Martinez-Rosell G.; De Fabritiis G. KDEEP: Protein-Ligand Absolute Binding Affinity Prediction via 3D-Convolutional Neural Networks. J. Chem. Inf. Model. 2018, 58, 287–296. 10.1021/acs.jcim.7b00650. [DOI] [PubMed] [Google Scholar]
- Kwon Y.; Shin W. H.; Ko J.; Lee J. AK-Score Accurate Protein-Ligand Binding Affinity Prediction Using an Ensemble of 3D-Convolutional Neural Networks. Int. J. Mol. Sci. 2020, 21, 8424–8440. 10.3390/ijms21228424. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meng Z.; Xia K. Persistent spectral-based machine learning for protein-ligand binding affinity prediction. Sci. Adv. 2021, 7, eabc5329 10.1126/sciadv.abc5329. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jones D.; Kim H.; Zhang X.; Zemla A.; Stevenson G.; Bennett W. F. D.; Kirshner D.; Wong S. E.; Lightstone F. C.; Allen J. E. Improved Protein-Ligand Binding Affinity Prediction with Structure-Based Deep Fusion Inference. J. Chem. Inf. Model. 2021, 61, 1583–1592. 10.1021/acs.jcim.0c01306. [DOI] [PubMed] [Google Scholar]
- Jiang H.; Fan M.; Wang J.; Sarma A.; Mohanty S.; Dokholyan N. V.; Mahdavi M.; Kandemir M. T. Guiding Conventional Protein-Ligand Docking Software with Convolutional Neural Networks. J. Chem. Inf. Model. 2020, 60, 4594–4602. 10.1021/acs.jcim.0c00542. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brown B. P.; Mendenhall J.; Geanes A. R.; Meiler J. General Purpose Structure-Based Drug Discovery Neural Network Score Functions with Human-Interpretable Pharmacophore Maps. J. Chem. Inf. Model. 2021, 61, 603–620. 10.1021/acs.jcim.0c01001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ye W. L.; Shen C.; Xiong G. L.; Ding J. J.; Lu A. P.; Hou T. J.; Cao D. S. Improving Docking-Based Virtual Screening Ability by Integrating Multiple Energy Auxiliary Terms from Molecular Docking Scoring. J. Chem. Inf. Model. 2020, 60, 4216–4230. 10.1021/acs.jcim.9b00977. [DOI] [PubMed] [Google Scholar]
- Yang J.; Shen C.; Huang N. Predicting or Pretending: Artificial Intelligence for Protein-Ligand Interactions Lack of Sufficiently Large and Unbiased Datasets. Front. Pharmacol. 2020, 11, 69. 10.3389/fphar.2020.00069. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang Z.; Zhong W.; Zhao L.; Chen C. Y.-C. Mutual Learning Mechanism for Interpretable Drug-Target Interaction Prediction. J. Phys. Chem. Lett. 2021, 12, 4247–4261. 10.1021/acs.jpclett.1c00867. [DOI] [PubMed] [Google Scholar]
- Gundelach L.; Fox T.; Tautermann C. S.; Skylaris C. K. Protein-ligand free energies of binding from full-protein DFT calculations: convergence and choice of exchange-correlation functional. Phys. Chem. Chem. Phys. 2021, 23, 9381–9393. 10.1039/d1cp00206f. [DOI] [PubMed] [Google Scholar]
- Wei L.; Chi B.; Ren Y.; Rao L.; Wu J.; Shang H.; Liu J.; Xiao Y.; Ma M.; Xu X.; Wan J. Conformation Search Across Multiple-Level Potential-Energy Surfaces (CSAMP): A Strategy for Accurate Prediction of Protein-Ligand Binding Structures. J. Chem. Theory Comput. 2019, 15, 4264–4279. 10.1021/acs.jctc.8b01150. [DOI] [PubMed] [Google Scholar]
- Wang R.; Fang X.; Lu Y.; Wang S. The PDBbind database: Collection of binding affinities for protein-ligand complexes with known three-dimensional structures. J. Med. Chem. 2004, 47, 2977–2980. 10.1021/jm030580l. [DOI] [PubMed] [Google Scholar]
- Liu Z.; Su M.; Han L.; Liu J.; Yang Q.; Li Y.; Wang R. Forging the Basis for Developing Protein-Ligand Interaction Scoring Functions. Acc. Chem. Res. 2017, 50, 302–309. 10.1021/acs.accounts.6b00491. [DOI] [PubMed] [Google Scholar]
- Sheridan R. P. Time-split cross-validation as a method for estimating the goodness of prospective prediction. J. Chem. Inf. Model. 2013, 53, 783–790. 10.1021/ci400084k. [DOI] [PubMed] [Google Scholar]
- Su M.; Yang Q.; Du Y.; Feng G.; Liu Z.; Li Y.; Wang R. Comparative Assessment of Scoring Functions: The CASF-2016 Update. J. Chem. Inf. Model. 2019, 59, 895–913. 10.1021/acs.jcim.8b00545. [DOI] [PubMed] [Google Scholar]
- Lee T. S.; Cerutti D. S.; Mermelstein D.; Lin C.; LeGrand S.; Giese T. J.; Roitberg A.; Case D. A.; Walker R. C.; York D. M. GPU-Accelerated Molecular Dynamics and Free Energy Methods in Amber18: Performance Enhancements and New Features. J. Chem. Inf. Model. 2018, 58, 2043–2050. 10.1021/acs.jcim.8b00462. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maier J. A.; Martinez C.; Kasavajhala K.; Wickstrom L.; Hauser K. E.; Simmerling C. ff14SB: Improving the Accuracy of Protein Side Chain and Backbone Parameters from ff99SB. J. Chem. Theory Comput. 2015, 11, 3696–3713. 10.1021/acs.jctc.5b00255. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang J.; Wolf R. M.; Caldwell J. W.; Kollman P. A.; Case D. Development and testing of a general amber force field. J. Comput. Chem. 2004, 25, 1157–1174. 10.1002/jcc.20035. [DOI] [PubMed] [Google Scholar]
- Jakalian A.; Jack D. B.; Bayly C. I. Fast, efficient generation of high-quality atomic charges. AM1-BCC model: II. Parameterization and validation. J. Comput. Chem. 2002, 23, 1623–1641. 10.1002/jcc.10128. [DOI] [PubMed] [Google Scholar]
- Xu L.; Sun H.; Li Y.; Wang J.; Hou T. Assessing the performance of MM/PBSA and MM/GBSA methods. 3. The impact of force fields and ligand charge models. J. Phys. Chem. B 2013, 117, 8408–8421. 10.1021/jp404160y. [DOI] [PubMed] [Google Scholar]
- Jorgensen W. L.; Chandrasekhar J.; Madura J. D.; Impey R. W.; Klein M. L. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 1983, 79, 926–935. 10.1063/1.445869. [DOI] [Google Scholar]
- Kräutler V.; Gunsteren W. F.; Hünenberger P. H. A fast, SHAKE algorithm to solve distance constraint equations for small molecules in molecular dynamics simulations. J. Comput. Chem. 2001, 22, 501–508. . [DOI] [Google Scholar]
- Miller B. R. 3rd; McGee T. D. Jr.; Swails J. M.; Homeyer N.; Gohlke H.; Roitberg A. E. MMPBSA.py: An Efficient Program for End-State Free Energy Calculations. J. Chem. Theory Comput. 2012, 8, 3314–3321. 10.1021/ct300418h. [DOI] [PubMed] [Google Scholar]
- Wang R.; Gao Y.; Lai L. SCORE: A New Empirical Method for Estimating the Binding Affinity of a Protein-Ligand Complex. J. Mol. Model. 1998, 4, 379–394. 10.1007/s008940050096. [DOI] [Google Scholar]
- Böhm H. J. The development of a simple empirical scoring function to estimate the binding constant for a protein-ligand complex of known three-dimensional structure. J. Comput.-Aided Mol. Des. 1994, 8, 243–256. 10.1007/bf00126743. [DOI] [PubMed] [Google Scholar]
- Pedregosa F.; Varoquaux G. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Chen T.; Guestrin C.. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining; Krishnapuram B., Shah A., Aggarwal C., Shen D., Rastogi R., Eds.; ACM: San Francisco, CA, 2016; pp 785–794.
- Tian S.; Zeng J.; Liu X.; Chen J.; Zhang J. Z. H.; Zhu T. Understanding the selectivity of inhibitors toward PI4KIIIalpha and PI4KIIIbeta based molecular modeling. Phys. Chem. Chem. Phys. 2019, 21, 22103–22112. 10.1039/c9cp03598b. [DOI] [PubMed] [Google Scholar]
- Burke J. E.; Inglis A. J.; Perisic O.; Masson G. R.; McLaughlin S. H.; Rutaganira F.; Shokat K. M.; Williams R. L. Structures of PI4KIIIbeta complexes show simultaneous recruitment of Rab11 and its effectors. Science 2014, 344, 1035–1038. 10.1126/science.1253397. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cang Z.; Wei G. W. TopologyNet: Topology based deep convolutional and multi-task neural networks for biomolecular property predictions. PLoS Comput. Biol. 2017, 13, e1005690 10.1371/journal.pcbi.1005690. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cang Z.; Mu L.; Wei G. W. Representability of algebraic topology for biomolecules in machine learning based scoring and virtual screening. PLoS Comput. Biol. 2018, 14, e1005929 10.1371/journal.pcbi.1005929. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu X.; Feng H.; Wu J.; Xia K. Persistent spectral hypergraph based machine learning (PSH-ML) for protein-ligand binding affinity prediction. Briefings Bioinf. 2021, 22, bbab127. 10.1093/bib/bbab127. [DOI] [PubMed] [Google Scholar]
- Wee J.; Xia K. Forman persistent Ricci curvature (FPRC)-based machine learning models for protein-ligand binding affinity prediction. Briefings Bioinf. 2021, 22, bbab136. 10.1093/bib/bbab136. [DOI] [PubMed] [Google Scholar]
- Bao J.; He X.; Zhang J. Z. H. DeepBSP-a Machine Learning Method for Accurate Prediction of Protein-Ligand Docking Structures. J. Chem. Inf. Model. 2021, 61, 2231–2240. 10.1021/acs.jcim.1c00334. [DOI] [PubMed] [Google Scholar]
- Stein R. M.; Yang Y.; Balius T. E.; O’Meara M. J.; Lyu J.; Young J.; Tang K.; Shoichet B. K.; Irwin J. J. Property-Unmatched Decoys in Docking Benchmarks. J. Chem. Inf. Model. 2021, 61, 699–714. 10.1021/acs.jcim.0c00598. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wee J.; Xia K. Ollivier Persistent Ricci Curvature-Based Machine Learning for the Protein-Ligand Binding Affinity Prediction. J. Chem. Inf. Model. 2021, 61, 1617–1626. 10.1021/acs.jcim.0c01415. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.