Abstract
Volumetric 3D printing motivated by computed axial lithography enables rapid printing of homogeneous parts but requires a high dimensionality gradient-descent optimization to calculate image sets. Here we introduce a new, simpler approach to image-computation that algebraically optimizes a model of the printed object, significantly improving print accuracy of complex parts under imperfect material and optical precision by improving optical dose contrast between the target and surrounding regions. Quality metrics for volumetric printing are defined and shown to be significantly improved by the new algorithm. The approach is extended beyond binary printing to grayscale control of conversion to enable functionally graded materials. The flexibility of the technique is digitally demonstrated with realistic projector point spread functions, printing around occluding structures, printing with restricted angular range, and incorporation of materials chemistry such as inhibition. Finally, simulations show that the method facilitates new printing modalities such as printing into flat, rather than cylindrical packages to extend the applications of volumetric printing.
Keywords: Volumetric, VAM, CAL, Computation, Object, Optimization
INTRODUCTION
Multi-step additive manufacturing (AM) is being pursued for many diverse applications [1] like: printing optics [2]-[4], microfluidics [5]-[7], composites requiring overprinting [8], [9], regenerative medicine [10]-[14], etc. However, multistep processes have some inherent challenges. From extrusion-based techniques to stereolithographic [15] printing, they struggle with three main challenges: 1. Structures must be connected and supported, 2. new printing-material must be transported to the part during the print, and 3. printed parts suffer from layering effects [16]. Challenge #1 has been addressed by a variety of approaches [17], but these present additional steps that slow down printing, and the final part-options are ultimately still limited. Challenge #2 not only limits print speed, but limits the resins that can be used for printing; e.g. printing cannot be done into solids, and the mechanical properties of parts are ultimately limited by the viscosity of the printing-resins [18], [19]. Challenge #3 is tolerable for some applications, but for others (e.g. printing optics, or parts that must be uniform in modulus), it can cause inhomogeneities in material properties (e.g. refractive index, modulus, chemical functionality, etc.) that limit its applications, and it is a problem that the field of AM is still working to solve.
The relatively new field of Volumetric Additive Manufacturing (VAM) performs printing in a single lithographic step [20]-[22]. While some approaches rely on two-color chemistry to print layer-by-layer in a fixed volume of resin [23], the most general VAM method to print into a single-photon absorbing photosensitive resin does so tomographically. In tomographic VAM printing (Fig. 1), a series of 2D optical patterns are projected into a rotating volume of photosensitive liquid resin. Over the course of tens of seconds to a few minutes, the accumulated optical dose distribution polymerizes the material, resulting in an arbitrary 3D structure, and the printed part is removed from the remaining liquid resin. VAM is free of many of the constraints inherent to multi-step AM. Most notably, non-contiguous parts become possible, layering effects are eliminated, and the lack of material movement mid-print enables high-viscosity resins, with no penalty to print-time, opening the doors to a host of new material properties [22]. However, a lack of control over optical dose delivery limits the scope of VAM applications.
Figure 1*.
Overview of tomographic VAM concept. (A*) Computed images, optically projected into a vial of photosensitive resin. (B) Cross-section of accumulated optical dose distribution (normalized units of dose). (C) Perfectly-gelled cross section of a “thinker”; resin gels where the optical dose is above a threshold, forming a 3D printed part that is removed from remaining liquid resin.
*Fig 1A reproduced courtesy of the American Association for the Advancement of Science (AAAS).
VAM tomographic computation methods that insufficiently control dose delivery can cause errors in the shape of a final gelled part, either for purely mathematical reasons or because they require perfect optics and materials. Real VAM is enabled by a combination of imperfect optics, material science, and computation. While significant progress has been reported on optics and materials [20]-[22], there is a lack of analysis in the literature about the inverse math problem of computing the images that, when projected into resin, integrate together to print a part [24]. An image-computation algorithm yielding perfectly-shaped gelation for complex parts, even with imperfect optics and materials, could expand the range of structures printable by tomographic VAM. Increased control over dose could also allow for control over resin conversion beyond just the state of gelation.
The typical objective of 3D polymeric printing generally, and VAM specifically, is to fabricate a 3D part in which voxels receive local optical dose to be either above or below the gelation threshold of the resin. We refer to this here as Binary VAM printing. Note that while optical dose is defined as the product of intensity and time, the dose to gelation in real resins changes with intensity (i.e. nonreciprocity [25], [26]), requiring a calibration step to determine dose to gelation for a given intensity. The VAM printing geometry introduced in [20], in which images are projected orthogonally to the resin’s axis of rotation (Fig. 1A), can be considered as a collection of independent 2D reconstruction problems. For each horizontal 2D slice-region in the resin (e.g. shown in red in Fig.1A), the computational problem is to choose the set of 1D projected images that integrate together to exceed a dose-to-gelation threshold for in-part voxels, while remaining below this threshold for out-of-part voxels, thus printing a desired geometry (Fig. 1B, C).
The Binary VAM computation problem has solutions necessarily involving various compromises because the projector images are constrained to be non-negative in intensity. This precludes the direct application of the well-known Filtered Back Projection (FBP) algorithm [27] which, although providing image sets to perfectly reconstruct objects (in the continuous limit and under ideal assumptions), produces images with negative intensity. Any non-negative image set solution can only approximate an ideal dose distribution, and must rely on a material non-linearity, like a gelation threshold, to convert a non-ideal optical dose to an ideal printed shape.
The most easily implemented methods of computing image sets for Binary VAM use FBP with its negative values set to zero [21] or offset to zero by a constant. However, this modification results in poor reconstructions with unwanted extra gelation outside of the desired part. Previous approaches [20], [22] mitigate this problem by using gradient-descent optimization to adjust image sets to improve the volumetric dose reconstruction. While these methods do, in fact, improve the outcome, VAM computation could significantly benefit from improvement in three areas: ease of implementation and use, computational flexibility, and print accuracy under material and optical imprecision.
Here we show that algebraically optimizing directly on the structure, instead of the set of external projection images, enables notable improvement in these areas. We refer to this approach as object-space model optimization (OSMO), and we discuss multiple advancements: 1. Print Accuracy. For complex parts, prior methods suffer from errors in the shape of a final part, especially when optical or material precision is imperfect. We show that by improving optical dose contrast between the target and surrounding regions, OSMO produces dose-reconstructions that can tolerate optical and material uncertainties, while still resulting in perfectly gelled prints. 2. Flexibility. We show that this approach naturally allows for the application of object-space constraints such as dose-limits, as well as the application of object-space physical models, such as resin oxygen inhibition, Gaussian beam models, and occlusions for over-printing applications. 3. Ease of implementation and use. The approach is intuitive and includes only two parameters, both of which directly set reconstruction dose constraints. While these parameters afford easy dose control, tuning them from their default values is unnecessary for fast and reliable convergence to desirable reconstructions. OSMO is easy to code in a handful of lines, and consists of only four algebraic steps per iteration.
The ease of use and flexibility of this approach additionally facilitate VAM modalities that do not yet exist in the field, but that could enable new applications of VAM. This includes new printing geometries that would enable printing into non-cylindrical packages such as flat slabs without index-matching baths. It also includes the problem of printing arbitrary functionally graded materials by controlling the degree of polymerization – not just the state of gelation – throughout a printed part, a problem that we refer to as Grayscale VAM. We conclude by discussing how the availability of generalized, efficient, and simple image-computation algorithms could help enable new applications in the field of VAM, while avoiding the need for researchers to understand and tune complex computation algorithms.
Section 1: Image Computation for Binary VAM Printing
In this section, we present an algebraic object space model optimization (OSMO) algorithm for computing image sets to 3D-print arbitrary structures in gel-threshold resins. The algorithm is easy to implement and run, it is flexible, and it yields improved accuracy compared to previously published alternatives, and has only two simple parameters that directly tune reconstruction properties in object space. We first describe the algorithm, we define and discuss reconstruction quality metrics, and we consider how to choose the two constraint parameters to achieve a desired balance of reconstruction quality metrics. We discuss an object-filtering step to reduce the number of OSMO iterations needed for convergence, and we compare the algorithm to previous methods. Note that the 2D reconstructions shown here can be trivially extended to 3D as a stack of independent 2D reconstructions for the printing geometry shown in Fig. 1. Computation for new printing geometries that cannot be decoupled into independent 2D regions is more challenging and is discussed in Section 4, but remains algorithmically unchanged from the basic 2D case.
S.1.1: OSMO Algorithm for Binary VAM
For a simple VAM projection model where each projection beam is assumed to be non-diverging, and attenuation through the resin obeys Beer-Lambert exponential intensity decay [28], transformation between volumetric dose and image set is well-described by the Attenuated Radon Transform (ART) [20], [22]. Back projection (projection from image-set into volume), as is physically implemented while printing, is similarly modeled with exponentially attenuated rays. Formally, back projection is the adjoint of the forward projection operator (from volume to image set) or, in the discrete case, its matrix transpose. The simplest method of generating an image set from a desired object is to mathematically perform a forward projection from object to image set, using the ART. However, back-projecting the resultant image-set results in a blurred reconstruction, a consequence of the suppressed high spatial frequencies inherent to forward then back projecting in a radial geometry [27]. Fig. 2, shows a target object, a binary model of the object, and the reconstructed dose that results from forward projecting the model, then back projecting the resultant set of images. Here, instead of optimizing the intermediate image-set to avoid this blurring, we instead iteratively optimize a model of the desired structure, which, when then used to compute an image set, results in a desirable dose reconstruction.
Figure 2.
Dose reconstruction via forward projecting a binary model of a target geometry, then back projecting the resultant set of images. The reconstruction is blurred due to suppressed high spatial frequencies inherent to forward then back projecting. Instead of optimizing image intensities in projection-space to improve the reconstructed dose, we will instead optimize the model to improve dose. This first reconstruction serves as an initial step in the model-optimization algorithm shown in the next figure. Note that since all projection values are non-negative in this case (as no filtering nor thresholding was applied), they can be represented by intensities with no modification.
The model can contain negative values, however it yields image sets and dose reconstructions that are nonnegative, and thus physically realizable. The process of optimizing a model is shown in Fig. 3A. The process of computing a non-negative image set (and its dose reconstruction) from a given model is shown in Fig. 3B – this process is used during the optimization procedure (Fig. 3A), as well as to compute a final image set and reconstruction. In this process, the model is forward-projected, and resultant negative image-values are set to zero. This image set is then back projected to form a reconstruction. The reconstruction is then normalized in preparation for optimization calculations (shown in Fig. 3A), or to produce a final reconstruction. Once optimization is complete, with a desired image set computed, the image set is scaled to match the intensity of a real optical projection system.
Figure 3.
Object space model optimization (OSMO) algorithm for binary-gelation VAM printing. (A) One model-update iteration of the OSMO loop. Each model in the loop produces a dose-reconstruction by the process shown in (B) forward projection, clipping any resultant negative values to zero, then back-projecting and normalizing to form a dose-reconstruction. Negative values must be clipped to convert projections to physically realizable intensities. Note that, unlike all subsequent models, the initial model (Fig. 2) has no negative values in its projections, and thus does not require a clipping step. (A, Left Column) A given ith model (in this case, the initial model is pictured) produces a reconstruction. (A, Step 1) Unwanted extra dose in the out-of-part regions of the reconstruction are computed and subtracted from the ith model to form an intermediate model. Only the extra dose that lies above a lower threshold, Dl, is included. (A, Middle Column) The intermediate model is then used to compute a dose-reconstruction. (A, Step 2) The prior step of subtracting out-of-part values from the model, inadvertently reduces some desired dose in the in-part regions. This missing in-part dose is calculated by comparing the in-part reconstruction voxels to an upper threshold, Dh. These values are then added to the intermediate model to form a (i+1)st model, completing one model-update iteration. (B) The model produced by m iterations, the dose reconstruction it produces, and the resultant perfectly gelled part. Computationally, the gel threshold is modeled by setting all voxels above a gelation-dose to unity, and setting all voxels below that dose to zero.
The OSMO algorithm (Fig. 3A) tries to push in-part dose to be above an upper threshold Dh, and out-of-part dose to be below a lower threshold Dl by adjusting the model. Increasing the value of an in-part voxel in a model will increase the corresponding voxel in the resultant dose reconstruction. However, it will also increase dose in other reconstruction voxels, some of which may be out-of-part. These unwanted out-of-part doses can then be reduced by decreasing their corresponding model voxels. The OSMO algorithm alternates between increasing in-part model voxels and decreasing out-of-part model voxels to achieve a model that yields a desirable reconstruction. The algorithm can be mathematically defined as follows:
Let fT be a target function (the desired geometry to print). Let P be any forward-projection operator (e.g. the ART), and P* the corresponding back-projection operator. That is, PfT is the forward projection of fT, from object to image set, and the dose reconstruction P*PfT is the back projection of that image set, back into object space. Let N be a normalizing operator that divides an input by its maximum. Let Dl and Dh be fixed high and low dose-threshold values, where 0 < Dl < Dh < 1. Let Mj,j be the object model after j iterations, where the initial model is defined to be M0,0 = fT. Lastly, let fj,j = NP*max{0, P Mj,j}. That is, the model is forward projected, any resultant negative values are set to zero, the result is back projected, and the reconstruction is normalized. Then, the steps to update a model Mj,j by one iteration to Mj+1,j+1 are as follows:
STEP 1: Update the model by subtracting from out-of-part voxels with an excess of dose. For only the out-of-part voxels (in-part voxels remain unchanged from previous model, Mj,j):
| (1) |
| (2) |
STEP 2: Update the model by adding missing dose to the in-part voxels. For only in-part voxels (out-of-part voxels remain unchanged from Mj+1,j):
| (3) |
| (4) |
The max{} operation in STEP 1 means that for each out-of-part voxel, some extra dose is subtracted from the previous model, but not all way to zero; instead, the value is subtracted only down to Dl. Similarly, the max{} operation in STEP 2 means that for each in-part voxel, some extra dose is added to the previous model, but only to reach the value of Dh, not to reach the highest-possible value of 1. Instead of trying to achieve a perfect reconstruction (a binary dose distribution), the algorithm is essentially pushing the reconstruction towards a reduced-contrast solution, allowing the in-part and out-of-part regions to be non-uniform in dose, as long as they lie above and below Dh and Dl, respectively. Thus, the two parameters have physical meaning in the object-space; they set the lower and upper goal-bounds on in-part and out-of-part dose, respectively.
This algorithm is succinct and easy to code, especially in any language that includes projection functions (see the supplemental information for a sample implementation in Matlab). It is also easy to understand, as computations are made in object space, not in the more abstract set of writing-images, and it has only two parameters, both which directly correspond to object space dose constraints.
The two parameters, Dl and Dh, push the solution in contradictory directions; one enforces a decrease of out-of-part dose, and one an increase of in-part dose. The choice of these values affects competing aspects of reconstruction quality. Before discussing how to best choose these values, we must first discuss what our objectives should be; that is, what makes for an accurate reconstruction.
S.1.2: Reconstruction quality metrics.
We define three metrics for evaluating the quality of a reconstruction: Voxel Error Rate (VER), Process Window (PW) size, and In-Part Dose-Range (IPDR). All three are simplest to understand while viewing in-part and out-of-part histograms of reconstruction dose, e.g. as shown in Fig. 4. In normalized units of dose, a perfect reconstruction would yield an out-of-part histogram with values only at 0, and an in-part histogram with values only at 1. In reality, accurate reconstructions yield two non-overlapping histogram peaks, such that when the gelation threshold lies between them, all in-part voxels gel, while all out-of-part voxels do not. An example of a reconstruction with non-overlapping in-part and out-of-part dose histograms is shown in Fig. 4.
Figure 4.
Reconstruction Quality Metrics. (A) A target geometry to be printed. (B) An optimized dose-reconstruction, shown in normalized units of dose. The parameter values were Dl = 0.6 and Dh = 0.8. (C) Voxel Error Rate (VER) converging to zero. (D) The distribution of doses in the reconstruction for the in-part and out-of-part regions. Since the histograms do not overlap, VER is 0, and thus the gel threshold is above all out-of-part voxels, and below all in-part voxels. Therefore, this dose-distribution will print a part that theoretically exactly matches the target geometry. The Process Window is the distance between histograms, and represents room for error with optics or materials, without a change in the final gelled shape. As long as dose is applied such that the gel threshold lies within the process window, the part will gel in the correct shape. The In-Part Dose Range (IPDR) is the range of doses, as a fraction of maximum dose, that in-part voxels receive.
We define Voxel Error Rate, to quantify histogram overlap, as VER = W/N, where W is the number of out-of-part voxels that receive more dose than the lowest-dosed in-part voxel, and N is the total number of voxels in the reconstruction. Graphically, VER is the area of the out-of-part histogram that overlaps with the in-part histogram, normalized to the sum of the histogram areas. Any overlap between histograms indicates errors in the final gelled part, as any gel threshold will result in some error voxels (voxels that gelled when they should not have, and vice versa). VER is roughly proportional to Jaccard Index [20] for gelled reconstructions. However, VER does not require that a gel threshold be chosen, and thus is a more fundamental to the evaluation of tomographic dose reconstructions than Jaccard Index. For any reconstruction with VER > 0, the final part will not match the target function, even when the gelation threshold is an ideal step function positioned optimally between the dose histograms.
We define Process Window to be the difference, in normalized units of dose, between the highest-dose out-of-part voxel, and the lowest-dose in-part voxel. Graphically, this is simply the distance between the inner edges of the histograms; it is negative when VER > 0. A large positive process window can allow for, without penalty to VER, a non-ideal gel threshold that occurs over a range of dose, for non-uniformities in optics, for uncertainty in the gel threshold dose location (e.g. due to imprecisions in measuring photo-initiator concentration when mixing resins), etc. Therefore, a large process window is desirable, as it makes it practically easier to gel the inpart voxels, without inadvertently delivering too much dose and also gelling any out-of-part voxels.
Lastly, we define In-Part Dose Range (IPDR) to be 1 minus the lowest dose in-part voxel, in normalized units of dose. It is an indication of dose-variation of in-part-voxels. This metric is important in VAM printing because we cannot deliver all optical dose instantly. Instead, it is delivered over time, by a projection system with limited dynamic range. A consequence of a large IPDR is that high-dose in-part voxels can surpass the gel threshold before the rest of the part. Once this happens, these gelled regions (with their increased index of refraction) will scatter subsequent writing beams, interfering with the completion of dose-delivery to the rest of the part. We will discuss this effect, and how to computationally mitigate it, in greater detail in section 3.3. All else equal, reconstructions with a small IPDR are desirable.
S.1.3: Choosing the two parameter values.
The choice of the two parameter values must reflect the fact that a perfect dose reconstruction (where dose is delivered only to in-part regions) is impossible without negative image values. If a perfect dose-reconstruction were possible, the parameter values would be chosen to be Dl = 0, and Dh = 1. Then the algorithm would push out-of-part dose to zero, and in-part dose to 1 (in normalized units of dose). However, since such a reconstruction is not possible (due to the lack of negative-intensity images), choosing these extreme values results in a poor reconstruction with non-zero VER (thus leading to poor print fidelity upon gelation). Relaxing these constraints reduces the contrast of the dose-reconstruction but can drive VER to zero. This is because choosing 0 < Dl, and Dh < 1 increases the freedom of the reconstruction, since voxels are constrained only to a range, not to particular values; in-part doses are above Dh, while out-of-part doses are below Dl. This produces reconstructions with reduced contrast, but with improved VER.
Tuning the parameter values for each new target is unnecessary for fast and reliable convergence to desirable reconstructions. While some parameter optimization may slightly improve particular target-functions, the default values Dl = 0.85, and Dh = 0.9 resulted in reliable convergence to a VER of zero for all targets we tested, with the number of iterations required for convergence depending on target-complexity, and ranging from tens to hundreds of iterations. Choosing lower values, such as Dl = 0.45, Dh = 0.5, results in a slightly larger process window, which is unsurprising, as the increase in IPDR relaxes some reconstruction constraints for in-part voxels - see the Supplemental Information (SI-Fig.1) for an example of this. Similarly, choosing values such as Dl = 0.99, and Dh = 1 results in a very small IPDR, at the cost process window size, and, for complex target structures, even reduced VER. Similarly, it is possible to request a larger than possible process window size from the algorithm, by choosing excessively separated parameter values. E.g. for all but simple targets, a choice like Dl = 0.2, and Dh = 0.9 will not only fail to increase process window size, but it may also increase VER from zero. Lastly, as the choice of parameter values changes the magnitude by which object-voxel doses change upon each iteration, they can slightly affect the rate of convergence of the algorithm. Regardless of optimization possibilities, the default values yield reconstructions that improve upon previous methods, as discussed in section 1.5.
S.1.4: Object-Space Frequency Filtering – An Improved Initial Model.
The OSMO algorithm reliably converges with the target geometry as the initial model. However, an improved initial model can significantly reduce the number of iterations needed to converge to the same result, saving computational run time. The initial model does not change the target nor any reconstruction constraints, but rather serves as initial guess for the OSMO algorithm. Using the target as an initial model results in an initially blurred reconstruction (Fig. 2), a consequence of the suppressed high spatial frequencies inherent to forward then back projecting in a radial geometry. FBP compensates for this by emphasizing high spatial frequencies with a linear frequency filter applied to the forward projected images [27]. While this results in negative-intensity projector image values, clipping these image-space values to zero yields an improved initial guess for gradient descent image-optimization methods [20]. We can use the same concept with OSMO by applying an object-space frequency filter to the target to generate an initial model.
An object-space filter for the standard tomographic geometry (Fig. 1) is a 2D linear frequency-ramp of the form fr, where is a radial coordinate in the Fourier-spectrum of a 2D object-slice, with Cartesian coordinates fx and fy. It is one dimension larger than FBP’s projection-space filter since it applies to the object, and not to the image-set. Unlike FBP’s filtering step which is computed for each 1D projection image, the object-space filtering step is computed for each object slice. This 2D filter is the same as is used in back projection filtration in which f = R2DP*Pf, where f is a 2D target slice, R2D is an operator applying fr, and P and P* are forward and back projection operators. That is, just as P*R1D is a left inverse of P in FBP (where R1D is the operator applying FBP’s 1D filter), R2DP* is also a left inverse of P. The difference between the filters emerges when negative-clipping projector-image values, since the negative values produced by the 2D filter are first smoothed by forward projection, while FBP’s 1D filter produces negative values after forward projection occurs. An example of the application of this 2D filter to a target function is shown in Fig. 5.
Figure 5.
Frequency-filtering a target to generate an improved initial model. This reduces the number of algorithm iterations necessary to converge to an accurate solution, compared to simply using the target as the initial model. For this target, with Dl = 0.85 and Dh = 0.9, required iterations were reduced by 25%. (A) A target geometry. (B) An initial reconstruction that results from using the target geometry as the initial model, a process illustrated in Fig. 3. (C) The target geometry with a 2D frequency ramp filter applied. (D) The initial reconstruction that results from using the filtered target as a model. Both initial models converge to qualitatively identical final dose reconstructions, with identical quality-metric values.
A filtered target does not provide a reconstruction with a VER of zero; iterative optimization is needed to achieve that because the forward projection of filtered target results in negative numbers. Nor does initial filtering change the quality metrics of a final optimized reconstruction. However, it does reduce the number of iterations needed to converge to a VER of zero. E.g., for the target in Fig. 5, filtering reduces the number of OSMO iterations to reach a VER of zero by 25% (with Dl = 0.85, Dh = 0.9). The exact iteration savings depends on the particular target and on the choice of parameter values, and can even be negligible. However, we observe significant iteration savings in most cases, at only the cost of the filtering step, which takes about 1% the run time of a single OSMO iteration. In summary, we find that applying a 2D ramp filter to the initial model significantly reduces the run time of the OSMO algorithm.
S.1.5: Performance Comparison Example to Prior Methods.
Here, we consider a binary VAM reconstruction example to compare OSMO to the state of the art in the literature: the CAL algorithm [20]. The original computed axial lithography (CAL) method [20] (referred to as “CAL2019” in what follows) uses gradient-descent optimization on image-sets. It converges to a VER of zero for simple geometries, and is available on GitHub [29]. Another recent method [30] based on thresholded FBP, reports a relatively large number of voxel errors even for a simple geometry, so we do not show comparison calculations to this method. We consider an example reconstruction to compare the performance of OSMO and CAL2019. To ensure that CAL2019 parameters were chosen with expertise for this comparison, the algorithm was run by a member (authored here) of the research group that maintains it.
We find that OSMO improves upon the reconstruction quality of CAL2019. Fig. 6A shows the object used for this comparison: a resolution target. Fig 6B shows the convergence of VER towards zero for the first 30 iterations of CAL2019 and OSMO. The initial VER for OSMO is slightly lower than that for CAL2019 because OSMO uses an object-space filtered initial guess while CAL2019 uses a clipped FBP initial guess. Both algorithms show an initial increase in VER as they work towards a reconstruction with the requested IPDR. CAL2019 plateaus to a VER near zero (~10 −5), while further iterations of OSMO drive the reconstruction past a VER of zero to a process window size of 5.9% of the maximum dose. While the number CAL2019 error voxels are few, its lack of process window means that a physical implementation would require perfect precision in optics and materials to achieve that low level of gelation errors. The OSMO 5.9% process window allows for some errors in material and dose-delivery, while still resulting in perfect gelation. See the supplemental information (SI-Figs.2-3) for exposure timing and optical non-uniformity error simulations for both CAL2019 and OSMO.
Figure 6.
Convergence comparison example with the previously-published CAL2019 method. (A) Binary target geometry. (B) VER convergence for the first 30 iterations of the OSMO and CAL2019 methods. Note that the initial VER value for OSMO is slightly smaller than for CAL2019, due to different initial guesses: 2D model filtering versus clipped FBP, respectively. While CAL2019 plateaus to a small VER near zero (~10 −5), further iterations of OSMO drive the reconstruction beyond a VER of zero, to a positive process window size. The CAL2019 reconstruction had an IPDR of 0.12 and a process window size of −0.23%. (C) & (D) OSMO dose reconstruction and histogram. The OSMO parameter values were Dl = 0.83, and Dh = 0.9, VER = 0, and the process window size was 5.9% of the maximum dose with an IPDR of 0.11. (E) & (F) CAL2019 dose reconstruction and histogram. The histogram overlap yields a non-zero VER value with no positive process window size. Since VER > 0, a print would have voxels with gelation error. While these voxels would be few, the lack of a process window would result in further error in a physical implementation, due to imperfect precision in optics and materials.
Both methods take on the order of a few seconds per iteration on a typical desktop computer. CAL2019 has six hyperparameters which control: (1) learning rate, (2) descent momentum, (3) prescribed or floating threshold (note: prescribed threshold, not originally in CAL2019, was added to make a fair comparison between OSMO and CAL2019), (4) non-negativity constraint relaxation, (5) width of sigmoid thresholding function, and (6) weight of robust thresholding heuristic. For more details, the reader is directed to the Supplementary Information of Kelly et al.[20]. Although, typically only the first two or three are manually tuned to arrive at a sufficient reconstruction given a new structure. OSMO has 2 parameters whose default values do not require tuning to produce a positive process window size for a new structure. OSMO uses four projection operations per iteration – twice the number that CAL2019 uses. In Matlab, with its relatively slow projections (compared to e.g. [31]), OSMO takes about 3 times longer per iteration than CAL2019, however OSMO iterations produce an improved reconstruction, and some of that additional time may be offset by a lack of parameter-tuning.
While this comparison (Fig. 6) is illustrated using a 2D object of relatively high complexity, it supports the observation that OSMO typically results in quality metric improvements - especially in increased process window size. OSMO’s improvement in final output, coupled with its simplicity - both to run and to code - provides a significant advancement in computation for binary VAM.
Section 2: Image Computation for Grayscale VAM Printing
One of the appealing features inherent to VAM is that it is possible to cure resin with spatial control over the dose delivered, creating functionally graded properties through a printed part. Whether the objective is to control modulus, refractive index, or any other dose-tunable property, arbitrary 3D property control requires arbitrary 3D dose control. The particular dose values required depend on the property-dose response of a given material, requiring a material calibration step. What we call the Grayscale VAM printing problem is to compute the image-set that will reconstruct such an optical dose distribution. Here we present an object space approach to image computation for grayscale VAM. As with binary VAM, we seek to compute a model that will yield a desirable dose reconstruction by the process shown in Fig. 3B. This can be done with two steps: first by computing an initial model, and then by adjusting that model to improve the final reconstruction.
An initial model will produce a grayscale dose reconstruction that suffers from reduced contrast and from nonuniformities. It can be computed by the same process as for binary VAM: by applying a frequency filter to the object, as detailed in Section 1.3. Fig. 7A-C shows a grayscale target, the initial model produced by filtering the target, and the dose reconstruction produced by that model. This initial reconstruction (Fig. 7C) exhibits reduced contrast, as well as non-uniformities in each region that should be constant in dose. This is unsurprising, as grayscale reconstructions are highly constrained since they attempt to achieve a particular function value at every point in a reconstruction – an impossible task without negative image intensities.
Figure 7.
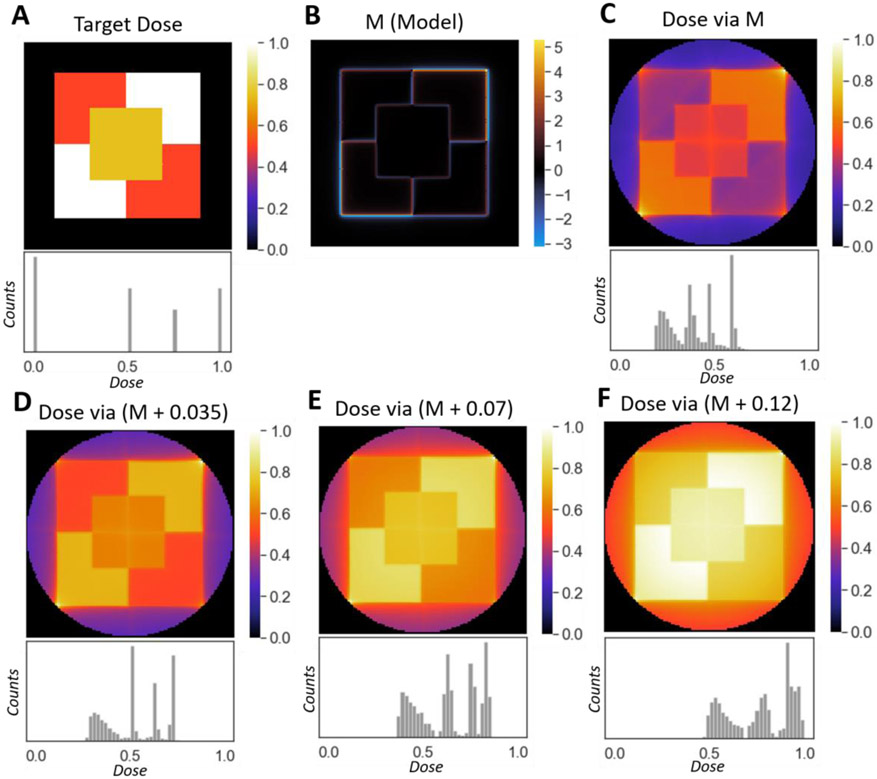
Grayscale tomographic reconstructions by non-negative projection sets. (A) A target dose to reconstruct and its histogram. (B) A model, M, formed by frequency-filtering the target. (C) The reconstruction and histogram yielded from the model. (D-F) Reconstructions and their histograms yielded by adding a constant to the model. The more the model is shifted, the higher the dose values that reconstruct the object in the necessarily reduced-contrast reconstructions. There is a tradeoff between uniformity and contrast. E.g. the average spread of each dose-region in the reconstruction in (F) is smaller than those in (C-E). However, the reconstructions shown in (C-E) exhibit a larger dose contrast than the reconstruction shown in (F).
The initial model can be adjusted to balance reconstruction contrast and uniformity, and to choose which dose values are best reproduced. This is done by shifting the initial model (M) by a constant value (c) before using it to produce a reconstruction (f). That is, using the notation from Section 1.1., f = NP*max{0, P (M + c)}. Fig. 7D-F shows examples of this. Adding a constant to the initial model (Fig. 7B) will shift where, in the reconstruction dynamic range, the object will be reproduced. Adding a negative constant to the model allows for adjustment in the opposite direction, better-matching the smaller values of the target function. This process lets us choose which values from our original target structure are most-accurately reproduced. Larger constants will better distinguish high dose regions, and will improve their uniformity, but at the cost of an overall reduction in contrast. This process is fast, making it computationally practical to check many shift values to find a desirable reconstruction for a given target. While this method of filtering and shifting does not control material properties perfectly, it allows for adjustable approximation, opening the doors to the application of VAM to the fabrication of functionally graded structures.
Section 3: Including Material Response
Section 1 used an idealized polymer resin described only by a threshold dose of gelation. Algebraic optimization in object space facilitates more general material response models.
S.3.1: Binary printing with inhibition.
Resins containing radical inhibitors exhibit a delay in optical dose accumulation before the start of polymerization. This delay, or inhibition period, is caused by radical inhibitors reacting with photo-generated radicals at a much higher rate than monomer-radical reactions. Only once inhibitor is locally depleted does significant conversion commence. Oxygen can provide a small inhibition period, and is often present in photosensitive resins when they are used in ambient conditions. A larger inhibition period can be engineered by the inclusion of a radical inhibitor [22]. In VAM printing, inhibition relaxes the requirements of an optical tomographic reconstruction, as it increases the allowable dose without gelation in the out-of-part regions. We find that even a small inhibitory dose significantly improves the contrast between in-part and out-of-part regions in a VAM print.
The OSMO algorithm can be easily changed to model this effect. With respect to conversion, inhibition effectively subtracts from the dose applied in object-space since some amount of dose causes no conversion. Including inhibition is mathematically equivalent to including negative values in image-sets, with larger inhibition periods corresponding to larger negative magnitudes. By the linearity of Radon Transform, this effect is equivalently described as a subtraction in image-space, resulting in negative values in simulated image-sets. Thus, for computational convenience, we can apply the subtracting effect of inhibition in image-space during the negative-clipping step when computing a reconstruction from a model (Fig. 3B). After forward projecting a model, instead of clipping all resultant negative values to zero, we clip them to the negative value gmin, where the ratio of -gmin to 1 is the same as the ratio of the inhibition period to the conversion period of the resin. Then, after calculating a reconstruction with a back projection, any negative dose values in object-space are set to zero, since they correspond to no polymeric conversion. That is, all of the reconstruction steps described in Section 1.1 such as fj,j = NP*max{0, P Mj,j), become fj,j = max{0, NP* max{gmin, P Mj,j}}. See SI-Fig.4 of the Supplemental Information for a graphical depiction of using an OSMO model with inhibition. Once a final image-set has been computed, the images are shifted by a constant such that their smallest value is zero (again relying on the linearity of the Radon Transform). The rest of the algorithm remains unchanged. See the Supplemental Information (SI-Fig.5) for an example of process window size increasing by a factor of 4 with the inclusion of only a 10% inhibition period.
S.3.2: Image computation for the control of material properties.
VAM is naturally suited to the problem of 3D printing structures with functionally graded properties since it has the ability to control optical dose throughout a print. However, tomographic computation addresses only the control and delivery of optical exposure. Here, we briefly discuss how the grayscale reconstruction algorithm described in Section 2 fits into the larger problem of material property control in VAM.
The problem of arbitrary property control by VAM requires multiple inversion steps. For material property being a function, f, of conversion, conversion being a function, q, of optical dose, and optical dose being a function, h, of projection image set, we can say that an arbitrary 3D distribution of material property, MP = f(q(h(image set))). Note that f and q are typically intensity-dependent, requiring system-specific calibration. To compute the image set that results in a desired distribution of material properties, we must solve the inverse problem: image set = h−1 (q−1(f−1(MP))). Inverting f and q is an experimental measurement calibration step yielding monotonic functions that are empirically collected [25]. Predicting and modeling such material property dependence on conversion, and the dependence of conversion on optical exposure is an active area of research [32], [33] and beyond the scope of this paper. However, once f and q are inverted, they provide a grayscale optical exposure target h (e.g. like the target shown in Fig. 7A). Inverting h can then be approximated by the grayscale reconstruction algorithm described in Section 2. The limitations of such a grayscale reconstruction will strongly depend on the particular target distribution, along with the particular material responses involved. Finally, the effects of inhibition can be included to increase reconstruction degrees of freedom. This is done, as in the binary-gelation printing case, by allowing negative values in the projection sets, the magnitude of which is determined by the inhibition period of the resin. While the limited fidelity of the grayscale algorithm constrains the ability to specify arbitrary material properties in 3D, the processed outlined here may provide sufficient control for many applications, and demonstrates a computational advancement for more potential control over VAM prints.
S.3.3: Controlling Print Dynamics.
Above, we have calculated final dose distributions and ignored the fact that this dose is deposited by the exposure of each image at a particular intensity for a finite time. However, the computed dose delivered by each image does not have to be applied in a single exposure. By visiting each angle many times in a single print it is possible to use different images for each rotation, which may result in additional control over the print dynamics. Instead of considering an image set to contain e.g. 360 images (1 per degree) that are then repeated over N rotations, we can instead consider the image set to contain 360xN independent images. This increases control over the dynamics of dose delivery within the total exposure time. We hypothesize this can improve print quality e.g. by reducing the early gelation of localized volumes which can sink or refract subsequent writing beams.
We can avoid gelling a portion of the print long before the rest of the part forms by delivering the majority of the dose at the end of the of the printing process (see Supplementary Video-1 and Supplementary-Fig.5 for experimental results demonstrating such an avoidance of early gelation). While the OSMO algorithm does not inherently account for temporal variations in the resin, the approximate energy doses delivered over time can be estimated by considering a fraction of the total projections. By choosing to order the projections such that the high intensity projections occur at the end of the build, the in-part regions are expected to cross the gelation dose-threshold nearly simultaneously. Equivalent dose distributions can be generated by re-distributing the pixel intensities across multiple rotations as given by equation 5.
| (5) |
where:
g0(θ, y, x) = image set assuming a single rotation, where θ ranges from 0 to 360°
gi(θ, y, x, i) = image set for i of nrot rotations
nrot = number of rotations over which to vary the light field
While any combination of gi can be used such that equation 5 is satisfied, to deliver the majority of the dose at the end of the build, we define gi as:
| (6) |
where:
where: i = the rotation number 1, … nrot. Note that ki is defined up to i = nrot + 1 to calculate gi up to i = nrot.
For an example reconstruction, when the same image set is used over 10 rotations, voxels in the object start reaching the gelation threshold after 6 rotations (Fig. 8). However, when the pixel intensities are redistributed across 10 rotations as described by equation 6, object voxels do not surpass the gelation dose-threshold until the final rotation.
Figure 8:
Re-binning pixels across multiple rotations enables simultaneous part formation. (A) Binary target geometry. (B) When a constant image set (gray squares) is projected across 10 rotations, the object starts forming (surpassing the gel threshold) after 9 rotations. When the intensity of pixels is re-binned such that the majority of the dose is delivered at the end of the build (orange circles), the object does not form until the final rotation. (C) Rate of gelation for a constant image set versus the image-set with value redistributed as per Eqn. 6. (C, Top Row) Dose reconstruction after the 8th, 9th and 10th rotation for redistributed image set. (C, Bottom Row) Dose reconstruction after the 8th, 9th and 10th rotation for the constant image set. See the Supplemental Information (SI-Fig.6 and SI Video-1) for an example of an experimental implementation of this method.
This process can be applied to any build to minimize the time between when the first and last in-part voxel crosses the gelation threshold. This method allows all regions of a given part to cross the gelation dose-threshold nearly simultaneously, with the largest benefit gained by reconstructions with a large IPDR. We hypothesize that simultaneous gelation will minimize the scattering due to increases in index of refraction as the polymer gels, and the problem of parts sinking during the build process since gelled regions are denser than their monomer counterparts.
SECTION 4: ADDITIONAL PRINTING GEOMETRIES AND OPTICAL MODELS FOR BINARY VAM.
S.4.1: Image Computation for More Complex Projection Models.
Real VAM printing does not occur with ideal, perfectly sharp, perfectly non-diverging beams. Likewise, when over-printing around occluding structures, the ideal tomographic condition where each beam spatially overlaps with all other beams, is broken. Fortunately, the OSMO algorithm still works, without modification, for more complex projection models than the Attenuated Radon Transform (ART). Here, we demonstrate its outputs for two projection models: for Gaussian beams, and for printing around occlusions.
Gaussian beam projections can be modeled by changing the line integrals used in the ART from straight paths, to curved paths represented by a Gaussian kernel. This tends to concentrate dose towards the center of a reconstruction. It also effectively reduces the degrees of freedom of a reconstruction, since each image-set pixel addresses a larger region within the reconstruction (the out-of-focus parts of the Gaussian beams), resulting in an increased overlap with other writing beams. Both effects increase the difficulty of achieving accurate tomographic reconstructions, with more iterations needed to achieve an inferior reconstruction (e.g. reduced process window size), as compared to the ideal non-diverging beam case. An example of this in 2D is shown in Fig. 9. Note that extending this to 3D would break the independence of slice-regions in a print, but the optimization process would remain algorithmically unchanged. The ability to model Gaussian beam projections becomes especially important when a long depth of focus relative to the maximum target dimension cannot be achieved experimentally, resulting in beams that are significantly non-collimated. This may occur when using LED illumination instead of lower etendue laser-sources [21], or when applying VAM at especially large or micro scales.
Figure 9.
(A) Gaussian point spread function (PSF) (B) Back projection with Gaussian-pixel-PSF projector (C) Optimized reconstruction with Dl = 0.5, Dh = 0.6, and 150 iterations. Optical parameters: wavelength = 405 nm, numerical aperture = 0.1, digital micromirror device pixel pitch = 10.8 μm, and magnification = 0.36. (D) Thresholded reconstruction, threshold = 0.545. Here, VER was 0.074, IPDR was 0.512, and process window size was −15.5%. See Supplemental Information (SI-Fig.7) for additional details.
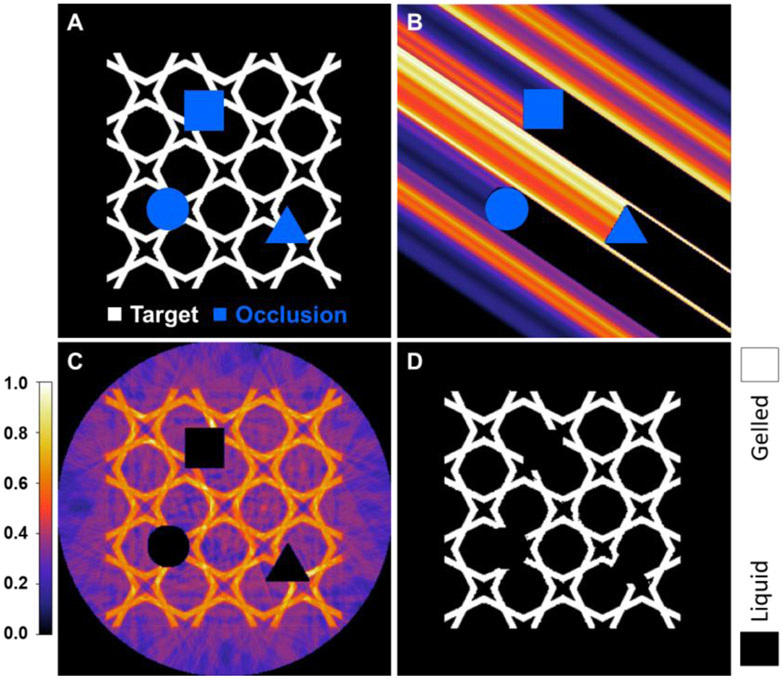
Similarly, image computation for printing around occlusions requires that ART line integrals be truncated at the occlusions. This also reduces the freedom of a tomographic reconstruction, however the OSMO algorithm still works without modification. An example of such a reconstruction is shown in Fig. 10, with an additional example with a dense target shown in the Supplemental Information (SI-Fig.9). Such computation would be necessary for applications involving over-printing around existing, occluding structures.
Figure 10.
(A) Target and occluding geometries. (B) Back projection with custom projector; occluded regions are shown as black regions adjacent to the occluding geometries. (C, D) Optimized raw and thresholded reconstructions with Dl = 0.35, Dh = 0.60, threshold = 0.515, and 120 iterations. Here, VER was 0.0694, IPDR was 0.605, and process window size was −24.1%. Note: IPDR and process window size are large, compared to a visual inspection of the dose histogram (SI-Fig.8), because a small number of in-part pixels are in error. See Supplemental Information (SI-Fig.8) for additional details.
S.4.2. Image Computation for Alternate Printing Geometries.
In prior VAM literature [20]-[22], only a basic tomographic projection geometry was considered; one in which writing beams are normal to the axis of rotation, and are evenly distributed about a rotation. Other printing geometries, however, are possible and may have application advantages. In particular, the standard geometry requires access to the sample from all directions normal to the rotation axis. One simple modification is to use only a limited angular range for printing. Fig. 11, A, B shows an example of a reconstruction slice of a thinker geometry. Here, only an angular range of 130° was used, yet the OSMO algorithm was able to produce a reconstruction with a VER of zero. Another geometry, inspired by tomosynthetic medical imaging and computed laminography, uses a ring of projections that are at a fixed, non-normal angle, to the axis of rotation (see Fig. 11. C, D). Although this geometry excludes a cone of available spatial frequencies, it is commonly used for imaging and provides sufficient resolution for many applications [34], [35]. This could allow for VAM printing into flat sample packages, perhaps with applications in microfluidics. In this case, the OSMO algorithm achieved a VER near zero (1.7E-4). However, deviations from the standard geometry come at a cost, particularly as a reduction in process window size.
Figure 11.
(A) A 2D dose reconstruction yielding a VER of zero, made by a set of projections over only a 130° range, with Dl = 0.78 and Dh = 0.79. (B) A gelation threshold applied to the dose shown in (A) yields a perfectly gelled slice of a thinker geometry. (C) A tomosynthetic printing geometry, with projection direction vertically angled by 40° from the standard printing geometry. (D) A slice of a 3D thinker-geometry dose-reconstruction with VER near zero (1.7E-4), made with the tomosynthesis writing geometry shown in (C), with Dl = 0.74 and Dh = 0.75. The process window size was −0.70%, and the IPDR was 0.26. Note that (D) shows a 2D slice of a 3D reconstruction, not a 2D reconstruction. In this case, 360 angles, all at a 50° to the axis of rotation, were used. See Supplemental Information (SI-Fig.10) for additional details.
For both the limited angular range reconstruction, as well as the tomosynthesis reconstruction, while a VER of zero or near zero was achieved, the resultant process window sizes were much smaller than what a standard tomographic geometry could achieve. In both cases, this is due to a reduction in the degrees of freedom of the reconstruction process. For the limited angular range case, only 130° (36%) of a full rotation was used. Note that since attenuation is included, a 0° projection is different from a 180° projection, and 130° is 36% of a full rotation image set. If attenuation were not included, a 130° range would comprise 72% of the images in a full rotation. With tomosynthesis, the degrees of freedom of the reconstruction are reduced because the volume can no longer be de-coupled into slices addressed by 1D projections, and there is an increased spatial overlap of writing beams. Small deviations from the standard geometry hardly suffer a decrease in reconstruction performance, with larger deviations (the limit being 90 degrees for tomosynthesis) exhibiting worse reconstructions. However, in spite of these fundamental limitations, image sets can be generated for complex, arbitrary target-objects by the OSMO algorithm.
Tomosynthetic VAM printing, in particular, could enable new applications of VAM. The flat package geometry is more convenient than cylindrical in many cases and could enable hybrid printing methods such as printing into microfluidic devices. Further, the flat package enables a step-and-repeat scheme such that tomosynthetic VAM could allow for writing into very large areas, one small, high-resolution area at a time.
CONCLUSIONS
The new, relatively immature field of VAM has potential applications in multiple fields requiring fast, high-resolution manufacturing. Advances in optics, materials, and image computation will be necessary to realize such applications; this paper presents improvement on the last of these aspects by introducing an object-domain optimization paradigm for VAM computation. We presented an object space model optimization algorithm (OSMO) that is easy to implement and to use, is flexible, and has been demonstrated on simulated data to produce highly accurate prints even with imperfect optical and material precision (SI-Figs.2-3) via an improved optical dose contrast between the target and surrounding regions. We defined reconstruction-quality metrics and showed the OSMO algorithm to be a significant improvement on prior methods for binary VAM computation, most notably with respect to convergence rate and dose separation between in-part and out-of-part regions. We applied the object space concept to the problem of grayscale VAM image computation for the printing of arbitrary functionally graded materials, and we discussed its inherent limitations. We demonstrated how the OSMO algorithm can easily be modified to account for material inhibition, and we demonstrated the flexibility of the method by computing reconstructions with both Gaussian beam projections, and reconstructions around occluding features. Lastly, we applied the OSMO algorithm to computing images for a new tomosynthetic VAM geometry that could allow for printing into a traditional planar geometry, illustrating how the proposed image computation method facilitates new printing geometries and applications of VAM.
Supplementary Material
Highlights.
Object-space optimization for VAM image computation yields multiple advantages.
A simple and high-performing algebraic image computation algorithm is presented.
Volumetric 3D printing accuracy is improved over prior CAL computation methods.
A grayscale reconstruction algorithm allows for functionally graded materials.
Novel volumetric 3D printing geometries and sample packaging are proposed.
Funding:
This work was partially performed under the auspices of the U.S. Department of Energy by Lawrence Livermore National Laboratory under Contract DE-AC52-07NA27344 with funding from the LLNL LDRD program. LLNL-JRNL-820693.
Research reported in this publication was supported by the Office of The Director of the National Institutes of Health under award numbers 1OT2OD023852-01 and R01NS118188. Portion of project Federally funded: 87% and $331K. Portion of project non-governmentally funded: 13% and $50K. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health.
Joseph Toombs was supported in part by the National Science Foundation under Cooperative Agreement No. EEC-1160494.
For assistance with proof reading, we thank: Amy Sullivan, Jamie Kowalski, and Gabriel Seymour, with special thanks to Martha Bodine.
Footnotes
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
REFERENCES
- [1].Schubert C, van Langeveld MC, and Donoso LA, “Innovations in 3D printing: a 3D overview from optics to organs,” Br. J. Ophthalmol, vol. 98, no. 2, pp. 159–161, February. 2014, doi: 10.1136/bjophthalmol-2013-304446. [DOI] [PubMed] [Google Scholar]
- [2].Nguyen DT et al. , “3D-Printed Transparent Glass,” Adv. Mater, vol. 29, no. 26, p. 1701181, 2017, doi: 10.1002/adma.201701181. [DOI] [PubMed] [Google Scholar]
- [3].Gissibl T, Thiele S, Herkommer A, and Giessen H, “Two-photon direct laser writing of ultracompact multi-lens objectives,” Nat. Photonics, vol. 10, no. 8, Art. no. 8, August. 2016, doi: 10.1038/nphoton.2016.121. [DOI] [Google Scholar]
- [4].Thiele S, Arzenbacher K, Gissibl T, Giessen H, and Herkommer AM, “3D-printed eagle eye: Compound microlens system for foveated imaging,” Sci. Adv, vol. 3, no. 2, p. e1602655, February. 2017, doi: 10.1126/sciadv.1602655. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Gong H, Bickham BP, Woolley AT, and Nordin GP, “Custom 3D printer and resin for 18 μm × 20 μm microfluidic flow channels,” Lab. Chip, vol. 17, no. 17, pp. 2899–2909, August. 2017, doi: 10.1039/C7LC00644F. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6].Waheed S et al. , “3D printed microfluidic devices: enablers and barriers,” Lab. Chip, vol. 16, no. 11, pp. 1993–2013, 2016, doi: 10.1039/C6LC00284F. [DOI] [PubMed] [Google Scholar]
- [7].Amin R et al. , “3D-printed microfluidic devices,” Biofabrication, vol. 8, no. 2, p. 022001, June. 2016, doi: 10.1088/1758-5090/8/2/022001. [DOI] [PubMed] [Google Scholar]
- [8].Jianu C, Lamanna G, and Opran CG, “Research Regarding Embedded Systems of Robotic Technology for Manufacturing of Hybrid Polymeric Composite Products,” Mater. Sci. Forum Pfaffikon, vol. 957, pp. 267–276, June. 2019, doi: 10.4028/www.scientific.net/MSF.957.267. [DOI] [Google Scholar]
- [9].Jahangir MN, Cleeman J, Hwang H-J, and Malhotra R, “Towards out-of-chamber damage-free fabrication of highly conductive nanoparticle-based circuits inside 3D printed thermally sensitive polymers,” Addit. Manuf, vol. 30, p. 100886, December. 2019, doi: 10.1016/j.addma.2019.100886. [DOI] [Google Scholar]
- [10].Bishop ES et al. , “3-D bioprinting technologies in tissue engineering and regenerative medicine: Current and future trends,” Genes Dis., vol. 4, no. 4, pp. 185–195, December. 2017, doi: 10.1016/j.gendis.2017.10.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Noor N, Shapira A, Edri R, Gal I, Wertheim L, and Dvir T, “3D Printing of Personalized Thick and Perfusable Cardiac Patches and Hearts,” Adv. Sci, vol. 6, no. 11, p. 1900344, 2019, doi: 10.1002/advs.201900344. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12].Grigoryan B et al. , “Multivascular networks and functional intravascular topologies within biocompatible hydrogels,” Science, vol. 364, no. 6439, pp. 458–464, May 2019, doi: 10.1126/science.aav9750. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13].Randazzo M, Pisapia JM, Singh N, and Thawani JP, “3D printing in neurosurgery: A systematic review,” Surg. Neurol. Int, vol. 7, no. Suppl 33, pp. S801–S809, November. 2016, doi: 10.4103/2152-7806.194059. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14].Hockaday LA et al. , “Rapid 3D printing of anatomically accurate and mechanically heterogeneous aortic valve hydrogel scaffolds,” Biofabrication, vol. 4, no. 3, p. 035005, August. 2012, doi: 10.1088/1758-5082/4/3/035005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [15].Bártolo PJ, Ed., Stereolithography: Materials, Processes and Applications. Springer US, 2011. doi: 10.1007/978-0-387-92904-0. [DOI] [Google Scholar]
- [16].Quan H, Zhang T, Xu H, Luo S, Nie J, and Zhu X, “Photo-curing 3D printing technique and its challenges,” Bioact. Mater, vol. 5, no. 1, pp. 110–115, March. 2020, doi: 10.1016/j.bioactmat.2019.12.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [17].Jiang J, Xu X, and Stringer J, “Support Structures for Additive Manufacturing: A Review,” J. Manuf. Mater. Process, vol. 2, no. 4, Art. no. 4, December. 2018, doi: 10.3390/jmmp2040064. [DOI] [Google Scholar]
- [18].Wang X, Jiang M, Zhou Z, Gou J, and Hui D, “3D printing of polymer matrix composites: A review and prospective,” Compos. Part B Eng, vol. 110, pp. 442–458, February. 2017, doi: 10.1016/j.compositesb.2016.11.034. [DOI] [Google Scholar]
- [19].Tekinalp HL et al. , “High modulus biocomposites via additive manufacturing: Cellulose nanofibril networks as ‘microsponges,’” Compos. Part B Eng, vol. 173, p. 106817, September. 2019, doi: 10.1016/j.compositesb.2019.05.028. [DOI] [Google Scholar]
- [20].Kelly BE, Bhattacharya I, Heidari H, Shusteff M, Spadaccini CM, and Taylor HK, “Volumetric additive manufacturing via tomographic reconstruction,” Science, vol. 363, no. 6431, pp. 1075–1079, March. 2019, doi: 10.1126/science.aau7114. [DOI] [PubMed] [Google Scholar]
- [21].Loterie D, Delrot P, and Moser C, “High-resolution tomographic volumetric additive manufacturing,” Nat. Commun, vol. 11, no. 1, p. 852, December. 2020, doi: 10.1038/s41467-020-14630-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [22].Cook CC et al. , “Highly Tunable Thiol-Ene Photoresins for Volumetric Additive Manufacturing,” Adv. Mater, vol. n/a, no. n/a, p. 2003376, doi: 10.1002/adma.202003376. [DOI] [PubMed] [Google Scholar]
- [23].Regehly M et al. , “Xolography for linear volumetric 3D printing,” Nature, vol. 588, no. 7839, Art. no. 7839, December. 2020, doi: 10.1038/s41586-020-3029-7. [DOI] [PubMed] [Google Scholar]
- [24].“OSA ∣ Correcting ray distortion in tomographic additive manufacturing.” https://www.osapublishing.org/oe/fulltext.cfm?uri=oe-29-7-11037&id=449502 (accessed May 16, 2021). [DOI] [PubMed] [Google Scholar]
- [25].Uzcategui AC, Muralidharan A, Ferguson VL, Bryant SJ, and McLeod RR, “Understanding and Improving Mechanical Properties in 3D printed Parts Using a Dual-Cure Acrylate-Based Resin for Stereolithography,” Adv. Eng. Mater, vol. 20, no. 12, p. 1800876, 2018, doi: 10.1002/adem.201800876. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [26].Wydra JW, Cramer NB, Stansbury JW, and Bowman CN, “The reciprocity law concerning light dose relationships applied to BisGMA/TEGDMA photopolymers: Theoretical analysis and experimental characterization,” Dent. Mater, vol. 30, no. 6, pp. 605–612, June. 2014, doi: 10.1016/j.dental.2014.02.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [27].Natterer F, The Mathematics of Computerized Tomography. SIAM, 2001. [Google Scholar]
- [28].Shusteff M et al. , “One-step volumetric additive manufacturing of complex polymer structures,” Sci. Adv, vol. 3, no. 12, p. eaao5496, December. 2017, doi: 10.1126/sciadv.aao5496. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [29].computed-axial-lithography/CAL-software. Computed Axial Lithography, 2020. Accessed: Oct. 11, 2020. [Online]. Available: https://github.com/computed-axial-lithography/CAL-software [Google Scholar]
- [30].Pazhamannil RV, Govindan P, and Edacherian A, “Optimized projections and dose slices for the volumetric additive manufacturing of three dimensional objects,” Mater. Today Proc, December. 2020, doi: 10.1016/j.matpr.2020.10.807. [DOI] [Google Scholar]
- [31].van Aarle W et al. , “Fast and flexible X-ray tomography using the ASTRA toolbox,” Opt. Express, vol. 24, no. 22, p. 25129, October. 2016, doi: 10.1364/OE.24.025129. [DOI] [PubMed] [Google Scholar]
- [32].Peterson GI et al. , “Production of Materials with Spatially-Controlled Cross-Link Density via Vat Photopolymerization,” ACS Appl. Mater. Interfaces, vol. 8, no. 42, pp. 29037–29043, October. 2016, doi: 10.1021/acsami.6b09768. [DOI] [PubMed] [Google Scholar]
- [33].Kuang X et al. , “Grayscale digital light processing 3D printing for highly functionally graded materials,” Sci. Adv, vol. 5, no. 5, p. eaav5790, May 2019, doi: 10.1126/sciadv.aav5790. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [34].Viergever M and Todd-Pokropek A, Eds., Mathematics and Computer Science in Medical Imaging. Berlin Heidelberg: Springer-Verlag, 1988. doi: 10.1007/978-3-642-83306-9. [DOI] [Google Scholar]
- [35].Xu F, Helfen L, Baumbach T, and Suhonen H, “Comparison of image quality in computed laminography and tomography,” Opt. Express, vol. 20, no. 2, pp. 794–806, January. 2012, doi: 10.1364/OE.20.000794. [DOI] [PubMed] [Google Scholar]
- [36].Moran B, Fong E, Cook C, and Shusteff M, “Volumetric additive manufacturing system optics,” in Emerging Digital Micromirror Device Based Systems and Applications XIII, Online Only, United States, March. 2021, p. 2. doi: 10.1117/12.2577670. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.