Gaussian accelerated molecular dynamics (GaMD): principles and applications

Abstract

Gaussian accelerated molecular dynamics (GaMD) is a robust computational method for simultaneous unconstrained enhanced sampling and free energy calculations of biomolecules. It works by adding a harmonic boost potential to smooth biomolecular potential energy surface and reduce energy barriers. GaMD greatly accelerates biomolecular simulations by orders of magnitude. Without the need to set predefined reaction coordinates or collective variables, GaMD provides unconstrained enhanced sampling and is advantageous for simulating complex biological processes. The GaMD boost potential exhibits a Gaussian distribution, thereby allowing for energetic reweighting via cumulant expansion to the second order (i.e., “Gaussian approximation”). This leads to accurate reconstruction of free energy landscapes of biomolecules. Hybrid schemes with other enhanced sampling methods, such as the replica exchange GaMD (rex-GaMD) and replica exchange umbrella sampling GaMD (GaREUS), have also been introduced, further improving sampling and free energy calculations. Recently, new “selective GaMD” algorithms including the ligand GaMD (LiGaMD) and peptide GaMD (Pep-GaMD) enabled microsecond simulations to capture repetitive dissociation and binding of small-molecule ligands and highly flexible peptides. The simulations then allowed highly efficient quantitative characterization of the ligand/peptide binding thermodynamics and kinetics. Taken together, GaMD and its innovative variants are applicable to simulate a wide variety of biomolecular dynamics, including protein folding, conformational changes and allostery, ligand binding, peptide binding, protein-protein/nucleic acid/carbohydrate interactions, and carbohydrate/nucleic acid interactions. In this review, we present principles of the GaMD algorithms and recent applications in biomolecular simulations and drug design.

Graphical Abstract

Gaussian accelerated molecular dynamics (GaMD) and its applications to a wide range of biological systems.

1. Introduction

Biological processes are mediated by biomolecules such as proteins, nucleic acids, lipids, and carbohydrates. Biomolecules often visit different functional conformations during various biological functions, including cellular signaling, protein folding, gene translation/editing, and biomolecular recognition^1–4. The underlying free energy landscapes of biomolecules determine their conformations^{5, 6}. Molecular dynamics (MD) is an advanced technique that allows us to simulate biomolecular dynamics at an atomistic level⁷. It is now possible to run longer and cheaper MD simulations with remarkable advances in computing hardware (e.g., the Anton supercomputer and GPUs) and software developments⁸. Even so, conventional MD (cMD) is often limited to typically hundreds of nanoseconds to tens of microseconds^9–12. On the other hand, many biological processes of interest take place over milliseconds or even longer timescales, due to high energy barriers (e.g., 8–12 kcal/mol)^{1, 13, 14}. Due to this gap, it remains challenging to sufficiently sample different conformations and accurately calculate free energy profiles of biomolecules through cMD simulations.

To overcome the above challenges, numerous enhanced sampling techniques have been introduced since the dawn of MD as reviewed in a number of previous articles^15–18. One class of these methods use predefined collective variables (CVs) or reaction coordinates, including umbrella sampling (US)^{19, 20}, metadynamics^{21, 22}, adaptive biasing force (ABF)^{23, 24}, steered MD (SMD)²⁵, conformational flooding^{26, 27}, and so on. Typical CVs include root-mean square deviation (RMSD) relative to a reference conformation, dihedrals, atom distances, eigenvectors of principal component analysis (PCA)²⁷, etc. These methods greatly improve the sampling of biomolecular dynamics and the accuracy of free energy calculations along the chosen CVs. However, it is rather challenging to define proper CVs in prior because the system needs to be studied in detail beforehand. Furthermore, the predefined CVs could largely limit sampling of the conformational space during the biasing simulations. This usually slows convergence of the simulations and suffers from the “hidden energy barrier” problem once crucial CVs are missing in the simulation setup²².

Another kind of enhanced sampling techniques have been introduced without using predefined CVs, including replica exchange molecular dynamics (REMD)^{28, 29} or parallel tempering³⁰, self-guided Langevin or molecular dynamics^31–34, essential energy space random walk^35–37 and accelerated molecular dynamics (aMD)³⁸. In particular, Voter introduced aMD by adding a boost potential in non-barrier regions to accelerate infrequent transitions in solids³⁹. Hamelberg et al. further developed this technique to perform biomolecular simulations³⁸. The boost potential in aMD enables simulations to sample different low-energy conformational states by smoothing the system potential energy surface and reducing the energy barriers^{38, 40}. Despite the advantage of unconstrained enhanced sampling, aMD can suffer from high statistical noise, affecting the description of the correct statistical ensemble⁴¹. In detail, the ensemble canonical average is reached by reweighting each point in the configuration space on the modified potential by the strength of the Boltzmann factor of the bias energy, at that particular point. By using the early aMD method, this has shown to lead to high statistical noise, since the points with the largest biases dominate the reweighted result^42–45. In comparison with the CV-biasing methods, aMD has typically much higher boost potential with wider distributions (tens to hundreds of kcal/mol)⁴³, making it very challenging to accurately reweight free energies from aMD simulations, especially for biological macromolecules^{44, 46, 47}. This issue can be severe for large biomolecular systems, such as transmembrane proteins and ribonucleoproteins, where the standard reweighting procedure has often been prohibitive, given the large statistical noise⁴³.

Gaussian accelerated molecular dynamics (GaMD) has been developed to smooth the surface of potential energy with a harmonic boost potential, following three newly formulated enhanced sampling principles⁴⁸. Similar to the previous aMD, no predefined CV is needed for GaMD simulations. Furthermore, the new harmonic boost potential in GaMD exhibits a Gaussian distribution, which enables us to accurately recover the original biomolecular free energy landscapes by Gaussian approximation, i.e., cumulant expansion to the second order. This useful scheme substantially reduces the statistical noise, thereby overcoming the limitations of the early aMD methodology (vide supra). Therefore, GaMD simultaneously enables enhanced sampling without any constraints and accurately calculates free energy landscapes of biomolecules. As previously reported^{49, 50}, GaMD has been successfully applied to simulate ligand binding^{48, 51, 52}, protein folding^{48, 52}, activation of G-protein-coupled receptors (GPCRs)⁵¹, human dystonia related protein⁵³, ion channels⁵⁴, agonist and antagonist binding in the μ-OR^{55, 56}, virus enzymes^{57, 58}, bacterial effector proteins⁵⁹, etc.

In addition, GaMD has been combined with REMD to further improve conformational sampling and free energy calculations^{60, 61}. More recently developed “selective GaMD” algorithms, including ligand GaMD (LiGaMD)⁶² and peptide GaMD (Pep-GaMD)⁶³, have enabled unprecedented microsecond simulations to capture repetitive binding and dissociation of small-molecule ligands and highly flexible peptides. Accurate ligand/peptide binding free energies and kinetic rate constants are thus calculated through the selective GaMD simulations.

In this review, we will present the principles and the most recent applications of GaMD. Robust GaMD has been established for advanced simulation studies of a wide range of biomolecular systems, especially the protein-nucleic acid interactions^64–66 such as the CRISPR (clustered regularly interspaced short palindromic repeats)-Cas9 gene editing system^{67, 68}, protein-protein/peptide interactions^69–73, protein-ligand binding^{56, 57, 74–77}, protein folding⁷⁸, protein enzymes^{53, 59, 79–93}, membrane proteins (including GPCRs^{69, 70, 74, 77, 94–96}, ion channels^{54, 97} and γ-secretase⁹⁸) and carbohydrates^99–101, as well as drug design^{102, 103}.

2. Theory

2.1. Gaussian Accelerated Molecular Dynamics (GaMD)

A harmonic boost potential is added in GaMD to smooth the system potential energy surface and enhance the conformational sampling of biomolecules (Fig. 1)⁴⁸. Consider a system with N atoms at positions $\stackrel{⃑}{r}=\left\{{\stackrel{⃑}{r}}_{\mathit{1}},\cdots {\stackrel{⃑}{r}}_N\right\}$, when the system potential $V(\stackrel{⃑}{r})$ is lower than a threshold energy E, a boost potential is added as:

$$\Delta V(\stackrel{⃑}{r})=\frac{\mathit{1}}{\mathit{2}}k{(E-V(\stackrel{⃑}{r}))}^{\mathit{2}},V(\stackrel{⃑}{r})<E,$$ (1)

where k is the harmonic force constant. The modified system potential, $V^{*}(\stackrel{⃑}{r})=V(\stackrel{⃑}{r})+\Delta V(\stackrel{⃑}{r})$ is given by:

$$V^{*}(\stackrel{⃑}{r})=V(\stackrel{⃑}{r})+\frac{\mathit{1}}{\mathit{2}}k{(E-V(\stackrel{⃑}{r}))}^{\mathit{2}},V(\stackrel{⃑}{r})<E.$$ (2)

Otherwise, when the system potential is above the threshold energy, i.e., $V(\stackrel{⃑}{r})\ge E$, the boost potential is set to zero and $V^{*}(\stackrel{⃑}{r})=V(\stackrel{⃑}{r})$.

Figure 1.

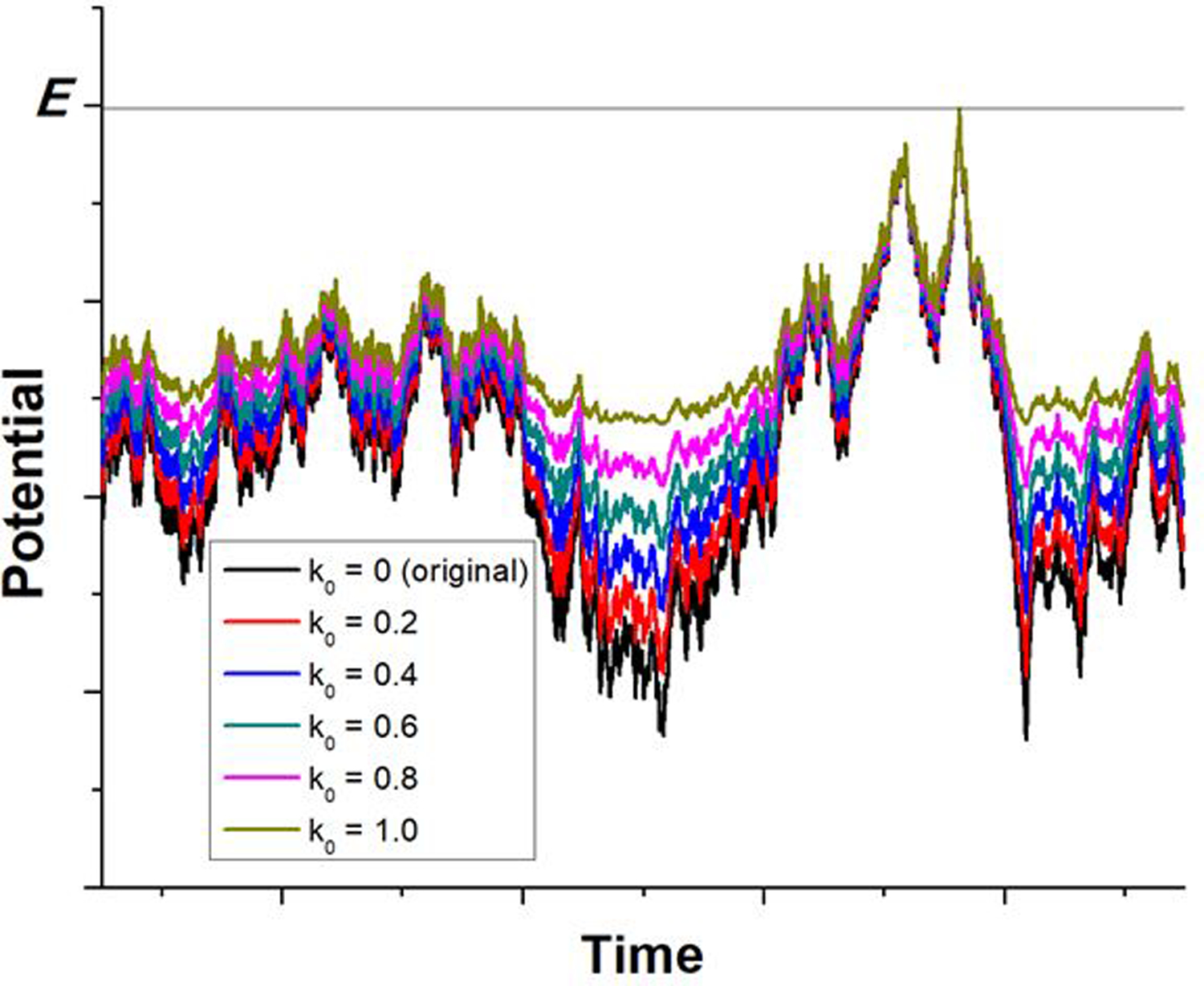
Scheme illustration of Gaussian accelerated molecular dynamics (GaMD). When the threshold energy is set to the maximum potential (E=Vmax), the system potential energy surface is smoothened by adding a harmonic boost potential that follows Gaussian distribution. The coefficient k₀ in the range of 0−1 determines the magnitude of the applied boost potential. With greater k₀, higher boost potential is added to the original energy surface in conventional molecular dynamics (cMD), which provides enhanced sampling of biomolecules across decreased energy barriers. Adapted with permission from Miao et al. (2015). Copyright 2015 American Chemical Society. https://pubs.acs.org/doi/abs/10.1021/acs.jctc.5b00436. Further permissions related to the material excerpted should be directed to the American Chemical Society.

Three enhanced sampling principles are applied to the boost potential in GaMD to smooth the potential energy surface. First, for any two arbitrary potential values $V_{\mathit{1}}(\stackrel{⃑}{r})$ and $V_{\mathit{2}}(\stackrel{⃑}{r})$ found on the original energy surface, if $V_{\mathit{1}}(\stackrel{⃑}{r})<V_{\mathit{2}}(\stackrel{⃑}{r})$, ΔV should be a monotonic function that does not change the relative order of the biased potential values, i.e., $V_{\mathit{1}}^{*}(\stackrel{⃑}{r})<V_{\mathit{2}}^{*}(\stackrel{⃑}{r})$. By replacing $V^{*}(\stackrel{⃑}{r})$ with Equation (2) and isolating E, we then obtain:

$$E<\frac{\mathit{1}}{\mathit{2}}\left[V_{\mathit{1}}(\stackrel{⃑}{r})+V_{\mathit{2}}(\stackrel{⃑}{r})\right]+\frac{\mathit{1}}{k}.$$ (3)

Second, if $V_{\mathit{1}}(\stackrel{⃑}{r})<V_{\mathit{2}}(\stackrel{⃑}{r})$, the potential difference observed on the smoothened energy surface should be smaller than that of the original, i.e., $V_{\mathit{2}}^{*}(\stackrel{⃑}{r})-V_{\mathit{1}}^{*}(\stackrel{⃑}{r})<V_{\mathit{2}}(\stackrel{⃑}{r})-V_{\mathit{1}}(\stackrel{⃑}{r})$. Similarly, by replacing $V^{*}(\stackrel{⃑}{r})$ with Equation (2), we can derive:

$$E>\frac{\mathit{1}}{\mathit{2}}\left[V_{\mathit{1}}(\stackrel{⃑}{r})+V_{\mathit{2}}(\stackrel{⃑}{r})\right].$$ (4)

With $V_{\text{min}}\le V_{\mathit{1}}(\stackrel{⃑}{r})<V_{\mathit{2}}(\stackrel{⃑}{r})\le V_{\text{max}}$, we need to set the threshold energy E in the following range by combining Equations (3) and (4):

$$V_{\text{max}}\le E\le V_{\text{min}}+\frac{\mathit{1}}{k},$$ (5)

where V_min and V_max are the system minimum and maximum potential energies. To ensure that Equation (5) is valid, $V_{\text{max}}\le V_{\text{min}}+\frac{\mathit{1}}{k}$ and k have to satisfy:

$$k\le \frac{\mathit{1}}{V_{\text{max}}-V_{\text{min}}}.$$ (6)

Let us define $k\equiv k_{\mathit{0}}•\frac{\mathit{1}}{V_{\text{max}}-V_{\text{min}}}$, then 0 < k₀ ≤ 1. As illustrated in Fig. 1, k₀ determines the magnitude of the applied boost potential. With higher k₀, larger boost potential is added to the potential energy surface, which facilitates enhanced sampling of biomolecules across decreased energy barriers.

Third, in order to ensure accurate reweighting using cumulant expansion to the second order⁴³, the standard deviation of ΔV needs to be small enough (i.e., narrow distribution):

$${\sigma }_{\Delta V}=\sqrt{{\left({\frac{\partial \Delta V}{\partial V}|}_{V=V_{avg}}\right)}^{\mathit{2}}}{\sigma }_V^{\mathit{2}}=k\left(E-V_{avg}\right){\sigma }_V\le {\sigma }_{\mathit{0}},$$ (7)

where V_avg and σ_V are the average and standard deviation of the system potential energies, σ_ΔV is the standard deviation of ΔV with σ₀ as a user-specified upper limit (e.g., 10k_BT) for accurate reweighting.

Provided Equation (5) that gives the range of threshold energy E, when E is set to the lower bound E = V_max, we substitute in E and k, and obtain:

$$k_{\mathit{0}}\le \frac{{\sigma }_{\mathit{0}}}{{\sigma }_V}•\frac{V_{\text{max}}-V_{\text{min}}}{V_{\text{max}}-V_{avg}}.$$ (8)

Let us define the right-hand side in Equation (8) as $k_{\mathit{0}}^{\prime }=\frac{{\sigma }_{\mathit{0}}}{{\sigma }_V}•\frac{V_{\text{max}}-V_{\text{min}}}{V_{\text{max}}-V_{avg}}$. For efficient enhanced sampling with the highest possible acceleration, k₀ can then be set to its upper bound as:

$$k_{\mathit{0}}=\text{min}\left(\mathit{1.0},k_{\mathit{0}}^{\prime }\right)=\text{min}\left(\mathit{1.0},\frac{{\sigma }_{\mathit{0}}}{{\sigma }_V}•\frac{V_{\text{max}}-V_{\text{min}}}{V_{\text{max}}-V_{avg}}\right).$$ (9)

The larger σ_ΔV is obtained from the original potential energy surface (particularly for large biomolecules), the smaller k₀ may be applicable to allow for accurate reweighting. Alternatively, when the threshold energy E is set to its upper bound $E=V_{\text{min}}+\frac{l}{k}$ according to Equation (5), we substitute in E and k in Equation (7) and obtain:

$$k_{\mathit{0}}\ge \left(\mathit{1}-\frac{{\sigma }_{\mathit{0}}}{{\sigma }_V}\right)•\frac{V_{\text{max}}-V_{\text{min}}}{V_{avg}-V_{\text{min}}}.$$ (10)

Let us define the right-hand side in Equation (10) as $k_{\mathit{0}}^{″}\equiv \left(\mathit{1}-\frac{{\sigma }_{\mathit{0}}}{{\sigma }_V}\right)•\frac{V_{\text{max}}-V_{\text{min}}}{V_{avg}-V_{\text{min}}}$. Note that a smaller k₀ will give higher threshold energy E, but smaller force constant k. When $\mathit{0}<k_{\mathit{0}}^{″}\le \mathit{1}$, k₀ can be set to either $k_{\mathit{0}}^{″}$ for the highest threshold energy E or its upper bound 1.0 for the greatest force constant k. In this regard, $k_{\mathit{0}}=k_{\mathit{0}}^{″}$ is applied in the current GaMD. Otherwise, k₀ is calculated using Equation (9).

Given E and k₀, we can calculate the boost potential as:

$$\Delta V(\stackrel{⃑}{r})=\frac{\mathit{1}}{\mathit{2}}{k}_{\mathit{0}}\frac{\mathit{1}}{V_{\text{max}}-V_{\text{min}}}{(E-V(\stackrel{⃑}{r}))}^{\mathit{2}},V(\stackrel{⃑}{r})<E.$$ (11)

GaMD provides different options to add only the total potential boost ΔV_p, only dihedral potential boost ΔV_D, or the dual potential boost (both ΔV_P and ΔV_D). The dual-boost GaMD generally provides higher acceleration than the other two types of simulations for enhanced sampling⁴⁰. The simulation parameters comprise of the threshold energy values and the effective harmonic force constants, k_0P and k_0D for the total and dihedral potential boost, respectively.

2.2. Energetic Reweighting of GaMD for Free Energy Calculations

For simulations of a biomolecular system, the probability distribution along a selected reaction coordinate A(r) is written as p*(A), where r denotes the atomic positions {r₁,…,r_N}. Given the boost potential ΔV(r) of each frame, p*(A) can be reweighted to recover the canonical ensemble distribution, p(A), as:

$$p\left(A_j\right)=p^{*}\left(A_j\right)\frac{{\langle e^{\beta \Delta V(r)}\rangle }_j}{\sum _{i=\mathit{1}}^M{\langle p^{*}\left(A_i\right)e^{\beta \Delta V(r)}\rangle }_i},j=\mathit{1},\cdots ,M,$$ (12)

where M is the number of bins, β = k_BT and 〈e^βΔV(r)〉_j is the ensemble-averaged Boltzmann factor of ΔV(r) for simulation frames found in the j^th bin. In order to reduce the energetic noise, the ensemble-averaged reweighting factor can be approximated using cumulant expansion^{104, 105}:

$$e^{\beta \Delta V}=\text{exp}\left\{\sum _{k=\mathit{1}}^{\infty }\frac{{\beta }^k}{k!}{C}_k\right\},$$ (13)

where the first three cumulants are given by:

$$\begin{gathered} C_{\mathit{1}}=\langle \Delta V\rangle , \\ {C}_{\mathit{2}}=\langle \Delta V^{\mathit{2}}\rangle -{\langle \Delta V\rangle }^{\mathit{2}}={\sigma }_{\Delta V}^{\mathit{2}}, \\ {C}_{\mathit{3}}=\langle \Delta V^{\mathit{3}}\rangle -\mathit{3}\langle \Delta V^{\mathit{2}}\rangle \langle \Delta V\rangle +\mathit{2}{\langle \Delta V\rangle }^{\mathit{3}}. \end{gathered}$$ (14)

When the boost potential follows near-Gaussian distribution, cumulant expansion to the second order (or “Gaussian Approximation”) provides the accurate approximation for free energy calculations⁴³. The reweighted free energy $F(A)=-k_{B}T\text{\hspace{0.17em}ln\hspace{0.17em}}p(A)$ is calculated as:

$$F(A)=F^{*}\left(A\right)-\frac{\mathit{1}}{\beta }\sum _{k=\mathit{1}}^{\mathit{2}}\frac{{\beta }^k}{k!}{C}_k+F_c,$$ (15)

where $F^{*}(A)=-k_{B}T\text{\hspace{0.17em}ln\hspace{0.17em}}{p}^{*}(A)$ is the modified free energy obtained from GaMD simulation and F_c is a constant.

To characterize the extent to which ΔV follows a Gaussian distribution, its distribution anharmonicity γ is calculated as⁴³:

$$\gamma =S_{\text{max}}-S_{\Delta V}=\frac{\mathit{1}}{\mathit{2}}\text{ln}\left(\mathit{2}\pi e{\sigma }_{\Delta V}^{\mathit{2}}\right)+{\int }_{\mathit{0}}^{\infty }p(\Delta V)\text{\hspace{0.17em}ln\hspace{0.17em}}(p(\Delta V))d\Delta V,$$ (16)

where ΔV is dimensionless as divided by k_BT with k_B and T being the Boltzmann constant and system temperature, respectively, and $S_{\text{max}}=\frac{\mathit{1}}{\mathit{2}}\text{ln}\left(\mathit{2}\pi e{\sigma }_{\Delta V}^{\mathit{2}}\right)$ is the maximum entropy of ΔV⁴³. When γ is zero, ΔV follows exact Gaussian distribution with sufficient sampling. Reweighting by approximating the exponential average term with cumulant expansion to the second order is able to accurately recover the original free energy landscape. As γ increases, the ΔV distribution becomes less harmonic and the reweighted free energy profile obtained from cumulant expansion to the second order would deviate from the original. The anharmonicity of ΔV distribution serves as an indicator of the enhanced sampling convergence and accuracy of the reweighted free energy. Nevertheless, with the GaMD theoretical framework, the GaMD boost potential does not change shape of the biomolecular overall energy landscape. A near Gaussian distribution is achieved for the GaMD boost potential. A toolkit of Python scripts for GaMD/aMD reweighting “PyReweighting”⁴³ is developed and distributed free of charge at http://miao.compbio.ku.edu/PyReweighting/.

2.3. Replica Exchange-GaMD

Replica exchange and GaMD have been combined in a rex-GaMD approach to further improve the sampling and free energy calculations of biomolecules⁶⁰. According to Equation (11), both the threshold energy E and the effective force constant k₀ could adjust the boost potential. Therefore, two versions of rex-GaMD were proposed: force constant rex-GaMD and threshold energy rex-GaMD. During simulations of force constant rex-GaMD, the boost potential can be exchanged between replicas, in which the threshold energy is fixed and harmonic force constants are different. Whereas the algorithm of threshold energy rex-GaMD tends to switch the threshold energy between lower and upper bounds for generating different levels of boost potential.

The rex-GaMD simulations allow replicas exchanged between each pair of neighboring σ_0P or threshold energy based on the probability that meets the Metropolis criterion. In the simulation system, each state x can be weighted by the Boltzmann factor,

$$W_B\left(x\right)=\text{exp}\left(\frac{\mathit{1}}{k_{B}T}H\left(x\right)\right),$$ (17)

where k_B is the Boltzmann constant, T is the system temperature and H(x) is the system Hamiltonian. The weight factor for the state X here is given by the product of the Boltzmann factor of each replica:

$$W_{RE}\left(X\right)=\text{exp}\left(-{\sum }_{i=\mathit{1}}^N\frac{\mathit{1}}{k_{B}T}H\left(x_i\right)\right),$$ (18)

where N is the number of total states. Thus, the replica exchange probability can be written as w(X_i → X_j), which needs to meet the Metropolis criterion to calculate the exchange probability:

$$w\left(X_i\to X_j\right)=\text{min}\left(\mathit{1.0},e^{\Delta }\right),$$ (19)

where X_i and X_j are the states of the two nearby replicas, and $\Delta =\frac{\mathit{1}}{k_{B}T}(V_i^{*}-V_j^{*})$ and V*_i and V*_j are the total modified system potential energies calculated from the last conformation of the GaMD simulations at replica i and j. These exchange processes will keep repeating until the end of the simulation. The rex-GaMD simulations were tested on three model systems, including the alanine dipeptide, chignolin, and HIV protease, demonstrating that the distribution width of the boost potential is narrowed down, and the system conformational space is enhanced sampled.

Recently, Sugita et al.⁶¹ proposed another approach (GaREUS) that combined GaMD with replica exchange umbrella sampling (REUS). GaREUS was successfully demonstrated on accurate calculations of free energy landscapes underlying the N-glycan equilibration, conformational change of adenylate kinase and chignolin folding. The computational resource for GaREUS was the same as that required for REUS, while the sampling in GaREUS was more efficient than REUS or GaMD.

2.4. Ligand Gaussian Accelerated Molecular Dynamics (LiGaMD)

Based on GaMD, LiGaMD⁶² has been proposed to more efficiently simulate both binding and dissociation of small-molecule ligands for calculating the ligand binding free energies and kinetics. For such simulations, the system contains ligand L, protein P and the biological environment E. The system comprises of N atoms with their coordinates $r\equiv \left\{{\stackrel{⃑}{r}}_{\mathit{1}},\cdots ,{\stackrel{⃑}{r}}_N\right\}$ and momenta $p\equiv \left\{{\stackrel{⃑}{p}}_{\mathit{1}},\cdots ,{\stackrel{⃑}{p}}_N\right\}$. The system Hamiltonian can be expressed as:

$$H\left(r,p\right)=K\left(p\right)+V\left(r\right),$$ (20)

where K(p) and V(r) are the system kinetic and total potential energies, respectively. Then, the potential energy could be decomposed into the following terms:

$$V\left(r\right)=V_{P,b}\left(r_P\right)+V_{L,b}\left(r_L\right)+V_{E,b}\left(r_E\right)+V_{PP,nb}\left(r_P\right)+V_{LL,nb}\left(r_L\right)+V_{EE,nb}\left(r_E\right)+V_{PL,nb}\left(r_{PL}\right)+V_{PE,nb}\left(r_{PE}\right)+V_{LE,nb}(r_{LE}).$$ (21)

where V_P,b, V_L,b and V_E,b are the bonded potential energies in protein P, ligand L and environment E, respectively. V_PP,nb, V_LL,nb and V_EE,nb are the self non-bonded potential energies in protein P, ligand L and environment E, respectively. V_PL,nb, V_PE,nb and V_LE,nb are the non-bonded interaction energies between P-L, P-E and L-E, respectively. According to molecular mechanics force fields,^{106, 107} the non-bonded potential energies are usually calculated as:

$$V_{nb}=V_{\mathit{\text{elec}}}+V_{vdW},$$ (22)

where V_elec and V_vdW are the system electrostatic and van der Waals potential energies. Presumably, ligand binding mainly involves the non-bonded interaction energies of the ligand, V_L,nb(r) = V_LL,nb(r_L) + V_PL,nb(r_PL) + V_LE,nb(r_LE). Therefore, we add a boost potential selectively to the ligand non-bonded potential energy according to the GaMD algorithm:

$$\Delta V_{L,nb}\left(r\right)=\{\begin{array}{ll}\hfill \frac{\mathit{1}}{\mathit{2}}{k}_{L,nb}{\left(E_{L,nb}-V_{L,nb}\left(r\right)\right)}^{\mathit{2}},& V_{L,nb}\left(r\right)<E_{L,nb}\hfill \\ \hfill \mathit{0},& V_{L,nb}\left(r\right)\ge E_{L,nb} \hfill \end{array}$$ (23)

where E_L,nb is the threshold energy for applying boost potential and k_L,nb is the harmonic constant. These parameters in LiGaMD are derived similarly as in the GaMD algorithm.

Next, one can add multiple ligand molecules in the solvent to facilitate ligand binding to proteins in MD simulations. This is based on the fact that the average ligand unbound time τ_U is inversely proportional to the ligand concentration [L], i.e., ${\tau }_U=\frac{\mathit{1}}{k_{on}\bullet \left[L\right]}$ with k_on being the ligand binding rate constant. The higher the ligand concentration, the faster the ligand binds, provided that the ligand concentration is still within its solubility limit. In addition to selectively boosting the bound ligand, another boost potential could thus be applied on the unbound ligand molecules, protein, and solvent to facilitate both ligand dissociation and rebinding. The second boost potential is calculated using the total system potential energy other than the non-bonded potential energy of the bound ligand as:

$$\Delta V_D\left(r\right)=\{\begin{array}{rr}\hfill \frac{\mathit{1}}{\mathit{2}}{k}_D{\left(E_D-V_D\left(r\right)\right)}^{\mathit{2}},& \hfill V_D\left(r\right)<E_D\\ \hfill \mathit{0},& \hfill V_D\left(r\right)\ge E_D\end{array}$$ (24)

where V_D is the total system potential energy other than the non-bonded potential energy of the bound ligand, E_D is the corresponding threshold energy for applying the second boost potential and k_D is the harmonic constant. This leads to dual-boost LiGaMD (LiGaMD_Dual) with the total boost potential ΔV(r) = ΔV_L,nb(r) + ΔV_D(r).

2.5. Peptide Gaussian Accelerated Molecular Dynamics (Pep-GaMD)

Large conformational changes of peptides often occur via peptides binding to the target proteins, being distinct from small-molecule ligand binding or protein-protein interactions (PPIs). We have developed another algorithm called peptide GaMD or “Pep-GaMD” that enhances sampling of peptide-protein interactions⁶³.

In Pep-GaMD, we consider a system of ligand peptide L binding to a target protein P in a biological environment E. We decompose the potential energy into similar terms as in Equation (21). Presumably, peptide binding mainly involves in both the bonded and non-bonded interaction energies of the peptide since peptides often undergo large conformational changes during binding to the target proteins. Thus, the essential peptide potential energy is V_L(r) = V_LL,b(r_L) + V_LL,nb(r_L) + V_PL,nb(r_PL) + V_PL,nb(r_LE). In Pep-GaMD, we add boost potential selectively to the essential peptide potential energy according to the GaMD algorithm:

$$\Delta V_L\left(r\right)=\{\begin{array}{rr}\hfill \frac{\mathit{1}}{\mathit{2}}{k}_L{\left(E_L-V_L\left(r\right)\right)}^{\mathit{2}},& \hfill V_L\left(r\right)<E_L\\ \hfill \mathit{0},& \hfill V_L\left(r\right)\ge E_L\end{array}\begin{array}{c} \\ \end{array}$$ (25)

where E_L is the threshold energy for applying boost potential and k_L is the harmonic constant.

In addition to selectively boosting the peptide, another boost potential is applied on the protein and solvent to enhance conformational sampling of the protein and facilitate peptide rebinding. The second boost potential is calculated using the total system potential energy other than the peptide potential energy as:

$$\Delta V_D\left(r\right)=\{\begin{array}{rr}\hfill \frac{\mathit{1}}{\mathit{2}}{k}_D{\left(E_D-V_D\left(r\right)\right)}^{\mathit{2}},& \hfill V_D\left(r\right)<E_D\\ \hfill \mathit{0},& \hfill V_D\left(r\right)\ge E_D\end{array}$$ (26)

where V_D is the total system potential energy other than the peptide potential energy, E_D is the corresponding threshold energy for applying the second boost potential and k_D is the harmonic constant. This leads to dual-boost Pep-GaMD (Pep-GaMD_Dual) with the total boost potential ΔV(r) = ΔV_L(r) + ΔV_D(r).

3. Applications

Without the need to set predefined reaction coordinates or CVs, GaMD enables a wide range of applications in enhanced sampling of biomolecules. Furthermore, accurate reweighting using cumulant expansion to the 2^nd order could be achieved in GaMD simulations because the boost potential exhibits a Gaussian distribution, allowing recovery of the original free energy landscapes even for large biomolecules^{48, 51, 52}. Depending on the system size, orders of magnitude speedup for biomolecular simulations could be achieved in GaMD. As demonstrated on alanine dipeptide, GaMD simulations achieved ~36–67 times speedup for sampling of the backbone dihedral transitions compared with the long cMD simulations¹⁰⁸. Higher acceleration could be potentially achieved for larger systems with greater boost potential applied in the GaMD simulations. Hundreds-of-nanosecond to microsecond GaMD simulations could capture millisecond timescale events. Here, we summarize recent application studies of GaMD.

3.1. Protein-nucleic acid interactions

CRISPR-Cas9 system is a bacterial immune system that has introduced a powerful genome editing technology, which has revolutionized life sciences¹⁰⁹. At the molecular level, CRISPR-Cas9 is a protein/nucleic acid complex, composed of the Cas9 protein associated with a guide RNA and matching sequences of DNA¹¹⁰. Cas9 site-specifically recognizes the DNA by binding its Protospacer-Adjacent Motif (PAM), a short trinucleotide that enables the selection of the DNA across the genome. Upon PAM binding, the DNA binds Cas9 by matching the RNA with one strand (the target strand, TS), such forming an RNA:DNA heteroduplex structure. The second non-target strand (NTS) of the DNA gets displaced and also accommodated within the protein. Structures of the Streptococcus Pyogenes Cas9 (SpCas9) revealed a bilobed architecture (Fig. 2A). One lobe – viz., the recognition lobe (REC) – includes three regions that mediate nucleic acid binding (REC1–3), while the second is the nuclease lobe (NUC)^111–113. The latter comprises two catalytic domains, HNH and RuvC, which cleave the DNA TS and NTS, respectively. X-ray crystallography and cryo-EM studies portrayed the structure of SpCas9 in different states, as apo protein¹¹³, in complex with RNA¹¹⁴ and upon DNA binding^{111, 112}. These structural studies have been a stepping stone to understand the mechanism of action of CRISPR-Cas9. However, although critical, this information could not access the dynamics and the complex conformational transitions of this ribonucleoprotein, raising fundamental questions on the system’s biological function. In this regard, we have successfully applied GaMD to decipher the molecular mechanism of nucleic acid processing and selectivity of this genome editing tool.

Figure 2.

(A) Overview of the Streptococcus pyogenes CRISPR-Cas9 system. The Cas9 protein is represented in molecular surface, showing individual domains in different colors. The RNA (yellow), target DNA (TS, violet), and non-target DNA (NTS, cyan) are also shown. (B) Energetic landscape associated to the conformational transition of the Cas9 protein from the apo form to the RNA-bound state, computed using GaMD. The potential of mean force (PMF), which describes the free energy landscape, was computed along the E945-D435 FRET distance and the root mean square deviation (RMSD) with respect to the apo state. The simulations identified three minima: M1 corresponding to the crystallographic apo, M2 that is the RNA-bound structure and M3, which is an intermediate characterized by the solvent exposure of an arginine-rich helix. For selected states, the ensemble averaged electrostatic potential has been computed, revealing the formation of a positively charged cavity (blue) in the intermediate states. Adapted with permission from Palermo et al. (2017). https://www.pnas.org/content/114/28/7260. Copyright 2017 National Academy of Sciences.

3.1.1. Conformational changes underlying RNA binding to CRISPR-Cas9

Based on structural data, large structural transitions of the protein have been hypothesized to enable RNA binding^{113, 114}. To characterize this process, we applied a GaMD in combination with Targeted MD (TMD) approach, which reduces the RMSD between an initial and final target conformations¹¹⁵. By using TMD, we obtained an initial pathway of the conformational change from the apo protein to the RNA-bound form. We observed that the REC1–3 regions of the protein moved in opposite directions relative to each other, leading to the closure of the REC lobe to accommodate RNA. This observation agreed well with previous hypotheses based on cryo-EM^{113, 114}. Then, we used GaMD to precisely describe the energetic landscape associated to this conformational change (Fig. 2B). The free energy landscape described three local minima: M1 corresponds to the crystallographic apo structure, M2 is the RNA-bound structure, while M3 is an intermediate state, characterized by the solvent exposure of an arginine-rich helix. The latter directly binds the RNA guide in both RNA-bound and DNA-bound structures of Cas9¹¹⁴, suggesting a mechanism for the recruitment of RNA, in which the electrostatics could play a key role. By further computing the ensemble averaged electrostatic potential, we found that a positively charged cavity is formed at the level of the arginine-rich helix and is suitable for RNA binding (Fig. 2B). Overall, these simulations indicated that the arginine helix is critical for the recruitment of RNA, and that the formation of positively charged cavity allows for the formation of the Cas9:RNA binary complex.

3.1.2. Conformational activation of the Cas9 protein for DNA cleavage

The process of conformational activation of the Cas9 protein toward DNA cleavages involves a critical transition of the catalytic HNH domain. The latter undergoes a structural change from an inactive form to the active state prone to perform DNA cleavages^{111, 112, 116}. Our first study based on cMD highlighted a “striking plasticity” of the catalytic HNH nuclease¹¹⁷. That study revealed the critical dynamic interplay between the DNA NTS and HNH, suggesting that the binding of the NTS would allow increased dynamics of HNH and, thereby, its activation toward DNA cleavage. After this first computational study, single-molecule Förster Resonance Energy Transfer (FRET) experiments have investigated the large scale dynamics of the system, showing that the dynamical docking of HNH at the cleavage site critically requires the presence of the NTS,¹¹⁸ and thereby confirming the predictions of molecular simulations. Overall, that early MD study has been instrumental in characterizing the atomic level details of the CRISPR-Cas9 dynamics. Nevertheless, considering that cMD simulations are limited to short timescales (i.e., ns–to–μs), that investigation could not fully address the activation mechanism of the catalytic HNH domain. To overcome the inherent timescale limits of cMD and characterize the HNH activation process, we performed GaMD simulations, capturing multiple states of the HNH conformational landscape¹¹⁵. As expected, the simulations broadly sampled various possible configurations of the HNH domain. Energetic reweighting of the conformational landscape revealed that the energetic minima identified through GaMD correspond to the conformational states found by FRET experiments^{112, 114, 116, 119} and structural studies¹¹¹ (Fig. 3A). Notably, this extensive GaMD sampling (collecting >20 μs) identified a “bona-fide” conformation of the active state (viz., active #4 in Fig. 3A), which was shown to be thermodynamically stable. This conformation predicted the active state two years before structural data was made available¹¹¹, allowing also to start in-depth studies of the catalysis though hybrid quantum-classical methods^{120, 121}. Moreover, to better describe the conformational change from the pre-active state (captured in PDB ID: 5f9r) to the active configuration where HNH catalytic residue (H983) docks at the DNA TS (Fig. 3B, top panel), the specialized supercomputer Anton-2¹²² has been used to carry out continuous multi-μs cMD simulations¹²³. These simulations captured the late step of HNH activation over ~16 μs of continuous simulations (Fig. 3B, bottom panel). The dynamical docking of HNH at the cleavage site on the TS occurred by following the same pathway previously observed over multiple GaMD replicas (Fig. 3B, central panel). Indeed, while the continuous simulation performed on Anton-2 recovered the transition over ~16 μs, GaMD captured the conformational change by running ~400 ns and in three replicas. This finding indicates that GaMD reliably captures structural transitions of biomolecules that occur over longer time scales. Finally, it is notable that the activated state, which was early identified though GaMD¹¹⁵ and later refined using Anton-2 simulations¹²³, resulted in notable agreement with the cryo-EM structure of the active complex¹¹¹. This showed the reliability of the early predictions that have been obtained based on GaMD.

Figure 3.

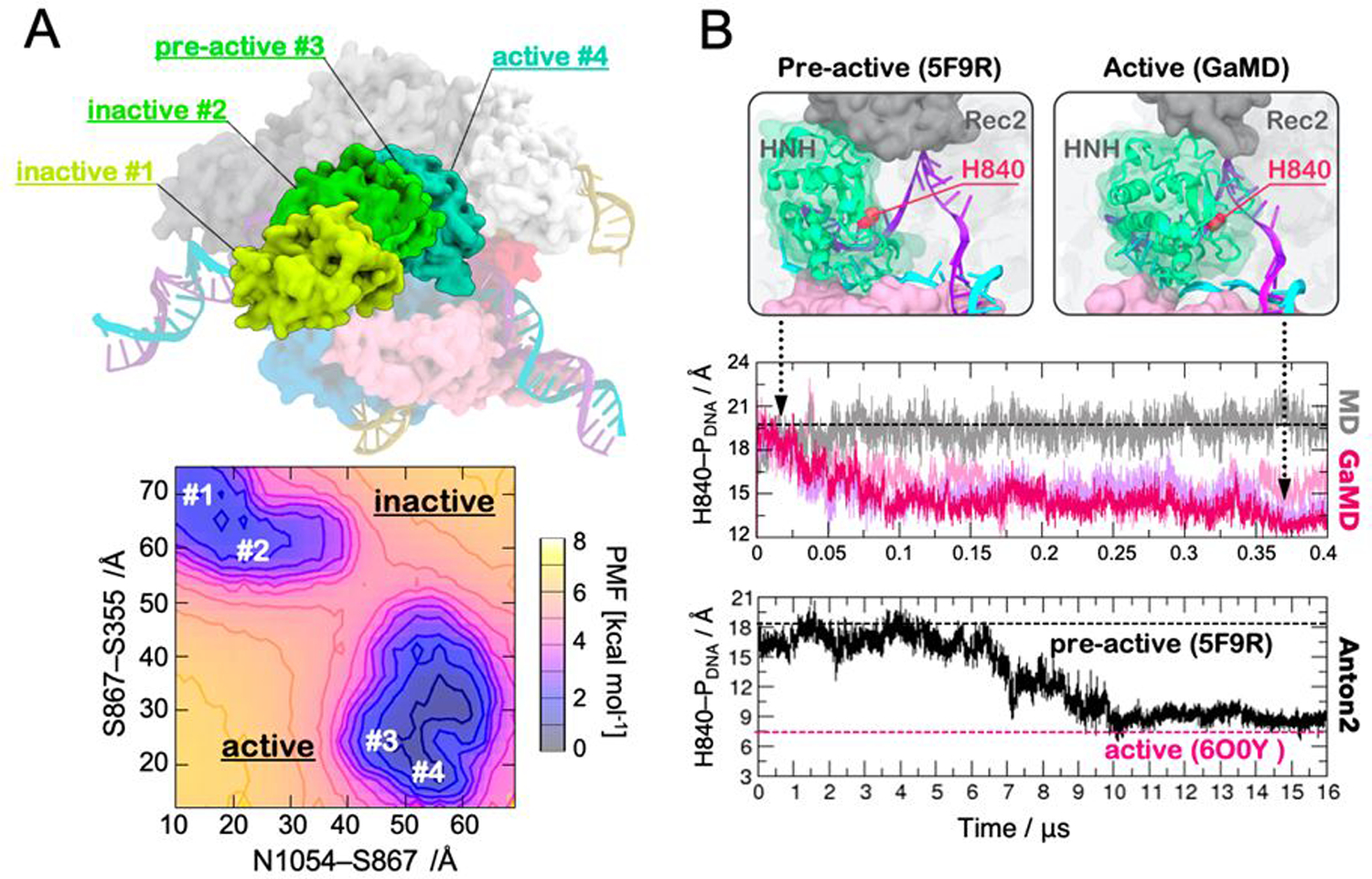
(A) Conformations of the HNH domain (green) in its inactive (#1, #2), pre-active (#3) and active (#4) states, as experimentally determined through single-molecule FRET and structural approaches (top panel). The free energy landscape (i.e., Potential of Mean Force, PMF) associated to the conformational changes of the HNH domain from its inactive to active states is shown in the bottom panel. The minima correspond to the four states experimentally found (top). The PMF was computed along the S867-S355 and N1054-S867 FRET distances. Adapted with permission from Palermo et al. (2017). https://www.pnas.org/content/114/28/7260. Copyright 2017 National Academy of Sciences. (B) Conformational change of the HNH domain from its pre-active conformation (captured in the PDB ID: 5F9R, left) to the active state identified through GaMD (right). The active state displays the catalytic residue H983 close to the DNA target strand (TS). The distance between the catalytic H840 and the scissile phosphate (H840–PDNA) has been computed along ~400 ns GaMD (central panel) and ~16 μs of continuous MD using the specialized supercomputer Anton-2 (bottom panel). The black dashed line indicates the pre-active conformation (PDB ID: 5F9R) used as a starting point for MD simulations, while the magenta dashed line indicates the active conformation more recently captured through cryo-EM (PDB ID: 6O0Y). Reprinted with permission from Palermo et al. (2018). Copyright 2018 Cambridge University Press. https://doi.org/10.1017/S0033583518000070.

3.1.3. Molecular mechanism of off-target effects of CRISPR-Cas9

An important mechanistic question relates to the onset of off-target effects, which arise from the binding of DNA sequences that do not fully match the guide RNA, resulting in RNA:DNA hybrids containing mismatched pairs. Off-target effects result in cleavages at DNA sites, representing a limitation for the application of CRISPR-Cas9 for in vivo and ex vivo genome editing. Kinetic and single-molecule FRET studies provided critical hints on the molecular basis of off-target effects. Indeed, it has been shown that DNAs containing one to three mismatches located at the RNA:DNA hybrid ends result in a flexible and catalytically active HNH domain^{118, 124, 125}. Contrariwise, four (or more) mismatches result in decreased flexibility of HNH and in its catalytic inactivation. The single-molecule experiments, however, could not explain how a different number of DNA mismatches at the RNA:DNA hybrid ends could affect the activation of HNH. Knowing the molecular basis of this mechanism is of critical importance, as it could help in developing more specific CRISPR-Cas9 systems, in which a single base pair mismatch is sufficient for reducing the HNH dynamics and catalytic function, thereby inhibiting the cleavage of incorrect DNA sequences. Considering that GaMD has been successful in describing the activation mechanism of HNH¹¹⁵ (Fig. 3), we employed the method to investigate the effect of base pair mismatches on its conformational dynamics^{68, 126}. For this application, we employed GaMD without carrying out energetic reweighting, increasing the sampling of low-energy states and providing a semi-quantitative ranking of the associated probabilities. This enabled us to broadly explore the system’s conformational dynamics in the presence of base pair mismatches. The simulations revealed that four or more mismatches induce a broad opening of the RNA:DNA hybrid (Fig. 4A), which results in newly formed interactions between the TS and the L2 loop. These interactions importantly reduce the HNH flexibility, hampering its conformational activation. On the other hand, one to three base pair mismatches do not result in sensible openings of the heteroduplex, as evinced by the minor groove width (measured at position 17, Fig. 4B), resulting in a negligible effect on the HNH conformational dynamics and thereby not affecting its activation for cleavage. Overall, the simulations could discriminate the different effects of base pair mismatches on the HNH activation, providing a mechanistic rationale to previous kinetic and single-molecule experiments. Building on the outcomes of GaMD simulations, we suggested that altering the TS-L2 interactions could reduce off-target binding. This speculation has been supported by the experimental engineering of the L2 loop in several variants of the Cas9 enzyme^{125, 127, 128}, which increase the system’s specificity toward on-target sequences.

Figure 4.

(A) Extended opening of the RNA:DNA hybrid and newly formed interactions with the L2 loop (magenta) of the HNH domain (green), observed during GaMD simulations of CRISPR-Cas9 in the presence of four base pair mismatches at the RNA:DNA hybrid ends. (B) RNA:DNA minor groove width computed along MD simulations of CRISPR-Cas9 bound to an on-target DNA (black) and in the presence of one to four mismatches at the hybrid ends. A vertical bar indicates the experimental minor groove width (i.e., 11 Å from X-ray crystallography). The minor groove width has been measured at the level of base pair 17 (shown on the right). Adapted with permission from Ricci et al. (2019). Copyright 2019 American Chemical Society. https://pubs.acs.org/doi/full/10.1021/acscentsci.9b00020. Further permissions related to the material excerpted should be directed to the American Chemical Society.

3.1.4. Allosteric effects across the CRISPR-Cas9 complex

Multiple evidences including experiments and computations have indicated that CRISPR-Cas9 is also an intriguing “allosteric engine”^{125, 129–131}. Indeed, CRISPR-Cas9 requires an intricate allosteric activation to accomplish DNA cleavages. Biochemical experiments have indicated that the central element of the CRISPR-Cas9 allosteric signaling is the HNH domain, since its high flexibility can allow the signal transmission. To describe the allosteric signaling across HNH and how it transfers the information of DNA binding (occurring within the REC lobe) to the catalytic sites for cleavage, GaMD was combined with graph theory¹³². This combination allowed inclusion of long timescale motions in the calculation of the allosteric pathways⁶⁷. Specifically, while GaMD characterized the long timescale system’s dynamics, network models derived from graph theory accurately described the allosteric network and information transfer. This approach revealed the existence of a millisecond timescale dynamic pathway across HNH, which connects the RuvC nuclease domain to the recognition lobe REC. This allosteric route was validated through NMR relaxation experiments, showing that a contiguous pathway of slow residues overlaps with the prediction from GaMD and graph theory-based analysis. In summary, the combination of GaMD simulations with graph theory provided a useful approach for determining the signal transduction in CRISPR-Cas9, laying the foundations for characterizing allostery in other protein/nucleic acid complexes whose biological function relies on slow dynamical motions associated to the (re)organization of protein domains and long-range effects.

3.2. Protein-protein/peptide interactions

Protein–protein interactions (PPIs) and protein-peptide interactions are central to biological functions and have thus been targeted to design novel therapeutic drugs^133–137. Here, we will summarize recent GaMD applications in simulation studies of PPIs and protein-peptide interactions.

3.2.1. Protein-protein interactions

The recognition of T cell receptor (TCR) and peptides presented by major histocompatibility molecules (pMHC) initiates adaptive immune responses. The pMHC binding affinity often correlates with the TCR-signaling strength. However, frequent high-affinity of pMHC in the human T cell repertoire are not stimulatory. Recently, enhanced sampling methods including GaMD, ABF and SMD were performed to distinguish stimulators from non-stimulatory ligands by simulating the TCR-pMHC disengagement⁷¹. The GaMD was first performed to reveal the structural flexibility of the complex and identify important CVs, including the orientation angle of the TCR about the pMHC assembly, salt bridges and hydrogen bonds. Then, the identified CVs were used for free energy calculation using the ABF method. Constant velocity SMD simulations were performed starting from the free energy minima identified by ABF. The simulations revealed that dynamic interactions in the TCR-pMHC interface play a critical role in determining the TCR specificity. One collective property of the entire TCR-pMHC interface is the formation of a catch or slip bond, being consistent with the results from single-molecule force measurements. In addition to simulations of PPIs with globular proteins such as the TCR-pMHC complex, GaMD have also been successfully applied to investigate PPIs with membrane proteins such as GPCR-G protein interactions^{69, 70}, which will be described in Section 3.5. In summary, GaMD is suitable to study large biomolecular complexes and provide important insights into functionally important PPIs.

3.2.2. Protein-peptide interactions

Petrizzelli et. al.⁷³ applied GaMD to investigate the pathogenic mechanisms caused by missense mutations of KDM6A on the histone H3, including P941S, D980V, S1025G, H1060L, L1200F, G1223D, Q1248R and R1255W. GaMD simulations showed that the interaction between the linker and JmjC domains was significantly impacted by residue mutations, leading to a loss of function. All mutants exhibited movements of the disordered linker domain, leading to increased flexibility of the KDM6A-H3 complex, which induced wrong exposure and orientation of the trimethylated lysine in the catalytic site. Therefore, GaMD simulations revealed important pathogenic mechanisms of the KDM6A-H3 interaction⁷³.

We developed a novel approach, namely PeptiDock+GaMD, in which the global peptide docking-ClusPro PeptiDock and GaMD simulations were combined for improving modeling of protein-peptide interactions¹³⁸. For three model peptides (peptide 1–3), docking models generated with PeptiDock¹³⁹ showed 3.3 Å, 3.5 Å and 4.8 Å RMSD of the peptide backbone relative to their experimental structures. The peptide docking poses were refined by GaMD simulations. Then, the PyReweighting toolkit⁴³ was applied to reweight and calculate free energies of the peptide structural clusters obtained from GaMD simulations. RMSDs of Peptides 1 and 2 in the 1^st top-ranked cluster were 0.9 Å and 0.6 Å, respectively. The 3^rd top-ranked cluster in Peptide 3 exhibited the smallest RMSD of 2.7 Å. Thus, the PeptiDock+GaMD could be used to accurately predict the peptide-protein interaction. In comparison, cMD simulations with same simulation time were much less efficient in refining the peptide docking poses.¹³⁹ Only 1 among 4 cMD simulations of Peptide 2 improved the peptide binding pose. RMSD decrease was not observed in any of cMD simulations of Peptide 3. The top-ranked models obtained by clustering of cMD snapshots were of high quality for only Peptide 1 but medium for both Peptides 2 and 3. Therefore, GaMD simulations refined peptide docking poses and provided significantly improved sampling than cMD.

The PeptiDock+GaMD approach was further applied to model interactions of cyclic peptides with proteins, including peptide binding to MDM2/MDMX¹⁴⁰ and Tsg101 UEV protein⁷². Compared with the linear peptides, cyclic peptides often possess longer lifetime and better biological activity. To facilitate cyclic peptide design, the PeptiDock+GaMD approach was applied to investigate binding interactions between the UEV domain protein and three cyclic peptides⁷². The predicted peptide binding mode identified from GaMD simulations was further validated by binding free energy calculations, which agreed well with the experimental binding affinities. Therefore, GaMD simulations provided important insights to protein-peptide interactions and were applicable to both linear and cyclic peptides.

3.2.3. Binding thermodynamics and kinetics of peptide

Pep-GaMD⁶³ has been developed to simulate both peptide binding and dissociation, which allows us to calculate the binding free energies and kinetics of flexible peptides. It has been demonstrated on binding of three model peptides to the SH3 domains^{141, 142}, which include “PPPVPPRR” (PDB: 1CKB), “PPPALPPKK” (PDB: 1CKA) and “PAMPAR” (PDB: 1SSH) (Figs. 5A–5C). Repetitive peptide binding and unbinding events were captured in independent 1 μs Pep-GaMD simulations, allowing us to calculate peptide binding thermodynamics and kinetics (Figs. 5D–5I). Peptide kinetics especially the dissociation rate was accelerated by ~3–4 orders of magnitude in the Pep-GaMD simulations. The predicted values from Pep-GaMD were in good agreement with available experimental data. Furthermore, the Pep-GaMD simulations revealed the important role of long-range electrostatics in peptide binding and the binding mainly followed a conformational selection model.

Figure 5.

Pep-GaMD simulations have captured repetitive dissociation and binding of three model peptides to the SH3 domains: (A-C) X-ray structures of the SH3 domains bound by peptides (A) “PAMPAR” (PDB: 1SSH), (B) “PPPALPPKK” (PDB: 1CKA) and (C) “PPPVPPRR” (PDB: 1CKB). The SH3 domains and peptides are shown in green and magenta cartoon, respectively. Key protein residues Asp19 and Trp40 in the 1SSH structure and Asp150 and Trp169 in the 1CKA and 1CKB structures, and peptide residues Arg10 in the 1SSH structure, Lys8 in the 1CKA structure and Arg7 in the 1CKB structure are highlighted in sticks. The “N” and “C” labels denote the N-terminus and C-terminus of the peptides. (D–F) time courses of peptide backbone RMSDs relative to X-ray structures with the protein aligned calculated from three independent 1 μs Pep-GaMD simulations of the (D) 1SSH, (E) 1CKA and (F) 1CKB structures. (G–I) The corresponding PMF profiles of the peptide backbone RMSDs averaged over three Pep-GaMD simulations of the (G) 1SSH, (H) 1CKA and (I) 1CKB structures. Error bars are standard deviations of the free energy values calculated from three Pep-GaMD simulations. Reprinted from “Jinan Wang, Yinglong Miao, J Chem Phys 2020, 153:154109”, with the permission of AIP Publishing.

3.3. Protein-ligand binding

3.3.1. Protein-ligand interactions

Use of EGFR tyrosine kinase inhibitors is a promising approach to improve progression-free survival in cancer patients. Osimertinib was approved as a third generation EGFR mutant selective inhibitor. Unfortunately, resistances were detected against the osimertinib therapy. Brown et al.⁸⁰ identified G724S as an osimertinib resistance mutation. Microsecond GaMD simulations were performed on EGFR mutants in presence and absence of osimertinib to investigate the underlying mechanism. The GaMD simulations showed that the G724S mutation disrupts the osimertinib binding to the enzyme with exon 19 in-frame deletion (Ex19Del) mutation, while does not affect the enzyme with exon 21 missense mutation (L858R). The G724S mutation induces hyper stabilization of glycine-rich P-loop in β-bend conformation. It disrupts the interaction between indole ring of osimertinib and phenyl ring of F723. These results were further verified in animal cell culture experiments and in cancer patients. Overall, GaMD simulations elucidated the molecular mechanisms of ligand binding in EGFR mutations for treatment of non-small cell lung carcinomas, as well as many other protein-ligand interactions^{56, 57, 74–77}.

3.3.2. Ligand binding thermodynamics and kinetics characterized by LiGaMD

LiGaMD has been proposed to quantitatively characterize ligand binding thermodynamics and kinetics⁶². Host-guest and protein-ligand binding model systems have been used to validate the LiGaMD algorithm. Hundreds-of-nanosecond LiGaMD simulations captured repetitive guest binding and unbinding in the β-cyclodextrin host. The calculated guest binding free energies were in good agreement with experimental data, for which the errors were <1.0 kcal/mol. The sampling errors of LiGaMD simulations were < 1.0 kcal/mol in comparison with converged μs-timescale cMD simulations. Additionally, ligand kinetic rate constants were accurately predicted using Kramers’ rate theory. Furthermore, repetitive binding and unbinding of the benzamidine inhibitor in trypsin was observed in 1 μs LiGaMD simulations, allowing us to accurately calculate ligand binding free energy and kinetic rate constants. The ligand dissociation rate was remarkably accelerated by 7 orders of magnitude in the LiGaMD simulations. The predicted values were in excellent agreement with the experimental data⁶².

3.4. Protein enzymes

3.4.1. Structural dynamics of protein kinases

Casein kinase 1δ (CK1δ) has been regarded as an important component in metazoan circadian rhythms regulation. Despite its importance, little was known about substrate selectivity and activity of the enzyme in molecular detail. Philpott et. al.⁹⁰ performed GaMD simulations on wildtype and tau mutant CK1δ systems and discovered a conformational switching mechanism of the activation loop. The switch regulates two different regions of the PER2 protein, which in turn regulates the protein stability and circadian timings in eukaryotes. The GaMD simulations further revealed that anion binding to a highly conserved site monitors the conformation in the activation loop and thereby regulating the overall conformation of the substrate binding cleft. The tau mutant, on the other hand, disrupts the allosteric regulation between the anionic sites. This disturbs the conformational flexibility of the activation loop and affects the stability of the PER2 protein. GaMD simulations thus provided molecular basis of the decreased activity in the tau mutant CK1δ.

Brassinosteroid insensitive 1-associated kinase 1 (BAK1) is an important receptor like kinase which initiates numerous immune and growth signaling pathways in plants. Moffett et al.⁸⁹ applied GaMD simulations to explore physiochemical basis of BAK1 activation through phosphorylation. GaMD simulations revealed the effects of various phosphorylation patterns and ATP binding on the enzyme conformation. GaMD simulations identified a metastable inactive enzyme conformation using activation-loop cracking. This activation loop conformation had been also found in other kinases like the ERK2. Phosphorylation of residues T450 and T455 played important roles in stabilizing the active-like activation loop without cracking. During the GaMD simulations, phosphorylation helped αC helix of the enzyme maintain its position near the N-lobe. In contrast, the αC helix of the unphosphorylated systems switched to an inactive state as the activation loop changed into a “cracked” conformation. Overall, GaMD simulations revealed the mechanism of phosphorylation controlled BAK1 activation. In another study, Koh et. al.⁸⁸ performed GaMD simulations for mechanistic insights into the flux-dependent transport signaling by Bce-like antibiotic resistance systems. They found that the transport activity is directly related to histidine kinase activity even with different antibiotic concentrations.

3.4.2. Active site dynamics of protein enzymes

The oncoprotein AlkB homolog 5 (Alkbh5) is involved in cancers such as leukemia, brain cancer and breast cancer. NMR experiments and GaMD simulations were combined to generate the structural model of the apo human Alkbh5⁸¹. The Alkbh5 active site was observed to be more disordered than that in the x-ray structure (PDB:4NJ4). It was likely due to the absence of the Cys²³⁰–Cys²⁶⁷ disulfide bond in solution, which limited the protein conformational accessibility. GaMD simulations captured breathing motions of the protein, which expands the α-ketoglutarate binding pocket and permits binding of small molecules.

FabA and FabZ are two Escherichia coli dehydratases involved in production of the unsaturated fatty acids (UFAs) from fatty acid biosynthesis⁸³. Both FabA and FabZ are known to catalyze dehydration reactions, however, only FabA can further catalyze isomerization reaction. A combined approach involving chemical biology, structural biology and GaMD simulations was applied to understand the substrate selectivity and divergent activity of the two enzymes. Cross-linking experiments were performed to produce the acyl-AcpP•FabA and acyl-AcpP•FabZ complexes, which were used for GaMD simulations to elucidate the dehydration mechanism catalyzed by FabA and FabZ. GaMD simulations revealed dynamic mechanism of the unique isomerase activity of FabA and successfully differentiated the substrate preferences of FabA and FabZ. Moreover, GaMD simulations showed that only FabA selectively sampled the (−) gauche conformer of trans-2-decenoyl-AcpP for allylic rearrangement.

Furthermore, GaMD was successfully applied on simulations of protein enzymes for structure-based drug design of anti-malarial drugs,⁸² design of inhibitors targeting Staphylococcus aureus enzyme MnaA,⁸⁵ investigation of soybean lecithin–gallic acid complex formation to aid in alcoholic liver disease (ALD),⁸⁷ usefulness of antioxidative agent for treating vascular endothelial deficits,⁸⁶ and understanding of drug resistance mechanism of rifampin⁹². Simulations using GaMD and replica exchange solute tempering (REST2)¹⁴³ were performed to understand mechanism of the transactivation of estrogen receptor⁷⁹.

3.4.3. Protein allostery

The interaction between HCV NS5A-D2 and human prolyl isomerase cyclophilin A (CypA) plays an essential role in viral RNA replication. Dujardin et al.⁸⁴ employed GaMD simulations and NMR to investigate the role of a short structural motif PW-turn (³¹⁴PXWA³¹⁷) on the structural disorder in NS5A-D2. There is a conformational equilibrium between folded and disordered states in the PW-turn motif, which is allosterically regulated by the cis/trans isomerization of 5 prolines residues (P306, P310, P315, P319 and P320). Moreover, the HCV RNA replication efficiency correlates well with the fraction of the structured PW-turn obtained from GaMD simulations.

Another study by Sztain et al.⁹¹ employed GaMD to identify cryptic pockets of the SARS-CoV-2 main protease (Mpro), which are far away from the active site. Four systems including the monomer and dimer of Mpro in the absence and presence of the co-crystalized N3 inhibitor were built to perform GaMD simulations. Three regions including the distal allosteric site, active site and dimer interface region were identified as potential drug pockets using the PockDrug webserver.¹⁴⁴ Virtual screening against the above-mentioned pockets allowed to identify more hit molecules than using only the active site in the crystal structure. Furthermore, correlation analysis suggested that the three pockets could be allosterically regulated by each other. Therefore, the above identified pockets could be useful in virtual screening to identify novel inhibitors of SARS-CoV-2.

3.5. Membrane proteins

Membrane proteins including GPCRs, intramembrane proteases and ion channels play essential roles in cellular signaling and serve as important drug targets. Here, we will summarize recent applications of GaMD in studies of GPCRs (including muscarinic acetylcholine, adenosine, opioid and chemokine receptors), γ-secretase, etc.

3.5.1. Binding mechanism of G protein mimetic nanobody to M₂ muscarinic GPCR

GaMD simulations were performed to capture the spontaneous binding of nanobody Nb9–8, a G protein mimetic, to the M₂ muscarinic GPCR¹⁴⁵. The agonist and nanobody in the X-ray structure of the active M₂ receptor were placed to be >20 Å far away from the receptor to build the starting model. Five independent GaMD simulations lasting ~4500 ns were performed. One GaMD simulation successfully captured the binding of the nanobody to the receptor G-protein coupling site of M₂ with a minimum RMSD of 2.48 Å in the nanobody core domain relative to the X-ray conformation, although the agonist still not reached its binding site (Figs. 6A and 6B). Both the orthosteric ligand-binding pocket and intracellular domains of the M2 receptor involved conformational change along with the binding of the nanobody (Fig. 6B). The orthosteric pocket in the X-ray structures of antagonist-bound and agonist nanobody-bound receptor are “open” and “closed”, respectively. Binding of the nanobody induced the orthosteric pocket from the “open” to “closed” state. Moreover, activation of the M₂ receptor was occurred during the binding of the nanobody, as measured by the distance between intracellular transmembrane helix 3 and 6 (TM3–TM6 distance) (Fig. 6B). Free energy profile of the nanobody RMSD relative to the 4MQS X-ray conformation and the receptor Arg121^3.50-Thr386^6.34 distance were calculated to characterize the nanobody binding pathways (Fig. 6C). Three low-energy conformational states including the unbound (“U”), intermediate 1 (“I1”), and intermediate 2 (“I2”) were identified from the potential of mean force (PMF) profile. The bound (“B”) conformation identified in the GaMD simulations is similar to that sampled in previous simulations of the 4MQS X-ray structure.¹⁴⁵ On the intracellular side, the nanobody core domain especially the β2, β3, β6, β7 and β8 strands overlapped well with the 4MQS X-ray structure when the nanobody RMSD decreased to 2.48 Å (Fig. 6D). Therefore, the GaMD provided important insights into the binding mechanism of the nanobody to the M₂ receptor.

Figure 6.

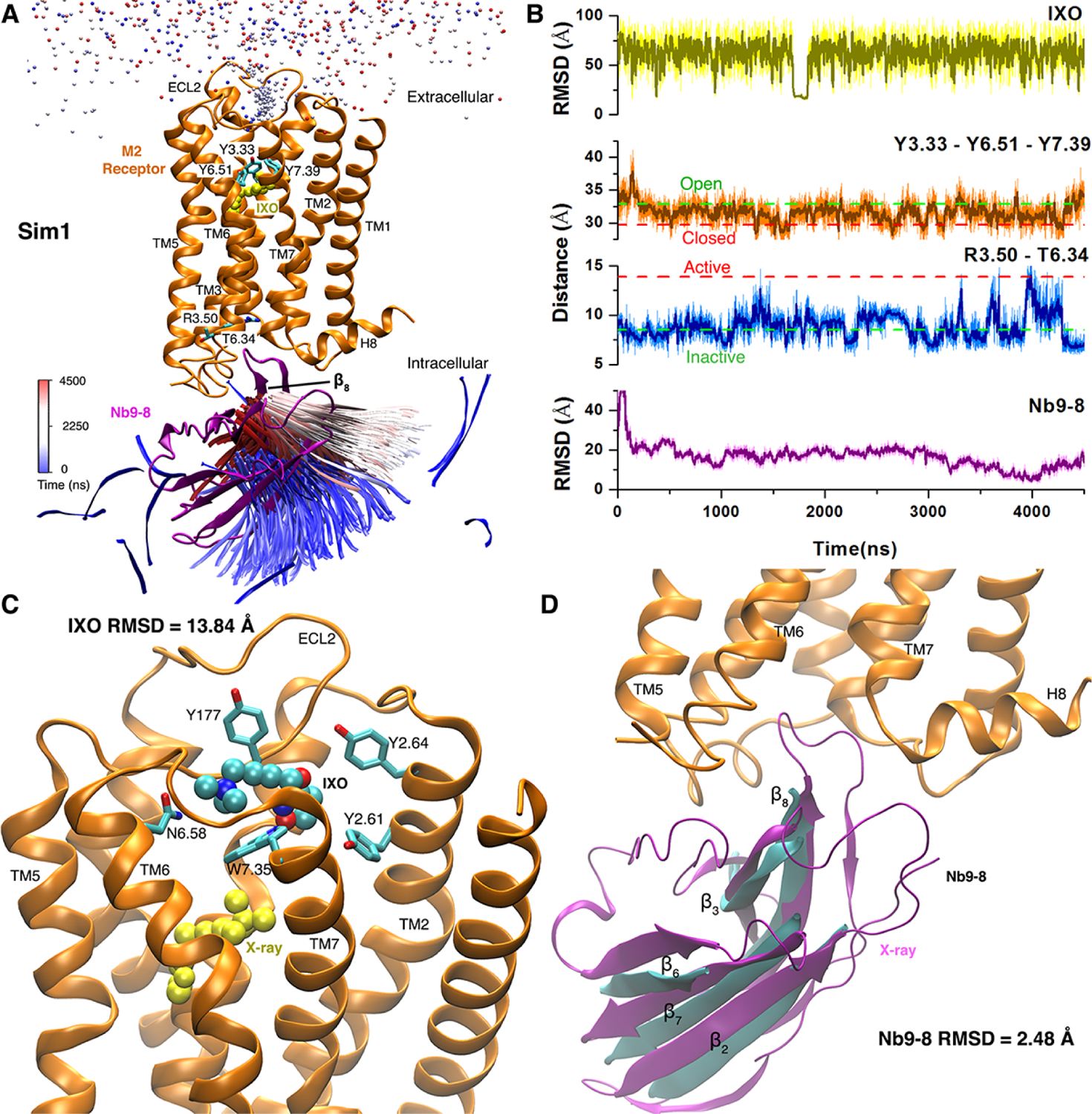
Binding of agonist IXO and G_i protein mimetic nanobody Nb9–8 to the M2 muscarinic GPCR was captured in one of five GaMD simulations: (A) Trajectories of a nitrogen atom in IXO (beads) and the β8 strand of Nb9–8 (ribbons) colored by simulation time in a blue (0 ns)–white (2250 ns)–red (4500 ns) scale. (B) RMSDs of the IXO and Nb9–8 relative to the X-ray structure, Tyr104^3.33-Tyr403^6.51-Tyr426^7.39 triangle perimeter and Arg121^3.50-Thr386^6.34 distance calculated from the simulation. Dashed lines indicate X-ray structural values of the M2 receptor (3UON: green and 4MQS: red). (C) Binding pose of IXO (spheres) in the receptor extracellular vestibule with 13.84 Å RMSD relative to the X-ray conformation (yellow spheres). Residues found within 5 Å of IXO are highlighted in sticks. (D) Binding of Nb9–8 (cyan), which exhibits only 2.48 Å RMSD in the protein core (the β2, β3, β6, β7 and β8 strands). X-ray conformations of the M2 receptor and nanobody are shown in orange and purple ribbons, respectively. Adapted with permission from Miao et al. (2018). https://www.pnas.org/content/115/12/3036. Copyright 2018 National Academy of Sciences.

3.5.2. Mechanism of specific G protein coupling to adenosine receptors

There are four subtypes of adenosine receptors (A₁, A_2A, A_2B, and A₃) in human, which mediate the effects of adenosine (ADO). The odd ARs including A₁AR and A₃AR mainly couple to the G_i/o proteins, while the even ARs (A_2AAR and A_2BAR) preferentially couple to the G_s proteins. In one of our recent studies⁶⁹, we employed GaMD simulations on four AR-G protein models, including the native structures of ADO-A₁AR-G_i with ADO and G_i protein bound¹⁴⁶ and the NECA-A_2AAR-G_s with 5’-N-ethylcarboxamidoadenosine (NECA) and an engineered G_s protein bound¹⁴⁷, as well as “decoy” complexes ADO-A₁AR-G_s and NECA-A_2AAR-G_i generated by switching the G proteins. In the ADO-A₁AR-G_i and NECA-A_2AAR-G_s complexes, GaMD identified only one stable low-energy conformation, which is similar to the cryo-EM structure (Figs. 7A and 7B). Similarly, only one low-energy conformation was identified in the NECA-A_2AAR-G_i complex, suggesting that agonist NECA binding in the A_2AAR could be still stabilized by coupling to the G_i protein (Fig. 7C). While the binding of G_s protein in the A₁AR led to increased fluctuations of both the receptor and ADO (Fig. 7D). The ADO agonist exhibited high fluctuations and sampled two different binding poses (“L1” and “L2”) in the ADO-A₁AR-G_s complex. In the “L2” binding pose, ADO interacted with residues Tyr12^1.35 and Tyr271^7.36 in the sub-pocket 2 of the A₁AR, which is described earlier¹⁴⁸. GaMD simulations indicated that coupling with the G_i protein was preferred to the G_s in the A₁AR (Fig. 7E), while both the G_s and G_i proteins could be coupled with the A_2AAR (Fig. 7F), being well agreement with experimental data of the ARs^149–151. In summary, the dynamic mechanism of specific GPCR-G protein interactions could be obtained from the GaMD simulations.

Figure 7.

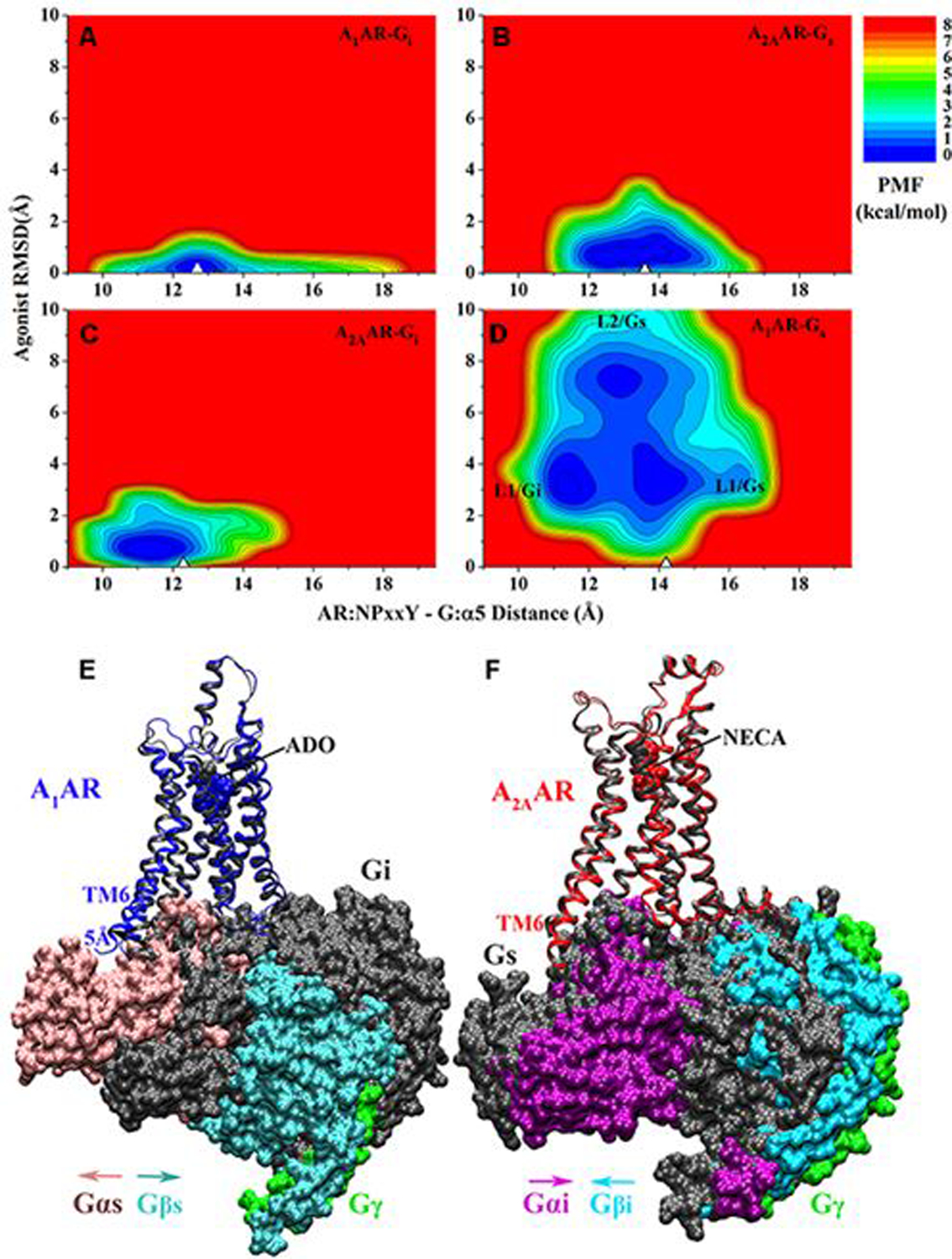
2D potential of mean force (PMF) profiles of the (A) ADO-bound A₁AR-G_i, (B) NECA bound A_2AAR-G_s, (C) NECA bound A_2AAR-G_i and (D) ADO bound A₁AR-G_s complex systems regarding the agonist RMSD relative to the cryo-EM conformation and AR:NPxxY-G:α5 distance. The white triangles indicate the cryo-EM or simulation starting structures. Summary of specific AR-G protein interactions: (E) the ADO-bound A₁AR prefers to bind the G_i protein to the G_s. The latter could not stabilize binding of agonist ADO in the A₁AR and tended to dissociate from the receptor. (F) The A_2AAR could bind both the G_s and G_i proteins, which adopted distinct conformations in the complexes. Adapted with permission from Wang et al. (2019). Copyright 2019 American Chemical Society. https://pubs.acs.org/doi/10.1021/acs.jpcb.9b04867. Further permissions related to the material excerpted should be directed to the American Chemical Society.

3.5.3. GPCR-membrane interactions depend on the receptor activation state

The phospholipid membrane bilayer plays an important role in GPCR transiting among different conformational states. Elucidation of the lipid-protein interactions could facilitate to understand the functional mechanism of GPCRs. In one of our recent study⁹⁶, the cryo-EM structure of the active ADO-A₁AR-Gi¹⁴⁶ and the X-ray structure^{148, 152} of the inactive antagonist PSB36-bound A₁AR (PSB36-A₁AR) were used to perform GaMD simulations. They were embedded in a 1-palmitoyl-2-oleoyl-glycero-3-phosphocholine (POPC) lipid bilayer. GaMD simulations revealed important role of the membrane lipids in stabilizing different states of the A₁AR. Different structural flexibility profiles of the inactive and active A₁AR were obtained by the GaMD simulations. In comparison with the inactive state, higher fluctuations of the A₁AR ECL2 region, intracellular ends of TM6 and TM5 were found in the active state. Furthermore, the -S_CD order parameter values obtained from GaMD simulations were consistent with experimental data.¹⁵³ Particularly, the inactive and active A₁AR systems exhibited similar values of the -S_CD order parameters of sn-2 acyl chains of POPC in the upper leaflet. However, the active A₁AR exhibited smaller value of the same -S_CD order parameters in the lower leaflet than those in the inactive A₁AR, suggesting that POPC lipids in the lower leaflet of the active A₁AR system were more fluid than in the inactive A₁AR system. One reliable explanation is that the outward movement of TM6 in the active A₁AR could induce higher inclination of the C-H bonds to be aligned along the bilayer normal. Thus, GaMD simulations showed that the protein-membrane interactions depended on different conformational states of the A₁AR.

3.5.4. Mechanism of allosteric drug lead binding to an adenosine GPCR

Preclinical studies suggest that the A₁AR is an important drug target for treating diseases including reduce neuropathic pain and ischemia-reperfusion injury^154–156. However, off-target side effects have hindered the therapeutic development of A₁AR agonists, which mainly originated from the high conservation of the endogenous agonist binding (“orthosteric”) site across different AR subtypes¹⁵⁷. Positive allosteric modulators (PAMs), which bind to a less conserved “allosteric” site, have the potential to develop high subtype selective A₁AR therapeutics¹⁵⁸. Using the X-ray structure of the A₁AR (PDB: 5UEN)¹⁴⁸ as a model, GaMD simulations¹⁵⁹ were performed to investigate binding mechanisms of two PAMs, VCP171 and PD81723. Each PAM was initially placed at >20 Å away from the receptor. Spontaneous binding of PAMs to the A₁AR was captured in GaMD simulations using both AMBER⁴⁸ and NAMD⁵² at different acceleration levels (dihedral and dual boost).

GaMD simulations identified similar binding modes of PD81723 and VCP171 that bound to a site around ECL2 in the A₁AR from different acceleration levels of GaMD simulations performed using different software packages. They were in highly agreement with experimental results of site-directed mutagenesis obtained by the Christopoulos group¹⁶⁰. In the mutagenesis experiments, numerous ECL2 residues including Asn148^ECL2, Glu153^ECL2, Ser161^ECL2, Ile167^ECL2 and Glu172^ECL2 were mutated to alanine, which caused significant alterations in PAM binding affinity, efficacy, and cooperativity^{160, 161}. These residues were found to interact with the bound PAMs in the GaMD simulations. Additionally, agonist binding affinity was enhanced by PAM binding. In the absence of PAM, the agonist sampled a large conformational space in the receptor orthosteric pocket without binding of PAM. Upon PAM binding at the ECL2, movement of agonist was significantly reduced.

3.5.5. Mechanism of drug binding to a chemokine GPCR

Chemokine receptors are regarded as one of the important GPCRs with implications in human health and therapeutics. CXCR4 is an important subtype with involvement in different human diseases including cancer and HIV infection. Despite its important, less is known about the mechanism of drug interaction with the receptor. GaMD simulations⁷⁴ were performed to study the binding mechanism of the drug Plerixafor (PLX) and its pathway to CXCR4. Simulation systems were built by placing ten unbound ligand molecules at a distance >15 Å away from the receptor. GaMD_Dual_NB boost scheme was used in which system nonbonded and dihedral energy terms were boosted. The GaMD_Dual_NB simulations captured spontaneous binding of the PLX from the bulk solvent to the receptor orthosteric site in one of five production runs. The complete binding of PLX was observed at ~480 ns timescale with minimum RMSD relative to the bound conformation of 2.76 Å. In the binding pocket of CXCR4, the positively charged PLX formed stable salt bridges with residues Asp97^2.63, Asp262^6.58 and Glu288^7.39 occupying both the minor and major sub-pockets of the receptor. In 2D PMF profile calculated from the GaMD simulations, “unbound”, “intermediate 1” (I1), “intermediate 2” (I2) and “bound” PLX low-energy conformational states were identified. In the intermediate conformational states I1 and I2, same polar and charged residues in the receptor ECL2-TM5-TM6 region, namely Asp187^ECL2, Asp193^5.32 and Asp262^6.58, formed favorable interactions with the positively charged nitrogen atoms of PLX. Thus, the ECL2-TM5-TM6 region of CXCR4 formed a novel intermediate drug binding site. Furthermore, GaMD simulations identified PLX drug binding pathway to the CXCR4. These studies are expected to greatly facilitate drug design of CXCR4.

3.5.6. Mechanisms of γ-secretase activation and substrate processing

The mechanism of activation of γ-secretase bound to amyloid precursor protein (APP) was investigated using GaMD simulations⁹⁸. The Cryo-EM structures of two substrates App and Notch bounded γ-secretase were simulated to investigate substrate processing by γ-secretase of wildtype and APP mutant causing the familial Alzheimer’s disease (FAD)¹⁶² (Fig. 8A). Mutations in the cryo-EM structure introduced unnatural enzyme-substrate interactions and hindered the activation process. With a combined study of GaMD simulations, mass spectrometry and western blotting, a model highlighting the process of intramembrane proteolysis of APP by γ-secretase was presented.

Figure 8.

GaMD simulations revealed the activation and its ε cleavage mechanisms of γ-secretase in the wildtype and mutant APP substrates. Summary of the (A) inactive cryo-EM, (B) active (wildtype), and (C) shifted active (M51F) conformational states of the APP-bound γ-secretase. Distinct AICD products were generated from the wildtype and M51F mutant APP. GaMD free energy profiles of (D) wildtype and (E) M51F APP-bound γ-secretase regarding the Asp257:Cγ–Asp385:Cγ and Asp257:protonated O–Leu49:O distances. Adapted with permission from Bhattarai et al. (2020). Copyright 2020 American Chemical Society. https://pubs.acs.org/doi/abs/10.1021/acscentsci.0c00296. Further permissions related to the material excerpted should be directed to the American Chemical Society.

Spontaneous activation of γ-secretase in complex with wildtype APP in the presence of a water molecule was captured by GaMD simulations (Figs. 8A and 8D). The water molecule that entered the presenilin active site was trapped between two catalytic Asp residues that were ~7 Å apart forming stable hydrogen bonds. A carbonyl oxygen of the scissile amide bond present between Leu49 and Val50 residues of the APP substrate formed a hydrogen bond with γ-secretase residue Asp257. During activation of γ-secretase, TM1, TM2 and TM8 helices of catalytic PS1 subunit showed some flexibility while TM6a was observed interacting directly with the substrate. Free energy profiles revealed four low-energy conformations of γ-secretase bound to wildtype APP, namely “Inactive”, “Intermediate”, “Inhibited” and “Active” (Fig. 8D). The active conformational state resembled the activation of the enzyme whereas the inactive state correlated with the starting cryo-EM structure (Figs. 8A & 8B). The active conformational state resembled the activation of the enzyme whereas the inactive state correlated with the starting cryo-EM structure. The inhibited conformational state closely resembled the γ-secretase structure in complex with DAPT inhibitor¹⁶³. The intermediate conformational state resembled the transitional structure in between these states.

In addition to wildtype, GaMD simulations were performed on the APP mutants namely I45F, T48P and M51F that lead to FAD. The I45F and T48P system systems revealed faster activation compared to the wildtype system which were in good agreement with the experimental mass spectrometry data of APP intracellular domain (AICD) proteolytic products that showed greater AICD50–99/AICD49–99 ratio in comparison to the wildtype. Four low-energy conformations, similar to those observed in wildtype, were identified in the FAD mutant systems. Furthermore, the GaMD simulation of M51F mutant shifted the ε cleavage between Thr48-Leu49 (Figs. 8C & 8E). The mass spectrometry analysis validated the AICD products formed as a result of proteolysis cleavage between Thr48-Leu49 was observed higher. In vitro assay showed significant high production of AICD in M51F system as compared to other systems. This was consistent with the GaMD free energy landscape as the inhibited state was observed in wildtype, I45F and T48P system but not in M51F system. The experimental validations strongly correlated with the GaMD simulation model of γ-secretase.

GaMD simulations of the wildtype and FAD mutant APPs of the different γ-secretase enzyme systems were analyzed with respect to their secondary structures. In particular, the M51F mutant APP shifted ~4 Å downwards with Thr48 and Leu49 residues flipping its side chain. The C-terminus of APP lost its β-sheet conformation as required for local rearrangements during the shift in ε cleavage. The sub-pockets S1’, S2’ and S3’ in the active site could also be visualized in the wildtype and FAD mutant APPs bound to γ-secretase via GaMD simulations. Overall, the combination of GaMD simulations, mass spectrometry and western blots enabled deep understanding of substrate processing by γ-secretase and its activation.

3.5.7. Structural dynamics of cytochrome P450

Cytochrome P450 3A4 (CYP34A) enzyme plays a crucial role in mammalian metabolic pathways including synthesis and breakdown of fatty acids and hormones. It undergoes large conformational changes in the active site and other structural components of the enzyme. Redhair et. al.⁹³ performed GaMD simulations to understand the protein dynamics and protein-ligand interactions induced by allosteric drug benzodiazepine midazolam (MDZ) in a lipid bilayer. The GaMD simulations showed that F- and G-helical regions could be a possible allosteric site for MDZ drug, which were further verified by hydrogen-deuterium exchange mass spectrometry. The GaMD simulations showed that the local environment at the Phe-cluster comprising the region between the active site and the lipid bilayer was dynamic and could be a possible allosteric site. Even in the presence of a ligand at the active site, the enzyme generated flexible allosteric site nearby. Overall, GaMD simulations provided the molecular basis of enzyme activity and allosteric drug interaction in cytochrome CYP34A.

3.6. Carbohydrates

Here, we summarize recent GaMD studies of carbohydrates, fundamental components of cells that engage in energy functions and form structural components. We review how GaMD has been applied to describe the dynamic interplay of carbohydrates with DNA¹⁰¹ and proteins,⁵⁹ and how the method has been used to facilitate the development of carbohydrate force field parameters.⁹⁹

3.6.1. The importance of carbohydrates conformation on DNA triplex

DNA triplexes are higher-order structural arrangements important for gene regulation and biotechnological applications. GaMD simulations were recently employed to examine the impact of substituting deoxyribose sugars by conformationally locked sugars on the DNA triplex structure.¹⁰¹ Multiple GaMD simulations were performed on both 3’–5’ and 5’–3’ modified triplexes, as well as on an unmodified DNA triplex, which was used as a control. The simulations revealed that the DNA triplexes, in which the deoxyribose was replaced by locked sugar, lost their structural integrity, and disintegrated resembling the structure of a duplex. On the other hand, the control DNA triplex preserved the structural integrity during the simulations. As a notable observation, both modified triplexes changed conformation reaching duplex structures containing a modified strand and a regular strand, while the third DNA strand was dissociated from the complex. In-depth analysis of the trajectories indicated a significant reduction in the major groove width and diminished solvent accessible surface area in the modified triplexes, as compared to reference systems. On this basis, the authors suggested that the newly introduced locked sugars impose a remarkable steric constraint, which alters the DNA structure and results in the inefficient binding of the third DNA strand. Overall, the authors concluded that knowledge of the structural changes induced by modified sugars could be leveraged for the design of new antisense oligonucleotides, as well as to understand the role of modified oligonucleotides in anticancer therapy.

3.6.2. Carbohydrate-protein interactions

Protein glycosylation is a post-translational modification that is involved in several cellular and biological processes.⁵⁹ Glycosyltransferases (GTs) catalyze the transfer of a sugar moiety to acceptor amino acids, such as serine, threonine (O-linked glycosylation) and asparagine (N-linked glycosylation). The glycosylation process also occurs in bacterial proteins, where it plays a critical role in the immune response against pathogens. Some bacterial effectors leverage the glycosylation process to suppress the nuclear factor NF-κB, which is central in regulating the immune response. The non-locus of enterocyte effacement effector protein B (NleB) has glycosyltransferase activity and inhibits NF-κB by transferring N-acetyl glucosamine (GlcNAc). To further understand the glycosylation process, Park and co-authors⁵⁹ focused on the SseK1 and SseK2 effectors, which are orthologs of NleB from Salmonella typhimurium. The authors combined X-ray crystallography, NMR, enzyme kinetics, GaMD simulations and in vivo experiments. Structural evidences revealed a glycosyltransferase architecture displaying a helix-loop-helix (HLH) domain relevant to protein substrate recognition and a catalytic core, which includes the conserved catalytic triad (His-Glu-Asn) critical for enzyme catalysis and bacterial virulence. GaMD simulations showed large amplitude motions of the HLH domain, with significant differences in SseK1 and SseK2 that affect the HLH approach toward the substrate binding pocket. Specifically, SseK1 was considerably more flexible than SseK2 in the loop region connecting the HLH, in line with the increased specificity toward the substrate that has been measured experimentally.⁵⁹ The simulations also suggested a possible conformation of the catalytically competent active site, showing that the binding of GlcNAc properly orients the substrate, viz., an arginine residue target of the glycosylation process, for the chemical reaction.

3.6.3. Development of carbohydrate force field parameters with GaMD simulations

Heparin is a highly sulphated, linear polysaccharide belonging to the family of glycosaminoglycans. Endogenous heparin critically regulates blood coagulation by interacting with the small protein antithrombin (AT), through the pentasaccharide domain responsible for the heparin activity.^{99, 164} The capability of a heparin penta-saccharide to bind AT is determined by the conformational dynamics of the sugar rings, and particular by the conformation of the L-iduronic acid residue. On this basis, idraparinux derivatives, which are non-glycosaminoglycan analogues of the heparin penta-saccharide, are promising anticoagulant drug candidates. However, computational simulations of carbohydrates for drug discovery are difficult due to their high flexibility. Moreover, the difficulty of computationally modelling idraparinux derivatives is increased by the presence of sulfonato-methyl moieties, which are highly charged. Therefore, to attain a proper description of heparin and idraparinux derivatives, Balogh and co-authors assessed the performance of the GAFF1,¹⁶⁵ GLYCAM06^{166, 167} and CHARMM^{168, 169} force fields using GaMD simulations.⁹⁹ This enabled enhancing the conformational landscape of the pentasaccharide domain obtaining agreement with NMR experiments. The analysis of simulations and their comparison with NMR demonstrated that the CHARMM force field was better reproducing best the experimental data on the ring conformations, producing also good agreement with the Nuclear Overhauser Effects (NOE) distances on L-iduronic acid ring conformations. Therefore, the use of the CHARMM force field was proposed for the exhaustive and comparative conformational analyses of idraparinux derivatives.

3.7. Drug Design

3.7.1. Retrospective ensemble docking of allosteric modulators of A₁AR

Virtual screening has been widely used for agonist/antagonist design targeting GPCRs.¹⁷⁰ The success rate for virtual screening of GPCRs in the orthosteric pocket is mostly >20%, which is even higher than that of globular proteins.¹⁷¹ However, it is rather challenging to apply virtual screening to identify allosteric modulators due to their low affinity compared with the agonist/antagonist. In a recent study¹⁰³, we tested whether receptor structural ensembles obtained from GaMD simulations could be used to increase docking performance of known PAMs using the A₁AR as a model GPCR. Retrospective ensemble docking calculations of PAMs to the A₁AR combining GaMD simulations and Autodock¹⁷² were performed.

The GaMD simulations implemented in AMBER and NAMD were applied to generate receptor ensemble. The flexible docking and rigid-body docking at different levels (short, medium, and long) were all evaluated. Docking scores corrected by the GaMD reweighted free energy of the receptor structural cluster further improved the docking performances. The calculated docking enrichment factors (EFs) and the area under the receiver operating characteristic curves (AUC) are increased using ranking by the average binding energy (BE_avg) in comparison with the minimum binding energy (BE_min). Ensemble obtained from AMBER dual-boost GaMD simulations of the VCP171-bound ADO-A₁AR-Gi complex outperformed other ensembles for docking. Interactions between the PAM and receptor ECL2 in the VCP171-bound ADO-A₁AR-Gi complex might induce more suitable conformations for PAM binding, which were difficult to be sampled in the simulations of PAM-free (apo) A₁AR. Dual-boost GaMD with higher boost potential was observed to perform better than the dihedral-boost GaMD for ensemble docking. Overall, flexible docking performed significantly better than the rigid-body docking at different levels with AutoDock, suggesting that the flexibility of protein side chains is also important in ensemble docking. In summary, the docking performance has been highly improved by combining GaMD simulations and flexible docking, which effectively account for the flexibility of backbone and side chain in receptors. Such an ensemble docking protocol will greatly facilitate future PAM design of the A₁AR and other GPCRs.

3.7.2. Discovery of Novel Small-Molecule Calcium Sensitizers for Cardiac Troponin C

Cardiac troponin C (TnC) is a calcium-dependent protein in the troponin complex responsible for the activation of muscle contraction. Disorder of TnC may trigger heart diseases and then cause death. One of the current therapies¹⁷³ is to design small molecules that can stabilize an open structure of the TnC and facilitate binding of the TnC switch peptide. To identify potential small molecules for the treatment, Coldren et al.¹⁰² combined GaMD and high-throughput virtual screening to predict binding conformations and affinities of small molecules in TnC. The simulations were compared with experiments for the TnC protein structures in complex with calcium sensitivity modulators. 300 ns GaMD simulations were performed on each system to obtain protein conformations. The simulation trajectory snapshots were clustered into ten most representative conformations based on an agglomerative hierarchical algorithm, which were the structures used for virtual screening and docking studies. The work identified a number of novel compounds that reduced the calcium dissociation rate and showed an overall calcium sensitization effect. One of the compounds exhibited high binding affinity in TnC and was further verified by the stopped-flow kinetic experiment.

4. Software

GaMD has been implemented in the common MD simulation packages, including both GPU and CPU versions of AMBER^{48, 174}, NAMD⁵² and GENESIS⁶¹ (Table 1). All the above-mentioned GaMD algorithms have been incorporated into the latest GPU version of AMBER 20¹⁷⁵.

Table 1.

The implemented GaMD algorithms in different MD software packages.

	AMBER CPU version	AMBER GPU version	NAMD	GENESIS
Dihedral GaMD	X	X	X	X
Total boost GaMD	X	X	X	X
Dual boost GaMD	X	X	X	X
Nonbonded dual-boost GaMD	X	X
Selective GaMD (LiGaMD & Pep-GaMD)		X

5. Conclusions

Without the need to set predefined reaction coordinates or collective variables, GaMD can be advantageous for exploring biomolecular conformational space and complex biomolecular interactions without a priori knowledge or constraints. Additionally, the boost potential in GaMD simulations exhibits a Gaussian distribution, allowing for accurate reweighting of the simulations using cumulant expansion to the second order. Thus, GaMD is applicable to a wide range of biological systems as described in this review.

Based on GaMD, novel approaches including rex-GaMD⁶⁰, GaREUS⁶¹ and selective GaMD (LiGaMD and Pep-GaMD)^{62, 63} have been developed. The selective LiGaMD and Pep-GaMD algorithms appear to be more efficient and easier to use as compared with other existing methods, including the cMD^{176, 177}, replica exchange^178–180 and metadynamics^{180, 181}. For example, a binding event of drug Dasatinib to its binding site of Src Kinase was captured in a total of 35 μs Anton cMD simulation¹⁷⁷. Repetitive binding and unbinding of an IDP peptide was captured in 200 μs Anton cMD simulations at elevated temperature (400 K)¹⁷⁶. Replica exchange algorithm needs to simultaneously simulate many replicas to model ligand/peptide binding and dissociation^178–180. In comparison, LiGaMD and Pep-GaMD simulations was able to capture multiple events of ligand/peptide binding and unbinding within microsecond simulation time. These highly efficient simulations allowed us to accurately characterize the ligand/peptide binding thermodynamics and kinetics^{62, 63}.

Finally, more efficient GaMD algorithms and enhanced sampling methods in general are still needed to characterize the thermodynamics and kinetics of important protein-protein/nucleic acid interactions, which could involve difficult simulations of both binding and dissociation of large biomolecular complexes. Moreover, structural dynamics in systems of increasing sizes such as viruses and cells present grand challenges for computational modelling and enhanced sampling simulations. Continued innovations in both supercomputing hardware and method developments may help us to address these challenges in the future.