Supervised Multisensory Calibration Signals Are Evident in VIP But Not MSTd

Abstract

Multisensory plasticity enables our senses to dynamically adapt to each other and the external environment, a fundamental operation that our brain performs continuously. We searched for neural correlates of adult multisensory plasticity in the dorsal medial superior temporal area (MSTd) and the ventral intraparietal area (VIP) in 2 male rhesus macaques using a paradigm of supervised calibration. We report little plasticity in neural responses in the relatively low-level multisensory cortical area MSTd. In contrast, neural correlates of plasticity are found in higher-level multisensory VIP, an area with strong decision-related activity. Accordingly, we observed systematic shifts of VIP tuning curves, which were reflected in the choice-related component of the population response. This is the first demonstration of neuronal calibration, together with behavioral calibration, in single sessions. These results lay the foundation for understanding multisensory neural plasticity, applicable broadly to maintaining accuracy for sensorimotor tasks.

SIGNIFICANCE STATEMENT Multisensory plasticity is a fundamental and continual function of the brain that enables our senses to adapt dynamically to each other and to the external environment. Yet, very little is known about the neuronal mechanisms of multisensory plasticity. In this study, we searched for neural correlates of adult multisensory plasticity in the dorsal medial superior temporal area (MSTd) and the ventral intraparietal area (VIP) using a paradigm of supervised calibration. We found little plasticity in neural responses in the relatively low-level multisensory cortical area MSTd. By contrast, neural correlates of plasticity were found in VIP, a higher-level multisensory area with strong decision-related activity. This is the first demonstration of neuronal calibration, together with behavioral calibration, in single sessions.

Introduction

When executing actions, like throwing darts, we want to be both accurate (unbiased, darts centered on target) and precise (darts tightly clustered). If only one of these two properties were attainable, it might be better to choose accuracy over precision; this is because precision is advantageous only when behavior is accurate. Yet, whereas multiple studies have explored how combining cues from different sensory modalities leads to improved precision (Ernst and Banks, 2002; van Beers et al., 2002; Alais and Burr, 2004; Knill and Pouget, 2004; Fetsch et al., 2009; Butler et al., 2010), perceptual accuracy, which is perhaps more important functionally, has received relatively little attention.

Behavioral adaptation and plasticity are normal capacities of the brain throughout the lifespan (Pascual-Leone et al., 2005; Shams and Seitz, 2008). Intriguingly, sensory cortices can functionally change to process other modalities (Pascual-Leone and Hamilton, 2001; Merabet et al., 2005), with multisensory regions demonstrating the greatest capacity for plasticity (Fine, 2008). Sensory substitution devices and neuro-prostheses aim to harness this intrinsic capability of the brain to restore lost function (Bubic et al., 2010). In addition to lesion or pathology, perturbation of environmental dynamics, such as in space or at sea, also results in multisensory adaptation (Black et al., 1995; Nachum et al., 2004; Shupak and Gordon, 2006). However, despite its importance in normal and abnormal brain function, the neural basis of adult multisensory plasticity remains a mystery.

Past studies that presented discrepant visual and vestibular stimuli have established robust changes in heading perception when the directions of optic flow and platform motion are not aligned (Zaidel et al., 2011, 2013). When spatially conflicting cues are presented without external feedback, we and others have shown that an unsupervised (perceptual) plasticity mechanism reduces the experimentally imposed conflict by shifting single-cue perceptual estimates toward each other (Burge et al., 2010; Zaidel et al., 2011). When feedback on accuracy is provided, a supervised (cognitive) plasticity mechanism acts to correct the multisensory percept, thereby shifting the single cues together in the same direction according to the combined cue error (Zaidel et al., 2013). These two plasticity mechanisms superimpose during tasks with feedback, and together ultimately achieve both internal consistency and external accuracy. The supervised mechanism operates more rapidly than the unsupervised mechanism. Therefore, when feedback is present, supervised calibration initially dominates, leading to an overall behavioral shift of both cues in the same direction (Zaidel et al., 2013).

Here we explore the neural basis of this plasticity. Neural correlates of multisensory heading perception have been found in several cortical regions, including the dorsal medial superior temporal (MSTd) and ventral intraparietal (VIP) areas (Britten and Van Wezel, 1998; Bremmer et al., 2002; Page and Duffy, 2003; Gu et al., 2006, 2008; Zhang and Britten, 2010, 2011; Chen et al., 2013). Although the basic visual-vestibular response properties of VIP and MSTd appear similar (Maciokas and Britten, 2010; Chen et al., 2011a,b), VIP shows stronger correlations with behavioral choice than MSTd (Chen et al., 2013; Zaidel et al., 2017). We test the hypothesis that VIP cells show shifts in their response tuning in a direction consistent with the superposition of both plasticity mechanisms, thus directly proportional to simultaneously recorded behavioral changes. This hypothesis is motivated by the high prevalence of choice-related signals in VIP (Chen et al., 2013; Zaidel et al., 2017). In contrast, we hypothesize that MSTd neuron activity, which shows limited choice-related signals (Gu et al., 2008; Zaidel et al., 2017), lacks this property.

Materials and Methods

Experimental design and setup

Two male rhesus monkeys (Macaca mulatta; Monkeys Y and A) were chronically implanted with a circular plastic ring for head restraint and a scleral coil for monitoring eye movements in a magnetic field (CNC Engineering). All experimental procedures complied with national guidelines and were approved by institutional review boards.

During experiments, the monkeys were head fixed and seated in a primate chair, which was anchored onto a 6 df motion platform (6DOF2000E; Moog). A stereoscopic projector (Mirage 2000; Christie Digital Systems) and rear-projection screen were also mounted on the platform, in front of the monkey. The projection screen was located ∼30 cm in front of the monkey's eyes and spanned 60 × 60 cm, subtending a visual angle of ∼90° × 90°. The monkeys wore red-green stereo glasses custom-made from Wratten filters (red #29 and green #61, Kodak) through which they viewed the visual stimulus, rendered in 3D.

Self-motion stimuli were vestibular-only (inertial motion generated by the motion platform, without visual optic flow), visual-only (optic flow simulating self-motion through a 3D star field, without inertial motion), or combined vestibular and visual self-motion cues. Visual stimuli were presented with 100% motion coherence (i.e., all stars in the star field simulated coherent self-motion, without the addition of visual noise). Each stimulus comprised a single-interval linear trajectory of self-motion, with 1 s duration and a total displacement of 0.13 m (Gaussian velocity profile with peak velocity 0.35 m/s and peak acceleration 1.4 m/s²). Self-motion stimuli were primarily in a forward direction, with varying deviations to the right or to the left of straight ahead, in the horizontal plane. Heading was varied in log-spaced steps around straight ahead.

The monkeys' task was to discriminate whether their self-motion was to the right or to the left of straight ahead (two-alternative forced choice) after each stimulus presentation. During stimulus presentation, the monkeys were required to maintain fixation on a central target. After the fixation point was extinguished, they reported their choice by making a saccade to one of two choice targets (located 7° to the right and left of the fixation target). A random delay, uniformly distributed between 0.3 and 0.7s, was added after stimulus offset before the fixation point was extinguished to jitter the monkeys' responses in relation to the motion stimuli. If the monkeys broke fixation during the stimulus or before the fixation point was extinguished, the trial was aborted. Monkeys were rewarded for correct heading selections (or rewarded statistically, as described below) with a portion of water or juice.

Calibration protocol

To elicit calibration, we used the same supervised calibration protocol previously tested behaviorally in humans and monkeys (Zaidel et al., 2011, 2013), with minor alterations for neuronal recording. Each experimental session comprised three main consecutive blocks: precalibration, calibration, and postcalibration (blocks 1-3, respectively). When the monkey was willing to continue performing the task beyond these three main blocks, recordings of the same cells continued as the calibration stimulus switched to the reverse direction (block 4, reverse-calibration; and block 5, post-reverse-calibration).

The precalibration block (block 1) comprised visual-only, vestibular-only and combined (visual-vestibular) cues, interleaved. Straight ahead was defined as 0° heading with positive headings to the right and negative headings to the left. Heading values were ±12°, ±6°, ±1.5° and 0° (0° was an ambiguous condition). The stimulus set was presented according to the method of constant stimuli. This block comprised: 10 repetitions × 3 cues (visual-only/vestibular-only/combined) × 7 headings = 210 trials. The monkey was rewarded for correct choices 95% of the time and not rewarded for incorrect choices. This reward rate gets the monkey accustomed to not being rewarded all the time, as occurs in the post-adaptation block described below. Data from this block were used to deduce the baseline behavioral and neuronal responses, per cue.

In the calibration block (block 2), only combined (visual-vestibular) cues were presented, with a consistent discrepancy of Δ = 10° or −10° introduced between the visual and vestibular headings for the entire duration of the block. Positive Δ represents an offset of the vestibular heading to the right and visual heading to the left; negative Δ represents the reverse arrangement. During this block, reward was consistently contingent on one of the cues (either visual or vestibular). The reward-contingent cue was considered “externally accurate” (the other, “inaccurate”) in that it was consistent with external feedback. Only one sign of discrepancy (positive or negative Δ, pseudo-randomly counterbalanced across sessions) and one reward contingency (visual or vestibular, primarily vestibular since that condition elicits larger shifts) were used for block 2 in each session. For most sessions (104 of 155, ∼67%), this block comprised 30 repetitions × 7 headings (210 trials). The remaining sessions had between 20 and 40 repetitions (apart from one, which had 50 repetitions).

During the postcalibration block (block 3), individual (visual and vestibular) cue performance was measured by single-cue trials, interleaved with combined-cue trials (with Δ = 10° or −10°, as in the calibration block). For the single-cue trials, the identical headings as precalibration were presented. The combined-cue trials were run in the same way as in the calibration block, and included here to retain calibration, while it was measured. For this block, the reward for single-cue trials worked slightly differently from the precalibration block, in order not to perturb the calibration: when the single-cue trial heading lay within ± Δ of 0° (symmetrically), a reward was always given. When the single-cue trial heading lay outside this range (i.e., clearly to the right or left), the monkey was rewarded for making a correct choice (and not rewarded for incorrect). This block typically comprised: 10 repetitions × 3 cues (visual-only/vestibular-only/combined) × 7 headings = 210 trials. Some blocks with <10 repetitions were also included (minimum 5); however, the vast majority (>95% for both VIP and MSTd cells) had ≥10 repetitions. Data from the single-cue trials in this block were compared with the baseline behavioral and neuronal responses from the precalibration block.

After the postcalibration block, if the monkey was still willing to perform the task, a reverse-calibration block (block 4) was run, followed by a post-reverse-calibration block (block 5). These followed the same protocol as the calibration and postcalibration blocks (with the same number of repetitions), but with Δ having the opposite sign.

We found previously that, when the less reliable cue is “accurate” (i.e., in accordance with external feedback) and the more reliable cue “inaccurate,” the difference between the multisensory percept and feedback is largest, and thus multisensory calibration (and the phenomenon of yoking) is best revealed (Zaidel et al., 2013). The data in this study were collected with 100% visual coherence (a highly reliable cue). Thus, to best expose multisensory calibration, neural activity was mostly monitored during the “vestibular accurate” condition (144 sessions; 97 and 47 for Monkeys Y and A, respectively). For comparison, 11 sessions were also gathered under the “visual accurate” reward contingency (7 and 4 for Monkeys Y and A, respectively). Reverse-calibration blocks were run in 70 (of 144) and 7 (of 11) sessions for vestibular and visual accurate (reward) conditions, respectively.

Electrophysiology

Single units were recorded extracellularly from areas VIP and MSTd in Monkeys Y and A during calibration (and reverse calibration). An electrode array (Plexon; 16-channel U-probe, 100 µm electrode spacing) or a single tungsten electrode (Frederick Haer; impedance ∼1-2 mΩ at 1 kHz) was advanced into the cortex through a custom transdural guide-tube using a micromanipulator (Frederick Haer) mounted on top of the head restraint ring. Recording locations were targeted using MRI scans, and were initially mapped along a stereotaxic grid (using single electrodes) to identify cortical gyri and sulci (according to white/gray matter transitions) and neurophysiological response properties, as described previously (Gu et al., 2008; Chen et al., 2013).

When recording with the microelectrode array, it was slowly inserted until all contacts were in the target region (according to prior mapping and online neurophysiological identification). Next, the array was retracted slightly (50-100 µm) and left to settle for ∼20-30 min, to improve stability before starting the recording session. Neuronal data were displayed online, but neurons were not specifically prescreened for visual or vestibular tuning, to reduce any selection biases. Rather, the data from all channels were saved using a Plexon multichannel data acquisition system (Plexon) and later sorted offline using the Plexon Offline Sorter.

In offline sorting, each neuron's isolation was confirmed to be stable across blocks, by consistency of its spike shape, interspike interval histogram, and firing properties. If the baseline firing rate (FR) changed by a factor of >2 across calibration blocks 1-3 (or reverse-calibration blocks 3-5), the cell was excluded from that comparison. Baseline FR was defined as the median FR in the 1 s interval before stimulus onset (computed across the block). In total, the sample consisted of N = 223 cells from VIP and N = 147 cells from MSTd. Among the VIP cells, 206 were stable across the first three blocks of calibration (182 and 24 recorded during vestibular and visual accurate conditions, respectively), 118 were stable across reverse calibration (106 and 12 during vestibular and visual accurate conditions, respectively), and 101 were stable across all five blocks. Among the MSTd cells, 127 were stable across the first three blocks of calibration (all in the vestibular accurate condition), 76 across reverse calibration, and 56 were stable across all five blocks. Most of the cells (177 of 223 in VIP and 142 of 147 in MSTd) were recorded using linear electrode arrays. The remainder were collected using standard tungsten microelectrodes.

Data and statistical analyses

Behavioral and neuronal data analyses were performed using custom scripts in MATLAB R2014b (The MathWorks). Psychometric functions were constructed (per block and cue) by calculating the proportion of rightward choices as a function of heading, and fitting these data with a cumulative Gaussian distribution using the psignifit toolbox for MATLAB (version 2.5.6) (Wichmann and Hill, 2001). The bias (point of subjective equality [PSE]) and psychophysical threshold were defined by the mean (µ) and SD (σ) of the fitted cumulative Gaussian distribution, respectively. We quantified the goodness of fit for the psychometric functions using McFadden's pseudo-R². The median pseudo-R² for the psychometric fits (pooling across precalibration and postcalibration blocks, visual and vestibular cues, and conditions) was 0.97; 98% of the psychometric fits had pseudo-R² > 0.80, and the minimum value was 0.69.

Neuronal heading tuning curves were constructed (per block and cue) by computing the average FR (in units of spikes/s) for each heading, over a time period from t = 0.2 s after stimulus onset until the end of the stimulus (t = 1 s). This time period was determined by cutting off 100 ms from the beginning and the end of the stimulus epoch (where stimulus motion is close to zero) and shifting by 100 ms to approximately account for response latency. Since stimulus intensity and neuronal responses are strongest during the middle of the stimulus time course, average FRs calculated in this manner are fairly robust to modest variations in exactly how much time is excluded at the beginning and end of the stimulus epoch.

Heading tuning curves were constructed from neural responses measured during successfully completed trials of the discrimination task. A neuron was considered tuned to a specific cue if the linear regression of FR versus heading (over the narrow range −12° to 12°) had a slope significantly different from zero (p < 0.05). We confirmed that this method indeed sorted the cells into two groups (tuned and not tuned) adequately, by looking at the Bayes factors (BFs) of the cells' tuning. BF₁₀ values >1 support the hypothesis that the cell is tuned (H₁) and BF₁₀ values <1 support the null hypothesis (H₀) that the cell is not tuned, with a factor of 3 (i.e., > 3 or < ⅓) providing substantial evidence (Raftery, 1995; Wagenmakers, 2007; Jarosz and Wiley, 2014). The median BF₁₀ for the significantly (and nonsignificantly) tuned cells from the precalibration block was: 161 (0.14) and 25 (0.13) for VIP visual and vestibular responses, respectively, and 1732 (0.14) and 5.4 (0.12) for MSTd visual and vestibular responses, respectively. These values indicate that p < 0.05 was a suitable threshold for determining significant neuronal tuning. Shifts in neuronal tuning associated with calibration were calculated only if both the precalibration and postcalibration tuning curves had significant tuning. This resulted in 87 and 58 VIP neurons tuned to visual and vestibular cues, respectively (42 of which were tuned to both). Of these, most were from the vestibular accurate condition (78 and 50 tuned to visual and vestibular cues, respectively; 37 tuned to both), with the remainder from the visual accurate condition. In MSTd, only the vestibular accurate condition was tested, resulting in 56 and 19 MSTd neurons tuned to visual and vestibular cues, respectively (14 of which were tuned to both).

Similarly, reverse-calibration shifts in neuronal tuning were calculated only if both the postcalibration and post-reverse-calibration tuning curves had significant tuning. This resulted in 51 and 35 VIP neurons tuned to visual and vestibular headings, respectively (26 of which were tuned to both). Of these, most were from the vestibular accurate (reverse calibration) condition (46 and 31 tuned to visual and vestibular headings, respectively; 23 tuned to both). For reverse calibration, there were 35 and 12 MSTd neurons tuned to visual and vestibular headings, respectively (9 of which were tuned to both).

Changes in perceptual bias were calculated as the change in PSE of the fitted psychometric curves from precalibration to postcalibration. Shifts in neuronal tuning were calculated by the shift in the corresponding tuning curves, as follows: first, baseline FRs were subtracted (per block, as described above). Then, the neuronal shift (along the heading axis) was estimated by dividing the difference between the y intercepts of the two linear regression fits of FR (at x = 0° heading) by the average slope of the two fits. This provides an estimate of the shift of straight ahead for the postcalibration (relative to precalibration) neuronal tuning. Similarly, reverse-calibration shifts (behavior and neuronal) were calculated from postcalibration to post-reverse-calibration. The use of linear fits here does not imply that neuronal tuning for heading was linear, although it was commonly monotonic. Rather, linear fits provided a simple and adequate measure (i.e., relatively robust to noise) of tuning shifts.

Because heading tuning curves can deviate from being linear, we assessed the robustness of our findings by also calculating neuronal biases as shifts in neurometric functions (Fetsch et al., 2011). Specifically, we fit separate neurometric functions (cumulative Gaussian distributions) to the precalibration and postcalibration data (baseline subtracted FRs). Precalibration and postcalibration responses were z-scored using the precalibration mean and SD (for both), and neurometric curves were calculated from the z-scored responses. We then calculated the difference in PSE between precalibration and postcalibration neurometric curves. To reduce the influence of neurometric shift outliers, the PSE shifts were capped at ±20°. This was less of an issue for the linear tuning curve fits, which did not have large outliers. In addition, the linear fits were also more robust when computed in short time windows. Thus, we present the data for both methods (linear and neurometric fits) for the main analysis window, and used the linear fits for shorter time-step analyses.

Analyses that examined response metrics as a function of time relied on calculations of instantaneous FRs (IFRs) in a range of smaller time windows. IFRs were calculated as the average FR within a 0.2 s rectangular window that was stepped through the data in intervals of 0.1 s. Thus, the time index (which was taken from the center of the window) ranged from t = 0.1 s to t = 1.2 s. This time range extended beyond the end of the stimulus (t = 1.0 s) but did not include the saccade, which could only take place after t = 1.3 s because of the random delay period (0.3-0.7 s) that was inserted after the end of the stimulus. Permutation-based cluster analysis was used to test for significance of neuronal shifts over time. This was calculated by performing a t test at each time step, and then searching for a cluster of significant t values (at the 5% significance level). The cluster “mass” was calculated by the sum of t values above this threshold, and a permutation test (5000 bootstrap samples) was used to determine whether this mass was significant.

Targeted dimensionality reduction

In order to visualize population responses, and to test how these changed after multisensory calibration, we projected the responses of the 182 VIP neurons recorded during the vestibular accurate condition (those that were stable from block 1 through block 3) onto a low-dimensional subspace. All stable neurons were included in this analysis (i.e., they were not screened for significant tuning). For this analysis, we used the targeted dimensionality reduction method developed by Mante et al. (2013) that captures the variance associated with specific task variables of interest (in our case, “heading” and “choice”). The advantage of this technique (over standard principal component analysis) is the ability to attribute meaning to the axes in the low-dimensional subspace. Here, we applied the methodology to examine the neural representation for the heading (stimulus) and choice parameters, and to assess how these representations changed after multisensory calibration. We performed the targeted dimensionality reduction using the responses from block 1, and then projected the responses of both blocks 1 and 3 (using the same projection axes) to see how the population responses changed after multisensory calibration. This allowed us to probe whether the change in responses was primarily in the heading or choice dimensions.

The data were prepared for the dimensionality reduction analysis by calculating a spike density function (SDF) per trial for each single unit (sorted offline, as described above); this was done by convolving the spike raster with a Gaussian kernel (σ = 30 ms). SDFs were then downsampled to 10 ms time steps for the rest of the analysis. For each unit, we sorted trials into different stimulus conditions by cue (visual or vestibular stimulus) and heading, and then averaged the responses within each condition. We define the population response for a given condition c, at time t, as a vector x_c,t of length N_unit (the number of units in the population). We found that we did not need the denoising step described by Mante et al. (2013), as it made little difference for our data, and we subtracted the mean SDF from each cell rather than having a constant term in the regression (these two options are equivalent). The specifics of the procedure are described below, with similar notation to that used by Mante et al. (2013).

First, linear regression was used to determine how specific variables relate to the responses of each recorded unit at specific times. We used two task variables, which were indexed by ν, as follows: heading (ν = 1) and choice (ν = 2). Our goal was to find a vector of coefficients β_i,t that describes how much the FR of unit i at time t depends on the corresponding task variables (i.e., a column vector β_i,t for each i and t, has elements β_i,t(ν), and is of length N_coeff = 2). To achieve this, we first define a matrix F_i for each unit i, of size N_coeff × N_trial (where k =1 to N_trial represents the trial number) as follows:

$$F_i=\left[\begin{array}{ccc}\cdots & heading(k)& \cdots \\ \cdots & choice(k)& \cdots \end{array}\right]$$ (1)

where heading(k) represents the stimulus heading (normalized to range from −1 to 1, where negative and positive values reflect leftward and rightward headings, respectively) and choice(k) represents the monkey's choice (−1 and 1, for leftward and rightward choices, respectively) on trial k. The responses of unit i at time t are then represented by the linear combination as follows:

$$r_{i,t}=F_i{}^T\cdot {\beta }_{i,t}$$

where $r_{i,t}$ is a column vector specific to unit i and time t (of length N_trial), taken from the SDFs described above (using the responses from block 1). Accordingly, the regression coefficients can be estimated by the following: 7

$${\beta }_{i,t}={\left(F_i{F}_i^T\right)}^{-1}{F}_i{r}_{i,t}$$

As described by Mante et al. (2013), the regression coefficients can then be rearranged to identify the dimensions in state space containing variance related to the variables of interest. Namely, vector β_i,t (with elements β_i,t(ν), defined above) was rearranged to form vector β_ν,t, with elements β_ν,t(i). This rearrangement corresponds to the fundamental step of viewing the regression coefficients as the directions in state space along which the underlying task variables are represented at the level of the population (rather than properties of individual units). Each vector, β_ν,t, thus corresponds to a direction in state space that accounts for population response variance at time t, because of variation in task variable ν.

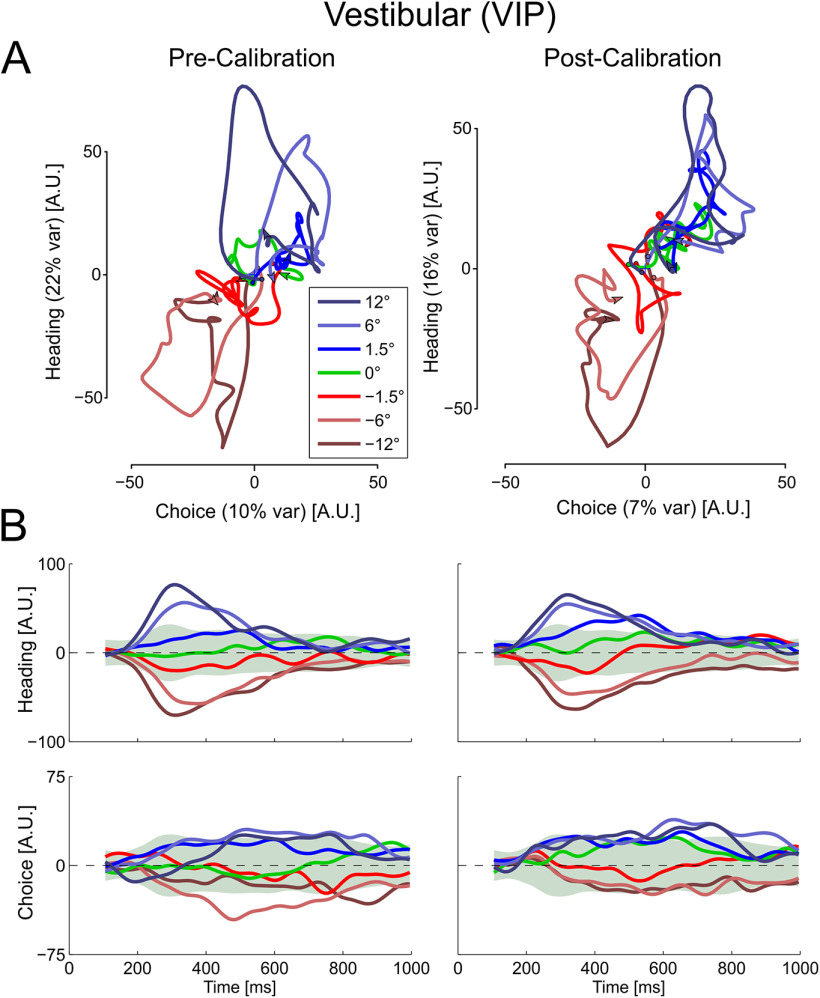
Next, for each task variable ν, we collapsed β_ν,t over time, by taking the vector at the time which gave the maximum vector norm, to get ${\beta }_v^{max}$. The vectors were then orthogonalized using QR-decomposition (to form ${\beta }_v^{\perp }$) such that each vector explains distinct portions of the variance in the response. The orthogonalization process starts with one axis and then orthogonalizes the second axis with respect to the first. The resulting interpretation is that whatever variance is plotted along the second axis is specific to that axis, since it is not accounted for by the first. Here choice was orthogonalized secondary to heading, indicating that whatever variance is accounted for by the choice axis is independent of that explained by the heading axis. The fraction of variance explained was calculated as the amount of variance accounted for by each targeted axis divided by the variance of the original data. Finally, the average population responses (for both blocks 1 and 3) were projected onto these orthogonal axes, resulting in the trajectories and time courses in Figures 5 and 6 (for the visual and vestibular conditions, respectively).

Figure 5.

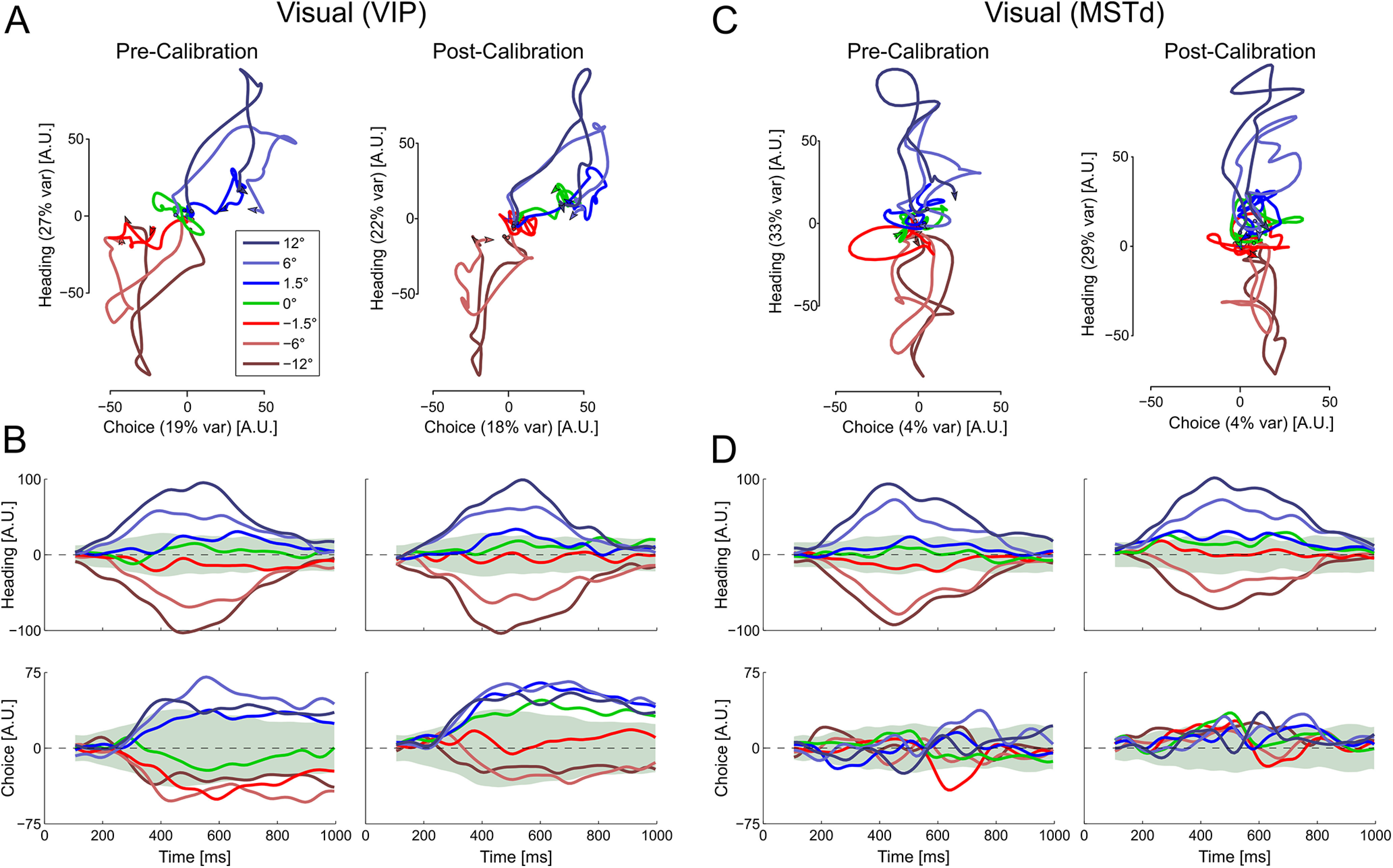
Multisensory calibration of visual responses in state space. (A) VIP and (C) MSTd population responses for each heading direction are projected onto a two-dimensional state space that captures variance related to heading (stimulus) and choice. Time is embedded within the state space trajectories (these start around the origin; arrows indicate the end of each trajectory). B, D, State space projections for VIP and MSTd, respectively, as a function of time. The state space axes were constructed from the precalibration responses (using only neurons that were stable both precalibration and postcalibration). Responses of these same neurons were projected both precalibration and postcalibration onto the same axes (left and right columns, respectively, in each subplot). Data are presented as Δ = 10° (data collected with Δ = −10° were flipped). Green shaded regions represent 95% distribution intervals (from surrogate data) for the 0° heading condition. The choice axis was orthogonalized relative to the heading axis. Therefore, the percentage of explained variance (presented in parentheses in A and C) represents the unique variance explained by choice, whereas the heading value represents its unique component plus any overlap between the two. Multisensory calibration is seen for VIP primarily in the choice domain as the projections shift toward more rightward choices. This is best seen for the 0° heading condition (green) and the near central headings (−1.5° and 1.5°). N = 182 for VIP, and N = 127 for MSTd.

Figure 6.

Multisensory calibration of vestibular responses from VIP in state space. (A) Population responses projected onto state space. (B) State space projections as a function of time. Conventions are the same as in Figure 5.

Results

The monkeys were trained to discriminate heading around the straight-ahead direction after presentation of a single-interval stimulus (Gu et al., 2008; Fetsch et al., 2011). They were required to fixate on a central target during stimulus presentation and then to report their choice by making a saccade to one of two choice targets (right or left; for details, see Materials and Methods). The self-motion stimulus contained vestibular cues only, visual cues only, or a simultaneous combination of vestibular and visual cues.

Each experiment comprised at least three consecutive blocks of trials (Zaidel et al., 2011, 2013). The preadaptation (control) block consisted of interleaved vestibular-only, visual-only, and combined heading stimuli, with no cue conflict (Δ = 0). In the adaptation block, only combined visual-vestibular cues were presented with a discrepancy of Δ = 10° (vestibular heading offset to the right) or −10° (visual heading offset to the right). In the postadaptation block, shifts of individual (visual and vestibular) percepts were measured by presenting single-cue trials, which were interleaved with combined-cue trials having same Δ as in the adaptation block, to retain plasticity while calibration effects were measured.

We previously found that, in the presence of external feedback, discrepant sensory cues were calibrated according to the multisensory (combined) percept (Zaidel et al., 2013). This supervised calibration leads to an interesting phenomenon of cue “yoking.” Namely, both cues are calibrated together, in the same direction. This leads to a striking outcome in which the initially “accurate” cue (consistent with external feedback) shifts away from feedback, becoming less accurate in the process (Fig. 1). We present the data in Figure 1 with headings (x values) offset in accordance to external feedback (i.e., the “inaccurate” cue's heading is shifted by Δ). Accordingly, the “inaccurate” cue would be expected to calibrate toward zero heading (and for both cues to ultimately converge on PSE ∼ 0°).

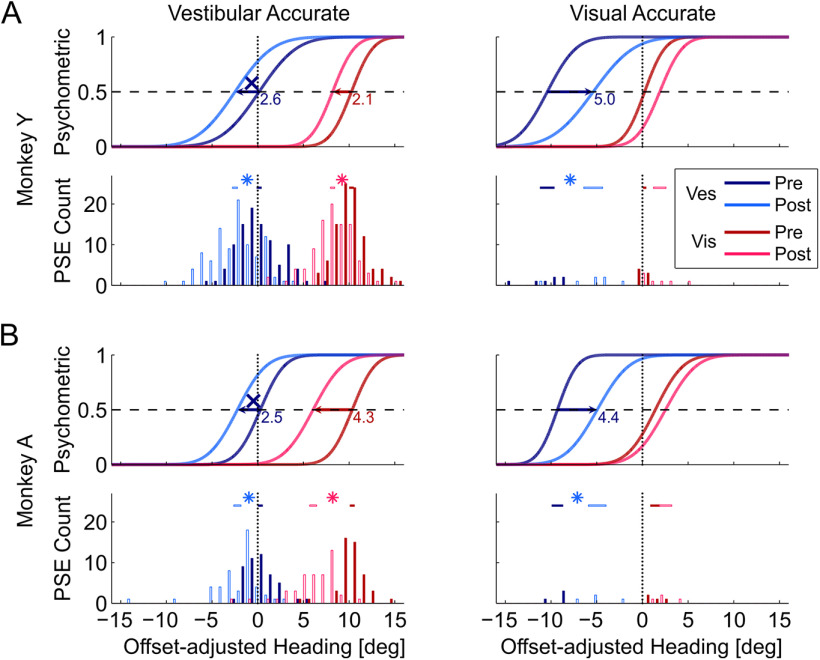
Figure 1.

Behavioral shifts during multisensory calibration. Behavioral responses from the recording sessions are presented for Monkey Y (A) and Monkey A (B), for the “vestibular accurate” and “visual accurate” conditions (left and right columns, respectively). All data are presented as though Δ = 10°, and data collected with Δ = −10° were flipped before pooling. Blue and red colors represent the vestibular and visual responses, respectively. Dark hues represent precalibration (baseline) behavior. Lighter hues represent postcalibration data. The psychometric plots (Gaussian cumulative distribution functions) represent the proportion of rightward choices as a function of heading, adjusted according to external feedback; that is, the visual “inaccurate” plots (left column) were shifted by 10°, and the vestibular “inaccurate” plots (right column) were shifted by −10°. Here, these represent the average behavior (per condition, cue, block, and monkey). Intersection of each psychometric function with the horizontal dashed line (y = 0.5) marks the PSE (perceptual estimate of straight ahead). Vertical dotted lines indicate the expected PSE for “accurate” perception, according to external feedback. PSE histograms present the data from all sessions. Horizontal bars above the PSE histograms represent the mean ± SEM intervals. Significant shifts (p < 0.05) are marked by asterisk symbols above the histograms, and by horizontal arrows on the psychometrics (with the shift size presented in degrees). X represents significant shifts away from feedback (becoming less accurate).

In the vestibular accurate condition (for which most data were collected) both cues demonstrated significant shifts (Fig. 1, left column, 144 sessions). The visual PSEs (red curves) shifted to be better aligned with feedback (p = 4.5 × 10⁻¹⁸ and 1.2 × 10⁻¹³ for Monkeys Y and A, respectively; paired t test), while the vestibular PSEs (blue curves) were yoked, shifting away from external feedback (marked by X symbols; p = 2.8 × 10⁻¹⁶ and 1.9 × 10⁻⁷ for Monkeys Y and A, respectively; paired t test). These average data were computed by normalizing to the condition Δ = 10° (i.e., for Δ = −10°, PSE values were flipped for pooling).

In the visual accurate condition (Fig. 1, right column; 11 sessions), the vestibular PSEs shifted significantly to be aligned with external feedback (p = 1 × 10⁻⁶, paired t test pooled across animals). The visual PSEs shifted (more moderately) away from feedback (p = 2.7 × 10⁻², pooled across animals).

Over the long experimental sessions involved in this study, performance could deteriorate, thus potentially complicating comparisons across calibration conditions. We tested this by comparing precalibration with postcalibration thresholds. For Monkey Y, there were no significant differences: visual thresholds precalibration and postcalibration were 1.85 ± 0.18° and 1.89 ± 0.18°, respectively (geometric means ± SEM, pooled across visual and vestibular “accurate” conditions; p = 0.99, paired t test); vestibular thresholds precalibration and postcalibration were 3.19 ± 0.14° and 3.27 ± 0.14°, respectively (p = 0.46, paired t test). Thresholds did increase somewhat for Monkey A: visual thresholds precalibration and postcalibration were 1.96 ± 0.21° and 2.55 ± 0.21°, respectively (p = 0.001, paired t test); vestibular thresholds precalibration and postcalibration were 2.02 ± 0.20° and 2.49 ± 0.20°, respectively (p = 0.001, paired t test). However, performance was still good across all blocks of trials; and importantly, calibration was measured by the shift of the psychometric curve PSEs (µ of the Gaussian fits), not by changes in slope (σ), which is an independent parameter. Thus, modest changes in threshold should have little effect on estimates of biases. Also, because of the balanced study design (Δ = 10° and Δ = −10°), it is unlikely that any changes in threshold would affect measures of calibration.

VIP, but not MSTd, neuronal tuning shifts in accordance with the behavioral shifts

Figure 2B presents the responses of an example VIP neuron (taken from a “vestibular accurate” session with Δ = 10°; behavior in Fig. 2A), showing a shift of its tuning curve for both visual and vestibular cues in accordance with the behavioral shifts. Before calibration, the monkey's vestibular and visual PSEs were close to zero (dark blue and red psychometric curves, respectively; Fig. 2A). After calibration, they both shifted leftwards (medium blue and red dashed lines, respectively; Fig. 2A). After reverse-calibration, they both shifted rightward (light blue and red dashed lines, respectively; Fig. 2A), overshooting the baseline (precalibration) PSE.

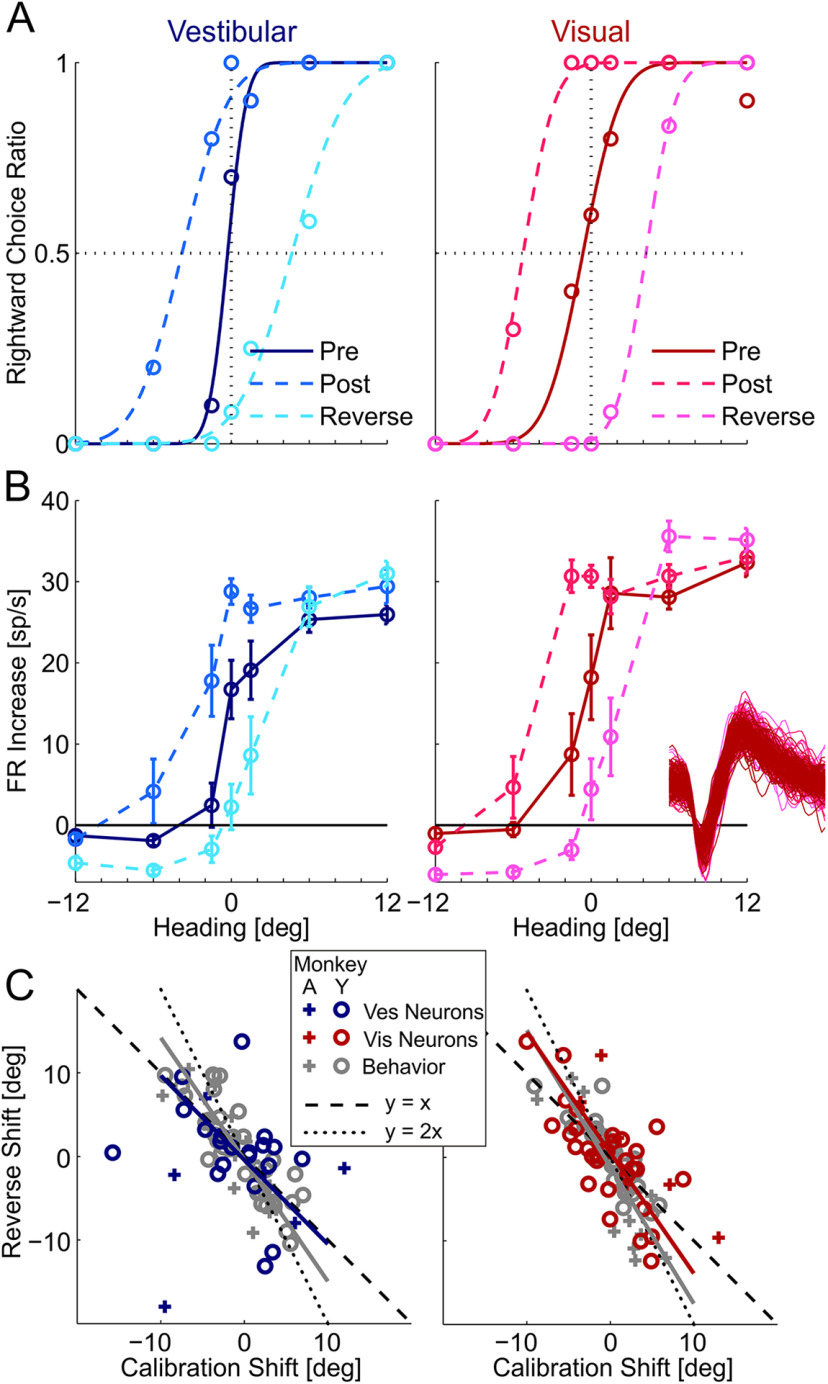
Figure 2.

Example VIP recording during multisensory calibration. Behavior (A) and neuronal responses (B) for an example neuron from a single session. Blue represents vestibular responses. Red represents visual responses. Darkest hues represent precalibration. Medium hues represent postcalibration. Lightest hues (cyan and magenta) represent the responses after reverse calibration. For behavior (A), circles represent the proportion of rightward choices (fit by cumulative Gaussian psychometric curves). For the neuronal responses (B), circles and error bars represent mean FR (baseline subtracted) ± SEM. Inset, One hundred (randomly selected) overlaid spikes from each block. The tuning curves are presented in relation to the original (veridical) headings (not adjusted according to external feedback as in Fig. 1). C, Reverse versus primary calibration shifts for vestibular (left) and visual (right) cues. Gray represents behavioral shifts. Blue and red represent neuronal shifts (vestibular and visual, respectively). Solid lines indicate Type II regressions (excluding the + outlier on the bottom left of the left plot).

This example neuron was tuned for both visual and vestibular cues to self-motion and preferred rightward headings for both modalities (FRs were increased for rightward vs leftward headings; Fig. 2B). Before calibration, both the vestibular and visual tuning curves demonstrate a sharp slope at ∼0° heading (dark blue and dark red, respectively; Fig. 2B). After calibration, both the vestibular and visual tuning curves shifted leftward (medium blue and red dashed lines, respectively) together with the behavioral shifts. Similarly, after reverse-calibration, both tuning curves shifted rightward (light blue and red dashed lines, respectively), also in parallel with the behavioral shifts. Therefore, the tuning of this neuron shifted in accordance with the behavioral (PSE) shifts.

To compare neuronal and behavioral shifts across the population of neurons, the neuronal responses for each cue were fit with a linear regression (across the narrow heading range from −12° to 12°), precalibration and postcalibration, as well as after reverse-calibration. The shift in a neuron's tuning curve was estimated by the shift in the regression line (see Materials and Methods). Only cells with significant (p < 0.05) regression fits, both precalibration and postcalibration (blocks 1 and 3), and with significant regression fits, both postcalibration and after reverse-calibration (blocks 3 and 5) were used to estimate neuronal shifts across the respective blocks. We also estimated the neuronal shifts using neurometric curves, referenced to the precalibration condition (see Materials and Methods). The main findings were similar using both approaches, but the linear fits were more robust in short time windows. Hence, we focus on results from the linear fits, but corresponding main results from the neurometric curve analysis are also presented in Figure 3.

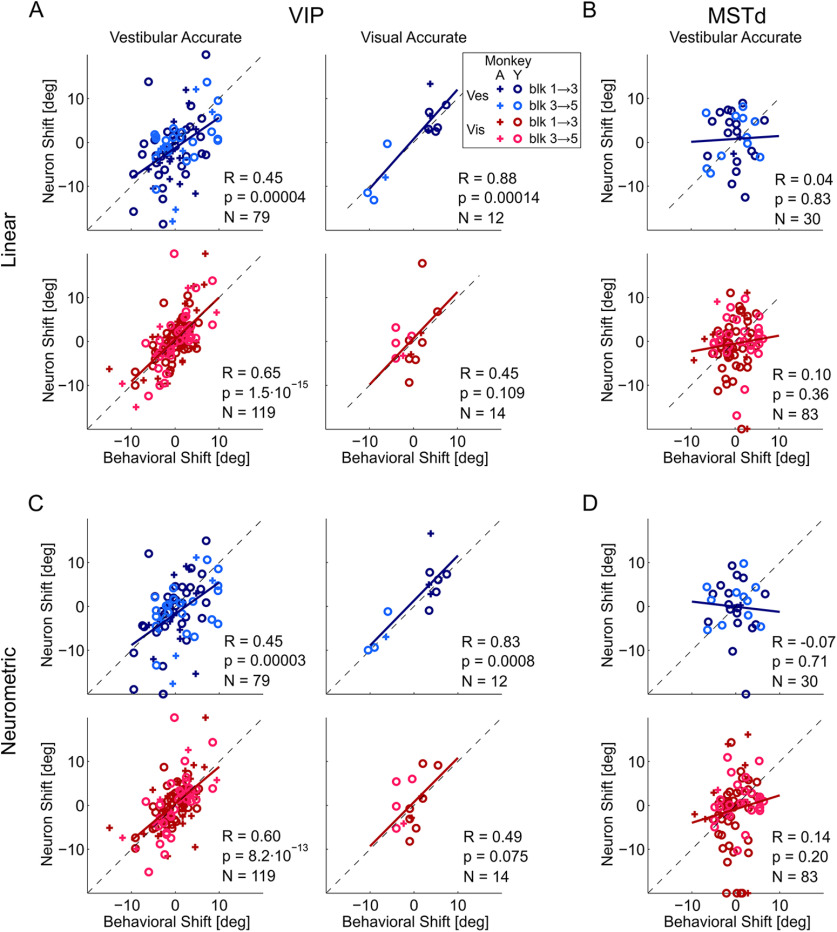
Figure 3.

VIP neuronal shifts correlate with behavioral shifts. Correlations between neuronal shifts (calculated using linear fits in A,B; and neurometric fits in C,D) and behavioral shifts, are presented for VIP (A,C; both vestibular and visual accurate conditions) and MSTd (B,D; vestibular accurate condition; the visual accurate condition was not tested in MSTd). Blue represents vestibular data. Red represents visual data. Darker hues represent the primary calibration sequence (blocks 1-3). Lighter hues represent the reverse-calibration sequence (blocks 3-5). + and open circle represent Monkeys A and Y, respectively. Black dashed lines indicate the diagonal (y = x). Solid lines indicate regression lines of the data.

In the example of Figure 2A, B, responses were plotted in relation to veridical heading. Therefore, the reverse-calibration shifts (calculated between the “post” and “reverse” curves: light blue to cyan for vestibular, and light red to magenta for visual) were larger than the primary calibration shifts (which were calculated between the “pre” and “post” curves: dark blue to light blue for vestibular, and dark red to light red for visual). Namely, reverse-calibration shifts not only returned to, but extended beyond, the initial precalibration baseline. This is expected because the Δ (systematic heading discrepancy) jumped from 10° to –10° (or vice-versa) for reverse calibration (a larger change vs the primary calibration stage, which went from Δ = 0° precalibration to Δ = ±10°). Figure 2C presents a scatter plot of reverse versus primary calibration shifts for the vestibular and visual cues (left and right plots, respectively). If reverse calibration were to simply “undo” the calibration shift, the data would lie along the negative diagonal y = –x (dashed line; i.e., equal in magnitude but opposite in direction). If reverse calibration were to calibrate beyond (in the reverse direction) to a similar extent as the primary calibration shift (as the example in Fig. 2A,B), the data would lie along the line y = –2x (dotted line). The data (behavioral in gray and neuronal in color) generally lay between these two options.

Across the population of VIP neurons, there was a significant correlation between the neuronal and behavioral shifts (computed across sessions and animals) for both visual and vestibular cues (Fig. 3A,C). This was highly significant in the vestibular accurate condition (Fig. 3, left column) for which most of the data were collected (p = 3.7 × 10⁻⁵ and 1.5 × 10⁻¹⁵ for the vestibular and visual cue shifts, respectively). In the visual accurate condition, a significant correlation was seen for the vestibular shifts (p = 1.4 × 10⁻⁴), but not for the visual shifts (p = 0.109; however, the visual shifts were smaller, and there were fewer data for this condition). Linear regression fits largely lay superimposed on the diagonal lines (for the vestibular accurate condition, the regression slopes were 0.69 and 0.96 for the vestibular and visual cues, respectively; for the visual accurate condition, the slopes were 1.13 and 1.06, respectively). These slopes were calculated with Type I regressions, using the neuronal and behavioral shifts as the dependent and independent variables, respectively. Type I regressions were used because (1) Type II regressions are sensitive to differences in variability, that is, the larger variability associated with neuronal (vs behavioral) shifts could itself “pull” the regression to be more vertical; and (2) neuronal shifts were unique, whereas behavioral shifts could be repeated (for neurons recorded in the same session) and Type I regressions minimize only the y axis (i.e., neuronal) mean squared error. (This was not an issue in Fig. 2C, where each data point reflects a unique combination of calibration and reverse-calibration values.)

When testing the 2 monkeys separately, significant correlations were observed individually for both Monkey Y (R = 0.54, p = 3.9 × 10⁻⁶ for vestibular and R = 0.58, p = 9.1 × 10⁻¹⁰ for visual cues) and for Monkey A (R = 0.53, p = 0.0036 for vestibular and R = 0.69, p = 1.0 × 10⁻⁶ for visual cues). For these individual monkey analyses, we pooled the data from the vestibular accurate and visual accurate conditions. Although the shifts are expected to differ for the conditions, correlations between behavioral and neuronal shifts are not expected to differ (i.e., they are expected to shift together; Fig. 3); hence, the data were pooled. Also, when testing calibration and reverse calibration separately (pooling across monkeys and conditions), significant correlations were observed for both calibration (R = 0.50, p = 0.00007 for vestibular and R = 0.60, p = 8.5 × 10⁻¹⁰ for visual cues) and for reverse calibration (R = 0.58, p = 0.0004 for vestibular and R = 0.67, p = 3.7 × 10⁻⁷ for visual cues).

By stark contrast, the neuronal shifts in MSTd, for which only the vestibular accurate condition was tested, did not follow the behavioral shifts (Fig. 3, right column), the correlations between neuronal and behavioral shifts were small and not significant (p = 0.83 and p = 0.36 for the vestibular and visual cues, respectively). Therefore, the tight relationship between neuronal and behavioral shifts was specific to VIP.

We tested whether there was a difference between VIP multisensory and unisensory neurons in terms of their correlations with behavioral shifts. For this analysis, we analyzed multisensory and unisensory (visual-only and vestibular-only) neurons separately (pooling across visual and vestibular “accurate” conditions, and calibration and reverse calibration). We found that multisensory neurons' shifts were significantly correlated with the behavioral shifts (R = 0.79, p = 5.0 × 10⁻¹⁵, slope = 1.00 for visual responses and R = 0.66, p = 1.2 × 10⁻⁹, slope = 0.75 for vestibular responses, N = 66). Visual-only neurons' shifts were also significantly correlated with the behavioral shifts (R = 0.42, p = 3.4 × 10⁻⁴, slope = 0.87, N = 67), with vestibular-only neurons showing a similar trend (R = 0.38, p = 0.06, slope = 0.98, N = 25). Thus, the correlations were robust and evident separately for multisensory, and visual-only neurons, with a similar, but not robust, trend for vestibular-only neurons.

VIP tuning shifts as a function of time

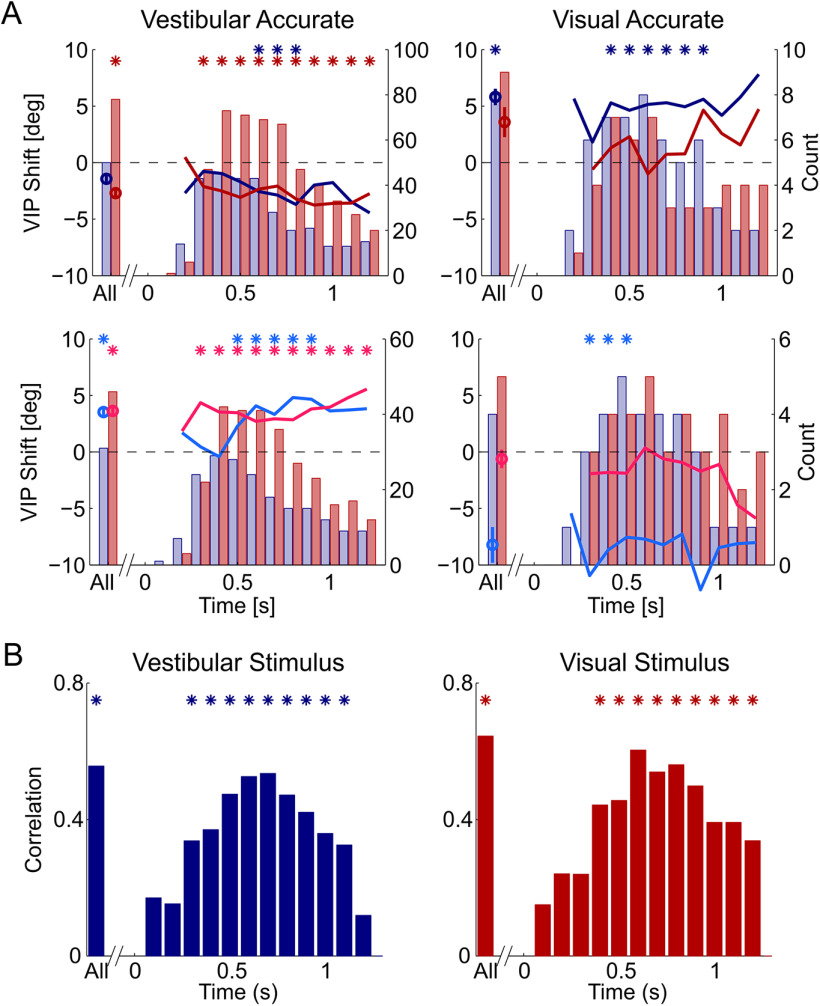
To assess at which times (within and beyond the stimulus period) the neuronal responses to the stimuli reflected the behavioral shifts, we calculated IFRs (using a 200 ms time window, shifted in increments of 100 ms) and assessed how tuning curves based on IFR shifted at different time points relative to stimulus onset (Fig. 4A, shifts for the primary and reverse-calibration blocks are presented in the top and bottom rows, respectively). For the vestibular accurate condition (left column), the visual cue showed significant shifts throughout the stimulus response (red and magenta asterisk markers for the primary and reverse-calibration shifts, respectively), while the vestibular cue showed significant shifts for a shorter duration (mainly around the middle of the stimulus; blue and cyan asterisk markers). Permutation-based cluster analysis found that each of these clusters (visual/vestibular × primary/reverse calibration) was significant (p < 0.003).

Figure 4.

Calibration of VIP responses as a function of time. A, Average visual and vestibular neuronal shifts (red and blue lines, respectively) as a function of time for the primary calibration (top row) and reverse calibration (second row). Red and blue bars represent the number of visual and vestibular neurons, respectively, with significant tuning (per time step) used to calculate the shifts. Stimulus onset was at x = 0 s, and stimulus offset at x = 1 s. Data are presented as though Δ = 10° (data collected with Δ = −10° were flipped for pooling). Positive values reflect rightward shifts. Circle markers represent mean ± SEM shifts for the regular time window (0.2-1 s; All). Asterisks indicate significant clusters. B, Correlation of VIP neuronal versus behavioral shifts over time (pooling the primary and reverse-calibration data). Asterisks indicate significant correlations (p < 0.05).

For the visual accurate condition (right column), only the vestibular shifts were significant (blue and cyan asterisk markers, permutation-based cluster tests, p < 0.002); visual shifts were not significant (p > 0.26). This is in accordance with larger vestibular versus visual behavioral shifts (and the smaller N) in this condition (Fig. 1). The neuronal shifts were largely commensurate with the sizes of the behavioral shifts. Because relatively few neurons were significantly tuned at the beginning and toward the end of the stimulus (vs the middle, Fig. 4A, histograms) we did not test for differences in shift size over time. Rather, we only compared the shifts at each time step versus zero, and identified significant clusters (with the permutation test).

Correlating the neuronal shifts (computed from IFRs over time) versus the behavioral shifts (Fig. 4B) demonstrates that correlations are maximal near peak stimulus velocity (around the middle of the stimulus epoch). For this analysis, the same cells were used for the calculations at each time point. Specifically, we included all neurons that were significantly tuned when using the whole time window (i.e., all cells from Fig. 3A,C). Significant correlations are marked by asterisk (p < 0.05, after Bonferroni correction for 12 comparisons). Although these correlations are reduced toward the end of the stimulus period, significant correlations persist beyond the end of the stimulus (>1 s), especially evident for the visual cues. Thus, the correlates of multisensory calibration are seen throughout the stimulus-driven responses.

Population shifts

To test the hypothesis that these tuning curve shifts reflect response modulations related to choice rather than heading, we visualized dynamics of population tuning (for the “vestibular accurate” condition) by plotting neuronal responses in a two-dimensional state space (Figs. 5 and 6). The state space was found using a method of targeted dimensionality reduction that is able to dissociate the effects of specific task variables (Mante et al., 2013). For this analysis, the data gathered with Δ= −10° were flipped along the stimulus axis. Namely, the neuronal responses to positive and negative headings were switched symmetrically (for all blocks), such that postcalibration shifts were expected in the same direction (in accordance with Δ = 10°). Before calibration, the VIP population responses to the visual stimulus (Fig. 5A, left) can be seen first extending along the heading axis, which is most easily seen for the 12° heading stimulus (dark blue line, which moves upward initially) and the −12° heading stimulus (brown line, which moves downward). At later time points, the trajectories move substantially along the choice axis as well, such that they become separated both horizontally and vertically. Headings closer to zero follow a shorter path. The projections of VIP population activity onto the heading and choice axes can also be seen as a function of time in Figure 5B (left).

After calibration, the heading-related responses of the VIP population are similar to before calibration (compare the top two plots in Fig. 5B). By contrast, the choice-related responses were changed after calibration (compare the bottom two plots in Fig. 5B). To assess these changes, we generated 100 surrogate datasets of the precalibration data using the “corrected Fisher randomization” (surrogate-TNC) method from Elsayed and Cunningham (2017), and calculated 95% distribution intervals (±1.96 × SD) for the 0° heading condition (green shaded regions). While the choice trajectory for the 0° condition (green curve) lay within the 95% distribution interval before calibration (Fig. 5B, bottom left), it lay above this interval after calibration (bottom right), reflecting a significant shift toward more rightward choices. Also, choice trajectories for the negative heading conditions (red, light and dark brown), which lay below the 95% interval for 0° heading before calibration, became more positive after calibration (the −1.5° condition trajectory even crossed into positive values). This result of a rightward choice bias (normalized to Δ = 10°) is in accordance with the leftward shifts of the neuronal tuning curves described above (Fig. 4A, top left). Finally, projecting error trials for the smallest headings (−1.5° to 1.5°) confirmed that there were strong choice signals when the heading information was weak (choice projections for error trials split from the correct trials; data not shown). Similar results are seen for the vestibular response dynamics in VIP (Fig. 6). After calibration, the choice trajectory for the 0° condition (green curve) straddled the upper edge of the 95% distribution interval, and lay in proximity of the rightward heading conditions (Fig. 6, bottom right, blue curves).

By contrast, the visual population responses from MSTd show little choice-related response projection and no clear differences between the precalibration and postcalibration data (Fig. 5C,D). Thus, the population trajectories in state space summarize the main conclusions: (1) behavioral effects of calibration are reflected in VIP, but not MSTd, neuronal activity; and (2) the observed shifts in tuning curves of VIP neurons reflect modulations related to choice, rather than the stimulus heading.

Discussion

Proficiency of sensory perception can be assessed by two complementary (but independent) properties: reliability (or precision) is defined by the inverse-variance of the underlying perceptual estimate (reflected by the steepness of the psychometric function), whereas accuracy is defined by the bias of the percept in relation to the actual stimulus (mean of psychometric function). An ideal percept is both precise (low variance) and accurate (unbiased). However, a precise estimate could still be inaccurate (because the two properties are independent). Many model-based studies have shown that multisensory integration can lead to small improvements in precision through statistically optimal cue combination, brought about by cue-weighting (Ernst and Banks, 2002; van Beers et al., 2002; Alais and Burr, 2004; Knill and Pouget, 2004; Fetsch et al., 2009; Butler et al., 2010). However, it is often not appreciated that reliability-based multisensory integration can lead to compromised accuracy if the more reliable cue is inaccurate because the combination rule (Ernst and Banks, 2002) pushes the combined estimate closer to the most reliable cue, even if it is inaccurate. In general, we know little about how the brain maintains multisensory accuracy, which could be more important than reliability for behavioral success in everyday life.

One solution to avoid inaccurate behavior would be for robust calibration mechanisms to maintain and ensure accuracy in multisensory perception. Indeed, such plasticity mechanisms have been shown to maintain the accuracy of sensory perception during development (Gori et al., 2008, 2010, 2011, 2012a,b; Nardini et al., 2008; Burr et al., 2011; Stein and Rowland, 2011) and in adulthood (Burge et al., 2010; Ernst and Di Luca, 2011; Zaidel et al., 2011, 2013).

Thus, for multisensory perception to be accurate, it must maintain both “internal consistency” (estimates from different sensory modalities must agree with one another) and “external accuracy” (perception must represent the real world). Behavioral studies have indeed demonstrated multisensory plasticity at the level of perception (Canon, 1970; Radeau and Bertelson, 1974; Zwiers et al., 2003; Burge et al., 2010; Bruns et al., 2011; Wozny and Shams, 2011; Zaidel et al., 2011, 2013; Frissen et al., 2012; Badde et al., 2020). Specifically, Zaidel et al. (2011, 2013) identified two plasticity mechanisms for multisensory heading discrimination: unsupervised plasticity, which can be isolated during no-feedback tasks; and supervised plasticity, which is also recruited during feedback tasks. Kramer et al. (2020) also recently showed that cross-modal (audiovisual) recalibration is changed by top-down influences. Based on these studies, multisensory plasticity has been categorized into two types (supervised and unsupervised), which serve different purposes. The goal of unsupervised plasticity is internal consistency, which is achieved by comparing cues to one another and calibrating them individually. The goal of supervised plasticity is external accuracy, which is achieved by comparing the combined estimate to feedback from the environment.

While unsupervised plasticity is more implicit and thus likely to represent a sensory or perceptual shift, supervised plasticity is a more explicit, cognitive process, possibly targeting the mapping between perception and action. In combination, these two plasticity mechanisms can achieve both internal consistency and external accuracy (Adams et al., 2001; but see Knudsen and Knudsen, 1989a,b). A similar distinction between implicit and explicit components is found in studies of sensorimotor plasticity (Mazzoni and Krakauer, 2006; Simani et al., 2007; Haith et al., 2008; Taylor and Ivry, 2011).

To explore neural correlates of this plasticity, we recorded from both MSTd and VIP, as these areas are known to contain a large proportion of multisensory visual-vestibular cells, and are heavily interconnected with each other anatomically (Gu et al., 2007, 2008; Chen et al., 2013). The two areas have generally similar stimulus-driven responses (Colby et al., 1993; Bremmer et al., 1997, 2002; Duffy, 1998; Page and Duffy, 2003; Zhang et al., 2004; Gu et al., 2006, 2007; Takahashi et al., 2007; Maciokas and Britten, 2010; Zhang and Britten, 2010; Chen et al., 2011b), but show major differences in choice-related activity: while the choice-related signals in MSTd are modest, VIP shows large choice-related activity (Chen et al., 2013; Zaidel et al., 2017).

We found that changes in behavior associated with calibration are reflected in neuronal activity in VIP, but not MSTd. One caveat is that the analyses used relied on monotonic tuning (linear as well as sigmoid neurometric analysis). Thus, we cannot rule out the possibility that other (nonlinear) decoding of MSTd activity might show calibration effects. Applying nonlinear decoding here would be complex because the data come from separate blocks of trials, and are thus sensitive to slow fluctuations in neural activity over time. In addition, we found that the observed shifts in tuning curves of VIP neurons mainly reflect response components related to the choice, rather than stimulus heading. Given its explicit, cognitive nature, we have speculated previously that supervised plasticity is mediated by choice signals, which presumably arises from areas that transform sensory cues into a perceptual decision (Zaidel et al., 2013). VIP is thus a more likely candidate to play a role in supervised plasticity by analogy to the lateral intraparietal area, where neurons are thought to represent task-related decision variables (Katz et al., 2016).

One interpretation of our findings is that VIP responses reflect behavioral calibration simply because VIP activity is strongly modulated by choice. In this interpretation, VIP might not play a specific role in the calibration process itself. In a recent study, Sasaki et al. (2020) found that VIP activity was modulated by task reference frame, and that these modulations were independent of choice-related modulations from trial to trial. This raises the possibility that VIP population activity might represent signals that drive calibration (e.g., the visual-vestibular cue conflict or expected reward) as well as choices. However, it is difficult to apply the analyses of Sasaki et al. (2020) to our data since responses during the different calibration conditions were, by necessity, measured in different blocks of trials. Thus, our findings leave open the question of whether VIP plays a role in the calibration process itself or simply reflects the behavioral consequences of calibration because of strong modulations by choice (or other cognitive factors).

Because supervised calibration operates more rapidly than unsupervised calibration (Zaidel et al., 2013), and the overall shifts for both visual and vestibular cues were “yoked” in the same direction (a signature of supervised calibration), the results here predominantly reflect supervised calibration. To identify neural correlates of unsupervised plasticity is more difficult, given that their magnitude is small, they build up slowly and are overwhelmed by the larger and faster supervised plasticity (Zaidel et al., 2013). It was not viable in this study to separate these two components in the (limited) neuronal data. Nevertheless, it is tempting to speculate that unsupervised plasticity reflects sensory-driven signals, thus possibly present in MSTd. This would be in line with findings of audiovisual recalibration in auditory cortices with concurrent decisional recalibration in fronto-parietal cortices (Aller et al., 2021). To further explore this hypothesis and to isolate the unsupervised component, one could use calibration protocols without performance feedback (as in Burge et al., 2010; Zaidel et al., 2011) and perhaps chronically implanted electrodes, which would allow long recordings (given that unsupervised plasticity is slow).