Abstract
Timely diagnostic testing for active SARS‐CoV‐2 viral infections is key to controlling the spread of the virus and preventing severe disease. A central public health challenge is defining test allocation strategies with limited resources. In this paper, we provide a mathematical framework for defining an optimal strategy for allocating viral diagnostic tests. The framework accounts for imperfect test results, selective testing in certain high‐risk patient populations, practical constraints in terms of budget and/or total number of available tests, and the purpose of testing. Our method is not only useful for detecting infections, but can also be used for long‐time surveillance to detect new outbreaks. In our proposed approach, tests can be allocated across population strata defined by symptom severity and other patient characteristics, allowing the test allocation plan to prioritize higher risk patient populations. We illustrate our framework using historical data from the initial wave of the COVID‐19 outbreak in New York City. We extend our proposed method to address the challenge of allocating two different types of diagnostic tests with different costs and accuracy, for example, the RT‐PCR and the rapid antigen test (RAT), under budget constraints. We show how this latter framework can be useful to reopening of college campuses where university administrators are challenged with finite resources for community surveillance. We provide a R Shiny web application allowing users to explore test allocation strategies across a variety of pandemic scenarios. This work can serve as a useful tool for guiding public health decision‐making at a community level and adapting testing plans to different stages of an epidemic. The conceptual framework has broader relevance beyond the current COVID‐19 pandemic.
Keywords: COVID‐19 diagnostic RT‐PCR test, false negatives, rapid antigen testing, safe reopening
1. INTRODUCTION
The importance of testing for SARS‐CoV‐2 viral infections has been widely accepted by public health professionals around the world. 1 , 2 , 3 Identifying infections early in their infectious period through large‐scale testing efforts can help prevent disease transmission, guide contact tracing and isolation strategies, reduce rates of severe downstream outcomes and contribute to estimation of expected healthcare needs. While immunoglobulin antibody tests can evaluate past SARS‐CoV‐2 viral infections, many public health interventions such as contact tracing are based on detection of active infections. Several testing options for detecting an active SARS‐CoV‐2 viral infection are currently available, and these tests have varying levels of accuracy (as characterized by their sensitivity and specificity) and different barriers to access. Expensive RT‐PCR tests are based on nasopharyngeal swabs, whereas less accurate rapid antigen tests (RATs) require only a saliva sample and are much less expensive. 4 , 5 It is easy to perform RATs and at‐home self‐sampling rapid testing kits are available. 6 Tests may be administered for many reasons, including diagnostic testing for symptomatic or exposed individuals, population surveillance to detect an outbreak, or enhanced screening in high‐risk strata (eg, essential workers). A central public health challenge is defining “optimal” test allocation strategies under resource constraints and/or multiple competing test options. The conceptual framework in this paper is broadly applicable to test allocation designs, beyond the COVID‐19 pandemic.
One testing strategy for estimating the population infection rate is universal random testing, 7 where a large random sample of the entire population is tested. This process is repeated regularly to track the pandemic over time. However, this approach requires conducting an enormous number of tests and is impractical for countries or regions such as the United States or India with large heterogeneous population and limited number of tests available. Several approaches have been suggested for allocating tests under resource constraints. Cleevely et al 8 proposed stratified periodic testing, where tests are administered at different rates (in terms of test frequency and volume) for patients at different levels of risk of infection. Combined with other mitigation strategies such as isolating individuals who have tested positive, they determined the required testing rate for a targeted reduction in disease transmission, which is in turn reflected by a reduction in the effective reproduction number. Although this approach highlights the importance of stratifying the population and prioritizing testing of high‐risk groups, the authors did not consider how exactly to distribute the tests across different prioritization groups. Another approach that has been suggested for finding cases or community surveillance is pooled/group testing, 9 , 10 , 11 , 12 , 13 where a single test is applied to merged samples from a group of people. Under pooled testing, the number of required tests is dramatically reduced. Nevertheless, dilution due to combined samples is always one of the major concerns in the pooled/group testing approach. 10 , 11 , 12 Ely et al 14 described allocation of fixed numbers of multiple different test types with different sensitivities and specificities to populations at high/low risk. Under this approach, tests are allocated by a decision‐making process for maximizing the value of the tests, mathematically defined as the sum of the test specificity and sensitivity weighted by the loss of the corresponding decision error. Ely et al's approach requires quantification of the relative loss of false negatives and false positives for each individual. This problem setting is similar to ours, but the two objective functions are very different, leading to different interpretation of the results and different allocation strategies.
In this article, we develop a comprehensive mathematical framework illustrated in Figure 1 for defining an optimal test allocation strategy, accounting for (1) imperfect viral test results, (2) intensified testing in certain patient populations, (3) resource limitations in terms of budget and/or total number of available tests, and (4) the goal of testing. In our proposed approach, tests are allocated across population strata defined by symptom severity and other patient characteristics (eg, age, comorbidities, occupation), allowing our test allocation plan to prioritize higher risk patient populations. Since the goal of testing may vary at different points of the pandemic, our proposed objective function provides flexible testing strategies across different phases of a pandemic, for example finding as many cases as possible during the growing phase of a surge/outbreak (called detecting mode) and long‐term surveillance for new outbreaks during decay/containment period of a pandemic (called surveillance mode). During the detecting mode, our approach allocates tests with the goal of finding as many of the positive tests as we can to guide contact tracing efforts and isolation interventions. During surveillance mode, our approach allocates tests to give a test positive rate near a target threshold (eg, 3%). An observed test positive rate exceeding this threshold provides an indicator of rising community prevalence. Unlike universal random testing procedures and many other existing approaches, neither the detecting mode nor the surveillance mode aims to directly estimate the infection rate or prevalence in the population. However, we show that control of the test positive rate at a target level implies an upper bound on the population infection rate under certain conditions. Our framework assumes that the selection for testing is independent of the true infection status, conditional on the symptoms and patient characteristics and that people with severe symptoms are always tested. Defining population strata based on symptom severity and age group, we use extensive simulation studies to evaluate the proposed method for test allocation strategy. We illustrate how these methods can be applied to determine test allocation through different stages of the pandemic in New York City (NYC).
FIGURE 1.
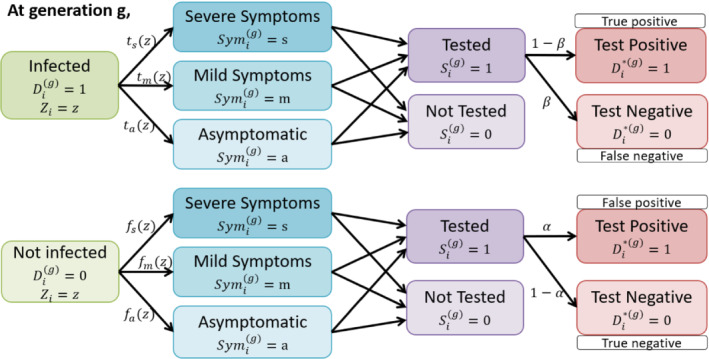
Illustration of data structure at generation g with the incorporation of selection and misclassification. For a person i with the characteristic information(or risk factors) at the beginning of generation g, the true infection status is unobserved, with 1 indicating being infected and 0 being uninfected. The probability for an infected person of developing severe(s)/mild(m)/no(a) symptoms is , where , which is based on the characteristics. An uninfected person may also develop similar symptoms due to other diseases, for example, influenza, and the probability is . Often, people are tested/selected based on symptoms and some other risk factors. and are the false negative and positive rate for the test
We then extend this framework to address the question of how to allocate two different types of diagnostic tests with differing accuracy, for example, RT‐PCR tests versus RATs. This approach can provide guidance about allocation of multiple types of tests at the workplace level (eg, for colleges and universities) under budget constraints.
We provide a R Shiny app available at https://umich‐biostatistics.shinyapps.io/Testing_Optimization/ that implements all of the proposed methods. In this app, users can specify their goals of testing as well as other key variables to obtain a customized optimal test allocation strategy.
2. METHODS
2.1. Conceptual framework
Consider a population of size N, and let be a binary variable representing person i's true (unobserved) infection status (infected‐1 vs not infected‐0) at the gth generation of infectious disease circulation. Here, the length of a generation is the time interval between the time when an individual is infected by a carrier and the time when this index carrier was infected. For COVID‐19, the generation interval is around 5 days. 15 It is common to use “generation” for describing infectious disease spread. 15 , 16 , 17 Dividing the time period by generation intervals allows us to capture the variation in disease prevalence, guided by transmission dynamics, which is critical to make public health interventions. At the gth generation, some subset of the population will be tested, with binary indicator representing whether person i in the population is tested during generation g. Let denote the test result (positive‐1 vs negative‐0) for person i during generation g, which may or may not be the correct result (may or may not equal ). If person i is not tested, will be 0. Let denote the number of tests available for generation g. With limited testing capacity, current test strategies prioritize tests based (at least in part) on severity of symptoms. Let be a categorical variable which takes value in corresponding to severe, mild, and asymptomatic symptom levels respectively. We assume that testing may also depend on other covariates, , such as patient age.
In modeling symptoms, we assume the probability is the same for any g. Let be the probability of developing symptom j conditional on and , and let be the probability of developing symptom j conditional on and . Namely, and . We summarize the notations in Table 1.
TABLE 1.
A summary of notations
| Notation | Definition/Meaning | |
|---|---|---|
|
|
Covariate vector for person i | |
|
|
True infection status for person i at generation g | |
|
|
Symptom level for person i at generation g | |
|
|
Selection indicator for testing person i at generation g | |
|
|
Observed infection status for person i at generation g | |
|
|
Probability of developing symptom j conditional on being infected with covariate z | |
|
|
Probability of developing symptom j conditional on being uninfected with covariate z | |
|
|
False positive rate of the diagnostic test | |
|
|
False negative rate of the diagnostic test | |
| N | Total population eligible for testing | |
|
|
True total number of cases in generation g | |
|
|
Observed total number of positive tests in generation g | |
|
|
Total number of available tests in generation g |
We further make the following independence assumption about the testing model:
A1. , so is independent of given and .
A summary of model notations at generation g is presented below:
Under this framework, we can establish the probabilistic relationship between obtaining a positive test () and the test allocation strategy (). We can use this relationship to predict the number of people testing positive at generation g, denoted as , as a function of test allocation strategy. Predicting the number of positive tests requires inputting probabilities from the infection model, symptom model and model for observed test results. For example, if age is the covariate under consideration, in the infection model represents the infection rate in age group z. Although it is possible to obtain estimates for from the reported age‐stratified case number in some regions, for example, New York City, this approach would underestimate the true infection rate in age group z due to a large proportion of asymptomatic cases. Moreover, in many other regions where the age information of the infected individual is not publicly available, obtaining estimates for in the infection model and in the model for observed test results would be difficult. Therefore, to facilitate the calculation of predicted number of positive tests when reliable estimates for conditional probabilities and are not available, we make the following assumptions:
A2. , so is independent of .
A3. , so is independent of and given and .
Let be the test false positive rate and be the test false negative rate. In the next section, we provide a general form of the expected number of positive tests, , and a specific expression under assumption A.1 to A.3.
2.2. Predicting , the number of people who will test positive
For a tested/selected person i, we express the probability of testing positive as:
| (1) |
In this article, we consider as a discrete variable so that the whole population is partitioned into several strata based on the symptom severity and covariate levels. The first term of the summation captures the likelihood of a positive test in the selected population given and . The second term describes the joint distribution of symptoms and in the selected population. We now take a closer look at each of the terms in the summation.
The probability of person i testing positive can be expressed as a function of and as follows:
| (2) |
The joint distribution of and conditional on getting tested can be expressed as:
| (3) |
Putting these two expressions together, the probability that person i in the selected population has a positive test can be expressed as:
| (4) |
In our framework, we treat the selection indicator corresponding to each individual as random. Therefore, we have the following expression for the expected number of positive tests, :
The expectation is taken with respect to the distribution of the selection indicator . Summing over the tested people, the number of positive tests with population N is predicted as
| (5) |
Equation (5) is the general form for the expected number of positive tests. Under assumptions A.1 to A.3, Equation (5) can be simplified as:
| (6) |
where and are the probabilities of developing symptom j conditional on the infection status and the covariate level. To predict the number of positive tests, some quantities are needed as inputs, including the test false positive rate (), false negative rate (), total number of true cases (), the covariate distribution (), and the probabilities of developing symptom j conditional on the covariate information and the infection status ( and ). Many studies have investigated the test false positive rate and test false negative rate. 18 , 19 Although the true number is unknown, predicted values for can often be obtained from forecasting models (such as SEIR model 20 , 21 ). Taking age as the covariate, we obtained the empirical estimates for and using the reported case counts and hospitalization data and the influenza surveillance data. 22 , 23 Details of estimating and can be found in Section 3.1. In addition, Equation (6) depends on , which is the probability of testing in generation g for a person i with and . This term represents the testing protocol in the population, and constraints on testing in terms of (1) test availability and (2) testing prioritization correspond to constraints on .
Remark 1
In this paper, we consider the population that is eligible for testing as a constant N, ignoring potential changes in this number across generations. For example, someone who is tested positive once may not get tested again within 90 days, due to immunity induced by past infections. Our model can be easily extended to incorporate such dependencies in the number of tests across generations by subtracting the number of people ineligible for testing from the total population N and using as the population eligible for testing in generation g. Mathematically speaking, , where is the number of people tested positive at generation , and where K is the number of generations for 90 days, say 18, if one generation interval is 5 days.
2.3. Optimal testing strategy
Since the number of positive tests is an important metric for measuring the extent of the pandemic, we use , the expected number of positive tests, for constructing our objective function. The quantity is directly related to the test allocation strategy by the term which we aim to calculate. Since the entire population is divided into several strata based on symptom severity and covariate levels (covariates and symptom measures are both assumed to be categorical), the selection probability within a population stratum is the same for all individuals. We thus construct the following objective function:
| (7) |
where is a pre‐fixed target test positive rate for detecting the outbreak of the pandemic and is the marginal probability for a person in the entire population to be selected for testing. The first term controls the difference between the number of positive tests and the true case counts. The second term controls the difference between test positive rate and the target outbreak threshold c. In our objective function, we use which includes both true and false positive tests because in practice, the true infection status for someone with a positive test is unknown and we have to use for public health decision making and intervention. w takes value 0 or 1, indicating the preference for either component in defining the optimal testing strategy. For example, when , the objective function reduces to , which corresponds to a goal of finding the test allocation strategy to detect the greatest number of positive tests (detecting mode). By dividing the whole population into several strata based on symptom severity and covariate levels, our detecting mode assigns tests to each population stratum by the order of the likelihood of detecting a positive test. On the other hand, corresponds to a goal of detecting if the test positive rate has crossed a predesignated outbreak threshold (surveillance mode). In Supplementary Material, we show that the population disease prevalence is bounded by a function of the test positive rate under mild conditions, so a low test positive rate implies a low disease prevalence in the population. Here, we do not take w between 0 and 1, because the loss function for the detecting mode and for the surveillance mode are not on the same scale, and the average of the two losses has no practical meaning. The first constraint in Equation (7) ensures that everyone with severe symptoms is prioritized for testing. Constraint 2 is to guarantee that the expected number of people tested does not exceed the total number of available tests. We obtain the optimal testing strategy in Equation (7) using R package optiSolve. 24
Our objective function involves the most commonly‐used information metrics for COVID‐19, including the overall number of positive tests and the overall test positive rate, which are straightforward and easy to understand for the general public. Neither the detecting mode or the surveillance mode in our objective function aims for estimating the true prevalence in the population, which is usually the goal of universal random testing. It is worthy to mention that if testing is performed randomly in the population, for example, universal random testing, then an unbiased estimator of the population prevalence would be , where is the observed test positive rate.
2.4. Extension to allocation of two different types of diagnostic tests
The above framework can be extended to handle allocation of two different types of tests with different costs and accuracy constrained by a fixed total budget. We suppose the first test option is cheap but has low sensitivity (eg, rapid antigen testing) and the second test option is more expensive but has higher sensitivity (eg, RT‐PCR testing). Let represent whether an individual is untested or given the first or second type of test, respectively. Following Equation (6), the predicted numbers of positive tests of each type, denoted as and are:
where , , , are the false positive and negative rates corresponding to two tests. Suppose that costs for one test of each type are and . In the special case where our goal is to detect the greatest number of positive tests ( in Equation (7)), we construct the following objective function for allocating two types of tests subject to a fixed total budget:
| (8) |
The first constraint guarantees that all the severe patients will be tested, and the second constraint ensures that the expected total spending does not exceed the budget. For the problem of assigning two tests, we do not consider to set because it would always recommend to use the less accurate test for a lower test positive rate.
3. SIMULATION
3.1. Simulation design
We first explore by simulation how the optimal strategy for allocating a single type of diagnostic test varies by 1) the number of available tests; and 2) the probability of being asymptomatic for a truly infected individual, denoted as .
Design phase for the test allocation strategy: We consider a hypothetical region of population 8 million similar to New York City. Although the true proportion of asymptomatic infections is likely to be unknown, existing literature suggests this proportion varies across regions, with estimates from around 30% to almost 90%. 25 , 26 , 27 We estimate and using the publicly available historical data. 22 , 23 More specifically, let and denote the probabilities of developing symptom j in the infected and uninfected populations; that is, and . For a given value of , the probability for a truly infected person to be an asymptomatic carrier, the probability of developing severe symptoms for an infected person is assumed to be roughly of all COVID‐19 symptomatic cases (, which is roughly the ratio of the number of hospitalizations to the cases until September 18, 2020 in New York City. 28 For the uninfected person, the probabilities of having severe () or mild () symptoms are set to and , respectively, using the data from the New York State Department of Health 2019‐2020 Flu Monitoring Archives. 22 In obtaining these estimates, hospitalized patients with flu‐like symptoms are treated as severe cases, and the remaining laboratory‐confirmed cases are treated as mild cases. We suppose represents age and is grouped into four categories: age 0 to 17, age 18 to 49, age 50 to 64 and age . From the probabilistic relationship , we first estimate probabilities of having severe and mild symptoms for an infected person in age group z, namely, and , where is the age distribution in symptom group j of COVID‐19 case counts and hospitalized counts from the New York City Department of Health and Mental Hygiene through September 18, 2020. 23 Next, the probability of being asymptomatic for an infected person in age group z is . Similarly, is estimated using data from the New York State Department of Health 2019 to 2020 Flu Monitoring Archives by age group. 22 Table S1 provides estimates of and when .
We consider settings with high and low infection rate separately, which correspond to being near or past the pandemic peak, respectively. We assume that 175 000 people are truly infected at generation g (), which mimics the situation of the peak of the pandemic. We suppose , the number of available tests, to be either 50 000 or 200 000. These two scenarios correspond to the setting with limited testing resources and the setting with relatively sufficient testing resources. Due to a large number of infections in the population, the test strategy in this setting should be aimed at detecting cases, so the weight w in the objective function Equation (7) is set as 1. After the peak of the pandemic, we assume that the number of infected cases in the population decreases to 10 000 () with 200 000 tests available. In this setting, our goal is for long‐term surveillance to detect outbreaks, and we obtain optimal test allocation by setting in Equation (7). We define the outbreak threshold c to be 0.03. 29
We compare our proposed optimal strategy to four alternative allocation strategies, named as the risk‐based strategy, the symptom‐based strategy, the severe‐only strategy, and the universal random testing strategy. The risk‐based strategy prioritizes the group with higher risk of being hospitalized; that is, it prioritizes the severe and mild symptomatic people, but within each symptom group, elderly people are always tested first. The symptom‐based strategy allocates tests based only on the severity of symptoms, and tests are randomly assigned to individuals within symptom groups, regardless of age or other risk factors. The severe‐only strategy prioritizes testing the severely‐ill patients and randomly assigns the remaining tests to the rest of the population. The universal random testing strategy randomly tests the entire population without prioritizing any selected group.
Evaluation of the allocation strategy to achieve its desired goal: After we obtain the test allocation strategy from our strategy as well as other competing methods, we then generate the individual level data, including infection status , covariate , symptom information from the assumed distribution. We apply each strategy to the population and simulate the test result to compare the performance of all strategies. More specifically, we generate the individual‐level data as follows. For the i‐th person, :
Generate age information from a multinomial distribution. The probability corresponding to the four age groups is .
Under the assumption that , we generate the true infection status, from a binomial distribution with probability from the assumed infection rate, namely .
Generate the symptom from a multinomial distribution with three symptom categories. The probability for each symptom conditional on the true infection status and the covariate is or .
Generate the selection indicator . Conditional on and , the selection indicator is generated from a binomial distribution, whose probability is given by the allocation strategy .
Generate the testing result . if . Otherwise, conditional on the true infection status, , where is the test false negative rate; and , where is the test false positive rate.
In the fourth step, we apply our test allocation strategy as well as other competing strategies and summarize the number of true positive, true negative, false negative, false positive and the number of missing cases under the detecting mode. For the surveillance mode, we report the total number of positive tests and test positive rate since these two measures are critical targets. We repeat the above procedure 100 times and provide the mean and standard deviation for each measure.
3.2. Simulation results
Characteristic properties of allocation strategy, detecting mode: Figure 2A,B corresponds to the setting with limited number of tests and high population infection rate. In this setting, the majority of tests are allocated to people with severe and mild symptoms unless the probability of being asymptomatic among infected individuals is very high (eg, 0.75). This is because, unless is very large, the probability of a random person with mild symptoms testing positive is larger than the probability of a random person without symptoms testing positive. In contrast, when we have an abundance of tests available (Figure 2C,D), the majority of the tests are allocated to asymptomatic patients, partially due to a limited number of patients with severe and mild symptoms overall. When tests are scarce and the goal is to detect more cases, tests are allocated across all four age groups based on the assumed marginal proportion of infected people who are asymptomatic, . These age distributions among the tested patients are largely driven by differences in symptoms across age categories. Since younger people are more likely to be asymptomatic, 25 the majority of tests among asymptomatic people are allocated to young (ages 0 to 17) people. For example, when the marginal probability of being asymptomatic for an infected person is 0.55 () and when we have an abundance of tests as 200 000, 4.3% of tests are allocated to people aged 65+ with mild symptoms compared to 1.5% to people aged 0 to 17 with mild symptoms. After satisfying the prioritized testing for the severe and mild symptom groups, the remaining 59.5% of tests are allocated to the young (age 0 to 17) asymptomatic group.
FIGURE 2.
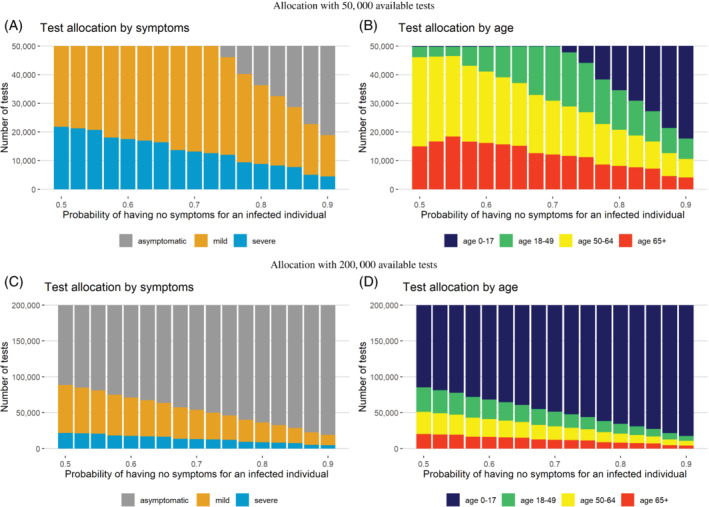
Tests allocated to each symptom and age group near the peak of the pandemic under the detecting mode, assuming either 50 000 or 200 000 tests are available and that the number of true infected cases is 175 000 in a region of eight million people
Characteristic properties of allocation strategy, surveillance mode: Figure 3 shows the optimal test allocation when the infection rate in the population is low and many tests are available. In this situation, we are in a surveillance mode and want to monitor when the test positive rate exceeds a certain threshold (c), for example, 3%. A test positive rate exceeding the threshold level c obtained under this testing strategy may provide a good indicator that the prevalence of disease is going up in the population (Figure S1 in the Supplementary Material). The optimal testing strategy does not require all available tests to be used, and the majority of allocated tests are given to people aged 50+. Close monitoring of older asymptomatic patients may provide a good strategy for capturing an outbreak as indicated by a raising test positive rate.
FIGURE 3.
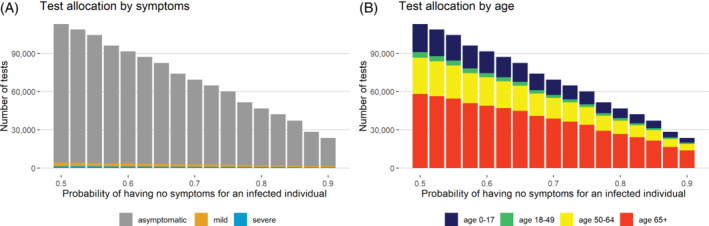
Tests allocated to each symptom and age group for surveillance past the peak of the pandemic, assuming 200 000 tests are available and the number of true infected cases is low (10 000) in a region of eight million people. The test positive rate for the disease outbreak is 0.03
Evaluation of the allocation strategy, detecting mode: The test allocation strategies under the detecting mode and from other approaches are provided in Table S2 and their performance is shown in Table 2. On average, our proposed optimal allocation strategy under the detecting mode can identify more true cases in the population than all the other allocation methods across most scenarios. In a limited testing resources scenario with , the strategy determined by our detecting mode finds 1.4 times more true cases than the severe‐only strategy and 44.5 times more than the universal random testing strategy. In this scenario, our detecting mode strategy performs essentially similar as the risk‐based strategy. This is because these two approaches give the same allocation strategy when the number of tests are limited and no asymptomatic people can be tested. However, there is a difference when we have a sufficient number of tests. Our proposed strategy assigns 59.9% of available tests to the young (aged 0 to 17) asymptomatic people, rather than to the elderly (aged ) asymptomatic people as the risk‐based strategy does (Table S2). With a sufficient number of tests, our detecting mode on average finds 2.7% more true cases than the risk‐based strategy. At the same time, our strategy misses fewer true infections than all the other methods, with 2.6%, 2.2%, 38.2%, 45.0% fewer than the risk‐based strategy, symptom‐based strategy, severe‐only strategy and universal random testing. In terms of the false negatives, the risk‐based method has fewer false negative tests than our method, which is because the former method overall select fewer true cases. Our method outperforms all other approaches considered as the probability of being asymptomatic among true cases increases, for example, .
TABLE 2.
The mean and standard deviation of the true positive tests, true negative tests, false negative tests, false positive tests, and the missing cases who are not tested in the population, using the test allocation strategy determined by the proposed detecting mode and alternative allocation methods
| True positive | True negative | False negative | False positive | Missing cases | |
|---|---|---|---|---|---|
| Mean (SD) | Mean (SD) | Mean (SD) | Mean (SD) | Mean (SD) | |
| Limited number of tests as 50 000; =0.55 | |||||
| Detecting mode | 34654 (178.3) | 463 (23.7) | 14833 (121.6) | 5 (2.0) | 125497 (336.3) |
| Risk‐based | 34654 (178.3) | 463 (23.7) | 14833 (121.6) | 5 (2.0) | 125497 (336.3) |
| Symptom‐based | 34415 (207.9) | 795 (29.0) | 14736 (122.0) | 8 (2.9) | 125834 (317.5) |
| Severe‐only | 14178 (108.7) | 29425 (157.6) | 6075 (70.4) | 299 (18.6) | 154732 (359.6) |
| Universal random | 761 (27.4) | 48412 (208.2) | 331 (17.3) | 491 (23.1) | 173893 (400.0) |
| Sufficient number of tests as 200 000; =0.55 | |||||
| Detecting mode | 56840 (248.6) | 117589 (326.0) | 24333 (162.1) | 1186 (35.5) | 93811 (265.0) |
| Risk‐based | 55364 (234.9) | 119617 (314.4) | 23720 (145.0) | 1209 (31.8) | 95901 (269.5) |
| Symptom‐based | 56128 (219.4) | 118583 (311.7) | 24046 (154.3) | 1195 (34.0) | 94811 (267.7) |
| Severe‐only | 16214 (118.0) | 175026 (408.7) | 6950 (79.8) | 1766 (38.1) | 151821 (352.2) |
| Universal random | 3051 (49.9) | 193643 (404.0) | 1317 (36.4) | 1954 (41.4) | 170617 (397.3) |
| Limited number of tests as 50 000; =0.90 | |||||
| Detecting mode | 12720 (105.6) | 31528 (177.9) | 5445 (80.5) | 320 (19.4) | 156820 (364.6) |
| Risk‐based | 12628 (122.4) | 31609 (172.2) | 5415 (75.5) | 320 (20.1) | 156942 (368.0) |
| Symptom‐based | 12676 (117.5) | 31566 (168.9) | 5430 (64.9) | 321 (19.2) | 156879 (365.3) |
| Severe‐only | 3728 (56.9) | 44212 (193.4) | 1605 (42.5) | 448 (21.4) | 169652 (401.7) |
| Universal random | 759 (28.9) | 48414 (207.1) | 330 (17.8) | 491 (23.3) | 173896 (412.7) |
| Sufficient number of tests as 200 000; =0.90 | |||||
| Detecting mode | 14988 (114.6) | 176771 (385.7) | 6419 (80.7) | 1787 (41.1) | 153578 (351.7) |
| Risk‐based | 14492 (123.9) | 177427 (431.4) | 6212 (80.3) | 1790 (41.7) | 154280 (364.3) |
| Symptom‐based | 14742 (119.0) | 177124 (400.1) | 6318 (70.9) | 1788 (38.3) | 153925 (365.3) |
| Severe‐only | 5971 (71.8) | 189521 (388.4) | 2561 (52.0) | 1913 (41.2) | 166453 (405.0) |
| Universal random | 3048 (49.9) | 193644 (396.6) | 1315 (39.3) | 1954 (41.4) | 170621 (408.5) |
Note: The assumed number of true infected cases near the peak of the pandemic is 175 000, and the population is eight million. The test false negative rate is 0.3 and the test positive rate is 0.01. Results are based on 100 repetitions. is the probability for a person of being asymptomatic after being infected.
Evaluationof the allocation strategy, surveillance mode: Unlike the other testing strategies that use all available tests, the proposed optimal test strategy uses only 51.5% of available tests when our goal is conducting disease surveillance (Table S3). For comparison, we also present optimal test allocations obtained from our method under the detecting mode. Our surveillance model approach finds about 37% fewer cases than the proposed method under detecting mode and then purely risk‐based and symptom‐based strategies, but it still finds more cases than the severe‐only and universal random testing strategies (Table 3). Even using fewer tests than other methods, our approach can obtain a nominal 3% test positive rate, and observed deviations from this target positive rate can be used as an indicator that the population prevalence is larger than expected.
TABLE 3.
The mean and standard deviation of the true positive tests, true negative tests, false negative tests, false positive tests, the missing cases who are not tested, the total number of positive tests and the test positive rate in the population, using the test allocation strategy determined by the proposed surveillance mode and alternative allocation methods
| True positive | True negative | False negative | False positive | Missing cases | Total no of positive | Positive rate | |
|---|---|---|---|---|---|---|---|
| Mean (SD) | Mean (SD) | Mean (SD) | Mean (SD) | Mean (SD) | Mean (SD) | Mean (SD) | |
| Surveillance | 2086 | 99098 | 905 | 1003 | 7027 | 3088 | 0.03 |
| (43.9) | (314.8) | (31.4) | (29.8) | (78.8) | (52.4) | (5e‐04) | |
| Risk‐based | 3175 | 193456 | 1366 | 1951 | 5476 | 5126 | 0.02 |
| (56.2) | (435.5) | (39.3) | (41.7) | (72.3) | (69.7) | (3e‐04) | |
| Symptom‐based | 3244 | 193386 | 1398 | 1952 | 5376 | 5195 | 0.03 |
| (57.8) | (392.1) | (40.0) | (41.5) | (73) | (74.2) | (4e‐04) | |
| Severe‐only | 938 | 196642 | 408 | 1985 | 8672 | 2922 | 0.01 |
| (29.7) | (396.3) | (20.7) | (42.4) | (88.8) | (48.8) | (2e‐04) | |
| Universal random | 175 | 197719 | 75 | 1996 | 9768 | 2171 | 0.01 |
| (12.3) | (397.4) | (9.0) | (42.5) | (92.8) | (42.7) | (2e‐04) | |
| Detecting mode | 3314 | 193262 | 1423 | 1951 | 5281 | 5264 | 0.03 |
| (61.4) | (419.7) | (40.9) | (44.6) | (71.5) | (76.4) | (4e‐04) |
Note: The assumed number of true infected cases near the peak of the pandemic is 10 000, and the population is 8 million. The test false negative rate is 0.3 and the test positive rate is 0.01. Results are based on 100 repetitions. The probability for a person of being asymptomatic after being infected is 0.55 ().
Remark 2
To understand how the test allocation strategy will be affected by false positive tests, we compare the test allocation with and without consideration of false positive tests. An easy way to obtain the test allocation strategy without false positive tests is to set equal to 0 in the strategy design phase. For comparison purposes, we set and obtain the test allocation strategy with false positive tests. Overall, our simulation studies indicate that low levels of false positive tests will not affect the test allocation strategy under the detecting mode (Figure S2). Although we would need fewer tests for the surveillance mode based only on true positive tests (Figure S3), the resulting test positive rate cannot be guaranteed at the prefixed level if we ignore the false positives (Table S4).
4. A SAMPLE CASE‐STUDY: TEST ALLOCATION STRATEGY IN NEW YORK CITY
We illustrate how our framework can be applied to determine test allocation through different stages of the pandemic in New York City () between March 3 and November 1 in the year 2020. The case numbers and the total available tests for each week/generation are obtained from data released by the New York City Department of Health and Mental Hygiene. 30 Existing work studying the magnitude of under‐reported cases and the proportion of asymptomatic cases suggest that the true number of cases is about 10 times the reported cases in the United States. 31 However, since New York City has tested nearly 70% of its population until November 11, 30 which is far above the national level of 45%, 32 the fraction of under‐reported cases should be smaller. We assume the multiplicative under‐reporting factor to be 4, meaning we assume the true number of cases in the New York City to be 4 times the reported cases. Following Rahmandad et al, 31 we set the marginal probability that a true case is asymptomatic, , to be 55%. Although the accuracy varies across different types of diagnostic tests, the false negative rate is known to be appreciable and depends on the type of test. 33 We set the false positive () and false negative () rates to 0.01 and 0.3, 33 respectively. Other details regarding assumed parameter settings can be found in Table S1 in the Supplementary Material. Alternative parameter values can be explored dynamically using our R Shiny app.
Figure 4 shows the optimal test allocation strategy our method would have recommended for New York City throughout the pandemic. We suppose we had allocated tests with the goal of detecting as many cases as possible between March 3 and July 21, during which the disease prevalence was high in the population. Under this method, we predict that the test positive rate would have fallen below 0.03 during the week of July 21st. We then switched to the surveillance mode for monitoring disease outbreaks thereafter. When the goal is to detect as many cases as possible (detecting mode), symptomatic and the elderly patients should be prioritized, especially when we are short of tests. From March 3 to April 7, for example, our method would test only people with severe and mild symptoms, and people of age 0 to 17 would be rarely tested, because the probability of finding a positive test in the symptomatic group is higher than the asymptomatic group. As the number of available tests gradually increased, more tests would have been allocated to asymptomatic patients and to young people, because the younger people would be more likely to be asymptomatic and the symptomatic elderly people would have already been offered a test. After switching to surveillance mode, our method would have allocated just 53.9% of the tests that are actually conducted. These tests would primarily be allocated to older asymptomatic people.
FIGURE 4.
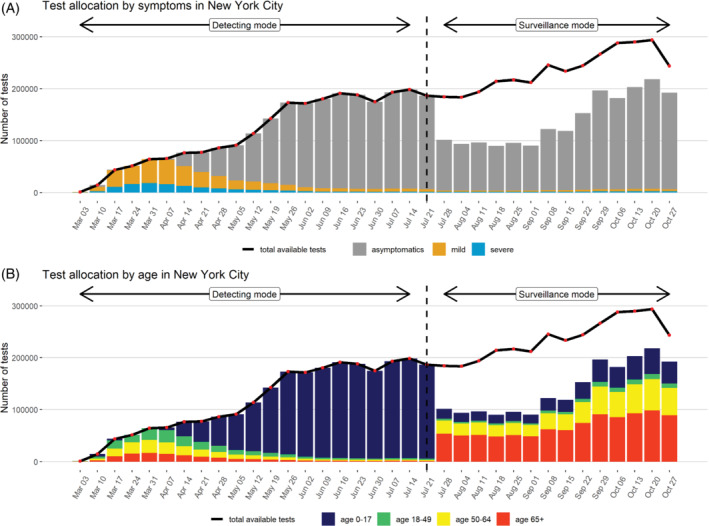
Test allocation strategy for New York City in the year 2020 assuming a case under‐reporting factor of 4, stratified by symptoms and age
To validate our proposed method, we compare the number of cases and the test positive rate reported for New York City to the predicted values under our optimal testing strategy method in Figure 5. Since in practice, the true infection status is unknown, we do not distinguish the false positive tests from the true positive tests when obtaining the total number of positive tests from our proposed strategy. Under our assumptions about the rate of case under‐reporting, the proposed testing strategy is able to detect a greater number of cases than were actually observed in New York City between March 3rd to July 21st. After July 21st, the optimal test strategy detects a similar number of reported cases but uses far fewer tests than were actually administered during this time period for New York City.
FIGURE 5.
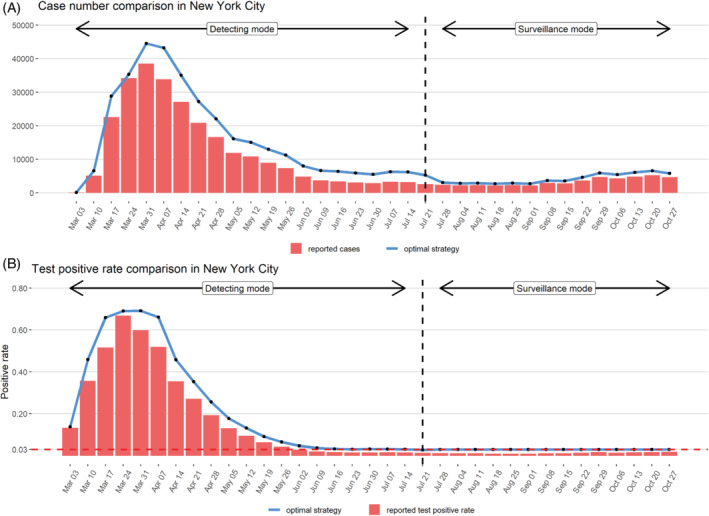
Comparison of predicted positive test number and test positive rates under optimal testing strategy to values observed for New York City in the year 2020 assuming a case under‐reporting factor of 4
5. EXAMPLE OF ALLOCATING TWO DIFFERENT TYPES OF DIAGNOSTIC TESTS
For universities and colleges, test allocation strategy needs to be customized according to the local disease rates and community testing capacity, 34 as are often characterized by the budget for testing, the total number of tests available, the observed number of positive tests and test positive rate. As tests of different costs and accuracy become available, the question of test allocation becomes even more challenging. Subject to budget constraints, we extend our proposed test allocation method to address allocation of two competing tests with differing costs and accuracy as a function of symptoms and patient characteristics. We consider the hypothetical scenario where we want to allocate a fixed budget to a mixture of RATs and RT‐PCR tests. The RT‐PCR test, which is considered to be the gold‐standard test in COVID‐19 diagnosis, costs about $100 per test and has sensitivity as high as 0.9. 35 , 36 , 37 RATs, in contrast, cost $ 5 per test but have much lower sensitivity. 35 , 36 , 38 Mirroring current market information, we set the price for the RAT and for the RT‐PCR test as $5 and $135, respectively, and we assume test sensitivity values are 0.45 and 0.9, respectively. 37 , 38 Specificity is set to 0.99 for both tests. We suppose that at a certain generation, the number of truly infected cases in a population of 8 million is 10 000 and the budget is one million. Alternative scenarios (including different budgets, population size, age distributions) can be explored using our R Shiny app.
Figure 6 provides the optimal budget allocation between the two tests as a function of the marginal probability that a true case is asymptomatic (). As seen in Supplementary Material Figure S4, RT‐PCR tests are only allocated to people with severe and mild symptoms, and the majority of RATs are allocated to asymptomatic people. Since the absolute number of symptomatic people decreases when increases under a fixed number of total cases, the proportion of the budget allocated to RT‐PCR testing decreases with increased .
FIGURE 6.
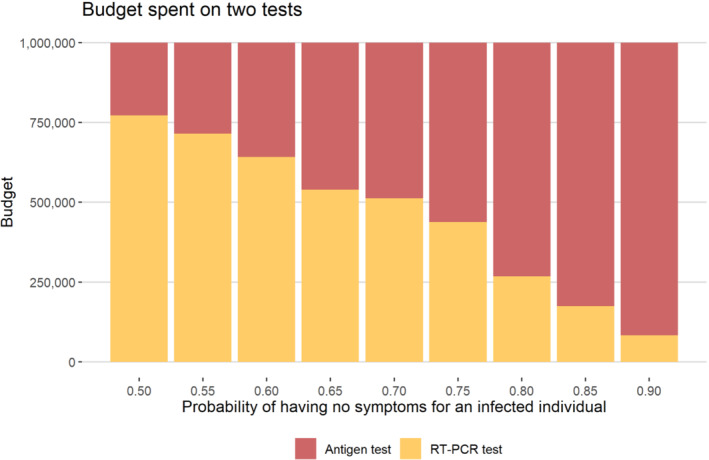
A total of one million budge divided for RATs and RT‐PCR tests. The price of a single antigen test and RT‐PCR test are $ 5 and $ 135, respectively. The number of infected cases is assumed to be 10 000 in a region of population eight million
6. DISCUSSION
In this article, we provide a mathematical framework for developing test allocation strategy with imperfect diagnostic tests. We develop a strategy for obtaining optimal allocation of diagnostic tests across population strata defined by symptom severity and other risk factors such as age. This method adapts to different scenarios in terms of public health objectives. For example, when the goal is to detect as many infected cases as possible in the acceleration phase of the pandemic with high community prevalence, tests should be allocated with targeted testing in population strata most likely to contain cases. When our goal is to detect new disease outbreaks as part of population surveillance after a disease wave has passed and we are in a state of containment, fewer tests may be needed, and a substantial proportion of tests should be allocated to asymptomatic people. In the setting where we have a sufficient number of tests, we demonstrate that our proposed detecting mode strategy can find 2.7% more cases than the risk‐based strategy. Under the surveillance mode, our strategy only uses 51.5% of tests that are available. Although our simulation results rely on the assumption that a person's infection status is independent of his/her characteristics, this assumption can be relaxed if the distribution of true infection status given patient characteristics is known.
We demonstrate this optimal test allocation strategy in a special case where the population is stratified based on age and the severity of symptoms, using New York City as a illustrative example. If tests had been allocated as suggested by our method, we may have used only 53.9% of the tests that were actually conducted and have still found as many cases as were reported. We provide a R Shiny web app (available at https://umich‐biostatistics.shinyapps.io/Testing_Optimization/) allowing users to explore the optimal test allocation as a function of test positive/negative rates, number of available tests, and the true rate of infection among asymptomatic people.
In an extension of the proposed method, we develop a strategy for obtaining optimal allocation of two tests with different false negative rates and cost (eg, cheap RATs vs expensive RT‐PCR tests) subject to overall budget constraints. We show that the expensive but more accurate RT‐PCR tests should be used on the severe or mild symptomatic people, which is in accordance with the finding in the existing work. 14 This approach can be used to help inform test allocation decisions currently being made by many universities, communities, businesses, etc. for planning their reopening. Through our R Shiny app, users can explore the impact of comparative cost, total budget, population age profile, and other key factors on the optimal test allocation at different points in a pandemic wave.
Our R Shiny web app can also be used to explore the problem of repeated testing, where RATs are repeatedly used to improve sensitivity. We found that the probability of correctly identifying an infected individual goes up with repeated rapid antigen testing, but the ability to detect cases in the entire population decreases as fewer different people are able to be tested under a fixed overall test budget.
An advantage of the proposed test allocation method is that it directly incorporates test accuracy and can be applied to allocation of different types of tests, including RATs and/or RT‐PCR tests. We focus on the particular case where population strata are defined based on age as well as symptom severity, but this method can be extended to also incorporate occupation, geographical location, and other key factors into defining population strata. We provide an example R script for implementing the methods with strata defined by age and symptoms in the Supplementary Material. Users can adapt this code to apply our methods under different strata definitions. Care must be taken when specifying model parameters, since the resulting test allocation may be sensitive to these choices. We recommend, therefore, that users explore test allocation across a spectrum of plausible input parameters to inform decision‐making in practice.
With the emergence of new variants of concern and global vaccine inequity, testing will play a key role in safely reopening any nation for the foreseeable future. Assays for diagnostic tests will possibly need to be adapted to detect new strains, but the fundamental problem of who to test given a limited number of available tests in a detection or surveillance phase will remain relevant as we continue to combat this global pandemic. For any new infectious virus such testing strategies and tools will prove to be useful beyond the ongoing pandemic. We hope this general framework leads to cost‐saving and effective strategies, particularly in developing countries where resources are limited.
AUTHOR CONTRIBUTIONS
Jiacong Du, Lauren J. Beesley, and Bhramar Mukherjee: Conceptualized and formulated the mathematical framework. Jiacong Du: Drafted the manuscript, collected data, and wrote codes. Lauren J. Beesley: Built the R Shiny app and co‐drafted the manuscript. Seunggeun Lee, Xiang Zhou, Walter Dempsey, and Bhramar Mukherjee: Revised the manuscript. All participated in reading, editing, and revising the initial draft of the manuscript.
CONFLICT OF INTEREST
The authors declare no potential conflict of interests.
Supporting information
Data S1 Supplementary Material
ACKNOWLEDGEMENTS
The work is supported by NSF DMS 1712933 and a pilot grant by the Michigan Institute of Data Science. The authors would like to thank Mike Kleinsasser from the department of Biostatistics, University of Michigan for helping to build the R Shiny application.
Du J, J Beesley L, Lee S, Zhou X, Dempsey W, Mukherjee B. Optimal diagnostic test allocation strategy during the COVID‐19 pandemic and beyond. Statistics in Medicine. 2022;41(2):310–327. doi: 10.1002/sim.9238
DATA AVAILABILITY STATEMENT
The data that support the findings of this study are openly available. These data were derived from the following resources available in the public domain:
1. New York City Department of Health and Mental Hygiene. Daily COVID‐19 case counts and tests. https://www1.nyc.gov/site/doh/covid/covid‐19‐data.page
2. New York City Department of Health and Mental Hygiene. Cases, Hospitalizations and Deaths. https://www1.nyc.gov/site/doh/covid/covid‐19‐data.page
3. New York State Department of Health. Weekly Influenza Surveillance Report. https://www.health.ny.gov/diseases/communicable/influenza/surveillance/
REFERENCES
- 1. Salathé M, Althaus CL, Neher R, et al. COVID‐19 epidemic in Switzerland: on the importance of testing, contact tracing and isolation. Swiss Med Weekly. 2020;150(1112). [DOI] [PubMed] [Google Scholar]
- 2. Manabe YC, Sharfstein JS, Armstrong K. The need for more and better testing for COVID‐19. Jama. 2020;324(21):2153‐2154. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Grassly N, Pons Salort M, Parker E, et al. Report 16: role of testing in COVID‐19 control; 2020.
- 4. U.S. Food & Drug Administration . Coronavirus testing basics. https://www.fda.gov/consumers/consumer‐updates/coronavirus‐testing‐basics. Accessed May 19, 2021.
- 5. Service RF . Coronavirus antigen tests: quick and cheap, but too often wrong; 2020. https://www.sciencemag.org/news/2020/05/coronavirus‐antigen‐tests‐quick‐and‐cheap‐too‐often‐wrong. Accessed May 19, 2021.
- 6. U.S. Food & Drug Administration . Update: FDA authorizes first COVID‐19 test for self‐testing at home; 2020.
- 7. Romer P. Webinar: how to re‐start the economy after COVID‐19; 2021. https://bcf.princeton.edu/event‐directory/covid19_04/. Accessed May 19, 2021.
- 8. Cleevely M, Susskind D, Vines D, Vines L, Wills S. A workable strategy for Covid‐19 testing: stratified periodic testing rather than universal random testing1. Covid Economics. 2020;44. [Google Scholar]
- 9. Eliaz Y, Danovich M, Gasic GP. Poolkeh finds the optimal pooling strategy for a population‐wide COVID‐19 testing (Israel, UK, and US as Test Cases). MedRxiv; 2020.
- 10. Crist C. Group screening could help COVID‐19 test shortages; 2020. https://www.webmd.com/lung/news/20200514/group‐screening‐could‐help‐covid‐19‐test‐shortages. Accessed May 19, 2021.
- 11. Broadfoot M. Coronavirus test shortages trigger a new strategy: group screening; 2020. https://www.scientificamerican.com/article/coronavirus‐test‐shortages‐trigger‐a‐new‐strategy‐group‐screening2/#:∼:text=Such%20false%20negatives%20have%20plagued,of%20a%20pathogen%20remains%20low. Accessed May 19, 2021.
- 12. Lefkowitz M. Group testing could screen entire US, research suggests; 2020. https://news.cornell.edu/stories/2020/06/group‐testing‐could‐screen‐entire‐us‐research‐suggests. Accessed May 19, 2021.
- 13. Jonnerby J, Lazos P, Lock E, et al. Maximising the benefits of an acutely limited number of COVID‐19 tests; 2020. arXiv preprint arXiv:2004.13650.
- 14. Ely J, Galeotti A, Steiner J. Optimal test allocation. Technical report. Mimeo; 2020.
- 15. Ganyani T, Kremer C, Chen D, et al. Estimating the generation interval for coronavirus disease (COVID‐19) based on symptom onset data. Eurosurveillance. 2020;25(17):2000257. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Champredon D, Dushoff J. Intrinsic and realized generation intervals in infectious‐disease transmission. Proc Royal Soc B Biol Sci. 2015;282(1821):20152026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Griffin J, Casey M, Collins Á, et al. Rapid review of available evidence on the serial interval and generation time of COVID‐19. BMJ Open. 2020;10(11):e040263. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Brooks ZC, Das S. COVID‐19 testing: impact of prevalence, sensitivity, and specificity on patient risk and cost. Am J Clin Pathol. 2020;154(5):575‐584. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Böger B, Fachi MM, Vilhena RO, Cobre AF, Tonin FS, Pontarolo R. Systematic review with meta‐analysis of the accuracy of diagnostic tests for COVID‐19. Am J Infect Control. 2021;49(1):21‐29. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. Wang L, Zhou Y, He J, et al. An epidemiological forecast model and software assessing interventions on the COVID‐19 epidemic in China. J Data Sci. 2020;18(3):409‐432. [Google Scholar]
- 21. Hao X, Cheng S, Wu D, Wu T, Lin X, Wang C. Reconstruction of the full transmission dynamics of COVID‐19 in Wuhan. Nature. 2020;584(7821):420‐424. [DOI] [PubMed] [Google Scholar]
- 22. New York State Department of Health . Weekly influenza surveillance report; 2021. https://www.health.ny.gov/diseases/communicable/influenza/surveillance/2019‐2020/archive/. Accessed May 19, 2021.
- 23. New York City Department of Health and Mental Hygiene . Coronavirus case counts and hospitalized counts by age; 2021. https://www1.nyc.gov/site/doh/covid/covid‐19‐data.page. Accessed May 19, 2021.
- 24. Wellmann R. R package optiSolve; 2020.
- 25. Dong Y, Mo X, Hu Y, et al. Epidemiology of COVID‐19 among children in China. Pediatrics. 2020;145(6). [DOI] [PubMed] [Google Scholar]
- 26. Gupta M, Mohanta SS, Rao A, et al. Transmission dynamics of the COVID‐19 epidemic in India, and evaluating the impact of asymptomatic carriers and role of expanded testing in the lockdown exit strategy: a modelling approach. medRxiv; 2020.
- 27. Subramanian R, He Q, Pascual M. Quantifying asymptomatic infection and transmission of COVID‐19 in New York City using observed cases, serology, and testing capacity. Proc Nat Acad Sci. 2021;118(9). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28. New York City Department of Health and Mental Hygiene . Cases, hospitalizations and deaths; 2021. https://www1.nyc.gov/site/doh/covid/covid‐19‐data.page. Accessed May 19, 2021.
- 29. Siddarth D, Katz R, Graeden E, Allen D, Tsai T. Evidence roundup: why positive test rates need to fall below 3%; 2020.
- 30. New York City Department of Health and Mental Hygiene . Daily COVID‐19 case counts and tests; 2021. https://www1.nyc.gov/site/doh/covid/covid‐19‐data.page. Accessed May 19, 2021.
- 31. Rahmandad H, Lim TY, Sterman J. Estimating COVID‐19 under‐reporting across 86 nations: implications for projections and control; 2020.
- 32. The COVID Tracking Project . https://covidtracking.com/data/national. Accessed May 19, 2021.
- 33. Woloshin S, Patel N, Kesselheim AS. False negative tests for SARS‐CoV‐2 infection‐challenges and implications. New Engl J Med. 2020. [DOI] [PubMed] [Google Scholar]
- 34. Elbanna A, Wong GN, Weiner ZJ, et al. Entry screening and multi‐layer mitigation of COVID‐19 cases for a safe university reopening. medRxiv; 2020.
- 35. Vandenberg O, Martiny D, Rochas O, Belkum vA, Kozlakidis Z. Considerations for diagnostic COVID‐19 tests. Nature Rev Microbiol. 2020;1‐13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36. Nagura‐Ikeda M, Imai K, Tabata S, et al. Clinical evaluation of self‐collected saliva by quantitative reverse transcription‐PCR (RT‐qPCR), direct RT‐qPCR, reverse transcription–loop‐mediated isothermal amplification, and a rapid antigen test to diagnose COVID‐19. J Clin Microbiol. 2020;58(9). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37. IGeneX, Inc . Description of COVID‐19 tests; 2021. https://igenex.com/igenex‐covid‐19‐testing/. Accessed May 19, 2021.
- 38. Abbott Laboratories . Abbott's fast, $5, 15‐minute, easy‐to‐use COVID‐19 antigen test receives FDA emergency use authorization; mobile app displays test results to help our return to daily life; ramping production to 50 million tests a month; 2020. https://abbott.mediaroom.com/2020‐08‐26‐Abbotts‐Fast‐5‐15‐Minute‐Easy‐to‐Use‐COVID‐19‐Antigen‐Test‐Receives‐FDA‐Emergency‐Use‐Authorization‐Mobile‐App‐Displays‐Test‐Results‐to‐Help‐Our‐Return‐to‐Daily‐Life‐Ramping‐Production‐to‐50‐Million‐Tests‐a‐Month#:∼:text=ABBOTT%20PARK%2C%20Ill.%2C%20Aug,sell%20this%20test%20for%20%245. Accessed May 19, 2021.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data S1 Supplementary Material
Data Availability Statement
The data that support the findings of this study are openly available. These data were derived from the following resources available in the public domain:
1. New York City Department of Health and Mental Hygiene. Daily COVID‐19 case counts and tests. https://www1.nyc.gov/site/doh/covid/covid‐19‐data.page
2. New York City Department of Health and Mental Hygiene. Cases, Hospitalizations and Deaths. https://www1.nyc.gov/site/doh/covid/covid‐19‐data.page
3. New York State Department of Health. Weekly Influenza Surveillance Report. https://www.health.ny.gov/diseases/communicable/influenza/surveillance/


