Avoiding bias in self‐controlled case series studies of coronavirus disease 2019

Abstract

Many studies, including self‐controlled case series (SCCS) studies, are being undertaken to quantify the risks of complications following infection with severe acute respiratory syndrome coronavirus 2 (SARS‐CoV‐2), the virus that causes coronavirus disease 2019 (COVID‐19). One such SCCS study, based on all COVID‐19 cases arising in Sweden over an 8‐month period, has shown that SARS‐CoV‐2 infection increases the risks of AMI and ischemic stroke. Some features of SARS‐CoV‐2 infection and COVID‐19, present in this study and likely in others, complicate the analysis and may introduce bias. In the present paper we describe these features, and explore the biases they may generate. Motivated by data‐based simulations, we propose methods to reduce or remove these biases.

1. INTRODUCTION

The coronavirus disease 2019 (COVID‐19) pandemic has prompted several studies to describe the natural course of the infection and quantify the risks presented by COVID‐19 in relation to population baselines. This task is complicated by the fact that severe acute respiratory syndrome coronavirus 2 (SARS‐CoV‐2) incidence and COVID‐19 severity vary greatly according to factors that are not, as yet, completely documented, the understanding of which is still evolving. These factors include age, sex, ethnic background, socioeconomic circumstances, underlying state of health, and location.

To date, three studies using the self‐controlled case series (SCCS) method have been undertaken to evaluate the risk of acute myocardial infarction (AMI) and ischemic stroke after SARS‐CoV‐2 infection. ¹ , ² , ³

The present case study concerns the second of these SCCS studies, ² which was undertaken in Sweden. This was a nationwide study, based on all COVID‐19 cases arising between February and September 2020. It is motivated by two methodological issues, which are likely to arise more widely in SCCS studies of SARS‐CoV‐2 infection and cardiovascular disease or other severe complications; the first is likely to affect study designs other than SCCS as well.

The first issue we consider relates to the definition of the risk period for cardiovascular events following COVID‐19. The data reveal a sharp peak of events occurring on the day COVID‐19 first becomes apparent. We call these day‐zero events. We will discuss the reasons why such spikes may arise in these data, and show that including day‐zero events in the postexposure risk period introduces bias. Our proposal is to redefine the risk period to start on day 1 after COVID‐19. Day‐zero events are instead included in a pre‐exposure risk period. We show in simulations that this simple solution removes the bias, which may otherwise be large.

The second issue we consider relates to mortality. Individuals may die for reasons unconnected to COVID‐19 or its complications. Some, however, may die of cardiovascular disease: in such cases, the observation period is event‐dependent, thus violating one of the assumptions of the standard SCCS method. An extension of the SCCS method is available in such circumstances. ⁴ However, this extension was developed under the assumption that the exposure is not an independent cause of mortality. This is not the case for SARS‐CoV‐2 infection. Nevertheless, we show through simulations that the extended SCCS method of event‐dependent observation periods still provides reliable results.

The paper is organized as follows. In the next section, we give some details of the SCCS method and its extension. Then we describe the Swedish study, illustrate the two methodological issues of interest, and detail our proposed solutions. In the following two sections, we outline the simulations and describe their results. The paper ends with a discussion of the findings and of their likely applicability.

2. THE SCCS METHOD

In this section we give brief details of the SCCS method. Further information is available in a Statistics in Medicine tutorial paper, ⁵ and in a book on the topic. ⁶

The SCCS study design is obtained from a retrospective Poisson cohort model by conditioning on the number of events observed for each individual in the cohort over the period of observation. Individuals with zero events drop out of the conditional likelihood, which includes only cases (whence the CS in SCCS), individual likelihood terms being of the form:

$$\frac{\lambda (t;x)}{{\int }_a^b\lambda (s;x)ds},$$

where $(a,b]$ is the observation period, t is the event time, $\lambda (s;x)$ is the event rate at time s, and x is the exposure history for this individual. The form of this conditional likelihood contribution implies that each case acts as its own control (whence the SC in SCCS): in particular, time‐invariant covariates acting multiplicatively on the event rate factor out of the likelihood. Note also that the integral in the denominator involves observation time both before and after the event time t.

Thus, multiplicative time‐invariant confounders are automatically adjusted (time‐varying confounders, on the other hand, are not). This feature of the method is likely to be advantageous in the context of studies of COVID‐19, since, as noted above, full information on potential confounders is unavailable.

In the standard SCCS model, the event rate is represented as piecewise constant, with parameters for exposure levels and time effects. In the present paper, the exposure levels are determined by risk intervals before and after COVID‐19. Days outside the risk periods correspond to the reference exposure level. The standard SCCS model may be fitted using standard Poisson modelling software. The loglinear models used in this paper are all of the form:

$$\mathtt{\text{Exposure level + Seasonal effect.}}$$

The exposure level parameters are log relative incidences $\log (\rho )$, where

$$\rho =\frac{\lambda (s;s\text{in risk period})}{\lambda (s;s\text{not in risk period})}.$$

Standard likelihood theory applies, thus guaranteeing consistency of the parameter estimators.

However, for inferences about the event rate $\lambda (s;x)$ from the conditional likelihood to be valid, some strict exogeneity conditions are required. In particular, the observation period $(a,b]$ should not depend on the event time t: this condition may be violated if the event can cause an early death. In order to overcome this limitation, an extended SCCS model was developed. ⁴ In this model, the likelihood contribution is modified:

$$\frac{\lambda (t;x)w(b;t,I)}{{\int }_a^b\lambda (s;x)w(b;s,I)ds},$$

where $w(b;s,I)$ is a weighting function that depends on the distribution of the time of death, given an event at time s; I is an indicator function to specify whether the end of observation b is a death. This weighted version of the standard SCCS likelihood requires an extra step, to estimate the time from event to death and hence the weights. The procedure yields consistent estimators. ⁴

In the R functions used here, the distribution of times to death is estimated using four inbuilt parametric mixture models, the best‐fitting of which is selected. We chose optimal starting values to estimate this mixture model. ⁶

3. SWEDISH STUDY OF COVID‐19 AND CARDIOVASCULAR DISEASE

The aim of the Swedish study was to quantify the relative risk of AMI and ischemic stroke after confirmed infection with SARS‐CoV‐2, using both a SCCS design and a matched cohort design. We focus on the SCCS design.

The study was based on data extracted from several linked Swedish registers with data on COVID‐19, hospital inpatient and outpatient admissions, and deaths. These data were used to define dates of COVID‐19, cardiovascular disease (AMI or ischemic stroke), and death. ² The SCCS study included all individuals with confirmed COVID‐19 and a first AMI or ischemic stroke between 1 February and 14 September 2020; these dates determined the observation period for the study. The post‐COVID‐19 risk period was 28 days; temporal effects were adjusted in calendar months, February to September. Significantly elevated relative incidences were found during the risk period for both AMI and ischemic stroke, motivating the conclusion that COVID‐19 increases the risk of cardiovascular disease.

The results reported here are based on preliminary data sets used for investigative purposes, and differ slightly from those published. ² The main differences relate to numbers of cases and the criteria used to determine the date of confirmed COVID‐19 (see Appendix S1).

3.1. Day‐zero events and the choice of risk periods

Histograms of the interval between COVID‐19 and AMI or ischemic stroke are shown in Figure 1. The dominant features of this plot are the spikes in the 7‐day periods up to and including day zero; events on day zero are those whose COVID‐19 and event dates are the same.

FIGURE 1.

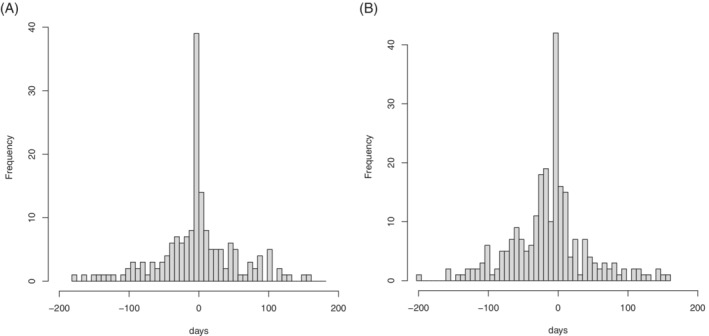
Days from coronavirus disease 2019 to event (7‐day bins). Left: acute myocardial infarction; right: ischemic stroke

The likely reason for these spikes is as follows. The COVID‐19 date is likely to be later than the date of SARS‐CoV‐2 infection. Some cardiovascular events, perhaps caused by the infection, will occur before symptoms have developed sufficiently to result in the patient being identified as having COVID‐19. In this case, the AMI or ischemic stroke will precipitate the admission to hospital, at which point COVID‐19 is identified.

The proposed mechanism behind the observed day‐zero spike is a complex type of reverse causation: the stroke, which may have been caused by the infection, precipitates a hospital admission and a test upon admission, and thus results in the identification of the infection.

Inclusion of such day‐zero events in the post‐exposure risk period is likely to bias the results, by inducing or inflating a positive association between COVID‐19 infection and AMI or ischemic stroke. To see this, consider that a similar mechanism would induce an association between negative COVID‐19 tests and cardiovascular events, owing to their coincidence with date of admission. The bias reflects the association between the event (which precipitates a hospital admission) and testing for COVID‐19, irrespective of the result of the test, or of any causal link between SARS‐CoV‐2 infection and the event.

In the present study, it is likely that some (perhaps many) day‐zero events are causally linked to COVID‐19. In consequence, clinical arguments for their inclusion in the post‐COVID‐19 risk period compete with statistical arguments against. The statistical argument against including such cases in the post‐exposure risk period is that this would introduce a selection bias related to delay between SARS‐CoV‐2 infection and its identification.

A second, simpler, type of reverse causation may also arise: an individual with AMI or ischemic stroke may be admitted to hospital, whereupon that individual may contract nosocomial SARS‐CoV‐2 infection.

In order to separate out these effects, we undertook SCCS analyses both excluding and including day zero in the post‐COVID‐19 risk period. This was split into three segments: [0 or 1, 7] days, [8, 14] days, and [15, 28] days, day zero being the COVID‐19 day. To remove the effect of reverse causation, we also included two pre‐exposure risk periods: [$-$28, $-$4] days and [$-$3, $-$1 or 0] days; these periods are not of substantive interest. Note that no data are excluded from the analysis as a result of the redefinition of risk periods.

Very different results are obtained according to whether the post‐COVID‐19 risk period includes day zero or not. The results using the preliminary data are shown in Table 1. For AMI, the relative incidence in the first week after COVID‐19 is 3.18 when day zero is excluded from the risk period, but 9.72 when it is included. For ischemic stroke, the values are 2.50 and 7.18, respectively. In the next section, we show using simulations that, in order to avoid bias, the post‐COVID‐19 risk period should not include day zero: day‐zero events should be included in pre‐exposure risk periods.

TABLE 1.

Relative incidence (RI) and 95% confidence interval (CI) for acute myocardial infarction (AMI) and ischemic stroke by risk period, with day zero excluded from or included in the post‐COVID‐19 risk period

(a) Day zero excluded from post‐exposure risk period
	AMI			Ischemic stroke
Risk period (days)	Events	RI	95 % CI	Events	RI	95 % CI
$-$28 to $-$4	25	1.76	(1.09, 2.86)	51	1.94	(1.33, 2.83)
$-$3 to 0	36	11.12	(10.92, 26.84)	38	10.97	(7.15, 16.83)
1 to 7	14	3.18	(1.72, 5.88)	16	2.50	(1.41, 4.44)
8 to 14	8	1.79	(0.83, 3.88)	15	2.66	(1.47, 4.80)
5 to 28	10	1.34	(0.67, 2.69)	11	1.18	(0.60, 2.30)

(b) Day zero included in postexposure risk period
	AMI			Ischemic stroke
Risk period (days)	Events	RI	95 % CI	Events	RI	95 % CI
$-$28 to $-$4	25	1.75	(1.08, 2.84)	51	1.95	(1.34, 2.85)
$-$3 to $-$1	2	1.44	(0.35, 5.97)	2	0.87	(0.21, 3.57)
0 to 7	48	9.72	(6.37, 14.84)	52	7.18	(4.80, 10.75)
8 to 14	8	1.91	(0.88, 4.11)	15	2.83	(1.56, 5.13)
15 to 28	10	1.38	(0.69, 2.77)	11	1.25	(0.64, 2.44)

3.2. Handling deaths

Twenty percent (36 of 176) of AMI cases and 29% (72 of 247) of ischemic stroke cases died before the end of the predetermined end of the observation period, 14 September 2020. Figure 2 shows the time from event to death for those who died.

FIGURE 2.

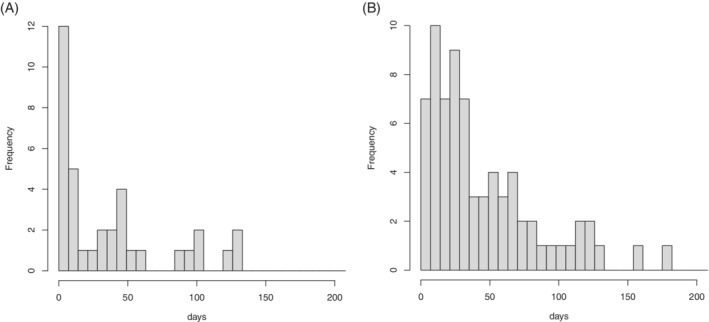
Days from event to death (7‐day bins). Left: acute myocardial infarction; right: ischemic stroke

Figure 2 shows that a high proportion of deaths occurred soon after the event (AMI or ischemic stroke), consistent with it being the cause of death. If this is the case, there is event‐dependent censoring of the observation period, and the extended SCCS model ⁴ should be used in preference to the standard SCCS model. However, this extension assumes that the exposure, which in this application is COVID‐19, is not itself a direct cause of increased mortality. This assumption may be incorrect.

If information were available on whether deaths were due directly to COVID‐19 (rather than to AMI or ischemic stroke), this information could be used to apply the SCCS extension without any concern, since such deaths are not event‐dependent. But this information is not available. Thus, it is not immediately clear which analysis strategy is to be preferred: standard SCCS model, or extended SCCS model. The results using the two methods for the post‐COVID‐19 risk periods (with day zero excluded) are shown in Table 2; the pre‐COVID‐19 risk periods are omitted as they are not of primary interest.

TABLE 2.

Relative incidence (RI) and 95% confidence interval (CI) for acute myocardial infarction (AMI) and ischemic stroke by risk period with the standard and the extended self‐controlled case series (SCCS) models

(a) AMI
	Standard model		Extended model
Risk period (days)	Events	RI	95 % CI	RI	95 % CI
1 to 7	14	3.28	(1.79, 6.00)	3.18	(1.72, 5.88)
8 to 14	8	2.07	(0.97, 4.40)	1.79	(0.83, 3.88)
15 to 28	10	1.50	(0.75, 2.98)	1.34	(0.67, 2.69)
1 to 28	32	2.16	(1.37, 3.40)	1.81	(1.14, 2.87)

(b) Ischemic stroke
	Standard model		Extended model
Risk period (days)	Events	RI	95 % CI	RI	95 % CI
1 to 7	16	2.79	(1.59, 4.91)	2.50	(1.41,4.44)
8 to 14	15	3.10	(1.73, 5.55)	2.66	(1.47, 4.80)
15 to 28	11	1.42	(0.74, 2.75)	1.18	(0.60, 2.30)
1 to 28	42	2.30	(1.52, 3.48)	1.82	(1.19, 2.78)

Table 2 also presents results for the combined 1‐ to 28‐day post‐COVID‐19 risk period. Note that likelihood ratio tests provide only weak evidence that the relative incidences in the three post‐COVID‐19 risk periods differ (P = 0.087 for AMI and P = 0.055 for stroke).

Table 2 shows that the two methods give broadly similar results, but that the RI values in the postexposure risk periods obtained with the extended SCCS model are systematically lower than those obtained with the standard model. This will be explored in simulations based on the fitted extended model, varying the proportion of deaths that are attributed to AMI and ischemic stroke, in order to ascertain which analysis method is preferable for these data.

4. DESIGN AND IMPLEMENTATION OF THE SIMULATIONS

In the next two subsections we describe the design of the simulations. These were implemented in R; the SCCS models were fitted using the R package SCCS. ⁷ , ⁸ The R code for the analysis and the simulations is available from the journal website. All SCCS models fitted in the simulations included temporal effects in calendar months.

4.1. Simulations for day‐zero events

This set of simulations are focused on whether day‐zero events should be included or excluded from the post‐COVID‐19 risk period. Accordingly, we ignored the possible effects of event‐dependent deaths.

We used the observation periods in the preliminary data, and took the dates of infection as occurring 12 days prior to the COVID‐19 date. ⁹ We then simulated event times for AMI and ischemic stroke, conditional on an event occurring within the observation period. This conditional distribution of event times, for each case, is multinomial. To match a post‐test risk period of r days in the analysis, we took the postinfection risk period to be $r+12$ days, with r = 7, 14, and 28 days. We assumed that the true relative incidence in the risk period was $\rho$ = 1, 2, 3, or 4. The multinomial probability (for simplicity we assume no calendar effects are present) is then proportional to $\rho$ for each day in the risk period, and proportional to 1 on days outside the risk period.

We then redefined the COVID‐19 dates as follows. If the simulated event occurred less than 12 days after infection, we redefined the COVID‐19 day to be that same day. Otherwise we left the COVID‐19 date unchanged. This mimics the situation in which an individual is admitted to hospital for AMI or stroke and is tested for COVID‐19, before symptoms have indicated that such a test is necessary. It will lead to a spike of events on the (redefined) COVID‐19 day, as observed in the data.

The data are then analyzed using a post‐COVID‐19 risk period of r days, in two ways: excluding day zero from the risk period (which thus stretches from day 1 to day r post‐COVID‐19), and including day zero in the risk period (which goes from day 0 to day r). Two pre‐COVID‐19 risk periods were also included, as in the substantive analyses.

For each combination of r and $\rho$, this procedure was repeated $N=10\hspace{0.17em}000$ times. The mean estimate $\widehat{\rho }$ of $\rho$ was compared for each of the two models, along with the empirical mean squared error (MSE) of the estimator $\log (\widehat{\rho })$, the log scale being that on which the parameters are estimated:

$$\text{MSE}=\frac{1}{N}{\displaystyle \sum _{i=1}^N}{(\log ({\widehat{\rho }}_i)-\log (\rho ))}^2.$$

In this expression, ${\widehat{\rho }}_i$ is the estimate of $\rho$ obtained in the ith simulation run.

4.2. Simulations for handling deaths

This set of simulations are focused on how best to handle deaths in this context. It is not possible to ignore day‐zero events, since these may determine dates of death. Thus the simulations use the relative incidences estimated with the extended SCCS model, with day zero excluded from the postexposure risk period.

As previously, we used the starts and ends of the observation periods and the COVID‐19 dates in the preliminary data, and simulated AMI and ischemic stroke event times. These event times were simulated conditionally on the times of death (for the cases who died during the observation period), under a range of assumptions about the proportions of deaths attributed to AMI or ischemic stroke. In view of the small numbers in some post‐COVID‐19 risk periods, we grouped them into a single 1‐ to 28‐day interval. (Simulations were also undertaken with the ungrouped risk periods; these are reported in Appendix S1.) There are thus three risk periods: $-$28 to $-$4, $-$3 to 0, and 1 to 28 days post‐COVID‐19. Let ${\rho }_j$, $j=1,2,3$ denote the relative incidences for these three periods, obtained from the fitted models, and set $\mathit{\rho }=({\rho }_1,{\rho }_2,{\rho }_3)$.

For each of the cases who died (36 for AMI and 72 for ischemic stroke), let t denote the days from event (as observed in the preliminary data) to death, and consider the empirical distribution of these intervals, as shown in Figure 2. We shall assume that individuals with t within a specified percentile p of this distribution died of AMI or ischemic stroke, the remainder dying of other causes (whether connected to COVID‐19 or not), for p = 0%, 25%, 50%, 75%, and 100%. Let $s_p$ denote the mean of the values of t within percentile p.

For each case i, let $m_i(k;\mathit{\rho })$ denote the following multinomial distribution, for days k within the observation period for case i. If k lies within risk interval j, the multinomial probability is proportional to ${\rho }_j$, while for other values k it is proportional to 1.

For individuals deemed not to have died of the event, we simulated an event day using this multinomial distribution, much as described in the previous subsection. Suppose now that, in a simulation scenario based on percentile p, individual i is deemed to have died of the event on day $b_i$. We shall assume that the probability distribution of the time from event to death is exponential with mean $s_p$, and independent of the exposure time. Using Bayes' Theorem, it may be shown that, conditionally on having died of the event at $b_i$, the event time distribution is:

$$d_i(k;r,\mathit{\rho },p)\propto \exp \{-(b_i-k)/s_p\}{m}_i(k;\mathit{\rho }).$$

This is a weighted version of the multinomial distribution $m_i(k;\mathit{\rho })$. The event for individual i was randomly generated using this distribution.

The simulated data were analyzed with two SCCS models: the standard model, and the extended SCCS model for event‐dependent observation periods. For each value of p, this procedure was repeated $N=1000$ times, for each of the AMI and ischemic stroke data sets. We report the empirical bias and MSE of the estimator $\log (\widehat{{\rho }_3})$, the bias being:

$$\text{Bias}=\frac{1}{N}{\displaystyle \sum _{i=1}^N}\log ({\widehat{{\rho }_3}}_i)-\log ({\rho }_3).$$

In this expression, ${\widehat{{\rho }_3}}_i$ is the estimate of parameter ${\rho }_3$ obtained in the ith simulation run.

5. RESULTS OF THE SIMULATIONS

5.1. Results for day‐zero events

Table 3 shows the mean estimates $\widehat{\rho }$ of the relative incidence for the post‐COVID‐19 risk periods, for each assumed value of $\rho$. This shows that the estimates are virtually unbiased when day‐zero events are excluded from the post‐COVID‐19 risk period, but severely upwardly biased when day‐zero events are included in this risk period. The discrepancy is greatest for shorter post‐COVID‐19 risk periods.

TABLE 3.

Mean estimated relative incidence $\widehat{\rho }$ with day zero excluded or included, by post‐coronavirus disease 2019 risk period (days) and true relative incidence $\rho$

(a) Acute myocardial infarction
	Day zero excluded			Day zero included
$\rho$	1‐7	1‐14	1‐28	0‐7	0‐14	0‐28
1	1.02	1.01	1.01	2.62	1.93	1.53
2	2.04	2.03	2.03	5.24	3.85	3.09
3	3.07	3.06	3.05	7.91	5.81	4.67
4	4.08	4.07	4.09	10.53	7.76	6.33

(b) Ischemic stroke
	Day zero excluded			Day zero included
$\rho$	1‐7	1‐14	1‐28	0‐7	0‐14	0‐28
1	1.01	1.01	1.01	2.69	1.98	1.60
2	2.03	2.02	2.02	5.38	3.98	3.24
3	3.03	3.00	3.04	8.08	5.97	4.94
4	4.05	4.02	4.04	10.8	8.03	6.67

Table 4 shows the corresponding values of the MSE (for the log relative incidence). These are much higher when day‐zero events are included in the risk period, as expected, since the bias term dominates. The MSE declines as the risk period increases: this is because the estimates are increasingly precise, as they are based on larger numbers of events within the risk period. This is also true when $\rho$ increases, for the same reason, but only when day‐zero events are excluded from the risk period.

TABLE 4.

Mean squared error of the log relative incidence $\log \widehat{\rho }$ with day zero excluded or included, by post‐coronavirus disease 2019 risk period (days) and true relative incidence $\rho$

(a) Acute myocardial infarction
	Day zero excluded			Day zero included
$\rho$	1‐7	1‐14	1‐28	0‐7	0‐14	0‐28
1	0.211	0.111	0.070	0.933	0.454	0.213
2	0.122	0.070	0.048	0.931	0.445	0.213
3	0.089	0.058	0.044	0.942	0.451	0.218
4	0.074	0.052	0.045	0.939	0.452	0.232

(b) Ischemic stroke
	Day zero excluded			Day zero included
$\rho$	1‐7	1‐14	1‐28	0‐7	0‐14	0‐28
1	0.142	0.077	0.049	0.981	0.481	0.243
2	0.080	0.051	0.037	0.980	0.484	0.251
3	0.062	0.042	0.035	0.983	0.484	0.265
4	0.053	0.039	0.034	0.989	0.495	0.277

The Monte Carlo SEs of the MSEs were at most 0.0049 for AMI and 0.0043 for ischemic stroke. Note that the simulation models and analysis models differ: in the simulations, the postinfection risk period is r + 12 days, while the post‐coronavirus disease 2019 risk period is r days in the analysis. Some residual bias is expected as a result of this mismatch and the possibly low numbers of events (especially in the 1‐ to 7‐day risk period with $\rho =1$), though as shown here this residual bias is small.

In all simulations, a large peak of day‐zero events was observed, which greatly inflated the relative risk in the $-$3 to 0 day risk period, when fitted. This spike accounts for the difference in the estimates obtained under the two methods in Table 3. Note that the way this peak was generated—by mimicking a situation in which patients with a stroke caused by SARS‐CoV‐2 infection are hospitalised for stroke before COVID‐19 becomes apparent—produces a compensatory dearth of stroke events in the period immediately preceding day zero. Thus, in all simulations, the relative incidence in the $-$28 to $-$4 day pre‐COVID‐19 risk period was less than 1 (typically about 0.65).

5.2. Results for handling deaths

Figure 3 shows the plots of the bias and MSE of $\log (\widehat{\rho })$ plotted against the percentile p of deaths attributed to AMI or ischemic stroke, obtained with the standard and extended SCCS models, for the combined 1‐ to 28‐day post‐COVID‐19 risk period.

FIGURE 3.

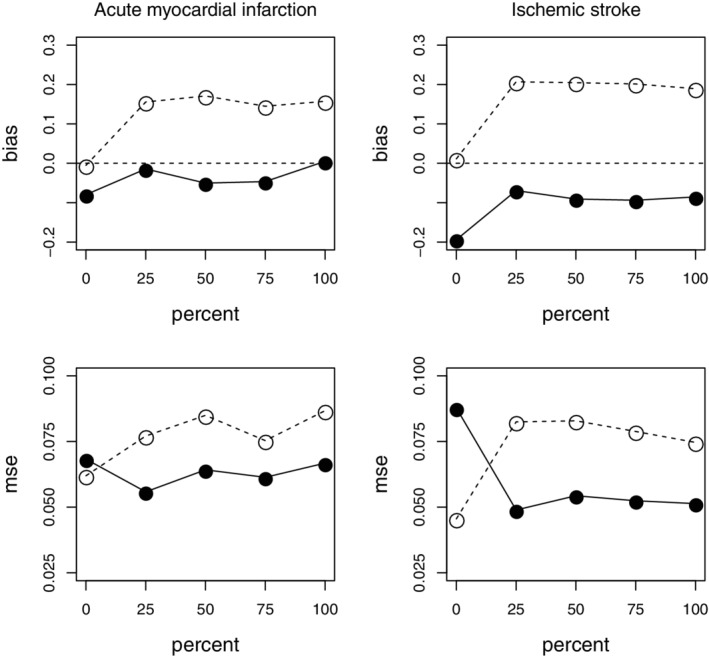
Bias (top row) and mean squared error (bottom row) of the log relative incidence of Acute myocardial infarction (AMI) and ischemic stroke for the 1‐ to 28‐day post‐coronavirus disease 2019 risk period, by percentile of deaths attributed to the event. Circles: standard self‐controlled case series (SCCS) model. Full dots: extended SCCS model. Left: AMI; right: ischemic stroke

When $p=0\%$, none of the deaths are attributed to the event. In that case, the optimal method of analysis is the standard SCCS method. This is reflected in Figure 3: for $p=0\%$, both the bias (in absolute value) and the MSE are less for the standard model compared to the extended model. As p increases, the situation reverses, lower bias (in absolute value) and MSE being obtained for the extended model. Neither the bias nor the MSE vary much for p beyond 25%: sensitivity to model assumptions is greatest for deaths occurring very soon after the event. In all such cases, the extended SCCS model is preferable to the standard model.

The Monte Carlo SEs for the MSEs were at most 0.0040 for AMI and 0.0035 for ischemic stroke. There is some residual bias, especially for the stroke data, when using the extended model. This is likely attributable to the fact that the parametric mixture model used to represent the distribution of the time from event to death may not provide a perfect fit to the data.

The simulations were repeated with the three separate risk periods 1‐7, 8‐14, and 15‐28 days. The results of these simulations are affected to some degree by the low numbers of cases in individual risk periods, resulting in larger MSEs. The results (see Appendix S1) nevertheless still favor the use of the extended model when some deaths are attributable to the event of interest.

6. DISCUSSION

6.1. Day‐zero events

The simulation results we have obtained indicate that SCCS analyses with post‐COVID‐19 risk periods that include day‐zero events, that is, events whose date of occurrence coincide with the COVID‐19 date, are likely to produce biased results. The bias is removed by the simple expedient of excluding day zero from the risk period, and including suitable pre‐COVID‐19 risk periods in the SCCS model.

The spike of day‐zero events we observed in these data is by no means unique to them. A similar spike was observed in a very different context: influenza vaccine and asthma or COPD exacerbations. ¹⁰ However, in this case, the spike was caused by taking patient histories on the day of vaccination, which were coded to that day. These retrospectively ascertained events were causally unconnected to vaccination. In the present data, this is not the case: many of the day‐zero AMI or ischemic stroke events are likely to be attributable to SARS‐CoV‐2 infection. However, it is essential to exclude them from the risk period for the purpose of obtaining an unbiased estimate of the association parameter, which in our case is the relative incidence $RI$.

On the other hand, if the purpose of the analysis were to estimate AMI and ischemic stroke burden attributable to COVID‐19, a proportion of day‐zero events should be included in the calculation. Assuming that the strength of association for the day‐zero events is at least that estimated in the immediate post‐COVID‐19 risk period, namely $RI=3.18$ for AMI and $RI=2.5$ for ischemic stroke, then a proportion of at least $(RI-1)/RI$ of these events—about 23 of the 34 AMIs and 22 of the 36 ischemic strokes observed on day zero—are attributable to SARS‐CoV‐2 infection.

Our simulation findings for the immediate post‐COVID‐19 risk period broadly match those obtained for the first post‐COVID‐19 risk period, 0 or 1 to 7 days, in the analysis of the preliminary data reported in Table 1. The same applies to the $-$3 to $-$1 or 0 days pre‐COVID‐19 risk period. However, for the $-$28 to $-$4 days pre‐COVID‐19 risk period, our simulations always indicated a relative incidence of about 0.65, contrasting with the value 1.9 obtained with the actual data in Table 1. Our explanation for this discrepancy is that our simulations did not attempt to mimic the reverse causality resulting from patients acquiring nosocomial SARS‐CoV‐2 infection after admission to hospital for ischemic stroke. This reverse causality would produce an excess risk in the pre‐COVID‐19 period. We conclude that nosocomial acquisition of SARS‐CoV‐2 infection was a factor in our study.

6.2. Handling deaths

The second issue we investigated was the appropriate method of SCCS analysis in the presence of deaths due to AMI or ischemic stroke and COVID‐19. In our data, 20% of patients with AMI and 29% of those with ischemic stroke died during the observation period: these proportions are perhaps too high to ignore, though the results of Table 2 suggest that the impact of deaths (unlike day zero events) is only moderate. We conclude from our simulations that the extended SCCS model should be used with our data, as it produces lower bias and MSE than the standard method when some deaths are due to ischemic stroke. When no deaths are due to the event of interest, the best method is the standard SCCS model.

The extended SCCS model ⁴ was derived under the assumption that the exposure does not directly increase the risk of death; this assumption is invalid in this application, as COVID‐19 can cause death. The model could, in theory, be further extended to include exposure related deaths. However, the main requirement is to obtain a reasonable empirical description of the distribution of intervals from the event to death. ⁶ It would appear that the inbuilt functions in the R package SCCS achieve this.

6.3. Implications for other studies

The bias induced by day‐zero events is likely to occur in any setting in which (a) the true exposure time is unknown, exposure being ascertained with delay, and (b) occurrence of the event of interest precipitates a test for the exposure. It is very likely present in other studies of COVID‐19 infection. A simple diagnostic is the plot shown in Figure 1: a spike of events at day zero indicates its likely presence.

This bias is not related to the SCCS method of analysis, and so is likely to apply to other study designs, notably cohort methods. Indeed, we found a corresponding discrepancy when excluding or including day zero in the post‐COVID‐19 risk period in a matched cohort model fitted to the same data. ²

In contrast, the possible bias related to event‐dependent deaths is specific to the SCCS method. It is not generally possible in advance to know the direction of this bias or its magnitude. Indeed, the curtailing of observation periods due to event‐dependent deaths does not necessarily induce any substantial bias. The presence of bias can be checked by fitting both standard and extended SCCS models and comparing the results. If substantive discrepancies are found between the two models and it is known that the event is associated with higher short‐term mortality, the extended model is likely to be preferable. Simulations based on the fitted models like those displayed in Figure 3 can be used to explore such discrepancies further. These simulations can be simplified by restricting them to the two settings where 0% and 100% of deaths are assumed to be due to the event.

Supporting information

Appendix S1. Supporting information

Fonseca‐Rodríguez O, Fors Connolly A‐M, Katsoularis I, Lindmark K, Farrington P. Avoiding bias in self‐controlled case series studies of coronavirus disease 2019. Statistics in Medicine. 2021;40(27):6197–6208. 10.1002/sim.9179

DATA AVAILABILITY STATEMENT

The licensing conditions under which the data were obtained preclude data sharing. We have therefore prepared a simulated dataset that mimics key features of the original data. This dataset, and the R code to analyze it and run the simulations described in the paper, are freely available from the SIM website.