Abstract
The preparedness of Indian states and union territories (UTs) against the COVID‐19 pandemic has been evaluated. Ten parameters related to demographic, socioeconomic, and healthcare aspects have been considered and the performances of 27 states and three UTs have been evaluated applying the Fuzzy Analytic Hierarchy Process. Opinions of medical experts have been considered to ascertain the relative importance of decision criteria as well as subcriteria. The scores of various states and UTs in each of the decision subcriteria have been calculated by using the secondary data collected from authentic sources. It is found that Kerala and Bihar are the best prepared and worst prepared states, respectively, to combat COVID‐19 pandemic. Karnataka, Goa, and Tamil Nadu have very good preparedness whereas Chhattisgarh, Jharkhand, and Bihar have very poor preparedness. Maharashtra, the most affected state in India, has average preparedness. As around 650 million people are vulnerable due to the poor and very poor preparedness of their states, the country needs to make region specific mitigation strategies to combat the COVID‐19 pandemic and the preparedness map will be helpful in that direction.
Keywords: COVID‐19, fuzzy analytic hierarchy process, India, pandemic
1. INTRODUCTION
Coronavirus disease 2019 (COVID‐19) caused by the serious acute breathing syndrome corona‐virus 2 (SARS‐CoV‐2) is arguably the most cursed pandemic in the last one century (WHO, 2020a). The disease was first detected in the city Wuhan of China in December 2019 (Huang et al., 2020). On January 30, 2020, the World Health Organization (WHO) declared an international public health emergency, and on March 11, a nationwide emergency. Till the end of July 2021, almost 197 million COVID‐19 cases have been registered, resulting in around 4.2 million deaths (John Hopkins CCSC, 2021). The viruses are mainly transmitted to humans during close contact, mainly through small droplets released to the environment while coughing, sneezing, and talking (CDC, 2020a). The droplets generally fall onto the ground or floor instead of traveling long distances through the air. When a person touches this infected surface and then rubs his or her face, he or she can also get infected. It is most contagious within the first three days after the initial infection, although it is more likely to spread from the asymptomatic individuals before symptoms start appearing (CDC, 2020a).
Fever, cough, tiredness, breathlessness, and loss of smell are the typical symptoms of this disease (Rubio‐Romero, Pardo‐Ferreira, Torrcialla‐Garcìa, & Calero‐Castro, 2020) whereas serious complications can occur in the form of acute respiratory distress syndrome (Huynh, 2020). The symptoms typically take about five days to surface, however, it can vary from two to 14 days (Velavan & Meyer, 2020). So far, no specific antiviral treatment is available for this disease through research work is going on across the world to find some remedies (Haas, 2020). It is advised to take precautions such as frequent washing of hands, covering one's mouth while coughing and sneezing, maintaining social distances and wearing face masks in public places. Monitoring and self‐isolation are recommended for people suspected of being infected. Authorities have adopted travel bans, lockdowns, and closure of offices, schools, malls, and so on to thwart the community spread of the virus. Walensky and del Rio (2020) suggested rapid contact tracing using digital technologies and quarantining within 24 hours.
India, which reported the first case on 30 January 2020, currently has the second highest number of confirmed cases after the United States. The Indian government took some strict decisions including lockdowns in four stages across the country during March–May 2020 to mitigate the spread of the disease. As of July 31st 2021, the Ministry of Health and Family Welfare, Government of India has confirmed a total of 30.78 million recoveries and 0.42 million deaths in the country. Nevertheless, the fatality rate in India is 1.34%, which is lower compared to the global fatality rate.
Several works related to patient's care and pandemic spread have already been published related to COVID‐19 (Bhatraju et al., 2020; Holshue et al., 2020; Zhou et al., 2020). Adhikari et al. (2019) have worked on the bioaerosol transport model in a hospital setting with the aid of Monte Carlo Simulation to predict the risk of infection. They found that within the same room the risk of infection is the maximum for the healthcare workers including nurses and the lowest for the visitors. Solé et al. (2020) showed how to take care of neuromuscular patients during the COVID‐19 pandemic. Hirsch et al. (2020) studied patients with acute kidney problems who were hospitalized for COVID‐19. Kushnir et al. (2020) tried to reactivate gastroenterologist practices following this disease. deBruin et al. (2020) have analyzed various methods and strategies adopted by countries to contain the spread of COVID‐19. For the COVID‐19 epidemic in Italy, Giordano et al. (2020) estimated the model parameters based on data from February 20th, 2020 (day 1) to April 5th, 2020 (day 46) and showed how the progressive restrictions and lockdown have affected the spread of the epidemic. They opined that a combination of voluntary and enforceable measures are expected to give the best results. It has now become quite obvious that the disease is going to stay for some time before some effective medical intervention is discovered. Therefore, it is important to evaluate the preparedness of countries and states to combat against this pandemic so that effective strategies can be formulated by the government.
With 1.35 billion population, India is the second most populated country in the world. According to size, it is the 7th largest country. It has 28 states and 8 union territories (UTs) which vary widely in various demographic, socioeconomic, and healthcare parameters. Therefore, the preparedness of Indian states and UTs to counter the COVID‐19 pandemic is expected to be different. However, evaluation of this preparedness is not an easy task as multiple criteria having different weights or importance are involved. Some of these criteria may have a beneficial effect in containing the pandemic whereas some others may have a negative effect (Sangiorgio & Parisi, 2020). Flanagan, Gregory, Hallisey, Heitgerd, and Lewis (2011) proposed a percentile based ranking approach to determine social vulnerability index against disaster. The authors used simple sum approach to combine the percentile ranking in various criteria. However, the weightage of various criteria in determining the vulnerability of states to any pandemic is different. Therefore, multiple criteria decision making (MCDM) should be invoked to solve such a decision‐making problem. Among the MCDM methods, the analytic hierarchy process (AHP) is probably the most popular one as it can handle subjective as well as objective criteria (Saaty, 1983, 1986). However, the original AHP can only handle the use of crisp numbers. Therefore, incorporation of fuzzy set theory and fuzzy numbers in AHP is required as the expert's opinion may have vagueness and ambiguity. In recent years, fuzzy AHP has been used to solve various decision‐making problems related to the internet of things (Ly, Lai, Hsu, & Shih, 2018), financial distress in aviation companies (Mahtania & Garg, 2018), site selection (Karasan, Ilbahar, & Kahraman, 2019), and supply chain risk quantification (Majumdar, Sinha, Shaw, & Mathiyazhagan, 2020). Besides, some researchers have modified the AHP by using Gini coefficient and other approaches to overcome the drawbacks of parent AHP (Choudhury, Howladar, Majumder, & Saha, 2019; Choudhury, Saha, & Majumder, 2020). However, our literature search shows that there is no reported research using MCDM approaches to evaluate the preparedness of a country or its states against a pandemic.
The main objective of this research is to evaluate the preparedness of Indian states and UTs by considering important demographic, socioeconomic and healthcare parameters (subcriteria) and performance scores of each state and UT in each of these subcriteria. The research makes an attempt to group the Indian states and UTs into few clusters based on their preparedness. The results reveal that there exists stark contrast in terms of preparedness in various parts of India. Therefore, the government can develop and implement zone wise pandemic mitigation strategy rather than adopting a uniform strategy across the whole country.
2. BASIC DEFINITION AND TERMINOLOGY
The following definitions have been recalled and used in this study.
2.1. Fuzzy Set Theory
The crisp set theory was extended by Zadeh (1996) to the fuzzy set theory. In an ambiguous and vague scenario, fuzzy set theory can deal with real‐life problems (Viadiu, Fa, & Saizarbitoria, 2006). Fuzzy set theory has been characterized by a membership function which maps from 0 to 1. Till now, many researchers have improved the concept of fuzzy methods to use in several fields e.g., optimization problems, multiobjective problems, and multicriteria decision‐making problems (Bajpai, Sachdeva, & Gupta, 2010; Chen & Sanguansat, 2011; Wang, Chen, Shi, & Chen, 2011).
2.2. Definition 1: Fuzzy Sets
Let X be a collection of objects denoted by . A fuzzy set in X is a set of ordered pairs defined as
| (1) |
where, is the membership function of in .
2.3. Definition 2: Triangular Fuzzy Number
A fuzzy number is called Triangular Fuzzy Number (TFN) if its membership function is defined as:
| (2) |
where, is the most probable value, and are the smallest and largest value. The basic operations of TFN are shown in Table I.
Table I.
The Basic Operations Between two Triangular Fuzzy Numbers
| Operation | Explanation | |
|---|---|---|
| Addition |
|
|
| Subtraction |
|
|
| Multiplication |
|
|
| Division |
|
|
| Inverse |
|
where, represent two TFN with lower, modal, and upper values.
2.4. Analytic Hierarchy Process
The Analytic Hierarchy Process (AHP) was developed by Saaty (1983, 1986). It is one of the most widely used methods of decision making when several qualitative and quantitative criteria and alternatives are involved. In AHP, a decision‐making problem is first broken down into many subproblems by arranging them in a hierarchy which includes a number of criteria and subcriteria at respective levels. The top layer of the hierarchy reflects the goal or objective of the problem and the intermediate levels represent the criteria and subcriteria related to the element at the next higher level. The alternatives of the decision problem are placed at the lowest level of the hierarchy. After formulating the problem hierarchy, a team of experts prepare the pairwise comparison matrix of criteria with respect to the objective and pairwise comparison matrices of subcriteria with respect to the corresponding criteria. The perception of the experts about the dominance of one element (criterion or subcriterion) over the other is converted by using Saaty's scale given in Table II. Thereafter, Eigen vectors of these matrices are determined to elicit weights of criteria and subcriteria. The scores of alternatives with respect to criteria or subcriteria are then derived either by using actual objective data or by using pairwise comparison for subjective data. Finally, the weights and scores are synthesized to elicit the priority or ranking of alternatives.
Table II.
Pairwise Comparison Used in AHP (Saaty, 1983)
| Rating | Description |
|---|---|
| 1 | Equal importance |
| 3 | Moderate importance |
| 5 | Strong importance |
| 7 | Very strong importance |
| 9 | Extreme importance |
2.5. Fuzzy‐AHP
One of the drawbacks of classical AHP is that the vagueness and ambiguity of decisionmakers in case of priority of criteria of alternatives cannot be handled. To overcome this drawback, fuzzy AHP was developed by integrating the fuzzy theory with AHP (van Laarhoven & Pedrycz, 1983). Various forms of fuzzy numbers, namely triangular, trapezoidal, sigmoidal, and Gaussian can be used to represent the vagueness. TFN is a special case of trapezoidal fuzzy number. The former is used in conservative cases as full membership is given only at a specific value of universe of discourse whereas the latter is used in tolerant cases where full membership is given for large regions of universe of discourse (Berkan & Trubatch, 1997). In this research, TFNs have been used as they are easy to comprehend and are computationally simple. Table III shows the linguistic judgements and corresponding TFN. Fuzzy AHP also has some variants. Chang (1996) proposed the extent analysis approach of fuzzy AHP. However, it is computationally more complicated than the approach that has been used in this work following the work of Triantaphyllou and Lin (1996).
Table III.
Linguistic Expressions and Equivalent Triangular Fuzzy Numbers (Wang, Liu, Fan, & Feng, 2009)
| Linguistic judgment | Fuzzy number | |
|---|---|---|
| Approximately equal |
|
|
| Approximately x times more significant |
|
|
| Approximately x times less significant |
|
|
| Between y and z times more significant |
|
|
| Between y and z times less significant |
|
3. METHODOLOGY
This study has been conducted in four stages. The flowchart of the steps involved is depicted in Fig. 1.
Fig 1.
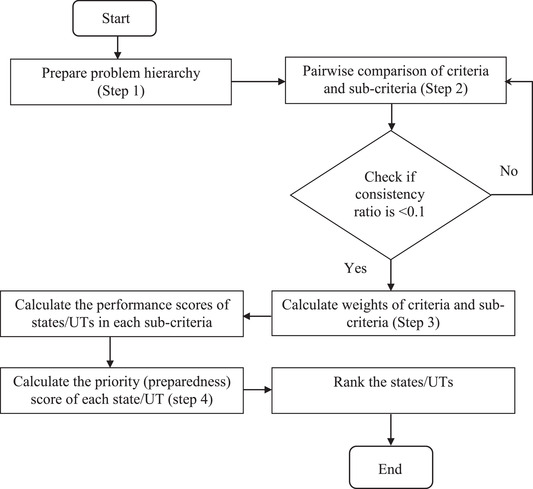
Flow chart of fuzzy AHP methodology
First, a conceptual hierarchical model comprising of all the criteria and subcriteria relevant to the objective of the study was formulated as depicted in Fig. 2. The decision criteria, namely, demographic, socioeconomic, and healthcare were placed at level 2 of the hierarchy. Level 3 of the hierarchy contained 10 sub‐criteria, divided into three, three, and four, respectively for demographic, socioeconomic, and healthcare criteria. At the lowest level of the hierarchy, were all the states and UTs to be ranked based on their priority score of preparedness against COVID‐19. Table IV presents a brief description of decision criteria and subcriteria.
Fig 2.
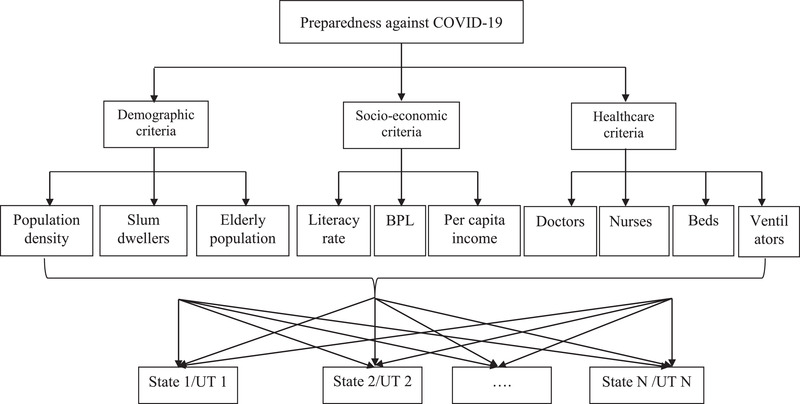
Hierarchical model
Table IV.
Decision Criteria and Subcriteria
| Criteria | Subcriteria | Description |
|---|---|---|
| Demographic | Population density (km−2) | Population per square km |
| Slum‐dwellers (%) | Percentage of urban population living in slums | |
| Elderly population (%) | Percentage of people over 60 years of age | |
| Socioeconomic | Literacy rate (%) | Percentage of people who are literate |
| Poverty level (%) | Percentage of people below the poverty level | |
| Per capita income | Per capita income of each state/UT | |
| Medical | Doctors/1000 people | Total number of registered doctors available in 2020 |
| Nurses/1000 people | Total number of registered nurses available in 2020 | |
| Beds/105 people | Total number of hospital beds available in 2020 | |
| Ventilators/105 people | Total number of ventilators available in 2020 |
In the second stage, pairwise comparison was made for criteria and subcriteria. Fuzzy numbers were used to compare the criteria as well as subcriteria based on their importance with respect to the element at the next higher level. In the third stage, weights of criteria and subcriteria were determined. In the fourth stage, weights of subcriteria and scores of all the states and UTs in each of these subcriteria were synthesized to get the priority values. Finally, the states were ranked according to the descending values of the priority and a preparedness map was delineated.
After preparing the problem hierarchy, the fuzzy pairwise comparison matrix of criteria with respect to the objective of the problem was formulated as shown in (Equation 3).
| (3) |
where, represents the dominance of the criterion in the row in terms of TFN with respect to the criterion in the column.
As the formulation of the pair‐wise comparison matrix requires domain knowledge of pandemic mitigation, telephonic discussions were made with the doctors of a COVID‐19 hospital located in the state of West Bengal, India. The perception of experts was converted to TFN using the scale given in Table II. Afterward, the geometric mean of each row () of the pairwise comparison matrix was calculated as shown in Equation (4).
| (4) |
Furthermore, normalization was done to obtain the fuzzy weights of criteria as shown in Equation (5).
| (5) |
In the next step, pairwise comparison was done among sub‐criteria (of a criteria) to elicit local fuzzy weights of subcriteria with respect to corresponding criteria. Then, the global fuzzy weight of a sub‐criterion was determined by multiplying the weight of a criterion and local weight of a subcriterion with respect to the criterion.
The data of Indian states and UTs in selected nine subcriteria were collected from authentic government sources. Andhra Pradesh and Telangana, two separate states at present, were considered as a single state as only unified data were available. Similarly, Jammu and Ladakh, two UTs at present, were considered as Jammu and Kashmir state. Table V shows the data used in this research. As the units are different for various subcriteria, it is important to normalize the data so that the effect of scale is neutralized. Sub‐criteria where higher values are desirable (literacy rate, doctors/1000 persons, etc.), were normalized using Equation (6). On the other hand, cost criteria (population density, below poverty line %, etc.) were normalized using Equation (7).
| (6) |
| (7) |
Table V.
Data Collected for States and UTs
| Demographic | Socioeconomic | Healthcare | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Name of state/ UT | Slum popu. (%) | Pop density (km−2) | Elderly population (%) | Literacy rate (%) | Poverty level (%) | Percapita income | Doctors (Per 1000 persons) | Nurses (per 1000 persons) | No. of beds (per lakhs) | Ventilators (per lakhs) | |
| A & N Islands | 9.88 | 46 | 6.7 | 86.6 | 1.0 | 1,59,664 | 0.367 | 1.080 | 431.3 | 10.67 | |
| Andhra Pradesh | 36.10 | 308 | 9.8 | 67.0 | 9.2 | 151173 | 1.047 | 2.811 | 98.5 | 2.46 | |
| Arunachal | 4.90 | 17 | 4.6 | 65.4 | 34.7 | 139588 | 0.646 | 0.722 | 201.8 | 5.08 | |
| Assam | 4.48 | 398 | 6.7 | 72.2 | 32.0 | 82078 | 0.722 | 0.676 | 77.5 | 1.94 | |
| Bihar | 10.53 | 1106 | 7.4 | 61.8 | 33.7 | 43822 | 0.385 | 0.091 | 29.7 | 0.74 | |
| Chhattisgarh | 31.98 | 189 | 7.8 | 70.3 | 39.9 | 96887 | 0.271 | 0.512 | 68.4 | 1.71 | |
| Delhi | 10.91 | 11320 | 6.8 | 86.2 | 9.9 | 365529 | 0.963 | 3.665 | 234.9 | 5.87 | |
| Goa | 2.80 | 394 | 11.2 | 88.7 | 5.1 | 458304 | 2.405 | – | 327.4 | 8.21 | |
| Gujarat | 6.53 | 308 | 7.9 | 78.0 | 16.6 | 197447 | 0.893 | 1.796 | 107.4 | 2.69 | |
| Haryana | 18.8 | 573 | 8.7 | 75.6 | 11.2 | 236147 | 0.226 | 1.121 | 142.8 | 3.57 | |
| Himachal Pradesh | 8.90 | 123 | 10.2 | 82.8 | 8.1 | 179188 | 0.413 | 3.034 | 232.5 | 5.81 | |
| Jammu & Kashmir | 19.28 | 124 | 7.4 | 67.2 | 10.3 | 91882 | 1.146 | 0.320 | 64.0 | 1.60 | |
| Jharkhand | 4.70 | 414 | 7.1 | 66.4 | 37.0 | 76019 | 0.155 | 0.101 | 80.5 | 2.01 | |
| Karnataka | 13.93 | 319 | 7.7 | 75.4 | 20.9 | 210887 | 1.718 | 3.797 | 429.7 | 10.74 | |
| Kerala | 1.27 | 860 | 12.6 | 94.0 | 7.1 | 204105 | 1.654 | 7.370 | 297.1 | 7.43 | |
| Madhya Pradesh | 28.35 | 236 | 7.9 | 69.3 | 31.6 | 90998 | 0.473 | 1.636 | 89.4 | 2.24 | |
| Maharashtra | 23.32 | 365 | 9.9 | 82.3 | 17.4 | 191736 | 1.367 | 1.074 | 206.4 | 5.16 | |
| Manipur | – | 128 | 7.0 | 76.9 | 37.0 | 69978 | 0.476 | 2.798 | 63.9 | 1.61 | |
| Meghalaya | 9.64 | 132 | 4.7 | 74.4 | 11.9 | 89024 | 0.202 | 1.576 | 180.8 | 4.52 | |
| Mizoram | 13.74 | 52 | 6.3 | 91.3 | 20.4 | 168626 | 0.133 | 3.405 | 249.6 | 6.20 | |
| Nagaland | – | 119 | 5.2 | 79.6 | 18.9 | 116882 | 0.422 | 0.789 | 134.8 | 3.37 | |
| Odisha | 22.28 | 270 | 9.5 | 72.9 | 32.6 | 95164 | 0.517 | 1.804 | 61.2 | 1.53 | |
| Punjab | 14.04 | 551 | 10.3 | 75.8 | 8.3 | 154996 | 1.613 | 2.768 | 220.2 | 5.51 | |
| Rajasthan | 12.13 | 200 | 7.5 | 66.1 | 14.7 | 110606 | 0.592 | 2.922 | 136.0 | 3.40 | |
| Sikkim | 20.43 | 86 | 6.7 | 81.4 | 8.2 | 357643 | 0.480 | 1.573 | 325.3 | 8.17 | |
| Tamil Nadu | 16.61 | 555 | 10.4 | 80.1 | 11.3 | 193750 | 1.753 | 3.644 | 215.5 | 5.39 | |
| Tripura | 14.54 | 350 | 7.9 | 87.2 | 14.0 | 113102 | 0.417 | 0.785 | 129.6 | 3.25 | |
| Uttar Pradesh | 14.02 | 829 | 7.7 | 67.7 | 29.4 | 66512 | 0.358 | 0.313 | 140.8 | 3.52 | |
| Uttrakhand | 15.99 | 189 | 8.9 | 78.8 | 11.3 | 198738 | 0.706 | 0.151 | 238.4 | 5.96 | |
| West Bengal | 22.06 | 1028 | 8.5 | 76.3 | 20.0 | 109491 | 0.734 | 0.666 | 124.5 | 3.11 | |
Source: National Health profile, 2018; NITI Aayog Health index 2019; and Census data 2011.
where, , and are the normalized score, maximum score, and minimum score of states and UTs in a subcriteria.
4. RESULTS AND DISCUSSION
The priority scores obtained from the fuzzy AHP indicate the preparedness of states and UTs against the pandemic. Table VI presents the first step of fuzzy AHP where demographic, socioeconomic, and healthcare criteria are compared with each other using TFN. Healthcare criteria are the most important followed by socioeconomic ones to combat a pandemic like COVID‐19. From the normalized fuzzy weights shown in Table VI, it is noted that the modal value of the weight of healthcare criteria is 0.645 implying that it is contributing around 65% to the objective whereas socioeconomic criteria, with a modal value of the weight of 0.231, is contributing around 23%. Tables VII, VIII, and IX show the pair‐wise comparison of subcriteria with respect to demographic, socioeconomic, and healthcare criteria, respectively. The last column of these tables shows the local weights of sub‐criteria in terms of TFN with respect to the corresponding criteria. Table X shows the global weights of all subcriteria in terms of TFN which have been defuzzified using Kaufman and Gupta's (1988) method. The last column of Table X shows the final weights of subcriteria after normalization.
Table VI.
Pairwise Comparison Matrix and Weight of Criteria
| Criteria | Demographic | Socioeconomic | Medical | Normalized fuzzy weight | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Demographic | 1.00 | 1.00 | 1.00 | 0.33 | 0.50 | 1.00 | 0.17 | 0.20 | 0.25 | 0.083 | 0.124 | 0.211 |
| Socioeconomic | 1.00 | 2.00 | 3.00 | 1.00 | 1.00 | 1.00 | 0.25 | 0.33 | 0.50 | 0.137 | 0.231 | 0.381 |
| Medical | 4.00 | 5.00 | 6.00 | 2.00 | 3.00 | 4.00 | 1.00 | 1.00 | 1.00 | 0.429 | 0.645 | 0.950 |
Table VII.
Pairwise Comparison Matrix and Local Weights Demographic Subcriteria
| Socioeconomic | Population density | Slumdwellers | Elderly population | Normalized fuzzy weight | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Population density | 1.00 | 1.00 | 1.00 | 0.33 | 0.50 | 1.00 | 0.25 | 0.33 | 0.50 | 0.097 | 0.164 | 0.332 |
| Slum dwellers | 1.00 | 2.00 | 3.00 | 1.00 | 1.00 | 1.00 | 0.33 | 0.50 | 1.00 | 0.153 | 0.297 | 0.603 |
| Elderly population | 2.00 | 3.00 | 4.00 | 1.00 | 2.00 | 3.00 | 1.00 | 1.00 | 1.00 | 0.278 | 0.539 | 0.957 |
Table VIII.
Pairwise Comparison Matrix and local Weights of Socioeconomic subcriteria
| Socioeconomic | Literacy rate | Poverty level | Per capita income | Normalized fuzzy weight | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Literacy rate | 1.00 | 1.00 | 1.00 | 0.50 | 1.00 | 2.00 | 2.00 | 3.00 | 4.00 | 0.217 | 0.428 | 0.827 |
| Poverty level | 0.50 | 1.00 | 2.00 | 1.00 | 1.00 | 1.00 | 2.00 | 3.00 | 4.00 | 0.217 | 0.428 | 0.827 |
| Per capita income | 0.25 | 0.33 | 0.50 | 0.25 | 0.33 | 0.50 | 1.00 | 1.00 | 1.00 | 0.087 | 0.144 | 0.264 |
Table IX.
Pairwise Comparison Matrix and Local Weights of Medical Subcriteria
| Medical | Doctors | Nurses | Beds | Ventilators | Normalized fuzzy weight | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Doctors | 1.00 | 1.00 | 1.00 | 1.00 | 1.50 | 2.00 | 2.00 | 3.00 | 4.00 | 5.00 | 6.00 | 7.00 | 0.279 | 0.451 | 0.704 |
| Nurses | 0.50 | 0.67 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 2.00 | 3.00 | 4.00 | 5.00 | 6.00 | 0.186 | 0.318 | 0.530 |
| Beds | 0.25 | 0.33 | 0.50 | 0.33 | 0.50 | 1.00 | 1.00 | 1.00 | 1.00 | 2.00 | 3.00 | 4.00 | 0.100 | 0.166 | 0.306 |
| Ventilators | 0.14 | 0.17 | 0.20 | 0.17 | 0.20 | 0.25 | 0.25 | 0.33 | 0.50 | 1.00 | 1.00 | 1.00 | 0.044 | 0.064 | 0.102 |
Table X.
Global Weights of Subcriteria
| Subcriteria | Fuzzy weight | Defuzzified weight | Normalized defuzzified weight | ||
|---|---|---|---|---|---|
| Population density | 0.008 | 0.020 | 0.070 | 0.030 | 0.023 |
| Slum dwellers | 0.013 | 0.037 | 0.127 | 0.053 | 0.042 |
| Elderly population | 0.023 | 0.067 | 0.202 | 0.090 | 0.071 |
| Literacy rate | 0.030 | 0.099 | 0.315 | 0.136 | 0.107 |
| Poverty level | 0.030 | 0.099 | 0.315 | 0.136 | 0.107 |
| Per capita income | 0.012 | 0.033 | 0.100 | 0.045 | 0.035 |
| Doctors | 0.120 | 0.291 | 0.669 | 0.343 | 0.271 |
| Nurses | 0.080 | 0.205 | 0.504 | 0.249 | 0.196 |
| Beds | 0.043 | 0.107 | 0.291 | 0.137 | 0.108 |
| Ventilators | 0.019 | 0.041 | 0.097 | 0.050 | 0.039 |
It is observed from Table X that the number of doctors per 1000 persons is the most important subcriterion followed by the number of nurses per 1000 persons. Table XI presents the preparedness scores of all states and UTs in descending order. Kerala has the highest preparedness score (0.690) followed by Karnataka (0.596). It is noteworthy that Kerala is the only state to acquire a preparedness score of more than 0.6. Our results are in agreement with the fact that Kerala has emerged out to be the model state in India to contain the spread of COVID‐19 though the first case was reported from this state (Arentz et al., 2020). At the end of July 2021, Kerala has a case fatality (ratio of number of deaths to number of infections) of 0.6% which is much lower than the Indian national average (1.34%). Goa and Tamil Nadu are the other two states which have a preparedness score of more than 0.5 implying that they are also very well prepared. Andaman and Nikobar Islands, Punjab, and Delhi have good preparedness with score higher than 0.4. On the other hand, Chhattisgarh, Jharkhand, and Bihar have score ≤ 0.2 implying very poor preparedness. The number of doctors per 1000 persons in these three states is 0.271, 0.155, and 0.385, respectively, which is much lower than the WHO's guideline of 1 doctor per 1000 persons. Moreover, Bihar has the lowest numbers of nurses per 1000 persons (0.091) and lowest number of hospital beds per lakhs of population (29.7). Besides, there are 11 other states and UTs (Meghalaya, Jammu and Kashmir, Manipur, Nagaland, West Bengal, Assam, Tripura, Madhya Pradesh, Haryana, Odisha, and Uttar Pradesh) which have poor preparedness (0.2 < score ≤0.3). Together, these 14 states and UTs have a population of around 650 million accounting for almost half of the entire Indian population. This study reveals that a huge population is under the pandemic risk as the preparedness of these states is either poor or very poor. Therefore, it important for the Indian government to make region‐specific pandemic mitigation strategy. Fig. 3 depicts the preparedness map by grouping the states and UTs in five clusters: very good (score: >0.5; green), good (0.4 <score ≤ 0.5; yellow), average (0.3 <score ≤ 0.4; pink); poor (0.2 <score ≤ 0.3; orange) and very poor (score ≤ 0.2; red). It is observed that the southern part of India is better placed with preparedness level of average and above. However, the central and eastern part of India have poor or very poor preparedness, thus requiring immediate attention. According to British medical journal Lancet, pandemic vulnerability is dynamic as a group of people may not be vulnerable at the beginning. However, they may become vulnerable with time as the pandemic spreads (The Lancet, 2020). The experts suggested that it would be very difficult to increase the number of doctors or nurses overnight. However, trained medical volunteers should be recruited to monitor patients with mild and moderate symptoms locally and only the patients with severe symptoms should be hospitalized as beds are bound to be limited. They expressed that most of the critical patients have suffered from micro‐vascular clots in the lungs and other parts of the body. Therefore, the oxygen saturation level in the body should be monitored after every two hours as the conditions of patients deteriorate very quickly.
Table XI.
Preparedness Score of Various States and UTs
| State/UT | Score | State/UT | Score |
|---|---|---|---|
| Kerala | 0.69 | Uttrakhand | 0.32 |
| Karnataka | 0.60 | Meghalaya | 0.30 |
| Goa | 0.59 | Jammu & Kashmir | 0.30 |
| Tamil Nadu | 0.52 | Manipur | 0.30 |
| A & N Islands | 0.50 | Nagaland | 0.29 |
| Punjab | 0.48 | West Bengal | 0.28 |
| Delhi | 0.48 | Assam | 0.28 |
| Maharashtra | 0.40 | Tripura | 0.27 |
| Sikkim | 0.40 | Madhya Pradesh | 0.26 |
| Mizoram | 0.38 | Haryana | 0.26 |
| Himachal Pradesh | 0.37 | Odisha | 0.26 |
| Andhra Pradesh | 0.36 | Uttar Pradesh | 0.23 |
| Arunachal | 0.35 | Chhattisgarh | 0.20 |
| Gujarat | 0.35 | Jharkhand | 0.19 |
| Rajasthan | 0.33 | Bihar | 0.18 |
Fig 3.
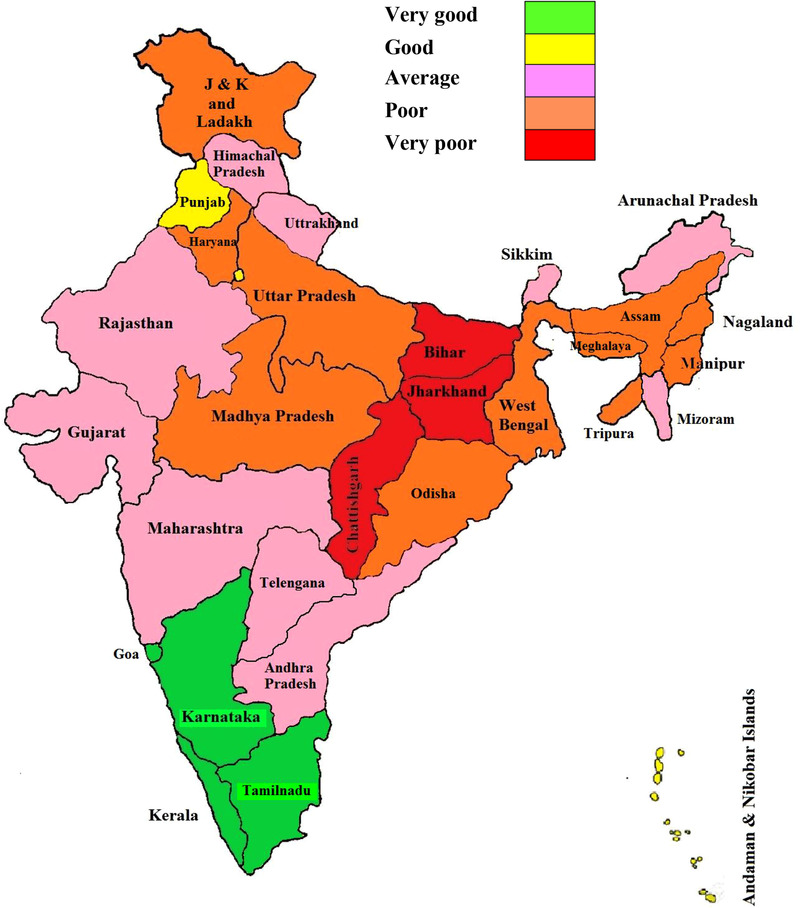
Preparedness Map of Indian States and UTs
5. CONCLUSIONS
The preparedness of Indian states and UTs against the COVID‐19 pandemic has been evaluated using the fuzzy AHP method of multi‐criteria decision making. Demographic, socioeconomic, and healthcare‐related criteria and subcriteria have been considered. Weights or importance of these decision criteria and subcriteria were determined by converting the perception of medical experts using triangular fuzzy numbers. It is found that the preparedness of the states and UTs, represented by preparedness score, varies widely. Kerala, Karnataka, Goa, and Tamil Nadu are the states which have very good preparedness against the pandemic. The southern states, in general, have average or better preparedness. On the other hand, Bihar Jharkhand and Chhattisgarh have very poor preparedness. Besides, a large number of states in the central and eastern part of India have poor preparedness. A population of around 650 million is under the risk of COVID‐19 as the preparedness of states is either poor or very poor.
Therefore, fuzzy AHP presents a sound and logical decision‐making platform based on which policymakers can formulate pandemic mitigation strategies. As India is on the cusp of third wave, this study will be helpful to devise region specific strategy to combat against the COVID‐19 pandemic. As an extension of this study, district wise mapping can be done for the states having poor and very poor preparedness.
REFERENCES
- Adhikari, U. , Chabrelie, A. , Weir, M. , Boehnke, K. , McKenzie, E. , Ikner, L. , & Mitchell, J. (2019). A case study evaluating the risk of infection from Middle Eastern Respiratory Syndrome Coronavirus (MERS‐CoV) in a hospital setting through bioaerosols. Risk Analysis, 39(12), 2608–2624. 10.1111/risa.13389 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Arentz, M. , Yim, E. , Klaff, L. , Lokhandwala, S. , Riedo, F. X. , Chong, M. , & Lee, M. (2020). Characteristics and outcomes of 21 critically ill patients with COVID‐19 in Washington State. Journal of the American Medical Association, 323(16), 1612–1614. 10.1001/jama.2020.4326 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bajpai, S. , Sachdeva, A. , & Gupta, J. P. (2010). Security risk assessment: Applying the concepts of fuzzy logic. Journal of Hazardous Materials, 173(1‐3), 258–264. 10.1016/j.jhazmat.2009.08.078 [DOI] [PubMed] [Google Scholar]
- Berkan, R. C. , & Trubatch, S. L. (1997). Fuzzy systems design principles: Building fuzzy if‐then rule bases (pp. 22–131). New York: IEEE Press. [Google Scholar]
- Bhatraju, P. K. , Ghassemieh, B. J. , Nichols, M. , Kim, R. , Jerome, K. R. , Nalla, A. K. , & Mikacenic, C. (2020). Covid‐19 in critically ill patients in the Seattle region‐ Case series. The New England Journal of Medicine, 382(21), 2012–2022. 10.1056/NEJMoa2004500 [DOI] [PMC free article] [PubMed] [Google Scholar]
- CDC . (2020a). How COVID‐19 Spreads | Coronavirus Disease 2019 (COVID‐19) | Centers for Disease Control and Prevention. Retrieved from: https://www.cdc.gov/coronavirus/2019‐ncov/prevent‐getting‐sick/how‐covid‐spreads.html
- Chang, D.‐Y. (1996). Applications of the extent analysis method on fuzzy AHP. European Journal of Operational Research, 95(3), 649–655. 10.1016/0377-2217(95)00300-2 [DOI] [Google Scholar]
- Chen, S.‐M. , & Sanguansat, K. (2011). Analyzing fuzzy risk based on a new fuzzy ranking method between generalized fuzzy numbers. Expert Systems with Applications, 38(3), 2163–2171. 10.1016/j.eswa.2010.08.002 [DOI] [Google Scholar]
- Choudhury, S. , Howladar, P. , Majumder, M. , & Saha, A. K. (2019). Application of novel MCDM for location selection of surface water treatment plant. IEEE Transactions on Engineering Management, 1–13. 10.1109/TEM.2019.2938907 [DOI] [Google Scholar]
- Choudhury, S. , Saha, A. K. , & Majumder, M. (2020). Optimal location selection for installation of surface water treatment plant by Gini coefficient‐based analytical hierarchy process. Environment, Development and Sustainability, 22, 4073–4099. 10.1007/s10668-019-00373-w [DOI] [Google Scholar]
- deBruin, Y. B. , Lequarre, A.‐S. , McCourt, J. , Clevestig, P. , Pigazzani, F. , Jeddi, M. Z. , … Goulart, M. (2020). Initial impacts of global risk mitigation measures taken during the combatting of the COVID‐19 pandemic. Safety Science, 128, 104773. 10.1016/j.ssci.2020.104773 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Flanagan, B. E. , Gregory, E. W. , Hallisey, E. J. , Heitgerd, J. L. , & Lewis, B. (2011). A social vulnerability index for disaster management. Journal of Homeland Security and Emergency Management, 8(1). Article 3. 10.2202/1547-7355.179 [DOI] [Google Scholar]
- Giordano, G. , Blanchini, F. , Bruno, R. , Colaneri, P. , Di Filippo, A. , Di Matteo, A. , & Colaneri, M. (2020). Modelling the COVID‐19 epidemic and implementation of population‐wide interventions in Italy. Nature Medicine, 26, 855–860. 10.1038/s41591-020-0883-7 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haas, C. (2020). Coronavirus and risk analysis. Risk Analysis, 40(4), 660–661. 10.1111/risa.13481 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hirsch, J. S. , Ng, J. H. , Ross, D. W. , Sharma, P. , Shah, H. H. , Barnett, R. L. , … & Jhaveri, K. D. (2020). Acute kidney injury in patients hospitalized with COVID‐19. Kidney International, 98(1), 209–218. 10.1016/j.kint.2020.05.006s [DOI] [PMC free article] [PubMed] [Google Scholar]
- Holshue, M. L. , DeBolt, C. , Lindquist, S. , Lofy, K. H. , Wiesman, J. , Bruce, H. , … Diaz, G. (2020). First case of 2019 novel coronavirus in the United States. The New England Journal of Medicine, 382(10), 929–936. 10.1056/NEJMoa2001191 [DOI] [PMC free article] [PubMed] [Google Scholar]
- John Hopkins CCSE . (2021). COVID‐19 Dashboard by the Center for Systems Science and Engineering (CSSE) at Johns Hopkins University (JHU). Retrieved from: https://coronavirus.jhu.edu/map.html
- Huynh, T. L. D. (2020). Does culture matter social distancing under the COVID‐19 pandemic? Safety Science, 130, 104872. 10.1016/j.ssci.2020.104872 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang, C. , Wang, Y. , Li, X. , Ren, L. , Zhao, J. , Hu, Y. , … Cao, B. (2020). Clinical features of patients infected with 2019 novel coronavirus in Wuhan, China. The Lancet, 395(10223), 497–506. 10.1016/S0140-6736(20)30183-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kaufmann, A. , & Gupta, M. M. (1988). Fuzzy mathematical models in engineering and management science. Amsterdam, The Netherlands: Elsevier Science. [Google Scholar]
- Karasan, A. , Ilbahar, E. , & Kahraman, C. (2019). A novel pythagorean fuzzy AHP and its application to landfill site selection problem. Soft Computing, 23(21), 10953–10968. 10.1007/s00500-018-3649-0 [DOI] [Google Scholar]
- Kushnir, V. M. , Berzin, T. M. , Elmunzer, B. J. , Mendelsohn, R. B. , Patel, V. , Pawa, S. , … Keswani, R. N. (2020). Plans to reactivate gastroenterology practices following the COVID‐19 pandemic: A survey of North American centers. Clinical Gastroenterology and Hepatology, 18(10), 2287–2294. 10.1016/j.cgh.2020.05.030 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ly, P. T. M. , Lai, W.‐H. , Hsu, C.‐W. , & Shih, F.‐Y. (2018). Fuzzy AHP analysis of Internet of Things (IoT) in enterprises. Technological Forecasting and Social Change, 136, 1–13. 10.1016/j.techfore.2018.08.016 [DOI] [Google Scholar]
- Majumdar, A. , Sinha, S. K. , Shaw, M. , & Mathiyazhagan, K. (2020). Analysing the vulnerability of green clothing supply chains in South and Southeast Asia using fuzzy analytic hierarchy process. International Journal of Production Research, 59(3), 752–771. 10.1080/00207543.2019.1708988 [DOI] [Google Scholar]
- Mahtania, U. S. , & Garg, C. P. (2018). An analysis of key factors of financial distress in airline companies in India using fuzzy AHP framework, Transportation Research Part A: Policy and Practice, 117, 87–102. 10.1016/j.tra.2018.08.016 [DOI] [Google Scholar]
- Rubio‐Romero, J. C. , Pardo‐Ferreira, M. D. C. , Torrecilla‐García, J. A. , & Calero‐Castro, S. (2020). Disposable masks: Disinfection and sterilization for reuse, and non‐certified manufacturing, in the face of shortages during the COVID‐19 pandemic. Safety Science, 129. 10.1016/j.ssci.2020.104830 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saaty, T. L. (1983). Priority setting in complex problems. IEEE Transactions on Engineering Management, 30(3), 140–155. 10.1109/TEM.1983.6448606 [DOI] [Google Scholar]
- Saaty, T. L. (1986). Axiomatic foundation of the Analytic Hierarchy Process. Management Science, 32(7), 841–855. 10.1287/mnsc.32.7.841 [DOI] [Google Scholar]
- Sangiorgio, V. , & Parisi, F. (2020). A multicriteria approach for risk assessment of Covid‐19 in urban district lockdown. Safety Science, 130, 104862. 10.1016/j.ssci.2020.104862 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Solé, G. , Salort‐Campana, E. , Pereon, Y. , Stojkovic, T. , Wahbi, K. , Cintas, P. , … Attarian, S. (2020). Guidance for the care of neuromuscular patients during the COVID‐19 pandemic outbreak from the French rare health care for neuromuscular diseases network. Revue Neurologique, 176(6), 507–515. 10.1016/j.neurol.2020.04.004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- The Lancet (2020). Redefining vulnerability in the era of COVID‐19. Lancet, 395(10230), 1089. 10.1016/S0140-6736(20)30757-1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Triantaphyllou, E. , & Lin, C.‐T. (1996). Development and evaluation of five fuzzy multiattribute decision‐making methods. International Journal of Approximate Reasoning, 14(4), 281–310. 10.1016/0888-613X(95)00119-2 [DOI] [Google Scholar]
- van Laarhoven, P. J. M. , & Pedrycz, W. (1983). A fuzzy extension of Saaty's priority theory. Fuzzy Sets and Systems, 11(1–3), 229–241. 10.1016/S0165-0114(83)80082-7 [DOI] [Google Scholar]
- Viadiu, F. M. , Fa, M. C. , & Saizarbitoria, I. H. (2006). ISO 9000 and ISO 14000 standards: An international diffusion model. International Journal of Operations & Production Management, 26(2), 141–165. 10.1108/01443570610641648 [DOI] [Google Scholar]
- Velavan, T. P. , & Meyer, C. G. (2020). The COVID‐19 epidemic. Tropical Medicine &International Health, 25(3), 278–280. 10.1111/tmi.13383 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang, Z.‐X. , Liu, Y.‐J. , Fan, Z.‐P. , & Feng, B. (2009). Ranking L–R fuzzy number based on deviation degree. Information Sciences, 179(13), 2070–2077. 10.1016/j.ins.2008.08.017 [DOI] [Google Scholar]
- Wang, X. , Chen, J.‐F. , Shi, Z.‐G. , & Chen, K. S. (2011). Fuzzy‐control‐based particle filter for maneuvering target tracking. Progress in Electromagnetics Research, 118, 1–15. 10.2528/PIER11051907 [DOI] [Google Scholar]
- Walensky, R. P. , & del Rio, C. (2020). From mitigation to containment of the COVID‐19 pandemic: Putting the SARS‐CoV‐2 genie back in the bottle. Journal of the American Medical Association, 323(19), 1889–1890. 10.1001/jama.2020.6572 [DOI] [PubMed] [Google Scholar]
- WHO . (2020a). Naming the coronavirus disease (COVID‐19) and the virus that causes it | World Health Organisation. Retrieved from https://www.who.int/emergencies/diseases/novel‐coronavirus‐2019/technical‐guidance/naming‐the‐coronavirus‐disease‐(covid‐2019)‐and‐the‐virus‐that‐causes‐it
- Zadeh, L. A. (1996). Fuzzy sets. In Klir G. J. & Yuan B. (Eds.), Fuzzy sets, fuzzy logic, and fuzzy systems: Selected papers (Advances in Fuzzy Systems‐ applications and Theory) (Vol. 6, pp. 394–432). Hackensack, NJ: World Scientific Publishing Co., Inc. Retrieved from 10.1142/2895 [DOI] [Google Scholar]
- Zhou, F. , Yu, T. , Du, R. , Fan, G. , Liu, Y. , Liu, Z. , … Cao, B. (2020). Clinical course and risk factors for mortality of adult inpatients with COVID‐19 in Wuhan, China: A retrospective cohort study. The Lancet, 395(10229), 1054–1062. 10.1016/S0140-6736(20)30566-3 [DOI] [PMC free article] [PubMed] [Google Scholar]


