Abstract
Coronavirus disease 2019 or COVID-19 is one of the biggest challenges which are being faced by mankind. Researchers are continuously trying to discover a vaccine or medicine for this highly infectious disease but, proper success is not achieved to date. Many countries are suffering from this disease and trying to find some solution that can prevent the dramatic spread of this virus. Although the mortality rate is not very high, the highly infectious nature of this virus makes it a global threat. RT-PCR test is the only means to confirm the presence of this virus to date. Only precautionary measures like early screening, frequent hand wash, social distancing use of masks, and other protective equipment can prevent us from this virus. Some researches show that the radiological images can be quite helpful for the early screening purpose because some features of the radiological images indicate the presence of the COVID-19 virus and therefore, it can serve as an effective screening tool. Automated analysis of these radiological images can help the physicians and other domain experts to study and screen the suspected patients easily and reliably within the stipulated amount of time. This method may not replace the traditional RT-PCR method for detection but, it can be helpful to filter the suspected patients from the rest of the community that can effectively reduce the spread in the of this virus. A novel method is proposed in this work to segment the radiological images for the better explication of the COVID-19 radiological images. The proposed method will be known as SuFMoFPA (Superpixel based Fuzzy Modified Flower Pollination Algorithm). The type 2 fuzzy clustering system is blended with this proposed approach to get the better-segmented outcome. Obtained results are quite promising and outperforming some of the standard approaches which are encouraging for the practical uses of the proposed approach to screening the COVID-19 patients.
Keywords: COVID-19, Biomedical image interpretation, Image segmentation, Type 2 fuzzy systems, Superpixel, SuFMoFPA
1. Introduction
The use of automated systems is increasing rapidly and the advantages of the computer-based automated systems are exploited by different domains. With the recent advancements in artificial intelligence and computer vision, automated systems are gaining popularity which is increasing day by day. Automated systems which are equipped with artificial intelligence, are highly reliable and proves to be very helpful in various real-life scenario. Machine learning is a branch of artificial intelligence that allows a machine to learn from the input data sets and to perform a certain task based on the acquired knowledge. Machine learning methods have proven their efficiency and effectiveness in exploring many real-life data sets (Pesapane, Volonté, Codari, & Sardanelli, 2018). Some systems are proved to be more efficient than humans in certain circumstances. One of the initial applications of machine learning is observed in 1959 in the checker games (Samuel, 2000). After that, machine learning methods have evolved a lot and many complex problems are effectively solved with the application of some advanced machine learning methods (Chakraborty, Chatterjee, Ashour, Mali, & Dey, 2017). Typically, machine learning approaches can be divided in two ways. The first one is a supervised approach where some ground truth data are required to train the machine learning model. In the case of unsupervised learning approaches, no ground truth data are required and the machine learning model can efficiently explore the underlying data set to find some hidden patterns, and therefore, no supervision is required. Like many other domains, the field of biomedical image analysis is no exception and exploits several advantages of the machine learning systems (Chakraborty and Mali, 2020, Liu et al., 2019). Computer vision and machine learning-based approaches are helpful to automate the diagnostic procedures and machine learning-based decision support systems can act as a third eye to the physicians and other domain experts (Fourcade and Khonsari, 2019, Hore et al., 2016).
Radiological images are one of the important modalities of the biomedical imaging that serves as an important tool to assess the condition of various living organisms and some non-living objects in a non-invasive manner. In general, physicians have to study the radiological images manually, to interpret it and generate the reports in highly time-bound conditions (Kahn et al., 2009, Sistrom et al., 2009). But on many occasions, raw radiological images are not very suitable for interpretation and, different operations like enhancement, segmentation, etc. are to be performed (Chakraborty and Mali, 2020, Roy et al., 2017). Machine learning methods are not only useful in performing these jobs efficiently but also effective in performing some other relevant tasks like adjusting different parameters of the radiological imaging devices, determining the amount of radiation, etc. which are crucial from the diagnostic perspective. Machine learning-based automated systems can guide in different stages of the radiological image assessment including quality assurance. For example, Altan et. al. (Altan & Karasu, 2020) proposed a hybrid model to detect and analyze COVID-19. This approach combinedly applies a 2D curvelet transform, chaotic salp swarm algorithm, and deep learning approach to determine the status of the infection in a patient using X-ray images. The EfficientNet-B0 architecture is used for the diagnosis purpose.
COVID-19 is currently the biggest threat for mankind that creates a global pandemic scenario and the absence of a dedicated vaccine or drugs makes the situation more complicated. Officially 16,558,289 numbers of people found who are infected with this virus and 656,093 people are already expired due to this virus as of 30th July 2020, 5:36 pm CEST (WHO Coronavirus Disease (COVID-19) Dashboard | WHO Coronavirus Disease (COVID-19) Dashboard, n.d.). According to these statistics, it can be concluded that the mortality rate is not very high (approximately 3.96%) but the heavily infectious nature of this virus is a big reason to worry. Already 217 countries are suffering from this virus and trying to find the weapon to combat the spread of this highly infectious virus but, some precautionary steps are the only hope to prevent this virus in this present scenario. Early screening, appropriate sanitization, social distancing, use of masks, gloves, and other protective equipment can only stop the spread of this virus. The presence of this virus can be detected by only RT-PCR test to date but, radiological images can show some early signs of the COVID-19 disease (Kanne, Little, Chung, Elicker, & Ketai, 2020). Some researches show that the computerized tomography scans of the chest region can be useful in identifying some early signs of this disease (Fang et al., 2020). Still, the RT-PCR test has no alternative and the computerized tomography scans cannot be used as an alternative tool because of the false negatives (Aiet al., 2020, Bernheimet al., 2020) but, these images can be useful in the early screening purpose and it is helpful to isolate some suspected patients from the society that can reduce the risk of the community spread. In general, the ground truth segmented images are not widely available for the COVID-19 CT scan images but, the segmentation plays a vital role in interpreting the radiological images. It can help in easy understanding and decision-making process about the COVID-19 by interpreting some relevant features from the CT scan images of the chest region, which are reported in Table 1 (Torkian, Ramezani, Kiani, Bax, & Akhlaghpoor, 2020). Typically, modern CT scan devices are advanced enough to acquire high-quality images containing a large amount of spatial information. It is one of the challenging tasks to process a large amount of spatial information efficiently (Lei et al., 2019). The above discussion gives a glimpse of the motivation behind proposing a novel segmentation approach namely SuFMoFPA (Superpixel-based Fuzzy Modified Flower Pollination Algorithm). The proposed method incorporates the concept of superpixels to make the processing easier so that, a large amount of spatial information could not be a constraint anymore. The type 2 Fuzzy system is blended with this proposed method, to get the better-segmented outcome. The proposed method can be considered as a computer-assisted tool to combat the spread of the COVID-19 virus.
Table 1.
Some useful properties in the chest CT scan of the COVID-19 positive patients for the early screening purpose (Caruso et al., 2020).
| Property | Sample percentage |
|---|---|
| ground-glass opacities (GGO) | 100% |
| multilobe and posterior involvement | 93% |
| bilateral pneumonia | 91% |
| subsegmental vessel enlargement (>3 mm) | 89% |
1.1. A brief overview of the literature
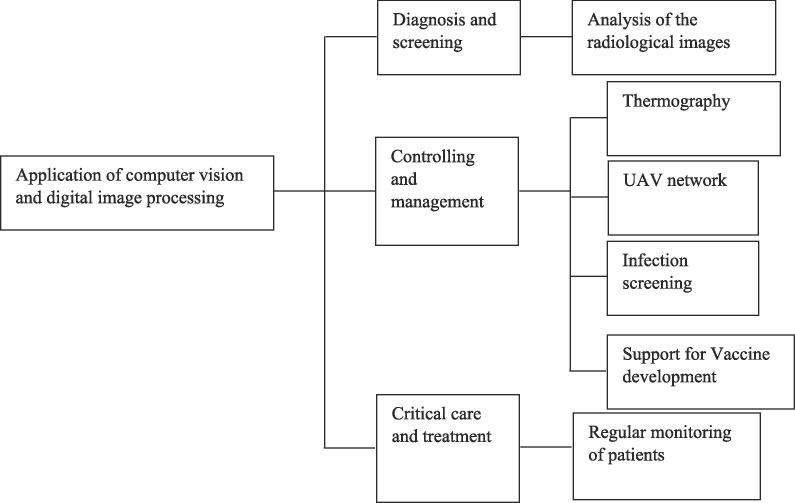
Computer vision and digital image processing are applied in different ways to cope up with this pandemic scenario. The application domain of the computer vision and image processing-based application can be broadly categorized into 3 categories. These categories and some of their subcategories are depicted in Fig. 1 .
Fig. 1.
A broad overview of the application domain of the computer vision and digital image processing in managing the COVID-19 pandemic.
In this work, CT scan images are investigated using an automated unsupervised approach for easy interpretation and early screening of the COVID-19 suspects. Therefore, the main focus of the study of the related literature is confined to the approaches related to the CT scan images. A comprehensive overview of some of the related works is presented in Table 2 which is beneficial to understand the current state-of-the-art research and also helpful in further progress.
Table 2.
A brief overview of the current state-of-the-art approaches.
| Approach | Type | Deployment details | Brief description |
|---|---|---|---|
| Chen et. al. (Chen et al., 2020) | Supervised | Renmin Hospital of Wuhan University | This approach is based on deep learning and used high-resolution CT scan images to automatically diagnose the COVID 19 infection. The UNet++ model is used to choose the appropriate regions of the CT images. This approach is useful to assist the radiologist to diagnose the CT images. This approach achieves 100% sensitivity, 93.55% specificity, and 95.24% accuracy. |
| Wang et. al. (S. Wang et al., 2020) | Supervised | Not available | A deep learning-based COVID-19 CT image analysis framework is proposed where the deep learning framework can explore the COVID-19 related features from the CT scan images of the chest region. This approach uses modified inception and transfers learning. The performance of this approach on the external testing achieves 79.3% accuracy, 83.00% specificity, and 67.00% sensitivity. |
| Butt et. al. (Butt et al., 2020) | Supervised | Not available | Multiple convolutional neural networks based automated CT image analysis technique is proposed in this work. The region of interest is segmented with the help of the 3D convolutional neural network. Noisy-or Bayesian function is used to determine the infection probability. This approach achieves a result of 98.2% sensitivity and a 92.2% specificity. |
| Xu et. al. (Xu et al., 2020) | Supervised | Not available | This approach uses two three-dimensional classification models based on convolutional neural networks. The ResNet-18 and location-Attention-oriented model are combined to analyze the CT scan images. Three different classes COVID-19, Influenza, and irrelevant to infection groups are identified by this approach. This approach achieves an overall accuracy of 86.7%. |
| Jin et. al. (Jin et al., 2020) | Supervised | 16 number of hospitals in China | This approach uses Transfer learning on ResNet-50 to design a computer-assisted CT image analysis framework to investigate COVID-19 from radiological images. A three-dimensional UNet++ model is used for segmentation purposes. This approach can effectively identify the infected region of the CT scan image efficiently. This approach achieves 97.4% sensitivity and 92.2% specificity. |
| Wang et. al. (X. Wang et al., 2020) | Weakly-supervised | Not available | A weakly-supervised lung lesion segmentation approach is proposed in this work that automatically identifies the lesion from the Ct scan images. A trained UNet architecture is used for lesion segmentation purposes. A three-dimension deep neural architecture is used to analyses the three-dimensional segmented region to determine the chances of COVID-19 infection. Experimental results prove the performance and the real-life applicability of this approach. |
| Mohammed et. al. (Mohammed et al., 2020) | Weakly-supervised | Not available | This approach is known as ResNext + . A lung segmentation mask is used to perform the segmentation operations and the spatial features are extracted with the help of the spatial and channel attention. This approach achieves 81.9% precision and 81.4% F1 score. |
| Laradji et. al. (Laradji, Rodriguez, Mañas, et al., 2020) | Weakly-supervised | Not available | This work uses a point marking scheme i.e. the infected regions are marked with the help of some points that significantly reduce the manual effort to make manual delineations. A consistency-based loss function is proposed in this work that helps in generating consistent outputs with the spatial transformations. Experimental results show the improvement of the proposed approach over the traditional approaches that are based on point level loss functions. |
| Laradji et. al. (Laradji, Rodriguez, Branchaud-Charron et al., 2020) | Weakly-supervised | Not available | This work is based on an active learning approach that is useful for fast and efficient labeling of the CT scan images. The proposed annotator ensures of producing a significantly high amount of information content cost-effectively. The experimental results prove that the 7% annotation effort can produce the 90% performance compared to the completely annotated dataset. |
| Gozes et. al. (Gozes et al., 2020) | Supervised | Not available | A two-dimensional deep convolutional neural network-based model is proposed to automatically analyze the CT scan images for efficient diagnosis of the COVID-19 infection. This approach uses the Resnet-50 model. Apart from this, U-net architecture is used for segmentation purposes. This approach achieves 98.2% sensitivity and 92.2% specificity. |
Apart from these recently developed works, related comprehensive overview of this topic can be found in (Dong et al., 2020, Shi et al., 2020, Shoeibi et al., 2020, Ye et al., 2020).
1.2. Motivation of the proposed work
As discussed earlier, the whole world is suffering in the mid of this pandemic scenario due to the COVID-19 virus. The entire mankind is trying to find some ways to get rid of this virus. COVID-19 is highly infectious in nature and early screening of the suspected patients can help to stop the drastic spread of this virus. The RT-PCR test is considered as the gold standard and it is frequently used worldwide to confirm the presence of this virus. It is a time-consuming procedure and sometimes, it can consume up to two days to produce the result. Investigation of the chest computed tomography (CT) scans can be beneficial in this context due to the presence of some prominent features which are discussed in Table 1. One prominent problem which is faced by the researchers is the absence of a sufficient amount of properly annotated ground truth data due to the need for manual or expert intervention (Mei, Lee, & Diao, 2020). It is very difficult to get and not practical to expect a manually annotated dataset for investigations purposes in this pandemic scenario (Yao, Xiao, Liu, & Zhou, 2020). Motivated from this, an unsupervised approach is proposed in this work to automatically analyze the CT scan images without depending on the expert delineations. Typically, modern CT scan images consist of a large amount of spatial information which is difficult to process. Motivated from this, a novel superpixel based approach is proposed to reduce the computational burden. The flower pollination algorithm is modified and combined with the type 2 fuzzy system to effectively handle the uncertainties.
1.3. Outline of the theoretical and practical contributions
This article proposes an unsupervised approach to automatically analyze CT scan images for early screening of COVID-19. This contribution can act as a third eye for the physicians and also helpful to resist the significant spread of this virus without depending on the manually annotated dataset and it makes the proposed approach beneficial and applicable to get adapted in practical scenarios. In this work, the traditional flower pollination algorithm is modified using the type 2 fuzzy system which is one of the major contributions. The advantages of type 2 fuzzy systems are mentioned in Section 3. The cluster centers updated using the flower pollination algorithm. The proposed algorithm is free from the dependency of the choice on the initial cluster centers. To reduce the associated computational burden of processing a large amount of spatial information, a novel superpixel based approach is proposed in which the noise sensitivity of the watershed-based superpixel computation method is handled by determining the local minima from the gradient image. Moreover, to exploit the advantage of the superpixels, the fuzzy objective function is modified accordingly. These are the major contributions to the existing literature from the practical as well as theoretical point of view. It is completely a unique and novel contribution to the literature compared to the other approaches that are designed for the same job.
1.4. Organization of the article
The remaining article is organized as follows: Section 2 briefly illustrates the flower pollination algorithm. Section 3 illustrates the type two fuzzy clustering system. The proposed algorithm and the obtained results are presented in 4, 5 respectively. Section 6 discusses some of the important points related to this article. Section 7 concludes the article.
2. A brief overview of the flower pollination algorithm
As the name suggests, the flower pollination algorithm is inspired by the pollination process of some flowers and it is developed by X.S. Yang in 2012 (Yang, 2012). It is a global optimization process that mimics the operation of the pollinators that helps in the reproduction process in the flower plants. This approach uses a global search as well as a local search scheme to effectively determine the local minima. Some basic assumptions of this approach are stated below:
-
a.
Global exploration is performed by mimicking the cross-pollination and biotic pollination process. The movement of the pollinators is controlled by the Lévy flight.
-
b.
Local exploitation is carried out by mimicking the self-pollination and abiotic pollination process.
-
c.
The local exploitation and global exploration are guided a probability factor .
-
d.
The probability of the reproduction is dependent on the similarities of the two flowers which are involved in the pollination process.
-
e.
A solution is mimicked by a pollen gamete.
-
f.
A single pollen gamete can be produced by a single flower and therefore, a candidate solution is also equivalent to a flower.
The local pollination and the global pollination are two prime steps of this algorithm. The global pollination helps to explore the solution space more effectively by mimicking the long-range movements of different pollinators. Eq. (1) can be used to update the solution Sp using the Lévy flight from an iteration itr to the next iteration itr + 1.
| (1) |
In this equation, ψ denotes the step size which is also known as ‘strength of the pollination’ and this value can be determined from the Lévy distribution of the form as given in Eq. (2). Sbest is the optimal solution found so far.
| (2) |
In this equation, represents the standard gamma function and ω is a parameter whose value is considered as 1.6 in this work. The local pollination process can be implemented using Eq. (3) where Sq and Srare the solutions (i.e. pollens) from different flowers. The value of φ can be drawn from a uniform distribution in [0,1].
| (3) |
3. Clustering based on type-2 fuzzy systems
Crisp clustering approaches are not applicable on many occasions due to its inherent limitations and restrictions (Liew, Leung, & Lau, 2000). Fuzzy clustering approaches are practically useful in various practical scenarios (Bezdek, Ehrlich, & Full, 1984) where the crisp clustering methods do not perform well. Fuzzy clustering approaches allow a single pixel to be a member of multiple classes simultaneously with some membership degree. The sum of the membership values for a certain point must be 1 i.e. the degree of membership can take any values between 0 and 1. The objective function is given in Eq. (4) which is optimized by the fuzzy c-means clustering approaches. It is a squared error function where μmn is the membership value of the point pm to the nth cluster and this value can be computed using Eq. (5) and the χ is the fuzzifier. The cluster centers can be updated using Eq. (6). nP and nC represents the number of data points and the number of cluster centers.
| (4) |
As noted above, the degree of membership can take any value from [0,1] and the sum must be 1 i.e. .
| (5) |
| (6) |
Noise can significantly affect the type 1 fuzzy clustering system. Moreover, the relative membership creates some additional problems in real-life applications. Type 2 fuzzy system is helpful in this context to overcome the inherent constraints of type 1 fuzzy systems by properly modeling the noise and uncertainty and controlling the impact of a data point depending on the value of the uncertainty. Some basic advantages of adapting the type 2 fuzzy system are mentioned below (Rhee & Cheul, n.d):
-
a.
Effective uncertainty modeling allows a point to have a greater impact if it has lesser uncertainty and vice-versa.
-
b.
Some realistic segmented output can be produced using the application of type 2 fuzzy system.
-
c.
Impact of noise can be reduced with the help of type 2 fuzzy systems.
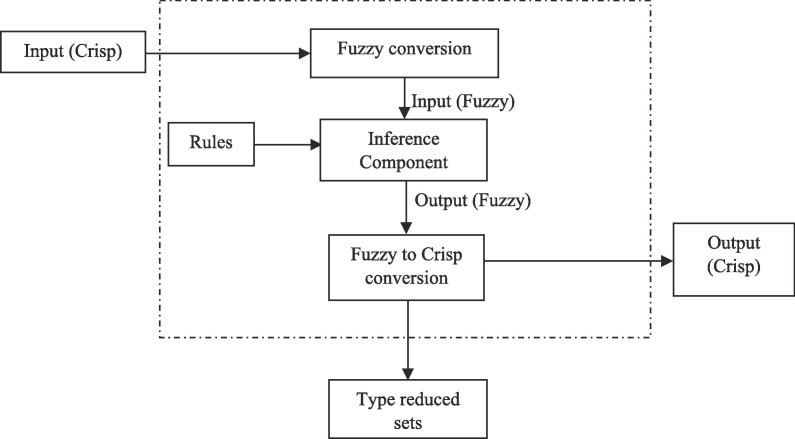
The fuzzy type 2 membership value can be derived from Eq. (5) and it is given in Eq. (7). The cluster centers can be updated using Eq. (8). Algorithm 1 illustrates the type 2 fuzzy system-based clustering approach and Fig. 2 demonstrates the working flow of type 2 fuzzy system as discussed above.
| (7) |
| (8) |
Fig. 2.
Working flow diagram of type 2 fuzzy system.
| Algorithm 1. Type 2 fuzzy system-based C-means clustering |
|---|
| Input: The dataset to be clustered and the number of clusters nC where, |
| Output: Computed near optimal cluster centers |
| 1: Choose the initial cluster centers randomly. |
| 2: Assign some membership values to the data points in a random manner. |
| 3: Set a tiny threshold ς. |
| 4: Update the cluster centers using Eq. (8). |
| 5: Compute the fitness of the objective function using Eq. (4). |
| 6: Check if then |
| a. Compute the membership value using Eq. (7). |
| b. Goto step 2. |
| end if |
| 9: Return the computed near optimal cluster centers. |
4. 4. Proposed SuFMoFPA approach
With technological advancements, the quality of the radiological imaging devices is increasing day by day and precise and sophisticated hardware allows us to capture high quality multi-slice radiological images. Although it is a blessing in the biomedical imaging and the diagnostic domain, the technological advancements also bring the challenge to automate the processing task of such a huge amount of spatial information. To process a high-quality image automatically and within the stipulated amount of time, it is necessary to develop an efficient computer-aided solution (Chakraborty and Mali, 2018, Chakraborty and Mali, 2020). Superpixels (Moore, Prince, Warrell, Mohammed, & Jones, 2008) are helpful in this context because, superpixels can efficiently represent a group of pixels that can reduce the computational burden and therefore, a superpixel based clustering approach is proposed in this work to accelerate the screening process of the COVID-19 infected patients.
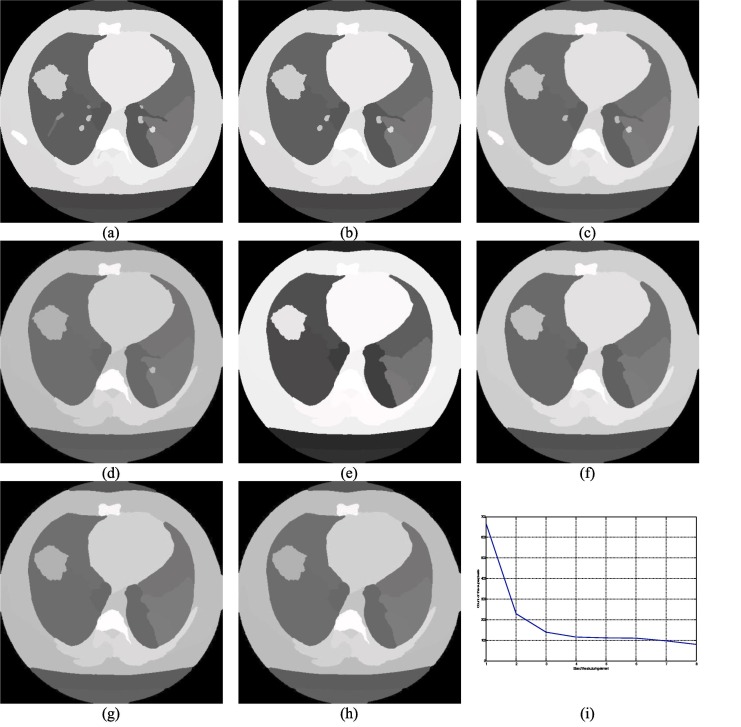
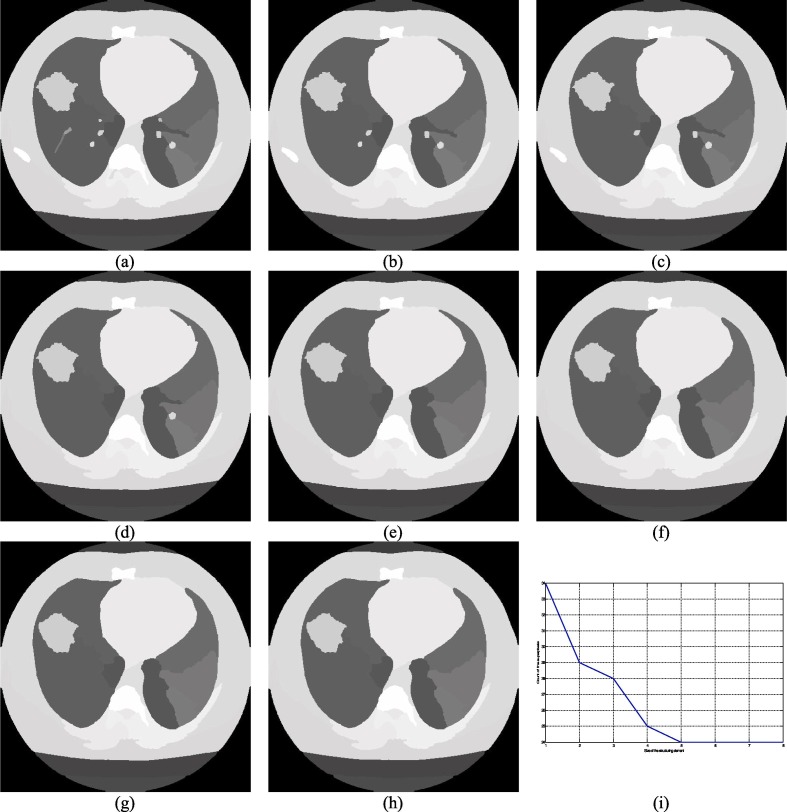
Superpixels are a frequently used concept to perform the segmentation task efficiently and a superpixel image can be constructed in various ways (Achanta et al., 2012, Comaniciu and Meer, 2002, Hu et al., 2015). The shape and size of the superpixels can vary with the method. For example, the SLIC (Achanta et al., 2012) method produces regular superpixels. Mean shift (Comaniciu & Meer, 2002) and the watershed (Hu et al., 2015) are another two methods that produce superpixels of irregular sizes. Typically, irregular superpixels are more useful for segmentation purposes (Lei et al., 2019). One major drawback of the watershed-based approach is its noise sensitivity and this is the main reason behind the widespread popularity of the mean shift method which happens to be more complex than the watershed-based superpixel approach. The watershed method is adapted due to its simplicity and the associated problem is addressed in this work by computing the local minima of the gradient image (Hore et al., 2015) of the corresponding input image. The essential gradient information is preserved by performing the morphological opening ξ and closing ς based reconstruction operation which is defined in 9 and 10 respectively where ζ and υ represents the morphological erosion and dilation respectively and these are defined in Eqs. (11) and (12) respectively. In Eqs. (11) and (12), V and represent the point wise maximum and the minimum value, Im and Im' are the actual and the marker images respectively and Im' can be expressed using Eqs. (13) and (14) where se is the acronym for the structuring element and it plays a vital role in generating the superpixel images and the choice of the correct controlling parameter essential for precise segmentation outcome and it can be easily understood from Fig. 3, Fig. 4 where the disk and square structuring elements are used with different sizes on I001 (please refer Table 2). Fig. 2, Fig. 3 demonstrate the effect of the size of the structuring elements on the number of superpixels.
| (9) |
| (10) |
| (11) |
| (12) |
| (13) |
| (14) |
Fig. 3.
Demonstration of the impact of the size of the disk structuring elements on the superpixel image (a)–(h) superpixel image corresponding to the I001 generated using se of size 3 to 10 respectively, (i) Size of superpixels vs. number of superpixels.
Fig. 4.
Demonstration of the impact of the size of the circle structuring elements on the superpixel image (a)–(h) superpixel image corresponding to the I001 generated using se of size 3 to 10 respectively, (i) Size of superpixels vs. number of superpixels.
Now, it is not practically feasible to determine the correct structuring element for every image manually. This issue is addressed by determining the pointwise maximum values from the mixture of the gradient images (Chakraborty & Mali, 2020) which are generated using different structuring elements and the number of structuring elements can be selected depending on the which is nothing but the range of the guiding parameter ρ for the corresponding structuring element and . It can be achieved using Eq. (15) which is derived from Eq. (9) and the upper bound can be computed using Eq. (16) where γ is a threshold to control the error rate.
| (15) |
| (16) |
The superpixels can represent a group of pixels nPm using a representative pixel and it can be computed using Eq. (17). With the help of this representative pixel value, Eq. (4) is updated and the modified as given in Eq. (18) and the degree of membership can be determined using Eq. (19) which is used to find the type 2 membership value as given in Eq. (7).
| (17) |
| (18) |
| (19) |
The cluster centers are guided and updated using the modified flower pollination algorithm instead of the fuzzy cluster center updation equation. In this work, the local pollination method is modified to improve the segmentation output. The exploitation is typically performed by searching the neighborhood of a particular solution but it may not worth always. Searching around the best solutions may discover some potentially better solutions and can reduce the overall exploitation overhead (Eiben & Schippers, 1998). The concept of Fitness Euclidean distance Ratio () in this work to update the Eq. (1) and the updated version of Eq. (1) is given in Eq. (20) where is defined in Eq. (21) and FER is defined in Eq. (22). Algorithm 2 demonstrates the proposed SuFMoFPA method.
| (20) |
| (21) |
| (22) |
This approach will help to exploit the fittest individuals near a solution.
5. Results of the simulation
The SuFMoFPA approach is applied and evaluated using some CT scan images of the chest region which are collected from the COVID-19 infected patients from the different geographic regions of the world. The proposed approach can be helpful in the easy explication of the COVID-19 disease without the ground truth and annotated segmented image. It can be highly useful to restrict and isolate suspected patients from the community. RT-PCR test can be performed for the confirmation purpose but, the proposed method can be effective for the screening purpose. The effectiveness of the proposed approach is established through both visual and quantitative analyses using four well-known cluster validity parameters.
| Algorithm 2. The proposed SuFMoFPA approach |
|---|
| Input: Input image which is to be segmented |
| Output: Segmented output image |
| 1: Find the gradient image corresponding to the input image using the method proposed in (Hore et al., 2015). |
| 2: Apply Eqs. (9) and (10) to find the superpixel image corresponding to the input image. |
| 3: Determine the representative point τ of a superpixel. |
| 4: Randomly initialize the cluster centers where and denotes the upper and lower bound respectively for a representative point. |
| 5: Randomly assign the fuzzy membership values to the superpixels. |
| 6: //Iteration counter |
| 7: Repeat until //evalCnt is the maximum number of iterations |
| 8: Determine the fitness values |
| 9: Perform global pollination |
| 10: Perform local pollination |
| 11: Update the solutions using Eq. (20) |
| 12: Check if is worse than then |
| 13: |
| end if |
| 14: Update the global best |
| end until |
| 15: Prepare the output segmented image by assigning the superpixels to their nearest cluster centers. |
| 16: Return the segmented image. |
5.1. Description of the dataset
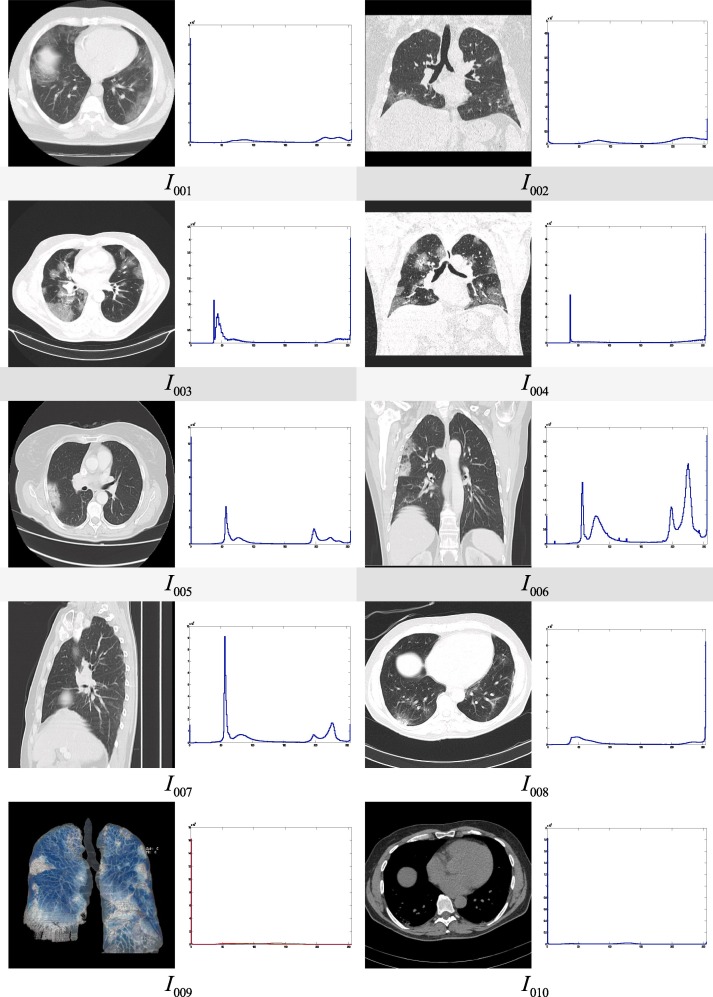
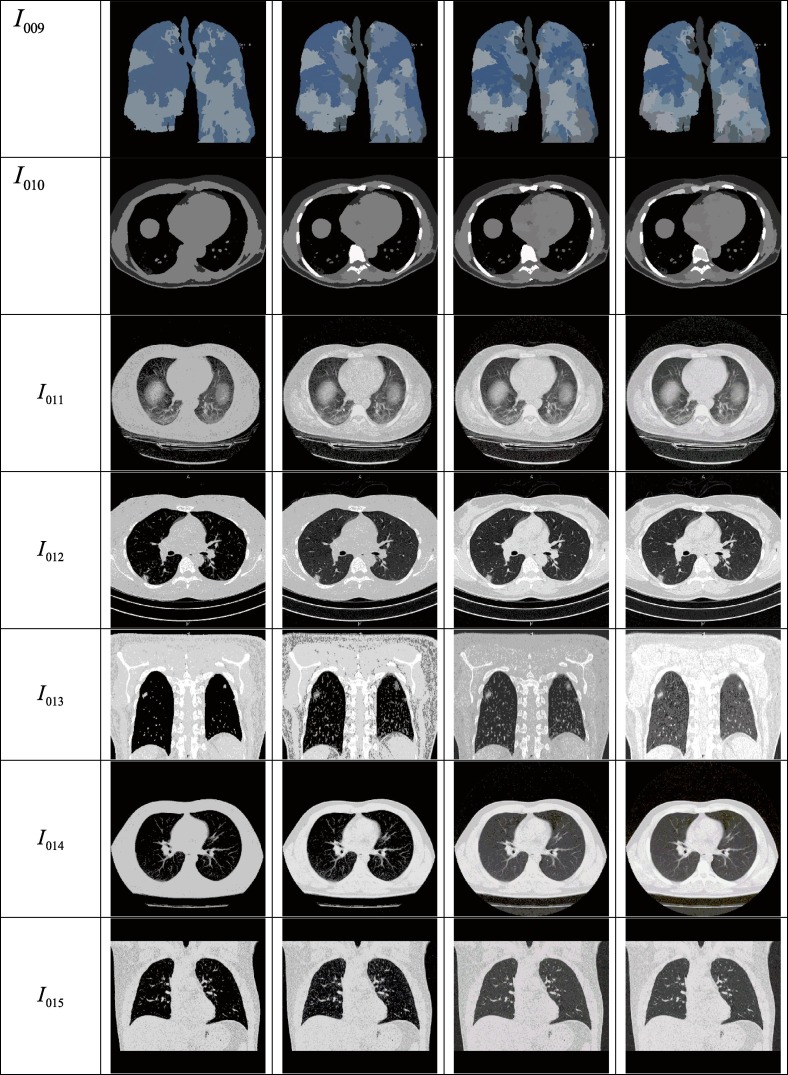
115 CT scan images of the chest region are considered for the experimental purpose out of which, details of the 18 images are presented in this article. The test images are collected from the COVID-19 infected patients from various geographic regions and different views are considered of the works. Moreover, patients from different age groups are considered for this experiment. 10 images are considered from the age group greater than or equal to 50 years and 8 images are considered from the age group less than 50 years in this article to demonstrate and compare the performance of the proposed approach. The sample test images along with their histograms are given in Fig. 5 and the description of the dataset is given in Table 3 .
Fig. 5.
Test images under consideration and their histograms.
Table 3.
Description of the images under test.
| Image Id | View | Source | Gender | Age | Features observed | Comments |
|---|---|---|---|---|---|---|
| I001 | Axial | (COVID-19 Pneumonia | Radiology Case | Radiopaedia.Org, n.d.-a) | M | 50 | ground-glass opacities (GGO) crazy paving air space consolidation |
Case courtesy of Dr Bahman Rasuli, Radiopaedia.org, rID: 74,576 |
| I002 | Coronal | |||||
| I003 | Axial | (COVID-19 Pneumonia | Radiology Case | Radiopaedia.Org, n.d.-b) | M | 65 | ground-glass opacities (GGO) crazy paving |
Case courtesy of Dr Elshan Abdullayev, Radiopaedia.org, rID: 76,015 |
| Coronal | ||||||
| I005 | Axial | (COVID-19 Pneumonia | Radiology Case | Radiopaedia.Org, n.d.-c) | F | 70 | ground-glass opacities (GGO) crazy paving air space consolidation bronchovascular thickening |
Case courtesy of Dr Ammar Haouimi, Radiopaedia.org, rID: 75,665 |
| I006 | Coronal | |||||
| I007 | Sagittal | |||||
| I008 | Axial | (COVID-19 Pneumonia | Radiology Case | Radiopaedia.Org, n.d.-d) | M | 60 | ground-glass opacities (GGO) crazy paving air space consolidation |
Case courtesy of Dr Antonio Rodrigues de Aguiar Neto, Radiopaedia.org, rID: 77,067 |
| I009 | Coronal | |||||
| I010 | Axial (Non-contrast) | |||||
| Axial | (COVID-19 Pneumonia | Radiology Case | Radiopaedia.Org, n.d.-e) | M | 45 | multilobar and bilateral peripheral ground glass opacities | Case courtesy of Dr Fateme Hosseinabadi , Radiopaedia.org, rID: 74,868 | |
| Axial | (COVID-19 Pneumonia - Early-Stage | Radiology Case | Radiopaedia.Org, n.d.) | F | 45 | small patchy ground glass opacities and consolidations are scattered at both lungs | Case courtesy of Dr Mohammad Taghi Niknejad, Radiopaedia.org, rID: 75,829 | |
| Coronal | ||||||
| Axial | (COVID-19 Pneumonia | Radiology Case | Radiopaedia.Org, n.d.-f) | M | 25 | Air space consolidation is present at the right lower lobe and ground glass opacity nodules can also be observed | Case courtesy of Dr Bahman Rasuli, Radiopaedia.org, rID: 74,879 | |
| Coronal | ||||||
| Axial | (COVID-19 Pneumonia | Radiology Case | Radiopaedia.Org, n.d.-g) | M | 40 | multiple patchy, peripheral and basal, bilateral areas of ground-glass opacity is observed | Case courtesy of Dr Maksym Kovratko, Radiopaedia.org, rID: 75,350 | |
| Axial | (COVID-19 Pneumonia | Radiology Case | Radiopaedia.Org, n.d.-h) | F | 35 | bilateral confluent ground-glass opacities | Case courtesy of Henri Vandermeulen, Radiopaedia.org, rID: 75,417 | |
| Coronal |
To establish the practical applicability of the proposed approach and analyze it quantitatively, four well-known cluster validity measures are used in this work. These are Davies–Bouldin index (Davies & Bouldin, 1979), Xie-Beni index (Xie & Beni, 1991), Dunn index (Dunn, 1974) and β index (Pal, Ghosh, & Shankar, 2000).
5.2. Experimental results
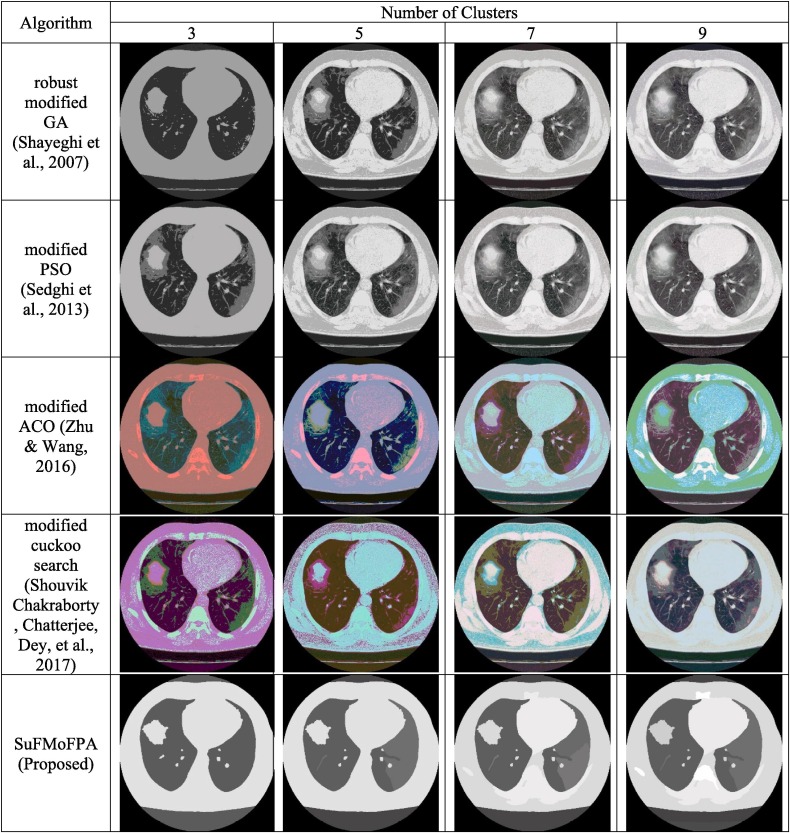
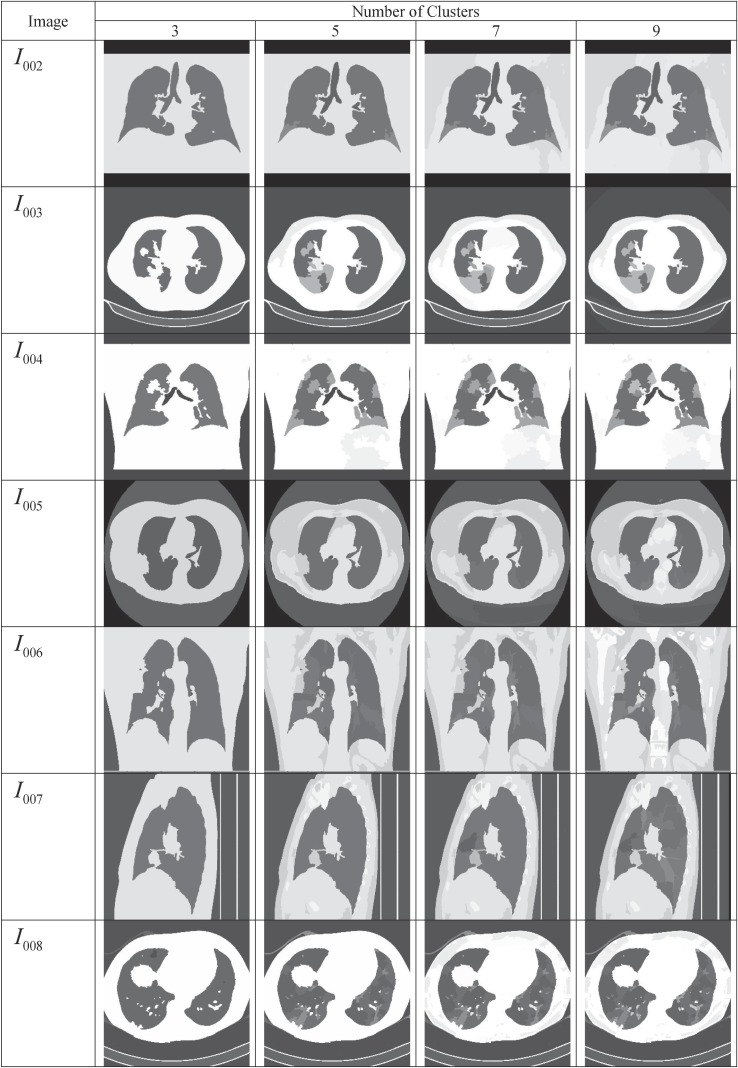
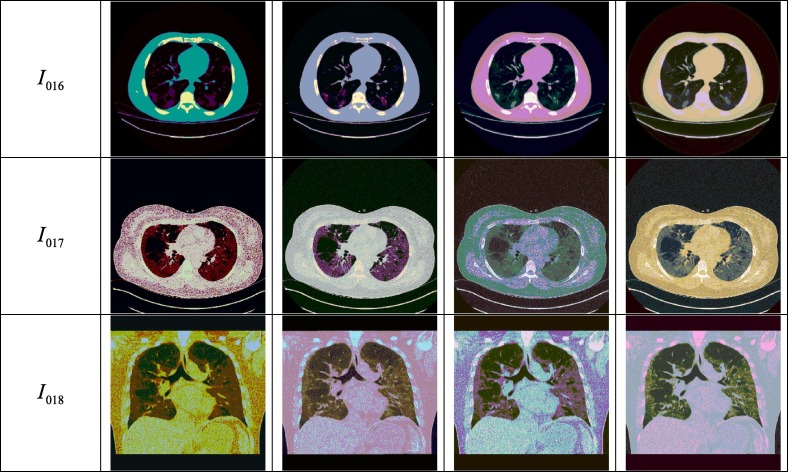
The proposed approach is evaluated and compared through qualitative and quantitative measures. Experiments are performed using MatLab R2014a with a computer that is equipped with an Intel i3 processor (1.8 GHz) and 4 GB of RAM. The proposed SuFMoFPA approach is evaluated and compared with some of the standard methods like robust modified GA (Shayeghi, Jalili, & Shayanfar, 2007) based clustering, modified PSO (Sedghi, Aliakbar-Golkar, & Haghifam, 2013) based clustering, modified ACO (Zhu & Wang, 2016) based clustering and modified cuckoo search (Chakraborty, Chatterjee, Dey, et al., 2017) based clustering approaches. A comparison of the proposed method with these standard approaches can be found in Fig. 6 where the image used for the study and the segmentation results of the remaining 9 images are reported in Fig. 7 . The quantitative comparison is presented in Table 4, Table 5, Table 6, Table 7 for the Davies–Bouldin index, Xie-Beni index, Dunn index and β index respectively. The acceptable values are marked in boldface.
Fig. 6.
Comparison of different methods using for different number of clusters.
Fig. 7.
Segmented output for different number of clusters which are obtained by applying the SUFEMO method.
Table 4.
Comparison of different segmentation methods with the Davies–Bouldin index values (Highlighted values denotes the acceptable values).
| Image Id | Algorithm | No. of Clusters |
|||
|---|---|---|---|---|---|
| 3 | 5 | 7 | 9 | ||
| robust modified GA (Shayeghi et al., 2007) | 1.46566084 | 1.74543298 | 2.90550813 | 1.166586138 | |
| modified PSO (Sedghi et al., 2013) | 1.27069619 | 1.71228711 | 2.75030941 | 2.271593017 | |
| modified ACO (Zhu & Wang, 2016) | 0.71499362 | 1.12138179 | 2.09958914 | 1.7088708 | |
| modified cuckoo search (Chakraborty, Chatterjee, Dey, et al., 2017) | 1.85023122 | 2.20605136 | 0.95728619 | 2.292252512 | |
| SuFMoFPA (Proposed) | 1.08842834 | 1.07747973 | 0.53539368 | 1.778431432 | |
| robust modified GA (Shayeghi et al., 2007) | 1.62773175 | 1.31925593 | 2.40392655 | 1.191051933 | |
| modified PSO (Sedghi et al., 2013) | 2.57308165 | 2.63202031 | 3.11996996 | 2.123245072 | |
| modified ACO (Zhu & Wang, 2016) | 2.7662899 | 3.22557015 | 2.50463222 | 1.795131518 | |
| modified cuckoo search (Chakraborty, Chatterjee, Dey, et al., 2017) | 2.01832075 | 1.34648767 | 1.67138427 | 0.998082371 | |
| SuFMoFPA (Proposed) | 1.18390271 | 0.95679948 | 1.65405987 | 1.32410342 | |
| robust modified GA (Shayeghi et al., 2007) | 1.91583123 | 1.1671004 | 1.03516035 | 1.828472656 | |
| modified PSO (Sedghi et al., 2013) | 1.85688108 | 1.07056686 | 1.107896 | 0.665328328 | |
| modified ACO (Zhu & Wang, 2016) | 1.09573718 | 0.9340154 | 1.61607886 | 1.566379073 | |
| modified cuckoo search (Chakraborty, Chatterjee, Dey, et al., 2017) | 0.53000143 | 0.66238182 | 1.34665728 | 1.212108295 | |
| SuFMoFPA (Proposed) | 0.95124587 | 2.2761225 | 1.82915305 | 1.349001333 | |
| robust modified GA (Shayeghi et al., 2007) | 1.6600279 | 2.4451295 | 2.31047531 | 2.643031826 | |
| modified PSO (Sedghi et al., 2013) | 1.06648072 | 1.79694851 | 1.76383591 | 2.094111557 | |
| modified ACO (Zhu & Wang, 2016) | 1.50860621 | 0.85245887 | 1.02585668 | 1.901277409 | |
| modified cuckoo search (Chakraborty, Chatterjee, Dey, et al., 2017) | 2.99528813 | 1.34999352 | 1.13965062 | 0.737896183 | |
| SuFMoFPA (Proposed) | 1.71026086 | 0.76668142 | 1.31795642 | 1.64507146 | |
| robust modified GA (Shayeghi et al., 2007) | 2.25838317 | 2.55455974 | 1.87962855 | 1.805648018 | |
| modified PSO (Sedghi et al., 2013) | 1.57623769 | 1.98474109 | 2.14412299 | 2.951422852 | |
| modified ACO (Zhu & Wang, 2016) | 1.47407174 | 2.01603748 | 1.36439983 | 2.404545846 | |
| modified cuckoo search (Chakraborty, Chatterjee, Dey, et al., 2017) | 1.38990864 | 3.86711577 | 2.1478699 | 1.830888571 | |
| SuFMoFPA (Proposed) | 1.81518141 | 1.09159251 | 1.66683998 | 2.989766006 | |
| robust modified GA (Shayeghi et al., 2007) | 1.23138832 | 1.01014988 | 0.95618714 | 0.787057999 | |
| modified PSO (Sedghi et al., 2013) | 2.16222311 | 0.81622082 | 1.72504726 | 2.16507972 | |
| modified ACO (Zhu & Wang, 2016) | 0.80889272 | 1.66389743 | 1.5421688 | 1.835921993 | |
| modified cuckoo search (Chakraborty, Chatterjee, Dey, et al., 2017) | 0.43185735 | 1.29048782 | 0.50438778 | 0.682941573 | |
| SuFMoFPA (Proposed) | 1.17476198 | 0.98550436 | 1.31757186 | 0.335980865 | |
| robust modified GA (Shayeghi et al., 2007) | 1.57652908 | 1.6194884 | 1.9736603 | 2.097535382 | |
| modified PSO (Sedghi et al., 2013) | 1.10447081 | 1.26272695 | 1.36844449 | 2.675402245 | |
| modified ACO (Zhu & Wang, 2016) | 2.31158307 | 2.11203941 | 1.52910585 | 1.531703371 | |
| modified cuckoo search (Chakraborty, Chatterjee, Dey, et al., 2017) | 2.25098064 | 2.16640854 | 2.00816908 | 1.560587542 | |
| SuFMoFPA (Proposed) | 1.61738912 | 3.01887919 | 2.35125854 | 1.007280189 | |
| robust modified GA (Shayeghi et al., 2007) | 2.87594572 | 3.08027 | 2.69379274 | 2.876237664 | |
| modified PSO (Sedghi et al., 2013) | 2.34842572 | 1.23482571 | 1.541943 | 1.475744307 | |
| modified ACO (Zhu & Wang, 2016) | 1.92449742 | 1.76792302 | 1.75173512 | 2.07728695 | |
| modified cuckoo search (Chakraborty, Chatterjee, Dey, et al., 2017) | 1.96624057 | 1.40574191 | 0.91283874 | 1.76713855 | |
| SuFMoFPA (Proposed) | 1.44323534 | 1.8190357 | 2.41462487 | 1.089341918 | |
| robust modified GA (Shayeghi et al., 2007) | 1.5124999 | 1.82220571 | 1.69599381 | 2.487036546 | |
| modified PSO (Sedghi et al., 2013) | 2.031554 | 2.00024885 | 1.57173881 | 3.129046095 | |
| modified ACO (Zhu & Wang, 2016) | 1.29799698 | 1.65648242 | 2.68760426 | 2.50496945 | |
| modified cuckoo search (Chakraborty, Chatterjee, Dey, et al., 2017) | 2.40913356 | 1.25466882 | 1.45602541 | 2.464918427 | |
| SuFMoFPA (Proposed) | 1.00272734 | 0.52918873 | 2.23226914 | 2.943121702 | |
| robust modified GA (Shayeghi et al., 2007) | 2.10490036 | 2.63338268 | 3.23131984 | 1.527199305 | |
| modified PSO (Sedghi et al., 2013) | 1.51393914 | 2.03440721 | 3.1910575 | 2.364745851 | |
| modified ACO (Zhu & Wang, 2016) | 1.42880839 | 1.72549789 | 1.59589807 | 1.409002754 | |
| modified cuckoo search (Chakraborty, Chatterjee, Dey, et al., 2017) | 1.77377859 | 1.8807976 | 1.37702388 | 1.631550862 | |
| SuFMoFPA (Proposed) | 1.49954426 | 1.80651403 | 0.80097162 | 2.595115205 | |
| robust modified GA (Shayeghi et al., 2007) | 1.53482292 | 2.68752282 | 3.4813301 | 2.06306391 | |
| modified PSO (Sedghi et al., 2013) | 0.91109125 | 2.59537271 | 2.5134342 | 2.954316867 | |
| modified ACO (Zhu & Wang, 2016) | 1.43064584 | 1.17580191 | 1.20036121 | 2.004273422 | |
| modified cuckoo search (Chakraborty, Chatterjee, Dey, et al., 2017) | 4.04527618 | 2.27041931 | 2.42526682 | 1.946313785 | |
| SuFMoFPA (Proposed) | 1.01088876 | 2.18670769 | 3.23843823 | 1.237978898 | |
| robust modified GA (Shayeghi et al., 2007) | 1.22658437 | 3.17522974 | 2.27317978 | 0.344527227 | |
| modified PSO (Sedghi et al., 2013) | 2.54989016 | 1.57511342 | 1.2428984 | 0.689328996 | |
| modified ACO (Zhu & Wang, 2016) | 0.28415421 | 2.74713111 | 1.02942694 | 2.712611798 | |
| modified cuckoo search (Chakraborty, Chatterjee, Dey, et al., 2017) | 2.8764765 | 3.23680059 | 1.39796326 | 2.361006173 | |
| SuFMoFPA (Proposed) | 1.07310418 | 2.0509123 | 1.32380555 | 1.530585878 | |
| robust modified GA (Shayeghi et al., 2007) | 0.61510902 | 1.41130686 | 2.31081462 | 2.454117072 | |
| modified PSO (Sedghi et al., 2013) | 0.69302372 | 2.23337638 | 2.6482827 | 2.660312932 | |
| modified ACO (Zhu & Wang, 2016) | 0.90384693 | 0.80032964 | 1.71976028 | 0.74821378 | |
| modified cuckoo search (Chakraborty, Chatterjee, Dey, et al., 2017) | 2.32272452 | 0.3677459 | 1.17416408 | 2.161732805 | |
| SuFMoFPA (Proposed) | 1.00737929 | 1.43298693 | 1.1225014 | 1.420251346 | |
| robust modified GA (Shayeghi et al., 2007) | 1.3731039 | 2.22284221 | 1.54779963 | 2.335616159 | |
| modified PSO (Sedghi et al., 2013) | 1.58257822 | 3.18142561 | 3.38494164 | 1.796379355 | |
| modified ACO (Zhu & Wang, 2016) | 2.53668303 | 2.53703367 | 2.76676462 | 1.256570426 | |
| modified cuckoo search (Chakraborty, Chatterjee, Dey, et al., 2017) | 1.45128835 | 0.92768719 | 2.83487868 | 1.638298952 | |
| SuFMoFPA (Proposed) | 1.84160988 | 1.79008218 | 2.7911172 | 0.761798871 | |
| robust modified GA (Shayeghi et al., 2007) | 0.97732237 | 1.50302038 | 1.28425245 | 1.357409005 | |
| modified PSO (Sedghi et al., 2013) | 3.54852343 | 2.89261202 | 3.28192626 | 0.845549773 | |
| modified ACO (Zhu & Wang, 2016) | 3.03732267 | 1.78607349 | 1.51302288 | 1.024783073 | |
| modified cuckoo search (Chakraborty, Chatterjee, Dey, et al., 2017) | 2.21838199 | 2.66022916 | 2.85416128 | 3.347336396 | |
| SuFMoFPA (Proposed) | 2.04570242 | 2.20236741 | 1.53215432 | 1.269017534 | |
| robust modified GA (Shayeghi et al., 2007) | 0.96299427 | 2.90984857 | 1.17120698 | 2.642412232 | |
| modified PSO (Sedghi et al., 2013) | 2.43261273 | 2.47702112 | 2.01797272 | 3.266493868 | |
| modified ACO (Zhu & Wang, 2016) | 1.59364378 | 1.85125757 | 3.0135343 | 3.339244033 | |
| modified cuckoo search (Chakraborty, Chatterjee, Dey, et al., 2017) | 3.23768482 | 3.4428074 | 3.61698754 | 3.057258286 | |
| SuFMoFPA (Proposed) | 1.02819889 | 2.88473661 | 2.63056273 | 1.718441873 | |
| robust modified GA (Shayeghi et al., 2007) | 1.5158794 | 0.90469494 | 1.1378578 | 2.157363193 | |
| modified PSO (Sedghi et al., 2013) | 1.45799655 | 1.51945747 | 3.10569445 | 4.308694749 | |
| modified ACO (Zhu & Wang, 2016) | 1.61444958 | 0.67963783 | 2.55840916 | 0.981993266 | |
| modified cuckoo search (Chakraborty, Chatterjee, Dey, et al., 2017) | 4.33053578 | 3.60084369 | 2.66888415 | 1.489080936 | |
| SuFMoFPA (Proposed) | 0.41959794 | 1.39546262 | 1.5516554 | 1.183681245 | |
| robust modified GA (Shayeghi et al., 2007) | 2.92505535 | 3.04178458 | 2.45828714 | 2.454949186 | |
| modified PSO (Sedghi et al., 2013) | 0.92664642 | 0.98893148 | 1.29211482 | 0.594085259 | |
| modified ACO (Zhu & Wang, 2016) | 1.17945546 | 2.05736916 | 2.2385389 | 2.056917812 | |
| modified cuckoo search (Chakraborty, Chatterjee, Dey, et al., 2017) | 2.68811487 | 4.12460479 | 2.72524349 | 2.601467668 | |
| SuFMoFPA (Proposed) | 1.85109038 | 1.23907301 | 1.09513163 | 1.224494386 | |
| Average | robust modified GA (Shayeghi et al., 2007) | 1.631098 | 2.069624 | 2.041688 | 1.901073 |
| modified PSO (Sedghi et al., 2013) | 1.755908 | 1.88935 | 2.209535 | 2.168382 | |
| modified ACO (Zhu & Wang, 2016) | 1.550649 | 1.706108 | 1.875383 | 1.825539 | |
| modified cuckoo search (Chakraborty, Chatterjee, Dey, et al., 2017) | 2.265901 | 2.114515 | 1.845491 | 1.876714 | |
| SuFMoFPA (Proposed) | 1.320236 | 1.639451 | 1.744748 | 1.522415 | |
Table 5.
Comparison of different segmentation methods with the Xie-Beni index values (Highlighted values denotes the acceptable values).
| Image Id | Algorithm | No. of Clusters |
|||
|---|---|---|---|---|---|
| 3 | 5 | 7 | 9 | ||
| robust modified GA (Shayeghi et al., 2007) | 3.21817245 | 1.36519126 | 1.37370621 | 0.832343158 | |
| modified PSO (Sedghi et al., 2013) | 2.17940336 | 2.00732781 | 1.91394161 | 1.736100633 | |
| modified ACO (Zhu & Wang, 2016) | 2.19583107 | 1.24738026 | 1.40991562 | 2.590986787 | |
| modified cuckoo search (Chakraborty, Chatterjee, Dey, et al., 2017) | 1.13218772 | 2.48575471 | 1.36003351 | 1.827333414 | |
| SuFMoFPA (Proposed) | 2.36627797 | 0.92609827 | 1.48464329 | 0.42034107 | |
| robust modified GA (Shayeghi et al., 2007) | 2.68233984 | 3.52564787 | 2.64236667 | 2.717464341 | |
| modified PSO (Sedghi et al., 2013) | 2.28652953 | 2.30104937 | 0.97089446 | 1.67302776 | |
| modified ACO (Zhu & Wang, 2016) | 1.63053092 | 3.33795819 | 3.68980214 | 1.507676081 | |
| modified cuckoo search (Chakraborty, Chatterjee, Dey, et al., 2017) | 2.91912589 | 1.8666488 | 1.92677413 | 2.582014527 | |
| SuFMoFPA (Proposed) | 0.8117843 | 1.28927477 | 1.04297006 | 2.266470147 | |
| robust modified GA (Shayeghi et al., 2007) | 4.87045671 | 3.21325653 | 2.26552738 | 2.477519609 | |
| modified PSO (Sedghi et al., 2013) | 3.68718368 | 3.61315881 | 2.9575926 | 3.603151966 | |
| modified ACO (Zhu & Wang, 2016) | 3.76907001 | 3.93736001 | 3.03620985 | 2.160024412 | |
| modified cuckoo search (Chakraborty, Chatterjee, Dey, et al., 2017) | 2.27505226 | 2.42443772 | 2.83502179 | 3.103077692 | |
| SuFMoFPA (Proposed) | 1.71822942 | 2.02281672 | 3.87167305 | 1.979848481 | |
| robust modified GA (Shayeghi et al., 2007) | 2.74340266 | 2.78224527 | 3.12958372 | 2.737426929 | |
| modified PSO (Sedghi et al., 2013) | 1.62907192 | 1.64898948 | 2.82690111 | 2.656397918 | |
| modified ACO (Zhu & Wang, 2016) | 1.21734389 | 1.01377112 | 1.80297714 | 2.111560047 | |
| modified cuckoo search (Chakraborty, Chatterjee, Dey, et al., 2017) | 2.23264547 | 1.07518795 | 1.93924806 | 1.464449536 | |
| SuFMoFPA (Proposed) | 1.05084803 | 1.86424393 | 1.58397303 | 2.474808563 | |
| robust modified GA (Shayeghi et al., 2007) | 2.88523588 | 1.874593 | 2.15274233 | 1.086324633 | |
| modified PSO (Sedghi et al., 2013) | 2.32294144 | 1.81637124 | 1.42260397 | 2.745273247 | |
| modified ACO (Zhu & Wang, 2016) | 2.67335291 | 2.06601942 | 1.79012347 | 2.410216274 | |
| modified cuckoo search (Chakraborty, Chatterjee, Dey, et al., 2017) | 2.86329968 | 1.24600699 | 1.24162556 | 1.623343707 | |
| SuFMoFPA (Proposed) | 1.63114379 | 1.05156975 | 1.43117277 | 0.965257035 | |
| robust modified GA (Shayeghi et al., 2007) | 2.63300482 | 1.18379706 | 1.13787659 | 2.704963143 | |
| modified PSO (Sedghi et al., 2013) | 1.40202358 | 0.94763653 | 1.18797854 | 3.008681424 | |
| modified ACO (Zhu & Wang, 2016) | 1.25010936 | 0.84928892 | 1.25056741 | 1.164569476 | |
| modified cuckoo search (Chakraborty, Chatterjee, Dey, et al., 2017) | 2.21819335 | 0.94250707 | 1.81469575 | 2.28152942 | |
| SuFMoFPA (Proposed) | 0.86378523 | 0.57133645 | 1.25309223 | 1.427646696 | |
| robust modified GA (Shayeghi et al., 2007) | 4.1891548 | 4.88492581 | 3.96898641 | 3.719715939 | |
| modified PSO (Sedghi et al., 2013) | 4.27485496 | 3.33563516 | 1.71947535 | 2.175527606 | |
| modified ACO (Zhu & Wang, 2016) | 3.004285 | 3.72027465 | 3.18668583 | 3.470873592 | |
| modified cuckoo search (Chakraborty, Chatterjee, Dey, et al., 2017) | 2.8890883 | 2.06306755 | 3.07727844 | 2.664247727 | |
| SuFMoFPA (Proposed) | 1.88280107 | 3.95342752 | 2.3180929 | 2.715312615 | |
| robust modified GA (Shayeghi et al., 2007) | 3.46905142 | 2.47990393 | 1.66895615 | 2.365868215 | |
| modified PSO (Sedghi et al., 2013) | 1.27976206 | 2.99584076 | 3.27660735 | 2.513513065 | |
| modified ACO (Zhu & Wang, 2016) | 1.88795608 | 2.25034876 | 1 0.7877613 | 2.588727005 | |
| modified cuckoo search (Chakraborty, Chatterjee, Dey, et al., 2017) | 1.1942788 | 3.11714096 | 2.95424688 | 2.31370579 | |
| SuFMoFPA (Proposed) | 2.2580697 | 1.20701143 | 1.56911353 | 2.606214047 | |
| robust modified GA (Shayeghi et al., 2007) | 1.24618871 | 0.64676108 | 0.7108075 | 2.923074858 | |
| modified PSO (Sedghi et al., 2013) | 3.1905011 | 1.80549786 | 1.66312933 | 1.670702967 | |
| modified ACO (Zhu & Wang, 2016) | 1.518378 | 2.94049124 | 1.55888295 | 2.844178345 | |
| modified cuckoo search (Chakraborty, Chatterjee, Dey, et al., 2017) | 1.62117672 | 1.42795605 | 2.2731199 | 0.804572159 | |
| SuFMoFPA (Proposed) | 0.99415379 | 1.5837012 | 1.39345292 | 1.368263896 | |
| robust modified GA (Shayeghi et al., 2007) | 3.5664172 | 2.11307998 | 0.52173083 | 0.705577543 | |
| modified PSO (Sedghi et al., 2013) | 2.39855285 | 2.01074484 | 2.88952903 | 1.415173255 | |
| modified ACO (Zhu & Wang, 2016) | 1.33526641 | 1.02509423 | 1.55461444 | 3.077377137 | |
| modified cuckoo search (Chakraborty, Chatterjee, Dey, et al., 2017) | 0.42095703 | 1.83375494 | 1.10662455 | 1.351317264 | |
| SuFMoFPA (Proposed) | 2.90165104 | 1.17241288 | 1.26429887 | 0.24945176 | |
| robust modified GA (Shayeghi et al., 2007) | 1.10477625 | 2.81995288 | 2.58449323 | 2.618595149 | |
| modified PSO (Sedghi et al., 2013) | 0.08541246 | 1.91146671 | 2.02244803 | 4.384603468 | |
| modified ACO (Zhu & Wang, 2016) | 2.19733738 | 0.43085828 | 1.8402415 | 2.691986128 | |
| modified cuckoo search (Chakraborty, Chatterjee, Dey, et al., 2017) | 4.29823505 | 1.80859507 | 2.93591826 | 1.839428366 | |
| SuFMoFPA (Proposed) | 0.98436623 | 2.223423 | 3.94400992 | 1.859826731 | |
| robust modified GA (Shayeghi et al., 2007) | 1.42854313 | 2.564549 | 2.50745286 | 1.01021662 | |
| modified PSO (Sedghi et al., 2013) | 2.55044632 | 1.44757483 | 1.97426354 | 1.320351713 | |
| modified ACO (Zhu & Wang, 2016) | 1.08783035 | 2.89308407 | 1.80323366 | 3.180526833 | |
| modified cuckoo search (Chakraborty, Chatterjee, Dey, et al., 2017) | 2.39079188 | 3.40368176 | 1.88121939 | 2.135322085 | |
| SuFMoFPA (Proposed) | 2.20279543 | 1.54105389 | 2.84407727 | 2.187520039 | |
| robust modified GA (Shayeghi et al., 2007) | 0.99301454 | 1.32707249 | 2.28544596 | 3.428079106 | |
| modified PSO (Sedghi et al., 2013) | 0.7490175 | 1.91574923 | 2.46777988 | 2.055655827 | |
| modified ACO (Zhu & Wang, 2016) | 0.82664572 | 0.59339851 | 2.77438008 | 1.048554517 | |
| modified cuckoo search (Chakraborty, Chatterjee, Dey, et al., 2017) | 2.79289801 | 0.59131407 | 1.02416727 | 1.763133485 | |
| SuFMoFPA (Proposed) | 1.7610329 | 3.81683047 | 2.81223407 | 2.364123586 | |
| robust modified GA (Shayeghi et al., 2007) | 0.22006745 | 0.86055227 | 1.82069224 | 2.242449359 | |
| modified PSO (Sedghi et al., 2013) | 1.72968283 | 2.78441235 | 2.87998407 | 2.007299512 | |
| modified ACO (Zhu & Wang, 2016) | 2.92256927 | 2.0446814 | 2.06883674 | 1.70090367 | |
| modified cuckoo search (Chakraborty, Chatterjee, Dey, et al., 2017) | 2.03300801 | 2.12343218 | 2.8543342 | 1.551431688 | |
| SuFMoFPA (Proposed) | 1.83154788 | 2.65621274 | 2.12845904 | 1.817467588 | |
| robust modified GA (Shayeghi et al., 2007) | 0.35249741 | 2.11438251 | 1.98098198 | 0.833641185 | |
| modified PSO (Sedghi et al., 2013) | 2.51857315 | 2.5984684 | 2.89267801 | 1.569651809 | |
| modified ACO (Zhu & Wang, 2016) | 3.26182455 | 1.6343017 | 1.81108183 | 0.807782546 | |
| modified cuckoo search (Chakraborty, Chatterjee, Dey, et al., 2017) | 2.2698238 | 2.36713893 | 2.88798836 | 3.999939242 | |
| SuFMoFPA (Proposed) | 3.13955162 | 2.53717758 | 2.26363163 | 2.176438597 | |
| robust modified GA (Shayeghi et al., 2007) | 1.92818846 | 3.3276728 | 2.51147115 | 1.829572857 | |
| modified PSO (Sedghi et al., 2013) | 1.98628832 | 2.60809164 | 1.30794522 | 3.881667058 | |
| modified ACO (Zhu & Wang, 2016) | 0.57874494 | 1.16557843 | 2.36074575 | 3.155892364 | |
| modified cuckoo search (Chakraborty, Chatterjee, Dey, et al., 2017) | 2.95600656 | 3.16356094 | 2.95930208 | 2.763235569 | |
| SuFMoFPA (Proposed) | 1.76006559 | 2.11442515 | 5.14117809 | 1.560251665 | |
| robust modified GA (Shayeghi et al., 2007) | 1.0189718 | 0.1566355 | 1.32292613 | 1.906411138 | |
| modified PSO (Sedghi et al., 2013) | 2.06525797 | 1.83796498 | 3.27385569 | 3.954765376 | |
| modified ACO (Zhu & Wang, 2016) | 0.97340241 | 1.15638837 | 1.54883415 | 1.336527526 | |
| modified cuckoo search (Chakraborty, Chatterjee, Dey, et al., 2017) | 4.63174044 | 4.85891753 | 2.95700702 | 1.416670977 | |
| SuFMoFPA (Proposed) | 1.04984083 | 4.29808824 | 1.98875903 | 1.945587123 | |
| robust modified GA (Shayeghi et al., 2007) | 3.48061386 | 3.14204392 | 2.13706718 | 2.247345259 | |
| modified PSO (Sedghi et al., 2013) | 0.71351645 | 1.22469501 | 1.36076698 | 1.464676443 | |
| modified ACO (Zhu & Wang, 2016) | 1.18504581 | 1.90007151 | 2.11212867 | 2.464056407 | |
| modified cuckoo search (Chakraborty, Chatterjee, Dey, et al., 2017) | 1.28985517 | 2.70210051 | 3.02767788 | 2.755097766 | |
| SuFMoFPA (Proposed) | 1.41875201 | 2.28290882 | 2.54149114 | 2.424585243 | |
| Average | robust modified GA (Shayeghi et al., 2007) | 2.335005411 | 2.243459064 | 2.040156362 | 2.13258828 |
| modified PSO (Sedghi et al., 2013) | 2.05827886 | 2.156148612 | 2.167131932 | 2.435345614 | |
| modified ACO (Zhu & Wang, 2016) | 1.86197356 | 1.900352726 | 2.09407419 | 2.239578842 | |
| modified cuckoo search (Chakraborty, Chatterjee, Dey, et al., 2017) | 2.357131341 | 2.194511318 | 2.280904613 | 2.124436134 | |
| SuFMoFPA (Proposed) | 1.701483157 | 2.061778489 | 2.270906824 | 1.822745271 | |
Table 6.
Comparison of different segmentation methods with the Dunn index values (Highlighted values denotes the acceptable values).
| Image Id | Algorithm | No. of Clusters |
|||
|---|---|---|---|---|---|
| 3 | 5 | 7 | 9 | ||
| robust modified GA (Shayeghi et al., 2007) | 1.12535573 | 1.61578897 | 4.08857997 | 1.905081252 | |
| modified PSO (Sedghi et al., 2013) | 3.74240514 | 4.53644815 | 3.93796563 | 2.206052346 | |
| modified ACO (Zhu & Wang, 2016) | 4.07813945 | 2.22984218 | 3.0136908 | 3.430451366 | |
| modified cuckoo search (Chakraborty, Chatterjee, Dey, et al., 2017) | 3.02336228 | 3.40532418 | 2.6234403 | 4.045114582 | |
| SuFMoFPA (Proposed) | 1.20465098 | 4.72691948 | 0.72556603 | 2.230860023 | |
| robust modified GA (Shayeghi et al., 2007) | 0.67388477 | 0.37924682 | 1.01229087 | 0.371401309 | |
| modified PSO (Sedghi et al., 2013) | 2.12379148 | 0.13614716 | 3.09316933 | 0.702857413 | |
| modified ACO (Zhu & Wang, 2016) | 0.83057152 | 0.72541859 | 1.53110771 | 1.798947306 | |
| modified cuckoo search (Chakraborty, Chatterjee, Dey, et al., 2017) | 1.4247201 | 1.39796129 | 2.9206735 | 1.79260722 | |
| SuFMoFPA (Proposed) | 1.77849394 | 2.26010929 | 3.21819337 | 1.54670362 | |
| robust modified GA (Shayeghi et al., 2007) | 0.27645967 | 1.08953352 | 1.85659804 | 1.584958757 | |
| modified PSO (Sedghi et al., 2013) | 0.5135087 | 0.0277859 | 1.76580402 | 0.598600031 | |
| modified ACO (Zhu & Wang, 2016) | 1.02015134 | 1.18862089 | 1.62740649 | 0.199552398 | |
| modified cuckoo search (Chakraborty, Chatterjee, Dey, et al., 2017) | 2.76700722 | 1.61928839 | 1.5456074 | 3.114432622 | |
| SuFMoFPA (Proposed) | 1.86738691 | 1.1010286 | 2.99042464 | 2.198167978 | |
| robust modified GA (Shayeghi et al., 2007) | 0.43265393 | 0.9089483 | 0.31715197 | 1.664270374 | |
| modified PSO (Sedghi et al., 2013) | 0.48782614 | 0.29953957 | 1.80272564 | 2.283849511 | |
| modified ACO (Zhu & Wang, 2016) | 2.0973503 | 0.804764 | 0.90457287 | 0.784878997 | |
| modified cuckoo search (Chakraborty, Chatterjee, Dey, et al., 2017) | 0.94912988 | 1.47172469 | 1.40035734 | 1.831345324 | |
| SuFMoFPA (Proposed) | 3.03713567 | 1.7705106 | 0.41365583 | 2.273399184 | |
| robust modified GA (Shayeghi et al., 2007) | 1.75251283 | 2.10414104 | 1.19411085 | 0.930799564 | |
| modified PSO (Sedghi et al., 2013) | 0.16893279 | 0.38204891 | 1.82656744 | 1.157408411 | |
| modified ACO (Zhu & Wang, 2016) | 0.80168041 | 0.53885776 | 2.21644001 | 3.33477766 | |
| modified cuckoo search (Chakraborty, Chatterjee, Dey, et al., 2017) | 1.52392077 | 0.43724981 | 2.59218063 | 1.705536748 | |
| SuFMoFPA (Proposed) | 3.85647327 | 2.10913175 | 2.10302368 | 2.453340434 | |
| robust modified GA (Shayeghi et al., 2007) | 1.98274446 | 1.6841264 | 1.18028628 | 0.863347565 | |
| modified PSO (Sedghi et al., 2013) | 0.26504151 | 2.62308356 | 4.01097655 | 2.458085347 | |
| modified ACO (Zhu & Wang, 2016) | 2.99658324 | 3.00682622 | 1.41340446 | 2.640352682 | |
| modified cuckoo search (Chakraborty, Chatterjee, Dey, et al., 2017) | 1.98771487 | 1.18145786 | 1.43427534 | 2.725758672 | |
| SuFMoFPA (Proposed) | 1.61986091 | 1.0012967 | 4.52813153 | 1.828473353 | |
| robust modified GA (Shayeghi et al., 2007) | 0.03567237 | 0.74251006 | 3.30533244 | 2.960232017 | |
| modified PSO (Sedghi et al., 2013) | 1.65448103 | 2.08776357 | 2.18141231 | 0.008377465 | |
| modified ACO (Zhu & Wang, 2016) | 0.28990355 | 0.50583374 | 0.74786489 | 1.751319553 | |
| modified cuckoo search (Chakraborty, Chatterjee, Dey, et al., 2017) | 1.01823885 | 0.88426808 | 0.14329284 | 3.076938017 | |
| SuFMoFPA (Proposed) | 4.65062371 | 1.81888595 | 1.19360059 | 2.341863431 | |
| robust modified GA (Shayeghi et al., 2007) | 0.46762575 | 0.98111232 | 0.2363378 | 1.301492095 | |
| modified PSO (Sedghi et al., 2013) | 3.50159548 | 0.03993424 | 0.83938028 | 0.770974762 | |
| modified ACO (Zhu & Wang, 2016) | 2.56030394 | 1.79836797 | 0.81428664 | 1.799451758 | |
| modified cuckoo search (Chakraborty, Chatterjee, Dey, et al., 2017) | 0.63599478 | 1.2713109 | 0.08120175 | 1.838166072 | |
| SuFMoFPA (Proposed) | 3.64491352 | 3.02948476 | 1.68982292 | 2.139971306 | |
| robust modified GA (Shayeghi et al., 2007) | 0.87124016 | 1.36016844 | 1.81508208 | 2.746990589 | |
| modified PSO (Sedghi et al., 2013) | 4.19588116 | 1.84804193 | 1.88863398 | 1.080175537 | |
| modified ACO (Zhu & Wang, 2016) | 0.37935729 | 2.97962137 | 2.61451103 | 2.060206272 | |
| modified cuckoo search (Chakraborty, Chatterjee, Dey, et al., 2017) | 3.31761798 | 3.66026645 | 3.59355705 | 4.578409411 | |
| SuFMoFPA (Proposed) | 2.9280758 | 4.41427395 | 3.90686462 | 1.889027695 | |
| robust modified GA (Shayeghi et al., 2007) | 1.71308337 | 2.57918531 | 3.472013 | 2.894621015 | |
| modified PSO (Sedghi et al., 2013) | 3.51067707 | 3.6804834 | 4.20999705 | 2.040446984 | |
| modified ACO (Zhu & Wang, 2016) | 3.91554431 | 1.69577549 | 3.01877796 | 3.33552876 | |
| modified cuckoo search (Chakraborty, Chatterjee, Dey, et al., 2017) | 2.90294354 | 3.97209268 | 2.19230993 | 4.039165139 | |
| SuFMoFPA (Proposed) | 1.84609008 | 3.9931925 | 1.04178473 | 1.796884647 | |
| robust modified GA (Shayeghi et al., 2007) | 2.11605621 | 2.7016858 | 2.32089956 | 2.040890622 | |
| modified PSO (Sedghi et al., 2013) | 0.19326148 | 1.29244744 | 3.1218127 | 3.959432542 | |
| modified ACO (Zhu & Wang, 2016) | 1.20819205 | 0.74549486 | 0.41027461 | 2.578597498 | |
| modified cuckoo search (Chakraborty, Chatterjee, Dey, et al., 2017) | 3.92946018 | 2.58444185 | 2.17711825 | 2.186020531 | |
| SuFMoFPA (Proposed) | 1.95707205 | 2.03946121 | 4.6878584 | 2.073638044 | |
| robust modified GA (Shayeghi et al., 2007) | 0.838755 | 3.59989836 | 1.51810874 | 0.546175437 | |
| modified PSO (Sedghi et al., 2013) | 3.60942136 | 0.71660202 | 2.18079874 | 1.325483556 | |
| modified ACO (Zhu & Wang, 2016) | 0.88814174 | 2.83481384 | 1.27071954 | 3.244886146 | |
| modified cuckoo search (Chakraborty, Chatterjee, Dey, et al., 2017) | 2.39904194 | 2.95128964 | 2.19801115 | 2.623335759 | |
| SuFMoFPA (Proposed) | 1.88991079 | 1.43751981 | 3.46975149 | 2.164342801 | |
| robust modified GA (Shayeghi et al., 2007) | 1.22925491 | 1.42229243 | 2.73024479 | 2.559421351 | |
| modified PSO (Sedghi et al., 2013) | 0.44568111 | 1.64928522 | 2.33534677 | 2.943228742 | |
| modified ACO (Zhu & Wang, 2016) | 1.93856904 | 0.47494083 | 2.18503931 | 1.550660621 | |
| modified cuckoo search (Chakraborty, Chatterjee, Dey, et al., 2017) | 2.41472033 | 0.69026251 | 1.0381164 | 1.184316929 | |
| SuFMoFPA (Proposed) | 2.59614135 | 4.08411025 | 2.23356922 | 2.289015299 | |
| robust modified GA (Shayeghi et al., 2007) | 2.3478567 | 2.23264276 | 1.78127824 | 1.596607169 | |
| modified PSO (Sedghi et al., 2013) | 1.836135 | 2.80021459 | 3.39016033 | 1.707833052 | |
| modified ACO (Zhu & Wang, 2016) | 2.95217015 | 2.29434247 | 2.57750903 | 0.686348581 | |
| modified cuckoo search (Chakraborty, Chatterjee, Dey, et al., 2017) | 1.84350732 | 2.38885812 | 2.92955856 | 1.604039136 | |
| SuFMoFPA (Proposed) | 1.92531342 | 2.05327029 | 4.62150971 | 2.014009802 | |
| robust modified GA (Shayeghi et al., 2007) | 0.69394011 | 2.48058702 | 1.02352207 | 1.958463577 | |
| modified PSO (Sedghi et al., 2013) | 2.87660663 | 3.2850893 | 2.86999687 | 1.896004966 | |
| modified ACO (Zhu & Wang, 2016) | 2.63362583 | 2.7087012 | 2.03774092 | 0.682257146 | |
| modified cuckoo search (Chakraborty, Chatterjee, Dey, et al., 2017) | 2.40016767 | 2.55868281 | 2.68173452 | 4.203708965 | |
| SuFMoFPA (Proposed) | 2.26261551 | 4.06478279 | 3.24136536 | 2.00582908 | |
| robust modified GA (Shayeghi et al., 2007) | 1.28057124 | 3.12410702 | 1.34990754 | 1.701904384 | |
| modified PSO (Sedghi et al., 2013) | 2.28967642 | 2.58036004 | 0.8950637 | 3.579965207 | |
| modified ACO (Zhu & Wang, 2016) | 1.54549966 | 1.48056375 | 2.75748805 | 2.750500444 | |
| modified cuckoo search (Chakraborty, Chatterjee, Dey, et al., 2017) | 2.3260119 | 3.24011433 | 2.72159848 | 2.787082695 | |
| SuFMoFPA (Proposed) | 2.9428701 | 2.31184632 | 4.4780755 | 2.140141906 | |
| robust modified GA (Shayeghi et al., 2007) | 1.72957874 | 0.68293573 | 1.01932287 | 2.862744247 | |
| modified PSO (Sedghi et al., 2013) | 1.9693704 | 1.97936832 | 3.4024238 | 3.981022433 | |
| modified ACO (Zhu & Wang, 2016) | 0.98140635 | 1.01289196 | 1.85292021 | 0.920427273 | |
| modified cuckoo search (Chakraborty, Chatterjee, Dey, et al., 2017) | 3.87030128 | 4.23734844 | 2.24640752 | 0.643010075 | |
| SuFMoFPA (Proposed) | 0.0388915 | 3.02172489 | 1.61481739 | 1.876040136 | |
| robust modified GA (Shayeghi et al., 2007) | 2.96208646 | 2.69070595 | 2.18238358 | 2.212471484 | |
| modified PSO (Sedghi et al., 2013) | 0.45375751 | 1.45264234 | 0.83294531 | 0.715728097 | |
| modified ACO (Zhu & Wang, 2016) | 1.31021766 | 1.89294933 | 1.98705276 | 2.449007895 | |
| modified cuckoo search (Chakraborty, Chatterjee, Dey, et al., 2017) | 2.69220643 | 3.57281612 | 3.06597316 | 3.088158888 | |
| SuFMoFPA (Proposed) | 2.83685521 | 4.85155301 | 2.27747269 | 2.745606669 | |
| Average | robust modified GA (Shayeghi et al., 2007) | 1.392228 | 1.953287 | 2.508091 | 1.879283 |
| modified PSO (Sedghi et al., 2013) | 1.838011 | 1.872875 | 2.185965 | 1.573213 | |
| modified ACO (Zhu & Wang, 2016) | 1.813528 | 1.734997 | 2.051701 | 2.291343 | |
| modified cuckoo search (Chakraborty, Chatterjee, Dey, et al., 2017) | 1.833804 | 1.819202 | 1.86698 | 2.422787 | |
| SuFMoFPA (Proposed) | 2.68384 | 2.691592 | 2.270533 | 2.167687 | |
Table 7.
Comparison of different segmentation methods with the index values (Highlighted values denotes the acceptable values).
| Image Id | Algorithm | No. of Clusters |
|||
|---|---|---|---|---|---|
| 3 | 5 | 7 | 9 | ||
| robust modified GA (Shayeghi et al., 2007) | 1.08030166 | 2.54577616 | 3.22490003 | 2.347810386 | |
| modified PSO (Sedghi et al., 2013) | 0.12896068 | 1.0972991 | 2.50810354 | 3.105269436 | |
| modified ACO (Zhu & Wang, 2016) | 0.95460335 | 1.10476818 | 1.52963416 | 2.744418936 | |
| modified cuckoo search (Chakraborty, Chatterjee, Dey, et al., 2017) | 3.67130847 | 1.32872736 | 2.13048943 | 1.894271413 | |
| SuFMoFPA (Proposed) | 0.39961555 | 2.05274396 | 3.95434278 | 2.433800915 | |
| robust modified GA (Shayeghi et al., 2007) | 1.60888678 | 2.52923119 | 2.17984335 | 0.17301238 | |
| modified PSO (Sedghi et al., 2013) | 3.4656689 | 0.7370578 | 1.34864831 | 1.062931572 | |
| modified ACO (Zhu & Wang, 2016) | 0.75240613 | 2.52461831 | 1.90775524 | 2.708374815 | |
| modified cuckoo search (Chakraborty, Chatterjee, Dey, et al., 2017) | 2.28630694 | 2.71348371 | 1.84906597 | 2.303622357 | |
| SuFMoFPA (Proposed) | 1.25105943 | 1.26202883 | 3.56707587 | 1.50230463 | |
| robust modified GA (Shayeghi et al., 2007) | 0.85462328 | 1.13172637 | 2.44214648 | 2.332910353 | |
| modified PSO (Sedghi et al., 2013) | 0.05850133 | 1.54902953 | 2.48389261 | 2.474018521 | |
| modified ACO (Zhu & Wang, 2016) | 1.15553341 | 0.11922888 | 2.25133489 | 0.96989777 | |
| modified cuckoo search (Chakraborty, Chatterjee, Dey, et al., 2017) | 2.62117707 | 1.22497331 | 1.46286087 | 2.202865732 | |
| SuFMoFPA (Proposed) | 2.01391643 | 3.60499596 | 2.54503349 | 2.478372258 | |
| robust modified GA (Shayeghi et al., 2007) | −0.323756 | 2.1072883 | 1.53166572 | 1.130117436 | |
| modified PSO (Sedghi et al., 2013) | 2.52282579 | 2.99556638 | 3.05567925 | 2.597314922 | |
| modified ACO (Zhu & Wang, 2016) | 3.84312474 | 1.46517086 | 1.77834996 | 1.627108032 | |
| modified cuckoo search (Chakraborty, Chatterjee, Dey, et al., 2017) | 2.40700832 | 1.9367675 | 1.96927611 | 2.334228243 | |
| SuFMoFPA (Proposed) | 2.22061779 | 2.9231381 | 4.04870654 | 0.389403893 | |
| robust modified GA (Shayeghi et al., 2007) | 0.90736785 | 1.09738243 | 1.1964885 | 1.965702243 | |
| modified PSO (Sedghi et al., 2013) | 2.70120004 | 3.10898795 | 2.83360465 | 0.799582251 | |
| modified ACO (Zhu & Wang, 2016) | 2.80200617 | 2.25668212 | 1.80455619 | 0.565179198 | |
| modified cuckoo search (Chakraborty, Chatterjee, Dey, et al., 2017) | 1.24901793 | 2.9797685 | 4.00365635 | 3.211382077 | |
| SuFMoFPA (Proposed) | 2.50442646 | 3.45505346 | 3.95273903 | 1.710608254 | |
| robust modified GA (Shayeghi et al., 2007) | 1.48932711 | 2.64378217 | 1.61909543 | 2.715290484 | |
| modified PSO (Sedghi et al., 2013) | 2.18962706 | 3.19300694 | 2.23155991 | 2.6998225 | |
| modified ACO (Zhu & Wang, 2016) | 1.17775759 | 1.6740792 | 2.82040535 | 2.854924226 | |
| modified cuckoo search (Chakraborty, Chatterjee, Dey, et al., 2017) | 2.46858705 | 3.25291566 | 2.55103456 | 2.180550543 | |
| SuFMoFPA (Proposed) | 0.19171251 | 3.04508239 | 4.83691179 | 1.876129512 | |
| robust modified GA (Shayeghi et al., 2007) | 1.03190965 | 0.92863533 | 1.70238882 | 2.033984423 | |
| modified PSO (Sedghi et al., 2013) | 2.66441796 | 1.84029684 | 3.02041233 | 3.328463297 | |
| modified ACO (Zhu & Wang, 2016) | 1.01154939 | 1.77237091 | 2.61272764 | 0.885098898 | |
| modified cuckoo search (Chakraborty, Chatterjee, Dey, et al., 2017) | 4.31950134 | 4.03012854 | 2.61867249 | 1.208037556 | |
| SuFMoFPA (Proposed) | 0.90437179 | 3.99787823 | 2.42973167 | 1.957067206 | |
| robust modified GA (Shayeghi et al., 2007) | 3.38371626 | 2.6349559 | 2.25267573 | 1.651698877 | |
| modified PSO (Sedghi et al., 2013) | 1.30299086 | 1.53569527 | 1.21467864 | 0.931970088 | |
| modified ACO (Zhu & Wang, 2016) | 1.26054601 | 2.10699216 | 1.89587126 | 2.524847925 | |
| modified cuckoo search (Chakraborty, Chatterjee, Dey, et al., 2017) | 3.17034431 | 3.80187904 | 3.4724212 | 2.526850986 | |
| SuFMoFPA (Proposed) | 2.60614501 | 4.9605439 | 2.39995219 | 2.92391514 | |
| robust modified GA (Shayeghi et al., 2007) | 0.71399444 | 2.14788247 | 2.72756786 | 2.616832182 | |
| modified PSO (Sedghi et al., 2013) | 2.44888085 | 0.52143725 | 1.7003886 | 1.505823292 | |
| modified ACO (Zhu & Wang, 2016) | 3.0116282 | 3.45612248 | 2.40811288 | 2.035794501 | |
| modified cuckoo search (Chakraborty, Chatterjee, Dey, et al., 2017) | 2.59708775 | 2.17195911 | 2.00127627 | 3.378663995 | |
| SuFMoFPA (Proposed) | 2.83994234 | 1.92787401 | 5.00456648 | 3.639328475 | |
| robust modified GA (Shayeghi et al., 2007) | 1.81960457 | 2.35468121 | 3.5681476 | 1.597325231 | |
| modified PSO (Sedghi et al., 2013) | 0.60991396 | 0.83944781 | 1.65777353 | 3.498810794 | |
| modified ACO (Zhu & Wang, 2016) | 0.76997978 | 1.37772079 | 0.71073799 | 2.016448483 | |
| modified cuckoo search (Chakraborty, Chatterjee, Dey, et al., 2017) | 4.0215901 | 1.64210239 | 3.31696429 | 1.34090451 | |
| SuFMoFPA (Proposed) | 0.22223857 | 2.30889269 | 3.95499191 | 1.228755654 | |
| robust modified GA (Shayeghi et al., 2007) | 1.15289064 | 1.5291455 | 2.05372676 | 3.03432955 | |
| modified PSO (Sedghi et al., 2013) | 0.48630903 | 2.5296523 | 1.78686171 | 2.5096375 | |
| modified ACO (Zhu & Wang, 2016) | 1.18699733 | 1.08986712 | 2.34039959 | 1.006494197 | |
| modified cuckoo search (Chakraborty, Chatterjee, Dey, et al., 2017) | 2.36262768 | 0.8773631 | 0.75446494 | 1.701325217 | |
| SuFMoFPA (Proposed) | 1.05915599 | 2.96080359 | 2.2682372 | 3.215903931 | |
| robust modified GA (Shayeghi et al., 2007) | 1.099847 | 1.95694211 | 1.26228229 | 1.294054493 | |
| modified PSO (Sedghi et al., 2013) | 1.33645051 | 2.65755194 | 3.91970296 | 2.117279192 | |
| modified ACO (Zhu & Wang, 2016) | 2.31398358 | 2.69638937 | 2.67147565 | 2.171889289 | |
| modified cuckoo search (Chakraborty, Chatterjee, Dey, et al., 2017) | 1.90548359 | 2.01335749 | 2.1705331 | 2.171304072 | |
| SuFMoFPA (Proposed) | 2.91573865 | 2.3324229 | 4.03121674 | 1.097428558 | |
| robust modified GA (Shayeghi et al., 2007) | 1.3966156 | 1.89421075 | 0.62674073 | 2.074990828 | |
| modified PSO (Sedghi et al., 2013) | 3.09948678 | 2.80258726 | 3.01168379 | 0.417157951 | |
| modified ACO (Zhu & Wang, 2016) | 3.68787034 | 1.93767678 | 2.18609032 | 1.93744153 | |
| modified cuckoo search (Chakraborty, Chatterjee, Dey, et al., 2017) | 2.459167 | 2.51295226 | 4.05511791 | 4.112032152 | |
| SuFMoFPA (Proposed) | 3.09240172 | 4.6510254 | 3.39698465 | 2.503391612 | |
| robust modified GA (Shayeghi et al., 2007) | 1.75901468 | 2.89057369 | 1.48593163 | 1.940841246 | |
| modified PSO (Sedghi et al., 2013) | 1.91261272 | 3.0947708 | 1.51191584 | 3.398500184 | |
| modified ACO (Zhu & Wang, 2016) | 1.01082091 | 1.71159966 | 3.14750022 | 2.67908343 | |
| modified cuckoo search (Chakraborty, Chatterjee, Dey, et al., 2017) | 3.22703421 | 2.71169602 | 3.68267574 | 2.413376839 | |
| SuFMoFPA (Proposed) | 1.23079627 | 2.75525092 | 4.22777124 | 2.234653012 | |
| robust modified GA (Shayeghi et al., 2007) | 1.63630722 | 0.34174905 | 1.1411655 | 2.268922039 | |
| modified PSO (Sedghi et al., 2013) | 1.92343591 | 2.57740959 | 4.13875254 | 3.438041968 | |
| modified ACO (Zhu & Wang, 2016) | 1.32360399 | 1.15506857 | 1.85106544 | 1.451104932 | |
| modified cuckoo search (Chakraborty, Chatterjee, Dey, et al., 2017) | 3.6072077 | 4.77845301 | 3.77258317 | 1.23872438 | |
| SuFMoFPA (Proposed) | 0.29891733 | 4.14725366 | 1.69171125 | 1.261310612 | |
| robust modified GA (Shayeghi et al., 2007) | 3.43809754 | 3.0480546 | 2.74492167 | 2.627967634 | |
| modified PSO (Sedghi et al., 2013) | 0.24807311 | 0.80150704 | 1.20288975 | 0.4368312 | |
| modified ACO (Zhu & Wang, 2016) | 2.0218355 | 2.05944617 | 2.27188204 | 1.973079218 | |
| modified cuckoo search (Chakraborty, Chatterjee, Dey, et al., 2017) | 3.90131485 | 3.44227838 | 3.10907189 | 3.029066541 | |
| SuFMoFPA (Proposed) | 1.50412711 | 5.06291945 | 2.6895786 | 2.641977937 | |
| robust modified GA (Shayeghi et al., 2007) | 1.15958777 | 2.37983691 | 2.75183093 | 1.785976134 | |
| modified PSO (Sedghi et al., 2013) | 2.73704867 | 0.31549428 | 2.11261402 | 1.168603999 | |
| modified ACO (Zhu & Wang, 2016) | 3.5972623 | 3.40862177 | 2.19918987 | 1.847951785 | |
| modified cuckoo search (Chakraborty, Chatterjee, Dey, et al., 2017) | 2.4957426 | 1.80301025 | 2.82065921 | 3.476861333 | |
| SuFMoFPA (Proposed) | 2.83342366 | 2.13269299 | 4.28523577 | 3.113438599 | |
| robust modified GA (Shayeghi et al., 2007) | 1.43661557 | 1.75386802 | 2.15887356 | 1.38820541 | |
| modified PSO (Sedghi et al., 2013) | 0.71616599 | 1.81928812 | 2.27493676 | 3.379698838 | |
| modified ACO (Zhu & Wang, 2016) | 1.02390364 | 1.03870838 | 1.30638805 | 3.652735604 | |
| modified cuckoo search (Chakraborty, Chatterjee, Dey, et al., 2017) | 4.28406919 | 1.17302868 | 2.1763827 | 2.444311055 | |
| SuFMoFPA (Proposed) | 2.41350136 | 1.44933675 | 4.2196256 | 1.040516042 | |
| Average | robust modified GA (Shayeghi et al., 2007) | 1.42472 | 1.995318 | 2.037244 | 1.943332 |
| modified PSO (Sedghi et al., 2013) | 1.697365 | 1.889783 | 2.334117 | 2.159431 | |
| modified ACO (Zhu & Wang, 2016) | 1.828078 | 1.830841 | 2.094082 | 1.98066 | |
| modified cuckoo search (Chakraborty, Chatterjee, Dey, et al., 2017) | 2.947476 | 2.46638 | 2.662067 | 2.398243 | |
| SuFMoFPA (Proposed) | 1.694562 | 3.057219 | 3.528023 | 2.06935 | |
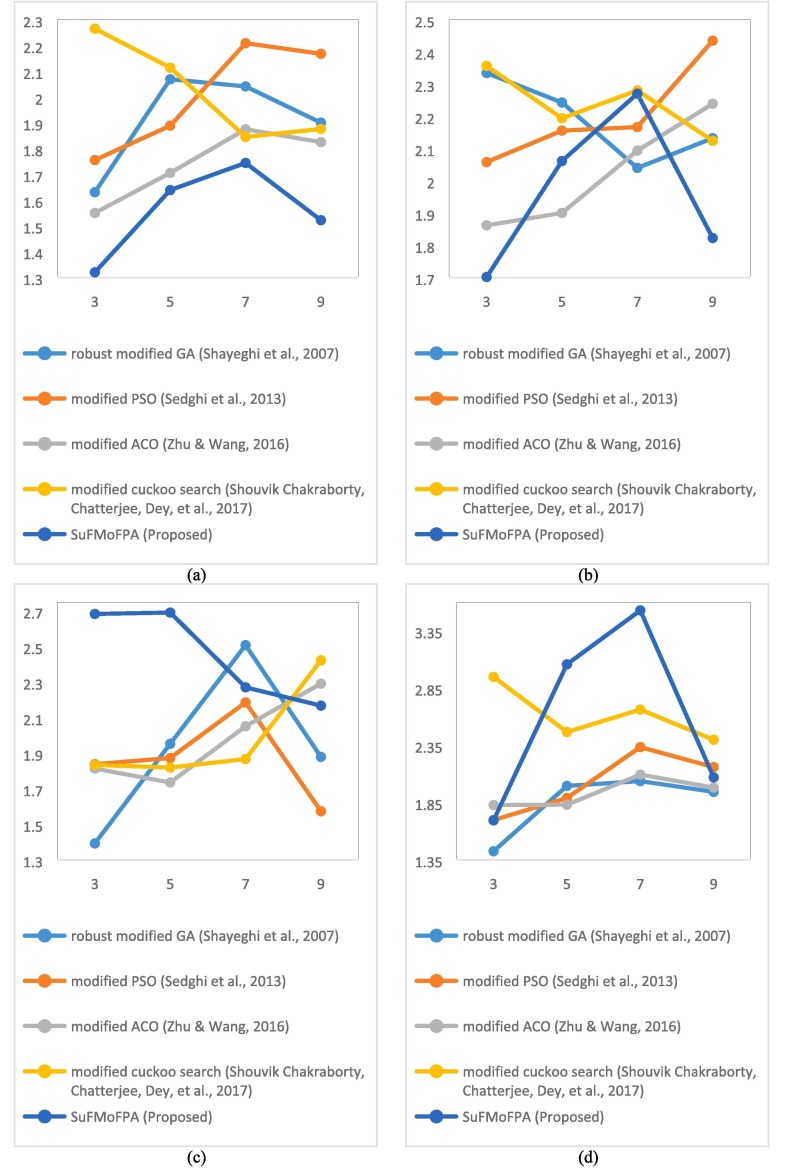
To get an overall understanding about the performance of all five approaches in terms of four different approaches and to interpret the obtained results in a better way, the average of 10 images for all approaches and different clusters are added at the end of each table and a graphical comparison is presented in Fig. 8 . In the average part of each table, the values in boldface denote the acceptable values for a certain number of clusters which are different from the rest of the table where the values in boldface indicate the best values in a row i.e. the best value for a particular approach. From this analysis, it can be observed that the proposed approach outperforms other approaches in most of the occasions. For example, in Fig. 8(a), it can be observed that the proposed approach completely outperforms all other approaches for all clusters.
Fig. 8.
Comparison of the average performance of all five algorithms for four different cluster validity indices i.e. (a) Davies-Bouldin, (b) Xie-Beni, (c) Dunn, and (d) index.
5.3. Analysis of the convergence rate
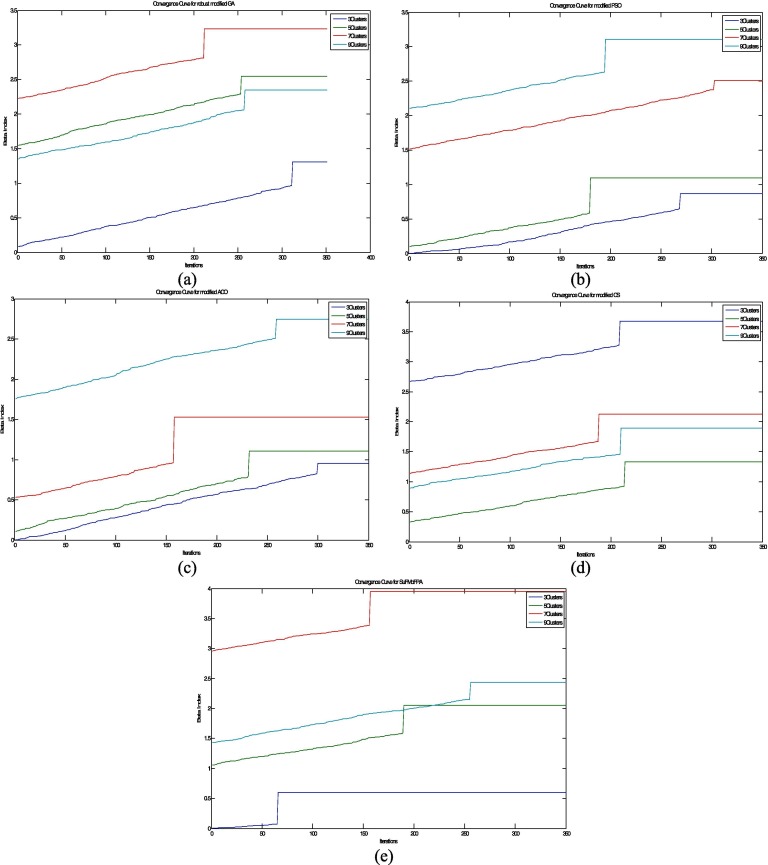
The convergence analysis is one of the important perspectives to analyze and compare the proposed approach with other methods. This subsection gives a graphical analysis of the convergence in terms of the index using. The higher value of the index indicates good clustering result. From Fig. 9 , it can be clearly understood that the proposed approach outperforms some standard approaches in terms of convergence. It also establishes the effectiveness and the real-life applicability of the proposed approach. The experiment is carried out for the different number of clusters and the performance of the proposed method is quite satisfactory for the higher number of clusters compared to other standard algorithms.
Fig. 9.
The analysis and comparison of the rate of convergence for different methods and for different number of clusters. These plots corresponds to the index and shows the convergence rate of (a) robust modified GA (Shayeghi et al., 2007), (b) modified PSO (Sedghi et al., 2013), (c) modified ACO (Zhu & Wang, 2016), (d) modified cuckoo search (Chakraborty, Chatterjee, Dey, et al., 2017), (e) SuFMoFPA (Proposed).
5.4. Analysis of the complexity
In this subsection, the complexity of the proposed approach is analyzed. The proposed algorithm is mainly divided into two phases. In the first phase, the superpixels are computed from the actual image based on the watershed-based approach. The noise sensitivity of the watershed-based superpixel computation approach is handled by determining the local minima from the gradient image. In the second phase, the fuzzy modified flower pollination approach is adapted to determine the optimal segmentation outcome. Now, the watershed-based approach is a simple approach to determine the superpixels that provide the linear complexity (Hu et al., 2015) which is one of the major motivations behind adapting this approach in this work. Now, the modification introduced in the flower pollination algorithm is nothing the incorporation of the type 2 fuzzy system where the fuzzy modified objective function is optimized by the flower pollination algorithm. It is known that the flower pollination algorithm takes linear time (Abdel-Basset & Shawky, 2019) for the optimization problems. So, the proposed approach is simple to implement as well as computational friendly.
5.5. Analysis of the parameter uncertainty
At first, during the computation of the superpixel image, it is always challenging to determine the structuring element and it is vital to choose the appropriate structuring element for a certain application. From Fig. 3, Fig. 4, the effect of the size of the structuring element can be observed. Secondly, the choice of the size of the initial population is another challenging job. The small size of the initial population can lead to a significant delay in the convergence. Similarly, a large initial population can cause introduce significant redundancy and can spoil the whole optimization process. So, the correct choice of this parameter is also essential. Thirdly, the choice of the number of clusters is very significant because it has a direct impact on the segmented outcome. In this work, it is chosen experimentally but automated processes can be incorporated to decide these values which will certainly increase the practical significance of this work.
6. Discussion
From the detailed analysis of the proposed SuFMoFPA approach, it can be concluded that the proposed approach can produce significant outcomes from the CT images which is beneficial to analyze the suspected COVID-19 patients without depending on any manual delineations. This approach significantly outperforms some other standard approaches in terms of both quantitatively and qualitatively. This work proposes a novel superpixel-based fuzzy objective function that is minimized using the fuzzy modified flower pollination algorithm. One major drawback of this approach is that the number of clusters cannot be automatically determined. In this work, the number of clusters is selected randomly. It can be incorporated in the future to make the proposed approach more realistic and suitable for practical applications. The proposed approach helps to significantly reduce the overhead of processing a huge amount of spatial information and it is beneficial from the perspective of quick and accurate diagnosis. From Fig. 8, it can be observed that the proposed approach completely outperforms some other approaches in terms of all four cluster validity indices. Therefore, this approach is useful for real-life COVID-19 screening purposes. Apart from producing satisfactory segmentation outcomes, the proposed approach not only performs well in terms of four cluster validity indices but also performs well in terms of the convergence. From Fig. 9(e), it can be noted that the proposed approach also works well for the higher number of clusters which are the major results of the proposed approach.
7. Conclusion
A novel method is proposed in this article to screen the COVID-19 patients at the earliest so that, the spread of this highly infectious disease can be restricted. The proposed SuFMoFPA approach uses the concept of superpixel to efficiently process the spatial information of the CT scan images. The type 2 fuzzy system and the modified flower pollination algorithm helps to efficiently exploit and explore the search space. The proposed approach is tested and compared using 115 CT scan images and out of them, the results of the 18 different CT scan images are reported. Four well-known cluster validity indices are used for the quantitative evaluation and the obtained results are quite promising and outperform some of the related approaches under discussion. This approach achieves significantly better segmentation results from both qualitative and quantitative points of view. From the obtained average values, the average values reported at the end of each table from Table 4, Table 5, Table 6, Table 7 and the graphical comparison in Fig. 8 reveals that on average, the proposed approach outperforms most of the other competitors. Moreover, Fig. 9 demonstrates the convergence performance of the proposed approach which is also quite satisfactory specifically for the higher number of clusters. It is an important point because, most of the time, an image consists of several small overlapping regions which are very difficult to segment. The proposed approach shows an impressive performance in terms of determining segments from the CT images without depending on any expert delineations which are highly beneficial in assessing COVID-19 suspects as well as in analyzing biomedical images in general. The proposed computer-aided approach helps determine the early signs of the COVID-19 infection from the CT scan image and detection of some prominent features (which are mentioned in Table 1) can be helpful in early isolation and treatment. This approach cannot replace the RT-PCR test to confirm the COVID-19 infection but can be helpful to take some early precautionary measures and can accelerate the treatment process.
CRediT authorship contribution statement
Shouvik Chakraborty: Conceptualization, Methodology, Software, Investigation. Kalyani Mali: . : Formal analysis, Resources, Writing - review & editing.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgement
The authors would like to express their gratitude and thank the editors, anonymous reviewers, and referees for their valuable comments and suggestions which are helpful in further improvement of this research work.
References
- Abdel-Basset, M., & Shawky, L. A. (2019). Flower pollination algorithm: a comprehensive review. In Artificial Intelligence Review (Vol. 52, Issue 4, pp. 2533–2557). Springer Netherlands. https://doi.org/10.1007/s10462-018-9624-4.
- Achanta R., Shaji A., Smith K., Lucchi A., Fua P., Süsstrunk S. SLIC superpixels compared to state-of-the-art superpixel methods. IEEE Transactions on Pattern Analysis and Machine Intelligence. 2012;34(11):2274–2281. doi: 10.1109/TPAMI.2012.120. [DOI] [PubMed] [Google Scholar]
- Ai T., Yang Z., Hou H., Zhan C., Chen C., Lv W.…Xia L. Correlation of Chest CT and RT-PCR Testing in Coronavirus Disease 2019 (COVID-19) in China: A Report of 1014 Cases. Radiology. 2020;200642 doi: 10.1148/radiol.2020200642. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Altan A., Karasu S. Recognition of COVID-19 disease from X-ray images by hybrid model consisting of 2D curvelet transform, chaotic salp swarm algorithm and deep learning technique. Chaos, Solitons and Fractals. 2020;140 doi: 10.1016/j.chaos.2020.110071. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bernheim A., Mei X., Huang M., Yang Y., Fayad Z.A., Zhang N.…Chung M. Chest CT Findings in Coronavirus Disease-19 (COVID-19): Relationship to Duration of Infection. Radiology. 2020;200463 doi: 10.1148/radiol.2020200463. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bezdek J.C., Ehrlich R., Full W. FCM: The fuzzy c-means clustering algorithm. Computers & Geosciences. 1984;10(2–3):191–203. doi: 10.1016/0098-3004(84)90020-7. [DOI] [Google Scholar]
- Butt C., Gill J., Chun D., Babu B.A. Deep learning system to screen coronavirus disease 2019 pneumonia. Applied Intelligence. 2020;1 doi: 10.1007/s10489-020-01714-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Caruso D., Zerunian M., Polici M., Pucciarelli F., Polidori T., Rucci C.…Laghi A. Chest CT Features of COVID-19 in Rome, Italy. Radiology. 2020;201237 doi: 10.1148/radiol.2020201237. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chakraborty, S., & Mali, K. (2018). Application of multiobjective optimization techniques in biomedical image segmentation—A study. In Multi-objective optimization (pp. 181–194). Springer Singapore. https://doi.org/10.1007/978-981-13-1471-1_8.
- Chakraborty, S., & Mali, K. (2020). An overview of biomedical image analysis from the deep learning perspective. In S. Chakraborty & K. Mali (Eds.), Applications of advanced machine intelligence in computer vision and object recognition: Emerging research and opportunities. IGI Global. https://doi.org/10.4018/978-1-7998-2736-8.ch008.
- Chakraborty S., Chatterjee S., Dey N., Ashour A.S., Ashour A.S., Shi F., Mali K. Modified cuckoo search algorithm in microscopic image segmentation of hippocampus. Microscopy Research and Technique. 2017;80(10):1051–1072. doi: 10.1002/jemt.22900. [DOI] [PubMed] [Google Scholar]
- Chakraborty, S., Chatterjee, S., Ashour, A. S., Mali, K., & Dey, N. (2017). Intelligent computing in medical imaging: A Study. In N. Dey (Ed.), Advancements in applied metaheuristic computing (pp. 143–163). IGI Global. https://doi.org/10.4018/978-1-5225-4151-6.ch006.
- Chen, J., Wu, L., Zhang, J., Zhang, L., Gong, D., Zhao, Y., Hu, S., Wang, Y., Hu, X., Zheng, B., Zhang, K., Wu, H., Dong, Z., Xu, Y., Zhu, Y., Chen, X., Yu, L., & Yu, H. (2020). Deep learning-based model for detecting 2019 novel coronavirus pneumonia on high-resolution computed tomography: A prospective study. MedRxiv, 2020.02.25.20021568. https://doi.org/10.1101/2020.02.25.20021568. [DOI] [PMC free article] [PubMed]
- Comaniciu D., Meer P. Mean shift: A robust approach toward feature space analysis. IEEE Transactions on Pattern Analysis and Machine Intelligence. 2002;24(5):603–619. doi: 10.1109/34.1000236. [DOI] [Google Scholar]
- Davies D.L., Bouldin D.W. A Cluster Separation Measure. IEEE Transactions on Pattern Analysis and Machine Intelligence. 1979;PAMI-1(2):224–227. doi: 10.1109/TPAMI.1979.4766909. [DOI] [PubMed] [Google Scholar]
- Dong D., Tang Z., Wang S., Hui H., Gong L., Lu Y.…Li H. The role of imaging in the detection and management of COVID-19: A review. IEEE Reviews in Biomedical Engineering. 2020 doi: 10.1109/RBME.2020.2990959. [DOI] [PubMed] [Google Scholar]
- Dunn J.C. Well-separated clusters and optimal fuzzy partitions. Journal of Cybernetics. 1974;4(1):95–104. doi: 10.1080/01969727408546059. [DOI] [Google Scholar]
- Eiben, A. E., & Schippers, C. A. (1998). On evolutionary exploration and exploitation. In Fundamenta Informaticae (Vol. 35). 1{16 1 IOS Press.
- Fang Y., Zhang H., Xie J., Lin M., Ying L., Pang P., Ji W. Sensitivity of Chest CT for COVID-19: Comparison to RT-PCR. Radiology. 2020;200432 doi: 10.1148/radiol.2020200432. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fourcade A., Khonsari R.H. Deep learning in medical image analysis: A third eye for doctors. Journal of Stomatology, Oral and Maxillofacial Surgery. 2019;120(4):279–288. doi: 10.1016/j.jormas.2019.06.002. [DOI] [PubMed] [Google Scholar]
- Gozes, O., Frid-Adar, M., Greenspan, H., Browning, P. D., Zhang, H., Ji, W., Bernheim, A., & Siegel, E. (2020). Rapid AI Development Cycle for the Coronavirus (COVID-19) Pandemic: Initial Results for Automated Detection & Patient Monitoring using Deep Learning CT Image Analysis. http://arxiv.org/abs/2003.05037.
- Hore S., Chakroborty S., Ashour A.S., Dey N., Ashour A.S., Sifaki-Pistolla D.…Chaudhuri S.R.B. Finding contours of hippocampus brain cell using microscopic image analysis. Journal of Advanced Microscopy Research. 2015;10(2):93–103. doi: 10.1166/jamr.2015.1245. [DOI] [Google Scholar]
- Hore, S., Chakraborty, S., Chatterjee, S., Dey, N., Ashour, A. S., Van Chung, L., Nguyen, G., & Nhuong Le, D. (2016). An integrated interactive technique for image segmentation using stack based seeded region growing and thresholding. International Journal of Electrical and Computer Engineering (IJECE), 6(6), 2773–2780. https://doi.org/10.11591/ijece.v6i6.11801.
- Hu, Z., Zou, Q., & Li, Q. (2015). Watershed superpixel. In Proceedings - International conference on image processing, ICIP, 2015-December (pp. 349–353). https://doi.org/10.1109/ICIP.2015.7350818.
- Jin, S., Wang, B., Xu, H., Luo, C., Wei, L., Zhao, W., Hou, X., Ma, W., Xu, Z., Zheng, Z., Sun, W., Lan, L., Zhang, W., Mu, X., Shi, C., Wang, Z., Lee, J., Jin, Z., Lin, M., … Xu, W. (2020). AI-assisted CT imaging analysis for COVID-19 screening: Building and deploying a medical AI system in four weeks. MedRxiv, 2020.03.19.20039354. https://doi.org/10.1101/2020.03.19.20039354.
- Kahn C.E., Langlotz C.P., Burnside E.S., Carrino J.A., Channin D.S., Hovsepian D.M., Rubin D.L. Toward best practices in radiology reporting. Radiology. 2009;252(3):852–856. doi: 10.1148/radiol.2523081992. [DOI] [PubMed] [Google Scholar]
- Kanne J.P., Little B.P., Chung J.H., Elicker B.M., Ketai L.H. Essentials for radiologists on COVID-19: An update-radiology scientific expert panel. Radiology. 2020;200527 doi: 10.1148/radiol.2020200527. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Laradji, I., Rodriguez, P., Mañas, O., Lensink, K., Law, M., Kurzman, L., Parker, W., Vazquez, D., & Nowrouzezahrai, D. (2020). A weakly supervised consistency-based learning method for COVID-19 segmentation in CT images. http://arxiv.org/abs/2007.02180.
- Laradji, I., Rodriguez, P., Branchaud-Charron, F., Lensink, K., Atighehchian, P., Parker, W., Vazquez, D., & Nowrouzezahrai, D. (2020). A weakly supervised region-based active learning method for COVID-19 segmentation in CT images. http://arxiv.org/abs/2007.07012.
- Lei T., Jia X., Zhang Y., Liu S., Meng H., Nandi A.K. Superpixel-Based Fast Fuzzy C-Means Clustering for Color Image Segmentation. IEEE Transactions on Fuzzy Systems. 2019;27(9):1753–1766. doi: 10.1109/TFUZZ.2018.2889018. [DOI] [Google Scholar]
- Liew A.W.C., Leung S.H., Lau W.H. Fuzzy image clustering incorporating spatial continuity. IEE Proceedings: Vision, Image and Signal Processing. 2000;147(2):185–192. doi: 10.1049/ip-vis:20000218. [DOI] [Google Scholar]
- Liu, S., Wang, Y., Yang, X., Lei, B., Liu, L., Li, S. X., Ni, D., & Wang, T. (2019). Deep learning in medical ultrasound analysis: A review. In Engineering (Vol. 5, Issue 2, pp. 261–275). Elsevier Ltd. https://doi.org/10.1016/j.eng.2018.11.020.
- Mei, X., Lee, H. C., Diao, K. yue, Huang, M., Lin, B., Liu, C., Xie, Z., Ma, Y., Robson, P. M., Chung, M., Bernheim, A., Mani, V., Calcagno, C., Li, K., Li, S., Shan, H., Lv, J., Zhao, T., Xia, J., … Yang, Y. (2020). Artificial intelligence–enabled rapid diagnosis of patients with COVID-19. Nature Medicine, 26(8), 1224–1228. https://doi.org/10.1038/s41591-020-0931-3. [DOI] [PMC free article] [PubMed]
- Mohammed A., Wang C., Zhao M., Ullah M., Naseem R., Wang H.…Cheikh F.A. Weakly-supervised network for detection of COVID-19 in Chest CT Scans. IEEE Access. 2020;8:155987–156000. doi: 10.1109/ACCESS.2020.3018498. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moore, A. P., Prince, S. J. D., Warrell, J., Mohammed, U., & Jones, G. (2008). Superpixel lattices. In 26th IEEE conference on computer vision and pattern recognition, CVPR. https://doi.org/10.1109/CVPR.2008.4587471.
- Pal S.K., Ghosh A., Shankar B.U. Segmentation of remotely sensed images with fuzzy thresholding, and quantitative evaluation. International Journal of Remote Sensing. 2000;21(11):2269–2300. doi: 10.1080/01431160050029567. [DOI] [Google Scholar]
- Pesapane, F., Volonté, C., Codari, M., & Sardanelli, F. (2018). Artificial intelligence as a medical device in radiology: ethical and regulatory issues in Europe and the United States. In Insights into imaging (Vol. 9, Issue 5, pp. 745–753). Springer Verlag. https://doi.org/10.1007/s13244-018-0645-y. [DOI] [PMC free article] [PubMed]
- Rhee, F. C. H., & Cheul H. (n.d.). A type-2 fuzzy C-means clustering algorithm. In Proceedings joint 9th IFSA World Congress and 20th NAFIPS International Conference (Cat. No. 01TH8569), 4 (pp. 1926–1929). https://doi.org/10.1109/NAFIPS.2001.944361.
- Roy, M., Chakraborty, S., Mali, K., Chatterjee, S., Banerjee, S., Chakraborty, A., Biswas, R., Karmakar, J., & Roy, K. (2017). Biomedical image enhancement based on modified Cuckoo Search and morphology. In 2017 8th Industrial automation and electromechanical engineering conference, IEMECON 2017. https://doi.org/10.1109/IEMECON.2017.8079595.
- Samuel A.L. Some studies in machine learning using the game of checkers. IBM Journal of Research and Development. 2000;44(1–2):207–219. doi: 10.1147/rd.441.0206. [DOI] [Google Scholar]
- Sedghi M., Aliakbar-Golkar M., Haghifam M.R. Distribution network expansion considering distributed generation and storage units using modified PSO algorithm. International Journal of Electrical Power and Energy Systems. 2013;52(1):221–230. doi: 10.1016/j.ijepes.2013.03.041. [DOI] [Google Scholar]
- Shayeghi H., Jalili A., Shayanfar H.A. Robust modified GA based multi-stage fuzzy LFC. Energy Conversion and Management. 2007;48(5):1656–1670. doi: 10.1016/j.enconman.2006.11.010. [DOI] [Google Scholar]
- Shi F., Wang J., Shi J., Wu Z., Wang Q., Tang Z.…Shen D. Review of artificial intelligence techniques in imaging data acquisition, segmentation and diagnosis for COVID-19. IEEE Reviews in Biomedical Engineering. 2020 doi: 10.1109/RBME.2020.2987975. [DOI] [PubMed] [Google Scholar]
- Shoeibi, A., Khodatars, M., Alizadehsani, R., Ghassemi, N., Jafari, M., Moridian, P., Khadem, A., Sadeghi, D., Hussain, S., Zare, A., Sani, Z. A., Bazeli, J., Khozeimeh, F., Khosravi, A., Nahavandi, S., Acharya, U. R., & Shi, P. (2020). Automated detection and forecasting of COVID-19 using deep learning techniques: A review. http://arxiv.org/abs/2007.10785.
- Sistrom C.L., Dang P.A., Weilburg J.B., Dreyer K.J., Rosenthal D.I., Thrall J.H. Effect of computerized order entry with integrated decision support on the growth of outpatient procedure volumes: Seven-year time series analysis. Radiology. 2009;251(1):147–155. doi: 10.1148/radiol.2511081174. [DOI] [PubMed] [Google Scholar]
- Torkian P., Ramezani N., Kiani P., Bax M.R., Akhlaghpoor S. Common CT findings of novel coronavirus disease 2019 (COVID-19): A case series. Cureus. 2020;12(3) doi: 10.7759/cureus.7434. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang X., Deng X., Fu Q., Zhou Q., Feng J., Ma H.…Zheng C. A weakly-supervised framework for COVID-19 classification and lesion localization from Chest CT. IEEE Transactions on Medical Imaging. 2020;39(8):2615–2625. doi: 10.1109/TMI.2020.2995965. [DOI] [PubMed] [Google Scholar]
- Xie X.L., Beni G. A validity measure for fuzzy clustering. IEEE Transactions on Pattern Analysis and Machine Intelligence. 1991;13(8):841–847. doi: 10.1109/34.85677. [DOI] [Google Scholar]
- Xu X., Jiang X., Ma C., Du P., Li X., Lv S.…Wu W. Deep Learning System to Screen Coronavirus Disease 2019 Pneumonia. Applied Intelligence. 2020;2019:1–5. http://arxiv.org/abs/2002.09334. [Google Scholar]
- Yang, X. S. (2012). Flower pollination algorithm for global optimization. Lecture Notes in Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics), 7445 LNCS (pp. 240–249). https://doi.org/10.1007/978-3-642-32894-7_27.
- Yao, Q., Xiao, L., Liu, P., & Zhou, S. K. (2020). Label-free segmentation of COVID-19 Lesions in Lung CT. http://arxiv.org/abs/2009.06456. [DOI] [PMC free article] [PubMed]
- Ye Z., Zhang Y., Wang Y., Huang Z., Song B. Chest CT manifestations of new coronavirus disease 2019 (COVID-19): A pictorial review. European Radiology. 2020;30(8):4381–4389. doi: 10.1007/s00330-020-06801-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhu F., Wang H. A modified ACO algorithm for virtual network embedding based on graph decomposition. Computer Communications. 2016;80:1–15. doi: 10.1016/j.comcom.2015.07.014. [DOI] [Google Scholar]