Maximizing mechanical stress in small urinary stones during burst wave lithotripsy

Abstract

Unlike shock wave lithotripsy, burst wave lithotripsy (BWL) uses tone bursts, consisting of many periods of a sinusoidal wave. In this work, an analytical theoretical approach to modeling mechanical stresses in a spherical stone was developed to assess the dependence of frequency and stone size on stress generated in the stone. The analytical model for spherical stones is compared against a finite-difference model used to calculate stress in nonspherical stones. It is shown that at low frequencies, when the wavelength is much greater than the diameter of the stone, the maximum principal stress is approximately equal to the pressure amplitude of the incident wave. With increasing frequency, when the diameter of the stone begins to exceed about half the wavelength in the surrounding liquid (the exact condition depends on the material of the stone), the maximum stress increases and can be more than six times greater than the incident pressure. These results suggest that the BWL frequency should be elevated for small stones to improve the likelihood and rate of fragmentation.

I. INTRODUCTION

Urinary stone management often depends on the size and location of a stone. Stones found in the ureter smaller than 7 mm are often addressed by medical expulsion therapy, pain medication, and observation.^1,2 However, observation can leave patients debilitated for weeks before stone passage and many still require later intervention to remove a stone.^2,3 Similarly, smaller stones in the kidney that do not cause symptoms often receive active surveillance until they grow or move and cause later symptoms. Because of the pain and other potential symptoms associated with stones, many patients opt for earlier intervention rather than watchful waiting. However, these decisions are balanced against the potential complications and side effects of stone removal procedures.^4,5

Lithotripsy is one of the most common technologies used for urinary stone intervention. With this technology, stones are fragmented by transcutaneous ultrasonic pulses with the expectation that fragments will then spontaneously pass through the urinary tract.⁶ The most widely used method is shock wave lithotripsy (SWL), in which short, broadband ultrasonic pulses (∼1 cycle) containing a shock front, are generated by an electrohydraulic, electromagnetic, or piezoelectric source and focused onto the stone to fragment it.⁷ Since the pulse duration is usually not adjustable for SWL, the fragmentation efficiency is commonly related to the magnitude of the positive and negative pressures, the spatial width of the focal beam waist, and the pulse repetition rate.⁸ Modeling and experiments have indicated that lithotripter designs with a beam larger than the width of the stone to be most effective.^9,10 Studies have shown that careful selection of these parameters can improve stone fragmentation in SWL.⁶ SWL is not commonly used in stones smaller than 5 mm because of their high rate of spontaneous passage and concern for tissue injury from the procedure.¹¹

Unlike SWL, burst wave lithotripsy (BWL) uses longer tone bursts, consisting of multiple periods of a sinusoidal profile.¹² Such pulses are narrow-band and thus, a new spatial scale (the wavelength) and a new timescale—the wave period of the center frequency—appear. As a result, the fracture density and size of fragments produced by BWL has been shown to be strongly dictated by the ultrasound frequency.^12,13 Previous studies have identified a frequency of 350 kHz for effectively fragmenting stones into 1–2 mm pieces,¹⁴ which can be accomplished with minimal trauma to the kidney tissue. These benefits and BWL's minimal risk suggest BWL may be useful to treat small stones that might otherwise be observed in order to alleviate symptoms and accelerate stone passage.

Based on previous work, one might also expect that the internal stress and the internal stress distribution within stones depends on this central frequency relative to stone size,¹³ and that both fragmentation time and fragment size might be optimized simultaneously with proper selection of frequency.¹² In larger stones, periodic elastic wave patterns constructively interfere to amplify the stress and lead to fracture.^13,15 However, when the stone diameter is similar to the wavelength or smaller, the edges of the stone serve as acoustically soft boundaries for internal waves, and the stress is limited. Thus, treatment of small stones requires special consideration. Analytical and numerical models can be used to assist in the understanding of how stress in the stone varies with frequency. Numerical models of linear stress within stones for SWL research have been previously published,^9,16,17 and have been demonstrated to predict the location and rate of stone fracture based on the location of maximum principal stress.⁹ Spherical, cylindrical, and irregular-shaped stones have been modeled and show similar response to acoustic pulses in SWL.

The goal of the current study is to develop an analytical model, validate it against a numerical (finite difference) model, and then use both to investigate the effect of frequency on stress magnitude in stones exposed to BWL pulses. These investigations lead to identification of specific ranges for frequency where BWL may be most effective in producing stress and fracturing small stones.

II. MATERIALS AND METHODS

An analytical model is derived for the spherical stone and validation against a previously employed numerical model. In addition, we use the numerical model to evaluate the dependance of the results on stone geometry and composition. Both spherical and nonspherical geometries are representative of actual kidney stones, although in clinical practice, the shape of an individual's stone can only be estimated from computed tomography with a resolution on the order of 1 mm.¹⁸ The material properties of urinary stones of different types have been characterized,^19,20 although clinically, the composition is usually unknown at the time of the procedure; thus, we evaluate these over their natural range. These results are used to describe the maximum principal stresses occurring in the stones as a function of frequency for different properties.

A. Analytical description

Here, an analytical description of elastic waves in a spherical stone in a liquid caused by an axisymmetric acoustic beam is derived. We consider that the continuous wave (CW) case, and physical quantities $\tilde{F}(\mathbf{r},t)$ (e.g., acoustic pressure $\tilde{p}$, stress components ${\tilde{T}}_{ij}$, particle displacement $\stackrel{\mathbf{~}}{\mathbf{u}}$, etc.) depend on time sinusoidally: $\tilde{F}(\mathbf{r},t)=\mathrm{Re}[F(\mathbf{r})\text{exp}\hspace{0.17em}(-i\omega \hspace{0.17em}t)]$, where $F$ is a complex amplitude of $\tilde{F}$. In the liquid, the wave equation results in the following Helmholtz equation:

$$\Delta p+k^{2}p=0.$$ (1)

Here, $p$ is the complex amplitude of the acoustic pressure, $k=\omega /c_0$ is the wavenumber, $\omega$ is angular frequency, and $c_0$ is the speed of sound in the liquid. According to the equation of motion, for the mentioned time dependence $\sim e^{-i\omega \hspace{0.17em}t}$, the particle displacement complex amplitude $\mathbf{u}$ in the liquid is expressed as follows:

$$\mathbf{u}=\frac{1}{{\rho }_0{c}_0^2{k}^2}\nabla p,$$ (2)

where ${\rho }_0$ is the liquid density.

The motion of the solid material (inside the sphere) is convenient to describe using the particle displacement vector $\mathbf{u}$. In the general case, it can be represented by the scalar and vector potentials $\Phi$ and $\mathbf{A}$:²¹

$$\mathbf{u}=-\nabla \Phi +\nabla \times \mathit{A}.$$ (3)

The scalar and vector potentials $\Phi$ and $\mathbf{A}$ describe the longitudinal and shear waves, correspondingly, and as such, are governed by the following Helmholtz equations:

$$\Delta \Phi +k_l^2\Phi =0,$$ (4)

$$\Delta \mathbf{A}+k_t^2\mathbf{A}=0.$$ (5)

Here, $k_l=\omega /c_l$ and $k_t=\omega /c_t$ are the wavenumbers for the longitudinal and shear waves. The corresponding wave velocities $c_l$ and $c_t$ are expressed as follows: $c_l=\sqrt{(\lambda +2\mu )/{\rho }_{\ast }}$, $c_t=\sqrt{\mu /{\rho }_{\ast }}$, where $\lambda$ and $\mu$ are the Lamé constants, and ${\rho }_{\ast }$ is the density of the sphere material. According to Hooke's law, the mechanical stress tensor is expressed through the displacement vector $\mathbf{u}=(u_1,u_2,u_3)$:

$$T_{ij}=\lambda {\delta }_{ij}\nabla \cdot \mathbf{u}+\mu \left(\frac{\partial u_i}{\partial x_j}+\frac{\partial u_j}{\partial x_j}\right),$$ (6)

where ${\delta }_{ij}$ is the Kronecker delta.

Let an axisymmetric beam with its axis directed along the z axis be scattered from an elastic sphere in a liquid. Let the center of the sphere be positioned at the origin of the coordinate system. In such a case, it is convenient to use spherical coordinates:

$$p_i=\sum _{n=0}^{\infty }{Q}_n{P}_n\left(\text{cos}\hspace{0.17em}\theta \right)j_n\left(kr\right),$$ (7)

where $r$ is radial distance (distance to origin, i.e., the stone center), $\theta$ is the polar angle (the angle with respect to axis $z$ axis), $P_n(.)$ and $j_n(.)$ are the Legendre polynomials and spherical Bessel functions, correspondingly, and the coefficients $Q_n$ describe the structure of the axisymmetric incident beam. For instance, in the case of a plane incident wave propagating along the $z$ axis, $p_i=p_0\hspace{0.17em}\text{exp}\hspace{0.17em}(\mathit{ikz})$,²²

$$Q_n^{\left(\text{plane}\hspace{0.17em}\text{wave}\right)}=p_0\hspace{0.17em}{i}^n\left(2n+1\right).$$ (8)

Another important case is a quasi-Gaussian beam focused on the center of the scatterer. The expression for $Q_n$ in such a case can also be presented analytically.²³

The scattered wave in fluid will be of the form

$$p_s=\sum _{n=0}^{\infty }{Q}_n{c}_n{h}_n{}^{(1)}(kr)P_n\left(\text{cos}\hspace{0.17em}\theta \right),$$ (9)

where $h_n^{(1)}(.)$ are the spherical Hankel functions of the first kind, and $c_n$ are coefficients that depend on sphere diameter and acoustic properties of the liquid and solid materials.

Because the incident acoustic beam has an axially symmetric structure, there is no dependence on the azimuthal angle $\phi$ (angle of rotation around the $z$ axis). Therefore, there is no displacement tangential to the direction of rotation ( $u_{\phi }=0$). The two other components of the vortical part of the displacement vector are ${(\nabla \times \mathbf{A})}_r=[\partial (A_{\phi }\hspace{0.17em}\text{sin}\hspace{0.17em}\theta )/\partial \theta -\partial A_{\theta }/\partial \phi ]/(r\hspace{0.17em}\text{sin}\hspace{0.17em}\theta )$ and ${(\nabla \times \mathbf{A})}_{\theta }=[(\partial A_r/\partial \phi )/\hspace{0.17em}\text{sin}\hspace{0.17em}\theta -\partial (r{A}_{\phi })/\partial r]/r$. Because $\partial A_r/\partial \phi =\partial A_{\theta }/\partial \phi =0$, only the azimuthal component $A_{\phi }$ is needed, i.e., the pair of functions $\Phi$ and $A_{\phi }$ fully describe the displacement field. These potentials can be expressed in the following form:^21,24

$$\Phi =\sum _{n=0}^{\infty }{a}_n{P}_n\left(\text{cos}\hspace{0.17em}\theta \right)j_n\left(k_{l}r\right),$$ (10)

$$A_{\phi }=\sum _{n=0}^{\infty }{b}_n{j}_n\left(k_{t}r\right)\frac{d{P}_n\left(\text{cos}\hspace{0.17em}\theta \right)}{d\theta }.$$ (11)

Here, $a_n$ and $b_n$ are coefficients and, similar to $c_n$, depend on the sphere diameter and acoustic properties of the media.

Because previous publications solving the problem of acoustic wave scattering from an elastic sphere do not describe the stress and displacement fields inside the sphere,^21,24,25 the corresponding expressions are derived here. Let us introduce the following notations for the spherical Bessel functions arguments: $\xi =k_{l\hspace{0.17em}}r$, $\eta =k_{t}r$, and $\varsigma =kr$. According to Eqs. (7) and (9), the complex amplitude of the total pressure $p=p_i+p_s$ has the following form:

$$p=\sum _{n=0}^{\infty }{Q}_n\left[j_n\left(\varsigma \right)+c_n{h}_n^{\left(1\right)}\left(\varsigma \right)\right]P_n\left(\hspace{0.17em}\text{cos}\hspace{0.17em}\theta \right).$$ (12)

The stress tensor components in the spherical coordinates are expressed by the following equations, which follow from Eqs. (3) and (6):

$$T_{rr}=\sum _{n=0}^{\infty }\{{\widehat{a}}_n\left[\nu j_n\left(\xi \right)-j_{\mathit{n}}^{″}\left(\xi \right)\right]+{\widehat{b}}_{n}n\left(n+1\right)\left[\frac{j_n\left(\eta \right)}{{\eta }^2}-\frac{j_{\mathit{n}}^{\prime }\left(\eta \right)}{\eta }\right]\}{P}_n\left(\text{cos}\hspace{0.17em}\theta \right),$$ (13)

$$\begin{array}{c}{T}_{\theta \theta }=\sum _{n=0}^{\infty }\left\{ {\widehat{a}}_n\left[\nu j_n\left(\xi \right)+n\left(n+1\right)\frac{j_n\left(\xi \right)}{{\xi }^2}-\frac{j_{\mathit{n}}^{\prime }\left(\xi \right)}{\xi }\right]+{\widehat{b}}_{n}n\left(n+1\right)\frac{j_{\mathit{n}}^{\prime }\left(\eta \right)}{\eta }\right\}{P}_n\left(\text{cos}\hspace{0.17em}\theta \right)\\ +\sum _{n=0}^{\infty }\left\{{\widehat{a}}_n\frac{j_n\left(\xi \right)}{{\xi }^2}+{\widehat{b}}_n\left[\frac{j_n\left(\eta \right)}{{\eta }^2}+\frac{j_{\mathit{n}}^{\prime }\left(\eta \right)}{\eta }\right]\right\}\frac{\hspace{0.17em}\text{cos}\hspace{0.17em}\theta }{\hspace{0.17em}\text{sin}\hspace{0.17em}\theta }\frac{d{P}_n\left(\text{cos}\hspace{0.17em}\theta \right)}{d\theta },\end{array}$$ (14)

$$\begin{array}{c}{T}_{\phi \phi }=\sum _{n=0}^{\infty }\left\{{\widehat{a}}_n\left[\nu j_n\left(\xi \right)-\frac{{j^{\prime }}_{\mathit{n}}\left(\xi \right)}{\xi }\right]-{\widehat{b}}_{n}n\left(n+1\right)\frac{j_n\left(\eta \right)}{{\eta }^2}\right\}{P}_n\left(\text{cos}\hspace{0.17em}\theta \right)\\ -\sum _{n=0}^{\infty }\left\{{\widehat{a}}_n\frac{j_n\left(\xi \right)}{{\xi }^2}+{\widehat{b}}_n\left[\frac{j_n\left(\eta \right)}{{\eta }^2}+\frac{{j^{\prime }}_{\mathit{n}}\left(\eta \right)}{\eta }\right]\right\}\frac{\hspace{0.17em}\text{cos}\hspace{0.17em}\theta }{\hspace{0.17em}\text{sin}\hspace{0.17em}\theta }\frac{d{P}_n\left(\text{cos}\hspace{0.17em}\theta \right)}{d\theta },\end{array}$$ (15)

$$T_{r\theta }=\sum _{n=0}^{\infty }\left\{{\widehat{a}}_n\left[\frac{j_n\left(\xi \right)}{{\xi }^2}-\frac{{j^{\prime }}_{\mathit{n}}\left(\xi \right)}{\xi }\right]-\frac{1}{2}{\widehat{b}}_n[j_{\mathit{n}}^{″}\left(\eta \right)+\left(n-1\right)\left(n+2\right)\frac{j_n\left(\eta \right)}{{\eta }^2}]\right\}\frac{d{P}_n\left(\text{cos}\hspace{0.17em}\theta \right)}{d\theta }.$$ (16)

Here, ${\widehat{a}}_n=2\mu k_l^2{a}_n$, ${\widehat{b}}_n=2\mu k_t^2{b}_n$, the prime indicates the derivative over the function argument, and the second derivative of the spherical Bessel function is expressed as $j_{\mathit{n}}^{″}(\xi )=[n(n+1)/{\xi }^2-1]j_n(\xi )-2{j^{\prime }}_n(\xi )/\xi$. Also, $\nu =\lambda /(2\mu )=\sigma /(1-2\sigma )$ is an auxiliary constant, where $\sigma =0.5(c_l^2-2c_t^2)/(c_l^2-c_t^2)$ is Poisson's ratio.

The particle displacement components in the liquid, according to Eqs. (2) and (12), are expressed as follows:

$$u_r=\sum _{n=0}^{\infty }\frac{Q_n}{k{\rho }_0{c}_0^2}\left[{j^{\prime }}_{\mathit{n}}\left(\varsigma \right)+c_n{h}_n^{\left(1\right)\prime }\left(\varsigma \right)\right]P_n\left(\text{cos}\hspace{0.17em}\theta \right),$$ (17)

$$u_{\theta }=\sum _{n=0}^{\infty }\frac{Q_n}{k{\rho }_0{c}_0^2}\left[\frac{j_n\left(\varsigma \right)}{\varsigma }+c_n\frac{h_n^{\left(1\right)}\left(\varsigma \right)}{\varsigma }\right]\frac{d{P}_n\left(\text{cos}\hspace{0.17em}\theta \right)}{d\theta }.$$ (18)

In the sphere, the corresponding expressions follow from Eqs. (3), (10), and (11):

$$u_r=-\sum _{n=0}^{\infty }\left\{k_l{a}_n{j^{\prime }}_{\mathit{n}}\left(\xi \right)+k_t{b}_{n}n\left(n+1\right)\frac{j_n\left(\eta \right)}{\eta }\right\}{P}_n\left(\text{cos}\hspace{0.17em}\theta \right),$$ (19)

$$u_{\theta }=-\sum _{n=0}^{\infty }\left\{k_l{a}_n\frac{j_n\left(\xi \right)}{\xi }+k_t{b}_n\left[\frac{j_n\left(\eta \right)}{\eta }+{j^{\prime }}_{\mathit{n}}\left(\eta \right)\right]\right\}\frac{d{P}_n\left(\text{cos}\hspace{0.17em}\theta \right)}{d\theta }.$$ (20)

Note that the related axial and lateral components of the particle displacement, $u_{\parallel }$ and $u_{\perp }$, are expressed through the components $u_r$ and $u_{\theta }$ as follows:

$$u_{\parallel }=u_r\hspace{0.17em}\text{cos}\hspace{0.17em}\theta -u_{\theta }\hspace{0.17em}\text{sin}\hspace{0.17em}\theta ,$$ (21)

$$u_{\perp }=u_r\hspace{0.17em}\text{sin}\hspace{0.17em}\theta +u_{\theta }\hspace{0.17em}\text{cos}\hspace{0.17em}\theta .$$ (22)

The expansions' coefficients $a_n$, $b_n$, and $c_n$ are derived from the boundary conditions on the surface of the sphere ( $r=a$), which are continuity of the normal stress $p=-T_{rr}$, absence of the tangential stress $T_{r\theta }=0$, and continuity of the normal component of the displacement $u_r$. The corresponding expressions can be represented in the following form:

$${\widehat{a}}_n={\beta }_n{W}_n,$$ (23)

$${\widehat{b}}_n=2{\alpha }_n{W}_n,$$ (24)

$$c_n=\frac{-{\Gamma }_n{j}_n\left(ka\right)+{j^{\prime }}_{\mathit{n}}\left(ka\right)}{{\Gamma }_n{h}_n^{\left(1\right)}\left(ka\right)-h_n^{{\left(1\right)}^{\prime }}\left(ka\right)},$$ (25)

where the following auxiliary notations are used:

$${\Gamma }_n=\frac{{\rho }_0{c}_0}{2{\rho }_{\ast }{c}_t}\frac{{\beta }_n{\gamma }_n+{\alpha }_n{\delta }_n}{{\beta }_n{\epsilon }_n+{\alpha }_n{\chi }_n},$$ (26)

$$W_n=\frac{Q_n}{{\beta }_n{\epsilon }_n+{\alpha }_n{\chi }_n}\frac{j_n\left(ka\right)h_n^{{\left(1\right)}^{\prime }}\left(ka\right)-j_{\mathit{n}}^{\prime }\left(ka\right)h_n^{\left(1\right)}\left(ka\right)}{{\Gamma }_n{h}_n^{\left(1\right)}\left(ka\right)-h_n^{{\left(1\right)}^{\prime }}\left(ka\right)},$$ (27)

$${\alpha }_n=\frac{j_n\left(k_{l}a\right)}{{\left(k_{l}a\right)}^2}-\frac{j_{\mathit{n}}^{\prime }\left(k_{l}a\right)}{k_{l}a},$$ (28)

$${\beta }_n=j_{\mathit{n}}^{″}\left(k_{t}a\right)+\left(n-1\right)\left(n+2\right)\frac{j_n\left(k_{t}a\right)}{{\left(k_{t}a\right)}^2},$$ (29)

$${\gamma }_n=\frac{c_l}{c_t}{j}_{\mathit{n}}^{\prime }\left(k_{l}a\right),$$ (30)

$${\delta }_n=2n\left(n+1\right)\frac{j_n\left(k_{t}a\right)}{k_{t}a},$$ (31)

$${\epsilon }_n=\frac{\sigma }{1-2\sigma }j\left(k_{l}a\right)-j_{\mathit{n}}^{″}\left(k_{l}a\right),$$ (32)

$${\chi }_n=2n\left(n+1\right)\left[\frac{j_n\left(k_{t}a\right)}{{\left(k_{t}a\right)}^2}-\frac{j_{\mathit{n}}^{\prime }\left(k_{t}a\right)}{k_{t}a}\right].$$ (33)

Note also that

$$a_n=\frac{{\widehat{a}}_n}{2{\rho }_{\ast }{\omega }^2}\frac{c_l^2}{c_t^2},$$ (34)

$$b_n=\frac{{\widehat{b}}_n}{2{\rho }_{\ast }{\omega }^2}.$$ (35)

Equations (12)–(35) provide the exact analytical solution of the considered problem.

In lithotripsy, the fracture of stones is the primary effect of interest. The maximum principal stress and peak elastic energy in the stone can be used as parameters that indicate the possibility to initiate appearance and growth of cracks. To find these values, it is necessary to express the time-dependent stress tensor components:

$${\tilde{T}}_{i j}\left(r,\theta ,t\right)=\mathrm{Re}\left[T_{i j}\left(r,\theta \right)\text{exp}\hspace{0.17em}\left(-i\omega \hspace{0.17em}t\right)\right].$$ (36)

The principal stress components can be expressed as follows:

$$T_{I,\hspace{0.17em}II}=\frac{{\tilde{T}}_{rr}+{\tilde{T}}_{\theta \theta }}{2}\pm \sqrt{{\left(\frac{{\tilde{T}}_{rr}-{\tilde{T}}_{\theta \theta }}{2}\right)}^2+{\tilde{T}}_{r\theta }{}^2},$$ (37)

$$T_{\mathit{III}}={\tilde{T}}_{\phi \phi }.$$ (38)

From here, the time-dependent maximum principal stress in different points in the stone can be calculated:

$$T_{\text{max}}=\text{max}\left(T_I,T_{II},T_{\mathit{III}}\right).$$ (39)

Elastic potential energy distribution in the stone can be characterized by the free energy density, which is expressed through the stress tensor:²⁶

$$E=\frac{1}{4\mu }{\tilde{T}}_{ik}{\tilde{T}}_{ik}-\left(\frac{1}{12\mu }-\frac{1}{18K}\right){\tilde{T}}_{ll}{}^2.$$ (40)

Here, $K=\lambda +2\mu /3$ is the bulk modulus, ${\tilde{T}}_{ik}{\tilde{T}}_{ik}={\tilde{T}}_{rr}^{\hspace{0.17em}2}+{\tilde{T}}_{\theta \theta }^{\hspace{0.17em}2}+{\tilde{T}}_{\phi \phi }^{\hspace{0.17em}2}+2{\tilde{T}}_{r\theta }^{\hspace{0.17em}2}$, and ${\tilde{T}}_{ll}={\tilde{T}}_{rr}+{\tilde{T}}_{\theta \theta }+{\tilde{T}}_{\phi \phi }$.

Note that for stones that are not too large in comparison with the wavelength, the greatest stresses and free energy density are achieved near the center of the stone. In the center of the sphere, expressions for the maximum principal stress and free energy density are simplified and do not require the use of infinite sums and special functions, since at $r=0$ only the terms of Eqs. (13)–(16) corresponding to the indices $n=0$ and $n=2$ are nonzero (see the Appendix).

B. Finite-difference model

The analytical solution described above is applicable only to the case of a uniform spherical stone. For stones of arbitrary shape and structure, the analysis can be performed using direct numerical modeling, e.g., in finite differences. Such an approach was applied to the problems of lithotripsy earlier.^9,15,16 In the axisymmetric case, it is convenient to use cylindrical coordinates $(r_{\perp },z,\phi )$, where $r_{\perp }$ is the transverse coordinate. Because of the axial symmetry, the velocity vector $\stackrel{\mathbf{~}}{\mathbf{v}}=\partial \stackrel{\mathbf{~}}{\mathbf{u}}/\partial t$ has only two components: radial, ${\tilde{v}}_{r_{\perp }}$, and axial, ${\tilde{v}}_z$, and the stress tensor has only four nonzero components: ${\tilde{T}}_{r_{\perp }{r}_{\perp }}$, ${\tilde{T}}_{zz}$, ${\tilde{T}}_{\phi \phi }$, and ${\tilde{T}}_{r_{\perp }z}$. Here, as earlier, the tilde indicates the full time-dependent quantity versus the complex amplitudes of the quantity. These six functions describing the mechanical field are governed by the following evolution equations:²⁷

$$\frac{\partial {\tilde{v}}_{r_{\perp }}}{\partial t}=\frac{1}{\rho }\left\{\frac{1}{r_{\perp }}\frac{\partial \left[r_{\perp }\left({\tilde{T}}_{r_{\perp }{r}_{\perp }}-{\tilde{T}}_{\phi \phi }\right)\right]}{\partial r_{\perp }}+\frac{\partial {\tilde{T}}_{r_{\perp }z}}{\partial z}+\frac{\partial {\tilde{T}}_{\phi \phi }}{\partial r_{\perp }}\right\},$$ (41)

$$\frac{\partial {\tilde{v}}_z}{\partial t}=\frac{1}{\rho }\left[\frac{1}{r_{\perp }}\frac{\partial \left(r_{\perp }{\tilde{T}}_{r_{\perp }z}\right)}{\partial r_{\perp }}+\frac{\partial {\tilde{T}}_{zz}}{\partial z}\right],$$ (42)

$$\frac{\partial {\tilde{T}}_{r_{\perp }{r}_{\perp }}}{\partial t}=\lambda \left[\frac{1}{r_{\perp }}\frac{\partial \left(r_{\perp } {\tilde{v}}_r\right)}{\partial r_{\perp }}+\frac{\partial {\tilde{v}}_z}{\partial z}\right]+2\mu \frac{\partial {\tilde{v}}_{r_{\perp }}}{\partial r_{\perp }},$$ (43)

$$\frac{\partial {\tilde{T}}_{zz}}{\partial t}=\lambda \frac{1}{r_{\perp }}\frac{\partial \left(r_{\perp } {\tilde{v}}_{r_{\perp }}\right)}{\partial r_{\perp }}+\left(\lambda +2\mu \right)\frac{\partial {\tilde{v}}_z}{\partial z},$$ (44)

$$\frac{\partial {\tilde{T}}_{\phi \phi }}{\partial t}=\lambda \frac{\partial {\tilde{v}}_z}{\partial z}+\left(\lambda +2\mu \right)\frac{1}{r_{\perp }}\frac{\partial \left(r_{\perp } {\tilde{v}}_{r_{\perp }}\right)}{\partial r_{\perp }}-2\mu \frac{\partial {\tilde{v}}_{r_{\perp }}}{\partial r_{\perp }},$$ (45)

$$\frac{\partial {\tilde{T}}_{r_{\perp }z}}{\partial t}=\mu \left(\frac{\partial {\tilde{v}}_z}{\partial r_{\perp }}+\frac{\partial {\tilde{v}}_{r_{\perp }}}{\partial z}\right).$$ (46)

In the numerical modeling, it is convenient to consider the liquid and stone as one inhomogeneous medium, whose parameters $\rho$, $\lambda$, and $\mu$ are functions of the coordinate locations. In the liquid, $\rho ={\rho }_0$, $\lambda ={\rho }_0{c}_0^2$, and $\mu =0$. In the stone, $\rho ={\rho }_{\ast }$, $\lambda ={\rho }_{\ast }(c_l^2-2c_t^2)$, and $\mu ={\rho }_{\ast }{c}_t^2$. When such parameters are used in Eqs. (41)–(46), the boundary conditions at the stone surface are satisfied automatically.

To solve the system of Eqs. (41)–(46) numerically, the partial differential equations are discretized using a central differencing scheme with staggered grids in both space and time. To account for an incident acoustic wave, a proper boundary condition is set at the calculation box boundary. The typical spatial grid step for the coordinates was 50 μm, and the temporal step was 10 ns, which was sufficient to maintain stability and accuracy. A perfectly matched layer (PML) of 1.5 mm thickness is placed at the boundary of the calculation region of 50 × 50 mm size.

Similar to the analytical approach, the results of numerical modeling are analyzed using maximum principal stress and free energy density. The principal stress components are expressed similar to Eqs. (37):

$$T_{I,\hspace{0.17em}II}=\frac{{\tilde{T}}_{r_{\perp }{r}_{\perp }}+{\tilde{T}}_{zz}}{2}\pm \sqrt{{\left(\frac{{\tilde{T}}_{r_{\perp }{r}_{\perp }}-{\tilde{T}}_{zz}}{2}\right)}^2+{\tilde{T}}_{r_{\perp }z}^{\hspace{0.17em}2}},$$ (47)

and the third principal stress is described by Eq. (38), i.e., $T_{\mathit{III}}={\tilde{T}}_{\phi \phi }$. The maximum principal stress then is calculated according to Eq. (39). The free energy density has the form of Eq. (40), in which ${\tilde{T}}_{ik}{\tilde{T}}_{ik}={\tilde{T}}_{r_{\perp }{r}_{\perp }}^{\hspace{0.17em}2}+{\tilde{T}}_{zz}^{\hspace{0.17em}2}+{\tilde{T}}_{\phi \phi }^{\hspace{0.17em}2}+2{\tilde{T}}_{r_{\perp }z}^{\hspace{0.17em}2}$ and ${\tilde{T}}_{ll}={\tilde{T}}_{r_{\perp }{r}_{\perp }}+{\tilde{T}}_{zz}+{\tilde{T}}_{\phi \phi }$.

In lithotripsy, the formation of cracks under the action of a tensile load is of interest; therefore, it is convenient to use the maximum principal stress $T_{\text{max}}$ as a parameter. As our interest is the effect of the wave frequency on $T_{\text{max}}$ and since the maximum principal stress also depends on time, it makes sense to use the peak value of the maximum stress in time, $\underset{\text{time}}{\text{max}}(T_{\text{max}})$, as an indicator of the impact at the selected point of the stone, and to characterize the possibility of stone fragmentation, use the largest value within the entire stone, $\underset{\text{space}}{\text{max}}[\underset{\text{time}}{\text{max}}(T_{\text{max}})]$. This value depends on the frequency of the wave and the size of the stone by means of a dimensionless frequency $ka$. Here, data are presented versus $ka$ for the sounds speed in the surrounding water.

C. Material properties

To relate the study to lithotripsy, the properties of the sphere are chosen to represent natural kidney stones and commonly used artificial stone models for testing as shown in Table I.^28–30 The liquid was water with the density ${\rho }_0$ = 1000 kg/m³ and the speed of sound $c_0$ = 1500 m/s, which is reasonable for urine or tissue that surrounds the stone. The shape of the stone was spherical for the analytical theory, and spherical, cylindrical, or biconical (with diameter equal to the length) for the finite-difference modeling.

TABLE I.

Material properties of common natural and artificial kidney stone compositions: calcium oxalate monohydrate (COM), calcium oxalate dihydrate (COD), struvite-magnesium ammonium phosphate hexahydrate (MAPH), and Ultracal-30 (United States Gypsum Company, Chicago, Illinois) gypsum artificial stone (U-30).

Material	Density ${\rho }_{\ast }$ (kg/m3)	Longitudinal velocity, $c_l$ (m/s)	Shear velocity $c_t$ (m/s)
COM	1823	4476	2247
COD	1875	2687	1344
MAPH	1587	2798	1634
U-30	1693	3180	1880

III. RESULTS

A. Analytical modeling results

The theory described in Sec. II A allows one to calculate all the characteristics of the process of mechanical loading of a stone when an acoustic wave is incident on it. For small stones, the beam width is much larger than the diameter of the stone, therefore, below the incident wave is considered as a plane (not focused) harmonic wave.

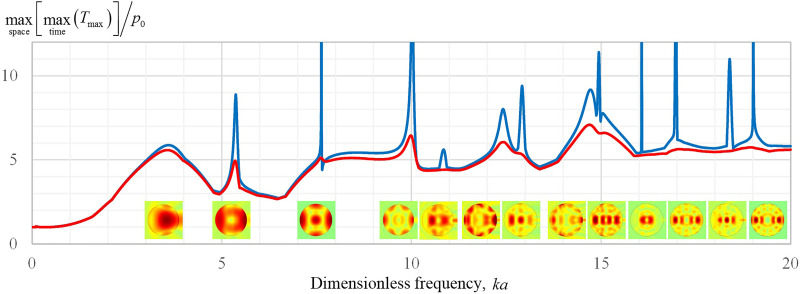
Figure 1 shows the results of calculations of the largest maximum stress, $\underset{\text{space}}{\text{max}}[\underset{\text{time}}{\text{max}}(T_{\text{max}})]$, normalized to the pressure amplitude $p_0$ in the incident wave for a spherical calcium oxalate monohydrate (COM) stone in a wide range of variation of the dimensionless frequency $ka$. This curve has a characteristic behavior: at low frequencies, the highest stress coincides with the pressure amplitude of the incident wave, $p_0$, and weakly depends on the frequency. With increasing frequency, an increase in the stress in the stone is observed at $ka>1$, and a local maximum is reached at the frequency $ka\approx 3.6$, at which the stress is approximately six times higher than the amplitude of the incident wave, $p_0$. With a further increase in frequency, many narrower resonance peaks are observed, which appear above a plateau level that is several times higher than $p_0$. The presence of resonances is expected, since a stone, like any volume with reflecting boundaries, is a resonator for elastic waves. At each resonant frequency, a particular stress distribution is formed inside the stone. For clarity, in Fig. 1, the distributions of the quantity $\underset{\text{time}}{\text{max}}(T_{\text{max}})$ at the corresponding resonant frequencies are shown below the curve. The narrow peaks are reduced or completely disappear when elastic wave absorption is present. As an example, this effect is illustrated in Fig. 1 by a red line when a moderate absorption is introduced in the model by adding an imaginary part to the elastic wavenumbers $k_l$ and $k_t$, the value of which is consistent with the range of attenuation measured in a sample of stones.¹⁹

FIG. 1.

(Color online) Maximum in space and time of the maximum principal stress, $\underset{\text{space}}{\text{max}}[\underset{\text{time}}{\text{max}}(T_{\text{max}})]$, normalized by the incident plane wave amplitude p₀, versus dimensionless frequency ka, where k is the wavenumber in the liquid, a is the stone radius. The modeled spherical stone is made from COM material. The blue line corresponds to the case when no losses are present in the stone, the red line represents simulations when an absorption that grows linearly with frequency is introduced to the elastic waves in the stone: $k_t\to k_t(1+0.01\hspace{0.17em}i)$, $k_l\to k_l(1+0.01\hspace{0.17em}i)$. Images below the curve represent spatial distribution of the maximum-in-time of the maximum principal stress, $\underset{\text{time}}{\text{max}}(T_{\text{max}})$, for the frequencies where the curve has local maxima (i.e., the resonance frequencies).

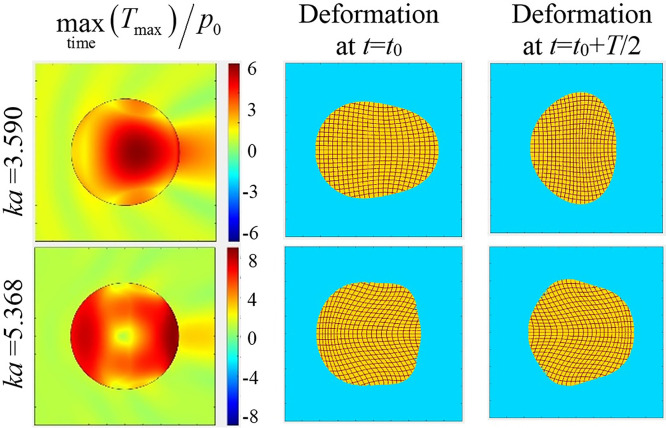
Consider in more detail the two lowest resonances: $ka=3.590$ and $ka=5.368$. Figure 2 shows the distribution of the maximum-in-time of the maximum principal stress for a COM stone, as well as the pattern of the stone deformation in the process of its oscillations at the corresponding frequencies. The scale deformation of the stones has been exaggerated for display. Note the maximum stress is not always at the stone center. The deformation is shown by the grid, which is a square grid in the unperturbed state. At the lowest resonance frequency, $ka=3.590$, the vibration of the stone has the structure of a quasi-longitudinal standing wave, in which particle displacement mainly occurs in the longitudinal direction, and transverse deformations are due to the Poisson effect. At the second resonant frequency, $ka=5.368$, the deformation of the stone has the form of bending vibrations. It should be noted that at the lowest frequency, the resonance peak is relatively wide, with the maximum stress being achieved near the center of the stone. At higher frequencies, stress is more likely to be concentrated near the border of the stone (see also Fig. 1).

FIG. 2.

(Color online) The distribution of the maximum-in-time of the maximum principal stress for a COM stone (left), as well as the pattern of the stone deformation in the process of its oscillations (center and right) at the 1st and 2nd lowest resonance frequencies, $ka=3.590$ and $ka=5.368$. Here, $t_0$ is a moment in time and $T$ is the wave period.

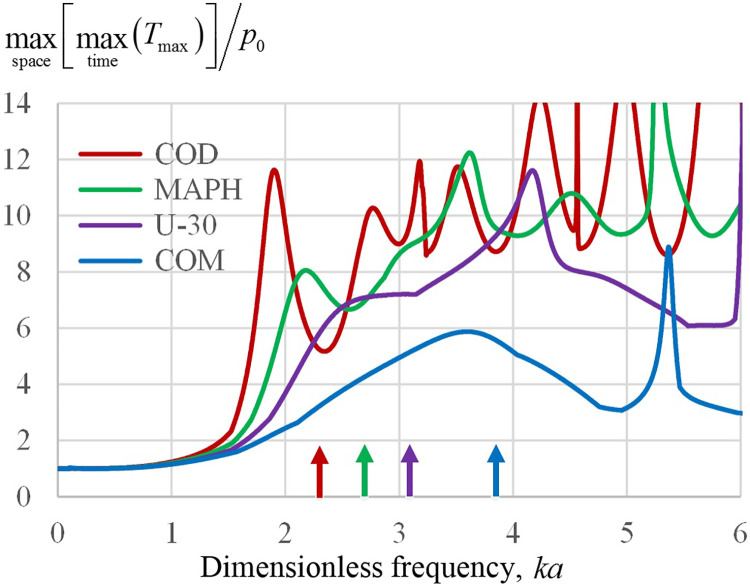
The values of the resonances depend on the stone composition. Figure 3 shows a view of the lowest-frequency resonance curve for several materials. It can be seen that both the resonance frequency and the magnitude of the maximum stress achieved are different for different materials, and the magnitude of the resonance peak increases with decreasing the resonance frequency. The arrows show the values of the resonance frequency, calculated under the assumption of the lowest resonance of the quasi-longitudinal standing wave in a thin rod with a length equal to the diameter of a spherical stone. The speed of the indicated bar wave is $c_{\mathit{rod}}=\sqrt{E/{\rho }_{\ast }}$, where $E$ is Young's modulus, which corresponds to the expression $c_{\mathit{rod}}=c_t\sqrt{(3c_l^2-4c_t^2)/(c_l^2-c_t^2)}$. This gives an estimate for the lowest resonance frequency, $f_{\mathit{res}}=c_{\mathit{rod}}/(4a)$, which in terms of the dimensionless frequency $ka$ is written as follows: ${(ka)}_{\mathit{res}}=(\pi /2)c_{\mathit{rod}}/c_0$.

FIG. 3.

(Color online) Normalized maximum stress $\underset{\text{space}}{\text{max}}[\underset{\text{time}}{\text{max}}(T_{\text{max}})]/p_0$ in a stone as a function of dimensionless frequency ka varying stone composition: COD, MAPH, U-30, and COM. Arrows indicate the lowest resonance frequency for quasi-longitudinal standing waves in a thin rod with length equal to the stone diameter.

B. Comparison of analytical and finite-difference modeling approaches

The analytical method described in Sec. II A provides an exact solution of the considered problem but is limited to the case of a spherical stone. The finite-difference numerical approach presented in Sec. II B can be used for any stone shape and thus, is more general, although it needs more computing resources and calculation time. However, such numerical method is approximate by its nature because the derivatives are replaced by finite differences, i.e., it provides sufficiently high accuracy only for a sufficiently small calculation steps in space and time. The proper choice of calculation steps and boundary conditions can be verified by using the analytical solution where both approaches are possible.

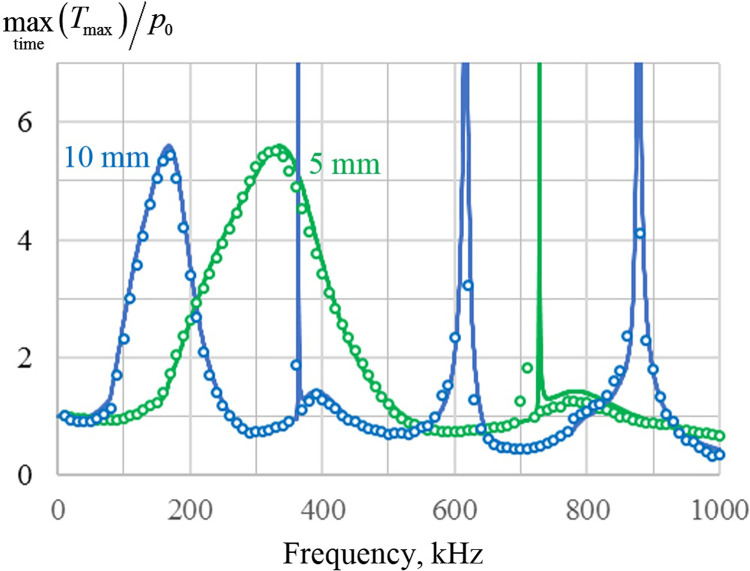
For such a comparison, the problem of the incidence of a plane wave on a spherical COM stone of different diameters is considered. To be specific, the maximum principal stress, $\underset{\text{time}}{\text{max}}(T_{\text{max}})$, normalized by the incidence pressure amplitude in the absence of the stone, $p_0$, is calculated at the stone center for a frequency range from 0 to 1 MHz for the stones of diameters 5 and 10 mm. In the stone center, only two terms in Eqs. (10) and (11) are nonzero, so the analytical expressions are simplified as shown in the Appendix.

Finite-difference modeling of CW regimes for a series of frequencies requires considerable calculation time. To avoid this difficulty, an impulse response approach was employed. Specifically, a plane wave in the form of a short pulse was used in the finite-difference simulation as an incident wave, and then, the frequency response was reconstructed using the Fourier transform of the transient stresses in the absence of the stone (to find the incident pressure amplitude as a function of frequency) and with the stone (to find the principal stresses as functions of frequency).

The modeling results are shown in Fig. 4. The exact analytical solution is shown by solid lines and the finite-difference modeling results are shown by circles. It is seen that the two modeling approaches provide nearly identical results.

FIG. 4.

(Color online) Maximum principal stress $\underset{\text{time}}{\text{max}}(T_{\text{max}})$ at the center (r = 0) of 5 and 10 mm diameter COM stones normalized by the incident plane wave amplitude p₀. The exact analytical solution is presented as solid lines, whereas the finite-difference modeling results are shown as circles with 10 kHz frequency steps. Note, we discuss only the peak at the stone center to consider the resonance behavior here, but higher values exist above the lowest resonance off axis.

C. Finite-difference modeling results for nonspherical stones

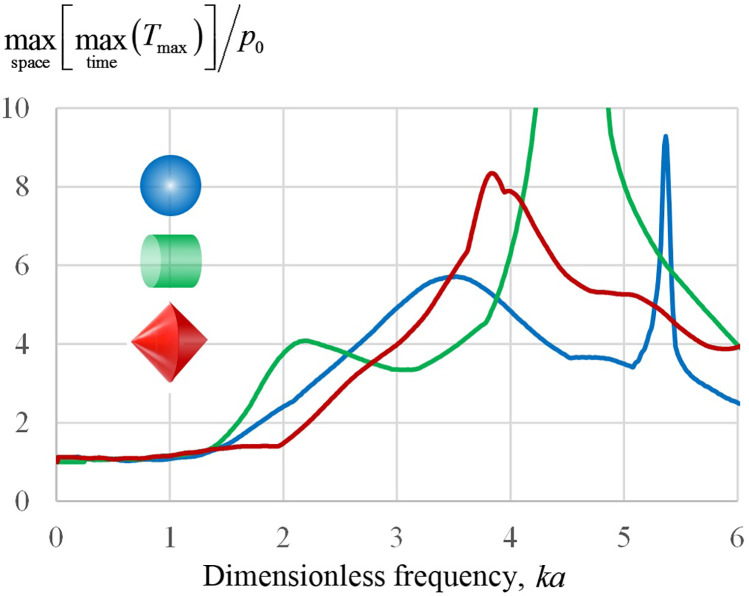
Since real kidney stones are commonly nonspherical, a natural question arises whether the conclusions drawn from the analysis of mechanical stresses for spherical stones can be extended to the more general case of stones of a different shape. To answer this question, a finite-difference simulation of the frequency dependence of the maximum principal stress in stones of various shapes under the action of a plane acoustic wave was carried out. The calculation of the frequency dependence was performed by the impulse response method described in Sec. III B. However, in comparison with Secs. III A and III B, the maximum principal stress, $T_{\text{max}}$, was calculated not only in the center of the stone, but in the entire stone. To characterize the efficiency of mechanical loading of the stone, the highest value of this value was considered, $\underset{\text{space}}{\text{max}}[\underset{\text{time}}{\text{max}}(T_{\text{max}})]$. Figure 5 shows the results of calculations for three stone shapes: in addition to the previously mentioned spherical shape, a cylindrical stone with a diameter equal to the length was considered, as well as a stone in the form of two oppositely oriented cones with a common base, the length of which was chosen equal to its transverse diameter. From the curves shown in Fig. 5, one can conclude that the qualitative form of the dependences of the maximum stress on frequency for nonspherical stones remained the same as for spherical stones: in the low-frequency region, there is an initial section extending to the value $ka\approx 1.5-2$ at which the maximum stress weakly depends on the frequency and remains close to the amplitude of the incident wave. Note that at this frequency the stone diameter is $2a\approx {\lambda }_0/2$, where ${\lambda }_0$ is the wavelength in the liquid. With a further increase in frequency, the maximum stress begins to grow and increases several times. The degree of the stress amplification depends on the shape of the stone: for example, for the cases shown in Fig. 5, at the first peak of the curve, the stress amplification for a cylindrical stone is about 4, for a spherical stone about 6, and for a stone with conical ends about 8. The frequency at which the corresponding peak occurs also depends on the shape of the stone. However, in any case, the indicated amplification effect occurs at $ka$ in the range from 2 to 5, a similar range to that was observed earlier when considering spherical stones made from different materials (see Fig. 3).

FIG. 5.

(Color online) Normalized maximum stress $\underset{\text{space}}{\text{max}}[\underset{\text{time}}{\text{max}}(T_{\text{max}})]/p_0$ in an axisymmetric COM stone as a function of the dimensionless frequency ka for stones of different shapes (shown in different colors): spherical, cylindrical, and in the form of two connected cones. For nonspherical stones, the parameter a corresponds to the radius of a sphere of equal volume.

IV. DISCUSSION AND CONCLUSIONS

An analytical model of stress in a spherical stone was developed and compared to a finite-difference model which was, in turn, used to calculate the stress in nonspherical stones. A range for $ka$ was found above which the incident BWL pressure was significantly amplified within the stone. Amplification was 6 for COM stones and greater for other stone compositions. About half of the stones are of pure composition—calcium stones are most common but also range substantially in properties.³¹ Stones can also be of mixed composition, and this was not addressed here. However, mixed compositions likely have properties in the range addressed by considering different pure compositions.

Amplification could be maximized at specific resonance peaks, although in clinical practice, this would be difficult to achieve without foreknowledge of the stone composition. However, the model suggests that high stresses can be achieved in all compositions provided ka is sufficiently high for those with the greatest sound speed (COM), around ka ∼5. The general trend observed in the simulations was not the result of the perfect symmetry of the stone, as similar behavior was seen for this range of ka with cylindrical and biconical stones as well.

Simulation shows (see Fig. 1) that the mechanical stresses are generally somewhat higher for higher frequencies. However, in this case, the zone of increased stresses is localized near the surface of the stone and, therefore, does not lead to fragmentation of the stone, but only to its surface erosion. Surface erosion also occurs at low frequencies through the cavitation mechanism (at low frequencies it is even more effective because of the greater growth of bubbles and the formation of jets when they collapse). To increase the efficiency of stone comminution by means of near-surface erosion, it is necessary to increase the surface of the stones, i.e., to split them into multiple fragments. That is why it is important to create high stresses inside the stone, closer to its center. This is exactly what happens at the first low-frequency resonance. Thus, the choice of the frequency in the vicinity of the first low-frequency resonance is advantageous for two reasons—both due to the growth of the stone splitting into fragments, and due to the increase in the surface area, which determines the efficiency of erosion both caused by cavitation and the direct action in the case of transition to higher BWL source frequency.

The analysis showed that when the stone diameter is less than the wavelength in the liquid, the tension created in it by the incident wave drops sharply. For small stones, the stress in the stone is practically equal to the amplitude of the incident wave (see Figs. 1, 3, and 5). This feature can be explained by the fact that at low frequencies the effect of external pressure on the stone becomes the same as in the static mode, when the stress inside the stone coincides with the external pressure. Important for practice is the result that with an increase in frequency, the maximum principal stress in the stone can be several times (from four and more) higher than the amplitude of the incident wave. The physical reason is the occurrence of resonant vibrations of the stone. At the lowest resonance, the deformation of the stone resembles a resonance in an elastic rod, when the displacement of particles occurs mainly along the direction of wave propagation. However, due to the Poisson effect, there is some deformation in the transverse direction (see Fig. 2). In this case, the Q-factor of the first resonance is low, i.e., it occurs over a wide range of frequencies, and the very fact of the occurrence of this resonance (and the corresponding increase in stress amplification in the stone) does not depend on either the shape or the material of the stone; only the specific value of the resonance frequency and the degree of stress amplification depend on these factors.

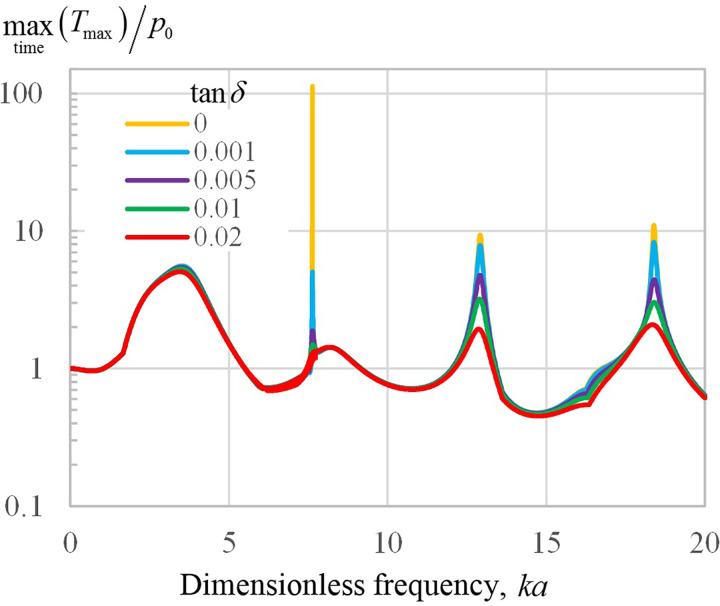
One of the significant limitations of modeling for stones is that only limited data are available regarding the attenuation; moreover, it can be expected that attenuation strongly depends on the type of stone, its structure, and the frequency of the incident wave. To assess the effect of losses, let's assume for simplicity that the attenuation of elastic waves increases linearly with frequency. Then, the analytical model can be modified as follows: $k_t\to k_t(1+i\hspace{0.17em}\text{tan}\hspace{0.17em}{\delta }_t)$, $k_l\to k_l(1+i\hspace{0.17em}\text{tan}\hspace{0.17em}{\delta }_l)$, where $\text{tan}\hspace{0.17em}{\delta }_t$ and $\text{tan}\hspace{0.17em}{\delta }_l$ are the corresponding loss tangents for shear and longitudinal waves. A rough estimate of the loss tangent can be made from a study by Singh and Dhawan,¹⁹ who measured the attenuation coefficient for natural kidney stones in the range of 3–11 dB/cm at 2.5 MHz. This gives a range of change in $\text{tan}\hspace{0.17em}{\delta }_l$ from 0.004 to 0.016 and is likely an overestimation for lower-frequency BWL. Figure 6 shows the modeling results of the maximum stress in the center of the COM stone (see the Appendix) for the case of equal loss tangents for shear and longitudinal waves: $\text{tan}\hspace{0.17em}{\delta }_t=\text{tan}\hspace{0.17em}{\delta }_l=\text{tan}\hspace{0.17em}\delta$. Different colors correspond to a set of different $\text{tan}\hspace{0.17em}\delta$= 0, 0.001, 005, 0.01, and 0.02. Simulations show that taking into account even moderate losses dampens the narrow peak at $ka\approx 7.6$ almost completely, and significantly reduces wider high-frequency resonances. On the contrary, the lowest-frequency resonance of interest to us in the current paper, with a central frequency of $ka\approx 3.6$, is practically insensitive to the presence of absorption. This shows that the simulation results obtained in Sec. III the approximation of zero losses are valid even in absorbing stones, i.e., neglect of absorption is reasonable, particularly for small stones.

FIG. 6.

(Color online) Maximum principal stress $\underset{\text{time}}{\text{max}}(T_{\text{max}})$ at the center (r = 0) of a COM stone normalized by the incident plane wave amplitude p₀ as a function of the dimensionless frequency ka. Vertical axis is presented in logarithmic scale, the curves of different colors correspond to different degree of the elastic waves' absorptions characterized by loss tangent $\text{tan}\hspace{0.17em}\delta$.

Important to the clinical application of BWL for small stones, the low-frequency mode has a single position of high stress, and its likely outcome would be to bisect the stone into two smaller fragments. Once fragmented, the smaller individual pieces may no longer experience amplified stress, but a stress closer to $p_0$. While larger stones require fragmentation into numerous pieces, even a single fracture can benefit the passage of an obstructing ureteral stone or even relieve obstruction of urine flow. Previous preclinical¹⁴ and clinical³² work evaluating stone comminution of COM stones¹⁴ found that fragments produced with a 350 kHz transducer were reduced to 1–2 mm (ka ∼1.5–2.9), consistent with the range for onset of amplified stress in the model. This model, therefore, explains why stones are not necessarily reduced to fine particles but remain a specific size related to the wavelength. The notion of bisecting a stone sequentially through a fundamental resonance gives the possibility to use a low frequency and break a stone into larger pieces, and then use a higher frequency to break them further. This strategy could prove faster than using only high frequency, which can take a substantial time to completely fragment a stone on its own. As a result, very small fragments could be produced in a clinically reasonable timeframe and pass asymptomatically. Future work will evaluate this promising technique to accelerate stone fragmentation in BWL.

APPENDIX: STRESSES AND FREE ENERGY DENSITY AT THE SPHERICAL STONE CENTER

At the stone center, $r=0$, the spherical Bessel functions provide nonzero terms only for the indices $n\le 2$, which follows from the following expressions for the spherical Bessel functions: $j_0(x)=1-x^2/6+\cdots$, $j_1(x)=x/3-x^3/30+\cdots$, $j_2(x)=x^2/15+\cdots$ Substitution of these expansions into Eqs. (13)–(16) and the transition to the limit $r\to \hspace{0.17em}0$ leads to the conclusion that the stress is completely characterized by two components of the stress tensor–axial and lateral (perpendicular to the axis), which have the following complex amplitudes:

$$T_{\parallel }=\left(\nu +\frac{1}{3}\right){\widehat{a}}_0-\left(\frac{2}{15}{\widehat{a}}_2+\frac{2}{5}{\widehat{b}}_2\right),$$ (A1)

$$T_{\perp }=\left(\nu +\frac{1}{3}\right){\widehat{a}}_0+\frac{1}{15}{\widehat{a}}_2+\frac{1}{5}{\widehat{b}}_2.$$ (A2)

According to Eq. (39), the corresponding maximum principal stress is ${T_{\text{max}}|}_{r=0}=\text{max}({\tilde{T}}_{\parallel },{\tilde{T}}_{\perp })$, where,

$${\tilde{T}}_{\parallel }=\mathrm{Re}\left(T_{\parallel }{e}^{-\mathit{\text{iω\hspace{0.05em}t}}}\right),$$ (A3)

$${\tilde{T}}_{\perp }=\mathrm{Re}\left(T_{\perp }{e}^{-\mathit{\text{iω\hspace{0.05em}t}}}\right).$$ (A4)

The peak value (maximum in time) of ${T_{\text{max}}|}_{r=0}$ is therefore

$${T_{\text{max}}^{\text{peak}}|}_{r=0}=\text{max}\left(\left|T_{\parallel }\right|,\left|T_{\perp }\right|\right).$$ (A5)

The corresponding free energy density in accordance with Eq. (40) is

$${E|}_{r=0}=\frac{1}{4\mu }\left({\tilde{T}}_{\parallel }^{\hspace{0.17em}2}+2{\tilde{T}}_{\perp }^{\hspace{0.17em}2}\right)-\left(\frac{1}{12\mu }-\frac{1}{18K}\right){\left({\tilde{T}}_{\parallel }+2{\tilde{T}}_{\perp }\right)}^2.$$ (A6)

Here, $K=\lambda +2\mu /3$ is the bulk modulus. As is seen from Eqs. (13)–(16), the solution at $r=0$ is completely defined by three coefficients ${\widehat{a}}_0$, ${\widehat{a}}_2$, and ${\widehat{b}}_2$. According to Eqs. (23)–(33), these coefficients are expressed through elementary functions. Indeed, the spherical Hankel and Bessel functions in Eqs. (23)–(33) are expressed through the trigonometric functions:³³

$$h_0^{\left(1\right)}\left(x\right)=-i\frac{e^{ix}}{x},$$ (A7)

$$h_2^{\left(1\right)}\left(x\right)=\left(-i\frac{3}{x^3}-\frac{3}{x^2}+i\frac{1}{x}\right)e^{ix},$$ (A8)

$$j_0\left(x\right)=\frac{\hspace{0.17em}\text{sin}\hspace{0.17em}x}{x},$$ (A9)

$$j_2\left(x\right)=\left(\frac{3}{x^3}-\frac{1}{x}\right)\text{sin}\hspace{0.17em}x-\frac{3\hspace{0.17em}\text{cos}\hspace{0.17em}x}{x^2}.$$ (A10)

The above equalities enable the coefficients presented by Eqs. (23)–(33) to be expressed by elementary (trigonometric) functions and thus easily calculated at the spherical stone center.