Abstract
Background and objective:
The stepped wedge cluster randomized trial is a study design increasingly used in a wide variety of settings, including public health intervention evaluations, clinical and health service research. Previous studies presenting power calculation methods for stepped wedge designs have focused on continuous outcomes and relied on normal approximations for binary outcomes. These approximations for binary outcomes may or may not be accurate, depending on whether or not the normal approximation to the binomial distribution is reasonable. Although not always accurate, such approximation methods have been widely used for binary outcomes. To improve the approximations for binary outcomes, two new methods for stepped wedge designs (SWDs) of binary outcomes have recently been published. However, these new methods have not been implemented in publicly available software. The objective of this paper is to present power calculation software for SWDs in various settings for both continuous and binary outcomes.
Methods:
We have developed a SAS macro %swdpwr, an R package swdpwr and a Shiny app for power calculations in SWDs. Different scenarios including cross-sectional and cohort designs, binary and continuous outcomes, marginal and conditional models, three link functions, with and without time effects under exchangeable, nested exchangeable and block exchangeable correlation structures are accommodated in this software. Unequal numbers of clusters per sequence are also allowed. Power calculations for a closed cohort employ a block exchangeable within-cluster correlation structure that accounts for three intracluster (intraclass) correlations: the within-period, between-period, and within-individual correlations. Cross-sectional cohorts allow for nested exchangeable or exchangeable correlation structures defined by the within-period and the between-period intracluster correlations only. Our software assumes a complete design and equal cluster-period sizes. While the methods accommodate correlation structures of constant within-period intracluster correlation coefficient (ICC) as well as a different within- and between-period ICC, it does not allow the between-period ICC to decay.
Results:
swdpwr provides an efficient tool to support investigators in the design and analysis of stepped wedge cluster randomized trials. swdpwr addresses the implementation gap between newly proposed methodology and their application to obtain more accurate power calculations in SWDs.
Conclusions:
In an effort to make computationally efficient (and non-simulation-based) power methods under both the cross-sectional and closed-cohort designs for continuous and binary outcomes more accessible, we have developed this user-friendly software. swdpwr is implemented under two platforms: SAS and R, satisfying the needs of investigators from various backgrounds. Additionally, the Shiny app enables users who are not able to use SAS or R to implement these methods online straightforwardly.
Keywords: sample size estimation, cross-sectional designs, cohort designs, correlation structure, generalized estimating equations, generalized linear mixed models, R Shiny
1. Introduction
In cluster randomized trials (CRTs), the unit of randomization is the cluster, improving administrative convenience and reducing treatment contamination [1]. In stepped wedge designs (SWDs), all clusters start out in the control condition and switch to the intervention condition in a unidirectional and randomly assigned order, and once treated, the clusters maintain their intervention status until the end of the study. At pre-specified time periods, a random subset of clusters cross over from the control to the intervention condition. Stepped wedge randomization may be preferred for estimating intervention effects when it is logistically more convenient to roll-out intervention in a staggered fashion and when the stakeholders or participating clusters perceive the intervention to be beneficial to the target population [2].
Two different stepped wedge designs have been considered: the cross-sectional design and the closed cohort design [3]. We do not consider open-cohort designs in this work as the related methods for binary outcomes are currently unavailable. Only complete designs with no transition periods are included. In a cross-sectional design, different participants are recruited at each time period in each cluster; while in a closed cohort design (which for simplicity will be referred to as a cohort design hereafter), participants are recruited at the beginning of the study and have repeated outcome measures at different time periods [4]. A distinguishing feature of all CRTs is that outcomes within the same cluster tend to be correlated with one another [5]. Because in SWDs outcomes are measured at different time periods, the within-period and between-period intracluster correlation coefficients may be different and thus should be separately considered in designing SWDs [5]. An additional withinâĂŘindividual correlation should be included when it is a cohort SWD to account for the repeated measures within the same individual over time [6]. Two statistical models can be used to account for these three levels of intraclass correlation: the conditional model and the marginal model. Conditional models are based on mixed effects models [7, 8], which accommodate the intraclass correlations via latent random effects. Marginal models describe the population-averaged responses across cluster-periods, and are usually fitted with generalized estimating equations (GEE) [9]. The interpretations of regression parameters can be different under these two models, with the important exception of the identity and log links when random effects and the covariates are independent, as is typically assumed [10]. The design and analysis of SWDs have been mostly based on conditional models, for instance, Hussey and Hughes [2], Woertman et al. [11], Hemming et al. [12], Hooper et al. [13], Li et al. [14]. As a complementary approach, the marginal models separately consider the mean and correlation models and carry a straightforward populationâĂŘaveraged interpretation. Accordingly, assuming a continuous or binary outcome, Li et al. [15] proposed methods for the design and analysis of SWDs using marginal models. Alternatively, the conditional model considers the causal effect of interventions on individuals, under the assumption of no unmeasured confounders present or other source of bias.
Binary outcomes are frequently seen in cluster randomized trials as endpoints. However, existing methods for sample size calculation of SWDs have been almost exclusively focused on continuous outcomes. Hussey and Hughes [2] proposed an approach based on linear mixed effects models, estimated by weighted least squares for continuous outcomes, and provided an approximation to this approach for binary outcomes. Systematic reviews indicate that the majority of SWDs with binary outcomes used this approximation method [16, 17], which may either overestimate or underestimate the power in different scenarios [18]. To improve this approximation, Zhou et al. [18] developed a maximum likelihood method for power calculations of SWDs with binary outcomes based on the mixed effects model and Li et al. [15] proposed a method for binary outcomes within the framework of GEE that employed a block exchangeable withinâĂŘcluster correlation structure with three correlation parameters.
These new methods have not yet been implemented in publicly available software, making it difficult for researchers and practitioners to apply these new methods to rigorously design their studies. There are a few current software packages for power calculations in SWDs. The Hussey and Hughes approach [2] was implemented by the swCRTdesign [19] in R and an Excel spreadsheet (http://faculty.washington.edu/jphughes/pubs.html). Hemming and Girling [20] developed a Stata menu-driven program steppedwedge based on the Hussey and Hughes model. These approaches consider the linear mixed effects model for continuous outcomes and perform approximate calculations for binary outcomes. Hemming et al. [21] developed the Shiny CRT Calculator programmed in R using linear mixed effects models for continuous outcomes and included the normal approximation for binary outcomes (https://github.com/karlahemming/Cluster-RCT-Sample-Size-Calculator). This method accommodated cross-sectional and cohort designs with three intraclass correlations (intracluster correlation, cluster autocorrelation (CAC) and individual autocorrelation (IAC)) [13] that are different from those in our work. The IAC and CAC are both cluster mean correlations, however, the intacluster correlation coefficients in our software are defined for within-cluster individual level observations (their differences are clarified in Li et al. [22]). These approximations for binary outcomes may or may not be accurate, depending on whether or not the normal approximation to the binomial distribution is reasonable. Alternatively, Baio et al. [23] developed the R package SWSamp (https://sites.google.com/a/statistica.it/gianluca/swsamp), which allows simulation-based sample size and power calculations for several general scenarios including cross-sectional and cohort designs for continuous, binary and count outcomes. However, this package does not allow for random cluster-by-time interaction (therefore assuming the within-period intracluster correlation coefficient (ICC) is the same as the between-period ICC). In addition, two more recent R packages, clusterPower [24] and CRTpowerdist [25] also allow for simulation-based power calculation for continuous, binary and count outcomes, but with a focus on cross-sectional designs. Hence, in an effort to make computationally efficient (and non-simulation-based) power methods under both the cross-sectional and closed-cohort designs for continuous and binary outcomes more accessible, we have developed user-friendly software for methods proposed by Zhou et al. [18] and Li et al. [15] based on the conditional and marginal models, respectively. Particularly, we focus on the exchangeable, nested exchangeable, and block exchangeable within-cluster correlation structures. Methods of binary outcomes for other types of correlation structures (eg. exponential decay structure) are not implemented in the current version of our software. The software engine has been developed in Fortran and is incorporated into the SAS macro %swdpwr, the R package swdpwr and a Shiny app.
2. Methods
Throughout this article, the regression parameter β denotes the treatment effect. For testing the treatment effect, we consider the following hypothesis:
| (1) |
where βA is the true value of β under the alternative hypothesis that βA ≠ 0. In this software, power is calculated based on a two-sided Wald-type test given by:
| (2) |
where Φ(·) is the cumulative distribution function of the standard normal distribution, α is the significance level, and Z1−α/2 is the (1 − α/2)th quantile of the standard normal distribution. The variance of is defined by either asymptotic theory for maximum likelihood estimation (MLE) in a conditional model, or by the theory of generalized estimating equations in a marginal model.
A SWD is defined by I clusters and J time periods, each including Kij individuals at time period j for cluster i (i in 1, ⋯ , I; j in 1, ⋯ , J). A SWD consists of several sequences, which are determined by different periods when participants crossover to receive the intervention [26]. The clusters are randomly assigned to each sequence, and unequal clusters per sequence are supported in our software. In a cross-sectional SWD, the size of cluster i is given by ; in a cohort SWD, assuming that Kij = Ki over the active study period, the size of cluster i is Ni = Ki. In this paper, we adopt the equal cluster-period size assumption, and thus Kij = K. In practice, when cluster-period sizes vary, it’s conventional to assume K to be the average cluster-period size for the purpose of sample size calculation. Let Yijk be the response corresponding to individual k at time period j from cluster i (k in 1, ⋯ , Kij), which can be continuous or binary outcomes (for example: success or failure of surgery, getting the disease or not). For both outcome types, we first present the general models with three correlation parameters and then give more details about the cases implemented in this software. More remarks on these methods can be found in Appendix A.
2.1. Models for binary outcomes
Due to the correlated nature of the outcomes in SWDs, a generalized linear mixed effects model can be written:
| (3) |
where g(·) is a link function, Xij is a binary treatment assignment (1=intervention; 0=standard of care) in cluster i at time period j, μ is the baseline outcome rate on the scale of the link function in the control group, γj is the fixed time effect corresponding to time period j (j in 1, ⋯ , J, and γ1 = 0 for identifiability), and β is the parameter of interest in this study, the treatment effect. We assume that bi is the cluster-level random effect distributed by , cij is the cluster-by-time interaction random effect distributed by , and πik is the random effect for repeated measures of one individual distributed by . We assume that bi, cij and πik are independent of each other. Let pijk = E(Yijk∣Xij, bi, cij, πik) = Pr(Yijk = 1∣Xij, bi, cij, πik) be the probability of the outcome for individual k conditioned on the random effects and design allocation, interpreted as the conditional mean response of the individual.
To account for the correlation of outcomes, a block exchangeable within-cluster correlation structure with three levels of correlation [15] is employed: (1) α0, the within-period intracluster correlation, which measures the similarity between responses from different individuals within the same cluster during the same time period (corr(Yijk, Yijk′) = α0 for k ≠ k′); (2) α1, the between-period intracluster correlation, which measures the similarity between responses from different individuals within the same cluster in different time periods (corr(Yijk, Yij′k′) = α1 for j ≠ j′, k ≠ k′); (3) α2, the within-individual correlation, which measures the similarity between responses from the same individual across time periods (corr(Yijk, Yij′k) = α2 for j ≠ j′). The correlation parameters are calculated on the proportional scale for binary outcomes, Appendix A provides details for the calculations.
This framework can accommodate three common link functions g(·): identity, log and logit links. In a cross-sectional design, the correlation structure depends only on α0 and α1 since different sets of individuals are included at each time period, and α2 is no longer relevant. However, in this circumstance, α1 and α2 are, by definition, the same, since actually different individuals are assessed at each time period, to obtain a two-level nested exchangeable correlation model to accommodate the cross-sectional design [15]. Otherwise, a cohort design is implied.
Model (3) accommodates both cross-sectional and cohort SWDs. These designs can also be fitted by the marginal model with the same correlation structure but without random effects:
| (4) |
In our software, we implemented specific cases of designs with binary outcomes under conditional and marginal model assumptions. For binary outcomes, the marginal and conditional mean responses limit the ranges of the correlation coefficients inside [−1, 1] [27, 28]. Thus, we need additional restrictions for α0, α1, α2 beyond those required to ensure a positive definite working correlation matrix and that the correlations are between 0 and 1. To ensure valid probabilities between 0 and 1 under the identity and log link functions, we also need restrictions for parameters related to the treatment effect, baseline outcome rate and time effect parameters on the scale of the link function. For example, μ + β + γj should not exceed 0 under log link function. These restrictions apply to both the conditional and marginal models. When the input parameters for power calculations are out of range, the software will return an error message. More details will be discussed in Appendix B.
2.1.1. Conditional model based on GLMM
Zhou et al. [18] considered a cross-sectional SWD modelled by the generalized linear mixed model (GLMM) as a special case of Model (3):
| (5) |
All notations are as defined previously. We assume a normal distribution for random effects, bi ~ N(0, τ2), although Zhou et al. [18] showed that results are insensitive to the assumed form of the distribution of the random effects. This model only considers fixed time effects and does not include cluster-by-time interaction random effects. As α2 is undefined for cross-sectional studies, the correlation structure for this case reduces to an exchangeable structure with α0 = α1 and it’s shown that they are equal to [18], where ρ represents an intracluster correlation coefficient which measures the correlation between individuals in the same cluster.
In this work, we consider three link functions for g(·): identity, log and logit. Then, the likelihood for the outcomes is based on the conditional probability under the specific link function. Because the likelihood involves integrating out the unobserved random effects bi, we use the Gaussian quadrature for numerical integration [29]. The large-sample variance and power are calculated based on the theory of maximum likelihood estimation.
We also consider SWDs with no time effects (all γj = 0). The model is
| (6) |
It applies when time effects are expected to be minimum [30]. The derivation of the likelihood formula and the calculation of the variance of and power are similar to the procedures with time effects.
2.1.2. Marginal model based on GEE
Cohort SWDs with three correlation parameters, where individuals from each cluster are enrolled at the start of the trial and followed up for repeated measurements [15], have been studied. The marginal model based on GEE is:
| (7) |
Here we slightly abuse the notation, and denote pijk = E(Yijk∣Xij) = P(Yijk = 1∣Xij), interpreted as the marginal mean response of individuals, μ is the marginal outcome rate on the scale of the link function in the control group, γj is the fixed time effect, β is the parameter of interest in this study, interpreted as the marginal treatment effect. We also consider two settings: with time effects (j in 1, ⋯ , J, and γ1 = 0 for identifiability) and without time effects (all γj = 0). When assuming Kij = Ki for each j, the block exchangeable working correlation matrix for cluster i is written as [15]:
| (8) |
where Ju is a u * u matrix with all elements of 1, Ik is a k * k identity matrix. Li et al. [15] showed that Ri has four distinct eigenvalues and all of them should have positive values, in order to ensure a positive-definite correlation structure. We define η = (μ, γ2, γ3, …, γJ, β)∨ˋ& to be the vector of parameters in Model (7), and η = (μ, β)∨ˋ& to be the parameter vector without time effects. Let Yi = (Yi11, Yi12…, YiJ Ki)∨ˋ& and pi = (pi11, pi12…, piJ Ki)∨ˋ&. The GEE estimator is solved from , where Di = ∂pi/∂η′, Vi = Ai1/2RiAi1/2, and Ai is the J Ki–dimensional diagonal matrix with elements ϕv(pijk), with ϕ representing the dispersion parameter (ϕ = 1 for binary outcomes) and the variance function v(pijk) = pijk(1 − pijk). Assuming the correlation structure is correctly specified, is approximately multivariate normal with mean η and covariance estimated by the model-based estimator . Hence, we can calculate the variance of .
Cross-sectional SWDs can also be designed under the marginal model with appropriate specification of the correlation parameters α0 and α1 for the nested exchangeable correlation structure.
2.2. Models for continuous outcomes
Hooper et al. [13] assumed a linear mixed effects model for correlated continuous outcomes in SWDs:
| (9) |
Notations are as defined previously. Here we assume that , and as previously, bi, cij, πik and ϵijk are independent of each other, and the total marginal variance of Yijk is . We note that, for k ≠ k′, for j ≠ j, k ≠ k′, and for j ≠ j′. The correlation structure Ri and the specification for cross-sectional and cohort designs are as in Section 2.1.
This general Model (9) agrees with the population-averaged marginal model used by Li et al. [15] for SWDs:
| (10) |
where μijk is the marginal expected mean response of Yijk. Our software allows for SWDs both with time effects (j in 1, ⋯ , J, and γ1 = 0 for identifiability) and without time effects (all γj = 0).
Li et al. [15] and Hooper et al. [13] both considered scenarios for continuous outcomes that accommodate three correlation parameters (although not the same), under marginal and conditional model, respectively. In both models, the covariance is estimated by the model-based estimator , where Zi is the J Ki * (J + 1) design matrix corresponds to the parameter vector η under the SWD framework within cluster i and Vi is the working covariance matrix within cluster i based on a block exchangeable correlation structure, in which . Our software implements Li et al. [15] for cross-sectional and cohort SWDs with continuous outcomes. Regarding restrictions on the allowable parameter space for continuous outcomes, the correlations are within [−1, 1]. When two or three correlation parameters are used for cross-sectional and cohort designs, respectively, a positive definite correlation matrix Ri should be ensured.
3. Software Description
Table 1 displays all the scenarios and correlation structures that are implemented in the software, accommodating cases and methods with and without time effects. The input parameters are the same for R and SAS. Hereafter, the mean response refers to the average outcome and the proportion for continuous and binary outcomes, respectively. Different input parameters values, including for the anticipated mean response in the control group at the start of the study, the anticipated mean response in the control group at the end of the study, the anticipated mean response in the intervention group at the end of the study, the study design, and the intraclass correlations, can be specified based on preliminary data. The arguments of software swdpwr are shown in Table 2.
Table 1.
Methods implemented in swdpwr and correlation structures accommodated.
| Conditional model | Marginal model | ||
|---|---|---|---|
| Binary outcomes (identity, log, logit links) | Cross-sectional design | Zhou et al. [18] (exchangeable structure) | Li et al. [15] (nested exchangeable structure) |
| Cohort design | N/A | Li et al. [15] (block exchangeable structure) | |
| Continuous outcomes (identity link) | Cross-sectional design | Hussey and Hughes [2]; Li et al. [15]; Zhou et al. [30] (nested exchangeable structure) | |
| Cohort design | Hooper et al.[13]; Li et al. [14]; Li et al. [15] (block exchangeable structure) | ||
Table 2.
Arguments of software swdpwr.
| Argument | Description | Default |
|---|---|---|
| K | number of individuals at each time period in a cluster, or the average cluster-period size under variable cluster-period sizes | |
| design | I*J dimensional data set that the study design, unequal allocation of sequences and only complete designs with no transition periods are allowed | |
| family | specify family="gaussian" for continuous outcome, family="binomial" for binary outcome | "binomial" |
| model | specify model="conditional" for conditional model, model="marginal" for marginal model | "conditional" |
| link | choose link function from link="identity", link="log" and link="logit" | "identity" |
| type | specify type="cohort" for closed cohort study, type="cross-sectional" for cross-sectional study | "cross-sectional" |
| meanresponse_start | the anticipated mean response in the control group at the start of the study | NA |
| meanresponse_end0 | the anticipated mean response in the control group at the end of the study | meanresponse_start |
| meanresponse_end1 | the anticipated mean response in the intervention group at the end of the study | NA |
| effectsize_beta | the anticipated effect size | NA |
| sigma2 | marginal variance of the outcome (only allowed if is continuous outcome) | 0 |
| typeIerror | Two-sided Type I error | 0.05 |
| alpha0 | within-period intracluster correlation α0 | 0.1 |
| alpha1 | between-period intracluster correlation α1 | alpha0/2 |
| alpha2 | within-individual correlation α2 (only allowed if type="cohort") | NA |
In this section, we give a detailed description for implementation in R and SAS. Examples under different scenarios will be discussed in Section 4. We assume balanced cluster-period sizes so that Kij = K over all i and j.
3.1. Specification of regression model parameters
First we give the interpretations of meanresponse_start, meanresponse_end0 and meanresponse_end1. meanresponse_start refers to the mean response in the first period when all clusters are in the control condition. meanresponse_end0 represents the mean response at the last period under the counterfactual had the intervention not been introduced. The difference between them is due to secular trends (or time effects). meanresponse_end1 is the mean response at the last period when all clusters are in the intervention condition. Based on these input parameters, the software will automatically calculate the time effects on the link function scale. To account for time effects, we assume that the secular trend is linear on the link function scale such that γj increases linearly in j. Hence, the parameter returned by the software for time effects γJ is a single parameter. This software considers two complementary ways for users to provide the regression model parameters μ, β and γJ. One approach is to specify meanresponse_start, meanresponse_end0 and meanresponse_end1, which will help calcualte and identify the baseline outcome rate μ, the treatment effect β and the time effect γJ on the link function scale. The alternative approach is to specify meanresponse_start, meanresponse_end0 and effectsize_beta. This approach provides the treatment effect β directly, while μ and γJ can also be calculated from the input parameters.
It has been shown in Li et al. [15] that power calculations for continuous outcomes only depend on β, and do not depend on μ or γJ. Hence users are allowed to obtain power results from our software by just providing values for effectsize_beta without the secular trend for a continuous outcome. However, users will additionally need to specify different values for meanresponse_start and meanresponse_end0 to indicate the presence of time effects, although the values are not required to be accurate. If assuming no time effects and continuous outcomes, Equation (D.19) in Appendix D also shows the independence of power on β, and users can just supply effectsize_beta to conduct the calculation, as the default is of no time effects.
In case of potentially contradictory parameter specification, only one of the following approaches is allowed in the software. To elaborate, one approach is to specify meanresponse_start, meanresponse_end0 and meanresponse_end1, and another approach is to specify meanresponse_start, meanresponse_end0 and effectsize_beta. Users are not allowed to supply meanresponse_start, meanresponse_end0, meanresponse_end1 and effectsize_beta at the same time.
3.2. Description of the R package
This package swdpwr provides statistical power calculations for SWDs with both binary and continuous outcomes through the swdpower function. The arguments of swdpower are
1 swdpower (K, design, family = "binomial", model = "conditional", link = "identity", 2 type = "cross-sectional", meanresponse_start = NA, meanresponse_end0 = meanresponse_start, 3 meanresponse_end1 = NA, effectsize_beta = NA, sigma2 = 0, typeIerror = 0.05, alpha0 = 0.1, 4 alpha1 = alpha0/2, alpha2 = NA)
with details provided in Table 2 along with defaults if any (those above with an equal sign have default values). The input argument design is a matrix generated in R with elements of 0 (control) or 1 (intervention) for users to define the detail of the SWD, in which each row represents a cluster and each column represents a time period. Unequal allocation to different sequences is allowed in design. The argument sigma2 is only allowed for continuous outcomes. The argument alpha2 should not be an input under cross-sectional designs although it is numerically identical to alpha1 in this scenario by definition. The object returned by swdpower function has a class of swdpower, which includes a list of the design matrix, summary features of the design and the power for the scenario specified. This package also contains an associated print method for the class of swdpower, which hides the list output and just shows the readable power under the alternative hypothesis.
This package also incorporates two functions for the calculations of ICCs of continuous and binary outcomes, respectively. There is a function ContICC for the calculations of the correlation parameters given the random effects variances for continuous outcomes as in Section 2.2. This function returns alpha0, alpha1, and alpha2 that can be used in the main function swdpower with continuous outcomes. For binary outcomes, we provide a function BinICC that calculates a single intracluster correlation coefficient given the cluster level random effects variance τ2 (also denoted as ) for different link functions in Section 2.1. The ICC returned by this function can be used for cross-sectional SWDs with α0 = α1 for both the conditional and marginal models. However, we recommend that users provide the three correlation parameters directly based on calculations on the proportional scale, as noted in Appendix A, due to the fact that the correlation parameters might not have a closed form under different link functions for binary outcomes.
3.3. Description of the SAS macro
The SAS macro %swdpwr plays the same role as the function swdpower in R package swdpwr described above, and this macro also needs a pre-prepared data set for the study design matrix generated in SAS. For illustration, a toy data set design is created, which contains the allocation of control (0) or intervention (1) for each cluster at different time periods as well as the number of clusters for each allocation shown the first column. The step to generate this data set in SAS is as follows, in which 3 clusters are allocated to the first two sequences and the last sequence has 2 clusters.
1 data design; 2 input numofclusters time1 time2 time3 time4; 3 cards; 4 3 0 1 1 1 5 3 0 0 1 1 6 2 0 0 0 1 7 ; 8 run;
The procedure of data set generation is the common DATA step, but is supposed to include a header with correct time period description.
Sharing the same utility with the function swdpower in R package swdpwr, the input arguments of %swdpwr are
% macro swdpwr(K, design, family = "binomial", model = "conditional", link = "identity", type = "cross-sectional", meanresponse_start = NA, meanresponse_end0 = meanresponse_start, meanresponse_end1 = NA, effectsize_beta = NA, sigma2 = 0, typeIerror = 0.05, alpha0 = 0.1, alpha1 = alpha0/2, alpha2 = NA)
with details given in Table 2 together with defaults if any. This macro will return an output of summary features of the design, as well as the power value under the particular scenario, which can be referred in Section 5.
4. Examples
The usage of the software is based on platforms of R and SAS, which requires separate illustrations. The following sections are organized according to different scenarios such as continuous and binary outcomes, cross-sectional and cohort settings, different model options, different link functions, different time effects assumptions. Each section will contain examples under both platforms. The implementation of SAS macro for these examples will be shown in Appendix C. When the input arguments are inappropriate, warnings and error messages may occur in the software. Appendix B will give an illustration of these scenarios and advise users how to correct for the errors. Besides the hypothetical examples in this section, we provide two real-data applications implemented by SAS in Section 5: the Washington Expedited Partner Therapy (EPT) trial and the Tanzania postpartum intrauterine device (PPIUD) study. We would like to point out that, although the examples in our paper all have equal allocation to different sequences, unequal allocation of clusters to each sequence is absolutely accommodated by our software.
4.1. Conditional model with binary outcome and cross-sectional design
Zhou et al. [18] proposed this maximum likelihood method under cross-sectional settings, which discussed scenarios with time effects and without time effects. With binary outcomes, the variance argument sigma2 is undefined and should not be specified. Due to this specific cross-sectional setting, we specify α0 = α1 in the function and α2 is also undefined as discussed in Section 2.1.2.
The study design should be supplied by an I*J matrix, where I is the number of clusters, J is the number of time periods. We will utilize the rep() function to specify the elements of the study design matrix by providing different allocations and repeated times of each allocation. More details can be found in the following examples.
An investigator plans to conduct a cross-sectional stepped wedge design with 12 clusters and 3 periods, in which clusters are randomly allocated to one of the two sequences (6 clusters per sequence). This trial has an average of 50 individuals per cluster per period with a total sample size of 1800, and measurements on the binary outcome will be taken. The baseline proportion is assumed to be 0.2 and is expected to increase to 0.25 by the end of the study even in the absence of the intervention (due to the secular trend). The risk difference (RD) by the end of the study is specified to be 0.13 and thus it’s convenient to use the identity link under the conditional model (with the treatment effect β to be also 0.13 for this model configuration). The investigator assumes a constant intracluster correlation coefficient (ICC) over time, equal to 0.01 on the proportions scale, here interpreted as the correlation between different individuals within the same cluster. The treatment effect is to be tested at a two-sided 5% level of significance. Fitting the model with all required inputs in R:
1 R> library("swdpwr")
2 R> dataset = matrix(c(rep(c(0, 1, 1), 6), rep(c(0, 0, 1), 6)), 12, 3, byrow = TRUE)
3 R> swdpower(K = 50, design = dataset, family = "binomial", model = "conditional",
4 + link = "identity", type = "cross-sectional", meanresponse_start = 0.2,
5 + meanresponse_end0 = 0.25, meanresponse_end1 = 0.38, typeIerror = 0.05, alpha0 = 0.01,
6 + alpha1 = 0.01)
7 This cross-sectional study has total sample size of 1800
8 Power for this scenario is 0.899 for the alternative hypothesis treatment effect
9 beta = 0.13 ( two-sided Type I error = 0.05 )
The power obtained from swdpower for this scenario is 0.899 for the alternative hypothesis βA = 0.13.
The model can also be considered under other link functions such as log and logit link functions. For instance, when the investigator assumes the odds ratio (OR) at the end of the study to be , then it’s intuitive to adopt the logit link function. Other assumptions are the same with the previous example, however, the treatment effect β is now different (β is anticipated to be around log(1.84) under the conditional model) and will be returned by the software. As the ICC is based on the proportional scale, it is applicable to different link functions and is still assumed to be 0.01. Fitting the model with all required inputs in R:
1 R> library("swdpwr")
2 R> dataset = matrix(c(rep(c(0, 1, 1), 6),rep(c(0, 0, 1), 6)), 12, 3, byrow = TRUE)
3 R> swdpower (K = 50, design = dataset, family = "binomial", model = "conditional",
4 + link = "logit", type = "cross-sectional", meanresponse_start = 0.2,
5 + meanresponse_end0 = 0.25, meanresponse_end1 = 0.38, typeIerror = 0.05, alpha0 = 0.01,
6 + alpha1 = 0.01)
7 This cross-sectional study has total sample size of 1800
8 Power for this scenario is 0.838 for the alternative hypothesis treatment effect
9 beta = 0.616 (two-sided Type I error = 0.05 )
R package gives the power of 0.838 for the alternative hypothesis βA = 0.616.
If considering scenarios without time effects (secular trend), users can provide the same value for meanresponse_start and meanresponse_end0.
4.2. Marginal model for binary outcomes with cross-sectional and cohort designs
A method for the marginal model based on GEE was proposed in Li et al. [15], employing a block exchangeable correlation structure applicable to both cohort and cross-sectional designs. This method accommodates scenarios with and without time effects as well as three link functions. When the outcome is binary, because the variance is a strict function of the mean, the marginal variance argument sigma2 is undefined.
4.2.1. R package with cohort design
We first utilize a cohort design example to illustrate the use of the software in R for function swdpower in package swdpwr. A cohort design requires the specification of α0, α1 and α2. The examples are as follows:
An investigator plans to conduct a closed cohort stepped wedge design with 12 clusters and 4 periods, in which clusters are randomly allocated to one of the two sequences (6 clusters per sequence). This trial has an average of 100 individuals per cluster with a total sample size of 1200, and repeated measurements on each individual at each period for the binary outcome will be taken. The baseline proportion is assumed to be 0.156 and is expected to increase to 0.1765 by the end of the study even in the absence of the intervention (due to the secular trend). The relative risk (RR) by the end of the study is specified to be e0.75 and thus it’s intuitive to use the log link under the marginal model (with the treatment effect β to be 0.75 for this model configuration). The investigator is anticipating a within-period ICC of 0.03, a between-period ICC of 0.015, and a within-individual correlation in repeated measures on the same individual of 0.2 on the proportions scale. The treatment effect is to be tested at a two-sided 5% level of significance. Fitting the model with all required inputs in R:
1 R> library("swdpwr")
2 R> dataset = matrix(c(rep(c(0, 1, 1, 1), 6), rep(c(0, 0, 1, 1), 6)), 12, 4, byrow = TRUE)
3 R> swdpower(K = 100, design = dataset, family = "binomial", model = "marginal",
4 + link = "log", type = "cohort", meanresponse_start = 0.156, meanresponse_end0 = 0.1765,
5 + effectsize_beta = 0.75, typeIerror = 0.05, alpha0 = 0.03, alpha1 = 0.015, alpha2 = 0.2)
6 This cohort study has total sample size of 1200
7 Power for this scenario is 0.983 for the alternative hypothesis treatment effect
8 beta = 0.75 (two-sided Type I error = 0.05 )
In this example, the treatment effect effectsize_beta is given as an alternatively to meanresponse_end1. The power calculated given by R for this scenario is around 0.983 for the alternative hypothesis βA = 0.75.
Similarly, different link functions can be considered for the calculation. For instance, with the same regression model parameters and other inputs but under the logit link function due to the focus of interest in OR=e0.75 by the end of the study, the power obtained is then 0.843 for the alternative hypothesis βA = 0.75.
1 R> library("swdpwr")
2 R> dataset = matrix(c(rep(c(0, 1, 1, 1), 6), rep(c(0, 0, 1, 1), 6)), 12, 4, byrow = TRUE)
3 R> swdpower(K = 100, design = dataset, family = "binomial", model = "marginal",
4 + link = "logit", type = "cohort", meanresponse_start = 0.1349, meanresponse_end0 = 0.1499,
5 + effectsize_beta = 0.75, typeIerror = 0.05, alpha0 = 0.03, alpha1 = 0.015, alpha2 = 0.2)
6 This cohort study has total sample size of 1200
7 Power for this scenario is 0.843 for the alternative hypothesis treatment effect
8 beta = 0.75 (two-sided Type I error = 0.05 )
4.2.2. R package with cross-sectional design
We next consider the cross-sectional design under the marginal model, where α0 and α1 should be specified. In this example, an investigator plans to conduct a cross-sectional stepped wedge design with 12 clusters and 4 periods, in which clusters are randomly allocated to one of the two sequences (6 clusters per sequence). This trial has an average of 100 individuals per cluster per period with a total sample size of 4800, and measurements on the binary outcome will be taken. The baseline proportion is assumed to be 0.15 and no changes are expected by the end of the study even in the absence of the intervention (no secular trend). The risk difference (RD) by the end of the study is specified to be 0.05 and thus it’s convenient to use the identity link under the marginal model (with the treatment effect β to be also 0.05 for this model configuration). The investigator is anticipating a within-period ICC of 0.02 and a between-period ICC of 0.015 on the proportions scale. The treatment effect is to be tested at a two-sided 5% level of significance. Fitting the model with all required inputs in R:
1 R> library("swdpwr")
2 R> dataset = matrix(c(rep(c(0, 1, 1, 1), 6), rep(c(0, 0, 1, 1), 6)), 12, 4, byrow = TRUE)
3 R> swdpower(K = 100, design = dataset, family = "binomial", model = "marginal",
4 + link = "identity", type = "cross-sectional", meanresponse_start = 0.15,
5 + meanresponse_end0 = 0.15, meanresponse_end1 = 0.2, typeIerror = 0.05, alpha0 = 0.02,
6 + alpha1 = 0.015)
7 This cross-sectional study has total sample size of 4800
8 Power for this scenario is 0.946 for the alternative hypothesis treatment effect
9 beta = 0.05 (two-sided Type I error = 0.05 )
The power given by R is around 0.946 for the alternative hypothesis βA = 0.05.
4.3. Method with continuous outcomes under identity link
Linear mixed effects models have been widely used in the design and analysis of SWDs, for example, see: Hussey and Hughes [2], Hemming et al. [12], Hooper et al. [13]. Li et al. [15] proposed methods for analyzing SWDs for continuous outcomes under the identity link function. Because it has been shown that conditional and marginal models are equivalent when the regression is linear with mean 0 random effect and the identity or log link functions [10], with the addition of a new proof for equivalence of variance of treatment effect in Appendix D, the procedures in Li et al. [15] are used for power calculations with continuous outcomes, with three levels of correlation parameters considered.
The designs for continuous outcomes are conducted under the identity link function. Both cross-sectional and cohort designs with and without time effects can be accommodated in our software. Here, the argument sigma2 must be specified, which equals as in Section 2.2.
An example from Li et al. [15] is used for illustrating the use of function swdpower in R. In this example, an investigator plans to conduct a closed cohort stepped wedge design with 8 clusters and 3 periods, in which clusters are randomly allocated to one of the two sequences (4 clusters per sequence). This trial has an average of 24 individuals per cluster per period with a total sample size of 192, and measurements on the continuous outcome will be taken. Continuous outcomes will be explained under the marginal model with identity link. The baseline mean response is assumed to be 0.1 and is expected to increase to 0.2 by the end of the study even in the absence of the intervention (due to the secular trend). The mean response difference by the end of the study is specified to be 0.2 (with the treatment effect β to be also 0.2 for this model configuration). The investigator is anticipating a within-period ICC of 0.03, a between-period ICC of 0.015, and a within-individual correlation in repeated measures on the same individual of 0.2. The marginal variance of the outcomes is set to be 0.095, which is a required input for continuous outcomes. The treatment effect is to be tested at a two-sided 5% level of significance. The implementation in R is:
1 R> library("swdpwr")
2 R> dataset = matrix(c(rep(c(0, 1, 1),4), rep(c(0, 0, 1), 4)), 8, 3, byrow = TRUE)
3 R> swdpower(K = 24, design = dataset, family = "gaussian", model = "marginal",
4 + link = "identity", type = "cohort", meanresponse_start = 0.1, meanresponse_end0 = 0.2,
5 + effectsize_beta = 0.2, sigma2 = 0.095, typeIerror = 0.05, alpha0 = 0.03, alpha1 = 0.015,
6 + alpha2 = 0.2)
7 This cohort study has total sample size of 192
8 Power for this scenario is 0.965 for the alternative hypothesis treatment effect
9 beta = 0.2 (two-sided Type I error = 0.05 )
In this example trial, the power obtained from the software is around 0.965 for the alternative hypothesis βA = 0.2.
We also consider the same example without secular trends (time effects are zero):
1 R> library("swdpwr")
2 R> dataset = matrix(c(rep(c(0, 1, 1), 4), rep(c(0, 0, 1), 4)), 8, 3, byrow = TRUE)
3 R> swdpower(K = 24, design = dataset, family= "gaussian", model = "marginal",
4 + link = "identity", type = "cohort", effectsize_beta = 0.2, sigma2 = 0.095,
5 + typeIerror = 0.05, alpha0 = 0.03, alpha1 = 0.015, alpha2 = 0.2)
6 This cohort study has total sample size of 192
7 Power for this scenario is 1 for the alternative hypothesis treatment effect
8 beta = 0.2 (two-sided Type I error = 0.05 )
In this example, only effectsize_beta is specified and the trial was conducted without time effects by default. The calculated power is around 1 for the alternative hypothesis βA = 0.2.
5. Application
We provide two real-data applications and show the implementation by SAS.
5.1. The EPT Trial
The Washington Expedited Partner Therapy (EPT) trial was a community-based trial employing a cluster randomized SWD for promoting EPT. The outcome was Chlamydia status, a binary variable. 24 local health jurisdictions (LHJs) were included in this trial and each represented a cluster. There were 5 time periods and the intervention was initiated at four of them, with 6 clusters entering the intervention group at each time period (6 clusters per sequence). We can describe this design in the SAS data set ept:
1 data ept; 2 input numofclusters time1 time2 time3 time4 time5; 3 cards; 4 6 0 1 1 1 1 5 6 0 0 1 1 1 6 6 0 0 0 1 1 7 6 0 0 0 0 1 8 ; 9 run;
The design used a generalized linear mixed model under the log link function with covariates for intervention status and time period [31]. This cross-sectional design assumes 162 individuals in each cluster at each time period for a total sample size of 19440. Based on preliminary data, the baseline prevalence of Chlamydia was about 0.05, the cluster effect coefficient of variation was 0.3, the two-sided Type I error was set of 0.05, and a prevalence ratio of 0.7 was to be tested. The coefficient of variation is defined to characterize the cluster effects on the variance of responses [32] and is closely related to regular intraclass correlation. Following Hussey and Hughes [2] that the coefficient of variation was τ/μ′, where μ′ is denoted as the baseline prevalence of Chlamydia 0.05, the intraclass correlation [2] was approximately 0.0047 on the proportional scale and hence in this study α0 = α1 = 0.0047. We also assumed the presence of time effects. The input parameters were calculated and summarized based on these information. Hussey and Hughes [2] used the conditional model and the approximation method for binary outcomes, here, we conducted this design using the marginal model, as follows:
1 %swdpwr(K = 162, design = ept, family = "binomial", model = "marginal", 2 link = "log", type = "cross-sectional", meanresponse_start = 0.05, 3 meanresponse_end0 = 0.049, meanresponse_end1 = 0.035, typeIerror = 0.05, 4 alpha0 = 0.0047, alpha1 = 0.0047)
At a two-sided 5% level of significance, we obtained power of 0.812 for the alternative hypothesis βA = −0.336 from the marginal model in Table 3, which corresponds to the anticipated power of 80% from similar scenarios with the conditional model considered in Golden et al. [31] and Hussey and Hughes [2].
Table 3.
Output from macro %swdpwr for EPT trial
| Result |
|---|
| I = 24 J = 5 K = 162 Total sample size = 19440 Family = binomial Model = marginal Link = log Type = cross-sectional Baseline (mu): −2.996 Treatment effect (beta): −0.336 Time effect (gamma J): −0.020 alpha0: 0.005 alpha1: 0.005 alpha2: 0.005 Type I error = 0.050 Power = 0.812 |
5.2. The PPIUD Study
The Tanzania PPIUD study utilized a SWD to assess the causal effect of a PPIUD intervention on subsequent pregnancy [33]. The binary outcome was defined as a current or terminated pregnancy at 18 months postpartum. 6 hospitals were selected into the trial and the study lasted for 18 months with 4 time periods (3 clusters per sequence). We can describe this design in a SAS data set PPIUD:
1 data PPIUD; 2 input numofclusters time1 time2 time3 time4; 3 cards; 4 3 0 1 1 1 5 3 0 0 0 1 6 ; 7 run;
A generalized linear mixed model under identity link without time effects was employed for design. For illustrative purposes, we consider a small cluster size and this cross-sectional design assumes 120 individuals in each cluster at each time period for a total sample size of 2880. As in Canning et al. [33], the baseline proportion of pregnancy was assumed to be 0.24, the intraclass correlation was 0.15, the two-sided Type I error was set of 0.05, and a prevalence ratio of around 0.8 was to be tested. We estimated from preliminary data that the effect size was −0.046, assuming no time effects. We conducted this design using the conditional model in SAS. The macro called for this power calculation would be:
1 %swdpwr(K = 120, design= PPIUD, family = "binomial", model = "conditional" 2 link = "identity", type = "cross-sectional", meanresponse_start = 0.24 3 meanresponse_end0 = 0.24, effectsize_beta = −0.046, typeIerror = 0.05, 4 alpha0 = 0.15, alpha1 = 0.15)
At a two-sided 5% level of significance, we get the power 0.846 for the alternative hypothesis βA = −0.046 by the conditional model in Table 4. The result is consistent with the conclusion of 80% power or more in Canning et al. [33].
Table 4.
Output from macro %swdpwr for PPIUD study
| Result |
|---|
| I = 6 J = 4 K = 120 Total sample size = 2880 Family = binomial Model = conditional Link = identity Type = cross-sectional Baseline (mu): 0.240 Treatment effect (beta): −0.046 Time effect (gamma J): 0.000 alpha0: 0.150 alpha1: 0.150 alpha2: 0.150 Type I error = 0.050 Power = 0.846 |
6. Discussion
This article has described the use of the R package swdpwr and the SASmacro %swdpwr for power calculations in SWDs. The software is designed under two computer platforms where users specify input parameters for different scenarios of interest, accommodating cross-sectional and cohort designs, binary and continuous outcomes, marginal and conditional models, three link functions, with and without time effects, and unequal allocation of clusters per sequence. This software addresses the implementation gap between newly proposed methodology and their application to obtain more accurate power calculations for binary outcomes in SWDs, rather than relying on the approximation method in Hussey and Hughes [2]. The core of the software is developed in Fortran to ensure efficient computations, and is linked to SAS and R by the foreign function interface. As the number of time periods and individuals in each cluster increases, the calculations may become time-consuming, thus we have implemented some methods to decrease the computational cost. For example, we applied a simplified closed-form expression for matrix inversion under the marginal model, as derived in Li et al. [15]. The SAS macro swdpwr can be accessed at: https://github.com/jiachenchen322/swdpwr. Package swdpwr is available via the Comprehensive R Archive Network (CRAN) as a contributed package at: https://CRAN.R-project.org/package=swdpwr. The package is also available as a Shiny [34] app, available online at: https://jiachenchen322.shinyapps.io/swdpwr_shinyapp/ to enable users without SAS or R programming skills to also use this software easily.
One limitation of our study is that our software assumes equal cluster sizes. However, the average power under the conditional models or marginal models is generally robust to moderate cluster size variability under stepped wedge trials, as shown in Zhou et al. [18] and Tian et al. [35]. Future work is needed to accommodate unequal cluster-period sizes to make our software even more flexible. Furthermore, we are working to implement the partition method developed in Zhou et al. [18] for the conditional model with binary outcomes to permit power and sample size calculations with cluster sizes, K, greater than 150 as occurs in practice. In addition, current software only accommodates exchangeable, nested exchangeable and block exchangeable correlation structures, which could be further extended to allow for damped exponential correlation structures [36] and proportional decay correlation structures [37] that allow the between-period ICC to decay.
Highlights.
User-friendly SAS macro, R package and Shiny app for stepped wedge designs power calculations
Accommodation of various scenarios for binary and continuous outcomes
Addressing the implementation gap and providing more accurate power calculations for binary outcomes
Acknowledgments
This work was supported by the grants NIH/R01AI112339 and NIH/DP1ES025459.
Appendix
A. Remarks for methods
This software includes procedures for power calculations in SWDs with binary outcomes under the identity, logit and log link functions, based on Zhou et al. [18] and Li et al. [15], and also incorporates procedures for continuous outcomes as in Hussey and Hughes [2], Hooper et al. [13] and Li et al. [15] with the identity link function. The treatment effect β is the same under the conditional and marginal model with the identity and log link functions [10].
In Appendix D, by proving the equivalence of the variance of the intervention effect in the conditional and marginal models with continuous outcomes, we showed that Li et al. [15] incorporated the cross-sectional designs in Hussey and Hughes [2] and the cohort designs in Hooper et al. [13], and obtained the same power formulae for the conditional and marginal models for each of these designs. Hence, we can directly implement Li et al. [15] in our software for all of these continuous outcome scenarios.
Regarding the cross-sectional settings where α0 = α1 with binary outcomes, we implement both the conditional [18] and the marginal [15] models, for which the variance of these two estimates are different. As shown by Ritz and Spiegelman [10], the treatment effect, β, is the same for these two models under the identity and log link functions given the same mean responses. However, the estimates of the conditional and marginal model have different variances, and we found in numerical calculations that neither is globally greater than the other. Under the logit link, the parameter β has different interpretations for the two models given the same mean responses, and again, neither has a greater power than the other although variance comparisons are not meaningful with parameters having different interpretations. Figure A.1 provides some examples of this pattern, which is expected because GLMM is likelihood based, while the marginal models relies on unbiased estimating equations.
We emphasize that our software considers designs with and without time effects. In most literature, see, for instance, Hussey and Hughs [2], Hemming et al. [12], Hooper et al. [13], Li et al. [14] and Li et al. [15], time effects are assumed. However, Zhou et al. [30] argued that SWDs are mostly used in the study of relatively short-term outcomes with short-term interventions, thus, it is reasonable to assume no time effects in the primary analysis. Zhou et al. [18] developed their method considering cases with and without time effects. When developing this software, we include and generalize all the methods to cases with and without time effects.
Of note, for binary outcomes, the correlation parameters are calculated on the proportional scale, which can be obtained based on preliminary data. We give the general definitions of the correlation parameters with binary outcomes as follows [38], which correspond to the equations for continuous outcomes in Section 2.2:
| (A.1) |
| (A.2) |
| (A.3) |
Specifically, for continuous outcomes only, for k ≠ k′, for j ≠ j′, k ≠ k′, and for j ≠ j′. The total marginal variance of Yijk is . For binary outcomes, we recommend that investigators utilize the Equations A.1, A.2, and A.3 for calculations as sometimes the correlation parameters for binary outcomes do not have closed forms (eg. under the logit link).
B. Warnings and error messages generation
The program will output reliable results although warnings are returned due to some invalid input arguments, including mainly five scenarios. First, conditional model with binary outcomes only allows for cross-sectional settings, so if "cohort" is specified for the argument type, a warning message will occur and type=âĂIJcross-sectionalâĂİ will be forced to resume the power calculation. Second, α0 = α1 is to be ensured for conditional model with binary outcome and cross-sectional designs, if it is violated, the value of α1 is set to the value of α0 and a warning will be returned. Third, for cross-sectional designs, if α2 is specified, it will be ignored and a warning message will remind users that α2 is undefined and should not be an input. Fourth, when sigma2 is supplied for binary outcomes, it will be ignored and the software will return a warning that marginal variance should not be specified for binary outcomes. Last, if it is continuous outcome supplied by link functions of logit or log, a warning message will explain that the program will be conducted with the link function forced to be identity.
There are also cases where error messages occur and the program will be stopped, then users will need to revise the input arguments. The most common errors will be missing of input arguments. However, users will need to notice that although the software includes two complementary ways to supply regression model parameters as in Section 3.1, an error will be generated if users specify meanresponse_start, meanresponse_end0, meanresponse_end1 and effectsize_beta_ simultaneously, in case that contradictions occur for the value of parameters. Besides, the specification of input arguments cannot be identified when typos occur in arguments such as family, model, link and type, then errors will be reported.
When input parameters, including the correlation parameters, two-sided Type I error rate, or response for binary outcomes, are out of range, an error message will be returned. Before giving the detailed examples, we discuss the specification of correlation parameters for both cross-sectional and cohort designs. As described in Section 2.1.2, these correlations represent the within-period intracluster, between-period intracluster, and within-individual correlations, respectively, with the natural restriction of within [−1, 1]. For the correlation structure of SWDs, Li et al. [14] identified four linear eigenvalue constraints to ensure a positive definite correlation matrix. These constraints are enforced in our software for all models and both outcome types. In a cross-sectional design, because there are no repeated measures within subjects, α2 is not required and the block exchangeable correlation structure reduces to the nested exchangeable structure as in Teerenstra et al. [39]. Thus, in cross-sectional designs, a single intracluster correlation coefficient which measures the correlation between individuals in the same cluster describes the correlation structure in Zhou et al. [18] such that the working correlation reduces to α0 = α1.
Additional restrictions for α0, α1 and α2 are needed as the marginal and conditional means limit the ranges of correlation due to binary outcomes [27], where i ≠ j:
| (B.4) |
This can be written to require that, the following three criteria must be satisfied over i = 1, 2, …, I; j, l = 1, 2, …, J; k, m = 1, 2, …, K:
| (B.5) |
| (B.6) |
| (B.7) |
where μijk = μij and vijk = vij are the mean and variance of the outcome for individual k at time period j from cluster i, and j ≠ l plus k ≠ m. These restrictions apply to both the conditional and marginal model with binary outcomes.
Now, we give examples for scenarios where representative errors occur in R, so that users can check the input parameter according to the error message and obtain suggestions about how to revise them. The same errors will occur if conducted in SAS as well.
In the first example, the requirement that the 2- or 3-way working correlation matrix Ri is positive definite is violated as correlation parameters exceed plausible ranges although they are still within [0, 1]. This error could occur for both outcome types and in all models.
1 R> library("swdpwr")
2 R> dataset = matrix(c(rep(c(0, 1, 1, 1), 4), rep(c(0, 0, 1, 1), 4),
3 + rep(c(0, 0, 0, 1), 4)), 12, 4, byrow = TRUE)
4 R> swdpower(K = 100, design = dataset, family = "gaussian",
5 + model = "marginal", link = "identity", type = "cohort",
6 + effectsize_beta = 0.05, sigma2 = 0.095, typeIerror = 0.05, alpha0 = 0.015,
7 + alpha1 = 0.2, alpha2 = 0.1)
8 Error in swdpower(K = 100, design = dataset, family = "gaussian",
9 model = "marginal", : Correlation matrix R is not positive definite. Please
10 check whether the between-period intracluster correlation is unrealistically larger
11 than the within-period intracluster correlation or the within-individual correlation.
The fix to this error can be revising alpha1 to be much smaller, then the program will be processed without errors:
1 R> swdpower(K = 100, design = dataset, family = "gaussian", 2 + model = "marginal", link = "identity", type = "cohort", 3 + effectsize_beta = 0.05, sigma2 = 0.095, typeIerror = 0.05, alpha0 = 0.015, 4 + alpha1 = 0.01, alpha2 = 0.1) 5 This cohort study has total sample size of 1200 6 Power for this scenario is 0.994 for the alternative hypothesis treatment 7 effect beta = 0.05 ( two-sided Type I error = 0.05 )
The second example occurred with a binary outcome. This error is also related to the correlations values given because they are additionally restricted by means due to binary outcomes [27, 28] as discussed before.
1 R> library("swdpwr")
2 R> dataset = matrix(c(rep(c(0, 1, 1, 1), 4), rep(c(0, 0, 1, 1), 4),
3 + rep(c(0, 0, 0, 1), 4)), 12, 4, byrow = TRUE)
4 R> swdpower (K = 100, design = dataset, family = "binomial",
5 + model = "marginal", link = "identity", type = "cohort",
6 + meanresponse_start = 0.1, meanresponse_end0 = 0.2, effectsize_beta = 0.7,
7 + typeIerror = 0.05, alpha0 = 0.1, alpha1 = 0.05, alpha2 = 0.2)
8 Error in swdpower(K = 100, design = dataset, family = "binomial",
9 model = "marginal", : Correlation parameters do not satisfy the
10 restrictions of Qaqish (2003). Please check whether it is possible to reduce
11 the effect size, or make adjustments to the intraclass correlations.
This error can be fixed by revising the intraclass correlations, for example:
1 R> swdpower(K = 100, design = dataset, family = "binomial", 2 + model = "marginal", link = "identity", type = "cohort", 3 + meanresponse_start = 0.1, meanresponse_end0 = 0.2, effectsize_beta = 0.7, 4 + typeIerror = 0.05, alpha0 = 0.05, alpha1 = 0.05, alpha2 = 0.1) 5 This cohort study has total sample size of 1200 6 Power for this scenario is 1 for the alternative hypothesis treatment 7 effect beta = 0.7 ( two-sided Type I error = 0.05 )
The third example also pertains to a binary outcome. Sometimes, the input parameters related to mean responses may exceed the range for valid probability between [0, 1]. This error is easy to handle with and is not relevant to continuous outcomes. For instance:
1 R> library("swdpwr")
2 R> dataset = matrix(c(rep(c(0, 1, 1, 1), 4), rep(c(0, 0, 1, 1), 4),
3 + rep(c(0, 0, 0, 1), 4)), 12, 4, byrow = TRUE)
4 R> swdpower(K = 100, design = dataset, family = "binomial",
5 + model = "marginal", link = "identity", type = "cohort",
6 + meanresponse_start = 0.1, meanresponse_end0 = 0.2, effectsize_beta = 0.9,
7 + typeIerror = 0.05, alpha0 = 0.05, alpha1 = 0.05, alpha2 = 0.1)
8 Error in swdpower(K = 100, design = dataset, family = "binomial",
9 model = "marginal", : Violation of valid probability, given input parameters:
10 max(meanresponse_start, meanresponse_end0, meanresponse_end1)>1. Please
11 check whether any of these values are out of range and revise one or more of
12 them.
The fourth example occurs only in scenarios of binary outcomes under conditional models with time effects. It is discussed in Zhou et al. [18] that as the sample size K for each cluster at each time period increases, the estimated running time increases prohibitively to beyond what is possible even for high performance computing under these scenarios. Hence, we set an upper limit of 150 for K in the current software. However, even with values of K within this allowable range, computing time may still be low. To address this, users can consider switching to the marginal model specification or dropping time effects. An example for this error is:
1 R> library("swdpwr")
2 R> dataset = matrix(c(rep(c(0, 1, 1, 1), 4), rep(c(0, 0, 1, 1), 4),
3 + rep(c(0, 0, 0, 1), 4)), 12, 4, byrow = TRUE)
4 R> swdpower(K = 160, design = dataset, family = "binomial",
5 + model = "conditional", link = "logit", type = "cross-sectional",
6 + meanresponse_start = 0.1, meanresponse_end0 = 0.2, effectsize_beta = 0.6,
7 + typeIerror = 0.05, alpha0 = 0.05, alpha1 = 0.05)
8 Error in swdpower(K = 100, design = dataset, family = "binomial",
9 model = "conditional", : K should be at least smaller than 150 for this
10 scenario as the running time is too long with this K for the power
11 calculation of binary outcomes under conditional model with time effects.
12 Please reduce K or use the model without time effects or use
13 marginal models.
In addition, the intraclass correlations and two-sided Type I error must be between 0 and 1 as well for all models, for instance:
1 R> library("swdpwr")
2 R> dataset = matrix(c(rep(c(0, 1, 1, 1), 4), rep(c(0, 0, 1, 1), 4),
3 + rep(c(0, 0, 0, 1), 4)), 12, 4, byrow = TRUE)
4 R> swdpower(K = 100, design = dataset, family = "binomial",
5 + model = "marginal", link = "identity", type = "cohort",
6 + meanresponse_start = 0.1, meanresponse_end0 = 0.2, effectsize_beta = 0.5,
7 + typeIerror = 0.05, alpha0 = 1.1, alpha1 = 0.05, alpha2 = 0.1)
8 Error in swdpower(K = 100, design = dataset, family = "binomial",
9 model = "marginal", : Violate range of intraclass correlations:
10 max(alpha0, alpha1, alpha2)>1. Please correct the values of correlation
11 parameters, they must be between 0 and 1.
12 R> swdpower(K = 100, design = dataset, family = "binomial",
13 + model = "marginal", link = "identity", type = "cohort ",
14 + meanresponse_start = 0.1, meanresponse_end0 = 0.2, effectsize_beta = 0.5,
15 + typeIerror = 1.05, alpha0 = 0.1, alpha1 = 0.05, alpha2 = 0.1)
16 Error in swdpower(K = 100, design = dataset, family = "binomial",
17 model = "marginal", : two-sided Type I error provided is larger than 1, it must be
18 between 0 and 1, and is usually 0.05.
C. Examples implemented by SAS macro
C.1. Conditional model with binary outcome and cross-sectional design
The macro %swdpwr is used in SAS. The same examples are illustrated in SAS as the paper. As in R, %swdpwr in SAS requires that the input of a design matrix and a SAS data set exmple as follows is a pre-requisite:
1 data example; 2 input numofclusters time1 time2 time3; 3 cards; 4 6 0 1 1 5 6 0 0 1 6 ; 7 run;
The call to %swdpwr is:
1 %swdpwr(K = 50, design = example, family = "binomial", model = "conditional", 2 link = "identity", type = "cross-sectional", meanresponse_start = 0.2, 3 meanresponse_end0 = 0.25, meanresponse_end1 = 0.38, typeIerror = 0.05, 4 alpha0 = 0.01, alpha1 = 0.01) 1 %swdpwr(K = 50, design = example, family = "binomial", model = "conditional", 2 link = "logit", type = "cross-sectional", meanresponse_start = 0.2, 3 meanresponse_end0 = 0.25, meanresponse_end1 = 0.38, typeIerror = 0.05, 4 alpha0 = 0.01, alpha1 = 0.01)
The data set example should be generated as described in Section 3.3. The inputs of the SAS are the same as the R examples. Calculations were based on the conditional model with time effects. The same results are obtained as in the R examples. SAS gives the power of 0.899 under this scenario with the identity link function for the alternative hypothesis βA = 0.13, and the power of 0.838 under this scenario with the logit link function for the alternative hypothesis βA = 0.616, at a two-sided 5% level of significance.
C.2. Marginal model for binary outcomes with cohort designs
Next, we illustrate the use of SAS macro %swdpwr for cohort design examples under marginal model for binary outcomes and a SAS data set design2 is required:
1 data design2; 2 input numofclusters time1 time2 time3 time4; 3 cards; 4 6 0 1 1 1 5 6 0 0 1 1 6 ; 7 run;
To implement the same examples in R, the macro called to do power calculations would be:
1 % swdpwr(K = 100, design = design2, family = "binomial", model = "marginal", 2 link = "log", type = "cohort", meanresponse_start = 0.156, 3 meanresponse_end0 = 0.1765, effectsize_beta = 0.75, typeIerror = 0.05, 4 alpha0 = 0.03, alpha1 = 0.015, alpha2 = 0.2) 1 % swdpwr(K = 100, design = design2, family = "binomial", model = "marginal", 2 link = "logit", type = "cohort", meanresponse_start = 0.1349, 3 meanresponse_end0 = 0.1499, effectsize_beta = 0.75, typeIerror = 0.05, 4 alpha0 = 0.03, alpha1 = 0.015, alpha2 = 0.2)
Based on the sample stepped wedge cohort trial and conducting design using the marginal model with time effects, we obtain the same calculated power: power of 0.983 under the log link function and power of 0.843 under the logit link function for the alternative hypothesis βA = 0.75, at a two-sided 5% level of significance.
C.3. Marginal model for binary outcomes with cross-sectional designs
To illustrate the cross-sectional settings in SAS, we use the same example in R. Similarly, we use the data set design2 generated previously as the study design.
The macro called to do power calculations would be:
1 %swdpwr(K = 100, design = design2, family = "binomial", model = "marginal", 2 link = "identity", type = "cross-sectional", meanresponse_start = 0.15, 3 meanresponse_end0 = 0.15, meanresponse_end1 = 0.2, typeIerror = 0.05, 4 alpha0 = 0.02, alpha1 = 0.015)
With a total sample size of 4800,, at a two-sided 5% level of significance, the power under this scenario is 0.946 for the alternative hypothesis βA = 0.05, which accords with the results in R.
C.4. Method with continuous outcomes under identity link
Next, we illustrate the R examples in macro %swdpwr using SAS, and prepare a SAS data set design3:
1 data design3; 2 input numofclusters time1 time2 time3; 3 cards; 4 4 0 1 1 5 4 0 0 1 6 ; 7 run;
The macro called to do power calculations would be:
1 %swdpwr(K = 24, design = design3, family = "gaussian", model = "marginal", 2 link = "identity", type = "cohort", meanresponse_start = 0.1, 3 meanresponse_end0 = 0.2, effectsize_beta = 0.2, sigma2 = 0.095, 4 typeIerror = 0.05, alpha0 = 0.03, alpha1 = 0.015, alpha2 = 0.2) 5 6 %swdpwr(K = 24, design = design3, family = "gaussian", model = "marginal", 7 link = "identity", type = "cohort", effectsize_beta = 0.2, sigma2 = 0.095, 8 typeIerror = 0.05, alpha0 = 0.03, alpha1 = 0.015, alpha2 = 0.2)
The same results were obtained as in R, with the power of around 0.965 considering time effects and 1 considering no time effects, respectively, for the alternative hypothesis βA = 0.2, at a two-sided 5% level of significance.
D. Equivalence of the variance for continuous outcomes
In this paper, we include procedures for power calculations in SWDs with continuous outcomes based on Li et al. [15], which employed a block exchangeable correlation structure with three correlation parameters accommodating both cohort and cross-sectional designs under the GEE framework. Hussey and Hughes [2] developed methods based on a linear mixed effects model with a continuous outcome for a cross-sectional design with a single random cluster effect. Hooper et al. [13] generalized Hussey and Hughes [2]’s method to closed cohort CRTs with random effects of individuals within cluster, between- and within-period effect, as in Li et al. [15].
Here, we show the equivalence of power obtained by Hussey and Hughes [2], Hooper et al. [13], and Li et al. [15] for a continuous outcome. Then, power calculations for continuous outcomes under all scenarios covered in this software can all be incorporated by Li et al. [15] directly.
D.1. With time effects
With I clusters and J time periods, Hussey and Hughes [2] defined:
| (D.8) |
where Yijk is the individual continuous response in cluster i at time period j of individual k, Xij is a binary treatment assignment (1=intervention; 0=standard of care) in cluster i at time period j, β is the treatment effect, μ is the baseline outcome rate on the scale of the link function in control groups, γj is the fixed time effect corresponding to time period j (with γ1 = 0), bi is the random effect for cluster i with bi ~ N(0, τ2), and . We also assume that ϵijk is independent of bi, and K individuals at each time period in each cluster.
It can be shown that, the cluster means model obtained by summing over individuals within a cluster is:
| (D.9) |
where ϵij = Σk ϵijk/K ~ N(0, σ2) and .
The estimate of the fixed parameter vector η = (μ, γ2, γ3, …, γJ, β) is obtained by weighted least squares (WLS). We assume that Z is the I J * (J + 1) design matrix corresponding to the parameter vector η under SWD. To obtain power, we are interested in the variance of , which is the (J + 1) × (J + 1) element of (Z′V−1Z)−1, where V is an I J * I J block diagonal matrix that measures the covariance of mean response between different time periods in all clusters. With K individuals at each time period per cluster, Hussey and Hughes [2] gave:
| (D.10) |
where U = Σij Xij, W = Σj(Σi Xij)2 and V = Σi(Σj Xij)2.
To generalize cross-sectional SWDs considered by Hussey and Hughes [2] to cohort SWDs, Hooper et al. [13] also assumed a linear mixed effects model:
| (D.11) |
The notations are the same as Section 2.2. We also assume that bi, cij, πik and ϵijk are independent of each other, and the total variance of Yijk is . The working correlation matrix is the same as the three-level correlation structure Ri given in Section 2.2 for cross-sectional and cohort designs. Model (D.11) corresponds to individual-level responses based on mixed effects model, which agrees with the population-averaged marginal model in Li et al. [15]:
| (D.12) |
where μijk is the mean response of Yijk under both the marginal and conditional model. Li et al. [15] and Hooper et al. [13] are developed to accommodate the same three correlation parameters, under marginal and conditional models, respectively. In both models, the covariance is estimated by the model-based estimator , where Zi is the J Ki * (J + 1) design matrix corresponding to the parameter vector η under SWD within cluster i and is the working covariance matrix within cluster i based on a block exchangeable correlation structure. Hence, the estimators of β under Model (D.11) and (D.12) are equivalent and obtain the same power.
As shown in Li et al. [15], this variance for the estimated intervention effect is:
| (D.13) |
where U = Σij Xij, W = Σj(Σi Xij)2, V = Σi(Σj Xij)2, λ3 = 1 + (K − 1)(α0 − α1) − α2, λ4 = 1 + (K − 1)α0 + (J − 1)(K − 1)α1 + (J − 1)α2.
The equivalence of Model (D.9) and (D.12) is proved under the cross-sectional setting in Hussey and Hughes [2] with , where Equation (D.10) is equal to Equation (D.13). The treatment effect β is the same under the conditional and marginal model with the identity link function Ritz and Spiegelman [10]. Thus we can conclude the equivalence of these three models in cases with time effects.
D.2. Without time effects
Here, we consider cases without fixed time effects and derive the three models by Hussey and Hughes [2], Hooper et al. [13], and Li et al. [15] accordingly.
The Hussey and Hughes [2] model without time effects is denoted as:
| (D.14) |
The notations are the same as previously.
The cluster means model obtained by summing over individuals within a cluster is:
| (D.15) |
where ϵij = Σk ϵijk/K ~ N(0, σ2) and .
The estimate of the fixed parameter vector η = (μ, β) is obtained by weighted least squares (WLS). We assume that Z is the I J * 2 design matrix corresponding to the parameter vector η under SWD. To obtain power, we are interested in the variance of , which is the 2×2 element of (Z′V−1Z)−1, where is an I J * I J block diagonal matrix that measures the covariance of mean response between different time periods in all clusters. With K individuals at each time period per cluster, Liao et al. [40] showed that the variance of the estimated intervention effect is:
| (D.16) |
where U = Σij Xij and V = Σi(Σj Xij)2.
The model that accounts for closed cohort designs without time effects under Hooper et al. [13] is:
| (D.17) |
The notations are defined in the same way as in the previous section. This model is described at individual-level responses based on mixed effects model, which still agrees with the population-averaged marginal model in Li et al. [15]:
| (D.18) |
where μijk is the mean response of Yijk under both the marginal and conditional model. Li et al. [15] and Hooper et al. [13] are developed to accommodate the three three correlation parameters, under marginal and conditional models, respectively. In both models, the covariance is estimated by the model-based estimator , where Zi is the J Ki *2 design matrix corresponding to the parameter vector η under SWD within cluster i and Vi is the working covariance matrix within cluster i based on a block exchangeable correlation structure. Hence, Model (D.17) and (D.18) are equivalent and obtain the same power.
According to our derivation following Li et al. [15], the variance of the estimated intervention effect under cases without time effects is:
| (D.19) |
where U = Σij Xij and V = Σi(Σj Xij)2, λ3 = 1 + (K − 1)(α0 − α1) − α2, λ4 = 1 + (K − 1)α0 + (J − 1)(K − 1)α1 + (J − 1)α2.
The equivalence of Model (D.15) and (D.18) is proved under the cross-sectional setting in Hussey and Hughes [2] with , where Equation (D.16) equals to Equation (D.19). The treatment effect β is the same under the conditional and marginal model with the identity link function [10]. Thus we can conclude the equivalence of these three models in cases without time effects.
Figure A.1:
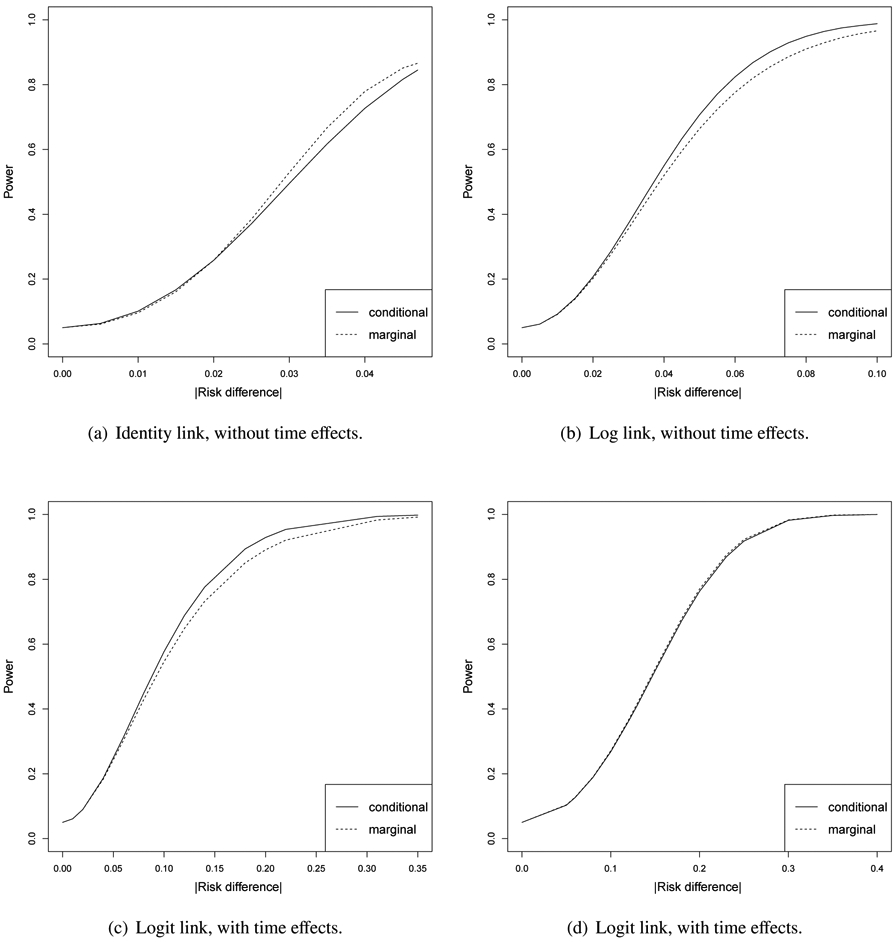
Power vs. the absolute value of risk difference between the control and intervention group at the end of the cross-sectional study, for I = 6, J = 3, K = 40, and α0 = α1 = 0.02. There are no time effects in the first row. Figure A.1 has the identity link and the baseline mean response in the control group of 0.05. The conditional model has a slightly larger power when the absolute value of risk difference is smaller, the opposite conclusion is shown when the absolute value of risk difference is larger. Figure A.1 has the log link and the baseline mean response in the control group of 0.045. The conditional and marginal models have almost the same power when risk difference is smaller, and conditional model has a larger power when risk difference increases. The second row considers time effects and the logit link. In Figure A.1, the baseline mean response in the control group is 0.03 and the mean response in the control group at the end of the study is 0.04. The conditional model has a larger power as risk difference increases. In Figure A.1, the baseline mean response in the control group is 0.3 and the mean response in the control group at the end of the study is 0.4. The marginal model has a larger power as risk difference increases.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Declaration of Competing Interest
The authors have declared no conflict of interest.
References
- [1].Murray DM, et al. , Design and Analysis of Group-Randomized Trials, Vol. 29, Oxford University Press, USA, 1998. [Google Scholar]
- [2].Hussey MA, Hughes JP, Design and analysis of stepped wedge cluster randomized trials, Contemporary Clinical Trials 28 (2) (2007) 182–191. doi: 10.1016/j.cct.2006.05.007. [DOI] [PubMed] [Google Scholar]
- [3].Copas AJ, Lewis JJ, Thompson JA, Davey C, Baio G, Hargreaves JR, Designing a stepped wedge trial: Three main designs, carry-over effects and randomisation approaches, Trials 16 (1) (2015) 352. doi: 10.1186/s13063-015-0842-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4].Hemming K, Girling A, The efficiency of stepped wedge vs. cluster randomized trials: Stepped wedge studies do not always require a smaller sample size, Journal of Clinical Epidemiology 66 (12) (2013) 1427. doi: 10.1016/j.jclinepi.2013.07.007. [DOI] [PubMed] [Google Scholar]
- [5].Martin J, Girling A, Nirantharakumar K, Ryan R, Marshall T, Hemming K, Intra-cluster and inter-period correlation coefficients for cross-sectional cluster randomised controlled trials for type-2 diabetes in uk primary care, Trials 17 (1) (2016) 402. doi: 10.1186/s13063-016-1532-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6].Hughes JP, Granston TS, Heagerty PJ, Current issues in the design and analysis of stepped wedge trials, Contemporary Clinical Trials 45 (2015) 55–60. doi: 10.1016/j.cct.2015.07.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7].Pinheiro J, Bates D, Mixed-Effects Models in S and S-PLUS, Springer Science & Business Media, 2006. [Google Scholar]
- [8].Breslow NE, Clayton DG, Approximate inference in generalized linear mixed models, Journal of the American statistical Association 88 (421) (1993) 9–25. doi: 10.1080/01621459.1993.10594284. [DOI] [Google Scholar]
- [9].Liang K-Y, Zeger SL, Longitudinal data analysis using generalized linear models, Biometrika 73 (1) (1986) 13–22. doi: 10.1093/biomet/73.1.13. [DOI] [Google Scholar]
- [10].Ritz J, Spiegelman D, Equivalence of conditional and marginal regression models for clustered and longitudinal data, Statistical Methods in Medical Research 13 (4) (2004) 309–323. doi: 10.1191/0962280204sm368ra. [DOI] [Google Scholar]
- [11].Woertman W, de Hoop E, Moerbeek M, Zuidema SU, Gerritsen DL, Teerenstra S, Stepped wedge designs could reduce the required sample size in cluster randomized trials, Journal of Clinical Epidemiology 66 (7) (2013) 752–758. doi: 10.1016/j.jclinepi.2013.01.009. [DOI] [PubMed] [Google Scholar]
- [12].Hemming K, Lilford R, Girling AJ, Stepped-wedge cluster randomised controlled trials: A generic framework including parallel and multiple-level designs, Statistics in Medicine 34 (2) (2015) 181–196. doi: 10.1002/sim.6325. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13].Hooper R, Teerenstra S, de Hoop E, Eldridge S, Sample size calculation for stepped wedge and other longitudinal cluster randomised trials, Statistics in Medicine 35 (26) (2016) 4718–4728. doi: 10.1002/sim.7028. [DOI] [PubMed] [Google Scholar]
- [14].Li F, Turner EL, Preisser JS, Optimal allocation of clusters in cohort stepped wedge designs, Statistics & Probability Letters 137 (2018) 257–263. doi: 10.1016/j.spl.2018.02.002. [DOI] [Google Scholar]
- [15].Li F, Turner EL, Preisser JS, Sample size determination for gee analyses of stepped wedge cluster randomized trials, Biometrics 74 (4) (2018) 1450–1458. doi: 10.1111/biom.12918. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [16].Hemming K, Taljaard M, Sample size calculations for stepped wedge and cluster randomised trials: A unified approach, Journal of Clinical Epidemiology 69 (2016) 137–146. doi: 10.1016/j.jclinepi.2015.08.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [17].Martin J, Taljaard M, Girling A, Hemming K, Systematic review finds major deficiencies in sample size methodology and reporting for stepped-wedge cluster randomised trials, BMJ Open 6 (2) (2016) e010166. doi: 10.1136/bmjopen-2015-010166. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [18].Zhou X, Liao X, Kunz LM, Normand S-LT, Wang M, Spiegelman D, A maximum likelihood approach to power calculations for stepped wedge designs of binary outcomes, Biostatistics 21 (1) (2020) 102–121. doi: 10.1093/biostatistics/kxy031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [19].Hughes J, Hakhu NR, Voldal E, swCRTdesign: Stepped Wedge Cluster Randomized Trial (SW CRT) Design, r package version 3.1 (2019). URL https://CRAN.R-project.org/package=swCRTdesign [Google Scholar]
- [20].Hemming K, Girling A, A menu-driven facility for power and detectable-difference calculations in stepped-wedge cluster-randomized trials, The Stata Journal 14 (2) (2014) 363–380. doi: 10.1177/1536867X1401400208. [DOI] [Google Scholar]
- [21].Hemming K, Kasza J, Hooper R, Forbes A, Taljaard M, A tutorial on sample size calculation for multiple-period cluster randomized parallel, cross-over and stepped-wedge trials using the shiny crt calculator, International journal of epidemiology 49 (3) (2020) 979–995. doi: 10.1093/ije/dyz237. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [22].Li F, Hughes JP, Hemming K, Taljaard M, Melnick ER, Heagerty PJ, Mixed-effects models for the design and analysis of stepped wedge cluster randomized trials: An overview, Statistical Methods in Medical Research 30 (2) (2021) 612–639. doi: 10.1177/0962280220932962. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [23].Baio G, Copas A, Ambler G, Hargreaves J, Beard E, Omar RZ, Sample size calculation for a stepped wedge trial, Trials 16 (1) (2015) 354. doi: 10.1186/s13063-015-0840-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [24].Kleinman K, Sakrejda A, Moyer J, Nugent J, Reich N, Obeng D, clusterPower: Power Calculations for Cluster-Randomized and Cluster-Randomized Crossover Trials, r package version 0.7.0 (2021). URL https://CRAN.R-project.org/package=clusterPower [Google Scholar]
- [25].Ouyang Y, Xu L, Karim ME, Gustafson P, Wong H, Crtpowerdist: An r package to calculate attained power and construct the power distribution for cross-sectional stepped-wedge and parallel cluster randomized trials, Computer Methods and Programs in Biomedicine 208 (2021) 106255. doi: 10.1016/j.cmpb.2021.106255. [DOI] [PubMed] [Google Scholar]
- [26].Hemming K, Taljaard M, Grimshaw J, Introducing the new consort extension for stepped-wedge cluster randomised trials, Trials 20 (1) (2019) 1–4. doi: 10.1186/s13063-018-3116-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [27].Qaqish BF, A family of multivariate binary distributions for simulating correlated binary variables with specified marginal means and correlations, Biometrika 90 (2) (2003) 455–463. doi: 10.1093/biomet/90.2.455. [DOI] [Google Scholar]
- [28].Ridout MS, Demetrio CG, Firth D, Estimating intraclass correlation for binary data, Biometrics 55 (1) (1999) 137–148. doi: 10.1111/j.0006-341X.1999.00137.x. [DOI] [PubMed] [Google Scholar]
- [29].McCulloch CE, Maximum likelihood algorithms for generalized linear mixed models, Journal of the American Statistical Association 92 (437) (1997) 162–170. doi: 10.1080/01621459.1997.10473613. [DOI] [Google Scholar]
- [30].Zhou X, Liao X, Spiegelman D, âĂIJcross-sectionalâĂİ stepped wedge designs always reduce the required sample size when there is no time effect, Journal of Clinical Epidemiology 83 (2017) 108–109. doi: 10.1016/j.jclinepi.2016.12.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [31].Golden MR, Kerani RP, Stenger M, Hughes JP, Aubin M, Malinski C, Holmes KK, Uptake and population-level impact of expedited partner therapy (ept) on chlamydia trachomatis and neisseria gonorrhoeae: The washington state community-level randomized trial of ept, PLOS Medicine 12 (1). doi: 10.1371/journal.pmed.1001777. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [32].Hayes R, Bennett S, Simple sample size calculation for cluster-randomized trials., International Journal of Epidemiology 28 (2) (1999) 319–326. doi: 10.1093/ije/28.2.319. [DOI] [PubMed] [Google Scholar]
- [33].Canning D, Shah IH, Pearson E, Pradhan E, Karra M, Senderowicz L, Bärnighausen T, Spiegelman D, Langer A, Institutionalizing postpartum intrauterine device (iud) services in sri lanka, tanzania, and nepal: Study protocol for a cluster-randomized stepped-wedge trial, BMC Pregnancy and Childbirth 16 (1) (2016) 362. doi: 10.1186/s12884-016-1160-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [34].Chang W, Cheng J, Allaire J, Xie Y, McPherson J, shiny: Web Application Framework for R, r package version 1.5.0 (2019). URL https://CRAN.R-project.org/package=shiny [Google Scholar]
- [35].Tian Z, Preisser J, Esserman D, Turner E, Rathouz P, Li F, Impact of unequal cluster sizes for gee analyses of stepped wedge cluster randomized trials with binary outcomes, Biometrical Journal doi: 10.1002/bimj.202100112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [36].Munoz A, Carey V, Schouten JP, Segal M, Rosner B, A parametric family of correlation structures for the analysis of longitudinal data, Biometrics (1992) 733–742doi: 10.2307/2532340. [DOI] [PubMed] [Google Scholar]
- [37].Li F, Design and analysis considerations for cohort stepped wedge cluster randomized trials with a decay correlation structure, Statistics in Medicine 39 (4) (2020) 438–455. doi: 10.1002/sim.8415. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [38].Eldridge SM, Ukoumunne OC, Carlin JB, The intra-cluster correlation coefficient in cluster randomized trials: a review of definitions, International Statistical Review 77 (3) (2009) 378–394. doi: 10.1111/j.1751-5823.2009.00092.x. [DOI] [Google Scholar]
- [39].Teerenstra S, Lu B, Preisser JS, Van Achterberg T, Borm GF, Sample size considerations for gee analyses of three-level cluster randomized trials, Biometrics 66 (4) (2010) 1230–1237. doi: 10.1111/j.1541-0420.2009.01374.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [40].Liao X, Zhou X, Spiegelman D, A note on âĂIJdesign and analysis of stepped wedge cluster randomized trials", Contemporary Clinical Trials 45 (Pt B) (2015) 338. doi: 10.1016/j.cct.2015.09.011. [DOI] [PMC free article] [PubMed] [Google Scholar]


