Abstract
Background and Objective:
It is common to combine biomechanical modeling and medical images for multimodal analyses. However, mesh-image mismatch may occur that prevents direct information exchange. To eliminate mesh-image mismatch, we develop a simple but elegant displacement voxelization technique based on image voxel corner nodes to achieve voxel-wise strain. We then apply the technique to derive dense white matter fiber strains along whole-brain tractography (~35 k fiber tracts consisting of ~3.3 million sampling points) resulting from head impact.
Methods:
Displacements at image voxel corner nodes are first obtained from model simulation via scattered interpolation. Each voxel is then scaled linearly to form a unit hexahedral element. This allows convenient and efficient voxel-wise strain tensor calculation and displacement interpolation at arbitrary fiber sampling points via shape functions. Fiber strains from displacement interpolation are then compared with those from the commonly used strain tensor projection using either voxel- or element-wise strain tensors.
Results:
Based on a synthetic displacement field, fiber strains interpolated from voxelized displacement are considerably more accurate than those from strain tensor projection relative to the prescribed ground-truth (determinant of coefficient (R2) of 1.00 and root mean squared error (RMSE) of 0.01 vs. 0.87 and 0.10, respectively). For a set of real-world reconstructed head impacts (N=53), the strain tensor projection method performs similarly poorly (R2 of 0.80–0.90 and RMSE of 0.03–0.07), with overestimation strongly correlated with strain magnitude (Pearson correlation coefficient >0.9). Up to ~15% of the fiber strains are overestimated by more than the lower bound of a conservative injury threshold of 0.09. The percentage increases to ~37% when halving the threshold. Voxel interpolation is also significantly more efficient (15 sec vs. 40 sec for element strain tensor projection, without parallelization).
Conclusions:
Voxelized displacement interpolation is considerably more accurate and efficient in deriving dense white matter fiber strains than strain tensor projection. The latter generally overestimates with overestimation magnitude strongly correlating with fiber strain magnitude. Displacement voxelization is an effective technique to eliminate mesh-image mismatch and generates a convenient image representation of tissue deformation. This technique can be generalized to broadly facilitate a diverse range of image-related biomechanical problems for multimodal analyses. The convenient image format may also promote and facilitate biomechanical data sharing in the future.
Keywords: biomechanical model, medical imaging, finite element method, multimodal analysis, strain tensor, traumatic brain injury, Worcester Head Injury Model
1. Introduction
The finite element (FE) method has been widely applied to study a wide array of biomedical problems [1], including the simulation of biomechanical behavior of diverse biological tissues (e.g., soft tissue [2], bone [3]) under different loading conditions (e.g., surgery [4] and injury [5]). Combining FE-based biomechanical modeling with medical imaging is also a common practice as it allows for multimodal analysis to enable their mutual validation and the generation of personalized models [6,7]. Typically, biomechanical models use discretized mesh nodes and elements to sample displacement and stress/strain, respectively [8]. Mesh elements can be of many shapes or combinations of different shapes, such as triangles and quadrilaterals in two-dimension (2D), or tetrahedrons and hexahedrons in three-dimension (3D), provided that they satisfy numerical accuracy requirements. There are no size restrictions either, although smaller elements are desired for improved accuracy in FE simulation, and they are also typically used in regions that would experience greater response gradient. Both nodes and their connectivity relationship expressed in elements are necessary to determine the spatial discretization scheme.
In comparison, medical images typically employ regularly shaped pixels or voxels (in 2D or 3D, respectively) to sample anatomical and/or physiological information such as tissue property [9]. This sampling scheme is much more restrictive because pixels/voxels need to conform to a lattice or grid pattern. In addition, their spatial resolution (i.e., physical dimension for each pixel or voxel) along each anatomical axis is also fixed, although they may differ among the major axes. Because of these restrictions, an image resolution and the directions of major axes are sufficient to determine the spatial discretization scheme.
Nevertheless, when the mesh and image spatial discretization schemes do not align in space, mesh-image mismatch would occur. For example, mesh element centroids do not align with pixel/voxel centroids. This would prevent direct information exchange. To resolve mesh-image mismatch, deformation response resampling is often necessary, that is, to interpolate element-wise strains at image pixel/voxel centroids [10–12]. A maximum of 6 interpolations are necessary to generate a complete strain tensor field in 3D [12]. In addition, there could be concerns on the interpolation accuracy given that element-wise strains could be discontinuous at the element boundary. A systematic investigation is lacking on how best to resolve the mesh-image mismatch problem to yield maximum accuracy and efficiency.
In FE simulation and analysis, displacement field is first obtained by solving the system of equations, from which to derive stress/strain [8]. The latter are usually the response variables of interest across diverse biomechanical problems including, but not limited to, artery [13], tooth [14], stent [15], cartilage [16] and tendon [17] collagen, heart [18], and brain [5]. Both displacement and stress/strain sample a spatially continuous response field. Nevertheless, they are all “forced” to use a finite number of degrees-of-freedom (DOFs) for response sampling, which leads to discretization errors [8]. Further resampling the already discretized deformation field in order to conform to an image voxel lattice would seem to amplify the error. This is particularly of concern in downstream biomechanical analysis such as deriving fiber strains along white matter fiber tracts from head impact simulation in the field of traumatic brain injury [19–23]. Therefore, it is important to study how best to resample a deformation field to maximally preserve response accuracy and with high efficiency when transforming it into an image space for subsequent multimodal analysis.
For linear FE elements most widely used (and virtually exclusively used in head injury models [5,24]), displacement varies linearly across elements. They lead to element-wise constant strain [8], which is discontinuous at the element boundary. This suggests that deformation resampling based on displacement, rather than the commonly used strain, may be more accurate. Nevertheless, an extra voxel-wise strain tensor calculation is necessary for a voxelized displacement field, as the response of interest is typically strain rather than displacement, itself. However, this calculation can be much simplified because regularly shaped voxels are a special type of hexahedral element that can be simply scaled linearly to a unit element. Standard element shape functions are then readily applicable.
Therefore, the aim of this study is to develop a displacement voxelization scheme to resolve the common mesh-image mismatch problem and apply it to derive dense white matter fiber strains along the whole brain tractography due to head impact. We first verify our customized voxel-wise strain tensor calculation through hexahedral element shape functions against Abaqus simulation. We then compare fiber strain accuracy and efficiency using voxelized displacement interpolation with the commonly used strain tensor projection method, based on either voxel- or element-wise strain tensor from model simulation [19–23]. The latter approach could be slow (e.g., ~28 min to process just the transcallosal fiber tracts over the course of an impact using an unoptimized code [25]). More importantly, its accuracy has not been verified, but this is critical as fiber strain is now thought to be more predictive of injury [19,22,26,27].
If post-simulation displacement voxelization is effective for head impact simulation, it is anticipated to be applicable to other biomechanical problems as well. This simple but elegant technique allows generating an image representation of deformation to eliminate mesh-image mismatch. This could greatly simplify downstream calculations of voxel-wise strain tensor, which allows convenient image-based strain analyses and morphological operations without the usual disadvantage of a voxelized mesh used in numerical modeling. Given that mesh-image mismatch is common across diverse biomechanical fields [1], this technique can be generalized more broadly for seamless integration of biomechanical modeling and medical imaging for multimodal analyses. The convenient image format may also promote and facilitate biomechanical data sharing in the future, especially when it is not feasible to share the biomechanical model, itself.
2. Methods
2.1. Fiber strain and strain tensor from voxelized displacement field
In this study, we consider white matter fiber tracts from tractography as a set of ordered and discrete sampling points that define geometrical line segments of fibers. Fiber strain, by definition, describes the relative stretch of each line segment, or the relative change in distance between two neighboring fiber sampling points. In fact, it can be directly determined by their difference in displacement interpolated from those of the surrounding nodes (via scattered interpolation; referred to as “mesh interpolation”). However, this approach does not provide a voxelized deformation to resolve the mesh-image mismatch.
To rectify, we first “voxelize” the displacement field by interpolating displacements at voxel corner nodes. For an image volume of size of p × q × r, where p, q, and r are the number of rows, columns, and frames along the three anatomical directions, y, x, and z, respectively, this requires displacement resampling at voxel corner nodal locations of size of (p + 1) × (q + 1) × (r + 1), as illustrated in Fig. 1.
Fig. 1.
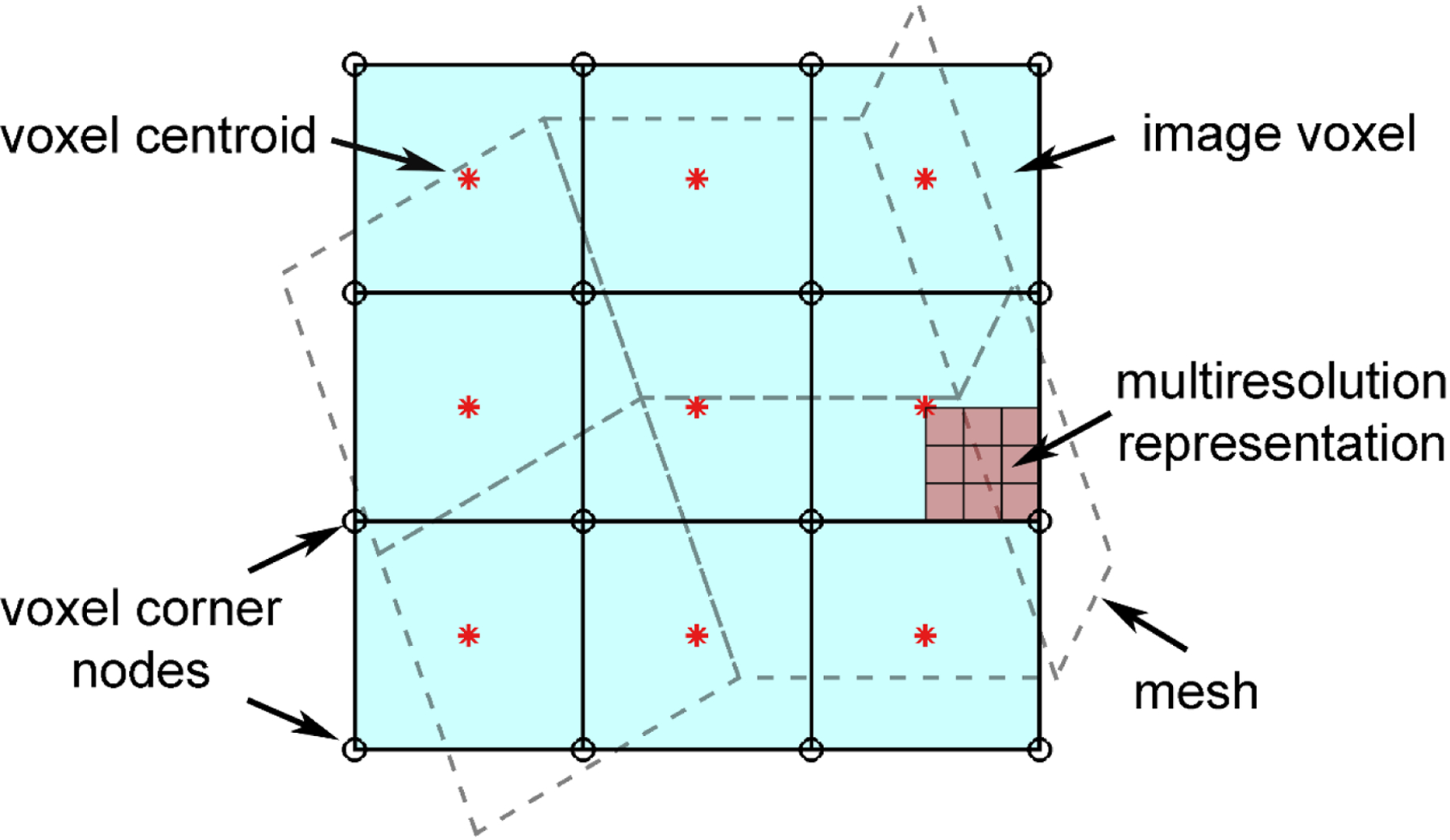
Illustration of mesh-image mismatch, where an image volume of size of p × q × r requires displacement resampling at voxel corner nodes of size of (p + 1) × (q + 1) × (r + 1) to generate a voxel-wise strain tensor field that will conform to the given image volume. To improve visualization, only a 2D projection is shown. An arbitrary region can be sampled at multiple and arbitrary resolutions to yield a multiresolution representation, if needed.
A voxel is a special 8-noded hexahedral element that can be simply scaled linearly to form a unit cube. This allows displacement interpolation at arbitrary fiber sampling points directly via hexahedral element shape functions (after proper scaling to yield an isotropic voxel resolution of dimensionless 2 in a natural coordinate system given by ξ, η, and ζ):
| (1) |
where ui are the voxel corner node displacements and Ni(ξ, η, ζ) are the shape functions represented as an 8×3 matrix for a given hexahedral element (with one integration point at element centroid).
Fiber strain can then be similarly determined by the difference in displacement of two neighboring fiber sampling points as interpolated from the corner nodes of the enclosing voxel (referred to as “voxel interpolation”). Localizing the corresponding enclosing voxel is greatly simplified into identifying the closest integer along the three major axes (round.m in MATLAB; after proper scaling).
To summarize, an image volume is first used to generate voxel corner nodes. Their displacements are obtained from FE nodal displacements via scattered interpolation. For each white matter fiber sampling point, the corresponding displacement is then determined through hexahedral shape functions based on the enclosing voxel. The displacement difference between two adjacent fiber sampling points readily determines the corresponding strain.
2.2. Strain tensor projection
To derive voxel-wise strain tensor, the deformation gradient, F, is calculated as:
| (2) |
where Xi are the voxel corner node coordinates in the global coordinate system, Ξ = Ξ(ξ, η, ζ) are their corresponding nodal coordinates in the natural coordinate system, and I is an identity matrix. is the Jacobian matrix, which is calculated as the transpose of the shape functions (matrix of size of 3×8) multiplied by the nodal coordinates of the 8 element nodes (matrix of size of 8×3, with each row representing the three coordinates of a given node). The outcome then leads to a 3×3 Jacobian matrix. In this study, we calculate engineering strain following the finite strain theory (which can be easily extended to other types of strain measures [8]), as it is directly available from Abaqus to verify our customized MATLAB implementation. The following hold:
| (3) |
| (4) |
where V is the left stretch tensor in the current configuration, and ε is the engineering strain tensor of interest [28]. For a regularly shaped voxel, J degenerates into a 3×3 matrix whose only non-zero elements are along the matrix diagonal. For an isotropic voxel of the same resolution along the three major axes, J further degenerates into an identity matrix, I (with a proper scaling). This greatly simplifies the customized implementation because no explicit and costly matrix inversion is necessary to calculate the inverse of J in Eqn. 2, which is also critical for achieving a high efficiency.
To project strain tensor based on voxelized displacement or FE elements (referred to as “voxel” or “element” tensor projection, respectively), the global coordinate system is rotated so that its z-axis is aligned with the fiber tangential direction determined from a forward difference method. Due to large rotation, it is important to account for the change in fiber orientation before strain tensor projection [29]. For voxelized displacement, the current fiber orientation is achieved by the updated fiber sampling point displacements via shape functions. For FE mesh-based displacement, the updated displacements are obtained through scattered interpolation instead.
Finally, strain tensor in the rotated coordinate system is obtained:
| (5) |
where the 4-by-4 matrix, T, is the rigid body transformation from the global to the local coordinates. Fiber strain, εf, at the given sampling point is then available through the following equation:
| (6) |
To summarize, voxel-wise strain tensor is efficiently calculated using hexahedral shape functions due to the degenerated Jacobian matrix. The current white matter fiber orientation is then determined from the updated fiber sampling point locations before stain tensor projection, for which the global coordinate system is rotated so that its z-axis is aligned with the current fiber tangential direction. Of note, the updated fiber sampling point locations can be directly used to determine fiber strain. Therefore, strain tensor projection is, in fact, unnecessary. Nevertheless, we employed this method for accuracy comparisons.
2.3. Anisotropic Worcester Head Injury Model V2.0
We employed the anisotropic Worcester Head Injury Model (WHIM) V2.0 (Fig. 2) [30] for testing. The model contains 227.4 k nodes and 202.8 k hexahedral elements for the brain (with an average element size of 1.8 ± 0.4 mm) and 221.1 k nodes and 440 k membrane elements for the cerebral vasculatures (with an average element size of 1 mm). It also has a co-registered companion whole-brain tractography consisting of ~35 k fibers, represented by a total of ~3.3 million ordered sampling points with 1 mm relative distance between two adjacent points [25]. The head coordinate system was chosen such that the posterior-to-anterior, right-to-left, and inferior-to-superior directions corresponded to the x, y, and z directions, respectively.
Fig. 2.
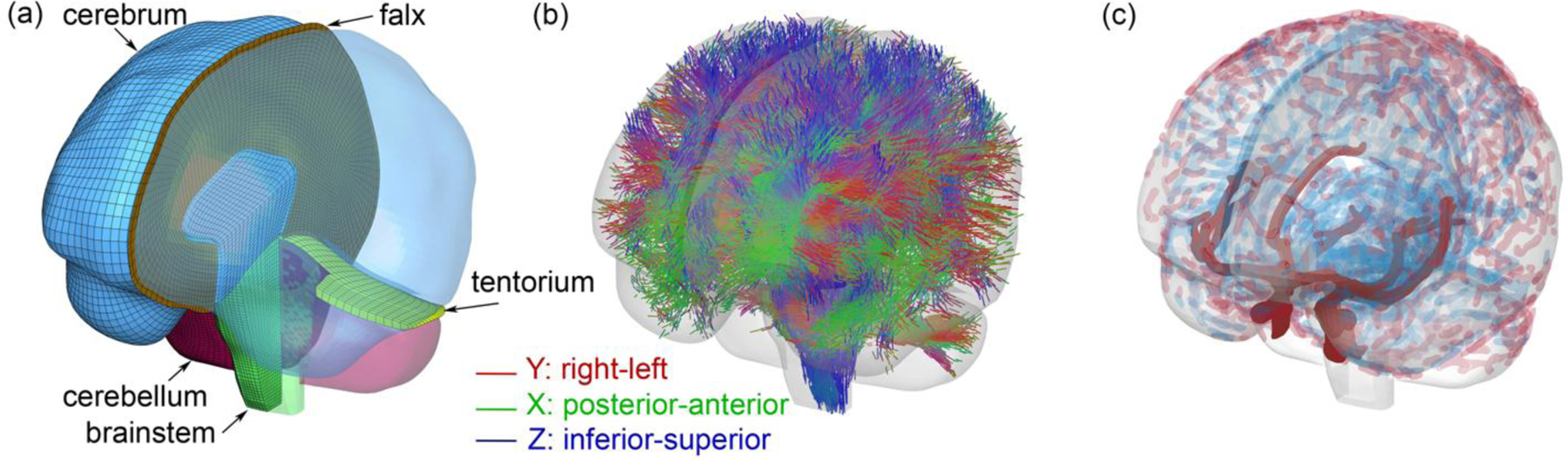
Anisotropic Worcester Head Injury Model V2.0 showing the mesh (a), element-wise fiber directions based on whole-brain tractography (b), and cerebral vasculatures including arteries, veins, and sinuses (c).
2.4. Synthetic displacement field to verify voxel-wise strain tensor calculation
To first verify our customized implementation of voxel-wise strain tensor calculation, a layer of voxels of size of 19×19×1 was generated, with an isotropic resolution of dimensionless 2. This led to voxel corner nodes of size of 20×20×2 (Fig. 3a). For each node at location, (x, y, z), a radial vector emanating from the origin, , was determined. The nodal displacement was then specified according to the following equation that uses a sine function to regulate a nonlinear deformation pattern:
| (7) |
The scaling factor, 0.5, was empirically chosen to produce a reasonable displacement magnitude without excessive distortion. The resulting deformed voxels are shown in Fig. 3b. Their voxel-wise strain tensors were calculated according to Eqns. 1–4 in MATLAB. To compare with the “ground-truth” from Abaqus simulation, each voxel was converted into a hexahedral element, with displacements of its eight nodes prescribed as boundary conditions. Element type, C3D8R, was used, which has one integration point as adopted in the customized implementation.
Fig. 3.
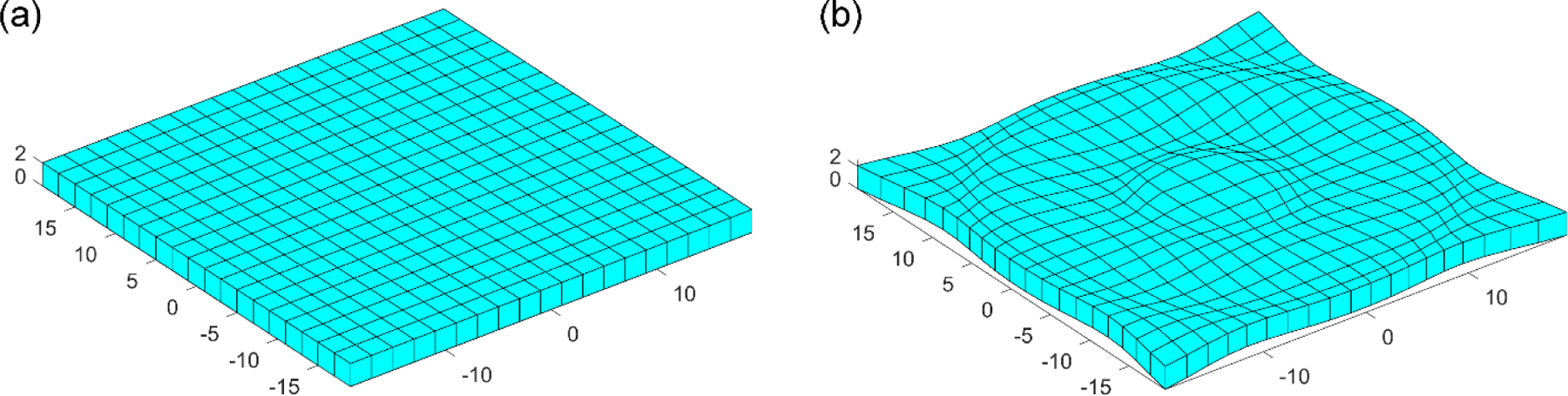
Comparison of the (a) undeformed and (b) deformed block of voxels also shown as meshes. Each voxel has an isotropic resolution of dimensionless 2 and is converted into the corresponding hexahedral element.
2.5. Synthetic displacement field for white matter fiber strains
To benchmark accuracy of displacement voxelization to calculate white matter fiber strains, a synthetic, nonlinear, and in-plane axial shear deformation field was devised to simulate injury-causing shear strain [8]. The displacement magnitude, d, was determined by a sine function to emulate in vivo brain harmonic motion [31]:
| (8) |
where r (in mm) is the xy-plane distance relative to the head center of gravity:
| (9) |
and is the counter-clockwise tangential direction normal to the in-plane radial direction (Fig. 4). The displacement magnitude was chosen to produce typical strain levels that could occur in real-world concussive impacts.
Fig. 4.

Synthetic displacement field is applied to element nodes and fiber sampling points to compute “ground-truth” fiber strains for 100 randomly selected fiber tracts (a; only displacement magnitude is shown). Element nodal displacements are used to resample at voxel corner nodes of an image volume (isotropic “pixel” resolution on an axial imaging plane is set to 4 mm here to improve visualization, vs. an isotropic resolution of 1.8 mm used in analysis; b). Illustration of engineering fiber strain calculation (c).
The displacement field was applied to all WHIM nodes and white matter fiber sampling points, which would generate the “ground-truth”. Element nodal displacements were then used to resample at voxel corner nodes of an image volume. Its isotropic voxel resolution was set to be 1.8 mm to match with the average brain element size. Ground-truth fiber strains at 100 randomly selected fiber tracts (~9000 sampling points and fiber segments) were used to benchmark accuracy among the four methods: mesh interpolation, voxel interpolation, and strain tensor projection based on either voxels or elements.
2.6. Application to real-world head impacts
Laboratory reconstructed head impacts from the National Football League (NFL) [32] were used for further accuracy comparison. This dataset includes 53 reconstructed head impacts and offers a range of impact severities and strain magnitudes for evaluation (Fig. 5). For each impact, the head rotational velocity temporal profile was used as input for impact simulation. Fiber strains along the whole brain tractography were calculated at the time when the peak maximum principal strain (MPS; assessed at the 95th percentile level) was reached. This ensured that strains were compared for a given unique displacement field.
Fig. 5.
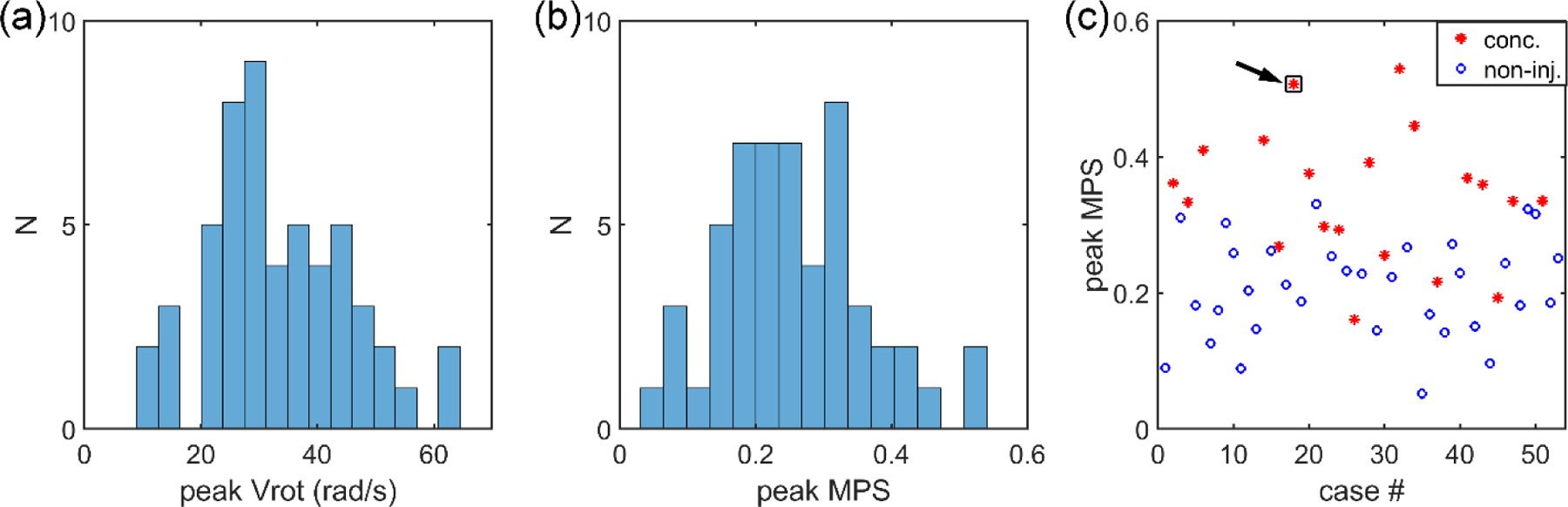
Histogram of the peak rotational velocity (a) and peak MPS (b) for the 53 reconstructed head impacts, along with the distribution of the peak MPS across the 20 concussive and 33 non-injury cases (c). One concussive case (‘Case077HD02’) was selected for further detailed illustration (arrow).
2.7. Data analysis
For the synthetic displacement field designed to stress test the customized strain tensor calculation, the determinant of coefficient, R2, and root mean squared error, RMSE, relative to result from Abaqus simulation were evaluated for each strain tensor component. To obtain R2 between a pair of predicted and observed data (fi and yi, respectively, with i ranging from 1 to the number of samples), the residual sum of squares and total sum of squares (SSres and SStot, respectively) are first obtained:
| (10) |
| (11) |
where is the mean of the observed data. Then, R2 is defined as the following:
| (12) |
When R2 is 1.0, SSres will be zero, indicating that the predicted values exactly match the observed counterparts.
For the synthetic displacement field used to benchmark the accuracy of white matter fiber strain using the four competing techniques (i.e., mesh interpolation, voxel interpolation, voxel tensor projection, and element tensor projection), R2, and RMSE were compared against the known or prescribed ground-truth fiber strains to identify the “most accurate” baseline method.
For real-world impacts, “ground-truth” fiber strains were unavailable because of uncertainties in head injury model validation [33,34]. Therefore, the baseline method from the synthetic displacement comparison was used to benchmark the accuracies of other methods in terms of R2 and RMSE. Note, the accuracy assessment here is separate from a different issue of model validation against the unknown ground-truth. To provide context of the relative errors, fiber strain differences relative to the baseline method were also compared to the lower bound of an injury threshold of 0.09 determined from an animal injury study [35]. The threshold value is similar to the optimal injury threshold identified when using the average fiber strain from WHIM as the injury predictor based on the reconstructed NFL head impacts [36]. It is also on the same order relative to injury-causing axonal microtubule strains [37,38]. To further verify the customized strain tensor implementation (Eqns. 1–4), the resulting MPS of the whole brain for an example head impact case was compared against the Abaqus counterpart. We chose MPS because it is currently the primary response variable of interest for studying brain injury biomechanics [5,8,33]. The head rotational velocity and acceleration profiles for the selected case are given in the Supplementary Material (Fig. S1).
Finally, we suspected that the accuracy of the displacement voxelization technique as well as the voxel-wise strain tensor projection method would necessarily depend on the voxel spatial resolution. Therefore, we also increased the isotropic image voxel size from 1.8 mm to 4 mm to derive fiber strains using the displacement interpolation technique and strain tensor projection method for accuracy comparison.
All impact simulations were conducted in Abaqus (Version 2018; Dassault Systèmes, France) on a Linux workstation (double precision, 15 CPUs, Intel Xeon E5–2698 with 256 GB memory, and 4 NVidia Tesla K80 GPUs with 12 GB memory). All other programs were implemented and further optimized for maximum efficiency in MATLAB (R2020a; MathWorks, Natick, MA)). All MATLAB computations were executed on an ordinary Windows 10 desktop computer (Intel Xeon E52623 v4 with 2 CPUs and 32 GB memory). No parallelization was used for objective efficiency comparison in this study. Statistical significance was defined at the level of 0.05.
3. Results
3.1. Synthetic displacement field for voxel-wise strain tensor calculation
Fig. 6 compares our customized voxel-wise strain tensor calculation against Abaqus simulation for the synthetic displacement field illustrated in Fig. 3. Each sub-image shows the corresponding strain tensor component distribution on the undeformed image/mesh. For all components, the two were virtually identical, with R2 of 1.00 and RMSE of ~4×10−4, except for ε13 and ε23 with a slightly degraded performance (R2 of 0.99 and RMSE of 0.002). In part, this was due to loss of data precision when writing the displacement boundary conditions into text files as required for Abaqus simulation.
Fig. 6.

Comparison of the six strain tensor components between our customized voxel-wise strain tensor calculations (top) and counterparts from Abaqus simulation (bottom). The undeformed and deformed images/meshes are shown in Fig. 3.
3.2. Synthetic displacement field for fiber strains
Fiber strains from mesh and voxel interpolations were both virtually identical to the prescribed ground-truth (R2 of 1.00 with RMSE of 0.01). Voxel and element strain tensor projections also produced very similar results between themselves (R2 of 0.98 with RMSE of 0.02). However, they were poorer compared to the ground-truth (R2 of 0.87 with RMSE of 0.10; Fig. 7).
Fig. 7.
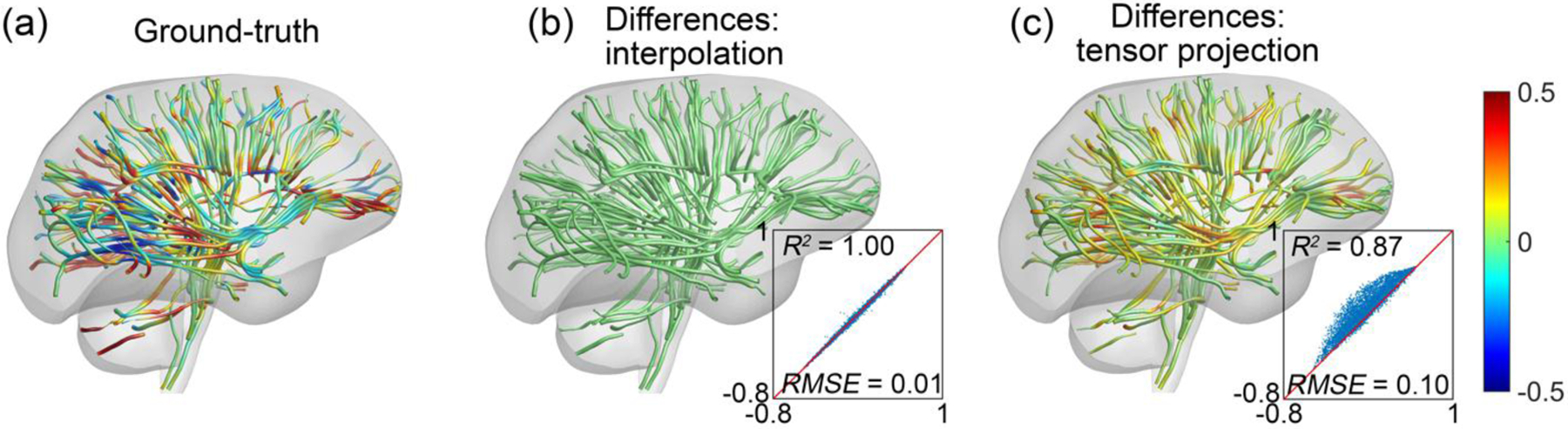
Ground-truth fiber strains for 100 random fiber tracts resulting from the synthetic deformation field (a). Mesh and voxel interpolations produced virtually identical results, and fiber strain differences relative to the ground-truth are only shown for one (b). Similarly, strain tensor projection based on either voxelized displacement or FE elements produced almost the same results, and their fiber strain differences relative to the ground-truth are also only shown for one (c). Overall, strain tensor projection overestimated fiber strain magnitudes.
3.3. Real-world head impacts
For the selected real-world head impact, the two interpolation methods produced nearly identical results once again (R2 of 0.99 with RMSE of 0.01). The two strain tensor projection methods based on voxelized displacement or FE elements also produced very similar results (R2 of 0.95 with RMSE of 0.03). However, they were considerably different from the baseline (R2 of 0.80 with RMSE of 0.09; Fig. 8). More specifically, 12.8–13.3% of the fiber segments had strain overestimation greater than the lower bound of injury threshold. The percentage increased to 34.8–35.6% when the threshold value was halved. In contrast, the voxel interpolation method only overestimated by 1.4% and 7.4%, respectively, relative to mesh interpolation method. The magnitude of fiber strain differences strongly correlated with the fiber strain magnitude, itself (Pearson correlation coefficient, r, of 0.94, p<0.001).
Fig. 8.
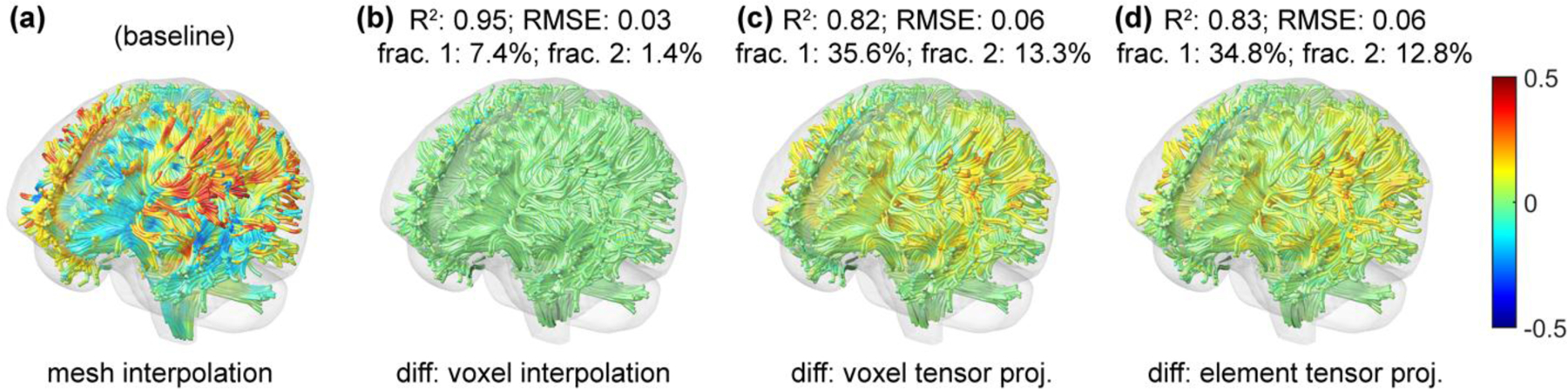
Fiber strains for the selected impact case using the mesh interpolation method (a). Relative to this baseline, fiber strain differences using the voxel interpolation (b), voxel tensor projection (c), and element tensor projection (d) methods are compared in terms of R2, RMSE, fractional percentage of fiber segments with the strain differences greater than 0.045 (frac. 1) or 0.09 (frac. 2) are reported. Both tensor projection methods overestimate fiber strains overall, with the magnitude of overestimation strongly correlated with fiber strain magnitude, itself. Only 10% of the whole-brain tractography is shown to improve visualization.
Fig. 9 summarizes the relative fiber strain differences using all the head impact cases. Mesh interpolation and voxel interpolation consistently had the least differences across all measurements. The correlation between R2 and whole-brain peak MPS was not significant for the two interpolation methods (p >0.3). However, their correlations for all other pairs of methods were significant and negative (r ranged from −0.75 to −0.59, p <0.001). For all other metrics, significant and positive correlations were found between all pairs of methods (r of 0.90–0.97 for RMSE, 0.90–0.96 for frac. 1, and 0.82–0.87 for frac. 2, all with p<0.001). Up to ~15% of the fiber segments had fiber strain overestimation relative to mesh interpolation greater than the injury threshold of 0.09. When the injury threshold was halved, the percentage could reach ~37%.
Fig. 9.
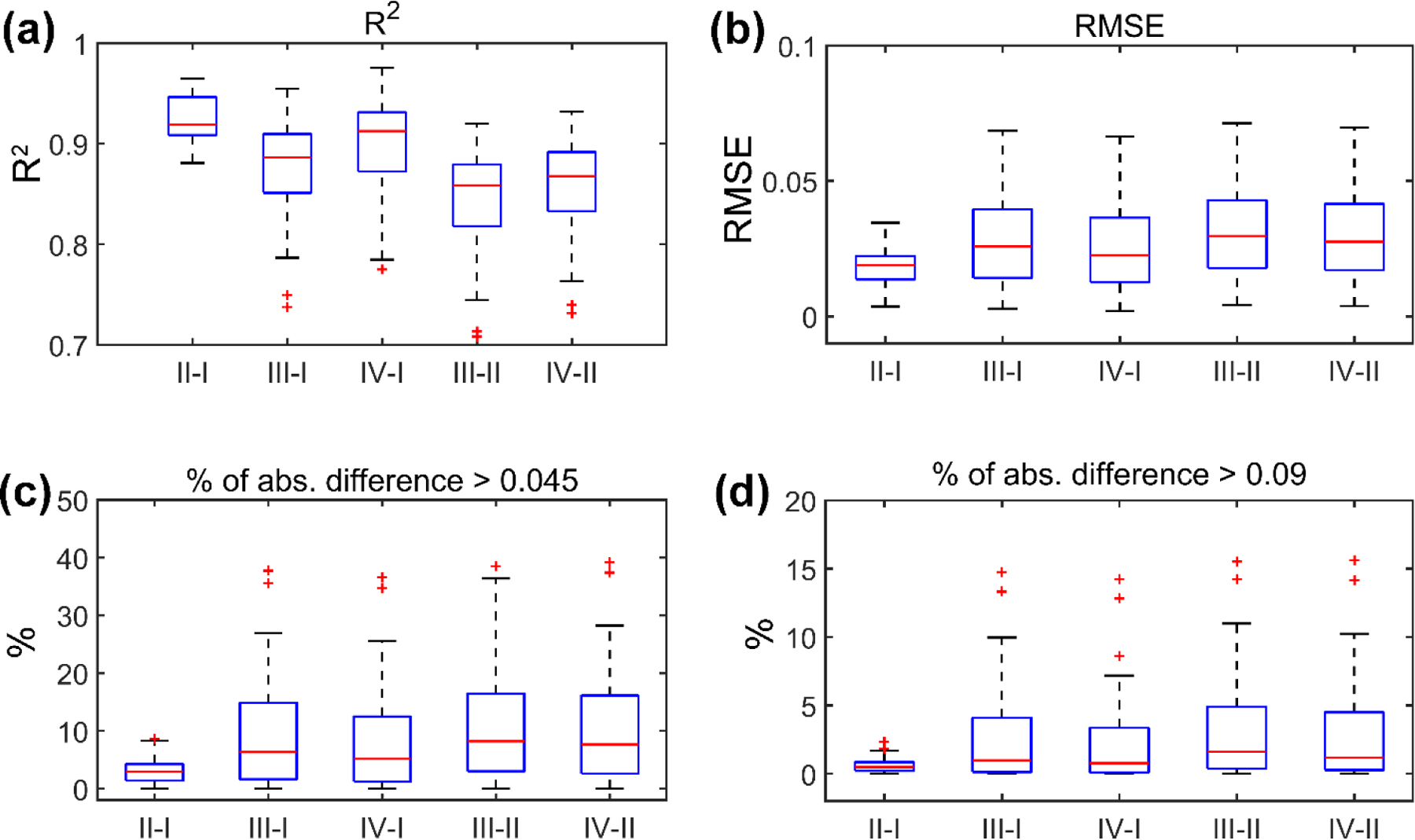
Summary of R2 (a), RMSE (b), the percentage of absolute fiber strain differences greater than 0.045 (half of the injury threshold; c) or greater than the injury threshold of 0.09 (d) for the 53 reconstructed head impacts. The comparisons are made between pairs of the four methods, including mesh interpolation (I), voxel interpolation (II), voxel tensor projection (III), and element tensor projection (IV).
3.4. Further verification of customized implementation
The previous synthetic displacement field has successfully verified the customized strain tensor calculation against Abaqus simulation (Fig. 6). We further used the same program to compute voxel-wise MPS values of the entire brain. For the selected head impact case (Fig. 5 and Fig. 8) based on the voxelized displacement at a sampling resolution of 1.8 mm, results from the customized calculation were nearly identical to the Abaqus counterparts once again (the latter were resampled on the same voxel centroids to facilitate one-to-one comparison; Fig. 10). Only mild differences occurred at the brain boundary.
Fig. 10.
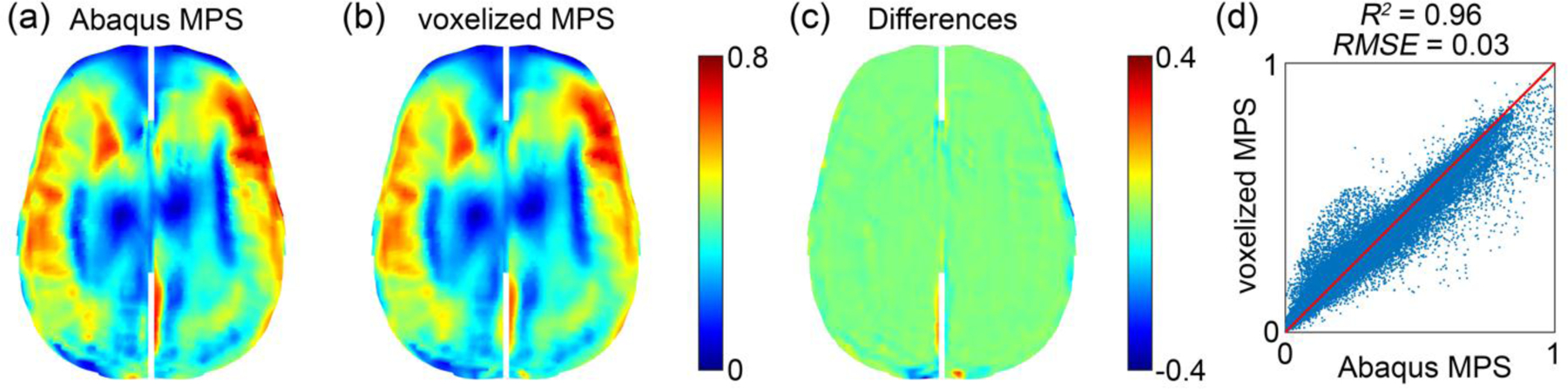
Comparison between baseline Abaqus MPS (a) and that computed from the voxelized displacement using the customized implementation (b) for the selected head impact case. They are virtually identical except mild differences at the brain boundary due to sampling discretization errors resulting from both displacement voxelization and resampling of Abaqus simulation result. Their differences are shown in fringe plot (c) and distribution (d). The head rotational velocity and acceleration profiles for the selected case are given in the Supplementary (Fig. S1).
3.5. Sensitivity on image voxel size
Increasing the isotropic image voxel size from 1.8 mm to 4 mm for displacement voxelization degraded the accuracy of fiber strains (Fig. 11). Relative to fiber strains from mesh interpolation (identical to Fig. 8a), voxel interpolation decreased R2 to 0.90 and increased RMSE to 0.05 (Fig. 11a and b). However, the performance degraded even more when using the voxel strain tensor projection method, achieving R2 of 0.77 and RMSE of 0.09, respectively (Fig. 11c and d).
Fig. 11.

Fiber strain differences relative to mesh interpolation (Fig. 8a) when using voxel interpolation (a and b) and voxel strain tensor projection (c and d) based on voxelized displacement resampled at an isotropic resolution of 4 mm.
3.6. Efficiency
Finally, the computational steps and their costs for each fiber strain calculation method are compared (Table 1). Voxel interpolation was significantly more efficient than all other competing methods.
Table 1.
Comparison of the computational cost (in sec) in each step for the four methods in deriving dense white matter fiber strains along the whole-brain tractography (~35 k tracts from ~3.3 million ordered fiber sampling points with ~1 mm between two adjacent points). No parallelization was used. N/A: not applicable
| Method | Mesh interpolation | Voxel interpolation | Voxel tensor projection | Elem. tensor projection |
|---|---|---|---|---|
| Host voxel/elem. identification | N/A | 0.02 | 0.02 | 1.6 |
| Displacement resampling | 33.3 | 11.6 | 11.6 | 33.3 |
| Strain tensor calculation | N/A | N/A | 10.5 | N/A |
| Fiber strain calculation | 0.2 | 3.2 | 4.7 | 4.7 |
| Total time | 33.5 | 14.8 | 26.8 | 39.6 |
4. Discussion
Mesh-image mismatch occurs whenever a discretized biomechanical model and the associated image do not align in space (Fig. 1). Therefore, this issue is very common across diverse biomechanical engineering fields [1]. However, it appears that little attention has been paid on how best to resolve this issue for maximum accuracy and efficiency. Given that the response variable is often strain that is already available from model simulation, a convenient approach is to resample or interpolate the strain field at image voxel centroids to facilitate biomechanical analysis in the image space [10–12]. In this study, we develop a displacement voxelization strategy to eliminate the mesh-image mismatch by resampling displacement at image voxel corner nodes instead. Voxel-wise strain can then be reconstructed at the voxel centroids through hexahedral element shape functions to conform to the given image volume (Fig. 1); thus, eliminating the mesh-image mismatch problem. We first verify the customized voxel-wise strain tensor calculation using a synthetic deformation field against Abaqus simulation. We then apply the voxelized displacement to derive fiber strain and compare with the commonly used strain tensor projection method [19–23] using a synthetic deformation field with prescribed ground-truth. Finally, we compare the performance based on simulated brain strains from 53 reconstructed real-world head impacts.
4.1. Accuracy performance
Our strain tensor calculation was successfully verified against Abaqus simulation (Fig. 6). For the synthetic fiber deformation, the mesh interpolation and voxel interpolation methods produced virtually identical results relative to the prescribed ground-truth. They were considerably more accurate than the two strain tensor projection methods, using either voxels or FE mesh elements (Fig. 7). The latter overestimated fiber strains overall.
Similar findings were also found with a real-world head impact (Fig. 8). However, the difference between the two interpolation methods increased. Strain tensor projection using both voxels and elements overestimated fiber strains overall, relative to either interpolation method. Up to ~13% of the fiber strains had an overestimation magnitude greater than the lower bound of a conservative strain threshold (of 0.09). When halving the threshold, the percentage with significant overestimations grew to ~35%. Within the deformation field, fiber strain overestimation strongly correlated with the fiber strain magnitude (Pearson correlation coefficient, r, of 0.94, with p<0.001).
The summary results from the 53 head impacts (Fig. 9) offer a range of fiber strain errors relative to the mesh and voxel interpolation methods. Across the impact cases, the overestimation errors strongly correlated with the peak MPS magnitude, with r typically >0.9 and p <0.001. Collectively, these observations suggest that strain tensor projection may overestimate the risk of injury, especially in regions of high strains and impacts of high kinematic severities. Therefore, this behavior may have important implications when applying the technique for real-world concussion detection [19,22,26,27].
The different accuracy in fiber strain estimation was not surprising because displacement is continuous throughout the spatial domain, while element-wise constant strain is discontinuous at element boundaries. Increasing the image voxel size would necessarily degrade the fiber strain accuracy, for both voxel-wise displacement interpolation (R2 of 0.95 and RMSE of 0.03 in Fig. 8b vs. 0.90 and 0.05 in Fig. 11b, respectively) and strain tensor projection (R2 of 0.82 and RMSE of 0.06 in Fig. 8c vs. 0.77 and 0.09 in Fig. 11d, respectively). However, voxel interpolation appears less sensitive to voxel resolution in retaining fiber strain accuracy, which once again suggests its potential advantage over voxel tensor projection.
4.2. Efficiency performance
Voxel interpolation not only performed well in accuracy, but it was also the most efficient method (Table 1). For example, it took 15 sec to process ~35 k fiber tracts and ~3.3 million points, vs. 40 sec using strain tensor projection based on “nearest” element. When using “enclosing” element for strain tensor projection [25], the computational cost would increase substantially (10 min required to identify the enclosing element in WHIM for each white matter fiber sampling point by explicitly testing whether the point is inside or outside of the element boundary [39]). However, the difference in fiber strains was negligible (result not shown). Therefore, it was not necessary to use “enclosing” element to calculate fiber strain.
The high efficiency with voxel interpolation stems from the fact that a voxel can be simply scaled linearly to a unit hexahedral element. This enables a direct application of shape functions (Eqn. 1) without the need for explicit coordinate system transformation through a Jacobian matrix that would decrease efficiency. In addition, identifying the enclosing “host voxel” for an arbitrary sampling point is trivial, as it is degenerated into finding the closest integer after proper scaling. The bottleneck for this method is to resample voxel corner node displacements via scattered interpolation (Table 1; more discussions below); albeit it is still more efficient than direct mesh interpolation at every fiber sampling points (11.6 sec for 256 thousand nodes vs. 33.3 sec for ~3.3 million sampling points, respectively).
It is also possible to resample strain tensor components directly at image voxel centroids to resolve the mesh-image mismatch [12]. However, this requires six resampling operations (6 unique components in a 3×3 tensor matrix due to symmetry), which is twice as that required in displacement voxelization (3 displacement components; albeit with an increase in image volume dimension of 1 along each direction). More importantly, strain tensor resampling allows tensor projection to derive fiber strain but not through element shape functions. As found in this study, the former method could considerably overestimate fiber strain (Figs. 8 and 9), and thus, is not recommended. Collectively, these findings suggest that voxelized displacement is an effective representation of the continuous deformation field that offers versatile and efficient post-processing capabilities.
4.3. Implications for traumatic brain injury biomechanics
The commonly used strain tensor projection method [19–23] may considerably overestimate fiber strains (Fig. 8 and 9). Therefore, this method is not recommended for future injury studies. In addition, fiber strain accuracy depends on the voxel size (Fig. 11). Both voxel interpolation and voxel strain tensor projection methods would suffer in accuracy with the increase in voxel size (albeit the former seems to maintain a better accuracy). A tradeoff is necessary when choosing the voxel resolution to balance accuracy and the amount of data to produce that could have practical implications for further downstream analysis, such as deriving dense fiber strains as conducted in this study. A multiresolution representation (Fig. 1) may be especially useful when there is a need for improved accuracy in specific regions of the brain with a refined voxel resolution.
There are also other alternative techniques to derive fiber strains, for example, by explicitly embedding fiber elements to export strain from model simulation. This would avoid any post-processing and the associated error [26,27]. However, this approach only allows embedding a rather small number of fibers due to the substantial increase in simulation runtime (e.g., the earlier studies used ~3–5% of the ~3.3 million fiber segments employed in this study). Recognizing the need to use the current rather than the initial fiber orientation for strain tensor projection, Zhou et al. performed an extra simulation with fiber truss elements of null material properties to track instantaneous fiber orientation [29]. However, this technique still depends on strain tensor projection that would degrade accuracy, independent of fiber orientation. In addition, the extra simulation is unnecessary because the current fiber orientation can be directly determined from the current fiber sampling point locations through mesh interpolation. This is likely significantly more efficient than direct impact simulation. In contrast, the displacement voxelization approach developed here avoids all these challenges, including the need for identifying the current fiber orientation through the less efficient mesh interpolation method (Table 1).
Using a voxel-based mesh directly for model simulation would also avoid mesh-image mismatch [40]. However, the unsmooth voxel boundaries, both externally with contact to the skull or internally between anatomical components and gray-white matter interfaces, could cause undesirable numerical issues and degrade accuracy in simulation, especially in high-rate contact simulation [41]. In contrast, post-processing displacement voxelization avoids any modeling numerical issues while at the same time, retains the convenience of a voxelized mesh for image-based morphological operation (e.g., segmentation) and multimodal analysis.
A particular application is to resolve a challenge in image-based brain biomechanics [23], where it is often necessary to transform image-based biomechanical strain and medical images of anatomical and/or physiological information into the same image space. Directly transforming a strain tensor field in one image volume into the other is possible but could similarly introduce voxel-voxel mismatch. With the technique developed in this study, displacement can be properly resampled at voxel corner nodes based on rigidly transformed voxels from the target image. The resulting voxel-wise strain tensor would then conform to the target image. A rigid rotation may be necessary prior to strain tensor calculation to ensure that unit hexahedral elements can be obtained by simple linear scaling.
4.4. Broader implications
Voxelized displacement benefits from image-based strain analyses and morphological operations but without the usual disadvantage of a voxelized mesh in numerical modeling due to unsmooth voxel boundaries [41]. Therefore, this technique may be generalized more broadly across diverse biomechanical engineering fields for seamless integration of biomechanical modeling and medical imaging to facilitate multimodal analysis in the future. This includes problems such as myofibers in the heart [18], collagen fiber in cartilage [16] and tendon [17], or deriving local strain fields along optical nerves [42] and cerebral vasculature network [30], or in 2D, where the same mesh-image mismatch can happen.
It is important to note that displacement voxelization does not limit the type (e.g., hexahedral vs. tetrahedral, or a mixture), order (e.g., linear vs. quadratic), or density of model elements. In addition, the voxel resolution does not need to be fixed or isotropic either, and can be adaptable for specific need (e.g., a finer resolution in more vulnerable or injury-predictive regions [43]; Fig. 1). In fact, the technique may potentially become a valuable add-on for FE analysis software packages in the future. By specifying the image origin, resolution, axis directions, and the region of interest in the FE model space, voxelized displacement and stress/strain fields can then be generated directly from the FE software to eliminate the need from the end user. The displacement voxelization may also be more accurate and efficient by using element shape functions [8] to mitigate the bottleneck in voxel corner node displacement resampling via scattered interpolation as adopted here (Table 1). This could further improve the overall efficiency, which is important when there is a need to increase the resampling voxel resolution and density of the white matter tractography.
Finally, voxelized displacement and the resulting voxel-wise strain can be considered as standard image volumes like MRI. This could greatly promote and facilitate data sharing of biomechanical model responses among research groups. Otherwise, the associated model (mesh nodes and elements), in addition to node-wise displacement and/or element-wise strain, is required for data sharing as well. This is not only cumbersome but may also be infeasible when it is not practical to share the biomechanical model, itself.
4.5. Limitations
A limitation with the displacement voxelization technique is the potentially incomplete sampling at tissue boundaries due to stepwise voxels that are often smooth in biological organs. This issue could be mitigated by increasing the local resampling spatial resolution, if this is an important region (hence, of dense meshes to achieve high accuracy in model simulation in the first place). Given that displacement voxelization can be performed at an arbitrary spatial resolution, a multiresolution voxelization strategy can be deployed in practice, with a coarse resolution for the global model but finer resolutions in specific, targeted regions for a multiresolution representation (Fig. 1).
From the study evaluation perspective, this work is also limited to using a single head injury model and with application only to head impact in traumatic brain injury. In the future, domain-specific investigations are necessary to quantify the effectiveness of displacement voxelization technique in resolving the mesh-image mismatch problem. However, we anticipate that at least the qualitative findings in this study will remain applicable.
5. Conclusion
An image voxel is a special hexahedral element that can be simply scaled linearly to form a unit cube. Using interpolated displacements at image voxel corner nodes, a voxelized displacement field takes advantage of a degenerated Jacobian matrix to allow convenient and efficient displacement interpolation and the calculation of voxel-wise strain tensor. Based on a synthetic displacement field and simulation of a series of head impacts in the context of traumatic brain injury, we showed that displacement interpolation from voxelized displacement achieve high accuracy and efficiency in deriving dense white matter fiber strains along the entire tractography. The technique is considerably more accurate and efficient than the commonly used strain tensor projection method based on either voxel- or element-wise strain tensors. Overall, strain tensor projection overestimates fiber strains, with the overestimation magnitude strongly correlates with the strain magnitude, itself. Increasing the image voxel size degrades the accuracy of fiber strain, but displacement interpolation appears less sensitive than the voxel-wise strain tensor projection. Therefore, displacement interpolation from voxelized displacement is recommended for fiber strain calculations in the future.
Finally, voxelized displacement benefits from image-based strain analyses and morphological operations but without the usual disadvantage of a voxelized mesh in numerical modeling. Therefore, this technique may be generalized more broadly across diverse biomechanical engineering fields for seamless integration of biomechanical modeling and medical imaging to facilitate multimodal analysis. The convenient image format may also promote and facilitate biomechanical data sharing in the future.
Supplementary Material
Highlights:
A displacement voxelization technique is developed to generate an image representation of deformation that will eliminate mesh-image mismatch.
The technique is considerably more accurate and efficient than the commonly used strain tensor projection method in deriving dense white matter fiber strains along tractography.
Displacement voxelization may be broadly applicable to eliminate mesh-image mismatch common in diverse biomechanical engineering problems.
Voxelized displacement and voxel-wise strains can be considered as standard image volumes to promote and facilitate biomechanical data sharing.
Acknowledgement
This work is partially supported by the NIH grant R01 NS092853 and the NSF award under grant No. 2114697. The sponsors do not have any role in the study.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Statements of Ethical Approval
This is not applicable: no animal or human data were generated from the current study.
References:
- [1].Yang Z, Finite Element Analysis for Biomedical Engineering Applications, Finite Elem. Anal. Biomed. Eng. Appl (2019). 10.1201/9780429061264. [DOI] [Google Scholar]
- [2].Freutel M, Schmidt H, Dürselen L, Ignatius A, Galbusera F, Finite element modeling of soft tissues: Material models, tissue interaction and challenges, Clin. Biomech 29 (2014) 363–372. 10.1016/j.clinbiomech.2014.01.006. [DOI] [PubMed] [Google Scholar]
- [3].Parashar SK, Sharma JK, A review on application of finite element modelling in bone biomechanics, Perspect. Sci 8 (2016) 696–698. 10.1016/j.pisc.2016.06.062. [DOI] [Google Scholar]
- [4].Phellan R, Hachem B, Clin J, Mac-Thiong JM, Duong L, Real-time biomechanics using the finite element method and machine learning: Review and perspective, Med. Phys 48 (2021) 7–18. 10.1002/mp.14602. [DOI] [PubMed] [Google Scholar]
- [5].Madhukar A, Ostoja-Starzewski M, Finite Element Methods in Human Head Impact Simulations: A Review, Ann. Biomed. Eng (2019) 1–23. 10.1007/s10439-019-02205-4. [DOI] [PubMed] [Google Scholar]
- [6].Soleimani M, Shipley RJ, Smith N, Mitchell CN, Medical imaging and physiological modelling: Linking physics and biology, Biomed. Eng. Online 8 (2009) 1. 10.1186/1475-925X-8-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7].Galbusera F, Cina A, Panico M, Albano D, Messina C, Image-based biomechanical models of the musculoskeletal system, Eur. Radiol. Exp 4 (2020) 49. 10.1186/s41747-020-00172-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8].Yang K, ed., Basic finite element method as applied to injury biomechanics, Academic Press, 2018. [Google Scholar]
- [9].Rebouças Filho PP, Sarmento RM, Holanda GB, de Alencar Lima D, New approach to detect and classify stroke in skull CT images via analysis of brain tissue densities, Comput. Methods Programs Biomed 148 (2017) 27–43. 10.1016/j.cmpb.2017.06.011. [DOI] [PubMed] [Google Scholar]
- [10].Zhao W, Ji S, White matter anisotropy for impact simulation and response sampling in traumatic brain injury, J. Neurotrauma 36 (2019) 250–263. 10.1089/neu.2018.5634. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Amidror I, Scattered data interpolation methods for electronic imaging systems: a survey, J. Electron. Imaging 11 (2002) 157–176. https://lspwww.epfl.ch/publications/other/sdimfeisas.html. [Google Scholar]
- [12].Yan H, Hu S, Martin RR, 3D morphing using strain field interpolation, J. Comput. Sci. Technol 22 (2007) 147–155. [Google Scholar]
- [13].Sandeep S, Shine SR, Effect of stenosis and dilatation on the hemodynamic parameters associated with left coronary artery, Comput. Methods Programs Biomed 204 (2021) 106052. 10.1016/j.cmpb.2021.106052. [DOI] [PubMed] [Google Scholar]
- [14].Dezzen-Gomide AC, de Carvalho MA, Lazari-Carvalho PC, de Oliveira HF, Cury AADB, Yamamoto-Silva FP, Silva B.S. de F., A three-dimensional finite element analysis of permanent maxillary central incisors in different stages of root development and trauma settings, Comput. Methods Programs Biomed 207 (2021) 106195. 10.1016/j.cmpb.2021.106195. [DOI] [PubMed] [Google Scholar]
- [15].Djukic T, Saveljic I, Pelosi G, Parodi O, Filipovic N, A study on the accuracy and efficiency of the improved numerical model for stent implantation using clinical data, Comput. Methods Programs Biomed 207 (2021) 106196. 10.1016/j.cmpb.2021.106196. [DOI] [PubMed] [Google Scholar]
- [16].Li J, Hua X, Jones AC, Williams S, Jin Z, Fisher J, Wilcox RK, The influence of the representation of collagen fibre organisation on the cartilage contact mechanics of the hip joint, J. Biomech 49 (2016) 1679–1685. 10.1016/j.jbiomech.2016.03.050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [17].Thomopoulos S, Marquez JP, Weinberger B, Birman V, Genin GM, Collagen fiber orientation at the tendon to bone insertion and its influence on stress concentrations, J. Biomech 39 (2006) 1842–1851. 10.1016/j.jbiomech.2005.05.021. [DOI] [PubMed] [Google Scholar]
- [18].Sack KL, Aliotta E, Ennis DB, Choy JS, Kassab GS, Guccione JM, Franz T, Construction and validation of subject-specific biventricular finite-element models of healthy and failing swine hearts from high-resolution DT-MRI, Front. Physiol 9 (2018) 1–19. 10.3389/fphys.2018.00539. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [19].Giordano C, Kleiven S, Evaluation of Axonal Strain as a Predictor for Mild Traumatic Brain Injuries Using Finite Element Modeling, Stapp Car Crash J 58 (2014) 29–61. 10.4271/2014-22-0002. [DOI] [PubMed] [Google Scholar]
- [20].Ji S, Zhao W, Ford JC, Beckwith JG, Bolander RP, Greenwald RM, Flashman LA, Paulsen KD, McAllister TW, Group-wise evaluation and comparison of white matter fiber strain and maximum principal strain in sports-related concussion, J. Neurotrauma 32 (2015) 441–454. 10.1089/neu.2013.3268. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [21].Li X, Zhou Z, Kleiven S, An anatomically accurate and personalizable head injury model: Significance of brain and white matter tract morphological variability on strain, Biomech. Model. Mechanobiol (2020) 1–29. 10.1101/2020.05.20.105635. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [22].Sahoo D, Deck C, Willinger R, Brain injury tolerance limit based on computation of axonal strain, Accid. Anal. Prev 92 (2016) 53–70. 10.1016/j.aap.2016.03.013. [DOI] [PubMed] [Google Scholar]
- [23].Knutsen AK, Gomez AD, Gangolli M, Wang W-T, Chan D, Lu Y-C, Christoforou E, Prince JL, Bayly PV, Butman JA, Pham DL, In vivo estimates of axonal stretch and 3D brain deformation during mild head impact, Brain Multiphysics. (2020) 100015. 10.1016/j.brain.2020.100015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [24].Yang KH, Hu J, White NA, King AI, Chou CC, Prasad P, Development of numerical models for injury biomechanics research: a review of 50 years of publications in the Stapp Car Crash Conference, Stapp Car Crash J. 50 (2006) 429–490. 10.4271/2006-22-0017. [DOI] [PubMed] [Google Scholar]
- [25].Zhao W, Ford JC, Flashman LA, McAllister TW, Ji S, White Matter Injury Susceptibility via Fiber Strain Evaluation Using Whole-Brain Tractography, J. Neurotrauma 33 (2016) 1834–1847. 10.1089/neu.2015.4239. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [26].Garimella HT, Kraft RH, Modeling the mechanics of axonal fiber tracts using the embedded finite element method, Int. j. Numer. Method. Biomed. Eng 33 (2017) 26–35. 10.1002/cnm.2823. [DOI] [PubMed] [Google Scholar]
- [27].Wu T, Alshareef A, Giudice JS, Panzer MB, Explicit Modeling of White Matter Axonal Fiber Tracts in a Finite Element Brain Model, Ann. Biomed. Eng (2019) 1–15. 10.1007/s10439-019-02239-8. [DOI] [PubMed] [Google Scholar]
- [28].Abaqus, Abaqus Online Documentation, Abaqus; 2020, (2020). [Google Scholar]
- [29].Zhou Z, Domel AG, Li X, Grant G, Kleiven S, Camarillo D, Zeineh M, White Matter Tract-Oriented Deformation Is Dependent on Real-Time Axonal Fiber Orientation, J. Neurotrauma (2021) neu.2020.7412. 10.1089/neu.2020.7412. [DOI] [PubMed] [Google Scholar]
- [30].Zhao W, Ji S, Incorporation of vasculature in a head injury model lowers local mechanical strains in dynamic impact, J. Biomech 104 (2020) 109732. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [31].Okamoto RJ, Romano AJ, Johnson CL, V Bayly P, Insights Into Traumatic Brain Injury From MRI of Harmonic Brain Motion, J. Exp. Neurosci 13 (2019) 117906951984044. 10.1177/1179069519840444. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [32].Sanchez EJ, Gabler LF, Good AB, Funk JR, Crandall JR, Panzer MB, A reanalysis of football impact reconstructions for head kinematics and finite element modeling, Clin. Biomech 64 (2018) 82–89. 10.1016/j.clinbiomech.2018.02.019. [DOI] [PubMed] [Google Scholar]
- [33].Zhao W, Ji S, Displacement- and strain-based discrimination of head injury models across a wide range of blunt conditions, Ann. Biomed. Eng 20 (2020) 1661–1677. 10.1007/s10439-020-02496-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [34].Zhao W, Wu Z, Ji S, Displacement Error Propagation From Embedded Markers to Brain Strain, J. Biomech. Eng 143 (2021) 1–10. 10.1115/1.4051050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [35].Bain AC, Meaney DF, Tissue-level thresholds for axonal damage in an experimental model of central nervous system white matter injury, J. Biomech. Eng 122 (2000) 615–622. 10.1115/1.1324667. [DOI] [PubMed] [Google Scholar]
- [36].Zhao W, Cai Y, Li Z, Ji S, Injury prediction and vulnerability assessment using strain and susceptibility measures of the deep white matter, Biomech. Model. Mechanobiol 16 (2017) 1709–1727. 10.1007/s10237-017-0915-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [37].Shamloo A, Manuchehrfar F, Rafii-Tabar H, A viscoelastic model for axonal microtubule rupture, J. Biomech 48 (2015) 1241–1247. 10.1016/j.jbiomech.2015.03.007. [DOI] [PubMed] [Google Scholar]
- [38].Ahmadzadeh H, Smith DH, Shenoy VB, Viscoelasticity of tau proteins leads to strain rate-dependent breaking of microtubules during axonal stretch injury: predictions from a mathematical model, Biophys. J 106 (2014) 1123–33. 10.1016/j.bpj.2014.01.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [39].de Berg M, Cheong O, van Kreveld M, Overmars M, Computational geometry algorithms and applications, Third Edit, Springer, 2008. [Google Scholar]
- [40].Miller LE, Urban JE, Stitzel JD, Development and validation of an atlas-based finite element brain model model, Biomech Model. 15 (2016) 1201–1214. 10.1007/s10237-015-0754-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [41].Mao H, Gao H, Cao L, Genthikatti VV, Yang KH, Development of high-quality hexahedral human brain meshes using feature-based multi-block approach, Comput. Methods Biomech. Biomed. Engin 16 (2013) 271–279. 10.1080/10255842.2011.617005. [DOI] [PubMed] [Google Scholar]
- [42].Li Y, Singman E, McCulley T, Wu C, Daphalapurkar N, The Biomechanics of Indirect Traumatic Optic Neuropathy Using a Computational Head Model With a Biofidelic Orbit, Front. Neurol 11 (2020). 10.3389/fneur.2020.00346. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [43].Wu S, Zhao W, Rowson B, Rowson S, Ji S, A network-based response feature matrix as a brain injury metric, Biomech Model Mechanobiol. 19 (2020) 927–942. 10.1007/s10237-019-01261-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


