A Dynamical Paradigm for Molecular Cell Biology

Abstract

The driving passion of molecular cell biologists is to understand the molecular mechanisms that control important aspects of cell physiology, but this ambition is often limited by the wealth of molecular details currently known about these mechanisms. Their complexity overwhelms our intuitive notions of how molecular regulatory networks might respond under normal and stressful conditions. To make progress we need a new paradigm for connecting molecular biology to cell physiology. We suggest an approach that uses precise mathematical methods to associate the qualitative features of dynamical systems, as conveyed by ‘bifurcation diagrams’, with ‘signal–response’ curves measured by cell biologists.

The Curse of Complexity and the Curse of Parameter Space

By gathering information from molecular genetics, biochemistry, and cell physiology, molecular biologists construct complex gene–protein interaction networks that they believe may underlie the vital and often mysterious behavior of living cells. These networks –for example, the molecular interaction map of the budding yeast cell cycle [1] – pose some serious challenges. How can we envisage, from a static diagram, the astonishing array of temporal responses of a living cell? Can we be sure that the proposed network accounts fully for the cell functions that it purports to explain? And can we count on the network to make reliable, accurate predictions about the behavior of a cell under novel conditions?

Because of the complexity of these diagrams, with multiple feedback and feed-forward loops and crosstalk, it is impossible to answer these questions with any confidence by intuitive reasoning alone. The human mind cannot keep track of all possible interactions that percolate through the network under any given conditions.

One way to get around this ‘curse of complexity’ is to convert the network diagram into a set of ordinary differential equations (ODEs; see Glossary), using well-established principles of biochemical kinetics, which associate the rates of chemical reactions with the concentrations of the reactant species (the ‘variables’ in the ODEs). We then solve these equations numerically, letting the computer work out the implications of the crosstalk among signaling pathways and the complex feedback and feed-forward loops in the network. There are two problems with this approach. It is no trivial task to write the ODEs in the first place. The network diagram itself may be uncertain: do we know all the essential molecular components and their interactions? However, the process of building a mathematical ‘model’ of biological reality has its own virtues: it forces us to be specific about the molecular players and interactions that we believe to be important in understanding some aspect of cell physiology. The model may be relatively simple, with only a few ODEs, or very complex, with 50–500 variables and equations; in either case it is a precise representation of what we believe to be true. Our challenge is to determine whether it is good/useful representation of the truth. To achieve this, we must solve the ODEs and compare the computed behavior of the model with the actual behavior of cells.

The second problem is that, before doing a numerical simulation, the modeler must know the numerical values of all the kinetic constants (the ‘parameters’) for every reaction in the proposed network, and these values are never known beforehand. They must be estimated from the same data that the model is trying to explain. For realistic models, with up to 100 unknown parameters, it is impossible to estimate parameter values from available experimental data by a systematic search of parameter space (were we to limit each parameter to 10 possible values, we would need to do 10¹⁰⁰ simulations to search the parameter space completely – a Sisyphean task given that there are only ∼10⁸⁰ hydrogen atoms in the known universe). This approach replaces the curse of complexity by the worse ‘curse of parameter space’.

In this article we describe an approach that bypasses these curses by employing a technique from the qualitative theory of dynamical systems. In that theory, a bifurcation diagram correlates the output of an ODE model (e.g., the level of a regulatory protein) with an input parameter (e.g., the total concentration of a transcription factor). We propose to associate a bifurcation diagram with a signal–response curve as measured experimentally. By making this association we can use the power of dynamical systems theory to connect molecular mechanisms to cell physiology. We will illustrate this idea with two examples: switch-like activation of mitosis-promoting factor in frog egg embryos, and circadian oscillations in mammalian cells. We intend that this ‘dynamical’ paradigm will help both modelers and experimentalists to better understand the complexities of molecular regulatory systems.

Bypassing the Curses

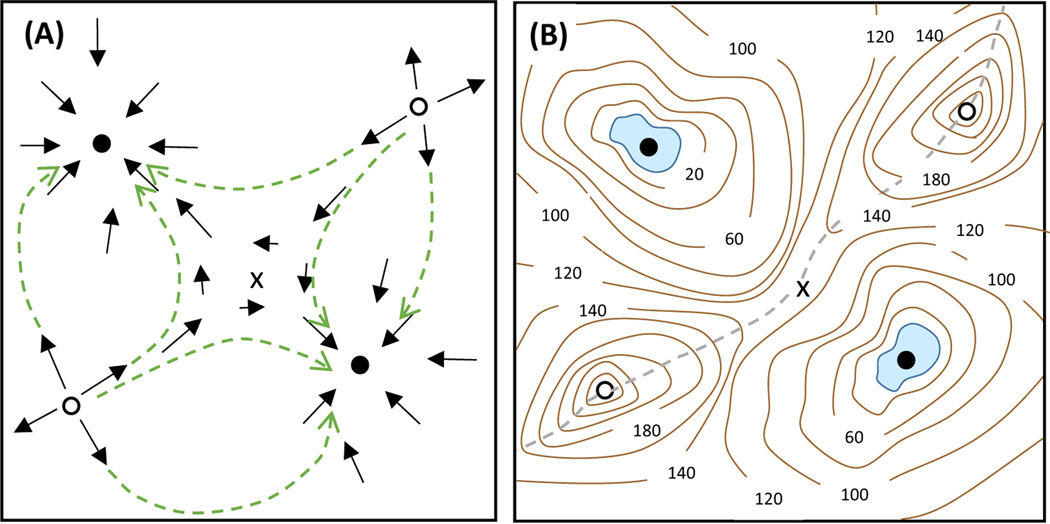
The qualitative theory of dynamical systems does not regard a set of ODEs primarily as a challenge for straightforward numerical simulation on a computer. Instead, dynamical systems theorists understand that the ODEs define a ‘vector field’ in a multidimensional state space (the n-dimensional Cartesian coordinate system spanned by the n variables – the mRNAs and proteins – that comprise the underlying biochemical network). To each point in this state space, the ODEs attach a small vector indicating the direction and speed in which the control system will change in the next small increment of time (Δt) (Figure 1A). By following these vectors, namely by stringing together a sequence of small Δt steps, we could, in principle, solve the ODEs from any initial condition and be led, for example, to a stable steady-state solution of the ODEs (indeed, this is exactly what a computer does in calculating a numerical solution from any particular initial condition). However, instead of trying to walk from point to point along the directions of the arrows, we want a global view of where all the arrows are pointing; in other words, we want to see the final states that can be adopted by the dynamical system from all possible initial states. These final states are called the attractors (if they are stable) or repellers (if they are unstable) of the dynamical system. This ‘global view’ is analogous to the topographic map in Figure 1B, where the lakes and peaks are the attractors and repellers (respectively) experienced by a mountaineer who prefers to walk downhill.

Figure 1. The Vector Field of a Dynamical System.

(A) The differential equations, dx/dt = f(x,y) and dy/dt = g(x,y), define a direction and rate of change at each point in the ‘state space’ (x,y). A solution of the differential equations follows the arrows from some starting point until the trajectory (any one of the green dashed lines) reaches a stable attractor (one of the two stable steady-states represented by the black circles). The white circles represent repellers, and the x marks a ‘saddle point’. (B) The vector field in panel A can be associated with this ‘topographic map’, where the contours are plotted at 20 m intervals above the ‘lake’ in the upper left corner. The stable attractors are lakes (blue zones) in two depressions (at elevations of 0 and 20 m), and the repellers are mountain peaks (the white circles, at elevation 260 m). In the middle of the landscape is a saddle point (at an elevation of 130 m), which lies on the boundary (the grey dashed line) between the watersheds of the two lakes.

The precise flow lines of a vector field are, of course, dependent on the values assigned to the parameters in the ODEs. However, the qualitative features of the attractors and repellers of the vector field are usually independent of these exact parameter values. Small perturbations of the parameter values may change the flow lines, but are unlikely to destroy the attractors and repellers. In the same way, a little erosion of the landscape in Figure 1B may alter the slopes and drainage patterns of the terrain, but will not remove the lakes or peaks of the countryside. Nonetheless, a sufficiently large change of parameter values may cause qualitative changes in the number and character of the attractors and repellers of a dynamical system, in the same way that an earthquake may shift the landscape so as to drain one of the lakes. In dynamical systems theory, such changes of the qualitative nature of the attractors and repellers of a system of ODEs are called ‘bifurcations’. As a dynamical system moves past a bifurcation point there is a dramatic change in the properties of the attractors and repellers of the system. For example, for values of a parameter p less than a critical value p_crit, the system may have one steady-state (a single attractor), but for p > p_crit the system may have three steady-states (two attractors and one repeller).

Dynamical systems theorists have characterized all the possible bifurcations that can occur in systems of nonlinear ODEs [2] and have devised convenient ways to visualize them. A one-parameter bifurcation diagram is a plot of how the final states (the attractors and repellers) of a dynamical system depend on one of the parameters in the ODEs. To connect this abstract mathematical notion to cell physiology we must recognize that a mathematician’s one-parameter bifurcation curve is closely related to the cell physiologist’s signal–response curve. In a physiology experiment, the biologist measures how some behavior of the cell (the response; e.g., the activity of an important regulatory protein) depends on the value of an experimentally controlled signal (e.g., the concentration of a hormone in the growth medium). The signal is held at a constant value until the response settles on a definitive value, then the signal is changed to a new value and the new response is recorded. Signal–response curves carry information about how particular combinations of signals and responses are embedded in the entire regulatory network. A one-parameter bifurcation diagram shows how the final states of a mathematical model (e.g., the activity of a protein kinase in the reaction network) depend on one of the parameters in the model (e.g., the concentration of a hormone in the equations). Bifurcation diagrams carry information about how particular combinations of variables and parameters are connected through the full array of regulatory signals in the network. In particular, one-parameter bifurcation diagrams identify values of the parameter, p_crit, where the dynamical system undergoes a qualitative change in behavior, analogous to dramatic changes in the response of a cellular system to continuous changes in an experimental signal.

Although it is too much to expect a one-to-one correspondence between the two curves (given the variety of ways that experimentalists characterize how cells respond to specific signals), the bifurcation diagram provides theoretical insights into the observed behaviors of cells, thereby alleviating the curse of complexity. In addition, the bifurcation diagram may suggest novel physiological experiments to test the theoretical connections (as illustrated below).

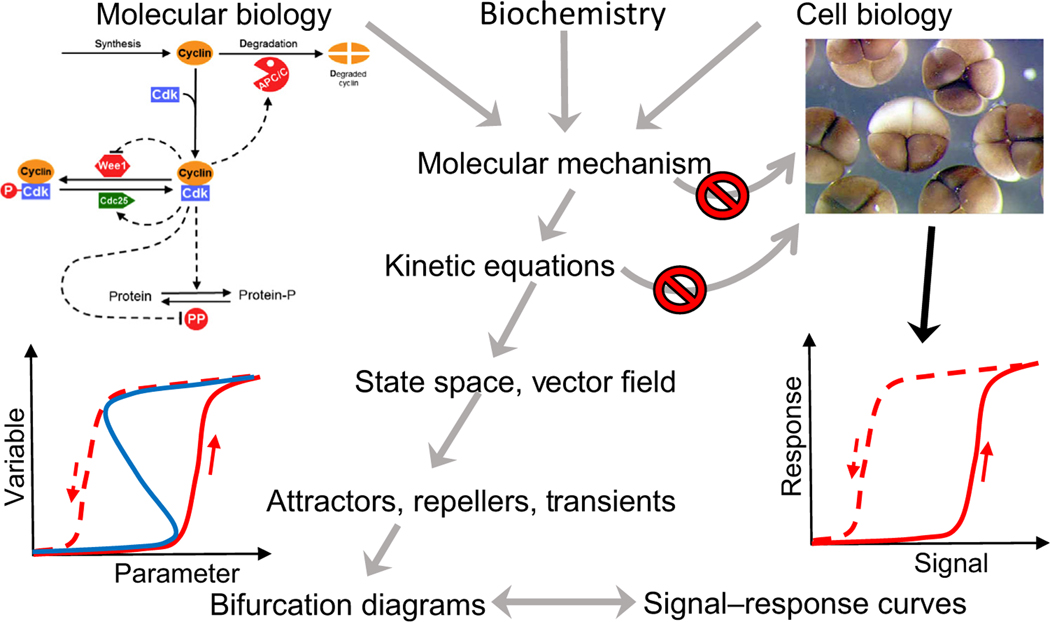
Bifurcation diagrams also afford a way around the curse of parameter space because they provide the modeler with information about parameter values where the model shows the same type of behaviors that are observed in cell physiology; for example, the sudden appearance of a new stable steady-state during cell differentiation. With this information as a starting point, the theoretician can use numerical solutions of the ODEs to simulate hundreds or thousands of experimental scenarios, to investigate the adequacy of the model to explain all known properties of a particular aspect of cell physiology, and to predict how the cell will respond under novel experimental conditions. This approach, summarized in Figure 2 (Key Figure), is what we call a ‘dynamical paradigm for molecular cell biology’.

Figure 2. Key Figure A Dynamical Paradigm for Molecular Cell Biology.

Biologists gather information from many types of experiments to propose a molecular mechanism for the control of some aspect of cell physiology; for example, the regulation of cyclin-dependent kinase (upper left) as an explanation of the early embryonic divisions of frog eggs (upper right). Nowadays, these mechanisms are so complex that intuitive arguments alone are insufficient to understand the full behavioral repertoire of cells (the ‘curse of complexity’, represented by the upper ‘no passage’ sign). In principle, one could convert the mechanism into a set of differential equations and use computer simulations to deduce the temporal responses of cells to signals (lower right), but this approach is stymied by our ignorance of the values of the rate constants and binding constants that enter into the kinetic equations (the ‘curse of parameter space’ – the lower ‘no passage’ sign). The curses can be bypassed by ‘dynamical systems theory’ which considers kinetic equations as defining a vector field in state space (Figure 1). The vector field defines key attractors, repellers, and transients of the dynamical system, which can be characterized by a one-parameter bifurcation curve (lower left) The theoretician’s bifurcation curve is directly comparable with the physiologist’s signal–response curve. By making this connection, dynamical systems theorists can work their way backward to the parameter values that are necessary to account for the signal–response characteristics of the cells, and from there to comprehensive simulations of the molecular mechanism under a variety of experimental conditions, including novel tests of the model. Abbreviation: P, phosphorylation.

Bistability

As an example, consider the control of mitotic division cycles in frog eggs and frog egg extracts (Figure 2, upper right). The hypothetical network controlling these cycles (upper left of the figure) is based on the activity of a cyclin-dependent kinase (Cdk1:CyclinB heterodimer, also known as MPF) and its interaction partners (Wee1, Cdc25, APC/C, etc.). The network diagram can be converted into a set of 10 differential equations, involving 26 ill-defined parameter values [3]. The key to understanding the dynamics of this network is the observation of a ‘cyclin threshold for MPF activation’ [4]: the solid red curve in the signal–response diagram in the lower right of the figure. By incrementally increasing the total amount of cyclin in a frog egg extract, Solomon et al. [4] observed, at first, no MPF activity and then an abrupt jump to high MPF activity for cyclin concentrations above a distinct threshold. To a dynamical systems theorist, this behavior is suggestive of a bistable switch. Novak and Tyson [3] showed that the MPF control network can indeed function as a bistable switch (the bifurcation diagram in the lower left of Figure 2). A plot of the steady-state activity of MPF (the dynamical variable) as a function of total cyclin level (the parameter value) is S-shaped, and contains two stable steady-states (low MPF activity, i.e., interphase; and high MPF activity, i.e., M phase) separated by an unstable, intermediary activity of MPF. The region of bistability is bounded by two ‘bifurcation points’ at the turning points of the S-shaped curve. Starting on the lower branch of the curve and increasing total cyclin B (as done by Solomon et al.), one observes little or no MPF activity until the level of cyclin B exceeds the right-most bifurcation point, beyond which the control system switches abruptly to the upper steady-state (the solid red curve on the bifurcation diagram). The right-most bifurcation point is Solomon’s ‘cyclin threshold for MPF activation’. The one-parameter bifurcation diagram immediately suggests a novel experiment to test the mathematical model: start on the upper steady-state (i.e., in mitosis) and reduce the level of cyclin in stages (the red dashed line), and the extract will remain in a mitotic state until cyclin level drops below a lower threshold (the left-most turning point of the S-shaped curve, i.e., a lower ‘cyclin threshold for MPF inactivation’). This prediction of the model was confirmed 10 years later by two groups independently [5,6], whose results are indicated schematically by the dashed red curve on the signal–response diagram in the lower right of the Figure 2.

Bistable behavior, such as this, is a consequence of positive feedback in molecular regulatory networks: either +/+ interactions (mutual activation) or −/− interactions (mutual inhibition). Bistability has been widely invoked as a basis for cell differentiation, as has been insightfully reviewed by Huang [7].

Solomon’s experiments were designed so that the total cyclin concentration in the frog egg extract could be held at a constant value to measure the steady-state activity of MPF at that particular cyclin concentration. In an intact frog embryo, the concentration of cyclin oscillates up and down during each mitotic cycle owing to a fundamental negative feedback in the reaction network. When MPF activity is low, the embryo synthesizes cyclin protein from maternal stores of cyclin mRNA, and cyclin concentration increases. As the cyclin concentration increases, MPF activity remains low because it continuously adjusts to a pseudo-steady-state value that tracks closely to the lower branch of the signal–response curve (Figure 2, solid red curve in the lower right corner). Eventually, the total concentration exceeds the bifurcation point on the signal–response curve, and MPF is rapidly activated (the up-arrow). The frog egg enters mitosis, and subsequently APC/C is turned on. As cyclin molecules are rapidly degraded by APC/C, cyclin concentration decreases, following the dashed red arrow on the signal–response curve. During this phase, MPF activity remains large because it is now tracking the upper branch of the signal–response curve. When cyclin concentration drops below the lower threshold for MPF inactivation, MPF activity drops abruptly (the down-arrow), cyclin degradation turns off, and cyclin concentration starts to increase again, to repeat the process of DNA synthesis, mitosis, and cell division. The analogous curves on the bifurcation diagram (Figure 2, lower left) describe a ‘hysteresis loop’ or (as a dynamical system theorist would say) a ‘stable limit cycle oscillation’.

Oscillations

Sustained oscillations are observed in many features of cell biology, from cAMP oscillations in cell signaling, to hormonal oscillations in organismal physiology, to ubiquitous circadian rhythms in the majority of organisms exposed to day/night cycles [8]. Cellular oscillations have been a favorite topic of mathematical biologists, and we shall use a recent model of the mammalian circadian clock by Kim and Forger [9] to illustrate the ‘dynamical perspective’. The circadian system in our body synchronizes and phase-locks most of our physiological functions to the 24 h cycle of light and darkness. Our underlying circadian ‘clock’ is an autonomous oscillator that has a free-running period close to 24 h (‘circa diem’).

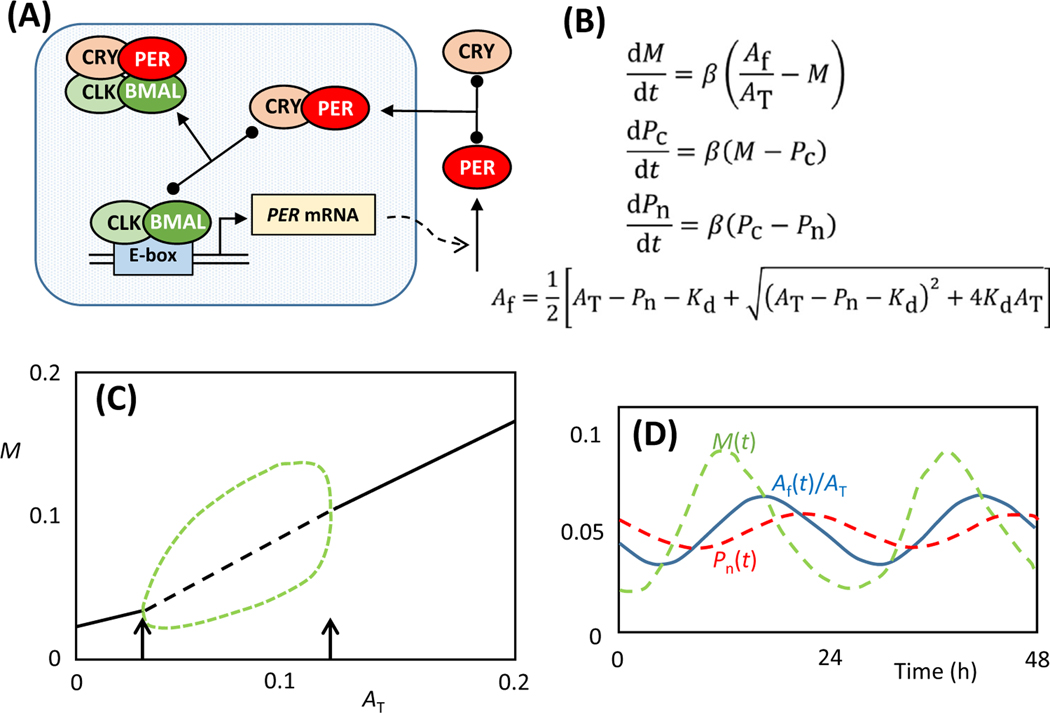
The core interactions of this clock comprise a negative feedback loop between a heterodimeric transcription factor, BMAL1:CLOCK, and a regulatory protein, PERIOD1/2 (Figure 3A). BMAL1: CLOCK binds to transcriptional regulatory sites (E-boxes) in front of hundreds of genes that are subject to circadian regulation. Among these are the genes that encode PER1/2; these proteins are synthesized in the cytoplasm, bind to partner proteins (CRY1/2), and return to the nucleus to bind to BMAL1:CLOCK and inhibit its transcription-promoting activity. The negative feedback of PER proteins on their own expression induces periodic synthesis of PER1/2 and periodic inactivation of BMAL1:CLOCK. Consequently, all the genes regulated by BMAL1:CLOCK are expressed periodically at the same ∼24 h rhythm. In the following model we combine PER1/2 and CRY1/2 into single protein variables, PER and CRY. We also drop the 1 from BMAL.

Figure 3. Kim–Forger Model of Circadian Rhythms.

(A) The core negative feedback loop of the mammalian circadian rhythm (main text for details). (B) Ordinary differential equations (ODEs) embodying the mechanism in panel A. M(t) = concentration of PER mRNA, P_c(t) = concentration of PER protein in cytoplasm, P_n(t) = concentration of PER:CRY complex in nucleus, A_T = total concentration of BMAL:CLOCK in nucleus, and A_f = nuclear concentration of ‘free’ BMAL:CLOCK (not bound to PER:CRY). K_d = dissociation constant of the BMAL:CLOCK::PER:CRY complex. (C) One-parameter bifurcation diagram plotting the attractor states for PER mRNA (M) as a function of total BMAL:CLOCK concentration (A_T). For these calculations, K_d = 10⁻⁴ and β = 1. Solid and dashed black lines denote (respectively) stable and unstable steady-states of the network. The green dashed lines denote the maximum and minimum levels of PER mRNA during the course of an oscillation at any fixed value of A_T in the interval 0.0305< A_T <0.1159. The arrows indicate the positions of two Hopf bifurcation points. (D) Circadian oscillations of PER mRNA (green), active BMAL:CLOCK (blue), and PER:CRY (red). Parameter values: A_T = 0.05, K_d = 10⁻⁴, β = 0.15; period = 25 h.

The Kim and Forger (KF) model of this control system (Figure 3B) consists of three ODEs (for PER mRNA, and PER protein in the cytoplasm and nucleus) and three parameters (A_T = total concentration of BMAL:CLOCK, K_d = dissociation constant of the BMAL:CLOCK::PER:CRY complex, and β = a rate constant that sets the timescale of the feedback loop). The KF model has a single steady-state for all values of the parameters, and this steady-state is stable for most values of the parameters. Oscillations are possible, but only over a restricted range of parameters. As is evident in the one-parameter bifurcation diagram in Figure 3C, the control system oscillates only over a range of values of A_T (0.031 < A_T < 0.116, for the case K_d = 10⁻⁴; the range is slightly larger for smaller values of K_d). The oscillatory domain is bounded by two ‘Hopf’ bifurcation points [9]. At a Hopf bifurcation, a stable steady-state solution of a system of ODEs loses stability and gives rise to a family of oscillatory solutions, illustrating the defining feature of a bifurcation point: that the solutions of the ODE system undergo a qualitative change as a parameter passes through the bifurcation point. In this case, as A_T passes through the value 0.031, the steady-state of the control system loses stability and gives birth to stable oscillations. These oscillations are tiny at first, but soon achieve a sizable amplitude. In Figure 3D we illustrate the waveforms of the oscillations for A_T = 0.05; we have chosen β = 0.15 to produce oscillations with a circadian period of 25 h.

The KF model oscillates only over a restricted range of A_T values because oscillations require a stoichiometric balance of BMAL:CLOCK and PER:CRY. If there is too little BMAL:CLOCK (A_T < 0.031), then most BMAL:CLOCK heterodimers will be bound to PER:CRY, and the transcription of E-box-regulated genes will be permanently turned down. On the other hand, if there is too much BMAL: CLOCK (A_T > 0.116), then the excess of BMAL:CLOCK over PER:CRY will ensure that all E-box-regulated genes are constitutively expressed.

From this model of a simple negative-feedback loop, Kim and Forger built up a ‘detailed’ model of the mammalian circadian rhythm, including additional negative and positive feedback loops (through REV-ERB and ROR proteins, respectively). Readers should consult the paper of Kim and Forger to see how the detailed model provides an excellent fit to experimental measurements of gene expression during mammalian circadian oscillations and the phenotypes of circadian mutants. Other groups have proposed similar ‘detailed’ models of mammalian circadian rhythms [10–12]. Battogtokh and Tyson [13] have published a detailed bifurcation analysis of Relogio’s model [12].

Extending the Paradigm

If this ‘paradigm’ is correct, then an understanding of the basic principles of cellular signaling is closely entwined with the theory of bifurcations in dynamical systems. Although cell behaviors may seem bewilderingly complex, they are all consequences of underlying molecular control systems that are adequately described by the nonlinear differential equations of biochemical kinetics. The signal–response characteristics of cells must derive from the types of bifurcations that are possible in such dynamical systems; and it is a remarkable and reassuring fact that there are only a small number (∼10) of elementary bifurcations of dynamical systems [2] from which all the complexities of cell responses must arise.

Not all signal–response curves show indications of bifurcations. Some curves exhibit a simple ‘linear’ or ‘hyperbolic’ response to increasing signal strength, or more interesting ‘sigmoidal’ responses. Other signal–response curves may be ‘bell-shaped’, where the response increases at low signal strength and then decreases at higher signal strengths. ‘S-shaped’ curves (e.g., in Figure 2) are typical of cases where a cell must make a binary ‘decision’ (e.g., to enter mitosis or to differentiate into a new cell type). Cellular oscillations arise from Hopf bifurcations (as in the example in Figure 3) or from more complex bifurcations, as illustrated in [14]. Examples of all these types of signal–response curves can be found in [15].

Although not widely recognized or understood by molecular cell biologists, this dynamical paradigm has been practiced by mathematical biologists for decades, as documented in Table 1. Some highlights: Goldbeter and Lefever [16] used bifurcation diagrams to find conditions under which glycolysis in yeast cells would exhibit sustained oscillations; Mackey and Glass [17] linked physiological dysfunctions of cells with dynamical bifurcations in the underlying biochemical control systems, a phenomenon they called ‘dynamical diseases’; Goldbeter and Segel’s [18] concept of a ‘developmental path’ associated physiological states of a differentiating cell with changes in parameter values that carry the control system past bifurcation points on a two-parameter bifurcation diagram; and recently Heldt et al. [19] used a one-parameter bifurcation diagram to illuminate the phenomenon of multiple-fission cycles in photosynthetic algae.

Table 1.

Selective Survey of Applications of the Dynamical Paradigm (1972–2020)

Year	Authors	Physiology	Molecular Mechanism
1972	Goldbeter and Lefever [16]	Glycolytic oscillations in yeast cells	Allosteric regulation of phosphofructokinase
1977	Mackey and Glass [17]	Pathological oscillations in blood cell counts	Negative feedback on gene expression
1980	Goldbeter and Segel [18]	Developmental transitions in the cAMP signaling system	Control of cAMP level by adenylate cyclase and phosphodiesterase
1987	Martiel and Goldbeter [31]	cAMP oscillations in Dictyostelium cells	Receptor desensitization in the cAMP signaling system
1989	Edgar et al. [32]	Patterns of gene expression in Drosophila embryos	Bistability generated by mutual inhibition of pair-rule genes
1991	Tyson [33]	Mitotic division cycles in fission yeast cells	Cyclin-dependent kinase regulation by Wee1, Cdc25, and APC/C
1995	Bertram et al. [34]	Bursting oscillations of pancreatic β cells	Fast inward Ca2+ current and slow outward K+ current
1998	Borisuk and Tyson [35]	Maturation and early division cycles in frog eggs	Regulation of activity of M phase-promoting factor (MPF)
2004	Battogtokh and Tyson [36]	Cell division cycles in budding yeast	Cdk1 regulation by cyclin synthesis and degradation
2004	Yates et al. [37]	Differentiation of Th1 and Th2 helper T cells	Expression of the master regulators Tbet and GATA3
2005	Ciliberto et al. [38]	Oscillations in the p53/Mdm2 network	Positive and negative feedback loops create oscillations of p53
2005	Ma et al. [39]	Digital response of p53 to DNA damage	Influence of double-strand breaks on p53 oscillations
2006	Legewie et al. [40]	Programmed cell death (apoptosis)	Inhibition of caspase-3 by IAPs (inhibitors of apoptosis)
2007	Dodd et al. [41]	Epigenetic memory by nucleosome modification	Positive feedback and cooperativity provide epigenetic memory
2008	van den Ham and de Boer [42]	Differentiation of helper T cells (Th1, Th2, Th17, …)	Expression of multiple master regulators
2008	Yao et al. [43]	The restriction point in the G1 phase of the mammalian cell cycle	A bistable E2F–Rb switch underlies the decision between quiescence and proliferation
2012	Hong et al. [44]	Heterogeneous differentiation of CD4+ T cells	Positive and double-negative feedback signals among the master-regulatory transcription factors
2012	Okaz et al. [45]	Yeast meiotic prophase–metaphase transition	Positive and double-negative feedback controlling entry into metaphase I
2013	Binder et al. [46]	Transcriptional regulation by histone modifications	Chromatin reorganization during cell differentiation
2014	Zhang et al. [47]	Epithelial-mesenchymal transition in human breast cells	Double-negative feedback loops between SNAIL1 and miR-34, and between ZEB1 and miR-200
2016	Barr et al. [48]	G1/S transition of human cells	A bistable switch controlling the initiation of DNA replication
2016	Mochida et al. [49]	Regulation of Cdk1-counteracting protein phosphatase	Bistability of the Greatwall–ENSA–PP2A:B55 pathway
2016	Kunche et al. [50]	Self-organizing morphogenesis	Positive and negative diffusible signals acting on tissue progenitor cells
2016	Tian et al. [51]	Cell fate decisions	Reciprocal regulation of mRNA and microRNA enables bistability
2018	Rata et al. [52]	Mitotic control in mammalian cells	Two interlinked bistable switches
2019	Nijhout et al. [53]	Robustness of homeostatic mechanisms in development	One-carbon metabolism: folate cycle, methionine cycle, and glutathione synthesis
2020	Heldt et al. [19]	Multiple-fission cycles in green alga cells	Cdk1 regulation by a bistable switch and a mitotic oscillator

An excellent review of the classical literature of mathematical cell biology is provided by Mogilner et al. [20]. For book-length treatments of dynamical systems theory and bifurcation diagrams with applications to cell physiology we refer the reader to Goldbeter [8], Strogatz [21], Keener and Sneyd [22], Forger [23], and Alon [24].

Concluding Remarks and Future Perspectives

A living cell is a dynamical system that is governed by nonlinear interactions among genes, proteins, and metabolites in time and space. It is extremely difficult – if not impossible – for the human mind to comprehend how such cellular control systems respond to the variety of conditions experienced by cells under laboratory conditions, or to predict how the system will react to novel conditions in the laboratory or in the wild. The only way to begin to make accurate, reliable assessments of cell behavior – based on the underlying interactions of genes and proteins – is to create realistic mathematical models of these dynamical systems, and to employ the well-established tools of analysis and simulation of nonlinear differential equations.

The path to useful mathematical models of molecular control systems – models that are realistic, accurate, and predictive – is barred by the twin roadblocks of network complexity and parameter uncertainty. We suggest that some basic ideas from dynamical systems theory – bifurcation diagrams in particular – provide a way around these roadblocks. Bifurcation diagrams tie dynamical properties, such as bistability and oscillations, to the interactions in underlying molecular networks, such as positive and negative feedback, respectively. The task of the modeler is to discover, among the myriad reactions of a molecular network, those interactions that are potentially responsible for the observed behaviors of a cell. After these reactions are cast in mathematical form, as a system of nonlinear ODEs, the theory of bifurcations of vector fields can determine, first of all, whether the system of ODEs does indeed exhibit the desired bifurcations, and second, the ranges of parameter values where these bifurcations occur. Once we have this level of detail, then numerical solutions of the ODEs can be used to fit the model in quantitative detail to a variety of experimental observations. This is the route we and others have taken to develop successful mathematical models of many aspects of cell physiology (Table 1). There is much work remaining to be done (see Outstanding Questions).

Outstanding Questions.

To model and understand complex molecular regulatory networks demands that they have a certain modular character. To what extent are the networks modular? How weak or strong are the interactions among the modules?

How do we process the information from omics studies into network diagrams that are sufficiently comprehensive to cover the details of a particular aspect of cell physiology without being weighed down by extraneous information?

Who will develop the next generation of useful computational tools to assist both theoreticians and experimentalists in building, analyzing, and simulating realistic mathematical models of molecular regulatory networks?

This approach to modeling has relied, in the past, on a degree of ‘modularity’ of molecular control systems. That is, complex networks of reactions have been dissected, to a first approximation, into smaller ‘units’ of control, for example, distinct bistable switches and oscillators [25]. These smaller control units are easier to analyze by the paradigm described here because there are fewer variables and parameters to keep track of. The subunits can then be combined into a larger set of equations, which can be studied numerically if not analytically (by bifurcation theory). The advantages of invoking modularity are two-fold. First, modular thinking is almost a prerequisite for gaining insight into the workings of a complex control system. Second, applying bifurcation theory to the modules helps the modeler to estimate parameter values in smaller, more manageable groups. When the modules are assembled, these initial estimates of parameter values provide a good first-guess for parameter values of the full system. Computational studies of the full system can then be carried out to adjust the parameter values to obtain good agreement with experimental observations.

Some limitations and extensions to the paradigm proposed here must be acknowledged. First, not all cellular responses to applied signals can be described in terms of steady-state behaviors or oscillations. Some interesting responses are transitory (e.g., perfectly adapting responses, such as odor detection). However, transitory responses are dynamical transitions between repellers and attractors in the state space of the system, and therefore characterization of the long-term steady-state and oscillatory behaviors of the system can shed considerable light on the qualitative trajectory of a transitory response. Although a trajectory can often be predicted from the locations of attractors and repellers, the timescale of the transition cannot. It will depend on particular values of the kinetic parameters in the model.

Second, our approach focuses on the regulation of physiological responses ‘in time’ and the description of underlying molecular mechanisms by nonlinear ODEs (i.e., biochemical kinetics in ‘well-stirred’ reaction vessels). Far from being well-stirred reaction vessels, eukaryotic cells are subdivided into distinct compartments, which may need to be modeled individually, with realistic rules for the movement of molecules between compartments. This complication can be handled by extending the set of ODEs to include all the relevant subcellular compartments (where each is considered to be a well-stirred vessel). However, this approach is inappropriate for nonmembrane-bounded, liquid–liquid phase-separated compartments that require a different paradigm based on equilibrium statistical mechanics, as described in the exceptional review by Hyman et al. [26]. Furthermore, some physiological processes (such as cell polarity, motility, and embryogenesis) are governed in part by physical movements of molecules in space (diffusion and motor-driven transport), and the description of these mechanisms requires nonlinear ‘partial differential equations’ (PDEs; i.e., reaction–diffusion–convection equations), a subject requiring a separate review (e.g., the textbook by Murray [27]).

Third, modeling cell physiology with ODEs or PDEs presumes a ‘deterministic’ view of molecular interactions and trafficking within cells and tissues, even though living cells are very small and stochastic fluctuations in molecular abundances and movements are likely to be significant. Furthermore, even in the context of deterministic models of cell behavior, individual cells within a tissue will make different decisions because they differ in terms of molecular constitution (initial conditions) and gene expression (parameter values). There are well-developed theories to account for such stochastic effects. Nevertheless, building effective ‘stochastic models’, in our experience, requires (i) a solid foundation based on a preliminary deterministic model, and (ii) substantial amounts of additional quantitative data about cell constituents (e.g., counts of mRNA and protein numbers within cells) and cell behavior (e.g., statistical distributions of cell responses to a particular signal). The roles of stochastic fluctuations in determining the variability of cell behavioral responses have been reviewed by Rao et al. [28], Paulsson [29], and Shahrezaie and Swain [30].

Our dynamical paradigm for molecular cell biology is not a sure-fire cure for all our uncertainties, but it is a systematic way to begin to ground our understanding of cellular behavior on molecular mechanisms. For this approach to be successful, cell biologists and mathematicians must learn to speak a common language. Our goal in this opinion article has been to introduce molecular cell biologists to the basic principles of dynamical systems theory such that they can collaborate effectively with computational cell biologists.

Highlights.

A dynamical system of interacting genes, proteins, and metabolites underlies the physiological properties of every living cell.

To understand the behavior of these molecular mechanisms requires a disciplined mathematical theory of biochemical reaction networks.

The proper approach to this problem is based on the ‘qualitative theory’ of nonlinear differential equations.

The link between theory and experiment is the identification of the mathematician’s ‘one-parameter bifurcation diagram’ with the physiologist’s signal–response curve.

Glossary

Attractor

a stable steady-state solution of a system of ordinary differential equations. A steady-state is stable if any small perturbation away from the steady-state returns to the steady-state as time proceeds

Bifurcation diagram

a plotted curve specifying how some characteristic property of a dynamical system (e.g., the steady-state value of a variable) depends on particular values of a parameter

Bistable switch

a dynamical system with three steady-state solutions (two stable steady-states separated by an unstable steady-state) is said to be bistable. The bifurcation diagram of a bistable system is S-shaped, where the upper and lower branches define the stable steady-states, and the middle branch defines the unstable steady-state. The property of bistability, which usually appears over a restricted range of parameter values, is often associated with decision-making in cellular control systems.

Dynamical system

a set of interacting components (mechanical, electrical, chemical, biological) that are governed by the basic laws of physics, chemistry, and biology, and that specify how the system will evolve in time from a given set of initial conditions. The system is composed of time-dependent variables (positions, currents, concentrations, population densities) and time-independent parameters (masses, resistances, rate constants, intrinsic growth rates).

Ordinary differential equations (ODEs)

equations of the form dx/dt = f(x,y,z,…) are often used to describe the time-evolution of a dynamical system. The function f(x,y,z,…) describes the rate of change of a variable x(t) as a function of (potentially) all the variables x,y,z,…that define the dynamical system. f(x,y,z,…) is typically a nonlinear function of its time-dependent variables and of a number of time-independent parameters.

Repeller

an unstable steady-state solution of a system of ordinary differential equations. A steady-state is unstable if some small perturbations move away from the steady-state as time proceeds.

Signal–response curve

a plotted curve specifying how some characteristic output of a physiological control system (e.g., the activity of an enzyme) depends on some aspect of the system that is under experimental control (e.g., the concentration of a hormone in the growth medium of the cells).

Steady-state solution

a dynamical system is at a steady-state for fixed values for the variables (x₀, y₀, …) if dx/dt = f(x₀,y₀,...) = 0, dy/dt = g(x₀,y₀,…) = 0, etc.