Abstract
Background
Accurate segmentation of pulmonary nodules is important for image-driven nodule analysis and nodule malignancy risk prediction. However, due to interobserver variability caused by manual segmentation, an accurate and robust automatic segmentation method has become an essential task. Therefore, the aim of the present study was to construct an accurate segmentation and malignant risk prediction algorithm for pulmonary nodules.
Methods
In the present study, we proposed a coarse-to-fine 2-stage framework consisting of the following 2 convolutional neural networks: a 3D multiscale U-Net used for localization and a 2.5D multiscale separable U-Net (MSU-Net) used for segmentation refinement. A multitask framework was proposed for nodules’ malignancy risk prediction. Features from encoding and decoding paths of MSU-Net were integrated for pathology or morphology characteristic classification.
Results
Experimental results showed that our method achieved state-of-art results on the Lung Image Database Consortium and Image Database Resource Initiative dataset. The proposed method achieved a Dice similarity coefficient (DSC) of 83.04% and an overlapping error of 27.47% on the dataset. Our method achieved accuracy of 77.8% and area under the receiver-operating characteristic curve of 84.3% for malignancy risk prediction. Moreover, we compared our method with the inter-radiologist agreement, and the average DSC difference was only 0.39%.
Conclusions
The results showed the effectiveness of the multitask end-to-end framework. The coarse-to-fine 2.5D strategy increased the accuracy and efficiency of pulmonary nodule segmentation and malignancy risk prediction of the computer-aided diagnosis system. In clinical practice, doctors can obtain accurate morphological characteristics and quantitative information of nodules by using the proposed method, so as to make future treatment plan.
Keywords: Pulmonary nodule segmentation, refinement segmentation framework, convolutional neural network (CNN), 2.5D multiscale separable U-Net (2.5D MSU-Net), malignancy risk prediction
Introduction
Lung cancer is one of the most aggressive cancers, with a 5-year survival of only 19% (1). Lung cancer is also the leading cause of disability-adjusted life years for men in developed and developing countries (2). Due to air pollution and a high cigarette smoking rate, lung cancer incidence and mortality are rising in emerging countries, such as Brazil, Russia, India, China, and South Africa (3). However, early detection and diagnosis can greatly reduce the mortality rate of lung cancer. Although the survival rate of lung cancer is low for advanced lung cancer patients, the estimated 10-year survival of stage I lung cancer is up to 75%. Therefore, detecting and diagnosing lung cancer in the early stage is important for patients’ survival. The helical thoracic computed tomography (CT) screen as a non-invasive method is an effective means for lung cancer detection (4). The nodule’s CT image characteristics can help radiologists assess the risk of malignant nodules. As quantitative measurements of morphological, texture, or gray-level characteristics are easily interfered by surroundings, it is necessary to perform accurate nodule edge segmentation.
A robust and accurate automatic pulmonary nodule segmentation method has clinical significance in avoiding tedious manual processing and reduces interobserver variability (5). However, automatic pulmonary segmentation is challenging for several reasons. First, some ground-glass opacities (GGOs) often have low contrast to the surrounding background. The obscure boundaries of GGOs make them hard to detect and segment. Second, the adhesive lesions’ edges (juxta-pleural and juxta-vascular) attached to pleural surfaces or vascular structures cannot be segmented easily using the traditional morphology-based method. Finally, it is hard to distinguish small nodules with a diameter less than 5 mm from the nodule-like lung structures in the noisy CT image.
Many computer-aided diagnosis (CADx) systems have been proposed to segment pulmonary nodules and perform benign and malignancy classifications. CADx systems can be divided into the following 2 categories: radiomics-based methods and deep learning methods (6). The radiomics workflow often involves imaging examination, nodule segmentation, quantitative imaging feature extraction, and analysis. Nodule segmentation methods, such as region growing (7,8), level set (9), or graph cut (10), often fail to segment juxta-pleural nodules and small nodules. These methods are sensitive to the size and morphological characteristics of the nodules. For quantitative imaging feature extraction, radiomics studies extract numerous hand-crafted features from segmented CT images. These features involve the nodule’s intensity distribution descriptors, spatial relationships to other structures, texture patterns, and morphological characteristics. However, an end-to-end scheme for the segmentation and classification cannot be constructed using the radiomics strategy. Although the nodule’s hierarchy and internal features can be learned automatically, more robust feature representation methods need to be constructed manually.
To overcome these issues, data-driven learning methods were implemented into medical segmentation and classification tasks. Recently, CADx systems have been developed based on convolutional neural networks (CNNs). Due to efficient and automatic feature extraction, CNN-based CADx systems have better performance and stronger flexibility than traditional CADx systems (11). In addition, state-of-art CNN structures, such as the feature pyramid network, region proposal network, and dual-path network, extract in-depth features that boost segmentation, detection, and classification performance in the pulmonary nodule CADx (12).
In terms of the medical segmentation area, the U-shape network U-Net has been widely applied as a backbone (13). This network has a more efficient structure compared with that of the fully connected network (FCN) (14). The U-Net structure has been modified with additional mechanisms since it was proposed. The attention mechanism was introduced for the construction of the attention U-Net (15), the recurrent structure was applied for the construction of the R2U-Net (16), and the squeeze-and-excitation blocks were used to construct the USE-Net (17). These mechanisms further improved efficiency and performance in the modified U-Net structures compared with the original U-Net structure (18). For malignant risk prediction of pulmonary nodules, deep learning methods can also achieve better performance. Due to the shortcut connection in the residual block, the ResNet can solve the problem of vanishing/exploding gradients in a deep CNN (19). To develop an end-to-end framework that can simultaneously complete segmentation and malignancy classification, we combined the residual block and U-Net structure to build a multitask learning network.
Because CT images contain 3D information, the model should possess a 3D, rather than 2D, structure. However, 3D-structured networks require relatively larger computational capacity and have lower accuracy in slice-level segmentation compared with those of 2D networks. Therefore, in the present study, we proposed a 2.5D structured network known as a multiscale separable U-Net (MSU-Net). A 2.5D image has 1 more slice axis compared with that of a 2D image. This strategy harnesses the advantage of 2D and 3D networks to increase feature extraction efficiency of the U-Net architecture. The features from the encoding and decoding paths of MSU-Net have been used for classification feature learning. Residual blocks can efficiently extract the nodule features and predict their probability for malignancy or other morphological characteristics.
Due to significant variability in the size of nodules, a single segmentation model often fails to achieve good results. Therefore, researchers use cascaded or parallel models to segment medical images from multiple perspectives or scales (20-23). With a similar aim, we designed a coarse-to-fine structure for pulmonary nodule segmentation and classification. A 3D multiscale U-Net (MU-Net) is used to quickly locate the nodule position in a 3D CT image. For the refinement stage, multitask 2.5D MSU-Net was proposed to refine the 3D network’s output and obtain the classification output.
We introduced a coarse-to-fine strategy for pulmonary nodule segmentation and classification. The algorithm applied the following 2-stage prediction: a 3D MU-Net for nodule localization and a 2.5D MSU-Net for refinement.
We proposed a multitask network. A 2.5D MSU-Net was introduced to perform the segmentation and classification task. The 2.5D input structure, multiscale, and separable convolution strategies increased the accuracy of segmentation and classification.
We integrated traditional hand-crafted features, such as texture, calcification, and margin characteristics, into the framework. These characteristics play important roles in the radiological diagnosis of benign and malignant nodules.
A series of 2D, 2.5D, and 3D networks were implemented to demonstrate the 2.5D MSU-Net’s performance. The MSU-Net’s encoding/decoding single-branch classification networks and machine learning methods were also implemented to compare the dual branch (encoding and decoding paths) of the MSU-Net network’s performance.
Methods
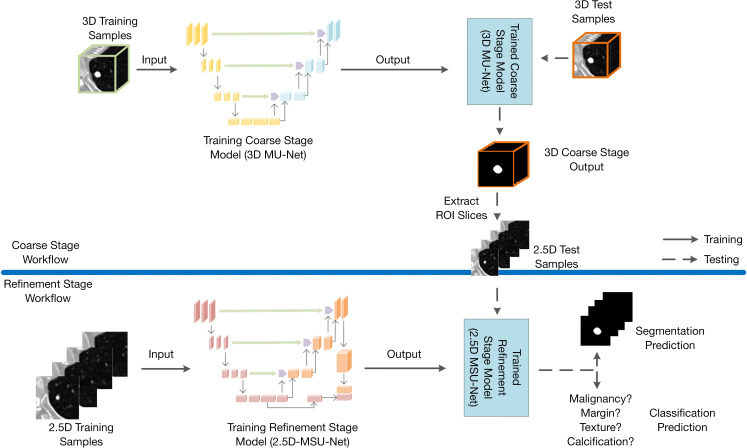
The proposed coarse-to-fine pipeline of pulmonary nodule segmentation and classification contains the following 2 networks: 3D MU-Net and 2.5D MSU-Net. These are both based on the U-Net structure. The proposed framework is shown in Figure 1.
Figure 1.
Proposed pipeline of pulmonary nodule segmentation and classification. MU-Net, multiscale U-Net; MSU-Net, multiscale separable U-Net; ROI, region of interest.
For training, the 3D and 2.5D training samples were simultaneously applied to train the 3D MU-Net and 2.5D MSU-Net to obtain the coarse and refinement stage model. First, for inference, the 3D MU-Net located the rough region of interest (ROI) of the 3D input. Then, based on the 3D segmentation result, the ROI slices were extracted automatically and fed into the trained 2.5D MSU-Net. Finally, we obtained the segmentation results and classification output from the trained multitask 2.5D MSU-Net.
Data preprocessing
Data preprocessing was aimed to reduce input redundancy and unify the spatial resolution of 3D CT. To reduce memory usage, the original 16-bit medical data were converted into a 10-bit unsigned integer. The pixel value of each data sample was bounded from –1,000 to 500 HU and quantized into an integer ranging from 0 to 1,023.
3D bilinear interpolation was used to unify the spatial resolution of 3D CTs. After reconstruction, the spatial resolution was unified to 1 mm × 1 mm × 1 mm. We extracted 64×64×64 3D cubes as input data of the 3D MU-Net and 64×64×4 2.5D slices as the input data for 2.5D MSU-Net.
Multitask 2.5D MSU-Net
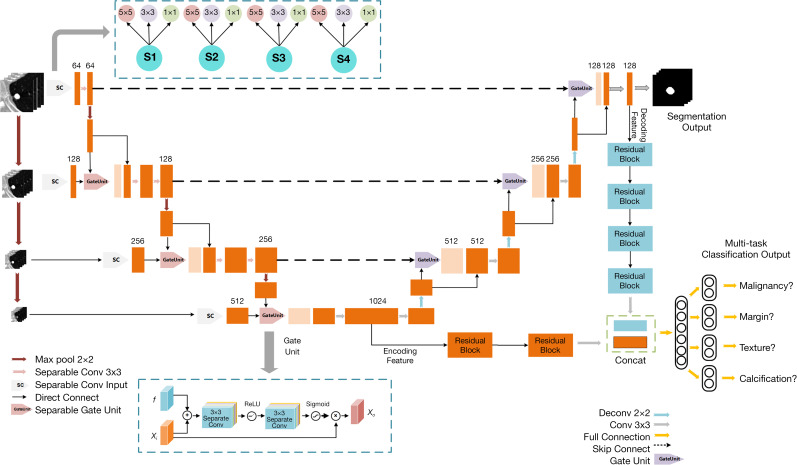
The proposed 2.5D MSU-Net is a deep end-to-end network consisting of the following main parts: an encoder and decoder. We used the following 3 strategies for constructing the network: separable convolution in the encoder to avoid the structural damage caused by the 2D convolution kernel, a gate unit for attention information extraction, and multiscale input for constructing the pyramid input (24).
Because the CT is a spatially continuous 3D image, the 3D network structure can fully utilize the information from the spatial 3D context (25). Moreover, the inference process of 3D networks is much faster than that of 2D networks (26); however, the 3D network’s training and deployment require a large computation capacity, especially in the semantic segmentation aspect. Due to its large input and relatively shallow network depth, the 3D network cannot rival the performance of the 2D network in the fine segmentation stage. To achieve the network learn context information of 3D CT but minimize the network’s computational requirements, we proposed a 2.5D network. This strategy combines the advantages of 2D and 3D networks. Different from the 2D network, the 2.5D network uses a series of ROI slices with a 4-slice image structure as the input. Interpolation is applied to nodules with less than 4 ROI slices. For nodules with more than 4 ROI slices, every 4 slices of the nodule serve as the input. The network structure is shown in Figure 2.
Figure 2.
Multitask 2.5D MSU-Net structure. Blue dotted boxes at top and bottom represent structures of the separable convolution and gate unit, respectively. MSU-Net, multiscale separable U-Net; Concat, concatenation operation; Conv, convolution layer.
The proposed network has the following 2 outputs: segmentation and classification. These 2 outputs share the network’s hidden layers and reserve 1 fully connected layer for implementation. This pattern of parameter sharing results in a low probability of overfitting. Due to semantic segmentation, results have a strong correlation with classification characteristics, shared encoding, and the decoding feature that widens the feature space and increases classification performance.
Given the k tasks, the model consists of a shared-bottom network. Two branches from the encoding feature and decoding feature were concatenated after passing the residual blocks. For classification tasks, the shared-bottom network fshare is:
| [1] |
where fenc represents the encoding branch model, fdec denotes the decoding branch model, and res represents the residual blocks. In this task, we used 2 residual blocks in the encoding branch and 4 residual blocks in the decoding branch.
For task k, the classification model yk can be formulated as:
| [2] |
where Lk represents the full connection layer after the shared-bottom network. For the classification task, prediction output is:
| [3] |
For segmentation, ys output is:
| [4] |
where Ws is the final convolution operator before output. The output of the multitask network is:
| [5] |
Output y consists of two parts, which are segmentation output ys and classification output .
Separable convolution
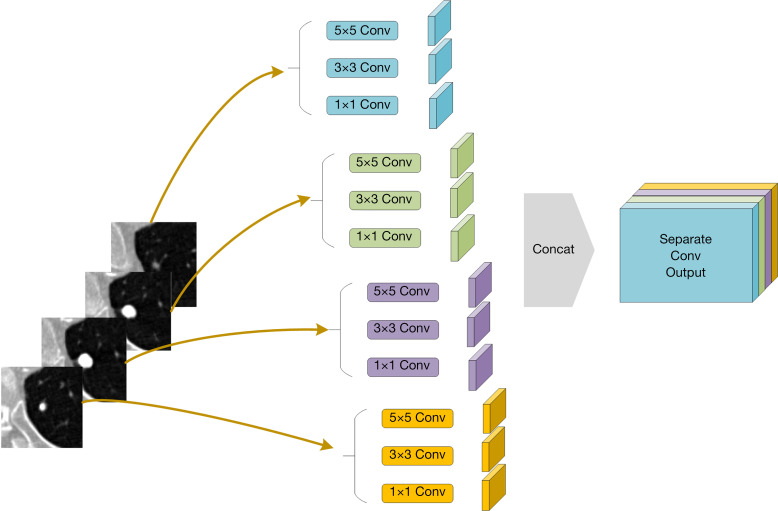
Previous 2.5D networks stack 2D convolutions as a basic network structure. This strategy causes the 2.5D structure to degrade into a 2D structure. To preserve the hierarchical features of the 2.5D structure and avoid the destruction of 2.5D information by the 2D convolution kernel, we applied separable convolution. Different from the normal convolution operation, separable convolution conducts a convolution operation for each slice-group feature map, as shown in Figure 3. In the encoding path of MSU-Net, separable convolution ensures that the network fully extracts the features in each slice. In the decoding path, the slice-separated features merge for semantic segmentation. This structure can reduce the network’s complexity.
Figure 3.
Separable convolution and structure of the multiscale input layer. Concat, concatenation operation; Conv, convolution layer.
Multiscale input layer
A multiscale input layer was applied to merge small-scale to large-scale features. The pyramid pooling structure was the key to forming a 2.5D network. Discrete pixels from the image had different aggregation modes in different imaging scales. The max pool operation reduced the original image to a scale of 2. In the CNN structure, the receptive field was presented as the feature scale that we extracted. Figure 3 shows the structure of a multibranch separable convolution input layer. This operation obtains different feature scales from any input image scale. The convolution outputs of each slice were concatenated for the next operation.
Gate unit
Gate unit operation integrates the multiscale feature and encoding-decoding feature. Due to the convolution operation and non-linearities, detailed spatial information becomes lost in the top-down structure of the encoder, and it is difficult to reduce false-positive predictions for small objects that show large shape variability (15). To prevent missing pixel-level information, we conducted a spatial attention mechanism to improve the accuracy of feature extraction.
Different from the squeeze-and-excitation block extraction of channel attention coefficients (17,27), the gate unit exploits the spatial attention of feature maps. The gate unit fuses the top-down/bottom-up feature with the multiscale-input/encoding feature. The gate unit produces the attention parameter Fatt. The concrete formula for calculating Fatt is:
| [6] |
For the encoder, f denotes the multiscale feature extracted by separable convolution, Xi represents top-down branch feature maps, σ2 denotes the sigmoid activation function, and σ1 denotes the rectified linear unit (ReLU) function. The multiscale feature f and top-down branch feature Xi are summed up, and then pass through 2 convolution layers. The sigmoid activation function was applied to normalize the attention coefficients Fatt between 0 and 1.
The output Xo of the gate unit is:
| [7] |
The top-down (bottom-up) feature Xi maps are multiplied with attention coefficients Fatt. The attention coefficients can progressively suppress irrelevant background information with different feature scales and can focus on the foreground ROI.
3D network for localization
As the segmentation algorithm is executed, the 3D network plays a vital role throughout the whole process. The network provides 2.5D MSU-Net with ROI slices in the test stage. The missing slice from the coarse segmentation stage would be ignored during the next fine segmentation stage.
To obtain more accurate location information from the coarse segmentation stage, we applied a 3D MU-Net to accomplish this task. The 3D gate unit applied the attention mechanism by fusing 2 types of feature maps. The multiscale strategy was applied to merge different scale inputs with that of the top-down feature maps. These strategies can improve segment performance compared with the traditional 3D U-Net structure without increasing too many parameters.
Loss function
In the medical community, Dice loss is widely applied for segmentation tasks (28). Dice loss is calculated as follows:
| [8] |
where pi represents the prediction of each pixel, gi denotes ground truth, and N represents the number of pixels.
Due to the different sizes of the nodules, the loss function must balance the foreground and background pixels. As small nodules, background pixels take up a large percentage of the total pixels. Most of the background pixels can be classified easily. The loss function should be focused on pixels that are difficult to classify. We used the focal loss to solve this problem (29). The loss of the network is:
| [9] |
Hyperparameters γ and α control the contribution of hard misclassified pixels and are set as 2 and 0.25. Classification loss can be formulated as:
| [10] |
where k represents the number of classification tasks and and denote the label and prediction in task I, respectively. The total loss is as follows:
| [11] |
When these 3 loss functions are combined, log is used to magnify the Dice loss and hyperparameter λ to shrink focal loss. Hyperparameter λ is set to 0.2 in the experiments.
Evaluation metrics
To investigate the performance of 2.5D MSU-Net and the 2-stage coarse-to-fine strategy, the Dice similarity coefficient (DSC), and overlapping error (OE) were used to measure the performance on pulmonary nodule segmentation. The Jaccard Index and DSCs have been widely used as performance metrics. The OE is calculated based on the 1-Jaccard Index. The DSC is the harmonic mean of precision and recall (30):
| [12] |
| [13] |
where Sg is the ground-truth mask; Sp is the predicted segmentation mask; Sg∩Sp and the Sg∪Sp are the interaction and union region of ground truth and prediction, respectively; and TP, FP, and FN represent the true positive, false positive, and false negative, respectively.
The receiver-operating characteristic (ROC) curve and the area under the ROC curve (AUC) were applied to analyze the classification results. Accuracy, sensitivity, and specificity were also used to evaluate the results.
Experiment implementation
For the experiments, we used a dynamic learning rate to prevent overfitting. The learning rate automatically changes when the training loss cannot decrease by 5 epochs. The experiments are based on the PyTorch framework and programmed in Python 3.6. The experiment was carried out on a server with 64 GB memory and 3 NVIDIA GTX-1080 graphics processing units (GPUs).
Results
Dataset
We used the public dataset Lung Image Database Consortium and Image Database Resource Initiative (LIDC-IDRI) (31) to perform the experiments. The tube peak potential energies used for CT scan acquisition ranged from 120 to 140 kV. The tube current ranged from to 627 mA (mean: 222.1 mA) (32). Each case in this dataset was labeled by 4 experienced radiologists. Due to differences in labels between the radiologists, in the present study, all 1,561 collected pulmonary nodules met a 50% consistency criterion. Each nodule was labeled by more than 2 radiologists, and its ground truth voxel points were also labeled by more than 2 radiologists. Furthermore, each nodule in the dataset was assessed by a panel that considered the nodule’s likelihood for malignancy, based on 8 nodule characteristics (33).
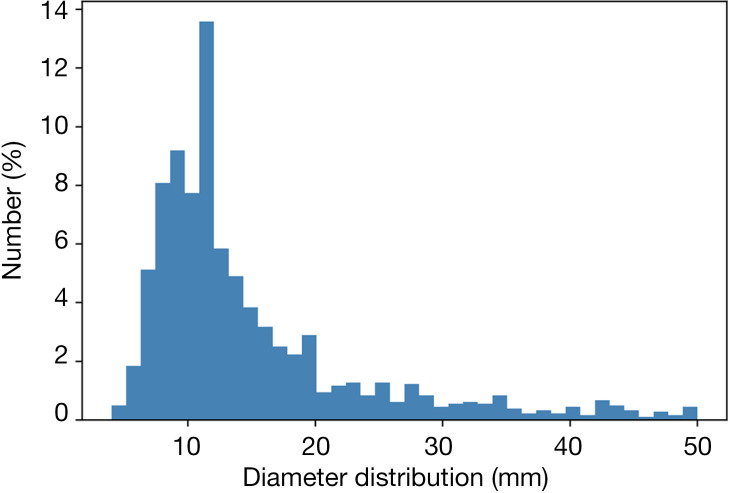
Five sections were used for 5-fold cross-validation to make the results more reliable (34). We use a pretrained U-Net and Gaussian mixture model for data division (35). This method ensures that the nodules in each section have a similar statistical distribution. Tables 1,2 show the characteristic distribution of each fold. Nodule diameters in this research ranged from 4 to 50 mm. As shown in Table 1 and Figure 4, the nodules were concentrated at a diameter of 10–15 mm.
Table 1. Data distribution of the divided 5 folds.
| Characteristics | Fold 1 | Fold 2 | Fold 3 | Fold 4 | Fold 5 |
|---|---|---|---|---|---|
| Diameter (mm) | 15.47±8.78 | 14.62±8.56 | 15.22±9.38 | 15.06±8.95 | 14.46±8.34 |
| Calcification | 5.66±0.97 | 5.64±0.98 | 5.63±0.98 | 5.67±0.98 | 5.71±0.88 |
| Internal structure | 1.01±0.17 | 1.01±0.16 | 1.00±0.12 | 1.02±0.29 | 0.01±0.18 |
| Lobulation | 1.66±0.96 | 1.60±0.85 | 1.60±0.91 | 1.70±0.99 | 1.60±0.99 |
| Margin | 4.02±1.06 | 3.94±1.13 | 4.00±1.20 | 4.03±1.08 | 4.10±1.10 |
| Sphericity | 3.67±0.94 | 3.67±0.95 | 3.76±0.88 | 3.71±0.98 | 3.64±0.97 |
| Spiculation | 1.67±1.11 | 1.47±0.85 | 1.42±0.87 | 1.60±1.01 | 1.47±0.91 |
| Subtlety | 3.80±1.13 | 3.75±1.08 | 3.75±1.19 | 3.73±1.16 | 3.77±1.16 |
| Texture | 4.49±1.10 | 4.49±1.09 | 4.45±1.16 | 4.52±1.06 | 4.53±1.05 |
| Malignancy | 2.83±1.14 | 2.71±1.16 | 2.80±1.17 | 2.96±1.19 | 2.77±1.15 |
Table 2. Detailed characteristic descriptions.
| Characteristics | Malignancy | Margin | Texture | Calcification |
|---|---|---|---|---|
| Description | Likelihood of malignancy | If the nodule’s margin is clear | Internal texture of the nodule | Appearance of the calcification |
| Rating | 1. Highly unlikely | 1. Fuzzy margin | 1. Non-solid | 1. Popcorn |
| 2. Moderately unlikely | 2. – | 2. – | 2. Laminated | |
| 3. Indeterminate | 3. – | 3. Part solid | 3. Solid | |
| 4. Moderately suspicious | 4. Clear margin | 4. – | 4. Non-central | |
| 5. Highly suspicious | 5. Sharp margin | 5. Solid | 5. Central | |
| 6. Absent |
We choose 4 nodule characteristics for the classification tasks. There were malignancy, margin, texture, and calcification. Scores for these 4 characteristics were binarized by their score meaning. The threshold was set as 4 for malignancy, margin, and texture characteristics. Label 0 represents the benign, fuzzy margin, and non-solid/partially solid internal density. Calcification was annotated by a rating of 1–6, with 6 indicating the “no calcification” pattern (label 1); all other ratings exhibited calcification (label 0).
Figure 4.
Distribution of nodule diameters.
Some researchers have applied the generative adversarial network (GAN) to augment the pulmonary nodule dataset. CT surroundings and nodule segments were used to generate the synthetic nodule samples (36,37). However, for some synthetic nodules, it was difficult to develop an accurate label for their malignant risk, texture, and calcification characteristic. Moreover, the augmentation amount required for this task was relatively small. Therefore, each characteristic was augmented by rotation, flipping, and scaling operations. Data distribution in the augmented dataset is shown in Table 3.
Table 3. Range of ratings defined for the label of Lung Image Database Consortium and Image Database Resource Initiative nodules and its percentage in the augmented dataset.
| Characteristics | Malignancy | Margin | Texture | Calcification |
|---|---|---|---|---|
| Label 0 | Range 1–3 | Range 1–3 | Range 1–3 | Range 1–5 |
| Percentage | 3,589 (55.8%) | 2,876 (44.7%) | 2,375 (36.9%) | 3,095 (48.1%) |
| Description | Benign | Fuzzy margin | Non-solid or partially solid internal density | Appearance of calcification |
| Label 1 | Range 4–5 | Range 4–5 | Range 4–5 | Range 6 |
| Percentage | 2,844 (44.2%) | 3,557 (55.3%) | 4,058 (63.1%) | 3,338 (51.9%) |
| Description | Malignant | Clear margin | Solid internal density | No calcification |
Coarse stage segmentation
Our method was constructed in 2 stages. The localization stage was applied to locate the appearance slices of the nodule, and the refinement stage was applied to precisely segment the nodule’s edge and characteristics classification.
We used 5-fold cross-validation to improve the reliability of the results. The 5 folds shown in Table 1 were divided into 3 training sets, 1 validation set, and 1 test set for each training phase. Therefore, each model used for the experiment collects 5 sets of experimental results. Each 3D nodule cube was extracted with a pixel size of 64×64×64. We used 3 popular 3D segmentation networks—3D U-Net (38), V-Net (28), and 3D FCN (14), as baselines to perform a comparison of the network performance.
Table 4 shows the results for the localization segmentation stage of the pulmonary nodule. The implementations of 3D FCN and 3D U-Net were borrowed from the semantic segmentation methods code base (39). The V-Net is provided by the code base (40). The parameter sizes of 3D FCN, V-Net, 3D U-Net, and 3D MU-Net were 15.40, 19.40, 25.88, and 25.97 M (M =106), respectively. The MU-Net achieved a 0.46% higher Dice with a 0.1 M parameter size increase compared with that of the U-Net 3D model, which verified that the multiscale input structure was effective for segmentation of the network’s performance.
Table 4. Segmentation of 3D networks in the localization stage.
| Method | DSC (%) | OE (%) | |||||
|---|---|---|---|---|---|---|---|
| AVG ± STD | Minimum | Maximum | AVG ± STD | Minimum | Maximum | ||
| 3D FCN | 70.62±24.31 | 69.0 | 72.2 | 43.41±22.21 | 42.1 | 44.01 | |
| V-Net | 71.01±14.02 | 69.1 | 73.3 | 42.82±15.23 | 40.8 | 42.9 | |
| 3D U-Net | 72.80±14.62 | 70.1 | 74.1 | 41.02±15.65 | 39.9 | 43.1 | |
| 3D MU-Net | 73.26±14.11 | 72.6 | 74.4 | 40.20±15.41 | 39.7 | 41.2 | |
Maximum and minimum, maximal and minimal average performance during 5-fold cross-validation. AVG, average; STD, standard deviation; DSC, Dice similarity coefficient; OE, overlapping error; FCN, fully connected network; MU-Net, multiscale U-Net.
Refinement stage segmentation
For the refinement training procedure, each input of 2.5D data consisted of 4 continuous image slices for the pulmonary nodule. We compared our method to 5 other semantic segmentation networks as follows: U-Net (13), attention U-Net (15), R2U-Net (16), nested U-Net (41), and DeepLabV3 (42). We also conducted an ablation study to measure the performance of the 2.5D strategy and MSU-Net separately. For the 2.5D strategy, we compared 2.5D segmentation methods with their 2D structure. Networks with 2.5D separable convolution strategy were used to verify the significance of separable convolution in the encoding path of U-shape structures.
Table 5 shows the results of the refinement segmentation stage of the algorithm. The U-Net family networks—U-Net, attention U-Net, R2U-Net, and nested-U-Net—use different feature merge techniques, such as the attention mechanism and recurrent convolution strategy. The 2.5D convolution neural networks achieved a 2.26% higher Dice and 2.66% lower OE compared with those 2D networks on average. The 2.5D neural network achieved a significant improvement compared with its 2D version. 2.5D MSU-Net obtained the highest Dice and the lowest OE compared with those of other networks. The S-Network parameters were reduced by approximately 3 times compared with those of the 2.5D networks. As shown by the results in Table 5, the proposed network MSU-Net achieved the best performance.
Table 5. Segmentation of networks in the refinement stage.
| Method | Parameter size (106) | DSC (%) | OE (%) | |||||
|---|---|---|---|---|---|---|---|---|
| AVG ± STD | Minimum | Maximum | AVG ± STD | Minimum | Maximum | |||
| 2D U-Net | 34.52 | 78.40±14.41 | 77.2 | 79.1 | 33.01±16.51 | 31.1 | 34.2 | |
| 2D Attention U-Net | 34.87 | 78.61±16.97 | 77.3 | 80.5 | 32.92±18.12 | 32.2 | 34.3 | |
| 2D R2U-Net | 39.09 | 75.02±16.54 | 69.5 | 79.2 | 37.61±18.24 | 33.2 | 44.4 | |
| 2D Nested-U-Net | 36.62 | 78.85±15.99 | 78.2 | 79.6 | 32.55±18.02 | 32.2 | 33.5 | |
| 2D DeepLabV3 | 58.04 | 78.09±15.21 | 77.2 | 78.4 | 33.05±17.25 | 32.7 | 34.4 | |
| 2.5D U-Net | 39.32 | 81.24±14.92 | 81.2 | 82.2 | 29.62±15.72 | 28.5 | 31.7 | |
| 2.5D Attention U-Net | 35.06 | 81.80±16.43 | 80.6 | 83.3 | 28.68±17.06 | 28.4 | 30.3 | |
| 2.5D R2U-Net | 34.71 | 76.41±23.32 | 74.6 | 76.1 | 35.63±21.81 | 34.5 | 38.2 | |
| 2.5D Nested-U-Net | 36.96 | 81.03±12.85 | 81.0 | 82.5 | 29.23±15.01 | 28.3 | 31.4 | |
| 2.5D DeepLabV3 | 59.34 | 79.83±18.51 | 73.3 | 81.3 | 32.66±14.63 | 32.1 | 33.6 | |
| 2.5D S-U-Net | 13.39 | 80.81±14.62 | 80.5 | 83.2 | 30.22±16.15 | 29.3 | 32.6 | |
| 2.5D S-Attention U-Net | 13.48 | 80.61±15.57 | 79.4 | 82.5 | 30.04±16.41 | 29.3 | 32.5 | |
| 2.5D S-R2U-Net | 14.54 | 77.03±18.33 | 75.6 | 78.4 | 35.81±18.97 | 34.0 | 37.4 | |
| 2.5D S-Nested-U-Net | 9.25 | 81.24±13.26 | 81.4 | 82.7 | 30.25±15.07 | 28.4 | 32.8 | |
| 2.5D MSU-Net | 21.81 | 83.04±12.96 | 82.5 | 84.6 | 27.42±14.27 | 26.4 | 28.1 | |
S-Network denotes the separate convolution strategy applied to the network’s encoder. Maximum and minimum, maximal and minimal average performance during 5-fold cross-validation. AVG, average; STD, standard deviation; DSC, Dice similarity coefficient; OE, overlapping error; MSU-Net, multiscale separable U-Net.
To demonstrate that the performance of the proposed method was comparable to the results obtained by human experts, we implemented a consistency comparison between the method’s prediction and 4 radiologists’ hand labels. Table 6 shows that the DSC between each radiologist and proposed method was 82.9% on average, which was 0.39% higher than that of the inter-radiologist result. Moreover, the results also showed that the proposed method achieved a more stable performance than that of human experts.
Table 6. Mean DSC (%) of consistency comparison between the proposed method and 4 radiologists.
| Radiologists | R1 | R2 | R3 | R4 | AVG ± STD |
|---|---|---|---|---|---|
| R1 | – | 82.41 | 82.30 | 82.26 | – |
| R2 | 82.41 | – | 83.70 | 82.21 | – |
| R3 | 82.30 | 83.70 | – | 82.19 | 82.51±0.59 |
| R4 | 82.26 | 82.21 | 82.19 | – | – |
| Proposed | 82.49 | 83.49 | 82.70 | 82.93 | 82.90±0.43 |
R1–R4 represent the 4 radiologists. AVG, average; STD, standard deviation; DSC, Dice similarity coefficient.
Multitask classification
To assess the performance of the dual feature branch (encoding and decoding feature) concatenated in MSU-Net, we used the single-branch (encoding/decoding feature branch) networks as baseline models. The encoding/decoding feature coupled with a random forest classifier model served as the experimental comparison.
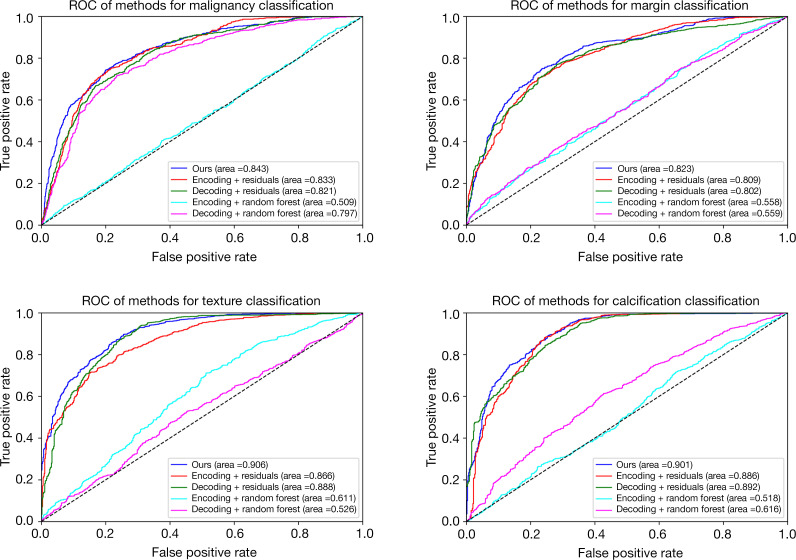
Table 7 shows the performance results of multitask prediction performance for each method. For the malignancy, margin, texture, and calcification characteristics, the MSU-Net achieved a mean accuracy of 77.8%, 75.6%, 85.2%, and 87.10%; mean sensitivity of 83.4%, 81.4%, 92.7%, and 92.4%; mean specificity of 76.2%, 81.4%, 78.2%, and 80%; and mean AUC of 84.3%, 83.2%, 90.6%, and 90.1%. The performance of MSU-Net was better than the baselines. Figure 5 shows the ROC curve and AUC for each task. The random forest model was set with 50 trees and 1,500 features, and the results indicated that the machine learning methods cannot predict multitask situations well. The AUCs suggested that the dual-feature branch concatenation in MSU-Net had better capability for feature extraction and multitask classification.
Table 7. Classification performance of different methods.
| Characteristics | Malignancy (%) | Margin (%) | Texture (%) | Calcification (%) |
|---|---|---|---|---|
| Methods | Acc/Sens/Spec | Acc/Sens/Spec | Acc/Sens/Spec | Acc/Sens/Spec |
| Encoding + RF | 50.3/51.6/46.6 | 52.7/49.2/57.2 | 58.5/71.5/31.0 | 68.7/88.6/22.4 |
| Decoding + RF | 75.2/66.3/79.0 | 53.2/52.9/53.6 | 63.4/70.5/49.0 | 65.4/51.1/70.0 |
| Decoding + residuals | 73.1/70.6/78.2 | 74.6/78.2/69.9 | 83.2/92.0/70.0 | 84.0/87.2/65.0 |
| Encoding + residuals | 75.6/71.8/80.0 | 73.4/79.7/65.4 | 80.0/89.4/64.8 | 86.9/93.4/69.0 |
| Proposed | 77.8/83.4/76.2 | 75.6/81.4/75.0 | 85.2/92.7/78.2 | 87.1/92.4/80.0 |
Encoding + RF/decoding + RF represent the encoding/decoding feature coupled with a random forest; Decoding + residuals/encoding + residuals represent the single branch (encoding/decoding) network; Acc, Sens, and Spec represent the accuracy, sensitivity, and specificity of each network.
Figure 5.
ROC curve of classification results for malignancy, margin, texture, and calcification of each method. Area represents the area under the ROC of each model. ROC, receiver-operating characteristic.
Discussion
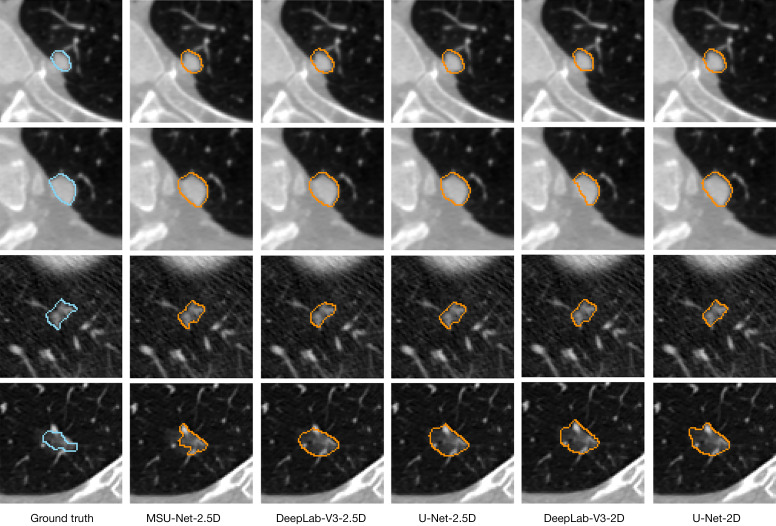
A visual comparison of the segmentation results using different methods is shown in Figure 6. From top to bottom, a small juxta-pleural nodule (diameter <6 mm), large juxta-pleural nodule, small and isolated nodule, and GGO are shown. All networks work well for the juxta-pleural nodules. For the small and isolated nodule, these networks also performed well, while for the DeepLabV3-2.5D network, these were slightly inferior to those of other networks. The prediction result of MSU-Net was closest to the ground truth, as it possessed the most detailed contour information. For GGO, the predictions for all networks included a partition of the surrounding material.
Figure 6.
Visual comparison of the prediction edges of different networks. Blue and orange lines depict the ground truth and predicted contours, respectively. MSU-Net, multiscale separable U-Net.
Table 8 shows the performance of several different methods. Tachibana et al. applied a distance-transformation method and watershed method to segment nodules automatically (43). Wang et al. adopted the dynamic programming and a multidirectional fusion strategy for constructing the algorithm (44). These 2 traditional methods did not work well for juxta-pleural nodules and small nodules. Wang et al. and Cao et al. each used a dual branch structure for segmentation (46,48); Messay et al. used a semi-automated system to improve segmentation performance (45); Singadkar et al. introduced the deconvolution residual blocks into 2D U-Net (49); and Pezzano et al. proposed the CoLe-CNN, which was focused on the nodule images’ context learning and loss calculation (50). These 6 networks are all a 1-stage structure. The general segmentation framework nnU-Net (51) is a 2-stage structure with 2 cascaded 3D U-Net segment nodule edges from a large to small scale. According to Table 8, the deconvolution residual network achieved better results than the proposed method. However, based on a larger dataset, the proposed method exhibited good segmentation performance. The localization step can limit the target nodule to a series of slices. The 2.5D MSU-Net can perform finer edge segmentation in a smaller range.
Table 8. Performance of various pulmonary nodule segmentation methods in the Lung Image Database Consortium and Image Database Resource Initiative dataset.
| Method | Year | Nodules (n) | DSC (%), AVG ± STD | OE (%), AVG ± STD | ||
|---|---|---|---|---|---|---|
| Training | Testing | |||||
| Tachibana et al. (43) | 2006 | – | 23 | – | 49.30±22.90 | |
| Wang et al. (44) | 2009 | 23 | 64 | – | 42.00 | |
| Messay et al. (45) | 2015 | 300 | 66 | – | 28.30±20.00 | |
| Wang et al. (46) | 2017 | 350 | 493 | 82.15±10.76 | 28.84±12.22 | |
| Zhao et al. (47) | 2019 | – | – | – | 37.20±06.50 | |
| Cao et al. (48) | 2020 | 387 | 544 | 82.74±10.19 | – | |
| Singadkar et al. (49) | 2020 | 272 | 89 | 94.68±12.00 | 11.63±12.00 | |
| Pezzano et al. (50) | 2021 | – | – | 82.50 | 27.40 | |
| Isensee et al. (20) | 2021 | 794 | 354 | 79.28±12.12 | 29.92±10.64 | |
| Proposed | 2021 | 781 | 390 | 83.04±12.96 | 27.42±14.27 | |
AVG, average; STD, standard deviation; DSC, Dice similarity coefficient; OE, overlapping error.
We also performed segmentation tests on each type of nodule. As shown in Table 9, the nodules with fuzzy edges or non-solid internal structure achieved relatively poor segmentation results, and the nodules with calcification or clear edges are better segmented. The experiment results show that the proposed method achieves 81.1% or more DSC and 31.4% or less OE performance on all kinds of nodules.
Table 9. Segmentation results of nodules with different characteristics.
| Characteristics | Category [n] | DSC (%) | OE (%) |
|---|---|---|---|
| Margin | Fuzzy margin [174] | 81.32±16.12 | 30.57±15.37 |
| Clear margin [216] | 83.67±10.12 | 24.88±12.51 | |
| Texture | Non-solid or partially solid [143] | 81.89±14.39 | 30.12±16.21 |
| Solid [247] | 83.71±11.54 | 25.86±12.38 | |
| Calcification | Appearance of calcification [187] | 85.14±11.65 | 23.15±14.59 |
| No calcification [203] | 81.10±15.18 | 31.35±14.07 | |
| Malignancy | Benign [173] | 82.95±13.56 | 26.91±14.28 |
| Malignant [217] | 83.11±12.49 | 27.82±14.33 |
DSC, Dice similarity coefficient; n, number of nodules for each label; OE, overlapping error.
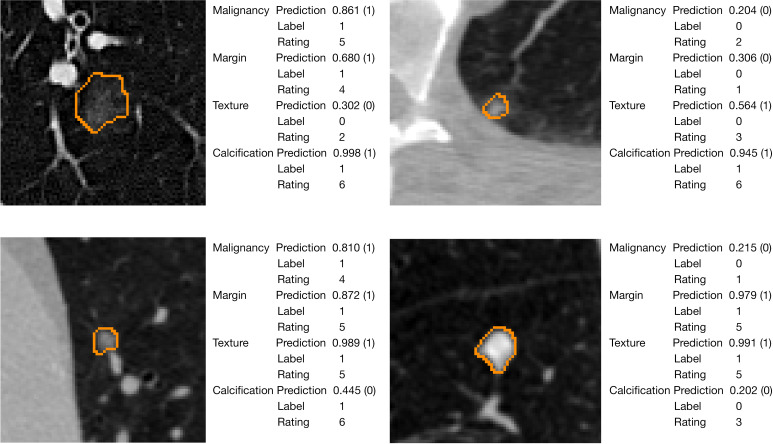
Pulmonary nodule segmentation and malignancy classification achieved significant improvement in clinical applications. The precise segmentation of the nodule boundary aids the network to accurately predict its shape characteristics and malignant risk. The segmentation and classification outputs of MSU-Net are shown in Figure 7. The classification predictions were given in a probability format, and the threshold in the present study was set to 0.5 to balance the sensitivity and specificity. The probability of malignancy indicates the likelihood that a nodule is benign or malignant. Moreover, when the threshold was set to 0.65, the prediction precision () reached 94.7%; for those nodules with prediction probability below 0.35, the benign-precision () reached 94.1%. Based on this probability, we can preliminarily determine the nodules as benign or malignant.
Figure 7.
Segmentation output and classification output of the MSU-Net (0.5 threshold). Orange lines depict the predicted contours. MSU-Net, multiscale separable U-Net.
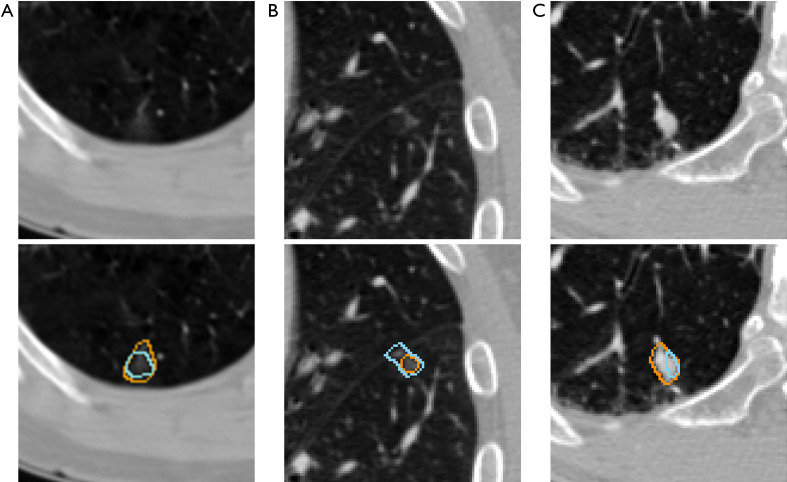
There are some limitations to the present study. Figure 8 shows the nodules with large deviations between prediction and ground truth, Figure 8A,8B are pure ground glass nodules; and Figure 8C is a juxta-vascular. Due to the indistinguishable edge, the present study has limitations in the segmentation of these 2 kinds of nodules. For the multitask classification, because of the small number for certain characteristics in the dataset, we had to augment the dataset for each characteristic, which may lead to model overfitting. Moreover, due to the limitation of the LIDC-IDRI dataset, we were unable to obtain more important characteristics of the nodules.
Figure 8.
Nodules with large deviation between prediction and ground truth. (A,B) Performance of the proposed method on pure ground glass nodules. (C) Prediction result on juxta-vascular. Blue and orange lines depict the ground truth and predicted contours, respectively.
Several improvements can be investigated in further research. First, the deconvolutional residual blocks could replace the rescale operation in the decoder of MSU-Net (48); the 2.5D strategy could extract more inter-layer information through spatial transformation, such as squeeze-and-excitation operation (17). These strategies could be used to potentially improve the segmentation performance. Second, for malignant risk prediction, the model could be finetuned by expert labels by weighting more significant features in difficulty cases. Finally, more clinical data with accurate edge and characteristic labels should be collected to improve the generalization performance of the method.
This coarse-to-fine algorithm operates within an end-to-end framework. The nodule’s contour and characteristics can be predicted simultaneously. These predictions may help doctors achieve a clear understanding of the nodule’s morphological characteristics and quantitative information. Doctors can refer to the probability of malignancy given by the network to form a preliminary judgment of the nodule.
Conclusions
In the present study, we proposed a coarse-to-fine framework for pulmonary nodule segmentation and classification. This framework was composed of a 3D MU-Net as the localization network and a multitask 2.5D MSU-Net as the refinement network. The novel 2.5D network was used to extract hierarchical features from the 3D CT. Moreover, features from the encoding and decoding paths of MSU-Net could be used to improve nodule classification accuracy by widening the feature space. Our method achieved state-of-the-art results in the LIDC-IDRI dataset for both nodule segmentation and classification. Therefore, this method can help radiologists obtain a more accurate nodule contour with quantitative nodule analysis and malignancy risk prediction.
Acknowledgments
Funding: This work was supported in part by the Ministry of Science and Technology of China (No. 2019YFC0118800).
Ethical Statement: The authors are accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved. This article does not contain any studies with human participants or animals performed by any of the authors. No ethical approval and written informed consent are required.
Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.
Footnotes
Conflicts of Interest: All authors have completed the ICMJE uniform disclosure form (available at https://dx.doi.org/10.21037/qims-21-19). The authors have no conflicts of interest to declare.
References
- 1.Siegel RL, Miller KD, Jemal A. Cancer statistics, 2020. CA Cancer J Clin 2020;70:7-30. 10.3322/caac.21590 [DOI] [PubMed] [Google Scholar]
- 2.Fitzmaurice C, Allen C, Barber RM, Barregard L, Bhutta ZA, et al. Global, Regional, and National Cancer Incidence, Mortality, Years of Life Lost, Years Lived With Disability, and Disability-Adjusted Life-years for 32 Cancer Groups, 1990 to 2015: A Systematic Analysis for the Global Burden of Disease Study. JAMA Oncol 2017;3:524-48. 10.1001/jamaoncol.2016.5688 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Barta JA, Powell CA, Wisnivesky JP. Global Epidemiology of Lung Cancer. Ann Glob Health 2019;85:8. 10.5334/aogh.2419 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Al Mohammad B, Brennan PC, Mello-Thoms C. A review of lung cancer screening and the role of computer-aided detection. Clin Radiol 2017;72:433-42. 10.1016/j.crad.2017.01.002 [DOI] [PubMed] [Google Scholar]
- 5.Kubota T, Jerebko AK, Dewan M, Salganicoff M, Krishnan A. Segmentation of pulmonary nodules of various densities with morphological approaches and convexity models. Med Image Anal 2011;15:133-54. 10.1016/j.media.2010.08.005 [DOI] [PubMed] [Google Scholar]
- 6.Kim H, Park CM, Goo JM, Wildberger JE, Kauczor HU. Quantitative Computed Tomography Imaging Biomarkers in the Diagnosis and Management of Lung Cancer. Invest Radiol 2015;50:571-83. 10.1097/RLI.0000000000000152 [DOI] [PubMed] [Google Scholar]
- 7.Dehmeshki J, Amin H, Valdivieso M, Ye X. Segmentation of pulmonary nodules in thoracic CT scans: a region growing approach. IEEE Trans Med Imaging 2008;27:467-80. 10.1109/TMI.2007.907555 [DOI] [PubMed] [Google Scholar]
- 8.Ren H, Zhou L, Liu G, Peng X, Shi W, Xu H, Shan F, Liu L. An unsupervised semi-automated pulmonary nodule segmentation method based on enhanced region growing. Quant Imaging Med Surg 2020;10:233-42. 10.21037/qims.2019.12.02 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Farag AA, El Munim HE, Graham JH, Farag AA. A novel approach for lung nodules segmentation in chest CT using level sets. IEEE Trans Image Process 2013;22:5202-13. 10.1109/TIP.2013.2282899 [DOI] [PubMed] [Google Scholar]
- 10.Ye X, Beddoe G, Slabaugh G. Automatic Graph Cut Segmentation of Lesions in CT Using Mean Shift Superpixels. Int J Biomed Imaging 2010;2010:983963. 10.1155/2010/983963 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Cao W, Wu R, Cao G, He Z. A comprehensive review of computer-aided diagnosis of pulmonary nodules based on computed tomography scans. IEEE Access 2020;8:154007-23.
- 12.Thakur SK, Singh DP, Choudhary J. Lung cancer identification: a review on detection and classification. Cancer Metastasis Rev 2020;39:989-98. 10.1007/s10555-020-09901-x [DOI] [PubMed] [Google Scholar]
- 13.Ronneberger O, Fischer P, Brox T. U-net: Convolutional networks for biomedical image segmentation. MICCAI 2015: International Conference on Medical image computing and computer-assisted intervention; 5-9 Oct 2015; Munich, Germany. Springer, 2015:234-41. [Google Scholar]
- 14.Long J, Shelhamer E, Darrell T. Fully convolutional networks for semantic segmentation. 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR); 8-10 Jun 2015; Boston, USA. IEEE, 2015:3431-40. [DOI] [PubMed] [Google Scholar]
- 15.Schlemper J, Oktay O, Schaap M, Heinrich M, Kainz B, Glocker B, Rueckert D. Attention gated networks: Learning to leverage salient regions in medical images. Med Image Anal 2019;53:197-207. 10.1016/j.media.2019.01.012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Alom MZ, Yakopcic C, Hasan M, Taha TM, Asari VK. Recurrent residual U-Net for medical image segmentation. J Med Imaging (Bellingham) 2019;6:014006. 10.1117/1.JMI.6.1.014006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Rundo L, Han C, Nagano Y, Zhang J, Hataya R, Militello C, Tangherloni A, Nobile MS, Ferretti C, Besozzi D, Gilardi MC, Vitabile S, Mauri G, Nakayama H, Cazzaniga P. USE-Net: Incorporating Squeeze-and-Excitation blocks into U-Net for prostate zonal segmentation of multi-institutional MRI datasets. Neurocomputing 2019;365:31-43. 10.1016/j.neucom.2019.07.006 [DOI] [Google Scholar]
- 18.Liu L, Cheng J, Quan Q, Wu FX, Wang YP, Wang J. A survey on U-shaped networks in medical image segmentations. Neurocomputing 2020;409:244-58. 10.1016/j.neucom.2020.05.070 [DOI] [Google Scholar]
- 19.He K, Zhang X, Ren S, Sun J. Deep residual learning for image recognition. 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR); 27-30 June 2016; Las Vegas, NV, USA. IEEE, 2016:770-8. [Google Scholar]
- 20.Isensee F, Jaeger PF, Kohl SAA, Petersen J, Maier-Hein KH. nnU-Net: a self-configuring method for deep learning-based biomedical image segmentation. Nat Methods 2021;18:203-11. 10.1038/s41592-020-01008-z [DOI] [PubMed] [Google Scholar]
- 21.Zhao N, Tong N, Ruan D, Sheng K. Fully automated pancreas segmentation with two-stage 3D convolutional neural networks. MICCAI 2019: International Conference on Medical Image Computing and Computer-Assisted Intervention; 2019 Oct 13-17; Shenzhen, China. Springer; 2019:201-9. [Google Scholar]
- 22.Wang S, Zhou M, Gevaert O, Tang Z, Dong D, Liu Z, Jie T. A multi-view deep convolutional neural networks for lung nodule segmentation. EMBC 2017: 39th Annual International Conference of the IEEE Engineering in Medicine and Biology Society; 11-15 Jul 2017; Jeju Island, Korea. IEEE, 2017:1752-5. [DOI] [PubMed] [Google Scholar]
- 23.Sun L, Jiang Z, Chang Y, Ren L. Building a patient-specific model using transfer learning for four-dimensional cone beam computed tomography augmentation. Quant Imaging Med Surg 2021;11:540-55. 10.21037/qims-20-655 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Zhao H, Shi J, Qi X, Wang X, Jia J. Pyramid scene parsing network. 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR); 21-26 July 2017; Honolulu, HI, USA. IEEE, 2017:2881-90. [Google Scholar]
- 25.Kang G, Liu K, Hou B, Zhang N. 3D multi-view convolutional neural networks for lung nodule classification. PLoS One 2017;12:e0188290. 10.1371/journal.pone.0188290 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Zheng H, Qian L, Qin Y, Gu Y, Yang J. Improving the slice interaction of 2.5D CNN for automatic pancreas segmentation. Med Phys 2020;47:5543-54. 10.1002/mp.14303 [DOI] [PubMed] [Google Scholar]
- 27.Hu J, Shen L, Sun G. Squeeze-and-excitation networks. CPVR 2018: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition; 19-21 Jun 2018; Salt Lake City, UT, USA. IEEE, 2018:7132-41. [Google Scholar]
- 28.Milletari F, Navab N, Ahmadi SA. V-net: Fully convolutional neural networks for volumetric medical image segmentation. 2016 Fourth International Conference on 3D Vision (3DV); 25-28 Oct 2016; Stanford, CA, USA. California: IEEE, 2016:565-71. [Google Scholar]
- 29.Lin TY, Goyal P, Girshick R, He K, Dollár P. Focal loss for dense object detection. 2017 IEEE International Conference on Computer Vision (ICCV); 22-29 Oct 2017; Venice, Italy. IEEE, 2017:2980-8. [Google Scholar]
- 30.Xie Z, Ling T, Yang Y, Shu R, Liu BJ. Optic Disc and Cup Image Segmentation Utilizing Contour-Based Transformation and Sequence Labeling Networks. J Med Syst 2020;44:96. 10.1007/s10916-020-01561-2 [DOI] [PubMed] [Google Scholar]
- 31.wiki.cancerimagingarchive.net [Internet]. LIDC-IDRI - The Cancer Imaging Archive (TCIA) Public Access - Cancer Imaging Archive Wiki; c2021 [cited 2021 May]. Available online: https://wiki.cancerimagingarchive.net/display/Public/LIDC-IDRI
- 32.Armato SG, 3rd, McLennan G, Bidaut L, McNitt-Gray MF, Meyer CR, Reeves AP, et al. The Lung Image Database Consortium (LIDC) and Image Database Resource Initiative (IDRI): a completed reference database of lung nodules on CT scans. Med Phys 2011;38:915-31. 10.1118/1.3528204 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.McNitt-Gray MF, Armato SG, 3rd, Meyer CR, Reeves AP, McLennan G, Pais RC, et al. The Lung Image Database Consortium (LIDC) data collection process for nodule detection and annotation. Acad Radiol 2007;14:1464-74. 10.1016/j.acra.2007.07.021 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Kohavi R, editor. A study of cross-validation and bootstrap for accuracy estimation and model selection. IJCAI 1995: International Joint Conferences on Artificial Intelligence Organization; 20-25 Aug 1995; Montreal, Canada. Morgan Kaufmann Publishers Inc., 1995:1137-45. [Google Scholar]
- 35.Zong B, Song Q, Min MR, Cheng W, Lumezanu C, Cho D, Chen H. Deep autoencoding gaussian mixture model for unsupervised anomaly detection. ICLR 2018: International Conference on Learning Representations; 2018 Apr 30-May 3; Canada. Vancouver, 2018. [Google Scholar]
- 36.O'Briain TB, Yi KM, Bazalova-Carter M. Technical Note: Synthesizing of lung tumors in computed tomography images. Med Phys 2020;47:5070-6. 10.1002/mp.14437 [DOI] [PubMed] [Google Scholar]
- 37.Han C, Kitamura Y, Kudo A, Ichinose A, Rundo L, Furukawa Y, Umemoto K, Li Y, Nakayama H. Synthesizing diverse lung nodules wherever massively: 3D multi-conditional GAN-based CT image augmentation for object detection. 3DV 2019: International Conference on 3D Vision; 16-19 Sep 2019; Canada. Quebec City: IEEE; 2019:729-37. [Google Scholar]
- 38.Çiçek Ö, Abdulkadir A, Lienkamp SS, Brox T, Ronneberger O. 3D U-Net: learning dense volumetric segmentation from sparse annotation. MICCAI 2016: International Conference on Medical Image Computing and Computer-Assisted Intervention; 17-21 Oct 2016; Greece. Athens: Springer; 2016:424-32. [Google Scholar]
- 39.github.com [Internet]. zijundeng/pytorch-semantic-segmentation: PyTorch for Semantic Segmentation; c2017 [cited 2017 Nov 19]. Available online: https://github.com/zijundeng/pytorch-semantic-segmentation
- 40.github.com [Internet]. mattmacy/vnet.pytorch: A PyTorch implementation for V-Net: Fully Convolutional Neural Networks for Volumetric Medical Image Segmentation; c2017 [cited 2017 Mar 25]. Available online: https://github.com/mattmacy/vnet.pytorch
- 41.Zhou Z, Siddiquee MMR, Tajbakhsh N, Liang J. UNet++: A Nested U-Net Architecture for Medical Image Segmentation. Deep Learn Med Image Anal Multimodal Learn Clin Decis Support (2018) 2018;11045:3-11. 10.1007/978-3-030-00889-5_1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Chen LC, Papandreou G, Kokkinos I, Murphy K, Yuille AL. DeepLab: Semantic Image Segmentation with Deep Convolutional Nets, Atrous Convolution, and Fully Connected CRFs. IEEE Trans Pattern Anal Mach Intell 2018;40:834-48. 10.1109/TPAMI.2017.2699184 [DOI] [PubMed] [Google Scholar]
- 43.Tachibana R, Kido S. Automatic segmentation of pulmonary nodules on CT images by use of NCI lung image database consortium. Medical Imaging 2006: Image Processing; 11-16 Feb 2006; USA. San Diego: International Society for Optics and Photonics, 2006. [Google Scholar]
- 44.Wang Q, Song E, Jin R, Han P, Wang X, Zhou Y, Zeng J. Segmentation of lung nodules in computed tomography images using dynamic programming and multidirection fusion techniques. Acad Radiol 2009;16:678-88. 10.1016/j.acra.2008.12.019 [DOI] [PubMed] [Google Scholar]
- 45.Messay T, Hardie RC, Tuinstra TR. Segmentation of pulmonary nodules in computed tomography using a regression neural network approach and its application to the Lung Image Database Consortium and Image Database Resource Initiative dataset. Med Image Anal 2015;22:48-62. 10.1016/j.media.2015.02.002 [DOI] [PubMed] [Google Scholar]
- 46.Wang S, Zhou M, Liu Z, Liu Z, Gu D, Zang Y, Dong D, Gevaert O, Tian J. Central focused convolutional neural networks: Developing a data-driven model for lung nodule segmentation. Med Image Anal 2017;40:172-83. 10.1016/j.media.2017.06.014 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Zhao X, Sun W, Qian W, Qi S, Sun J, Zhang B, Yang Z. Fine-grained lung nodule segmentation with pyramid deconvolutional neural network. Medical Imaging 2019: Computer-Aided Diagnosis; 16-21 Feb 2019; USA. San Diego: International Society for Optics and Photonics, 2019. [Google Scholar]
- 48.Cao H, Liu H, Song E, Hung CC, Ma G, Xu X, Jin R, Lu J. Dual-branch residual network for lung nodule segmentation. Applied Soft Computing 2020;86:105934. 10.1016/j.asoc.2019.105934 [DOI] [Google Scholar]
- 49.Singadkar G, Mahajan A, Thakur M, Talbar S. Deep Deconvolutional Residual Network Based Automatic Lung Nodule Segmentation. J Digit Imaging 2020;33:678-84. 10.1007/s10278-019-00301-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Pezzano G, Ribas Ripoll V, Radeva P. CoLe-CNN: Context-learning convolutional neural network with adaptive loss function for lung nodule segmentation. Comput Methods Programs Biomed 2021;198:105792. 10.1016/j.cmpb.2020.105792 [DOI] [PubMed] [Google Scholar]
- 51.github.com [Internet]. MIC-DKFZ/nnUNet. Available online: https://github.com/MIC-DKFZ/nnUNet