Primer: Cell-Size Control

Abstract

A fundamental and still mysterious question in cell biology is “How do cells know how big they are?”. The fact that they do is evident from the tight size homeostasis that populations of cells maintain, and has been verified by a variety of creative experiments over the past 100 years. An increasingly sophisticated understanding of cell-cycle-control mechanisms, and increasingly sophisticated cell imaging and analysis tools, have allowed recent progress in proposing and testing models of cell-size control. Nonetheless, biochemical understanding of how proposed cell-size mechanisms might work is only beginning to be developed. This primer introduces the field of cell-size control and discusses some of the big questions yet to be answered.

The Question of Cell-Size Control

Size is a biological variable that affects life on every scale, from organelles to ecosystems. One key scale is the size of cells. Cell size is remarkable both for its interspecies variability—ranging over 14 orders of magnitude, from 0.1 femtoliter ultramicrobacteria to 10 milliliter amoeba—and its intraspecies homogeneity—with populations of cells regularly exhibiting as little as 10% variance in size at division. Moreover, many factors can cause variation in cell size—from to external nutritional conditions to internal cell-cycle delays—requiring some sort of control system to counteract these drivers of cell-size heterogeneity. Therefore, how cells maintain size homeostasis over such a wide range of potential sizes has long fascinated biologists.

In framing the question of cell size, a few issues need to be addressed. The first is the definition of size itself. Generally, total cell mass is used as the primary definition of cell size and we will use that definition here. However, cells can vary independently in volume, length, surface area and protein content. Correlations between these parameters and other relevant parameters, such as density, growth rate and genome content, complicate the definition of cell size. Furthermore, it is unclear which of these parameters, if any, are actually measured by cells to facilitate cell-size regulation.

A second issue is the cellular life-history context in which cell size is considered. Size homeostasis in a vertebrate neuron that will not divide for 100 years is a much different problem than size homeostasis in a yeast cell that will divide every 100 minutes. We will leave to others the question of size homeostasis in terminally differentiated cells and other quiescent cells, and focus here on populations of growing and dividing cells. In such populations, cell size is controlled by a balance between growth and division, and the size of a newborn cell is determined by the size at which its parental cell divided.

Finally, it is important to consider the difference between the questions of how cells determine what size they should be and how they maintain homeostasis at that target size. The former question—How cell decide how big they should be—is influenced by nutritional status in single-cellular organisms and cellular differentiation in multi-cellular organisms and, in eukaryotes, involves the TOR signalling pathway. However, disruption of the mechanisms that determine the target size do not disrupt the ability of cells to maintain size homeostasis. Cells that have their target size perturbed may divide at the ‘wrong’ size, but they maintain that wrong size with a robustness comparable to normal cells. The latter question—How cells maintain size homeostasis—is the focus of this primer.

An important distinction between the cell-size control systems that determine a cell’s target size and the cell-size control systems that maintain that target size is that the target-size determination is not generally essential for cell viability, but target-size homeostasis generally is. Many mutations have been identified that cause cells to be bigger or smaller than their wild-type target size, without obvious fitness effects. The systems for maintaining size homeostasis, on the other hand, are expected to be essential. A cell that has no size homeostasis mechanism will either never divide or will divide repeatedly without sufficient growth, either of which is fatal. For this reason, mutations that perturb the distribution of cell sizes in a population usually affect the mechanisms that determine target size and rarely disturb the mechanisms that maintain size homeostasis.

The History of Cell-Size Control

A century’s worth of cell biology has produced a wealth of information on cell size and informs models of cell-size control. One well-established conclusion is that cell size is proportional to genome content. This correlation is seen clearly in ploidy series. In organisms across the eukaryotic domain, diploid cells are twice as big as haploids, tetraploid are twice as big as diploids, etc. (Figure 1A). Likewise, among bacteria, cell size scales linearly with chromosome number. From a more experimental angle, removing nuclei microsurgically from multinucleate amoeba or slime mold causes a concomitant reduction in cytoplasm size. These and other experiments have led to the conclusion that cells do not maintain size directly, but rather maintain a target nuclear-to-cytoplasmic (N:C) ratio.

Figure 1. Historical Evidence for Cell Size Control.

A) Drawings of the pronephric ducts from a salamander ploidy series, demonstrating that cell size scales roughly linearly with genome content. The cells form a circular epithelium around the lumen of the ducts. The shapes inside the cells are the nuclei, indicating cell number. Note that the size of the nuclei also scales with ploidy. Modified from Fankhauser (1945) J Exp Zool 100:445. Reproduced with permission.

B) The negative correlation between cell size at birth (labeled ‘millimicrograms reduced weight’) and length of the subsequent cell cycle in amoeba. Modified from Prescott (1956) Exp Cell Res 11(1):86. Reproduced with permission.

C) An interpretation of the phenomenon of excess mitotic delay. In unperturbed cells, an unstable accumulating mitotic activator increases in concentration with cell size until it reaches a threshold at which it can induce mitosis. A pulse of cycloheximide, a protein synthesis inhibitor, causes the concentration of the activator to rapidly decrease. When the cycloheximide is washed out, the activator can asymptotically return to its normal concentration. A pulse early in the cell cycle affords ample time to resynthesize the activator, minimizing the mitotic delay. However, as the pulse approaches mitosis, the delay increases.

Another common observation is that many cell types exhibit a negative correlation between size at birth and the amount of growth in the subsequent cell cycle (Figure 1B). This observation suggests that cells born small must grow more to reach their target cell size than cells born at the average size, whereas cells born large must grow less. Although this observation is not as universal as the constant N:C ratio, it has led to the conclusion that, at least in many cells, size is controlled by a checkpoint that prevents passage through the cell cycle until cells have reached a critical size. In various organisms, size checkpoints have been proposed to regulate the G1/S transition, the G2/M transition, or both.

Cells that are experimentally delayed from dividing, but allowed to continue growing, will divide at larger sizes than untreated cells. Consistent with the size-checkpoint hypothesis, the abnormally large progeny of such cells have shorter subsequent cell cycles, as they return to size homeostasis. However, as discussed below, the exact kinetics of the return to homeostasis can vary and not all observations support the size-checkpoint hypothesis.

A classic experiment that supports the size-checkpoint hypothesis was performed on amoeba in the 1920s by Max Hartmann and repeated in the 1950s by David Prescott. To investigate how cell size regulates cell division, they removed a portion of an amoeba’s cytoplasm by microdissection and found that the now-smaller cell delayed division until it grew to the size of division of untreated cells. This procedure can be repeated, delaying division for many cell-cycle equivalents. In a heroic experimental feat, Hartmann keep one poor amoeba from dividing for the equivalent of 65 cell cycles, dissecting it every day for four months. At the end of the experiment, the cell grew to its normal division size and divided normally.

In bacteria, experimental observation and mathematical modeling led to the conclusion that, under a wide range of growth rates, bacteria initiate DNA replication at a constant cell size, thus maintaining a balance between cell size and genome number. Although these results were initially taken to support a bacterial size-checkpoint, they are, as we will see below, also consistent with other size control strategies.

Given the lack of any biochemical understanding of cell cycle mechanics, it is not surprising that early cell size models were lacking mechanistic detail; in fact is amazing that they are as insightful as they are. In particular, early workers were able to infer, in some systems, the existence of a ‘division protein’, which was imagined as a protein required for division and proposed to be expressed in a size-dependent manner, such that only when cells achieve a threshold size is division possible. Initially, the division protein was envisioned as a subunit of some sort of structure required for division for which a critical number of subunits would be required before division would be possible. As we will see, this concept is impressively close to current thinking about bacterial size control.

One variant of the division-protein hypothesis—the unstable accumulating activator—is motivated by the phenomenon of excess mitotic delay, an observation made in a number of eukaryotes. The observation is that a brief interphase exposure to proteotoxic stress, such heat or cycloheximide, causes a brief delay in mitosis, but that the closer to mitosis the exposure occurs, the longer the delay lasts (Figure 1C). The interpretation is that an unstable division protein accumulates in a size-dependent manner until it reaches a concentration that triggers division. During the proteotoxic treatment, the division protein rapidly decays, along with all other unstable proteins, and has to be resynthesized before the cell can divide. If the treatment is early in the cell cycle, there is ample time for the protein to be resynthesized, resulting in minimal mitotic delay. However, as the treatment is moved closer to mitosis, there is less time for the division protein to be resynthesized, leading to an increasingly long mitotic delay.

The Theory of Cell-Size Control

The rich history of cell size observation and experimentation has been paralleled by an equally rich history of theoretical approaches to the problem. Three fundamental classes of theoretical size control strategies have been succinctly referred to as sizers, adders and timers. Although all three classes of models could regulate any particular cell cycle transition, we will use regulation of cell division as the default example here.

Sizer models posit that a size checkpoint must be satisfied before a cell can divide. Sizers lead to a constant size (± biological noise) at division, independent of the cell size at birth. This situation produces a negative correlation between size at birth and amount of growth during the subsequent cell cycle, because cells born large will grow less than cells born small before satisfying the checkpoint and dividing (Figure 2A). As discussed above, there is substantial evidence for sizers in eukaryotes, particularly in the form of this negative correlation. Sizers lead to the correction of size heterogeneity within one cell cycle (Figure 2B). The exception to this rule is if a cell is so big that even after dividing, it is still bigger than its target size. In such a case, the cell will divide as soon as it can, creating a timer mechanism (see below) in which the timer is the minimum time in which a cell can accomplish all of its essential cell-cycle functions, in particular DNA replication and mitosis. Sizers, in a fundamental sense, allow cells to know how big they are, or at least to know if they are bigger or smaller than their target size.

Figure 2. Size-Control Strategies.

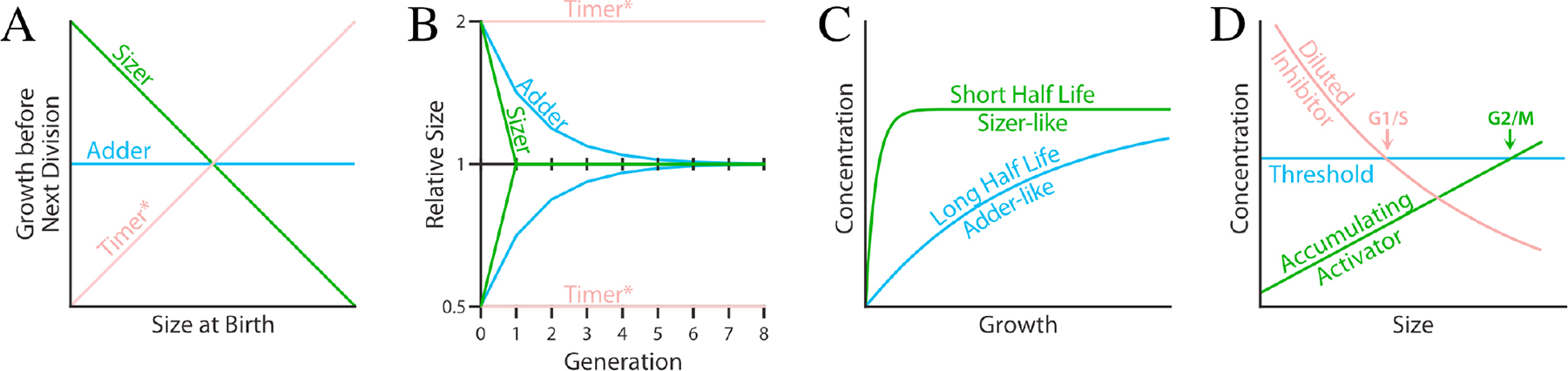
A) Three classes of size-control strategies—Sizers, Adders and Timers—are distinguished by the correlation they exhibit between size at birth and the amount of growth in the subsequent cell cycle. Sizers show a negative correlation because cells born large need less growth to reach their target size than cells born small. Adders show no correlation because they grow the same amount each cell cycle, regardless of their size at birth. Timers show a positive correlation because (in cells that grow exponentially) larger cells grow faster than smaller cells, thus growing more in the same amount of time. The asterisk indicates that the positive correlation for Timers is only expected if cells grow exponentially; if they grow linearly, no correlation is expected, and the Timer is equivalent to an Adder.

B) The three classes also differ in the kinetics of their return to size homeostasis. Sizers return to their target size in the next generation, unless they are more that two-fold too big, in which case they require multiple divisions to return to their target size. Adders return to their target size more slowly, reducing the difference between their actual size and their target size by half each generation. Timers do not enforce size homeostasis. Instead, cells divide at the size their parent divided, plus or minus any noise in the system. The asterisk indicates that this lack of homeostasis for Timers is only expected if cells grow exponentially; if they grow linearly, the Timer is equivalent to an Adder.

C) Division-protein half life can specify Adder or Sizer mechanisms. At its steady-state concentration, a protein’s synthesis is balanced by its degradation. The time it takes to reach that steady state is proportional to its half life. Shown are two proteins with the same steady-sate level, but different half lives. If a division protein has a long half life, reaching steady state takes a long time and during that time the number of protein molecules is proportional to the amount of growth that has occurred, regardless of size. Such division-protein expression kinetics create an adder mechanism. If the division protein instead has a short half life, it comes quickly to a steady-state concentration, independent of the amount of growth. In this case, the number of molecules is proportional to cell size, as required for a sizer mechanism.

D) One class of mechanisms for Sizers is size-dependent expression of a sizer protein. Two potential sizer-protein mechanisms are the Diluted Inhibitor and the Accumulating Activator. In a diluted-inhibitor model, a constant amount of the inhibitor is produced at the beginning of the cell cycle, regardless of cell size. As the cell grows, the concentration of the inhibitor is diluted until a threshold is reached and the cell cycle can proceed. Because all cells start with the same amount of the inhibitor, they all reach the threshold at the same size. In an accumulating-activator model, the activator is expressed at a size-dependent concentration. When cells are small, insufficient activator is present for cell-cycle progression. As cells grow, the concentration of the activator increases until it bypasses a threshold for the cell cycle to proceed. The diluted inhibitor is depicted as regulating G1/S and the accumulating activator is depicted as regulating G2/M, as they are proposed to do in budding and fission yeast, respectively; however, either mechanism could regulate either transition. Moreover, although the diluted inhibitor and accumulating activator are shown on the same graph, they are not expected to operate concurrently in the same cell.

Adder models posit that cells grow a fixed amount each cell cycle (Figure 2A). That fixed amount is one half the cell’s target size. So, a cell born at one half its target size will divide at its target size. If a cell is born too big, it will also divide too big; however, it will be closer to its target size than its parent. Likewise, a cell born small will divide small, but closer to its target size. Adders cause individual lineages of cells to return to their target size asymptotically (Figure 2B), but nonetheless maintain size homeostasis in a population. Moreover, adders cause cells to pass regulated cell cycle transitions at a constant target size, on average. So, adder size control, which seems to be the dominant approach to size control in bacteria, and perhaps also in archaea, is consistent with the observation that bacteria initiate DNA replication at a constant cell size, on average. Adders differ from sizers in that they do not allow cells to know how big they are, only how much they have grown.

Timer models posit that cells grow for a fixed amount of time each cycle (Figure 2A). The effect of a timer model depends on the growth rate of a cell. If a cell grows exponentially (i.e., its growth rate is proportional to its size), timers do not maintain size homeostasis because big cells will grow faster and small cells will grow slower, maintaining size heterogeneity in the population and amplifying any noise in the system. However, if a cell grows linearly (with the same growth rate at any size), then a timer is equivalent to an adder, with the same amount of mass added each cycle regardless of size. Specific claims to the contrary notwithstanding, the preponderance of evidence and analysis suggest that cells generally grow exponentially, a conclusion consistent with the observation that larger cells have proportionally greater synthetic capacity than smaller cells. Since timers are either ineffective at maintaining size homeostasis or equivalent to adders, we will not consider them further.

Regardless of whether size homeostasis is maintained by a sizer or adder strategy, there has to be some biochemical mechanism that differentiates a cell that is ready to divide from one that is not. A simple mechanism proposed for bacterial adders is a version of the original division-protein model, in which a certain number of molecules of a division protein is required to create a structure necessary for division. If the division protein is synthesized at a rate proportional to total protein synthesis (as most proteins are) then, after a fixed amount of growth, a fixed amount of the division protein will be synthesized, and the cell will be able to divide. If the division protein is degraded after division, the process starts anew each cell cycle. A cell’s target size can be adjusted by adjusting the rate of division protein synthesis. If its synthesis rate is increased, the critical number of division proteins will accumulate with less cell growth and cell size at division will be decreased. Likewise, a decreased synthesis rate will adjust cell size upwards.

A sizer could work by a similar mechanism, with one modification. If the division protein has a half life at least as long as the cell cycle, the number of division protein molecules accumulates proportional to the amount of cellular growth (Figure 2C), and such accumulation kinetics create an adder mechanism. However, if the half life of the division protein is much shorter than the length of the cell cycle, it quickly reaches a constant steady-state concentration, independent of the amount of cell growth. In this situation, the critical number of division-protein molecules will accumulate at a specific cell size, creating a sizer mechanism.

Sizers could also measure other parameters that correlate with cell size. One parameter that could work for some cells is surface area-to-volume ratio. However, the surface area-to-volume ratio is a robust measure of size only in cells that are close to spherical. In cylindrical cells, such as fission yeast, the surface area-to-volume ratio does not change as cell grow, and in irregularly-shaped flat cells, such a amoeba or fibroblasts, the correlation is weak, at best. So, measuring surface-to-volume ratio is not a general solution for cell-size control.

One parameter that varies with size in all cells is the ratio of protein to DNA, which increases with cell size. Many size control models have been proposed that take advantage of this changing ratio. A classic example is the nuclear-sites-titration model, which posits that an activator of division binds to, and is inhibited by, specific sites in the genome. If there are more DNA binding sites than proteins, the activator is titrated to those sites and inhibited. However, as the number of activator proteins increases, all of the nuclear sites become occupied and free activator can drive division. As with the division-protein models above, if the activator has a long half life, it accumulates proportional to growth, creating an adder mechanism, whereas if it has a short half life, it accumulates proportional to size, creating a sizer mechanism (Figure 2C).

Another class of sizer mechanism is based on sizer proteins. Sizer proteins are those expressed at a size-dependent concentration, either increasing in concentration in proportion to size (such that larger cells have higher concentrations), or decreasing in proportion to size. In the division-protein and nuclear-sites-titration models, the key protein maintains a constant concentration, and so the number of molecules of the protein increases with cell growth. Such protein-expression kinetics are common; in fact, proteins generally maintain a constant concentration as cells grow. Cells that are twice as big have twice as many ribosomes, twice as many polymerases, twice as much GAPDH, etc. The fact that the concentration of a protein is constant with cell size means that the number of molecules of that protein increases with size, so division-protein mechanisms can rely on achieving a threshold number of protein molecules to regulate cell size.

In sizer-protein models, it is the concentration of the protein that is critical, not the number of protein molecules. There are two general classes of sizer-protein models: inhibitor dilution and activator accumulation (Figure 2D). In inhibitor-dilution models, a fixed amount of inhibitor is made at the beginning of the cell cycle, independent of size at birth, and is diluted by growth until cells reach their target size, at which point the inhibitor is diluted below its effective concentration and cell cycle can progress. Since all cells start with the same amount of inhibitor regardless of their size at birth, the critical concentration for cell cycle progression is reached at the same size for all cells. In activator-accumulation models, a size-dependent concentration of the activator is too low to drive division in small cells, but achieves a sufficient concentration when cells grow to their target size. In neither case is the sizer protein likely to create a deterministic threshold at which division is triggered. Instead, an increasing concentration of activator, or decreasing concentration of inhibitor, will translate to an increasing probability of division, leading to a distribution of division sizes around the target size and contributing the biological noise seen in size control systems.

How a protein could be expressed at a size-dependent concentration is unclear. The problem is that the reactions that control protein expression are themselves protein-concentration dependent, and if the concentration of proteins is constant for cells of all sizes, there should be no difference in expression levels between small and big cells. The one thing that does change as cells grow is the ratio of protein to DNA. It seems likely that size-dependent expression of sizer proteins would need to exploit this ratio. Mechanisms that involve the size-dependent change of the protein-to-DNA ratio as cells grow could naturally explain the central role of the N:C ratio in cell-size control, because cells that have twice the DNA content would need to be twice the size to achieve the same protein:DNA ratio. However, how a changing protein:DNA ratio could affect the expression of sizer proteins, but not any other protein in the cell, is still a mystery.

Examples of Cell-Size Control

The work described above led directly to the yeast cell-cycle genetics that, along with the concurrent oocyte cell-cycle biochemistry, revolutionized our understanding of cell-cycle mechanics in the 1980s. The following decades elucidated the genetic and biochemical details of the cell cycle, which in turn provided the mechanistic understanding required for more robust and specific cell-size control models. The other critical advance in the field has been the development of automated methods for the acquisition and analysis of images of many cells growing over many generations. These large datasets have allowed for the quantitative analysis of cell-size parameters throughout the cell cycle and across generations, providing the grist for sophisticated computational models. Together, these conceptual and technical advances have led to number of plausible, detailed models for cell-size control in a variety of species. Nonetheless, important questions remain about all of them.

The best-established models for cell-size control are adder models in bacteria, particularly in model species such as E. coli and B. subtilis. Analysis of multigenerational movies of cell growth and division led to the observation that, instead of dividing at constant size, bacterial cells grow a constant amount each generation, regardless of birth size, showing that they use an adder strategy for size control. Early work suggested that E. coli regulates it size at replication initiation, but more recent analysis indicates that replication initiation and cell division are regulated by independent adder mechanisms. In both cases, a division-protein model has been proposed. In the case of replication initiation, a critical number of DnaA protein molecules—the initiator that is assembled into a homo-multimer at the replication origin and is required for replication initiation—is proposed to regulate the size at initiation. In the case of cell division, a critical number of FtsZ protein molecules—a tubulin homolog that assembles into the contractile ring—is proposed to regulate the size at division.

Another well-defined size-control model has been proposed for G1/S size control in budding yeast. The model proposes Whi5 as a diluted-inhibitor sizer protein. A constant amount of Whi5, an inhibitor of the G1 transcription that drives the G1/S transition, is synthesized at the beginning of the cell cycle, independent of the cell size at birth. The cell then needs to grow to its G1 target size in order to dilute Whi5 to the point at which G1 transcription can be activated and drive the G1/S transition. As for all models of size control, this one comes with caveats. In particular, competing models for G1 size control have been proposed and the importance of its central contention—the size-independence of Whi5 synthesis—has been directly contested. Furthermore, even if this model is correct, it does not explain how Whi5 could be synthesized to a size-independent amount, leaving a crucial mechanistic question unanswered.

Sizer-protein models for cell-size control have also been proposed in fission yeast. Both Cdc25, the phosphatase that activates Cdk1, and Cdc13, the cyclin subunit of Cdk1, have been proposed as accumulating activators for G2/M size control, consistent with the fact that the phenomenon of excess mitotic delay (Figure 1C) is observed in fission yeast. However, it is not known how these proteins could be expressed at size-dependent concentrations, leaving, as with the budding yeast model, crucial mechanistic questions unanswered.

Size control for multicellular organisms is more complicated than unicellular organisms both because different cell types may have different size-control mechanisms and because, in some cases, size can be affected by cell-cell interactions. Nonetheless, inhibitor-dilution models have been proposed for both mammalian and plant size control. In human epithelial cells, dilution of the G1/S inhibitor Rb has been proposed to regulate size at the G1/S transition, much as Whi5 has been proposed to do in budding yeast. However, as in budding yeast, how Rb could be expressed at a size-independent amount is unknown. In Arabidopsis meristems, the G1/S inhibitor KPR4 is also proposed to act as a diluted inhibitor. An interesting aspect of this model is that the abundance of KPR4 is proposed to be determined by chromatin binding. A fixed amount of KPR4 is proposed to bind to chromosomes and thus be protected from ubiquitin-mediated proteolysis, with any excess KPR4 being degraded. This twist on the classic nuclear-sites-titration model not only explains how a size-independent amount of the inhibitor could be expressed; it also explains how cell size could scale with ploidy.

Open Questions in Cell-Size Control

Although impressive progress has been made in understanding how cells maintain size homeostasis, fundamental conceptual and mechanistic questions remain.

One such question is the extent to which size-control mechanisms are conserved. Size control does not seem to be conserved between bacteria and eukaryotes, or even between budding yeast and fission yeast. Perhaps this observation should not be surprising, since as long as size homeostasis is maintained, the details of the mechanism may not provide any evolutionary advantage. Size could be similar to sex determination, where it is clear that it does not matter how sex is determined, as long as progeny of both sexes are produced. In flies, there can be three orthogonal, but mutually compatible, sex determination mechanisms circulating within one species.

A related question is why prokaryotes—bacteria and archaea—seem to prefer adder mechanisms, whereas eukaryotes seem to favor sizers. One possible explanation is that adders only work in actively growing cells. For single-celled organisms this limitation is not a problem, since they are generally either growing or nutrient limited. However, cells in multicellular organisms are not always growing. As noted above, size control in the quiescent cells of multicellular organisms is a conceptually different problem from size control in growing cells—one dependent on balancing catabolism and anabolism, instead of growth and division. Nonetheless, it is a problem that could be solved by—in fact, may only be solvable by—size-dependent gene expression. One might even speculate that a critical innovation in the evolution of multicellular organisms with quiescent tissues would be a sizer mechanism of size control. Presumably different sizer proteins would regulate size in growing and quiescent cells, but once size-dependent gene expression evolved, one could imagine it being applied in both cases.

Along those lines, it is interesting to observe that cell-cycle control mechanisms in bacteria seem to involve the assembly of structures of fixed subunit number—be it the assembly of the DnaA homomultimer or the assembly of the FtsZ contractile ring—which lend themselves to adder mechanisms. In contrast, cell-cycle regulatory mechanisms in eukaryotes are dominated by kinases and transcription factors, both of which are sensitive to protein concentration, not protein number, and thus can’t easily be regulated as adders.

This line of inquiry leads to perhaps the biggest current mystery in the field of cell-size control: how can sizer proteins be expressed at size-dependent concentrations. Both diluted inhibitors (which need to be produced at a certain amount, independent of cell size) and accumulating activators (which need to be expressed at a concentration proportional to cell size) deviate from the usual pattern, in which proteins maintain a constant concentration as cells grow. Although such expression patterns have been observed in yeast, mammals and plants, only in plants has a mechanism been proposed, namely a nuclear-sites-titration model. It seems likely that other sizer mechanisms will also need to rely on some variation of nuclear-sites titration, in which the number of protein molecules, titrated against a fixed number of DNA-dependent sites, regulates sizer protein expression. Nonetheless, how they may do so is very much an open question.

Figure 3. Examples of Size Control.

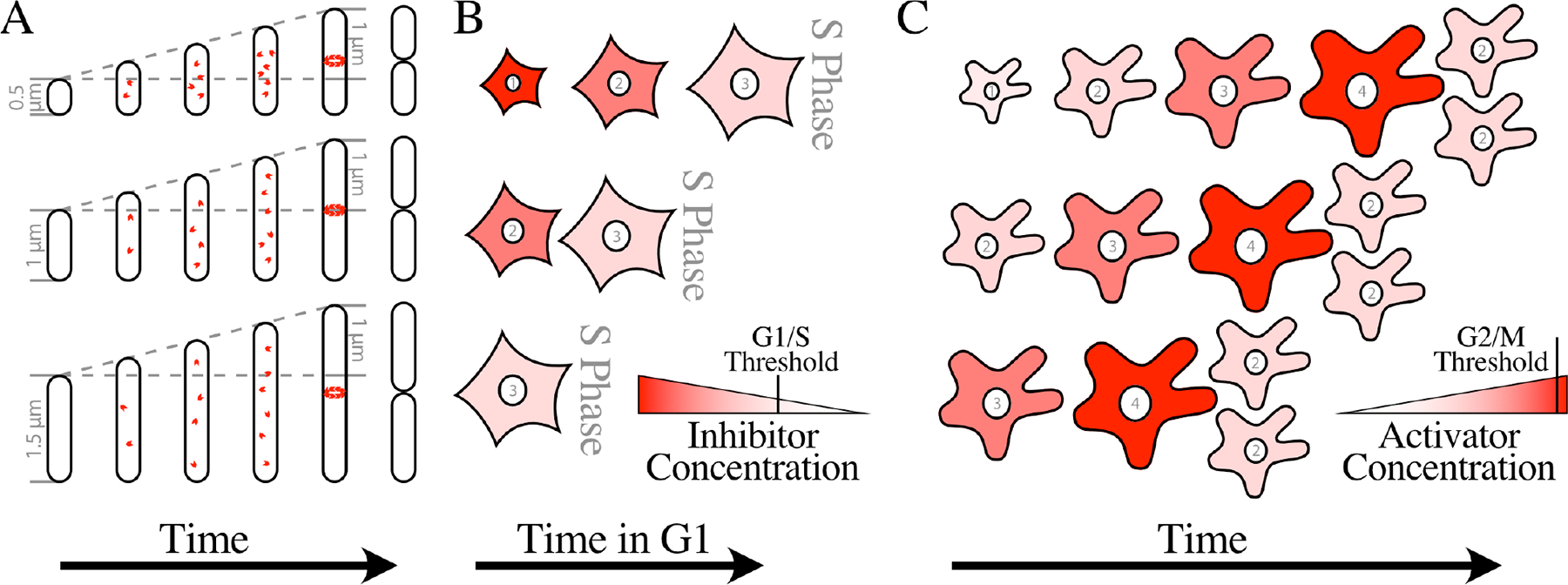
A) A Bacterial Adder. One model for how an adder mechanism could work is by way of a division protein, a protein that must accumulate to a certain number in order for a structure required for division to be formed. FtsZ, the tubulin homolog that forms to contractile ring required for cell division, shown here as red subunits, has been proposed to be such a division protein. If the division protein accumulates proportionally to cell growth, as most proteins do, a fixed amount of growth would be required each cell cycle, creating a adder mechanism. In the simplest division-protein models, the division protein is degraded at division, resetting the system. In this depiction, each cell grows 1 μm, regardless of its birth size. Note that the progeny of small cells are born smaller than the target size of 1 μm, but larger than their parent, moving the average population size towards the target size. A similar model has been proposed for regulation of DNA replication. In that case, a fixed number of DnaA, the replication initiator, are proposed to be required to build an initiation complex at the replication origin.

B) A Diluted-Inhibitor Sizer. In one version of the diluted-inhibitor model, every cell is born with the same amount of an inhibitor, regardless of size. Therefore, smaller cells, depicted here as mammalian fibroblasts, have a higher concentration of inhibitor. The numbers in the nuclei indicate the relative cell sizes, which are roughly equivalent to picoliters, and the intensity of the color indicates the concentration of the inhibitor. As cell grow, they dilute the inhibitor, eventually reaching a critical size that dilutes the inhibitor below a threshold that allows S phase to proceed. Budding yeast, mammalian cells and plants have all been proposed to use a diluted inhibitor to regulate size at the G1/S transition.

C) An Accumulating-Activator Sizer. Accumulating activators are proposed to increase in concentration in proportion to cell size, depicted here in amoeba. The numbers in the nuclei indicate the relative cell sizes, which are roughly equivalent to nanoliters, and the intensity of the color indicates the concentration of the activator. In small cells, the activator concentration is insufficient to drive mitosis, but as cells grow they reach a size at which the activator accumulates to a concentration sufficient to trigger division. Thus all cells divide at about the same size, regardless of their size at birth. Fission yeast, amoeba and Tetrahymena have all been proposed to use an accumulating activator to regulate size at the G2/M transition.