MULTI-DOMAIN LEARNING BY META-LEARNING: TAKING OPTIMAL STEPS IN MULTI-DOMAIN LOSS LANDSCAPES BY INNER-LOOP LEARNING

Abstract

We consider a model-agnostic solution to the problem of Multi-Domain Learning (MDL) for multi-modal applications. Many existing MDL techniques are model-dependent solutions which explicitly require nontrivial architectural changes to construct domain-specific modules. Thus, properly applying these MDL techniques for new problems with well-established models, e.g. U-Net for semantic segmentation, may demand various low-level implementation efforts. In this paper, given emerging multi-modal data (e.g., various structural neuroimaging modalities), we aim to enable MDL purely algorithmically so that widely used neural networks can trivially achieve MDL in a model-independent manner. To this end, we consider a weighted loss function and extend it to an effective procedure by employing techniques from the recently active area of learning-to-learn (meta-learning). Specifically, we take inner-loop gradient steps to dynamically estimate posterior distributions over the hyperparameters of our loss function. Thus, our method is model-agnostic, requiring no additional model parameters and no network architecture changes; instead, only a few efficient algorithmic modifications are needed to improve performance in MDL. We demonstrate our solution to a fitting problem in medical imaging, specifically, in the automatic segmentation of white matter hyperintensity (WMH). We look at two neuroimaging modalities (T1-MR and FLAIR) with complementary information fitting for our problem.

1. INTRODUCTION

In this paper, we consider the problem of Multi-Domain Learning (MDL) in which the goal is to take labeled data from some collection of domains {${\mathcal{D}}_i$}_i and minimize the risk on all of these domains. Note, this is in contrast to the related field of Domain Adaptation (DA) which minimizes risk on only a subset of these domains referred to as the target. Although our focus is MDL, it is not uncommon for Multi-Task Learning (MTL) solutions to be applicable to MDL problems. Where MDL assumes a collection of domains {${\mathcal{D}}_i$}_i all paired with the same task $\mathcal{T}$, MTL assumes a collection of tasks {${\mathcal{T}}_i$}_i all paired with a single domain $\mathcal{D}$ [1]. One simple model-agnostic solution to both problems comes in the form of a weighted loss function used to learn new tasks without “forgetting” old tasks [2]. This method can be simplified and adapted for the task of MDL by specifying loss functions for each domain and jointly training on all domains by optimizing for the convex combination (weighted average) of these loss functions. Inspired by this approach, our main contribution is to significantly build-upon this method by dynamically estimating the optimal weights of the convex combination throughout the training process. To achieve this, we appeal to the recently growing research area of learning-to-learn (or meta-learning) which uses the idea of hypothetical gradient steps taken during an inner-loop optimization to extract “meta-information” useful to the optimization task. Our method closely follows this idea to estimate a posterior distribution over the optimal weights of our loss function at each training iteration.

We showcase this method on a fitting problem in medical imaging, specifically, in the automatic segmentation of white matter hyperintensity (WMH) with multi-modal structural neuroimaging. Caused by various factors from neurological to vascular pathologies [3], WMH is prevalent in population of aging, e.g., Alzheimer’s disease (AD) [4]. Typically, the automatic WMH segmentation task focuses on identifying hyperintense, or bright, white matter regions in T2-weighted fluid attenuated inversion recovery (FLAIR). However, FLAIR is often acquired for neurological disorders that directly search for strokes or lesions, whereas, in observational AD studies of our focus, FLAIR is much less common and T1-weighted Magnetic Resonance (T1-MR) image is the norm. Unfortunately, detecting WMH in T1-MR is extremely difficult since contained WMH regions severely lack contrast – a key feature for segmentation (see Fig. 1 for the contrast difference and predictions). Hence, this setting provides a good opportunity for knowledge transfer across domains (T1-MR and FLAIR). While FLAIR may benefit from the higher quantity of T1-MR samples in a given dataset, T1-MR may additionally benefit from the much higher quality of the FLAIR samples. Further, considering how common it is for patients to only have either T1-MR or FLAIR, MDL is particularly relevant in this case (rather than DA) to perform well on both domains (i.e., train with T1-MR and FLAIR, but predicts well given T1-MR only, Fig. 1E). In this paper, we present a solution for MDL within this context. Importantly, the approach is model-agnostic, making it easily applicable to a myriad of MDL problems besides WMH segmentation.

Fig. 1.

A: FLAIR (bright WMH in the periventricular and deep white matter), B: Coregistered T1-MR (WMHs are less apparent), C: Manually segmented WMH, D: WMH prediction with FLAIR, E: WMH prediction T1-MR. T1-MR-based result (E), while reasonable, is still worse than FLAIR-based result (D).

2. MULTI-DOMAIN LEARNING (MDL)

Several early works on MDL combine domain-specific parameters with the classifier [5, 6]. More recent works separate shared parameters from domain-specific parameters [7]. These methods are model-dependent which requires explicit changes to network architecture. This is less desirable if one wishes to enable MDL in segmentation since standard existing methods cannot be trivially applied to U-Net [8]. Conversely, our approach is model-agnostic, making no model-dependent changes and is applicable to most existing models. This flexibility adds a great practical value for the end-users who wish to enable MDL in a “plug-and-play” manner.

Learning to Learn.

Learning-to-learn (meta-learning) is an algorithmic effort to not only learn some set of model parameters, but to learn the best way in which those model parameters can be learned. Many recent popularizations of this concept [9, 10] largely involve an inner- and outer-loop. The dual-loop scheme uses the inner-loop to extract hypothetical model performance if the model were optimized in some way. From this, in the outer-loop, the hyperparameters of interest (e.g., the way the model is optimized) can be updated [9, 10], or the model itself can be updated in a modified way [11]. Unlike many meta-learning solutions in the MTL problem space [10, 12, 13], we have only a single task, making it unclear how we could pre-train our hyperparameters as usual (i.e., using a distribution over tasks). Further, the majority of these solutions are fully gradient based – our technique, instead, uses MAP estimation during inner-loop optimization.

3. PROPOSED APPROACH

We describe our approach (Alg. 1, Fig. 2) which can be applied universally to nearly any neural network model without model-specific changes. Our meta-learning procedure with outer- and inner-loop is as follows: (i) outer-loop updates the model parameters θ based on (ii) inner-loop which learns and updates our hyperparameter (λ_θ). We first formalize the weighted loss function used in the outer-loop. Ultimately, we interpret this loss as an expectation over the optimal update choice, allowing us to learn λ_θ by MAP estimation.

Fig. 2.

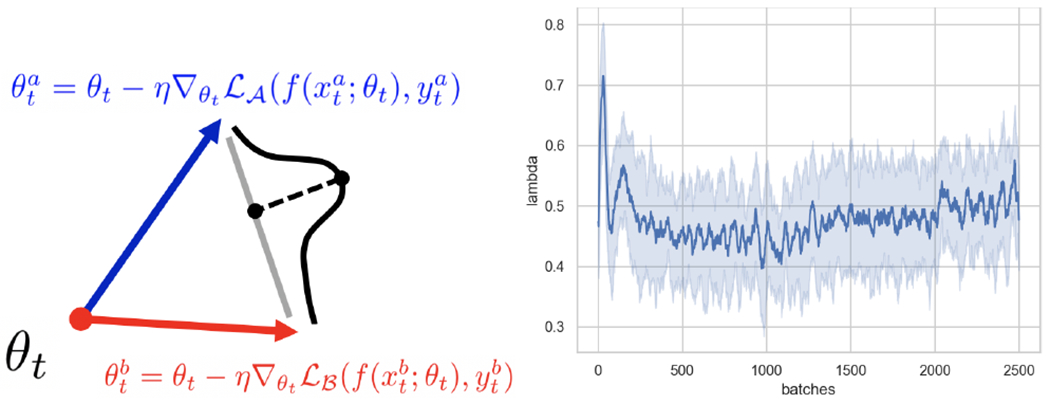
Left: Proposed Approach. We learn a distribution over the optimal convex-combination of the two gradient directions. Right: Visualization of how the optimal update choice λθ changes over time (U-Net 8F). Line shows mean. Band shows s.d. Early spikes favor more informative FLAIR samples.

3.1. Outer-loop Optimization of Model Parameter θ

We define domain $\mathcal{D}=(\mathcal{X},p(x))$ as a feature space $\mathcal{X}$ paired with a distribution of samples from that space p(x) [14]. For the remainder of the paper, we generally assume only two domains $\mathcal{A}=({\mathcal{X}}_{\mathcal{A}},p_{\mathcal{A}}(x))$ and $\mathcal{B}=({\mathcal{X}}_{\mathcal{B}},p_{\mathcal{B}}(x))$. We do this for brevity and for our two domain neuroimaging application, but in a subsequent section, we indeed show an easy extension to more than two domains. Further, we assume a single task $\mathcal{T}=(\mathcal{Y},q(y))$ (e.g., segmentation), a pre-specified model f (e.g., U-Net), and a possibly domain-specific loss function for both $\mathcal{A}$ and $\mathcal{B}$ written ${\mathcal{L}}_A$ and ${\mathcal{L}}_B$ respectively. Our method aims to dynamically determine the optimal weighting of these losses. We seek λ_θ with 0 ≤ λ_θ ≤ 1 for the training objective

$${\lambda }_{\theta }{\mathcal{L}}_{\mathcal{A}}(f(x^a;\theta ),y^a)+(1-{\lambda }_{\theta }){\mathcal{L}}_{\mathcal{B}}(f(x^b;\theta ),y^b)$$ (1)

where θ is the current model parameters. The mini-batches $(x^a,y^a)\sim (p_{\mathcal{A}}(x),q(y))\text{and}(x^b,y^b)\sim (p_{\mathcal{B}}(x),q(y))$ are (input,label) pairs from domains $\mathcal{A}$ and $\mathcal{B}$ respectively. In practice, this objective is achieved using a modified SGD to update θ. In particular, at step t, we set θ_t+1 to the quantity

$${\theta }_t-\eta {\nabla }_{{\theta }_t}[{\lambda }_t{\mathcal{L}}_{\mathcal{A}}(f(x_t^a;{\theta }_t),y_t^a)+(1-{\lambda }_t){\mathcal{L}}_{\mathcal{B}}(f(x_t^b;{\theta }_t),y_t^b)]$$ (2)

with η the learning rate and mini-batches $(x_t^a,y_t^a)$ and $(x_t^b,y_t^b)$. Since Eq. (2) involves two losses, the learned λ_t weights the effect of gradients ${\nabla }_{{\theta }_t}{\mathcal{L}}_{\mathcal{A}}$ and ${\nabla }_{{\theta }_t}{\mathcal{L}}_{\mathcal{B}}$ which are best for $\mathcal{A}$ and $\mathcal{B}$ respectively. This outer-loop optimization (Alg. 1 line 10) differs from standard SGD with weighted losses since λ_t depends on the current θ_t (rather than fixed).

3.2. Inner-Loop Optimization of Hyperparameter λ_θ

MAP Estimation of λ_θ.

We now discuss how to pick the best λ_θ. Before we describe the definition of best, for now, we assume some notion of an optimal update choice is given and that this choice boils down to taking a step in the direction best for $\mathcal{A}$ or $\mathcal{B}$. Thus, it is straightforward to interpret the multi-domain loss Eq. (1) as an expectation over the optimal update choice (i.e., the expected best gradient). We do this by assuming during the update process there exists a sequence of (not necessarily i.i.d.) Bernoulli random variables indicating whether a step in the direction best for domain $\mathcal{A}$ or $\mathcal{B}$ is optimal. We can write the sequence (Λ_t)_t where t indexes over the sequential update process given in Eq. (2), Λ_t ~ Bernoulli(λ_t), and Λ_t = 1 represents the event that taking a gradient step in the direction best for $\mathcal{A}$ is optimal.

Algorithm 1.

Approach using the conservative configuration

Domain $\mathcal{A}$ input, labels, loss: $x^a,y^a,{\mathcal{L}}_{\mathcal{A}}$
Domain $\mathcal{B}$ input, labels, loss: $x^b,y^b,{\mathcal{L}}_{\mathcal{B}}$
Model Parameters, Learned Loss Weighting, Learning-Rate: θ, λ, η
1:	procedure MetaLearningForMDL
2:	for mini-batch t do
3:	$\text{Split}{x}_t^a,y_t^a,x_t^b,y_t^b\text{into}{\dot{x}}_t^a,{\dot{y}}_t^a,{\dot{x}}_t^b,{\dot{y}}_t^b\text{and}{\ddot{x}}_t^a,{\ddot{y}}_t^a,{\ddot{x}}_t^b,{\ddot{y}}_t^b$
4:	${\theta }_t^a\leftarrow {\theta }_t-\eta {\nabla }_{{\theta }_t}{\mathcal{L}}_{\mathcal{A}}(f({\dot{x}}_t^a;{\theta }_t),{\dot{y}}_t^a)⊳\text{Inner-Loop Step for}\mathcal{A}$
5:	${\theta }_t^b\leftarrow {\theta }_t-\eta {\nabla }_{{\theta }_t}{\mathcal{L}}_{\mathcal{B}}(f({\dot{x}}_t^b;{\theta }_t),{\dot{y}}_t^b)⊳\text{Inner-Loop Step for}\mathcal{B}$
6:	$H_{\mathcal{A}}^t\leftarrow {\mathcal{L}}_{\mathcal{A}}(f({\ddot{x}}_t^a;{\theta }_t^a),{\ddot{y}}_t^a)+{\mathcal{L}}_{\mathcal{B}}(f({\ddot{x}}_t^b;{\theta }_t^a),{\ddot{y}}_t^b)$
7:	$H_{\mathcal{B}}^t\leftarrow {\mathcal{L}}_{\mathcal{A}}(f({\ddot{x}}_t^a;{\theta }_t^b),{\ddot{y}}_t^a)+{\mathcal{L}}_{\mathcal{B}}(f({\ddot{x}}_t^b;{\theta }_t^b),{\ddot{y}}_t^b)$
8:	$N_t\leftarrow {\sum }_{i=t-T}^t{\text{Λ}}_i(H_{\mathcal{A}}^i<H_{\mathcal{B}}^i)$
9:	${\lambda }_t\leftarrow \frac{\alpha +N_t-1}{\alpha +\beta +T-2}⊳$ Inner-Loop MAP Estimate for λt
10:	θt+1 ← Update via Eq. (2)     ⊳ Outer-Loop Gradient Update
11:	end for
12:	end procedure

It then becomes simple to optimize λ_t dynamically by assuming a prior and updating sequentially with Maximum a Posteriori (MAP) Estimation. To meet the requirements of MAP, we make the simplifying assumption that the Λ_t are i.i.d. in a small temporal window of size T (e.g., we perform our MAP updates using a history of length ≤ T). Thus, we can, as usual, assume the Beta(α, β) as our prior over λ_t and explicitly compute the MAP estimate (Alg. 1 line 8-9).

Defining the Optimal Update Choice.

Now, we need only define the optimal update choice by defining when Λ_t = 1. We do this by comparing model performance after computing hypothetical gradient steps (i.e., through an inner-loop) favoring $\mathcal{A}$ and $\mathcal{B}$. Specifically, in the case of domain $\mathcal{A}$, we randomly split the mini-batch $x_t^a,y_t^a$ into meta-train ${\dot{x}}_t^a,{\dot{y}}_t^a$ and meta-test ${\ddot{x}}_t^a,{\ddot{y}}_t^a$ (Alg. 1 line 3). Then, we compute the hypothetical gradient favoring $\mathcal{A}$ (Alg. 1 line 4)

$${\theta }_t^a={\theta }_t-\eta {\nabla }_{{\theta }_t}{\mathcal{L}}_{\mathcal{A}}(f({\dot{x}}_t^a;{\theta }_t),{\dot{y}}_t^a),$$ (3)

and the hypothetical loss favoring $\mathcal{A}$ at step t (Alg. 1 line 6)

$$H_{\mathcal{A}}^t={\mathcal{L}}_{\mathcal{A}}(f({\ddot{x}}_t^a;{\theta }_t^a),{\ddot{y}}_t^a)+{\mathcal{L}}_{\mathcal{B}}(f({\ddot{x}}_t^b;{\theta }_t^a),{\ddot{y}}_t^b).$$ (4)

We can similarly arrive ${\theta }_t^b$ and $H_{\mathcal{B}}^t$ (Alg. 1 line 5 and 7).

Now, we define two optimal update choices: (i) greedy: ${\text{Λ}}_t=1\text{ if }{H}_{\mathcal{B}}^t>H_{\mathcal{A}}^t$, otherwise Λ_t = 0; and (ii) conservative: ${\text{Λ}}_t=1\text{ if }{H}_{\mathcal{A}}^t>H_{\mathcal{B}}^t$, otherwise Λ_t = 0 (Alg. 1 line 8). These hypothetical losses are functions of the model parameters, so we can analyze them by looking at the dominant terms in their Taylor Expansions (centered at θ_t) to interpret our inner-loop [15, 11]. For instance, for $H_{\mathcal{A}}^t$, evaluated at ${\theta }_t^a$, the following holds¹ for small enough η:

$$H_{\mathcal{A}}^t={\mathcal{L}}_{\mathcal{A}}(f(x_t^a;{\theta }_t),y_t^a)+{\mathcal{L}}_{\mathcal{B}}(f(x_t^b;{\theta }_t,y_t^b)-\eta {\nabla }_{{\theta }_t}{\mathcal{L}}_{\mathcal{A}}{(f(x_t^a;{\theta }_t),y_t^a)}^{\text{T}}{\nabla }_{{\theta }_t}{\mathcal{L}}_{\mathcal{A}}(f(x_t^a;{\theta }_t),y_t^a)-\eta {\nabla }_{{\theta }_t}{\mathcal{L}}_{\mathcal{B}}{(f(x_t^b;{\theta }_t),y_t^b)}^{\text{T}}{\nabla }_{{\theta }_t}{\mathcal{L}}_{\mathcal{A}}(f(x_t^a;{\theta }_t),y_t^a)+O({\eta }^2)$$ (5)

Now, there are multiple common terms in the Taylor Expansion of $H_{\mathcal{A}}^t$ and $H_{\mathcal{B}}^t$ that can cancel out, so if we ignore O(η²) terms (which are small) and recognize the definition of the L2 norm, we have an approximation of $H_{\mathcal{A}}^t-H_{\mathcal{B}}^t$ as below

$$\eta {\Vert {\nabla }_{{\theta }_t}{\mathcal{L}}_{\mathcal{B}}(f(x_t^b;{\theta }_t),y_t^b)\Vert }_2^2-\eta {\Vert {\nabla }_{{\theta }_t}{\mathcal{L}}_{\mathcal{A}}(f(x_t^a;{\theta }_t),y_t^a)\Vert }_2^2.$$ (6)

Hence, in the greedy definition with $H_{\mathcal{B}}^t>H_{\mathcal{A}}^t$, we can infer $\Vert {\nabla }_{{\theta }_t}{\mathcal{L}}_{\mathcal{A}}(f(x_t^a;{\theta }_t),y_t^a)\Vert >\Vert {\nabla }_{{\theta }_t}{\mathcal{L}}_{\mathcal{B}}(f(x_t^b;{\theta }_t),y_t^b)\Vert$. Likewise, in the conservative definition with $H_{\mathcal{A}}^t>H_{\mathcal{B}}^t$, we can infer $\Vert {\nabla }_{{\theta }_t}{\mathcal{L}}_{\mathcal{B}}(f(x_t^b;{\theta }_t),y_t^b)\Vert >\Vert {\nabla }_{{\theta }_t}{\mathcal{L}}_{\mathcal{A}}(f(x_t^a;{\theta }_t),y_t^a)\Vert$. Since λ_t is the probability that ${\nabla }_{{\theta }_t}{\mathcal{L}}_{\mathcal{A}}$ is the optimal update choice, we see that the greedy definition prefers larger gradient steps, while the conservative definition prefers smaller.

More than Two Domains.

Generalizing our approach to more than two domains is straightforward. Eq. (1) is extended to a convex combination with additional weights for each added domain. Next, the sequence of Bernoulli Distributions becomes a sequence of Multinomial Distributions whose conjugate prior is a Dirichlet; the MAP Estimate is still analytic. Lastly, the optimal update choice (Alg. 1 line 8) is defined by argmax instead of > and argmin instead of <.

4. EXPERIMENTS

We randomly selected N=20 older participants with WMH from our local normal aging AD study who were cognitively normal at the time of scan with mean age of 81.2 (s.d.= 7.15), 14 females, and a mean education of 14.2 (s.d.= 2.44) years. For each subject, we used a 3T Siemens Trio TIM scanner and 12-channel head coil to collect T1-MR (TE=2.98ms, TR=2.3s, FA=9°, 1×1×1.2mm voxel) and FLAIR (TE=90ms, TR=9.16s, FA=150°, 1×1×3mm voxel). For each pair of T1-MR and FLAIR, we used FSL [16] to process them in the following order: (a) spatially align T1-MR to FLAIR (212×256×48 dims), (b) N4-correction [17], (c) skull-strip using FSL BET, and (d) intensity normalize using WhiteStripe [18]. The ground-truth WMH in each FLAIR was labeled by a neuroradiologist on 5 continuous and identical slices across the subjects where WMH is common.

4.1. Experiment Setup

We use two base networks: (i) the standard U-Net [8] and (ii) a light-weight (LW) variant of U-Net with 3% of the parameters and no pooling layers or skip-connects.

Our Methods.

We setup our methods as described in Section 3 with FLAIR for $\mathcal{A}$ and T1-MR for $\mathcal{B}$. We try T = {25, 100} for both the greedy (Ours-G-T) and conservative (Ours-C-T) versions. We use a Beta(5,5) as our prior for λ_t; this assumes equal likelihood for FLAIR/T1-MR to be optimal and imposes low likelihood of 0 or 1. These are applied to the base models (U-Net, LW) without any architecture changes.

Other Baselines.

The baselines are applied to both U-Net and LW as follows: (1) F50-T50: Fix the weighting of both FLAIR and T1-MR at 0.5 to treat them equally. This is the most naïve way to use any models without considering MDL. (2) F10-T90: Fix the weighting of FLAIR at 0.10 and T1-MR at 0.90, largely favoring T1-MR. (3) F90-T10: Fix the weighting of FLAIR at 0.90 and T1-MR at 0.10, largely favoring FLAIR. (4) Simple: Heuristically update the hyperparameter λ_θ in Eq. (1) proportional to the difference of the hypothetical losses: λ_t+1 = λ_t + γ($H_{\mathrm{FLAIR}}^t-H_{\mathrm{T1}}^t$)/|$H_{\mathrm{FLAIR}}^t$|. We set Simple-G with γ = −0.1 and Simple-C with γ = 0.1 to heuristically mimic Ours-G and Ours-C respectively.

Loss Function.

For both FLAIR and T1-MR we minimize the sum of the cross-entropy and dice score loss [19].

Simulating Variation in Data-Availability.

To show the efficacy of our method when the number of training subjects with FLAIR is reduced, we explore randomly down-sampling the number of subjects who have FLAIR during training. We try all FLAIR subjects (12F) and 2/3 of FLAIR subjects (8F).

Training Details.

We use SGD with an initial learning rate of 0.01 (multiply by 0.1 if no validation improvement for 20 epochs and stop after 50 epochs of no improvement). We randomly augment each training slice by rotation, shearing, and scaling. Each mini-batch of size 8 is randomly sampled from both FLAIR and T1-MR. For each setup, we use 5-fold CV (12 train, 4 validate, 4 test) and compute the mean and standard deviations over 5 repeated runs on NVIDIA RTX2080Ti. For additional details, see the publicly available code.²

Metrics.

We evaluated the methods by the mean Dice Similarity Coefficient (DSC = 2TP / (2TP + FP + FN)) and report standard deviation to measure consistency of performance.

4.2. Results and Analyses

Table 1 shows the results of all methods under various setups. We emphasize that our approach only modifies the baseline by allowing a dynamic weighting of the two domains. Therefore, our approach is intended to be a simple add-on to the weighted loss approach and we do not expect staggering performance jumps in all cases. Instead, we hypothesize our method will improve upon the baseline in low resource situations (e.g., using less of the more informative FLAIR samples and the much smaller LW network). To this end, we show U-Net (8F) to demonstrate improvement when the number of FLAIR samples is down-sampled but the network is still large. We also show LW (8F) and LW (12F) to show two cases where the network is very under-parameterized.

In all of these cases, our proposed approach demonstrates improvement over the compared baselines. Unlike ours, fixed weight setups (F10-T90 and F90-T10) are able to improve DSC on a single domain, but inevitably sacrifice performance on the others (i.e., giving worse overall performance). Fig. 2 emphasizes the importance of an adaptive weighting, showing how λ_t is modified throughout training. But, naive adaptive weighting may still fail. Poor performances of simple heuristics (Simple-G and Simple-C) show that λ_t needs to be learned as in our methods. Besides increased performance in DSC gain, our method also reduces the variability of the results across runs. In low data regimes, standard-deviation in performance during cross-validation can be very large – our reduction in this measure indicates robustness to difficulty of the testing data and quality of the training data.

5. CONCLUSION

We proposed a model-agnostic solution to the problem of MDL. The solution is an extension of a simple weighted loss which uses meta-learning with inner-loop MAP Estimation to dynamically learn the weights of our loss function. On a WMH segmentation problem, we show that our proposed method improves both performance and consistency in low resource scenarios. The approach is widely applicable for MDL, making no assumptions on the underlying model.

Table 1.

Means and standard deviations (s.d.) of metrics across all setups using two models (U-Net and LW) and two numbers of FLAIR subjects (12 and 8). -F and -T indicate the metrics are computed over FLAIR and T1-MR samples respectively. GAIN-μ is the total (summed) increase in DSC over the baseline F50-T50. GAIN-σ is the total decrease in s.d. of DSC from F50-T50. Our method increases DSC and reduces s.d. in low resource scenarios.

LW (12F)	DSC-F	DSC-T	GAIN-μ	GAIN-σ
F50-T50	0.757 ± 0.011	0.360 ± 0.031	0.0	0.0
F10-T90	0.729 ± 0.006	0.404 ± 0.026	0.016	0.010
F90-T10	0.766 ± 0.008	0.278 ± 0.033	−0.073	0.001
Simple-G	0.740 ± 0.023	0.152 ± 0.072	−0.225	−0.053
Simple-C	0.714 ± 0.062	0.325 ± 0.050	−0.078	−0.070
Ours-G-25	0.758 ± 0.009	0.366 ± 0.029	0.007	0.004
Ours-G-100	0.759 ± 0.010	0.375 ± 0.028	0.017	0.004
Ours-C-25	0.758 ± 0.007	0.356 ± 0.025	−0.003	0.010
Ours-C-100	0.755 ± 0.008	0.351 ± 0.018	−0.011	0.016
LW (8F)	DSC-F	DSC-T	GAIN-μ	GAIN-σ
F50-T50	0.753 ± 0.008	0.361 ± 0.023	0.0	0.0
F10-T90	0.725 ± 0.008	0.393 ± 0.026	0.004	−0.003
F90-T10	0.766 ± 0.013	0.291 ± 0.030	−0.057	−0.012
Simple-G	0.738 ± 0.020	0.152 ± 0.055	−0.224	−0.044
Simple-C	0.716 ± 0.063	0.311 ± 0.081	−0.087	−0.113
Ours-G-25	0.755 ± 0.007	0.361 ± 0.023	0.002	0.001
Ours-G-100	0.756 ± 0.010	0.368 ± 0.030	0.010	−0.009
Ours-C-25	0.752 ± 0.007	0.355 ± 0.021	−0.007	0.003
Ours-C-100	0.753 ± 0.013	0.364 ± 0.035	0.003	−0.017
U-Net (8F)	DSC-F	DSC-T	GAIN-μ	GAIN-σ
F50-T50	0.767 ± 0.013	0.556 ± 0.025	0.0	0.0
F10-T90	0.745 ± 0.014	0.574 ± 0.017	−0.004	0.007
F90-T10	0.775 ± 0.011	0.499 ± 0.028	−0.049	−0.001
Simple-G	0.745 ± 0.030	0.498 ± 0.129	−0.080	−0.121
Simple-C	0.750 ± 0.015	0.555 ± 0.025	−0.018	−0.002
Ours-G-25	0.769 ± 0.014	0.555 ± 0.022	0.001	0.002
Ours-G-100	0.769 ± 0.012	0.545 ± 0.022	−0.009	0.004
Ours-C-25	0.768 ± 0.014	0.566 ± 0.012	0.011	0.012
Ours-C-100	0.771 ± 0.009	0.561 ± 0.020	0.009	0.009