Abstract
Unsupervised anomaly detection for spatio-temporal data has extensive use in a wide variety of applications such as earth science, traffic monitoring, fraud and disease outbreak detection. Most real-world time series data have a spatial dimension as an additional context which is often expressed in terms of coordinates of the region of interest (such as latitude - longitude information). However, existing techniques are limited to handle spatial and temporal contextual attributes in an integrated and meaningful way considering both spatial and temporal dependency between observations. In this paper, a hybrid deep learning framework is proposed to solve the unsupervised anomaly detection problem in multivariate spatio-temporal data. The proposed framework works with unlabeled data and no prior knowledge about anomalies are assumed. As a case study, we use the public COVID-19 data provided by the Italian Department of Civil Protection. Northern Italy regions’ COVID-19 data are used to train the framework; and then any abnormal trends or upswings in COVID-19 data of central and southern Italian regions are detected. The proposed framework detects early signals of the COVID-19 outbreak in test regions based on the reconstruction error. For performance comparison, we perform a detailed evaluation of 15 algorithms on the COVID-19 Italy dataset including the state-of-the-art deep learning architectures. Experimental results show that our framework shows significant improvement on unsupervised anomaly detection performance even in data scarce and high contamination ratio scenarios (where the ratio of anomalies in the data set is more than 5%). It achieves the earliest detection of COVID-19 outbreak and shows better performance on tracking the peaks of the COVID-19 pandemic in test regions. As the timeliness of detection is quite important in the fight against any outbreak, our framework provides useful insight to suppress the resurgence of local novel coronavirus outbreaks as early as possible.
Keywords: Spatio-temporal anomaly detection, multivariate, unsupervised, deep learning, COVID-19, outbreak detection, Italy
I. Introduction
An anomaly is an observation whose properties are significantly different from the majority of other observations under consideration, which are called the normal data. Anomaly detection refers to the problem of finding these observations in data that do not conform to expected or normal behavior. A spatial-temporal outlier (ST-Outlier) is an object whose behavioral (non-spatial and non-temporal) attributes are significantly different from those of the other objects in its spatial and temporal neighborhoods [1]. Spatio-temporal data are extremely common in many problem settings where collecting data from various spatial locations at different times for the nature of the problem are important. In such settings, detection of ST-Outliers can lead to the discovery of unexpected and interesting knowledge such as local instability and deformations [2]. Some examples of such spatio-temporal datasets are as follows: meteorological data, traffic data, earth science, and disease outbreak data. Events that generate spatio-temporal data are evolving events, such as hurricanes and disease outbreaks, and both spatial and temporal continuity are important in modelling such events [3].
For a problem domain, obtaining the labelled training data for all types of anomalies is often too expensive if not impossible [4]. This highlights the need for unsupervised techniques to find spatio-temporal anomalies. Moreover, spatio-temporal datasets are generally multivariate, and have many contextual structures in them (spatial and temporal regularities), which makes them particularly difficult for labelling and well suited for unsupervised learning models. In the unsupervised scenarios, the type of anomalies and the ratio of anomalous events within the given dataset are generally not known. In such scenarios, we need to model the normal behavior of the underlying system in the presence of noise and anomaly which pose extra difficulty.
In this study, we address these challenges by proposing a hybrid deep learning framework. It is an autoencoder based anomaly detection framework. The hybrid framework structure is based on the idea of combining various deep neural network components. It has been successfully applied to multivariate time series forecasting [5], face detection [6], and video classification [7]. However, it has not yet been applied to unsupervised anomaly detection problem for non-image multivariate spatio-temporal data. Our proposed framework is composed of three stages: The first stage is the pre-processing of the multivariate spatio-temporal data so that the deep autoencoder network can exploit the spatial and temporal contexts jointly. The second stage is the data reconstruction stage, which is executed by a deep hybrid autoencoder network. The third stage is the anomaly detection stage, which is performed based on the reconstruction error. The hybrid autoencoder network is composed of a 3D convolutional neural network (CNN) based spatio-temporal encoder and a convolutional Long Short-Term Memory (ConvLSTM) network-based spatio-temporal decoder. It is designed to be trained in a truly unsupervised fashion for anomaly detection in non-image spatio-temporal datasets. We know that in a time series data set, data points with two adjacent timestamps are likely to have a higher similarity than data points with more distant timestamps. It is also true for spatio-temporal datasets that neighboring regions may have some strongly positively correlated patterns, such as traffic jam, climate change, and human activity. The hybrid deep learning framework is able to exploit contextual features of neighboring regions for anomaly detection in the absence of labels for normal or abnormal events.
The world has been fighting a pandemic caused by a new type of coronavirus (SARS-CoV-2) since it was discovered in China in December 2019. Almost all countries have been affected by the novel coronavirus (COVID-19) outbreak, and Italy is one of the hardest-hit European countries. As of May 15, the total number of positive cases reached 223,885 and the number of deaths exceeded 31,000. Following the identification of the first infections on the second half of February 2020 in northern Italy, authorities put an increasing number of restrictions in place [8]. Due to the high contagiousness of the infection, this did not stop further spreading of the epidemic by asymptomatic people. The peaks of the epidemic were delayed in Central and Southern Italian regions as expected compared to Lombardy and other northern regions [9]. As it has been shown by the COVID-19 outbreak, the biggest challenge is to detect the outbreak during its early stages and mitigate its effects. The lack of an early epidemic warning system eliminated the opportunity to prohibit the epidemic spread at the initial stage. We would like to apply the proposed hybrid framework to tackle the problem of early disease outbreak detection in the midst of this global health crisis.
There have been many studies that model the epidemiological dynamics of COVID-19 [10]–[16]. They use either SEIR or other statistical models to predict the spreading and peaks of the epidemic, duration of the epidemic, and an overall number of potentially infected individuals at a national or regional level. However, none of those studies have focused on building an anomaly detection system for early epidemic detection. We believe that the proposed deep learning-based anomaly detection framework will prove useful in detecting COVID-19 epidemic waves. According to an analysis by disease experts, cases may come in waves of different heights by the end of 2021 depending on control measures and other factors [17]. This makes it quite necessary to build a monitoring tool for the timely detection of COVID-19 waves in different regions.
For any anomaly detection algorithm to be successful in early detection of disease outbreaks, it must incorporate both spatial and temporal aspects of a disease [18]. On the other hand, accurate monitoring of the evolution of the COVID-19 epidemic becomes extremely meaningful for the decision-making authorities to take appropriate actions against any public health crisis. As the extreme timeliness of detection is the new requirement of public health [19], this data-driven approach may help us build an anomaly detection tool for a more timely detection of the COVID-19 outbreak.
We use public COVID-19 data provided by the Italian Department of Civil Protection [20] as a case study in this research. We test the proposed model with the dataset at a resolution of the region level. We train one unified model with the data from northern regions, and using that model, we track the progression of the COVID-19 epidemic in test regions, which are central and southern regions of Italy. The framework can detect anomalous trends in test regions, which may signal the possibility of an outbreak. The main assumption here is that the data generated by northern regions’ experience going through the epidemic can be used to derive an anomaly detection model. We evaluate the performance of the proposed framework against various univariate and multivariate methods including state-of-the art deep learning-based approaches proposed in recent years. Our framework has outperformed the state-of-the-art anomaly detection models in all test cases.
The main contributions of this study are the following:
-
1)
To the best of our knowledge, the proposed approach, which is composed of a novel data crafting and a hybrid deep learning model, is the first attempt in solving unsupervised anomaly detection problem in non-image multivariate spatio-temporal data.
-
2)
It achieves good generalization capabilities in scenarios where the training data are scarce and contaminated with anomalies. In the case study, only 82 daily data entries (data points) are available for each region. Even these contaminated outbreak data are sufficient to build a robust anomaly detection model due to its effective architecture to exploit spatial neighborhood data.
-
3)
The biggest challenge in anomaly detection for spatio-temporal data is to combine the contextual attributes in a meaningful way. In the proposed hybrid approach, spatial and temporal contexts are handled by different deep learning components as these contextual variables refer to different types of dependencies.
-
4)
The proposed hybrid framework is designed to be trained in a truly unsupervised fashion without any labels indicating normal or abnormal data. The architecture is robust enough to learn the underlying dynamics even if the training dataset contains noise and anomalies.
The rest of the paper is organized as follows. Section II provides an overview of existing methods for anomaly detection. Traditional anomaly detection methods are discussed in part A of Section II, whereas the state-of-the-art deep learning-based anomaly detection methods are mentioned and summarized in part B of Section II. Section III provides the related background information on traditional autoencoders and autoencoder based anomaly detection. The methodology including the problem formulation and the design of the proposed hybrid deep learning framework is presented in Section IV. Experiments and results are presented in Section V. Finally, Section VI concludes the paper and gives the directions for possible future work.
II. Related Work
A. Traditional Approaches
The task of detecting outliers or anomalous events in data has been studied extensively in the context of time series and spatial data separately. Time-series outlier detection studies find outliers considering only temporal context [21], [22]. For data with spatial context, several context-based anomaly detection techniques have been proposed [23]–[26]. In geoscience and environmental research, some statistical and simulation-based methods have been proposed for spatial anomaly detection [27], [28]. For spatio-temporal outlier detection, both spatial and temporal continuity should be considered for modeling. Hence, spatio-temporal outlier detection methods are significantly more challenging because of the additional difficulty of modeling the temporal and spatial components jointly [2], [3].
Distance and density-based outlier detection algorithms have also been applied to anomaly detection problems in spatial datasets, such as Local Outlier Factor (LOF) [29], [30], and DBSCAN [31]. LDBSCAN algorithm [32], created by the merge of DBSCAN and LOF, is a density-based algorithm for unsupervised anomaly detection problems in spatial databases with noise. Another popular proximity-based outlier detection approach is based on cluster analysis. The non-membership of a data point to any of the clusters can be used as a sign of being outlier [33]. Cluster-Based Local Outlier Factor (CBLOF) [34] is a clustering-based anomaly detection algorithm, in which the anomaly score of an instance is the distance to the next large cluster. Choosing the right number of clusters is very important since all clustering methods tend to be very sensitive to this choice.
In [35], Birant and Kut propose a neighborhood-based ST-Outlier detection algorithm. They use a modified version of DBSCAN algorithm to identify the spatial neighborhoods within the dataset. They define spatial outliers based on these neighborhoods. Then, they check the temporal context of spatial outlier objects by comparing them to temporal neighbor objects. However, their algorithm does not generate a score for data points. In [2], Cheng and Li propose a four-step approach to identify spatio-temporal outliers: classification (clustering), aggregation, comparison and verification. In [36], Gupta et al. introduce the notion of context-aware anomaly detection in distributed systems by integrating the information from system logs and time series measurement data. They propose a two-stage clustering methodology to extract context and metric patterns using a PCA-based method and a modified K-Means algorithm.
The aforementioned spatio-temporal anomaly detection methods have something in common: They first apply spatial (or non-temporal) context to find spatial outliers using a distance-based technique. Then, spatial outliers are compared with other spatial objects using temporal neighborhoods to identify if they are temporal outliers too. They do not combine the contextual (spatial and temporal) attributes in a meaningful way as these attributes refer to different types of dependencies. Despite the inherent unsupervised settings of distance and cluster-based algorithms, they may still not detect anomalies effectively due to the following reasons:
-
1)
In multivariate time series data, strong temporal dependency exists between time steps. Hence, distance-/ cluster-based methods, may not perform well since they cannot capture temporal dependencies properly across different time steps.
-
2)
The definition of distance between data points in multivariate spatio-temporal data with mixed attributes is often challenging. This difficulty may have an adverse effect on outlier detection performance of distance-based clustering algorithms.
-
3)
Another problem with distance-based methods is that they are well known to be computationally expensive and not suitable for large datasets.
IsolationForest [37], [38] is a powerful approach for anomaly detection in multivariate data without relying on any distance or density measure. In particular, it is an unsupervised, tree-based ensemble method that applies the novel concept of isolation to anomaly detection. It detects anomalies based on a fundamentally different model-based approach: an anomalous point is isolated via recursive partitioning by randomly selecting a feature, and then randomly selecting a split value for the selected feature. The output is the anomaly score for each data point. Although it establishes a powerful multivariate non-parametric approach, it works on continuous-valued data only. Numenta HTM [39], [40] is an unsupervised anomaly detection method for univariate streaming data based on Hierarchical Temporal Memory (HTM). It works based on the multiple predictions for the next time step which is done by a layer of HTM neurons. Anomaly score is generated based on the likelihood of the prediction error, which is a probabilistic metric defining how anomalous the current state is, based on prediction history. One-class SVM (OCSVM), which is a semi-supervised anomaly detection technique, has been applied extensively to anomaly detection problems in time series data [41]–[43]. However, OCSVM is sensitive to the outliers especially when used in an unsupervised fashion when there are no labels.
Several algorithms proposed in the statistics literature have been used widely for time series prediction and anomaly detection such as autoregressive integrated moving average (ARIMA) and Exponentially Weighted Moving Average (EWMA) [44]–[47]. Most detection algorithms in bio-surveillance which operate on univariate time series data have been taken from the field of quality control [48]. The common techniques include control charts [49] and CUmulative SUM Statistics (CUSUM) [47], [50]. What’s Strange About Recent Events (WSARE) [48] algorithm was developed for syndromic surveillance to the hospital setting, such as symptoms exhibited by patients at an Emergency Department (ED). WSARE is a rule-based algorithm specifically designed for patients’ pre-clinical data. It combines two approaches: association rule mining and Bayesian networks. Although the WSARE algorithm works on multidimensional data, it can only be used on categorical data sets. The Spatial Scan Statistic [51] can be considered the real-valued analog of WSARE. However, it is computationally expensive for large data sets. Neill and Cooper [52] proposed the multivariate Bayesian scan statistic (MBSS) for event detection in multivariate spatial time series data. However, their approach requires the prior probability of each event occurring in each space-time region. They need either an expert knowledge or labeled data to obtain the prevalence of each event type.
B. Deep Learning Based Approaches
Besides traditional anomaly detection methods, deep learning-based anomaly detection approaches have recently gained a lot of attention. In the literature, artificial neural networks have been widely applied to anomaly detection tasks for various types of datasets [53]. Reconstruction based and prediction based deep learning models are among the most widely used architectures for anomaly detection in videos and time-series data [54], [55].
Malhotra et al.
[56] proposes a deep Long Short-Term
Memory (LSTM) network to detect anomalies in univariate time series. They use
LSTM network architecture to predict next
 steps of the
input. Then, the prediction error is used to detect anomalies. The model is
trained using normal data to learn the Gaussian distribution of error vectors.
Malhotra et al.
[57] propose an LSTM network-based
encoder-decoder scheme for anomaly detection in univariate time series datasets.
Their model learns to reconstruct ‘normal’ time series data and
uses reconstruction error to detect anomalies. Hasan et al.
[58] propose a deep fully convolutional
autoencoder to reconstruct the input sequence of video frames to detect
anomalies. The network is trained in semi-supervised fashion with regular
videos. It learns the signature of each frame in regular motion videos. An
anomaly score of each frame in the test set is then calculated based on
reconstruction error.
steps of the
input. Then, the prediction error is used to detect anomalies. The model is
trained using normal data to learn the Gaussian distribution of error vectors.
Malhotra et al.
[57] propose an LSTM network-based
encoder-decoder scheme for anomaly detection in univariate time series datasets.
Their model learns to reconstruct ‘normal’ time series data and
uses reconstruction error to detect anomalies. Hasan et al.
[58] propose a deep fully convolutional
autoencoder to reconstruct the input sequence of video frames to detect
anomalies. The network is trained in semi-supervised fashion with regular
videos. It learns the signature of each frame in regular motion videos. An
anomaly score of each frame in the test set is then calculated based on
reconstruction error.
Various deep learning-based feature extraction methods have been proposed in the literature. The proposed architectures are used to extract useful (discriminative) features for anomaly detection, novelty detection or classification problems. Yang et al. [59] present a CNN-LSTM based recurrent autoencoder network for unsupervised extraction of highlights in video data, whereas in [60] a pre-trained 3D convolutional network is used to extract features from video segments for anomaly detection process. Munawar et al. [61] build an encoder composed of deep convolutional neural network and Restricted Boltzman Machine to extract features from videos. The extracted features are fed into an LSTM based prediction system to predict the next video frame in the learned feature space. Then, the difference between the prediction and actual observation in the feature space is used to detect anomalies. In a recent study, Perera and Patel [62] propose a one-class transfer learning schema for feature extraction based on Convolutional Neural Network (CNN). Estiri and Murphy [63] use a semi-supervised deep autoencoder for outlier detection in multivariate clinical observation data from Electronic Health Records (EHR).
D’Avino et al. [64] propose an LSTM-based autoencoder framework to detect forgeries in video frames. They train their model with pristine frames without any forgeries. They use reconstruction errors to detect any abnormalities in the frames with spliced areas. Chong and Tay [65] propose a spatiotemporal architecture for anomaly detection in videos. Their autoencoder based anomaly detection framework contains a spatial feature extractor and temporal encoder-decoder component. The spatial encoder component comprises two convolutional and two de-convolutional layers. They use a three-layer convolutional long short-term memory (LSTM) network as temporal encoder-decoder component. Munir et al. [66] present DeepAnT, a deep learning based unsupervised anomaly detection approach for time series data. DeepAnT architecture is based on 1D deep convolutional neural network to predict univariate time series data. They use the prediction-based approach where a window of time series is used as a context and the next time stamp is predicted. The anomaly detector module uses the prediction error and a pre-defined threshold value to tag each data point as normal or abnormal. Nogas et al. [67] use a deep spatio-temporal convolutional autoencoder schema, DeepFall, to detect falls in videos. They formulate the fall detection problem as one class classification problem. Their classification framework consists of a 3D convolutional autoencoder for learning spatio-temporal features from video frames. They use semi-supervised learning approach that their model is trained only on the videos with normal activities of daily living without fall frames in them. Then, they use annotated video data to detect fall frames which are considered abnormal.
Despite the effectiveness of those abovementioned deep learning approaches, they are either supervised or semi-supervised models. In the supervised approaches, models need labels for all targeted anomaly classes for training. In the semi-supervised approaches, models use only normal data to model the majority class (normal class) to further detect future anomalies. The proposed framework is designed to be trained in a truly unsupervised fashion without any labels indicating normal or abnormal data. The architecture is robust enough to learn the underlying dynamics even if the training dataset contains noise and anomalies. The main distinction between other deep learning based methods and the proposed hybrid approach is that they perform on either multivariate time series data or video data, and none of them is actually designed for non-image spatio-temporal multivariate datasets with both spatial and temporal contextual attributes.
III. Background
A. Autoencoders
Autoencoders are commonly used for dimensionality reduction of multidimensional data as a powerful non-linear alternative to PCA or matrix factorization [68]–[70]. If a linear activation function is used, the autoencoder becomes virtually identical to a simple linear regression model or PCA/matrix factorization model. When a nonlinear activation function is used, such as rectified linear unit (ReLU) or a sigmoid function, the autoencoder goes beyond the PCA, capturing multi-modal aspects of the input distribution [71], [72]. It is shown that carefully designed autoencoders with tuned hyperparameters outperform PCA or K-Means methods in dimension reduction and characterizing data distribution [73], [74]. They are also more efficient in detecting subtle anomalies and in computation cost than linear PCAs and kernel PCAs respectively [75].
A traditional autoencoder is a feed-forward multi-layer neural network which is trained to copy its input into the output. To prevent identity mapping, deep autoencoders are built with low dimensional hidden layers by creating non-linear representation of input data [68]. Usually, an autoencoder with more than one hidden layer is called a deep autoencoder [76]. Deep autoencoders have been successfully applied to dimensionality reduction, image denoising, and information retrieval tasks [77], [78].
An autoencoder is trained to encode the input
 into some latent
representation
into some latent
representation
 so that the
input can be reconstructed from that lower dimensional representation. An
autoencoder is usually trained using back-propagation in an unsupervised manner,
to learn how to build its original input by minimizing the reconstruction error
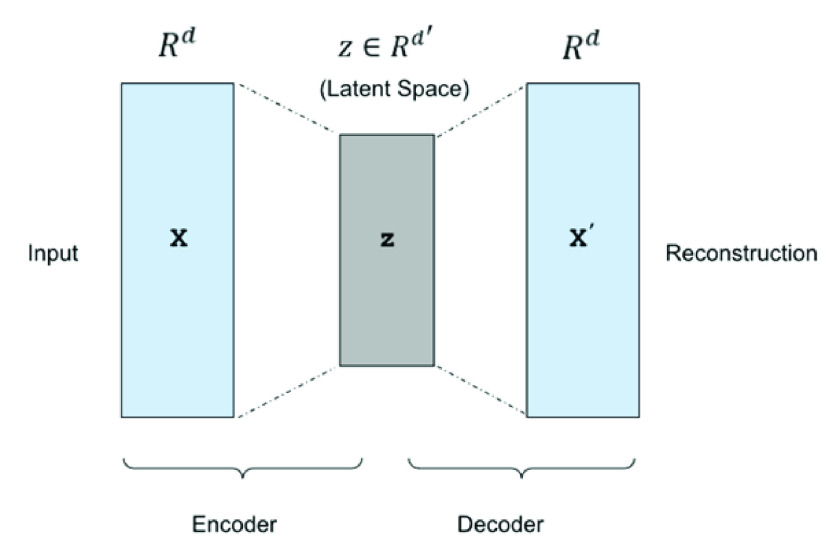
of the decoding results. Fig. 1 depicts a
typical autoencoder network structure with one hidden layer. They are composed
of two parts: an encoder and a decoder. Deep autoencoders learn a non-linear
mapping from the input to the output through multiple encoding and decoding
steps. An autoencoder takes an input vector
so that the
input can be reconstructed from that lower dimensional representation. An
autoencoder is usually trained using back-propagation in an unsupervised manner,
to learn how to build its original input by minimizing the reconstruction error
of the decoding results. Fig. 1 depicts a
typical autoencoder network structure with one hidden layer. They are composed
of two parts: an encoder and a decoder. Deep autoencoders learn a non-linear
mapping from the input to the output through multiple encoding and decoding
steps. An autoencoder takes an input vector
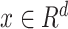 , and
first maps it to a latent representation
, and
first maps it to a latent representation
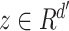 through a mapping:
through a mapping:
 |
where the
function
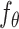 represents encoding steps and parameterized by
represents encoding steps and parameterized by
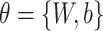 .
.
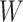 is a
is a
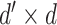 weight matrix and
weight matrix and
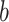 is a bias
vector. The lower dimensional latent representation of the input is then mapped
back to a reconstructed vector
is a bias
vector. The lower dimensional latent representation of the input is then mapped
back to a reconstructed vector
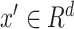 in the input space:
in the input space:
 |
where the function
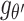 represents decoding steps and parameterized by
represents decoding steps and parameterized by
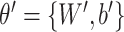 . The autoencoders training
procedure consists of finding a set of parameters
. The autoencoders training
procedure consists of finding a set of parameters
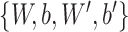 that make the reconstructed
vector
that make the reconstructed
vector
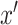 as
close as possible to the original input
as
close as possible to the original input
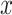 . The parameters
of autoencoder are optimized by minimizing a loss function that measures the
quality of the reconstructions. The loss function of an autoencoder is
sum-of-squared differences between the input and the output:
. The parameters
of autoencoder are optimized by minimizing a loss function that measures the
quality of the reconstructions. The loss function of an autoencoder is
sum-of-squared differences between the input and the output:
 |
where
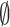 is the
training dataset.
is the
training dataset.
FIGURE 1.
Illustration of an autoencoder.
B. Anomaly Detection With Autoencoders
The main idea behind autoencoder based anomaly detection is to measure how much the reconstructed data deviates from the original data. An autoencoder has an unsupervised learning objective whose primary task is to copy the input to the output [77]. Therefore, an autoencoder is trained to reconstruct data by minimizing this objective function, or loss function. For anomaly detection, reconstruction error is used as the anomaly score. Data points which generate high reconstruction errors can be categorized as anomalous data points based on a threshold value. When autoencoders are used for anomaly detection, they are trained using only normal data instances as we have abundance of normal data. The training dataset should be cleaned from anomalous data points and outliers as much as possible for a successful model generation. After the training process, the autoencoder will generally reconstruct normal data with very small reconstruction error. As the autoencoder has not encountered the abnormal data during the training, it will fail to reconstruct them and generate high reconstruction errors which can be used as anomaly score [71], [75].
There are some practical issues in using autoencoders with contaminated training data (dataset with normal and anomalous data points). Since anomalies are treated as normal data points during the training phase, there will be inevitably more errors in the model compared to training with only normal data points. If we try to overcome these errors by tuning the network with more layers and neurons, we may face the problem of overfitting which is a significant problem in the case of deep neural networks. A sufficiently complex deep autoencoder may even learn how to represent each anomaly with sufficient training by generating low reconstruction errors which would be a problem in anomaly detection [71].
IV. Methodology
A. Problem Formulation
A univariate time series is a sequence of real valued data points with timestamps. A multivariate time series is a set of univariate time series with the same timestamps. In this paper, we focus on multivariate time series that are measured at successive points in time, spaced at uniform time intervals.
Let
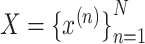 denote a multivariate time series dataset
composed of N data points. Let each data point
denote a multivariate time series dataset
composed of N data points. Let each data point
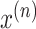 has
has
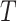 time steps, and
each observation at time step t, is a
time steps, and
each observation at time step t, is a
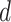 dimensional
vector. The dataset
dimensional
vector. The dataset
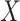 has dimensions
of (d,
has dimensions
of (d,
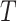 ), where
), where
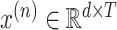 . Each data point
. Each data point
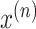 is a
two-dimensional data matrix and can be represented as:
is a
two-dimensional data matrix and can be represented as:
 |
The superscript
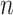 represents the
ordered number of each data point within the dataset
represents the
ordered number of each data point within the dataset
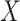 .
.
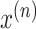 is a
multivariate time series data point with a contextual time attribute. Each
is a
multivariate time series data point with a contextual time attribute. Each
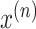 in the
dataset
in the
dataset
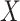 is ordered based
on the timestamp. As the number
is ordered based
on the timestamp. As the number
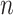 increases, the
time context changes, and time dimension, or timestamps, moves ahead.
increases, the
time context changes, and time dimension, or timestamps, moves ahead.
In a spatio-temporal dataset, each multivariate data point
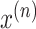 comes from
a different spatial location, or region, which has different spatial attributes
(such as latitude and longitude). We denote the multivariate spatio-temporal
dataset as
comes from
a different spatial location, or region, which has different spatial attributes
(such as latitude and longitude). We denote the multivariate spatio-temporal
dataset as
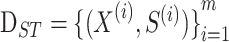 which contains multivariate time series data
points from
which contains multivariate time series data
points from
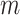 different
spatial regions. Each spatial region
different
spatial regions. Each spatial region
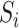 , where
, where
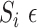 S, has a set of multivariate time series data represented by
the dataset
S, has a set of multivariate time series data represented by
the dataset
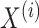 .
.
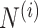 represents
the number of data points (or observations) in each spatial region
represents
the number of data points (or observations) in each spatial region
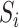 . In other
words, it is the size of
. In other
words, it is the size of
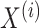 , which may be different for each region in
real-world scenarios.
, which may be different for each region in
real-world scenarios.
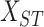 , which is
the multivariate spatio-temporal data matrix, can be represented as a
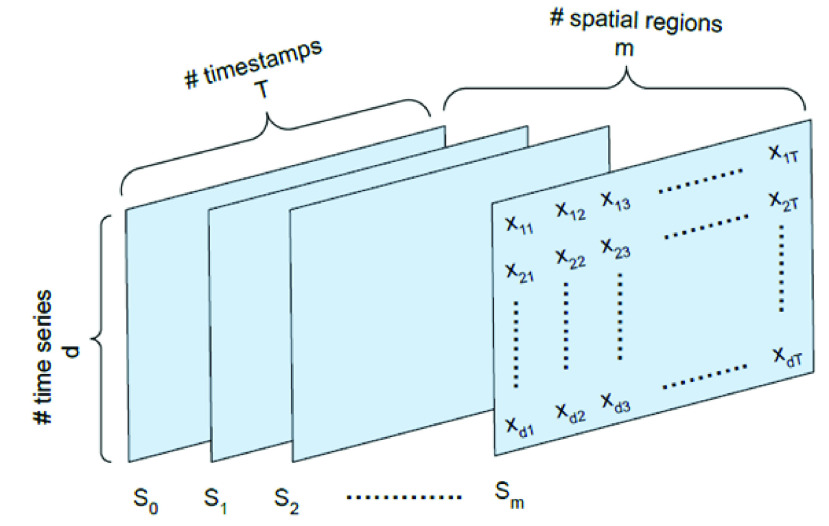
3-dimensional tensor as shown in Fig. 2.
It is built using multivariate time series data from
, which is
the multivariate spatio-temporal data matrix, can be represented as a
3-dimensional tensor as shown in Fig. 2.
It is built using multivariate time series data from
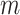 different
spatial regions or
different
spatial regions or
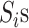 ,
where
,
where
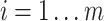 . The
sliding window technique which is used to build the 3-dimensional data matrix
. The
sliding window technique which is used to build the 3-dimensional data matrix
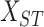 , is given
in Algorithm 1. It is composed of
, is given
in Algorithm 1. It is composed of
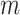 multivariate
time series data points from
multivariate
time series data points from
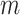 different
spatial regions and representing observations from the same time window with the
same timestamps.
different
spatial regions and representing observations from the same time window with the
same timestamps.
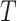 , which is called
the “input window-size”, represents the number of timestamps in
the multivariate data point, and
, which is called
the “input window-size”, represents the number of timestamps in
the multivariate data point, and
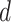 represents the
number of univariate time series.
represents the
number of univariate time series.
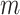 represents the
number of nearest spatial neighborhood to include in the anomaly detection
process. The best
represents the
number of nearest spatial neighborhood to include in the anomaly detection
process. The best
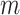 can be found
empirically for each problem domain. The
can be found
empirically for each problem domain. The
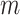 number of
nearest neighboring regions are selected from
number of
nearest neighboring regions are selected from
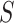 different
regions based on the pairwise spatial distance between regions.
different
regions based on the pairwise spatial distance between regions.
Algorithm 1 Sliding Window Algorithm Used in Subsequence Generation
# dataset: region dataset
# T: Number of timesteps, window size (T)
# region_list: region id list
# s: sliding step size
# depth: the number of spatial neighbors
# distance_matrix: distance matrix of regions
# output: multivariate spatio-temporal tensor data process_dataset (dataset, T, region_list, s, depth, distance_matrix)
-
1:
output = list()
-
2:
for each region in region_list:
# get region data from dataset
-
3:
data
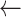 dataset[region]
dataset[region] -
4:
start_indx = 0
-
5:
end_indx = start_indx + T
# step through the region data
-
6:
while (end_indx < length(data)):
# get start and end timestamps of data slice of size
-
7:
start_date = getStartTimestamp (data, start_indx)
-
8:
end_date = getEndTimestamp(data, end_indx)
# get subsequence from region data:
# seqs: 3D spatio-temporal data
-
9:
seqs[n, 0] = data[start_indx..end_indx]
# get subsequences from depth-1 nearest neighbours:
-
10:
seqs[n, 1:depth] = getDataFromNeighbours(dataset, T, start_date_time, end_date_time, region_code, depth-1) output.append(seqs)
-
10.
start_indx = start_indx + s
-
11.
end_indx = start_indx + T
-
12.
n = n + 1, # end-while
-
13.
return output
FIGURE 2.
3-dimensional multivariate spatio-temporal data matrix structure used in anomaly detection procedure.
We formulate the spatio-temporal anomaly detection problem as detecting anomalous
multivariate observations (sample of
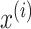 data
points) in the dataset
data
points) in the dataset
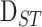 which differentiate significantly from their spatial and temporal neighbors.
Given the spatio-temporal 3-dimensional data matrix
which differentiate significantly from their spatial and temporal neighbors.
Given the spatio-temporal 3-dimensional data matrix
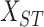 , the goal
is to reconstruct the multivariate-time series data from the region
, the goal
is to reconstruct the multivariate-time series data from the region
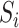 , where
, where
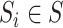 .
.
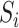 represents
the target region or the region of interest in which spatio-temporal anomalies
are investigated. Anomalous data points have large reconstruction errors because
they do not conform to the subspace patterns in the data. Therefore, the
aggregated reconstruction errors over the time dimension
represents
the target region or the region of interest in which spatio-temporal anomalies
are investigated. Anomalous data points have large reconstruction errors because
they do not conform to the subspace patterns in the data. Therefore, the
aggregated reconstruction errors over the time dimension
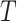 can be used as
the anomaly score for the autoencoder based proposed framework. All
can be used as
the anomaly score for the autoencoder based proposed framework. All
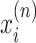 multivariate data points, or sub sequences, with high reconstruction errors from
the region
multivariate data points, or sub sequences, with high reconstruction errors from
the region
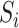 are
considered to be anomalies.
are
considered to be anomalies.
B. Proposed Hybrid Framework
The proposed approach consists of three main stages: The first stage is the data
pre-processing stage. At this stage, the multivariate spatio-temporal dataset is
processed in such a way that the deep autoencoder network can exploit the
spatial and temporal contexts jointly. Multivariate data from
 nearest spatial
neighbors are used to represent spatial dependency between different spatial
regions. The sliding window technique given in Algorithm 1 is applied to build the multivariate
spatial-temporal input data for the framework. By using the multistep
overlapping subsequences from
nearest spatial
neighbors are used to represent spatial dependency between different spatial
regions. The sliding window technique given in Algorithm 1 is applied to build the multivariate
spatial-temporal input data for the framework. By using the multistep
overlapping subsequences from
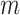 nearest spatial
neighborhood of each data point, we build a 3-dimensional data matrix as shown
in Fig. 2, which can represent the
spatial and temporal dependency within the dataset.
nearest spatial
neighborhood of each data point, we build a 3-dimensional data matrix as shown
in Fig. 2, which can represent the
spatial and temporal dependency within the dataset.
The important parameters of this algorithm are window size
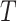 and step size
and step size
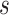 . They should be
chosen carefully based on the underlying dynamics of each dataset and the goal
of anomaly detection problem at hand. The length of each subsequence is equal to
the window size. Using sliding window technique, for a long sequence with length
L, the number of extracted subsequences can be given as:
. They should be
chosen carefully based on the underlying dynamics of each dataset and the goal
of anomaly detection problem at hand. The length of each subsequence is equal to
the window size. Using sliding window technique, for a long sequence with length
L, the number of extracted subsequences can be given as:
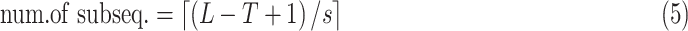 |
which gives the maximum number of subsequences we
can possibly extract for a given
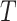 and
and
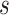 .
.
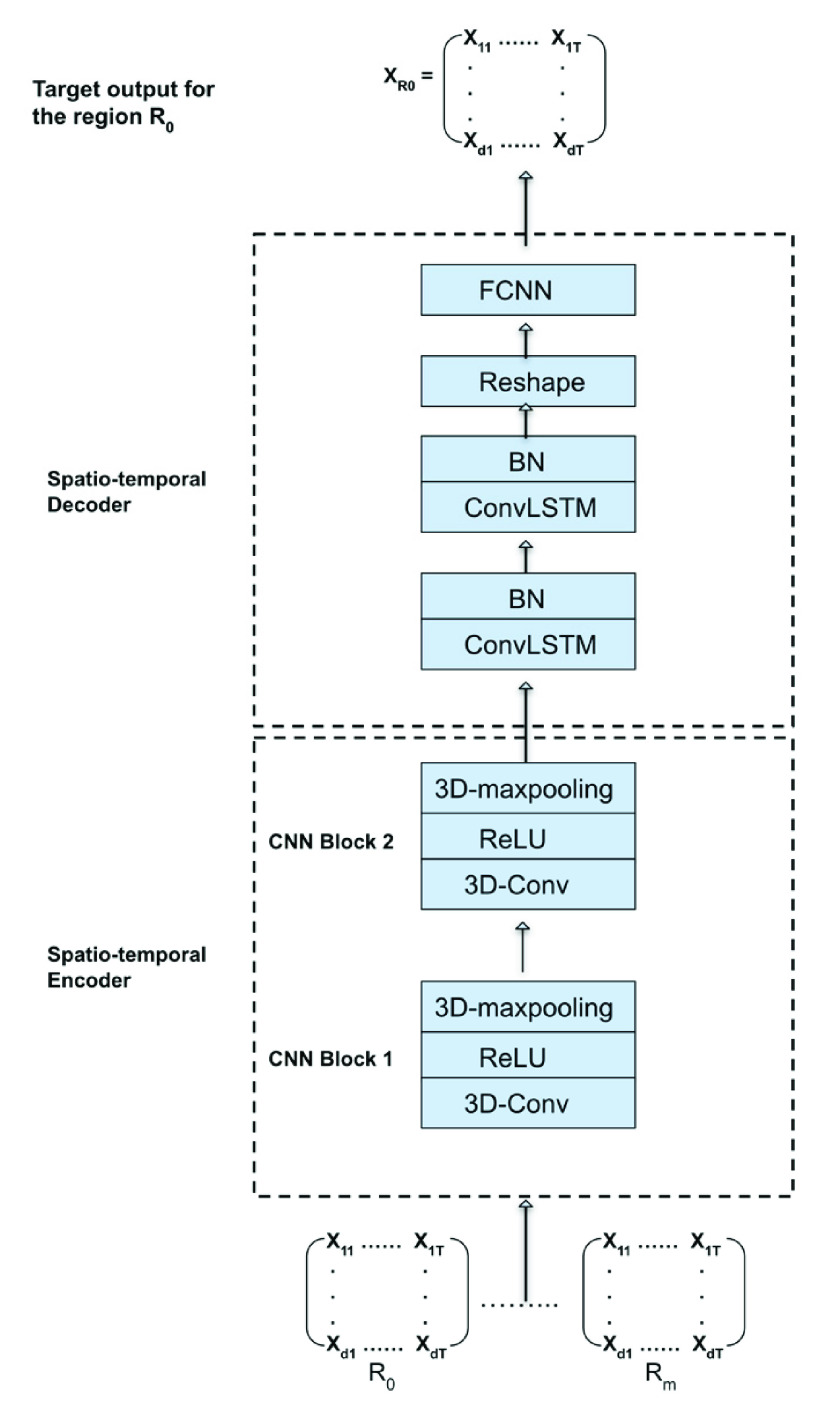
The second stage is the data reconstruction stage which is executed by the deep hybrid autoencoder network. The proposed hybrid autoencoder network consists of two main components: a spatio-temporal encoder component which has a 3D convolutional neural network (CNN), and a spatio-temporal decoder component which has a Convolutional Long Short-term Memory (ConvLSTM) network.
The third stage is the anomaly detection stage. The anomaly detection is
performed by calculating the reconstruction error as anomaly score. Let
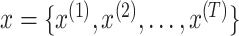 be a univariate time series data representing
one of the reconstructed features and
be a univariate time series data representing
one of the reconstructed features and
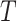 is the length of
the input window. Each data point
is the length of
the input window. Each data point
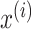 represents
a data reading for that feature at time instance
represents
a data reading for that feature at time instance
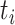 . The mean
absolute error (MAE) is used to calculate the reconstruction error for the given
time period (input window) for each feature as:
. The mean
absolute error (MAE) is used to calculate the reconstruction error for the given
time period (input window) for each feature as:
 |
where
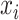 is the real
value and
is the real
value and
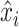 is
the reconstructed value at time instance
is
the reconstructed value at time instance
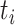 . The
reconstruction error for each feature and for all data points in the test set is
calculated. Each data point in the test set represents a window of size
. The
reconstruction error for each feature and for all data points in the test set is
calculated. Each data point in the test set represents a window of size
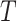 as the rolling
window. As each data point in the dataset is generated using sliding window
algorithm with step size set to
as the rolling
window. As each data point in the dataset is generated using sliding window
algorithm with step size set to
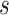 , we generate
rolling window estimation, and hence the rolling window errors.
, we generate
rolling window estimation, and hence the rolling window errors.
For an anomaly detection problem, we are only interested with the reconstruction
of a subset of original spatio-temporal multivariate dataset and not the fully
reconstructed version of it. The overall framework is trained to produce the
target multivariate time series
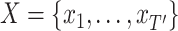 of length
of length
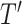 which
is the size of the reconstruction window. The length of
which
is the size of the reconstruction window. The length of
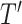 can be
equal to or smaller than the input window size
can be
equal to or smaller than the input window size
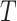 and should be
tuned for each problem. Each sequence
and should be
tuned for each problem. Each sequence
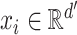 is an
is an
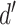 -dimensional vector where
-dimensional vector where
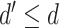 .
.
C. Spatio-Temporal Encoding
The encoder component uses 3D convolutions to capture complex spatial dependencies in each spatial neighborhood. By convolving a 3D kernel over the cube formed data, the encoder can extract better representative features. The cuboid data is formed by stacking the data from the nearest spatial neighbors of each data point as explained in Algorithm 1. This allows information across these spatially close neighbors to be connected to form feature maps, thereby capturing spatio-temporal information encoded in the close neighborhood.
In most typical CNNs for image recognition, the input data is a single image with
three channels for color images (R, G and B color channels) or one channel for
grayscale images. In anomaly detection networks, the input data is generally a
video clip consisting of multiple frames. In convolutional autoencoder based
applications,
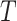 frames in the
channel dimension are stuck, and then fed into the autoencoder where
frames in the
channel dimension are stuck, and then fed into the autoencoder where
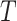 is the length of
the sliding window. In the case of 2D convolutional autoencoders, the temporal
features are rarely preserved as 2D convolution operations are performed only
spatially [58].
is the length of
the sliding window. In the case of 2D convolutional autoencoders, the temporal
features are rarely preserved as 2D convolution operations are performed only
spatially [58].
In this study, 3D convolutional operations are applied on multivariate
spatio-temporal data to better preserve the temporal features along with the
spatial features. The input data are re-constructed as a 3-dimensional cuboid by
stacking multivariate data frames as illustrated in Fig. 2. By applying this idea, we can accomplish
dimensionality reduction both in spatial and temporal context for a given input
window during the encoding phase. The main component of the spatio-temporal
encoder is the 3D convolutional layer, which is defined as follows: the value
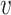 at position
at position
 of the
of the
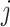 th feature map
in the
th feature map
in the
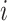 th 3D
convolutional layer, with bias
th 3D
convolutional layer, with bias
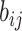 , can be
written by the following equation [79]:
, can be
written by the following equation [79]:
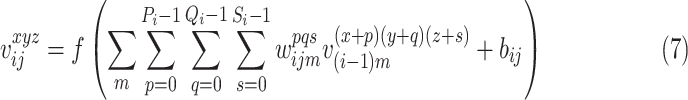 |
where
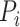 ,
,
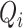 , and
, and
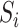 represent
the vertical (temporal depth, or window size,
represent
the vertical (temporal depth, or window size,
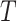 ), horizontal
(temporal width, or number of features,
), horizontal
(temporal width, or number of features,
 ), and spatial
depth (number of spatial neighbors,
), and spatial
depth (number of spatial neighbors,
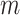 ) dimensions of
the kernel cube
) dimensions of
the kernel cube
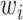 in the
in the
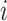 th layer. The set
of feature maps from the
th layer. The set
of feature maps from the
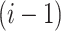 th layer is indexed by
th layer is indexed by
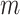 , and
, and
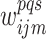 is
the value of the kernel cube at the position
is
the value of the kernel cube at the position
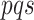 connected to
the
connected to
the
 th feature map in
the previous layer. The number of feature maps is defined by the number of
kernel cubes at each convolution layer.
th feature map in
the previous layer. The number of feature maps is defined by the number of
kernel cubes at each convolution layer.
D. Spatio-Temporal Decoding
For the decoding part of the framework, we use convolutional LSTM (ConvLSTM) network, which is a variant of LSTM network. It has been introduced by Shi et al. [80]. It has been recently utilized by Chong and Tay in [65] for abnormal event detection in videos and by Patraucean et al. in [81] for motion estimation in videos.
The major drawback of regular Long Short-Term Memory (LSTM) networks is that they are not capable of preserving the spatial information during the state transitions [80]. To overcome this problem, ConvLSTM units have convolutions operations in place of matrix operations in all gates and cell outputs. As they use convolution for both input-to-hidden and hidden-to-hidden connections, they require fewer weights and yield better spatio-temporal feature encoding and decoding performance. The formulation of a ConvLSTM unit can be given by the following equations from (8) through (13):
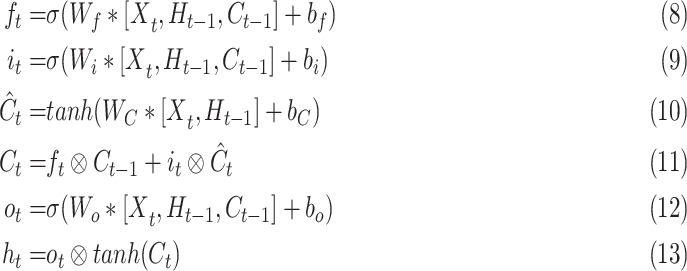 |
where ’*’ denotes the
convolution operator and ‘
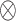 ’
denotes the Hadamard product. Equation (8) represents the forget gate, (9) and (10) are the gates where new
information (input
’
denotes the Hadamard product. Equation (8) represents the forget gate, (9) and (10) are the gates where new
information (input
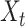 ) is added,
(11) combines the
new and old information factored by the forget gate, whereas (12) and (13) give the
output of the ConvLSTM unit for the next time step. The variable
) is added,
(11) combines the
new and old information factored by the forget gate, whereas (12) and (13) give the
output of the ConvLSTM unit for the next time step. The variable
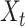 denotes the
input vector,
denotes the
input vector,
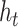 denotes the
hidden state, and
denotes the
hidden state, and
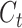 denotes the
cell state for the time step
denotes the
cell state for the time step
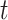 .
.
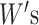 are the
trainable weight matrices and
are the
trainable weight matrices and
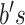 are the bias
vectors.
are the bias
vectors.
V. Experiment
A. Dataset
We use the public Italian COVID-19 time series dataset provided by the Italian Department of Civil Protection. It can be downloaded from the website [82], which is constructed as a national response effort for coronavirus emergency. For this study, we use the regional dataset which shows the daily progress of new coronavirus epidemic in regions of Italy. The regional dataset provides detailed epidemiological figures for all 21 regions (19 regions and 2 autonomous provinces) starting from February 24 and updated daily.
The regions dataset has 20 features as follows (translated into English): Date, country, region code, region name, latitude, longitude, hospitalized with symptoms, intensive care patients, total hospitalized patients, home isolation, total positives (current positives), change in total positive, new positives, recovered (discharged), deceased, total cases, tests performed, total number of people tested, notes in Italian, notes in English.
Features “date, country, region code, region name, latitude, longitude” are contextual attributes whereas the rest are regarded as behavioral attributes. The feature “tests performed” is part of the government intervention measures and shows significant differences between regions depending on the policies taken by each regional government in Italy [83]. As proactive testing and mobility can affect the epidemiological dynamics of the COVID-19 epidemic [84], it is regarded as contextual variable for the modelling, and is not included in the reconstruction space as a behavioral attribute.
All these features have been used during the modeling except the redundant and mostly empty attributes. The “total number of people tested” field is empty for most of the regions, so it is dropped for the modelling. Features “notes in Italian, notes in English, total number of people tested” are also discarded for this study as they are mostly empty. As the only country in the dataset is Italy, ‘country’ column is also dropped. On the website, the data format is explained as follows:
-
•
total positives: Total amount of current positive cases (hospitalized patients + home confinement)
-
•
change in total positive: New amount of current positive cases (total positives current day – total positives previous day)
-
•
new positives: New amount of current positive cases (total cases current day – total cases previous day)
-
•
total cases: Total amount of positive cases
Based on those detailed descriptions of dataset, we rename the feature “total positives” as “current positive cases” in our study to make the feature name more representative. We also regard the feature “new positives” as “daily confirmed new positive cases,” and renamed it as “new positive cases” for clarity. In addition to the regional epidemic data, we have also used population data of each region from ISTAT website [85]. By using population information, we have calculated three additional features: “total positive cases, new positive cases and deaths” on each 10,000 inhabitants. Using these engineered features, we have incorporated the case density information on each region to enrich spatial data.
Latitude and longitude are also provided for each region making this regional dataset a spatiotemporal dataset. Daily epidemic data entry for each region has two contextual attributes: a date attribute (temporal context) and latitude-longitude attributes (spatial context), which is static for each region. Besides these contextual attributes, the rest of the attributes including the engineered features are regarded as behavioral attributes. We use the min-max normalization method to scale all behavioral attributes in the dataset into the range of [0, 1] to accelerate the learning process and to avoid large weights which cause neural networks to overfit.
B. Data Preparation
We use the regional data entries between February 24 and May 15, inclusively. The model is trained with the data from northern regions which provides a complete epidemiological data in the sense that they have gone through all the peaks of COVID-19 outbreak showing a complete perspective for anomaly detection. The training dataset contains data from following northern regions: P.A. Bolzano, Emilia-Romagna, Liguria, Lombardia, Piemonte, P.A. Trento, Valle d’Aosta, Veneto, and Friuli Venezia Giulia. We use data from one central region (Marche) as validation set; data from one central region (Lazio), one region from southern Italy (Campania), and one island region (Sicilia) as test set. The total data entry for each region is 82, which means 82 days of COVID-19 epidemiological data are entered for each region.
The spatial attributes of all regions used in this study is given in Table 1. Using the latitude and longitude information, we calculate the distance matrix showing the pairwise distance of all regions used in this study. We use the haversine formula to calculate the shortest distance between regions, which is used to measure distances on a sphere [86].
TABLE 1. Region Information.
| Region Name | Latitude | Longitude | Population |
|---|---|---|---|
| Piemonte | 45.0733 | 7.68069 | 4356406 |
| Valle d’Aosta | 45.7375 | 7.32015 | 125666 |
| Lombardi | 45.4668 | 9.19035 | 10060574 |
| P.A. Bolzano | 46.4993 | 11.3566 | 531178 |
| P.A. Trento | 46.0689 | 11.1212 | 541098 |
| Veneto | 45.4349 | 12.3385 | 4905854 |
| Friuli Venezia Giulia | 45.6494 | 13.7681 | 1215220 |
| Liguria | 44.4115 | 8.9327 | 1550640 |
| Emilia-Romagna | 44.4944 | 11.3417 | 4459477 |
| Marche | 43.6168 | 13.5189 | 1525271 |
| Lazio | 41.8928 | 12.4837 | 5879082 |
| Campania | 40.8396 | 14.2508 | 5801692 |
| Sicilia | 38.1157 | 13.3624 | 4999891 |
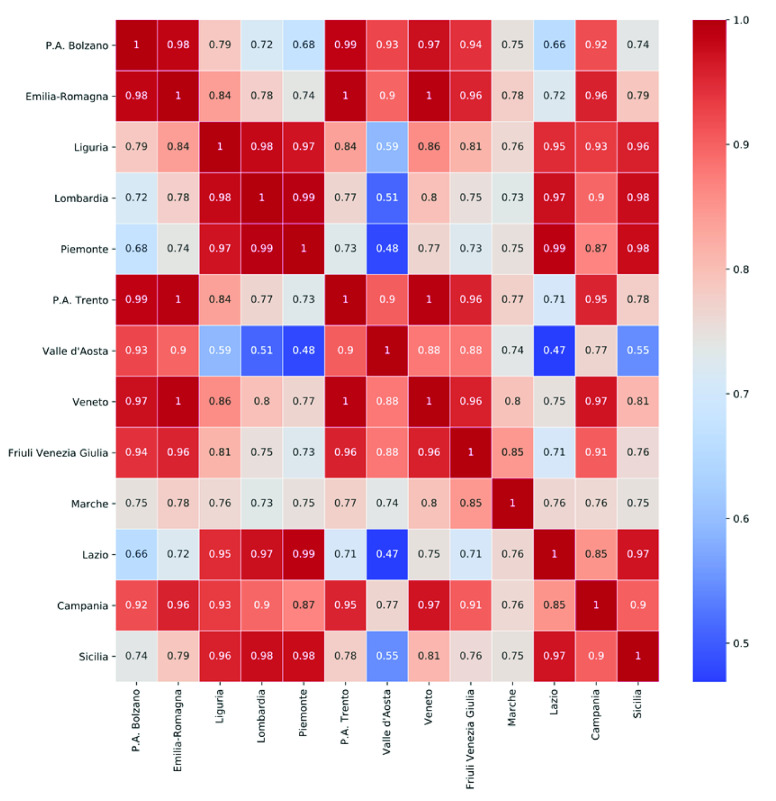
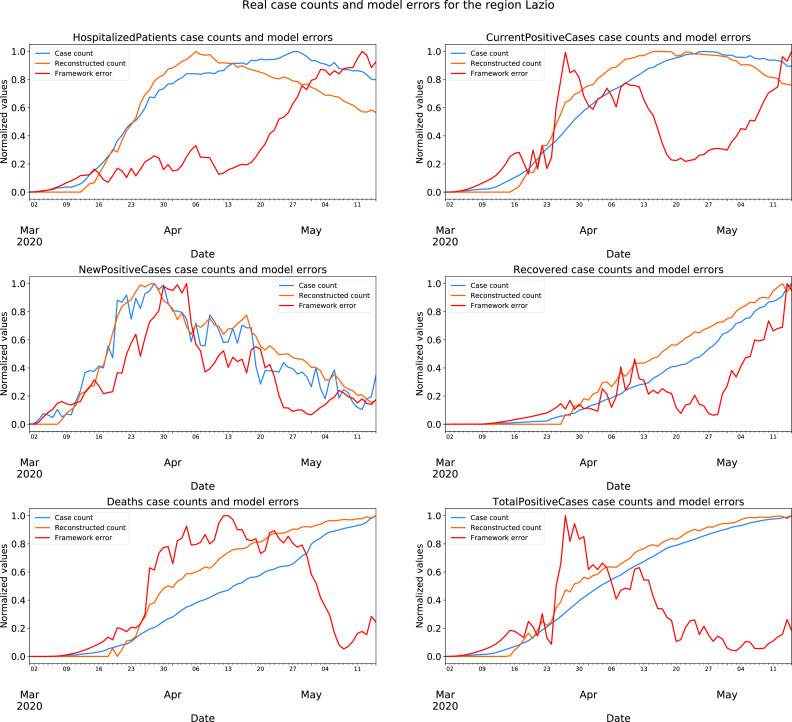
We calculate the correlation coefficients for the feature “current positive cases” between every pair of districts in the training data using Pearson correlation. The correlation heatmap matrix in Fig. 3 shows that all the neighboring regions have strong spatial correlations. Remote regions in the dataset, such as Valle d’Aosta and Marche, show weaker correlations between other regions. These results reflect that the spatial correlation of COVID-19 epidemic progression occurring in certain geographic regions at a certain spatial resolution is quite strong.
FIGURE 3.
Correlation matrix visualized as heatmap. It shows the strong spatial correlation between regions for the feature “Current Positive Cases”.
By using the spatial neighborhood of each region, we create a spatio-temporal
multivariate input for the model. The sliding window technique given in Algorithm 1 is applied to training,
validation, and test datasets to build spatio-temporal multivariate
subsequences. We apply the algorithm with parameters representing the number of
spatial neighbors (which is called depth in the algorithm) set to 10, the window
size set to 7 representing 7-day worth of data point, and step size to 1.
According to the formula given in (5) in which
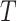 is set to 7,
is set to 7,
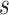 is set to 1 and
is set to 1 and
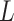 is set to 82, we
have 76 multivariate subsequences for each region. As the total number of
behavioral attributes is 13, excluding spatial features “region code,
region name, latitude, and longitude”, and with the depth of spatial
neighborhood is set to 10, we create
is set to 82, we
have 76 multivariate subsequences for each region. As the total number of
behavioral attributes is 13, excluding spatial features “region code,
region name, latitude, and longitude”, and with the depth of spatial
neighborhood is set to 10, we create
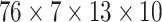 dimensional spatio-temporal multivariate
dataset from each region. By using this sliding window algorithm, we perform
data augmentation by moving the start of the T-day data entry by step size
resulting in a nearly six-fold expansion of the training data.
dimensional spatio-temporal multivariate
dataset from each region. By using this sliding window algorithm, we perform
data augmentation by moving the start of the T-day data entry by step size
resulting in a nearly six-fold expansion of the training data.
The parameter “number of spatial neighbors” represents the number
of nearest neighbors to use while building spatio-temporal multivariate
subsequences. It also corresponds to the spatial dimension of the 3D CNN
encoder. After data preprocessing step is completed, training, validation and
test sets are created. They are 4-dimensional data matrices with the following
sizes: The dimension of the training set is
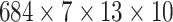 , the dimension of the validation set is
, the dimension of the validation set is
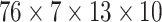 , and the dimension of the test set is
, and the dimension of the test set is
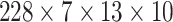 . Numbers 684, 76 and 228 represent the number
of data points or observations in training, validation, and test sets,
respectively. The proposed framework is trained to reconstruct the following
behavioral attributes: Hospitalized patients, intensive care patients,
total hospitalized patients, home confinement, current positive cases, new
positive cases, total positive cases, recovered, and deaths. The
size of the reconstruction space for the test set is
. Numbers 684, 76 and 228 represent the number
of data points or observations in training, validation, and test sets,
respectively. The proposed framework is trained to reconstruct the following
behavioral attributes: Hospitalized patients, intensive care patients,
total hospitalized patients, home confinement, current positive cases, new
positive cases, total positive cases, recovered, and deaths. The
size of the reconstruction space for the test set is
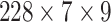 .
.
C. Framework Architecture and Tuning
Extensive experiments through grid search are executed to finalize the
architecture of the framework and its hyperparameters. Specifically, we use 2
CNN blocks in the encoder component, each of which has a 3D convolutional layer,
followed by a 3D max-pooling layer. Number of feature maps is set to 64 in the
first block and set to 32 in the second block with padding and no striding (or
with strides
 ). We set the kernel size to
). We set the kernel size to
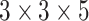 ,
where
,
where
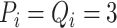 and
and
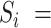 5 in
(7), for all convolutional
layers for the experiment, as these values are found to produce the best result
for the dataset. The max-pooling layers have pool size of
5 in
(7), for all convolutional
layers for the experiment, as these values are found to produce the best result
for the dataset. The max-pooling layers have pool size of
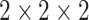 and strides of
and strides of
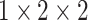 with padding. This means that the pooling operation is performed over all three
dimensions: (
with padding. This means that the pooling operation is performed over all three
dimensions: (
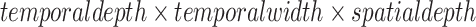 ). In addition,
temporal width and spatial depth dimensions are reduced by a factor of 2 with
every max-pooling layer. The activation function
). In addition,
temporal width and spatial depth dimensions are reduced by a factor of 2 with
every max-pooling layer. The activation function
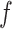 in (7) in all hidden convolutional
layers in the encoder component are set to Rectified Linear Unit
(ReLU) non-linearity,
in (7) in all hidden convolutional
layers in the encoder component are set to Rectified Linear Unit
(ReLU) non-linearity,
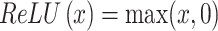 , which allows the deep neural networks converge
faster [87].
, which allows the deep neural networks converge
faster [87].
The decoder component is composed of two ConvLSTM layers with the number of
feature maps set to 32 and 64, respectively to preserve the symmetry of the
autoencoder framework. We apply 2D convolution operation over spatial and
temporal dimensions using the kernel size of
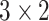 and the
stride of
and the
stride of
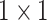 with
padding. Batch normalization (BN) [88]
is applied to each of the ConvLSTM layers, which accelerates the training of
deep neural networks. In the final layer, a fully connected neural network
(FCNN) is used to reconstruct the target output. Thus, we add a layer to reshape
the 4D output of final ConvLSTM layer before passing the output to the FCNN. The
FCNN layer is a time distributed dense layer which applies the same fully
connected operation to every time step. The number of units in the dense layer
is set to
with
padding. Batch normalization (BN) [88]
is applied to each of the ConvLSTM layers, which accelerates the training of
deep neural networks. In the final layer, a fully connected neural network
(FCNN) is used to reconstruct the target output. Thus, we add a layer to reshape
the 4D output of final ConvLSTM layer before passing the output to the FCNN. The
FCNN layer is a time distributed dense layer which applies the same fully
connected operation to every time step. The number of units in the dense layer
is set to
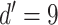 and
it is equal to the number of univariate time series (features) that we want to
reconstruct. The number of hidden units in the FCNN layer can be adjusted
according to the problem context at hand.
and
it is equal to the number of univariate time series (features) that we want to
reconstruct. The number of hidden units in the FCNN layer can be adjusted
according to the problem context at hand.
Activation functions of ConvLSTM units are set to hyperbolic tangent and the
activation functions in the final dense layer are set to ReLU.
Layer weights are initialized with the Glorot uniform initializer [89]. The deep learning framework is
optimized using the Adam optimizer with learning rate set to 0.0001. It ran for
100 epochs with batch size 16. The training is regularized by weight decay (the
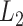 penalty
multiplier set to
penalty
multiplier set to
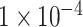 )
and dropout regularization for the two ConvLSTM layers (the dropout ratio set to
0.25). The model is trained to minimize the following mean absolute error (MAE)
loss function:
)
and dropout regularization for the two ConvLSTM layers (the dropout ratio set to
0.25). The model is trained to minimize the following mean absolute error (MAE)
loss function:
 |
where
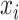 and
and
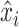 represent the true value and the reconstructed value, respectively, and
represent the true value and the reconstructed value, respectively, and
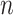 is the total
number of data points in each batch. The detailed architecture of the final deep
learning framework is illustrated in Fig.
4. The final framework has 299,241 trainable parameters. The data
structure of each component in the trained framework is given in Table 2, where
is the total
number of data points in each batch. The detailed architecture of the final deep
learning framework is illustrated in Fig.
4. The final framework has 299,241 trainable parameters. The data
structure of each component in the trained framework is given in Table 2, where
 represents
number of data points.
represents
number of data points.
FIGURE 4.
The proposed hybrid spatio-temporal autoencoder network architecture.
TABLE 2. Framework Data Structure.
| Layer Name | Output Shape | Param # |
|---|---|---|
| Input Layer (data) | [(
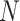 , 7, 13, 10, 1)] , 7, 13, 10, 1)] |
0 |
| 3D CNN Encoder | [(
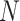 , 7, 4, 3, 32)] , 7, 4, 3, 32)] |
95,136 |
| ConvLSTM Decoder | [(
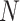 , 7, 4, 3, 64)] , 7, 4, 3, 64)] |
197,376 |
| Reshape Layer | [(
 , 7, 768)] , 7, 768)] |
0 |
| FCNN Layer | [(
 , 7, 9)] , 7, 9)] |
6921 |
D. Performance Comparison
We have compared the proposed framework with 15 different anomaly detection models which include several state-of-the-art deep learning-based approaches. Tested models fall under the following categories:
1). Statistical Models
The following univariate statistical models are used: CUmulative SUM Statistics (CUSUM) [47] and Shewhart control chart [49].
2). Prediction Based Models
Models under this category use the temporal dependencies of training data to build a model and predict the value of the test data. We employ three univariate time series regression models: Autoregressive Integrated Moving Average (ARIMA), Exponentially Weighted Moving Average (EWMA), and Fast Fourier Transform (FFT) extrapolation [90].
3). One-Class Classification Models
Models under this category learn a decision function during training to identify normal samples. Then, the trained classifier is applied to test data and generates an anomaly score based on being similar or dissimilar to the training set. The unsupervised variant of the OCSVM algorithm is used for this experiment. This unsupervised variant does not require its training set to be labeled to determine a decision surface [91].
4). Distance Based Models
These models use a distance metric to score data points in the test set. They have intrinsically unsupervised settings and don’t need training. Under this category, we employ the LOF algorithm [29], which is a locality-based outlier detection algorithm, and LDBSCAN algorithm [32], which is a local-density based spatial clustering algorithm.
5). Isolation Based Model
This model detects anomalies based on the concept of isolation without
employing any distance or density measure: Isolation Forest (
 Forest)
[37], [38].
Forest)
[37], [38].
6). Deep Learning Models
Various state of the art deep learning models which have been proven to be successful on anomaly detection problems are tested.
-
1)
Prediction based models: LSTM and CNN based deep learning predictor models are used under this category. A deep stacked LSTM predictor model based on the architecture proposed by Malhotra et al. in [56] and a 1D CNN based predictor model (namely DeepAnT) proposed by Munir et al. in [66] have been employed as multivariate time series prediction based models for anomaly detection.
-
2)
Reconstruction based models: Four different reconstruction based deep autoencoder architectures are tested. These architectures include a deep LSTM autoencoder architecture [57], a deep 2D CNN based autoencoder schema proposed by Hasan et al. in [58], a deep spatio-temporal autoencoder model for anomaly detection in videos proposed by Chong and Tay in [65], and a deep 3D CNN based spatio-temporal autoencoder model (namely DeepFall) proposed by Nogas et al. in [67].
All models are implemented using Python 3.6.8 programming language. Deep learning models including the proposed framework are implemented using the TensorFlow library [92]. For LOF, IsolationForest, and One-Class SVM methods, we use implementations available in the scikit-learn [93], which is a free machine learning library for Python programming language. To build the ARIMA model, we use the statsmodels library [94], which is a free Python module providing implementations of many different statistical models. Euclidean distance is used for all proximity-based algorithms since it has generated better results compared to other distance metrics.
E. Models Tuning
Shewhart control chart comes from the quality control and originated in 1931. It
uses previous data to estimate a reasonable upper limit or threshold value [49]. If future measurements stay under
the threshold value, the process is ‘under control’. New
measurements which exceed the calculated threshold limit may indicate that a
noteworthy change has occurred in the underlying process. In our early outbreak
detection scenario, it may indicate an anomalous daily data entry. The standard
detector was trained on training dataset to obtain the mean
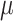 and variance
and variance
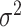 . The
control chart threshold value is calculated for each feature by the formula
given below as defined in [48]:
. The
control chart threshold value is calculated for each feature by the formula
given below as defined in [48]:
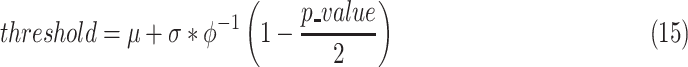 |
where
 is the
inverse to the cumulative distribution function of a standard normal, and the
is the
inverse to the cumulative distribution function of a standard normal, and the
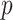 -value is
supplied by the user. Given a
-value is
supplied by the user. Given a
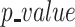 of 0.5,
we calculate the threshold level for the feature “new positive
cases” as 0.492.
of 0.5,
we calculate the threshold level for the feature “new positive
cases” as 0.492.
CUSUM charts are good at detecting small shift from the mean more quickly than Shewhart control charts [47]. CUSUM is calculated by taking the cumulative summation of the difference between each measured value and the estimated in-control mean value:
 |
where
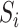 is the
is the
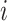 th cumulative
sum,
th cumulative
sum,
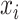 is the
is the
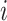 th observation
and
th observation
and
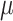 is the
in-control mean value. It keeps a running sum of excess values over the mean
each day. When this sum exceeds a threshold level, we can signal an alarm as an
indication of abnormality. For a process that is under control, each measured
value should be reasonably close to the mean. Thus, as long as the process
remains in control, the CUSUM plot of each calculated value of
is the
in-control mean value. It keeps a running sum of excess values over the mean
each day. When this sum exceeds a threshold level, we can signal an alarm as an
indication of abnormality. For a process that is under control, each measured
value should be reasonably close to the mean. Thus, as long as the process
remains in control, the CUSUM plot of each calculated value of
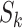 should be
centered about zero with small fluctuations. If the process mean shifts upward,
the CUSUM values for data points will eventually drift upwards.
should be
centered about zero with small fluctuations. If the process mean shifts upward,
the CUSUM values for data points will eventually drift upwards.
Standard moving average algorithm introduces lag into the original time series,
which means that changes in the trend are only seen with a delay. Exponentially
Weighted Moving Average (EWMA) reduces this lag effect by introducing the decay
parameter and puts more weight on more recent observations. The window (span) is
chosen as 7 days. The ARIMA model is represented by (p, d,
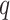 ) model
parameters which show the order of Auto-regressive (AR), the differencing
component, and Moving Average (MA), respectively. The integrated part of ARIMA
(the differencing component) helps in reducing the non-stationarity. The optimum
parameters of this model are selected by minimizing the Akaike information
criterion (AIC). The final model is built using the parameters ARIMA (2, 1, 3).
Fast Fourier Transform (FFT) is the discrete Fourier transform algorithm to
express a time series function as a sum of periodic components. We apply FFT to
univariate time series data (“new positive cases” attribute of
each region) and extrapolate to make one step prediction.
) model
parameters which show the order of Auto-regressive (AR), the differencing
component, and Moving Average (MA), respectively. The integrated part of ARIMA
(the differencing component) helps in reducing the non-stationarity. The optimum
parameters of this model are selected by minimizing the Akaike information
criterion (AIC). The final model is built using the parameters ARIMA (2, 1, 3).
Fast Fourier Transform (FFT) is the discrete Fourier transform algorithm to
express a time series function as a sum of periodic components. We apply FFT to
univariate time series data (“new positive cases” attribute of
each region) and extrapolate to make one step prediction.
An unsupervised version of the OCSVM algorithm is used for the anomaly detection in test regions. It learns a decision function during training and classifies the test data as similar to or different from the training set using the decision score. A OCSVM model with the Radial Basis Function kernel is used to build the classifier and detect anomalies in the unseen test dataset.
The Local Outlier Factor (LOF) algorithm is an unsupervised anomaly detection method based on local density deviation of a given dataset. It calculates the local density of a given data point with respect to its neighbors. It gives higher LOF scores to the samples that have a substantially lower density than their neighbors. For LOF model, we set the number of neighbors to 30 to use in k-nearest neighbor calculations and set the contamination ratio to 0.1.
The Local Density-Based Spatial Clustering of Applications with Noise (LDBSCAN)
algorithm is an extension to DBSCAN and takes the advantage of the LOF algorithm
in scoring data points and identifying clusters. The following values are
assigned to the LDBSCAN parameters since they give the best result: MinPts
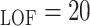 , MinPts
, MinPts
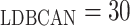 , LOFUB = 5, pct
, LOFUB = 5, pct
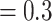 .
.
Isolation Forest algorithm returns an anomaly score for each observation and ’isolates’ anomalous points via recursive partitioning by randomly selecting a feature and then randomly selecting a split value for the selected feature. It can be represented by a tree structure and the number of splitting required to isolate a sample is used as a measure of normality. As the name infers, it is an ensemble of trees doing random partitioning to detect anomalies. The number of estimators (or trees) is selected as 100; and the rate of contamination is set to 0.1.
For the deep LSTM predictor model proposed in [56], we employ a stacked LSTM network with the history window size set to 7, and the prediction window size to 1 to perform the one-step prediction. The final LSTM predictor architecture is built with 3 hidden LSTM layers (having 64, 32 and 16 units, respectively) with ReLU activation function and a final fully connected neural network (FCNN) layer for inference of target variables. For the CNN based predictor, we follow the DeepAnT architecture proposed in [66]. Each 1D convolution layer has 32 filters followed by ReLU activation function and max pooling layer. The last layer of the network is a FCNN layer in which each neuron is connected to all the neurons in the previous layer. This layer generates the final prediction of the network for the next time stamp as in LSTM based predictor.
The encoder component in the deep CNN autoencoder model, which is similar to the
one proposed by Hasan et al. in [58], is composed of three convolutional layers:
Conv1-Conv3 with 64 kernels of size
 , 32
kernels of size
, 32
kernels of size
 , and 16
kernels of size
, and 16
kernels of size
 respectively with no strides. We use a max pooling layer after the first and the
second convolution layers with pool size of
respectively with no strides. We use a max pooling layer after the first and the
second convolution layers with pool size of
 and
strides
and
strides
 with
padding. The decoder component is built to maintain the symmetricity with three
convolutional layers and two unpooling layers with the same number of kernels of
size
with
padding. The decoder component is built to maintain the symmetricity with three
convolutional layers and two unpooling layers with the same number of kernels of
size
 . For the
deep LSTM autoencoder architecture proposed in [57], we use three LSTM layers in the encoder, and three LSTM layers
in the decoder with a fully connected neural network as the inference layer. On
the encoder side, the number of units in the LSTM layers are 64, 32, and 16. On
the decoder side, the same number of units are used in reverse order to build a
symmetric architecture.
. For the
deep LSTM autoencoder architecture proposed in [57], we use three LSTM layers in the encoder, and three LSTM layers
in the decoder with a fully connected neural network as the inference layer. On
the encoder side, the number of units in the LSTM layers are 64, 32, and 16. On
the decoder side, the same number of units are used in reverse order to build a
symmetric architecture.
We build the deep spatio-temporal autoencoder for abnormal event detection by
following the architecture proposed by Chong and Tay in [65]. The spatial encoder has two 2D convolutional layers
with 64 and 32 kernels of size
 and
and
 ,
respectively. Temporal encoder-decoder component is composed of three
convolutional LSTM (ConvLSTM) layers with the number of units are set to 16, 8,
and 16 with the convolution kernel size of
,
respectively. Temporal encoder-decoder component is composed of three
convolutional LSTM (ConvLSTM) layers with the number of units are set to 16, 8,
and 16 with the convolution kernel size of
 . The
spatial decoder has two deconvolutional layers with 32 and 64 kernels of size
. The
spatial decoder has two deconvolutional layers with 32 and 64 kernels of size
 and
and
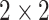 ,
respectively. It has a final FCNN layer to generate the reconstruction of the
selected test features.
,
respectively. It has a final FCNN layer to generate the reconstruction of the
selected test features.
To build the spatio-temporal 3D convolutional autoencoder, we follow the
architecture of DeepFall proposed in [67]. The encoder has two layers of 3D convolutions with
stride of
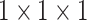 and padding. They have 16 and 8 kernels with kernel size set to
and padding. They have 16 and 8 kernels with kernel size set to
 .
After each convolution layer, 3D max pooling operation is applied with the
stride size of
.
After each convolution layer, 3D max pooling operation is applied with the
stride size of
 and pool size of
and pool size of
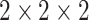 and
and
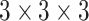 ,
respectively. The decoder has three layers of 3D deconvolutions with a stride of
,
respectively. The decoder has three layers of 3D deconvolutions with a stride of
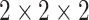 and padding. The kernel sizes are set to
and padding. The kernel sizes are set to
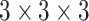 ,
,
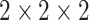 ,
,
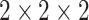 ,
respectively.
,
respectively.
All deep learning models are trained to minimize the mean absolute error with
Adam optimizer with learning rate set to 0.0001. The
 regularization with the penalty multiplier set to
regularization with the penalty multiplier set to
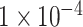 and dropout regularization with the dropout ratio set to 0.25 are applied for
training. Models are trained for 100 epochs with mini batches of size 16.
and dropout regularization with the dropout ratio set to 0.25 are applied for
training. Models are trained for 100 epochs with mini batches of size 16.
F. Performance Metric
In order to evaluate the performance of models, we measure the number of days until an anomaly is detected against the threshold level. In the context of this empirical study, an anomaly might mean that the COVID-19 pandemic might be moving out of control for the investigated region. According to European Centre for Disease Prevention and Control [95], the number of newly confirmed cases (or daily new positive cases) is one of the most accurate indicators of epidemic intensity. To compare the early COVID-19 outbreak detection performance, we compare the anomaly scores of models generated for the feature “new positive cases”. For the prediction-based model, we use the one step prediction errors as anomaly scores. For the reconstruction-based models, we use the reconstruction errors as anomaly scores. OCSVM, IsolationForest, LOF and LDBSCAN models generate one anomaly score for each multivariate observation regardless of the feature monitored.
VI. Results
A. Framework Performance
During the training process, the framework learns to reconstruct the selected features in each data point with the minimum possible error. In the case of anomalous events such as peaks of the COVID-19 pandemic, these reconstruction errors will get bigger, causing an alarm for the possible outbreak. The framework learns the normal data structure with the data from northern regions, which have gone through the pandemic earlier than other regions. To be able to detect the COVID-19 outbreak as early as possible, the framework must learn what the normal is when it is trained with highly contaminated data. As there is no label indicating anomalous events, the framework learns the distinctive patterns of abnormal events using the data from the nearest spatial neighbors.
We train one unified deep learning model using the training set, which has a total of 684 spatio-temporal multivariate data points from 9 different regions. Then, we use the model to calculate the reconstruction errors of each 228 data points in the test set. As we set the window size to 7 days during the data preparation process and sliding step size to 1 day, we calculate the rolling window errors of each feature.
The reconstructed values and reconstruction errors for features “hospitalized patients, current positive cases, new positive cases, recovered cases, deaths, and total positive cases” on test data are plotted against the real case numbers in figures from 5 to 7. Test results for the region Lazio are given in Fig. 5; test results for the region Campania are given in Fig. 6; and test results for the region Sicilia are given in Fig. 7. In these figures, the real data are depicted in blue; the reconstructions are depicted in orange; and the reconstruction errors are depicted in red. All values are min-max normalized into the range of [0, 1] before plotting.
FIGURE 5.
Model test results for the region Lazio are given for features HospitalizedPatients, CurrentPositiveCases, NewPositiveCases, Recovered cases, Death cases, and TotalPositiveCases. Real case counts are plotted in blue, reconstructed case counts are plotted in orange, and reconstruction errors are plotted in red.
FIGURE 6.
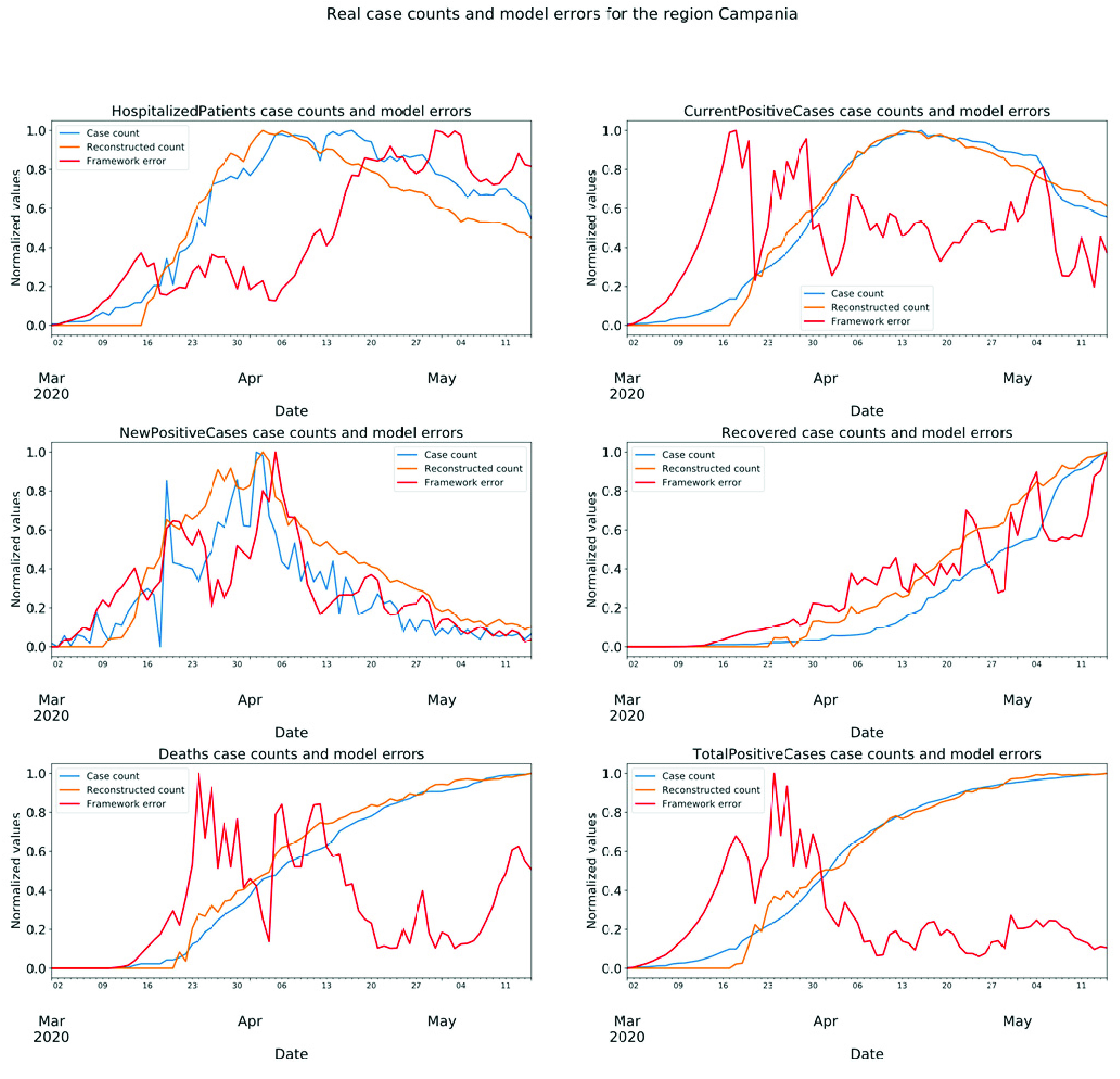
Model test results for the region Campania are given for features HospitalizedPatients, CurrentPositiveCases, NewPositiveCases, Recovered cases, Death cases, and TotalPositiveCases. Real case counts are plotted in blue, reconstructed case counts are plotted in orange, and reconstruction errors are plotted in red.
FIGURE 7.
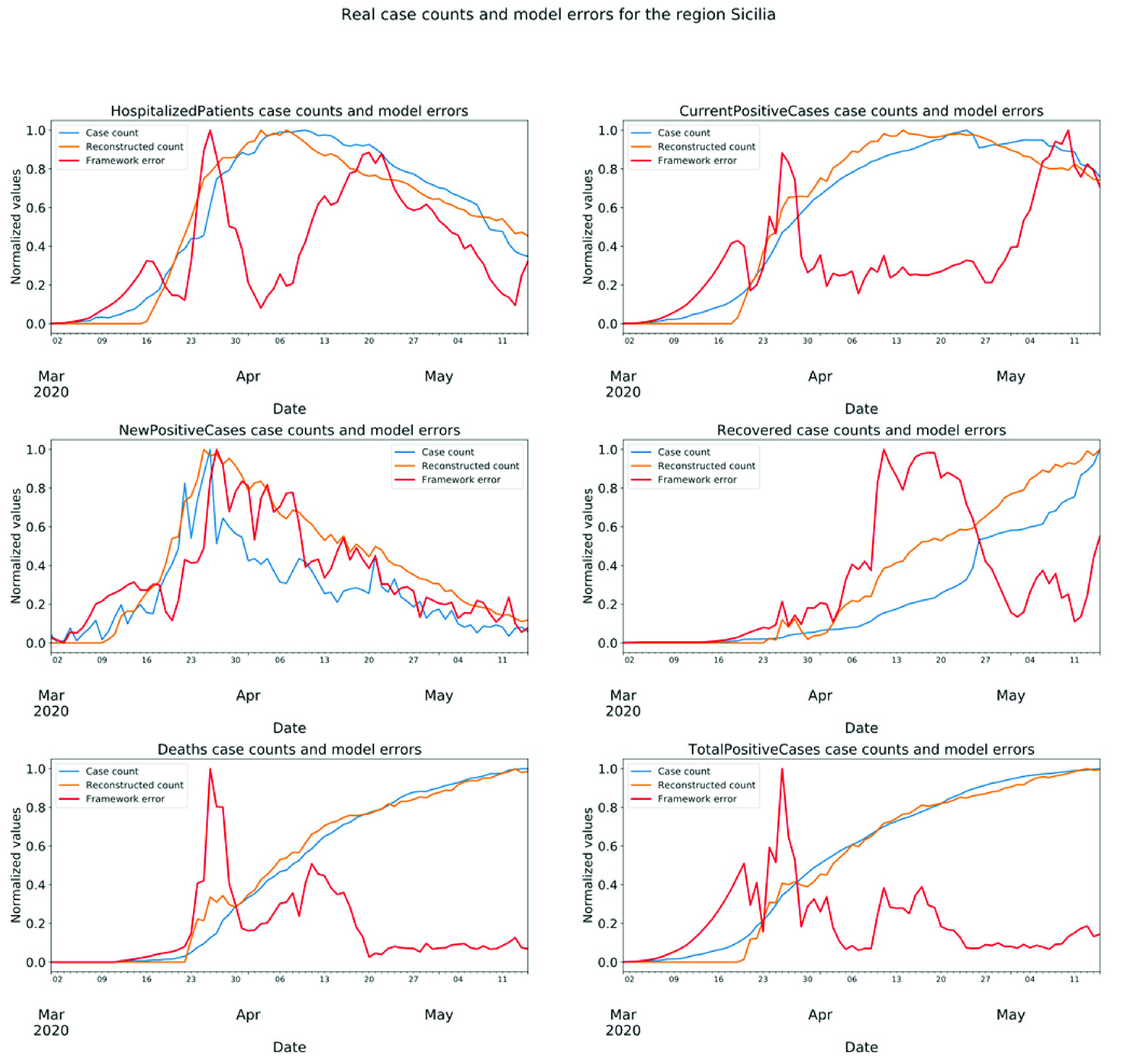
Model test results for the region Sicilia are given for features HospitalizedPatients, CurrentPositiveCases, NewPositiveCases, Recovered cases, Death cases, and TotalPositiveCases. Real case counts are plotted in blue, reconstructed case counts are plotted in orange, and reconstruction errors are plotted in red.
It can be seen in these plots that there is a subtle increase in the model error when the real case counts have peaks as each region goes through the COVID-19 pandemic. The progression of the COVID-19 pandemic in each test region is quite different: Lazio hits the peak of the epidemic earlier, and goes through a larger wave with many peaks, while Campania and Sicilia have shorter waves with a smaller number of peaks. Sicilia has the least number of peaks compared to other regions. The framework captures the overall structure of the real data and gives a good error margin to enable the early detection of the outbreak in each test region.
B. Detection Time
To compare the early outbreak detection performance of the proposed framework with other models, anomaly detection time in days is calculated. The Shewhart control chart value for the feature “new positive cases” is used as the threshold level for an alarm. Outbreak detection date is calculated as the date of the first alert raised when the alarm level passes the threshold line. Table 3 shows a comparison of all models based on the early outbreak detection performance. Best performing models on all three regions are highlighted.
TABLE 3. Outbreak Detection Date of Models.
| Model Name | Lazio | Campania | Sicilia | |
|---|---|---|---|---|
| Shewhart Control Chart | 18 March | 19 March | 22 March | |
| CUSUM | 12 March | 8 March | 12 March | |
| ARIMA | 13 March | 19 March | 21 March | |
| EWMA | 13 March | 19 March | 22 March | |
| FFT | 18 March | 19 March | 22 March | |
| IsolationForest | 13 March | 15 March | 18 March | |
| LOF | 13 March | 15 March | 17 March | |
| LDBSCAN | 12 March | 18 March | 16 March | |
| OCSVM | 15 March | 20 March | 17 March | |
| LSTM Predictor [56] | 13 March | 19 March | 8 March | |
| LSTM Autoencoder [57] | 13 March | 19 March | 19 March | |
| CNN Autoencoder [58] | 13 March | 19 March | 22 March | |
| Chong and Tay [65] | 16 March | 19 March | 21 March | |
| DeepAnT [66] | 12 March | 8 March | 4 March | |
| DeepFall [67] | 13 March | 19 March | 21 March | |
| Proposed Framework | 4 March | 5 March | 1 March | |
In this test dataset, the anomalies are not just the spike or point anomalies. They are contextual anomalies; and there is a trend in them showing the progression of the COVID-19 pandemic in each region. This makes this dataset difficult for an anomaly detection algorithm as contamination rate is very high in the training set.
The proposed framework outperforms all compared models in early outbreak detection for all test regions. Statistical models show similar performance on the regions Campania and Sicilia. The FFT falls behind other models on the region Lazio. LDBSCAN algorithm shows better early outbreak detection performance on the regions Lazio and Sicilia compared to IsolationForest and LOF. It can be seen that OCSVM does not work on such highly contaminated training data as it falls behind on early outbreak detection in all test regions. CUSUM, on the other hand, performs significantly better than other statistical and distance-based models. In general, other deep learning models show similar performance on each test region except DeepAnT, which shows better performance than other compared deep learning models.
We compare our model with the best performing models, namely the CUSUM, DeepAnT, and LDBSCAN. Fig. 8 to 10 illustrate the alarms generated by models, which are plotted against the standard threshold level and daily real case counts for the parameter “new positive cases”. The case counts and model alarm values (or anomaly scores) are min-max normalized into the range of [0, 1] before plotting. When an alarm value passes the threshold line, it is plotted in red to illustrate an outbreak signal.
FIGURE 8.
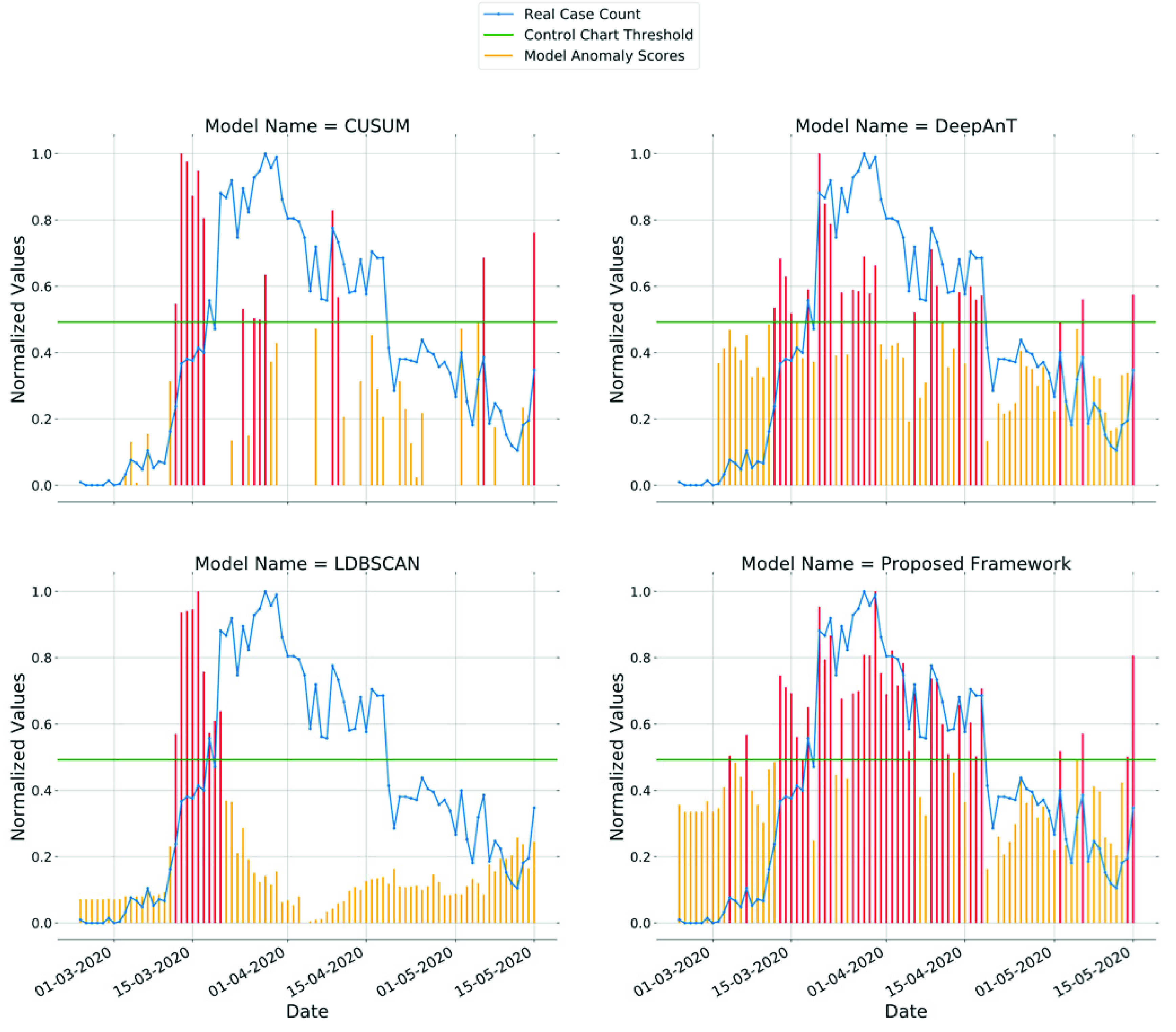
Region Lazio: Generated alarms of top performing models are plotted against daily real case counts for the parameter “new positive cases”. Shewhart control chart value is plotted as the threshold level. When a generated alarm signal passes the threshold level, it is plotted in red. A red alarm signal can be interpreted as an outbreak for the region.
FIGURE 9.
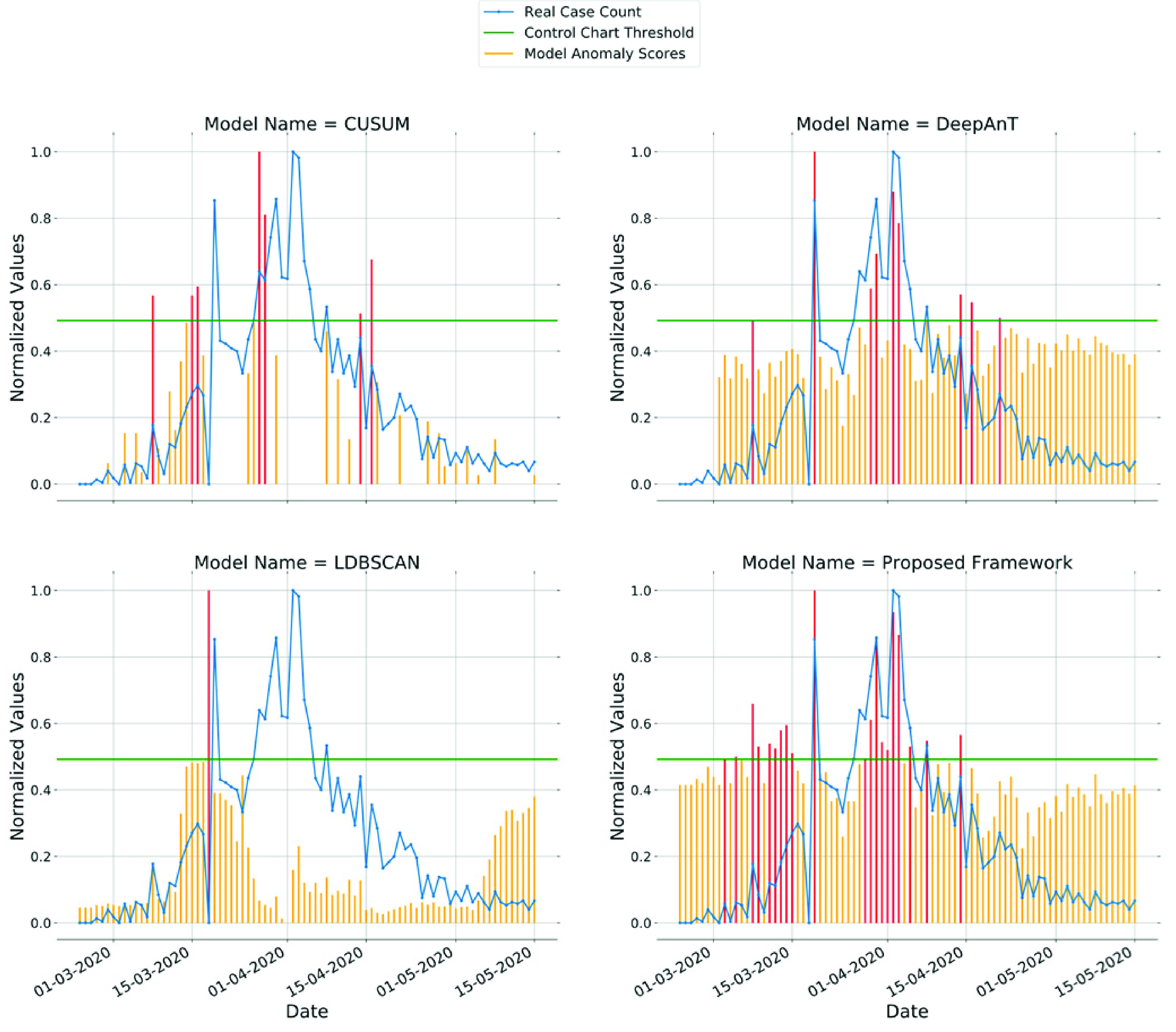
Region Campania: Generated alarms of top performing models are plotted against daily real case counts for the parameter “new positive cases”. Shewhart control chart value is plotted as the threshold level. When a generated alarm signal passes the threshold level, it is plotted in red. A red alarm signal can be interpreted as an outbreak for the region.
FIGURE 10.
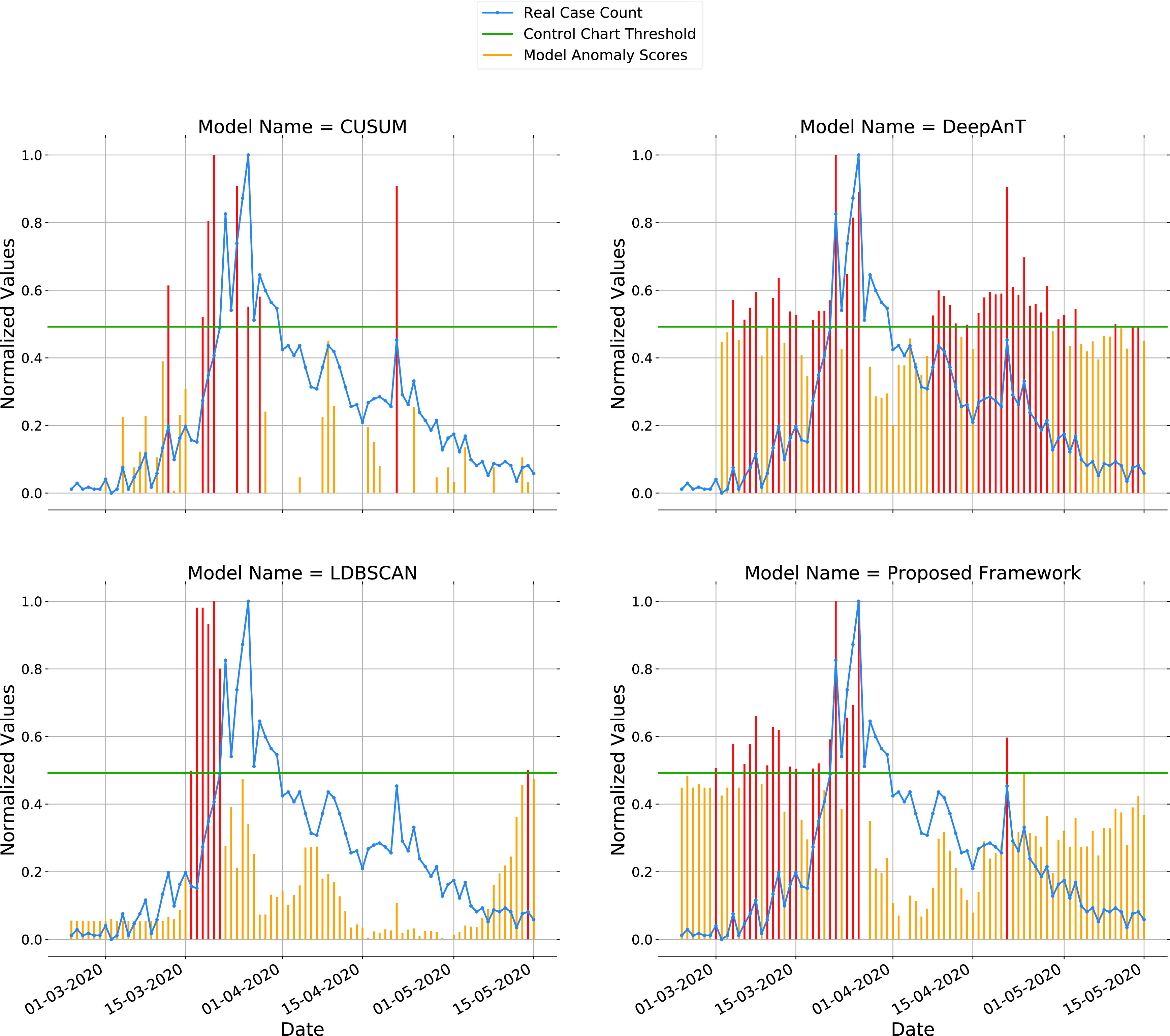
Region Sicilia: Generated alarms of top performing models are plotted against daily real case counts for the parameter “new positive cases”. Shewhart control chart value is plotted as the threshold level. When a generated alarm signal passes the threshold level, it is plotted in red. A red alarm signal can be interpreted as an outbreak for the region.
When we look at plots for the region Lazio in Fig. 8, the alarm level of the proposed framework passes the threshold line on March 4. It generates strong alarm signals through the wave of the COVID-19 pandemic. CUSUM, LDBSCAN and DeepAnT send first alarm signals on March 12, which is the date national lockdown was announced in Italy. Fig. 9 shows the test results for the region Campania. The proposed model can detect the early upswing trend in the epidemic while other models fall behind in detecting the outbreak. The proposed model gives the first outbreak signal which passes the threshold level on March 5, while CUSUM and DeepAnT give on March 8, and LDBSCAN gives the signal on March 18. The region Campania is very challenging for early outbreak detection as the upswing trend starts very late and suddenly in mid-March. Fig. 10 shows the test results for the region Sicilia. The proposed framework sends the first outbreak signal on March 1. It is followed by the DeepAnT model, which sends the first outbreak signal on March 4, followed by the CUSUM model, which sends the first outbreak signal on March 12, and followed by LDBSCAN, which sends the first outbreak signal on March 16. LDBSCAN shows good outbreak detection performance on Lazio and Campania but fails on the region Sicilia. DeepAnT is very successful in early outbreak detection in all regions, but significantly better on the region Sicilia compared to other base models. However, despite the downward trend of the pandemic in the region Sicilia after April 15, DeepAnT continues to send outbreak signals.
It can be observed that our model has the capability of detecting abnormal upswing trends in COVID-19 pandemic waves in each test region. The main advantage of the proposed framework is that once it is trained on the training set, it does not need the history of the tested region to detect any anomalous event. It can detect point anomalies as well as contextual anomalies in test regions. It is better at tracking the abnormal events and in detecting every major peak throughout the wave of the COVID-19 pandemic in each test region. What makes the proposed framework different from other deep learning-based models is the way it uses the spatio-temporal data. The nearest neighbor’s data, which is weighted based on the distance to the region, is exploited to extract the best spatio-temporal features. This makes the framework robust against noise and anomalies in the dataset.
C. Discussion on Other Parameters
The basic reproduction number (R0), which is an indicator of average number of secondary cases infected by the person who already had an infection, is one of the most important characteristics of an epidemic [96]. Health authorities and governments around the world build their preventive measures based on the reproduction number of the epidemic [97]. The most concerning characteristics of the current COVID-19 is its high reproduction number which was around 4.5 during the early outbreak and may evolve throughout the pandemic based on the mitigation measures taken by the governments such as rates of diagnostic testing, quarantine measures, case and contact isolation, face masks usage enforcement, and public education [98], [99]. In Italy, almost every day from February 25 until the start of national lockdown in March 12, new and stricter policies have been declared in many Italian provinces aimed at containing the outbreak and delaying the epidemic peak [8].
A recent study by Tahmasebi et al. [100] emphasizes the effect of different social distancing scenarios on the spread of COVID-19. They also discuss that other than government intervention scenarios, the pre-existing regional specific variables such as environmental, economic, and health factors may also have influenced the vulnerability to COVID-19. In order to build a more realistic early outbreak detection and pandemic tracking algorithm, all region-specific factors should be considered. In fact, many questions regarding the spread dynamics of COVID-19 have remained unanswered, such as why different regions experience different reproduction and fatality rates, which cultural and health variables have the most influence on the spread of COVID-19. As we gain more information on the COVID-19 pandemic, we will be able to build more effective models to detect the outbreak on each different region.
VII. Conclusion
In this study, a deep learning framework is presented for unsupervised detection of anomalies in multivariate spatio-temporal data. We also presented a novel way of pre-processing the non-image multivariate spatio-temporal data by using the nearest spatial neighborhood. The 3D cuboid data is formed by stacking the data from the nearest spatio-temporal neighbors of each multivariate data point. The proposed hybrid framework is designed to be trained in a truly unsupervised fashion without any labels indicating normal or abnormal data. The proposed approach is robust enough to learn the underlying dynamics even if the training dataset is highly contaminated with anomalies (more than 5%).
In all distance/clustering-based algorithms, the biggest challenge is to combine the contextual features along the spatial and temporal dimensions in a meaningful way. In the proposed approach, we handle spatial and temporal context by different deep learning components as these contextual variables refer to different types of dependencies. The proposed framework requires no prior knowledge on anomalies such as the distribution and types of anomalies.
There have been many studies that model the epidemiological dynamics of Covid-19. However, none of them have been focused on building an anomaly detection system for early epidemic detection. We conducted experiments using COVID-19 Italy dataset provided by the Italian Department of Civil Protection. We used northern Italian regions data to train the model and then used this one unified model to detect anomalous patterns of central and southern regions of Italy. We evaluated the performance of the proposed framework against 15 different anomaly detection algorithms including state-of-the art deep learning-based approaches proposed in recent years. It outperformed the state-of-the-art deep learning approaches in both early detection and tracking the COVID-19 outbreak. Experiments have shown that the framework is capable of handling the small amount of data event if the contamination level is too high as in the case of COVID-19 Italy dataset.
Our contributions can be summarized as follows:
-
1)
To the best of our knowledge, the proposed framework, which is composed of a novel data crafting and a hybrid deep learning model, is the first attempt in solving unsupervised anomaly detection problem which is designed specifically for non-image multivariate spatio-temporal data.
-
2)
It achieves good generalization capabilities in scenarios where the training data are scarce and contaminated with anomalies. In the case study, only 82 daily data entries (data points) are available for each region. Even these contaminated outbreak data are sufficient to build a robust anomaly detection model due to its effective architecture to exploit spatio-temporal neighborhood data.
-
3)
The biggest challenge in anomaly detection for spatio-temporal data is to combine the contextual attributes in a meaningful way. In the proposed hybrid approach, spatial and temporal contexts are handled by different deep learning components as these contextual variables refer to different types of dependencies.
This study illustrates the capability of the proposed approach to detect anomalous patterns and disease outbreaks in a timely manner. Our framework is aimed to provide useful insight for the crisis management against the novel coronavirus. It might help monitoring COVID-19 pandemic progression in various regions simultaneously to detect any signs of an outbreak.
The proposed framework has some limitations. The main limitation is that it is based on the assumption that similar control measures to suppress the outbreak are taken by all regions. However, it is not true as some regions put more restrictions on mobility resulting less correlation on daily pandemic data between neighboring regions. Further improvements can be achieved by including the control measures taken by each region into the model as part of the spatial context. Another limitation is the selection of the hyper parameters for each dataset for optimum performance. We plan to explore optimization-based techniques to select framework’s hyper-parameters to further enhance the performance. Finally, we plan to enhance the framework by adding the attention mechanism to tackle the weaknesses in analyzing long sequences.
Biographies

Yildiz Karadayi received the B.Eng. degree in computer engineering from Istanbul Technical University, Istanbul, Turkey, in 1998, the M.A.Sc. degree in data mining from the School of Engineering Science, Simon Fraser University, Burnaby, BC, Canada, in 2006, and the Ph.D. degree in computer engineering (artificial intelligence) from Kadir Has University, Istanbul, in 2020. She has been with various companies from different sectors, such as telecommunications, finance, and retail, since 1998. She has led various big data and data science projects as a Senior Data Scientist. She also led applied machine learning to solve business problems, such as fraud detection, anomaly detection, sales prediction, and predictive maintenance. Her research interests include machine learning, deep learning, unsupervised learning, anomaly detection, and spatio-temporal data analysis.

Mehmet N. Aydin (Member, IEEE) received the Ph.D. degree in management information systems from the University of Twente, The Netherlands. He was with the Institute for Innovation and Technology Management, Ryerson University, Toronto, ON, Canada, and the Department of Information Systems and Change Management, University of Twente. He is currently an Associate Professor of MIS with the Faculty of Management, Kadir Has University. He has provided organizations with proven expertise in data science, cloud computing, management information, and network science. He has published over 70 articles as journal articles, such as Journal of Database Management, Information Systems Frontiers, Journal of Enterprise Management, Computers and Education, book chapters, such as Springer series on Lecture Notes in Computer Science, and conference proceedings (IFIP 8.1, CAISE). His contribution to the research field of method engineering is laudable and cited in various studies.

Arif Selçuk Öǧrencí (Senior Member, IEEE) received the B.S., M.S., and Ph.D. degrees in electrical electronics engineering from Bogazici University, Turkey, in 1992, 1995, and 1999, respectively, and the double major degrees in mathematics. He has been a Faculty Member in electrical electronics engineering with Kadir Has University, Turkey, since 1999. He was a Manager with the Enterprise Knowledge Management System from 2001 to 2015. He offers courses in electronics, computational intelligence, and the IoT. His research interests include computational intelligence, the IoT (edge computing and analytics), machine learning (big data analytics and anomaly detection), and effective learning.
Funding Statement
This work was supported in part by Kadir Has University individual research grant.
References
- [1].Gupta M., Gao J., Aggarwal C. C., and Han J., “Outlier detection for temporal data: A survey,” IEEE Trans. Knowl. Data Eng., vol. 26, no. 9, pp. 2250–2267, Sep. 2014, doi: 10.1109/TKDE.2013.184. [DOI] [Google Scholar]
- [2].Cheng T. and Li Z., “A multiscale approach for spatio-temporal outlier detection,” Trans. GIS, vol. 10, no. 2, pp. 253–263, Mar. 2006, doi: 10.1111/j.1467-9671.2006.00256.x. [DOI] [Google Scholar]
- [3].Aggarwal C. C., “Spatial outlier detection,” in Outlier Analysis, 2nd ed. New York, Ny, USA: Springer Nature, 2017, pp. 345–367. [Google Scholar]
- [4].Hodge V. and Austin J., “A survey of outlier detection methodologies,” Artif. Intell. Rev., vol. 22, no. 2, pp. 85–126, Oct. 2004, doi: 10.1023/b:aire.0000045502.10941.a9. [DOI] [Google Scholar]
- [5].Du S., Li T., Yang Y., and Horng S.-J., “Deep air quality forecasting using hybrid deep learning framework,” IEEE Trans. Knowl. Data Eng., eraly access, Nov. 20, 2020, doi: 10.1109/tkde.2019.2954510. [DOI]
- [6].Sun Y., Wang X., and Tang X., “Hybrid deep learning for face verification,” IEEE Trans. Pattern Anal. Mach. Intell., vol. 38, no. 10, pp. 1997–2009, Oct. 2016, doi: 10.1109/TPAMI.2015.2505293. [DOI] [PubMed] [Google Scholar]
- [7].Jiang Y.-G., Wu Z., Tang J., Li Z., Xue X., and Chang S.-F., “Modeling multimodal clues in a hybrid deep learning framework for video classification,” IEEE Trans. Multimedia, vol. 20, no. 11, pp. 3137–3147, Nov. 2018, doi: 10.1109/TMM.2018.2823900. [DOI] [Google Scholar]
- [8].Pepe E., Bajardi P., Gauvin L., Privitera F., Lake B., Cattuto C., and Tizzoni M., “COVID-19 outbreak response, a dataset to assess mobility changes in Italy following national lockdown,” Sci. Data, vol. 7, no. 1, pp. 1–7, Dec. 2020, doi: 10.1038/s41597-020-00575-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Distante C., Pereira I. G., Goncalves L. G., Piscitelli P., and Miani A., “Forecasting COVID-19 outbreak progression in Italian regions: A model based on neural network training from Chinese data,” MedRxiv, Jan. 2020, doi: 10.1101/2020.04.09.20059055. [DOI]
- [10].Ziff A. L. and Ziff R. M., “Fractal kinetics of Covid-19 pandemics (with update 3/1/20),” MedRxiv, Mar. 2020, doi: 10.1101/2020.02.16.20023820. [DOI]
- [11].Yang Z., Zeng Z., Wang K., Wong S. S., Liang W., Zanin M., Liu P., Cao X., Gao Z., Mai Z., and Liang J., “Modified SEIR and AI prediction of the epidemics trend of COVID-19 in China under public health interventions,” J. Thoracic Disease, vol. 12, no. 3, pp. 165–174, Mar. 2020, doi: 10.21037/jtd.2020.02.64. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12].Zhong L., Mu L., Li J., Wang J., Yin Z., and Liu D., “Early prediction of the 2019 novel coronavirus outbreak in the mainland China based on simple mathematical model,” IEEE Access, vol. 8, pp. 51761–51769, 2020, doi: 10.1109/ACCESS.2020.2979599. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13].Wangping J., Ke H., Yang S., Wenzhe C., Shengshu W., Shanshan Y., Jianwei W., Fuyin K., Penggang T., Jing L., and Miao L., “Extended SIR prediction of the epidemics trend of COVID-19 in Italy and compared with Hunan, China,” Frontiers Med., vol. 7, p. 169, May 2020, doi: 10.3389/fmed.2020.00169. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14].Megna R., “First month of the epidemic caused by COVID-19 in Italy: Current status and real-time outbreak development forecast,” Medrxiv, pp. 1–14, Mar. 2020, doi: 10.1101/2020.03.26.20044628. [DOI] [PMC free article] [PubMed]
- [15].Perone G., “An ARIMA model to forecast the spread of COVID-2019 epidemic in Italy,” SSRN Electron. J., Mar. 2020, doi: 10.2139/ssrn.3564865. [DOI]
- [16].Dandekar R. and Barbastathis G., “Neural network aided quarantine control model estimation of COVID spread in Wuhan, China,” 2020, arXiv:2003.09403. [Online]. Available: http://arxiv.org/abs/2003.09403
- [17].Moore K. A., Lipsitch M., Barry J. M., and Osterholm M. T., “COVID-19: The CIDRAP viewpoint. Part 1: The future of the COVID-19 pandemic: Lessons learned from pandemic influenza,” Center Infectious Disease Res. Policy (CIDRAP), Univ. Minnesota, Minneapolis, MN, USA, Tech. Rep., Apr. 2020. [Online]. Available: https://www.cidrap.umn.edu/sites/default/files/public/downloads/cidrap-covid19-viewpoint-part1_0.pdf [Google Scholar]
- [18].Wong W.-K., Moore A., Cooper G., and Wagner M., “Rule-based anomaly pattern detection for detecting disease outbreaks,” in Proc. Nat. Conf. Artif. Intell. (AAAI), Aug. 2002, pp. 217–223. [Google Scholar]
- [19].Wagner M. M., Tsui F. C., Espino J. U., Dato V. M., Sittig D. F., Caruana R. A., McGinnis L. F., Deerfield D. W., Druzdzel M. J., and Fridsma D. B., “The emerging science of very early detection of disease outbreaks,” J. Public Health Manag. Pract., vol. 7, no. 6, pp. 9–51, Jul. 2001, doi: 10.1097/00124784-200107060-00006. [DOI] [PubMed] [Google Scholar]
- [20].The COVID-19 Data Italy Website by Italian Department of Civil Protection. Accessed: May 15, 2020. [Online]. Available: https://github.com/pcm-dpc/COVID-19
- [21].Takeuchi J. and Yamanishi K., “A unifying framework for detecting outliers and change points from time series,” IEEE Trans. Knowl. Data Eng., vol. 18, no. 4, pp. 482–492, Apr. 2006, doi: 10.1109/TKDE.2006.1599387. [DOI] [Google Scholar]
- [22].Cheng H., Tan P. N., Potter C., and Klooster S., “Detection and characterization of anomalies in multivariate time series,” presented at the SIAM Int. Conf. Data Mining, vol. 2, 2009, doi: 10.1137/1.9781611972795.36. [DOI] [Google Scholar]
- [23].Shekhar S., Lu C. T., and Zhang P., “A unified approach to detecting spatial outliers,” GeoInformatica, vol. 7, pp. 139–166, Jun. 2003, doi: 10.1023/A:1023455925009. [DOI] [Google Scholar]
- [24].Lu C.-T., Chen D., and Kou Y., “Algorithms for spatial outlier detection,” in Proc. 3rd IEEE Int. Conf. Data Mining, Melbourne, FL, USA, Nov. 2003, pp. 597–600, doi: 10.1109/ICDM.2003.1250986. [DOI] [Google Scholar]
- [25].Shekhar S., Lu C.-T., and Zhang P., “Detecting graph-based spatial outliers: Algorithms and applications (a summary of results),” in Proc. 7th ACM SIGKDD Int. Conf. Knowl. Discovery Data Mining (KDD), San Francisco, CA, USA, 2001, pp. 371–376. [Google Scholar]
- [26].Sun P. and Chawla S., “On local spatial outliers,” in Proc. 4th IEEE Int. Conf. Data Mining (ICDM), Brighton, U.K., Nov. 2004, pp. 209–216, doi: 10.1109/ICDM.2004.10097. [DOI] [Google Scholar]
- [27].McKenna S. A., “Statistical parametric mapping for geoscience applications,” in Handbook of Mathematical Geosciences, Fifty Years of IAMG, 1st ed. Cham, Switzerland: Springer, 2018, pp. 277–298. [Google Scholar]
- [28].Tahmasebi P., “Multiple point statistics: A review,” in Handbook of Mathematical Geosciences, Fifty Years of IAMG, 1st ed. Cham, Switzerland: Springer, 2018, pp. 613–644. [Google Scholar]
- [29].Breunig M. M., Kriegel H.-P., Ng R. T., and Sander J., “LOF: Identifying density-based local outliers,” ACM SIGMOD Rec., vol. 29, no. 2, pp. 93–104, Jun. 2000, doi: 10.1145/335191.335388. [DOI] [Google Scholar]
- [30].Pokrajac D., Lazarevic A., and Latecki L. J., “Incremental local outlier detection for data streams,” in Proc. IEEE Symp. Comput. Intell. Data Mining, Honolulu, HI, USA, Mar./Apr. 2007, pp. 504–515, doi: 10.1109/CIDM.2007.368917. [DOI] [Google Scholar]
- [31].Ester M., Kriegel H.-P., Sander J., and Xu X., “A density-based algorithm for discovering clusters in large spatial databases with noise,” in Proc. 2nd ACM Int. Conf Knowl. Discovery Data Mining, 1996, pp. 226–231. [Google Scholar]
- [32].Duan L., Xu L., Guo F., Lee J., and Yan B., “A local-density based spatial clustering algorithm with noise,” Inf. Syst., vol. 32, no. 7, pp. 978–986, Nov. 2007, doi: 10.1016/j.is.2006.10.006. [DOI] [Google Scholar]
- [33].Aggarwal C. C., “Proximity-based outlier detection,” in Outlier Analysis, 2nd ed. New York, NY, USA: Springer Nature, 2017, pp. 111–148. [Google Scholar]
- [34].He Z., Xu X., and Deng S., “Discovering cluster-based local outliers,” Pattern Recognit. Lett., vol. 24, nos. 9–10, pp. 1641–1650, Jun. 2003, doi: 10.1016/s0167-8655(03)00003-5. [DOI] [Google Scholar]
- [35].Birant D. and Kut A., “Spatio-temporal outlier detection in large databases,” J. Comp. Inf. Tech., vol. 14, no. 4, pp. 291–297, 2006. [Google Scholar]
- [36].Gupta M., Sharma A. B., Chen H., and Jiang G., “Context-aware time series anomaly detection for complex systems,” in Proc. SDM Workshop Data Mining Service Maintenance, 2013, p. 14. [Google Scholar]
- [37].Liu F. T., Ting K. M., and Zhou Z.-H., “Isolation forest,” in Proc. 8th IEEE Int. Conf. Data Mining, Dec. 2008, pp. 413–422, doi: 10.1109/ICDM.2008.17. [DOI] [Google Scholar]
- [38].Liu F. T., Ting K. M., and Zhou Z.-H., “Isolation-based anomaly detection,” ACM Trans. Knowl. Discov. Data, vol. 6, no. 1, pp. 3:1–3:39, Mar. 2012. [Google Scholar]
- [39].Lavin A. and Ahmad S., “Evaluating real-time anomaly detection algorithms - the numenta anomaly benchmark,” in Proc. IEEE 14th Int. Conf. Mach. Learn. Appl. (ICMLA), Dec. 2015, pp. 38–44. [Google Scholar]
- [40].Ahmad S., Lavin A., Purdy S., and Agha Z., “Unsupervised real-time anomaly detection for streaming data,” Neurocomputing, vol. 262, pp. 134–147, Nov. 2017. [Google Scholar]
- [41].Evangelista P., Bonnisone P., Embrechts M., and Szymanski B., “Fuzzy ROC curves for the 1 class SVM: Application to intrusion detection,” in Proc. 13th Eur. Symp. Artif. Neural Netw., 2005, pp. 345–350. [Google Scholar]
- [42].Ma J. and Perkins S., “Time-series novelty detection using one-class support vector machines,” in Proc. Int. Joint Conf. Neural Netw., vol. 3, 2003, pp. 1741–1745. [Google Scholar]
- [43].Szymanski B. K. and Zhang Y., “Recursive data mining for masquerade detection and author identification,” in Proc. 5th Annu. IEEE SMC Inf. Assurance Workshop, Jun. 2004, pp. 424–431. [Google Scholar]
- [44].Bianco A. M., García Ben M., Martínez E. J., and Yohai V. J., “Outlier detection in regression models with ARIMA errors using robust estimates,” J. Forecasting, vol. 20, no. 8, pp. 565–579, Dec. 2001. [Google Scholar]
- [45].Yaacob A. H., Tan I. K. T., Chien S. F., and Tan H. K., “ARIMA based network anomaly detection,” in Proc. 2nd Int. Conf. Commun. Softw. Netw., 2010, pp. 205–209. [Google Scholar]
- [46].Yu Q., Jibin L., and Jiang L., “An improved ARIMA-based traffic anomaly detection algorithm for wireless sensor networks,” Int. J. Distrib. Sensor Netw., vol. 12, no. 1, Jan. 2016, Art. no. 9653230, doi: 10.1155/2016/9653230. [DOI] [Google Scholar]
- [47].Montgomery D. C., “Cumulative sum and exponentially weighted moving average control charts,” in Introduction to Statistical Quality Control, 6th ed. Hoboken, NJ, USA: Wiley, 2009, pp. 399–432. [Google Scholar]
- [48].Wong W., Moore A., Cooper G., and Wagner M., “What’s strange about recent events (WSARE): An algorithm for the early detection of disease outbreaks,” J. Mach. Learn. Res., vol. 6, Dec. 2005, pp. 1961–1998. [Google Scholar]
- [49].Montgomery D. C., “Control charts for variables,” in Introduction to Statistical Quality Control, 6th ed., Hoboken, NJ, USA: Wiley, 2009, pp. 259–268. [Google Scholar]
- [50].Hutwagner L., Thompson W., Seeman G. M., and Treadwell T., “The bioterrorism preparedness and response early aberration reporting system (EARS),” J. Urban Health, vol. 80, pp. 89–96, Mar. 2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [51].Kulldorff M., “A spatial scan statistic,” Commun. Statist.-Theory Methods, vol. 26, no. 6, pp. 1481–1496, 1997. [Google Scholar]
- [52].Neill D. B. and Cooper G. F., “A multivariate Bayesian scan statistic for early event detection and characterization,” Mach. Learn., vol. 79, no. 3, pp. 261–282, Jun. 2010, doi: 10.1007/s10994-009-5144-4. [DOI] [Google Scholar]
- [53].Chalapathy R. and Chawla S., “Deep learning for anomaly detection: A survey,” 2019, arXiv:1901.03407. [Online]. Available: http://arxiv.org/abs/1901.03407
- [54].Kiran B., Thomas D., and Parakkal R., “An overview of deep learning based methods for unsupervised and semi-supervised anomaly detection in videos,” J. Imag., vol. 4, no. 2, p. 36, Feb. 2018, doi: 10.3390/jimaging4020036. [DOI] [Google Scholar]
- [55].Aggarwal C. C., “Time series and multidimensional streaming outlier detection,” in Outlier Analysis, 2nd ed. New York, NY, USA: Springer Nature, 2017, pp. 273–311. [Google Scholar]
- [56].Malhotra P., Vig L., Shroff G., and Agarwal P., “Long short term memory networks for anomaly detection in time series,” in Proc. 23rd Eur. Symp. Artif. Neural Netw. Comput. Intell. Mach. Learn., 2015, pp. 89–94. [Google Scholar]
- [57].Malhotra P., Ramakrishnan A., Anand G., Vig L., Agarwal P., and Shroff G., “LSTM-based encoder-decoder for multisensor anomaly detection,” presented at the ICML Anomaly Detection Workshop, Jul. 2016. [Google Scholar]
- [58].Hasan M., Choi J., Neumann J., Roy-Chowdhury A. K., and Davis L. S., “Learning temporal regularity in video sequences,” in Proc. IEEE Conf. Comput. Vis. Pattern Recognit. (CVPR), Jun. 2016, pp. 733–742. [Google Scholar]
- [59].Yang H., Wang B., Lin S., Wipf D., Guo M., and Guo B., “Unsupervised extraction of video highlights via robust recurrent auto-encoders,” in Proc. IEEE Int. Conf. Comput. Vis. (ICCV), Dec. 2015, pp. 4633–4641. [Google Scholar]
- [60].Sultani W., Chen C., and Shah M., “Real-world anomaly detection in surveillance videos,” in Proc. IEEE/CVF Conf. Comput. Vis. Pattern Recognit., Jun. 2018, pp. 6479–6488. [Google Scholar]
- [61].Munawar A., Vinayavekhin P., and De Magistris G., “Spatio-temporal anomaly detection for industrial robots through prediction in unsupervised feature space,” in Proc. IEEE Winter Conf. Appl. Comput. Vis. (WACV), Santa Rosa, CA, USA, Mar. 2017, pp. 1017–1025, doi: 10.1109/WACV.2017.118. [DOI] [Google Scholar]
- [62].Perera P. and Patel V. M., “Learning deep features for one-class classification,” IEEE Trans. Image Process., vol. 28, no. 11, pp. 5450–5463, Nov. 2019, doi: 10.1109/TIP.2019.2917862. [DOI] [PubMed] [Google Scholar]
- [63].Estiri H. and Murphy S. N., “Semi-supervised encoding for outlier detection in clinical observation data,” Comput. Methods Programs Biomed., vol. 181, Nov. 2019, Art. no. 104830, doi: 10.1016/j.cmpb.2019.01.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [64].D’Avino D., Cozzolino D., Poggi G., and Verdoliva L., “Autoencoder with recurrent neural networks for video forgery detection,” Proc. IS&T Int. Symp. Electron. Imag. Media Watermarking Secur. Forensics, 2017, pp. 92–99.
- [65].Chong Y. S. and Tay Y. H., “Abnormal event detection in videos using spatiotemporal autoencoder,” in Proc. Int. Symp. Neural Netw. Cham, Switzerland: Springer, 2017, pp. 189–196. [Google Scholar]
- [66].Munir M., Siddiqui S. A., Dengel A., and Ahmed S., “DeepAnT: A deep learning approach for unsupervised anomaly detection in time series,” IEEE Access, vol. 7, pp. 1991–2005, 2019, doi: 10.1109/ACCESS.2018.2886457. [DOI] [Google Scholar]
- [67].Nogas J., Khan S. S., and Mihailidis A., “DeepFall: Non-invasive fall detection with deep spatio-temporal convolutional autoencoders,” J. Healthcare Inform. Res., vol. 4, pp. 50–70, Mar. 2020, doi: 10.1007/s41666-019-00061-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [68].Hinton G. E. and Salakhutdinov R. R., “Reducing the dimensionality of data with neural networks,” Science, vol. 313, no. 5786, pp. 504–507, Jul. 2006, doi: 10.1126/science.1127647. [DOI] [PubMed] [Google Scholar]
- [69].Bengio Y., “Learning deep architectures for AI,” Found. Trends Mach. Learn., vol. 2, no. 1, pp. 1–127, 2009, doi: 10.1561/2200000006. [DOI] [Google Scholar]
- [70].Hecht-Nielsen R., “Replicator neural networks for universal optimal source coding,” Science, vol. 269, no. 5232, pp. 1860–1863, Sep. 1995, doi: 10.1126/science.269.5232.1860. [DOI] [PubMed] [Google Scholar]
- [71].Aggarwal C. C., “Linear models for outlier detection,” in Outlier Analysis, 2nd ed. New York, NY, USA: Springer Nature, 2017, pp. 65–111. [Google Scholar]
- [72].Japkowicz N., Hanson S. J., and Gluck M. A., “Nonlinear autoassociation is not equivalent to PCA,” Neural Comput., vol. 12, no. 3, pp. 531–545, Mar. 2000. [DOI] [PubMed] [Google Scholar]
- [73].Vincent P., Larochelle H., Lajoie I., Bengio V., Manzagol P. A., and Bottou L., “Stacked denoising autoencoders: Learning useful representations in a deep network with a local denoising criterion,” J. Mach. Learn. Res., vol. 11, pp. 3371–3408, Dec. 2010. [Google Scholar]
- [74].Rifai S., Vincent P., Muller X., Glorot X., and Bengio Y., “Contractive auto-encoders: Explicit invariance during feature extraction,” in Proc. Int. Conf. Mach. Learn., Jul. 2011, pp. 833–840. [Google Scholar]
- [75].Sakurada M. and Yairi T., “Anomaly detection using autoencoders with nonlinear dimensionality reduction,” in Proc. MLSDA 2nd Workshop Mach. Learn. Sensory Data Anal. (MLSDA), 2014, p. 4, doi: 10.1145/2689746.2689747. [DOI] [Google Scholar]
- [76].LeCun Y., Bengio Y., and Hinton G., “Deep learning,” Nature, vol. 521, no. 7553, pp. 436–444, May 2015, doi: 10.1038/nature14539. [DOI] [PubMed] [Google Scholar]
- [77].Goodfellow I., Bengio Y., and Courville A., “Autoencoders,” in Deep Learning. Cambridge, MA, USA: MIT Press, 2016, pp. 502–525. [Online]. Available: http://www.deeplearningbook.org [Google Scholar]
- [78].Baldi P., “Autoencoders, unsupervised learning, and deep architectures,” in Proc. ICML Unsupervised Transf. Learn., 2012, pp. 37–50. [Google Scholar]
- [79].Ji S., Xu W., Yang M., and Yu K., “3D convolutional neural networks for human action recognition,” IEEE Trans. Pattern Anal. Mach. Intell., vol. 35, no. 1, pp. 221–231, Jan. 2013, doi: 10.1109/TPAMI.2012.59. [DOI] [PubMed] [Google Scholar]
- [80].Shi X., Chen Z., Wang H., Yeung D.-Y., Wong W., and Woo W., “Convolutional LSTM network: A machine learning approach for precipitation nowcasting,” in Proc. Adv. Neural Inf. Process. Syst., 2015, pp. 802–810. [Google Scholar]
- [81].Patraucean V., Handa A., and Cipolla R., “Spatio-temporal video autoencoder with differentiable memory,” CoRR, vol. abs/1511.06309, 2015. [Google Scholar]
- [82].The COVID-19 Data Italy Website by Italian Department of Civil Protection. Accessed: May 15, 2020. [Online]. Available: https://github.com/pcm-dpc/COVID-19
- [83].Boccia S., Ricciardi W., and Ioannidis J. P. A., “What other countries can learn from Italy during the COVID-19 pandemic,” JAMA Intern Med., vol. 180, no. 7, pp. 927–928, Apr. 2020, doi: 10.1001/jamainternmed.2020.1447. [DOI] [PubMed] [Google Scholar]
- [84].Kraemer M. U. G., Yang C.-H., Gutierrez B., Wu C.-H., Klein B., Pigott D. M., du Plessis L., Faria N. R., Li R., Hanage W. P., Brownstein J. S., Layan M., Vespignani A., Tian H., Dye C., Pybus O. G., and Scarpino S. V., “The effect of human mobility and control measures on the COVID-19 epidemic in China,” Science, vol. 368, no. 6490, pp. 493–497, 2020, doi: 10.1126/science.abb4218. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [85].Italian National Institute of Statistics Website. Accessed: May 15, 2020. [Online]. Available: http://dati.istat.it/Index.aspx?lang=en&SubSessionId=50f87960-20d5-44f2-b405-5fe16f91da73
- [86].Ingole P. V. and Nichat M. K., “Landmark based shortest path detection by using Dijkestra algorithm and Haversine formula,” Int. J. Eng. Res. Appl., vol. 3, no. 3, pp. 162–165, 2013. [Google Scholar]
- [87].Simonyan K. and Zisserman A., “Very deep convolutional networks for large-scale image recognition,” in Proc. Int. Conf. Learn. Represent., 2015, pp. 1–12. [Online]. Available: https://arxiv.org/abs/1409.1556 [Google Scholar]
- [88].Ioffe S. and Szegedy C., “Batch normalization: Accelerating deep network training by reducing internal covariate shift,” in Proc. ICML, 2015, pp. 1–11. [Online]. Available: https://arxiv.org/abs/1502.03167 [Google Scholar]
- [89].Glorot X. and Bengio Y., “Understanding the difficulty of training deep feedforward neural networks,” in Proc. AISTATS, 2010, pp. 249–256. [Google Scholar]
- [90].Wojtak A., “Attempt to predict the stock market,” Interactive qualifying project, Math. Sci., Worcester Polytec. Inst., Worcester, MA, USA, Project no. MH-0777, Feb. 2008. [Online]. Available: https://digitalcommons.wpi.edu/cgi/viewcontent.cgi?article=3117&context=iqp-all [Google Scholar]
- [91].Eskin E., Arnold A., Prerau M., Portnoy L., and Stolfo S., “A geometric framework for unsupervised anomaly detection: Detecting intrusions in unlabeled data,” in Applications of Data Mining in Computer Security (Advances in Information Security), vol. 6. Boston, MA, USA: Springer, 2002, pp. 77–101, doi: 10.1007/978-1-4615-0953-0_4. [DOI] [Google Scholar]
- [92].Abadi M.et al. (2015). Tensorflow: Large-Scale Machine Learning on Heterogeneous Systems. [Online]. Available: https://www.tensorflow.org [Google Scholar]
- [93].Pedregosa F., Varoquaux G., Gramfort A., Michel V., Thirion B., Grisel O., Blondel M., Prettenhofer P., Weiss R., Dubourg V., and Vanderplas J., “Scikit-learn: Machine learning in Python,” J. Mach. Learn. Res., vol. 12, pp. 2825–2830, Oct. 2011. [Google Scholar]
- [94].Seabold S. and Perktold J., “Statsmodels: Econometric and statistical modeling with Python,” in Proc. 9th Python Sci. Conf., 2010, p. 61. [Google Scholar]
- [95].European Centre for Disease Prevention and Control, Stockholm. (Apr. 2020). Strategies for the Surveillance of COVID-19. [Online]. Available:https://www.ecdc.europa.eu/sites/default/files/documents/COVID-19-surveillance-strategy-9-Apr-2020.pdf
- [96].Chintalapudi N., Battineni G., Sagaro G. G., and Amenta F., “COVID-19 outbreak reproduction number estimations and forecasting in Marche, Italy,” Int. J. Infectious Diseases, vol. 96, pp. 327–333, Jul. 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [97].Ferguson N., Laydon D., Nedjati-Gilani G., Imai N., Ainslie K., Baguelin M., Bhatia S., Boonyasiri A., Cucunubá Z., Cuomo-Dannenburg G., and Dighe A., “Report 9: Impact of non-pharmaceutical interventions (NPIs) to reduce COVID-19 mortality and healthcare demand,” Fac. Med., School Public Health, Imperial College London, London, U.K., Tech. Rep., Mar. 2020, doi: 10.25561/77482. [DOI] [Google Scholar]
- [98].Layne S. P., Hyman J. M., Morens D. M., and Taubenberger J. K., “New coronavirus outbreak: Framing questions for pandemic prevention,” Sci. Transl. Med., vol. 12, no. 534, Mar. 2020, Art. no. eabb1469, doi: 10.1126/scitranslmed.abb1469. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [99].Linka K., Pierlinck M., and Kuhl E., “The reproduction number of COVID-19 and its correlation with public health interventions,” Comput. Mech., pp. 1–16, Jul. 2020, doi: 10.1007/s00466-020-01880-8. [DOI] [PMC free article] [PubMed]
- [100].Tahmasebi P., Shokri-Kuehni S. M. S., Sahimi M., and Shokri N., “How do environmental, economic and health factors influence regional vulnerability to COVID-19?” MedRxiv, Apr. 2020, doi: 10.1101/2020.04.09.20059659. [DOI]