ROBUST WHITE MATTER HYPERINTENSITY SEGMENTATION ON UNSEEN DOMAIN

Abstract

Typical machine learning frameworks heavily rely on an underlying assumption that training and test data follow the same distribution. In medical imaging which increasingly begun acquiring datasets from multiple sites or scanners, this identical distribution assumption often fails to hold due to systematic variability induced by site or scanner dependent factors. Therefore, we cannot simply expect a model trained on a given dataset to consistently work well, or generalize, on a dataset from another distribution. In this work, we address this problem, investigating the application of machine learning models to unseen medical imaging data. Specifically, we consider the challenging case of Domain Generalization (DG) where we train a model without any knowledge about the testing distribution. That is, we train on samples from a set of distributions (sources) and test on samples from a new, unseen distribution (target). We focus on the task of white matter hyperintensity (WMH) prediction using the multi-site WMH Segmentation Challenge dataset and our local in-house dataset. We identify how two mechanically distinct DG approaches, namely domain adversarial learning and mix-up, have theoretical synergy. Then, we show drastic improvements of WMH prediction on an unseen target domain.

1. INTRODUCTION

In traditional machine learning, an underlying assumption is that the model is trained on training data that is well representative of the testing data. That is, both the training and testing samples come from an identical distribution. However, this assumption has become difficult to satisfy in the modern medical imaging analysis community as it rapidly grows with multiple sites or scanners [1, 2]. Notably, datasets often exhibit heterogeneity (e.g., differing distributions of intensity) due to systematic variability induced by various site/scanner dependent factors, and commonly, imaging protocols.

In this work, we view sites or scanners as distinct distributions or domains and consider learning in the presence of multiple domains where the identical distribution assumption no longer holds. Under this new training regime, a model is trained on data arising from some sites/scanners and tested on samples from a new site/scanner unseen during the training process. Formally, at train-time, we observe k domains (sites/scanners) refer to as sources which have distributions ${\mathbb{P}}_1,{\mathbb{P}}_2,\dots ,{\mathbb{P}}_k$ over some space $\mathcal{X}$. At test-time, we test the model on a distinct target domain with distribution $\mathbb{Q}$ over $\mathcal{X}$.

This multi-domain construct appears in the literature in several medical image segmentation problems. When a model pretrained on sources is further trained on additional target samples with labels, this is often referred to as Transfer Learning [3]. Adding constraints to this setup, Domain Adaptation (DA) assumes access to samples from $\mathbb{Q}$ but without their labels [4, 5]. This is a prevalent situation for tasks requiring costly data annotations (e.g., manual tracing of brain lesions). Without labels, DA techniques may still utilize the target information to learn domain-agnostic features [4, 6, 7], so that task performance is promising irrespective of the input domain. Importantly, these solutions still assume unlabeled data from $\mathbb{Q}$, and this assumption of pre-existing knowledge may be too strong in some practical scenarios.

We therefore consider the problem of Domain Generalization (DG) where we make no assumptions about the target distribution, i.e., no access to the samples from $\mathbb{Q}$ during training. This recently developing construct has been deemed more challenging, but also, more useful to real world problems where we want to generalize without any data from our target [8, 9]. Yet, while a few DG approaches exist [10, 11], DG is still a nascent concept in medical imaging especially on segmentation problems. Several reasons contribute to this hindered progress, including the lack of theoretical understanding of the existing DG methods and their non-trivial adaptation to segmentation models such as U-Net. Nonetheless, a domain generalizable model is expected to bring practical benefits: retrospectively, we may better leverage existing siloed multi-domain datasets, and prospectively, we can reliably use these models on unseen datasets.

Contribution.

In this work, we ask the following question: Can we devise a segmentation model that generalizes well to unseen data? We answer this as follows: (1) We investigate two mechanically different DG methods, namely domain adversarial neural network and mixup, and identify their theoretical commonality. (2) We use these DG methods to build upon a U-Net segmentation model, tackling the WMH segmentation problem on a multi-site WMH Challenge Dataset [1] and drastically improving performance of a traditional U-Net on the DG task. (3) We further test our model on our local data which is not a part of the aforementioned multi-site dataset. We make our code publicly available.¹

2. METHODS

Intuition tells us that if our features are invariant to the domain, then the main task should not be affected by the domain of the input. In fact, recent theoretical argument [9] formally suggests such domain invariance in the feature space as a solution for DG. This motivates our proposed approach. We first employ the common domain adversarial training algorithm DANN which learns domain invariant features that fool a domain discriminator. We further show the data-augmentation algorithm mixup [12] may also be viewed as promoting domain invariance. We then propose to use both DANN and mixup after identifying their theoretical connection in DG.

2.1. Domain Adversarial Neural Network for DG

Based on the seminal theoretical work of Ben-David et al. [13, 14], Ganin and Lempitsky [5] proposed the commonly used algorithm DANN which learns domain invariant feature representations as desired. This algorithm breaks the model used for the task into two components: a feature extractor r_θ parameterized by θ and a task-specific network c_σ parameterized by σ. In addition to these, we also train a domain discriminator d_μ to classify from which domain each data point is drawn. To learn a domain invariant representation, the feature extractor is trained to fool this domain discriminator. Intuitively, if d_μ cannot identify the domain, then the feature representation learned by r_θ must be void of domain-specific features. In more detail, we may write the DANN objective computed for multiple source domains ${\mathbb{P}}_1,\dots ,{\mathbb{P}}_k$ as below

$$\underset{\sigma ,\theta }{\text{min}}\underset{\mu }{\text{max}}{\mathbf{E}}_{(x_i{)}_i\sim ({\mathbb{P}}_i{)}_i}\left[{\sum }_i{\mathcal{L}}_T(\sigma ,\theta ,x_i)-\gamma {\sum }_i{\mathcal{L}}_D(\mu ,\theta ,x_i)\right]$$ (1)

where ${\mathcal{L}}_D$ is the cross-entropy loss for domains

$$-{\mathcal{L}}_D(\mu ,\theta ,x)={\sum }_j\mathbb{I}[x\sim {\mathbb{P}}_j]\log ((d_{\mu }\circ r_{\theta }(x){)}_j)$$ (2)

and ${\mathcal{L}}_T$ is a task specific loss (e.g., in our segmentation setting, this might be the DSC loss). From this objective, the learned model c_σ ∘ r_θ may be adept at the task (i.e., by minimizing ${\mathcal{L}}_T$), but also invariant of domains (i.e., by maximizing ${\mathcal{L}}_D$). As is usual, we optimize this objective by simultaneous gradient descent implemented by inserting a Gradient Reversal Layer [5] between d_μ and r_θ.

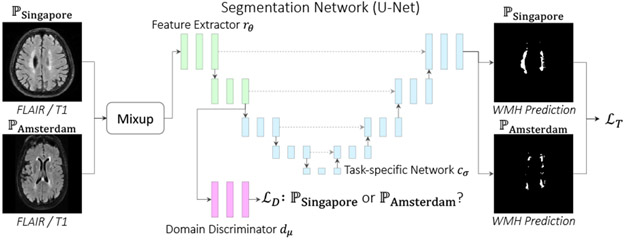
More specific to our segmentation task, it is unclear how to break up a fully convolutional neural network into a feature extraction component and a task-specific component. Motivated by [15], suggesting domain information is typically found in the earlier convolutional layers of a network, we generally limit r_θ to a few blocks in the downward path of a U-Net (Fig. 1). We provide exact details in the code.

Fig. 1:

MixDANN with Amsterdam and Singapore sources.

2.2. Mixup

Besides application of DANN, we also propose to use the common data-augmentation algorithm Mixup [12]. At first glance, this extension is fairly simple. Still, in the presence of multiple domains ${\mathbb{P}}_1,\dots ,{\mathbb{P}}_k$, this algorithm complements the optimization objective in Eq. (1) because it also aims to produce domain invariance in our learning algorithm (discussed in the next sub-section). The algorithm is defined as follows. Suppose we have a batch of data-points {x_i}_i with x_p and x_q two distinct data-points from this sample. Further, let λ ~ Beta(α, α). Then, we define the new mixed data-point:

$${\tilde{x}}_{p,q}=\lambda x_p+(1-\lambda )x_q.$$ (3)

With a certain probability (e.g., 0.5 in all our experiments), we can then substitute every data-point in the batch {x_i}_i with a mixed counterpart by randomly pairing the elements of {x_i}_i and using Eq. (3) to combine them. We do remark that the original proposal for mixup also mixes across the label space. Our segmentation setting is slightly different due to the common use of a Dice score loss. Thus, we adopt a loss balancing strategy similar to [7]: $\mathcal{L}({\tilde{x}}_{p,q})=\lambda {\mathcal{L}}^p({\tilde{x}}_{p,q})+(1-\lambda ){\mathcal{L}}^q({\tilde{x}}_{p,q})$ where ${\mathcal{L}}^i$ is the loss with the label y_i of x_i.

2.3. Theoretical Motivations

DANN and the $\mathcal{H}$-divergence.

While many works have used the motivation of domain invariant features for DG [8, 16], we note that the original theoretical motivation of DANN was based on the domain adaptation theory proposed by Ben-David et al. [14]. Further, recent work [9] has extended this theory to demonstrate that the application of DANN in DG is justified. In particular, it is shown that the $\mathcal{H}$-divergence – a measure of the difference between two domains – appears in an upper bound of the error on an unseen target. Therefore, to proxy minimization of the unseen target error, we can minimize the $\mathcal{H}$-divergence in the upper-bound (amongst other quantities, such as the error on the sources). The objective described in Eq. (1) can be interpreted as minimizing the $\mathcal{H}$-divergence in a fairly formal sense because the $\mathcal{H}$-divergence measures a classifier’s ability to distinguish between domains. Motivated by this, we learn invariant features in Eq. (1) by maximizing the errors of the domain classifier d_μ.

Algorithm 1 MixDANN for Domain Generalization

$$\begin{array}{cc}\hfill & \mathrm{Data}:\text{Set of sample}x\text{and label}y\text{from Sources}{\mathbb{P}}_1,\dots ,{\mathbb{P}}_k\text{and Target}\mathbb{Q}\hfill \\ \hfill & \mathrm{Models}:\text{U-Net (Feature Extractor}{r}_{\theta }\text{and Task-specific Network}{c}_{\sigma }),\text{Do-}\hfill \\ \hfill & \text{main Discriminator}{d}_{\mu }\hfill \\ \hfill & 1:\mathbf{procedure}\text{TRAIN MIXDANN USING SOURCES}({\mathbb{P}}_i{)}_i\hfill \\ \hfill & 2:\mathbf{for}\text{mini-batch}\text{of}\text{samples from}\text{sources}(x_i{)}_i\sim ({\mathbb{P}}_i{)}_i\mathbf{do}\hfill \\ \hfill & 3:\mathrm{Mixup}:{\tilde{x}}_{p,q}\leftarrow \lambda x_p+(1-\lambda )x_q\text{for}p,q\text{pairs},\lambda \sim Beta(0.7,0.7)\hfill \\ \hfill & 4:\mathbf{Task}\mathrm{Update}:\theta ,\sigma \leftarrow {\text{arg min}}_{\sigma ,\theta }\sum {\mathcal{L}}_T(\sigma ,\theta ,{\tilde{x}}_{i,j})\hfill \\ \hfill & 5:\mathbf{Domain}\mathrm{Update}:\theta ,\mu \leftarrow \text{arg}[{\text{min}}_{\theta }{\max }_{\mu }-\gamma \sum {\mathcal{L}}_D(\mu ,\theta ,{\tilde{x}}_{i,j})]\hfill \\ \hfill & 6:\mathbf{end}\mathbf{for}\hfill \\ \hfill & 7:\mathbf{end}\mathbf{procedure}\hfill \\ \hfill & 8:\mathbf{procedure}\text{TESTING MIXDANN ON TARGET}\mathbb{Q}\hfill \\ \hfill & 9:\mathrm{Prediction}:y_i\leftarrow c_{\sigma }\circ r_{\theta }(x_i)\text{for samples from target}{x}_i\sim \mathbb{Q}\hfill \\ \hfill & 10:\mathbf{end}\mathbf{procedure}\hfill \end{array}$$

A Formal Discussion of Mixup.

Mixup [12] is a special case of Vicinal Risk Minimization [17]. Usually, in machine learning, we use Empirical Risk Minimization which suggests estimating the true data-distribution by the empirical measure $P(x,y)=\frac{1}{n}{\sum }_{i=1}^n{\delta }_{x_i}(x){\delta }_{y_i}(y)$, with the Dirac measure δ_* estimating density at each data-point. In the more general case of Vicinal Risk Minimization, we allow freedom to use a density estimate in the vicinity of the data-point x_i using the vicinal measure v_* as $P_v(x,y)=\frac{1}{n}{\sum }_{i=1}^n{v}_{x_i}(x){\delta }_{y_i}(y)$. In Mixup, the modifications to our data described in Eq. (3) equate to sampling from a certain vicinal distribution u_*: $u_{x_i}(x)=\frac{1}{n}{\sum }_{j=1}^n{\mathbf{E}}_{\lambda }\left[{\delta }_{\lambda x_i+(1-\lambda )x_j}(x)\right]$ where λ ~ Beta.

Connecting Mixup to the $\mathcal{H}$-divergence.

From the perspective of the mentioned theory motivating DANN for DG (above), this form of density estimation has interestingly been linked to invariant learning by data-augmentation [17]. In particular, the vicinal measure v_* may be defined to promote learning which is invariant to features of our data (e.g., augmentation by noise seeks to make a neural network’s prediction invariant to noise in the input). By applying Mixup as defined in Eq. (3), we coincidentally mix features across the domains ${\mathbb{P}}_1,\dots ,{\mathbb{P}}_k$ because x_p and x_q may be drawn from differing domains. In this sense, the proposed vicinal distribution u_* estimates the density of a data point x_i to promote invariance to domain features in our learning algorithm. Hence, Mixup in the presence of multiple domains may be viewed as a technique complementary to DANN. It too is aimed at training r_θ and c_σ to be invariant to domain features so that the errors of the domain discriminator d_μ are maximized, and subsequently, the $\mathcal{H}$-divergence is minimized. Alg. 1 shows MixDANN, our algorithmic and theoretical combination of Mixup and DANN for DG.

3. EXPERIMENTS

3.1. Experimental Setup

Datasets.

We evaluate on two WMH datasets consisting of FLAIR (Fluid Attenuated Inverse Recovery), T1, and manual WMH segmentation for each subject: (1) a multi-site public MICCAI WMH Challenge Dataset [1] from three sites (Amsterdam (A), Singapore (S), Utrecht (U)) and (2) our local in-house dataset [18] from a single site (Pittsburgh (P)). See Fig. 2 for distinct scanners/protocols and [1, 18] for details.

Fig. 2:

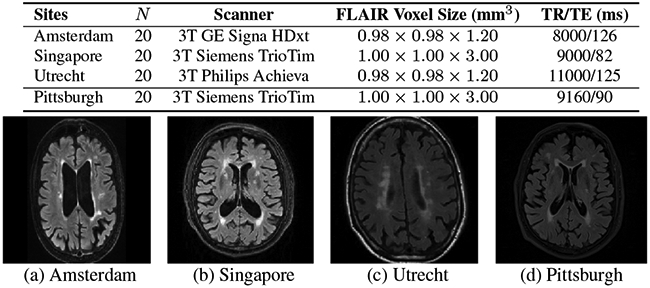
Top: Datasets with FLAIR and T1 (coregistered to FLAIR). Bottom: Sample FLAIR images.

Metrics.

We use five evaluation metrics to assess the WMH prediction mask Ŷ against the ground truth segmentation mask Y (TP: true positive, FP: false positive, FN: false negative). (1) Dice Similarity Coefficient (DSC): 2(Y⋂Ŷ)/(∣Y∣ + ∣Ŷ∣), (2) Housdorff Distance (H95): H95 = max{sup_x∈Y inf_y∈Ŷ d(x, y), sup_yy∈Ŷ inf_x∈Ŷ d(x, y)} using the 95-th percentile distance, (3) Absolute Volume Difference (AVD) between the predicted and true WMH volume, (4) Lesion Recall: Computes the # of correctly detected WMH over the # of true WMH, (5) Lesion F1: TP / (TP + 0.5(FP+FN)).

Baseline Models.

These baselines build on U-Net [19], and we report their results by a recent DA/DG work [4]: (1) DeepAll is the baseline U-Net with no DA or DG mechanisms which the following models build on. (2) UDA [4] is an unsupervised DA method using all target scans but not their labels. Note this DA method requires target thus has an advantage over DG methods. (3) BigAug [10] is a state-of-the-art DG medical imaging segmentation method with heavy data augmentations. See [4, 10] for full details.

Our Model.

Our proposed approaches also build on U-Net. Standard data augmentations (rotation, scale, shear) are applied. (1) We implement our own DeepAll comparable to the DeepAll by [4] to our best effort for fair comparison. (2) DANN: We introduce the domain discriminator (Conv-Conv-Conv-FC-FC-FC) d_μ to U-Net to the output of the second downsampling layer (Fig. 1). For the purpose of DANN (Eq. (1)), we can treat the U-Net as c_σ ∘ r_θ where r_θ is before and c_σ is after the second downsampling. We slowly introduce ${\mathcal{L}}_D$ to r_θ by setting γ = (2 · ξ)/(1 + exp(−κ · p)) − 1 in Eq. (1) with p = epoch/max_epoch, κ = 3, and ξ = 0.1. (3) Mixup: We randomly mix the samples following Eq. (3) to induce domain invariance. (4) MixDANN: Our final model combines DANN and Mixup. The initial learning rate is 2e-4 for all models. We trained on 80% of the training data against the comparing methods using 2 x NVIDIA RTX2080Ti.

3.2. Results and Analysis

Each model tests on one target domain after training on the remaining sources (Sources→Target). Generally, the comparison in DG is subjective across different experimental setups. For instance, despite the near identical architectures, our DeepAll slightly under-performs on some targets. As such, we pay special attention to the relative performance gain over the respective DeepAll to assess the domain generalizability.

Exp 1: DG within WMH Challenge Dataset.

We test on each target by training on the remaining two sources. Table 1 shows the results of all targets and the average across them. We see that despite our weaker DeepAll, MixDANN shows the best absolute avg on three metrics (DSC, AVD, and Lesion F1) and the best relative gain on all metrics. We ablate and see improvements in the order of DANN, Mixup, and MixDANN, also visualized in Fig. 3. We note that AVD assessing the accuracy of the predicted WMH volume, which is often considered as a biomarker of vascular pathology, is most accurate by MixDANN. We also pay special attention to the improvement in the hardest case of A+S→U: This exactly exemplifies a possible scenario where a DeepAll may fail on an unseen dataset but MixDANN can assure robustness.

Table 1:

WMH Challenge Results. Sources→Target: Trained on Sources and tested on Target among Amsterdam, Singapore, and Utrecht. avg: Average of the target results. gain: avg gain over the respective DeepAll.

Model	A+S→U	U+S→A	A+U→S	avg	gain
DSC ↑ (Higher is better)
DeepAll ([4] Setup)	0.430	0.674	0.682	0.595	-
BigAug [10]	0.534	0.691	0.711	0.645	0.050
UDA [4]	0.529	0.737	0.782	0.683	0.087
DeepAll (for Ours)	0.183	0.619	0.781	0.528	-
DANN	0.315	0.674	0.773	0.587	0.060
Mixup	0.619	0.691	0.835	0.715	0.187
MixDANN	0.694	0.700	0.839	0.744	0.217
H95 ↓ (Lower is better)
DeepAll (Our Setup)	11.46	11.51	9.22	10.73	-
BigAug	9.49	9.77	8.25	9.17	−1.56
UDA (Full Set)	10.01	7.53	7.51	8.35	−2.38
DeepAll	42.69	18.05	4.56	21.77	-
DANN	38.56	15.48	5.15	19.73	−2.03
Mixup	24.08	13.21	5.70	14.33	−7.44
MixDANN	20.57	12.75	3.10	12.14	−9.63
AVD ↓ (Lower is better)
DeepAll	54.84	37.60	45.95	46.13	-
BigAug	47.46	30.64	35.41	37.84	−8.29
UDA (Full Set)	54.95	30.97	22.14	36.02	−10.11
DeepAll	384.19	43.28	23.26	150.24	-
DANN	134.03	26.65	24.09	61.59	−88.66
Mixup	42.09	33.47	13.41	29.66	−120.59
MixDANN	23.40	26.48	12.81	20.89	−129.35
Lesion Recall ↑ (Higher is better)
DeepAll	0.634	0.692	0.641	0.656	-
BigAug	0.643	0.709	0.691	0.681	0.025
UDA (Full Set)	0.652	0.841	0.754	0.749	0.093
DeepAll	0.309	0.623	0.705	0.546	-
DANN	0.349	0.630	0.740	0.573	0.028
Mixup	0.556	0.700	0.790	0.682	0.136
MixDANN	0.604	0.685	0.797	0.695	0.150
Lesion F1 ↑ (Higher is better)
DeepAll	0.561	0.673	0.592	0.609	-
BigAug	0.577	0.704	0.651	0.644	0.035
UDA (Full Set)	0.546	0.739	0.649	0.645	0.036
DeepAll	0.288	0.554	0.697	0.513	-
DANN	0.309	0.610	0.708	0.542	0.029
Mixup	0.515	0.642	0.724	0.627	0.114
MixDANN	0.602	0.651	0.728	0.660	0.147

Fig. 3:

Visualization of WMH predictions (A+S→U). True Positive: Green, False Positive: Yellow, False Negative: Red.

Exp 2: A+S+U→Pitt.

We do a “cross-dataset” DG: train on A+S+U and test on Pitt. We could not include Pitt as a source since it only has 5 consecutive slices of manual segmentation available. Nonetheless, when we test it as a target as shown in Table 2, we again see consistent improvements over DeepAll. Interestingly, DANN best performs, implying that Mixup and DANN may also individually bring benefits. Our MixDANN with a single U-Net is now ranked 6^th on the leader board of the WMH Challenge [1], competitive against other top ensemble U-Nets. We observe poor performance by Mixup on the WMH counting metrics (Recall and F1), suspecting this to be from the different manual annotation standards between the two datasets. We consider this as our future work.

Table 2:

WMH Segmentation Results of A+S+U→Pitt

Model	DSC ↑	H95 ↓	AVD ↓	Recall ↑	F1 ↑
DeepAll	0.434	18.49	68.56	0.543	0.630
DANN	0.499	16.04	62.31	0.622	0.680
Mixup	0.462	16.92	65.92	0.501	0.606
MixDANN	0.488	15.93	63.41	0.466	0.566

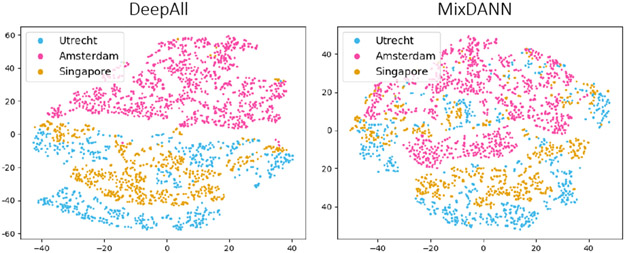
Do we learn domain-invariance?

Fig. 4 shows the t-SNE [20] plots of the second downsampling layer (r_θ) output. We see that the features by DeepAll can easily identify certain domains while those by MixDANN blur the boundary among domains as intended. In the context of WMH prediction, MixDANN explicitly suppresses the site/scanner dependent information, thus is more robust when test on unseen data.

Fig. 4:

t-SNE plots of U-Net features trained on Amsterdam (pink), Singapore (gold) and Utrecht (blue) as sources.

4. CONCLUSION

We investigate the domain generalizability of a WMH segmentation deep model to be trained on sources and operate well on an unseen target. We identify a theoretical connection between two DG approaches, namely DANN and Mixup, and jointly incorporate them into U-Net. Using a multi-site WMH dataset and our local dataset, we show our domain invariant learning frameworks bring drastic improvements over other DA/DG methods in both relative and absolute performances.