Fragility indices for only sufficiently likely modifications

Significance

In frequentist hypothesis testing, P values are used to establish statistical significance. Currently, there is an active movement to use alternative metrics, such as the fragility index, which measures how many outcome modifications in a clinical trial are required to reverse statistical significance. The fragility index approach compares to alternative outcomes that could have arisen from the same clinical trial. However, the existing fragility index does not take into account the likelihood of the outcomes and is defined only for 2 × 2 tables. We introduce methods that provide intuitive remedies to these problems.

Abstract

The fragility index is a clinically meaningful metric based on modifying patient outcomes that is increasingly used to interpret the robustness of clinical trial results. The fragility index relies on a concept that explores alternative realizations of the same clinical trial by modifying patient measurements. In this article, we propose to generalize the fragility index to a family of fragility indices called the incidence fragility indices that permit only outcome modifications that are sufficiently likely and provide an exact algorithm to calculate the incidence fragility indices. Additionally, we introduce a far-reaching generalization of the fragility index to any data type and explain how to permit only sufficiently likely modifications for nondichotomous outcomes. All of the proposed methodologies follow the fragility index concept.

Statistical hypothesis testing is a mainstay in the scientific method. Scientific conclusions typically rely on P values and related summaries to achieve validity. However, P values are widely misunderstood (1, 2). A complement to the P value for 2 × 2 tables that is gaining a foothold in the medical literature is the fragility index (3, 4), which is a measure of evidence that is in “patient” units instead of probability units.

Here, a 2 × 2 contingency table stores data from a clinical trial that has a control and a treatment group and a dichotomous outcome such as event or nonevent. A hypothesis test to determine whether the first group and the second group have different event rates is classically conducted by determining whether a P value is less than a significance threshold.

The fragility index is defined as the minimum number of patients whose outcomes (i.e., event or nonevent) must be modified to reverse significance of a statistical test (4). The measure is used to determine whether the significance of a statistical test is “fragile” and thus should not be firmly trusted. Researchers in several fields have found that surprisingly often the primary results in their field hinge on the outcomes of a few patients (5).

The concept underlying the fragility index is largely the same as the P value. Both consider hypothetical outcomes from the same clinical trial. In one case, P values rely on alternative patient outcomes and their distributional impact on test statistics; in the other, the fragility indices directly explore alternative patient outcomes. We feel that this is the most fundamental aspect of the fragility index: Each modification underlying the fragility index could have been observed in the clinical trial due to random variation.

The fragility index is commonly calculated using an algorithm from Walsh et al. (4) or a close extension, which we call the original algorithm. However, this algorithm can malfunction and fail to return the correct value of the fragility index. Due to this, some researchers have relied on ad hoc or alternative arguments to calculate the fragility index (6, 7). In this work, we describe serious shortcomings of the original algorithm and then present an exact algorithm to calculate the fragility index.

In the years since Walsh et al. (4) reintroduced the fragility index, the approach has been widely used but also criticized. One of the more interesting criticisms has been raised by Walter et al. (6). They argued that the modifications to patient outcomes that are behind the fragility index can be unlikely to occur in practice. This is certainly true, and we feel that the outcome probability is a crucial companion to the fragility index. This allows researchers to contextualize the fragility index in terms of the likelihood of the outcome modifications that reversed statistical significance. However, researchers currently cannot choose this outcome probability associated and are forced to accept whichever event modifications the algorithm happened to use. In this way, the traditional fragility index is roughly associated with an “anything goes” principle and is derived by assuming that any outcome modification can occur.

Another thread of critique argues that the fragility index, which is defined only for 2 × 2 tables, is not defined for useful data types and covariate controls and hence tends to be used inappropriately (8–13). Many who wish to use the fragility index in this case coerce their data into a 2 × 2 format, potentially losing valuable information or fundamentally changing the research question.

In this paper, we contribute methods that generalize the fragility index. To do this, we change the relationship between the fragility index and a fixed outcome probability and instead provide a fragility index for any given outcome modification probability. This enables researchers to have a version of the fragility index that incorporates their assessment of which outcomes in either group are too rare to permit modifications into. For 2 × 2 tables, the measures take into account the incidence in each group and hence we call the measures the incidence fragility indices (14). For general data types, we propose the generalized fragility indices, a broad generalization of the fragility index, which are appropriate for any data type or statistical test. These methods conform to the fragility index concept that only variables subject to random variation are modified. Several examples illustrate the incidence fragility indices and generalized fragility indices and their corresponding algorithms. Code to reproduce the examples is available in the R package FragilityTools (15).

This article proceeds by developing the fragility indices and algorithms presented in Table 1. In the next section, we review the formulation of the fragility index for testing a treatment effect on 2 × 2 tables. After extending the existing formulations by defining the traditional fragility index, we explain fundamental shortcomings of the associated original algorithm. In the following section, we introduce an extension of the 2 × 2 fragility index that permits only sufficiently likely modifications. In the following section, we introduce a broad generalization of the fragility index to any data type and statistical test, propose a class that permits only sufficiently likely modifications, and present an efficient approximation algorithm. In the final section, we summarize our contributions and conclude the paper.

Table 1.

The nomenclature for the methods and algorithms for various fragility measures

Method	Algorithm
Forward fragility index	Walsh’s algorithm
Reverse fragility index	Johnson’s algorithm
	Khan’s algorithm
Traditional fragility index	Original algorithm
	Exact algorithm
Incidence fragility index $F{I}_q$	Exact algorithm
Generalized fragility index
Sufficiently likely construction $GF{I}_q$	Greedy algorithm

The Traditional Fragility Index

In this section we formalize and study the fragility index that was introduced by Walsh et al. (4). We rely on Tables 2 and 3 to explain the fragility index. Table 2 shows the raw data from a clinical trial of the kind considered in this paper, with two groups and a dichotomous outcome. For example, there are a events in group 1 with a + b total patients in group 1 and c events in group 2 with c + d total patients in group 2. Table 3 shows the result of modifying the outcomes within each group of the trial. For example, when f₁ is positive, f₁ patients have their outcome modified from nonevent to event in group 1; when f₁ is negative, $-f_1$ patients have their outcome modified from event to nonevent in group 1. These outcome modifications preserve the number of patients in each group and are the driving force behind the fragility index.

Table 2.

The hypothetical sample data

	Event	Nonevent
Group 1	a	b
Group 2	c	d

Table 3.

The hypothetical sample data with outcome modifications

	Event	Nonevent
Group 1	$a+f_1$	$b-f_1$
Group 2	$c+f_2$	$d-f_2$

We will frequently refer to statistical significance without describing a particular statistical test. The authors believe that researchers should determine statistical significance for the fragility index in the same manner that they initially determined statistical significance. For example, if a researcher is using Fisher’s exact or Pearson’s ${\chi }^2$ test, the same test should be used for the fragility index.

We can view the fragility index as being a supplementary measure of evidence to this underlying statistical test. However, the fragility index concept is more broadly applicable than just to P values. For example, the fragility index concept has been applied to sensitivities instead of P values (16). In this article, we mostly use P values with the significance threshold 0.05 for the underlying statistical test because this is standard in the fragility index literature; however, readers should contextualize the presentation in terms of their preferred measure of evidence.

In this section, first, we briefly review the fragility index definitions and algorithms used in the literature. Next, we explain and appraise existing critiques of the fragility index. Next, we define the traditional fragility index and the original algorithm as modest extensions of the definitions of and algorithms for the reviewed fragility indices. Next, we highlight three shortcomings of the original algorithm in calculating the traditional fragility index. Next, we introduce an exact algorithm that remedies the shortcomings.

“Forward” and Reverse Fragility Indices

We start by reviewing the variants of the fragility index commonly used for 2 × 2 tables and their associated algorithms. We will sometimes refer to the fragility index as the” forward” fragility index to maintain parity with the reverse fragility index.

Forward fragility index

The fragility index was defined by Walsh et al. (4) for only statistically significant results. In their work, Walsh et al. extended an earlier fragility measure discussed by Feinstein (3).

When modifying a small number of a trial’s outcomes reverses the significance of a statistical test, the trial result is said to be fragile. The algorithm provided in Walsh et al. (4) is widely used to calculate the fragility index. It has three steps:

• 1)Choose the group with the fewest events.
• 2)Within that group, modify nonevents to events until statistical significance vanishes.
• 3)Report the total number of outcome modifications as the fragility index.

The algorithm starts by determining a group in which to modify outcomes. Then, the algorithm iteratively modifies patients’ outcomes from nonevent to event until the statistical test is no longer significant. We stress that Walsh’s algorithm can be used to (approximately) calculate the fragility index but is not itself the fragility index defined earlier.

Reverse fragility index

Johnson et al. (17) defined a fragility index for clinical trials with statistically insignificant results by introducing the reverse fragility index. The reverse fragility index is defined as the minimum number of patient outcome modifications that reverses the significance of a nonsignificant statistical test.

To calculate the reverse fragility index, Johnson et al. (17) used an algorithm that changed the number of patients in either group but kept (approximately) constant the total number of events. However, this algorithm is plainly inappropriate since it violates the fragility index concept that the number of patients within each group should be kept constant.

More recently, Khan et al. (18) reintroduced the reverse fragility index and proposed an accompanying algorithm, which has three steps:

• 1)Choose the group with the fewest events.
• 2)Within that group, modify events to nonevents until statistical significance appears.
• 3)Report the total number of outcome modifications as the reverse fragility index.

Khan’s algorithm is similar to Walsh’s, except that Khan’s algorithm modifies events to nonevents in a particular group instead of vice versa. The algorithm iteratively removes events from the group with the fewest events to increase the effect size and drive toward statistical significance.

Existing Fragility Index Critiques

First, there is a critique of the fragility index from Walter et al. (6) that the fragility index can be driven by inappropriately rare outcome modifications. The incidence fragility index and the sufficiently likely construction will be introduced in part to address this critique.

A second critique is that the fragility index can be calculated only for clinical trials with a particular kind of data structure such as a 2 × 2 table. This was true, but additional methods for other data types are increasingly being published. We review these methods, explain that they do not conform to the fragility index concept, and then present an improved measure that does.

A third critique is that well-designed clinical trials will tend to have low fragility indices because P values from such trials are designed to only barely cross the significance threshold (9, 13). A consequence of this critique would be that the fragility index should not be considered because it will always be low in well-designed trials. However, this critique is based on a statistical misunderstanding. There is no evidence that the distribution of P values under the alternative hypothesis will tend to cluster around the significance threshold after a sample size calculation with chosen power such as 0.80. Indeed, previous work shows that natural quantiles of the fragility index in well-designed studies are not always a low number such as one (19).

A fourth critique is connected to the dependence of the fragility index on the sample size (20–22). It has empirically been observed that larger trials tend to have larger fragility indices. Potter (22) made this critique by reviewing properties of posterior odds as evidence measures. In particular, Potter (22) reviewed that larger trials provide less evidence for the alternative hypothesis than smaller trials with the same P value. Then, in contrast, Potter (22) showed via a simulation that larger trials tend to have higher fragility indices (and hence more evidence for the alternative hypothesis) than smaller trials with the same P value. This conflict led Potter (22) to argue that the fragility index had been dismantled.

However, the conflict is immediately resolved by considering the fragility index quotient instead of the fragility index (23). The fragility index quotient is the fragility index divided by the sample size. Throughout simulations, we found that the sample size consistently had a negative relationship with the fragility index quotient while controlling for the P value.*

Further, researchers who prefer Bayesian measures of evidence could use or study a variant of the fragility index that determines statistical significance using Bayesian methods since the fragility index is more broadly applicable than just to P values.

We ultimately feel that, despite critiques and along with our extensions, the fragility index is sufficiently compelling to warrant thorough investigation. Connecting statistical significance to practical matters such as patient outcomes is clinically meaningful and can have an impact on statistical practice.

Definition

There are several disparate approaches to fragility indices and their calculation in the literature. To simplify our later discussion and to clarify concepts, we simply use a single traditional fragility index that combines the forward and reverse fragility indices. This definition is faithful to the previous definitions.

The traditional fragility index is the forward fragility index when the test is initially significant and is the negative of the reverse fragility index when the test is initially insignificant. We use the notation $F{I}_0$ for the traditional fragility index, for reasons that will become clear in the next section. The choice of the sign is consistent with treating the traditional fragility index as connected to the P value and specifically the significance margin $\alpha -p$ associated with a significance threshold α (20). If $\alpha -p$ is negative, so is the traditional fragility index that represents the reverse fragility index. If $\alpha -p$ is positive, so is the traditional fragility index that represents the forward fragility index.

For example, if $F{I}_0=-99$, then 99 patients must have their outcome modified to turn an insignificant test into a significant test. Similarly, if $F{I}_0=99$, then 99 patients must have their outcome modified to turn a significant test into an insignificant test.

The traditional fragility index $F{I}_0$ is formally determined for a given way to assess statistical significance by the number of patient outcome modifications defined below:

$$\underset{f_1,f_2\in \mathbb{Z}}{\min }\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\left|f_1\right|+\left|f_2\right|$$ [1]

subject to Table 2 and Table 3 have reversed significance

$$-a\le f_1\le b,\hspace{0.17em}\hspace{0.17em}-c\le f_2\le d,$$

where the second constraint and that $f_1,f_2\in \mathbb{Z}$ are integers ensure that the entries of Table 3 are not negative. The traditional fragility index is then either that value if the statistical test is initially significant or minus that value otherwise. Under these constraints, the optimization problem returns the fewest total outcome modifications $\left|f_1\right|+\left|f_2\right|$ which reverses statistical significance.

Unifying the forward and reverse fragility indices is conceptually useful. We can determine whether a statistical test is significant at level α by checking whether $F{I}_0>0$ since this is equivalent to $p<\alpha$ by definition. By preferring that the number of patients whose outcomes need to be modified to reverse statistical significance is not small, we are expressing that $F{I}_0>\phi$ for some positive number $\phi$. From this perspective, the traditional fragility is a more stringent test that is stacked on top of the usual P-value–based test. Having a test that is more stringent than the usual significance level 0.05 has been widely called for and is well justified using Bayesian arguments (24).

We could have also chosen $\phi$ to be a small negative number so that the rejection region $F{I}_0>\phi$ provides a test that is less stringent than the usual P-value test. In this case, the traditional fragility index being a small negative number or higher would indicate a soft rejection of the null hypothesis (18). Throughout, the cutoff $\phi$ can be interpreted in a clinically meaningful manner since it is a count of patients (19).

We can calculate the traditional fragility index simply by using Walsh’s algorithm when the statistical test is initially significant and Khan’s algorithm otherwise. This calculation procedure is called the original algorithm.

Algorithmic Shortcomings

The original algorithm suffers from several shortcomings. Despite being intuitive, the algorithm does not reliably find the minimum defined in the traditional fragility index and hence malfunctions and is not exact. This is becoming increasingly well known in the fragility index literature (6, 7). Below, we consider two ways in which the original algorithm fails. Each failure is illustrated with an example. We will see that the original algorithm clearly should not be trusted to calculate the traditional fragility index.

An immediate but minor shortcoming is that, in step 1, the algorithm does not prescribe how to choose a group when both groups have the same number of events.

Direction of outcome modifications

In step 2, there is a more interesting limitation: The direction of outcome modifications is constant within Walsh’s and Khan’s algorithm and so depends only on the initial statistical significance in the original algorithm. There are two prominent ways in which this limitation can lead to the algorithm failing.

First, there is an implicit assumption that events are rarer than nonevents. Because the statistical tests commonly used, such as Fisher’s exact and Pearson’s ${\chi }^2$ tests, treat the event and nonevent outcomes symmetrically, Walsh’s algorithm is really intending to just move the most likely outcome to the least likely outcome within the chosen group and vice versa for Khan’s algorithm.

For example, in the case that there are no events within the chosen group, step 2 in Khan’s algorithm would be impossible to carry out and so the statistical significance could not reverse. Instead of meaning that the statistical significance cannot reverse, in this example Khan’s algorithm seeks to make modifications in an inappropriate direction.

Second, the original algorithm was designed for two-sided statistical tests and can severely malfunction for one-sided tests. The problem is particularly clear when the statistical test is initially insignificant. In that case, both groups’ estimated event rates ($\frac{a}{a+b}$ and $\frac{c}{c+d}$) are close enough that the expected difference is not statistically significantly distinct from zero. Running the original algorithm will drive the chosen group’s event rate downward since events will be modified to nonevents. If the alternative hypothesis is one sided in the opposite direction, then the original algorithm will increase the P value rather than decrease the P value. This makes the statistical significance impossible to reverse for any number of outcome modifications considered by the original algorithm.

Modifying outcomes in only one group

A third shortcoming is that the original algorithm fixates on only one group to make outcome modifications. This is overly restrictive and unnecessary. Modifying patient outcomes in both groups can help to find fewer patients for which modifying their outcomes reverses statistical significance. This shortcoming was nicely discussed by Lin (8).

A clear example of this deficiency can be found in the experiment that motivated R.A. Fisher in 1935 to introduce Fisher’s exact test and also provide an early use of a null hypothesis (25).

The goal of the experiment was to determine whether Fisher’s colleague, Muriel Bristol, could taste whether milk or tea was added first to her cup of tea. The experiment was roughly conducted by presenting Bristol with eight cups of tea: four cups with milk added first and four cups with tea added first. She then tasted the cups of tea and predicted which four cups had milk added first. Table 4 shows the data that are commonly taken to be the outcome of the experiment (26). The test is one sided and was insignificant with P = 0.24.

Table 4.

The lady tasting tea experiment, introduced by Fisher (25)

	Guessed milk	Guessed tea
Poured milk	3	1
Poured tea	1	3

Interestingly, no number of outcome modifications within a single group can reverse the statistical significance of this test. Certainly then, the original algorithm would return that the traditional fragility index is not finite. However, this is not true. Modifying one incorrect guess to a correct guess in both the groups where milk was poured first and tea was poured first produces statistical significance (P = 0.014) and shows that the traditional fragility index is –2.

An Exact Algorithm

To close the gap between the output of the original algorithm and the correct minimum number of patients defined through the optimization problem (1), we study an exact algorithm for the traditional fragility index. The exact algorithm addresses all three shortcomings described in the previous section. As we were writing this article, we found an excellent article by Lin (8) that already presents this same algorithm. The steps of the algorithm are shown below:

• 1)Initialize the total number of outcomes modifications f = 0.
• 2)Increase the total number of outcome modifications f by 1.
• 3)Calculate the statistical significance of Table 3 for all outcome modifications (f₁, f₂) that satisfy $\left|f_1\right|+\left|f_2\right|=f$ and make Table 3 have nonnegative entries.
• 4)Repeat steps 2 and 3 until significance reverses and then report $\pm f$ as the traditional fragility index, where the sign is determined by the initial statistical significance.

In step 3 of the exact algorithm, there is an exhaustive search over all outcome modifications (f₁, f₂) that have a given total number of outcome modifications. For example, when f = 2, all $(f_1,f_2)$ pairs among $(2,0),(1,1),(0,2),$ $(-2,0),(-1,1),$ $(1,-1),(0,-2),$ and $(-1,-1)$ that make Table 3 have nonnegative entries have their corresponding P value calculated. This addresses the shortcomings of the previous subsection by not restricting the values of f₁ and f₂ so that only one is nonzero.

The Incidence Fragility Indices

In this section, we introduce and study a generalization of the traditional fragility index that allows researchers to specify that they want to permit only sufficiently likely outcome modifications. As in the previous section, we again use Tables 2 and 3 to define the sample data of a clinical trial and the sample data with outcome modifications, respectively.

Definition

Define the incidence fragility index $F{I}_q$ for any probability $q\in [0,1]$ as the minimum number of patient outcome modifications that have probability at least q and reverses the significance of a statistical test, appropriately signed. Compared to the index defined in the previous section, the incidence fragility index includes a restriction on the permitted patient outcome modifications to permit only sufficiently likely modifications. The line between modifications that are sufficiently likely or not is determined by the likelihood threshold q, which adds an extra dimension to the traditional fragility index.

We measure the probability of an outcome modification as the in-sample probability of observing the outcome for a given group. For example, in Table 2 the in-sample probability of a patient in group 1 having an event is $\frac{a}{a+b}$ since there were a events among a + b patients. Therefore, we take the in-sample probability $\frac{a}{a+b}$ as the probability of a patient in group 1 having the event instead of a nonevent.

The incidence fragility index $F{I}_q$ is formally determined for a given way to assess statistical significance by the number of patient outcome modifications defined below:

$$\underset{f_1,f_2\in \mathbb{Z}}{\min }\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\left|f_1\right|+\left|f_2\right|$$

subject to Table 2 and Table 3 have reversed significance

$$\begin{array}{l}-a\le f_1\le b,\hspace{0.17em}-c\le f_2\le d\\ f_1\le 0 \text{if} \frac{a}{a+b}<q,\hspace{0.17em}\hspace{0.17em}{f}_1\ge 0 \text{if} \frac{b}{a+b}<q\\ f_2\le 0 \text{if} \frac{c}{c+d}<q,\hspace{0.17em}\hspace{0.17em}{f}_2\ge 0 \text{if} \frac{d}{c+d}<q,\end{array}$$ [2]

where the second constraint and that $f_1,f_2\in \mathbb{Z}$ are integers ensure that the entries of Table 3 are not negative. Like the traditional fragility index, the incidence fragility index is then either that value if the statistical test is initially significant or minus that value otherwise.

This definition differs from the traditional fragility index via Eq. 1 by the inclusion of the last four constraints which ensure that all outcome modifications are sufficiently likely. For example, the $f_1\le 0$ constraint prevents patients in group 1 from having their outcome modified from nonevent to event if the group 1 event probability is not sufficiently likely, i.e., $\frac{a}{a+b}<q$.

Note that when q = 0, the incidence fragility index $F{I}_0$ is the traditional fragility index defined in Walsh et al. (4) since any outcome modification has probability at least 0 and thus all outcome modifications are permitted. In terms of the formal definition in the optimization problem in Eq. 2, having q = 0 forces the last four constraints to be inactive since none of the in-sample probabilities are negative.

When q = 1, the value of the incidence fragility index $F{I}_1$ is more complicated. If no outcome for either group has probability one, the possible outcome modifications are restricted so severely that reversing significance is not possible. In this case, we write that $F{I}_1$ is infinite. In terms of the formal definition in the optimization problem in Eq. 2, having q = 1 when no outcome in either group has probability 1 forces all of the last four constraints to be active so that $f_1\le 0,\hspace{0.17em}{f}_1\ge 0,\hspace{0.17em}{f}_2\le 0$, and $f_2\ge 0$ (that is, $f_1=0$ and $f_2=0$). This makes Table 3 necessarily equal to Table 2 and thus makes reversing the statistical significance impossible. Note that the value infinity is chosen in a theoretically natural way: The minimum in the optimization problem in Eq. 2 is considered to be an infimum, and the infimum of an empty set is infinity (27).

For likelihood thresholds q between 0 and 1, the incidence fragility index $F{I}_q$ shows the result of intermediate probability constraints that fine tune the researcher’s preferences; for example, the incidence fragility index $F{I}_{0.5}$ results from permitting only outcome modifications that are more likely than not.

Basic Properties

In this subsection we establish three basic properties of the incidence fragility indices. These are helpful to develop an initial intuition for the incidence fragility indices and are also crucial for the algorithm in the next subsection. Define the sample size $n=a+b+c+d$. First, the incidence fragility index $F{I}_q$ for any $q\in [0,1]$ will be an integer between – n and n, inclusive but not including 0, whenever it is finite. The number of outcome modifications associated with the incidence fragility index cannot exceed the sample size n, and statistical significance cannot be reversed by modifying the outcomes of 0 patients. In fact, we can tighten the range of the incidence fragility indices further. Since outcomes within a group will never be modified both from events to nonevents and vice versa, the incidence fragility index will actually be between – m and m, inclusive but not including 0, where $m=\max \{a,b\}+\max \{c,d\}$.

Second, the incidence fragility index $F{I}_q$ has at most five possible values as the likelihood threshold q varies over $[0,1]$, because the value of the incidence fragility index for a given trial is determined by which outcome modifications are permitted. There are four kinds of outcome modifications: modifying a nonevent to an event in group 1, vice versa, and likewise for group 2.

When q = 0, any outcome modification is permitted. As q grows, incrementally fewer kinds of outcome modifications will be permitted. When q crosses the lowest outcome probability in either group $\min \{\frac{a}{a+b},\frac{b}{a+b},\frac{c}{c+d},\frac{d}{c+d}\}$, there will be at least one fewer kind of outcome modification permitted since the rarest outcome across both groups can no longer receive modifications. As q grows, eventually q will be so high that no outcome modifications of any kind are permitted. Therefore, there are either all four kinds of outcome modifications permitted (e.g., when q = 0) or three, two, one, or zero kinds of outcome modifications permitted.

Third, the incidence fragility index $F{I}_q$ grows away from zero as q increases, because fewer of the four kinds of outcome modifications are permitted as q increases. When fewer outcome modifications are permitted, the incidence fragility index is increasingly handicapped, and the method needs to work harder to reverse statistical significance. In terms of the formal definition of the incidence fragility index in the optimization problem in Eq. 2, this is due to minimums being as large or larger when the constraint set is smaller.

An Exact Algorithm for Calculating $F{I}_q$ for q > 0

We now define an exact algorithm to compute the incidence fragility indices. We previously described an exact algorithm to calculate the traditional fragility index $F{I}_0$. Therefore, we now propose an algorithm to exactly calculate other incidence fragility indices $F{I}_q$ for q > 0.

The algorithm relies heavily on the properties established in the previous subsection. Starting at the traditional fragility index $F{I}_0$, we know that any incidence fragility index $F{I}_q$ for q > 0 will necessarily correspond to an as great or greater number of outcome modifications by the third basic property. Therefore, the exact algorithm will next choose the likelihood threshold $q_1=\min \{\frac{a}{a+b},\frac{b}{a+b},\frac{c}{c+d},\frac{d}{c+d}\}$ and find $F{I}_{q_1}$. To find $F{I}_{q_1}$, the exact algorithm searches through outcome modifications under the constraints in the optimization problem in Eq. 2 with increasingly many total outcome modifications.

By the second basic property, we know that $F{I}_q=F{I}_0$ for any $q<q_1$. The exact algorithm then iteratively continues this process by finding the incidence fragility index corresponding to each outcome probability in either group, in increasing order.

The steps of the exact algorithm are shown below:

• 1)Find $F{I}_0$ through the exact algorithm for the traditional fragility index and set this equal to f. Choose q to be the smallest nonzero outcome probability in either group.
• 2)Calculate the P value for all feasible outcome modifications (f₁, f₂) that have the given total number of outcome modifications f.
• 3)If statistical significance reverses, report $F{I}_q=f$. If not, increase f by one and go to step 2.
• 4)Go to step 2 for q equaling each outcome probability in either group, in increasing order.

A feasible outcome modification is a modification that satisfies all but the first constraint in the optimization problem in Eq. 2, i.e., which ensures all entries of Table 3 are not negative and permits only sufficiently likely modifications. The algorithm terminates when the total number of outcome modifications f exceeds the highest possible fragility index, as described in the first basic property.

Both of the presented algorithms for the traditional fragility index and for the incidence fragility indices are exact.

Examples

In this subsection we consider several examples of the exact algorithm applied to the incidence fragility indices FI_q. There are many possible behaviors as the likelihood threshold q varies and here we explore some of them. We will rely on both real and simulated trials. In each example, we use Fisher’s exact test to determine statistical significance at the $\alpha =0.05$ level. The trial examples are arranged into subsections according to the apparent stability of the fragility indices.

Stable incidence fragility indices examples

Walter et al. (6) argued that the traditional fragility index $F{I}_0$ can be driven by unlikely modifications by considering a simulated trial for which data are given in Table 5. In the trial, note that group 2 has no observed events. The trial has a statistically significant treatment effect, with a P value of 0.029. The original algorithm produces a traditional fragility index of 1, indicating that the statistical significance is fragile. Walter et al. (6) argued that the (traditional) fragility index being 1 is not evidence of the fragility of the trial result because the original algorithm reversed the significance of the test by modifying a nonevent to an event in group 2, a modification that seemingly has probability 0.

Table 5.

A simulated trial example due to Walter et al. (6)

	Event	Nonevent
Group 1	5	90
Group 2	0	96

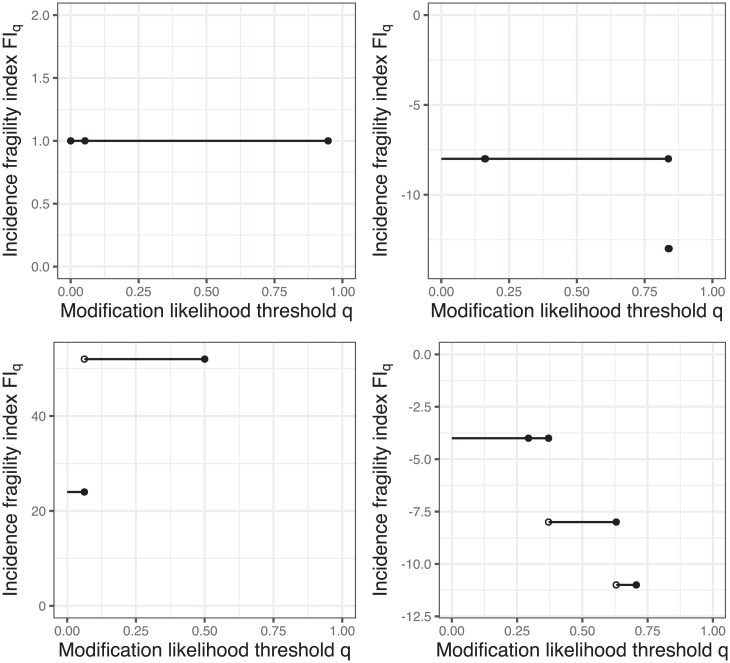
We agree with this argument in principle but note that the incidence fragility indices show that the simulated trial is not an example supporting the argument. [Based on the writing in Walter et al. (6), they seem to be aware of this.] The incidence fragility index $F{I}_q=1$ for any q < 0.947 and is infinite otherwise. The likelihood threshold 0.947 is so high that perhaps even the most conservative researcher would declare that 1 is a reasonable fragility measure of the simulated trial.

The three dots in Fig. 1, Top Left show the in-sample probabilities for various outcomes in either group. By the basic properties, these points are the only possible change point of the incidence fragility indices. The first two points (at q = 0 and q = 0.053) are the event probability in each group, and the last point (at q = 0.947) is the nonevent probability in group 1. There is no value plotted for q > 0.947 since the incidence fragility index is infinite there, indicating that reversing statistical significance is not possible.

Fig. 1.

Visualizations of the incidence fragility indices. Top Left, Top Right, and Bottom Left and Bottom Right correspond to Tables 5, 8, and 9 (top two rows and bottom two rows), respectively.

Second, the second Leicester Intravenous Magnesium Intervention Trial (LIMIT-2) (28) example considered by Walsh et al. (4) shows similar behavior. The 2 × 2 data for the trial are shown in Table 6. While introducing the modern version of the fragility index, Walsh et al. (4) highlighted that the fragility index was merely 1 in the trial despite the trial having thousands of patients. The incidence fragility indices show that this finding is stable in that $F{I}_q=1$ for any q < 0.897 and is infinite otherwise. The 0.897 threshold corresponds to survival probability in the placebo group.

Table 6.

A clinical trial example due to Woods et al. (28)

	Death	Survival
Magnesium	90	1,060
Placebo	118	1,032

Third, a stable example is demonstrated in the simulated trial whose data are shown in Table 7. There are only six patients in the trial, and the test is insignificant with a P value of 1. Every incidence fragility index is infinite, though: No number of outcome modifications can produce a significant test.

Table 7.

A simulated clinical trial example

	Event	Nonevent
Group 1	2	1
Group 2	1	2

Fourth, a borderline stable example is demonstrated in the simulated trial whose data are shown in Table 8. The test for a treatment effect is initially insignificant with a P value of 1. The original algorithm returns a fragility index of –8 patients. The incidence fragility index $F{I}_q=-8$ when $0\le q<0.8375,\hspace{0.17em}F{I}_q=-13$ when $0.8375\le q<0.84$, and $F{I}_q$ is infinite when $q\ge 0.84$. These values are shown in Fig. 1, Top Right.

Table 8.

A simulated clinical trial example

	Event	Nonevent
Group 1	24	126
Group 2	13	67

Unstable incidence fragility indices examples

We now focus on simulated trials for which the interpretation of the traditional fragility index $F{I}_0$ is strained upon taking into account the incidence fragility indices.

First, we consider the simulated trial whose 2 × 2 data are shown in Table 9. The test for a treatment effect is initially significant with P value of $1.6\times {10}^{-12}$, and the original algorithm returns a fragility index of 24 patients. On the other hand, the incidence fragility index $F{I}_q=24$ when $0\le q<0.063,\hspace{0.17em}F{I}_q=52$ when $0.063\le q<0.50$, and $F{I}_q$ is infinite when $q\ge 0.82$. These values are shown in Fig. 1, Bottom Left.

Table 9.

A simulated clinical trial example

	Event	Nonevent
Group 1	75	75
Group 2	5	75

This example has the opposite properties of the fourth example in the preceding subsection. The incidence fragility indices agree with the traditional fragility index only for very small likelihood thresholds q. For a wide range of likelihood thresholds q from nearly zero to one-half, the incidence fragility index is roughly double the traditional fragility index $F{I}_0$.

Second, a final example is given by the simulated trial whose data are provided in Table 10. The test for a treatment effect is initially insignificant with a P value of 0.48, and the original algorithm returns a fragility index of –8. The incidence fragility index is –4 when q < 0.37, –8 when $0.37\le q<0.63$, –11 when $0.63\le q<0.71$, and infinite otherwise. These values are displayed in Fig. 1, Bottom Right. The presence of three possible finite values makes the determination of a single fragility measure especially difficult.

Table 10.

A simulated trial example

	Event	Nonevent
Group 1	10	17
Group 2	27	65

The Generalized Fragility Indices

In this section, we introduce the generalized fragility indices, which provide a natural generalization of the fragility index to any data type or statistical test.

There have been various approaches to generalizing the fragility index beyond the case of $2\times 2$ contingency tables and dichotomous outcomes. All existing approaches that we are familiar with in the literature violate the fragility index concept of considering alternative realizations of the same clinical trial. That is, none of the approaches fix the sample size, fix any assigned variables such as control or treatment group, and then modify other measurements such as outcomes. Instead, one category of approach modifies the group of patients (29, 30), another adds patients into the study (30–32), and another removes patients from the study (17), each in such a way that statistical significance reverses. These approaches are interesting in their own right, but they must be interpreted differently from the fragility index. We provide a framework that offers particularly interpretable examples of generalized fragility indices by permitting only sufficiently likely modifications, analogous to the incidence fragility indices.

Restricting Outcome Modifications

The most foundational element underlying the fragility index concept is modifications to observed measurements. For the $2\times 2$ data case considered in the traditional and incidence fragility indices, this can be accomplished trivially. Since there are only two possible outcomes, either event or nonevent, each patient’s outcome can be kept constant or modified to the other one. However, the definitions are not readily generalizable to outcomes that are nondichotomous.

As a case study, let us consider a naive generalization of the traditional fragility index to nondichotomous outcomes that preserves that “fragility index is defined as the minimum number of patients whose outcomes must be modified to reverse significance of a statistical test” while ignoring the context of a dichotomous outcome. Therefore, this tentative generalization of the fragility index permits a patient’s outcome to be modified to any value. For illustration we calculate this tentative generalization of the fragility index for the simplest statistical test associated with nondichotomous data: the one-sample t test. Naturally, the ideas developed in this case study generalize to other data types, such as time to event.

Write that there are a total of n samples with observations $Y_1,\dots ,Y_n$. Suppose that the t test is initially significant and we use the significance threshold of 0.05. In the extreme, a patient’s outcome could be modified by sending it to infinity. When we do this (without loss of generality) for the first patient, the t-test statistic becomes $\underset{Y_1\to \infty }{\lim }\sqrt{n}(\overline{Y}-0)/S=n^{-1}/\sqrt{(1-n^{-1})/(n(n-1))}=1$, where $\overline{Y}$ is the sample mean and S is the sample SD. A test statistic of 1 corresponds to a nonsignificant test at the $\alpha =0.05$ level for any sample size n. For example, when the sample size n = 100, the P value is ∼0.32. Therefore, this tentative generalization of the fragility index of a statistically significant one-sample t test will always be 1.

We conclude that there is no information in this tentative generalization of the fragility index for this case: It does not depend on the characteristics of the clinical trial or the patient observations. Additionally, this case study is unsettling because measurements being arbitrarily large may not be possible in physical reality. The modifications permitted by a proper generalization of the fragility index must be restricted in some way.

Definition

We now define the generalized fragility index. The measure suitably generalizes the fragility index to any data type and statistical test. Crucially, we will see that the generalized fragility indices are faithful to the fragility index concept.

There are three elements that compose the definition of the generalized fragility indices:

• •A data frame Z for which each row represents patients and each column represents relevant measurements such as covariates and outcomes. Write that there are n patients so that Z has n rows.
• •A rejection region $\mathcal{R}$ for which interest lies in whether the data frame Z is in $\mathcal{R}$.
• •A function m that maps one row $Z_{i,}$ of the data frame Z to a set of modified values. The function is the outcome modifier and returns permitted modifications of each patient’s measurements. We force by convention that the original measurements are possible modifications; i.e., $Z_{i,}\in m(Z_{i,})$.

The generalized fragility index will be uniquely determined by the data Z, rejection region $\mathcal{R}$, and outcome modifier m. We refer to $(Z,\mathcal{R})$ as the statistical setup since they are necessary for any statistical testing problem; on the other hand, the outcome modifier m is designed for the generalized fragility index itself.

The outcome modifier m incorporates two noteworthy properties. First, we can specify that some measurements are not subject to modifications; i.e., ${\left(m(Z_{i,})\right)}_j=Z_{i,j}$ for all patients indexed by $i=1,\dots ,n$. Following the fragility index concept, all measurements that were assigned (and hence would be constant across all possible observed trial realizations) should have this property. Second, we can specify that the modified observations within $m(Z_{i,j})$ are close to the original observation $Z_{i,j}$ in some way. This would resolve the degeneracy highlighted in the previous subsection for the one-sample t test if done appropriately. For example, one choice of m that immediately presents itself is to permit outcomes to be modified by up to a constant translation so that $m(y)=[y-c,y+c]$ for some constant c.

We define the generalized fragility index for the outcome modifier m and statistical setup $(Z,\mathcal{R})$ as follows: Let $Z^{\text{mod}}$ be a variant of the data frame Z that has the same dimensions but with some rows possibly modified. Recall that each row represents a patient indexed by the notation i. Then we define the generalized fragility index to be a signed count of patients with modified outcomes, where the count of patients with modified outcomes is

$$\begin{array}{l}\min \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\left|M\right|\\ \text{subject} \text{to}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}Z\in \mathcal{R}\hspace{0.17em}\oplus \hspace{0.17em}{Z}^{\text{mod}}\in \mathcal{R}\\ Z_{i,}^{\text{mod}}\in m(Z_{i,}) \text{for} \text{all} i=1,\dots ,n\\ Z_{i,}^{\text{mod}}\ne Z_{i,}\hspace{0.17em} \text{for} i\in M.\end{array}$$ [3]

The sign of the generalized fragility index is determined by whether $Z\in \mathcal{R}$: The generalized fragility index is positive if $Z\in \mathcal{R}$ and is negative otherwise.

We now interpret the terms in the definition. The first constraint includes the exclusive or, ⊕, which denotes that either the original data frame Z or the modified data frame $Z^{\text{mod}}$ is in the rejection region $\mathcal{R}$, but not both. This formalizes that the modified data frame reverses inclusion in $\mathcal{R}$, i.e., statistical significance. The second constraint forces that the considered outcome modifications are permitted according to the outcome modifier m. The set M contains the indices of the patients whose outcomes are modified, due to the last constraint. Since the optimization problem is minimizing the cardinality $\left|M\right|$ of the set M, the generalized fragility indices find the fewest possible permitted modifications to patient outcomes that reverse whether $Z\in \mathcal{R}$.

Note that we could have rewritten the optimization problem in Eq. 3 as a projection onto the space of modified data frames (i.e., $Z^{\text{mod}}$) spanned by the first two constraints. The objective of this would be $\left|\right|Z-Z^{\text{mod}}|{|}_{\#}$, where $\left|\right|·|{|}_{\#}$ is the norm that counts the number of nonzero rows, i.e., the number of patients with modified outcomes.

The generalized fragility indices are indeed a generalization of the fragility index described by Walsh et al. (4). Let the data frame Z have two columns, with the first column representing the group (either control or treatment) and the second column representing the outcome (either event or nonevent). Let the outcome modifier fix the first entry since the group is assigned and permit any outcome modification so that $m(Z_{i,})=\{[Z_{i,1},\hspace{0.17em}\hspace{0.17em}\text{event}],[Z_{i,1},\hspace{0.17em}\hspace{0.17em}\text{nonevent}]\}.$ Then, this generalized fragility index is the traditional fragility index.

The Breakdown Point

In this subsection, we review a close relationship between fragility indices and the field of robust statistics (33). In the following subsection, we propose a construction technique for an outcome modifier m that permits only sufficiently likely modifications.

The field of robust statistics (33) studies the behavior of statistical methodologies under data distributions that deviate from standard distributions. A major body of work studies the sensitivity of statistical methods to outlier contamination. A fundamental measure in this context is the breakdown point (34), which classically measures how many patient outcomes must be modified for a statistic to diverge. When viewed as a proportion similar to the fragility index quotient (23), the breakdown point measures what percentage of patient outcomes must be arbitrarily contaminated for a statistic to lose all meaning. The tentative generalization of the fragility index we considered at the start of the section is an example of a sample breakdown point. The same calculation was done in Zhang (35) and Jolliffe and Lukudu (36) to show that the breakdown point of the one-sample t test when the test is significant is merely $1/n$ for sample size n. In robust statistics, this result shows that the t test is highly sensitive to outliers; however, we have different interests in this article. We are interested in the impact of minor perturbations of the data on rejection decisions, for which the breakdown point is not suitable.

Sufficiently Likely Modifications

The sufficiently likely construction of the outcome modifier requires information beyond the statistical setup $(Z,\mathcal{R})$ minimally needed to conduct a statistical hypothesis test. The source of additional information we use is the outcome distribution. We develop this approach for univariate numeric and categorical data types.

Numerical data types

First, we consider how to operationalize the sufficiently likely construction technique for numeric data types. We describe the construction for continuous variables with probability density functions, but an analogous construction works for discrete variables with probability mass functions.

There are three intuitive principles that underlie the construction:

• 1)The observed value should be in the set of permitted values,
• 2)likelier values have priority to be in the set, and
• 3)the set of permitted modifications is an interval.

The first principle is simply a restating of an assumption given in the previous section in the definition of the outcome modifier m. The second principle ensures that the set of outcome modifications contains values that plausibly could have arisen. This is the principle that relies on knowing the probabilistic distribution of the outcome. The third principle is reasonable because it arises from allowing the unobserved statistical error to smoothly vary, although it cannot hold for categorical data types.

From considering these three intuitive principles, a clear choice of the outcome modifier m emerges. The modifier function m should return the highest-density interval that includes the observation. Since highest-density regions are indexed by a coverage $1-q\in [0,1]$, this construction provides a family of outcome modifiers m_q. We call q the likelihood threshold, as we did for the incidence fragility indices. Define $GF{I}_q$ to be the generalized fragility index with modifier m_q and likelihood threshold q.

Note that $GF{I}_0$ is the breakdown point since the set of permitted modifications has full coverage and $GF{I}_1$ is infinite since the set of permitted modifications has coverage 0 and hence is empty.

To determine the likelihood of the permitted values, we use the most informative distribution possible. In general for parametric statistical testing problems, this will involve the estimated distribution that has the parameter estimated using all of the available data under no constraint.

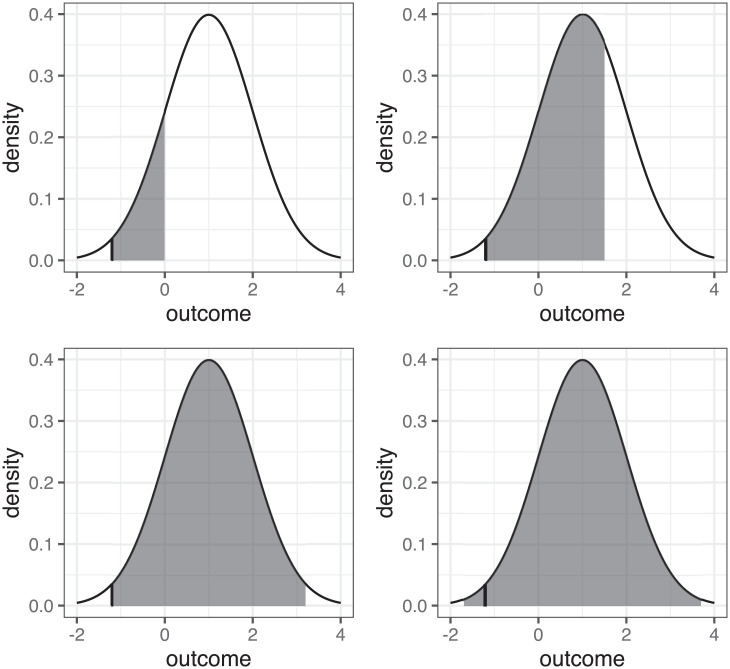
An illustration of the intervals that could be returned by m_q is in Fig. 2 for the case of a one-sample t test. Specifically, we consider the permitted modifications when the observation has the value –1.2, denoted by the vertical black line segment. Since an assumption for the t test to have exact error rates is that the outcome is normally distributed, we assume that the outcome satisfies this. The data we assume in Fig. 2 have sample size n = 100, sample mean $\overline{Y}\approx 1$, and sample variance $S^2\approx 1$. We consider the possible values of $m_q(-1.2)$ following the sufficiently likely construction. The density of the normal distribution with parameters $\overline{X}$ and S² is included in Fig. 2.

Fig. 2.

An illustration of four possible intervals that could be returned by the sufficiently likely construction of the outcome modifier relying on a normal distribution, for varying levels of confidence.

We consider a family of outcome modifiers m_q for $q\in [0,1]$. Note that we abuse the function notation and treat simply the outcome as the domain. The interval returned by the modifier m_q is the set of values that span the shaded region in Fig. 2, where each shaded region is chosen to have area equal to a user-supplied likelihood threshold $q\in [0,1].$ The Fig. 2, Top Left interval $m_{.855}(-1.2)=[-1.2,0]$ is derived with the likelihood threshold q = 0.855. It is the highest-density region that includes the observation. The Fig. 2, Top Right interval $m_{.322}(-1.2)=[-1.2,1.5]$ is similar yet with q = 0.322. The Fig. 2, Bottom Left interval $m_{.028}(-1.2)=[-1.2,3.2]$ is derived with q = 0.028 and is the largest interval that does not include any values lower than the observation –1.2. The Fig. 2, Bottom Right interval $m_{.007}(-1.2)=[-1.7,3.7]$ is derived with q = 0.007 and is symmetric. These sets returned by the modifiers m_q illustrate a clear pattern: As the likelihood threshold q grows, the interval grows and covers higher-density, more central values until the interval starts to grow symmetrically. More extreme values of the outcome are not permitted until the likelihood threshold q is large.

Categorical data types

Second, we consider how to operationalize the sufficiently likely construction for categorical nonnumeric data types. In this case, each of the three intuitive principles above cannot hold. Indeed, the third principle fails because the space is not ordered.

Therefore, we abandon the third principle while retaining the first two. This naturally leads to outcome modifications that contain the observation and some of the other possible values that are most likely. Let us now formally describe this set when, say, the observation is x. Let $S_p=\left\{x\right\}\cup \{x\prime \hspace{0.17em}:\hspace{0.17em}\mathrm{\mathbb{P}}[x\prime ]>p\}$ be such a set, where $\mathrm{\mathbb{P}}$ is the (possibly estimated) probability of the outcome. Then, for any probability $q\in [0,1]$, the sufficiently likely construction technique returns the set $S_{p(q)}$, where p(q) is the minimum p such that $\mathrm{\mathbb{P}}[S_p]\le q$.

When the outcome and explanatory variable are each dichotomous, the generalized fragility indices are simple transformations of the incidence fragility indices. Instead of using the set $S_{p(q)}$ as the permitted outcome modifications, the incidence fragility indices directly use the set S_q.

We can readily observe a basic property of the generalized fragility indices with outcome modifiers that follow the sufficiently likely construction. When q grows larger, the outcome modifier m_q covers a smaller region and hence fewer modifications are permitted. Therefore, in view of the variational definition, the generalized fragility indices grow away from zero as q grows.

A Greedy Algorithm

We now study calculating the generalized fragility indices. An exact algorithm can be readily derived by following the same approach as for the traditional and incidence fragility indices. First, all modifications that lead to the generalized fragility index to be $\pm 1$ could be checked. If any modification does reverse significance, then the algorithm terminates; otherwise, the algorithm does the same for $\pm 2$ and continues iteratively increasing until finding a modification that reverses statistical significance or all patient outcomes have been modified and reversal is deemed impossible. However, this combinatorial algorithm is intractable in practice: The first iteration considers modifications for each of the n patients, and the second iteration considers all $\left(\begin{array}{c}n\\ 2\end{array}\right)$ patient pairs, etc.

Since the above exact algorithm is slow in general, we propose a much faster approximate algorithm, inspired by the fast yet approximate original algorithm. The algorithm is a greedy approximation (37) and is stated in Algorithm 1. Note we assume the original data frame $Z\notin \mathcal{R}$ for notational simplicity. Write that $\mathcal{R}=\{Z\hspace{0.17em}:\hspace{0.17em}p(Z)>c\}$ for some significance threshold c.

Algorithm 1

Approximately find the modification count for generalized fragility indices

• 1.${\text{GFI}}_{\text{count}}\leftarrow 0$
• 2.$Z^{\text{mod}}\leftarrow Z$
• 3.$\text{SameSig}\leftarrow \text{TRUE}$
• 4.while SameSig do
• 5. ${\text{GFI}}_{\text{count}}\leftarrow {\text{GFI}}_{\text{count}}+1$
• 6. if ${\text{GFI}}_{\text{count}}>n$ then
• 7.  ${\text{GFI}}_{\text{count}}\leftarrow \infty$; break
• 8. for each patient i not yet modified do
• 9.  $S_i\leftarrow \{Z^a:Z_{k,}^a=Z_{k,}^{\text{mod}}\hspace{0.17em}\text{for}\hspace{0.17em}k\ne i,\hspace{0.17em}\hspace{0.17em}{Z}_{i,}^a\in m(Z_{i,}^{\text{mod}})\}$
• 10.  $p_i\leftarrow {\min }_{Z^a\in S_i}p(Z^a)$
• 11.  $Z^{a(i)}\leftarrow \arg {\min }_{Z^a\in S_i}p(Z^a)$
• 12. $I\leftarrow \arg {\min }_i{p}_i$
• 13. $Z^{\text{mod}}\leftarrow Z^{a(I)}$
• 14. if $p(Z^{\text{mod}})\le c$, then
• 15.  15. $\text{SameSig}\leftarrow \text{FALSE}$
• 16.return ${\text{GFI}}_{\text{count}}$

Algorithm 1 works by iteratively looking through outcome modifications for each patient. Within each iteration, the algorithm determines which patient has the outcome modification that makes the P value as small as possible. To do this, the best outcome modification for each patient is found. By best, we mean specifically the modification that drives p as low as possible within the set S_i of permitted modifications for each patient, where p is the P value. This is a sensible goal because recall that we are seeking a modified data frame $Z^{\text{mod}}$ for which $p(Z^{\text{mod}})$ is lower than the cutoff c. This optimization to find the best outcome modification may be time consuming, depending on the structure of p and m. With this information for each patient, the algorithm can readily determine which patient has the outcome modification that makes p as small as possible. The algorithm then commits to that modification and restarts the process, again exploring the permitted outcome modification of the remaining patients. This is repeated until inclusion of $\mathcal{R}$ reverses or there are no longer patients to receive outcome modifications.

This approach to approximating a fragility index has appeared earlier in the literature. Atal et al. (7) and Xing et al. (38) similarly relied on a greedy algorithm to calculate an extension of the fragility index for meta-analyses and network meta-analyses. They were in a data setting that was close to that originally considered by Walsh et al. (4): They had a dichotomous outcome variable (such as event or nonevent) and a dichotomous explanatory factor (such as control or treatment), together with an additional explanatory factor representing the study. They also explored altering the algorithm to consider only outcome modifications for a restricted class of patients, such as those in a particular study, for computational acceleration at the cost of further approximation.

We now explain more carefully why Algorithm 1 is greedy. Imagine that the generalized fragility index is 1 or –1 so that the corresponding count of outcome modifications is 1. Then, the proposed greedy algorithm will find an outcome modification that reverses inclusion in $\mathcal{R}$ and hence terminates at the correct value. When the generalized fragility index corresponds to a count of patient outcome modifications that is larger than 1, the same argument holds: The algorithm iteratively makes the best possible modification. Hence, it is greedy.

The algorithm creates a modified data frame $Z^{\text{mod}}$ that reverses inclusion in $\mathcal{R}$ when the algorithm finishes running, assuming it did not decide that reversing inclusion in $\mathcal{R}$ is impossible given the permitted outcome modifications via the modifier m. By construction, this modified data frame is feasible for the optimization problem in Eq. 3 defining the generalized fragility index; hence the corresponding count of patient modifications is an upper bound of the patient count for the generalized fragility index. The bound will tend to be tight due to the greedy nature of the algorithm, and we explore specific examples via simulation studies and real data examples in the following subsection.

Example

We now study the generalized fragility indices when they are applied to modify normally distributed outcomes compared via the one-sample t test. We used this example throughout the previous subsections to motivate the techniques. An existing approach for finding fragility measures for continuous outcomes was developed by Caldwell et al. (29); however, this method violates the fragility index concept. It modifies the control or treatment group of patients, which is assigned by the experimenter and hence not subject to variation.

We study a random vector $y\in {\mathbb{R}}^{500}$, where each entry $y_i\sim \mathcal{N}(\mu ,{\sigma }^2)$ is normally distributed and independent, where $\mu =0.1$ and ${\sigma }^2=1$. We estimate the sample mean $\overline{y}=0.099$ and variance $S^2=1.008$. Note that we use simulated data so that we can leverage the statistical model being known.

The data frame Z has only one column and contains the outcome. There are as many rows as there are patients, which is 500. The rejection region $\mathcal{R}$ is determined by whether a one-sample t test rejects at the 0.05 significance level. A data frame lying within $\mathcal{R}$ is equivalent to rejecting the null hypothesis μ = 0. Using the simulated data, the one-sample t test is statistically significant with P = 0.027, so we initially reject the null hypothesis and the generalized fragility indices must be positive yet.

We define the outcome modifier by following the sufficiently likely construction with an assumed normal distribution. Since the parameters of the normal distribution are not known in advance, we use the estimated distribution $\mathcal{N}(\overline{y},S^2)$. The sufficiently likely construction then defines a family of modifiers m_q for each likelihood threshold $q\in [0,1]$. For each combination of Z, $\mathcal{R}$, and the modifier m_q, a generalized fragility index is determined.

We efficiently approximate the generalized fragility indices using the greedy algorithm. Each pass of the greedy algorithm requires maximizing the P value over the interval returned by m_q. The maximizer must either make the derivative of the P value vanish or lie on the boundary of the interval. In the algorithm, we simply check each of these points. Note, for statistical tests or data types where the maximizer cannot be found in closed form, numerical procedures can be used.

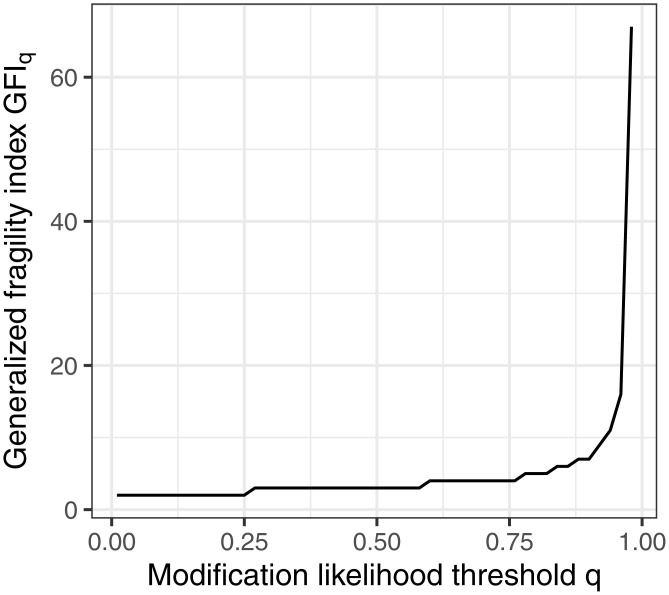
In Fig. 3, we visualize the generalized fragility indices. We used an equally spaced grid of 50 distinct values of q in an equally spaced grid to create Fig. 3. Fig. 3 illustrates some expected but notable behavior. The generalized fragility index is large when q is small so that outcomes can only marginally be modified; the generalized fragility index is near 1 when q is large, as shown earlier. For moderate q, the generalized fragility indices take many intermediate values. For example, with q = 0.5, the generalized fragility index equals 3. We interpret this as follows: There exist only three permitted outcome modifications that reverse statistical significance, where permitted is interpreted as being within the highest-density interval that includes the observation and has 0.50 coverage. The broad spectrum of generalized fragility index values here makes especially difficult the determination of a single number to summarize the family of generalized fragility indices. We note, however, that there is a sharp scree behavior in the generalized fragility indices, where the count approximately stabilizes at approximately $q\approx 0.1$. The calculation of the generalized fragility indices took in total 112 s or ∼2.25 s per generalized fragility index.

Fig. 3.

The generalized fragility indices for the t test indexed by the sufficiently likely threshold q.

Conclusion

We introduced the traditional fragility index and an exact algorithm to calculate it. Next, we introduced the incidence fragility indices, which are fragility measures that permit only outcome modifications that are more likely than the likelihood threshold q, and considered an exact algorithm to calculate them. We then considered several examples of the incidence fragility indices, and the exact algorithm crucially enabled us to have an honest look at the fragility measures and use values that are not biased due to algorithmic complications. The methodological development culminated with the definition of the generalized fragility indices that follow the sufficiently likely construction. The development finalized with the greedy algorithm for calculating generalized fragility indices.

Our analyses have shown that the incidence fragility indices can be sensitive to the outcome modification likelihood threshold q that is chosen. Therefore, the fragility index itself can be fragile, that is, sensitive to the likelihood threshold, if not handled appropriately. By being explicit about the likelihood threshold, the incidence fragility indices also allow researchers to be more precise about the likelihoods underlying the traditional fragility index. Of course, the incidence fragility indices are also interesting measures in their own right. Generalized fragility indices following the sufficiently likely construction can analogously be compared with the breakdown point.

The generalized fragility indices have a broad scope, far beyond Fisher’s exact test and the one-sample t test for illustration. The approach suitably defines fragility measures for tests with covariates. Some further examples are given in the R package FragilityTools (15). The sufficiently likely construction was defined only for univariate modifications, although higher-dimensional modifications are possible with a box construction.

There are many reasons why a fragility measure could be small. In small studies, the most compelling result possible could produce a small fragility index. For the lady tasting tea experiment reviewed previously, the largest possible fragility index is only 1: In some sense, the study was doomed to be insignificant or fragile. A recently proposed method to design studies to have nonfragile results can be directly modified to accommodate generalized fragility indices (19). This would allow studies to be designed to have a large enough fragility measure. Additionally, to better understand the largest possible fragility measure and other probabilistic summaries, researchers could visualize their fragility measure under null or alternative distributions (39).

There is much more work to do with fragility measures. In methodological future work, we plan to study alternative mechanisms for choosing patients’ underlying fragility measures. The generalized fragility indices establish only the existence of patients for which modifying their outcomes reverses statistical significance. However, these patients may be peculiar in some way and hence not readily interpretable (34). A measure that instead ensures that a random collection of patients with a given cardinality are more likely than not to have outcome modifications that reverse statistical significance seems to be an interesting direction. Additionally, we plan to study overall discrepancy measures between the original data and the modified data to supplement per-patient likelihood measures. Finally, theoretical descriptions of the sampling distribution of the measures described in this article would be very interesting.

Data Availability

All study data are included in the main text.