In situ investigation of water on MXene interfaces

Significance

Water organization at solid–liquid interfaces plays a critical role in a range of applications related to adsorption, membrane separations, energy storage, and catalysis. Currently, our understanding of molecular water at solid interfaces is limited to macroscopic and bulk measurement approaches. These interrogation techniques lack the spatial and temporal resolutions necessary to detect how water interacts with local heterogeneous chemical microenvironments governed by surface chemistry, solutes, etc. This work reveals the interaction between water and two-dimensional MXenes by combining in situ ambient-pressure X-ray photoelectron spectroscopy (XPS) and molecular dynamics simulation. This work demonstrates how the size of a solute (cation) governs transport within confined nanochannels and the hydration energy of the solute governs water adsorption/desorption properties at exposed surfaces.

Abstract

A continuum of water populations can exist in nanoscale layered materials, which impacts transport phenomena relevant for separation, adsorption, and charge storage processes. Quantification and direct interrogation of water structure and organization are important in order to design materials with molecular-level control for emerging energy and water applications. Through combining molecular simulations with ambient-pressure X-ray photoelectron spectroscopy, X-ray diffraction, and diffuse reflectance infrared Fourier transform spectroscopy, we directly probe hydration mechanisms at confined and nonconfined regions in nanolayered transition-metal carbide materials. Hydrophobic (K⁺) cations decrease water mobility within the confined interlayer and accelerate water removal at nonconfined surfaces. Hydrophilic cations (Li⁺) increase water mobility within the confined interlayer and decrease water-removal rates at nonconfined surfaces. Solutes, rather than the surface terminating groups, are shown to be more impactful on the kinetics of water adsorption and desorption. Calculations from grand canonical molecular dynamics demonstrate that hydrophilic cations (Li⁺) actively aid in water adsorption at MXene interfaces. In contrast, hydrophobic cations (K⁺) weakly interact with water, leading to higher degrees of water ordering (orientation) and faster removal at elevated temperatures.

Geologic clays are minerals with variable amounts of water trapped within the bulk structure (1) and are routinely used as hydraulic barriers where water and contaminant transport must be controlled (2, 3). These layered materials can exhibit large degrees of swelling when intercalated with a hydrated cation (4). Fundamentally, water adsorption at exposed interfaces and transport in confined channels is dictated by geometry, morphology, and chemistry (e.g., surface chemistry, local solutes, etc.) (5). Understanding water adsorption and swelling in natural clay materials has significant implications for understanding water interactions in nanoscale layered materials. At the nanoscale, the ability to control the interlayer swelling and water adsorption can lead to more precise control over mass and reactant transport, resulting in enhancement in properties necessary for next-generation energy storage (power and capacity) (6–8), membranes (selectivity, salt rejection, and water permeability), catalysis (9–13), and adsorption (14).

Two-dimensional (2D) and multilayered transition-metal carbides and nitrides (MXenes) are a recent addition to the few-atom-thick materials and have been widely studied in their applications to energy storage (6, 9, 15, 16), membranes (13), and adsorption (17). MXenes ($M_{n+1}{X}_n{T}_x$) are produced via selective etching of A elements from ceramic MAX ($M_{n+1}$ AX_n) phase materials (11, 18). The removal of A element results in thin $M_{n+1}$ X_n nanosheets with negative termination groups (T${}_x^{\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}-}$). MXene’s hydrophilic and negatively charged surface properties promote spontaneous intercalation of a wide array of ions and compounds. Cation intercalation properties in MXenes have been vigorously explored due to their demonstrated high volumetric capacitance, which may enable high-rate energy storage (6, 19). In addition, their unique and rich surface chemistry may enable selective ion adsorption, making them promising candidates for water purification and catalytic applications (20–22).

Water and ion transport within multilayered MXenes is governed by the presence of a continuum of water populations. The configuration of water in confined (interlayer) and nonconfined state (surface) influences the material system’s physical properties (13, 23–27). However, our current understanding of water–surface interactions and water structure at the molecular scale is incomplete due to limited characterization approaches (28). Most modern observations are limited to macroscopic measurements (e.g., transport measurement, contact angle, etc.), which do not capture the impact of local heterogeneity due to surface roughness, surface chemistry, solutes, etc. (29). Herein, we address this gap via combining theory with an ensemble of direct and indirect interrogation techniques. Water structure and sorption properties at MXene interfaces are directly probed by using ambient-pressure X-ray photoelectron spectroscopy (APXPS), X-ray diffraction (XRD), and diffuse reflectance infrared Fourier transform spectroscopy (DRIFTS). APXPS enables detection of local chemically specific signatures and quantitative analysis at near-ambient pressures (30). This technique provides the ability to spatially resolve the impact of surface chemistry and solutes on water sorption/desorption at water–solid interfaces. Model hydrophobic (e.g., K⁺) and hydrophilic (e.g., Li⁺) cations were intercalated into the layers via ion exchange to systematically probe the impacts of charged solutes on water orientation and sorption. Prior reports suggest that water within the confined interlayer transforms from bulk-like to crystalline when intercalated with bulky cations (31, 32). Furthermore, it has been demonstrated that water ordering is correlated with ion size (33, 34). Here, we expand upon this early work and examine the role that solute hydrophobicity and hydrophilicity impacts water adsorption on solid interfaces. Water mobility within the interlayer is impacted by the hydration energy of that cation. Results shed light on the intertwined role that surface counterions and terminating groups play on the dynamics of hydration and dehydration.

Results and Discussion

XRD

Multilayered MXene Ti₃C₂T_x was etched from Ti₃ AlC₂ (MAX phase) in 10 wt% hydrofluoric acid. The hydrophilic nature and negative surface charge of the MXene interlayers enable intercalation of a wide range of solvents and charged species (35, 36). Three different samples were prepared from the multilayered MXenes: “neat” (Ti₃C₂T_x), potassium-intercalated (K-Ti₃C₂T_x), and lithium-intercalated (Li-Ti₃C₂T_x). Neat-Ti₃C₂T_x lacks the presence of an interlayer intercalant or solute (Fig. 1 A and F). Potassium and lithium ions are model solutes employed to study the impact that solute hydration energy has on interlayer swelling. Samples were chemically preintercalated with a hydrophobic cation (e.g., K⁺) and a hydrophilic cation (e.g., Li⁺) (Fig. 1 B and C). All powders were washed and vacuum-dried. The powders were then uniaxially pressed at 200 MPa in a 6 mm diameter die to form free-standing discs.

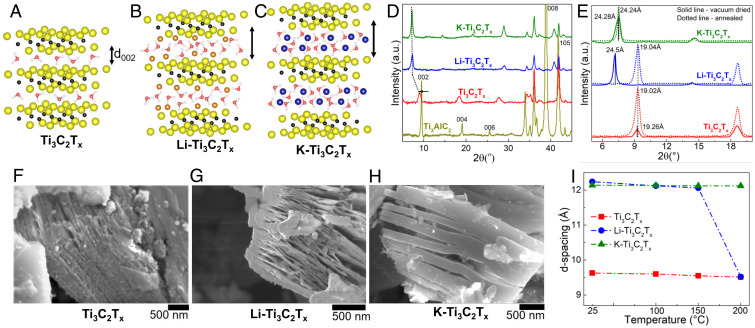
Fig. 1.

(A–C) Schematic of water residing in Ti₃C₂T_x (A), Li-Ti₃C₂T_x (B), and K-Ti₃C₂T_x (C). (D) XRD of Ti₃ AlC₂, vacuum-dried neat, Li${}^{+}$ and K${}^{+}$ intercalated Ti₃C₂T_x. (E) XRD of vacuum-dried and annealed (200 ${}^{°}$C) Ti₃C₂T_x highlighting (002) peak shifting with respect to temperature. (F–H) SEM images of vacuum-dried Ti₃C₂T_x (F), Li-Ti₃C₂T_x (G), and K-Ti₃C₂T_x (H). (I) Change of d-spacing in Ti₃C₂T_x samples with increased temperature. A.u., arbitrary units.

XRD of the etched MXene showed d-spacing shift due to Al removal during 10-HF etching. Upon washing with LiOH and KOH solution, the d-spacing further increased, as seen by a shift of the (002) peak toward the left (Fig. 1D). XRD of the MXene samples after vacuum-drying and annealing treatment (200 ${}^{°}$C) revealed changes to the interlayer structural properties (Fig. 1E). Neat-Ti₃C₂T_x demonstrated a prominent c-lattice (c-L) parameter of 19.26 Å. Upon intercalation of cations, the c-L parameter experienced a significant shift to lower angles, indicating an increase in the layer spacing due to the presence of both water and ions within the interlayer (6, 18). After vacuum annealing, there was little change in the c-L parameter for the neat-Ti₃C₂T_x and K-Ti₃C₂T_x, but a significant decrease was observed in the c-L parameter for the Li-Ti₃C₂T_x. Scanning electron microscopy of neat and chemically preintercalated powders supported XRD results. The neat samples demonstrated nonuniform “loose” layers (Fig. 1E). However, cation screening effects altered the long-range structural properties of the intercalated samples (Fig. 1 G and H) (31, 32). Intercalation of hydrophobic cations (e.g., K⁺) resulted in thick, multilayer lamellas with less interstack gaps (31). A slightly thinner lamellar structure was seen for Li⁺ intercalated samples and is attributed to the smaller solute size. Heating of the samples between 25 ${}^{°}$C and 200 ${}^{°}$C demonstrated very little water loss (dehydration) for both neat and K-Ti₃C₂T_x samples. However, noticeable loss of water was observed from the Li-Ti₃C₂T_x when heating between 150 ${}^{°}$C and 200 ${}^{°}$C (Fig. 1I). The structure of interlayer water undergoes a transition from disordered to ordered after cation intercalation (32). Prior works suggest that translational diffusion of water is greatly reduced when ions are intercalated within the interlayer (31). Yet, the current work demonstrates significantly more water mobility for Li⁺ (hydrophilic) intercalated samples than K⁺ (hydrophobic) intercalated samples. Water-mobility and layer-swelling dynamics are related to a range of surface properties, including surface terminating group and the presence of charged or uncharged solutes. To probe the effects of inorganic ions and layer terminating groups on hydration, in situ APXPS was performed on all samples.

APXPS

In situ APXPS was used to probe surface-hydration effects on nonconfined interfaces (outer surfaces) (Fig. 2A). This technique enables direct insight into how specific surface terminating groups and solutes (e.g., inorganic cations) impact water uptake in layered materials. Chemical ion exchange in an aqueous environment leads to surface hydroxylation and oxidation (TiC$\stackrel{}{\to }$ TiO₂). The latter was observed in the sharp oxide peak at 458.8 eV in the Ti2p spectra (SI Appendix, Fig. S3). TiO₂ constitutes 16, 34, and 42% of the Ti2P spectral weight for neat-Ti₃C₂T_x, Li-Ti₃C₂T_x, and K-Ti₃C₂T_x, respectively. The chemical-exchange process led to greater -O and -OH terminating groups when compared with samples that did not experience ion exchange (e.g., neat-Ti₃C₂T_x) (SI Appendix, Fig. S1). To minimize environmental effects to samples during loading into the vacuum chamber, all samples were heated at 200 ${}^{°}$C under ultrahigh vacuum (UHV) before any in situ experiment.

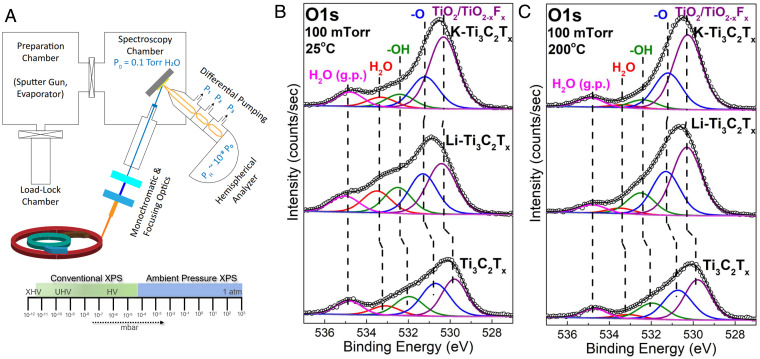
Fig. 2.

(A) Schematic of synchrotron-based APXPS. (B and C) O1s XPS spectra of neat and ion-intercalated Ti₃C₂ at 25 ${}^{°}$C (B) and 200 ${}^{°}$C (C) at 100 mTorr vapor pressure.

To explore the dynamic nature of hydration, each free-standing disc was exposed to 100 mTorr partial pressure of water (e.g., 25 ${}^{°}$C). APXPS is sensitive to the extent of water adsorption and enables a direct pathway for resolving water-solute–Ti₃C₂T_x interactions. Since the Ti₃C₂T_x surfaces are negatively charged, intercalated ions also exist as electrostatically bound species on the nonconfined external surface and represent model charged solutes. XPS spectra of Li1s and K2p clearly showed electrostatically bound ions (SI Appendix, Figs. S5 and S6). The Li1s and K2p spectra had the presence of LiF and KF fitted peaks. The highly negative surface terminating groups may act as active sites for solute adsorption.

The O1s spectra were fit with TiO₂, O-TiC, (OH)-TiC, H₂O, and gas-phase H₂O with respective binding energies at 530 eV, 531.1 eV, 532.1 eV, 533.15 eV, and 534.8 eV (Fig. 2 B and C) (37). The presence of gas-phase water at 100 mTorr vapor pressure signifies a stabilized configuration of physisorbed water (38). The physisorbed water is weakly bound to -OH groups, as OH-H₂O complexes and can be removed from the surface during heat treatment (<200 ${}^{°}$C) (39). Samples were heated from room temperature to 200 ${}^{°}$C to systematically track water desorption and dehydration mechanisms at nonconfined Ti₃C₂T_x interfaces. Increasing the temperature environment from 25 ${}^{°}$C to 200 ${}^{°}$C led to a continuous decrease in adsorbed water for each sample (Fig. 3 A and B). Prior XRD results (Fig. 1D) did not detect any water removal from the interlayer region (bulk) for the K-Ti₃C₂T_x and neat-Ti₃C₂T_x, and thus the reported water loss detected by APXPS can be ascribed to the exposed surface (nonconfined interface). Fig. 3A plots the normalized water coverage as a percentage the initial water uptake, whereas Fig. 3B plots the water coverage as a fraction of all detected components from O1s spectra (-O,-OH, H₂O, and Ti₂O). Rapid water removal occurred for all samples as the temperature increased from 25 ${}^{°}$C to 100 ${}^{°}$C. The rate of water removal decreased as the temperature increased from 150 ${}^{°}$C to 200 ${}^{°}$C (Fig. 3A). The rate of water removal with respect to annealing temperature was lowest for neat-Ti₃C₂T_x. The hydrophobic K-Ti₃C₂T_x demonstrated the fastest rate of removal and lowest water fraction after heating.

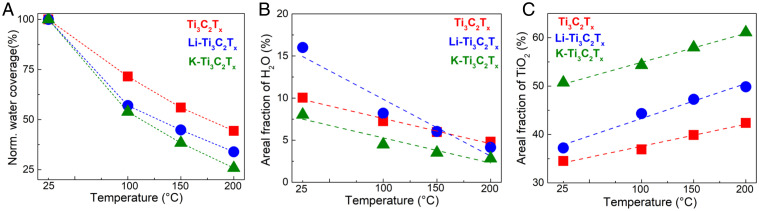
Fig. 3.

From O1s spectra at 100 mTorr, normalized (norm.) coverage of water adsorption depicting rate of water desorption at increasing temperature (A) and changes in H₂O coverage (B) and TiO₂ coverage (C) with increasing temperature. A linear fitting was applied (R² values are tabulated in SI Appendix). The coverage in B and C was normalized with respect to the total fraction of -O, -OH, H₂O, and TiO₂.

The largest quantity of physisorbed water was observed for the Li-Ti₃C₂T_x sample (Fig. 3B). The lowest quantity of physisorbed water was observed for the K-Ti₃C₂T_x (Fig. 3B). The presence of a hydrophilic cation allows for higher surface hydration, whereas the presence of a hydrophobic cation decreases hydration. The intensity for both the Li1P and K2P peaks remained constant during heating, which suggests that solutes are not lost during heating. Instead, the Li⁺ and K⁺ fitted peaks tended to broaden at 200 ${}^{°}$C, which signifies a change of hydration state (SI Appendix, Figs. S5 and S6). More water molecules can adsorb to lithium ions because lithium has larger hydration radii and a higher enthalpy of hydration (3.85 Åand -519 kJ/mol) than a potassium ion (3.3 Åand -322 kJ/mol) (40, 41). During heating experiments, the -OH terminating groups showed little change (SI Appendix, Fig. S2). Under increasing vapor pressure, the collective -OH groups may act as nucleation sites for physically bound water molecules. Fluoride functional groups can be replaced by -OH terminating groups during solution processing and chemical-exchange processes (42). The results suggest that the presence of a charged solute significantly outweighs local surface chemistry with respect to water uptake (Fig. 3B and SI Appendix, Fig. S2 and Tables S4 and S5). The samples demonstrated oxidation with increasing temperature (Fig. 3C). The K-Ti₃C₂T_x sample showed the highest degree of oxidation (TiC → TiO₂). Linear fittings were carried out for the changes in all functional groups, and R² values for linear regression are shown in SI Appendix, Table S6.

Initial heating (100 ${}^{°}$C) caused the farthest layer of surface water to desorb by breaking OH-H₂O complexes. As the temperature increases ($\approx$200 ${}^{°}$C), dehydration can expose additional -OH surface terminating groups. These exposed surface terminating groups (-OH) can undergo a dissociation reaction, which liberates a proton and leaves behind an -O terminating group. This reaction was observed while tracking the terminating groups. The total number of -OH terminating groups decreased slightly with annealing temperatures (SI Appendix, Table S5). Similar trends were observed when heating the samples at UHV and 1 mTorr partial pressure of water vapor (SI Appendix, Fig. S7).

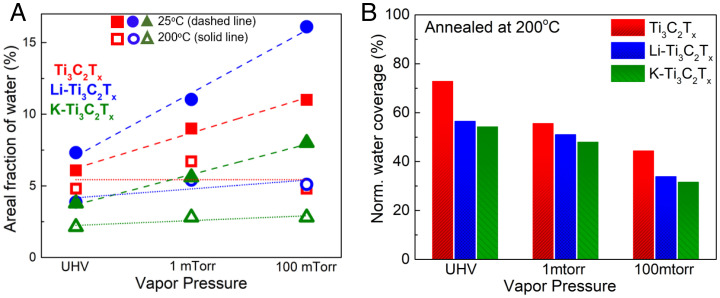
Water-adsorption properties on all samples were systematically evaluated with respect to vapor pressure (UHV, 1 mtorr and 100 mtorr). The areal fraction of absorbed water decreased for all samples as the temperature increased. The surface water uptake was highest for the sample with the hydrophilic solute (Li-Ti₃C₂T_x) at UHV, 1 mTorr and 100 mTorr (Fig. 4A) and lowest for the hydrophobic cation (K-Ti₃C₂T_x). A linear trend can be postulated showing the increasing trend of water adsorption at room temperature as vapor pressure increases. R² values for regression analysis of the areal fraction of water are presented in SI Appendix, Table S7. Neat-Ti₃C₂T_x demonstrated a nonlinear relationship between peak area of water detected and temperature, indicating the complex role of termination groups on water adsorption. Fig. 4B demonstrates the normalized water-coverage percentage after annealing at 200 ${}^{°}$C. Samples with no change in water coverage are designated as 100%. All samples at UHV were not exposed to water vapor and thus demonstrate the lowest initial concentration of surface water. When the samples are exposed to high temperatures, water is desorbed from all samples. At UHV, Ti₃C₂T_x, Li-Ti₃C₂T_x, and K-Ti₃C₂T_x saw water-desorption rates close to 25, 44, and 42%, respectively. At 100 mTorr vapor pressure, the water-removal rate was almost 50, 65, and 70%. We observed that K-Ti₃C₂T_x had the most water removed during heating, independent of vapor pressure (Fig. 4B). The presence of a hydrophobic solute at an exposed, nonconfined interface tends to accelerate water removal and/or local surface dehydration.

Fig. 4.

From O1s spectra, areal fraction adsorbed H₂O ($\approx 533.2eV$) at 25 ${}^{°}$C and 200 ${}^{°}$C (A) and normalized (norm.) water coverage after annealed at 200 ${}^{°}$C under UHV, 1 mTorr and 100 mTorr vapor pressure (B).

Surface hydration is fundamentally related to interfacial solute properties and the variety in concentration of surface terminating groups at the exposed interface. The surface terminating groups are dynamic and can change during heating and materials processing. Ion-intercalated samples (Li-Ti₃C₂T_x and K-Ti₃C₂T_x) demonstrated a greater number of water-accessible -OH and Li-bonded -O sites. Upon heating, dissociation of proton from hydroxyl groups can lead to increases in oxygen terminating groups for all samples. This is in agreement with prior density functional theory calculations (43). Furthermore, water dehydration during heating can expose surfaces that previously were undetectable to the probe (e.g., APXPS). The predicted total molar quantity of terminating group ($T_x^{-}$) for MXene at room temperature is 2 (44). APXPS measurements at 1 mTorr and 100 mTorr vapor pressure revealed similar magnitude of total number of moles of $T_x^{-}$ for neat-Ti₃C₂T_x (2.5) at 25 ${}^{°}$C (Fig. 5 A and B). However, slight differences in individual species’ composition were noted. A gradual decrease in -F terminating groups was observed during both hydration and heating experiments. Samples with interfacial solutes (e.g., cations) showed a more significant change in surface chemistry when exposed to water vapor and during heating experiments. The total number of $T_x^{-}$ moles at room temperature increased to ∼2.7 for both Li-Ti₃C₂T_x and K- Ti₃C₂T_x as the water-vapor partial pressure was increased. Table 1 shows the surface terminating groups for the “as-prepared” MXenes in UHV. Li-Ti₃C₂T_x had a higher content of detected water adsorption at UHV. Water-retention capacity at high temperatures was lower for K-Ti₃C₂T_x than Li-Ti₃C₂T_x. The inability of the K⁺ ion to retain a stable hydration complex at high temperature due to its hydrophobic nature, low charge density, and weak electrostatic interactions resulted in a higher degree of dehydration during annealing. It should be noted that both Li⁺ and K⁺ ion intercalation resulted in significantly higher (235 and 300% increase, respectively) surface oxidation (TiC → TiO₂). Subsequent vacuum heating also takes part in increasing the oxidation, which was evident from Ti2p spectra (SI Appendix, Fig. S3). This limits the potential for hydrophilic termination groups to adsorb water. Furthermore, the -OH dissociation and protonation (to -O and H⁺) at high temperature can also be attributed to the increased water loss at interfacial K⁺ ions (e.g., desolvation of solute). The strong correlation between -OH concentration and water adsorption in all samples caused dynamic changes in total number of $T_x^{-}$ mole at elevated temperatures. Further annealing (beyond the scope of this study) causes complete dissociation of -OH and -F and apparently severe phase transformations of MXenes (45).

Fig. 5.

Variation of number of $T_x^{-}$ moles in neat and ion-intercalated MXenes at different temperatures (25 to 200 ${}^{°}$C) under 1 mTorr (A) and 100 mTorr (B) vapor pressure.

Table 1.

Mole number of functional groups in MXenes (O)_x (OH)_y (F)_z (H₂O)_u (ion)_v

Vapor pressure	Temperature	Ti3C2Tx	Li- Ti3C2Tx	K-Ti3C2Tx
UHV (as-prepared)	25 ${}^{°}$C	O0.7OH0.5F1H2O0.3	O0.8OH0.7 F0.8 H2O0.4 Li0.3	O0.8 OH0.5 F0.9 H2 O0.3 K0.4
	200 ${}^{°}$C	O0.6 OH0.5 F0.9 H2 O0.2	O0.7 OH0.6 F0.7 H2 O0.2 Li0.3	O0.9 OH0.3 F0.8 H2 O${}_{0.1}$ K0.4
100 mTorr	25 ${}^{°}$C	O0.8 OH0.5 F0.8 H2 O0.4	O0.7 OH0.6 F0.6 H2 O0.5 Li0.3	O0.9 OH0.3 F0.8 H2 O0.3 K0.4
	200 ${}^{°}$C	O0.7 OH0.5 F0.7H2O0.2	O0.7 OH0.5 F0.5 H2 O0.2 Li0.3	O0.8 OH0.2 F0.7 H2 O${}_{0.1}$ K0.4

Molecular Simulations of MXenes

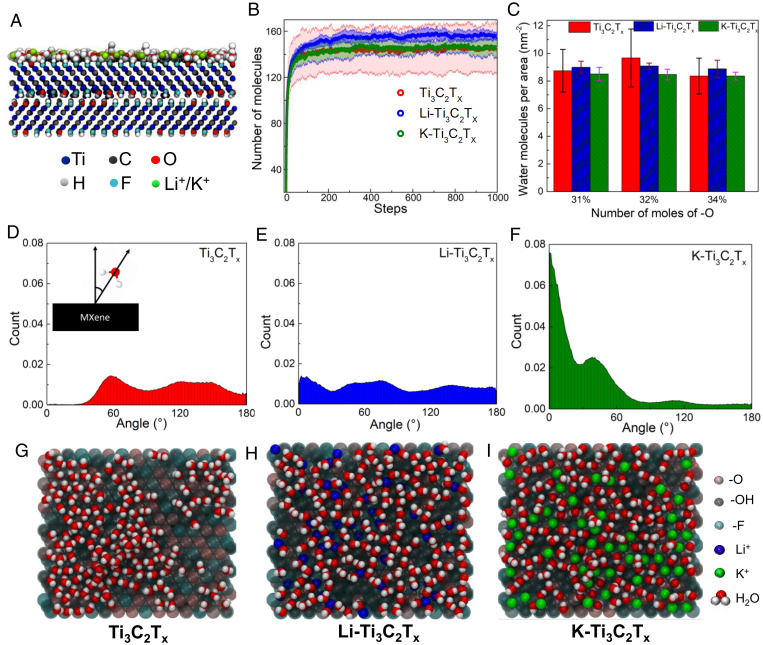
To support our findings from APXPS, Monte Carlo (MC) simulations were carried out for both neat and ion-adsorbed MXenes (details of simulations are discussed in SI Appendix). Grand Canonical MC (GCMC) simulations were performed in Cassandra (46) (version 1.2.5) for two Ti₃C₂T_x nanosheets with added surface terminations and cations (Fig. 6A). A total of 50 ions were initialized onto the Li-Ti₃C₂T_x and K-Ti₃C₂T_x surfaces. Periodic boundary conditions were applied in all directions. To prevent water molecules from translating through the periodic boundary conditions in the direction normal of the MXene surface, a graphene wall was constructed 10 nm above the MXene surface. A total of 10 nm of vacuum space below the MXene was also added to prevent MXene and graphene atoms from interacting. Once initialized, eight independent GCMC simulations of 100 million steps were run for each MXene system, in which water-molecule insertion and deletion moves were attempted. The average number of surface-adsorbed water molecules due to MC particle addition showed that 9.08 water molecules per nm² were inserted into the Li-Ti₃C₂T_x system, followed by 8.51 molecules per nm² in K-Ti₃C₂T_x and 8.36 molecules per nm² in Ti₃C₂T_x at room temperature (Fig. 6B). The surface-composition data were taken from APXPS experiments. This result also suggests that the equilibrium water concentration is highest on the surface of Li-Ti₃C₂T_x. Conversely, the equilibrium water concentration was roughly the same in Ti₃C₂T_x and K-Ti₃C₂T_x. We also looked into the change of water adsorption by slightly altering surface compositions, which still showed higher adsorption rate for Li-Ti₃C₂T_x (Fig. 6C). To elucidate more on the adsorption of water, additional MC simulations in the number, volume, and temperature canonical ensemble (NVT ensemble) were performed based on the equilibrated systems generated from the previous GCMC simulations. Initial equilibration was performed for 100 million MC steps, and production was performed for 300 million MC steps. The last 100 million steps were used for analysis.

Fig. 6.

(A) Snapshot of GCMC simulation of MXenes. (B) Number of water molecules adsorbed at the end of 100 million-step GCMC simulation. Corresponding shaded region represents error bars. (C) Comparison of number of molecules adsorbed at different $T_x^{-}$ compositions classified on -O mole numbers. (D–F) Orientation profiles of water relative to surface normal in neat-Ti₃C₂T_x (D), Li-Ti₃C₂T_x (E), and K-Ti₃C₂T_x (F). Schematic of orientation angle is shown in D, Inset. (G–I) Snapshot of top-views of water-surface interactions at Ti₃C₂T_x (G), Li-Ti₃C₂T_x (H), and K-Ti₃C₂T_x (I).

The angle-distribution profiles of water were calculated relative to the surface (Fig. 6 D–F). The angle was defined between the surface normal vector and the vector drawn from the midpoint of the hydrogen atoms going through the oxygen atom of a water molecule (dipole moment). All water molecules were considered in this analysis. In the Ti₃C₂T_x system, three distributions of angles exist around 0${}^{°}$, 60${}^{°}$, and 120${}^{°}$. The distribution of angles around 0${}^{°}$ corresponds to both hydrogen atoms of a water molecule interacting with the surface, resulting in the water vector being parallel with the surface normal. The distribution around 60${}^{°}$ corresponds to a conformation in which a single hydrogen atom is pointed toward the surface. Because the oxygen of the water molecules is most likely to interact with the surface via the hydrogen of the -OH group, the distribution around 120${}^{°}$ mostly corresponds to water molecules that interact with the surface via the oxygen atoms, with the hydrogen atoms pointed away from the surface. The water molecules in the Li-Ti₃C₂T_x system display the same three distributions of angles, albeit at different magnitudes. The distribution of angles around 0${}^{°}$ is highest, followed by the distribution around 60${}^{°}$ and 120${}^{°}$. Further, the peaks of these distributions are sharper, suggesting that the water molecules in this system are in more distinct orientations in comparison with those in the Ti₃C₂T_x system. The orientation profiles also include interactions between the Li⁺ ions and the water via the oxygen atoms. These interactions mostly correspond to the angles greater than 90${}^{°}$, but also sometimes corresponding to the angles around 60${}^{°}$, which suggests that Li⁺ plays an active role in water adsorption, facilitating an increment in total water adsorption. The K-Ti₃C₂T_x shows the biggest contrast of water orientations in comparison with the Ti₃C₂T_x and Li-Ti₃C₂T_x systems. The distribution of angles around 0${}^{°}$ is the dominant orientation, followed by the orientation around 50${}^{°}$ and a small distribution of angles around 110${}^{°}$. Based on these distributions, the water molecules are most likely to interact with the MXene surface via the hydrogen atoms. Because the dominant interaction of water with the surface in this system is with the hydrogen atoms, this suggests that the interaction between the K⁺ ions and water is lower than that of the Li⁺ ions and water. As a result, K⁺ ions play a smaller role in water adsorption that led to overall lower water adsorption in K-Ti₃C₂T_x. A correlation in the snapshots (Fig. 6 H and I) can be seen where Li⁺ ions are coordinated with up to three water molecules, whereas K⁺ ions show coordination with only one water molecule.

The structure of water and ions was also investigated through the calculation of number-density profiles. In neat-Ti₃C₂T_x, the hydrogen atoms displayed a slight tendency to be positioned away from the surface, as shown by the higher peak at $\approx$ 2.1 nm in the z direction (SI Appendix, Fig. S8A). In the ion systems, the first layer of hydrogen atoms is closer to the surface, likely due to the presence of ions. This closer position of the hydrogen atoms agrees well with the higher distribution of angles around 0${}^{°}$. The K⁺ ions are positioned in a single layer away from the surface at roughly 0.1 nm from -OH groups of the MXene (SI Appendix, Fig. S12C). However, the Li⁺ ions are positioned in roughly three layers on the MXene. The layer closest to the surface exists at 0.15 nm below the hydroxyl group; the next closest layers exist at roughly the same position as the hydroxyl groups; and the layer furthest away from the surface exists at roughly 0.05 nm away from the hydroxyl groups (SI Appendix, Fig. S12B). The positions of the ions suggests that the interactions of Li⁺ and K⁺ ions with the MXene surfaces are different and may affect the overall mechanisms of water adsorption.

When comparing the XPS and simulation results, there are several distinctions that should be made. First, the MXenes in the MC simulations are initialized with uniform surface compositions with no chemical defects. As a result, the simulations do not fully capture the surface functional group complexity regarding chemical-state changes. Further, the same number of ions (50) was used for both Li-Ti₃C₂T_x and K-Ti₃C₂T_x, which was done to maintain consistency between the two systems. Nonetheless, the results corroborate with the APXPS findings for different MXene samples, where presence of surface ions plays an important role in water physisorption.

DRIFTS analysis

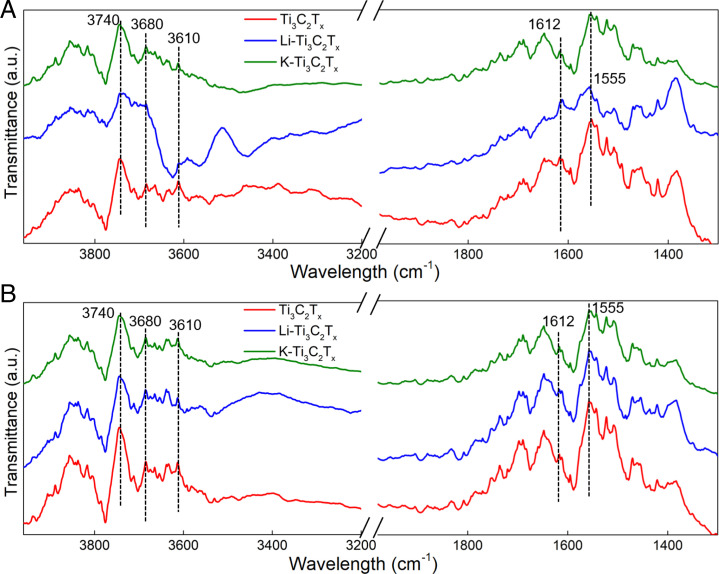
Temperature-dependent DRIFTS was conducted on all samples at 25 ${}^{°}$C and 200 ${}^{°}$C (Fig. 7). Both neat and ion-intercalated samples demonstrated distinctive peaks at 3,616; 3,634; and 3,740 cm^{– 1} (-OH stretching region) (47). Li-Ti₃C₂T_x demonstrated multiple peaks within the -OH stretching region, which suggests hydroxyl bonding and dissociative water adsorption. Water adsorption was also observed in the water-bending region between 1,640 and 1,560 cm^{– 1}. The weak vibrational mode of Li-Ti₃C₂T_x at 25 ${}^{°}$C in the -OH stretching region (3,400 cm^{– 1}) signified stable water adsorption. However, the vibrational mode is temperature-dependent for all samples, which is attributed to physically adsorbed water on the surface. Bending modes at 1,622 cm^{– 1} are evidence of water adsorption in between layers. After annealing at 200 ${}^{°}$C, surface-water loss leads to a more open -OH region.

Fig. 7.

DRIFTS spectra of Ti₃C₂T_x, Li-Ti₃C₂T_x, and K-Ti₃C₂T_x at 25 ${}^{°}$C (A) and 200 ${}^{°}$C (B). The left side of the split section is the -OH stretching region, and the right side represents the water bending region. The hydrogen-bonded adsorbed water region is at 3,400 cm^{– 1}.

Conclusions

Layered materials used as membranes in water applications and electrodes and energy-storage applications undergo variable degrees of hydration. Water and solute interactions can lead to material expansion and swelling. The properties of the fluid at the interface and within the bulk material can impact transport properties and system performance (e.g., capacity, permeability, etc.). State-of-the-art bulk-measurement approaches lack critical insight into the molecular nature of water ordering and adsorption in layered materials. Furthermore, bulk measurements lack spatial precision to capture variable surface properties. Herein, we combine XRD, APXPS, and MC simulations to examine the role that solutes and surface chemistry play in water-adsorption properties in multilayer ternary transition-metal carbide interfaces. The 2D MXenes exhibit significant volume swelling upon hydration and ion intercalation. The presence of electrostatically bound hydrophilic cations leads to greater water adsorption at the surface and slower water removal from the surface at elevated temperatures (>200 ${}^{°}$C). Solutes have a more significant impact on the kinetics of water adsorption and desorption than surface terminating groups. GCMC results suggest that the presence of solutes can affect the molecular orientation of water at MXene interfaces. Water is semiordered at surfaces with hydrophobic cations (e.g., K⁺). In particular, angle-distribution profiles of water in the potassium samples were dominated by water orientations 0${}^{°}$. Distribution angles at 0${}^{°}$ correspond to both hydrogen atoms of a water molecule interacting with the surface, resulting in water molecules that are parallel to the surface and fast water removal at elevated temperatures.

Materials and Methods

Synthesis of MXenes

The 2D Ti₃C₂T_x MXene was synthesized directly from its MAX precursor Ti₃ AlC₂ via hydrofluoric acid (HF) etching. Multilayered Ti₃ AlC₂ synthesis was carried out by mixing TiH₂, Al, and TiC (molar ratio 1:1.1:2) in a planetary ball mill. The resultant mixer was then sintered at 1,400${}^{°}$ for 2 h under Ar flow to achieve the layered MAX phase, followed by ball milling for 40 min (for size reduction) and drying. A total of 3 g of the as-produced powder was dissolved in 10% HF and stirred at room temperature for 24 h. The resultant suspension was then washed with deionized water and decanted multiple times until the pH was $\approx$ 5. After drying in vacuum, part of the as-produced pristine Ti₃C₂T_x powder was stored in an Ar-filled glovebox. For ion intercalation, the rest of the powder was separately dissolved in 2 M aqueous LiOH and KOH solutions, stirred for 1 h, and decanted via centrifuge. This process was repeated one more time, and then the decanted ion-intercalated Ti₃C₂T_x powders were dried in vacuum.

Sample Preparation

For XRD and DRIFTS measurements, MXene samples (Ti₃C₂T_x, Li-Ti₃C₂T_x, and K-Ti₃C₂T_x) were vacuum-annealed at 100 ${}^{°}$C, 150 ${}^{°}$C, and 200 ${}^{°}$C before taking the measurements. For APXPS, the vacuum-dried powders were cold-pressed at 200 MPa to form stable pellets of $\approx 600-700$ μm of thickness. The pellet diameter was 6 mm.

XRD and DRIFTS

XRD was carried on in Rigaku Smart Lab (Cu Kα X-ray). The diffraction patterns on the MXene pellets were taken from 5${}^{°}$ to 50${}^{°}$ with 0.01${}^{°}$ step size. For Fourier transform infrared (FTIR) analysis using the DRIFTS cell, the MXene samples were mixed with dry potassium bromide (KBr) with a ratio of 1:9 in a grinding bowl. The grounded powders were then passed through a sieve. The uniform mixture of MXenes–KBr was inserted into a DRIFTS chamber of Nicolet iS50 FTIR. Annealing the MXenes inside the chamber was controlled by a temperature controller. FTIR spectra were obtained from 4,000 cm^{– 1} to 1,000 cm^{– 1}. A total of 128 scans with a resolution of two were taken to get smoother data. Background analysis was done by using pure KBr before the MXenes–KBr mixtures.

APXPS

APXPS study on the MXenes was performed in the Advanced Light Source (Beamline 9.3.2) of Lawrence Berkeley National Laboratory. The APXPS analysis chamber is equipped with differentially pumped electrostatic lens systems, which allowed taking measurements up to 10^{– 5} mbar of gas pressure. The small MXene pellets were mounted on a ceramic heater, where K-type thermocouples were placed to control the temperature. A schematic of the APXPS is given in Fig. 2A. First, the samples were pumped down to UHV and heated up to 200 ${}^{°}$C to remove any previously adsorbed surface water. Then, by using the leak valve, water was introduced in the chamber at partial pressure of 1 and 100 mtorr. XPS spectra (Ti2P, C1s, O1s, F1s, Li1s, K2p, and valence band) were collected at 800 eV at different heating conditions (25 ${}^{°}$C, 100 ${}^{°}$C, 150 ${}^{°}$C, and 200 ${}^{°}$C), after holding at respective temperatures for 30 min. The same procedure was repeated for collecting the XPS spectra at 900 eV (only for Li-Ti₃C₂T_x and K-Ti₃C₂T_x samples and at 25 ${}^{°}$C and 200 ${}^{°}$C).

Molecular Simulations

Each GCMC system was built in a simulation box containing two sheets of Ti₃C₂T_x of lattice repeat units of 14 × 14 × 1. Functional groups were added to all systems with various compositions of -O, -OH, and -F (total T${}_x^{-}$ mole number 2). Periodic boundary conditions were applied in xyz coordinates. In order to prevent water molecules from getting stuck at the top of the box, a sheet of graphene was inserted 10 nm above the top layer of Ti₃C₂T_x to act as a repulsive wall. To prevent the graphene and MXene atoms interacting through the periodic boundary, 10 nm of vacuum space was built underneath the top layer of MXene. The Lennard–Jones sigma and epsilon parameters for the graphene atoms were set to 0.5 nm and 0.00001 kJ/mol, respectively. Specific pairwise interactions were defined between some MXene and water atoms, while Lorentz–Berthelot mixing rules were used for all other pair interactions. A total of 50 ions were added to the surface for the Li-Ti₃C₂T_x and K-Ti₃C₂T_x systems. The number of ions was estimated from the proportion of functional groups to ions and the number of functional groups (784). This value was then divided by four, as this is the number of surfaces containing functional groups, and ions were only placed on the uppermost surface of MXene. The number of Li⁺ and K⁺ ions estimated from Table 1 was 40 and 56, respectively. 50 ions were inserted into each Li⁺ and K⁺ system, as this is a convenient number roughly the average of these calculated values. To obtain reasonable configurations for the ions, steepest-descent energy minimization and molecular dynamics (MD) simulations of the ions on the MXene surface were first performed with GROMACS 2020 for 2,000 steps and 100 ps. All GCMC simulations were performed with Cassandra (46) (version 1.2.5) using the MoSDeF Cassandra (48) (version 0.2.3) wrapper. The MXene atoms were held rigid, and the water atoms and ions had maximum translations of 0.2 and 0.01 nm, respectively. The van der Waals and Coulomb interactions were cut off at 0.9 nm, and long-range Coulomb interactions were handled with the Ewald summation. The water bonds and angles were fixed. To determine the chemical potential at the desired pressure of 100 mTorr, a series of GCMC simulations of bulk water at various chemical potentials were run. Based on the results shown in SI Appendix, Fig. S11, a linear fit was calculated:

$$\log P=0.40931(\mu )+15.43,$$ [1]

where P is the bulk pressure, and μ is the chemical potential. Based on this equation, the initial chemical potential was chosen to be -59.5 kJ/mol at 300 K. Once the correct chemical potential was determined, a series of eight GCMC simulations of the three MXene systems were run for 100 million MC steps. The number of waters inserted into each system was determined by taking the average of the eight simulation runs. The average value of water molecules inserted was then used to initialize new MXene systems for MC simulations in the canonical ensemble with the purpose of calculating structural properties of each system.

NVT MC simulations were also performed with Cassandra (46) (version 1.2.5) using the MoSDeF Cassandra (48) (version 0.2.3) wrapper. Each system was equilibrated for 100 million steps, and sampling was performed for another 300 million steps for Ti₃C₂T_x and Li-Ti₃C₂T_x and 400 million steps for K-Ti₃C₂T_x (due to requiring further equilibration). The last 100 million steps of sampling were used for analysis. The number density profiles for the three systems are shown in SI Appendix, Fig. S12.

Angle distributions were calculated between the normal of the z vector and a vector drawn from the water molecule. The water-molecule vector was drawn from the midpoint between the two hydrogen atoms through the oxygen atom.

Data Availability

Excel files for all datasets used to analyze the results in the manuscript and SI Appendix have been deposited in Zenodo (DOI: 10.5281/zenodo.5695327).