Designing a sustainable closed-loop supply chain network of face masks during the COVID-19 pandemic: Pareto-based algorithms

Abstract

This study develops a novel mathematical model to design a sustainable mask Closed-Loop Supply Chain Network (CLSCN) during the COVID-19 outbreak for the first time. A multi-objective Mixed-Integer Linear Programming (MILP) model is proposed to address the locational, supply, production, distribution, collection, quarantine, recycling, reuse, and disposal decisions within a multi-period multi-echelon multi-product supply chain. Additionally, sustainable development is studied in terms of minimizing the total cost, total pollution and total human risk at the same time. Since the CLSCN design is an NP-hard problem, Multi-Objective Grey Wolf Optimization (MOGWO) algorithm and Non-Dominated Sorting Genetic Algorithm II (NSGA-II) are implemented to solve the proposed model and to find Pareto optimal solutions. Since Meta-heuristic algorithms are sensitive to their input parameters, the Taguchi design method is applied to tune and control the parameters. Then, a comparison is performed using four assessment metrics including Max-Spread, Spread of Non-Dominance Solution (SNS), Number of Pareto Solutions (NPS), and Mean Ideal Distance (MID). Additionally, a statistical test is employed to evaluate the quality of the obtained Pareto frontier by the presented algorithms. The obtained results reveal that the MOGWO algorithm is more reliable to tackle the problem such that it is about 25% superior to NSGA-II in terms of the dispersion of Pareto solutions and about 2% superior in terms of the solution quality. To validate the proposed mathematical model and testing its applicability, a real case study in Tehran/Iran is investigated as well as a set of sensitivity analyses on important parameters. Finally, the practical implications are discussed and useful managerial insights are given.

1. Introduction

Recent Coronavirus disease (COVID-19) is an infectious disease that was first found in December 2019 in Wuhan, China, while mortality rates from the disease have been reported to be up to 5%, often transmitted by tiny respiratory droplets from one person to another (Mardani et al., 2020a; Chen et al., 2020). Statistics show that as of 10.25.2020, the number of infected people with this deadly virus in Iran, the USA, China, Spain, and Germany is 526490, 8296249, 85659, 982723, and 357538, respectively. The number of deaths in these countries is 30123, 2223730, 4634, 33775, and 9838, respectively (World Health Organization, 2020).

The use of masks (N95, KN95, and surgical masks) is one of the preventive measures that can limit the prevalence of some respiratory viral diseases containing the COVID-19 (Nilashi et al., 2020; Kairon and Bhattacharyya, 2020; Liu et al., 2020). Most people in the world use face masks at the same time as the coronavirus outbreak because masks can prevent the transmission of large droplets that are released into the air after sneezing and coughing, so face masks are useful (Cheng et al., 2020; Omori et al., 2020; Ullah et al., 2020; Wang et al., 2020). In addition, the mask prevents the person from touching their nose and mouth with their hands, thus reducing their chances of contracting the virus following contact of their hands with the infected surface (Chan et al., 2020; Zuo et al., 2020).

According to the growing demand for masks and the scarcity of this vital commodity, production, supplier, distribution and inventory control seem essential to decision-makers (Gereffi, 2020). The decisions of the location of the production centers, distribution, collection, and disposal of masks affect the efficiency of the supply chain because the number and location of production, collection distribution, and disposal centers are established and the amount of stored masks in each center directly affects the costs of the supply chain and, more importantly, the health of the individual (Mollenkopf et al., 2021). For example, the production of the Shanghai-GM-Wuling (SGMW) car stopped production and resumed mask production in the COVID-19 situations because of decreasing vehicle demand and increasing mask demand (Betti and Ni, 2020).

Greenness, circularity and bioeconomy bring global sustainability concepts into the mainstream (D'Amato et al., 2017). Although they are interrelated towards sustainable utilization of natural resources within economic cycles, their dependencies, relations, advantages/disadvantages and best approaches have not been discussed enough in the literature, particularly referring to the public sector such as healthcare. During the COVID-19 pandemic, sustainable development of different supply chain networks becomes doubly important (Barbier et al., 2020; Tirkolaee et al., 2021). The growing importance of a sustainable supply chain design in today's turbulent world is not hidden from everyone (Mardani et al., 2020b). The supply chain of face masks as one of the most critical sanitary equipment is highly dependent on these requirements. It is obvious that a sustainable supply chain can minimize the social risks of mask production as well as its environmental impacts. Thus, the established production, distribution, and disposal centers should have the maximum distance from the densely populated urban areas. Other features of sustainability include treating environmental issues and reducing negative impacts (Tirkolaee et al., 2020a). Nowadays, due to the significance of environmental criteria, the effective and efficient use of waste and recycling, particularly face masks, can affect the success of organizations. This can both minimize environmental pollution and reduce supply chain costs to an acceptable level. On the other hand, reusable face masks must be promoted which can be provided for free with marketing targets (Filimonau, 2020).

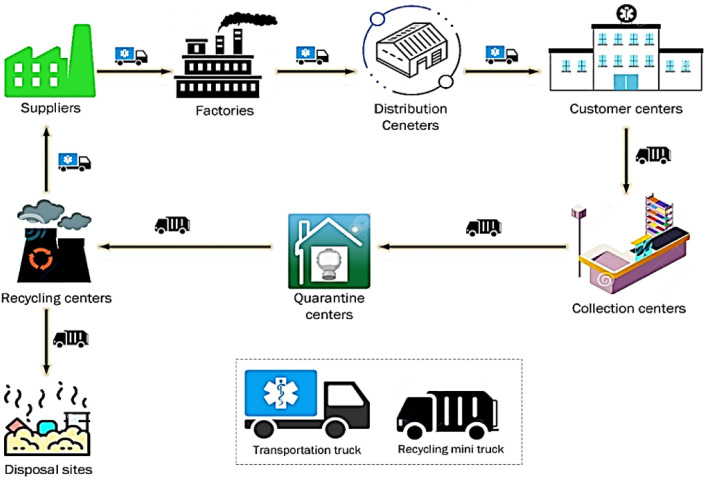
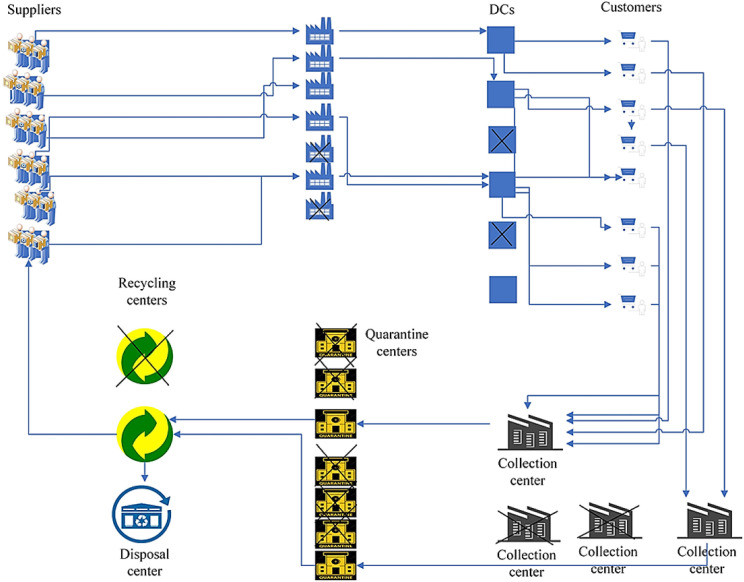
All in all, the importance of using mask is obvious to everyone as a preventive health principle during the pandemic. That is why it is so critical to consider the sufficiency of its supply, production and distribution by governments, while it can be very attractive for production managers in terms of economic aspect due to the growing demand. Furthermore, it is so important to take into account the possibility of timely disposal and treatment due to the environmental and health risks. This study tries to address all the above-mentioned issues and consider the chance of recycling COVID-19 related masks in terms of sustainable development within a Closed-Loop Supply Chain Network (CLSCN) for the first time. Therefore, a multi-objective mathematical model is developed for the mask CLSCN considering locational, supply, production, distribution, collection, quarantine, recycling, and reuse decisions as well as sustainability issues during the COVID-19 pandemic for the first time. Therefore, on the reverse flow, raw materials are transferred from suppliers to factories. Then, the produced masks from the factory are sent to the Distribution Centers (DCs) and finally to the customers. In the reverse direction, waste is sent by collection centers to quarantine centers and then to recycling centers. They are then crushed into small pieces and exposed to ultraviolet light to guarantee that they are thoroughly disinfected before the recycling process begins. In the next step, the disinfected masks are transported to recycling centers. In recycling centers, waste is sent to disposal centers and recycled waste is sent to suppliers for reuse. Also, there are two types of transportation systems in the proposed supply chain network, which include transportation trucks and recycling mini trucks. According to that shortages are not allowed in the main market (customer centers), so all masks produced in factories must be sent to distribution centers in the same period.

The first objective function (1) shows minimizing the total cost of the CLSCN design including the fixed establishment costs, fixed employment costs of trucks, transportation costs, and operational costs at different facilities. The second objective function (2) indicates minimizing the whole pollution emission incurred by transportation and operational processes. The third objective function (3) states minimizing the total human risk imposed by the establishment of facilities such as the number of people around collection centers, quarantine centers, recycling centers, and disposal centers is minimized.

The development of a multi-objective, multi-period, multi-echelon, and multi-commodity mathematical model considering location, supply, production, distribution, collection, quarantine, recycling, and burial decisions are some of the novelties of this research. In addition, considering the proposed sustainability in the proposed network for a real case study and simultaneous attention to the three pillars of sustainability including economic, environmental, and social aspects are among the other innovations of this research. The considered location in this research is as a discrete parameter. The location is such that the optimal points are selected from the pre-defined candidate points. The selection of optimal locations for the establishment of facilities will reduce transportation costs and as well as the resulting environmental pollution.

The framework of the rest sections is explained as follows. Section 2 provides a survey on similar research studies in the literature. Section 3 investigates the problem and formulates the presented mathematical model. Our proposed solution methodology is provided in Section 4. Section 5 proposes the validation of the presented methods. A real case study is then investigated in Section 6. Eventually, the discussion, concluding remarks, and outlook of the study are given in Section 7.

2. Survey on the related work

A variety of helpful research studies can be found in the literature, concentrating on CLSCN design (e.g., see Polo et al., 2019; Sazvar et al., 2021). However, in this section, the most relevant studies related to the supply chain of medical items are reviewed in brief. A resilient-sustainable model was proposed by Zahiri et al. (2017) to develop a supply chain of pharmaceutical distribution and production under uncertainty. They utilized possibilistic-stochastic programming to tackle the uncertainty of parameters. The establishment of production centers using built-in primary technology levels and considering intermodal freight transportation system was their main contribution. Finally, the proposed model was solved using the Pareto-based lower bound approach for the case study and the outcomes represented the proper performance of the mathematical model. Savadkoohi et al. (2018) designed a medical equipment supply chain network under uncertainty. The possibilistic programming method was utilized to cope with uncertainty. The main purpose of the presented model was to minimize supply chain costs in Iran. The location of the distribution and production centers and determining the inventory of the centers according to the perishability of medicines and equipment were among their strategic decisions. Xu et al. (2018) addressed the decision and coordination in the dual-channel supply chain network arising out of low-carbon preference and channel substitution. They developed the decision-making models of the centralized and decentralized supply chain network, which contain one manufacturer and one retailer. Additionally, they designed an improved revenue-sharing contract to effectively coordinate the manufacturer and retailer. De Melo Sathler et al. (2019) presented a model for the location of the medical equipment DCs and the allocation of the medical equipment to medical centers. Their main aim was to maximize the level of patient satisfaction in the face of resource scarcity. They considered a case study in Brazil and the results represented that with 4% more specialist staff, 15% more medical equipment can be delivered to medical centers. Nasrollahi and Razmi (2019) developed a medicine supply chain involving manufacturers, distributors, hospitals, and patients. They presented a multi-period model for determining the flow of medicines and transferred medical equipment between centers. The main purpose of their research was to clarify the demand coverage along with minimizing costs. Eventually, the proposed model was solved using two approaches including NSGA-II and Multi-Objective Particle Swarm Optimization (MOPSO). Weraikat et al. (2019) presented a mathematical model for managing the distribution of medical facilities. In addition, they considered sustainability along with the perishable products. The Vendor-Managed Inventory (VMI) approach was utilized to minimize unsatisfied demand. Moreover, the Monte-Carlo simulation approach was employed to cope with the uncertainty of the presented model. The outcomes demonstrated the suitable efficiency of the proposed model. Roshan et al. (2019) formulated a supply chain network for the distribution of medical equipment under crisis conditions. They designed a multi-objective mathematical model for minimizing distribution and production costs and maximizing unsatisfied demand. In order to increase social responsibility, they considered the maximization of employment rates in established centers. Finally, they reported the proposed sustainable model for the Seattle/USA case study. The main challenges, limitations, opportunities and innovations of solid waste management were discussed by Sharma et al. (2020) during and post COVID-19 pandemic. They pointed out the high importance of efficient medical and hazardous waste (e.g., face masks, gloves and other biomedical waste) management.

Sangkham (2020) estimated the number of face masks and the number of mask disposal centers during the COVID-19 outbreak. For this purpose, centers such as hospitals, mask manufacturers, and landfills in Asia were surveyed. The parameters to estimate the number of required masks included the number of population and the acceptance rate of the mask by the community. The acceptance rate of the mask by the community was estimated at 80%. Finally, the number of required masks and the number of disposal centers were estimated for 54 Asian countries including Iran. Klemeš et al. (2020) studied to minimize the effects of plastic waste and waste paper during the outbreak of the COVID-19. In addition, they investigated the effects of pandemics on the amount of plastic waste on the effects of pandemics on environmental pollutants, including carbon dioxide. They took into account a real case study including hospitals, landfills, and households. The obtained results demonstrated that in pandemic conditions, as the amount of released pollutants by vehicles decreases, the amount of plastic pollutants increase sharply, which results in increasing the number of landfills and job creation. Alizadeh et al. (2020) designed a direct and reverse medicine supply chain according to biological risks. In the direct direction, warehouses and DCs are located, and in the reverse direction, medical waste disposal centers are located. The goal of their suggested model was maximizing the difference between revenues and costs and minimizing the time distance between clinics and sterilization. The case study was examined in Tehran/Iran and the Bounded De Novo Programming method was utilized to solve it. Goodarzian et al. (2020) suggested a mathematical model for production and distribution in the pharmaceutical supply chain network. In their proposed model, the costs of ordering, purchasing, and production were considered as a fuzzy parameter and robust fuzzy technique was employed to deal with uncertain parameters. Then, the multi-modal transportation system was considered as one of the contributions. To minimize transportation costs and to minimize medicine delivery time were the most important objectives of their paper. The outcomes represented the suitable efficiency of their suggested model. Kargar et al. (2020a) examined a reverse supply chain for hospital waste disposal management. Therefore, they presented a multi-period and multi-item stochastic model with three objectives including decreasing transportation costs, inventory holding, and established disposal centers along with minimizing all stored hospital waste. Finally, the proposed model was solved by fuzzy goal programming and the outcomes indicate the proper performance of the model. In another research, Kargar et al. (2020b) proposed a mathematical model to optimally deal with hospital waste disposal, such as masks and face shields within a reverse logistics network during the COVID-19 pandemic. The allocation of hospitals to disposal centers along with the location of disposal centers was one of the decisions that did in their research. Their main goal was to minimize location and transportation costs while minimizing uncollected waste from the centers. A revised version of Multi-Choice Goal Programming (MCGP) approach was used to find the best solutions. Franco and Alfonso-Lizarazo (2020) introduced a simulation-optimization model for the distribution of medicines and medical equipment. They considered a bi-level supply chain network including hospitals and pharmacies. Moreover, two stochastic models were proposed for the considered problem. The first model considered the expiration date of medicines along with the level of service to patients and the second model considered inventory control and allocation of medical equipment to hospitals. Finally, the proposed models were solved using the ε-constraint approach and the results indicated a 16% reduction in supply chain costs.

Recently, Vanapalli et al. (2021) provided strategies and challenges for effective plastic waste management in the COVID-19 pandemic. They addressed the inefficiencies and inadequacies of the current waste management system to cope with the raised dependence on plastic. Then, these problems aggravated its leakage and mismanagement into the environment, then triggered a novel environmental crisis. Moreover, a futuristic review was conducted by Purnomo et al. (2021) on the possible thermochemical treatments for the COVID-19 related medical waste. They also examined the possible conversion to fuels by analyzing the characteristics of waste including face masks, clothes, goggles, gloves and disinfectant containers. Mosallanezhad et al. (2021) designed a disaster relief supply chain network for personal protection equipment in the COVID-19 condition. They formulated a multi-objective, multi-product, and multi-period model to minimize total cost and shortage considering the COVID-19 outbreak. To solve their model, they used four well-known multi-objective metaheuristics. They suggested the Taguchi method to tune the algorithm's parameters and compare the proposed algorithms based on assessment metrics. Goodarzian et al. (2021a) developed an integrated sustainable medical supply chain network in the COVID-19 pandemic. They designed a production-distribution–inventory–allocation–location problem for the multi-objective, multi-level, multi-product, and multi-period model. To solve their model, hybrid methods based on meta-heuristic algorithms were developed. In addition, they suggested the response surface method to tune the algorithms' parameters. Finally, a real case study was considered to validate their proposed model and show the performance of their proposed methods. Xu et al. (2021) investigated the effect of the COVID-19 epidemic on port performance in China. They considered a panel regression model to analyze the effect on port efficiency. Finally, 14 major ports in China were chosen as a case study. Goodarzian et al. (2021b) proposed a new sustainable-resilience healthcare network under uncertainty to handle the COVID-19 epidemic. They formulated and designed an optimization-simulation mixed-integer linear programming model for a multi-period, multi-product, multi-objective, and multi-echelon problem. To cope with uncertain parameters, stochastic chance-constraint programming was proposed. They developed three hybrid meta-heuristic algorithms to solve their model. Finally, they suggested a real case study to show the efficiency of their developed model. Pedroza-Gutiérrez et al. (2021) explained adaptive governance and coping strategies in the Yucatan Peninsula coasts facing COVID-19. They considered the COVID-19 crisis as a social driver of change with new and different forms of governance. Also, for coastal areas, a multi-level governance strategy to recover from the COVID-19 epidemic and economic crises was needed. Additionally, coastal communities had difficulties demonstrating non-fisheries-based or non-recreate-based resilience. Milanes et al. (2021) presented forty-three positive and negative practices and actions on beaches during the COVID-19 lockdown. In addition, they designed twenty-seven new recommendations for coastal planning and beach management, of which several recommendations were validated in the Republic of Cuba. Finally, experts in beach and coastal management from two Ibero-American networks were consulted. Goodarzian et al. (2021c) proposed a new multi-objective optimization approach for the pharmaceutical supply chain network design to minimize the total cost and the delivery time of pharmaceutical products while maximizing the reliability of the transportation system. Also, a new mixed-integer non-linear programming model was developed for the production-allocation-distribution-inventory-ordering-routing problem. Three new heuristics (H-1), (H-2), and (H-3) and two new meta-heuristic algorithms, namely, an Improved Social Engineering Optimization (ISEO) and Hybrid Firefly and Simulated Annealing Algorithm (HFFA-SA) were developed to solve their model. Finally, their proposed model was evaluated through extensive simulation experiments by analyzing different criteria.

According to the examined papers, the novelties of this study are discussed as follows:

• i.Developing a novel multi-objective, multi-period, multi-level, multi-product MILP model to design a sustainable mask CLSCN during the COVID-19 pandemic,
• ii.Addressing locational, supply, production, distribution, collection, quarantine, recycling, reuse and disposal decisions within the proposed network,
• iii.Studying the sustainability in mask CLSCN design problem in order to minimize the total human risk as much as possible and besides minimizing the total cost and total environmental pollution,
• iv.Developing two multi-objective meta-heuristic algorithms of Multi-Objective Grey Wolf Optimization (MOGWO) and NSGA-II to tackle the complexity of the problem,
• v.Enhancing the performance of the algorithms using the Taguchi design method,
• vi.Evaluating the performance of the algorithms using well-known metrics, problem instances and a statistical test,
• vii.Validating the proposed model and solution methods using a real case study in Tehran/Iran.

3. Problem definition and mathematical modeling

In this section, a sustainable mask CLSCN is modeled to deal with the production, distribution, and recycling processes of the face masks in the COVID-19 pandemic condition. In the forward supply chain structure, different levels of suppliers, factories, DCs, and customer centers are defined. On the other hand, in the reverse supply chain structure, recycling centers, collection centers, quarantine centers, and disposal centers are considered.

In addition to raw materials obtained from suppliers, factories produce different types of masks (N95, KN95, and surgical masks). With the help of the DCs, these products are transferred to customer centers including hospitals and infirmaries. A major part of demand at customer centers is then collected using sanitary packaging and transported to collection centers, then they are taken to the quarantine centers and placed there for four days. They are then crushed into small pieces and exposed to ultraviolet light to guarantee that they are thoroughly disinfected before the recycling process begins. In the next step, the disinfected masks are transported to recycling centers. Here, there are two output flows from recycling centers to disposal centers and suppliers. In forward logistics, since many products are dispatched and distributed among different levels, a fleet of vehicles with different sizes are used to handle the transportation process, but in reverse logistics, since fewer products are transported, a fleet of mini vehicles are used according to the economical aspect.

To address sustainable development, three objective functions are studied including social, economic, and environmental impacts. The 1st objective is minimizing the whole cost of the supply chain containing the establishment costs, transportation costs, and employment costs of vehicles. The 2nd objective tries to minimize the whole pollution emission throughout the supply chain. Finally, the 3rd objective seeks for minimizing the infection risk imposed on the population around newly-established sites. To better understand the components of the proposed CLSCN, Fig. 1 represents a schematic view.

Fig. 1.

Configuration of the proposed mask CLSCN.

The assumptions of the presented model are explained as follows:

• •Multiple levels of suppliers, factories, DCs, customer centers, disposal centers, recycling centers, collection centers, and quarantine centers are considered to configure the proposed closed-loop supply chain,
• •Locational decisions are made at the levels of factories, DCs, disposal centers, collection centers, quarantine centers, and recycling centers at the beginning of the time horizon,
• •Operations and transportations between different levels and operational activities at different facilities are the origins of pollution emission,
• •Two types of transportation systems are defined including transportation trucks and recycling mini trucks,
• •All produced masks at factories should be transported to DCs in each time period,
• •Facilities located on reverse logistics flow yield infection risks,
• •Parameters are deterministic,
• •Capacity of facilities is limited,
• •A time horizon is regarded,
• •Four raw materials and three final products are needed to be supplied,
• •Shortage in the main market (customer centers) is not allowed.

Now, the proposed mathematical model is given as follows:

Sets
$I$	Set of suppliers ($i\in I)$
$J$	Set of factories ($j\in J)$
$K$	Set of DCs ($k\in K)$
$L$	Set of customer centers ($l\in L)$
$C$	Set of collection centers ($c\in C$)
$Q$	Set of quarantine centers ($q\in Q$)
$R$	Set of recycling centers ($r\in R$)
$D$	Set of disposal centers ($d\in D$)
$F$	Set of raw materials ($f\in F;\left|F\right|=4$)
$M$	Set of masks ($m\in M;\left|M\right|=3$)
$D$	Set of disposal centers ($d\in D$)
$V$	Set of transportation trucks ($v\in V$)
$V^{\prime }$	Set of recycling mini trucks ($v^{\prime }\in V^{\prime }$)
$T$	Set of planning periods ($t\in T$)
Parameters
$F{J}_j$	Fixed establishment cost of factory $j$,
$F{K}_k$	Fixed establishment cost of DC $k$,
$F{C}_c$	Fixed establishment cost of collection center $c$,
$F{Q}_q$	Fixed establishment cost of quarantine center $q$,
$F{R}_r$	Fixed establishment cost of recycling center $r$,
$F{D}_d$	Fixed establishment cost of disposal center $d$,
$F{T}_v$	Fixed cost of using transportation truck $v$,
$FT{\prime }_{v^{\prime }}$	Fixed cost of using mini recycling truck $v^{\prime }$,
$S{C}_{fi}$	Unit purchasing cost of material $f$ from supplier $i$,
$P{J}_{mj}$	Unit production cost of mask $m$ by factory $j$,
$P{K}_{mk}$	Unit processing cost of mask $m$ by DC $k$,
$P{C}_{mc}$	Unit processing cost of mask $m$ by collection center $c$,
$P{Q}_{mq}$	Unit processing cost of mask $m$ by quarantine center $q$,
$P{R}_{mr}$	Unit processing cost of mask $m$ by recycling center $r$,
$P{D}_{md}$	Unit processing cost of mask $m$ by disposal center $d$,
$T{S}_{fij}$	Unit cost of the transportation of material $f$ from supplier $i$ to factory $j$,
$T{J}_{mjk}$	Unit cost of the transportation of mask $m$ from factory $j$ to DC $k$,
$T{K}_{mkl}$	Unit cost of the transportation of mask $m$ from DC $k$ to customer center $l$,
$T{L}_{mlc}$	Unit cost of the transportation of mask $m$ from customer center $l$ to collection center $c$,
$T{C}_{mcq}$	Unit cost of the transportation of mask $m$ from collection center $c$ to quarantine center $q$,
$T{Q}_{mqr}$	Unit cost of the transportation of mask $m$ from quarantine center $q$ to recycling center $r$,
$T{R}_{mrd}$	Unit cost of the transportation of mask $m$ from recycling center $r$ to disposal center $d$,
$T{M}_{mri}$	Unit cost of the transportation of mask $m$ from recycling center $r$ to supplier $i$,
$C{C}_{fm}$	Unit consumption coefficient of material $f$ to produce mask $m$,
$D{M}_{mlt}$	Demand of mask $m$ at customer center $l$ in time period $t$,
$D{U}_{lt}$	Return rate of used masks to be transported from customer center $l$ to collection centers in time period $t$,
$C{R}_{frt}$	Conversion rate of material $f$ to be transported to suppliers from recycling center $r$ in time period $t$,
$D{R}_{rt}$	Disposal rate of masks transported to recycling center $r$ in time period $t$,
$C{I}_{ift}$	Capacity of supplier $i$ to provide material $f$ in time period $t$,
$C{J}_{jmt}$	Capacity of factory $j$ to produce mask $m$ in time period $t$,
$C{K}_{kmt}$	Capacity of DC $k$ to process mask $m$ in time period $t$,
$C{M}_{ct}$	Capacity of collection center $c$ to process masks in time period $t$,
$C{Q}_{qt}$	Capacity of quarantine center $q$ to process masks in time period $t$,
$C{R}_{rt}$	Capacity of recycling center $r$ to process masks in time period $t$,
$C{D}_{dt}$	Capacity of disposal center $d$ to process masks in time period $t$,
$C{S}_{ift}$	Capacity of supplier $i$ to store recycled material $f$ transported by recycling centers in time period $t$,
$C{T}_v$	Capacity of transportation truck $v$,
$CT{\prime }_{v^{\prime }}$	Capacity of mini recycling truck $v^{\prime }$,
$E{S}_{fij}$	Unit pollution emission for transporting material $f$ from supplier $i$ to factory $j$,
$E{J}_{mjk}$	Unit pollution emission for transporting mask $m$ from factory $j$ to DC $k$,
$E{K}_{mkl}$	Unit pollution emission for transporting mask $m$ from DC $k$ to customer center $l$,
$E{L}_{mlc}$	Unit pollution emission for transporting mask $m$ from customer center $l$ to collection center $c$,
$E{C}_{mcq}$	Unit pollution emission for transporting mask $m$ from collection center $c$ to quarantine center $q$,
$E{Q}_{mqr}$	Unit pollution emission for transporting mask $m$ from quarantine center $q$ to recycling center $r$,
$E{R}_{mrd}$	Unit pollution emission for transporting mask $m$ from recycling center $r$ to disposal center $d$,
$E{M}_{mri}$	Unit pollution emission for transporting mask $m$ from recycling center $r$ to supplier $i$,
$K{I}_{fi}$	Unit pollution emission for providing material $f$ at supplier $i$,
$K{J}_{mj}$	Unit pollution emission for producing mask $m$ at factory $j$,
$K{K}_{mk}$	Unit pollution emission for processing mask $m$ at DC $k$,
$K{C}_c$	Unit pollution emission for processing masks at collection center $c$,
$K{Q}_q$	Unit pollution emission for processing masks at quarantine center $q$,
$K{R}_r$	Unit pollution emission for processing masks at recycling center $r$,
$K{D}_d$	Unit pollution emission for processing masks at disposal center $d$,
$S{C}_c$	Population size around collection center $c$,
$S{Q}_q$	Population size around quarantine center $q$,
$S{R}_r$	Population size around recycling center $r$,
$S{D}_d$	Population size around disposal center $d$.
Variables
$X{J}_j$	Binary variable expressing whether candidate factory $j$ is established or not,
$X{K}_k$	Binary variable expressing whether candidate DC $k$ is established or not,
$X{C}_c$	Binary variable expressing whether candidate collection center $c$ is established or not,
$X{Q}_q$	Binary variable expressing whether candidate quarantine center $q$ is established or not,
$X{R}_r$	Binary variable expressing whether candidate recycling center $r$ is established or not,
$X{D}_d$	Binary variable expressing whether candidate disposal center $d$ is established or not,
$V{I}_{vit}$	Binary variable expressing whether transportation truck $v$ is employed by supplier $i$ in time period $t$ or not,
$V{J}_{vjt}$	Binary variable expressing whether transportation truck $v$ is employed by factory $j$ in time period $t$ or not,
$V{K}_{vkt}$	Binary variable expressing whether transportation truck $v$ is employed by DC $k$ in time period $t$ or not,
$V{C}_{v^{\prime }lt}$	Binary variable expressing whether transportation truck $v^{\prime }$ is employed by customer center $l$ in time period $t$ or not,
$V{V}_{v^{\prime }ct}$	Binary variable expressing whether mini recycling truck $v^{\prime }$ is employed by collection center $c$ in time period $t$ or not,
$V{Q}_{v^{\prime }qt}$	Binary variable expressing whether mini recycling truck $v^{\prime }$ is employed by quarantine center $q$ in time period $t$ or not,
$V{R}_{vrt}$	Binary variable expressing whether transportation truck $v$ is employed by recycling center $r$ in time period $t$ or not,
$V{W}_{v^{\prime }rt}$	Binary variable expressing whether mini recycling truck $v^{\prime }$ is employed by recycling center $r$ in time period $t$ or not,
$Y{I}_{fijvt}$	Amount of material $f$ transported from supplier $i$ to factory $j$ by transportation truck $v$ in time period $t$,
$Y{F}_{mjkvt}$	Amount of mask $m$ transported from factory $j$ to DC $k$ by transportation truck $v$ in time period $t$,
$Y{K}_{mklvt}$	Amount of mask $m$ transported from DC $k$ to customer center $l$ by transportation truck $v$ in time period $t$,
$Y{L}_{lc{v}^{\prime }t}$	Amount of masks transported from customer center $l$ to collection center $c$ by recycling mini truck $v^{\prime }$ in time period $t$,
$Y{C}_{cq{v}^{\prime }t}$	Amount of masks transported from collection center $c$ to quarantine center $q$ by recycling mini truck $v^{\prime }$ in time period $t$,
$Y{Q}_{qr{v}^{\prime }t}$	Amount of masks transported from quarantine center $q$ to recycling center $r$ by recycling mini truck $v^{\prime }$ in time period $t$,
$Y{I}_{rivt}$	Amount of masks transported from recycling center $r$ to supplier $i$ by transportation truck $v$ in time period $t$,
$Y{D}_{rd{v}^{\prime }t}$	Amount of masks transported from recycling center $r$ to disposal center $d$ by recycling mini truck $v^{\prime }$ in time period $t$.

3.1. Mathematical model

$$\begin{array}{l}\text{minimize}Obj1=\sum _{j\in J}F{J}_{j}X{J}_j+\sum _{k\in K}F{K}_{k}X{K}_k+\sum _{c\in C}F{C}_{c}X{C}_c+\sum _{q\in Q}F{Q}_{q}X{Q}_q+\\ \sum _{r\in R}F{R}_{r}X{R}_r+\sum _{d\in D}F{D}_{d}X{D}_d+\sum _{v\in V}\sum _{i\in I}\sum _{t\in T}F{T}_{v}V{I}_{vit}+\sum _{v\in V}\sum _{j\in J}\sum _{t\in T}F{T}_{v}V{J}_{vjt}+\\ \sum _{v\in V}\sum _{k\in K}\sum _{t\in T}F{T}_{v}V{K}_{vkt}+\sum _{v\in V}\sum _{c\in C}\sum _{t\in T}F{T}_{v}V{C}_{vct}+\sum _{v^{\prime }\in V^{\prime }}\sum _{c\in C}\sum _{t\in T}F{T}_{v^{\prime }}^{\prime }V{V}_{v^{\prime }ct}+\\ \sum _{v^{\prime }\in V^{\prime }}\sum _{q\in Q}\sum _{t\in T}F{T}_{v^{\prime }}^{\prime }V{Q}_{v^{\prime }qt}+\sum _{v\in V}\sum _{r\in R}\sum _{t\in T}F{T}_{v}V{R}_{vrt}+\sum _{v^{\prime }\in V^{\prime }}\sum _{r\in R}\sum _{t\in T}F{T}_{v^{\prime }}^{\prime }V{W}_{v^{\prime }rt}+\\ \sum _{f\in F}\sum _{i\in I}\sum _{j\in J}\sum _{t\in T}\sum _{v\in V}T{S}_{fij}Y{I}_{fijvt}+\sum _{m\in M}\sum _{j\in J}\sum _{k\in K}\sum _{t\in T}\sum _{v\in V}T{J}_{mjk}Y{F}_{mjkvt}+\\ \sum _{m\in M}\sum _{k\in K}\sum _{l\in L}\sum _{t\in T}\sum _{v\in V}T{K}_{mkl}Y{K}_{mklvt}+\\ \sum _{m\in M}\sum _{l\in L}\sum _{c\in C}\sum _{t\in T}\sum _{v^{\prime }\in V^{\prime }}T{L}_{mlc}Y{L}_{lc{v}^{\prime }t}+\sum _{m\in M}\sum _{c\in C}\sum _{q\in Q}\sum _{t\in T}\sum _{v^{\prime }\in V^{\prime }}T{C}_{mcq}Y{C}_{cq{v}^{\prime }t}+\\ \sum _{m\in M}\sum _{q\in Q}\sum _{r\in R}\sum _{t\in T}\sum _{v^{\prime }\in V^{\prime }}T{Q}_{mqr}Y{Q}_{qr{v}^{\prime }t}+\sum _{m\in M}\sum _{r\in R}\sum _{i\in I}\sum _{t\in T}\sum _{v\in V}T{M}_{mri}Y{I}_{rivt}+\\ \sum _{m\in M}\sum _{r\in R}\sum _{d\in D}\sum _{t\in T}\sum _{v^{\prime }\in V^{\prime }}T{R}_{mrd}Y{D}_{rd{v}^{\prime }t}+\\ \sum _{f\in F}\sum _{i\in I}\sum _{j\in J}\sum _{t\in T}\sum _{v\in V}S{C}_{fi}Y{I}_{fijvt}+\sum _{m\in M}\sum _{j\in J}\sum _{k\in K}\sum _{t\in T}\sum _{v\in V}P{J}_{mj}Y{F}_{mjkvt}+\\ \sum _{m\in M}\sum _{k\in K}\sum _{l\in L}\sum _{t\in T}\sum _{v\in V}P{K}_{mk}Y{K}_{mklvt}+\sum _{m\in M}\sum _{l\in L}\sum _{c\in C}\sum _{t\in T}\sum _{v^{\prime }\in V^{\prime }}P{C}_{mc}Y{L}_{lc{v}^{\prime }t}+\\ \sum _{m\in M}\sum _{c\in C}\sum _{q\in Q}\sum _{t\in T}\sum _{v^{\prime }\in V^{\prime }}P{Q}_{mq}Y{C}_{cq{v}^{\prime }t}+\sum _{m\in M}\sum _{q\in Q}\sum _{r\in R}\sum _{t\in T}\sum _{v^{\prime }\in V^{\prime }}P{R}_{mr}Y{Q}_{qr{v}^{\prime }t}+\sum _{m\in M}\sum _{r\in R}\sum _{d\in D}\sum _{t\in T}\sum _{v^{\prime }\in V^{\prime }}P{D}_{md}Y{D}_{rd{v}^{\prime }t}\end{array}$$ (1)

$$\begin{array}{l}\text{minimize}Obj2=\sum _{f\in F}\sum _{i\in I}\sum _{j\in J}\sum _{t\in T}\sum _{v\in V}\left(K{I}_{fi}+E{S}_{fij}\right)Y{I}_{fijvt}+\\ \sum _{m\in M}\sum _{j\in J}\sum _{k\in K}\sum _{t\in T}\sum _{v\in V}\left(K{J}_{mj}+E{J}_{mjk}\right)Y{F}_{mjkvt}+\sum _{m\in M}\sum _{k\in K}\sum _{l\in L}\sum _{t\in T}\sum _{v\in V}\left(K{K}_{mk}+E{K}_{mkl}\right)Y{K}_{mklvt}+\\ \sum _{m\in M}\sum _{l\in L}\sum _{c\in C}\sum _{t\in T}\sum _{v^{\prime }\in V^{\prime }}\left(K{C}_c+E{L}_{mlc}\right)Y{L}_{lc{v}^{\prime }t}+\sum _{m\in M}\sum _{c\in C}\sum _{q\in Q}\sum _{t\in T}\sum _{v^{\prime }\in V^{\prime }}\left(K{Q}_q+E{C}_{mcq}\right)Y{C}_{cq{v}^{\prime }t}+\\ \sum _{m\in M}\sum _{q\in Q}\sum _{r\in R}\sum _{t\in T}\sum _{v^{\prime }\in V^{\prime }}\left(K{R}_r+E{Q}_{mqr}\right)Y{Q}_{qr{v}^{\prime }t}+\sum _{m\in M}\sum _{r\in R}\sum _{i\in I}\sum _{t\in T}\sum _{v\in V}E{M}_{mri}Y{I}_{rivt}+\\ \sum _{m\in M}\sum _{r\in R}\sum _{d\in D}\sum _{t\in T}\sum _{v^{\prime }\in V^{\prime }}\left(K{D}_d+E{R}_{mrd}\right)Y{D}_{rd{v}^{\prime }t}\end{array}$$ (2)

$$\text{minimize}Obj3=\sum _{c\in C}S{C}_{c}X{C}_c+\sum _{q\in Q}S{Q}_{q}X{Q}_q+\sum _{r\in R}S{R}_{r}X{R}_r+\sum _{d\in D}S{D}_{d}X{D}_d$$ (3)

subject to

$$\sum _{j\in J}\sum _{v\in V}Y{I}_{fijvt}\le C{I}_{ift}\forall i\in I,f\in F,t\in T,$$ (4)

$$\sum _{k\in K}\sum _{v\in V}Y{F}_{mjkvt}\le C{J}_{jmt}X{J}_j\forall j\in J,m\in M,t\in T,$$ (5)

$$\sum _{l\in L}\sum _{v\in V}Y{K}_{mklvt}\le C{K}_{kmt}X{K}_k\forall k\in K,m\in M,t\in T,$$ (6)

$$\sum _{l\in L}\sum _{v^{\prime }\in V^{\prime }}Y{L}_{lc{v}^{\prime }t}\le C{M}_{ct}X{C}_c\forall c\in C,t\in T,$$ (7)

$$\sum _{c\in C}\sum _{v^{\prime }\in V^{\prime }}Y{C}_{cq{v}^{\prime }t}\le C{Q}_{qt}X{Q}_q\forall q\in Q,t\in T,$$ (8)

$$\sum _{q\in Q}\sum _{v^{\prime }\in V^{\prime }}Y{Q}_{qr{v}^{\prime }t}\le C{R}_{rt}X{R}_r\forall r\in R,t\in T,$$ (9)

$$\sum _{r\in R}\sum _{v\in V}C{R}_{frt}Y{I}_{rivt}\le C{S}_{ift}\forall i\in I,f\in F,t\in T,$$ (10)

$$\sum _{d\in D}\sum _{v^{\prime }\in V^{\prime }}Y{D}_{rd{v}^{\prime }t}\le C{D}_{dt}X{D}_d\forall r\in R,t\in T,$$ (11)

$$\sum _{j\in J}\sum _{f\in F}Y{I}_{fijvt}\le C{T}_{v}V{I}_{vit}\forall i\in I,t\in T,v\in V,$$ (12)

$$\sum _{k\in K}\sum _{m\in M}Y{F}_{mjkvt}\le C{T}_{v}V{J}_{vjt}\forall j\in J,t\in T,v\in V,$$ (13)

$$\sum _{l\in L}\sum _{m\in M}Y{K}_{mklvt}\le C{T}_{v}V{K}_{vkt}\forall k\in K,t\in T,v\in V,$$ (14)

$$\sum _{c\in C}Y{L}_{lc{v}^{\prime }t}\le CT{\prime }_{v^{\prime }}V{C}_{v^{\prime }lt}\forall l\in L,t\in T,v^{\prime }\in V^{\prime },$$ (15)

$$\sum _{q\in Q}Y{C}_{cq{v}^{\prime }t}\le CT{\prime }_{v^{\prime }}V{V}_{v^{\prime }ct}\forall c\in C,t\in T,v^{\prime }\in V^{\prime },$$ (16)

$$\sum _{r\in R}Y{Q}_{qr{v}^{\prime }t}\le CT{\prime }_{v^{\prime }}V{Q}_{v^{\prime }qt}\forall q\in Q,t\in T,v^{\prime }\in V^{\prime },$$ (17)

$$\sum _{i\in I}Y{I}_{rivt}\le C{T}_{v}V{R}_{vrt}\forall r\in R,t\in T,v\in V,$$ (18)

$$\sum _{d\in D}Y{D}_{rd{v}^{\prime }t}\le CT{\prime }_{v^{\prime }}V{W}_{v^{\prime }rt}\forall r\in R,t\in T,v^{\prime }\in V^{\prime },$$ (19)

$$\sum _{f\in F}\sum _{i\in I}\sum _{v\in V}C{C}_{fm}Y{I}_{fijvt}=\sum _{v\in V}Y{F}_{mjkvt}\forall m\in M,j\in J,k\in K,t\in T,$$ (20)

$$\sum _{j\in J}\sum _{v\in V}Y{F}_{mjkvt}=\sum _{l\in L}\sum _{v\in V}Y{K}_{mklvt}\forall m\in M,k\in K,t\in T,$$ (21)

$$\sum _{k\in K}\sum _{v\in V}Y{K}_{mklvt}=D{M}_{mlt}\forall m\in M,l\in L,t\in T,$$ (22)

$$\sum _{k\in K}\sum _{m\in M}\sum _{v\in V}D{U}_{lt}Y{K}_{mklvt}=\sum _{c\in C}\sum _{v^{\prime }\in V^{\prime }}Y{L}_{lc{v}^{\prime }t}\forall l\in L,t\in T,$$ (23)

$$\sum _{l\in L}\sum _{v^{\prime }\in V^{\prime }}Y{L}_{lc{v}^{\prime }t}=\sum _{q\in Q}\sum _{v^{\prime }\in V^{\prime }}Y{C}_{cq{v}^{\prime }t}\forall c\in C,t\in T,$$ (24)

$$\sum _{c\in C}\sum _{v^{\prime }\in V^{\prime }}Y{C}_{cq{v}^{\prime }t}=\sum _{r\in R}\sum _{v^{\prime }\in V^{\prime }}Y{Q}_{qr{v}^{\prime }t}\forall q\in Q,t\in T,$$ (25)

$$\sum _{q\in Q}\sum _{v^{\prime }\in V^{\prime }}Y{Q}_{qr{v}^{\prime }t}=\sum _{i\in I}\sum _{v\in V}Y{I}_{rivt}+\sum _{d\in D}\sum _{v^{\prime }\in V^{\prime }}Y{D}_{rd{v}^{\prime }t}\forall r\in R,t\in T,$$ (26)

$$\sum _{i\in I}\sum _{v\in V}Y{I}_{rivt}=D{R}_{rt}\left(\sum _{q\in Q}\sum _{v^{\prime }\in V^{\prime }}Y{Q}_{qr{v}^{\prime }t}\right)\forall r\in R,t\in T,$$ (27)

$$X{J}_j,X{K}_k,X{C}_c,X{Q}_q,X{R}_r,X{D}_d,V{I}_{vit},V{J}_{vjt},V{K}_{vkt},V{C}_{v^{\prime }lt},V{V}_{v^{\prime }ct},V{Q}_{v^{\prime }qt},V{R}_{vrt},V{W}_{v^{\prime }rt}\in \left\{0,1\right\}$$

$$\forall i\in I,j\in J,k\in K,l\in L,c\in C,q\in Q,r\in R,d\in D,v\in V,v^{\prime }\in V^{\prime },$$ (28)

$$\begin{array}{l}Y{I}_{fijvt},Y{L}_{lc{v}^{\prime }t},Y{C}_{cq{v}^{\prime }t},Y{Q}_{qr{v}^{\prime }t},Y{I}_{rivt},Y{D}_{rd{v}^{\prime }t}\ge 0,Y{F}_{mjkvt},Y{K}_{mklvt}\in Z^{+},\\ \forall i\in I,j\in J,k\in K,l\in L,c\in C,q\in Q,r\in R,d\in D,v\in V,v^{\prime }\in V^{\prime },f\in F,m\in M.\end{array}$$ (29)

The first objective function (1) shows minimizing the total cost of the CLSCN design including the fixed establishment costs, fixed employment costs of trucks, transportation costs, and operational costs at different facilities. The second objective function (2) indicates minimizing the whole pollution emission incurred by transportation and operational processes. The third objective function (3) states minimizing the total human risk imposed by the establishment of facilities such as the number of people around collection centers, quarantine centers, recycling centers, and disposal centers is minimized. (4), (5), (6), (7), (8), (9), (10) represents the capacity constraints of suppliers, factories, DCs, collection centers, quarantine centers, recycling centers, and disposal centers, respectively. Furthermore, decisions on the facility location at different levels can be made according to these equations. (12), (13), (14), (15), (16), (17), (18), (19) indicate the capacity constraints of trucks employed by suppliers, factories, DCs, collection centers, quarantine centers, recycling centers, and disposal centers, respectively. Eq. (20) states the flow balance from suppliers to factories considering consumption rates of raw materials to produce masks. Eq. (21) expresses the flow balance between factories and DCs. Eq. (22) ensures that each customer center should receive its exact demand for masks. Eq. (23) shows the flow balance between customer centers and collection centers considering the converted amount of used masks to be collected and recycled possibly. Eq. (24) represents the flow balance between collection centers and quarantine centers. Eq. (25) indicates the flow balance between quarantine centers and recycling centers. Eqs. (26), (27) express the flow balance between recycling centers, disposal centers, and suppliers. These flow balances in (20), (21), (22), (23), (24), (25), (26), (27) are established based on the input and output items. In Eq. (27), a given amount of masks is recycled at each recycling center and then transported to suppliers. Moreover, the remaining amount of masks is transported to disposal centers based on Eq. (26). Eqs. (28), (29) display the types of variables.

4. Solution methods

In this research, MOGWO and NSGA-II are applied to tackle the complexity of the problem. The main reasons for choosing MOGWO and NSGA-II algorithms can be stated in two parts.

• I.The purpose of this study is to examine the performance of novel algorithms in the field of supply chain network design. Among the emerging multi-objective algorithms, MOGWO algorithm is chosen because of its strong structure in terms of both intensification and diversification (Mirjalili et al., 2016).
• II.To evaluate the performance of the proposed MOGWO algorithm, comparisons must be made with one of the strongest and well-known algorithms. In this regard, studies have demonstrated that the NSGA-II algorithm is one of the best multi-objective meta-heuristic algorithms (Tirkolaee et al., 2020b).

Therefore, in this research, MOGWO and NSGA-II algorithms are implemented and their results are evaluated both in terms of quality and dispersion of Pareto solutions using several performance metrics.

4.1. Multi-Objective Grey Wolf Optimization algorithm

Grey Wolf Optimization (GWO) algorithm is a meta-heuristic algorithm inspired by the hierarchical structure and social behavior of grey wolves while hunting. This algorithm is population-based, has a simple process, and can be easily generalized to large-scale problems (Makhadmeh et al., 2021). The GWO was introduced by Mirjalili et al. (2014). Grey wolves are regarded as apex predators, which are at the top of the food chain pyramid. Grey wolves prefer to live in a group, each group has an average of 5–12 members. All members of this group have a very precise hierarchy of social domination and have specific tasks. In each herd of wolves for hunting, there are 4°, which is modeled as a pyramidal structure including alpha ($\alpha$), beta ($\beta$), delta ($\delta$), omega ($\omega$). Leader wolves are called alpha groups, which can be male or female. These wolves dominate the herd. Beta wolves help alpha wolves in the decision-making process and are also prone to be chosen instead. Delta wolves are lower than beta wolves including older wolves, predators, and baby care wolves. Omega wolves show the lowest rank in the hierarchy that has the least rights over the rest of the group. After all, they eat and do not participate in the decision-making process. In GWO, the most appropriate solution is taken into account as alpha, and the second and third appropriate solutions are named beta and delta, respectively. The rest of the solutions are considered omega. In the GWO, hunting is driven by alpha, beta, and delta. Solution omega follows these three wolves. To model the circumvention behavior, Eqs. (30), (31) are formulated.

$$\overrightarrow{D}=\left|\overrightarrow{C}\overrightarrow{X_P}\left(t\right)-\overrightarrow{X}\left(t\right)\right|\text{,}$$ (30)

$$\overrightarrow{X}\left(t+1\right)=\overrightarrow{X_P}\left(t\right)-\overrightarrow{A}\overrightarrow{D},$$ (31)

where $t$, ($\overrightarrow{A},\overrightarrow{C}$), $\overrightarrow{X_P}$, and $\overrightarrow{X}$ represent the flow repetition, the vector coefficient, the hunting position vector, and the position vector of a grey wolf, respectively. Vectors $A$ and $C$ are computed based on Eqs. (32), (33).

$$\overrightarrow{A}=2\overrightarrow{a}\overrightarrow{r_1}-\overrightarrow{a}\text{,}$$ (32)

$$\overrightarrow{C}=2\overrightarrow{r_2}\text{,}$$ (33)

where the $\overrightarrow{a}$ elements are decreased linearly from 2 to 0 under the iteration route. Here, $r_1$ and $r_2$ are random vectors in the range [0, 1].

Grey wolves have the ability to detect the position of prey and bypass them. Hunting is guided by Alpha. Delta and Beta may also occasionally participate in hunting. Moreover, in an absolute search space, we have no solution for the optimal position (hunting). To mathematically simulate the hunting behavior of grey wolves, we suppose that Alpha (the best candidate solution), Delta, and Beta are sufficiently aware of the potential hunting position. So, the first three obtained solutions are saved and other search agents are obliged to update their position based on the position of the best search agents. This operation is performed based on (34), (35), (36):

$$\overrightarrow{D_{\alpha }}=\left|\overrightarrow{C_1}\overrightarrow{X_{\alpha }}-\overrightarrow{X}\right|,\overrightarrow{D_{\beta }}=\left|\overrightarrow{C_2}\overrightarrow{X_{\beta }}-\overrightarrow{X}\right|,\overrightarrow{D_{\delta }}=\left|\overrightarrow{C_3}\overrightarrow{X_{\delta }}-\overrightarrow{X}\right|,$$ (34)

$${\overrightarrow{X}}_1=\overrightarrow{X_{\alpha }}-\overrightarrow{A_1}\left({\overrightarrow{D}}_{\alpha }\right),{\overrightarrow{X}}_2=\overrightarrow{X_{\beta }}-\overrightarrow{A_1}\left({\overrightarrow{D}}_{\beta }\right),{\overrightarrow{X}}_3=\overrightarrow{X_{\delta }}-\overrightarrow{A_1}\left({\overrightarrow{D}}_{\delta }\right),$$ (35)

$$\overrightarrow{X}\left(t+1\right)=\frac{{\overrightarrow{X}}_1+{\overrightarrow{X}}_2+{\overrightarrow{X}}_3}{3}.$$ (36)

In GWO, the search process starts by creating a random population of grey wolves (candidate solutions). In the iteration time, Beta, Delta, and Alpha wolves estimate the probable hunting position. Each candidate solution updates its distance with the prey. Parameter $a$ is decreased from 2 to 0 to boost the detection and attack process to prey. If | $A$ |>1, candidate solutions diverge; else if |$A$ |<1, candidate solutions converge. In the MOGWO, the general framework of the grey wolf algorithm is implemented. The variation is that each iteration of the non-dominated solutions is separated in the manner presented in Sub-section 4.2.1. The pseudo-code of the MOGWO is represented in Fig. 2 .

Fig. 2.

Pseudo-code of the proposed MOGWO.

4.1.1. Fast non-dominated sorting

To rank a set of solutions and place them on various fronts in terms of the degree of non-dominated, first, the following two parameters are computed for each solution; $n_p$, which is actually the number of solutions that have overcome the solution $p$, and $S_p$, which is the set of solutions that have been dominated by the solution $p$. All solutions with $n_p$ = 0 are ranked first and placed in the first front. Then, for every solution of $p$ with rank one, every member ($q$) of the set $S_p$ is met and its $n_q$ is reduced by one unit. Thus, if $n_q$ = 0, then the solution $q$ takes second place and is in the second front. In the same way, the next fronts are formed. Fig. 3 shows the pseudo-code for how to fast non-dominated sorting (FNS) in the proposed MOGWO.

Fig. 3.

Pseudo-code of the FNS.

4.2. NSGA-II algorithm

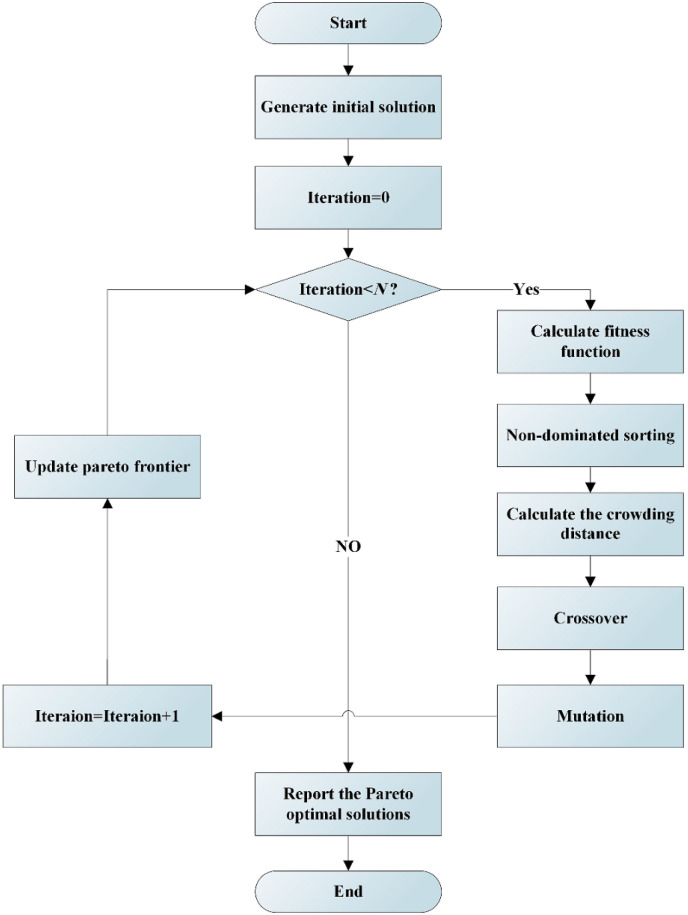
NSGA-II algorithm is one of the most widely-utilized and robust algorithms for treating multi-objective optimization problems and has an acceptable efficiency (Onan et al., 2015; Hu et al., 2020). Srinivas and Deb (1994) suggested the NSGA optimization method for solving multi-objective optimization problems. In general, the structure of the NSGA-II is given in Fig. 4 .

Fig. 4.

Structure of the proposed NSGA-II.

4.2.1. Generate the initial solution

In the first step of a multi-objective genetic algorithm, several initial solutions must be generated. Initial solutions must be randomly selected to cover the set of justified spaces. Therefore, random number generation functions are used in software environments.

4.2.2. Fitness function calculation

Fitness means that one solution is superior to another. In optimization problems, the superiority of one solution over another is specified by the objective function of the problem. Therefore, the fitness function will be the same as the objective function of the mathematical model. If the objective function is of the minimum sort, the fitness function is defined as $-f$ or $1/f$ ($f$ represents the formula of the objective function), but if the objective function is of the maximum sort, the concept of fitness is exactly the same as the objective function value.

4.2.3. Sorting non-dominated solutions

It is first necessary to define the concept of “dominance”:

• I.$X$ dominates all members of set $A$. The members of set $A$ shows points that are at least in one sense worse than $X$ and in no way better than $X$.
• II.$X$ is dominated by all members of set $C$. Here, $X$ is not better than any of the members in set $C$ and is worse in at least one respect. However, the members in sets $B$ and $D$ are better in one sense, so we cannot choose one.

In this step of NSGA-II, between the set of solutions, we select and separate the ones that are non-dominated to the other solutions are selected and separated. These non-dominated solutions are essentially the Pareto front or the front of efficiency found by the genetic algorithm. This Pareto front is improved in each iteration to report the best Pareto front by the NSGA-II at the end of the genetic algorithm.

4.2.4. Crossover

The crossover operation in the NSGA-II shows exactly the same as the crossover operation in the single-objective genetic algorithm. In this section, the solutions that were not non-dominated are separated, then composed in pairs according to a predetermined mechanism (tournament, random, or roulette wheel), and generate new solutions. This composition of solutions is done in methods such as uniform, single-point, two-point, etc. The aim of the crossover is to compose the features of various solutions with the aim of generating better solutions.

4.2.5. Mutation

The mutation operation in the NSGA-II is exactly the same as the mutation operation in the single-objective genetic algorithm. At this stage, some solutions are chosen at random and some of their cells are modified at random. The aim of the mutation is to make sudden alters in the solutions in order to escape the trap of optimal local.

4.3. Solution representation

Each solution of the studied problem consists of two different structures. The first structure is for location decision variables and the second structure is for transport decision variables in the presented network. In the first structure, a set of numbers between 0 and 1 is presented and numbers less than 0.5 mean no selection/establishment and numbers above 0.5 mean selection/establishment. For example, considering 5 potential points for the establishment of a DC, Fig. 5 shows an example of the first structure for the location of the DCs.

Fig. 5.

Representation of the first structure in a string.

According to Fig. 5, DCs 1, 2, and 4 are established. This structure is repeated for all network facilities (transport centers and equipment) that must be decided about selected/established.

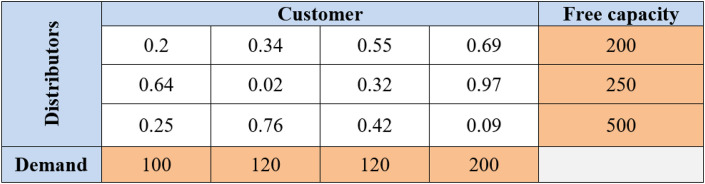
In the second structure, which determines the volume of transmission between different bases and destinations, a matrix with values between 0 and 1 is used. The number of rows in this matrix is equal to the number of bases and the number of columns is equal to the number of destinations. It should be noted that these matrices are repeated for each time period. For example, if we have 3 distributors and 4 customers, an example of the solution is indicated in Fig. 6 .

Fig. 6.

Example of a second structure for the distributor-customer.

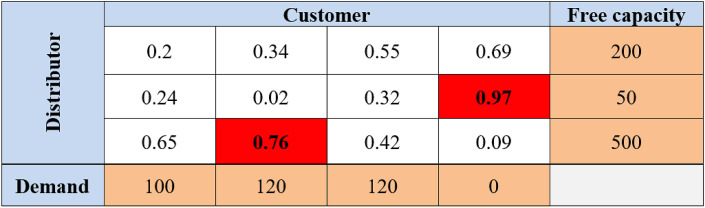
In order to decode the above matrix, several steps are performed sequentially. First, according to the generated random numbers from large to small, we start to meet the needs of the customer until all the needs of the customer are met. The first step is represented in Fig. 7 .

Fig. 7.

First step of decoding the second structure of the solution string.

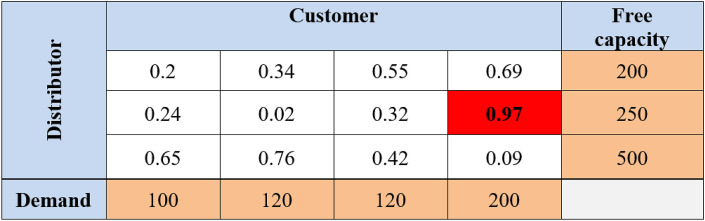
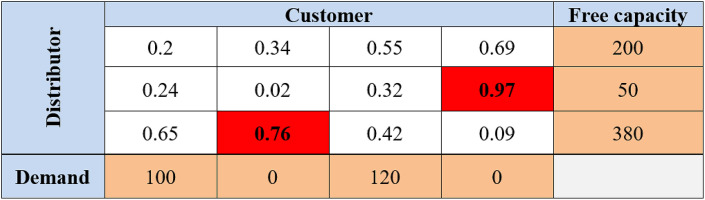
According to the selected random number, the amount of customer demand number 4 should be answered as much as possible first. Therefore, the amount of 200 units from distributor number 2 is allocated to customer 4. In the next step, a larger random number is selected from the available random numbers, the example of which is indicated in Fig. 8 .

Fig. 8.

Second step of decoding the second structure of the solution string.

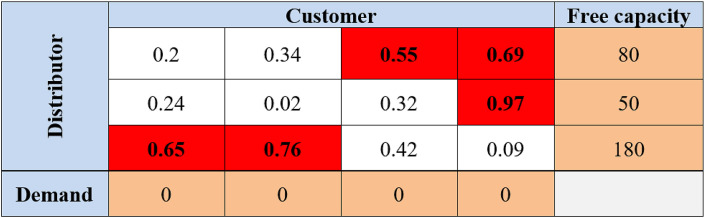
According to the selected random number, the amount of 120 units is transferred from distributor number 3 to customer 2 and the capacity and demand values are updated (according to Fig. 9 ).

Fig. 9.

First step of decoding the second structure of the solution string.

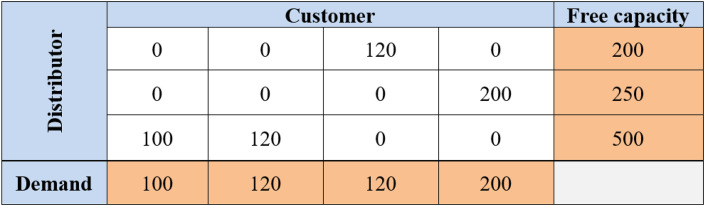
This process continues until the end of full coverage of customer demand. Fig. 10 shows how full coverage of customer demand by distributors. Therefore, customer demand was met in this way. Finally, the sent quantities from the distributor to the customer are presented in Fig. 11 .

Fig. 10.

Last step of decoding the second structure of the solution string.

Fig. 11.

Output of decoding the second structure of the solution string.

This designed structure for different types of bases, destinations, and in different periods as well as for different types of transportation systems are repeated to finally provide a complete solution to the closed-looped supply chain network design problem.

4.4. Assessment metrics for meta-heuristics

In this section, the suggested indicators are usually utilized to compare the performance of meta-heuristic algorithms that are explained in the next sub-sections.

4.4.1. Max-Spread

This index is utilized to compute the amplitude of the optimal Pareto front solutions gained by the algorithm. The larger the value of this index, the higher the priority of the algorithm. The value of this index is computed using Eq. (37):

$$\text{DM}=\sqrt{\sum _{i=1}^I{(\text{Min}{f}_i-\text{Max}{f}_i)}^2},$$ (37)

where $\text{Min}{f}_i$ and $\text{Max}{f}_i$ represent the minimum and maximum values of the objective function between all obtained non-dominated solutions from the algorithm, respectively.

4.4.2. Mean Ideal Distance (MID) metric

Using this metric, a close distance is obtained among the obtained non-dominated solutions and the ideal point. The smaller the value of this index, the higher the priority of the algorithm. The MID is calculated utilizing Eq. (38).

$$\text{MID}=\frac{{\sum }_{i=1}^n\sqrt{{\left(\frac{f{1}_i-f{1}_{best}}{f{1}_{total}^{max}-f{1}_{total}^{min}}\right)}^2+{\left(\frac{f{2}_i-f{2}_{best}}{f{2}_{total}^{max}-f{2}_{total}^{min}}\right)}^2}}{n},$$ (38)

where $f{1}_{total}^{max}$ and $f{2}_{total}^{min}$ are considered as the largest and the smallest value between non-dominated solutions, respectively.

4.4.3. Spread of Non-Dominance Solution (SNS) metric

This index also called the spread metric, is utilized to calculate the degree of variation of Pareto solutions. The larger the value of the SNS, the higher the priority of the algorithm. The value of the SNS is computed using Eq. (39).

$$SNS=\sqrt{\frac{{\sum }_{i=1}^n{\left(MID-C_i\right)}^2}{n-1}}$$ (39)

In Eq. (39), $n$ represents the number of non-dominated solutions and also the value of ${\text{C}}_{\text{i}}$ is calculated using Eq. (40):

$$C_i=\sqrt{{f_{1i}}^2+{f_{2i}}^2},$$ (40)

where Eq. (40), $f_{1i}$ and $f_{2i}$ are the values of the first and second objective functions, respectively, for the non-dominated solution $i$.

4.4.4. Number of Pareto Solution (NPS) metric

The NPS is employed to calculate the number of the gained non-dominated solutions by the proposed algorithm. The larger the NPS metric, the higher the priority of the algorithm.

4.5. Tuning the parameters

Here, the Taguchi design approach is used to tune the parameters of the algorithms efficiently. To design experiments in the proposed algorithms, firstly, three different levels are defined for its parameters. And then the predefined tests are performed in this algorithm utilizing random test problems in medium-sized. The proposed values for the parameters of the MOGWO and NSGA-II algorithms are shown in Table 1 . Then, with Taguchi L9 design, different experiments were created and the MOGWO and NSGA-II algorithms were implemented for each of them. The implementation results are reports in Table 2 .

Table 1.

Parameters and primary values of the proposed algorithms.

Algorithm	Parameter	Value of levels
		1	2	3
MOGWO	Maximum number of Iterations (Max_iter)	50	100	200
	Number of search agent (N_S)	50	100	150
	Change position rate (PR)	0.2	03	05
NSGA-II	Population size-Stopping criteria (PS)	50–200	100–150	200–100
	Crossover rate (CR)	0.5	0.7	0.9
	Mutation rate (MR)	0.2	03	05

Table 2.

MID values obtained by the Taguchi design method for the algorithms.

No.	Value of levels in MOGWO			MID index
	Max_iter	N_S	PR
1	1	1	1	0.679
2	1	2	2	0.712
3	1	3	3	0.682
4	2	1	2	0.663
5	2	2	3	0.702
6	2	3	1	0.681
7	3	1	3	0.647
8	3	2	1	0.739
9	3	3	2	0.739
No.	Value of levels in NSGA-II			MID index
	PS	CR	MR
1	1	1	1	0.534
2	1	2	2	0.612
3	1	3	3	0.537
4	2	1	2	0.491
5	2	2	3	0.576
6	2	3	1	0.637
7	3	1	3	0.599
8	3	2	1	0.973
9	3	3	2	0.642

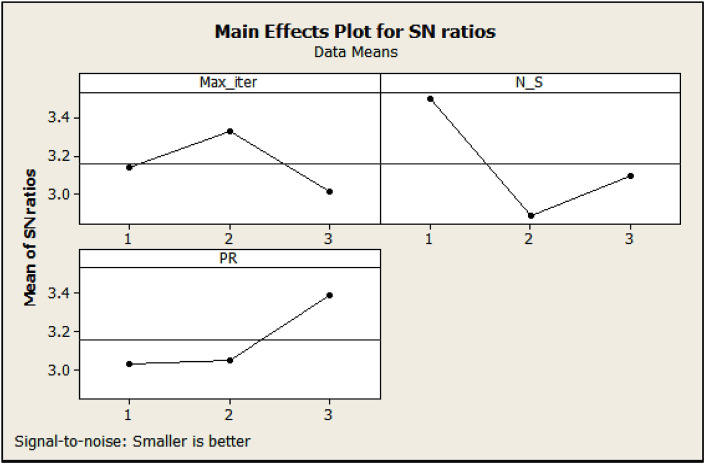
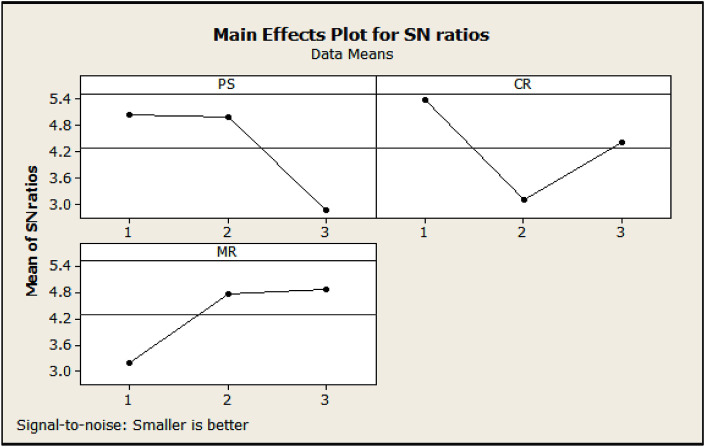
Therefore, by presenting these outputs by using MINITAB software, the S/N ratios of the proposed algorithms are displayed in Fig. 12, Fig. 13 .

Fig. 12.

S/N ratios obtained for the NSGA-II algorithm.

Fig. 13.

S/N ratios obtained for the NSGA-II algorithm.

Hence, according to the presented results in Fig. 12, Fig. 13, the best value of each parameter is determined and other examples are executed with these values of the algorithm parameters. Table 3 presents the optimal values of the parameters.

Table 3.

Optimal values for the parameters of the MOGWO and NSGA-II.

Algorithm	Parameter	Optimal value
MOGWO	Maximum number of Iterations (Max_iter)	200
	Number of search agent (N_S)	100
	Change position rate (PR)	0.2
NSGA-II	Population size (PS)	200–100
	Crossover rate (CR)	0.7
	Mutation rate (MR)	0.2

5. Numerical results

In this part, to validate the presented problem, the efficiency of the two algorithms was investigated. According to the superiority of NSGA-II in the MID metric is very slight, so in general, the MOGWO algorithm can be introduced as the superior algorithm. Since this analysis may not be complete and sufficient, thirty numerical problems in different sizes are generated and comparison metrics were calculated for both algorithms. It should be noted that the size of the test problems is divided into three groups: small, medium and large. The basis of this division is based on modeling from (Pahlevan et al., 2021). The input information for these thirty problems is presented in Table 4 . Also, the results related to different assessment metrics for the MOGWO algorithm are presented in Table 5 and for the NSGA-II algorithm in Table 6 .

Table 4.

Information of the problem instances.

Problem size	#P	#Suppliers	#Factories	#Collection centers	#DCs	#customers	#Quarantine centers	#Recycle centers	#Disposal centers	#Periods	#Trucks	#Mini trucks
Small scale	1	1	2	2	1	4	1	1	1	1	10	5
	2	1	3	2	2	5	1	1	2	1	10	5
	3	2	3	3	3	6	1	2	3	1	10	5
	4	2	4	3	4	7	2	2	3	2	15	8
	5	3	4	4	5	8	2	2	4	2	15	8
	6	3	5	4	7	9	2	3	4	2	15	8
	7	4	5	5	9	10	3	3	5	3	20	10
	8	4	6	5	10	11	3	3	5	3	20	10
	9	5	6	6	11	12	3	4	6	3	20	10
	10	5	7	6	12	13	4	4	6	4	25	13
Median Scale	11	6	8	7	13	15	6	4	7	6	30	15
	12	7	10	9	15	20	8	5	7	6	35	18
	13	8	12	11	17	25	10	5	7	8	40	20
	14	9	14	13	19	30	12	5	8	8	45	23
	15	10	16	15	21	35	14	6	8	10	50	25
	16	11	18	17	23	40	16	6	8	10	55	28
	17	12	20	19	25	45	18	6	9	12	60	30
	18	13	22	21	27	50	20	7	9	12	65	33
	19	14	24	23	29	55	22	8	9	14	70	35
	20	15	26	25	30	60	24	9	10	14	75	38
Large Scale	21	20	30	30	40	70	26	10	10	16	80	40
	22	25	40	35	50	80	28	11	10	18	90	45
	23	30	50	40	60	90	30	12	11	20	100	50
	24	35	60	45	70	100	40	13	12	22	120	60
	25	40	70	50	80	110	50	14	13	24	140	70
	26	45	80	60	90	120	60	15	14	26	160	80
	27	50	90	70	100	130	70	16	15	28	180	90
	28	55	100	80	110	140	80	17	16	30	200	100
	29	60	110	90	120	150	90	18	17	35	220	110
	30	65	120	100	130	160	100	19	18	40	250	125

Table 5.

Assessment metrics values of the MOGWO algorithm.

Problem size	No.	DM	MID	SNS	NPS
Small scale	1	241.196	0.173	316.431	3
	2	258.283	0.189	347.554	3
	3	274.296	0.207	374.511	3
	4	297.818	0.213	390.031	4
	5	303.228	0.214	396.462	4
	6	311.752	0.217	412.615	4
	7	318.568	0.230	424.654	5
	8	347.527	0.247	460.260	5
	9	361.972	0.269	493.717	5
	10	397.637	0.289	519.450	5
Median Scale	11	432.604	0.312	521.576	6
	12	468.866	0.331	543.823	6
	13	484.384	0.335	577.050	7
	14	508.802	0.362	634.302	7
	15	532.661	0.394	693.264	7
	16	542.116	0.401	727.036	7
	17	564.762	0.439	761.811	7
	18	613.951	0.444	823.359	8
	19	640.150	0.452	833.382	8
	20	654.266	0.493	855.750	8
Large Scale	21	672.367	0.515	917.400	9
	22	702.199	0.566	937.926	10
	23	771.150	0.607	951.755	11
	24	805.624	0.619	1002.409	12
	25	880.767	0.658	1055.105	13
	26	933.582	0.697	1105.337	13
	27	968.588	0.755	1187.458	13
	28	1047.115	0.779	1212.151	13
	29	1075.160	0.786	1241.729	15
	30	1080.784	0.839	1269.637	15
Average		583.072	0.434	732.932	7.836

Table 6.

Assessment metrics values of the NSGA-II algorithm.

Problem size	No.	DM	MID	SNS	NPS
Small scale	1	193.721	0.179	294.729	3
	2	201.235	0.189	316.515	3
	3	219.083	0.201	324.372	3
	4	238.059	0.218	335.879	3
	5	248.271	0.222	353.104	4
	6	265.823	0.240	362.473	4
	7	268.583	0.251	363.447	4
	8	274.798	0.262	393.232	4
	9	279.381	0.275	427.873	4
	10	281.318	0.289	448.088	4
Median Scale	11	301.667	0.313	478.610	5
	12	330.820	0.318	517.456	5
	13	348.891	0.331	522.779	5
	14	382.544	0.359	554.507	5
	15	417.119	0.363	573.487	5
	16	446.469	0.391	576.119	6
	17	446.577	0.428	632.250	6
	18	476.016	0.461	647.327	7
	19	505.150	0.475	652.730	7
	20	537.562	0.501	707.166	8
Large Scale	21	542.914	0.506	753.014	8
	22	596.915	0.536	787.730	8
	23	647.765	0.573	802.701	9
	24	668.586	0.578	811.838	10
	25	728.059	0.632	867.753	10
	26	740.416	0.664	897.247	11
	27	787.703	0.664	945.319	12
	28	819.619	0.730	961.630	13
	29	880.428	0.779	1048.001	14
	30	968.347	0.803	1055.756	14
Average		468.128	0.424	613.771	6.877554

It is clear that in Table 5, Table 6, both algorithms have been able to solve the optimal solutions of thirty problems and the process of the presented values can be seen quite logically. In the following, the results related to each metric are analyzed graphically.

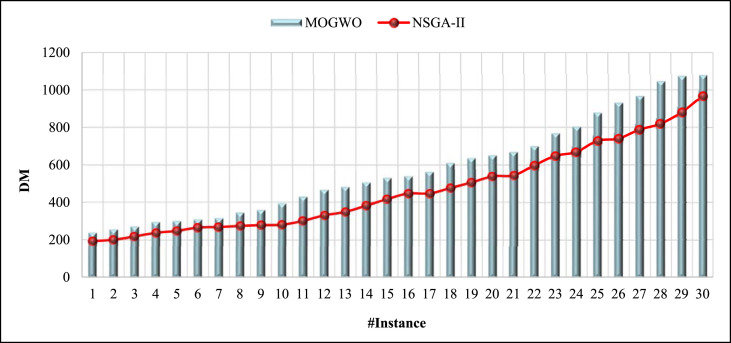
The obtained results of comparing the two algorithms MOGWO and NSGA-II based on the DM metric in Table 5, Table 6, and also Fig. 14 shows that the average value of DM for the MOGWO shows 583.07 and the NSGA-II indicates 468.12. As shown in Fig. 14, in all the solved problems, the MOGWO algorithm has obtained more than the DM metric. Overall, the MOGWO algorithm performed about 25% better than the NSGA-II in terms of DM metric.

Fig. 14.

Comparison of the algorithms based on DM metric.

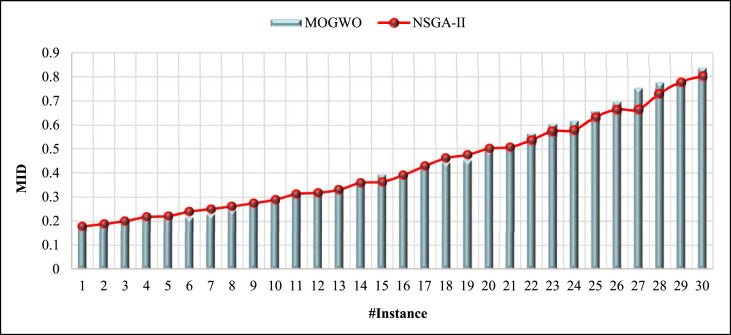
The results of comparing the two algorithms MOGWO and NSGA-II based on the MID metric in Table 5, Table 6 and also Fig. 15 show that the average value of MID for the MOGWO shows 0.434 and the NSGA-II is equal to 0.424. Also, as shown in Fig. 15, the two algorithms have obtained very close values in the MID assessment metric. In total, the MOGWO algorithm performed about 2% more than the NSGA-II in the MID. In terms of the MID, this indicates the very slight superiority of the NSGA-II.

Fig. 15.

Comparison of the algorithms according to the MID metric.

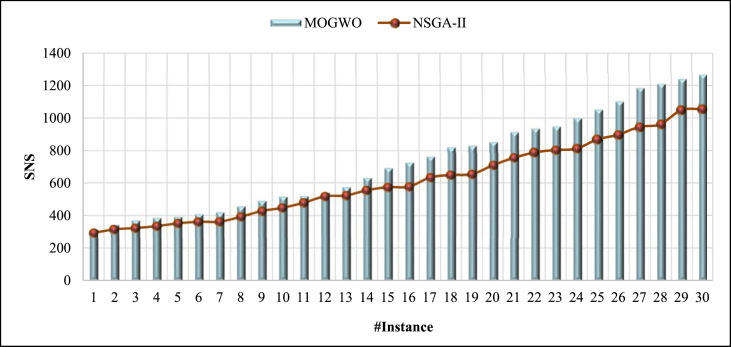
The results of comparing the two algorithms MOGWO and NSGA-II based on the SNS metric in Table 5, Table 6 as well as Fig. 16 show that the average SNS value for the MOGWO indicates 732.93 and the NSGA-II shows equal to 613.77. Also, as illustrated in Fig. 16, in all the solved problems, the MOGWO algorithm has obtained more than the SNS metric. The MOGWO algorithm shows about 19% superiority against the NSGA-II in terms of the SNS metric.

Fig. 16.

Comparison of the algorithms according to the SNS metric.

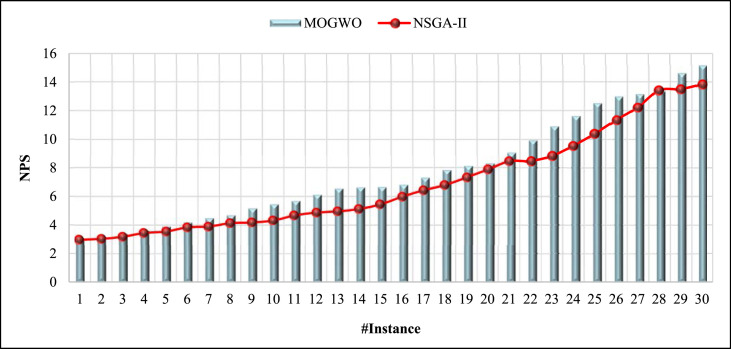
The results of comparing the two algorithms MOGWO and NSGA-II based on the NPS metric in Table 5, Table 6 as well as Fig. 17 show that the average NPS value for the MOGWO displays 7.83 and the NSGA-II represents equal to 6.87. Also, as represented in Fig. 17, in all the solved problems, the MOGWO algorithm has obtained more than the NPS metric. All in all, the MOGWO algorithm performed about 13% better than the NSGA-II in terms of the NPS metric.

Fig. 17.

Comparison of the algorithms according to the NPS metric.

To further assess the indicators, a paired t-test comparison between algorithms was performed. This test is performed separately for each indicator. The confidence level is 95%. Details of the results are provided in Table 7 .

Table 7.

Results of the statistical comparisons based on the assessment metrics.

Metric	Algorithm	Mean	Std. Deviation	Std. Error Mean	95% Confidence Interval of the Difference		$\mathit{t}$	$\mathit{df}$	Sig. (2-taled)
					Lower	Upper
DM	MOGWO – NSGA-II	114.94452	47.11774	8.60248	97.35047	132.53857	13.362	29	0.000
MID	MOGWO – NSGA-II	0.00989	0.02493	0.00455	−0.00058	0.01920	2.172	29	0.058
SNS	MOGWO – NSGA-II	119.16032	70.86008	12.93722	92.70073	145.61991	9.211	29	0.000
NPS	MOGWO – NSGA-II	1.06667	0.78492	0.14331	0.77357	1.35976	7.443	29	0.000

It is clear that in Table 7, the Sig value for the DM, SNS, and NPS assessment metrics is approximately equal to zero. Accordingly, the hypothesis test related to them is meaningful. This meaningful interpretation shows that the difference between the MOGWO and NSGA-II is also statistically proven and therefore the superiority of the MOGWO algorithm in terms of these assessment metrics is confirmed. Regarding the MID metric, the sig value is 0.058, which is more than 0.05, and therefore the significance of the difference among the two algorithms in terms of the MID metric is not confirmed, and it can be said that these two methods have the same average performance.

Overall, it can be argued that the MOGWO meta-heuristic algorithm, with its new and more powerful tools than the NSGA-II algorithm, can provide a better and stronger Pareto front on multi-objective optimization problems.

6. Case study

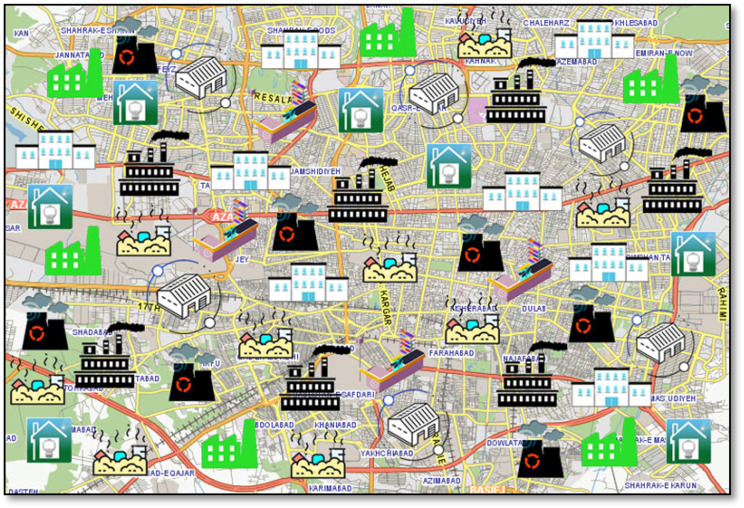
Tehran is the most populous city in Iran and one of the densest cities in Asia. The city, with a population of about 9 million people has faced many problems suffered great human and financial losses in the COVID-19 outbreak. The lack of masks is one of the main problems in this city and the supply chain management of the production, distribution, recycling, and disposal of masks in this city seems necessary. Therefore, in this study, the city of Tehran has been selected as a case study. Fig. 18 shows a case study map. As it is clear that, 6 suppliers, seven manufacturers, 6 DCs, 8 customer centers, 4 collection centers, 7 quarantine centers, 8 recycling centers, and 9 disposal centers are considered.

Fig. 18.

Geographical map of the case study problem.

Table 8 indicates the fixed cost of established quarantine centers and factories in dollars. For example, the fixed cost of an established Evin DC is $250,000. Then, the transportation costs from collection centers to quarantine centers for different types of masks in dollars are reported in Table 9 . For instance, the cost of transportation from Sabalan Collection Center to Shariati Quarantine Center for N95, KN95 masks, and surgical masks is $0.2, $0.4, and $0.3, respectively.

Table 8.

Fixed establishment cost of quarantine centers and factories.

Factories	Ozgol	Sadeqieh	Gholhak	Narmak	Azadi	Piroozi	Kahrizak
Fixed establishment cost ($)	300000	450000	400000	500000	300000	350000	400000
DCs	Evin	Gisha	Hakimieh	Majidieh	Vahidieh	Poonak	–
Fixed establishment cost ($)	250000	200000	300000	200000	350000	300000	–

Table 9.

Unit costs of transportation of masks from collection centers to quarantine center ($).

Collection centers	Mask Type	Quarantine center
		Jamaran	Qeitarieh	Pasdaran	Farjam	Shahran	Gandi	Shariati
Sabalan	N95	0.2	0.1	0.3	0.1	0.2	0.3	0.2
	KN95	0.3	0.2	0.2	0.3	0.4	0.2	0.4
	Surgical	0.4	0.5	0.4	0.2	0.3	0.5	0.3
Beryanak	N95	0.1	0.1	0.3	0.2	0.1	0.2	0.2
	KN95	0.3	0.3	0.1	0.2	0.3	0.3	0.4
	Surgical	0.3	0.3	0.4	0.5	0.3	0.2	0.3
Vanak	N95	0.1	0.2	0.2	0.3	0.3	0.2	0.3
	KN95	0.2	0.3	0.1	0.4	0.4	0.2	0.3
	Surgical	0.5	0.5	0.2	0.2	0.3	0.4	0.3
Vahidieh	N95	0.3	0.1	0.3	0.3	0.2	0.1	0.2
	KN95	0.4	0.3	0.4	0.4	0.2	0.3	0.2
	Surgical	0.2	0.3	0.4	0.3	0.5	0.5	0.4

Therefore, the raw material capacity for suppliers and the demand for different types of masks in the customer centers in kilograms are displayed in Table 10, Table 11 , respectively.

Table 10.

Capacity of suppliers (Kg).

Supplier/Material	Ferdousi	Ahang	Afsarieh	Tajrish	Mirdamad	Pastor
Material 1	600	500	700	500	800	700
Material 2	400	300	500	300	600	500
Material 3	2000	1800	3000	1600	6000	4000
Material 4	6000	5600	8000	5200	9000	8000

Table 11.

Demand distribution for the masks at customer centers (Kg).

Customer center/Mask type	Baharestan	Velenjak	Ekhtiarieh	Tehranpars	Roodaki	Molavi	Khavaran	Valiasr
N95	1100	1000	850	1200	1000	900	1400	1800
KN95	1500	1250	1000	1000	1600	1350	1500	2000
Surgical	500	800	300	750	500	650	450	700

After optimizing this problem with MOGWO algorithms, the Pareto front of each is obtained, which is shown in Fig. 19 . Moreover, the set of Pareto solutions are presented in Table 12 .

Fig. 19.

Pareto fronts obtained by the proposed algorithms.

Table 12.

Set of the Pareto optimal solutions obtained by MOGWO.

No. of the Pareto solution	1st objective function value (Z1)	2nd objective function value (Z2)	3rd objective function value (Z3)
1	158209.271	65.162	2176.587
2	188294.942	59.973	2264.951
3	243093.739	59.673	2465.338
4	720020.565	59.486	2531.964
5	815463.111	59.121	2769.854

It is clear that in Table 12, in Pareto optimal solutions, the values of the second objective function decreased as the first objective function value increased. In other words, the worse the solutions are in terms of the first objective function, the better the second function. The same is true of the second and third objective functions. The better the values of the second objective function, the worse the values of the third objective function. Therefore, none of the solutions is completely superior to the other and all the solutions are non-dominated.

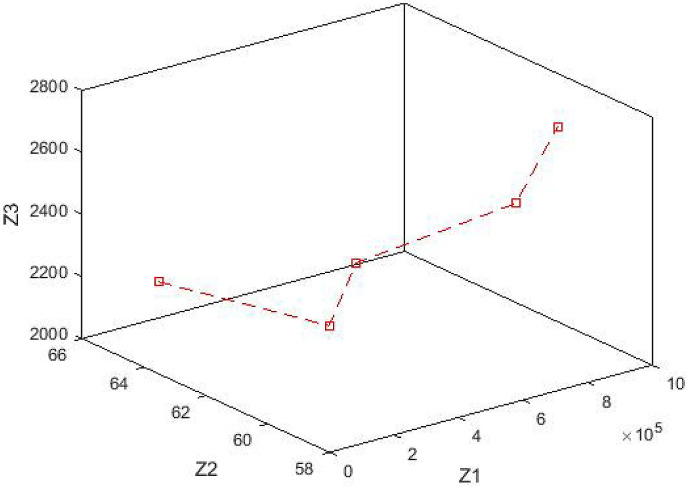
In order to examine the outputs of MOGWO in more detail, a solution from this algorithm is presented graphically in Fig. 20 .

Fig. 20.

One of the Pareto solutions of MOGWO algorithm.

As can be seen in Fig. 20, the obtained result from the MOGWO algorithms based on all the assumptions and conditions of the mathematical model are considered and are therefore sufficiently accurate.

6.1. Sensitivity analysis

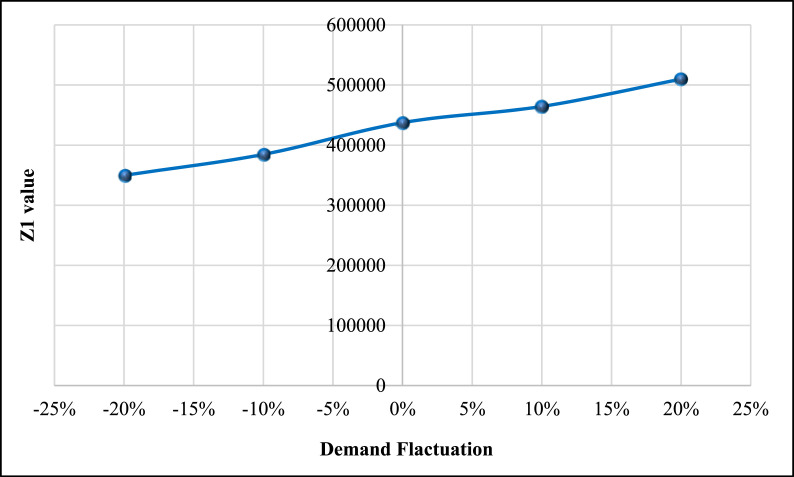
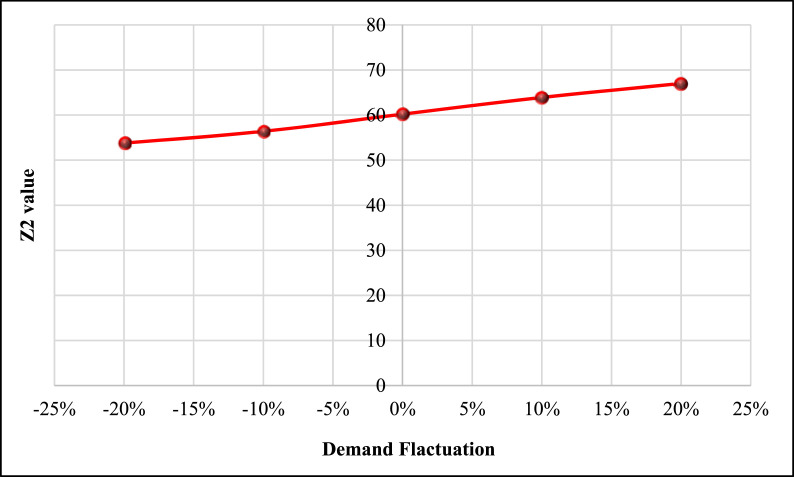
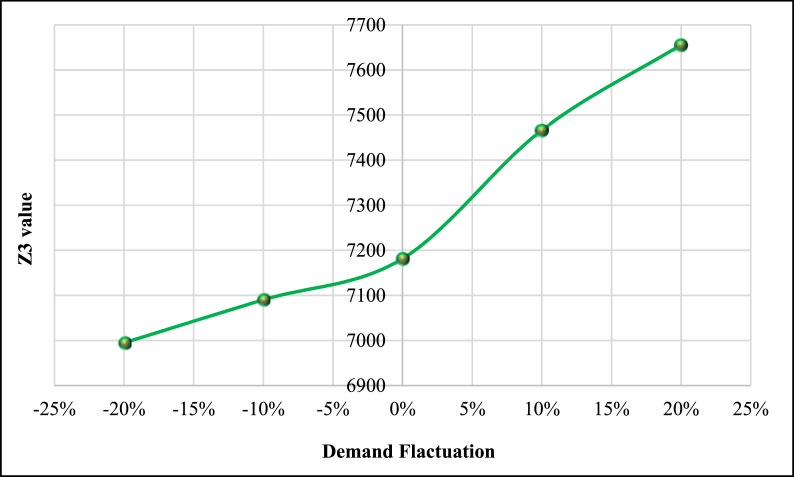
In this sub-section, the effect of one of the most important and significant parameters of the mathematical model on the Pareto front of the problem is investigated. In this regard, the raised problem in the validation section is examined. In the following, the value of the demand parameter fluctuates between −20% and +20%. For example, if the demand for a customer is equal to 10, the demand value between 8 and 12 is checked for that. Then, the values of Pareto solutions are reported. The outcomes are reported in Table 13 .

Table 13.

Output results of the sensitivity analysis of the demand parameter.

Pareto solution No.	−20%			−10%			0%			10%			20%
	Z1	Z2	Z3	Z1	Z2	Z3	Z1	Z2	Z3	Z1	Z2	Z3	Z1	Z2	Z3
1	141181.61	54.03	2177.93	143751.53	58.42	2189.98	152357.25	62.76	2263.97	165225.23	68.31	2272.26	191511.22	71.88	2385.02
2	152850.78	52.09	2218.86	164352.86	57.46	2299.73	185449.42	59.94	2376.62	201319.91	60.89	2489.96	226136.97	64.79	2537.40
3	218551.61	55.67	2408.88	250187.91	57.94	2474.61	258457.06	59.75	2496.13	268493.47	64.23	2519.13	304186.85	65.42	2572.34
4	544740.23	52.28	24793.20	641707.05	54.11	25136.97	729982.63	59.29	26067.24	801932.57	59.62	27056.45	819297.59	62.12	28349.32
5	690063.42	52.85	2661.09	775284.57	56.18	2675.84	861084.37	59.28	2703.93	953516.19	63.96	2711.73	998858.95	66.08	2734.48

In order to better analyze the results, the average values of each of the objectives are reported in Table 14 and the trend of changes of each of the objective functions in Fig. 21, Fig. 22, Fig. 23 is shown.

Table 14.

Average values of each objective function in the sensitivity analysis.

Objective function	−20%	−10%	0%	10%	20%
Z1	349682.98	384536.17	437466.14	464383.91	509848.31
Z2	53.78	56.39	60.21	63.91	67.01
Z3	6994.76	7090.20	7181.58	7466.65	7655.99

Fig. 21.

Trend of variation in the 3rd objective function against the changes of demand.

Fig. 22.

Trend of variation in the 2nd objective function against the changes of demand.

Fig. 23.

Trend of variation in the 3rd objective function against the changes of demand.

Sensitivity analyses indicate that raising the amount of demand causes raising each of the objective functions. In terms of the total cost, this trend is broken linearly, as well as in terms of total environmental pollution. However, in terms of human risk, there is a non-linear trend that with increasing demand, the slope of raising the third objective function value has also increased. Therefore, customer demand is a very important and key parameter that can have drastic changes in any of the objective functions.

7. Discussion, conclusion and outlook

Central governments and municipalities are mainly responsive for defining and enacting public strategies to move towards sustainable development during pandemics, especially in line with healthcare sectors as the frontline organizations to restrain destructive impacts as much as possible. The supply chain design of sanitary equipment such as face mask is one of the most significant issues in this regard. Evaluating the effects of policy actions within such a supply chain is in need of high-quality data, indicators and measures to surveil the chain performance considering the use of raw materials, production and distribution of final products, the management of waste flows, disposal, recycling and circularity practices. Accordingly, this study tried to configure a sustainable CLSCN of face masks during the COVID-19 outbreak using a novel multi-objective MILP for the first time. To this end, a multi-level, multi-period, multi-product network was considered in order to address the locational, supply, production, distribution, collection, quarantine, recycling, reuse, and disposal decisions. The objectives were to simultaneously minimize the total cost, environmental pollution and human risk caused by the establishment of facilities. To tackle the problem efficiently, two meta-heuristic algorithms of MOGWO and NSGA-II were utilized, which were calibrated optimally using the Taguchi design method. Then, four assessment metrics of MID, DM, SNS, and NPS were applied to assess the performance of the suggested algorithms. The outcomes showed that the average of the MID for MOGWO and NSGA-II is 0.4343 and 0.4244, respectively, and also the average of the DM for the MOGWO and NSGA-II was 583.0724 and 468.1279, respectively. Furthermore, the average of the SNS for MOGWO and NSGA-II was 732.9315 and 613.7712, respectively. The MOGWO outperformed the NSGA-II for 25%, 2%, 19%, and 13% in terms of the DM, MID, SNS, and NPS metrics, respectively. Accordingly, the outcomes of the t-test with a 95% confidence interval indicated the superiority of the MOGWO algorithm.

In the next stage, a real case study was investigated in Tehran/Iran using the MOGWO algorithm. The optimal policy was determined and discussed accordingly. Furthermore, the outcomes of the sensitivity analyses demonstrated that as demand increases, the total cost increase with a linear behavior approximately. Similarly, with increasing demand, the amounts of environmental pollution and human risk also increase.

As one of the most important management insights that can be considered in this research is providing several robust solutions for decision-makers in order to facilitate the process of decision-making. In this study, some intelligent methods were utilized to solve the problem that can ultimately provide several optimal solutions. This feature helps supply chain managers to choose and implement the most appropriate solutions based on their preferences which cannot be always considered in such optimization models. Here, to be more specific and according to the sensitivity of human risk and the possibility of human losses due to the establishment of facilities, it is suggested to managers and decision-makers to specify the potential locations of facilities as much as possible in areas with less population. This may increase transportation costs, but it seems necessary according to the priority of human risk. Moreover, air pollution can double the effects of COVID-19, especially in Tehran. Therefore, managers and decision-makers are advised to use hybrid vehicles that have less environmental pollution. Moreover, the optimal location of facilities can greatly reduce environmental pollution. In addition, supply chain costs can be reduced by using recycling operations. Finally, managers are recommended to focus on recycling operations due to high production costs.

The main limitations of the current paper include the following:

• ➢Usually, there is no specific database of transportation costs, so in this study, drivers' assessments were employed to estimate transportation costs,
• ➢The demand amount was just estimated based on the report of the Ministry of Health and based on the report of the medical centers,
• ➢Uncertainty was not addressed in the problem.

Finally, suggestions for future works are as follows:

• ➢Estimating the demand parameter using simulation methods to increase the accuracy,
• ➢Providing other aims such as minimizing the shortage of products and maximizing the reliability of the network to make the model more compatible with sustainable development,
• ➢Employing uncertainty approaches such as fuzzy programming (Das et al., 2020; Tirkolaee et al., 2021) and robust optimization (Özmen et al., 2017; Tirkolaee et al., 2020a), grey systems (Roy et al., 2017; Ju et al., 2019) and stochastic optimal control (Temoçin and Weber, 2014; Gao et al., 2019) to deal with the uncertain nature of the problem,
• ➢Integrating routing and inventory decisions in the proposed mask CLSCN for optimizing the problem more practically (Alinaghian et al., 2021).

CRediT authorship contribution statement

Erfan Babaee Tirkolaee: Conceptualization, Methodology, Supervision, Writing – review & editing. Alireza Goli: Data curation, Software, Validation. Peiman Ghasemi: Visualization, Investigation, Writing – original draft. Fariba Goodarzian: Writing – original draft, Validation.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Handling Editor: Cecilia Maria Villas Bôas de Almeida