Selection of 51 predictors from 13,782 candidate multimodal features using machine learning improves coronary artery disease prediction

Summary

Current cardiovascular risk assessment tools use a small number of predictors. Here, we study how machine learning might: (1) enable principled selection from a large multimodal set of candidate variables and (2) improve prediction of incident coronary artery disease (CAD) events. An elastic net-based Cox model (ML4H_EN-COX) trained and evaluated in 173,274 UK Biobank participants selected 51 predictors from 13,782 candidates. Beyond most traditional risk factors, ML4H_EN-COX selected a polygenic score, waist circumference, socioeconomic deprivation, and several hematologic indices. A more than 30-fold gradient in 10-year risk estimates was noted across ML4H_EN-COX quintiles, ranging from 0.25% to 7.8%. ML4H_EN-COX improved discrimination of incident CAD (C-statistic = 0.796) compared with the Framingham risk score, pooled cohort equations, and QRISK3 (range 0.754–0.761). This approach to variable selection and model assessment is readily generalizable to a broad range of complex datasets and disease endpoints.

Graphical abstract

Highlights

• •Elastic net regression is a useful selection tool with a large candidate variable space
• •This principled approach to predictor selection can improve CAD risk prediction
• •Performance improvement can be maintained in a simple Cox model using the 51 predictors

The bigger picture

Current cardiovascular risk stratification tools are based on a relatively small number of risk factors modeled with Cox proportional hazards models and are known to imperfectly estimate risk. The increasing prevalence of “multimodal” data sources—such as survey data, biomarker concentrations, anthropometric measures, and clinical diagnoses—offers a potential route for improvement, but simple Cox models are not well suited to these complex and often highly correlated inputs.

Here, we develop a framework to select a subset of candidate predictors for a coronary artery disease (CAD) risk prediction tool from a multimodal space of 13,782 features using elastic net regularized Cox regression. Our approach selected 51 of 13,782 candidate predictors, and the resulting model demonstrated improved prediction of incident CAD compared with clinically used algorithms among a held out set of participants.

Current cardiovascular risk stratification tools are based on a relatively small number of risk factors modeled with Cox proportional hazards models and are known to imperfectly estimate risk. Here, we develop a framework to select a subset of candidate predictors for a coronary artery disease (CAD) risk prediction tool from a multimodal space of 13,782 features using machine learning. This approach is readily generalizable to a broad range of large, complex datasets and disease endpoints.

Introduction

Machine learning—a discipline at the interface of statistics and computer science—is useful for identifying patterns in large, complex sets of candidate predictors.^1,2 While machine learning is now ubiquitous in applications such as advertising and finance modeling, its implementation within clinical medicine—particularly risk modeling—has been considerably slower, in part due to (1) the unique importance of model transparency when supporting clinical decisions and (2) the scarcity of large clinical cohorts that are well phenotyped enough to maximize and validate the utility of machine learning-based methods.^1,3 Accelerating the clinical adoption of machine learning will require identifying methods and clinical cohorts that address these caveats and applying them to clinically familiar problems, such as coronary artery disease (CAD) risk prediction.

The current paradigm for prevention of CAD is centered around risk factor modification targeting higher-risk groups as determined by the Framingham risk score (FRS) for CAD or the pooled cohort equations (PCE) and QRISK3 for cardiovascular disease (CVD).4, 5, 6 These risk calculators were developed using Cox proportional hazards models with tens of candidate risk factors, such as age, cholesterol, and smoking status and—while relatively easy to calculate—are known to imperfectly estimate risk.⁷ Prior studies have indicated that cardiovascular risk prediction may be improved by inclusion of additional risk factors across the domains of lifestyle, biomarkers, and genetics in a data-driven manner.8, 9, 10, 11, 12, 13, 14

As the number of candidate predictors of CAD increases from tens to thousands, the traditional approach using standard Cox regression models is prone to several limitations. First, such models do not adequately account for correlation between predictors—as the number of predictors becomes large, the correlation structure becomes increasingly complex and can lead to instability in estimates. Overfitting is also more likely in this setting, a statistical phenomenon in which a model becomes overly confident in the data used to train the model, reducing external validity. Finally, when presented with an excess of unrelated predictors, a simple Cox model may fail to converge entirely. In the setting of thousands of candidate predictors, a method is needed to prioritize a subset for subsequent integration into a risk prediction tool—machine learning methods are well-suited for this task.

The UK Biobank is a powerful cohort for the assessment of new risk prediction approaches enabled by machine learning owing to its combination of (1) genetic and phenotypic detail at the individual level, (2) detailed outcome definitions, and (3) large cohort size. In this study, we examined 13,782 candidate predictors across 173,274 individuals in the UK Biobank to predict risk of incident CAD. We developed the Machine Learning for Health—Elastic Net regularized Cox model (ML4H_EN-COX) and tested the hypothesis that ML4H_EN-COX would (1) be useful for selecting the most important predictors of CAD and (2) would outperform FRS, PCE, and QRISK3 in predicting incident CAD.

Results

Characteristics of the analyzed cohort

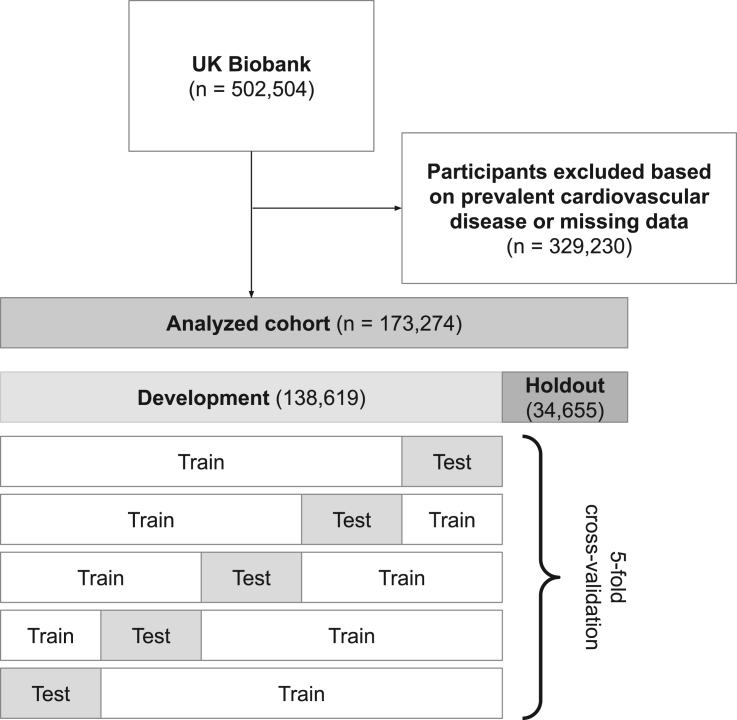
After excluding individuals with prevalent cardiovascular disease or missing data for candidate predictor variables, our study population included 173,274 UK Biobank participants (Tables S1–S4). Mean age was 56 years, 51% were male, and 95% were white. The analyzed cohort was randomly divided into 80% development cohort (n = 138,619) and 20% holdout cohort (n = 34,655) (Figure 1) with similar baseline characteristics (Table 1). Over a median follow-up of 11 years, 4,103 individuals developed incident CAD (3.0%) in the development cohort and 1,037 individuals developed incident CAD (3.0%) in the holdout cohort (Table S5). Individuals in the analyzed cohort were described by 13,782 candidate predictors spanning demographics, lifestyle, medical history, surgical history, family history, physical exam, genetics, and laboratory values (Tables 2 and S6).

Figure 1.

Flow diagram illustrating exclusion criteria and 5-fold cross-validation procedure

Prevalent cardiovascular disease included coronary artery disease, myocardial infarction, stroke, heart failure, and peripheral vascular disease. Five-fold cross-validation was used to select a range of models for subsequent clinician-review (Figure 2).

Table 1.

Baseline characteristics and predicted 10-year risk of cardiovascular events in UK Biobank

	Development (N = 138,619)	Holdout (N = 34,655)
Age (years)	56.2 (8.1)	56.1 (8.1)
Males	70,896 (51.1%)	17,606 (50.9%)
Ethnicity
White	132,610 (95.7%)	33,092 (95.5%)
Black	1,945 (1.4%)	499 (1.4%)
East Asian	1,095 (0.8%)	290 (0.8%)
South Asian	1,614 (1.2%)	402 (1.2%)
Other	1,355 (1.0%)	372 (1.1%)
Current smoker	14,501 (10.5%)	3,604 (10.4%)
Diabetes	6,568 (4.7%)	1,635 (4.7%)
Cholesterol (mg/dL)	217.5 (37.8)	217.4 (37.6)
HDL-C (mg/dL)	55.4 (13.9)	55.3 (13.9)
LDL-C (mg/dL)	136.3 (29.2)	136.2 (29.0)
SBP (mm Hg)	137.5 (18.4)	137.3 (18.3)
Antihypertensive	26,100 (18.8%)	6,501 (18.8%)
Genome-wide polygenic score for CAD(GPSCAD)	−0.03 (0.99)	−0.03 (0.99)
Incident CAD events over median 11-year follow-up	4,103 (3.0%)	1,037 (3.0%)
Predicted 10-year risk (%)
FRS	6.9 (6.4)	6.9 (6.4)
PCE	8.3 (7.7)	8.2 (7.7)
QRISK3-2017 (QRISK3)	10.0 (8.4)	9.9 (8.4)

The development cohort was used for a 5-fold cross-validation procedure to build ML4H_EN-COX, while the holdout cohort was used to test performance in unseen data (Figure 1). GPS_CAD was adjusted for the first four PCs of genetic ancestry and scaled to mean 0 and standard deviation 1. None of the above variables were significantly different between groups at the p < 0.05 level. HDL-C, high-density lipoprotein cholesterol; LDL-C, low-density lipoprotein cholesterol; SBP, systolic blood pressure.

Table 2.

Predictor space stratified by category

Category	Initial predictor space	Selected by ML4HEN-COX
Demographics	12 (0.09%)	3 (5.9%)	age
			sex
			Townsend deprivation index at recruitment
Lifestyle	11 (0.08%)	6 (11.8%)	overall health rating—fair
			smoking status—current
			smoking status—never
			overall health rating—excellent
			weight change compared with 1 year ago—none
			alcohol intake
Medical history	7,917 (57.4%)	5 (9.8%)	hypertension (self-reported)
			lipid-lowering medication
			diabetes
			hypertension (EHR)
			BP-lowering medication
Surgical history	5,740 (41.6%)	0
Family history	32 (0.23%)	2 (3.9%)	illnesses of father—heart disease
			illnesses of siblings—heart disease
Physical exam	7 (0.05%)	3 (5.9%)	systolic blood pressure
			hip circumference
			waist circumference
Genetics	5 (0.04%)	4 (7.8%)	genome-wide polygenic score for CAD (GPSCAD)
			principal component 3 of genetic ancestry (PC3)
			PC2
			PC4
Laboratory values	58 (0.42%)	28 (48.3%)	HDL cholesterol
			glycated hemoglobin
			LDL cholesterol
			testosterone
			apolipoprotein B
			cystatin C
			lipoprotein(a)
			neutrophil count
			apolipoprotein A
			alkaline phosphatase
			C-reactive protein
			monocyte count
			triglycerides
			red blood cell distribution width
			reticulocyte percentage
			alanine aminotransferase
			basophil count
			total protein
			calcium
			total bilirubin
			mean sphered cell volume
			white blood cell count
			mean corpuscular volume
			monocyte percentage
			hemoglobin concentration
			albumin
			urate
			platelet crit
	13,782	51

Predictor variables selected by ML4H_EN-COX are ranked by leave-one-out C-statistic change within each category (Table S4).

Building ML4H_EN-COX in the development cohort

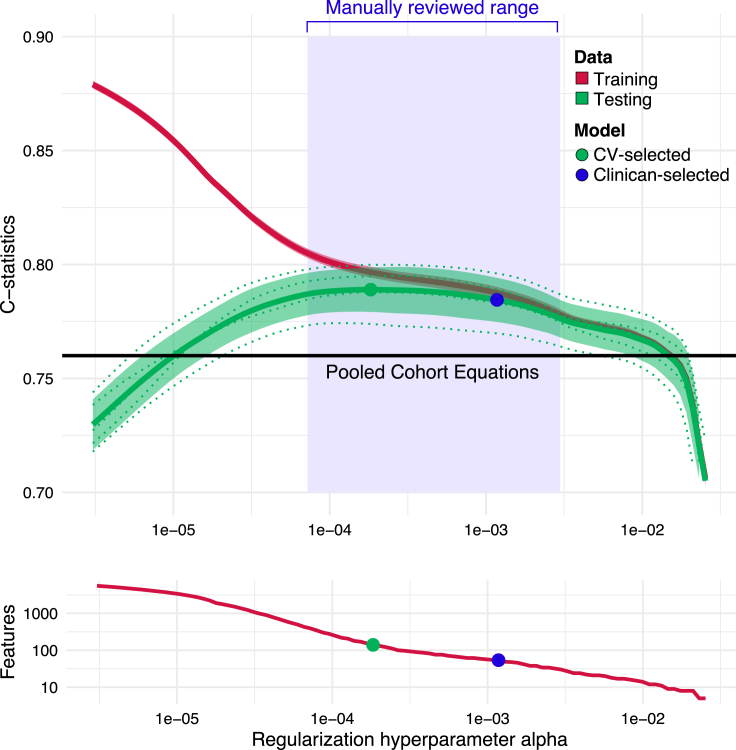
A two-step machine-learning approach with clinician review, ML4H_EN-COX, was implemented to develop a model that selected a subset of 13,782 candidate predictors (Table 2) to predict incident CAD. First, an elastic net regularized Cox proportional hazards model was fit in the development cohort with the goal of optimizing the hyperparameter $\lambda$, which determines how many predictors are selected in the final model. This optimization was done with 5-fold cross-validation (Figure 1). The output of this step was a range of models set by hyperparameter $\lambda$ and described by (1) number of predictors selected with that hyperparameter, (2) performance in the training data, and (3) performance in the testing data (Figure 2).

Figure 2.

C-statistics in training and testing data as a function of the regularization hyperparameter

The right white region represents an area of steep C-statistic growth on both the training and testing data, where adding predictors substantially improves prediction. In the left white region, the testing (green) and training (red) curves are diverging, representing a model that performs well in the training data but generalizes poorly to unseen test data. The blue region is an area of slow C-statistic growth, but continued rapid growth of the feature set. Using a single fold, models within this blue region were reviewed by an expert clinician panel and the model represented by the blue dot, corresponding to 51 features, was selected for further analyses. 95% confidence intervals are shaded around green testing and red training curves. Performance of the pooled cohort equations is drawn as a black line for reference.

A small range of models was identified wherein the performance improved marginally while the number of selected predictors significantly increased (Figure 2). An expert panel of clinicians reviewed the predictor sets in this range and ultimately selected one with 51 predictors resulting in ML4H_EN-COX (Table 2).

ML4H_EN-COX includes 51 predictors for CAD

ML4H_EN-COX included 51 predictors (Table 2) in the final model. Laboratory values made the greatest proportional contribution to the selected predictors (48.3%) followed by a relatively equal distribution across demographics (5.9%), lifestyle (11.8%), medical history (9.8%), family history (3.9%), physical exam (5.9%), and genetics (7.8%) (Table 2).

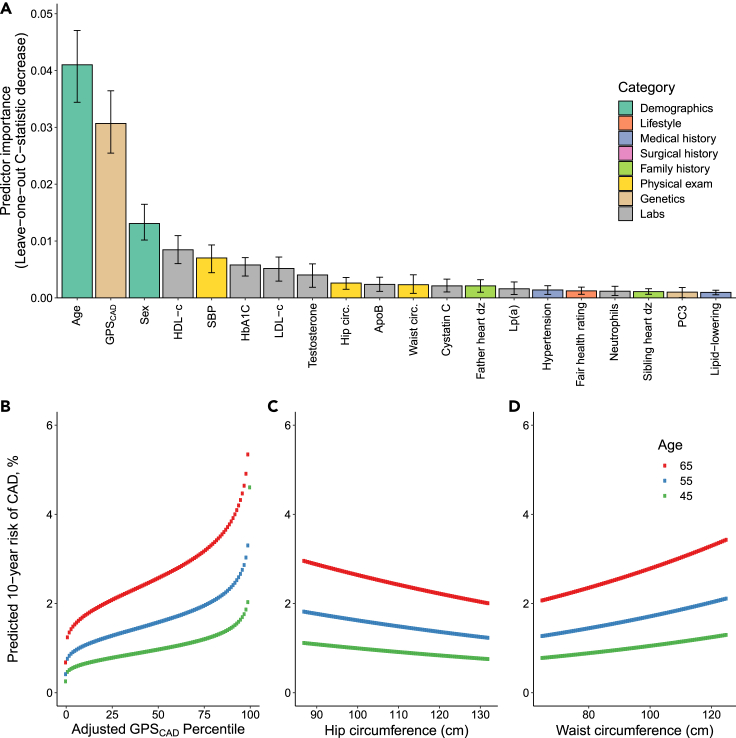
To understand the importance of each predictor in ML4H_EN-COX, we performed a “leave-one-out” analysis, systematically removing each variable and quantifying the decrease in model discrimination as assessed by the C-statistic (Table S7). The top 20 predictors ranked by leave-one-out analysis included several traditional cardiovascular risk factors, such as age, sex, HDL cholesterol, LDL cholesterol, systolic blood pressure, self-reported history of hypertension, and hemoglobin A1C (Figure 3A). In addition, the selection of cystatin C, paternal history of heart disease, and sibling history of heart disease mirrored chronic kidney disease and family history of heart disease considered in QRISK3.⁶

Figure 3.

Top 20 predictors selected by ML4H_EN-COX and predicted 10-year risk of CAD as a function of GPS_CAD, hip circumference, and waist circumference

(A) Predictors are ranked by leave-one-out decrease in C-statistic and colored by category (Table 2).

(B–D) Ten-year risk of CAD predicted by ML4H_EN-COX plotted at ages 45, 55, and 65 years as a function of GPS_CAD, hip circumference, and waist circumference, respectively. GPS_CAD, genome-wide polygenic score for CAD; HDL-c, HDL cholesterol; SBP, systolic blood pressure; HbA1c, hemoglobin A1C; LDL-c, LDL cholesterol; Hip circ., hip circumference; ApoB, apolipoprotein B; Waist circ., waist circumference; Father heart dz, paternal history of heart disease; Lp(A), lipoprotein a; Sibling heart dz, sibling history of heart disease; PC3, genetic principal component 3; Lipid-lowering, history of taking lipid-lowering medication.

Several emerging risk factors of CAD not considered in clinically used algorithms were selected by ML4H_EN-COX. For example, a genome-wide polygenic score for CAD (GPS_CAD) was the second most important predictor overall.¹⁴ The hazard ratio (HR) of this polygenic score (HR = 1.38 per standard deviation [SD] increment, Figure 3B) was comparable with previously reported effect sizes in the UK Biobank.¹⁵ This is consistent with the finding that the Pearson correlation coefficient between GPS_CAD and each of the other 50 predictors in this model never exceeds 0.25 in magnitude (Figure S1), suggesting that GPS_CAD is largely independent of most other proposed risk factors.

ML4H_EN-COX also nominated waist and hip circumference as important predictors of CAD. HRs within ML4H_EN-COX demonstrated an elevated risk of CAD with increasing waist circumference (HR = 1.12 per SD) and decreasing hip circumference (HR = 0.93 per SD), consistent with previous reports (Figures 3C and 3D).¹⁶ Apolipoprotein B, lipoprotein(a), and apolipoprotein A1 are elements of the lipid profile that are not directly considered in FRS, PCE, or QRISK3, but were selected by ML4H_EN-COX and have previously been shown to improve risk stratification in several studies.^17,18

Several hematologic parameters were also prioritized by ML4H_EN-COX, including neutrophil count, monocyte count, white blood cell count, red blood cell distribution width, mean corpuscular volume, and platelet crit. Each of these elements of the complete blood count has previously been associated with incident CVD.¹⁹ Along with the selection of C-reactive protein, these data point to the potential value of the inflammatory milieu in predicting future risk of CAD.

Principal components 3 and 4 of genetic ancestry (PC3, PC4) were selected by ML4H_EN-COX. In the UK Biobank, increasing PC3 and PC4 track with South Asian ethnicity (Figure S2), which is increasingly being identified as a high-risk group for cardiometabolic disease.²⁰ Interestingly, a marker of socioeconomic deprivation, the Townsend index, was also included in the final model. This index is computed based on geographical location and incorporates information about unemployment, household overcrowding, vehicle ownership, and home ownership, with a larger score reflecting greater material deprivation. ML4H_EN-COX assigned HR of 1.02 per SD to this predictor, meaning that increased material deprivation increased risk of incident CAD.

ML4H_EN-COX outperforms FRS, PCE, and QRISK3

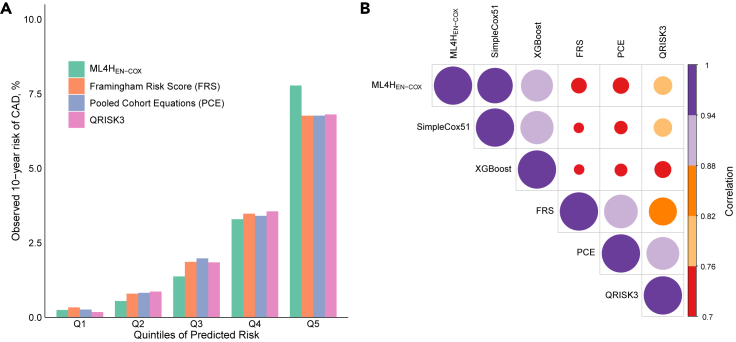
We began by investigating the change in 10-year CAD risk across predicted risk quintiles of ML4H_EN-COX in the holdout cohort. Individuals in the bottom quintile of predicted risk had 17 events (0.25%), those in the middle quintile had 95 events (1.4%), and those in the top quintile had 539 events (7.8%) (Figure 4). The increased risk for the top versus middle quintile was more pronounced for the ML4H_EN-COX model (5.7-fold) compared with FRS (3.6-fold), PCE (3.4-fold), and QRISK3 (3.7-fold). Individuals in the top quintile of predicted risk by ML4H_EN-COX were more likely to be older men with traditional cardiovascular risk factors (Table S8). Next, we investigated the extent to which ML4H_EN-COX was correlated with three clinical algorithms. Correlation coefficients between ML4H_EN-COX and the three clinical algorithms (FRS, 0.75; PCE, 0.76; QRISK3, 0.77) were lower than those for each pair of clinical algorithms (FRS-QRISK3, 0.86; PCE-QRISK3, 0.92; FRS-PCE, 0.93), suggesting that ML4H_EN-COX was contributing different information compared with FRS, PCE, and QRISK3 (Figure 4).

Figure 4.

Comparisons of risk predictions from ML4H_EN-COX, FRS, PCE, and QRISK3

(A) Observed 10-year risk of CAD plotted by quintiles of predicted risk for ML4H_EN-COX, FRS, PCE, and QRISK3—a steeper gradient is observed with ML4H_EN-COX.

(B) Correlation plot between 10-year risks of CAD predicted by ML4H_EN-COX, SimpleCox51, XGBoost, FRS, PCE, and QRISK3.

To benchmark the performance of each model, we calculated C-statistics, a measure of discrimination. The discrimination of a model measures the probability that, for a given incident CAD/no incident CAD pair, the model will correctly predict a higher risk for the individual who developed CAD. In the holdout cohort, ML4H_EN-COX demonstrated better discrimination (C-statistic = 0.796, 95% CI: 0.784–0.809) versus FRS (C-statistic = 0.756, 95% CI: 0.742–0.769), PCE (C-statistic = 0.754, 95% CI: 0.739–0.768), and QRISK3 (C-statistic = 0.761, 95% CI: 0.747–0.774) (Table 3). Discrimination was also assessed in subgroups stratified by sex and age (Table 3). Performance of ML4H_EN-COX was better in women (C-statistic = 0.780, 95% CI: 0.747–0.811) compared with men (C-statistic = 0.751, 95% CI: 0.735–0.767), although the performance gain compared with clinical risk algorithms was greater in men (0.06 improvement in men, 0.02 in women). These data are consistent with previous work showing that traditional cardiovascular risk factors had higher HRs for incident myocardial infarction in women compared with men in the UK Biobank²¹ and suggest that the value of added predictors included in ML4H_EN-COX is greater in men. In accordance with FRS, PCE, and QRISK3, performance of ML4H_EN-COX was better in younger participants (C-statistic = 0.825, 95% CI: 0.799–0.850) compared with older participants (C-statistic 0.755, 95% CI: 0.737–0.771).^6,7 Similar C-statistics were calculated in the development cohort, suggesting that no overfitting occurred (Table S9).

Table 3.

C-statistics for ML4H_EN-COX and comparator models in holdout cohort

Model	Entire holdout (n = 34,655)	Men (n = 17,606)	Women (n = 17,049)	Age < 55 (n = 15,134)	Age ≥ 55 (n = 19,521)
ML4HEN-COX	0.796 (0.784, 0.809) ref	0.751 (0.735, 0.767) ref	0.780 (0.747, 0.811) ref	0.825 (0.799, 0.850) ref	0.755 (0.737, 0.771) ref
FRS	0.756 (0.742, 0.769) p < 0.001	0.690 (0.670, 0.709) p < 0.001	0.758 (0.728, 0.790) p = 0.07	0.766 (0.736, 0.794) p < 0.001	0.712 (0.695, 0.730) p < 0.001
PCE	0.754 (0.739, 0.768) p < 0.001	0.689 (0.671, 0.707) p < 0.001	0.749 (0.719, 0.781) p = 0.01	0.770 (0.740, 0.796) p < 0.001	0.707 (0.688, 0.725) p < 0.001
QRISK3	0.761 (0.747, 0.774) p < 0.001	0.695 (0.676, 0.714) p < 0.001	0.763 (0.734, 0.793) p = 0.13	0.790 (0.763, 0.816) p = 0.001	0.709 (0.691, 0.727) p < 0.001

Bootstrapped 95% confidence intervals indicated in parentheses. p values listed below each C-statistic correspond to DeLong's test comparing each C-statistic with reference (ML4H_EN-COX). C-statistics in the development cohort are displayed in Table S7.

Performance of the ML4H_EN-COX model was further benchmarked by computing categorical net reclassification indices (NRIs). Reclassification indices compare the predicted risk assigned by two models at the individual level. For a given comparator model and cutoff risk, an updated model that moves cases that were predicted to be below the cutoff risk by the comparator model to above the cutoff risk and moves non-cases from above the cutoff risk to below will have a positive categorical NRI. Cutoffs of 2.5% and 5.0% were selected to investigate model behavior around the 10-year CAD event rate in the analyzed cohort and two times this rate, respectively. With a cutoff of 2.5%, categorical NRIs were favorable for ML4H_EN-COX when compared with FRS (6.0%, 95% CI: 3.5%–8.6%), PCE (6.6%, 95% CI: 4.1%–9.1%), and QRISK3 (5.8%, 95% CI: 3.3%–8.3%). Similar trends were observed with a cutoff of 5.0% (Table 4).

Table 4.

Categorical reclassification indices in holdout cohort when ML4H_EN-COX is compared with each of the three clinical risk algorithms

	Comparator model
Categorical NRI cutoff	FRS	PCE	QRISK3
2.5%	6.0% (3.5%–8.6%)	6.6% (4.1%–9.1%)	5.8% (3.3%–8.3%)
5.0%	6.1% (3.1%–9.1%)	8.2% (5.1%–11.2%)	7.5% (4.6%–10.5%)

All reclassification indices were significant at the p < 0.001 level.

Finally, ML4H_EN-COX was well calibrated in the development (calibration slope = 1.09, Hosmer-Lemeshow: p = 0.76) and holdout cohorts (calibration slope = 1.13, Hosmer-Lemeshow: p = 1) (Figure S3).

XGBoost and SimpleCox51 perform comparably with ML4H_EN-COX

We next benchmarked the performance of ML4H_EN-COX against (1) an alternate machine-learning method and (2) a simple Cox proportional hazards model. First, a survival model was developed based on XGBoost, an ensemble-based machine-learning method.^22,23 One advantage of this method compared with the elastic net regularization used in ML4H_EN-COX is that it naturally accounts for nonlinear relationships in the predictor space, although this comes at the cost of increased computational time. Despite the fact that XGBoost selected 115 predictors, including 46 of the 51 selected by ML4H_EN-COX (Table S10), its discriminatory performance in the holdout cohort (C-statistic = 0.797, 95% CI: 0.784–0.810) was almost identical to ML4H_EN-COX (Table S11). With a cutoff risk of 2.5%, categorical NRIs for XGBoost against FRS (5.9%, 95% CI: 3.3%–8.5%), PCE (6.4%, 95% CI: 3.8%–9.0%), and QRISK3 (5.6%, 95% CI: 3.1%–8.2%) were comparable with ML4H_EN-COX (Table S12). These results show that ML4H_EN-COX performed similarly well as a more complex machine-learning method, XGBoost, which included twice as many predictors.

We next investigated whether a simple Cox proportional hazards model containing the 51 predictors selected by ML4H_EN-COX, SimpleCox51, could be used to achieve similar performance. Discriminatory performance of SimpleCox51 was comparable with ML4H_EN-COX in the holdout cohort (C-statistic = 0.797, 95% CI: 0.784–0.811) (Table S11). With a cutoff risk of 2.5%, categorical NRIs for SimpleCox51 against FRS (6.6%, 95% CI: 4.0%–9.2%), PCE (7.1%, 95% CI: 4.6%–9.7%), and QRISK3 (6.3, 95% CI: 3.8%–8.9%) were comparable with ML4H_EN-COX (Table S12). Finally, we investigated the performance of SimpleCox20, a simple Cox proportional hazards containing only the top 20 predictors selected by ML4H_EN-COX (Figure 3A). In the holdout cohort, discriminatory performance (C-statistic = 0.794, 95% CI: 0.781–0.807) and reclassification indices were comparable with ML4H_EN-COX and SimpleCox51 (Tables S11 and S12). These results are consistent with the hypothesis that ML4H_EN-COX is most useful for prioritizing the most important predictors for an outcome, and that simple Cox proportional hazards models with all or a subset of selected predictors can be used for clinical implementation without a significant change in performance.

Discussion

In this study, we applied a machine-learning method, ML4H_EN-COX, to select 51 predictors of CAD from 13,782 in a data-driven manner. As large, deeply phenotyped cohorts become increasingly available, this approach offers a scalable, generalizable route for prioritizing salient predictors of a disease outcome. In this study, a relatively simple model containing only 51 predictors of CAD, ML4H_EN-COX, highlighted traditional cardiovascular risk factors along with emerging risk factors, such as GPS_CAD, waist and hip circumference, a measure of socioeconomic deprivation, and several hematologic parameters. The resulting model outperformed FRS, PCE, and QRISK3 in predicting 10-year risk of incident CAD.

The primary strength of this study is the magnitude of data-driven predictor reduction achieved while starting with a 13,782-dimensional predictor space spread across eight categories and with a mix of continuous and categorical predictors. Among studies with similar goals, the largest starting predictor space prior to this study contained 735 predictors.24, 25, 26, 27, 28, 29, 30 Indeed, because the initial predictor space is relatively small in most previous studies, they often utilize random survival forests to prioritize predictors. A random survival forest model did not converge with our data, reflecting the increased size and complexity of our predictor space. On the other hand, elastic net regression is likely to be robust to datasets even with an order of magnitude fewer candidate features and participants. Finally, both machine-learning methods developed in this study appropriately considered censoring compared with several contributions in this area that do not appropriately consider censoring, which may lead to substantial, systematic risk underestimation.³¹

Several risk factors for CAD not currently considered in clinically used risk algorithms were identified by ML4H_EN-COX. Our finding that GPS_CAD is the second most important predictor in our proposed model suggests that there is utility in integrated risk prediction tools that combine clinically established risk calculators with genetics. Several recent efforts exploring this have shown mixed results, most often demonstrating modest improvements in discrimination and reclassification with the addition of GPS_CAD.32, 33, 34, 35 Our work adds to this literature by demonstrating that GPS_CAD remains a continuous, independent predictor of CAD in an integrated risk calculator containing 50 other CAD risk factors. Waist and hip circumference were also selected as predictors of CAD and are anthropometric proxies for visceral adipose tissue and gluteofemoral adipose tissue, respectively. There is mounting evidence that these measures of fat distribution are causal determinants of cardiometabolic risk profiles.^16,36 ML4H_EN-COX also identified key hematologic indices describing white blood cell count and differential (neutrophil count, monocyte count), red blood cell characteristics (red blood cell distribution width, mean corpuscular volume), and platelet quantity (platelet crit), consistent with a previous survival analysis for CVD.¹⁹ Hence, there may be hidden predictive value for CAD in the complete blood count, even in the healthy patient.

Our model identified increasing PC3 and PC4 of genetic ancestry as risk factors for incident CAD. In the UK Biobank genetic ancestry principal component space, increasing PC3 and PC4 track with individuals of South Asian ethnicity (Figure S2). This ethnic group is increasingly being recognized as carrying an especially high cardiometabolic burden and recent efforts have focused on developing South Asian-specific risk-prediction tools.²⁰ Interestingly, none of the binary variables for ethnicity that were among the candidate predictors, including South Asian ethnicity, were selected by ML4H_EN-COX. This is a departure from how risk differences across ethnic groups have been handled in PCE and QRISK3, which have two and nine discretized ethnicity categories, respectively.^5,6 In addition, ML4H_EN-COX identified increasing material deprivation, measured by the Townsend index, as a risk factor for CAD. Given the mounting concerns surrounding the inclusion of race—a social construct without intrinsic biological meaning—in clinical calculators, our model proposes an alternate solution for capturing sociodemographic differences in risk by considering the PCs of genetic ancestry and socioeconomic indices.³⁷

Some previous studies similarly set out to predict CAD and related outcomes, noting value for inclusion of additional features, such as metabolites or imaging-based assessments of the coronary vasculature. Although such features were not available for our study, additional efforts that include multimodal forms of data input are likely to be of considerable interest.38, 39, 40

The performance increase of ML4H_EN-COX over FRS, PCE, and QRISK3 can be conceptualized as consisting of “predictor gain” and “modeling gain.” Predictor gain refers to added predictive value associated with adding more predictors to a model, while modeling gain refers to added predictive value associated with modeling those predictors in more complex ways, such as considering nonlinear relationships between predictors. Our finding that a simple Cox proportional hazards model, including the 51 predictors selected by ML4H_EN-COX, performs as well as ML4H_EN-COX suggests that the majority of the performance increase is attributable to predictor gain. The pattern of a simple Cox model performing as well as the machine-learning method that selected its predictors has previously been demonstrated in a medical context.²⁴ Our finding that XGBoost, an ensemble method that inherently considers nonlinear interactions, does not outperform ML4H_EN-COX provides further evidence for this conclusion.

A key barrier to the clinical implementation of machine-learning-derived tools for disease prediction is model complexity. While we report most performance metrics in this study in the context of a 51-predictor model, we note that the vast majority of performance improvement over clinically used algorithms could be achieved with a simple Cox proportional hazards model including only the top 20 predictors selected by ML4H_EN-COX. These results suggest a general paradigm for developing new, relatively simple disease prediction models from large, complex cohorts. First, elastic net regularization offers a computationally inexpensive approach for prioritizing a small fraction of predictors from tens of thousands. Our addition of a clinician-review step, a departure from some previous implementations of elastic net regularization, enables further model simplification with a trivial reduction in performance.^25,41 Finally, selected predictors—or even a subset of the most important predictors—can be combined in a simple Cox proportional hazards model. This paradigm may accelerate the incorporation of new insights from deeply phenotyped cohorts into clinical prediction tools.

Our results should be interpreted within the context of several limitations. First, ML4H_EN-COX does not inherently consider nonlinear relationships in the predictor space. This was addressed by verifying that the performance of an ensemble method that does consider nonlinear relationships, XGBoost, does not outperform ML4H_EN-COX. Second, the UK Biobank has a low incidence of CAD compared with the general population and consists predominantly of a white European population.⁴² It could be the case that the predictors identified by ML4H_EN-COX have predictive value specific to cohorts with these attributes. To minimize the risk of this, we used a rigorous cross-validation and holdout procedure and demonstrated that the vast majority of predictors selected by ML4H_EN-COX—particularly those among the top 20 in predictive value—have previously been associated with cardiovascular disease. Nonetheless, external validation of these results would be a crucial next step prior to any proposed clinical implementation. Third, the greater number of predictors included in ML4H_EN-COX compared with FRS, PCE, and QRISK3 inherently makes transportability more challenging. Automated input and calculation at the level of the health system or payer level using data in the electronic health records is possible in principle, but in practice has proven challenging to implement to date. Future work may implement an additional machine-learning step—possibly weighted by the clinical transportability of each feature—to further prioritize the 51 selected predictors in this study.

In conclusion, we proposed a machine-learning model, ML4H_EN-COX, that selected 51 predictors of CAD from 13,782 starting features in the UK Biobank. ML4H_EN-COX outperformed FRS, PCE, and QRISK3 for predicting 10-year risk of CAD on the basis of discrimination and reclassification indices. The methodology outlined here may be useful in developing relatively simple, population-specific risk prediction calculators.

Experimental procedures

Resource availability

Lead contact

Further information and requests for resources should be directed to and will be fulfilled by the lead contact, Amit V. Khera (avkhera@mgh.harvard.edu).

Materials availability

There were no physical materials associated with this study.

Study population and outcome definition

The UK Biobank is an observational study that enrolled over 500,000 individuals between the ages of 40 and 69 years between 2006 and 2010.⁴³ Detailed genetic and health information ascertained from nurse interviews, electronic health records, and blood tests are available for each individual. In this study, we excluded individuals with prevalent cardiovascular disease (defined as CAD, myocardial infarction, stroke, heart failure, or peripheral vascular disease ascertained by ICD-10 codes, ICD-9 codes, OPCS-4 surgical procedure codes, and national death registries) and individuals with missing data in the categories of demographics, lifestyle, family history, physical exam, genetics, and laboratory values (Tables S1–S4).

The 173,274 individuals included in this study were randomly assigned to either a development cohort (80%, n = 138,619) or a holdout cohort (20%, n = 34,655). The authors were blinded to the holdout cohort until model development was completed. For both machine-learning models developed in this study (ML4H_EN-COX and XGBoost), a 5-fold cross-validation procedure was performed in the development cohort to minimize risk of overfitting.

The primary outcome was incident CAD, defined as myocardial infarction, unstable angina, revascularization (PCI/CABG), or death from CAD as determined on the basis of ICD-10 codes, ICD-9 codes, OPCS-4 surgical procedure codes, and national death registries (Table S5).

Recalibrating clinical risk algorithms

The FRS for CAD, PCE for cardiovascular disease, and QRISK3 for cardiovascular disease were computed as described previously.4, 5, 6 QRISK3 was unavailable for 1.4% of the analyzed cohort. Mean 10-year predicted risk of the outcome from each of these calculators (FRS, 6.9%; PCE, 8.3%; QRISK3, 10.0%) was significantly greater than the observed 10-year event rate of CAD (2.6%) in the development cohort (Figures S4–S6). This discrepancy is likely due to a combination of (1) healthy volunteer selection bias in UK Biobank, (2) secular trends in lower rates of CAD in contemporary practice as compared with the data used to train these calculators, particularly FRS and PCE, and (3) the latter two calculators predicting a broader cardiovascular disease outcome (including stroke) rather than just CAD.⁴²

To account for this discrepancy, all three risk calculators were recalibrated to the incidence of CAD in the development cohort using methodology described previously.^44,45 Calibration plots plotted by predicted risk deciles supported successful recalibration for all three clinical algorithms (Figures S4–S6). Recalibrated models were used for all subsequent analyses.

Preparing candidate predictors

We curated 13,782 candidate predictors assessed at time of study enrollment across the domains of demographics, lifestyle, medical history, surgical history, family history, physical exam, genetics, and laboratory values (Table S6). Medical history and surgical history variables included both self-reported history collected during a verbal interview with a trained nurse at time of enrollment and ICD-10 and OPCS-4 surgical procedure codes from the participant’s electronic health record.

Candidate genetic variables included ancestral background as quantified by the first four PCs of genetic ancestry returned to the UK Biobank and a previously validated genome-wide polygenic score for CAD (GPS_CAD).¹⁴ This score has previously been associated with risk of prevalent disease among UK Biobank and other study participants.^15,46 In brief, raw GPS_CAD values were generated by multiplying the genotype dosage for each allele by its respective effect size followed by summing across all variants included in the score. To adjust for differences in variant frequencies according to genetic ancestry—needed to standardize the score distribution—an ancestry-adjusted GPS_CAD was generated by taking the residual of a linear regression model predicting raw GPS_CAD with the first four PCs of genetic ancestry.⁴⁶

Continuous variables were scaled to a mean of 0 and variance of 1. Categorical variables with n categories were split into n binary variables.

Development of machine-learning models for variable selection and prediction

We developed the ML4H_EN-COX using a two-step process.

First, an elastic net regularized Cox proportional hazards model was fit in the development cohort. Elastic net regularization was first developed in the context of linear regression and later extended to Cox survival analysis.^47,48 This approach is conceptually similar to a traditional Cox model, but adds an elastic net penalty term to the regression, which controls the fraction of candidate predictors that remain in the final model (Equation 1)

$$P_{\lambda ,\alpha }\left(\beta \right)=\sum _{j=1}^p\lambda \left(\alpha \left|{\beta }_j\right|+\frac{1}{2}\left(1-\alpha \right){\beta }_j^2\right)\text{,}$$ (Equation 1)

where $\left|{\beta }_j\right|$ corresponds to a lasso penalty (L1) and ${\beta }_j^2$ corresponds to a ridge regression penalty (L2). The hyperparameter $\alpha$ weights the relative contribution of the L1 and L2 terms, while the hyperparameter $\lambda$ controls the overall magnitude of the penalty term. In this study, $\alpha$was set to 0.5, allowing for an equal contribution of the L1 and L2 penalties. The overall magnitude $\lambda$ was optimized through a 5-fold cross-validation procedure (Figure 1). Increasing $\lambda$ corresponds to a more aggressive penalty, leading to fewer predictors selected in the final model (left side of Figure 2). Reciprocally, decreasing $\lambda$ results in more predictors in the final model (right side of Figure 2). The output of this step for each of the five folds was a matrix consisting of $\lambda$, a list of predictors selected at the given $\lambda$, the C-statistic in the training data at the given $\lambda$, and the C-statistic in the test data at the given $\lambda$.

Second, we implemented a clinician review step to investigate the models in a narrow window of $\lambda$ immediately prior to the largest C-statistic in the test data (peak of the test curve in Figure 2). We found that there was a range of $\lambda$ (green region in Figure 2) where the complexity of the model increased substantially (from 40 to 150 predictors) concomitant to a moderate increase in C-statistic (ranging from ∼0.005 to ∼0.01 increase). An expert panel of clinicians reviewed models in this range and ultimately chose the model containing 51 predictor variables as the most reasonable, balancing model performance with interpretability of included variables. The relative importance of the 51 predictors selected by ML4H_EN-COX was investigated by measuring the C-statistic decrease when a given predictor was removed from the model.

To benchmark ML4H_EN-COX against a more sophisticated machine-learning approach, we additionally developed a model using XGBoost, an ensemble machine-learning method that allows for nonlinear interactions between candidate variables.^22,23 Hyperparameter optimization of this model was performed with respect to the Cox partial log likelihood. The best-performing model resulted in 115 predictors (Table S10). Finally, we studied a simple, unregularized Cox proportional hazard model, SimpleCox51, using the 51 predictor variables selected by ML4H_EN-COX and SimpleCox20, using the top 20 predictors selected by ML4H_EN-COX.

Elastic net regression (ML4H_EN-COX) and XGBoost were the selected machine-learning approaches in this study because they had readily available implementations for survival analysis, penalized unimportant candidate variables to zero, and were computationally efficient enough to scale to tens of thousands of features across hundreds of thousands of participants.

ML4H_EN-COX and XGBoost models were developed with the scikit-survival 0.13.1, and xgboost 1.2.0 packages in Python. SimpleCox51 and SimpleCox20 were assessed with the survival package in R.

Statistical methods for benchmarking model performance

Calibration of developed models was assessed in the development and holdout cohorts by examining plots comparing predicted and observed 10-year risk of CAD and the Hosmer-Lemeshow test. To investigate the gradient in risk of CAD across a range of model predictions, the observed 10-year risk of CAD was determined for quintiles of risk predicted by ML4H_EN-COX, FRS, PCE, and QRISK3. The concordance of predicted risk between ML4H_EN-COX and the three clinical algorithms (FRS, PCE, and QRISK3) was investigated by computing the Pearson correlation coefficients between the models’ absolute risk predictions.

The evaluate model discrimination, C-statistics were computed for ML4H_EN-COX, FRS, PCE, QRISK3, XGBoost, SimpleCox51, and SimpleCox20; 95% confidence intervals were constructed with bootstrapping with 1,000 iterations. The DeLong test was used to evaluate statistical significance of differences between C-statistics. Categorical NRI comparing ML4H_EN-COX with FRS, PCE, and QRISK3 were calculated in the holdout cohort with cutoff risks of 2.5% and 5.0%. A cutoff of 2.5% was selected because it was close to the observed 10-year CAD event rate in the analyzed cohort, while 5.0% was selected to investigate model behavior at higher risk. Categorical NRI with identical cutoff risks were additionally computed comparing XGBoost, SimpleCox51, and SimpleCox20 with each of the three clinical algorithms. Statistical analyses were done in R 3.6.0.

Published: October 4, 2021

Data and code availability

The raw UK Biobank data are made available to researchers from universities and other research institutions with genuine research inquiries, following IRB and UK Biobank approval. Representative code used in this work can be found at the following Github repository: https://github.com/broadinstitute/ml4h/tree/master/model_zoo/mi_feature_selection.