Barn Owl's Auditory Space Map Activity Matching Conditions for a Population Vector Readout to Drive Adaptive Sound-Localizing Behavior

Abstract

Space-specific neurons in the owl's midbrain form a neural map of auditory space, which supports sound-orienting behavior. Previous work proposed that a population vector (PV) readout of this map, implementing statistical inference, predicts the owl's sound localization behavior. This model also predicts the frontal localization bias normally observed and how sound-localizing behavior changes when the signal-to-noise ratio varies, based on the spread of activity across the map. However, the actual distribution of population activity and whether this pattern is consistent with premises of the PV readout model on a trial-by-trial basis remains unknown. To answer these questions, we investigated whether the population response profile across the midbrain map in the optic tectum of the barn owl matches these predictions using in vivo multielectrode array recordings. We found that response profiles of recorded subpopulations are sufficient for estimating the stimulus interaural time difference using responses from single trials. Furthermore, this decoder matches the expected differences in trial-by-trial variability and frontal bias between stimulus conditions of low and high signal-to-noise ratio. These results support the hypothesis that a PV readout of the midbrain map can mediate statistical inference in sound-localizing behavior of barn owls.

SIGNIFICANCE STATEMENT While the tuning of single neurons in the owl's midbrain map of auditory space has been considered predictive of the highly specialized sound-localizing behavior of this species, response properties across the population remain largely unknown. For the first time, this study analyzed the spread of population responses across the map using multielectrode recordings and how it changes with signal-to-noise ratio. The observed responses support the hypothesis concerning the ability of a population vector readout to predict biases in orienting behaviors and mediate uncertainty-dependent behavioral commands. The results are of significance for understanding potential mechanisms for the implementation of optimal behavioral commands across species.

Introduction

The barn owl primarily relies on the interaural time difference (ITD) and interaural level difference (ILD) to locate sounds in azimuth and elevation, respectively (Moiseff, 1989). ITD is the delay for a sound to reach one ear before the other; ILD is the disparity in sound level between the two ears. Neurons in the owl's optic tectum (OT), homologous to the mammalian superior colliculus, respond to stimuli with distinct combinations of ITD and ILD and are arranged topographically based on their tuning (Knudsen, 1984; Olsen et al., 1989). Together, these neurons form a map of auditory space that supports sound-orienting behavior (du Lac and Knudsen, 1990; Masino and Knudsen, 1992, 1993; Fig. 1A). However, questions regarding how the neural population in the map is read out on a trial-by-trial basis remain unanswered. Previous work proposed that a population vector (PV) readout predicts the owl's sound-localizing behavior for varying reliability of sensory cues (Fischer and Peña, 2011; Cazettes et al., 2016, 2018). However, a critical open question is whether the response profile of the OT neural population matches the premises of a PV readout, which is required to predict behavioral outcomes.

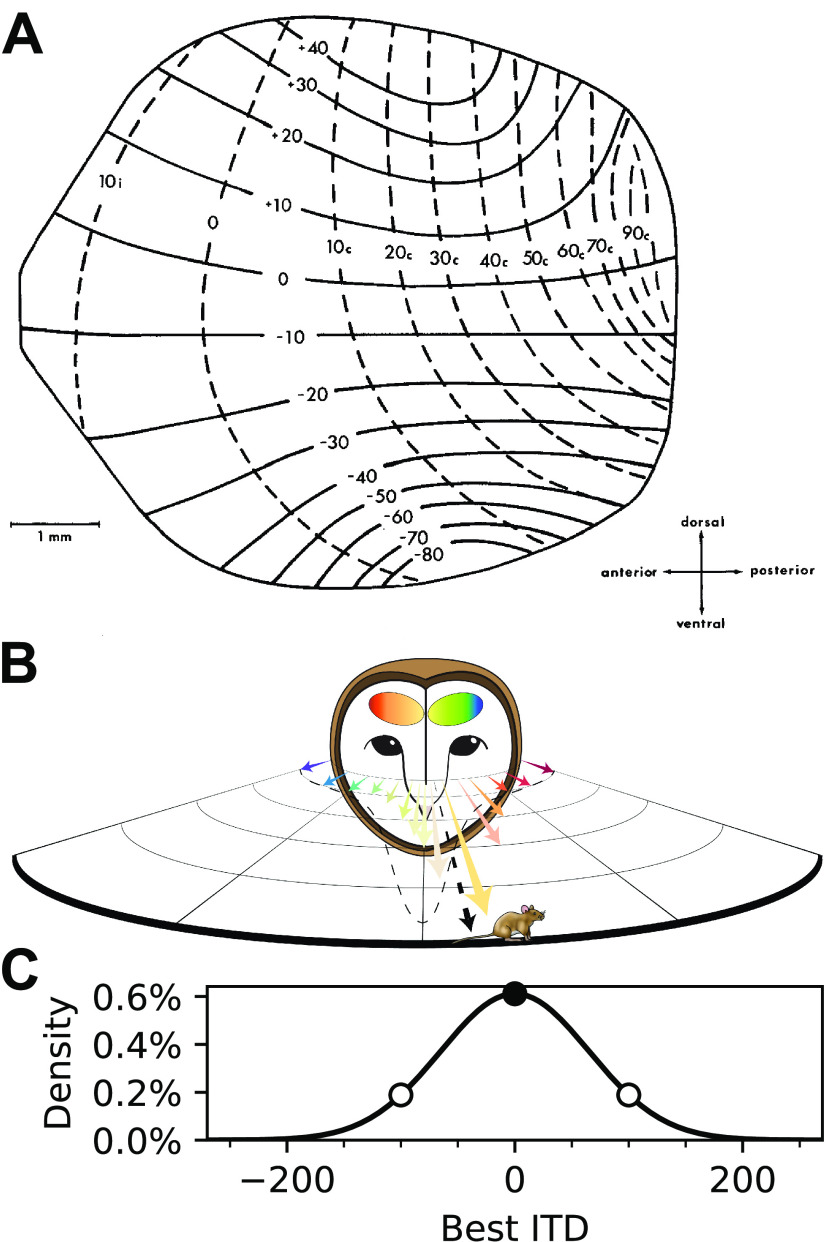
Figure 1.

Population vector readout of the owl's midbrain map of auditory space. A, Map of auditory space in the OT showing an overrepresentation of frontal space. Neural receptive fields are topographically arranged, where azimuthal tuning varies along the anterior–posterior axis (dashed lines) and tuning to elevation along the dorsoventral axis (solid lines), plotted in degrees (Adapted with permission from Knudsen, 1982, their Fig. 12). B, Population vector readout of the owl's midbrain space map. Each neuron in the space map is represented by a vector pointing toward its preferred direction (colored arrows). The overrepresentation of frontal space (dashed line) drives the resultant vector slightly more frontal than the actual location, matching the underestimation of sound sources observed across species. Adapted with permission from Peña et al., 2019 (their Fig. 1). C, Relative proportion of neuronal tuning to physiologically available ITDs. The Gaussian function predicted in Fischer and Peña (2011) was used to characterize the overrepresentation of frontal space, based on data in A. Approximately three times more neurons are tuned to frontal locations (ITDs near 0 µs; filled circle) than peripheral locations (ITDs > 100 µs; open circles).

A place code, implementing a “winner takes all” readout of the owl's OT map, fails to explain frontal biases observed in behavior (Knudsen et al., 1979; Hausmann et al., 2009). In contrast, a PV model can predict these biases (Fischer and Peña, 2011; Cazettes et al., 2016). In this model, the preferred direction of each neuron is described by a vector (Georgopoulos et al., 1986) and a PV is computed by summing preferred direction vectors weighted by the spike counts of the neurons across the entire population (Fig. 1B). Under the assumption that activity spreads across the map, frontal localization biases can be explained through the known overrepresentation of frontal space in the midbrain (Knudsen, 1982; Fischer and Peña, 2011; Fig. 1C). Additionally, the PV model predicts that the spread of population activity across the map broadens with increasing noise, leading to the recruitment of more neurons representing frontal directions. This prediction is consistent with the observed increase in frontal localization bias for binaurally decorrelated stimuli (Saberi et al., 1998). The change in patterns of population responses when noise increases have not been measured, limiting the ability to test predictions for how sensory reliability is represented on a trial-by-trial basis.

In the model proposed by Fischer and Peña (2011), a PV readout approximates Bayesian statistical inference under the premise that the overrepresentation of the front is proportional to a prior for stimulus direction and the population activity pattern is proportional to a likelihood for stimulus direction evaluated at the stimulus ITD. A consistent readout scheme was proposed for visual percepts of orientation in humans (Girshick et al., 2011). While previous work has shown that the nonuniformity of the map, acting as a prior, predicts behavioral bias (Fischer and Peña, 2011) and that single-cell tunings could shape the population response profile (Cazettes et al., 2016), whether activity across the population matches prior and likelihood functions remains unanswered. In this study, we conducted, for the first time, simultaneous recordings of multiple OT neurons across the map with different spatial tunings. We tested whether a decoder based on the PV model can estimate the stimulus ITD from single-trial responses. We found that this decoder could predict the source location from the readout of population responses and that the spread of activity across simultaneously recorded neurons was sufficient for the decoder to display the frontal bias normally observed for sounds in peripheral locations (Knudsen et al., 1979; Hausmann et al., 2009; Cazettes et al., 2018) and its increase in the presence of noise (Saberi et al., 1998). Together, these results provide direct physiological evidence that the activity in the owl's midbrain auditory space map could support a PV readout implementing statistical inference in the owl's sound localization pathway.

Materials and Methods

Experimental design and statistical analysis

The data for this study were collected through multielectrode array recordings in four anesthetized animals (male and female) while presenting acoustic stimuli via calibrated earphones. The use of independently moveable electrodes was found to be the most suitable method to reach the optic tectum (depth, 14–18 mm) while causing the least harm during in vivo recordings of multiple neurons simultaneously. To obtain the most informative results for trial-by-trial analysis, spike sorting was performed to isolate the responses of individual neurons. Alternative methods, such as larger connected arrays or wide-field imaging, were deemed unfeasible at this time. The details of animal handling and surgery, acoustic stimulation, electrophysiological recordings, and the multiple steps of data analysis are explained in the following sections. The statistical significance of the results was tested with nonparametric tests, comparing datasets for two groups/conditions against each other (Mann–Whitney U test) or one dataset against a fixed value (Wilcoxon signed-rank test), as detailed below.

Animal handling and surgery

Data were collected through in vivo recordings in four adult North American barn owls (Tyto furcata) of both sexes (two male, two female). Surgery and anesthesia were performed as described previously (Wang et al., 2012). Briefly, the birds were anesthetized with intramuscular injections of ketamine hydrochloride (Ketaset; 20 mg/kg) and xylazine (AnaSed; 4 mg/kg), followed by prophylactic antibiotics (ampicillin; 20 mg/kg, i.m.) and lactated Ringer's solution (10 ml, s.c.). An adequate level of anesthesia was maintained with supplemental injections of ketamine and xylazine during the experiment every 1–2 h. A metal head plate was implanted before the first electrophysiology recording. The head plate was used to restore the stereotaxic positioning of the head to locate the OT. Recording wells over the OT in each brain hemisphere were constructed out of dental acrylic to allow for repeated recordings.

After each recording session, the recording well was sealed with silicone (Quick-Pro, Warner Tech-Care). An analgesic, carprofen (Rimadyl; 3 mg/kg, i.m.), was administered at the end of each surgery to prevent inflammation and pain. Owls were given a minimum of 14 d between recording sessions. The brain hemisphere recorded was alternated for each owl to provide additional recovery time for brain tissue. All procedures complied with National Institutes of Health guidelines and were approved by the institutional animal care and use committee of the Albert Einstein College of Medicine.

Acoustic stimuli

All experiments were performed in a sound-attenuating chamber (Industrial Acoustic). Stimuli were generated by System II hardware [Tucker-Davis Technologies (TDT)] controlled by a computer running custom-made software. Dichotic stimuli were presented through custom-built earphones consisting of a speaker (model 1914, Knowles) and microphone (model EK-23 024, Knowles). The microphones were used to calibrate earphones once inserted into the ear canal to adjust for irregularities in phase and amplitude from 0.5 to 13 kHz, comprising the owl's hearing range. To create binaurally decorrelated sounds, a different independently generated noise was added to the signal for each ear, with the level of binaural correlation (BC) determined by the relative power between the signal and the noise.

Acoustic stimuli consisted of broadband (0.5–11 kHz) signals with a 5 ms rise–fall time. Tunings for ITD, ILD, and average binaural intensity were assessed using stimuli of 100 ms presented at a 200 ms interstimulus interval (ISI). For binaural correlation data, stimuli were 200 ms long and presented at a 500 ms ISI. This longer stimulus duration was chosen to ensure that enough response spikes could be recorded per stimulus, and the ISI was increased at the same time to avoid the potentially stronger response adaptation induced by these longer stimuli affecting responses in subsequent trials. Trial order was randomized to mitigate neuronal adaptation, which could affect the performance of a decoder.

Electrophysiological recordings

The OT was targeted stereotaxically (Knudsen and Knudsen, 1983). At the beginning of the first recording session, the coordinates of the OT were mapped by recordings with single tungsten electrodes. The multielectrode array (seven channels; Eckhorn Matrix System, Thomas Recording) was positioned within these coordinates. This system consisted of seven parallel electrodes arranged linearly (305 µm spacing) and moved independently. Electrode spacing was sufficient to bar recording the same neuron by multiple electrodes. OT single neurons were distinguished by their unambiguous tuning to ITD and ILD, bursty firing, and response to light stimulation (Knudsen, 1984). The array was aligned parallel to the midsagittal plane to cover regions of the map representing different azimuth positions. To ensure that results from each subset of neurons depend on the ensemble of different best ITDs rather than being distorted by systemic errors arising from differential ILD tunings, neurons were chosen such that all neurons in a subset responded strongly to a common ILD, which was used for all subsequent stimulation.

Recorded signals were amplified by a built-in preamplifier in the Eckhorn Matrix, digitized by an OmniPlex Amplifier (Plexon), and stored. Along with the continuous data and spike times, the Plexon files contained timestamps for TTL (transistor–transistor logic) pulses sent from the TDT system, marking the onset of acoustic stimuli.

Data analysis

Spike sorting.

Following the recordings, offline spike-sorting software (Offline Sorter) based on principal component analysis was used to isolate neuronal spikes for each electrode. Spike sorting was performed blinded to auditory properties of the isolated units. Isolated units that did not show a tuning to binaural cues after spike sorting were not included in the analysis.

Response rates and normalization.

Response rates were extracted from spike counts observed during the presentation period of acoustic stimuli. Consistent with the assumption of the previously proposed PV model (Fischer and Peña, 2011) and reported experimental evidence (Cazettes et al., 2016), the maximum firing rates of OT neurons showed a uniform distribution across the map. During recording sessions, which each lasted several hours, the responsiveness of some neurons fluctuated, possibly because of cycles of anesthetic clearance and re-administration, but there was no qualitative change in the tuning to binaural stimuli. Based on these premises, firing rates of each neuron were scaled by a factor minimizing the root mean square error (rmse) between mean responses from an ITD tuning curve collected at the start and scaled mean responses to the same ITDs collected later in the same recording session. These scaling factors were computed from responses to stimuli at 100% BC for each neuron and were applied across stimulus BCs. Responses were then normalized to the maximal firing rate of each neuron, observed in ITD tuning curves obtained at corresponding BCs.

Spread of activity.

For the proposed PV readout to predict the owl's behavior, activity must spread across the map, such that neurons display nonzero responses to nonpreferred stimuli. The predicted spread of activity is derived from the relationship between the PV and a Bayesian model that has been shown to match the owl's sound location behavior (Fischer and Peña, 2011). Fischer and Peña (2011) mathematically proved an equivalence between a Bayesian estimate and a PV estimate of sound direction under the following conditions: (1) the distribution of preferred directions in the population is equal to the prior distribution for stimulus direction; and (2) the population activity pattern, on a given trial, is proportional to the likelihood function for stimulus directions. It has been established that the distribution of preferred directions in OT is consistent with a Gaussian prior for stimulus direction (Fischer and Peña, 2011). However, testing the model also requires confirming that the population activity pattern, on average and, more importantly, on a given trial, is proportional to the likelihood function for stimulus direction.

The predicted spread of activity can be described as follows across neurons in the map by a Gaussian curve centered at the stimulus ITD:

$$\text{response}\left(IT{D}_{\text{unit}},IT{D}_{\text{stimulus}}\right)\propto e^{-0.5{\left(\frac{IT{D}_{\text{unit}}-IT{D}_{\text{stimulus}}}{219.34e^{-0.1131\times BC}+41.2\mu s}\right)}^2},$$

where ITD_unit is the best ITD of the neuron, ITD_stimulus is the ITD of the presented stimulus, and BC is the binaural correlation on a scale from 0 to 100. This formula is the function used by Fischer and Peña (2011) to describe the likelihood in a Bayesian framework modeling the owl's sound localization behavior. We tested the sufficiency of the spread of activity by fitting the Gaussian function to data from population recordings. Normalized responses of all recorded neurons (n = 222) across 500 presentations of stimuli with the same ITD were pooled. These responses were aligned based on their respective stimulus ITDs, yielding a population-wide response profile comparable to the assumed spread of activity used in the PV readout model. To fit this function to the response profile, the SD of the Gaussian curve was allowed to vary to minimize the rmse between the curve and the response profile. These fitted SD values for each BC were then used to rerun the original model and in a decoder, both of which are described below.

PV model simulation.

We tested the population vector model of Fischer and Peña (2011) using the measured values for the spread of activity over the OT population from the array recordings. As in the study by Fischer and Peña (2011), the model consisted of 500 neurons with a Gaussian distribution of preferred directions with a mean of 0° and an SD of 23.3°. On each stimulation trial, one of four sound source directions θ (±55° or ±75°) and one of three binaural correlations (20, 40, or 100%) were applied. We modeled the ITD in the sounds at the two ears as a sinusoidal function of source direction corrupted by Gaussian noise, as follows:

$$\text{ITD}=A\sin (\omega \theta )+\eta ,$$

where A = 260 μs is the maximum ITD, ω = 0.0143 radians/° is the angular frequency that determines the direction where ITD reaches the maximum, and $\eta$ is drawn from a zero-mean Gaussian distribution with SD ${\sigma }_{\eta }$. Fischer and Peña (2011) modeled the SD ${\sigma }_{\eta }$ to vary with binaural correlation as follows:

$${\sigma }_{\eta }(\text{BC})=219.34e^{-0.1131\times BC}+41.2\mu s.$$

Here, we tested the model using SD ${\sigma }_{\eta }$ values derived from the measured spread of activity over the OT population using array recordings (100% BC, ${\sigma }_{\eta }=34.0\mu s$; 40% BC, ${\sigma }_{\eta }=53.2\mu s$; 20% BC, ${\sigma }_{\eta }=65.0\mu s$).

The mean population response on a given stimulus trial was assumed to be proportional to the likelihood function of the stimulus direction (Fischer and Peña, 2011). Correspondingly, the response of the nth neuron to the observed ITD, $r_n\left(\text{ITD}\right)$, was drawn from a Poisson distribution with mean $a_n\left(\text{ITD}\right),$ as follows:

$$a_n\left(\text{ITD}\right)=10e^{-0.5{\left(\frac{\text{ITD}-{\mu }_n}{{\sigma }_{\eta }}\right)}^2},$$

where ${\mu }_n=A\sin (\omega {\theta }_n)$ is the preferred ITD corresponding to the preferred direction ${\theta }_n$.

The PV was computed as a linear combination of the preferred direction vectors of the neurons, weighted by the neural responses, as follows:

$$\text{PV}\left(\text{ITD}\right)=\frac{1}{N}{\displaystyle \sum }_{n=1}^N{r}_n\left(\text{ITD}\right)u({\theta }_n),$$

where $u({\theta }_n)$ is a unit vector pointing in the preferred direction of the nth neuron, and $r_n\left(\text{ITD}\right)$ is the response of the nth neuron, drawn from a Poisson with mean $a_n\left(\text{ITD}\right)$. The direction estimate was obtained by computing the angle of the PV.

Decoder.

To test whether the spread of activity in responses of subsets of simultaneously recorded neurons matched model expectations, we built a decoder based on a model for a PV readout implementing Bayesian inference reported previously (Fischer and Peña, 2011). The decoder uses the spread of activity to estimate the stimulus ITD from the responses of a subset of simultaneously recorded neurons. The evaluation of the performance of this decoder was conducted both for average and single-trial recorded responses.

For a given stimulus, the Gaussian function describing the spread of activity was centered at the stimulus ITD with an amplitude of 1 and an SD estimated from normalized responses across neurons in the map for stimulus ITD (see section Spread of activity). The curve was then shifted in ITD, fitting the ITD_stimulus parameter by minimizing the rmse between the function and the normalized mean responses of the neural subset. The ITD at the maximum of the fitted Gaussian function served as the ITD estimate of the decoder.

This ITD estimate was also used to predict a PV readout estimate from trial-by-trial responses of subsets of simultaneously recorded neurons across the map. Limited by technical constraints, preferred ITDs of simultaneously recorded subsets of neurons did not span across the entire ethological range available to the owl and could not reflect the overrepresentation of frontal space. However, given the proved equivalence between a Bayesian estimate and the PV estimate (Fischer and Peña, 2011), we used the fitted Gaussian as a likelihood function in a Bayesian model that would produce sound location estimates consistent with a PV from a full population of neurons that match the same Gaussian function. The position of the fitted Gaussian function's maximum served as the maximum likelihood ITD estimate. With the Gaussian form for the likelihood and prior, the Bayesian estimate from the posterior distribution is a weighted linear combination of the maximum likelihood estimate and the mean of the prior. Given that the mean of the prior describing the frontal bias is zero (Fischer and Peña, 2011), the Bayesian estimate is a scaling of the maximum likelihood estimate determined by the variance of the prior, Var(prior) = (23.3° × 2.8 µs/°)² (values from Fischer and Peña, 2011), and the variance of the maximum likelihood estimate, Var(ML) = σ² (SD σ determined by fitting a Gaussian function to the population data; see section Spread of activity). The estimate of the posterior mean, and thus the approximate PV readout, ITD_readout, was obtained from the ITD estimate (ITD_estimate):

$${\text{ITD}}_{\text{readout}}={\text{ITD}}_{\text{estimate}}\frac{\text{Var(prior)}}{\text{Var}\left(\text{prior}\right)+\text{Var}(\text{ML})}.$$

The performance of this decoder was quantified by the estimation error, calculated for every subset of neurons by the median across trials of the differences between ITD estimates and stimulus ITD. A Mann–Whitney U test was used to compare estimates for ITDs within and outside of the ITD range preferred by the neural subset. A Wilcoxon signed-rank test was used to test whether the estimation errors deviated from 0 µs (no error). Additionally, across-trial variability of estimated stimulus ITD was assessed by the interquartile range (IQR) of ITD estimates across trials, which is the difference between the 25th and 75th percentiles. A Mann–Whitney U test was used to compare the IQRs of estimates within or outside of the subset's preferred ITD range. For each subset of neurons and each stimulus ITD, responses to 500 trials were recorded and 330–500 trials were analyzed. We excluded trials where the average response across all neurons was <15% of their respective maximal firing rate, based on the assumption that such low overall activity would not lead to a behaviorally relevant readout and the observation that the fitting procedure yielded largely ambiguous results under these conditions.

Data availability

Custom Python code used for data analysis is available at https://github.com/penalab/Ferger-Shadron-et-al-2021 or available on request.

Results

Subsets (N = 36) of multiple simultaneously recorded OT single neurons (n = 5–7/subset; 222 total neurons) were collected from four barn owls (two males and two females). Each subset underwent a stimulation protocol aimed to characterize population responses to varying ITDs at different levels of signal-to-noise ratio implemented by manipulating the BC of acoustic signals (see Materials and Methods).

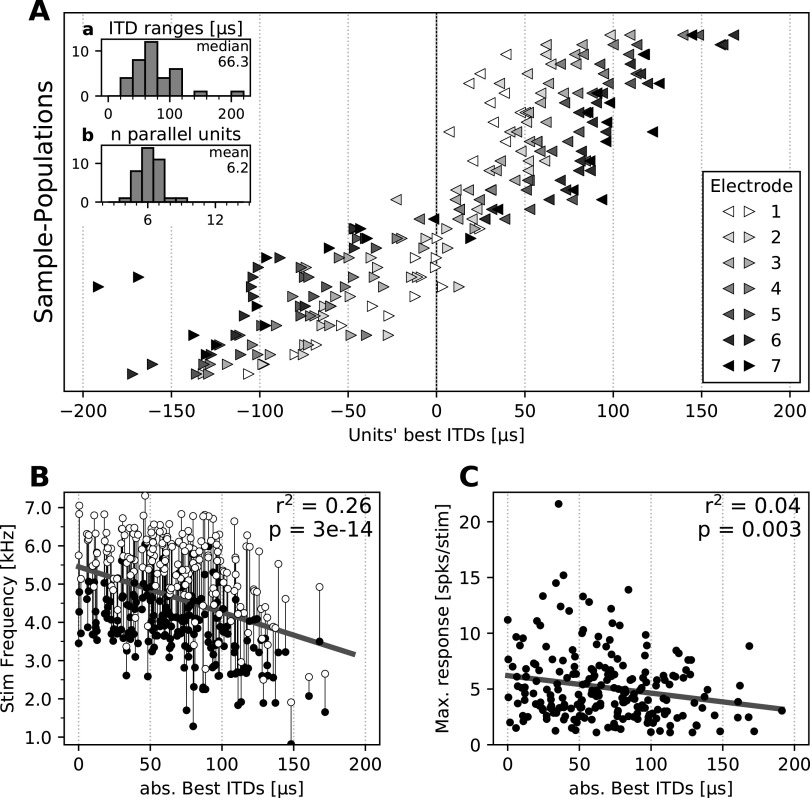
Recordings confirmed the expected topography of ITD tuning across OT (Knudsen, 1982; Fig. 1A). Along the anterior–posterior axis, preferred ITDs ranged from frontal (small ITDs) to lateral (large ITDs; Fig. 2A). Results were also consistent with the previously reported relationship between ITD and frequency tuning, where frontal neurons are tuned to higher frequencies (Knudsen, 1984; Cazettes et al., 2014; Fig. 2B), and there was no significant correlation between maximum firing rate and preferred ITD (Cazettes et al., 2016; Fig. 2C).

Figure 2.

Population tuning properties. A, Best ITDs of neurons in the dataset. Subsets of neurons recorded simultaneously are plotted as one row. Left and right pointing triangles show recordings from the left and right hemisphere, respectively. Gray scales indicate on which electrode in the array neurons were found, with the electrode 1 (white) located most anterior and the electrode 7 (black) located most posterior. Neurons recorded from the same electrode are plotted individually, with the same color. Inset a, Histogram of best ITD ranges for each subset of neurons. Inset b, Histogram of the number of neurons for each subset. B, Stimulus frequency range eliciting responses of all neurons as function of their absolute best ITD. Connected white and black circles indicate the top and bottom frequency bounds for which the unit responded at 50% of its maximum response, respectively. Solid line represents linear regression (linear fit properties shown on top right). C, Maximum firing rates of all neurons as a function of their absolute best ITD, computed as the maximal firing rates of each unit in ITD tuning curves (−240 to 240 µs, 20 µs steps), averaged over 10–20 repetitions. Solid line represents linear regression (linear fit properties shown on top right).

The PV model requires a spread of activity across the map where neurons show nonzero responses to nonpreferred ITDs, sufficient for the PV readout to predict a frontal bias that varies as a function of stimulus location and signal-to-noise level. The pattern of population responses across the map, the ability to decode stimulus ITD, and changes induced by signal-to-noise ratio are described below.

Spread of activity across the map

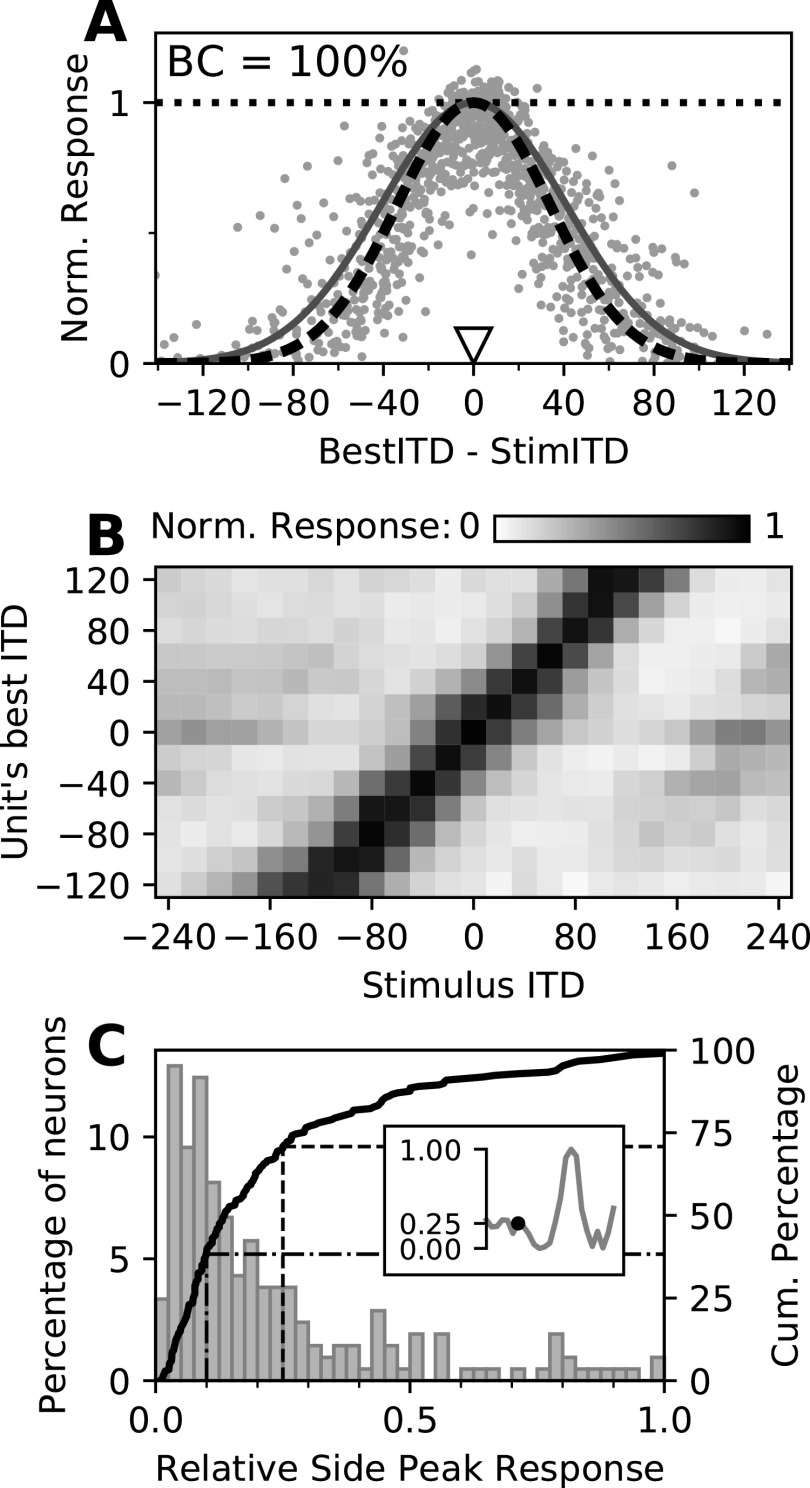
Population responses showed widespread activity across the map (Fig. 3A). A Gaussian function with an SD of 41.2 µs was used in a previous theoretical study (Fischer and Peña, 2011) to predict the spread of activity and a population response profile that would allow a PV decoder to match the owl's localization behavior. The population responses measured using multielectrode arrays were well correlated to this predicted pattern (r² = 0.61; Fig. 3A, dark gray curve). Fitting the SD of the Gaussian function to the response data of 222 recorded neurons showed a spreading width slightly smaller (SD = 34.0 µs, r² = 0.671; Fig. 3A, dashed black curve) than the predicted value but nevertheless following the shape required for a PV readout to match the owl's localization behavior.

Figure 3.

Spread of activity across the map. A, Normalized neural responses as a function of the best ITD of each unit relative to the stimulus ITD. Each dot represents the normalized response of one neuron across 500 repetitions of a particular stimulus. Note that each neuron appears multiple times, paired with stimuli of different ITDs. Responses were normalized by the maximum firing rate of each neuron in an ITD tuning curve, denoted by the dotted horizontal line. Solid dark gray curve, The spread of activity presumed in the population vector readout model (Fischer and Peña, 2011); dashed black curve, the same function with the best fitting SD, used in the PV model based decoder. B, Neural responses across the map as a function of the stimulus ITD (x-axis) and their best ITD (y-axis). Neurons were pooled according to their preferred ITD (8–26 units/row). Gray scales indicate the normalized response (color bar), averaged across pooled neurons. C, Relative side peak responses of OT neurons. Response of the highest side peak relative to the maximal response as histogram (left y-axis) and cumulative distribution (solid curve; right y-axis). The inset exemplifies the method. The dashed and dash-dotted lines indicate the proportion of relative side peak responses <25% and <10%, respectively.

Neurons across the map, with each one having a preferred ITD, still responded weakly to sounds away from their preferred ITDs (Fig. 3B). Peaks in the responses of midbrain space-specific neurons to ITDs away from their preferred ITDs are called side peak responses. The position and height of these side peaks relative to the main peak depend on the frequency range that a neuron responds to and on the frequencies contained in a stimulus. For the broadband stimuli used in this study, in 71% of the analyzed neurons, responses at the highest side peak were lower than one-fourth of the response at the best ITD (Fig. 3C, dashed line); in 38% of the neurons, these side peak responses were lower than one-tenth of the peak response (Fig. 3C, dash-dotted line). Additionally, this midbrain map population contains neurons with a range of best frequencies (Knudsen, 1984; Cazettes et al., 2014), and thus side peak positions across neurons are nonoverlapping. Therefore, side peak responses can be considered as being less important for shaping the population readout when broadband stimuli are presented. Thus, we used a single-peaked Gaussian to fit the response profile, as proposed in the PV readout model. Yet, we observed weak population responses that were mostly independent of stimulus ITD. In particular, neurons tuned to frontal ITDs showed sparse responses to stimuli away from the midline (Fig. 3B). This spread of responses, in conjunction with the known overrepresentation of frontal space, was suitable to drastically bias a PV readout toward the front, consistent with the prediction of the model.

Decoding stimulus ITD from population responses

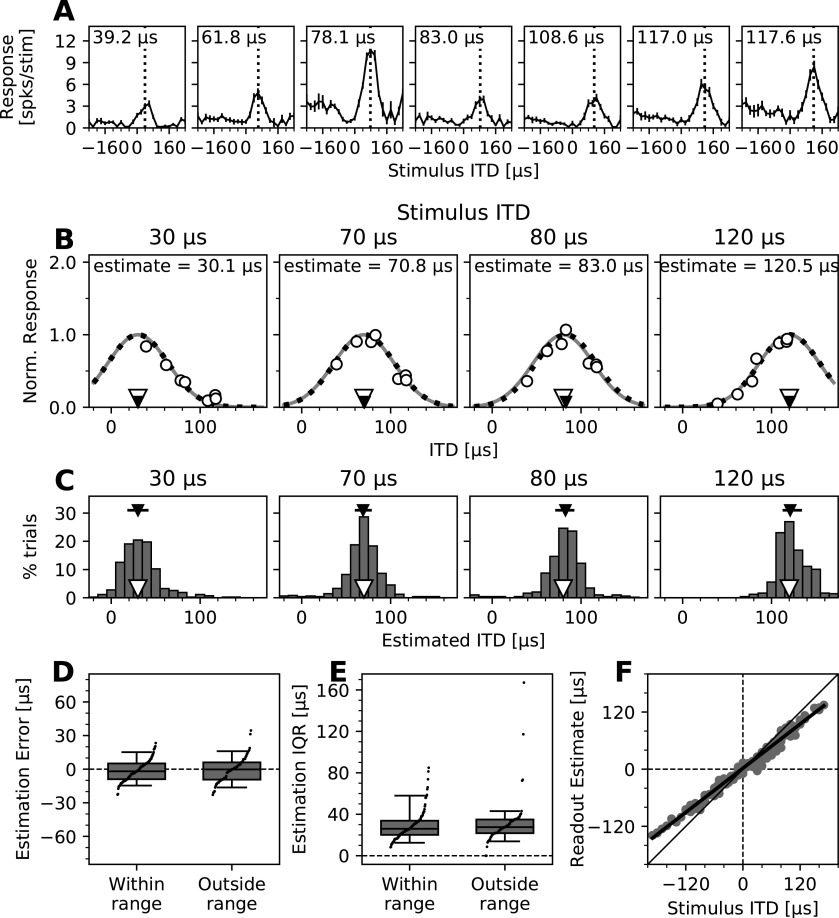
Subsets of five to seven OT neurons tuned to different ITDs were recorded simultaneously (Fig. 4A). The same Gaussian curve, representing the predicted response profile suitable for a PV readout model (Fischer and Peña, 2011) was fitted to the mean normalized responses across 500 trials of subsets of recorded neurons (for details, see Materials and Methods), and the position of the maximum of the fitted curve was used to estimate the stimulus ITD (Fig. 4B). These estimates deviated little from the stimulus ITD, with 50% of the absolute estimation errors <7.5 µs and 90% <18.2 µs. The distribution of estimates was nonsignificantly shifted toward frontal ITDs, with a median across all estimates of −1.05 µs, where negative values indicate an estimation error toward the front (p = 0.244, Wilcoxon signed-rank test). Adding to the above analysis of the spread of activity, this is further evidence that averaged population responses match the response profile required for a PV readout (Fig. 4B).

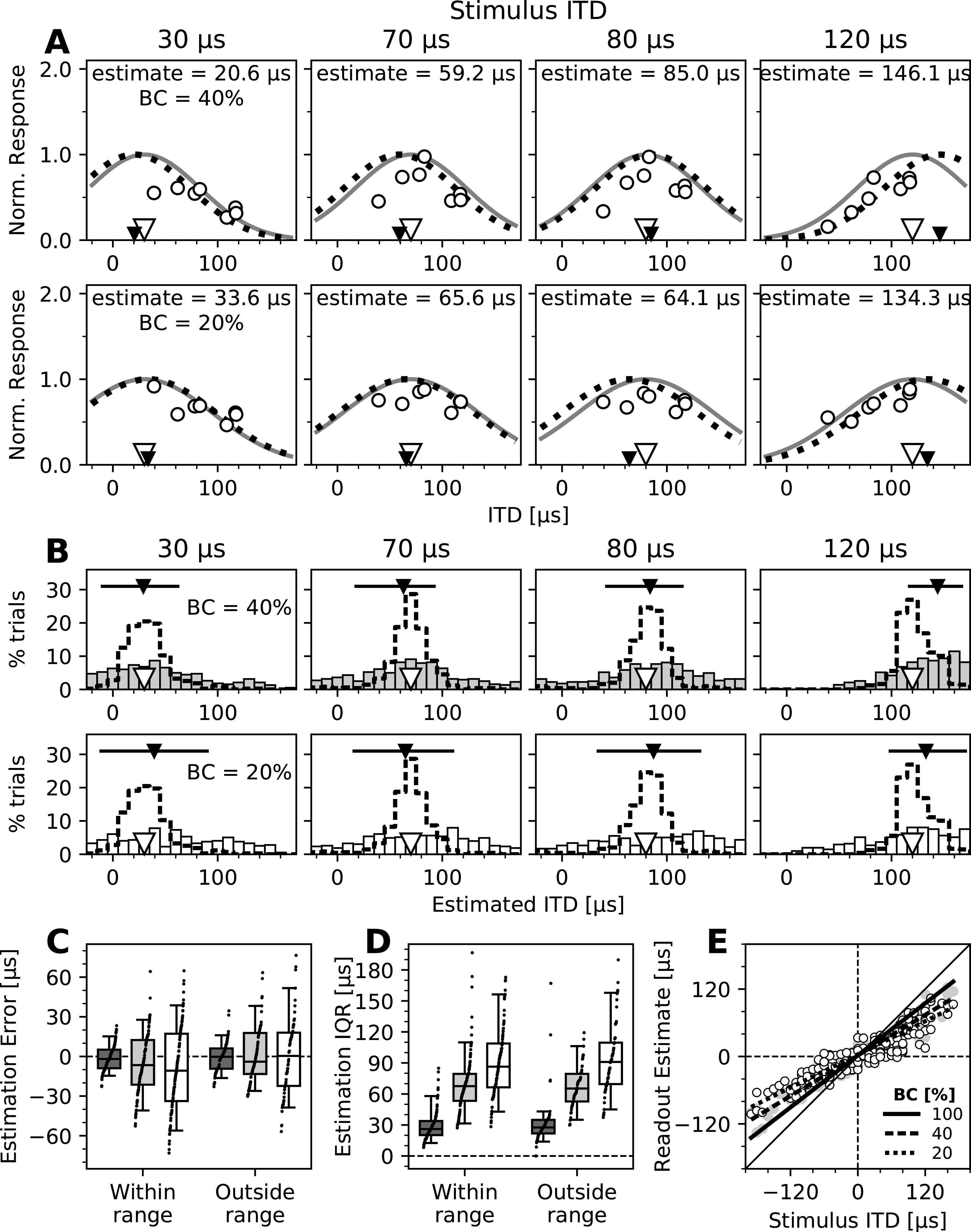
Figure 4.

Performance of the PV decoder based on simultaneous population recordings in the OT space map. A, ITD tuning curves of an example subset of neurons recorded simultaneously (left hemisphere). The best ITD of each neuron is indicated in the top left corner and by a vertical dotted line. Positive ITDs indicate that the stimulus to the right (contralateral) ear is leading. Error bars show the SEM. B, ITD decoding from response profiles of subsets of neurons. Normalized mean responses (open circles) of the neurons shown in A to stimuli of four different ITDs (indicated by open triangles; values shown above each plot) as a function of their best ITD. A Gaussian curve, representing the population response profile proposed by the model (Fischer and Peña, 2011; same as in Fig. 3A), was fitted to these neural responses through scaling (dark gray line) and then adjusting its ITD direction (black dotted line) to minimize the root mean square error. The peak of the fitted curve yielded the estimated ITD (indicated by small black triangles; values listed above each curve). C, Estimation of stimulus ITDs from recorded subsets of neurons on a trial-by-trial basis. Histograms of estimated ITDs using the same examples and decoding method described in B but based on single-trial responses. Stimulus ITDs are listed above each plot, indicated by open triangles. Median estimated ITDs are shown as black triangles, and across-trial variability is shown as horizontal black lines indicating the 25th to 75th percentile ranges (IQR). D, Errors of trial-by-trial ITD estimates for all subsets of recorded neurons and stimuli. Differences between stimulus ITD and subpopulation median ITD estimates are shown in groups, indicating whether stimulus ITDs were within or outside of the range of ITDs covered by the best ITDs of neurons. Positive and negative error values indicate estimates that were more lateral and more frontal than the stimulus ITD, respectively. Boxes range from the 25th to the 75th percentiles, and horizontal lines indicate the median. The bottom and top error bars indicate the 5th and 95th percentiles, respectively. Small black dots show all individual data. E, IQRs of trial-by-trial ITD estimates for all subsets of recorded neurons and stimuli. Data are grouped as in D, and boxplots and markers have the same formatting. F, Estimates of the population readout based on trial-by-trial ITD estimates. Median ITD estimates of all subsets of recorded neurons shown in D were combined with the Bayesian prior proposed to represent the overrepresentation of frontal space (Fig. 1C; Fischer and Peña, 2011) to estimate the overall population readout. Results are plotted as function of the stimulus ITD. Deviation from identity line (diagonal) shows the frontal bias in the readout for stimuli with lateral ITDs. Solid line indicates linear fit across estimates.

To further analyze this finding, neural responses on a trial-by-trial basis were assessed using the same model-driven decoder for estimating the stimulus ITD. A distribution of single-trial estimates was computed for every subset of neurons and stimulus ITD (Fig. 4C), described by the deviation of the median estimate from the stimulus ITD (estimation error) and the interquartile range of estimates (estimation IQR). Despite the limited number of neurons and the natural response variability of sparsely firing OT neurons, the decoder showed high accuracy, with 50% of the absolute estimation errors <6.5 µs for stimulus ITDs within the range of preferred ITDs of the recorded neurons, and <8.6 µs for stimuli outside that range (Fig. 4D). Estimation errors for both of these conditions were not significantly different (p = 0.367, Mann–Whitney U test) and slightly, but not significantly, shifted toward the front for stimuli within the represented range (median, −1.9 µs; p = 0.133, Wilcoxon signed-rank test) and even less for stimuli outside the range (median, −0.2 µs; p = 0.504, Wilcoxon signed-rank test; Fig. 4D). Estimates varied moderately across trials with 50% of the estimation IQRs <27.0 µs (90% <42.9 µs) and no significant difference between stimuli within and outside of the represented range (p = 0.293, Mann–Whitney U test; Fig. 4E). Despite the low number of neurons and the inherent variability of responses, these estimates are within physiologically plausible margins and approach behavioral reports of sound localization accuracy (Knudsen et al., 1979; Knudsen and Konishi, 1979) and minimum audible angles of 3–5°, equivalent to ∼8.4–14 µs ITD (Bala and Takahashi, 2000; Bala et al., 2003; Krumm et al., 2019). As this PV model-based decoder heavily relied on the spread of activity and performed equally well for stimuli within and outside the range of ITDs preferred by subsets of recorded neurons, these results confirm that the pattern of activity is sufficient for effective performance of this model, not only for averaged but also trial-by-trial responses.

Because of limitations in the size of our electrode array, a given subpopulation of recorded neurons would not be able to reflect the known overrepresentation of frontal space in the midbrain map (Knudsen, 1982). To circumvent this and obtain a physiologically relevant estimate of the population readout, we took advantage of the demonstrated mathematical equivalence of PV and Bayesian estimates (Fischer and Peña, 2011). The median of trial-by-trial ITD estimates and the overrepresentation of frontal space corresponded, respectively, to the maximum likelihood and prior estimates of the Bayesian readout model. Thus, applying the prior post hoc to ITD estimates from subsets of recorded neurons resulted in approximate estimates of the PV readout from a full population matching the observed response pattern. These readout estimates displayed a systematic underestimation of stimulus ITD, which was more pronounced at more lateral ITDs (Fig. 4F). These results are consistent with behavioral findings showing owls underestimate stimulus ITD in the periphery (Knudsen et al., 1979; Hausmann et al., 2009; Cazettes et al., 2016) and indicating that the PV decoder across the entire population could display this bias within individual trials.

Effect of sensory noise on population responses

The PV model explains biases toward the front, observed in behavior, by a combination of the overrepresentation of frontal space and an increased spread of responses for less reliable or less binaurally correlated stimuli (Fischer and Peña, 2011; Cazettes et al., 2016). The further responses to lateral stimuli spread throughout the map, the more neurons representing frontal locations will be active and contribute to a frontal bias of the PV readout. Thus, a prediction of the PV readout model is that the spread of activity should increase with decreasing levels of BC of an acoustic stimulus. It has been shown that responses of ITD-sensitive neurons to stimuli at their preferred ITDs are reduced by decorrelating stimulus signals across the ears (Albeck and Konishi, 1995; Saberi et al., 1998; Cazettes et al., 2016). However, it remained an open question whether binaurally decorrelated sounds increase responses to unfavorable ITDs and, as a consequence, the activity spreads further across the map. Consistent with the model predictions, the spread of responses across the population increased as the signal-to-noise ratio (BC) decreased (Fig. 5A,B). This increased width of the spreading of activity was measured by fitting a Gaussian function to the population activity, as was done before for stimuli at 100% BC. This fitting showed responses to stimuli at 40% BC (Fig. 5A) spreading slightly more (SD = 53.2 µs, r² = 0.08) than predicted in the model (Fischer and Peña, 2011; SD = 43.6 µs, r² = 0.06 for the presented data). Yet, this spreading further increased for stimuli at 20% BC (Fig. 5B; SD = 64.0 µs, r² = 0.004), matching the predictions of the model (SD = 65.0 µs, r² = 0.004). Importantly, we found that the increased spread of activity was because of both a decreased response to preferred ITDs and a relative increase in firing to nonpreferred ITDs (Fig. 5A,B). The diversity of response changes across neurons induced by increased noise explains the relatively low coefficients of determination for fitting Gaussian functions at the lower levels of BC, but matches the expected overall spread of activity induced by BC changes. This is consistent with premises of a PV readout model implementing the reported increase in frontal bias for stimuli with low BCs (Saberi et al., 1998; Fischer and Peña, 2011).

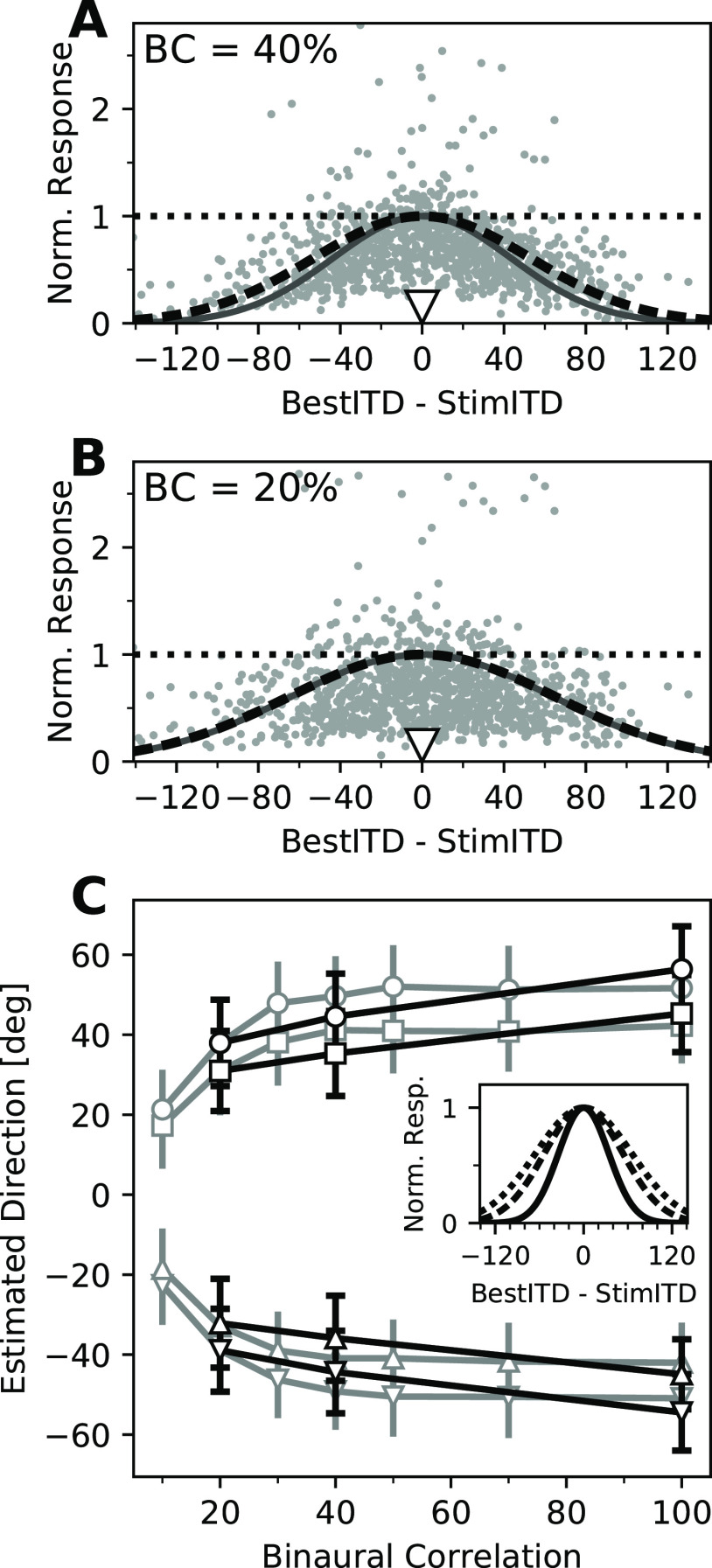
Figure 5.

Increased spread of activity for decorrelated stimuli. A, B, Normalized neural responses to stimuli with 40% (A) and 20% (B) BC (indicated in each panel), as a function of the best ITD of each unit, relative to the stimulus ITD. Responses were normalized to the maximal response of each unit in an ITD tuning curve with the same BC (dotted horizontal lines). Solid dark gray curves indicate the spread of activity presumed in the PV readout model (Fischer and Peña, 2011). The black dashed curves show the same functions with SDs that best fitted the data and that were used in the PV model-based decoder in this study. C, Direction estimates from the PV model (Fischer and Peña, 2011) using levels of SD from the original model (gray) and fitting a Gaussian function to population responses (black). Symbols indicate the stimulus directions (±55°, ±75°). Error bars indicate the SD across 500 model iterations. Inset, Comparison of the spreading widths (fitted SDs) of activity for 100% BC (solid), 40% BC (dashed), and 20% BC (dotted).

The spreads of activity of recorded neurons at different levels of BC were then applied to the original PV model described in the study by Fischer and Peña (2011). Briefly, a modeled population of 500 simulated OT neurons was constructed, responding to stimuli at ±55° and ±75° in azimuth and different levels of BC. Gaussian functions with SD values determined as described above were used to calculate the mean population pattern of activity from which simulated Poisson responses were drawn (see Materials and Methods). Responses were used as the amplitude of preferred direction vectors for each neuron to compute the PV readout from the direction of the sum of these vectors, leading to a direction estimate for the four stimulus directions at each level of BC (Fig. 5C, black lines). These results were compared with estimates produced by the same model when using the original SD values proposed by Fischer and Peña (2011). The PV model using the SD values from Fischer and Peña (2011) and the measured SD values produced similar results. The slightly smaller spread of activity at 100% BC found in the present study compared with Fischer and Peña (2011) estimation led to less underestimation of azimuth angles (19.6° at ±75° and 9.9° at ±55° on average, compared with 23.7° and 12.9° in the original model, respectively). The relatively larger spread of activity at 40% BC predicted a stronger frontal bias than the original model (30.5° and 19.4° compared with 25.6° and 14.0°). However, at 20% BC the width of the spread and the underestimation were almost identical (36.6° and 23.5° compared with 36.6° and 23.1°) to the original model. Despite these small quantitative differences, the use of experimentally obtained SD values did not affect the ability of the PV model to explain an increased frontal bias in response to decorrelated stimuli. These results are consistent with behavioral reports (Saberi et al., 1998) of the owl's performance and bias toward frontal directions at localizing decorrelated sounds. This supports the validity of our values for the spread of activity across the owl's map of auditory space and its increase for decorrelated stimuli and their feasibility to drive a PV readout.

Applying the same PV model-based decoder as before (Fig. 4B–E) to estimate stimulus ITDs based on mean population responses resulted in moderate estimation errors for stimuli with low BC, as could be expected (Fig. 6A). At 40% BC, the median absolute estimation error across subsets was 23.0 µs, and at 20% BC this increased to 39.2 µs, both considerably larger than at 100% BC, where it was only 7.4 µs. Interestingly, when analyzed on a trial-by-trial basis, increasing the noise level induced larger estimation errors (Fig. 6B). This was accompanied by an increased trial-to-trial variability of ITD estimates (Fig. 6B). Decreasing the signal-to-noise ratio decreased this decoding performance in two ways. First, the across-trial median estimates deviated more from the stimulus ITD, leading to median absolute estimation errors of 15.7 µs at 40% BC for stimuli within and outside of the range of ITDs represented by the subset of recorded neurons, and 23.7 µs (within) and 22.0 µs (outside) at 20% BC (Fig. 6C). Considering the direction of the deviation, there was a small but statistically significant frontal bias for stimuli within the represented range at 40% BC (median, −6.7 µs; p = 0.0143, Wilcoxon signed-rank test) and 20% BC (median, −10.8 µs; p = 0.00495), and less for stimuli outside that range (40% BC: median, −4.0 µs; p = 0.856; 20% BC: median, +0.38 µs; p = 0.856; Fig. 6C). Second, the intertrial variability increased drastically with noise, as expressed by the estimation IQR, which more than doubled at 40% BC (median across all subsets and stimuli, 67.1 µs) compared with 100% BC, and further increased at 20% BC (median, 90.1 µs; Fig. 6D). Similar to estimates at 100% BC, there was no difference between estimation IQRs for stimuli within and outside the range of best ITDs of neurons at either noise level (40% BC, p = 0.422; 20% BC, p = 0.237; Mann–Whitney U test). Both the increase in estimation error and the increase in trial-to-trial variability are consistent with larger behavioral variability reported at these noise levels (Saberi et al., 1998; Cazettes et al., 2016). This suggests that the spread of activity in response to decorrelated noise matches conditions of a PV model readout. Median ITD estimates were, as described before, combined with the overrepresentation of frontal space to yield population readout estimates. Consistent with model predictions (Fischer and Peña, 2011), the population readout underestimated the stimulus ITD for stimuli of lower BC (Fig. 6E). These results indicate that on a trial-by-trial basis, the population response profiles meet the criteria for a PV readout and together can explain the owl's behavioral bias (Saberi et al., 1998) and variability (Saberi et al., 1998; Cazettes et al., 2016) when localizing stimuli of low BC.

Figure 6.

Performance of the PV decoder across signal-to-noise levels. A, ITD decoding from normalized recorded responses (open circles) to stimuli of four different ITDs (indicated by open triangles and listed above each plot) and 40% (top row) and 20% (bottom row) BC as a function of the best ITDs of neurons. Black triangles indicate estimated ITDs. The same subset of neurons and decoding method shown in Figure 4B is presented. B, Estimation of stimulus ITDs on a trial-by-trial basis for stimuli of 40% (top row) and 20% (bottom row) BCs. Histograms of estimated ITDs from single-trial responses to four stimulus ITDs (same as in A). Dashed line histograms show results for stimuli of 100% BC (same as shown in Fig. 4C). C, Errors of trial-by-trial ITD estimates for all subsets of recorded neurons and stimuli, for stimuli at 100% BC (dark gray boxes; same data as in Fig. 4D), 40% BC (light gray boxes), and 20% BC (white boxes). Positive and negative error values indicate estimates that were more lateral and more frontal than the stimulus ITD, respectively. Boxes range from the 25th to the 75th percentile, and the horizontal line indicates the median. The bottom and top error bars indicate the 5th and 95th percentiles, respectively. Small black dots show all individual data. D, IQRs of the trial-by-trial estimates for all recorded subsets of neurons and stimuli, for stimuli of 100% BC (dark gray boxes), 40% BC (light gray boxes), and 20% BC (white boxes). Data are grouped as in C, and boxplots and markers have the same formatting. E, Estimates of the population readout based on trial-by-trial ITD estimates from population responses to stimuli of different BCs. Same as in Figure 4F, median ITD estimates of all subsets of recorded neurons were combined with the Bayesian prior and plotted as a function of stimulus ITD. Individual data are shown for stimuli of 40% BC (gray circles) and 20% BC (open white circles), and linear fits are shown for all three BC levels, as indicated in the legend. Larger deviation from the diagonal for stimuli of increased noise levels (bottom BCs) shows the increased frontal bias in the readout.

In sum, these results show that population responses support a PV readout of OT neurons on a trial-by-trial basis, and its performance across signal-to-noise levels is consistent with the predictions and behavioral observations of the model.

Discussion

This work provides physiological evidence for the viability of a PV readout of the auditory space map in the barn owl's optic tectum mediating probabilistic sound-localizing behavior. A decoder based on the PV model was able to infer stimulus ITD from subsets of simultaneously recorded neurons on a single-trial basis. In addition, response profiles of simultaneously recorded neurons matched premises of the PV model, including the spread of activity across the map, which, based on the nonuniform representation of space, allows a PV readout to predict physiological behavioral biases and to show how population responses change when noise levels vary.

Predictive power of stimulus ITD from population responses by a PV decoder

Decoding ITD using a model based on the PV from subsets of neurons allowed for reliable estimation of stimulus ITD (Fig. 4A–E), supporting the hypothesis that this decoding system can be implemented in the owl's OT. In addition to stimuli within the range of preferred ITDs among the subset of recorded neurons, decoding also allowed for estimating stimulus ITDs away from this range (Fig. 4D,E). This finding is consistent with the notion that PV decoding relies on readout of the entire population rather than responses of the most active neurons (Lee et al., 1988). Previous studies conducting lesions in lateral regions of the owl's OT showed a tendency of orienting behavioral responses short of the target (Knudsen et al., 1993) and reduced head-turning amplitude (Wagner, 1993), which is consistent with an increased frontal bias of a PV decoding because of a reduction in the number of neurons tuned to peripheral locations.

Spread of activity across the map sufficient to predict normal behavioral biases mediated by a PV readout

A critical open question regarding the readout of the owl's midbrain map of auditory space in predicting sound-localizing behavior is the spread of activity across the map. A classic place code mediated by the location of peak responses within the map cannot predict behavioral biases in sound localization, adaptive for natural and manipulated stimulus statistics (Knudsen et al., 1979; Hausmann et al., 2009; Fischer and Peña, 2011; Cazettes et al., 2016). Our results show a spread of activity across subsets of recorded neurons that is broad enough to support the prediction of the PV model of the natural frontal behavioral bias (Fig. 3; Fischer and Peña, 2011). The performance of our decoder to accurately estimate stimulus ITDs from single-trial responses further supports this prediction. This interpretation was made despite the relatively small number of simultaneously recorded neurons compared with the entire OT population and based on the assumption that all OT neurons contribute to the readout. As the decoder relies on this assumption by generalizing recorded response profiles to the full population, larger sample sizes might increase the trial-to-trial robustness of the estimation. However, recorded subpopulations were not selected based on the decoder performance and can be considered random samples, restricted by the configuration of the multielectrode array and search parameters (see Materials and Methods), supporting the premise that subpopulation responses are generalizable to the entire midbrain map. Furthermore, a PV readout model of recorded responses showed a consistent frontal bias (Fig. 4F).

Despite this strong evidence supporting a PV readout model, some conditions have not been addressed in this study. For example, space-specific neurons in the owl's external nucleus of the inferior colliculus (ICx) often show side peak responses (Takahashi and Konishi, 1986; Wagner, 1990; Mazer, 1998; Peña and Konishi, 2000), which could disrupt vector summation. However, in our data from the OT, downstream from the ICx (Knudsen and Knudsen, 1983) and the region known to drive behavioral output (du Lac and Knudsen, 1990; Masino, 1992; Cazettes et al., 2018), side peak responses were weak (Fig. 3C); thus, their influence would be minor. Another related challenge is the localization of pure tone stimuli that are phase ambiguous and lead to strong side peak responses in broadly frequency tuned neurons. Behavioral studies have demonstrated that owls, when presented with such ambiguous stimuli, localize either of the potential sound source directions (Knudsen and Konishi, 1979; Saberi et al., 1999; Kettler et al., 2017). The PV readout model alone would predict localization in between these ambiguous directions. Thus, another mechanism must influence the localization of tones. The PV readout may also be affected by the correlation between ITD and frequency tuning (Fig. 2B; Cazettes et al., 2014), which can lead to differential activity across the map. Ambiguous response patterns could further arise from multiple concurrent stimuli at different locations. One mechanism to implement stimulus selection is the previously reported global inhibition network in the owl's midbrain, inhibiting responses to all but the most salient stimulus (Mysore et al., 2010, 2011). While not part of this study, we judge that the combination of global inhibition and the PV readout may resolve this ambiguity.

In summary, we have shown that the profiles of population response in OT to single broadband stimuli, especially the spread of activity across the map, match the requirements of a PV readout, explaining the behavioral bias toward frontal locations. Future work should address the limitations of the model in relation to ambiguous stimuli and elucidate other predictive elements to resolve them.

Effect of signal-to-noise ratio on population responses supports behavioral predictions of a PV readout as noise levels change

As expected, neurons had overall lower responses when the signal was corrupted by decorrelated noise. Importantly, they also displayed a relative increase in responses to nonpreferred ITDs, which indicates that with increased noise the neuronal response spreads across the map, rather than being limited to the neurons tuned to the particular ITD (Fig. 5A,B). This increase in activity caused the ITD estimate based on single-trial responses to be systematically biased toward ITDs preferred by the neurons being recorded and, overall, to be more variable (Fig. 6B–D). When the known overrepresentation of frontal space in the owl's OT was combined with the ITD estimates, the bias was consistently directed toward frontal locations, with even larger underestimations of lateral ITDs for stimuli with increased noise than under no-noise conditions (Fig. 6E). These results are in line with previous behavioral reports showing increased frontal bias in lower signal-to-noise ratio stimulus conditions (Saberi et al., 1998; Cazettes et al., 2016) and predicted by the proposed PV readout (Fischer and Peña, 2011). Furthermore, decoding stimulus ITD from neural responses showed a larger trial-to-trial variability for decorrelated stimuli compared with non-noise conditions (Fig. 6B,C). This reflects the larger variability when noise is increased, which has been reported in behavioral studies (Saberi et al., 1998) and theoretical predictions (Cazettes et al., 2016), and emphasizes the importance of recording multiple neurons simultaneously and evaluating responses on a trial-by-trial basis, as opposed to averaging responses from single-neuron recordings.

Relevance of PV readout across systems

A PV readout has been a seminal population-decoding mechanism for the emergence of adaptive behavioral outputs (Georgopoulos et al., 1986; Lee et al., 1988; Groh, 2001; van Hemmen and Schwartz, 2008). This study examines the hypothesis of a PV readout mediating statistical inference, which has been proposed by studies in human visual perception (Girshick et al., 2011) and owl sound localization (Fischer and Peña, 2011). Following evidence that a PV readout of midbrain map responses could mediate optimal sound localization behavior in barn owls (Cazettes et al., 2018), this study tests the specific response properties of neuronal populations required for a PV readout. In contrast to the owl's midbrain, recordings in the mammalian IC were not reported as supporting a PV readout (Day and Delgutte, 2013). However, Day and Delgutte (2013) explained the poor predictive power of the PV decoder by the heterogeneous shapes of spatial tuning of mammalian IC neurons. In the superior colliculus of primates, the homolog of the owl's OT, a weighted sum readout, similar to a PV readout, has been reported to be feasible for use in guiding eye saccades to visual and auditory cues (Lee and Groh, 2014). Furthermore, evidence of an auditory space map was reported in the superior colliculus across mammalian species (Palmer and King, 1982; Middlebrooks and Knudsen, 1984; King, 1993; King et al., 1996; Gaese and Johnen, 2000), and population recordings of these regions may elucidate the potential role of PV in sound localization behavior across species. Overall, our study provides evidence of population response properties in a topographic representation of space, supporting premises for a PV readout mediating the implementation of statistical inference, possibly a common scheme across species and systems.

Conclusions

In sum, for the first time, population responses were recorded across the map of auditory space in the owl's OT, supporting the idea that a global readout of this population, rather than a place code, mediates behavioral responses. The effect of noise consistently led to an increased frontally biased population readout on a trial-by-trial basis. These findings support theories that PV readout of sensory neural populations can support behavioral optimality by incorporating prior information and sensory cue reliability in the behavioral command underlying sound-orienting responses on a trial-by-trial basis (Fischer and Peña, 2011; Cazettes et al., 2018) as well as human visual orientation perception (Girshick et al., 2011).