Comparison of Approaches for Determining Bioactivity Hits from High-Dimensional Profiling Data

Abstract

Phenotypic profiling assays are untargeted screening assays that measure a large number (hundreds to thousands) of cellular features in response to stimulus and often yield diverse and unanticipated profiles of phenotypic effects, leading to challenges in distinguishing active from inactive treatments. Here, we compare a variety of different strategies for hit identification in imaging-based phenotypic profiling assays using a previously published Cell Painting dataset. Hit identification strategies based on multi-concentration analysis involve curve-fitting at several levels of data aggregation: (individual feature-level, aggregation of similarly-derived features into categories and global modeling of all features), and on computed metrics (e.g. Euclidean and Mahalanobis distance metrics and eigenfeatures). Hit identification strategies based on single-concentration analysis included measurement of signal strength (i.e. total effect magnitude) and correlation of profiles among biological replicates. Modeling parameters for each approach were optimized to retain the ability to detect a reference chemical with subtle phenotypic effects while limiting the false positive rate to 10%. The percentage of test chemicals identified as hits was highest for feature-level and category-based approaches, followed by global fitting, while signal strength and profile correlation approaches detected the fewest number of active hits at the fixed false positive rate. Approaches involving fitting of distance metrics had the lowest likelihood for identifying high-potency false positive hits that may be associated with assay noise. The majority of methods achieved 100% hit rate for the reference chemical, and high concordance for 82% of test chemicals, indicating that hit calls are robust across different analysis approaches.

Introduction

High-throughput profiling (HTP) assays are untargeted screening assays that measure a large number (hundreds to thousands) of cellular features in order to capture the biological state (i.e. phenotype) of a cell¹. Examples of HTP assays are “omics” technologies, including transcriptomics^2–4, and image-based morphological profiling, such as Cell Painting^{5, 6}. HTP assays have been used in various research settings, including academia^{7, 8} and industry⁴, to characterize the biological activity of chemicals or genetic manipulations using a variety of different cell models and assay technologies. These types of assays are also of interest for broader use by regulatory organizations in the context of next generation chemical safety assessments^{9, 10}. One fundamental application for HTP data relevant to each of these sectors is reliable identification of “hits”: i.e. treatments that produce biologically and statistically significant changes in cellular phenotype that are associated with biological activity¹¹.

The high content nature of profiling assays introduces additional challenges to hit identification^{10, 12} as compared to targeted high-throughput screening (HTS) assays. Targeted HTS assays are designed to measure one (or a few) specific endpoints and response thresholds for hit identification are based on either the use of well-characterized negative and positive control treatments or defined based on separation of true signal from statistically characterized baseline activity (i.e. noise). Responses to test conditions falling below these thresholds are then classified as inactive, while responses above these thresholds are classified as active^{13, 14}. This strategy is difficult to generalize to HTP assays, for several reasons: (1) HTP assays often measure hundreds to thousands of features (i.e. have high dimensionality), and it would not be feasible to define a threshold for each individual feature in an analogous manner to targeted assays; (2) Measurement of many features allows for observation of a multitude of diverse cellular responses (i.e. phenotypes). Therefore, within the context of a large HTP screen it is not known a priori which phenotypic responses will be observed. Hence, there is not a single ‘positive control’ that can be used to establish hit thresholds for the multitude of phenotypes that may be observed. (3) Even without perturbation, stochastic variations in feature measurements can contribute to identification of false actives in high dimensionality datasets to a greater extent than in HTS assays. This is a classic manifestation of the multiple testing problem.

To date, there are no widely accepted standard practices for hit identification from HTP data^{15, 16}. As a consequence of the large number of features that are measured, there are a wide array of potential strategies for identification of hits and – for concentration-response screening – derivation of potencies. The choice of hit definition strategy also depends on the purpose of the screen. For example, for lead compound identification in the pharmaceutical sector, a hit definition strategy that minimizes false actives may be desirable^{17, 18}. In contrast, for toxicology screening the tolerance for identification of false actives using profiling assays will vary depending on the nature of the downstream application: i.e. comparatively higher tolerance in screening for prioritization versus comparatively lower tolerance for defining a specific hazard in the context of a risk assessment¹⁹.

The recently released Next Generation Blueprint for Computational Toxicology at the United States Environmental Protection Agency (USEPA) (i.e. USEPA Comptox Blueprint) advocates the use of HTP assays for initial characterization of the biological activity of environmental chemicals in human-derived cell models⁹. Use of HTP assays has been proposed as part of a tiered toxicity testing approach that relies on computational and non-animal based methods for chemical safety evaluation⁹. Applications for HTP data include identification of potency thresholds for perturbation of cellular biology, prediction of putative mechanism of action (MOA) and/or molecular initiating events (MIE)²⁰, and prioritization of chemicals for further testing and subsequent confirmation in targeted HTS or organotypic assay systems⁹. Chemicals with environmental exposure potential often lack a specific molecular target in human-based cell models and may have biological activity that is associated with ‘polypharmacology’ (i.e. promiscuous activity at multiple molecular targets) or general cell stress^21–23. All of these attributes contribute to the challenging task of hit identification when applying HTP assays to the universe of structurally diverse environmental chemicals. The variety of data analysis strategies that can be applied to profiling data and uncertainties regarding concordance of results, including active or inactive hit calls, across different analysis strategies represent a potential barrier to the broader use of these types of data in regulatory applications^{24, 25}.

We previously operationalized the Cell Painting HTP assay⁵ for concentration-response screening in U-2 OS osteosarcoma cells and screened 462 unique environmental chemicals²⁶. Following extraction of 1,300 features, concentration-response modeling was performed using the BMDExpress software package²⁷ to identify individual features affected by chemical treatment. We then grouped the features into biologically meaningful categories (based on the channel, compartment and analysis module). Chemicals where at least one category had ≥ 30% of constituent features identified as concentration-responsive were considered active, and their phenotype altering concentration (PAC) was defined as the median potency of the most sensitive (i.e. potent) category. Using this approach, 95% of tested chemicals were identified as active, which is helpful in terms of identifying a minimum bioactive concentration that can be used to prioritize chemicals using a bioactivity:exposure ratio^{26, 28}. Although a high rate of actives was expected due to the nature of the chemical test set (i.e. enriched in pesticides and chemicals with biological activity in ToxCast assays²⁸) and the use of a permissive benchmark response (BMR) (i.e. 1*standard deviation (SD) of controls²⁹), the proportion of false active hits using this approach was unclear. This was due to uncertainty regarding the identity and proportion of true negative (i.e. biologically inert) chemicals present in the test set in the concentration range tested and the aforementioned challenges in establishing hit criteria for HTP assays.

In the present study, we compared various approaches for identification of hits in imaging-based phenotypic profiling (i.e. Cell Painting) data using the above-mentioned data set. The goal of this work was to understand the impact of decisions made in the data analysis workflows on the resulting active or inactive hit calls and the associated PACs for perturbation of cellular biology, as these results may inform future chemical safety evaluations. With a focus on applications for in vitro bioactivity screening as the first step in a tiered toxicity testing strategy⁹, both multi-concentration and single-concentration approaches for hit identification were considered (Fig. 1). To optimize selection of a fit-for-purpose approach for hit identification, reference chemicals, test chemicals screened in duplicate, and a “null” or inactive data set constructed from conditions with no expected bioactivity were used to optimize and compare the performance of different approaches. Results were compared quantitatively to identify the approach(es) that provided the highest concordance of hit classifications (active vs. inactive), the lowest variability in PACs for reference chemicals and chemicals screening in duplicate and the lowest probability of observing high potency false active hit calls, as such approaches would be most informative and reliable for use in chemical safety evaluation.

Fig. 1: Approaches for Hit Determination from Imaging-Based Phenotypic Profiling Data.

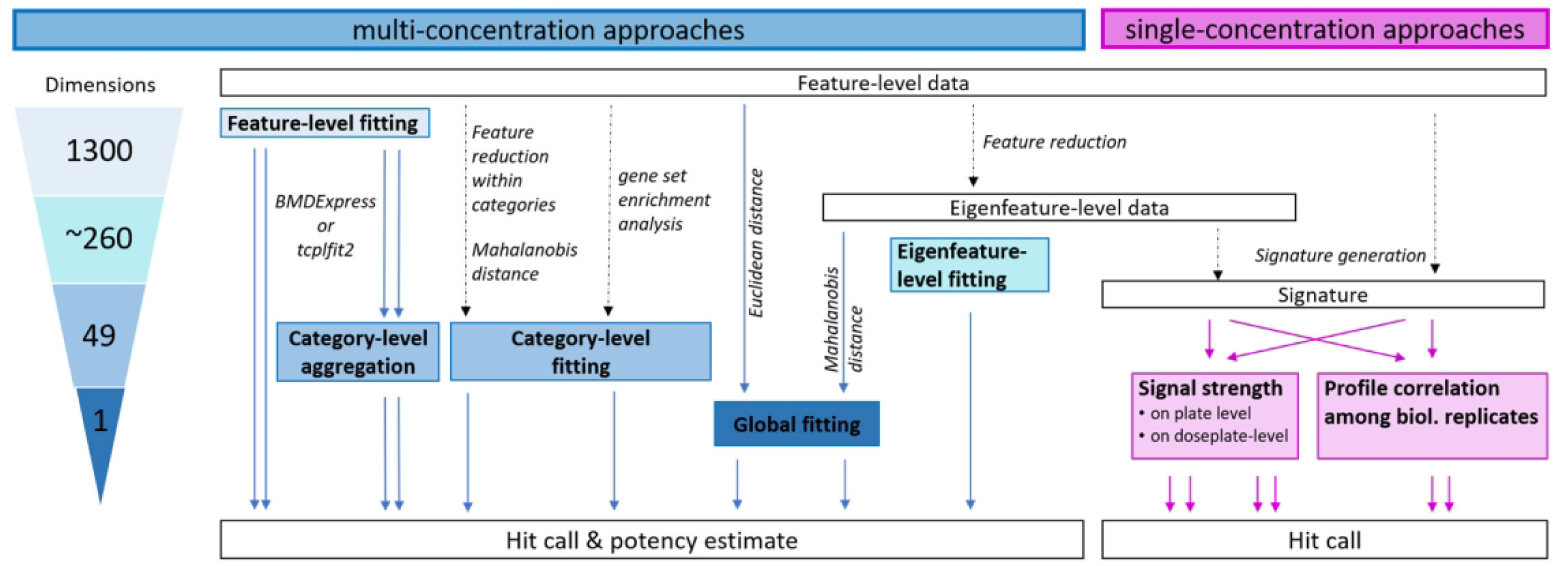
Multi-concentration approaches for hit determination are shown in blue. Single-concentration approaches for hit determination are shown in pink. The number of individual BMCs that could potentially be derived from each multi-concentration approach are shown in the triangle to the left. The starting point for all approaches was well-level data for each phenotypic feature. Feature-level data can be fit and directly used for potency estimation, or the fit results can be aggregated to the category level (i.e. collection of related features) before determining hit calls and calculating potency estimates. Data from our adaptation of the Cell Painting assay²⁶ can be reduced to 49 categories before curve-fitting using either feature reduction (PCA) or ssGSEA approaches. The 1300 individual features can also be used to calculate a Euclidean distance from controls and model this value as a single response variable. Similarly, feature-level data can be transformed to eigenfeatures to account for correlation among features and then distance from controls can be calculated using the Mahalanobis approach^{42, 43}. Eigenfeature-level data can also be used directly for curve fitting. For single concentration approaches, feature-level or eigenfeature-level data can be used to derive signatures and overall signal strength of the signature can be compared to controls. Alternatively, the correlation of signatures among biological replicates of the same treatment can be used as a hit calling criteria.

Materials and Methods

Experimental Data

The data set used for this study has been previously published²⁶ and is publicly available at (https://doi.org/10.23645/epacomptox.12132621).

Briefly, U-2 OS human osteosarcoma cells were treated for 24 h with 8 concentrations (1/2 log₁₀ spacing, typically 0.03 – 100 μM) of each chemical. The screen was performed in 384-well plate format. A total of 462 unique test chemicals from the ToxCast chemical library were screened. A total of 16 randomly selected chemicals were screened in duplicate which brought the total number of chemical samples evaluated to 478. The screen was performed using 12 dose plates, each with a different subset of test chemicals in a dilution series. Each chemical sample was screened in four independent cultures (i.e. biological replicates) with one technical replicate (i.e. well) per culture for each concentration of each chemical sample. Test plates from each biological replicate that were dosed with the same sub-set of test chemicals belong to the same plate group. Each test plate also contained 24 solvent control wells and six concentrations of four phenotypic reference chemicals: berberine chloride, Ca-074-Me, rapamycin and etoposide (see also Fig. S1 in Nyffeler, et al.²⁶). For the reference chemicals, each plate group was considered to be independent of one another; i.e., resulting in a total of 12 response profiles for each reference chemical, which we refer to as ‘replicates’.

For phenotypic profiling, labels were applied to visualize the nucleus (DNA), nucleoli (RNA), endoplasmic reticulum (ER), actin skeleton, golgi and plasma membrane (AGP) and mitochondria (Mito). Following image acquisition, 1300 features were extracted for each cell. Cell-level data was normalized to the solvent control using median absolution deviation (MAD) normalization⁵ and aggregated to well-level by calculating the median of normalized cell-level data within each well. Well-level data were further z-standardized within plate by scaling to the standard deviation (SD) of solvent control wells. These previously reported well-level results were used as the starting point for the present study.

A parallel set of plates was live-labeled with propidium iodide and Hoechst 33342 to assess cytotoxicity and cytostasis. Information from this cell viability (CV) assay was used to identify a benchmark concentration (BMC) for onset of cytotoxicity/cytostasis and subsequently identify the highest non-cytotoxic concentration (CV.NOEC) and the lowest cytotoxic concentration (CV.LOEC). As previously reported, data from wells above the CV.LOEC were not used for concentration-response analysis²⁶.

Data Analysis Software

The data processing, storage, analysis and visualization were performed using R v3.6.2³⁰. The R scripts are available at https://doi.org/10.23645/epacomptox.12589256.

Generation of a null data set

A null data set representative of inactive response profiles was constructed using the well-level data from concentrations of test chemicals that had a low probability of being bioactive. This consisted of data from the two lowest concentrations of each test chemical, but only using test chemicals for which there was no inferred bioactivity at or below the third lowest tested concentration in the previous study²⁶. Using these constraints, 472/478 test chemicals demonstrated no activity at the two lowest concentrations tested. Therefore, these wells were included in constructing the null data set.

For each test plate, well-level data for these inactive test chemical concentrations were randomly assigned to one of nine ‘null chemicals’ and one of 8 concentration indices (with ½ log₁₀ spacing, consistent with the actual design of the screening study). The test plate to plate group relationship was maintained. Of note, the four biological replicates of a null chemical × concentration were derived from different test chemicals through the random sampling process. A total of 108 ‘null chemicals’ were generated.

Metrics for Comparison of Analysis Approaches

Specificity was defined as the percentage of ‘null chemicals’ (n = 108) that were correctly identified as inactive. Conversely, the false positive rate (FPR) was calculated as 1 – specificity. Sensitivity (or true positive rate, TPR) was defined as the percentage of true positives that were correctly identified as active. While all four phenotypic reference chemicals could have served as true positives, we decided to only focus on replicate screenings of the reference chemical berberine chloride (n = 12) as a true positive for this analysis, as it had subtle, but reproducible effects in a small number of measured features²⁶. The “hit rate” was calculated as the percentage of test chemicals (n = 478) that were identified as active. Concordance was defined as the percentage of test chemicals screened in duplicate (n = 16) for which both replicates were identified as either inactive or active.

Parameters for each analysis approach were optimized to maximize TPR while maintaining an FPR of ~ 10%. Tunable parameters for the various approaches included: cutoff threshold (based on variance in the solvent control) and hit call probability for tcplfit2, threshold for effect size for BMDExpress or threshold for signature generation, as described below. A list of all fixed and tunable parameters, as well as the final choices is provided in Table S1. If multiple sets of parameters produced equivalent results according to these criteria, the most permissive threshold was chosen (e.g. the lowest threshold for signature generation, as described below) that retained maximal concordance.

Multi-concentration Analysis Approaches

The starting point for all multi-concentration approaches was well-level data. For each chemical, concentrations above the CV.LOEL were excluded from concentration-response modeling to avoid potential problems with non-monotonic curve behavior that can be observed at cytotoxic test concentrations. Different levels of data were modeled, in some cases preceded by feature reduction, to derive between 1 and 1300 potency estimates (benchmark concentrations, BMC). For all approaches, BMCs below the tested range were set to ½ order of magnitude below the lowest tested concentration (corresponding to dividing the concentration by 3), while BMCs above the tested range or above the CV.LOEC were discarded as invalid. Three test chemicals (disulfiram, thiram, ziram) had < 4 concentrations remaining and were not modeled with tcplfit2 in accordance with previous recommendations regarding the use of benchmark dose modeling in toxicology^{31, 32}. Therefore, some multi-concentration approaches and figures include only results from 475 test chemicals.

Feature-level fitting

Two different concentration-response modeling software packages were used: (1) BMDExpress²⁷ (https://www.sciome.com/bmdexpress/) and (2) tcplfit2, a curve-fitting package that includes constant, Hill, and gain-loss models from tcpl³³ and additional models to match the functionality of BMDExpress.

For BMDExpress, modeling parameters were identical to the previous study²⁶. Briefly, the command line version of BMDExpress (v2.2.180) was used. Only features with an absolute mean response > 1 in at least one test concentration were modeled. Four functions were fit to the data: Hill, power, and first- and second-degree polynomial. The model with the lowest Akaike information criterion (AIC) was selected as the winning model. The benchmark response (BMR) was set at ±1 (i.e. 1 SD from vehicle control). For the present study, an additional threshold for effect size was chosen to increase stringency. BMCs of features that had an absolute effect size ≤ 1.75 (designated as absolute maximal fold change of ≤ 2^1.75 in BMDExpress) were excluded.

For fitting with tcpl, a new version (tcplfit2, v.0.1.0, https://ncct-bitbucket.epa.gov/projects/TCPLFIT2/repos/tcplfit2/browse) of curve fitting was used, that allows fitting of effects in either direction and includes more fit functions: the four functions used with BMDExpress were run, as well as four exponential models (Exp2 – Exp5) and a constant model. Additionally, tcplfit2 returns a continuous hit call probability, ranging from 0 to 1. Analogous to BMDExpress, features were only modeled if there was at least one test concentration with an absolute mean response > 1. The BMR was defined using the median and normalized median absolute deviation (nMad, Nyffeler, et al.²⁶) of the vehicle controls (of the corresponding plate group) and was set at 1 nMad (corresponding to 1 SD). BMCs were only retained if the hit call probability was ≥ 0.95.

For both approaches, chemicals were considered active if more features were affected (i.e. had a valid BMC) as compared to the 90^th percentile of the null data set. For BMDExpress, chemicals with > 20 affected features were considered active. For tcplfit2, chemicals with > 24 affected features were considered active. The phenotype altering concentration (PAC) was calculated as the 5^th percentile of the valid BMCs (using R, function quantile with option type=7 for linear interpolation of the quantile from continuous data).

Category-level aggregation

Each of the 1300 features was assigned to exactly one of 49 categories, based on the channel, compartment and module it was derived from (Table S2 in Nyffeler, et al.²⁶). Analysis was conducted exactly as described in Nyffeler, et al.²⁶: For each category, a median BMC was calculated from the individual feature BMCs if ≥ 30% of features within a category were affected (i.e. had a valid BMC). Category-level aggregation was performed with both BMDExpress and tcplfit2 feature-level fitting results. Chemicals were considered active if they had at least one affected category (i.e. the category had a median BMC). The PAC was defined as the potency of the most potent category BMC.

Global fitting (Euclidean distance)

For each well, the Euclidean distance from the mean of the vehicle controls (of the corresponding culture plate) was calculated as $d_E(\overrightarrow{x},\overrightarrow{\mu })=\sqrt[2]{{\sum }_{i=1}^{1300}{\left(x_i-{\mu }_i\right)}^2}$ where $\overrightarrow{x}$ and $\overrightarrow{\mu }$ represent the vector of the 1300 features for the particular well and the mean of the vehicle controls, respectively. Subsequently, the Euclidean distances were modeled with tcplfit2, using nine functions and the median and nMad of the null data sets (of the corresponding plate group) to define the BMR, which was set at 1 nMad. BMCs were discarded if the hit call probability was < 0.2 or if the top of the curve was negative (smaller than the average distance to the mean of the vehicle controls is not considered an effect). Chemicals with a valid BMC were considered active, and the PAC was set equal to the BMC.

Feature reduction

For several of the approaches described below, well-level data was first transformed to a reduced set of eigenvectors, which we term ‘eigenfeatures’, using principal component analysis (PCA). Wells with < 100 cells were excluded, as was the null data set (because it was sampled from the original data). PCA was conducted using R (v3.6.2), package stats³⁰ and function prcomp with options center=F and scale.=F using the entire data set as input. The first 260 principal components, covering > 95% variance in the data set were used to transform the original data set to the eigenfeatures.

Eigenfeature-level fitting

Fitting of eigenfeature-level data was performed with tcplfit2, similarly as to described above. The BMR was defined based on the median and nMad of the vehicle control (of the corresponding plate group) and set at 1 nMad. Nine functions were fit, and eigenfeatures were only fit if there was at least one concentration that exceeded the BMR. BMCs were only retained if the hit call probability was ≥ 0.50. Hits and PACs were defined as described in ‘Feature-level fitting’.

Global fitting (Mahalanobis distance)

A covariance matrix was calculated from eigenfeature-level data using all wells with ≥ 100 cells (the null data set was not used). The inverse of the covariance matrix (Σ⁻¹) was then used to calculate the Mahalanobis distance. Analogous to the Euclidean distance, the Mahalanobis distance was calculated for each well $\overrightarrow{x}$ relative to the mean of solvent control wells $\overrightarrow{\mu }$ per culture plate as $d_M(\overrightarrow{x},\overrightarrow{\mu })=\sqrt[2]{{(\overrightarrow{x}-\overrightarrow{\mu })}^T{\Sigma }^{-1}(\overrightarrow{x}-\overrightarrow{\mu })}$. Well-level Mahalanobis distances were then modeled as described in ‘Global fitting (Euclidean distance)’.

Category-level fitting (Mahalanobis distance)

For each category, well-level data was transformed using PCA as described in ‘Feature reduction’, except that only the features within the category were used as input. The first N eigenfeatures that cover ≥ 90% of variance within that category were retained. Mahalanobis distance was then calculated for each category as described in ‘Global fitting (Mahalanobis distance)’.

Subsequently, the category-level Mahalanobis distances were modeled with tcplfit2, using nine functions and the median and nMad of the null data sets (of the corresponding plate group) to define the BMR, which was set at 1 nMad. BMCs were discarded if the hit call probability was < 0.80 or if the top of the curve was negative (smaller than average distance to the mean of the vehicle controls is not considered an effect). Chemicals with at least one valid BMC were considered active and the lowest BMC was defined as the PAC.

Category-level fitting (single sample gene set enrichment analysis, ssGSEA)

The ssGSEA approach was originally developed for transcriptomics data and was adapted for use with the HTPP data with slight modification³⁴. In brief, “gene sets” were defined as the set of features within each category as described in ‘Category-level aggregation’. Normalized feature data for each chemical and concentration were rank-ordered based on scaled response magnitude and zero-centered prior to calculating the Kolmogorov-Smirnov-like running sum statistic as described previously^{34, 35}. The category enrichment score is the sum integration of the Kolmogorov-Smirnov-like running sum of features within the category and features outside of the category. Enrichment scores were further normalized by the range of scores across all test samples and categories. Large positive or negative scores for a category indicate that a sample is enriched in features for that category in the top or bottom extremes of the ranked feature set distribution, respectively.

Category enrichment scores were modeled with tcplfit2, using nine functions and the median and nMad of the null data sets (of the corresponding plate group) to define the BMR, which was set at 1.349 nMad. BMCs were discarded if the hit call probability was < 0.50. Chemicals with at least one valid BMC were considered active and the lowest BMC was defined as the PAC.

Single-Concentration Analysis Approaches

To ‘simulate’ single concentration data, we tested approaches that utilize only one concentration for each test chemical. In this study, the tested concentration range varies across chemicals. As we have cell viability information for all chemicals, we chose to use the highest non-cytotoxic test concentration for each chemical (i.e. CV.NOEC) in evaluation of the single-concentration analysis approaches. This is the highest concentration below the threshold for cytotoxicity or cytostatic effects. For chemicals where no cytotoxicity or cytostatic effects were observed this value corresponds to the highest tested concentration.

Generation of profiles and signatures

A profile was defined as a vector consisting of the scaled response magnitude of the 1,300 features at the corresponding concentration. To reduce noise, signatures were constructed from profiles by replacing all values that were below a certain signature threshold with 0 (signature thresholds are applied uniformly across all features). For the following approaches, signature thresholds between 0 and 6 were evaluated. The best signature threshold was selected independently for each method below based on highest sensitivity with FPR ≤ 10%, followed by having the lowest (most permissive) signature threshold that produced high concordance of hit calls for chemicals screened in duplicate. The approaches described below were also used to model eigenfeature transformed data (covering > 95% of variance). In that case, no signature threshold was used.

Signal strength overall

Well-level data for a chemical was aggregated to a median across biological replicates (e.g. within plate group). Three different measures of signal strength (SS) were tested: (1) the Euclidean norm $\left(SS=\sqrt[2]{{\sum }_{i=1}^{1300}{\left|x_i\right|}^2}\right)$; (2) the Manhattan norm $\left(SS={\sum }_{i=1}^{1300}\left|x_i\right|\right)$; (3) the number of features with a value above the signature threshold. The measure with the best performance was the Euclidean norm with a signature threshold of 1.5 (for feature-based data). Chemicals were considered active if the chemical’s SS was above the 90^th percentile of the SS of the null data set.

Signal strength plate-wise

In this approach, SS was calculated for each biological replicate of a chemical. The same three measures as described above were evaluated. The four values for SS were then compared to the distribution of SS for null chemicals (from the same plate group, i.e. 36 values) using a Wilcoxon rank-sum test (R function wilcox.test with option alternative=”greater”) to test if the SS values of the chemical is greater than the SS distribution of the null data. For null chemicals, the four SS values were compared to the SS values from the remaining null chemicals (i.e. 32 values).

Chemicals were considered active if the resulting p-value was below the 10^th percentile of p-values of the null data set. The option with the best performance was Euclidean norm with a signature threshold of 2.25 (for feature-based data) and without a threshold (for eigenfeature-based data).

Profile correlation among biological replicates

The signatures of the four biological replicates were compared pairwise to each other using four different measures: (1) Pearson correlation; (2) cosine similarity $\left(\frac{\overrightarrow{x}\cdot \overrightarrow{y}}{\Vert \overrightarrow{x}\Vert \cdot \Vert \overrightarrow{y}\Vert }\right)$; (3) Jaccard similarity³⁶, and (4) p-value of Jaccard similarity³⁷. Jaccard similarity was calculated using the R function jaccard.test in package jaccard with option method=”asymptotic”. Each measure resulted in six comparisons, of which the third best value was used as the overall correlation/similarity score (this allows for the fact that if there was one outlier replicate, it would produce three low correlations).

Chemicals were considered active if the third best value was higher than the 90^th percentile of values of the null data set (or lower than the 10^th percentile for Jaccard p-values). The option with the best performance was Pearson correlation with a signature threshold of 1.75 (for feature-based data) and cosine similarity (for eigenfeature-based data).

Results

Overview of the Different Approaches

For this study we compared several multi-concentration and single-concentration approaches for hit identification as illustrated in Figure 1. Definitions for hit calls and potency estimates are summarized in Table S2. The different approaches have varying levels of mathematical and computational complexity. We hypothesized that the approaches would have differing abilities to identify chemicals as bioactive and varying susceptibility to assay noise; in particular, chemicals with weak or very specific effects might demonstrate the greatest variation in hit identification and potency across methods.

Comparison of Performance of Hit Determination Approaches

A previously published dataset²⁶ was reanalyzed and results compared using all the described approaches. The dataset comprised 462 unique test chemicals, of which 16 were screened in duplicate. Four reference chemicals were screened in concentration-response 12 times (corresponding to the number of plate groups in the study). In addition, a null data set comprised of 108 ‘null chemicals’ was constructed using data from the lowest two concentrations of test chemicals.

These various quality control datasets (i.e. duplicated test chemicals, reference chemicals, null data set) were used to optimize parameters for each individual modeling approach and to subsequently compare their performance. The FPR was empirically measured using the null data sets, while the TPR was based on the ability to reliably detect a subtle, specific reference chemical (berberine chloride). Concordance was based on hit calls for 16 chemicals screened in duplicate, i.e. the ability to consistently call both instances as inactive or bioactive. Parameters of each approach were optimized to achieve an FPR of ~ 10% and maximal TPR. If multiple sets of parameters produced equivalent results according to these criteria, the most permissive threshold with high concordance was chosen.

For 11/15 approaches, 100% TPR was achieved at an FPR ≤ 10% (Fig. 2, green triangles for FPR). Only the single concentration approaches using eigenfeature-level data and global fitting using Euclidean distance were not able to identify all berberine chloride replicates as bioactive. All approaches with 100% TPR also achieved concordance ≥ 75% (Fig.2, blue diamonds for concordance), with feature-level fitting using tcplfit2 achieving 100% concordance.

Fig. 2: Comparison of Performance of Hit Determination Approaches.

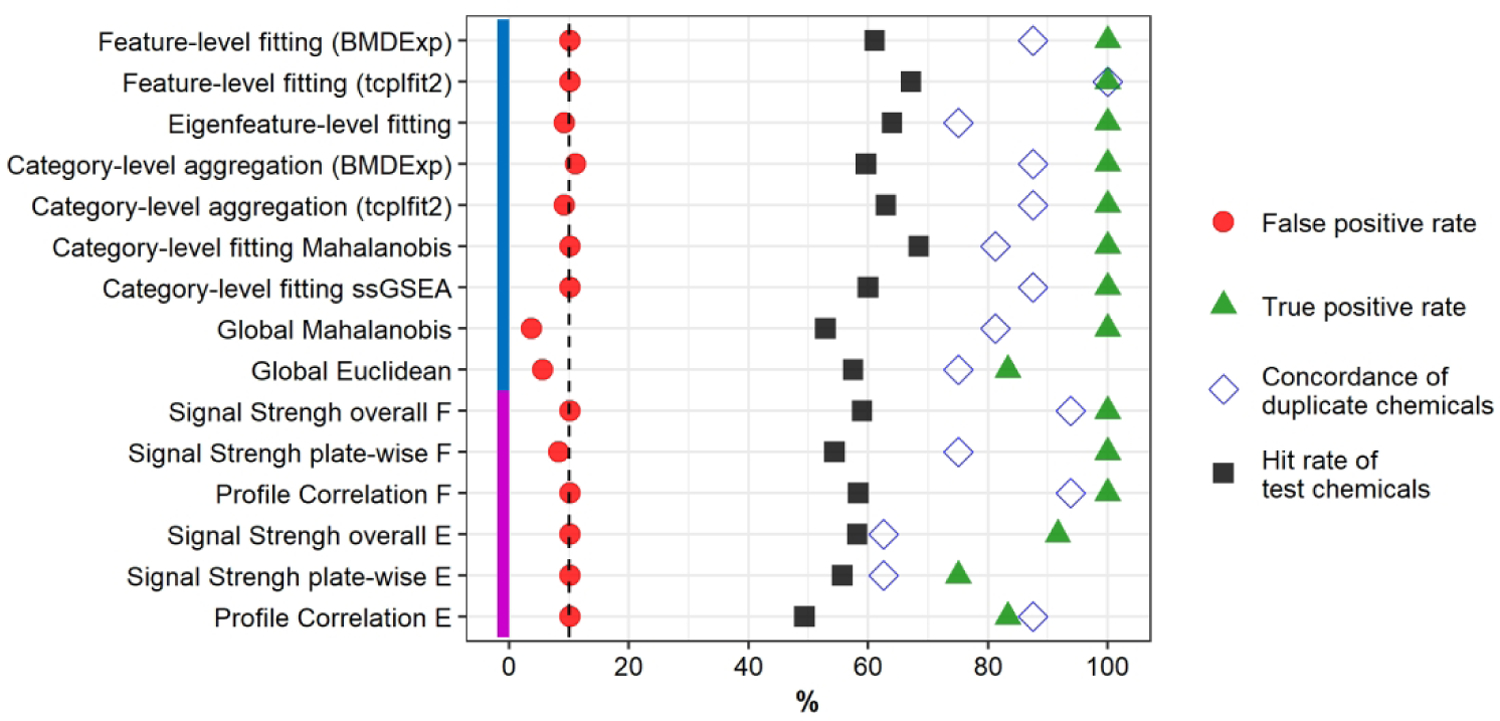
A previously published data set²⁶ was used to compare all approaches. U-2 OS cells were exposed for 24 h to the chemicals. Chemicals were tested in four biological replicates, resulting in a total of 48 assay plates organized as 12 plate groups. Approaches were optimized to a false positive rate of ~ 10% (vertical dashed line) based on a randomized null data set (red circles; n = 108) and the best possible true positive rate based on the reference chemical berberine chloride (green triangles; n = 12). Sixteen random test chemicals were screened in duplicate and used to calculate concordance (blue open diamonds) as the number of unique chemicals classified in both occurrences as either active or inactive. The hit rate of test chemicals (black squares) was calculated from 478 test chemicals, with the exception of approaches using tcplfit2 to fit, for which three chemicals had fewer than four concentrations and were excluded from concentration-response modeling. Method name abbreviations: ssGSEA: single sample gene set enrichment analysis; F: feature-based; E: eigenfeature-based.

Overall, the evaluated approaches identified between 49 – 68% of test chemicals as bioactive. Multi-concentration approaches had a slightly higher hit rate than single concentration approaches in general. Of note, fitting with tcplfit2 resulted in more chemicals identified as bioactive than fitting with BMDExpress, for both feature-level fitting and category-level aggregation of feature-level fits as the basis for hit calls.

Concordance of Hit Calls Among Approaches

Next, we wanted to investigate whether different approaches identify the same chemicals as bioactive. Overall, there was a large number of test chemicals that were identified as bioactive by all approaches, while another group of test chemicals, together with most null chemicals, were identified as inactive with all approaches (Fig. 3A). Single-concentration approaches clustered separately from the multi-concentration approaches; a small group of chemicals was bioactive in the latter but not the former group of approaches. For these 13 chemicals, the PAC approximated the highest non-cytotoxic concentration (data not shown). Feature-level fitting and category-level aggregation methods clustered together by curve-fitting strategy (i.e. tcplfit2 or BMDExpress) rather than by aggregation level.

Fig. 3: Concordance of Hit Calls Across Approaches.

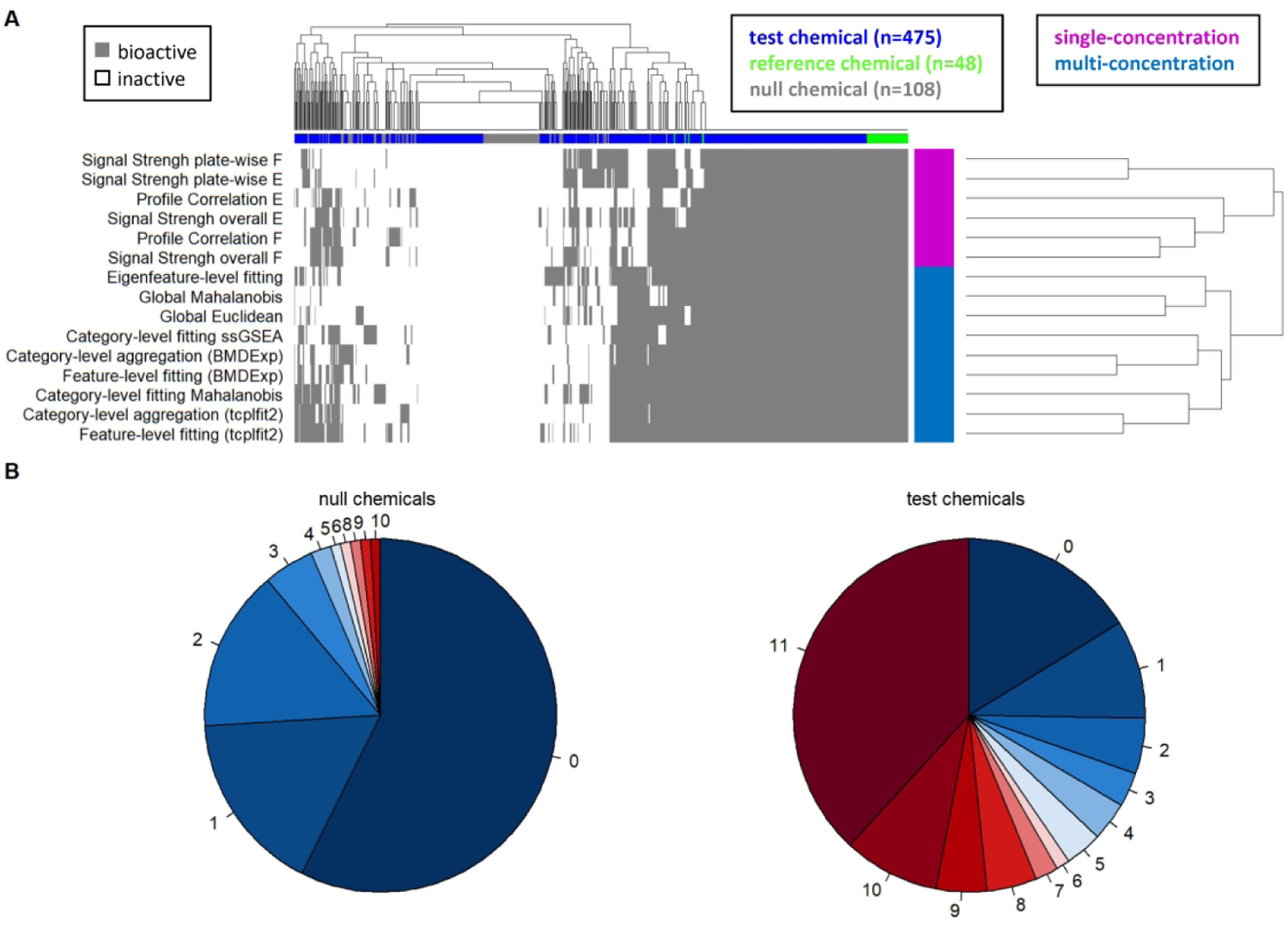
(A) Heatmap illustrating hit calls for all approaches (rows) and all chemicals (columns). Colors in the heatmap indicate whether the chemical was considered bioactive (gray) or inactive (white). The column annotation indicates the type of chemical: test chemical (blue), reference chemical (green), and null chemical (gray). The row annotation indicates multi-concentration approaches (blue) and single-concentration approaches (pink). (B) Pie charts summarizing the concordance among eleven approaches. Each pie chart slice indicates the proportion of 108 null chemicals (left) and 475 test chemicals (right), that were called as active by the number of approaches indicated by the numerical labels surrounding the pie charts. Four approaches with < 100% TPR were excluded (Global Euclidean, Signal Strength overall E, Signal Strength plate-wise E and Profile Correlation E). Three test chemicals had less than four concentrations, were not modelled with approaches that use tcplfit2, and were therefore excluded from the heatmap and pie chart. Abbreviations: ssGSEA: single sample gene set enrichment analysis; F: feature-based; E: eigenfeature-based.

To quantify the concordance among approaches, only the 11 approaches with 100% TPR were considered. These approaches identified the four reference chemicals (berberine chloride, Ca-074-Me, etoposide, rapamycin) as bioactive in all twelve replicates. For the null chemicals, 57% (62/108) were inactive with all approaches, with an additional 30% (32/108) identified as active by only one or two approaches (Fig. 3B, left).

In contrast, 38% (181/475) of test chemicals were considered active with all approaches, and an additional 13% (64/475) were called as active by nine or ten of the approaches (Fig. 3B, right). Approximately 30% (144/475) of chemicals were called as inactive by at least nine approaches. Overall, for 82% (389/475) of test chemicals, at least nine of the approaches agreed.

Concordance of Potency Estimates Among Multi-Concentration Approaches

One potential application of phenotypic profiling in regulatory toxicology is the derivation of potency estimates for perturbations of cellular biology from HTP data. For this purpose, limited detection of false actives is acceptable. However, avoiding false actives associated with highly potent estimates of bioactivity (i.e. those identified within the lower portion of the tested concentration range or below and associated with assay noise and not true biological activity) is desirable. Potency estimates such as these would not be an accurate representation of the biological activity of the chemical.

To evaluate these performance characteristics of the concentration-response modeling approaches, potency estimates (e.g. PAC) of reference chemical replicates were compared. While the true PAC is not known, previous analysis showed the reference chemical replicates yielded highly reproducible phenotypic profiles²⁶; therefore, PACs of individual replicates should be similar. This was the case for most approaches, particularly for the two reference chemicals with broad phenotypic effects (etoposide, rapamycin) (Fig. 4A). For berberine chloride, which has subtle and specific effects on a particular organelle (i.e. mitochondria), feature-based approaches produced PACs with low variability across replicates. PACs calculated from global approaches were less potent than those calculated from other approaches. Similarly, Ca-074-Me has very potent effects on Golgi morphology, which was detected by feature-level and category-level approaches; while global approaches, ssGSEA and eigenfeature-level fitting yielded less potent estimates.

Fig. 4: Concordance of Potency Estimates Across Multi-Concentration Approaches.

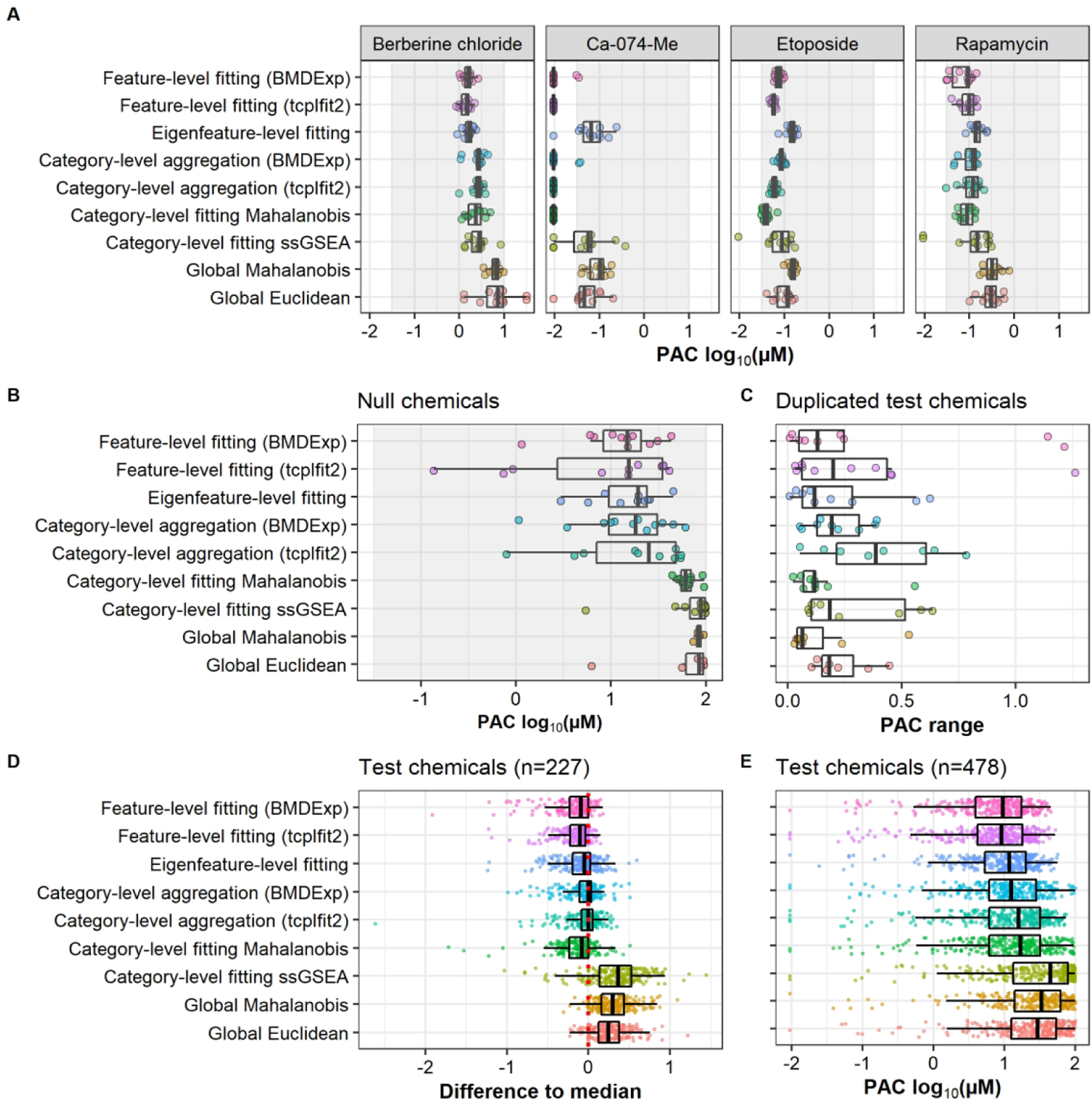
(A) Reproducibility of potency estimates of reference chemicals. All four reference chemicals were tested in twelve replicates within the study. The gray area indicates the range of tested concentrations. Replicates with potencies below the tested concentration range and replicates without a potency estimate (i.e. inactives) are displayed ½ an order of magnitude below or above the tested concentration range, respectively. (B) Potency estimates of null chemicals that were identified as active by each approach. Null chemicals were arbitrarily mapped to a concentration range of 0.03 – 100 μM with ½ log₁₀ spacing. (C) For the 16 test chemicals screened in duplicate, the difference of the two potency estimates is displayed for each test chemical that was identified as active in both instances for a respective approach (n = 7 – 10 per approach). The potency range is in units of log₁₀(μM). (D) Differences in potency estimates of test chemicals across the nine approaches. For each test chemical that was active across all nine approaches (n = 229), the median potency was estimated. Then, for each approach (rows), the difference of each chemical potency to the median potency was calculated. (E) Potency estimates for all test chemicals (n = 475 for approaches fit with tcplfit2, and n = 478 for all others) and all approaches. Abbreviation: PAC: phenotype altering concentration; ssGSEA: single sample gene set enrichment analysis.

We also compared the potency estimates from each method for null chemicals, which provides a model of false positive hits. As described above, each method was optimized to achieve an FPR of ~ 10%. Thus, by definition, only a small subset of null chemicals was identified as active and subsequently assigned a PAC by each approach. However, comparing the distribution of PACs for known false positives in each method provides an estimate of which methods are more prone to incorrectly calling bioactivity at higher potencies. We observed marked differences in the potencies estimated for null chemicals when comparing feature-level fitting and category-level aggregation approaches as compared to category-level and global fitting approaches: all feature-level and category-level aggregation approaches resulted in potency estimates well below the upper limit of the concentration range assigned to the null data set (i.e. 100 μM) (Fig. 4B). We term these ‘high-potency false actives’: i.e. potency estimates of ‘null chemicals’ that are lower than the second highest assigned dose (i.e. 30 μM). In contrast, global approaches and category level-fitting nearly exclusively estimated PACs close to the highest concentration level assigned to the null data sets and did not yield high-potency false active results.

Another important performance metric for each method is the similarity of PACs for chemicals screened in duplicate. Specifically, we computed “PAC range” as the log-scale difference in PAC estimates from the same method, between each pair of duplicate chemicals. Ideally, the PACs of duplicate chemicals should be close together (low PAC range). This was the case for the two global approaches and for category-level fitting of Mahalanobis distance (Fig. 4C). Overall, the PAC range was < ½ an order of magnitude for most chemicals, which in our opinion, indicates sufficient reproducibility for a first-tier screening assay.

Lastly, potency estimates of test chemicals were compared across the approaches. As the true potencies were not known, we calculated the median potency across all approaches for test chemicals called as active by all nine methods. We then investigated how individual approaches performed relative to this median. Feature-level and eigenfeature-level fitting resulted in the lowest PACs (highest potency estimates) for the majority of these test chemicals, sometimes > 1 order of magnitude below the median, followed by category-level fitting of Mahalanobis distance (Fig. 4D). Global approaches were mostly above the median, and ssGSEA yielded the highest PACs. In pairwise comparisons of each approach, correlations of potency estimates for complete cases (i.e. a chemical being identified as a hit in both of the approaches being compared) were high (Fig. S1). Of note, most bioactive chemicals identified by each method in our dataset had a PAC between 10 – 100 μM (Fig. 4E).

To summarize, feature-based approaches (feature-level fitting and category-level aggregation approaches) generally resulted in lower PACs, but also produced a greater frequency of high-potency false active results.

Comparison of Bioactivity Profiles Across Feature- and Category-Based Approaches

We also wanted to investigate whether the phenotypic features and feature categories identified as most sensitive for a given chemical were consistently identified using the multi-concentration modeling approaches. In this context, the “most sensitive” feature/category is defined as having the lowest potency estimate compared to other features/categories within a given method and is distinct from the calculation of TPR described above. For this purpose we leveraged the reference chemicals that were tested in twelve replicates and whose qualitative effects have been described previously^{6, 26}. Potency and effect size values for feature-level data were averaged across the twelve replicates and plotted (Fig. 5A). In addition, median potency values for affected categories were calculated and rank-ordered for each reference chemical (Fig. 5B). Only features/categories affected in the majority of replicates are shown. Thus, the displayed profiles represent a robust measure for each modeling approach.

Fig. 5: Comparison of Bioactivity Profiles Across Feature- and Category-Based Approaches.

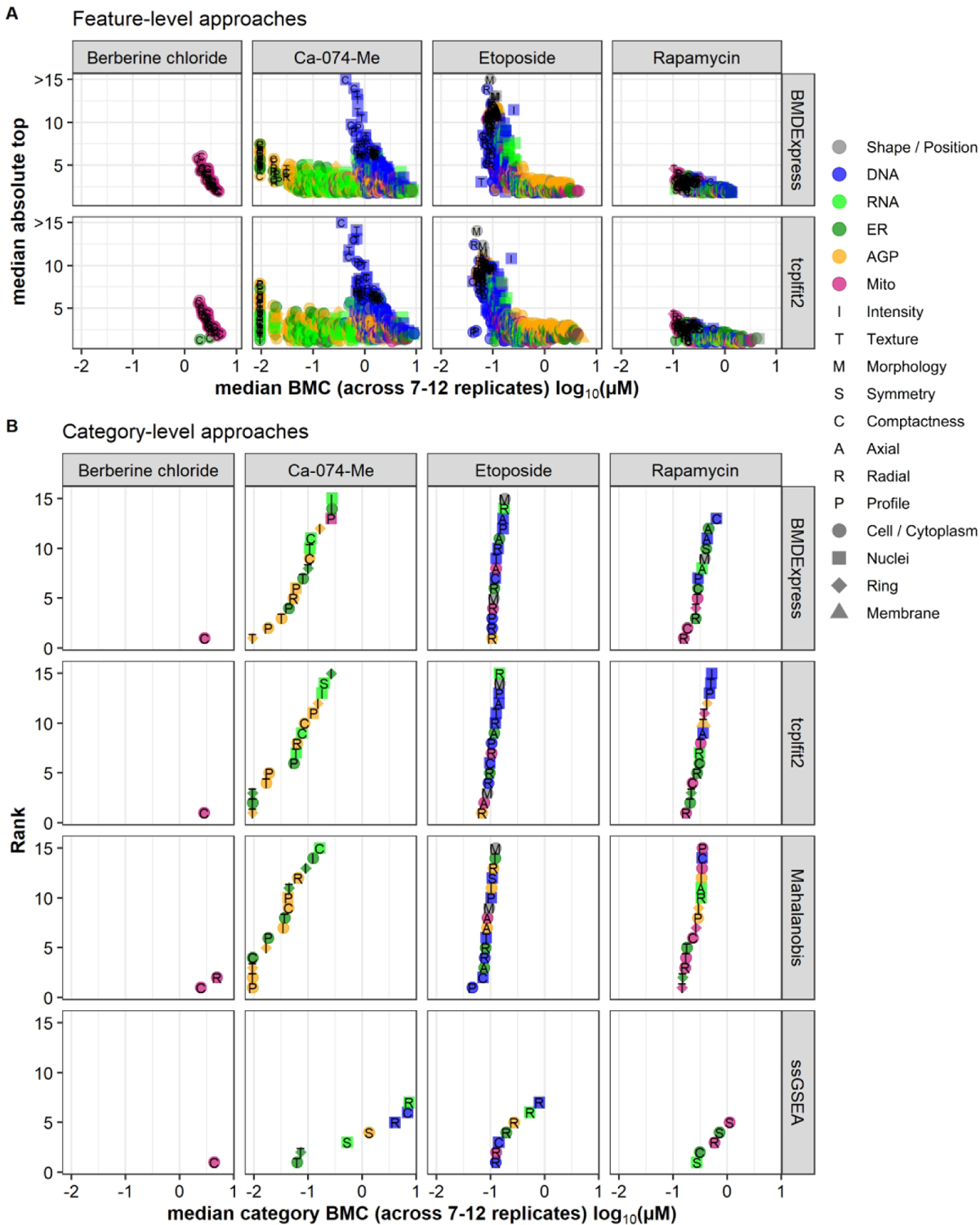
(A) Potency (x-axis) vs effect size (y-axis) for both feature-level approaches (BMDExpress and tcplfit2). For each reference chemical and feature, the median BMC and the median absolute top of the curve was calculated from the 12 replicates. Features are only displayed if they had a valid BMC in the majority of replicates (i.e. ≥ 7). (B) BMC accumulation plots for all category-based approaches. For each reference chemical and category, the median BMC was calculated from the 12 replicates. Categories that had a valid BMC in the majority of replicates (i.e. ≥ 7) were ranked according to their potencies. Only the 15 most potent categories are displayed. In both (A) and (B), features and categories, respectively, were coded with respect to shape/fluorescent channel (color), feature type (letter) or cellular compartment (shape).

Overall, fitting with BMDExpress and tcplfit2 resulted in very similar bioactivity profiles, both on the feature-level (Fig. 5A) and category-level (Fig. 5B). Mitochondrial compactness was identified as being affected by berberine chloride using all six approaches, consistent with previous qualitative observations. For Ca-074-Me, feature-level approaches showed that the AGP/ER channel was most sensitive (BMCs below the tested concentration) and that nucleus morphology was affected at higher concentrations, both of which are consistent with previous observations. This potent effect of Ca-074-Me is also captured with the category-aggregation approaches and category-level fitting of Mahalanobis distance, but not with ssGSEA. ssGSEA was less sensitive and did not identify the AGP phenotype in a manner similar to the other approaches (this phenotype is clearly visible upon manual inspection of images from Ca-074-Me treated cells²⁶). Many features/categories were affected following etoposide and rapamycin treatment. The rank order of the categories varied among the approaches, but there was a consensus regarding the potency estimate and the affected categories for all approaches except ssGSEA. ssGSEA again produced higher PACs and identified many fewer affected categories compared to the other three category-based approaches. A similar trend was observed for a sub-set of test chemicals (Fig. S2).

Overall, the two curve-fitting software tools BMDExpress and tcplfit2 had good agreement, both on the feature-level as well as with regards to category-aggregation. Category-level Mahalanobis was comparable to the aforementioned approaches, while category-level ssGSEA yielded largely discordant results.

Discussion

High-throughput profiling (HTP) assays are becoming increasingly popular in the pharmaceutical and toxicological sciences for investigating the effects of chemicals or genetic manipulations on cellular biology. The high dimensionality of these assays makes hit identification in the context of HTS very challenging. In the regulatory science arena, it has been proposed that HTP assays can be used to rapidly screen chemicals for the purpose of hazard identification and identification of bioactive concentrations^{9, 12}. However, at present there are no widely accepted standard practices for identifying hits or potency estimates from imaging-based HTP assays¹⁵. The lack of standardized approaches for data analysis, including demonstration of reliable approaches for classification of chemicals as inactive or bioactive with some accompanying estimation of potency, represents a barrier to broader use of imaging-based HTP data for application to regulatory decision-making. We previously screened a set of 462 environmental chemicals with the Cell Painting assay in U-2 OS cells²⁶. In the previous study, we used feature-level fitting with BMDExpress followed by category-level aggregation to identify bioactive chemicals and determine PACs. However, we did not explore other approaches for data analysis and PAC determination. The previously implemented category-level aggregation approach used an empirical threshold of 30% of features being concentration-responsive in order for a category to be considered active. One objective of the present study was to explore the use of category-based and global analysis approaches that were not dependent on this inflexible criteria for classifying chemical as inactive or bioactive. In the present study, we analyzed the data set from Nyffeler, et al.²⁶ with nine multi-concentration and six single concentration approaches (including the previously implemented category-aggregation approach using the BMDExpress software package) and systematically compared hit concordance and potency estimates where applicable. For the present study, we optimized each approach in terms of FPR as determined using a null data set and TPR as determined using a subtle, but reproducible, phenotypic reference chemical. For the vast majority of test chemicals, there was good agreement among the different approaches, both in terms of hit calls and potency estimates. However, we did observe differences among the approaches, in particular with regards to consistency of potency estimates for chemicals screened in duplicate and the risk of identifying high-potency false actives. Based on the comparisons performed in this work, category-wise Mahalanobis distance calculation followed by curve-fitting demonstrated the lowest variability in PACs determined from duplicate screening of chemicals and demonstrated the lowest risk of identifying high potency false active chemicals. Both of these performance characteristics are desirable for analysis of HTP data in the context of environmental chemical bioactivity screening and potential use in chemical safety assessment applications.

In the present study, we evaluated approaches with varying degrees of complexity that yield inactive versus bioactive hit calls (all approaches) and, for multi-concentration approaches, PACs based on calculation, aggregation and/or ranking of feature-, category-, or global-level potency values (Fig. 1). The starting point for the comparative analysis was category-level aggregation of BMDExpress fitted feature-level data, as described in Nyffeler, et al.²⁶. This approach was adapted from a standard approach used in transcriptomics research for concentration-response modeling of high-dimensional data that also provides biological context for interpretation of chemical effects by mapping to gene sets^{12, 29, 38, 39}. Phenotypic category-based analysis (similar to gene set-based analysis in transcriptomics) facilitates biological interpretation of high-dimensional feature data by aiding in identification of effects on organelles that may be associated with chemical bioactivity or toxicity. Feature-level fitting with BMDExpress was time consuming (~20 min per chemical for modeling 4 curve shapes on a computer with 20 processing cores) and documentation of and access to the underlying model executables was limited within the confines of the R computing environment. We therefore explored if modeling with the R package tcplfit2 would yield equivalent results, improve data processing efficiency, and make the curve-fitting procedure used more accessible. Tcplfit2 was faster (~3 min per chemical for modeling 9 curve shapes on a computer with 4 processing cores) and its code is amenable to adaptations for applications to this and other data streams. The slower processing efficiency of BMDExpress may be due to use of validated model executables deployed as part of the low-throughput BMDS modeling approach (https://www.epa.gov/bmds) and differences in the approaches BMDExpress and tcplfit2 use to calculate confidence intervals around the BMCs, a requirement for regulatory testing⁴⁰.

We also evaluated other approaches used frequently in image-based profiling for discrimination of treatment from control samples: namely, Euclidean and Mahalanobis distance metrics^{15, 41}. We had previously used the latter approach in a steroidogenesis screening assay that measures levels of 11 hormones (e.g. “features”) to calculate a single metric for discrimination of active and inactive environmental chemicals in a screening for prioritization context^{42, 43}. The Mahalanobis distance-based approach requires dimensionality reduction, a process frequently implemented in imaging-based profiling studies^{8, 15} and accounts for covariance among features, a common property of imaging-based profiling data. Here, we used feature reduction with PCA to derive eigenfeatures that were then used to calculate Mahalanobis distances. Both Euclidean and Mahalanobis distances were computed globally (i.e. using all the feature data). We then took the novel step of concentration-response modeling the global distance metrices (as well as the eigenfeatures used to derive the latter) using tcplfit2 to identify PACs. While an apparent advantage of the global-fitting approach was derivation of a single response variable for hit determination and calculation of PACs, a decided disadvantage was the loss of biological or mechanistic interpretability: i.e. it is unclear from the global modeling approaches which feature(s) or category(ies) are most sensitive to perturbation or driving the phenotypic response. We therefore implemented the Mahalanobis distance approach within the pre-defined phenotypic categories to maintain biological interpretability similar to the aforementioned category aggregation approaches while also accounting for correlations in similarly derived features. We adapted the ssGSEA approach from transcriptomics^{34, 35} using the phenotypic categories as de facto gene sets and z-standardized responses in lieu of fold-changes; ssGSEA scores were also modeled using tcplfit2. The signal strength approach in this study is a modification of the global Euclidean distance for the single-concentration application and has been used in a different form by others⁷. Finally, we evaluated profile comparison approaches that have been used in both transcriptomics studies^{37, 44–47} and image-based profiling¹⁵, although we repurposed the approach to measure similarity of biological replicates of a single chemical. While the primary focus of our research is concentration-response screening, the profile comparison and signal strength approaches are appropriate for use in hit determination by researchers conducting single-concentration screening studies, a common practice used to reduce the resources required to screen large chemical libraries. Overall, the described suite of hit determination approaches have trade-offs with regards to computational complexity, computing time, ease of biological interpretability, and provision of potency values that should be taken into account by researchers in the context of their particular research objectives.

The different approaches were compared by estimating FPR (from a null data set), TPR (from berberine chloride replicates) and concordance (from duplicated test chemicals). To compare the approaches in a consistent way, we first tuned each method to achieve a target FPR of 10% (Fig. 2). As Cell Painting is likely to be used as a first-tier toxicity screening assay, high sensitivity was preferred over high specificity. For all multi-concentration approaches (except global Euclidean) and all single-concentration approaches based on features (not eigenfeatures), a 100% TPR was achieved at an FPR of 10% or less, indicating high sensitivity of these approaches as implemented. For a subset of approaches (both global fitting approaches), the FPR was below 10% using a BMR of 1 nMad. Decreasing the BMR further to achieve the 10% FPR for these approaches didn’t seem reasonable for detecting meaningful biological effects. In addition, the concordance of hit calls for chemicals screened in duplicate was ≥ 75% for approaches where a TPR of 100% could be achieved. This indicated that each of those approaches reproducibly classified a random set of environmental chemicals as active or inactive a majority of the time. However, it should be noted that the TPR (and associated sensitivity) was estimated from only 12 replicates of a single phenotypic reference chemical, berberine chloride. Using only a single reference chemical could lead to ‘overtraining’ of approaches to detect this particular type of response. Therefore, this metric of sensitivity should be interpreted with caution. For a more thorough evaluation of sensitivity, it would be desirable to evaluate a larger set of chemicals with previously characterized biological activity that is representative of the environmental chemical space (such as chemicals selected from the ToxCast collection⁴⁸) and that have been evaluated repeatedly in our test system. As we are in an early stage of implementing the assay, we have not yet identified or screened a set of well-known “positive” chemicals within the environmental chemical space that could be used for this purpose. Instead, we decided to make use of the phenotypic reference chemicals run on each plate for the current sensitivity analysis. These reference chemicals (i.e. berberine chloride, Ca-074-Me, etoposide, rapamycin) were originally included in the screening study design to assess assay reproducibility as they produce robust, reproducible, visually discernable phenotypes. We decided to use only berberine chloride to estimate TPR, as this chemical is the one most closely resembling suspected behavior of environmental chemicals, with subtle, yet reproducible, phenotypic effects. Of note, the other three reference chemicals have larger effects and were identified by all approaches as active. Overall, there was large concordance among the approaches in terms of hit calls (Fig. 3A). There was a group of 13 chemicals that were identified as active using multi-concentration approaches but not identified as active with single-concentration approaches. Apart from this observation, there was no clear pattern among the approaches, suggesting that chemicals with discordant hit calls were probably chemicals with borderline activity and depending on the specifics of the approach they were classified as either active or inactive. This hypothesis is supported by the observation that there is a general trend of an increasing number of approaches that called a chemical as active with increasing signal strength (Fig. S3). Most null chemicals were consistently identified as inactive across different approaches (Fig. 3B, left), with only 4/108 null chemicals identified as active with the majority of approaches. For 96/108 null chemicals, ≤ 2 approaches identified them as hits. On the other hand, 82% of test chemicals were identified by all or most (9 out of 11) approaches as either active or inactive, with few chemicals in between (Fig. 3B, right). High concordance of hit calls across a variety of approaches provides a relatively greater weight-of-evidence that chemicals were either biologically active or inactive in our testing scenario (i.e. U-2 OS cells exposed to 24 h for up to 100 μM). Conclusions regarding the biological activity of chemicals associated with discordant hit calls across a variety of approaches would be associated with a relatively lower degree of confidence.

All the approaches we evaluated had a comparable hit rate for test chemicals, between 50 – 70%. This was surprising, as these approaches were implemented using different levels of “compressed” data. For example, Global fitting with the Mahalanobis approach worked surprisingly well, although the 1300 features were “compressed” to only one number (e.g. Mahalanobis distance) before curve fitting. Moreover, single-concentration approaches were able to identify a similar number of bioactive chemicals as compared to the multi-concentration approaches. Thus, if hit identification is the primary goal of a study (and not estimating potency), single-concentration screening might be sufficient for this purpose. However, it should also be noted that in the present study, we utilized information from multi-concentration cytotoxicity screening to choose the most informative (single) concentration to include in the analysis.

The hit rate of 50 – 70% was also substantially lower than the 95% hit rate reported in our previous analysis of these data²⁶. The main explanation for this difference was the more stringent hit call thresholds implemented in the present analyses, which were optimized to an upper limit of 10% FPR. Specifically, for feature-level fitting and subsequent category-level aggregation of BMDExpress results, an additional effect size threshold (not used in the previous study) had to be introduced to reduce the FPR to 10% and led to an overall reduction in the percentage of chemicals identified as hits; i.e. excluding chemicals with non-efficacious changes in phenotypic features. From a practical perspective, calibrating the hit call threshold to a set FPR using the noise structure inherent to HTP data provides a means to identify bioactive chemicals with greater confidence, an important consideration when triaging chemicals for hit confirmation within a tiered toxicity testing strategy or for considering HTP data for use in chemical safety assessment.

Of note, fitting with tcplfit2 led to a slightly higher hit rate than fitting with BMDExpress using either feature-level fitting or category-level aggregation. In instances where a chemical was identified as active using both approaches, the number of affected features and PACs were highly correlated (Fig. S4). While most parameters were kept constant between the two approaches, there were two notable differences in the implementation: (1) In order to reduce FPR to the target of ≤ 10%, an additional threshold for effect size was necessary to incorporate into the original BMDExpress approach; and (2) nine different models were used for tcplfit2 fitting compared to only four models with BMDExpress. Despite fitting more models, tcplfit2 was faster than BMDExpress, and increasing the number of models tested with BMDExpress would significantly increase analysis run times. We previously explored using more models in BMDExpress and found that performance was not increased substantially, while risk for identification of high-potency false actives increased (data not shown). Another difference is that BMDExpress does not have a ‘constant’ model but relies on pre-filtering steps (not applied here) and goodness-of-fit tests to decide if a concentration-dependent effect is present.

Concordance of potency estimates for reference chemicals was high, indicating that for chemicals with a robust signal most approaches give equivalent results (Fig. 4A). However, there were substantial differences among the approaches in terms of potency estimates for null chemicals (Fig. 4B). Eigenfeature-level fitting, feature-level fitting and category-level aggregation of feature-level null data all produced a number of high-potency false positives, while global fitting approaches and category-level fitting did not. One explanation is that the PAC for feature-level analysis was defined as the 5^th percentile of potencies for individual features. Null data sets should – by definition – represent baseline assay noise and thus generally only a few features should be identified as affected (e.g. have an estimated BMC). In that case, the 5^th percentile coincides with the most sensitive BMC. As such, we strongly discourage using the 5^th percentile of feature-level BMCs to derive a PAC as this could contribute to erroneous high potency hit calls for chemicals with little to no actual biological activity in the test system. Of note, category-aggregation approaches were not exempt from this problem, even though aggregating features within categories and defining the most sensitive category with ≥ 30% coverage as the PAC was an attempt to reduce the influence of spurious curve fits²⁶. Correlation of features within individual categories may have contributed to this finding, as the category-level aggregation approaches do not account for this phenomenon. The category-level fitting approaches using Mahalanobis distance does account for correlations in the feature data within categories and did not suffer from the same type of performance deficit as category-level aggregation (Fig. 4B). In addition, category-level fitting produced the least variable estimates of biological potency in chemicals screened in duplicate as compared to all other multi-concentration approaches (Fig. 4C). Overall, feature-based approaches gave the most potent PACs, but were not very robust in identifying chemicals with weak bioactivity (i.e. those that did not produce large effect sizes in individual feature measurements) and were prone to identification of high-potency false actives. Global approaches yielded slightly less potent PACs but had a much lower risk of identifying high-potency false actives. Category-level fitting of Mahalanobis distances was in between the two with relatively higher potency estimates (as compared to global fitting) and relatively lower risk for identifying high-potency false actives (as compared to feature-level fitting or category aggregation).

Category-level fitting of ssGSEA scores did not produce high potency false actives in the null chemicals but had large variability in terms of potency estimates for chemicals screened in duplicate. In addition, comparison of bioactivity profiles across feature-level fitting, category-level aggregation or category-level fitting approaches demonstrated marked qualitative differences between biological responses identified by ssGSEA and any of the other approaches (Fig. 5). The effect of berberine chloride on mitochondrial morphology was picked up by all these approaches, including ssGSEA, despite its specific effects on a few features/categories. This shows that all these approaches were overall capable of picking up such specific effects. However, category-level fitting of ssGSEA scores did not detect the effect of Ca-074-Me on the AGP channel. The effect of Ca-074-Me on the morphology of U-2 OS cells in the AGP channel can be discerned upon visual inspection of images, is associated with large magnitude changes in many features when measured quantitatively and is highly reproducible^{26, 49}. Therefore, ssGSEA did not reliably identify the most marked morphological effects associated with a well-characterized reference chemical. In addition, for the other reference chemicals, ssGSEA identified fewer categories as being affected and the range of category-level potency estimates was broader as compared to other category-level modeling approaches. Of note, the most sensitive category identified for Ca-074-Me with ssGSEA was at a higher concentration than other category-based approaches. These observations might be due to the fact that in the current implementation of ssGSEA scores are normalized across categories. This may result in low enrichment scores for chemicals with broad effects across many phenotypic features / categories, as no specific category will be enriched compared to all others in terms of being the extremes of the distribution. Overall, these results indicate that while ssGSEA has been applied successfully to transcriptomics data³⁴, it did not perform well on our phenotypic profiling data, at least in the present configuration.

In this study, the null data set was constructed from data from the lowest two test concentrations used for chemical screening. As chemicals with activity at these concentrations were excluded, we are confident that the null data set is an appropriate surrogate for inactive chemicals. However, other strategies to build null data sets could be used. For example, for some applications it might be desirable to randomly sample individual feature values independently, rather that randomly sample individual wells as we have done here. Our current strategy was chosen to maintain the observed correlation among features in our profiling data and to provide a fair comparative basis for approaches that inherently account for this correlation. In addition, while we included some approaches that model a reduced feature set (eigenfeatures), we haven’t explored all of the feature reduction and feature selection strategies that have been proposed in the imaging-based profiling research community, including machine-learning based approaches¹⁵. Because many features within imaging-based profiling data are inherently correlated, feature reduction could decrease the amount of data input into the analysis and equalize the weight of each feature. The benefit of feature reduction can be seen in the present study by comparing global fitting with Euclidean distance (all features) vs Mahalanobis distance (reduced feature set): global Mahalanobis had a higher TPR at the fixed FPR. We observed in preliminary work that the results of approaches based on eigenfeatures depend on the choice of input data to the PCA. More work is needed to find the optimal input data set, feature reduction method and number of retained eigenfeatures.

For our purposes, the Cell Painting assay is envisioned as a “first-tier” bioactivity assay for environmental chemicals⁹. As with any other in vitro assay, a low FPR is desirable. However, from the perspective of human health protection, identification of false positives is preferred over misclassification of true positives as inactive, particularly when only positive hit calls will undergo follow-up testing. With these principles in mind, the present study was tailored for screening of environmental chemicals, under the hypothesis that many (but not all) environmental chemicals will have marginal bioactivity as evaluated using the Cell Painting assay or produce nonspecific (i.e. promiscuous) molecular effects in human cells. This is in sharp contrast to pharmaceutical screenings, where bioactivity of small molecules is desired and expected. In our study, approaches were optimized for high sensitivity and consequently accepted a relatively high FPR of 10%. Overall, using the described optimization criteria, we found that feature-based approaches were sensitive but had a higher risk of high-potency false actives, and that category-based modelling with Mahalanobis distance had nearly as high a sensitivity, but a lower risk for high-potency false actives. This category-level fitting approach also facilitates biological interpretation of the profiling data, a utility that is lacking using the global fitting approaches. While some of these findings described here might be specific to the chemical space examined and the optimization schema, the general framework of comparing different approaches to gain confidence in hit identification should be of broad interest to both the high-throughput screening and regulatory research communities. In particular, this analysis framework can be applied to ongoing applications of the Cell Painting assay to a broader range of human-derived in vitro models and screening a larger chemical space to calculate thresholds for chemical bioactivity and discern putative cellular MOA for environmental chemicals.

Abbreviations

AGP

actin skeleton, golgi and plasma membrane

AIC

Akaike information criterion

BMC

benchmark concentrations

BMR

benchmark response

CV

cell viability

CV.LOEL

lowest cytotoxic concentration

CV.NOEL

highest non-cytotoxic concentration

ER

endoplasmic reticulum

FPR

false positive rate

HTP

high-throughput profiling

HTS

high-throughput screening

MOA

mechanism of action

MIE

molecular initiating events

nMad

normalized median absolute deviation

PAC

phenotype altering concentration

PCA

principal component analysis

SD

standard deviation

SS

signal strength

ssGSEA

single sample gene set enrichment analysis

TPR

true positive rate

USEPA

United States Environmental Protection Agency