Comparison of Statistical Approaches to Evaluate Factors Associated With Metabolic Syndrome

Abstract

J Clin Hypertens (Greenwich).

In statistical analyses, metabolic syndrome as a dependent variable is often utilized in a binary form (presence/absence) where the logistic regression model is used to estimate the odds ratio as the measure of association between health‐related factors and metabolic syndrome. Since metabolic syndrome is a common outcome the interpretation of odds ratio as an approximation to prevalence or risk ratio is questionable as it may overestimate its intended target. In addition, dichotomizing a variable that could potentially be treated as discrete may lead to reduced statistical power. In this paper, the authors treat metabolic syndrome as a discrete outcome by defining it as the count of syndrome components. The goal of this study is to evaluate the usefulness of alternative generalized linear models for analysis of metabolic syndrome as a count outcome and compare the results with models that utilize the binary form. Empirical data were used to examine the association between depression and metabolic syndrome. Measures of association were calculated using two approaches; models that treat metabolic syndrome as a binary outcome (the logistic, log‐binomial, Poisson, and the modified Poisson regression) and models that utilize metabolic syndrome as discrete/count data (the Poisson and the negative binomial regression). The method that treats metabolic syndrome as a count outcome (Poisson/negative binomial regression model) appears more sensitive in that it is better able to detect associations and hence can serve as an alternative to analyze metabolic syndrome as count dependent variable and provide an interpretable measure of association.

The metabolic syndrome is a cluster of conditions that occur together increasing the risk of heart disease, stroke, and diabetes. It is considered present when an individual has 3 or more of the following 5 syndrome components ¹ : (1) elevated waist circumference (≥102 cm in men, ≥88 cm in women); (2) elevated triglycerides (≥150 mg/dL); (3) reduced high‐density lipoprotein (HDL) cholesterol (<40 mg/dL in men, <50 mg/dL in women); (4) glucose intolerance (fasting glucose ≥100 mg/dL or diabetic medication use); and (5) hypertension (systolic blood pressure (SBP) ≥130 mm Hg or diastolic blood pressure (DBP) ≥85 mm Hg or antihypertensive medication use). Metabolic syndrome is highly prevalent among adults in the United States. ² The prevalence of metabolic syndrome is increasing, especially in North and South American countries and may present a major worldwide public health challenge in the future. ³ In light of this, studies on improved scientific approaches that would enable researchers to better understand factors that lead to or are associated with the metabolic syndrome could be worthwhile.

In cross‐sectional as well as prospective studies, investigators are frequently interested in determining the association between numerous health‐related variables and metabolic syndrome. ⁴ , ⁵ , ⁶ , ⁷ In a cross‐sectional design, when metabolic syndrome is the outcome of interest, the relationship between exposure variable(s) and metabolic syndrome is analyzed using two of the distributions from the class of generalized linear models; the logistic and the log‐binomial regression models where the odds and prevalence ratios are the measures of association, respectively. ⁸ , ⁹ , ¹⁰ , ¹¹ , ¹² Both models utilize metabolic syndrome as a binary outcome measure. Dichotomization of metabolic syndrome simplifies the statistical analysis and leads to easy interpretation of the results. However, dichotomizing an outcome variable that could otherwise be treated as discrete may lead to some loss of information and overall reduced statistical power. ¹³ The definition of metabolic syndrome can be modified, as the total count of syndrome components for an individual, to represent a discrete outcome (0, 1, 2, 3, 4, or 5) where statistical models for count data can be used as an alternative to assess the association between exposure variable(s) and metabolic syndrome. To our knowledge, the latter approach has not been used in research studies to date. Generalized linear models for discrete outcomes include the Poisson and the negative binomial regression models. ¹⁴ , ¹⁵ , ¹⁶ This study uses empirical data from the Buffalo Cardio‐Metabolic Occupational Police Stress (BCOPS) study ¹⁷ to evaluate the use of alternative generalized linear models for statistical analyses of metabolic syndrome as a discrete outcome measure and compares the results with the commonly used models that employ metabolic syndrome as a binary response variable. The paper first provides a review of generalized linear models including models for discrete and binary outcomes.

Generalized Linear Models

Traditional linear models are extensively used in statistical data analyses but departures from the restrictive assumption (continuous response, normally distributed data with constant variance) are common in practice. A powerful and flexible set of models called generalized linear models ¹⁸ , ¹⁹ , ²⁰ , ²¹ , ²² can handle a broader class of regression problems. The class of generalized linear models is simply an extension of the traditional linear model where: (1) the distribution of error terms can come from a family of exponential distributions rather than just the normal distribution; (2) the link function enables a wide variety of response variables to be modeled rather than just continuous variables; and (3) the variance can be a specified function of the mean rather than just being constant. Generalized linear models relate the mean of a population to a linear predictor through a nonlinear link function and allow the response probability distribution to be any member of an exponential family of distributions. The GENMOD procedure in SAS/STAT (SAS Institute, Cary, NC) provides a number of tools that are built to accommodate these different modeling situations.

Models for Discrete Outcome

Poisson Regression Model  Poisson regression is a widely used modeling technique for discrete, often highly skewed, count data where the response variable has only nonnegative integer values (0, 1, 2, 3, etc.) without an upper limit. ¹⁹ , ²² In Poisson regression it is assumed that the dependent variable, the number of occurrences of an event of interest, has a Poisson distribution conditional on the values of the independent variables X_1i, X_2i,…, X_ki. Since the Poisson mean is required to be positive, the Poisson regression uses a log link function to relate the expected value of the response variable (E(Y_i)=μ_i) to a linear combination of the explanatory variables (which could be continuous, ordinal, nominal, or a mixture of those) as follows:

(1)

The parameter estimates represent the expected change in the log scale. After some algebraic manipulation, it can be shown that the measure of association between an explanatory variable X_i and the response, referred from here on as ratios of means (RM), is

(2)

and represents a multiplicative effect on the estimated mean count (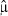) for a one‐unit increase in X_i. The expression 100 (RM−1) represents the percent change in the expected number of events with each one‐unit increase in the predictor variable X_i.

If Poisson regression is the method of choice to model count data, the sample distribution of the response variable should have a fairly small mean, ²³ below 10, preferably below 5, and ideally in the neighborhood of 1. An unusual property of the Poisson distribution is that the mean and variance are equal, μ=σ². This could be a limitation when modeling count data because count observations usually have variances much higher than the means, ²⁴ indicative of over‐dispersion. Over‐dispersion leads to underestimates of the standard errors (SEs) yielding large values of the chi‐square statistics which consequently increases the type I error. The deviance (DV), or the chi‐square (χ²) statistic divided by degrees of freedom (df), is often used to detect over‐dispersion (>1) or under‐dispersion (<1). There are two approaches to account for over‐dispersion in a Poisson regression model: (1) to use a multiplicative over‐dispersion factor (ψ) when defining the relationship between the variance and the mean ¹⁹ , ²⁴ or (2) to use the more flexible negative binomial distribution as the model. ¹⁶

Using the multiplicative over‐dispersion factor, the variance is now defined as Var (Y_i)=ψ×μ, where the multiplicative over‐dispersion factor (ψ) is ψ=DV/df or ψ=χ²/df. The SEs of each coefficient are adjusted by multiplying the unadjusted SEs by the square root of the multiplicative over‐dispersion factor; 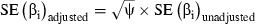. The introduction of the multiplicative dispersion factor does not introduce a new probability distribution, but rather adjusts the standard errors of the regression coefficients for testing the parameter estimates under the Poisson model. ²⁵ The second approach of accounting for over‐dispersion in Poisson regression is discussed below.

Negative Binomial Regression Model  The negative binomial regression is used to analyze count data when the Poisson estimation is inadequate due to over‐dispersion. Unlike the highly restrictive Poisson distribution, the negative binomial distribution has an additional parameter (m) that allows one to model subject heterogeneity and account for over‐dispersion. ¹⁶ , ²² The relationship between the variance and the mean for a negative binomial distribution has the following quadratic form: V(Y)=E(Y)+m[E(y)]² m>0, where m is the dispersion parameter that allows the variance to exceed the mean (m=0 yields the Poisson distribution). The negative binomial regression model assumes the same form as shown in “equation 1” above except for the additional dispersion parameter (m) that allows accounting for variation due to other factors not included in the model. If the dispersion parameter is much >0, then the negative binomial model is more appropriate than the Poisson model and the inferences from the negative binomial model are more accurate due to its accurate parameterization.

Models for Binary Outcome

Logistic Regression  The logistic regression model has been the principal method for studying the association between a set of exposure variables and a binary response variable adjusting for covariates. The method uses the logit link to produce odds ratio estimates as a measure of association. The usefulness of the odds ratio in epidemiological research has been questioned over a number of years, ⁸ particularly for prospective ²⁶ , ²⁷ and cross‐sectional ⁹ studies. The odds ratio adequately approximates the risk or prevalence ratio when the outcome is rare in all exposure and confounder categories ²⁷ but it increasingly overstates its target as the outcome becomes more common. Although there are procedures for converting odds ratios to risk ratios, they are not directly applicable when it involves adjustment for covariates. ²⁸

Log‐Binomial Regression  Several studies advocate the use of log‐binomial regression as the preferred method, compared with logistic regression, for prospective or cross‐sectional studies with common binary outcomes. ¹⁰ , ¹² , ²⁹ , ³⁰ The log‐binomial model is similar to logistic regression in assuming a binomial distribution of outcome. However, instead of using a logit link function, as is customary in standard logistic regression, a log link is applied. The regression coefficients from the log‐binomial regression model can be used to directly estimate risk ratios in prospective studies and prevalence ratios in cross‐sectional data. ¹² The log‐binomial model may produce confidence intervals (CIs) that are narrower since the estimated SEs are smaller but it can also have convergence problems.

Poisson Regression/Modified Poisson Regression  Poisson regression can also be used for analysis of cross‐sectional studies with binary outcomes ¹⁰ to provide correct estimates of the prevalence ratio and is considered a better alternative than logistic regression, since the prevalence ratio is more interpretable and easier to communicate. The application of Poisson regression to binary data follows from the fact that the standard generalized linear models parameterization of the mean of the Poisson model is of the same form as the log‐binomial model. ¹² Hence, the regression model and the measure of association have the same form as in log‐binomial regression except it assumes a Poisson distribution for the outcome. For binary data the Poisson regression model produces CIs that tend to be too wide ¹⁰ because the Poisson errors are overestimates of the binomial errors when the outcome is not rare. Hence the Poisson regression is conservative for binary outcomes (less likely to be statistically significant). To correct for this potential limitation, Zou ³¹ proposed a modified Poisson regression approach (ie, Poisson regression with a robust error variance) where the information sandwich estimator is used to obtain variance estimates that are robust to the error misspecification. The modified Poisson regression is functionally the same as the simple Poisson regression model except that to adjust for heterogeneity in the model, robust standard errors are estimated for the regression coefficients and it is more conservative. The Poisson and modified Poisson regression approaches for binary data require no data modification and can be easily performed using the GENMOD procedure in the SAS software.

Empirical Data  Data obtained from a cross‐sectional study of Buffalo police officers, BCOPS study, ¹⁷ were used to examine the association between depressive symptoms, as measured by the Center for Epidemiologic Studies Depression Rating Scale (CES‐D score), and metabolic syndrome, adjusting for age and education. The study had 115 randomly selected officers of which 96 had complete data on the primary variables of interest. Table I shows the characteristics of the study participants. For each participant, metabolic syndrome was defined in two ways: as a binary outcome representing presence (≥3 components) or absence of the syndrome (0, 1, or 2 components) and as a count of syndrome components (0, 1, 2, 3, 4, or 5). Fifteen of the participants had metabolic syndrome while the remaining 81 did not meet the criteria for metabolic syndrome. The count of metabolic syndrome components was derived for all participants (n=96) regardless of their metabolic syndrome status. Using the binary outcome, the logistic, the log‐binomial, the Poisson, and the modified Poisson regression models were fit to estimate the odds ratio (OR) for logistic and prevalence ratio (PR) for log‐binomial and Poisson models. The count of syndrome components as a discrete outcome variable was modeled by fitting the Poisson and the negative binomial regression models to estimate the RM as the measure of association. The CES‐D score and age in years are continuous variables while educational attainment is a nominal variable with 3 categories. The regression models were fit using PROC GENMOD in SAS. The same study sample data (n=96) were used for fitting all the statistical models. When fitting the Poisson regression for the discrete outcome, over‐dispersion was accounted for by using the PSCALE or DSCALE options in the model statement of PROC GENMOD. For the modified Poisson regression, the robust error variance was estimated using the REPEATED statement and the participant identifier and specifying the unstructured correlation matrix, even if there is only one observation per subject.

Table I.

 Characteristics of BCOPS Study Participants (1999–2000)

Characteristics	No.	% or Mean  ± SD
Age, y	96	39.80±7.66
CES‐D score	96	7.02±6.25
Count of syndrome components	96	1.19±1.33
Metabolic syndrome, %
Present	15	15.63
Absent	81	84.38
Education, %
≤High school/GED	18	18.75
College <4 y	30	31.25
College 4+ y	48	50.00

Abbreviations: BCOPS, Buffalo Cardio‐Metabolic Occupational Police Stress; CES‐D, Center for Epidemiologic Studies Depression Rating Scale; GED, General Equivalency Diploma; SD, standard deviation.

Results

Distribution of the Count of Syndrome Components

The distribution of the count of syndrome components shown in Figure 1 indicates that 39% had no components, 31% had 1, 15% had 2, 7% had 3, 5% had 4, and 3% had 5 components. The distribution of the count of syndrome components (Figure 1) has a mean of 1.19 which is relatively small (<10) and is highly skewed to the right. The high skewness, the small mean, and the discrete nature of the variable tend to suggest that the Poisson regression may be the appropriate model for the data. A chi‐square goodness of fit test was performed to compare the fit of the observed distribution of the count of syndrome components to the theoretical binomial, Poisson, and normal distributions using all data (Figure 2A) and excluding 5 influential observations (Figure 2B). The results suggest that the observed data closely follow the Poisson distribution and this model can be used as a basis to study the count of metabolic syndrome components. To detect nonlinearity between the response variable and the predictor we plotted the log means of the response variable by the continuous predictor (Figure 3). The plot is fairly linear indicating that the predictor variable meets the assumption of linearity in the log means needed to fit the Poisson regression model. If the plot had shown a nonlinear relationship (e.g., quadratic) then remedies would include adding a quadratic term of the predictor in the model or treating the predictor variable as a categorical variable by creating 3 or more groups.

Figure 1.

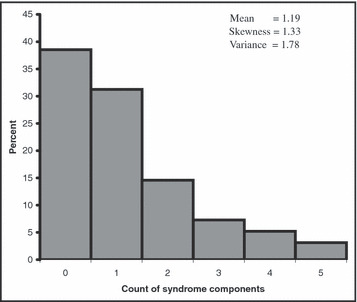
  Histogram of the count of syndrome components, the Buffalo Cardio‐Metabolic Occupational Police Stress (BCOPS) study (1999–2000).

Figure 2.

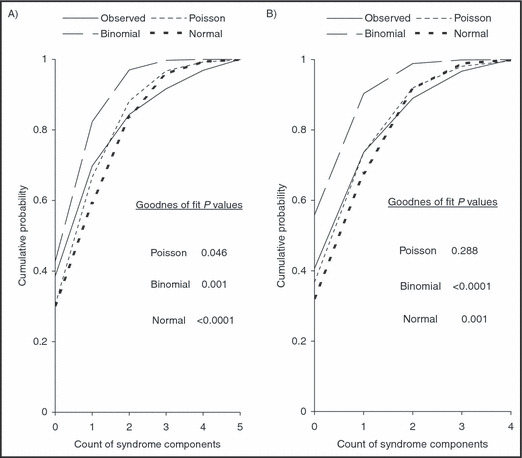
  The observed and expected cumulative distribution of the count of metabolic syndrome components, all data (A, n=96) and without influential observations (B, n=91), the Buffalo Cardio‐Metabolic Occupational Police Stress (BCOPS) study (1999–2000). The P values test the null hypothesis that the empirical data fit the specified probability distribution.

Figure 3.

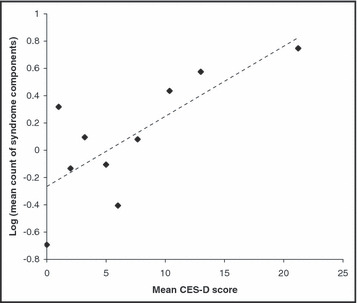
  Scatter plot of the log of the means for count of syndrome components by the Center for Epidemiologic Studies Depression Rating Scale (CES‐D score).

Measure of Association

The measures of association, their SE and 95% CI for the unadjusted and age‐and education‐adjusted association of CES‐D score with metabolic syndrome from the generalized linear models for binary and discrete outcomes are shown in Table II. The OR from the logistic model (OR, 1.51; 95% CI, 0.93–2.48) was larger than the PR from the log‐binomial model (PR, 1.37; 95% CI, 0.99–1.89) as this is usually the case with common outcomes where the OR overestimates the PR. The Poisson (PR, 1.38; 95% CI, 0.92–2.07) and the modified Poisson (PR, 1.38; 95% CI, 0.97–1.97) regression approaches for the binary outcome yielded a similar point estimate as the log‐binomial but with wider CIs. The PRs from log‐binomial and Poisson/modified Poisson regression approaches had smaller SEs and narrower CIs than the OR from the logistic regression model. However, all the models that are based on the binary outcome did not detect significant associations at the nominal level of significance in the unadjusted as well as the covariate‐adjusted models. For common binary outcomes, the modified Poisson regression is the preferred alternative when the log‐binomial model is numerically unstable. Generally, the modified Poisson estimates are not fully efficient when compared with log‐binomial estimators ³² but in this particular dataset the efficiency of the two models is similar as indicated by width of the CIs.

Table II.

 Associations Between CES‐D Score and Metabolic Syndrome Using Various Generalized Linear Models

Regression Model	Outcome Variable a	Measure of Association	Unadjusted				Age and Education Adjusted
			Estimate	Standard Error	95% CI	P Value	Estimate	Standard Error	95% CI	P Value b
Logistic	Binary	OR	1.514	0.3811	(0.925–2.480)	.0991	1.451	0.3760	(0.873–2.412)	.1507
Log‐binomial	Binary	PR	1.369	0.2269	(0.989–1.894)	.0582	1.340	0.2407	(0.943–1.906)	.1029
Poisson	Binary	PR	1.381	0.2873	(0.918–2.076)	.1212	1.324	0.2840	(0.870–2.016)	.1904
Modified Poisson	Binary	PR	1.381	0.2509	(0.967–1.971)	.0759	1.324	0.2395	(0.929–1.888)	.1205
Poisson	Count	RM	1.276	0.1015	(1.092–1.492)	.0022	1.264	0.1029	(1.077–1.483)	.0040
Poissonc	Count	RM	1.276	0.1242	(1.055–1.545)	.0122	1.264	0.1253	(1.041–1.535)	.0180
Poissond	Count	RM	1.276	0.1244	(1.055–1.545)	.0123	1.264	0.1254	(1.041–1.535)	.0181
Modified Poisson	Count	RM	1.276	0.1021	(1.091–1.493)	.0023	1.264	0.0988	(1.085–1.473)	.0027
Negative Binomial	Count	RM	1.294	0.1355	(1.054–1.588)	.0139	1.277	0.1311	(1.044–1.562)	.0174

Parameter estimates, standard errors and 95% confidence intervals (CIs) are for 1 standard deviation (6.25) increase in Center for Epidemiologic Studies Depression Rating Scale (CES‐D score). ^aMetabolic syndrome as the outcome was modeled as a binary (present/absent) as well as a discrete (count of syndrome components) variable. ^b P value tests the overall significance of the CES‐D score—metabolic syndrome association (tests significance of the variable adjusting for all other variables in the model). ^cPoisson regression model with correction for over‐dispersion, dispersion parameter (ψ) estimated as chi‐square statistic divided by degrees of freedom (χ²/df). ^dPoisson regression model with correction for over‐dispersion, dispersion parameter (ψ) estimated as deviance statistic divided by degrees of freedom (DV/df).

Abbreviations: OR, odds ratio; PR, prevalence ratio; RM, ratio of means.

The regression models that used the count of syndrome components as an outcome variable, the Poisson and the negative binomial regression models, yielded significant associations with CES‐D score. The RM from the Poisson (RM, 1.28; 95% CI, 1.09–1.49) and the negative binomial regression model (RM, 1.29; 95% CI, 1.05–1.59) indicate a significant positive association between CES‐D score and count of syndrome. Adjustment for age and educational attainment did not attenuate the association. The inference from the unadjusted and covariate‐adjusted models are similar; for every 1 standard deviation (SD) increase in CES‐D score, the participants would expect a 28% or 29% increase in the mean count of syndrome components.

The ratio of the DV or the chi‐square (χ²) statistic over the df for the unadjusted (DV/df=1.501, χ²/df=1.498) and covariate adjusted (DV/df=1.484, χ²/df=1.482) Poisson regression models was >1 suggesting some (but not serious) evidence of over‐dispersion. Over‐dispersion was then accounted for by using these ratios as estimates of the multiplicative over‐dispersion factor (ψ) and refitting the Poisson regression to obtain adjusted SEs of the estimated coefficients (Table II). For example, in the univariate Poisson regression model the SE for CES‐D score was 0.1015, this was adjusted to 0.1242 (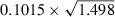) and 0.1244 (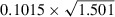) using χ²/df and DV/df as estimates of the multiplicative over‐dispersion factor, respectively. The estimates of the measures of association have not changed (Table II), but the SEs have all been inflated by the scale parameter (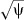). The result of this increase in the SEs has not affected the statistical significance of CES‐D score at the 0.05 level. However, over‐dispersion, when it is serious, can inflate the type I error and could lead to incorrect inferences regarding significance of associations. ²⁴ The alternative to the use of the multiplicative over‐dispersion factor to account for over‐dispersion is to fit the negative binomial regression model. The estimated dispersion parameter (m) for the unadjusted (m=0.3058) and covariate adjusted (m=0.2890) regression models is not much >0 but the likelihood ratio test for over‐dispersion (−2[log likelihood for Poisson−log likelihood for negative binomial]), which is distributed as chi‐square with 1 degree of freedom, showed that the dispersion parameter is significantly different from zero (P=.016 for unadjusted model, P=.041 for covariate adjusted model). The statistically significant evidence of over‐dispersion indicates that the negative binomial regression model is preferred to the Poisson regression model. However, for this example dataset the two procedures yield similar estimates and inferences.

Discussion

In this paper, we have explored and compared two approaches of modeling metabolic syndrome as an outcome (dependent) variable in cross‐sectional studies: (1) application of logistic, log‐binomial, Poisson, and the modified Poisson regression models that utilize the binary nature of metabolic syndrome; and (2) redefining metabolic syndrome as the count of syndrome components for an individual and applying alternative models for count data, the Poisson, and the negative binomial regression, to model the mean count of syndrome components as function of explanatory variables. A real dataset from the BCOPS study was used to model metabolic syndrome, employing both approaches, as a function of depression score adjusting for covariates. Analytic results from the empirical dataset demonstrate that our conclusion regarding the significance and effect size of the association between CES‐D score and metabolic syndrome is notably affected by the choice of the modeling approach. The models based on the binary metabolic syndrome failed to detect significant associations at the nominal level of significance while the Poisson and negative binomial regression models that treat count of syndrome components as a discrete outcome revealed strong associations. Ignoring the discrete nature of the outcome leads to an under‐statement of the statistical significance. In a cross‐sectional design, the RM from Poisson and negative binomial regression models can be interpreted as an (RM−1)×100 percent change in the mean number (count) of syndrome components for one unit increase in the exposure variable. The change is an increase if the quantity (RM−1)×100 is positive and a decrease otherwise. In this example, an RM of 1.276 is interpreted as a 27.6% increase in the mean count of metabolic syndrome components for each 1 SD increase in CES‐D score. This example shows the potential for Poisson/negative binomial regression models to provide an alternative way to analyze metabolic syndrome as a discrete outcome and yield a readily interpretable measure of association (RM) for cross‐sectional study designs. The limitation of modeling metabolic syndrome as a discrete outcome is that the count of syndrome components has an upper limit. The difference in statistical significance of CES‐D score between the two modeling approaches could be due to the small sample size. However, the alternative approach of using count of syndrome components as the dependent variable is more sensitive and can provide stronger association even in large sample‐based studies.

The current study has some epidemiological and clinical implications. The epidemiological implication is that the alternative analytic method provides a more sensitive measure of metabolic syndrome as a dependent variable for modeling purposes. Although this study is cross‐sectional and definitive recommendations as to how the analyses should be used in a clinical setting may need to follow confirmation in other studies, the count of syndrome components may serve as an additional tool in that early intervention could be recommended for patients with 0, 1, or 2 syndrome components to potentially reduce the risk of the full metabolic syndrome. More importantly, using the count of metabolic syndrome components, future prospective studies could develop models that estimate the change in number of syndrome components associated with changes in lifestyle, psychosocial and physiological characteristics, or combination of these factors. In addition, the count of syndrome components could also be used as a predictor in models that estimate the risk of future cardiovascular disease associated with a one unit increase in the number of syndrome components.

A situation that often arises when using the Poisson regression model for count data is over‐dispersion which occurs when the observed variance is larger than the nominal variance for the distribution and leads to inflation of type I error. Besides lack of fit, over‐dispersion could be a symptom of other problems such as an incorrectly specified model or outliers in the data. ¹⁶ , ¹⁹ Therefore, over‐dispersion occurs when the model is under‐specified, and the variability between subjects is not being adequately accounted for. Because there is no random error term in a Poisson regression model, there is no way to account for the extra variability caused by the omitted important predictor. ²⁵ Correcting these potential problems (missing predictors or quadratic terms or outliers) could eliminate the need for a multiplicative over‐dispersion factor. ³³ When there is a need to account for over‐dispersion, fitting a negative binomial regression model is a better way to account for over‐dispersion compared to the multiplicative over‐dispersion factors because the regression parameter estimates are more efficient. ²⁵ , ³⁴ The Poisson regression model that corrects for over‐dispersion with the multiplicative over‐dispersion factor usually has inefficient parameter estimates, meaning that they have more sampling variability than necessary. ³⁴ In the empirical dataset used in this paper over‐dispersion was mild, consequently the measure of association and inference from the Poisson regression, where over‐dispersion was accounted for by using the multiplicative over‐dispersion factor, and the negative binomial regression are similar but this may not be the case with other datasets.

Depending on the prevalence of metabolic syndrome in the specific study population, analysis of metabolic syndrome as a binary outcome should proceed as follows: the analyst should consider first fitting the logistic regression model followed by the more preferred log‐binomial regression for common outcomes; the log‐binomial model tends to have convergence problems and is less numerically stable than the logistic model. ³² In this situation, the modified Poisson regression with robust variance ³¹ should be used as an alternative. Finally, the count of syndrome components should be modeled using models for count data (the Poisson and the negative binomial regression models) and inferences/conclusions from the two approaches should be compared. We believe that the latter approach is more sensitive and should be favored especially when there is conflicting conclusions between the two approaches. In a study where the objective is to identify factors related to metabolic syndrome, we recommend that the analysis should certainly consider the discrete nature of the response variable in addition to the commonly used binary form.

From a theoretical stand point, the alternative method proposed for analysis of metabolic syndrome is justifiable regardless of the population under study, provided that the count of syndrome components approximately follows a Poisson probability distribution. In the current study, the analytic method is tested using sample data from a highly stressed occupational group which may not be representative of the general population. Confirmation of the utility of this analytic approach in other populations is warranted.

Disclosure:  This work was supported by the National Institute for Occupational Safety and Health (NIOSH), contract no. 200‐2003‐01580. The findings and conclusions in this report are those of the authors and do not necessarily represent the views of the NIOSH. No competing financial interests exist.