Marginal probabilities and point estimation for conditionally specified logistic regression

Abstract

Conditionally specified logistic regression (CSLR) models p binary response variables. It is shown that marginal probabilities can be derived for a CSLR model. We also extend the CSLR model by allowing third order interactions. We apply two versions of CSLR to simulated data and a set of real data, and compare the results to those from other modeling methods.

1. Introduction

In some situations it may be desirable to determine the effects of several (perhaps many) predictors on several outcomes simultaneously. If the outcomes are represented by binary variables, we have this problem:

$$\mathbf{Y}~\mathbf{X}$$ (1)

Y is a vector of p binary variables. X is a vector of n variables. Each of X₁, … , X_n is a potential predictor of Y_j, 1 ≤ j ≤ p.

Problems described by Equation (1) tend to arise in medicine and public health. Some examples:

• In Section 6.2, the responses are three medical conditions: kidney disease, hypertension, and diabetes. For some time it has been known in the field of public health that these tend to occur together.

• In [(Joe and Liu 1996)] an example is given based on a data set of cardiac surgery patients. Four binary response variables are modeled. Each is measured immediately after surgery. The four are, respectively, occurrence of: 1) renal complication, 2) pulmonary complication, 3) neurological complication, and 4) low-out syndrome (low cardiac output) complication.

• In [(O’Brien and Dunson 2004)] the given example is based on a neurotoxicology study. Litters of rat pups were exposed to a pesticide before and after birth. Each litter was exposed to one of five dosage levels. One male and one female pup was randomly selected from each litter and tested at three ages. The response variable was based on activity level: 0 for normal, 1 for elevated. Covariates were dose, age, and gender. So there are six responses for each litter.

• In [(García-Zattera et al. 2007)] the authors used data from a longitudinal study of oral health. They looked at the occurrence of caries in molars. Eight binary variables were modeled: occurrence of caries after one year in each of the eight molar teeth in the jaw.

Currently there is no one standard method for modeling problems described by Equation (1).

Conditionally specified logistic regression (to be referred to as CSLR) is a method for fitting the responses of Equation (1). CSLR was introduced in [(Joe and Liu 1996)]. A CSLR model may allow for a more meaningful interpretation of data than what alternative methods can give. However, until now the usefulness of CSLR was severely limited by an apparent inability to produce marginal probabilities. We now explain what this means.

The equations that define a CSLR model are as follows. Let Y_i = (Y_i1, … , Y_ip) be the vector of responses and X_i = (X_i1, … , X_in) the vector of covariates for observation i. Then

$$\text{logit\hspace{0.17em}}\left(P\left(Y_{ij}=1|X_i,\left\{Y_{ik},k\ne j\right\}\right)\right)={\mu }_j+\sum _{\mathcal{l}=1}^n{\alpha }_{j\mathcal{l}}{X}_{i\mathcal{l}}+\sum _{k\ne j}{\gamma }_{jk}{Y}_{ik},1\le j\le p$$ (2)

or

$$P\left(Y_{ij}=1|X_i,\left\{Y_{ik},k\ne j\right\}\right)=h\left({\mu }_j+\sum _{\mathcal{l}=1}^n{\alpha }_{j\mathcal{l}}{X}_{i\mathcal{l}}+\sum _{k\ne j}{\gamma }_{jk}{Y}_{ik}\right),1\le j\le p$$ (3)

where h(x): = e^x/(1 + e^x). Equation (2) specifies p distributions, each related to the others. If these p distributions do exist simultaneously, they are said to be compatible. The existence of such compatible conditional distributions is shown in [(Joe and Liu 1996)]. Equation (2) is an instance of a more general relationship between p binary variables Y₁, … , Y_p:

$$\text{logit\hspace{0.17em}}\left(P\left(Y_j=1|\left\{Y_1,\dots ,Y_{j-1},Y_{j+1},\dots ,Y_m\right\}\right)\right)={\mu }_j+\sum _{k\ne j}{\gamma }_{jk}{Y}_{ik},1\le j\le p,\text{ for }j=1,\dots ,p.$$ (4)

Equation (4) describes conditionally compatible logistic distributions. Conditionally compatible logistic distributions are in turn a particular instance of conditionally compatible distributions.

In Equation (2), γ_jk may be thought of as a measure of the association of Y_j and Y_k, distinct from their common reliance on X.

Consideration of Equation (2) leads to two questions:

• Equation(s) (2) implies that we must know the values of {Y_j : j ≠ ℓ} to estimate the probability that Y_ℓ = 1. This is not very useful, unless we have some reason for assuming values for all Y_j’s except one. Often it is desirable to estimate P(Y_ℓ = 1), without conditioning on other responses. If doing prediction or interpolation, no values for any of the Y_j’s are available. So in general the problem is to estimate P(Y_ℓ = 1) using only the covariate values x.

• Equation (2) includes second order interaction terms γ_jk. However, there are p responses. Could we modify the formula by including terms for higher order interactions?

Item 1 is asking for first order marginal probabilities. These are the probabilities {P(Y_ij = s), s ∈ {0, 1}|x_i}. For any subset S ⊂ {1, … , p}, the marginal probabilities for {Y_ij}_j∈S are of form P({Y_ij = s_j, j ∈ S}), where s ∈ {0, 1}^|S|. This is a marginal probability of order |S|. First order marginal probabilities are of most interest. In applied problems, we often need to know the marginal probability that response Y_j has value one. We may also wish to estimate the probability that Y_j = 1 when one or more covariates are set at hypothetical levels. Such counterfactual marginal probabilities are used to derive average treatment effects, used in econometrics and epidemiology (See [(Imbens and Wooldridge 2009)]).

However, marginal probabilities have another interpretation.

For a regression model of any kind, there is a response y and covariates x. One of the basic uses of a regression model is to provide point estimates, or predictions, of the response, for given covariate values:

$${\widehat{y}}_i=f(x_i).$$ (5)

Note f needs only x as an argument. If y is multivariate, we have several responses. Suppose we use a conditionally specified model. The model specifies the function for one response, conditional on the other responses:

$${\widehat{y}}_{ij}=f(x_i,\left\{y_{ik},k\ne j\right\}).$$ (6)

If y_ij is missing and needs to be estimated, we can’t assume that {y_ik, k ≠ j} will be present. For effective prediction or point estimation, we need an equation of form Equation (5).

The Y_j’s are binary, so P(Y_ℓ = 1|x) is the expected mean value of Y_ℓ. The estimated value $\widehat{p}$ of P(Y_ℓ = 1|x) is used as a point estimate of Y_i for many purposes, including goodness-of-fit statistics. For example, the Pearson goodness-of-fit statistic for a response variable Y is

$${\chi }^2=\sum _j\frac{{\left(y_j-{\widehat{p}}_j\right)}^2}{{\widehat{p}}_j}.$$ (7)

If the coefficients in Equation (2) are derived from a data set, then in calculating marginal probabilities we are modeling the data for each response Y_ℓ. We must ask: How well has the data been modeled? Are there better methods for modeling data for multiple binary responses?

In Section 2 we will show two methods for deriving marginal probabilities P(Y_ℓ = 1|x). Also, models with third order interactions are shown to exist.

in Section 3, alternative methods for fitting multiple binary random variables are introduced and briefly described.

In Section 5, some problems are discussed that would arise in fitting models of MPCSLR.

In Section 6, a set of real data is given, and all modeling methods are applied. The performances of the methods are assessed and compared.

The unifying concept is this: The ability to derive marginal probabilities (and model individual responses) is inseparable from assessment of goodness of modeling. CSLR can be made to yield fitted values $\left\{{\widehat{y}}_{ij}\right\}$, but it must be seen how much these fitted values deviate from data values {y_ij}.

1.1. Review of literature

Conditionally compatible distributions, and the conditions which must be satisfied for their existence, are discussed in [(Arnold and Press 1989)] and [(Arnold, Castillo, and Sarabia 2001)]. For a more recent discussion of conditionally compatible distributions, see [(Sarabia and Gómez-Déniz 2008)] or [(Arnold, Castillo, and Sarabia 1999)].

The concept of conditionally specified distributions arose from attempts to derive joint densities for multiple random variables. A good discussion of conditionally specified distributions and their marginal distributions is found in [(Arnold, Castillo, and Sarabia 2001)]. The authors compare the use of conditional distributions to characterize a multivariate distribution to the use of marginal distributions for the same purpose, and show that marginal distributions may be uninformative. However, they only discuss multiple Poisson or multiple normal responses. [(Joe 1996)] and [(Sarabia and Gómez-Déniz 2008)] extensively discuss conditionally specified distributions. The latter has a brief overview of applications of conditionally specified models. Alternatives to CSLR are given in [(O’Brien and Dunson 2004)] and [(García-Zattera et al. 2007)]. In [(García-Zattera et al. 2007)], CSLR was used to model actual data. Results from this were compared with results from a multivariate probit model (See Section 3). The authors derived conditional odds ratios as measures of association between pairs of response variables. [(Anderson, Li, and Vermunt)] extended CSLR to a model for polytomous responses. None of these authors attempted numerical calculation of marginal probabilities for individual responses or sets of responses. In [(Ghosh and Balakrishnan 2017)], explicit formulas for marginal distributions were given. However, they modeled continuous response variables, not binary. Also, their models were applied to a real data set, but marginal distributions were not used to find point estimates or residuals.

2. Marginal distributions and probabilities for CSLR

Assume that Y₁, … , Y_p is a set of p binary random variables, each taking values in {0, 1}, and that x = (x₁, … , x_n) is a vector of values for the covariates X₁, … , X_n.

Two methods will be presented for deriving marginal distributions for CSLR.

2.1. Marginal probabilities via joint density

By Equation (2.5) of [(Joe and Liu 1996)], the joint density of Y₁, … , Y_p is proportional to

$$\text{exp}\left(\sum _{j=1}^p{\mu }_j{y}_j+\sum _{1\le i<j\le p}{\gamma }_{ij}{y}_i{y}_u\right).$$

$$P\left(Y_i=y_i,i=1,\dots ,p\right)=\frac{\text{exp}\left({\sum }_{j=1}^p{\mu }_j{y}_j+{\sum }_{1\le i<j\le p}{\gamma }_{ij}{y}_i{y}_u\right)}{\sum \left\{\text{exp}\left({\sum }_{j=1}^p{\mu }_j{z}_j+{\sum }_{1\le i<j\le p}{\gamma }_{ij}{z}_i{z}_j\right):z\in {\{0,1\}}^p\right\}}.$$ (8)

To find marginal probabilities, proceed as follows. First, using Equation (8), calculate P(Y_i = y_i,i = 1, … , p) for all y ∈ {0, 1}^p. Then for any subset S ⊂ {1, … , p} and any bfz ∈ {0, 1}^|S|, the marginal probability $P\left(Y_{si}=z_i,i=1,\dots ,|\text{S}|\right)$ is

$$\sum \{P\left(Y_i=y_i,i=1,\dots ,p\right):\text{y}\in {\{0,1\}}^p\text{ and }{y}_{s_i}=z_i,i=1,\dots ,|S|\}.$$

This is the sum of 2^p−|S| summands.

2.2. Marginal probabilities via conditional probabilities

Notation. For S ⊂ {1, … , p}, Ev[S|] will denote the event {Y_ℓ = 1 : ℓ ∈ S}. Also, we will denote {1, … , p} by S_p.

Notice that Ev[S] can be written as a disjoint union:

$$Ev[S]={\cup }_{S^{\prime }}\{\mathit{\text{Event}}\left\{Y_{\mathcal{l}}=1,\mathcal{l}\in S^{\prime },Y_{\mathcal{l}}=0,\mathcal{l}\notin S^{\prime }\right\}:S\subset S^{\prime }\subset S_p\}.$$ (9)

Also, Ev[∅] = {0, 1}^p, so that P(Ev[∅]) = 1.

We need one more preliminary result before presenting our main lemma. Suppose S₁ ⊂ S_p, |S₁| < p, and a ∈ S^C = S_p/S₁. Then

$$P\left(Y_{\mathcal{l}}=1,\mathcal{l}\in S_1,Y_a=0|x\right)=P\left(Y_{\mathcal{l}}=1,\mathcal{l}\in S_1|x\right)-P\left(Y_{\mathcal{l}}=1,\mathcal{l}\in S_1\cup \left\{a\right\}|x\right)=P\left(Ev\left[S_1\right]|x\right)-P\left(Ev\left[S_1\cup \left\{a\right\}\right]|x\right).$$

If {a, b} ⊂ S_p/S₁, then

$$\begin{gathered} P\left(Y_{\mathcal{l}}=1,\mathcal{l}\in S_1,Y_a=Y_b=0|\mathbf{x}\right) \\ =P\left(Y_{\mathcal{l}}=1,\mathcal{l}\in S_1|\mathbf{x}\right)-P\left(Y_{\mathcal{l}}=1,\mathcal{l}\in S_1\cup \left\{a\right\}|x\right)-P\left(Y_{\mathcal{l}}=1,\mathcal{l}\in S_1\cup \left\{b\right\}|x\right)+P\left(Y_{\mathcal{l}}=1,\mathcal{l}\in S_1\cup \{a,b\}|x\right) \\ =P\left(Ev\left[S_1\right]|x\right)-P\left(Ev\left[S_1\cup \left\{a\right\}\right]|x\right)-P\left(Ev\left[S_1\cup \left\{b\right\}\right]|x\right)+P(Ev\left[S_1\cup \{a,b\}\right]|x). \end{gathered}$$

And in general, for S₁, S₂ ⊂ S_p. S₁ ⋂ S₂ = ∅,

$$\begin{gathered} P\left(Y_{\mathcal{l}}=1,\mathcal{l}\in S_1,Y_{\mathcal{l}}=0,\mathcal{l}\in S_2|x\right) \\ =\sum _{S^{”}}\left\{{(-1)}^{\left|S^{”}\right|-\left|S_1\right|}P\left(Ev\left[S^{”}\right]|x\right):S_1\subset S^{”}\subset S_1\cup S_2\right\}. \end{gathered}$$ (10)

Lemma 1. Let x be a vector of values of X₁, … , X_n. Then the vector of probabilities {P(Ev[S]|x) : S ⊂ S_p, |S| < p} is preserved by an nontrivial affine transformation with coefficients determined by x and by the coefficients of the defining conditional equations (2).

Proof. First, for any nonempty S ⊂ {1, … , p}, choose one element r(S) ∈ S. The vector r is defined by these arbitrary choices.

Let S ⊂ S_p and x be a vector of values of X₁, … , X_n. By Equations (9) and (10),

$$\begin{gathered} P(Ev[S]|x) \\ =P\left(Y_{\mathcal{l}}=1,\mathcal{l}\in S|x\right)(a) \\ =\sum _{S^{\prime }}\left\{P\left(Y_{\mathcal{l}}=1,\mathcal{l}\in S^{\prime },Y_{\mathcal{l}}=0,\mathcal{l}\notin S^{\prime }|x\right):S\subset S^{\prime }\subset S_p\right\}(b) \\ =\sum _{S^{\prime }}[P\left(Y_{r\left(S^{\prime }\right)}=1|Y_{\mathcal{l}}=1,\mathcal{l}\in S^{\prime }/\left\{r\left(S^{\prime }\right)\right\},Y_{\mathcal{l}}=0,\mathcal{l}\notin S^{\prime }\right)*P\left(Y_{\mathcal{l}}=1,\mathcal{l}\in S^{\prime }/\left\{r\left(S^{\prime }\right)\right\},Y_{\mathcal{l}}=0,\mathcal{l}\notin S^{\prime }|x\right)](c) \\ =\sum _{S^{\prime }}[P\left(Y_{r\left(S^{\prime }\right)}=1|Y_{\mathcal{l}}=1,\mathcal{l}\in S^{\prime }/\left\{r\left(S^{\prime }\right)\right\},Y_{\mathcal{l}}=0,\mathcal{l}\notin S^{\prime }\right)*(\sum _{S^{\prime \prime }}\left\{{(-1)}^{\left|S^{\prime \prime }\right|-\left(\left|S^{\prime }\right|-1\right)}P\left(Ev\left[S^{\prime \prime }\right]|x\right):S^{\prime }/\left\{r\left(S^{\prime }\right)\right\}\subset S^{\prime \prime }\subset S_p/\left\{r\left(S^{\prime }\right)\right\}\right\}(d) \\ =\sum _{S^{\prime \prime }\subset S_p}{q}_{S,S^{\prime \prime }}P\left(Ev\left[S^{\prime \prime }\right]|x\right) \end{gathered}$$ (11)

where

$$\begin{gathered} qS,S^{\prime \prime } \\ =\sum _{S^{\prime }}{(-1)}^{\left|S^{\prime \prime }\right|-\left|S^{\prime }\right|+1}P\left(Y_{r\left(S^{\prime }\right)}=1|Y_{\mathcal{l}}=1,\mathcal{l}\in S^{\prime }/\left\{r\left(S^{\prime }\right)\right\},Y_{\mathcal{l}}=0,\mathcal{l}\notin S^{\prime },\mathbf{x}\right) \end{gathered}$$ (12)

and the sum is over all subsets S′ ⊂ S_p such that (i) S ⊂ S′; (ii) S′/{r(S′)} ⊂ S″; (iii) r(S′) ∉ S″. If no S′ satisfy (i)-(iii), then q_S,S″ = 0.

In the Equation set (11), we used Equation (9) to go from (a) to (b) and Equation (10) to go from (c) to (d). The conditional probabilities on the right side of Equation (12) are determined by the coefficients in Equation (2).

Let $S_p^{*}$ denote S_p/{r(S_p)}. By condition (iii), S″ cannot be S_p. Equation (11) holds if S = S_p, but conditions (i)-(iii) imply that $q_{S_p},s^{\prime \prime }=0$ unless $S^{\prime \prime }=S_p^{*}$. In that case,

$$q_{S_p,S_p^{*}}=P\left(Y_{r\left(S_p\right)}=1|Y_j=1,j\ne r\left(S_p\right),x\right)$$

and Equation (11) simplifies to

$$\begin{gathered} P\left(Y_j=1,1\le j\le p|x\right) \\ =P\left(Ev\left[S_p\right]|x\right) \\ =q_{S_p,S_p^{*}}P\left(Ev\left[S_p^{*}\right]|x\right) \\ =P\left(Y_{r\left(S_n\right)}=1|Y_j=1,j\ne r\left(S_p\right),x\right)\cdot P\left(Y_j=1,j\ne r\left(S_p\right)|x\right). \end{gathered}$$

This is given by the definition of conditional probability, and adds no new information. So we can reduce our system of equations of form Equation (11) by omitting those for which |S| = p or |S″| = p.

If S = ∅, we have the trival equation P(Ev[∅]|x) = 1. S″ can be empty if and only if |S| = 1, that is, S = {ℓ}, some ℓ ∈ {1, … , p}. Then S′ must be {ℓ}, and Equation (12) simplifies to

$$q_{\left\{\mathcal{l}\right\},\varnothing }=P\left(Y_{\mathcal{l}}=1|Y_j=0,j\ne \mathcal{l},x\right).$$ (13)

This is the coefficient of P(Ev[∅]) = 1. So in Equation (11), P(Ev[S]|x) has a constant term if and only if |S| = 1.

So by Equations (11), (12), and (13), the set {P(Ev[S]|x) : S ⊂ S_p, 0 < |S| < p} satisfies the system

$$P(Ev[S]|x)=a_S+\sum \left\{q_{S,S^{\prime \prime }}P\left(Ev\left[S^{\prime \prime }\right]|x\right):S^{\prime \prime }\subset S_p,0<\left|S^{\prime \prime }\right|<p\right\}$$ (14)

where

$$a_S=\{\begin{array}{l}P\left(Y_{\mathcal{l}}=1|Y_j=0,j\ne \mathcal{l},x\right)\text{ if }S=\left\{\mathcal{l}\right\}\hfill \\ 0\text{ otherwise }\hfill \end{array}.$$ (15)

The Lemma holds with {a_S : S ⊂ S_p, 0 < |S| < p} and {q_S,S″ : S, S″ ⊂ S_p, 0 < |S|, |S″| < p} as the coefficients of the affine transformation. □

Notice that the proof used a vector r, indexed by nonempty subsets of {1, … , p}. r is chosen arbitrarily, so there is not a single canonical formula to calculate {q_S,S″}. However, r enters into Equation (11) at step (d). By the definition of conditional probability, the expression on line (c) equals that on line (d), no matter the choice of r.

Let U_p: = {S ⊂ S_p : 0 < |S| < p}. and let V denote the vector {P(Ev[S]) : S ∈ U_p}. Then Equation (14) can be expressed V = A + QV, or

$$(I-Q)V=A.$$ (16)

Choose a maximal subset T ⊂ S_p such that rows of I − Q indexed by T are linearly independent. For each j ∈ T^C, row j of I − Q is a linear combination of rows indexed by T. That is, P(Ev[S_j]|x) is determined by a linear combination of {P(Ev[S]|x) : S ∈ T} (plus a constant, if |S_j| = 1). So we have a new system

$$P(Ev[S]|x)=a_S^{*}+\sum _{S^{”}\in T}{q}_{S,S^{”}}^{*}P(Ev[S]|x),\forall S\in T$$

or V* = A* + Q*V*, so that

$$\left(I-Q^{*}\right)V^{*}=A^{*}$$ (17)

where (I − Q*) is nonsingular. If A* is nonzero, there is a unique solution V* of Equation (17), which implies a unique solution V of Equation (16). It is not clear as of now exactly when there is a unique solution of Equation (16), but so far there has been no difficulty in deriving the {P(Ev[S]|x)}.

Example. We show how the Lemma is applied for p = 2.

$$\begin{gathered} P\left(Y_1=1|x\right) \\ =P\left(Y_1=1,Y_2=1|\mathbf{x}\right)+P\left(Y_1=1,Y_2=0|\mathbf{x}\right) \\ =P\left(Y_1=1|Y_2=1,\mathbf{x}\right)P\left(Y_2=1|\mathbf{x}\right)+P\left(Y_1=1|Y_2=0,\mathbf{x}\right)P\left(Y_2=0|\mathbf{x}\right) \\ =P\left(Y_1=1|Y_2=1,\mathbf{x}\right)P\left(Y_2=1|\mathbf{x}\right)+P\left(Y_1=1|Y_2=0,\mathbf{x}\right)\left(1-P\left(Y_2=1|\mathbf{x}\right)\right) \\ =P\left(Y_1=1|Y_2=0,x\right)+\left(P\left(Y_1=1|Y_2=1,x\right)-P\left(Y_1=1|Y_2=0,x\right)\right)P\left(Y_2=1|x\right). \end{gathered}$$

Similarly,

$$\begin{gathered} P\left(Y_2=1|x\right) \\ =P\left(Y_2=1|Y_1=0,\mathbf{x}\right)+\left(P\left(Y_2=1|Y_1=1,\mathbf{x}\right)-P\left(Y_2=1|Y_1=0,\mathbf{x}\right)\right)P\left(Y_1=1|\mathbf{x}\right) \end{gathered}$$

so that

$$\left(\begin{array}{c}P\left(Y_1=1|\mathbf{x}\right)\\ P\left(Y_1=2|\mathbf{x}\right)\end{array}\right)={\left(\begin{array}{cc}{m}_{11}& m_{12}\\ m_{21}& m_{22}\end{array}\right)}^{-1}\left(\begin{array}{c}P\left(Y_1=1|Y_2=0,\mathbf{x}\right)\\ P\left(Y_2=1|Y_1=0,\mathbf{x}\right)\end{array}\right)$$

where

$$\begin{gathered} m_{11}=m_{22}=1 \\ {m}_{12}=P\left(Y_1=1|Y_2=0,\mathbf{x}\right)-P\left(Y_1=1|Y_2=1,\mathbf{x}\right) \\ {m}_{21}=P\left(Y_2=1|Y_1=0,\mathbf{x}\right)-P\left(Y_2=1|Y_1=1,\mathbf{x}\right). \end{gathered}$$

An explicit algorithm for p = 3 is given in Part A of the Appendix.

It should be noted that the two methods, of Sections 2.1 and 2.2, are methods of deriving marginal probabilities from conditional probabilities. They are not ways of fitting models, in the sense of estimating parameter values; both methods require that values of all parameters be given. The two methods, however, are quite different. The joint density method will be usually be simpler and quicker to calculate. The method of conditional probabilities is more difficult to program. It demands a great deal of calculation, and there are far more ways for errors to occur in the final results. In practice, the joint density method would be a safer choice in most cases. However, the two methods are based on different sets of ideas. The existence of a joint density for a system of conditionally specified logistic distributions is not obvious. Existence and specification for a joint density is based on a Theorem from [(Joe and Liu 1996)]. The joint density must be derived and calculated at all possible outcomes. The method of conditional probabilities does not require a clearly formulated joint density. It does require that all conditional probabilities be calculated. However, the conditional probabilities are defined by the system of conditionally specified logistic distributions; See Equation (2). That is, the method of conditional probabilities uses only the definition of CSLR. Lemma 1 says that marginal probabilities can be derived using only the the conditional probabilities that define a system, with no deeper theoretical results. In general, the joint density method is easier to implement and more reliable. The method of conditional probabilities, however, could be used in a case where for some reason an explicit formula for the joint density was not known. This would be the case if the conditional distributions of the respective outcomes were not compatible, and no unique joint density exists: See Part E of the Appendix.

2.3. CSLR with third order interaction

Equation (18 is a variation of Equation (2). It defines a variation of CSLR that includes third or higher order interactions of the responses. For p = 3, this model has one new parameter, γ₁₂₃.

$$\text{logit\hspace{0.17em}}\left(P\left(Y_{ij}=1|X_i,\left\{Y_{ik},k\ne j\right\}\right)\right)={\mu }_j+\sum _{\mathcal{l}=1}^n{\alpha }_{j\mathcal{l}}{X}_{i\mathcal{l}}+\sum _{k\ne j}{\gamma }_{jk}{Y}_{ik}+\sum _{k,\mathcal{l}\cancel{j},k\cancel{\mathcal{l}}}{\gamma }_{jk\mathcal{l}}{Y}_{ik}{Y}_{i\mathcal{l}},1\le j\le p.$$ (18)

By the way this is defined, γ_jkℓ = γ_jℓk, any (j, k, ℓ) distinct in 1, … , p).

Lemma 2. Assume that γ_jkℓ = γ_kjℓ. Then Equation(s) (18) define compatible conditional distributions,

Proof. Given in part B of the Appendix. □

3. Alternative methods for modeling multiple binary responses

3.1. Multivariate probit

Multivariate probit was probably the first method developed for multiple ordinal responses. A good introduction to fitting multivariate probit models with MCMC is given in [(Chib and Greenberg 1998)]. Multivariate probit and multivariate t-link both assume that each binary response Y_i arises from a continuous variable z_i, such that

$$Y_i=\{\begin{array}{l}1\text{ if }{z}_i>0\hfill \\ 0\text{ if }{z}_i\le 0.\hfill \end{array}$$ (19)

Multivariate probit is based on the multivariate normal density F(t|μ, Σ). The values of μ are given by linear regression. For observation i, the mean μ_ij of response j is

$${\mu }_{ij}={\alpha }_{j0}+\sum _{\mathcal{l}=1}^n{\alpha }_{j\mathcal{l}}{X}_{i\mathcal{l}}.$$ (20)

Then for y ∈ {0, 1}^p, the probability that Y_ij = y_j, 1 ≤ j < p is given by

$$P\left({\left\{Y_{ij}=y_j\right\}}_{j=1}^p|X_i\right)={\int }_{A_{i}1}\cdots {\int }_{A_{i}p}F\left(t|{\mu }_i,\Sigma \right)dt$$ (21)

where

$$A_{ij}=\{\begin{array}{l}(0,\infty )\text{ if }{y}_j=1\hfill \\ (-\infty ,0)\text{ if }{y}_j=0\hfill \end{array}.$$

3.2. Multivariate t-link

Multivariate t-link was introduced in [(O’Brien and Dunson 2004)]. This model is based on the multivariate density ${\mathcal{L}}_{p,\nu }(z|\mu ,R)$. Regression by way of μ and probability P(Y_i = y) are defined as in Equations (20) and (21). The multivariate t-link is defined so that the marginal densities of z_j are given by the univariate logistic densities $\mathcal{L}\left(z_j|{\mu }_j\right)$, where

$$\mathcal{L}(z|\mu )=\frac{\text{exp}(-(z-\mu ))}{{[1+\text{exp}(-(z-\mu ))]}^2}$$ (22)

The density ${\mathcal{L}}_{p,\nu }(z|\mu ,R)$ is difficult to work with. In [(O’Brien and Dunson 2004)], actual calculations were done with the density F_v of the multivariate F density with v degrees of freedom. If v = 7.3, then F_v closely approximates ${\mathcal{L}}_{p,\nu }(z|\mu ,R)$.

3.3. GLM with mixed effects

Generalized linear models with mixed effects (GLMMs) can be fitted with built-in procedures in standard statistical software packages such as SAS^© or R. The modeling problem of Equation (1) may be expressed in a way that allows fitting a GLMM. Suppose responses ${\left\{Y_i\right\}}_{i=1}^p$ are all to be modeled with predictors ${\left\{X_i\right\}}_{i=1}^n$:

$$Y_1,\dots ,Y_p~(X_1,\dots ,X_n).$$

This can be written as

$$\begin{array}{ll}{Y}_1\hfill & ~\left(X_1,\dots ,X_n,r_1\right)\hfill \\ Y_2\hfill & ~\left(X_1\dots \mathrm{..}{X}_n,r_2\right)\hfill \\ \hfill & ⋮\hfill \\ Y_p\hfill & ~\left(X_1,\dots ,X_n,r_p\right)\hfill \end{array}$$

Here r is a categorical variable with p levels. The relation between Y_j and (X₁, … , X_n) varies with r_j, so the predictors for Y_j are actually interactions of (X₁, … , X_n) with r. In Equation (1), the Y’s are binary, so the actual regression models would be forms for binary responses, such as logistic or probit. The predictor values (X₁, … , X_n) are repeated exactly p times, for each observation from the original data set. The relation between the responses may be modeled by adding a random effect for variation within subject.

This assumes that each response Y_j is to be modeled with the same set of predictors ${\left\{X_i\right\}}_{i=1}^n$. It will be made clear that this assumption does not apply to the methods discussed previously: CSLR, MVP, or MVTL. So the method of GLMM for multivariate responses (GLMM-MR for short) will not be used in the examples in the main text. An example comparing GLMM-MR with CSLR will be found in the Part C.3 of the Appendix.

3.4. Marginal distributions and probabilities

For the multivariate probit and multivariate t-link, each Y_j is determined by a latent variable z_j. The marginal distribution of a single Y_j is determined by the marginal distribution of z_j. For S ⊂ {1, … , n}, the marginal distribution of {Y_j}_j∈S is determined by the joint distribution of {z_j}_{j inS}. A marginal probability (of the Y_j’s) can be estimated by integrating the marginal p.d.f. of the z_j’s over a quadrant. For a first order marginal probability, the marginal distribution is univariate.

In the multivariate probit, the joint distribution of (z₁, … , z_n) is multivariate normal. The marginal distribution of any z_j is univariate normal. For the multivariate t-link, the marginal distribution of a single z_j is the logistic distribution $\mathcal{L}\left(\cdot |{\mu }_j\right)$. This is easily integrated.

For a higher order marginal probability of {Y_j }_j∈S, the marginal distribution of {z_j}_j∈S is multivariate normal for MVT. For MVTL, use F_v to find an approximate value for the marginal probability. In either case, the multivariate density must be integrated over a quadrant. Such integrations are feasible, but need much more computation than the univariate integrals of first order marginal probabilities.

4. Goodness of fit

As explained in Section 2, first order marginal probabilities model the binary responses. There are several measures of goodness of fit for models of binary responses. A standard older measure is the Hosmer-Lemeshow statistic. For definitions, see [(Hosmer, Lemeshow, and Sturdivant 2013)]. The Hosmer-Lemeshow statistic has some defects, however, which are discussed in [(Hosmer, Le Cessie, and Lemeshow 1997 and [(Allison 2014)]; it will not be used here. Three other statistics have more recently come into use as measures of goodness of fit for binary responses. These are the Cox-Snell R², McFadden’s R², and Tjur’s coefficient of determination. See [(Cox and Snell 1989)], [(McFadden 1974)], and [(Tjur 2009)] for definitions and examples. These statistics all have a simple interpretation: The larger the value of the statistic, the better the fit. Finally, we use two statistics that do not have monotonic interpretations. These are Pearson’s χ² and the unweighted sum of squares:

$$USS=\sum {\left(y_i-{\widehat{p}}_i\right)}^2.$$

For χ², see Equation (7).

The limit distributions of USS and χ² are known. Asymptotically E(χ²) → n and E(USS) → Σp_i(1 − p_i). Moreover, for a binary response,

$${\chi }^2-n\rightsquigarrow N\left(0,{\sigma }_{{\chi }^2}^2\right)USS-\sum p_i\left(1-p_i\right)\rightsquigarrow N\left(0,{\sigma }_{USS}^2\right)$$

where ${\sigma }_{{\chi }^2}^2$ and ${\sigma }_{USS}^2$ are determined by the parameters of the fitted model. See [(Copas 1980)], [(Hosmer, Le Cessie, and Lemeshow 1997)], and [(Osius and Rojek 1992)]. The conditions χ² ≫ n or $\mathit{\text{USS}}\gg \sum {\widehat{p}}_i\left(1-{\widehat{p}}_i\right)$ are evidence of lack of fit; χ² ≪ n or $\mathit{\text{USS}}\ll \sum {\widehat{p}}_i\left(1-{\widehat{p}}_i\right)$ are evidence of overfitting.

5. Some problems in modeling with MPCSLR

Here are discussed two issues that will arise in modeling actual data sets. Neither collinearity or missing outcomes were problems in the examples that follow, but these will appear if MPCSLR is applied to any extent. Also a short discussion of compatibility and modeling is given; this should make clear how compatibility can be assured.

5.1. Multicollinearity of potential covariates

Suppose x₁ and x₂ are potential covariates for Y₁, … , Y_m, but x₁ and x₂ are highly correlated. For modeling a single Y_j, if one of (x₁, x₂) is a significant predictor of Y_j, the other will almost certainly also be a significant predictor. To make a reliable regression model, choose one of (x₁, x₂) for modeling, but not both.

In this paper, the problem is to model multiple binary outcomes. If there are outcomes Y₁, … ,Y_m, the question of choosing x₁ or x₂ may arise several times. If variable selection for distinct Y_j’s is done completely independently, x₁ might be chosen for modeling Y_i and x₂ chosen for modeling Y_j. It would be more understandable to consistently choose either x₁ or x₂. This would help prevent the entire model for multiple outcomes from being unnecessarily complicated.

There may be a set of potential covariates {x_j : j ∈ S} that are highly collinear with each other. Simply choosing one of the x’s instead of the others may produce weaker models, because any one of the x’s may have only a fraction of the information of the set indexed by S. In this case it may be better to replace {x_j : j ∈ S} by a set of k principal components or factors, with k < |S|. Again, PCs or factors should be used consistently: If one or more of {x_j : j ∈ S} seem to be significant predictors of any Y_j, 1 ≤ j ≤ m, all of the PCs or factors should be used in a regression model for Y_j, and not the original covariates {x_j : j ∈ S}.

5.2. Missing data for outcome variables

If Y₁, … , Y_m are outcome variables and X₁, … , X_n potential covariates, any Y_j can be modeled with X and other Y’s. The conditional distribution of Y_j will fail to be defined if either (a) the value of Y_j is missing or (b) the value of at least one known covariate X_k of Y_j is missing. Here is described a method to model when some data are missing.

For any j ∈ {1, … , m}, let X^j be the variables in X used in modeling outcome Y_j, and β_j be the regression coefficients for Y_j. Suppose for observation i, Y_j and X^j have known values if and only if j ∈ S, for some subset S ⊂ {1, … , m}. Let t = |S| and s₁, … , s_t be the elements of S, in order. Let L_S,i denote the likelihood for {Y_j : j ∈ S} at observation i, given that only these Y’s have values for this observation. L_S,i can be calculated. It is proportional to

$$\sum _{j=1}^t{X}_i^{s_j}{\beta }_{s_j}{y}_{s_j,i}+\sum _{1\le j<k\le t}{\gamma }_{s_i{s}_j}{y}_{s_j,i}{y}_{s_k,i}$$

and the constant of proportionality is

$$\sum \left\{\sum _{j=1}^t{X}_i^{s_j}{\beta }_{s_j}{v}_j+\sum _{1\le j<k\le t}{\gamma }_{s_j{s}_k}{v}_j{v}_k:v\in {\{0,1\}}^t\right\}.$$

If there is a third order interaction, the likelihood is proportional to

$$\sum _{j=1}^t{X}_i^{s_j}{\beta }_{s_j}{y}_{s_j,i}+\sum _{1\le j<k\le t}{\gamma }_{s_j{s}_k}{y}_{s_j,i}{y}_{s_k,i}+\sum _{1\le j<k<\mathcal{l}\le t}{\gamma }_{s_j{s}_k{s}_{\mathcal{l}}}{y}_{s_j,i}{y}_{s_k,i}{y}_{s_{\mathcal{l}},i}$$

and the constant of proportionality likewise has ${\sum }_{1\le j<k<\mathcal{l}\le t}{\gamma }_{s_j{s}_k{s}_{\mathcal{l}}}{v}_j{v}_k{v}_{\mathcal{l}}$ added.

For S ∈ {1, … , m}, let T_S be the set of observations such that Y_i and Xⁱ have known values if and only if i ∈ S. The loglikelihood associated with T_S is ${\sum }_{\mathcal{l}\in T_S}\text{log\hspace{0.17em}}{L}_{S,\mathcal{l}}$. So the total loglikelihood associated with the entire data set is

$$\sum \left\{\left(\sum _{\mathcal{l}\in T_S}\text{log\hspace{0.17em}}{L}_{S,\mathcal{l}}\right):S\subset \{1,\dots ,m\},|S|>0\right\}.$$ (23)

So parameters appear only in likelihoods for some observations. Any element of β_j appears for all observations in ⋃{S ⊂ {1, … , m} : j ∈ S}. γ_jk appears for all observations in ⋃{S ⊂ {1, … , m} : j, k ∈ S}. And γ_jkℓ appears for all observations in ⋃{S ⊂ {1, … , m} : j, k, ℓ ∈ S}. If there are few observations for which Y_j, Y_k, X^j, and X^k all have values, there is little data with which to estimate γ_jk, and the only models that could be estimated with confidence are those for which γ_jk is assumed to be zero.

Part D of the Appendix gives an example of data with missing values for some outcomes.

5.3. Compatibility and modeling

The main result of [(Joe and Liu 1996)] is that conditionally specified logistic distributions are compatible if and only if interactions are commutative: γ_ij = γ_ji. But if interaction terms are estimated by fitting conditional distributions, a unique interaction value will not be found. To estimate the parameters of a joint density, it must be assumed that interactions are commutative. So compatibility must be imposed. Only one value of γ_ij can be allowed at any modeling step, for each distinct pair (i, j) drawn from {1, … , m}. This implies that modeling should be of the joint density of {Y₁, … , Y_m}, even though the problem began with the assumption of a set of conditional distributions: {(Y_j|Y_ℓ, ℓ ≠ j), 1 ≤ j ≤ m}.

Example. There are two outcomes, Y₁ and Y₂. It will be assumed that the parameter μ₁ of Y₁ is to be modeled as a linear combination of covariates X₁, X₂, and X₃: μ₁ = β₁x^[1], where X^[1] = (X₁, X₂, X₃). μ₂ will be modeled as a linear combination of X₂, X₄, and X₅. Let X^[2] = (X₂, X₄, X₅). So the joint density of Y₁ and Y₂ is proportional to

$$\text{exp\hspace{0.17em}}\left({\beta }_1{\mathbf{x}}^{[1]}\cdot y_1+{\beta }_2{\mathbf{x}}^{[2]}\cdot y_2+{\gamma }_{12}{y}_1{y}_2\right).$$

To find the normalizing constant, sum the last expression with respect to (y₁, y₂) ∈ {0, 1}². The total normalizing constant is

$$C(\mathbf{x})≔1+\text{exp\hspace{0.17em}}\left({\beta }_1{\mathbf{x}}^{[1]}\right)+\text{exp\hspace{0.17em}}\left({\beta }_2{\mathbf{x}}^{[2]}\right)+\text{exp\hspace{0.17em}}\left({\beta }_1{\mathbf{x}}^{[1]}+{\beta }_2{\mathbf{x}}^{[2]}+{\gamma }_{12}\right).$$

The joint loglikelihood is then

$$\sum _{j=1}^n\left[{\beta }_1{x}_i^{[1]}{y}_{1i}+{\beta }_2{x}_i^{[2]}{y}_{2i}+{\gamma }_{12}{y}_{1i}{y}_{2i}-log\left(C\left(x_i\right)\right)\right].$$

To fit the joint model of Y₁ and Y₂, use any optimization algorithm to find the parameter set (β₁, β₂, γ₁₂) that will maximize the joint loglikelihood. Notice that the modeling is based on the joint loglikelihood, that is, on the joint density. The regression terms β₁ for Y₁ and β₂ for Y₂ are estimated together with γ₁₂.

It may seem that imposing compatibility by unique interaction terms is to make a strong assumption. It is not unjustified, however. Compatibility is a mathematical way of saying that each Y_j is affected by {Y_ℓ, ℓ ≠ j}, and this is true simultaneously, for j = 1, … , m. If Y₁, … , Y_m are variables all measured at the same time and place for each observation, it would be difficult not to assume that the distribution of each is affected by the other outcomes: that is, that their distributions are conditional, and compatible.

It is important to understand that compatibility of conditional distributions is determined by interaction terms {γ_ij}, and is not affected by regression terms {β_j}. If some regression coefficients are difficult to estimate, or if some X_j’s are collinear or could be replaced by a latent variable, this will affect the modeling of one or more outcomes, but will not affect the compatibility of the outcomes.

Since compatibility needs to be assumed, there is the possibility of having multiple outcomes with conditionally specified distributions that are not compatible. This is actually another research topic, but is considered in Part E of the Appendix.

6. Examples

6.1. Summary of simulation examples

Two examples were done with simulated data and are presented fully in Section C of the Appendix. A summary description will be given here.

Example 1. Five responses, generated from six normally distributed covariates, using standard distributions. All responses generated by same algorithm. For modeling, only four of the covariates were available. Univariate logistic regressions modeled two responses poorly, three fairly well. Responses modeled jointly with CSLR, MVTL, and MVP. Modeling results: When CSLR was used, point estimates derived by the joint density method fitted the true outcomes better than point estimates derived by the method of conditional probabilities. CSLR (using joint density based estimates) modeled each response about as well as a univariate model. CSLR did not perform better than MVTL on the three responses modeled well; CSLR did model the other two responses, and MVTL failed to model these two at all. MVP modeled all responses worse than either CSLR or MVTL.

Example 1a. Two subsets of three response variables, chosen from the three of Example 1. Each was modeled twice, with two sets of covariates. In each model, the responses all had the same set of covariates. CSLR and GLMM-MR used to model each set of responses and covariates. Results: CSLR modeled the data somewhat better than GLMM-MR for the three responses that were fairly correlated. The other set of three responses had low correlations. For this set of responses, GLMM-MR produced the same point estimates and coefficients as individual univariate regressions; it modeled the actual outcomes as well as CSLR, but failed to capture any sort of relationship among responses.

Example 2. Three responses, each derived from a characteristic quantity for a correlated random walk. Responses modeled jointly with CSLR, MVTL, and MVP. For each response, CSLR and the univariate regression gave fitted values that were very close. CSLR modeled each response better than MVTL or MVP. For CSLR, point estimates derived using conditional probabilities were almost identical to those derived from the joint density.

6.2. Example: Application to a data set

Data comes from the survey of the DiNEH Project. Between the 1940’s and the 1980’s, mining and milling of uranium was done on the Navajo Nation. The DiNEH Project was a study to assess the effects on health of exposure to uranium mine and mill sites. It was carried out from 2004 to 2011. As part of the study, a survey was administered to 1,304 individuals, all living on and members of the Navajo Nation. For a description of the study, see [(Hund et al. 2014)].

Here we consider three yes/no questions on the survey. Each question concerned the presence or absence of a medical condition in a participant. The responses represent three different medical conditions. The medical conditions are 1) kidney disease (KD); 2) hypertension (HT); and 3) diabetes (Di). There were missing values for some of the relevant covariates (see below). So, for purposes of modeling, there were N = 1272 observations. Table 1 shows frequencies of the three conditions.

Table 1:

Frequencies of three medical conditions in sample from the DiNEH survey.

	KD	HT	DI
1 (present)	70	456	316
0 (absent)	1202	816	956

There are twelve covariates. They include the physiological variables age, gender (1=female, 0=male), and BMI (body mass index); three family history markers; and six variables defined for this study. The family history markers will be denoted FH_KD, FH_HT, and FH_Di. Each family history marker corresponds to a response, and records the presence or absence of the medical condition for that response in the family of a participant. The six remaining covariates are

• M: A measure of exposure to mine waste during active mining era. A score taking values 0 to 5.

• E: A measure of exposure to mine waste at abandoned mines. This is continuous and positive; actual values fell in (0, 2).

• NavajoUse: A measure of intensity of use of the Navajo language. This is a score, taking values 0 to 4.

• StoreTime: A binary variable, indicating whether individual lived far from a food store.

• EducationScore: Level of education attained. A score taking values 0 to 11.

• IncomeScore: A discrete variable. The middle of income bracket to which individual belongs.

Before modeling KD, HT, and Di together, each was modeled individually with the twelve potential covariates. For each response, Bayesian model averaging was used to remove variables that were not significant predictors. The remaining variables were used as covariates for that response in multivariate modeling. These are the covariates for each response, in the CSLR model:

• KD: M, NavajoUse, FH_KD.

• HT: age, gender, BMI, E, FH_HT.

• Di: age, gender, BMI, Storetime, EducationScore, IncomeScore, FH_Di.

Note that KD, HT, and Di are different variables; they have different sets of covariates, and it will be seen that their coefficients are also very different. However, the data for all responses and covariates were gathered together. The data were based on survey questions, and the survey was administered to each participant in one sitting.

6.2.1. Modeling

The response-covariate relations given above were used for all models. Multivariate probit and multivariate t-link models were fit. A conditionally specified logistic regression model was fit using Equation (2). Another CSLR model was fit, with a third order interaction (See Equation (18).) A CSLR model with this interaction will be denoted CSLR(3OI). All these models were fit by MCMC. In addition, a univariate logistic regression model was fit for each response, using the covariates listed above. Each fitted model gave a set of point estimates for coefficients. The coefficient estimates are shown in Table 2.

Table 2:

Point estimates of coefficients for models of multiple binary responses. Methods used to fit models: Multivariate probit (MVP), multivariate t-link (MVTL), conditionally specified logistic regression (CSLR), and CSLR with a three-way interaction term, and univariate logistic regression models (UV).

	MVP	MVTL	CSLR	CSLR(3OI)	UV
Intevcept:KD	−2.279	−2.548	−4.966	−4.947	−4.370
M:KD	0.2456	0.3009	0.4409	0.4401	0.5103
NavajuUse:KD	0.1829	0.1641	0.2207	0.2067	0.3883
FHKD:KD	0.3118	0.4921	0.7791	0.7530	0.8636
Intercept:HT	−4.219	−4.413	−6.756	−6.803	−7.244
age:HT	0.04119	0.04187	0.05977	0.0598	0.0696
gender:HT	−0.1269	−0.03376	−0.1773	−0.1860	−0.0403
BMI:HT	0.0398	0.04127	0.05525	0.0564	0.06575
E:HT	0.5578	0.6682	1.323	1.363	1.346
FHHT:HT	0.5021	0.5388	0.8184	0.8194	0.9368
Intercept:Di	−3.796	−4.014	−5.582	−5.206	−6.452
age:Di	0.03072	0.03048	0.02923	0.0261	0.0518
gender:Di	0.1212	0.1583	0.4359	0.4314	0.3197
BMI:Di	0.03226	0.03646	0.03486	0.0307	0.0546
Storetime:Di	0.1435	0.1357	0.215	0.2495	0.2096
EducationScore:Di	−0.03606	−0.04536	−0.08611	−0.1017	−0.0811
IncomeScore:Di	−4.976e-06	−4.976e-06	−7.833e-06	−1.027e-05	−8.265e-06
FHDi:Di	0.5757	0.6104	0.9691	0.9630	1.095
γKD,HT	0.367	0.3386	0.6466	0.7048	NA
γKD,Di	0.485	0.466	1.574	1.5800	NA
γHT,Di	0.6314	0.6383	1.93	1.9540	NA
γKD,HT,Di	NA	NA	NA	−0.0357	NA

6.2.2. Results

The coefficient estimates for the CSLR shown in Table 2 were used to calculate marginal probabilities. In light of results from the two examples with simulated data, the joint density was used to derive marginal probabilities. The coefficient estimates for the MVP and MVTL shown in Table 2 were used to specify multivariate densities. Then marginal probabilities for MVP and MVTL were calculated by integration of marginal distributions, as described in Section 3.4. Both first and second order marginal probabilities were found. The first order marginal probabilities found are of form P(Y_i = 1|x); the second order marginal probabilities are of form P(Yi = 1, Y_j = 1|x). This is sufficient; if we know P(Y_i = 1|x), P(Y_j = 1|x), and P(Y_i = 1, Y_j = 1|x), we can find P(Y_i = 0|x P(Y_j = 0|x, and P(Y_i = s₁,Y_j = s₂|x) for any x ∈ {0, 1}². So for each method there are marginal probabilities for all responses (and pairs of responses), for each of 1272 participants.

Correlations are shown in Table(s) 3. These are between first order marginal probabilities of different methods, with separate correlations for each response. Table 3 shows that for all three responses:

Table 3:

Correlations of first order marginal probabilities. (A): Correlations of marginal probabilities for KD. (B): Correlations of marginal probabilities for HT. (C): Correlations of marginal probabilities for Di.

(A)
	MVP	MVTL	CSLR	CSLR(3OI)	UV	response
MVP	1	0.9636	0.2155	0.2142	0.5631	0.08905
MVTL	0.9636	1	0.3318	0.3298	0.6538	0.1144
CSLR	0.2155	0.3318	1	0.9997	0.8961	0.1997
CSLR.3OI	0.2142	0.3298	0.9997	1	0.8955	0.2
UV	0.5631	0.6538	0.8961	0.8955	1	0.22
response	0.08905	0.1144	0.1997	0.2	0.22	1
(B)
	MVP	MVTL	CSLR	CSLR(3OI)	UV	response
MVP	1	0.9943	0.8206	0.8182	0.8809	0.4053
MVTL	0.9943	1	0.8163	0.8136	0.8801	0.4038
CSLR	0.8206	0.8163	1	0.9999	0.9889	0.4561
CSLR.3OI	0.8182	0.8136	0.9999	1	0.9877	0.4557
UV	0.8809	0.8801	0.9889	0.9877	1	0.4572
response	0.4053	0.4038	0.4561	0.4557	0.4572	1
(C)
	MVP	MVTL	CSLR	CSLR(3OI)	UV	response
MVP	1	0.9926	0.648	0.6591	0.7391	0.2705
MVTL	0.9926	1	0.6016	0.6134	0.7	0.251
CSLR	0.648	0.6016	1	0.9985	0.9823	0.3857
CSLR.3OI	0.6591	0.6134	0.9985	1	0.9813	0.3866
UV	0.7391	0.7	0.9823	0.9813	1	0.3809
response	0.2705	0.251	0.3857	0.3866	0.3809	1

(a) The marginal probabilities from MVP and CSLR have low correlation; (b) the m.p.’s for these two methods have higher correlation with the m.p.’s from MVTL; and (c) the correlation between the m.p.’s from MVP and those from MVTL is very high, as is that between the m.p.’s from CSLR and those from CSLR(3OI). For each response, the m.p.’s from CSLR have the highest correlation with the actual binary response, and those from MVP or MVTL have the lowest correlation.

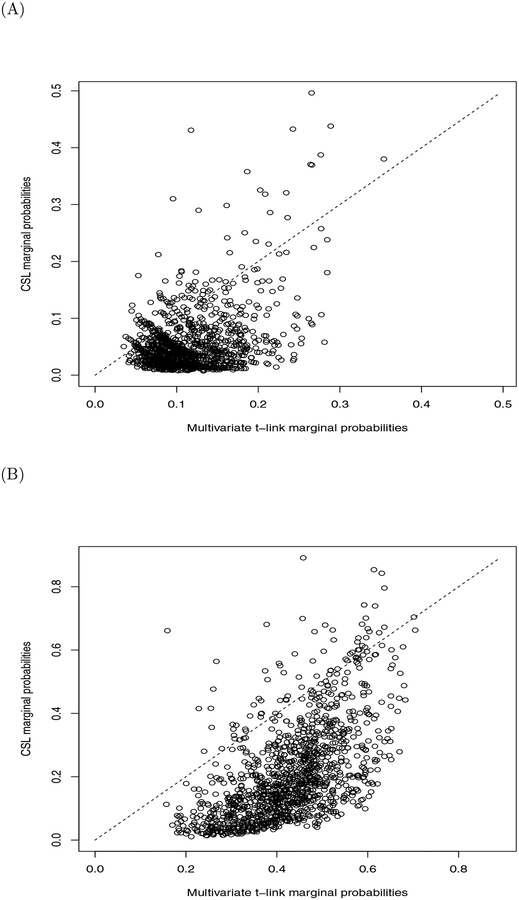
All plots can be seen in the Supplementary material. The plots of marginal probabilities from CSLR vs. those from MVP (Figure 1), do not clearly indicate linear relations; for Figure 1 (A), no linear relation can be seen. Figure 1(B) implies a curve, not a straight line. The same can be said for the plots of marginal probabilities from CSLR against those from MVTL (Figure 2). Also, in Figures 1 and 2, most points fall below the diagonal x = y, so that CSLR produces smaller marginal probabilities than do MVP or MVTL. So, for this data set, MVP and MVTL tend to overestimate marginal probabilities, or CSLR tends to underestimate. Figure 3 shows the marginal probabilities from MVP plotted against those from MVTL, for two responses. These plots have little scatter and close approximation to the diagonal, and indicate near-linear relationships. Figure 4 shows the marginal probabilities from CSLR(3OI) plotted against those from CSLR, for two responses. These plots follow the diagonal almost exactly, and show relationships that are close to identity.

Figure 1:

First order marginal probabilities from conditionally specified logistic regression plotted against first order marginal probabilities from multivariate probit. (A): Marginal probabilities for first response (KD). (B): Marginal probabilities for second response (HT).

Figure 2:

First order marginal probabilities from conditionally specified logistic regression plotted against first order marginal probabilities from multivariate t-link. (A): Marginal probabilities for first response (KD). (B): Marginal probabilities for third response (Di).

Figure 3:

First order marginal probabilities from multivariate probit plotted against first order marginal probabilities from multivariate t-link. (A): Marginal probabilities for first response (KD). (B): Marginal probabilities for second response (HT).

Figure 4:

First order marginal probabilities from conditionally specified logistic regression with 3-way interaction plotted against first order marginal probabilities from conditionally specified logistic regression. (A): Marginal probabilities for first response (KD). (B): Marginal probabilities for third response (Di).

It should be noted that the extremely close match of results from CSLR and CSLR(3OI) is partly accidental. Several MCMC runs were made to fit both CSLR and CSLR(3OI). Each run produced slightly different coefficient estimates, and slightly different marginal probabilities. However, the overall variation in results across various runs was small, and showed no significant difference between results of CSLR and results of CSLR(3OI).

Table 4 shows values of McFadden’s R², the Cox-Snell R², and Tjur’s coefficient of determination.

Table 4:

R²-like statistics for goodness of fit, applied to results of modeling with real data. (A): McFadden’s R². (B): Cox-Snell R². (C): Tjur’s coefficient of determination.

(A)
	KD	HT	Di
MVP	−0.04064	−0.02129	−0.1312
MVTL	−0.2205	−0.0008258	−0.1498
CSLR	0.06651	0.1802	0.1434
CSLR.3OI	0.06685	0.18	0.1434
UV	0.07188	0.1821	0.1419
(B)
	KD	HT	Di
MVP	−0.01747	−0.02817	−0.1584
MVTL	−0.0985	−0.001078	−0.1829
CSLR	0.02794	0.2095	0.1485
CSLR.3OI	0.02808	0.2094	0.1485
UV	0.03017	0.2116	0.1471
(C)
	KD	HT	Di
MVP	0.0241	0.1714	0.1049
MVTL	0.03082	0.1165	0.06707
CSLR	0.04568	0.2173	0.1577
CSLR.3OI	0.04496	0.2164	0.1561
UV	0.04549	0.2135	0.1509

Table 5(A) shows $\mathit{\text{USS}}-\sum {\widehat{p}}_i\left(1-{\widehat{p}}_i\right)$, for all responses and methods, for first order marginal probabilities. Table 5(B) shows the same statistics, divided by the estimated standard errors. The standard errors are estimated by a bootstrap: 1000 resamples (with replacement) of size N = 1272 were taken from the 1272 pairs $\left\{\left(y_i,{\widehat{p}}_i\right)\right\}$. Table 5(C)–(D) are similar to Table 5(A)–(B), but show values of χ² − N.

Table 5:

Unweighted sum of squares and χ² statistics. Asymptotic expected value of USS is Σp_i(1 − p_i). Asymptotic expected value of χ² is number of observations (N = 1272). (A): $\mathit{\text{USS}}-\sum {\widehat{p}}_i\left(1-{\widehat{p}}_i\right)$, for first order marginal probabilities, for five methods. (B): $\mathit{\text{USS}}-\sum {\widehat{p}}_i\left(1-{\widehat{p}}_i\right)$ divided by bootstrap estimate of SE(USS). (C): χ² − N, for first order marginal probabilities, for five methods. (D): χ² − N divided by bootstrap estimate of SE(χ²).

(A)
	KD	HT	Di
MVP	−23.742	38.927	1.7579
MVTL	−83.813	2.5849	−12.093
CSLR	3.295	6.2083	5.8401
CSLR.3OI	3.42	5.8618	4.6413
UV	−0.36014	2.6474	2.8614
(B)
	KD	HT	Di
MVP	−3.474	5.642	0.3316
MVTL	−14.97	0.5443	−3.227
CSLR	0.466	0.8885	0.7952
CSLR.3OI	0.4832	0.8411	0.6322
UV	−0.05116	0.3868	0.3986
(C)
	KD	HT	Di
MVP	−49.105	270.87	11.257
MVTL	−664.5	10.426	−56.039
CSLR	150.66	−40.803	−62.308
CSLRR.3OI	141.77	−43.706	−67.28
UV	8.654	−74.118	−95.641
(D)
	KD	HT	Di
MVP	−0.2416	5.143	0.3789
MVTL	−13.14	0.4505	−3.304
CSLR	0.681	−0.7345	−1.013
CSLR.3OI	0.6509	−0.7927	−1.101
UV	0.04562	−1.48	−1.699

In all these tables, y varies by column; y is successively KD, HT, and Di. p varies by row, and is the vector of marginal probabilities for a fixed y for, successively, MVP, MVTL, CSLR, CSLR(3OI), and univariate fits.

Observing Tables 4 and 5, we see:

1. In modeling first order marginal probabilities, McFadden’s R², Cox-Snell R², and Tjur’s coefficient of determination are all larger for CSLR and CSLR(3OI) than for MVP or MVTL. This is true for all three responses.

2. These same statistics ($R_{McF}^2$, $R_{CS}^2$, and Tjur’s COD) are better for the univariate models than for CSLR or CSLR(3OI). The only exception is Tjur’s COD for KD; this is slightly smaller for the univariate model, but not significantly so. However, for any statistic and response, the difference between the value for the univariate model and those for CSLR and CSLR(3OI) is not great. For example, McFadden’s R² for the CSLR fits of the three responses has values {0.06651, 0.1802, 0.1434}. For the univariate logistic fits, R² has values {0.07188, 0.1821, 0.1419} (See Table 4(A)).

3. For first order marginal probabilities again, $R_{McF}^2$, and $R_{CS}^2$ for the MVP modeling of KD are better than the same statistics for the MVTL modeling of KD. However, the same statistics for the MVP modeling for HT and Di are much worse than the same statistics for the MVTL modeling of the same two responses. Tjur’s COD does not indicate that MVP has modeled HT or Di worse than MVTL.

4. Look at the difference between unweighted sum of squares and the estimate of the asymptotic mean $(\sum {\widehat{p}}_i\left(1-{\widehat{p}}_i\right)$, scaled by estimated standard deviation, for first order marginal probabilities (Table 5(A)). For the univariate fits, the values of this statistic are not significantly different from zero. For CSLR and CSLR(3OI), the values are all positive but less than one. For MVP, the statistic is rather large for HT, not significantly different from zero for Di, and much less than zero (< (−3)) for KD; this indicates some overfitting. For MVTL, the values of the statistic are less than −9 for KD and Di. This indicates that MVTL is overfitting some part of these two responses.

5. Consider the difference between the χ² statistic and the asymptotic mean (N = 1272), scaled by estimated standard deviation, for first order marginal probabilities (Table 5(B)). The comments in item 3 can be repeated here, except that for CSLR and CSLR(3OI), the statistics are not significantly larger than zero.

The univariate models did best at fitting the individual responses. CSLR and CSLR(3OI) did almost as well as the univariate models. However, the univariate models say nothing about the relationships between KD, HT, and Di. Recall that the odds of a binary random variable Z is P(Z = 1)/P(Z = 0). The CSLR model says that

$$\text{ for }X,Di\text{ fixed }\{\begin{array}{ll}\text{log}(\mathit{\text{odds}}(KD|HT=1))=\hfill & 0.6466+\text{log}(\mathit{\text{odds}}(KD|HT=0)\hfill \\ \text{log}(\mathit{\text{odds}}(HT|KD=1))=\hfill & 0.6466+\text{log}(\mathit{\text{odds}}(HT|KD=0)\hfill \end{array}$$

$$\text{for }X,HT\text{ fixed }\{\begin{array}{l}\text{log}(\mathit{\text{odds}}(KD|Di=1))=1.574+\text{log}(\mathit{\text{odds}}(KD|Di=0)\hfill \\ \text{log}(\mathit{\text{odds}}(Di|KD=1))=1.574+\text{log}(\mathit{\text{odds}}(Di|KD=0)\hfill \end{array}$$

$$\text{for }X,KD\text{ fixed }\{\begin{array}{l}\text{log}(\mathit{\text{odds}}(HT|Di=1))=1.93+\text{log}(\mathit{\text{odds}}(HT|Di=0)\hfill \\ \text{log}(\mathit{\text{odds}}(Di|HT=1))=1.93+\text{log}(\mathit{\text{odds}}(Di|HT=0)\hfill \end{array}$$

See Table 2 for values of {γ_KD,HT, γ_KD,Di, γ_HT,Di} The corresponding equations for CSLR(3OI) would be more complex, but the third order interaction is very small.

MVP and MVTL did not model individual responses nearly as well as CSLR or CSLR(3OI). MVP modeled HT and Di very poorly, much worse than any other method. There were indications that MVTL overfitted some part of the data for each response.

7. Discussion

It is possible to find marginal probabilities for the conditionally specified logistic regression model. This means that CSLR can model multiple binary data, in the sense of making point estimates ${\widehat{p}}_{ij}=\widehat{P}\left(Y_i=1|x_j\right),1\le i\le p,1\le j\le N$. Two methods were shown for finding marginal probabilities. One is to use the joint density of all responses, as given in [(Joe and Liu 1996)]. The alternative method is to consider the marginal probabilities of form P(Y_i,j = 1, j ∈ S|x), for any subset S of {1, … , p}. These satisfy a system of affine equations. If the system can be solved, the marginal probabilities are found. In addition, the marginal distribution of each response can be modeled using the first order marginal probabilities. The two methods were used and compared in the examples with simulated data. The two methods gave approximately the same results for p = 3 responses. However, when p = 5, the methods gave sets of marginal probabilities that clearly differed. Those derived by the method of conditional probabilities did not fit the data as well. This method is also more difficult to program.

CSLR was applied to two examples based on simulated data and an example using real data. In these examples, the number p of responses was successively 5, 3, and 3. In simulation 1, the all responses were generated by the same algorithm, from standard distributions for random variables. In simulation 2, the responses were based on very different characteristics of an underlying process (correlated random walk). In the second simulated example and the example with real data, CSLR models were fitted both with and without a third order interaction.

In the first simulation example, the results were ambiguous; most of the test for goodness of fit indicated that CSLR modeled the response variables better than MVP or MVTL, but some important statistics (versions of R² and Tjur’s coefficient) were better for MVTL on three responses. In this example, the response variables were roughly equivalent, all generated in a uniform manner by a single algorithm. In both the second simulation and the example with real data, the responses were essentially different from each other. In the second simulation, each response was derived from a characteristic quantity of a correlated random walk. In the example with real data, the responses were occurrences of three very different diseases. For these examples, CSLR with and without third order interaction modeled this data better than the two alternative methods, MVP and MVTL. For modeling individual responses, univariate logistic regressions did best; but the two versions of CSLR did almost as well, and also modeled relationships between responses.

In a supplemental example, in the Appendix, CSLR was compared with GLMM-MR. GLMM-MR assumes that all response variables will have the same set of predictors, and so would not be as widely applicable as the other methods for modeling multiple binary responses. The example indicated that CSLR may model as well or better than GLMM-MR, and GLMM-MR may sometimes fail to capture interactions of response variables.

The results for this data set indicate what might be expected when applying CSLR to other data sets. CSLR may be the most effective method in many problems that involve modeling multiple binary responses that are dissimilar but measured simultaneously.